Modeling Latent Carbon Emission Prices for Japan: Theory and Practice

Abstract

Climate change and global warming are significantly affected by carbon emissions that arise from the burning of fossil fuels, specifically coal, oil, and gas. Accurate prices are essential for the purposes of measuring, capturing, storing, and trading in carbon emissions at regional, national, and international levels, especially as carbon emissions can be taxed appropriately when the price is known and widely accepted. This paper uses a novel Capital (K), Labor (L), Energy (E) and Materials (M) (or KLEM) production function approach to calculate the latent carbon emission prices, where carbon emission is the output and capital (K), labor (L), energy (E) (or electricity), and materials (M) are the inputs for the production process. The variables K, L, and M are essentially fixed on a daily or monthly basis, whereas E can be changed more frequently, such as daily or monthly, so that changes in carbon emissions depend on changes in E. If prices are assumed to depend on the average cost pricing, the prices of carbon emissions and energy may be approximated by an energy production model with a constant factor of proportionality, so that carbon emission prices are a function of energy prices. Using this novel modeling approach, this paper estimates the carbon emission prices for Japan using seasonally adjusted and unadjusted monthly data on the volumes of carbon emissions and energy, as well as energy prices, from December 2008 to April 2018. The econometric models show that, as sources of electricity, the logarithms of coal and oil, though not Liquefied Natural Gas (LNG,) are statistically significant in explaining the logarithm of carbon emissions, with oil being more significant than coal. The models generally displayed a high power in predicting the latent prices of carbon emissions. The usefulness of the empirical findings suggest that the methodology can also be applied for other countries where carbon emission prices are latent.

1. Introduction

Climate change and global warming are two of the most important environmental issues presently facing the international community. Global warming is typically defined as the observed century-scale rise in the average temperature of the Earth’s climate system and its related effects, while climate change refers to change in the statistical distribution of weather patterns, specifically average weather conditions, over an extended period, such as a century. Neither climate change nor global warming refer to changing weather conditions on a daily basis (see [1] Allen and McAleer (2018)).

Both climate change and global warming are significantly affected by carbon emissions that arise from the burning of fossil fuels, specifically coal, oil, and gas. One of the major environmental challenges of the climate policy of the European Union Emissions Trading Scheme (or System) is the reduction and mitigation of greenhouse gas emissions by capturing and storing carbon emissions.

Although the clear leader in the battle to reduce and mitigate the effects of carbon emissions is the European Union, China has also started to mitigate the effects of greenhouse gases through the development of domestic regional carbon emission trading markets, with the goal of extending it to the national level in the near future. The creation of such markets that trade in carbon emissions is intended to establish prices that can be used to buy and sell carbon emissions, and to reduce the harmful effects of such emissions on the social and physical environment.

Accurate prices are essential for the purposes of measuring, capturing, storing, and trading in carbon emissions at the regional, national, and international levels, especially as carbon emissions can be taxed appropriately when the price is known and widely accepted. In the absence of an active trading market for carbon emissions, the prices are typically decided through arbitrary administrative deliberations, and hence are not efficient or even necessarily accurate. In this sense, carbon emission prices are latent.

The purpose of this paper is to price the latent carbon prices through a novel econometric approach that can be used to calculate realized latent prices of carbon emissions as a function of capital (K), labor (L), energy (E) (that is, electricity), and materials (M) inputs. The novelty is in extending the KLEM production function to the multivariate setting, modeling latent carbon emission prices, and providing a novel method of estimating monthly latent carbon emission prices that are based on the observed monthly prices of alternative forms of energy using innovative econometric time series models.

The inputs K, L, and M are typically fixed at a monthly observation interval, and are not readily available on any well-known website, whereas E can be changed daily, so that changes in carbon emissions will depend on changes in E. If prices are assumed to depend on the average cost pricing, the prices of carbon emissions and energy may be approximated by an energy production model with a constant factor of proportionality, so that carbon emission prices are a function of energy prices.

Given the relationship between the prices of carbon emissions and energy, econometric models of the latent carbon emission prices are specified, estimated, evaluated, and used for forecasting carbon emissions prices for Japan, based on monthly data from December 2008 to April 2018. The econometric models will show that, as sources of electricity, the logarithms of coal and oil, though not LNG, as well as a deterministic time trend and a tax change dummy variable, are statistically significant in explaining the logarithm of carbon emissions, with oil being more significant than coal.

The plan of the remainder of the paper is as follows. A review of the literature on pricing carbon emissions for the European Union, and at the regional and national levels for China, is given in Section 2. Section 3 discusses the KLEM production function that obtains prices for the output of carbon emissions as a function of the inputs of capital, labor, energy (or electricity), and materials. The formal models of latent carbon emission prices are discussed in Section 4, estimation of the models is presented in Section 5, the monthly data and diagnostic checks are analyzed in Section 6, the empirical estimates and analysis are evaluated in Section 7, and some concluding remarks are given in Section 8.

Proof of the derivation of the correct standard errors for valid statistical inference for realized latent carbon emissions and the ranking of important underlying factors, a discussion on the theoretical structure for latent endogenous and exogenous variables, and extensions to more complicated decision strategies, are given in the Appendix A.

2. Literature Review

Much of the research literature on pricing carbon emissions in recent years has concentrated on Europe and China. The European Union Emissions Trading Scheme established the world’s first greenhouse gas emissions trading scheme in 2005, and remains the largest and most influential organization mitigating the effects of global warming and climate change.

In the sparse literature for Europe, most of which has been based on the European Union Emissions Trading Scheme (EUETS), [2] Daskalakis and Mrkellos (2009) developed a framework for future pricing and hedging, and examined data from EEX, Nord Pool, and Powernext, to analyze whether electricity risk premia were affected by the prices of emission allowances. [3] Daskalakis et al. (2009) provided evidence from modeling the prices of CO₂ emissions allowances and derivatives using European Trading Scheme data.

More recently, [4] Bushnell et al. (2013) examined profiting from regulation, based on European carbon market data. [5] Oestreich and Tsiakas (2015) analyzed carbon emissions and stock returns using EUETS data. Additionally, [6] Martin et al. (2016) examined the impacts of the EUETS on regulated firms for ten years from inception.

China’s market for national carbon emissions was established at a later stage than in Europe, and has been progressing steadily. The development of such markets since their inception in China in 2013 has not necessarily been based on competitive market principles. The National Government in Beijing has made it clear that the regional markets are a first step in the development of a national carbon emission pricing scheme. Just as the market for carbon emissions trading is presently at a formative stage in China, the academic theoretical and empirical research on the emerging regional and national carbon emissions pricing markets is also at a development stage.

A review of the admittedly sparse literature on the prices of carbon emissions in Europe and China, as well as a comprehensive analysis regarding the availability of price data at the domestic regional level, is analyzed in [7,8] Chang et al. (2018, 2019). Following earlier work, the authors discuss a number of developments in China since 2005. [9] Chen (2005) evaluated the costs associated with mitigating carbon emissions. [10] Gregg et al. (2008) analyzed the carbon emissions patterns associated with fossil fuel consumption and cement production. Moreover, [11] Li and Colombier (2009) evaluated carbon emissions and energy efficiency. Using a multivariate modeling approach, [12] Chang (2010) developed a multivariate causality test of various combinations of carbon dioxide emissions, energy consumption, and economic growth.

In more recent years, there have been analyses of interactions between China and one or more other regions. For example, [13] Nam et al. (2014) compared the synergy between China and the USA associated with pollution and carbon emissions controls. For China alone, [14] Zhang et al. (2014) considered the effects of emissions trading on progress and future prospects, [15] Zhang et al. (2014) used the Shapley value to analyze carbon emissions quotas across regions, [16] Liu et al. (2015) reviewed trading in carbon emissions and future challenges, [17] Tang et al. (2015) evaluated the trading scheme for carbon emissions using a multi-agent-based model, and [18] Zhang (2015) reformulated a strategy for low-carbon green growth. [19] Xiong et al. (2017) provided a comparison of China’s carbon trading allowance scheme and related schemes in the EU and California.

There seems to be even less research on pricing carbon emissions at an international level. [20] Zhang and Sun (2016) applied a Full BEKK multivariate conditional volatility model to analyze the time-varying covariances and the associated dynamic spillovers between the respective markets for Euro carbon and fossil fuel (for caveats regarding the Full BEKK model, particularly regarding the lack of mathematical regularity conditions, invertibility, the absence of a likelihood function, and hence the lack of valid asymptotic statistical properties, see [21] Chang and McAleer (2019)) [22]. Chang et al. (2017) and [21] Chang and McAleer (2019) analyzed the novel issues of volatility spillovers and Granger causality on the basis of daily data for the futures prices of EU carbon emissions, spot prices of US carbon emissions, and spot and future prices of oil and coal.

Interesting recent research has been undertaken on analyses of price and volatility from the perspective of derivative markets and alternative volatility models, such as the price impact, trading volume and volatilities associated with mission permits and the announcement of realized emissions in [23] Hitzemann, Uhrig-Homburg, and Ehrhart (2015); a Bayesian approach to the stochastic volatility of future prices of emission allowances in [24] Kim, Park, and Ryu (2017); and the empirical performance of reduced form models for emission permit prices in [25] Hitzemann and Uhrig-Homburg (2019).

As stated above, there seems to have been no published research on pricing carbon emissions in Japan. The existing published research seems to have primarily focused on Europe and, very recently, China. For these reasons, this paper makes a novel contribution to the pricing of carbon emissions for Japan. The usefulness of the empirical findings suggests that the methodology can also be applied for other countries where carbon emission prices are latent.

3. KLEMS Production Function for Carbon Emissions and Energy

Inputs are required to produce outputs, and the relationship is captured in a production function. A relatively broad specification is the KLEMS production function ([26] OECD, 2001), which uses capital ($K$), labor ($L$), energy ($E$), materials ($M$), and services (S) as the inputs for the production process. The function captures the most widely-used inputs for producing the output. Typically, the most widely observable input is energy, which is based on the use of electricity, whereas the services associated with a specific output are typically difficult to observe.

As a special case of KLEMS, consider the KLEM production function (see, for example, [27] Lecca et al., 2011) that is given as

$$CE=A{K}^{a1}{L}^{a2}{E}^{a3}{M}^{a4}exp\left(u\right),$$

(1)

where CE denotes the production of the output of carbon emissions; capital ($K$), labor ($L$), energy or electricity ($E$), and materials ($M$) are the inputs; $A$ is a constant; for simplicity, the partial production parameters are assumed to satisfy constant returns to scale, that is, $a1+a2+a3+a4=1$ (as in the Cobb-Douglas production function); and the random error term is assumed to be $u~iid\left(0,1\right).$

In practice, the output $CE$ and input $E$ may be observed at daily or monthly data frequencies, whereas the inputs $K$, $L$, and $M$ are generally fixed at much lower data frequencies, such as one year. Consequently, when the data are observed at monthly frequencies, as in this paper, $CE$ and $E$ may be assumed to be proportional, with the random factor of proportionality given by

$$k=A{K}^{a1}{L}^{a2}{M}^{a4}exp\left(u\right).$$

(2)

It is worth noting that $k$ is not restricted in its range, such as (0, 1). As $k$ has a unit of measurement, $k$ can take any value, depending on the units of measure of the variables, such as

$$CE=k{E}^{a3}$$

(3a)

or

$$\log \left(CE\right)=\log \left(k\right)+a3\log \left(E\right),$$

(3b)

where $a3$ is a scalar. If it is assumed that output prices are set according to an average cost pricing rule (see [28] Chang et al. (2018)), the prices of $CE$ and $E$ may be approximated by a model with a constant factor of proportionality. Let this relationship be given as

$$P_{CE}=k{P}_E,$$

(4)

where $P_{CE}$ is the price of $CE$, and $P_E$ is the price of energy (such as electricity), such that k in Equation (4) is the constant factor of proportionality. In practice, k may be known in advance or may be determined empirically using appropriate modeling techniques. [28] Chang et al. (2018) considered estimating k through the use of Equations (3b) and (4). The estimation of $P_{CE}$ through the use of econometric models, and acknowledging the presence of measurement errors, will be developed in the next section.

4. Modeling Latent Carbon Emission Prices

The definitional relationship for a random variable, Y, can be seen in Equation (5):

Y = Y* + measurement error,

(5)

where Y is the measured value of the random variable, which is subject to measurement error, and Y* is the true value of the random variable, with no measurement error, for which the following four relationships are possible:

(i)

$Y=P_{CE}, Y^{*}=P_{CE}^{*}$;

(ii)

$Y=P_{CE}, Y^{*}=P_E^{*}$;

(iii)

$Y=P_E, Y^{*}=P_E^{*}$;

(iv)

$Y=P_E, Y^{*}=P_{CE}^{*}$.

Here, $P_{CE}$ and $P_{CE}^{*}$ denote the (possibly) observed prices of carbon emissions and their underlying true prices, respectively, and $P_E$ and $P_E^{*}$ denote the observed and underlying true prices of energy, respectively.

In cases (i) and (ii), the price of carbon emissions is not available, together with the true underlying prices of carbon emissions and energy, respectively. case (iii) is not of particular interest as it relates to the observed and true underlying prices of energy, respectively. In case (iv), the price of energy is available, but the true underlying price of carbon emissions is not. Therefore, this paper is concerned with case (iv).

The remainder of the paper uses a novel econometric model to calculate the latent prices of carbon emissions, as will be discussed below. The approach has been used in the literature to calculate latent variables, and this paper is the first to use the methodological approach to calculate latent carbon emission prices.

For the sake of argument, in case (iv), if the price of energy is stationary, $P_E$ can be regressed on a set of observable variables using Ordinary Least Squares (OLS), as given in Equation (6):

$$P_E=b_0+b_1{Z}_1+b_2{Z}_2+b_3{Z}_3+error,$$

(6)

to yield estimated fitted values, as given in Equation (7):

$$\widehat{P_E}=\widehat{b_0}+\widehat{b_1}{Z}_1+\widehat{b_2}{Z}_2+\widehat{b_3}{Z}_3=\frac{1}{k}\widehat{P_{CE}^{*}},$$

(7)

where $\widehat{b_i}$ denotes the OLS estimates of the unknown parameters $b_i$ (i = 0, 1, 2, 3), and $\widehat{P_E}$ denotes the estimated fitted values of energy prices from Equation (6), which are equivalent to the estimated fitted values of carbon emissions, ($\widehat{P_{CE}^{*}}$), adjusted by the factor (1/k) (see Equation (4)), where k may be known in advance or may be determined empirically.

If energy prices are nonstationary rather than stationary, the price model for energy in Equation (6) can be estimated using a cointegrating relationship or a vector autoregressive distributed lag model to accommodate the nonstationarity. Alternatively, prices can be transformed into log differences in prices, which are equivalent to the rate of growth in prices, and then estimated by OLS (in empirical finance, log differences in prices are referred to as rates of return), which would be based on stationary processes.

5. Estimating Latent Carbon Emission Prices

This section describes a novel method of estimating monthly latent carbon emissions prices for Japan that are based on the observed monthly prices of alternative forms of energy and the models presented in the previous section.

Monthly prices (p) and volumes (quantities, q) of the following energy variables are typically available in a variety of energy databases, where almost ethanol refers to bio-ethanol:

(1)

Volume of carbon emissions;

(2)

Prices and volume of electricity;

(3)

Prices and volume of oil;

(4)

Prices and volume of crude coal;

(5)

Prices and volume of natural gas;

(6)

Prices and volume of nuclear energy;

(7)

Prices and volume of solar energy;

(8)

Prices and volume of wind energy;

(9)

Prices and volume of hydro energy;

(10)

Prices and volume of wave energy;

(11)

Prices and volume of bio-mass;

(12)

Prices and volume of ethanol;

(13)

Prices and volume of bio-ethanol.

In what follows, the models presented in the previous section will be estimated using the available price and volume data to obtain estimated fitted latent prices of carbon emissions. It is assumed that there is a known expected relationship between carbon emissions and the generation of electricity using the data in cases (2)–(12) above. This is based on applied engineering practice and structural form modeling, as presented in the previous section, as follows:

$$p_0{q}_0=k{p}_1{q}_1\exp \left(u\right)$$

(8)

or equivalently as

$$\log (p_0{q}_0)=\log \left(k\right)+\log \left(p_1{q}_1\right)+u,$$

(9)

where k is assumed to be a known factor of proportionality, and u is assumed to be a random measurement error, possibly independently and identically distributed, with a mean of 0 and constant variance.

Equation (8) relates the unknown price and known quantity of carbon emissions to the known price and known quantity of energy (or electricity), which confirms that the resulting price equation directly refers to carbon emissions. Equation (9) is the logarithmic equivalent of Equation (8).

Let $pq=e$ (expenditure), with $k=1$, without a loss of generality, so that Equation (8) becomes

$$\log \left(e_0\right)=\log \left(e_1\right)+u.$$

(10)

It follows that

$$\mathrm{E}\left[\log \left(e_0\right)\left]=E\right[\log \left(e_1\right)\right]$$

(11)

as $\mathrm{E}\left(u\right)=0$, such that the estimated fitted value of Equation (10) is given as

$$\widehat{\log \left(e_0\right)}=\widehat{\log \left(e_1\right)}.$$

(12)

A regression of $\log \left(e_1\right)$ on $\log \left(e_2\right),\dots ,\log \left(e_{12}\right)$ gives

$$\log \left(e_1\right)=c+{\delta }_2\log \left(e_2\right)+\dots +{\delta }_{12}\log \left(e_{12}\right)+error,$$

(13)

for which the estimated fitted value of $log\left(e_1\right)$ is given as

$$\widehat{\log \left(e_1\right)}=\widehat{c}+\widehat{{\delta }_2}\log \left(e_2\right)+\dots +\widehat{{\delta }_{12}}\log (e_{12}),$$

(14)

where $\widehat{c}, \widehat{{\delta }_2 },\dots ,\widehat{{\delta }_{12}}$ are the OLS estimates of $c, {\delta }_2,\dots ,{\delta }_{12}$, respectively.

Recalling Equation (11), it follows that

$$\widehat{\log \left(e_0\right)}=\widehat{\log \left(e_1\right)}= \widehat{c}+\widehat{{\delta }_2}\log \left(e_2\right)+\dots +\widehat{{\delta }_{12}}\log \left(e_{12}\right),$$

(15)

which gives an “optimal” estimate of $\log \left(e_0\right)$.

As $\log \left(e_0\right)=\log \left(p_0{q}_0\right)$ and $\widehat{\log e_0}=\widehat{\log \left(p_0\right)}+\log q_0$, the prices of carbon emissions can be “optimally” calculated as

$$\widehat{\log \left(p_0\right)}=\widehat{\log \left(e_0\right)}-\log \left(q_0\right).$$

(16)

Equation (16) gives the estimated fitted value, $\widehat{\log p_0}$, as the “optimal” estimate of carbon emission prices as it uses valid statistical techniques that are efficient and optimal.

This novel method would seem to be the first to calculate carbon emissions prices in theory, as well as in practice, using monthly data for Japan.

Further to the above discussion, if data were available for $p_0$, the price of energy (or electricity), as well as prices on some renewable ($Z_1$, say) and nonrenewable ($Z_2$, say) energy inputs, we could compare whether $Z_1$ jointly was more or less significant than $Z_2$ in explaining $p_0$.

The Japanese Government imposes energy taxes on industry, in particular, as well as on households. The use of government data is crucial for consumers and businesses that use energy, as they are expected to pay carbon taxes as users of energy. This is not a financial product, but an application of optimal carbon tax policies.

6. Monthly Data and Diagnostic Checks

The empirical analysis uses a monthly sample period from December 2008 to April 2018 for Japan, where carbon emission prices have not yet been calculated by any government agency or research institute. The definitions of the variables are given in Table 1 as the volume of seasonally unadjusted and seasonally adjusted (using X12) values of coal, LNG, petroleum, electricity, carbon emissions, the spot electricity price, the total transaction volume of electricity, and the price of electricity that represents the price of energy. The sources of the data are the Trade Statistics of Japan, Ministry of Finance, Government of Japan; the Japan Metrological Agency; and the Japan Electricity Power eXchange.

Table 1. Definition of variables.

Variable	Definition	Source
$Coal$	Value of coal (Import value of coal)	Trade Statistics of Japan, Ministry of Finance
$Coa{l}_{SA}$	Value of coal seasonally adjusted by X12
$LNG$	Value of LNG (Import value of LNG)	Trade Statistics of Japan, Ministry of Finance
$LN{G}_{SA}$	Seasonally adjusted value of LNG
$Oil$	Value of petroleum (Import value of petroleum)	Trade Statistics of Japan, Ministry of Finance
$Oi{l}_{SA}$	Value of petroleum seasonally adjusted by X12
$E$	Value of electricity obtained by P_E × E vol
$E_{SA}$	Value of electricity seasonally adjusted by X12
$CE$	Volume of carbon emission (ppm) Average of observations	Japan Metrological Agency
$C{E}_{SA}$	Volume of carbon seasonally adjusted by X12
$P_E$	Spot electricity price (Day ahead, 24 h)	Japan Electricity Power eXchange
$E_{vol}$	Total transaction volume of electricity	Japan Electricity Power eXchange
$E_{vol,SA}$	Total transaction volume of electricity seasonally adjusted by X12

Note: The sample period is monthly from December 2008 to April 2018.

Prior to econometric estimation, the seasonally unadjusted and adjusted volumes of the logarithms of electricity, coal, oil, and LNG were tested for unit roots, for both levels and first differences of the variables, using the non-parametric Phillips-Perron (PP) test of stationarity to ensure that asymptotic theory was valid for the purposes of drawing statistical inferences (see [29] Phillips and Perron (1979)). The test of the null hypothesis that a time series is integrated by an order of 1 is robust to unspecified autocorrelation and heteroscedasticity in the errors of the auxiliary test equation.

The PP tests of the logarithms of the levels and first differences of the seasonally unadjusted and adjusted volumes of electricity, coal, oil, and LNG in Table 2 were conducted using a constant term with a deterministic trend in order to provide alternative simulated critical values of the non-standard test. OLS was used to obtain the estimator of the residual spectrum at a frequency of zero. The PP test detects unit roots of the logarithmic levels of the variables at all reasonable levels of significance, but rejects the null hypothesis of unit roots in logarithmic first differences, so that the log differences of the data are stationary.

Table 2. Phillips-Perron unit root tests.

(a) Levels
Variable	Test Statistic	p-value
$\log \left(E\right)$	−2.320	0.420
$\log \left(E\right)\log {\left(E\right)}_{SA}$	−1.209	0.904
$\log \left(Coal\right)$	−3.309	0.070
$\log {\left(Coal\right)}_{SA}$	−2.727	0.228
$\log \left(Oil\right)$	−2.541	0.308
$\log {\left(Oil\right)}_{SA}$	−2.069	0.557
$\log \left(LNG\right)$	−2.166	0.504
$\log {\left(LNG\right)}_{SA}$	−1.321	0.878
Notes: SA denotes a seasonally adjusted variable. The auxiliary regression included a constant term and time trend. OLS was used to obtain the estimator of the residual spectrum at a frequency of zero.
(b) First Differences
Variable	Test Statistic	p-value
$\Delta \log \left(E\right)$	−11.862	0.000
$\Delta \log {\left(E\right)}_{SA}$	−10.960	0.000
$\Delta \log \left(Coal\right)$	−15.262	0.000
$\Delta \log {\left(Coal\right)}_{SA}$	−14.411	0.000
$\Delta \log \left(Oil\right)$	−12.241	0.000
$\Delta \log {\left(Oil\right)}_{SA}$	−12.639	0.000
$\Delta \log \left(LNG\right)$	−32.051	0.000
$\Delta \log {\left(LNG\right)}_{SA}$	−11.336	0.000
Notes: SA denotes a seasonally adjusted variable. The auxiliary regression included a constant term. The number of lags for the auxiliary regression was determined by the Akaike Information Criterion (AIC). Ordinary Least Squares (OLS) was used to obtain the estimator of the residual spectrum at a frequency of zero.

The correlations in the logarithmic levels of the seasonally unadjusted and adjusted data are shown in Table 3(a), with the corresponding correlations in the logarithmic first differences of the seasonally unadjusted and adjusted data shown in Table 3(b). The highest correlations for the logarithmic levels of the seasonally unadjusted and adjusted data are between oil and LNG, with surprisingly close values of 0.73 and 0.737, respectively. The highest correlations for the logarithmic first differences of the seasonally unadjusted and adjusted data are quite different, with the highest correlation for the former being between oil and LNG at 0.445, and at a much lower 0.267 for coal and oil, as well as for coal and LNG.

Table 3. (a) Correlation: Levels. (b) Correlation: First differences.

(a) Seasonally unadjusted data
	$\mathbf{log}\left(\mathit{E}\right)$	$\mathbf{log}\left(\mathit{Coal}\right)$	$\mathbf{log}\left(\mathit{Oil}\right)$	$\mathbf{log}\left(\mathit{LNG}\right)$
$\log \left(E\right)$	1.000	0.159	−0.008	0.379
$\log \left(\mathit{Coal}\right)$	0.159	1.000	0.317	0.341
$\log \left(\mathit{Oil}\right)$	−0.008	0.317	1.000	0.730
$\log \left(\mathit{LNG}\right)$	0.379	0.341	0.730	1.000
Seasonally adjusted data
	$\mathbf{log}{\left(\mathit{E}\right)}_{\mathit{S}\mathit{A}}$	$\mathbf{log}{\left(\mathit{Coal}\right)}_{\mathit{S}\mathit{A}}$	$\mathbf{log}{\left(\mathit{Oil}\right)}_{\mathit{S}\mathit{A}}$	$\mathbf{log}{\left(\mathit{LNG}\right)}_{\mathit{S}\mathit{A}}$
$\log {\left(E\right)}_{SA}$	1.000	0.146	−0.008	0.375
$\log {\left(\mathit{Coal}\right)}_{SA}$	0.146	1.000	0.294	0.295
$\log {\left(\mathit{Oil}\right)}_{SA}$	−0.008	0.294	1.000	0.737
$\log {\left(\mathit{LNG}\right)}_{SA}$	0.375	0.295	0.737	1.000
(b) Seasonally unadjusted data
	$\mathbf{\Delta }\mathbf{log}\left(\mathit{E}\right)$	$\mathbf{\Delta }\mathbf{log}\left(\mathit{Coal}\right)$	$\mathbf{\Delta }\mathbf{log}\left(\mathit{Oil}\right)$	$\mathbf{\Delta }\mathbf{log}\left(\mathit{LNG}\right)$
$\Delta \log \left(E\right)$	1.000	0.066	0.125	0.211
$\Delta \log \left(\mathit{Coal}\right)$	0.066	1.000	0.299	0.401
$\Delta \log \left(\mathit{Oil}\right)$	0.125	0.299	1.000	0.445
$\Delta \log \left(\mathit{LNG}\right)$	0.211	0.401	0.445	1.000
Seasonally adjusted data
	$\mathbf{\Delta }\mathbf{log}{\left(\mathit{E}\right)}_{\mathit{S}\mathit{A}}$	$\mathbf{\Delta }\mathbf{log}{\left(\mathit{Coal}\right)}_{\mathit{S}\mathit{A}}$	$\mathbf{\Delta }\mathbf{log}{\left(\mathit{Oil}\right)}_{\mathit{S}\mathit{A}}$	$\mathbf{\Delta }\mathbf{log}{\left(\mathit{LNG}\right)}_{\mathit{S}\mathit{A}}$
$\Delta \log {\left(\mathit{E}\right)}_{SA}$	1.000	0.043	0.177	0.038
$\Delta \log {\left(\mathit{Coal}\right)}_{SA}$	0.043	1.000	0.267	0.267
$\Delta \log {\left(\mathit{Oil}\right)}_{SA}$	0.177	0.267	1.000	0.200
$\Delta \log {\left(\mathit{LNG}\right)}_{SA}$	0.038	0.267	0.200	1.000

The [30] Johansen (1991) Trace and Maximum Eigenvalue tests of the number of cointegrating vectors for the seasonally unadjusted and adjusted values of coal, LNG, oil, and electricity are presented in Table 4. The null hypothesis of no cointegration (that is, R = 0) can be rejected at the 5% level of significance using both tests for the combination of logarithms of the seasonally unadjusted and adjusted volumes of coal, LNG, oil, and electricity.

Table 4. Johansen Trace and Maximum Eigenvalue tests of cointegrating vectors.

Trace or Maximum Eigenvalue Test	Number of Cointegrating Vectors	Test Statistic (p-Value)
Trace $\log \left(Coal\right),\log \left(LNG\right),\log \left(Oil\right),\mathrm{and}\log \left(E\right)$	$R=0$	66.725 (0.028)
Maximum Eigenvalue $\log \left(Coal\right),\log \left(LNG\right),\log \left(Oil\right),\mathrm{and}\log \left(E\right)$	$R=0$	37.215 (0.011)
Trace $\log {\left(Coal\right)}_{SA},\log {\left(LNG\right)}_{SA},\log {\left(Oil\right)}_{SA},\mathrm{and}\log {\left(E\right)}_{\mathrm{SA}}$	$R=0$	77.143 (0.003)
Maximum Eigenvalue $\log {\left(Coal\right)}_{SA},\log {\left(LNG\right)}_{SA},\log {\left(Oil\right)}_{SA},\mathrm{and}\log {\left(E\right)}_{\mathrm{SA}}$	$R=0$	40.017 (0.004)

Notes: SA denotes a seasonally adjusted variable. R is the number of cointegrating vectors.

7. Empirical Estimates and Analysis

The results of the PP unit root tests and Johansen tests of the number of cointegrating vectors in the previous section led to fully-modified OLS estimation ([31] Phillips and Hansen, 1990) of the cointegrating regressions, presented in Table 5.

Table 5. Cointegrating regression (fully-modified OLS) for carbon emissions. Case 1: Seasonally unadjusted data. Case 2: Seasonally adjusted data.

	Case 1	Case 2
Constant	−3.180 (0.409)	−4.141 (0.253)
$\log (Coal)$	0.410 (0.056) *
$\log {\left(Coal\right)}_{SA}$		0.451 (0.025) **
$\log (LNG)$	0.215 (0.210)
$\log {\left(LNG\right)}_{SA}$		0.265 (0.125)
$\log (Oil)$	0.612 (0.001) ***
$\log {\left(Oil\right)}_{SA}$		0.573 (0.002) ***
Trend	0.027 (0.000) ***	0.026 (0.000) ***
Dummy	0.669 (0.000) ***	0.772 (0.000) ***
Adjusted R2	0.943	0.958

Notes: ***, **, and * denote statistical significance at the 1%, 5%, and 10% levels, respectively. Numbers in parentheses indicate p-values of the t-tests. The dummy variable, which was introduced to accommodate the influence of increases in electricity prices on May 2017 arising from tax changes in Japan, equals 0 before September 2017, and 1 after September 2017.

Two cases are considered, as follows:

• Case 1: Seasonally unadjusted data, with a deterministic trend and dummy variable;
• Case 2: Seasonally adjusted data, with a deterministic trend and dummy variable.

The dummy variable, which was introduced to accommodate the influence of increases in electricity prices on May 2017 arising from tax changes in Japan, equals 0 before September 2017, and 1 after September 2017.

For both seasonally unadjusted and seasonally adjusted data, that is, Cases 1 and 2, the logarithms of coal and oil, as well as the deterministic time trend and the tax change dummy variable, are statistically significant in explaining the logarithm of carbon emissions, with oil being more significant than coal. The logarithm of LNG is not statistically significant at any conventional level of significance in explaining the logarithm of carbon emissions in either Case 1 or Case 2. The adjusted R² values are reasonably high, at 0.943 and 0.958 for Cases 1 and 2, respectively, which suggests that the models are quite successful in explaining the logarithm of carbon emissions using both seasonally unadjusted and seasonally adjusted data.

The forecasts of $\log \left(E\right)$ for seasonally unadjusted and seasonally adjusted data are shown in Figure 1a,b, respectively, where two standard errors in each figure provide the 95% confidence intervals. In each case, there were noticeable falls in the forecasts of the logarithm of electricity from mid-2015 through to early-2016, and substantial rises toward the end of 2017.

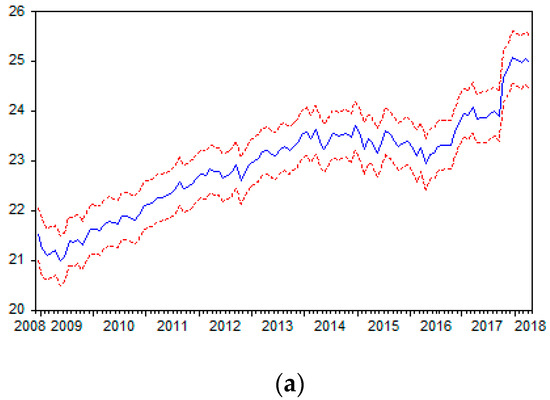
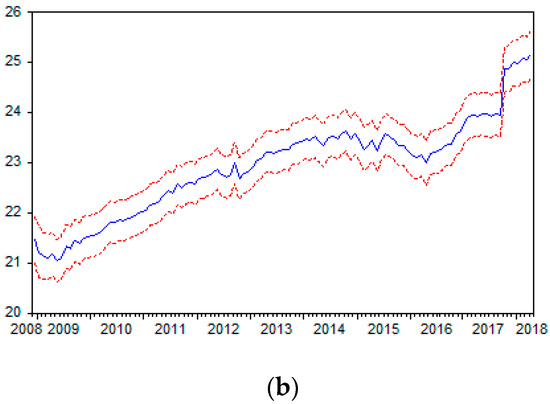
Figure 1. (a) Forecast of $\log \left(E\right)$ ($\pm 2$ standard errors). (b). Forecast of $\log {\left(\mathrm{E}\right)}_{\mathrm{SA}}$ ($\pm 2$ standard errors).

The predicted latent carbon emission prices for seasonally unadjusted and adjusted data are depicted in Figure 2a,b respectively.

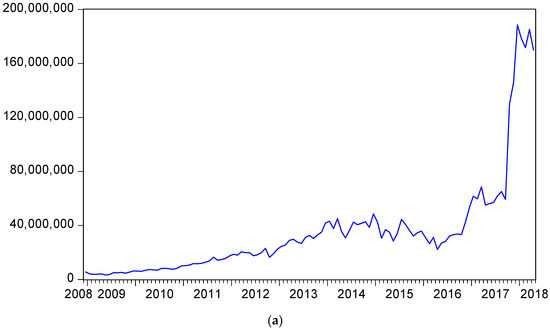
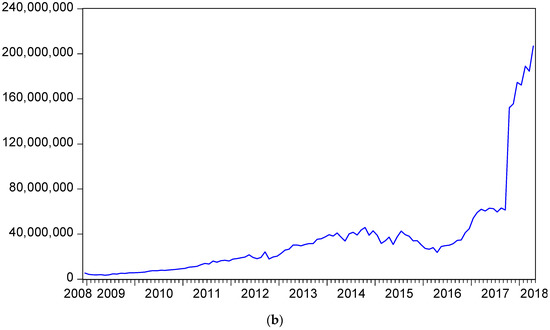
Figure 2. (a) Predicted carbon emission prices. $\widehat{\log \left(C{E}_p\right)}=\widehat{\log \left(E\right)}-\log \left(E_{vol}\right)$. $\widehat{C{E}_p}=\exp \left[\widehat{\log \left(E\right)}-\log \left(E_{vol}\right)\right]$. (b) Predicted carbon emission prices (SA). $\widehat{\log \left(C{E}_{p,SA}\right)}= \widehat{\log \left(E_{SA}\right)}-\log \left(E_{vol,SA}\right)$. $\widehat{C{E}_{p,SA}}=\exp \left[\widehat{\log (E_{SA})}-\log (E_{vol, SA})\right]$.

The predicted values are based on the formulae for the logarithmic values presented in Equation (16), with the predicted carbon emissions prices having been obtained using the exponential function for the seasonally unadjusted data, as follows:

$$\widehat{\log \left(C{E}_p\right)}=\widehat{\log \left(E\right)}-\log \left(E_{vol}\right)$$

(17a)

$$\widehat{C{E}_p}=\exp \left[\widehat{\log \left(E\right)}-\log \left({\mathrm{E}}_{vol}\right)\right]$$

(17b)

and for the seasonally adjusted data, as follows:

$$\widehat{\log \left(C{E}_{p,SA}\right)}= \widehat{\log \left(E_{SA}\right)}-\log \left(E_{vol,SA}\right)$$

(18a)

$$\widehat{C{E}_{p,SA}}=\exp \left[\widehat{\log (E_{SA})}-\log (E_{vol, SA})\right].$$

(18b)

The patterns of the predicted carbon emissions prices in Figure 2a,b emulate the patterns described in Figure 1a,b with significant upward movements in both the seasonally unadjusted and seasonally adjusted data after mid-2017.

The correlation between $\widehat{\log \left(E\right)}$ and $\widehat{\log {\left(E\right)}_{SA}}$ of 0.997 is given in Table 6, while the correlation between the seasonally unadjusted and seasonally adjusted predicted carbon emissions prices of 0.992 is given in Table 7. It is clear that the forecasts of carbon emission prices are very similar, regardless of whether seasonally unadjusted or seasonally adjusted data are used.

Table 6. Correlation between $\widehat{\log \left(\mathrm{E}\right)}$ and $\widehat{\log {\left(\mathrm{E}\right)}_{\mathrm{SA}}}$.

	$\widehat{\mathbf{log}\left(\mathit{E}\right)}$	$\widehat{\mathbf{log}{\left(\mathit{E}\right)}_{\mathit{S}\mathit{A}}}$
$\widehat{\log \left(\mathit{E}\right)}$	1.000	0.997
${\widehat{\log \left(\mathit{E}\right)}}_{SA}$	0.997	1.000

Note: SA denotes seasonally adjusted values.

Table 7. Correlation between predicted carbon emissions price and predicted carbon emissions price (SA).

	$\widehat{\mathit{C}{\mathit{E}}_{\mathit{p}}}$	$\widehat{\mathit{C}{\mathit{E}}_{\mathit{p},\mathit{S}\mathit{A}}}$
$\widehat{\mathit{C}{\mathit{E}}_{\mathit{p}}}$	1.000	0.992
$\widehat{\mathit{C}{\mathit{E}}_{\mathit{p},\mathit{S}\mathit{A}}}$	0.992	1.000

Note: SA denotes seasonally adjusted values.

8. Concluding Remarks

It is widely accepted in the international scientific and global communities that climate change and global warming are significantly affected by carbon emissions that arise from the burning of fossil fuels, specifically coal, oil, and gas. Although prices of fossil fuels are readily available, the prices of carbon emissions arising from competitive markets for the product are not yet commercially available.

As carbon emissions can be taxed appropriately when accurate commercial market prices are known and accepted at an international level, carbon emissions can be taxed appropriately for the purposes of measuring, capturing, storing, and trading in carbon emissions at regional, national, and international levels.

This paper used a novel KLEM production function approach to calculate the latent carbon emission prices, where carbon emissions are regarded as the output and capital (K), labor (L), energy (E) (or electricity), and materials (M), are the inputs for the production process. As the inputs K, L, and M are essentially fixed on a monthly basis, whereas E can be changed daily, it follows that changes in carbon emissions are functions of changes in E.

On the condition that prices depend on the average cost pricing, the prices of carbon emissions and energy may be approximated by an energy production model with a constant factor of proportionality, so that carbon emission prices will be a function of energy prices. Using this novel modeling approach, this paper estimated carbon emission prices for Japan using seasonally adjusted and unadjusted monthly data on the volumes of carbon emissions and energy, as well as energy prices, from December 2008 to April 2018.

The novel methods presented in the paper are straightforward to understand and implement, based on simple methods of estimation. The usefulness in establishing carbon emission prices goes to the heart of tackling global warming and climate change.

The econometric models showed that, as sources of electricity, the logarithms of coal and oil, though not LNG, are statistically significant in explaining the logarithm of carbon emissions, with oil being more significant than coal. The models generally displayed a high power in predicting the latent prices of carbon emissions. In particular, the forecasts of carbon emission prices were very similar, regardless of whether seasonally unadjusted or seasonally adjusted data were used. The usefulness of the empirical findings suggests that the methodology can also be applied for other countries where carbon emission prices are latent.

The theoretical approach and empirical application developed in the paper should be useful for purposes of public policy debate and decision making. Accurate predictions of the latent prices of carbon emissions, and the imposition of appropriate environmental taxes, are essential in order to mitigate the effect of carbon emissions on global warming and climate change.

Appendix A.1. Derivation of Correct Standard Errors for Realized Latent Carbon Emissions and Ranking of Important Underlying Factors

The novelty of the paper includes the development of innovative methods of analyzing latent exogenous and endogenous variables. There has been little, if any, research undertaken on latent variables, such as unobservable endogenous or exogenous variables, including rankings of the importance of various factors in explaining the latent prices of carbon emissions.

An analysis of latent variables is such that the choice of important and influential explanatory informational variables is typically arbitrary, that is, not based on any optimizing criterion. The final rankings may be based on averaging aggregated using Pythagorean arithmetic, geometric, or harmonic means. Consequently, any rankings based on arbitrary explanatory informational variables are themselves arbitrary.

The purpose of this paper is to determine and forecast latent endogenous variables, in particular, the latent prices for carbon emissions, and rankings using optimization methods, so that the rankings will also be optimal. The extensive list of references applies technical methods to show how the estimation and calculation of correct standard errors can be performed.

A wide range of alternative rankings include, but are not limited to the following:

(1)

Academic rankings of individuals, departments, faculties/schools/colleges, institutions, states, countries, and regions, which are of both academic and practical interest from individual students, parents, and institutions, to public and private policy advisors (for robust methods of ranking academic journals see, for example, [32,33,34,35,36,37] Chang and McAleer (2013, 2014a, 2014b, 2014c, 2015, 2016); [38,39,40,41,42] Chang, McAleer, and Oxley (2011a, 2011b, 2011c, 2011d, 2013); and [43] Chang, Maasoumi and McAleer (2016));

(2)

International rankings of universities, namely “Academic Ranking of World Universities (ARWU)” by Shanghai Ranking Consultancy (originally compiled and issued by Shanghai Jiao Tong University), “World University Rankings” by Times Higher Education (THE), and “QS World University Rankings” by Quacquarelli Symonds (QS), are based on arbitrary measures.

Appendix A.2. Theoretical Structure for Latent Endogenous and Exogenous Variables

The fundamental ideas and theoretical structure underlying a critical analysis of latent exogenous and latent endogenous variables can be presented in the following basic model, with extensions to models involving more complicated decision strategies to be presented subsequently.

Suppose the true linear relationship between a dependent variable, or an endogenous variable that is determined within the model, and a set of explanatory variables, that is, exogenous variables that are determined outside the model, can be represented as

$$y_t^{*}={\left(X_t^{*}\right)}^{\prime }\beta +{ϵ}_t,$$

(A1)

where t = 1, 2, 3, … n observations; $y_t^{*}$ is the latent endogenous variable; $X_t^{*}$ is a kx1 vector of latent exogenous variables; the unknown parameter vector $\beta$ is kx1; and $e_t$ is an uncorrelated and homoskedastic (or possibly an independently and identically distributed) random error term. The parameter $\beta$ in Equation (A1) cannot be estimated as $y_t^{*}$ and $X_t^{*}$ are not observable.

A standard approach to estimating $\beta$, calculating the in-sample estimates (that is, fitted values) of $y_t^{*}$, and forecasting out-of-sample values of $y_t^{*}$, is to use proxy variables for both $y_t^{*}$ and $X_t^{*}$. However, the use of a proxy for $X_t^{*}$ will almost certainly lead to problems in estimation and sub-optimal statistical properties of the associated estimators.

The use of proxy variables is called the problem of measurement error, which is inevitable whenever latent variables are considered:

$$y_t=y_t^{*}+u_t$$

(A2)

$$X_t=X_t^{*}+V_t$$

(A3)

in which the proxy $y_t$ for $y_t^{*}$ in Equation (A2) is decomposed into two components, namely the latent component, which is the true measure of $y_t$, and a measurement error $u_t$ that is the difference between $y_t$ and $y_t^{*}$. Similarly, the proxy $X_t$ for $X_t^{*}$ in Equation (A3) is decomposed into two components, namely the latent component, which is the true measure of $X_t$, and a measurement error $V_t$ that is the difference between $X_t$ and $X_t^{*}$.

Such measurement error problems frequently arise in the social sciences, especially in economics and finance, where $X_t^{*}$ may represent latent expectational, desired, perceived, equilibrium, or long-run variables. Rankings across a wide range of academic disciplines are also typically based on using a proxy for $y_t^{*}$ that depends on arbitrary rather than optimal measures, so that the rankings are arbitrary.

There are two approaches to trying to accommodate the problem of measurement error, namely a primitive approach that includes the measurement errors, and an alternative approach that quarantines and improves upon the incorporation of measurement errors.

Appendix A.2.1. Primitive Approach

Substituting $y_t^{*}=y_t-u_t$ and $X_t^{*}=X_t-V_t$ in (A1) leads to

$$y_t={\left(X_t\right)}^{\prime }\beta +\left(e_t+u_t-{\left(V_t\right)}^{\prime }\beta \right),$$

(A4)

where $\left(e_t+u_t-{\left(V_t\right)}^{\prime }\beta \right)$ is the composite error arising from Equations (A1)–(A3).

In Equation (A4), $\beta$ can be estimated by OLS, as both $y_t$ and $X_t$ are measurable, to obtain the in-sample estimated or fitted values, represented by “hat” (or circumflex) of $y_t$, as follows:

$$\widehat{y_t}=\widehat{y_t^{*}}=\left(X_t\right)\prime \widehat{\beta },$$

(A5)

where $\widehat{y_t}$ is the fitted value of both $y_t$ and $y_t^{*}$, which follows from (A2), and $\widehat{\beta }$ is the OLS estimate of $\beta$. Equation (A5) can be used to calculate the in-sample fitted values of $y_t^{*}$ or forecast out-of-sample values of $y_t^{*}$.

It is well-known that the OLS estimate of $\beta$ is biased, inconsistent, and inefficient as $X_t$ in (A4) is correlated with $V_t$ in the composite error. However, this does not mean that out-of-sample forecasts based on $\widehat{y_t}$ will be inaccurate in comparison with forecasts obtained from using an alternative consistent estimator of $\beta$. This is also well-known, but does not seem to have been applied to the issue of computing and forecasting latent endogenous variables, such as carbon emission prices and important ranking factors.

Appendix A.2.2. Generated Regressors and Realized Latents

The second approach is more sophisticated mathematically and statistically, and leads to consistent and efficient estimators of $\beta$ by reducing the impact of informational ignorance in the presence of latent exogenous and endogenous variables. Returning to Equation (A1), the substitution of $y_t$ for $y_t^{*}$ gives

$$y_t={\left(X_t^{*}\right)}^{\prime }\beta +\left(e_t+u_t\right),$$

(A6)

in which it is reasonably assumed that $X_t^{*}$ is not correlated with $e_t$ or $u_t,$ the random errors in $y_t^{*}$ and $y_t$, respectively. The parameter $\beta$ cannot be estimated in Equation (A6) as $X_t^{*}$ is a latent exogenous variable, even though $y_t$ is observed.

Rather than simply replacing $X_t^{*}$ with a proxy variable such as $X_t$, in economics, it is frequently assumed that the latent $X_t^{*}$ depends on a vector of observable variables $Z_t$, as follows:

$$X_t^{*}=\left(Z_t\right)\prime C,$$

(A7)

where $Z_t$ is gx1, and the unknown matrix of parameters C is gxk.

What is quite remarkable about Equation (A7) is that a latent exogenous variable, $X_t^{*}$, which is unmeasurable for all n observations on k variables, is now given as a function of n measurable observations on g variables in $Z_t$ and g unknown in C.

The assumption based on (A7) effectively reduces the ignorance and lack of informational content from n latent observations in $X_t^{*}$ to g unknown parameters in C.

Using the definition of $X_t$ in Equation (A3) and the assumption for $X_t^{*}$ in Equation (A7) gives

$$X_t={\left(Z_t\right)}^{\prime }C+V_t.$$

(A8)

As both $X_t$ and $Z_t$ are measurable, the OLS estimation of C in Equation (A8) leads to

$$\widehat{C}=\left[{\left(Z^{\prime }Z\right)}^{-1}\right]Z^{\prime }X,$$

(A9)

which gives an estimate in Equation (A10) of the latent variable $X_t^{*}$, $\widehat{X_t^{*}}$, based on estimating $X_t$ in Equation (A8) and $\widehat{C}$ from Equation (A9):

$$\widehat{X_t}=\widehat{X_t^{*}}={\left(Z_t\right)}^{\prime } \widehat{C}.$$

(A10)

Equation (A8) is the foundation of the “rational expectations” literature in economics as $\widehat{X_t}=\widehat{X_t^{*}}$ in Equation (A10) is used as a “rational” (or, more accurately, a model-consistent) estimate of the latent exogenous variable, $X_t^{*}$. $\widehat{X_t}$ is called a “generated (or realized) regressor” as it can be used to replace the latent $X_t^{*}$ to estimate $y_t$ and $y_t^{*}$. Returning to Equation (A6), the substitution of $\widehat{X_t^{*}}={\left(Z_t\right)}^{\prime } \widehat{C}$ for $X_t^{*}$ gives

$$y_t={\widehat{(X_t^{*}})}^{\prime }\beta +\left(e_t+u_t+{\left(X_t^{*}-\widehat{X_t^{*}}\right)}^{\prime }\beta \right).$$

(A11)

The substitution of $X_t^{*}$ from Equation (7), $\widehat{C}$ from Equation (9), and $\widehat{X_t^{*}}$ from Equation (10), in Equation (11), leads to

$$y_t={\widehat{(X_t^{*}})}^{\prime }\beta +\left(e_t+u_t-{[{\left(Z_t\right)}^{\prime }{\left(Z_t^{\prime }{Z}_t\right)}^{-1} Z_t^{\prime }{V}_t]}^{\prime }\beta \right),$$

(A12)

in which $\widehat{X_t^{*}}$ is an observable generated regressor.

As $\widehat{X_t^{*}}$ is uncorrelated with each of the components in the combined error in Equation (A12), namely $e_t$, $u_t$, and ${[{\left(Z_t\right)}^{\prime }{\left(Z_t^{\prime }{Z}_t\right)}^{-1} Z_t^{\prime }{V}_t]}^{\prime }\beta$, it follows that the OLS estimation of $\beta$ by regressing $y_t$ on $\widehat{X_t^{*}}$ is unbiased.

Calculation of the correct standard errors for statistical inference to be valid is dependent on using the correct error structure in Equation (A12), as given in Equation (A13):

$$\left(e_t+u_t-{\left[{\left(Z_t\right)}^{\prime }{\left(Z_t^{\prime }{Z}_t\right)}^{-1} Z_t^{\prime }{V}_t\right]}^{\prime }\beta \right)$$

(A13)

which is based on the composite error term $\left(e_t+u_t-{\left(V_t\right)}^{\prime }\beta \right)$ in Equation (A4), rather than on $e_t$ alone.

Using the incorrect standard errors from the OLS estimation of Equation (A12) based on $e_t$ rather than on the composite error in Equation (A13) will lead to standard errors that are biased downward as the variance of

$$\left(u_t-{\left(V_t\right)}^{\prime }\beta \right)=u_t-{[{\left(Z_t\right)}^{\prime }{\left(Z_t^{\prime }{Z}_t\right)}^{-1} Z_t^{\prime }{V}_t]}^{\prime }\beta$$

(A14)

is positively definite. Therefore, the calculated t-ratios will be biased upward, thereby incorrectly leading to findings of spurious statistical significance.

An alternative approach to calculating the correct standard errors based on the OLS estimation of Equation (A12) when $u_t$ = 0, that is, when only the exogenous regressors are latent, is to incorporate the [44] Newey and West (1987) Heteroskedasticity and AutoCorrelation (HAC) consistent covariance matrix estimator. [45] Smith and McAleer (1994) have shown that the HAC covariance matrix estimator is reasonably accurate for purposes of drawing inferences in finite samples in the presence of generated regressors. The finite sample properties of the OLS estimation of Equation (A12) when $u_t$ = 0 does not hold, that is, when the endogenous variable is latent, remains a topic for future research.

Moreover, using the necessary and sufficient Rao–Zyskind condition (also sometimes referred to as Kruskal’s Theorem) for OLS to be efficient (see [46] McAleer, 1992), the OLS estimator of $\beta$ in Equation (A12) can be shown to be efficient, and hence to enable valid statistical inference (for further details see, for example, [47] Pagan (1984), [48,49,50,51] McAleer and McKenzie (1991, 1992, 1994, 1997), and [52] Fiebig et al. (1992)).

Using the OLS estimate of $\beta$ from Equation (A12) will provide in-sample fitted values of $y_t$ and out-of-sample forecasts of $y_t$, and hence of $y_t^{*}$. The fitted values of $y_t$ are $\widehat{y_t}=\widehat{y_t^{*}}$, which are “realized latents” as they are the fitted or realized in-sample values of the latent variable $y_t^{*}$ in Equation (A1), and the realized out-of-sample forecasts of $y_t^{*}$.

The rankings literature provides a novel example of how it is possible to estimate true latent rankings, $y_t^{*}$, using realized latent rankings, $\widehat{y_t^{*}}$, that are obtained from generated (or realized) regressors and observed rankings, $y_t$, which are subject to measurement error. The realized latent rankings can also be used to obtain out-of-sample forecasts.

Appendix A.3. Extensions to More Complicated Decision Strategies

The presentation of the basic model concentrated on developing a theoretical approach and structure to generate univariate “realized latent rankings” for unobservable latent endogenous variables, and establishing the theoretical properties of the new measures, as well as of the associated parametric estimators.

Generated regressors and realized latents can be applied to obtain measurable and optimal rankings of any latent endogenous variables, with interesting and challenging extensions to a wide range of models arising from more complicated and sophisticated decision strategies.

The development of innovative methods of analyzing latent endogenous variables can be extended to the following topical and practical issues:

(i)

Extending “realized latent rankings” to multivariate unobserved latent endogenous variables, and establishing the theoretical properties of the new measures, as well as of the associated parametric estimators, using extensions of the technical developments in the basic model. These could include structural models, recursive models, and probabilistic models;

(ii)

OLS is the simplest technique that can be employed to obtain optimal weights through estimation, but it is possible to use Logistic regression to obtain optimal weights and the inherent associated probabilities;

(iii)

In the context of Cognitive Computing, it is widely argued that computers, computing facilities, machine hardware, mathematical algorithms, and computer software should be perceived as aids to learn dynamically, to reach managerial decisions, and to achieve strategic aims;

(iv)

As advanced machines can be programmed to learn through feedback, an important implication is that the outputs obtained from inputs and processing systems are not the same if learning is allowed because the outputs can differ. Consequently, outputs from such processing systems should be modeled and analyzed in a probabilistic context which, in turn, helps to make managerial decisions.

The cognitive approach is precisely related to realized latent rankings models, in which the probabilistic outputs, namely realized rankings, can change dynamically according to the generated (or realized) regressors and dynamic learning. Therefore, the probabilities would assist in strategic management decision making.

Conditional on the sets of features (such as the latent endogenous variable, and measurable or latent exogenous variables), the model can provide different realized latencies, such as latent carbon emission prices, which can assist management in making optimal decisions. It is assumed in latent probabilistic models that the exogenous regressors are measurable, such as

$$y^{*}=X^{\prime }\beta +e,$$

(A15)

where y* in Equation (A15) is latent, but we observe a binary variable y that takes the value of 1 or 0, according to whether or not y* crosses a threshold, that is, y = 1 if y* > 0, and 0 otherwise.

The probabilistic model is given by

$$P(y=1|x)=P(y^{*}>0)=P(-e<X^{\prime }\beta )=F(X^{\prime }\beta )$$

(A16)

where F in Equation (A16) is typically a normal or logistic cumulative distribution function (CDF). Then, y* is given in Equation (A17) by

$$y^{*}=\mathrm{F}\left(X^{\prime }\widehat{\beta }\right).$$

(A17)

The model and associated analysis change drastically if the basic latent regression model is changed to incorporate X*, as in Equation (A18), rather than X in Equation (A15):

$$y^{*}=X^{*\prime }\beta +e$$

(A18)

as an appropriate model would be required for X* to obtain generate regressors for X* and realized latencies for y*.

Such an extension of logistic probabilistic models to incorporate latent exogenous variables to estimate and forecast latent endogenous variables is a novel extension of the classical latent probabilistic model, and can be analyzed as follows:

(v)

Defining and measuring a wide range of latent variables, such as unknown carbon emission prices and academic quality; ranking individuals, departments, faculties, and institutions based on the new measure; and establishing the theoretical properties of the new measures, as well as the associated parametric estimators;

(vi)

Ranking individuals, departments, faculties and institutions based on non-academic measures, and establishing the theoretical properties of the new measures, as well as of the associated parametric estimators;

(vii)

Applying the approach based on “realized latent rankings” commercially to any decision making strategies in business, using structural models; multiple decision making based on recursive models, that is, sequential decision making; and strategic decision making using probabilistic models, among others.

For example, if $y_1^{*}$ and $X_1^{*}$ are latent endogenous and exogenous variables, respectively, in stage 1 of a decision making process, the model may capture sequential decision making in Equations (A19)–(A21), as follows:

$$y_1^{*}={X_1^{*}}^{\prime }{\beta }_1+e_1;$$

(A19)

$$y_2^{*}={X_2^{*}}^{\prime }{\beta }_2+c_1\widehat{y_1^{*}}+e_2;$$

(A20)

$$y_3^{*}={X_3^{*}}^{\prime }{\beta }_3+c_2 \widehat{y_2^{*}}+e_3.$$

(A21)

where $y_1^{*}$ in Equation (A20) is obtained at the first stage from Equation (A19), $y_2^{*}$ in Equation (A21) is obtained at the second stage from Equation (A20), and so on.

It is clear that sequential models will be necessary to obtain “sequential generated regressors”, and subsequent “sequential realized latencies”, which would present challenging and novel theoretical and practical developments. The approach given above could also be extended to probabilistic models, which would be an entirely new and innovative development.

Each of the points stated above is novel from theoretical and practical perspectives, namely applications of generated regressors and realized latents to obtain measurable and optimal rankings of any latent endogenous variables, and extensions to a wide range of more complicated models and decision strategies. The techniques of the basic model presented above can be extended, and are portable to different problems and disciplines, such as latent carbon emission prices, rankings of important factors, and associated management decisions.