Potential Analysis of Hybrid Renewable Energy Systems for Self-Sufficient Residential Use in Germany and the Czech Republic
Abstract
1. Introduction
- -
- -
- Many of the studies are mostly based on environmental data (wind speeds, solar irradiation) of single locations [16,17,18] not accounting for local long- and short-term availability and intermittency of natural resources, which are crucial to sustain self-sufficiency at all times. Furthermore, these studies usually neglect the potential of harnessing complementarity of wind and solar resources to decrease total system costs while increasing efficiency, stability and reliability of electricity generation [16,25]. Studies on larger regions [25,27], however, imply connection to the grid and therefore do not apply to the concept of self-sufficiency of sparsely populated regions in the future, but at the aim of maximizing self-consumption or minimizing residential load.
- -
- While in other studies, analyses were based on data of high temporal resolution, e.g., per minute [10], spatial resolution is generally low in the existing literature or the analysis is restricted only to single sites or smaller areas such as cities [10,11,13,16,17,18,27] or single NUTS-3 regions [25], reducing conclusions about applicability of investigated systems only to limited locations. In order to be of use to political and planning stakeholders, however, it is necessary to be able to compare sites covering larger regions in a high spatial resolution considering local resource availability. This can act as a decision-making basis for finding optimal locations and planning as well as investing accordingly. Studies covering large geographical areas with high spatial and temporal resolutions can be found only for assessments of complementarity of wind and PV power generation and not for hybrid systems sizing and costs.
2. Materials and Methods
2.1. Electricity Generation from PV and Wind Turbines
2.2. Identification of Potential Locations and Energy Demand
2.3. Mixed Integer Linear Program to Size Hybrid PV-Wind-Battery Systems
2.4. Scenario Assumptions
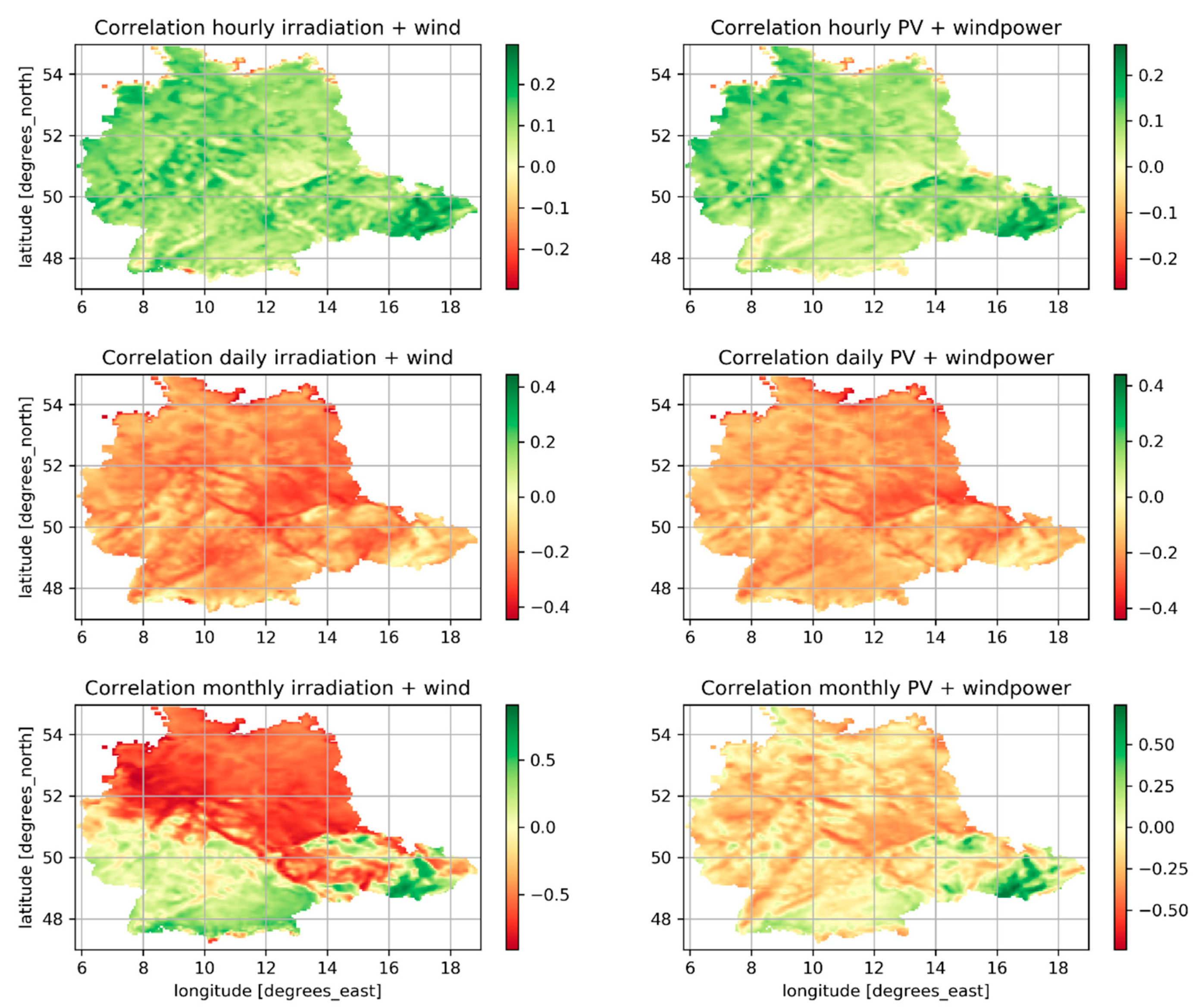
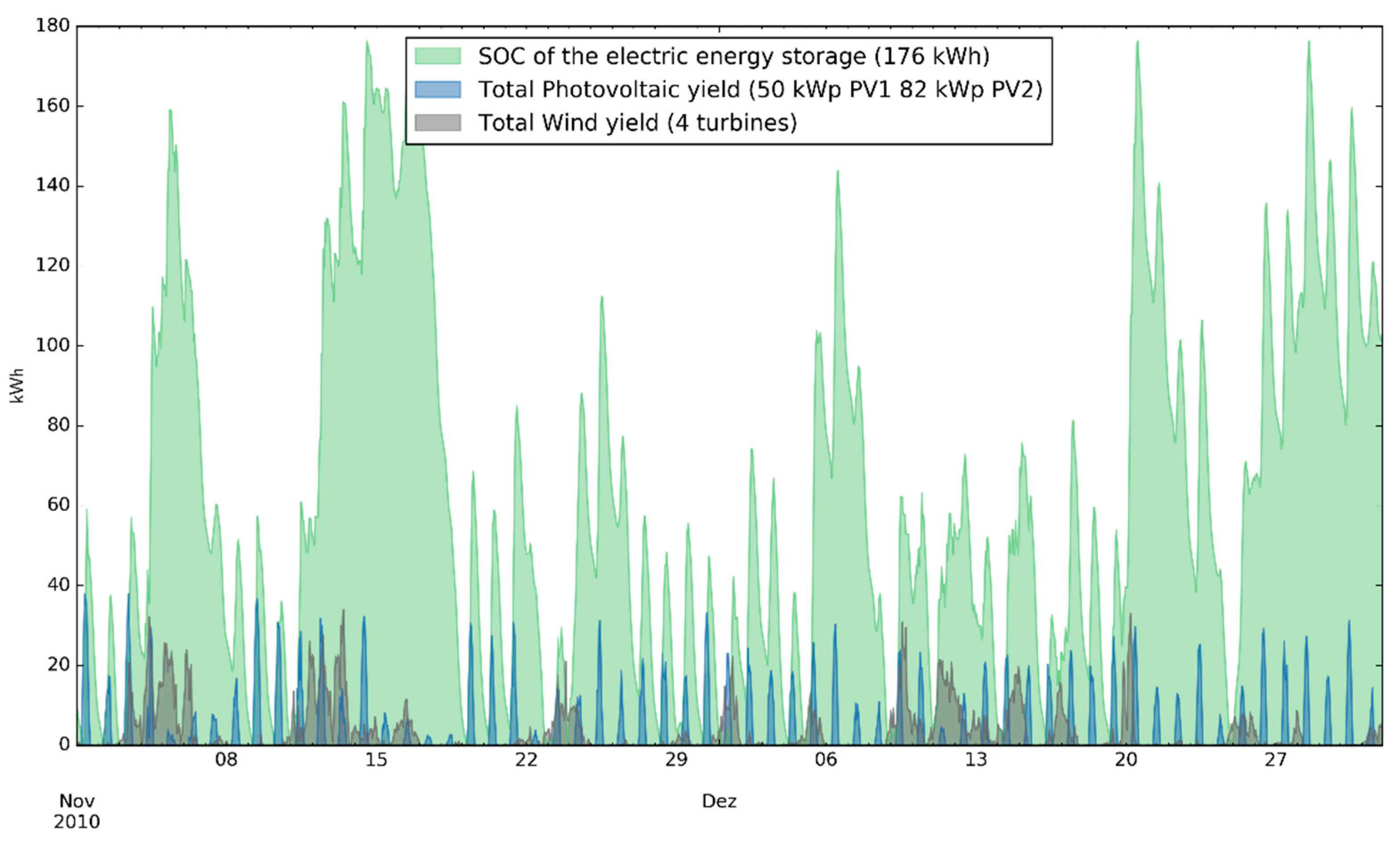
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IEA. Energy Technology Perspectives 2017; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Lang, T.; Gloerfeld, E.; Girod, B. Don’t just follow the sun—A global assessment of economic performance for residential building photovoltaics. Renew. Sustain. Energy Rev. 2015, 42, 932–951. [Google Scholar] [CrossRef]
- Eurostat Database—Energy Statistics. Available online: https://ec.europa.eu/eurostat/web/energy/data/database (accessed on 30 July 2019).
- GfK Belgium Consortium. Study on “Residential Prosumers in the European Energy Union”; EAHC/2013/CP/04; European Commission: Brussels, Belgium, 2017.
- Scarpa, R.; Willis, K. Willingness-to-pay for renewable energy: Primary and discretionary choice of British households’ for micro-generation technologies. Energy Econ. 2010, 32, 129–136. [Google Scholar] [CrossRef]
- Ramirez Camargo, L.; Pagany, R.; Dorner, W. Optimal Sizing of Active Solar Energy and Storage Systems for Energy Plus Houses. In EuroSun2016; International Solar Energy Society: Palma de Mallorca, Spain, 2016; pp. 1–12. [Google Scholar]
- Chauhan, A.; Saini, R.P. A review on Integrated Renewable Energy System based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- Kompil, M.; Aurambout, J.P.; Ribeiro Barranco, R.; Barbosa, A.; Jacobs-Crisioni, C.; Pisoni, E.; Zulian, G.; Vandecasteele, I.; Trombetti, M.; Vizcaino, P.; et al. European Cities, Territorial Analysis of Characteristics and Trends: An Application of the LUISA Modelling Platform (EU Reference Scenario 2013—Updated Configuration 2014); Publications Office: Luxembourg, 2015; ISBN 978-92-79-54594-8. [Google Scholar]
- Ropuszyńska-Surma, E.; Węglarz, M. Profiling End User of Renewable Energy Sources among Residential Consumers in Poland. Sustainability 2018, 10, 4452. [Google Scholar] [CrossRef]
- Weniger, J.; Tjaden, T.; Quaschning, V. Sizing of Residential PV Battery Systems. Energy Procedia 2014, 46, 78–87. [Google Scholar] [CrossRef]
- Hoppmann, J.; Volland, J.; Schmidt, T.S.; Hoffmann, V.H. The economic viability of battery storage for residential solar photovoltaic systems—A review and a simulation model. Renew. Sustain. Energy Rev. 2014, 39, 1101–1118. [Google Scholar] [CrossRef]
- Nižetić, S.; Papadopoulos, A.M.; Tina, G.M.; Rosa-Clot, M. Hybrid energy scenarios for residential applications based on the heat pump split air-conditioning units for operation in the Mediterranean climate conditions. Energy Build. 2017, 140, 110–120. [Google Scholar] [CrossRef]
- Widén, J.; Wäckelgård, E.; Lund, P.D. Options for improving the load matching capability of distributed photovoltaics: Methodology and application to high-latitude data. Sol. Energy 2009, 83, 1953–1966. [Google Scholar] [CrossRef]
- Merei, G.; Moshövel, J.; Magnor, D.; Sauer, D.U. Optimization of self-consumption and techno-economic analysis of PV-battery systems in commercial applications. Appl. Energy 2016, 168, 171–178. [Google Scholar] [CrossRef]
- Bruch, M.; Müller, M. Calculation of the Cost-effectiveness of a PV Battery System. Energy Procedia 2014, 46, 262–270. [Google Scholar] [CrossRef]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- Amrollahi, M.H.; Bathaee, S.M.T. Techno-economic optimization of hybrid photovoltaic/wind generation together with energy storage system in a stand-alone micro-grid subjected to demand response. Appl. Energy 2017, 202, 66–77. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L. A feasibility study of a stand-alone hybrid solar—Wind—Battery system for a remote island. Appl. Energy 2014, 121, 149–158. [Google Scholar] [CrossRef]
- Al-falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Khare, V.; Nema, S.; Baredar, P. Solar–wind hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2016, 58, 23–33. [Google Scholar] [CrossRef]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A.B. Sizing methods and optimization techniques for PV-wind based hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Khan, F.A.; Pal, N.; Saeed, S.H. Review of solar photovoltaic and wind hybrid energy systems for sizing strategies optimization techniques and cost analysis methodologies. Renew. Sustain. Energy Rev. 2018, 92, 937–947. [Google Scholar] [CrossRef]
- Bilir, L.; Yildirim, N. Modeling and performance analysis of a hybrid system for a residential application. Energy 2018, 163, 555–569. [Google Scholar] [CrossRef]
- Quoilin, S.; Kavvadias, K.; Mercier, A.; Pappone, I.; Zucker, A. Quantifying self-consumption linked to solar home battery systems: Statistical analysis and economic assessment. Appl. Energy 2016, 182, 58–67. [Google Scholar] [CrossRef]
- Killinger, S.; Mainzer, K.; McKenna, R.; Kreifels, N.; Fichtner, W. A regional optimisation of renewable energy supply from wind and photovoltaics with respect to three key energy-political objectives. Energy 2015, 84, 563–574. [Google Scholar] [CrossRef]
- Calif, R.; Schmitt, F.G. −5/3 Kolmogorov Turbulent Behaviour and Intermittent Sustainable Energies; Intech: London, UK, 2016; p. 16. [Google Scholar]
- Zappa, W.; van den Broek, M. Analysing the potential of integrating wind and solar power in Europe using spatial optimisation under various scenarios. Renew. Sustain. Energy Rev. 2018, 94, 1192–1216. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’Isidoro, M.; Lacal-Arántegui, R. Assessing complementarity of wind and solar resources for energy production in Italy. A Monte Carlo approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- Ramirez Camargo, L.; Nitsch, F.; Gruber, K.; Dorner, W. Electricity self-sufficiency of single-family houses in Germany and the Czech Republic. Appl. Energy 2018, 228, 902–915. [Google Scholar] [CrossRef]
- Ramirez Camargo, L.; Gruber, K.; Nitsch, F.; Dorner, W. Hybrid renewable energy systems to supply electricity self-sufficient residential buildings in Central Europe. Energy Procedia 2019, 158, 321–326. [Google Scholar] [CrossRef]
- Hans-Ertel-Zentrum für Wetterforschung COSMO Regional Reanalysis—COSMO-REA6. Available online: http://reanalysis.meteo.uni-bonn.de/?COSMO-REA6 (accessed on 24 January 2018).
- Bollmeyer, C.; Keller, J.D.; Ohlwein, C.; Wahl, S.; Crewell, S.; Friederichs, P.; Hense, A.; Keune, J.; Kneifel, S.; Pscheidt, I.; et al. Towards a high-resolution regional reanalysis for the European CORDEX domain. Q. J. R. Meteorol. Soc. 2015, 141, 1–15. [Google Scholar] [CrossRef]
- Schulzweida, U.; Kornblueh, L.; Quast, R. CDO User’s Guide Version 1.0.1; Max-Planck Institute for Meteorology: Munich, Germany, 2006. [Google Scholar]
- Ramirez Camargo, L.; Gruber, K.; Nitsch, F. Assessing variables of regional reanalysis data sets relevant for modelling small-scale renewable energy systems. Renew. Energy 2018, 133, 1468–1478. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Schachner Kleinwindkraft Windrad SW10 Produktbeschreibung. Available online: http://www.kleinwind.at/Windrad-SW10 (accessed on 9 May 2018).
- Bauer, L.; Matysik, S. Windkraftanlagen Datenbank. Available online: https://www.wind-turbine-models.com/turbines (accessed on 9 May 2018).
- Trigo, I.F.; Dacamara, C.C.; Viterbo, P.; Roujean, J.L.; Olesen, F.; Barroso, C.; Camacho-de-Coca, F.; Carrer, D.; Freitas, S.C.; García-Haro, J.; et al. The Satellite Application Facility for Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- The EUMETSAT Satellite Application Facility on Land Surface Analysis. Product User Manual Snow Cover (SC) 2016. Available online: https://landsaf.ipma.pt/GetDocument.do?id=659 (accessed on 12 March 2018).
- The EUMETSAT Satellite Application Facility on Land Surface Analysis. Algorithm Theoretical Basis Document (ATBD) Snow Cover (SC) 2016. Available online: https://landsaf.ipma.pt/GetDocument.do?id=657 (accessed on 12 March 2018).
- Siljamo, N.; Hyvärinen, O. New Geostationary Satellite–Based Snow-Cover Algorithm. J. Appl. Meteorol. Climatol. 2011, 50, 1275–1290. [Google Scholar] [CrossRef]
- Wirth, G.; Schroedter-Homscheidt, M.; Zehner, M.; Becker, G. Satellite-based snow identification and its impact on monitoring photovoltaic systems. Sol. Energy 2010, 84, 215–226. [Google Scholar] [CrossRef]
- Andrews, R.W.; Stein, J.S.; Hansen, C.; Riley, D. Introduction to the open source PV LIB for python Photovoltaic system modelling package. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 0170–0174. [Google Scholar]
- Mehleri, E.D.; Zervas, P.L.; Sarimveis, H.; Palyvos, J.A.; Markatos, N.C. Determination of the optimal tilt angle and orientation for solar photovoltaic arrays. Renew. Energy 2010, 35, 2468–2475. [Google Scholar] [CrossRef]
- University of West Bohemia; Technische Hochschule Deggendorf. Ostbayerische Technische Hochschule Regensburg Crossenergy: Cross-Border Energy Infrastructure—Future Perspectives for a Region in Change. Available online: http://crossenergy.eu (accessed on 22 January 2018).
- Dijkstra, L.; Poelman, H. A Harmonised Definition of Cities and Rural Areas: The New Degree of Urbanisation; European Commission: Brussels, Belgium, 2014; p. 28.
- World Energy Council. Energy Efficiency Indicators. Available online: https://wec-indicators.enerdata.net/household-electricity-use.html (accessed on 8 November 2018).
- Ramirez Camargo, L.; Nitsch, F. Maps of Germany and the Czech Republic with photovoltaic and battery system sizes for electricity self-sufficient single-family houses under 18 technical and weather dependent scenarios. Mendeley Data 2018, 1. [Google Scholar] [CrossRef]
- Ghaith, A.F.; Epplin, F.M.; Frazier, R.S. Economics of household wind turbine grid-tied systems for five wind resource levels and alternative grid pricing rates. Renew. Energy 2017, 109, 155–167. [Google Scholar] [CrossRef]
- Brooke, A.; Rosenthal, R.E. General Algebraic Modeling System; GAMS Development Corporation: Washington, DC, USA, 2003. [Google Scholar]
- Downey, A. Think Python; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2012. [Google Scholar]
- Eurostat Electricity Price Statistics—Statistics Explained. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics (accessed on 23 January 2019).
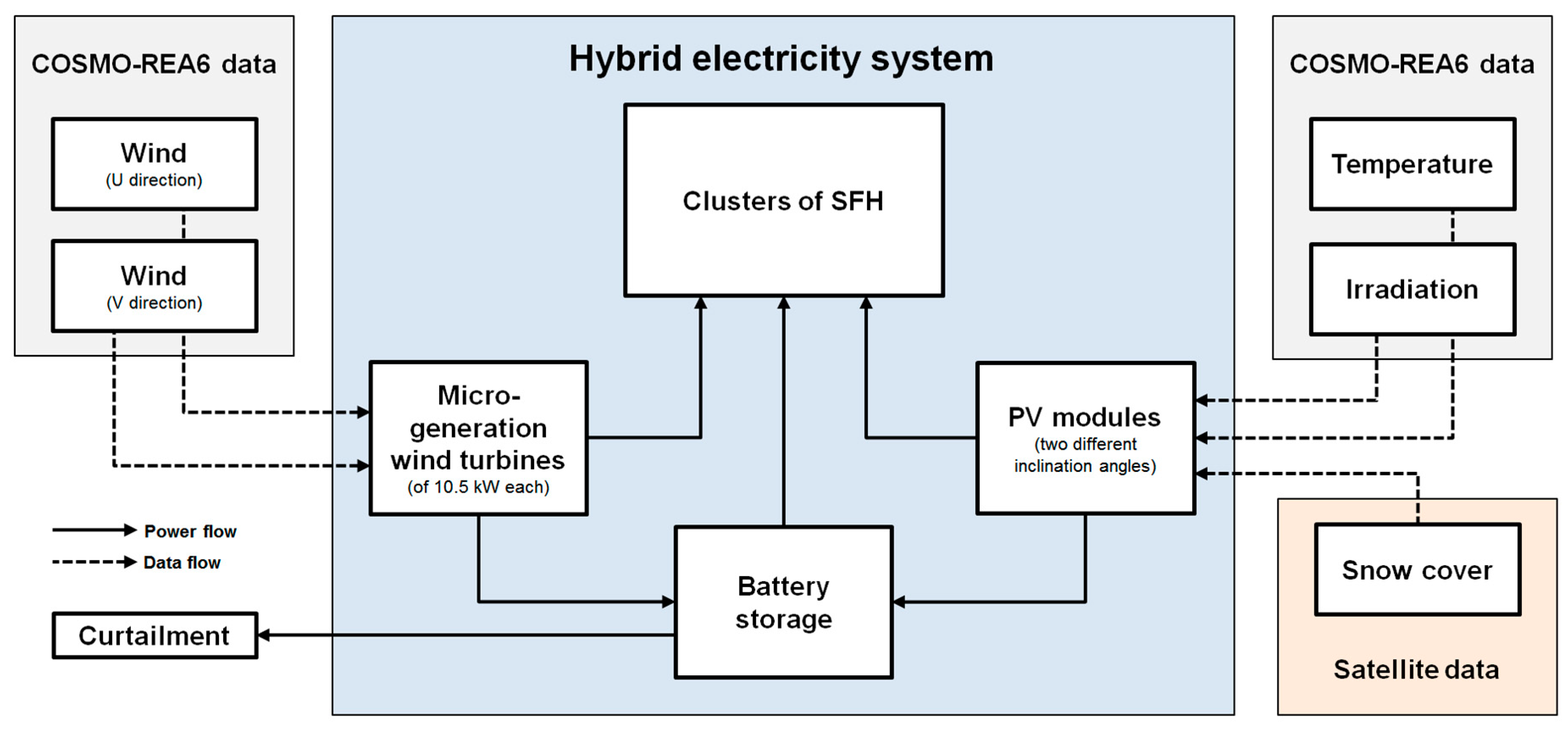

| Source | Type of Product (Variable Name) | Provider | Spatial Resolution | Temporal Resolution | Unit | Data Format |
|---|---|---|---|---|---|---|
| COSMO-REA6 | Downward diffuse short-wave radiation flux at surface (SWDIFDS_RAD) | DWD | 6 km × 6 km | 1 hour | W/m2 | GRIB |
| COSMO-REA6 | Downward direct short-wave radiation flux at surface (SWDIRS_RAD) | DWD | 6 km × 6 km | 1 hour | W/m2 | GRIB |
| COSMO-REA6 | Ambient temperature at two-meter height (T2M) | DWD | 6 km × 6 km | 1 hour | K | GRIB |
| COSMO-REA6 | Wind velocity at 10 m above ground, u direction (U_10M) | DWD | 6 km × 6 km | 1 hour | m/s | GRIB |
| COSMO-REA6 | Wind velocity at 10 m above ground, v direction (V_10M) | DWD | 6 km × 6 km | 1 hour | m/s | GRIB |
| Satellite images MSG | Snow Cover (SC) | LSA-SAF | 3 km × 3 km at nadir | 15 min | Classification in integer values from 0 to 5 | HDF5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramirez Camargo, L.; Nitsch, F.; Gruber, K.; Valdes, J.; Wuth, J.; Dorner, W. Potential Analysis of Hybrid Renewable Energy Systems for Self-Sufficient Residential Use in Germany and the Czech Republic. Energies 2019, 12, 4185. https://doi.org/10.3390/en12214185
Ramirez Camargo L, Nitsch F, Gruber K, Valdes J, Wuth J, Dorner W. Potential Analysis of Hybrid Renewable Energy Systems for Self-Sufficient Residential Use in Germany and the Czech Republic. Energies. 2019; 12(21):4185. https://doi.org/10.3390/en12214185
Chicago/Turabian StyleRamirez Camargo, Luis, Felix Nitsch, Katharina Gruber, Javier Valdes, Jane Wuth, and Wolfgang Dorner. 2019. "Potential Analysis of Hybrid Renewable Energy Systems for Self-Sufficient Residential Use in Germany and the Czech Republic" Energies 12, no. 21: 4185. https://doi.org/10.3390/en12214185
APA StyleRamirez Camargo, L., Nitsch, F., Gruber, K., Valdes, J., Wuth, J., & Dorner, W. (2019). Potential Analysis of Hybrid Renewable Energy Systems for Self-Sufficient Residential Use in Germany and the Czech Republic. Energies, 12(21), 4185. https://doi.org/10.3390/en12214185





