Model Predictive Control Tuning by Inverse Matching for a Wave Energy Converter
Abstract
:1. Introduction
2. Methods
2.1. Controller Matching Problem
2.2. An Analytical Solution When
3. Results: Application to a WEC
3.1. Numerical Simulations
- The system has no constraints.
- The system has a nearly hard constraint on its position.
- The system has a hard constraint on its control input and a soft constraint on its position.
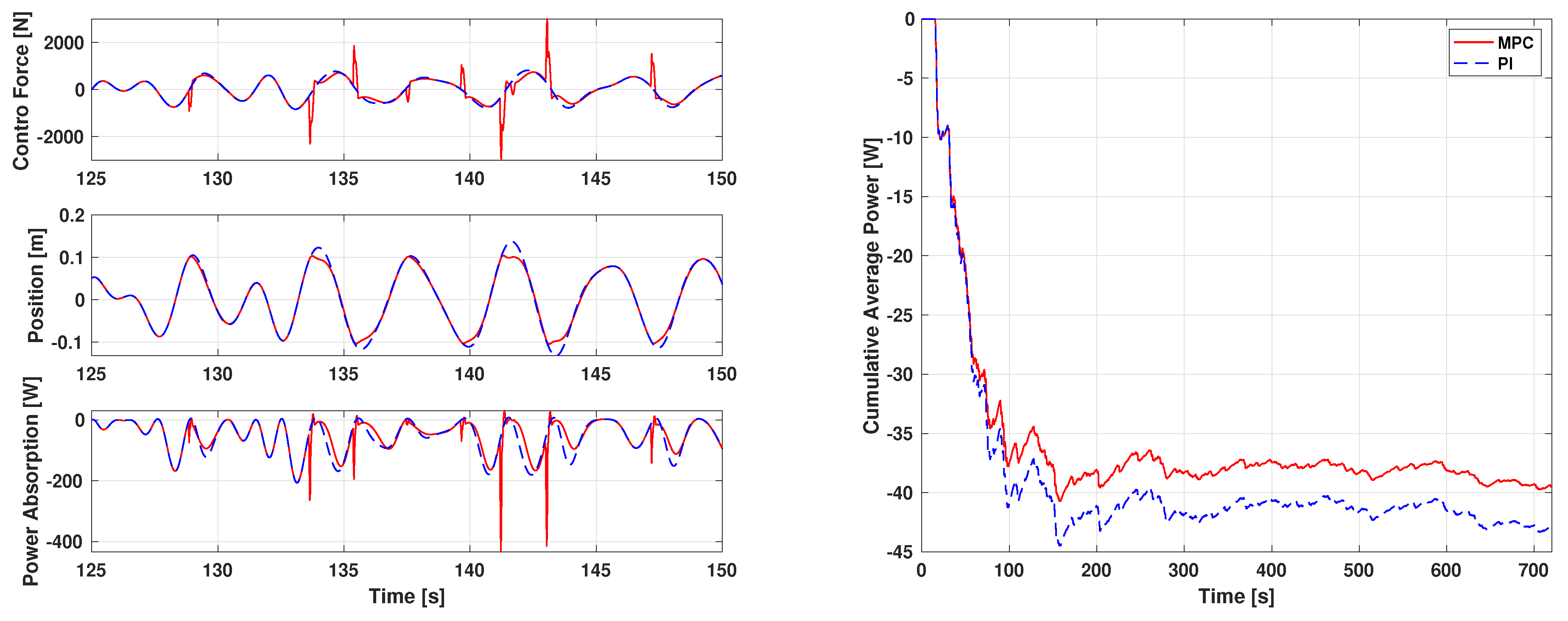
3.1.1. Scenario 1: System with No Constraint
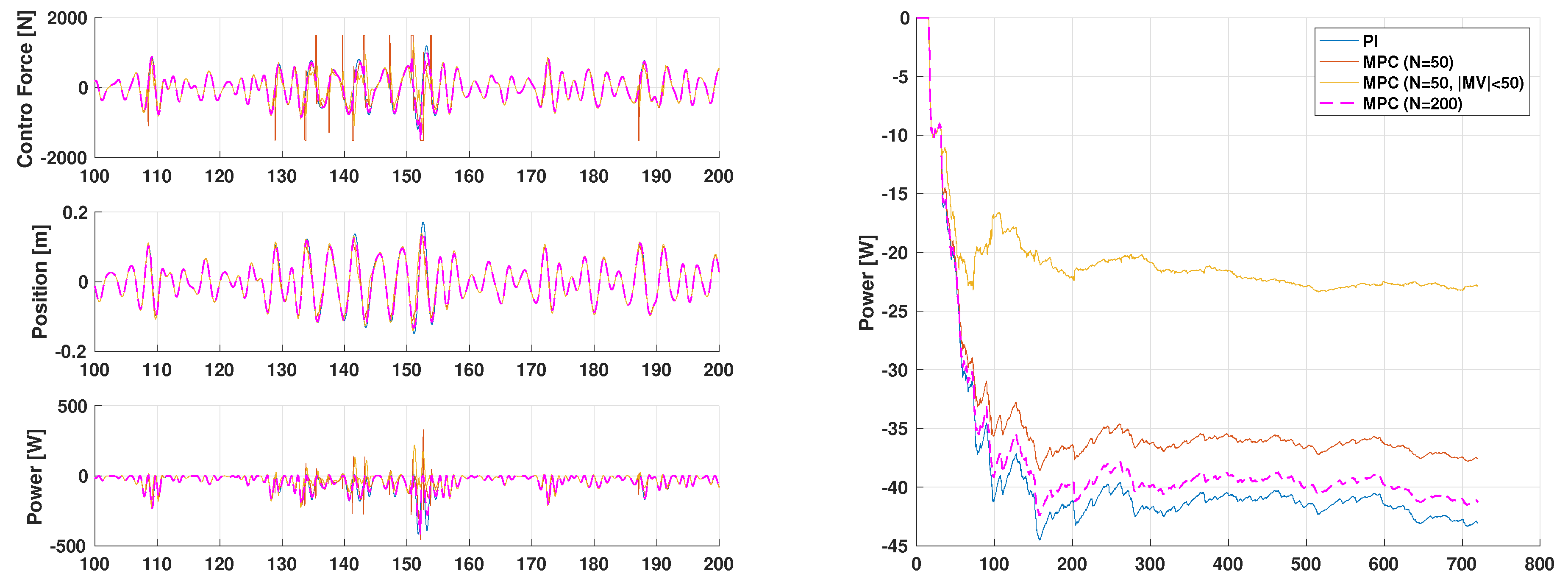
3.1.2. Scenario 2: System with Nearly Hard Constraint on the Position
3.1.3. Scenario 3: System with Hard Constraint on the Control Force and Soft Constraint on the Position
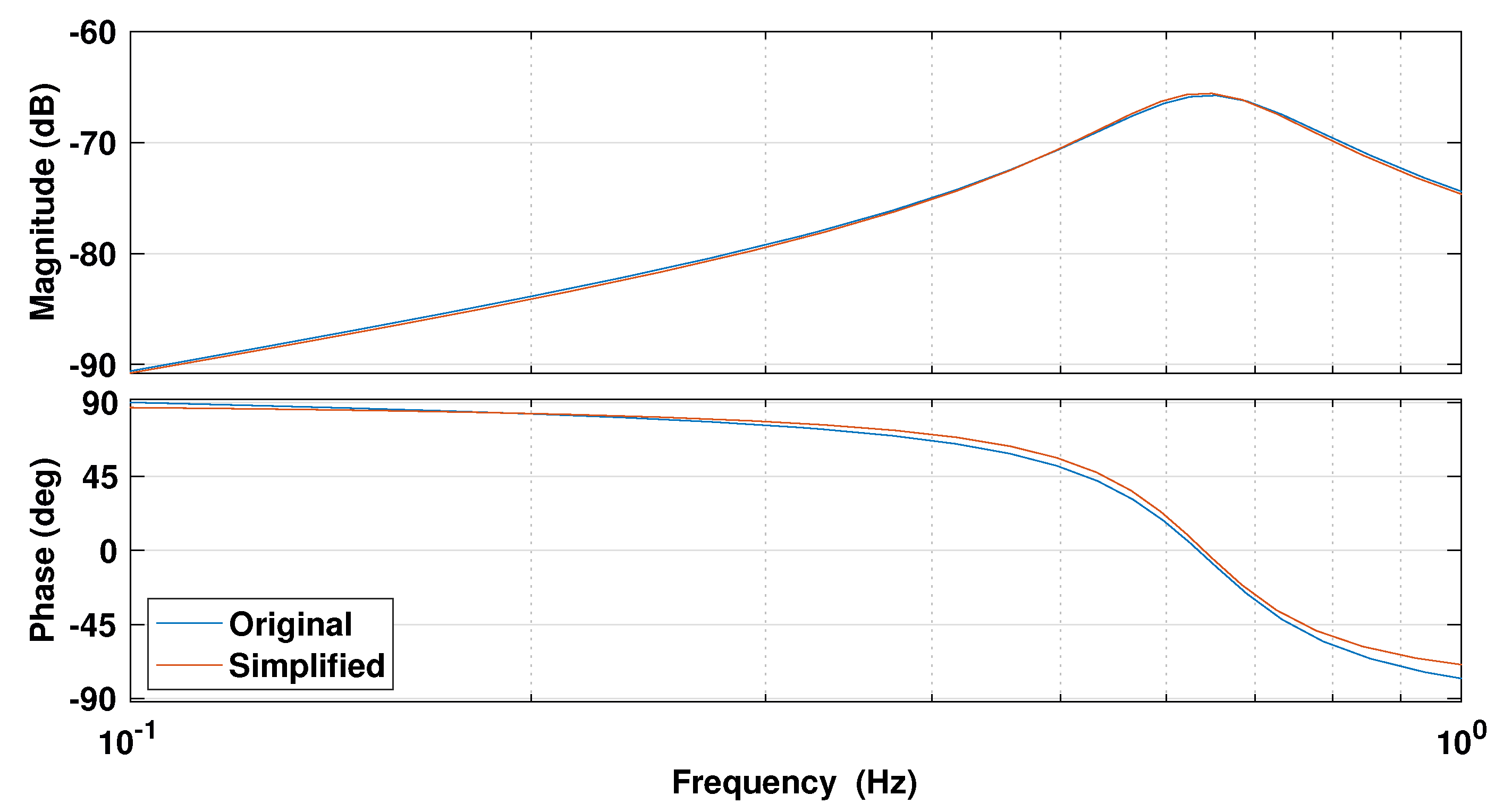
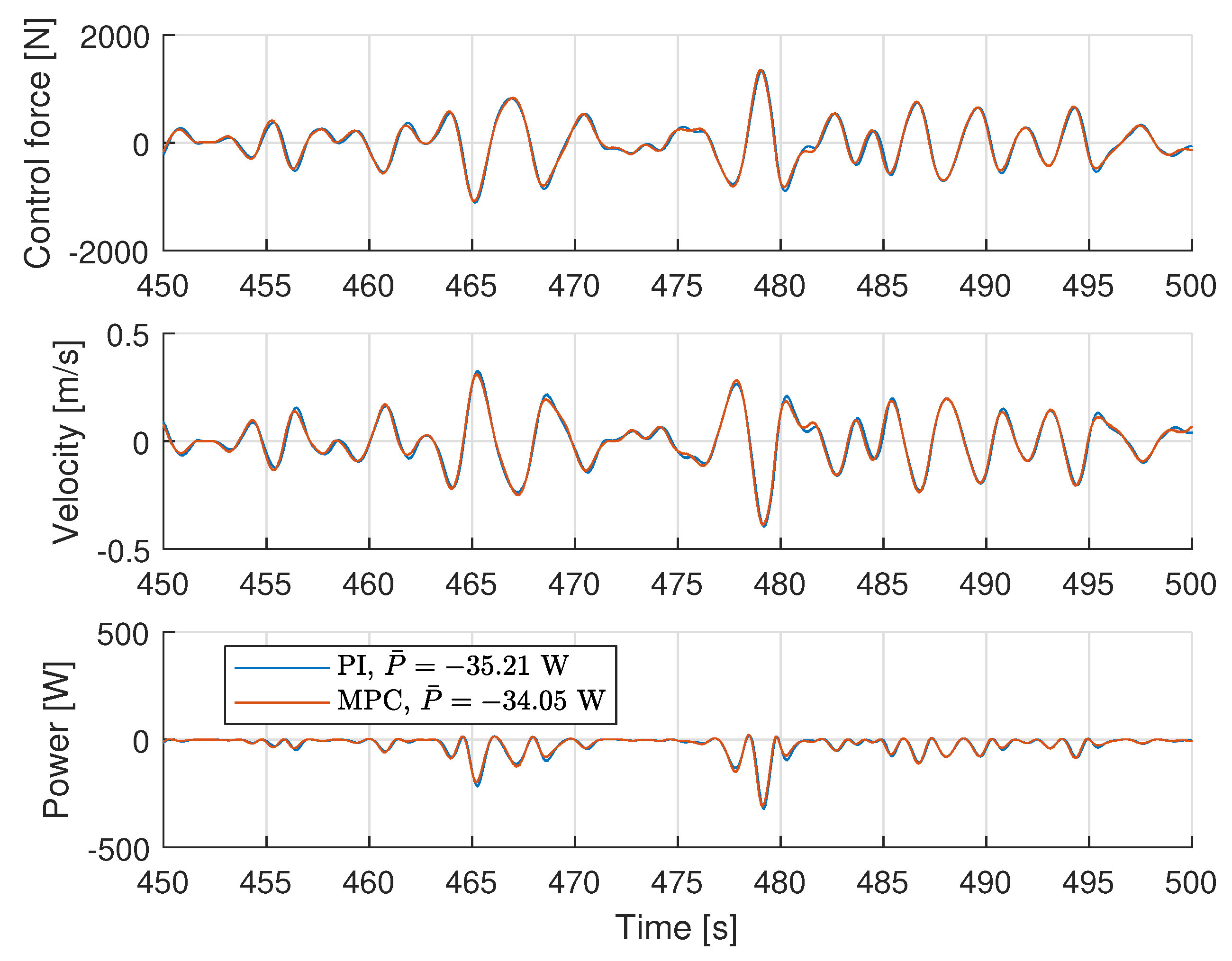
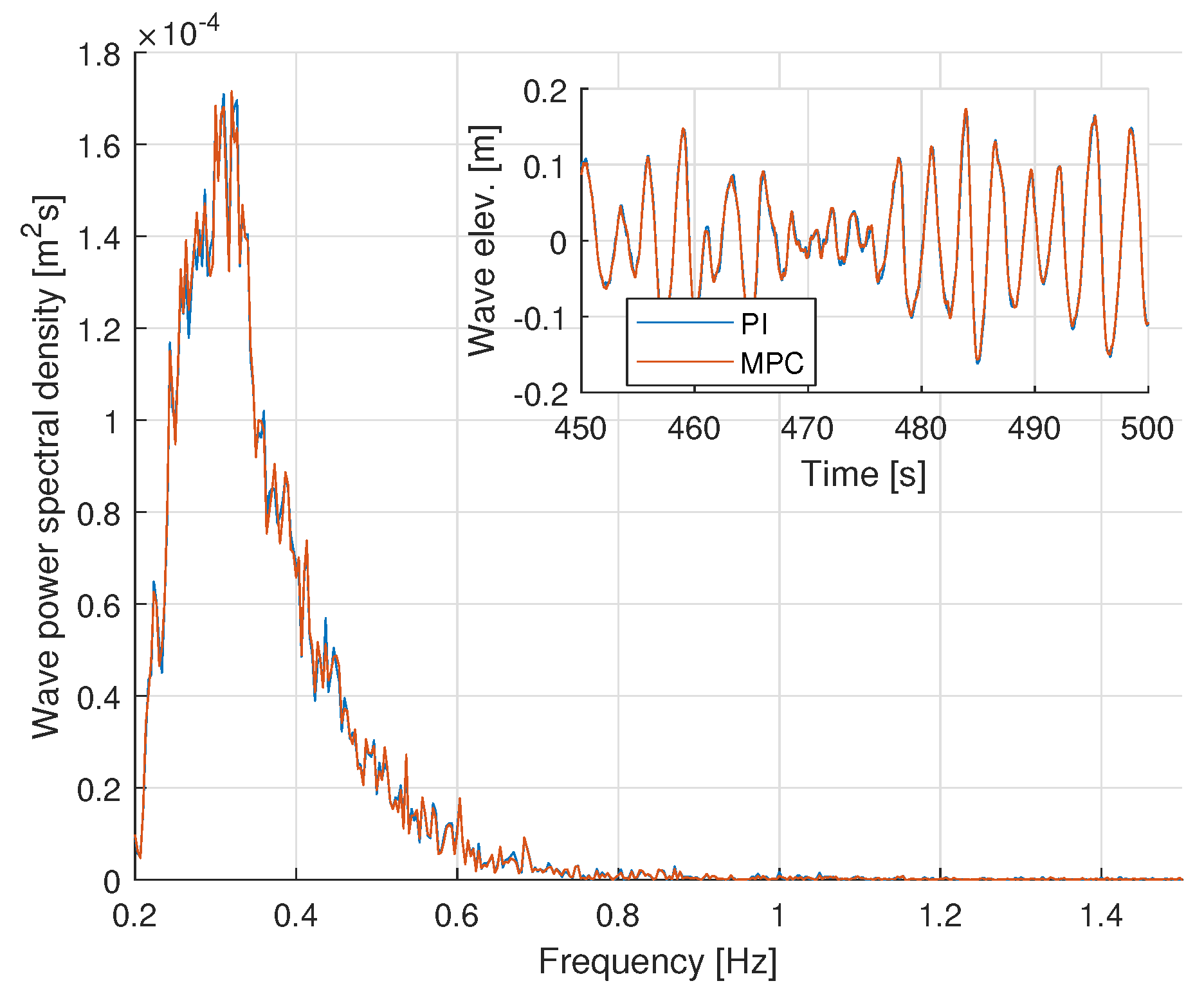
3.2. Experimental Tests
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Korde, U. Efficient primary energy conversion in irregular waves. Ocean Eng. 1999, 26, 625–651. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2002. [Google Scholar]
- Budal, K.; Falnes, J. Interacting point absorbers with controlled motion. In Power from Sea Waves; Count, B., Ed.; Academic Press London: Edinburgh, UK, 1979; pp. 381–399. [Google Scholar]
- Korde, U. Control system applications in wave energy conversion. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, 11–14 September 2000; pp. 1817–1824, Conference Proceedings (Cat. No.00CH37158); Volume 3. [Google Scholar] [CrossRef]
- Salter, S.; Taylor, J.; Caldwell, N. Power conversion mechanisms for wave energy. Proc. Inst. Mech. Eng. Part M J. Eng. Maritime Environ. 2002, 216, 1–27. [Google Scholar] [CrossRef]
- Scruggs, J.T.; Lattanzio, S.M.; Taflanidis, A.A.; Cassidy, I.L. Optimal causal control of a wave energy converter in a random sea. Appl. Ocean Res. 2013, 42, 1–15. [Google Scholar] [CrossRef]
- Li, G.; Weiss, G.; Mueller, M.; Townley, S.; Belmont, M.R. Wave energy converter control by wave prediction and dynamic programming. Renew. Energy 2012, 48, 392–403. [Google Scholar] [CrossRef] [Green Version]
- Bacelli, G.; Ringwood, J.; Gilloteaux, J.C. A control system for a self-reacting point absorber wave energy converter subject to constraints. IFAC Proc. Vol. 2011, 44, 11387–11392. [Google Scholar] [CrossRef] [Green Version]
- Schoen, M.; Hals, J.; Moan, T. Robust control of heaving wave energy devices in irregular waves. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 779–784. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Robinett, R.; Zou, S.; Bacelli, G.; Coe, R.; Bull, D.; Wilson, D.; Korde, U. On the control design of wave energy converters with wave prediction. J. Ocean Eng. Mar. Energy 2016, 2, 473–483. [Google Scholar] [CrossRef] [Green Version]
- Faedo, N.; Scarciotti, G.; Astolfi, A.; Ringwood, J.V. Energy-maximising control of wave energy converters using a moment-domain representation. Control Eng. Pract. 2018, 81, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Belmont, M.R. Model predictive control of a sea wave energy converter: a convex approach. IFAC Proc. Vol. 2014, 47, 11987–11992. [Google Scholar] [CrossRef] [Green Version]
- Maciejowski, J.M. Predictive Control with Constraints; Pearson: London, UK, 2002. [Google Scholar]
- Mayne, D.; Rawlings, J.; Rao, C.; Scokaert, P. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Maciejowski, J. Reverse-engineering existing controllers for MPC design. IFAC Proc. Vol. 2007, 40, 436–441. [Google Scholar] [CrossRef]
- Foo, M.; Weyer, E. On reproducing existing controllers as Model Predictive Controllers. In Proceedings of the 1st Australian Control Conference, Melbourne, VIC, Australia, 10–11 November 2011. [Google Scholar]
- Cairano, S.D.; Bemporad, A. Model Predictive Control Tuning by Controller Matching. IEEE Trans. Autom. Control 2010, 55, 185–190. [Google Scholar] [CrossRef]
- Kong, H.; Goodwin, G.; Seron, M.M. Predictive metamorphic control. Automatica 2013, 49, 3670–3676. [Google Scholar] [CrossRef]
- Cretel, J.A.M.; Lightbody, G.; Thomas, G.P.; Lewis, A.W. Maximisation of Energy Capture by a Wave-Energy Point Absorber using Model Predictive Control. IFAC Proc. Vol. 2011, 44, 3714–3721. [Google Scholar] [CrossRef] [Green Version]
- Bacelli, G.; Coe, R.G.; Patterson, D.; Wilson, D. System Identification of a Heaving Point Absorber: Design of Experiment and Device Modeling. Energies 2017, 10, 472. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Loftberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. Proceedings of 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar]
- Bemporad, A.; Morari, M.; Ricker, N. Model Predictive Control Toolbox: User’s Guide; MathWorks: Natick, MA, USA, 2017. [Google Scholar]
- Schmid, C.; Biegler, L.T. Quadratic programming methods for reduced hessian SQP. Comput. Chem. Eng. 1994, 18, 817–832. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive control in power electronics and drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Muller, C.; Quevedo, D.E.; Goodwin, G.C. How good is quantized model predictive control with horizon one? IEEE Trans. Autom. Control 2011, 56, 2623–2638. [Google Scholar] [CrossRef]
- Coe, R.G.; Bacelli, G.; Nevarez, V.; Cho, H.; Wilches-Bernal, F. A Comparative Study on Wave Prediction for WECs; Technical Report SAND2018-10945; Sandia National Laboratories: Albuquerque, NM, USA, 2018. [Google Scholar]
- Bacelli, G.; Ringwood, J.V. A geometric tool for the analysis of position and force constraints in wave energy converters. Ocean Eng. 2013, 65, 10–18. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Rigid-body mass (float & slider), M (kg) | 858 |
| Displaced volume, ∀ (m) | 0.858 |
| Float radius, r (m) | 0.88 |
| Float draft, T (m) | 0.53 |
| Water density, (kg/m) | 1000 |
| Water depth, h (m) | 6.1 |
| Linear hydrostatic stiffness, S (kN/m) | 23.9 |
| Infinite-frequency added mass, (kg) | 782 |
| Max vertical travel, (m) | 0.6 |
| Scenario | Constraint | ECR Values | N |
|---|---|---|---|
| 1 | No constraint | N/A | 2 |
| 2 | Nearly hard constraint on position | OV.minECR = OV.maxECR = | 50 |
| 3 | Hard constraint on control input Soft constraint on position | MV.minECR = MV.maxECR = 0 OV.minECR = OV.maxECR = 0.01 | 50 |
| Name | Prediction Steps | Slew Rate Limit | Power Absorbed [W] |
|---|---|---|---|
| PI | N/A | N/A | −42.7 |
| MPC () | 50 | (None) | −37.6 |
| MPC (, ) | 50 | −22.8 | |
| MPC () | 200 | (None) | −41.2 |
| Controller | Power Capture [W] | % Reduction |
|---|---|---|
| Unconstrained | −34.1 | 0 |
| N (75%) | −33.8 | 0.7 |
| N (50%) | −31.9 | 6.3 |
| N (25%) | −23.5 | 31.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.; Bacelli, G.; Coe, R.G. Model Predictive Control Tuning by Inverse Matching for a Wave Energy Converter. Energies 2019, 12, 4158. https://doi.org/10.3390/en12214158
Cho H, Bacelli G, Coe RG. Model Predictive Control Tuning by Inverse Matching for a Wave Energy Converter. Energies. 2019; 12(21):4158. https://doi.org/10.3390/en12214158
Chicago/Turabian StyleCho, Hancheol, Giorgio Bacelli, and Ryan G. Coe. 2019. "Model Predictive Control Tuning by Inverse Matching for a Wave Energy Converter" Energies 12, no. 21: 4158. https://doi.org/10.3390/en12214158
APA StyleCho, H., Bacelli, G., & Coe, R. G. (2019). Model Predictive Control Tuning by Inverse Matching for a Wave Energy Converter. Energies, 12(21), 4158. https://doi.org/10.3390/en12214158






