Simplified Model Predictive Current Control of Primary Permanent-Magnet Linear Motor Traction Systems for Subway Applications

Abstract

In this paper, a simplified model predictive current control (MPCC) is proposed for the primary permanent-magnet linear motor traction system in subway applications, which is fed by one two-level voltage-source-inverter (VSI). Based on the deadbeat concept, the reference voltage vector is calculated to eliminate the difference between the measured and reference currents in the next sampling period. Due to the discrete feature of the VSI, the reference voltage vector usually cannot be provided. Hence, the distance of a voltage vector is defined, and the voltage vector with the shortest distance is selected as the optimal one, which is called as the shortest distance principle in this paper. According to the shortest distance principle, the distribution of the reference voltage vector is divided into seven sectors, and the optimal voltage vector can be easily determined considering the location of the reference voltage vector. As a result, the computation cost is significantly reduced. However, the performances of MPCC are not affected by this simplification. The equivalence between the proposed and conventional MPCCs is proved in theory. All the theoretical analyses are verified by experimental results.

1. Introduction

Recently, the linear motor has attracted more attentions in subway applications due to the following advantages: (1) the direct production of thrust force; (2) smaller turning radius and less requirement of cross-sectional area of a tunnel; (3) better climbing ability and faster acceleration; and (4) less maintenance and lower noise [1,2,3,4,5]. Compared with the linear induction motor, which has been already employed in some subway projects [6,7], the permanent-magnet linear motor (PMLM) is always gone in actual subway applications in spite of its high efficiency and high power factor [8,9,10]. One important reason is the expensive construction cost since the permanent-magnets or armature windings must be equipped in the stator (rail) of the conventional PMLM. However, this problem can be solved by the primary PMLM (PPMLM) since both the permanent-magnets and armature windings can be mounted in the mover of PPMLM [11,12,13,14,15]. Generally, existing topologies of PPMLM can be divided into three main categories: double-salient type [11], flux-switching type [12,13,14], and flux reversal type [15].

Compared with PPMLM itself, the control has received less attention while it is important for the successful application of PPMLM in subway fields in the future. Due to a fast dynamic response and the simple structure, the direct thrust force control (DTFC) has attracted more attentions for PMLM [16]. In order to enhance the reliability, a fault-tolerant DTFC is proposed for the flux reversal PMLM with open-end windings [17]. To cope with current sensor failures, an improved DTFC scheme is proposed for PPMLM using only a single direct current (DC)-link current sensor [18]. Comparing with DTFC, the average switching frequency of model predictive control (MPC) can be significantly reduced while the MPC also inherits the advantages of the fast dynamic response and simple structure [19]. However, the MPC of PMLM has not received its deserved attention. That is why the MPC is investigated for PPMLM in this paper.

Finite control set MPC (FCS-MPC) is the original form of MPC, which takes full advantage of the discrete feature of voltage source inverter (VSI) [20,21]. Firstly, the values of control variables are predicted by each candidate voltage vector (VV) according to the discrete-time state-space model. Secondly, a cost function is designed by involving the errors between the reference and predictive values of control variables. Finally, the optimal VV is determined by minimizing the value of the cost function. According to the selected control variables, various FCS-MPCs have been proposed. In motor drives, model predictive torque/thrust control (MPTC) and model predictive current control (MPCC) are two main categories. In MPTC, stator flux and electromagnetic torque/thrust force are selected as the control variables [22]. However, these control variables usually cannot be measured directly, and they are often observed by mathematical methods. Besides, a weighting factor is usually required in cost function since the selected control variables have different units. In MPCC, direct- and quadrature-axis currents are selected as the control variables, which can be measured directly and no weighting factor is required [23].

As is known, high computation cost is the common challenge of FCS-MPC. For example, seven current predictions and same cost function calculations are required to determine the optimal VV for three-phase motor drives [24]. Furthermore, Nⁿ VVs will be evaluated for an N-level n-phase VSI. Obviously, the computation cost is significantly increased. The heavy computation cost will require longer calculation time, and then reduces the average switching frequency of the VSI, especially in multi-phase motor or multi-motor drives. Consequently, some methods have been proposed to reduce the computation cost of FCS-MPC. In [25], only the VVs with single switch state changed are considered for a five-leg dual-motor system. Compared with the conventional FCS-MPC, the amount of candidate VVs is reduced from 31 to 10. In [26], several predefined constraints are designed and the candidate VVs are reduced from 64 to 16 in the six-phase VSI supplied system. In the induction motor drive with asymmetrical dual three-phase winding, only 12 largest active VVs and zero VVs are considered [27]. However, the system performances using aforementioned simplified FCS-MPCs are usually affected since these modified solutions are not equivalent to the original ones. An equivalent simplified MPTC is proposed for PM motor drives, in which the deadbeat concept is involved and the candidate VVs are reduced from 7 to 4 [28].

However, to the best of authors’ knowledge, there is no literature to present an equivalent simplified MPCC for not only rotary permanent-magnet synchronous motor (PMSM) drives but also PMLM drives. The main contribution of this paper is to propose an equivalent MPCC for the PPMLM traction systems in subway applications, in which a shortest distance principle is designed and the cost function is eliminated. As a result, the computation cost can be further reduced comparing with the modified MPTC in [28] while the performances of PPMLM traction systems are not affected. It should be emphasized that the proposed MPCC is novel for not only PMLM drives but also rotary PMSM drives, and the PPMLM traction system is just taken as an example to present the proposed MPCC in this paper. This paper contains six sections. The studied PPMLM traction system is described in Section 2. The two MPCCs are introduced in Section 3. Equivalence analysis of two MPCCs is conducted in Section 4. The theoretical analysis is verified by experiment results in Section 5. Finally, some conclusions are drawn in Section 6.

2. Studied PPMLM Traction System

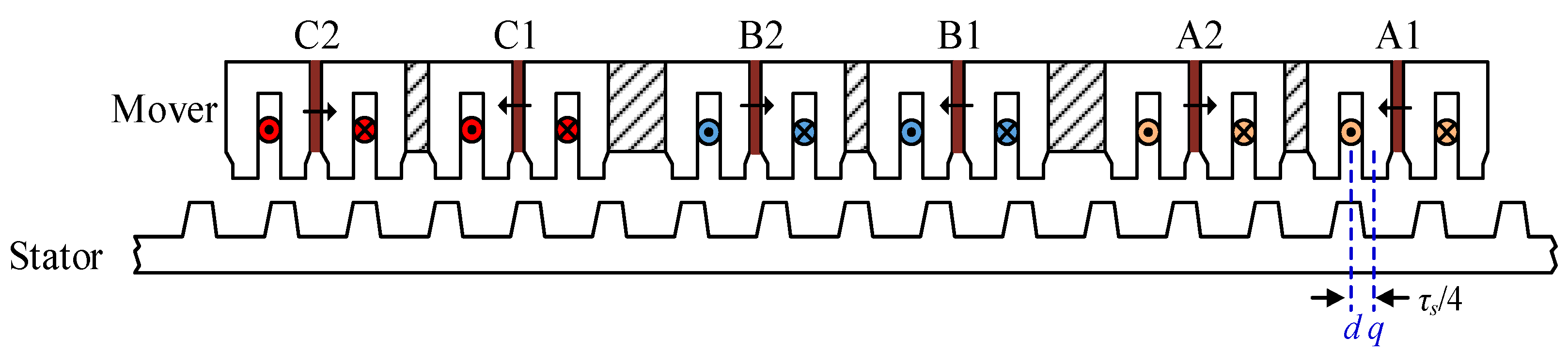
The studied PPMLM is composed of a primary mover and secondary stator as illustrated in Figure 1. Both the permanent-magnets and armature windings are equipped in movers. As is shown in Figure 1, the middle of stator teeth is defined as the d-axis with the maximum PM flux linkage. Meanwhile, the primary position is defined as the q-axis where PM flux linkage is minimum (zero). τ_s is the stator pole pitch, and the distance between two axes is τ_s/4. When the positive permanent-magnet flux linkage in phase-A winding is maximum, the corresponding primary position θ_e is defined as zero.

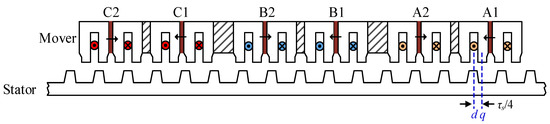
Figure 1. Structure of the studied primary permanent-magnet linear motor (PPMLM).

According to the previous definition, the voltage equation of the studied PPMLM in dq coordinate system is expressed as:

$$\{\begin{array}{l}{u}_d=R_s{i}_d+\frac{d{\psi }_d}{dt}-\frac{2\pi v_m}{{\tau }_s}{\psi }_q\\ u_q=R_s{i}_q+\frac{d{\psi }_q}{dt}+\frac{2\pi v_m}{{\tau }_s}{\psi }_d\end{array},$$

(1)

with

$$\{\begin{array}{l}{\psi }_d={\psi }_{PM}+L_s{i}_d\\ {\psi }_q=L_s{i}_q\end{array},$$

(2)

where R_s and L_s are the mover resistance and inductance; ψ_PM is the permanent-magnet flux linkage; u_d, u_q and i_d, i_q are the synchronous voltage and current components, respectively; ψ_d and ψ_q are the synchronous flux linkage components; and v_m is the mover speed.

The thrust force F_e can be deduced as:

$$F_e=\frac{3\pi {\psi }_{PM}{i}_q}{{\tau }_s}.$$

(3)

The motion equation is designed as:

$$F_e-F_l=m_t\frac{d{v}_m}{dt}+B{v}_m,$$

(4)

where F_l is the load force; m_t is the weight of PPMLM; B is the friction coefficient.

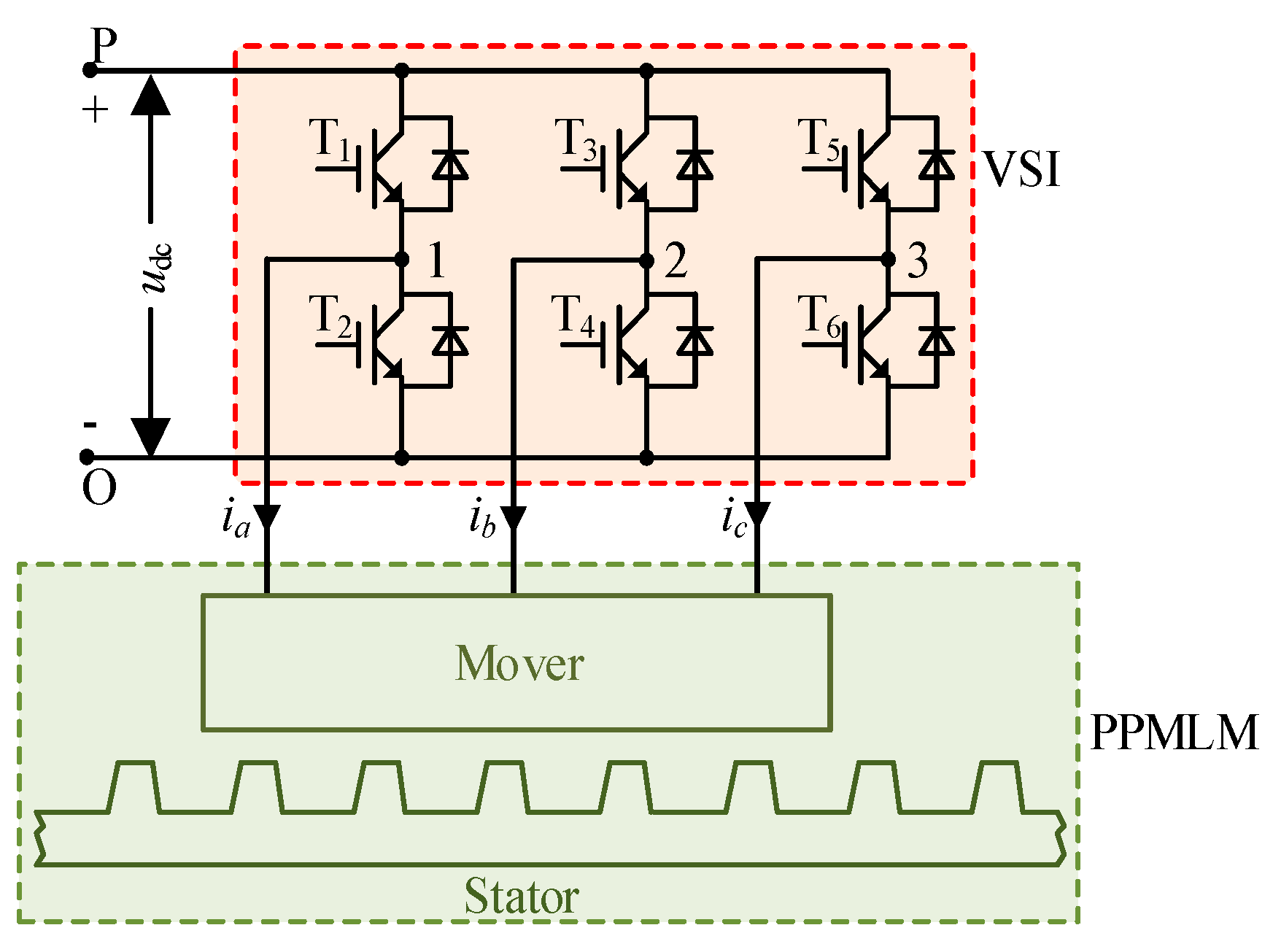
The studied PPMLM is fed by a two-level VSI, which is illustrated in Figure 2. The VSI consists of six power switches. The switch state s_x of x^th leg is defined as:

$$s_x=\{\begin{array}{l}1\mathrm{if}{x}^{\mathrm{th}}\mathrm{leg}\mathrm{upper}\mathrm{switch}\mathrm{is}\mathrm{ON}\\ 0\mathrm{else}\end{array}(x=a,b,c).$$

(5)

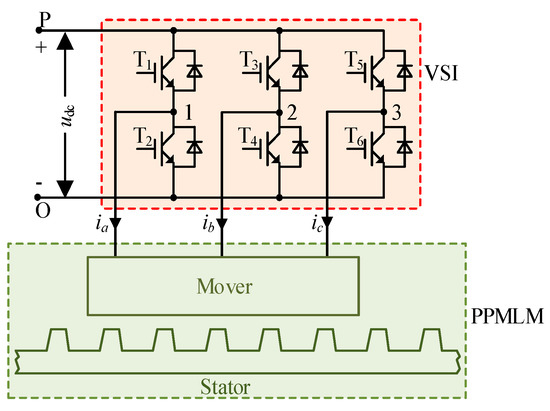
Figure 2. Studied PPMLM traction system.

The VV of the VSI is defined as [s_a s_b s_c]. All candidate VVs of VSI are presented in Table 1.

Table 1. Voltage vectors (VVs) of voltage source inverter (VSI).

VV	U0	U1	U2	U3	U4	U5	U6	U7
sa sb sc	000	100	110	010	011	001	101	111

3. Two MPCCs for PPMLM

To clarify the description, the conventional and proposed MPCCs were defined as MPCC-I and MPCC-II in this paper, respectively. To simplify the analysis, two assumptions were given as follows: (1) the variation of mover speed v_m could be neglected in one sampling period T_s; (2) the phase inductance L_s, the phase resistance R_s, and the peak value of PM flux linkage ψ_PM are considered unchanged during the entire operation.

3.1. MPCC-I

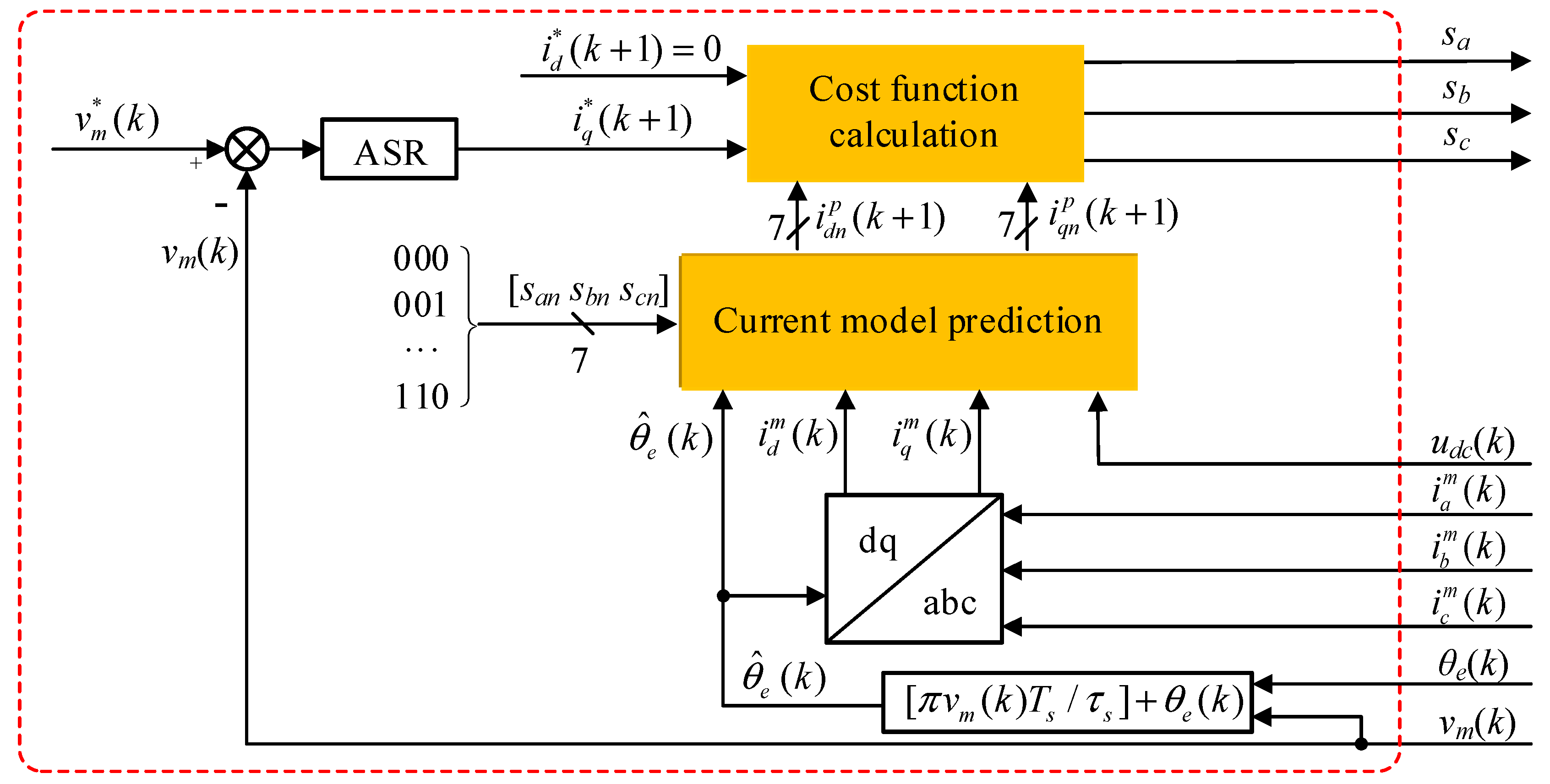
MPCC-I for the PPMLM traction system is shown in Figure 3, which contains two main modules: current model prediction and cost function calculation. In this paper, the average primary position ${\hat{\theta }}_e$ was used in the model prediction, which is determined by ${\hat{\theta }}_e=(\pi v_m{T}_s/{\tau }_s)+{\theta }_e$. The primary position θ_e can be detected by the linear encoder.

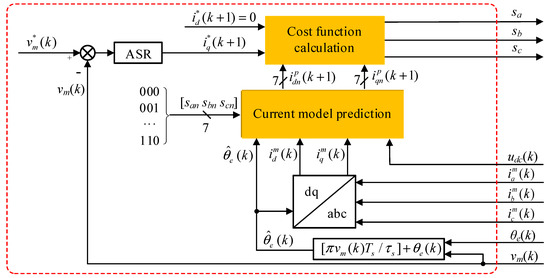
Figure 3. Model predictive current control (MPCC)-I for the PPMLM traction system.

(1) Current model prediction:

In MPCC-I, synchronous currents of PPMLM are selected as control variables to calculate their predictive values. Substituting (2) into (1) gives:

$$\{\begin{array}{l}{u}_d=R_s{i}_d+L_s\frac{d{i}_d}{dt}-\frac{2\pi v_m}{{\tau }_s}{L}_s{i}_q\\ u_q=R_s{i}_q+L_s\frac{d{i}_q}{dt}+\frac{2\pi v_m}{{\tau }_s}{L}_s{i}_d+\frac{2\pi v_m}{{\tau }_s}{\psi }_{PM}\end{array}.$$

(6)

According to the discrete time state-space model and Euler’s prediction formula, the current differential can be simplified as:

$$\frac{di\left(k\right)}{dt}\approx \frac{i^p(k+1)-i^m\left(k\right)}{T_s}.$$

(7)

In this paper, the superscripts p and m indicate predictive and measured quantities; the symbol k indicates the kth sampling period.

Substituting (7) into (6) gives the predictive currents:

$$\{\begin{array}{l}{i}_{dn}^p(k+1)=K_1{i}_d^m\left(k\right)+K_2{i}_q^m\left(k\right)+G{u}_{dn}\left(k\right)\\ i_{qn}^p(k+1)=-K_2{i}_d^m\left(k\right)+K_1{i}_q^m\left(k\right)+G{u}_{qn}\left(k\right)-I_{PM}\end{array}n=0\dots 7,$$

(8)

with

$$\{\begin{array}{l}{K}_1=1-\frac{R_s{T}_s}{L_s},K_2=\frac{2\pi v_m}{{\tau }_s}{T}_s\\ G=\frac{T_s}{L_s},I_{PM}=\frac{2\pi v_m{T}_s}{{\tau }_s{L}_s}{\psi }_{PM}\end{array},$$

(9)

$${[u_{dn}\left(k\right)u_{qn}\left(k\right)]}^T={\mathbf{T}}_{\mathit{3}s/\mathit{2}r}{u}_{dc}{[s_{an}{s}_{bn}{s}_{an}]}^T,$$

(10)

where $i_{dn}^p(k+1)$ and $i_{qn}^p(k+1)$ are the predictive synchronous currents by using the VV U_n, respectively. T_3s/2r is the transformation matrix from abc coordinate system to d-q coordinate system; u_dc is the dc bus voltage; u_dn and u_qn are the synchronous components of the VV U_n, respectively. The measured synchronous currents $i_d^m\left(k\right)$ and $i_q^m\left(k\right)$ can be calculated from the measured phase currents ($i_a^m$,$i_b^m$,$i_c^m$) and the primary position θ_e(k).

(2) Cost function calculation:

According to (8), the cost function of MPCC-I is designed as:

$$J_n={\left[i_d^{*}\right(k+1)-i_{dn}^p(k+1\left)\right]}^2+{\left[i_q^{*}\right(k+1)-i_{qn}^p(k+1\left)\right]}^2,n=0\dots 7,$$

(11)

where $i_q^{*}(k+1)$ is the reference q-axis current. According to the difference between the reference speed $v_m^{*}(k)$ and the actual value $v_m(k)$, $i_q^{*}(k+1)$ can be obtained from the automatic speed regulator (ASR). $i_d^{*}(k+1)$ is the reference d-axis current, which is set as 0. The optimal VV U_op is selected to minimize J_n:

$$J_{op}=\underset{0\le n\le 7}{\min }{J}_n.$$

(12)

3.2. MPCC-II

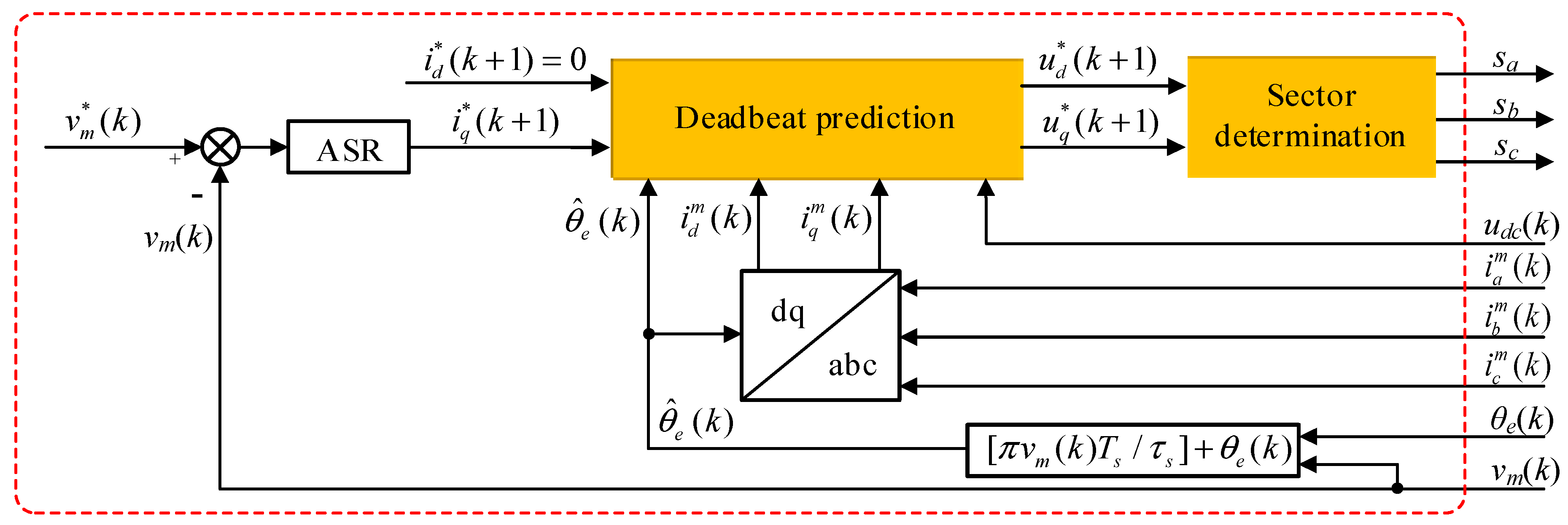
MPCC-II for the PPMLM traction system is shown in Figure 4, which contains two main modules: deadbeat prediction and sector determination.

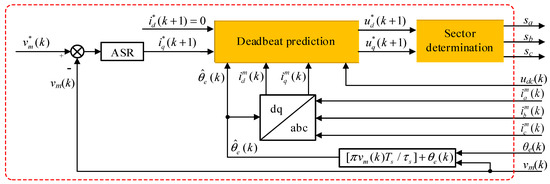
Figure 4. MPCC-II for the PPMLM traction system.

(1) Deadbeat prediction:

It is assumed in this module that the reference currents $i_d^{*}(k+1)$ and $i_q^{*}(k+1)$ can be achieved in next sampling period. In other words, the predictive synchronous currents $i_d^p(k+1)$ and $i_q^p(k+1)$ should be equal to $i_d^{*}(k+1)$ and $i_q^{*}(k+1)$, respectively. Substituting these equivalent relationships into (8) gives the reference synchronous voltages $u_d^{*}(k+1)$ and $u_q^{*}(k+1)$:

$$\left[\begin{array}{l}{u}_d^{*}(k)\\ u_q^{*}(k)\end{array}\right]={\mathit{M}}^{-1}(\left[\begin{array}{l}{i}_d^{*}(k+1)\\ i_q^{*}(k+1)\end{array}\right]-\mathit{P}\left[\begin{array}{l}{i}_d^m(k)\\ i_q^m(k)\end{array}\right]+\mathit{Q}),$$

(13)

with

$$\mathit{P}=\left[\begin{array}{r}\begin{array}{cc}{K}_1& K_2\end{array}\\ \begin{array}{cc}-K_2& K_1\end{array}\end{array}\right]\mathit{M}=\left[\begin{array}{r}\begin{array}{cc}G& 0\end{array}\\ \begin{array}{cc}0& G\end{array}\end{array}\right]\mathit{Q}=\left[\begin{array}{c}0\\ I_{PM}\end{array}\right].$$

(14)

However, the reference synchronous voltages $u_d^{*}(k+1)$ and $u_q^{*}(k+1)$ usually cannot be achieved since the candidate VVs of VSI are discrete as listed in Table 1.

(2) Sector determination:

To simplify the analysis, the distance of the VV U_n is defined as L_n:

$$L_n=\sqrt{{(u_d^{*}-u_{dn})}^2+{(u_q^{*}-u_{qn})}^2},n=0,1\dots 7.$$

(15)

According to (13) and (15), the selection of the optimal VV U_op becomes to find the VV with the shortest distance, which was defined as the shortest distance principle in this paper. According to (10), seven Park transformations from abc coordinate system to dq coordinate system (u_dn, u_qn) must be implemented to determine the optimal VV. To reduce the computation burden of coordinate transformation, dq components are expressed by αβ components:

$$\left[\begin{array}{c}{u}_d^{*}\\ u_q^{*}\end{array}\right]=\left[\begin{array}{cc}\cos {\hat{\theta }}_e& \sin {\hat{\theta }}_e\\ -\sin {\hat{\theta }}_e& \cos {\hat{\theta }}_e\end{array}\right]\left[\begin{array}{c}{u}_{\alpha }^{*}\\ u_{\beta }^{*}\end{array}\right],$$

(16)

$$\left[\begin{array}{c}{u}_{dn}\\ u_{qn}\end{array}\right]=\left[\begin{array}{cc}\cos {\hat{\theta }}_e& \sin {\hat{\theta }}_e\\ -\sin {\hat{\theta }}_e& \cos {\hat{\theta }}_e\end{array}\right]\left[\begin{array}{c}{u}_{\alpha n}\\ u_{\beta n}\end{array}\right],n=0,1\dots 7.$$

(17)

Substituting (16) and (17) into (15) gives:

$$L_n=\sqrt{{(u_{\alpha }^{*}-u_{\alpha n}^{})}^2+{(u_{\beta }^{*}-u_{\beta n}^{})}^2},n=0,1\dots 7,$$

(18)

where u_αn and u_βn are the α- and β-axis components of the VV U_n, respectively. The values of u_αn and u_βn are discrete, and they are listed in Table 2. According to (18), only one inverse Park transformation is implemented from dq coordinate system ($u_d^{*}$, $u_q^{*}$) to αβ coordinate system ($u_{\alpha }^{*}$, $u_{\beta }^{*}$):

$$\left[\begin{array}{l}{u}_{\alpha }^{*}\\ u_{\beta }^{*}\end{array}\right]=\left[\begin{array}{rr}\hfill \cos {\widehat{\theta }}_e& \hfill -\sin {\widehat{\theta }}_e\\ \hfill \sin {\widehat{\theta }}_e& \hfill \cos {\widehat{\theta }}_e\end{array}\right]\left[\begin{array}{l}{u}_d^{*}\\ u_q^{*}\end{array}\right].$$

(19)

Table 2. VVs in α-β coordinate system.

VV	sa sb sc	[uα, uβ]
U0	0 0 0	0
U1	1 0 0	[2/3udc, 0]
U2	1 1 0	[1/3udc, $\sqrt{3}$udc/3]
U3	0 1 0	[−1/3udc, $\sqrt{3}$udc/3]
U4	0 1 1	[−2/3udc, 0]
U5	0 0 1	[−1/3udc, −$\sqrt{3}$udc/3]
U6	1 0 1	[1/3udc, −$\sqrt{3}$udc/3]
U7	1 1 1	0

Comparing (18) with (15), the computation burden of (18) is significantly reduced. Comparing with the MPTC [28], the prediction amount has reduced from 4 to 1 by using MPCC-II, and the computation burden can be further reduced.

According to (18), a new cost function is developed as:

$${\lambda }_n=[{(u_{\alpha }^{*}-u_{\alpha n}^{})}^2+{(u_{\beta }^{*}-u_{\beta n}^{})}^2],n=0,1\dots 7.$$

(20)

The optimal VV U_op is selected to minimize λ_n:

$${\lambda }_{op}=\underset{0\le n\le 7}{\min }{\lambda }_n.$$

(21)

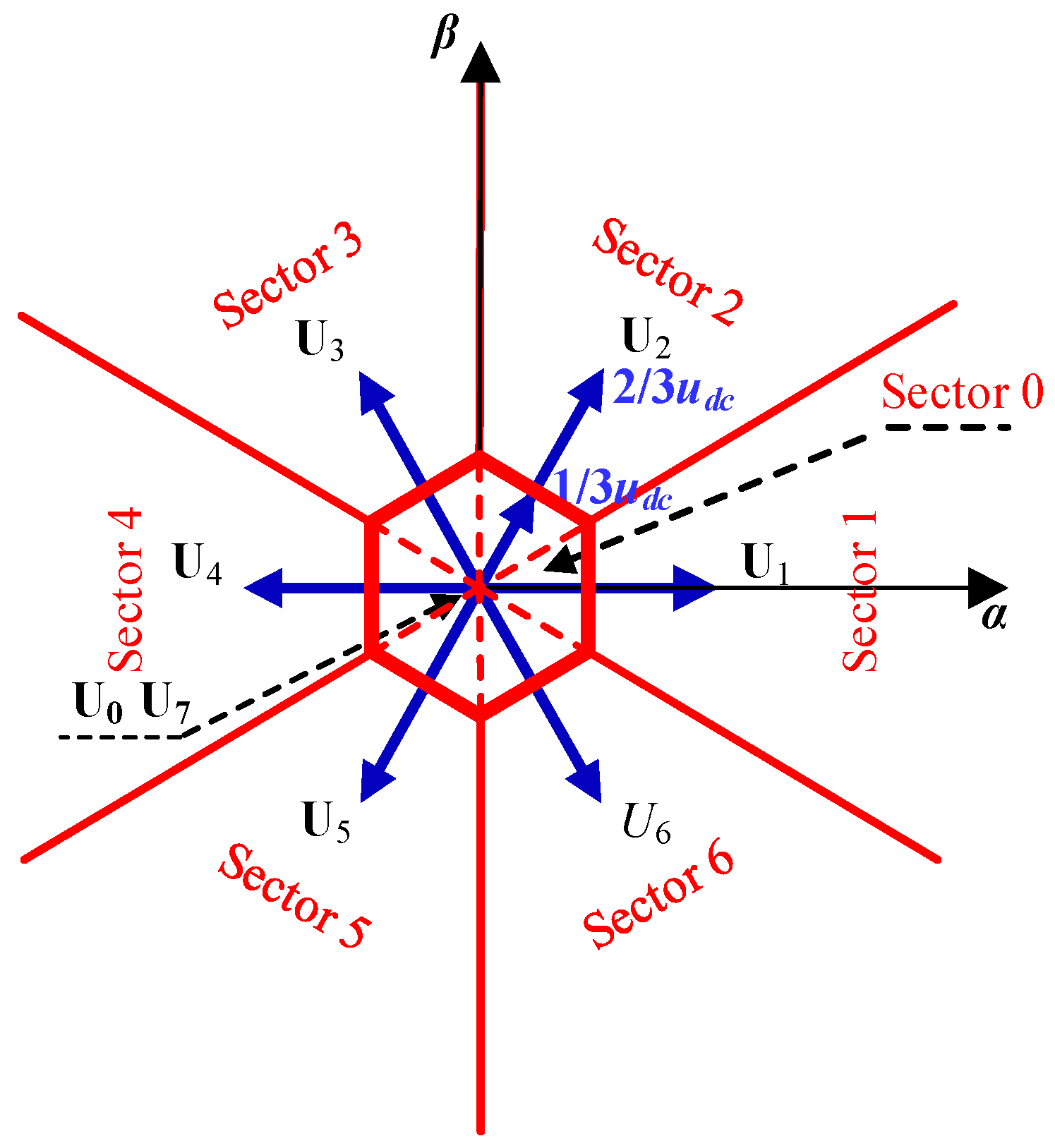
Based on the shortest distance principle, the distribution of the reference voltage vector U* was divided into seven sectors (Sector 0–6), as illustration in Figure 5. U_n was chosen as the optimal VV when the reference voltage vector U* was located in Sector n. Especially, the central hexagon with radial length u_dc/3 is Sector 0, and one zero VV was chosen by minimum switching actions principle. To reduce the computation burden, a fast determination method of the optimal VV was designed for MPCC-II.

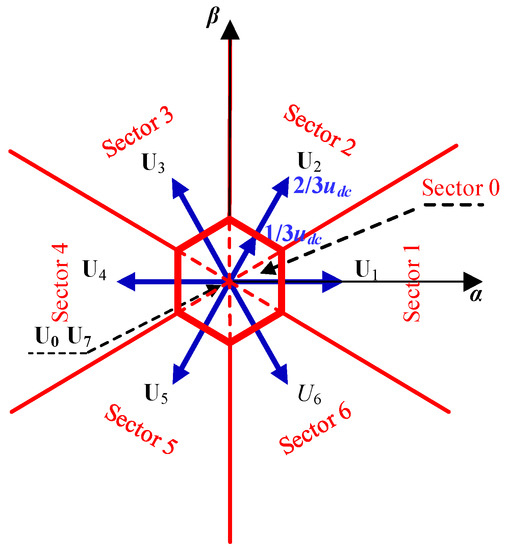
Figure 5. Distribution of the reference voltage vector.

Firstly, the phase angle φ and the magnitude U* of the reference voltage vector $[u_{\alpha }^{*}{u}_{\beta }^{*}]$ are determined as:

$$\{\begin{array}{l}{U}^{*}=\sqrt{{\left(u_{\alpha }^{*}\right)}^2+(u_{\beta }^{*}{)}^2}\\ \phi =\arctan (u_{\alpha }^{*}/u_{\beta }^{*}),\phi \in [0,2\pi )\end{array}.$$

(22)

Secondly, the direction code M of the reference voltage vector $[u_{\alpha }^{*}{u}_{\beta }^{*}]$ is determined according to the value of φ:

$$M=\{\begin{array}{l}1,0\le \phi <\pi /6and11\pi /6\le \phi <2\pi \\ 2,\pi /6\le \phi <\pi /2\\ 3,\pi /2\le \phi <5\pi /6\\ 4,5\pi /6\le \phi <7\pi /6\\ 5,7\pi /6\le \phi <3\pi /2\\ 6,3\pi /2\le \phi <11\pi /6\end{array}.$$

(23)

Thirdly, the relationship between the reference voltage vector $[u_{\alpha }^{*}{u}_{\beta }^{*}]$ and the central hexagon as shown in Figure 5 is determined by:

$$H=\{\begin{array}{l}0,U^{*}\cos (\phi -\frac{M-1}{3}\pi )\le \frac{u_{dc}}{3}\\ 1,U^{*}\cos (\phi -\frac{M-1}{3}\pi )\text{>}\frac{u_{dc}}{3}\end{array}.$$

(24)

According to (24), the reference voltage vector $[u_{\alpha }^{*}{u}_{\beta }^{*}]$ locates in the central hexagon if H = 0; otherwise, the reference voltage vector $[u_{\alpha }^{*}{u}_{\beta }^{*}]$ locates outside of the central hexagon.

Finally, the optimal VV U_op is determined as:

$${\mathit{U}}_{op}=\{\begin{array}{l}{\mathit{U}}_0,H=0\\ {\mathit{U}}_M,H=1\end{array}.$$

(25)

4. Equivalence Analysis

The difference between two MPCCs is how to determine the optimal VV. For MPCC-I, the optimal VV is determined by the cost function (11), which can minimize the value of (11). As is listed in Table 1, there are eight VVs. If two zero VVs are considered as same, the number of candidate VVs can be reduced to 7. Therefore, seven different current groups [$i_{dn}^p(k+1)$, $i_{qn}^p(k+1)$] can be predicted, and the cost function (11) will be calculated seven times. In some degree, MPCC-I is similarly like classical PWM. On the other hand, the reference synchronous voltages $u_d^{*}(k+1)$ and $u_q^{*}(k+1)$ are calculated by (13), and then the optimal VV can be determined by the location of the reference synchronous voltages in Figure 5. In fact, MPCC-II has referred to the SVM theory. However, both MPCCs can select the same optimal VV, and the equivalence of two MPCCs was analyzed in this section.

(8) is rewritten as:

$$\left[\begin{array}{l}{u}_{dn}(k)\\ u_{qn}(k)\end{array}\right]={\mathit{M}}^{-1}(\left[\begin{array}{l}{i}_{dn}^p(k+1)\\ i_{qn}^p(k+1)\end{array}\right]-\mathit{P}\left[\begin{array}{l}{i}_d^m(k)\\ i_q^m(k)\end{array}\right]+\mathit{Q}).$$

(26)

Comparing (13) with (26), the voltage error can be calculated by:

$$\left[\begin{array}{l}{u}_d{}^{*}-u_{dn}(k)\\ u_q{}^{*}-u_{qn}(k)\end{array}\right]={\mathit{M}}^{-1}\left[\begin{array}{l}{i}_d{}^{*}(k+1)-i_{dn}^p(k+1)\\ i_q{}^{*}(k+1)-i_{qn}^p(k+1)\end{array}\right].$$

(27)

Consequently, the initial form (11) can be simplified as:

$$J_n=G^2\{{[u_d^{*}-u_{dn}(k)]}^2+{[u_q^{*}-u_{qn}(k)]}^2\},n=0,1\dots 7.$$

(28)

According to (15) and (18), (28) can be rewritten as:

$$J_n=G^2\{{[u_{\alpha }^{*}-u_{\alpha n}(k)]}^2+{[u_{\beta }^{*}-u_{\beta n}(k)]}^2\},n=0,1\dots 7.$$

(29)

According to (20) and (29), two cost function formulas can be expressed as:

$$J_n=G^2{\lambda }_n,n=0,1\dots 7.$$

(30)

According to (30), MPCC-I and MPCC-II will select the same optimal VV. Hence, both MPCCs are equivalent.

5. Experimental Validation

To verify the effectiveness of the proposed MPCC, the hardware should be able to measure the dc bus voltage, two phase currents and the primary position. There was no special requirement for the software. According to the hardware/software requirements, a test bench was designed as illustrated in Figure 6, and the parameters of the studied PPMLM are listed in Table 3. A dSPACE DS1103 controller was adopted to execute the control algorithm. DC bus voltage was measured by a voltage sensor (LEM LV25-P, LEM, Geneva, Switzerland). Phase currents are sensed by two current sensors (LEM LA55-P/SP50, LEM, Geneva, Switzerland). The primary position was detected by the linear encoder. The VSI was manufactured by Infineon, and its switch states were determined by the dSPACE DS1103 controller. The sampling frequency was 20 kHz. To compare the two MPCCs, several experiments were carried out.

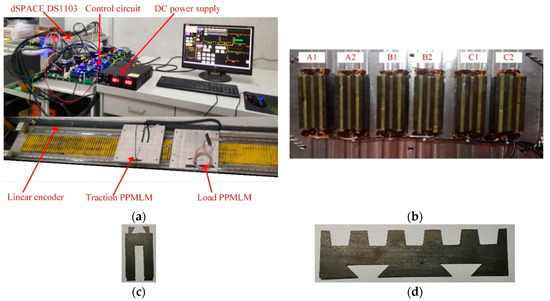
Figure 6. Test bench: (a) Entire view, (b) bottom view of mover, (c) stator teeth, and (d) stator teeth.

Table 3. Parameters of PPMLM.

Parameter	Value
Mover width, wm (mm)	160
Mover pole pitch, τm (mm)	26
Stator pole pitch, τs (mm)	24
Mover tooth width, wmt (mm)	τm/4
Mover slot mouth width wmsm (mm)	τm/4
Mover slot width wms (mm)	τm/4
Slot width (Under PM), wms (mm)	τm/4
Mover height, hm (mm)	35
Mover yoke height, hmy (mm)	10
Magnet height, hpm (mm)	0.9 × hm
Magnet width, wpm (mm)	5
Air gap length, g (mm)	2
Stator tooth width, wst (mm)	1.6 × τm/4
Stator teeth yoke width, wsty (mm)	2 × τm/4
Stator tooth height, hst (mm)	10
Stator yoke height, hsy (mm)	13
Stator height, hs (mm)	23
Coil spacing, λ1 (mm)	(2 + 1/2) × τs
Phase spacing, λ2 (mm)	(5 + 1/3) × τs
Number of turns per coil, Ncoil	114
Phase resistance (Ω), Rs	3
Stack factor	0.95
Rate current Irms (A)	3
Rated speed (m/s)	1.2
Maximum load (N)	150

5.1. Steady-State Experiment

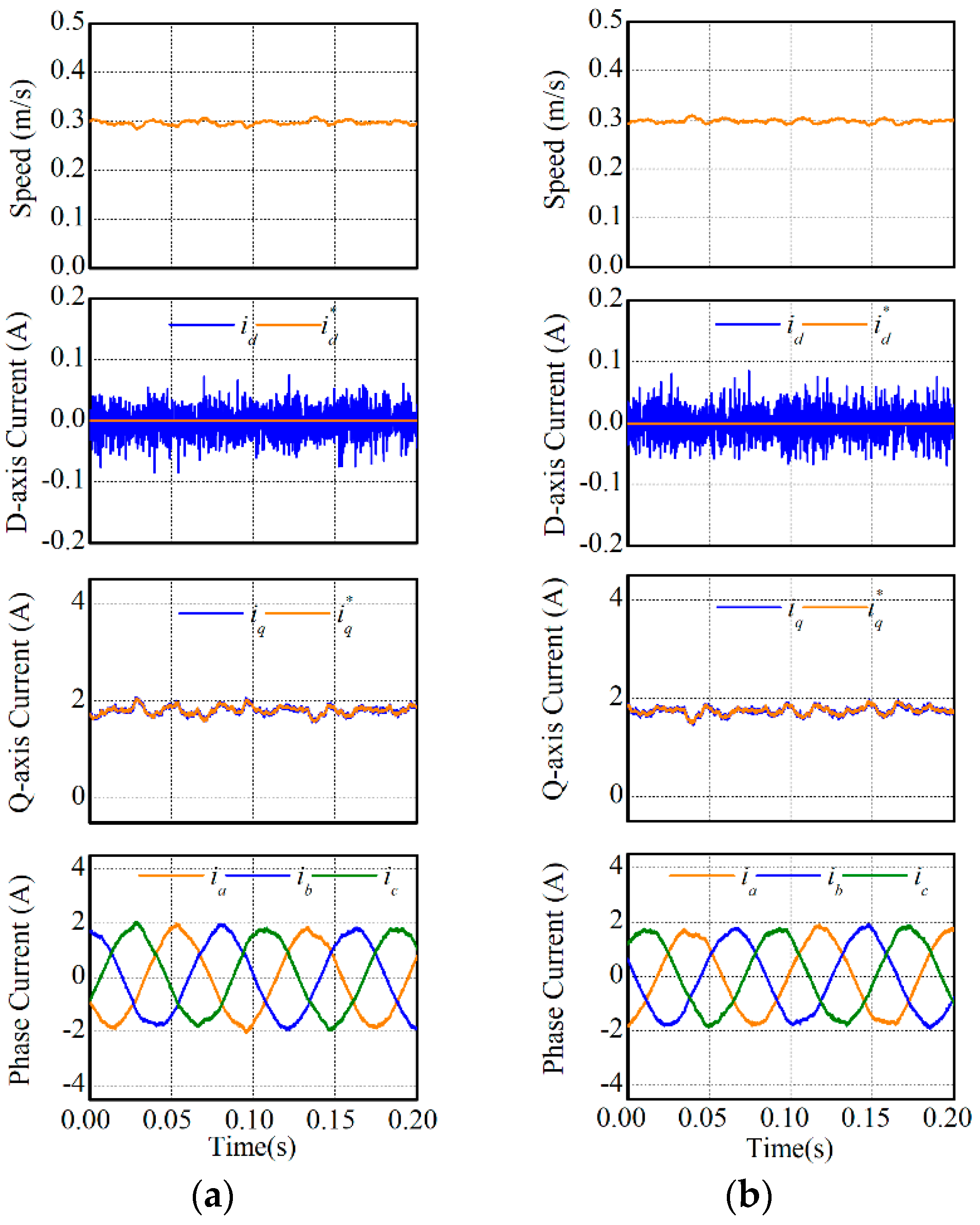
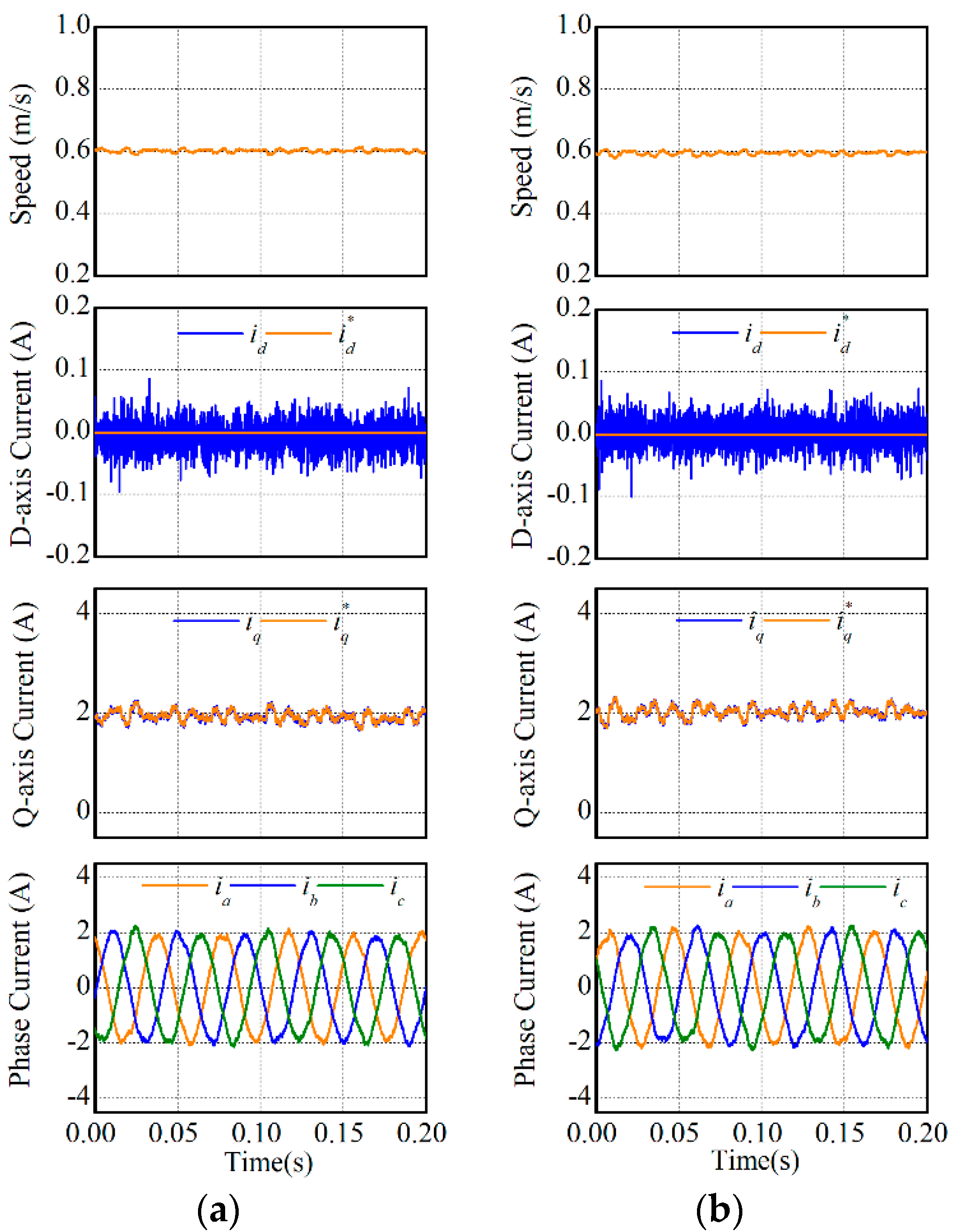
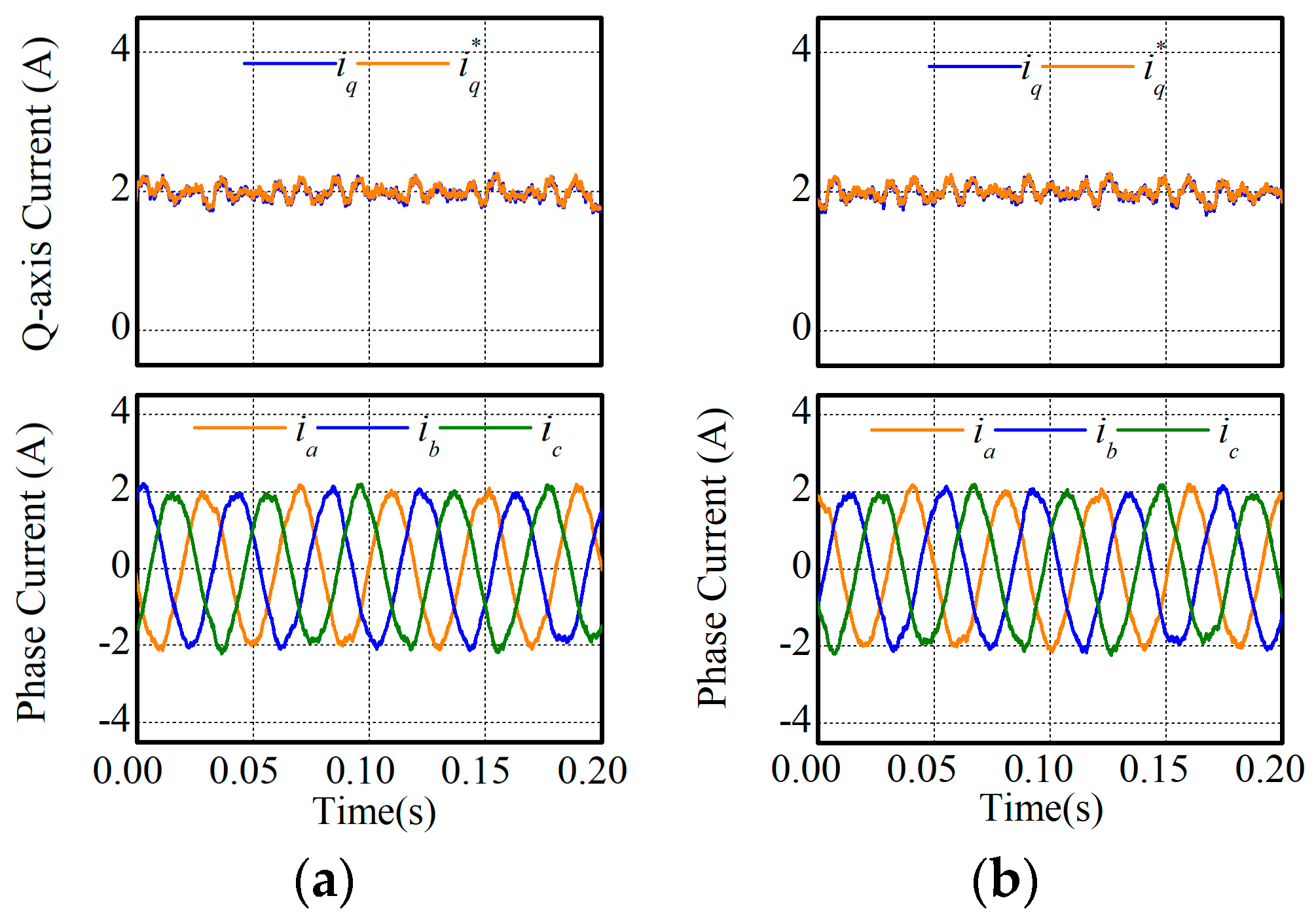
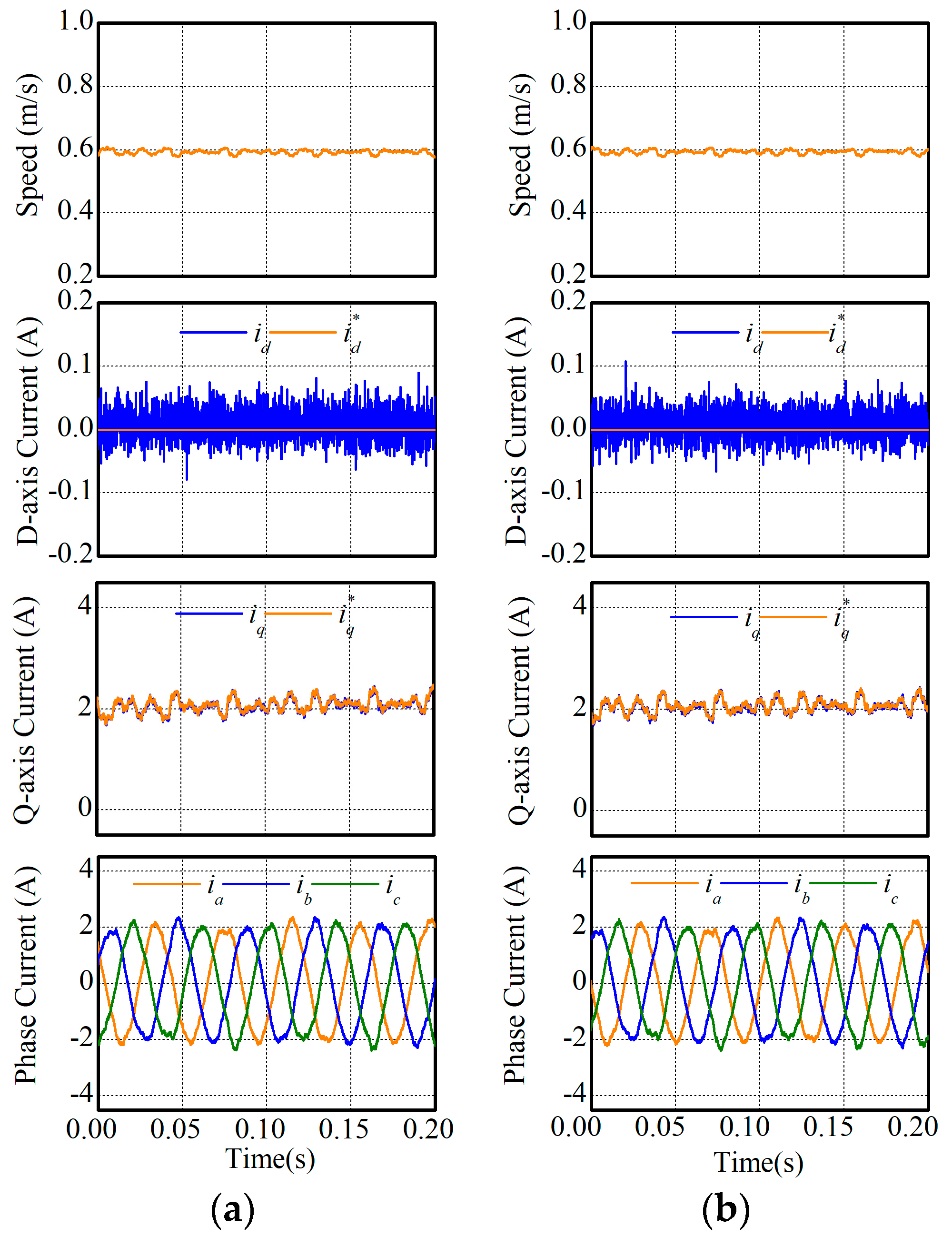
In this experiment, the steady-state performances of two MPCCs were compared. The reference speed was respectively set as 0.3 m/s and 0.6 m/s, and experimental results are respectively illustrated in Figure 7 and Figure 8. According to the experimental results, speed, synchronous currents, and phase currents were compared in Table 4. It can be found in Table 4 that MPCC-I and MPCC-II had nearly the same performance regarding speed, synchronous currents, and phase currents.

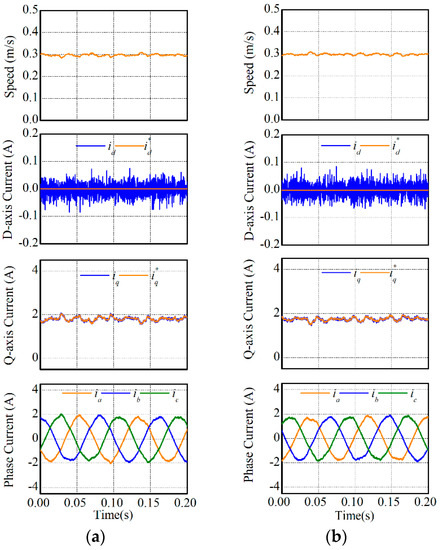
Figure 7. Steady-state performances under 0.3 m/s: (a) MPCC-I and (b) MPCC-II.

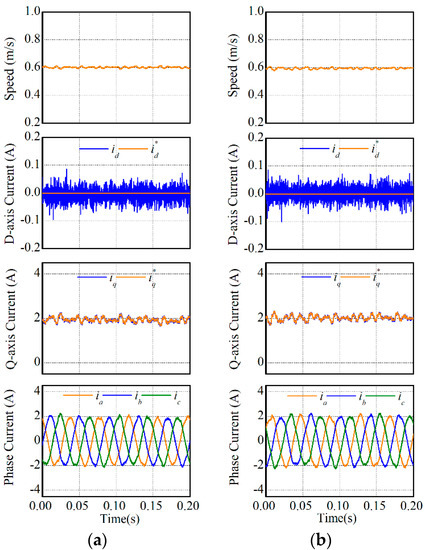
Figure 8. Steady-state performances under 0.6 m/s: (a) MPCC-I and (b) MPCC-II.

Table 4. Comparison of steady-state performances.

Operation Condition		Standard Deviation			THD of Phase Currents
Ref. Speed	MPCC	Speed (m/s)	id (A)	iq (A)
0.3 m/s	MPCC-I	0.00367	0.0219	0.0789	4.09%
	MPCC-II	0.00369	0.0223	0.0783	4.07%
0.6 m/s	MPCC-I	0.00528	0.0225	0.106	4.22%
	MPCC-II	0.00534	0.0229	0.108	4.24%

In the steady-state operation, the implement times of MPCC-I and MPCC-II in one sampling period were 12 μs and 9 μs, respectively. Hence, the computation burden could be reduced by 25% if MPCC-II was employed.

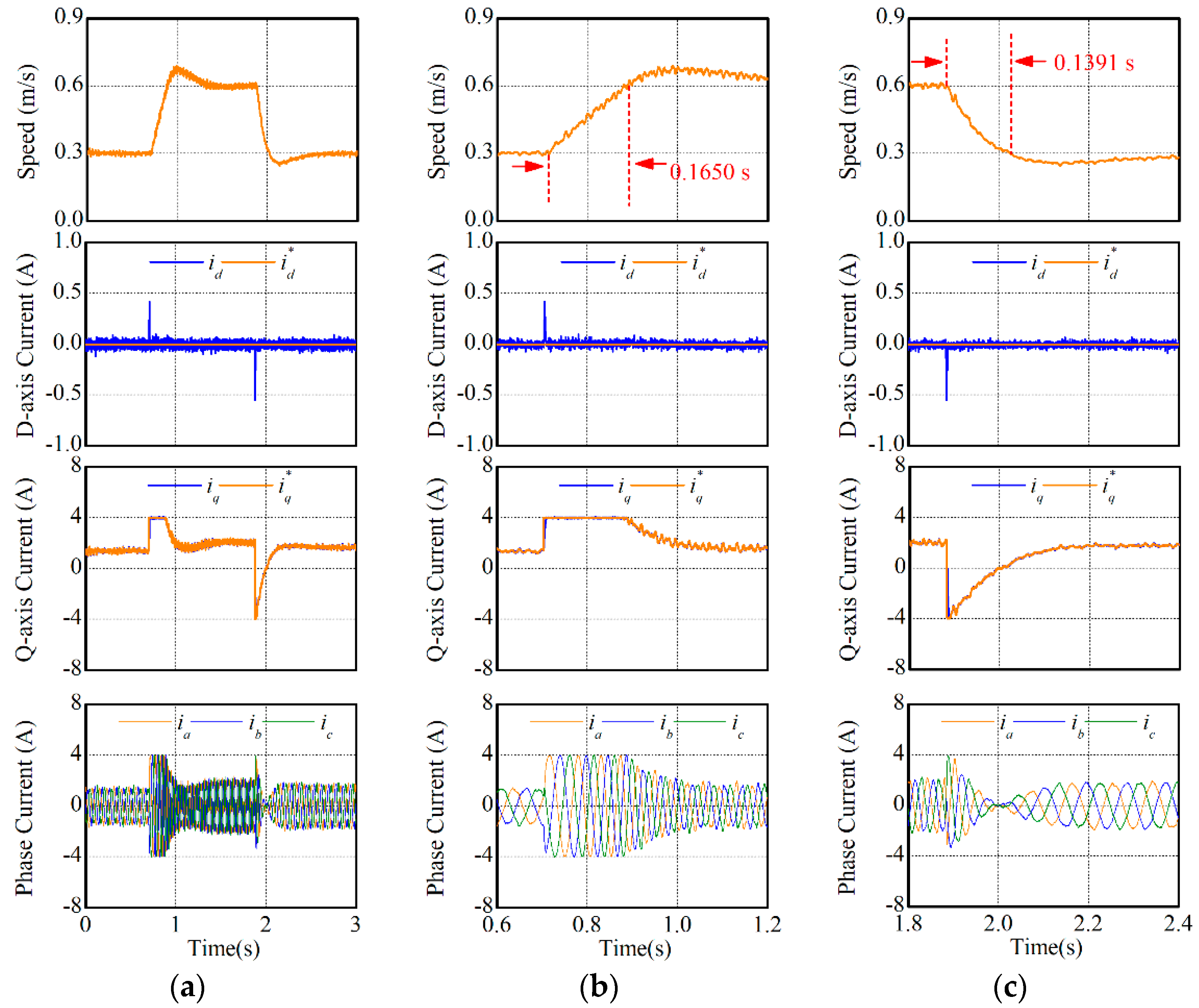
5.2. Speed Response Experiment

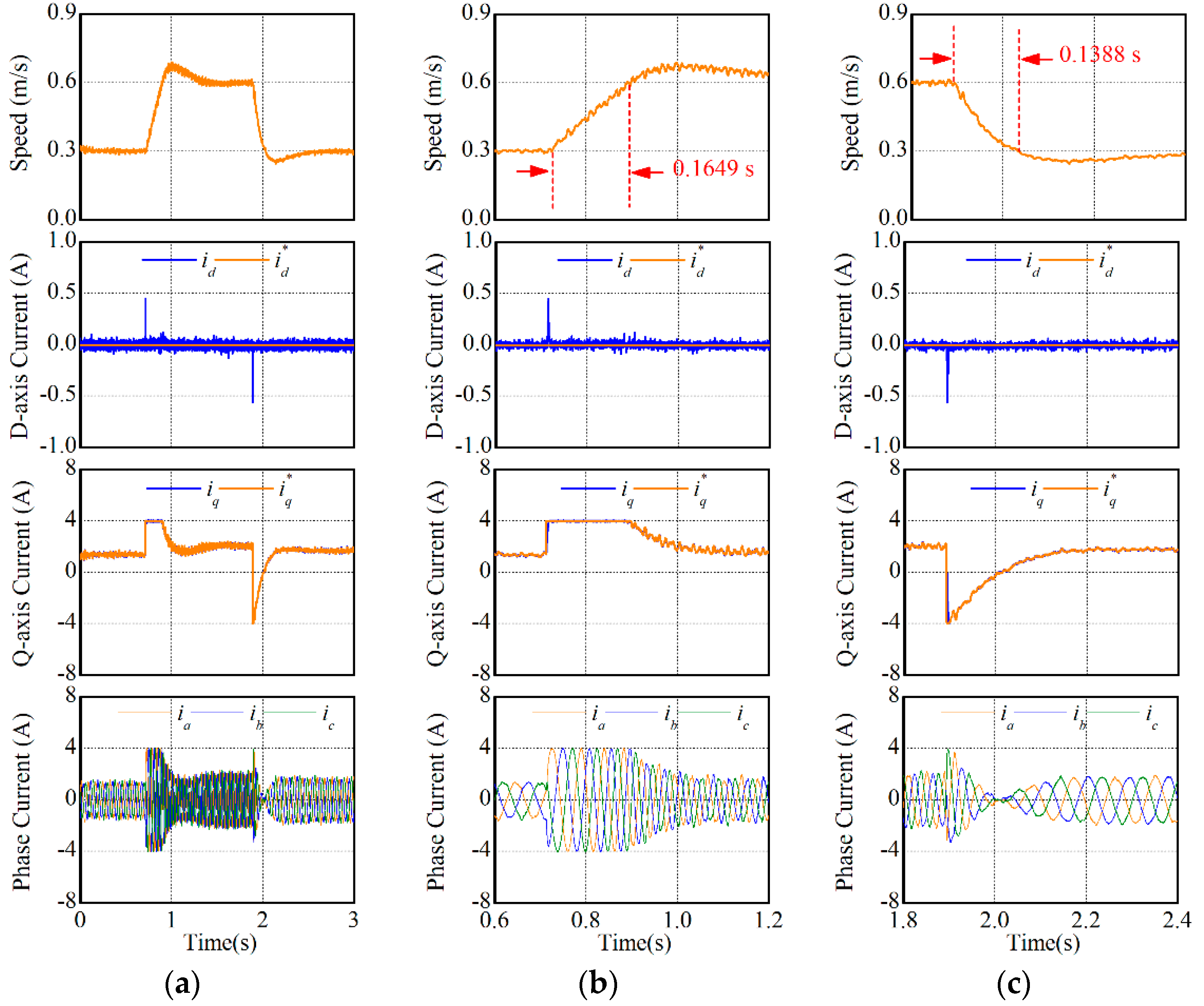
In this experiment, the speed response performances of two MPCCs were compared. The reference speed was changed between 0.3 m/s and 0.6 m/s. The experimental results are shown in Figure 9 and Figure 10. The integral time absolute error (ITAE) was introduced in this paper to evaluate the transient performances. The rising time of MPCC-I and MPCC-II were respectively 0.1649 s (ITAE value: 0.00743 m∙s) and 0.1650 s (ITAE value: 0.00746 m·s), while the falling time were respectively 0.1388 s (ITAE value: 0.00402 m·s) and 0.1391 s (ITAE value: 0.00400 m·s). The dynamic performances of synchronous currents and phase currents were also the same in two MPCCs. Hence, both MPCCs nearly demonstrated the same speed response performance.

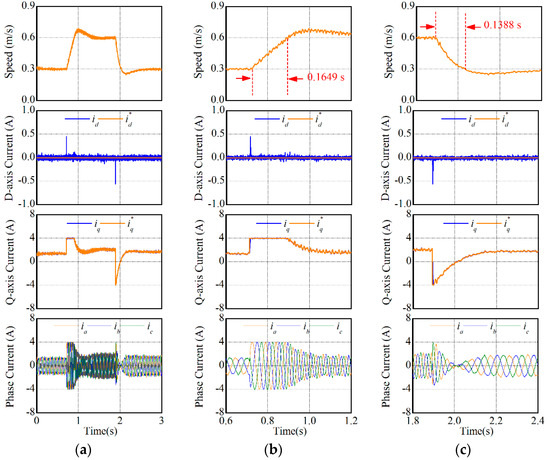
Figure 9. Speed response performances of MPCC-I. (a) t = 0–3 s, (b) t = 0.6–1.2 s, and (c) t = 1.8–2.4 s.

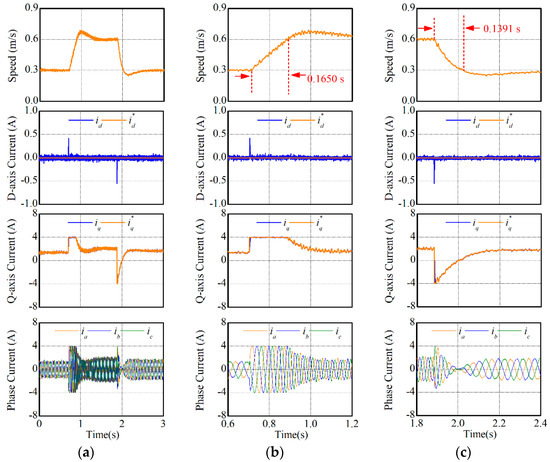
Figure 10. Speed response performances of MPCC-II. (a) t = 0–3 s, (b) t = 0.6–1.2 s, and (c) t = 1.8–2.4 s.

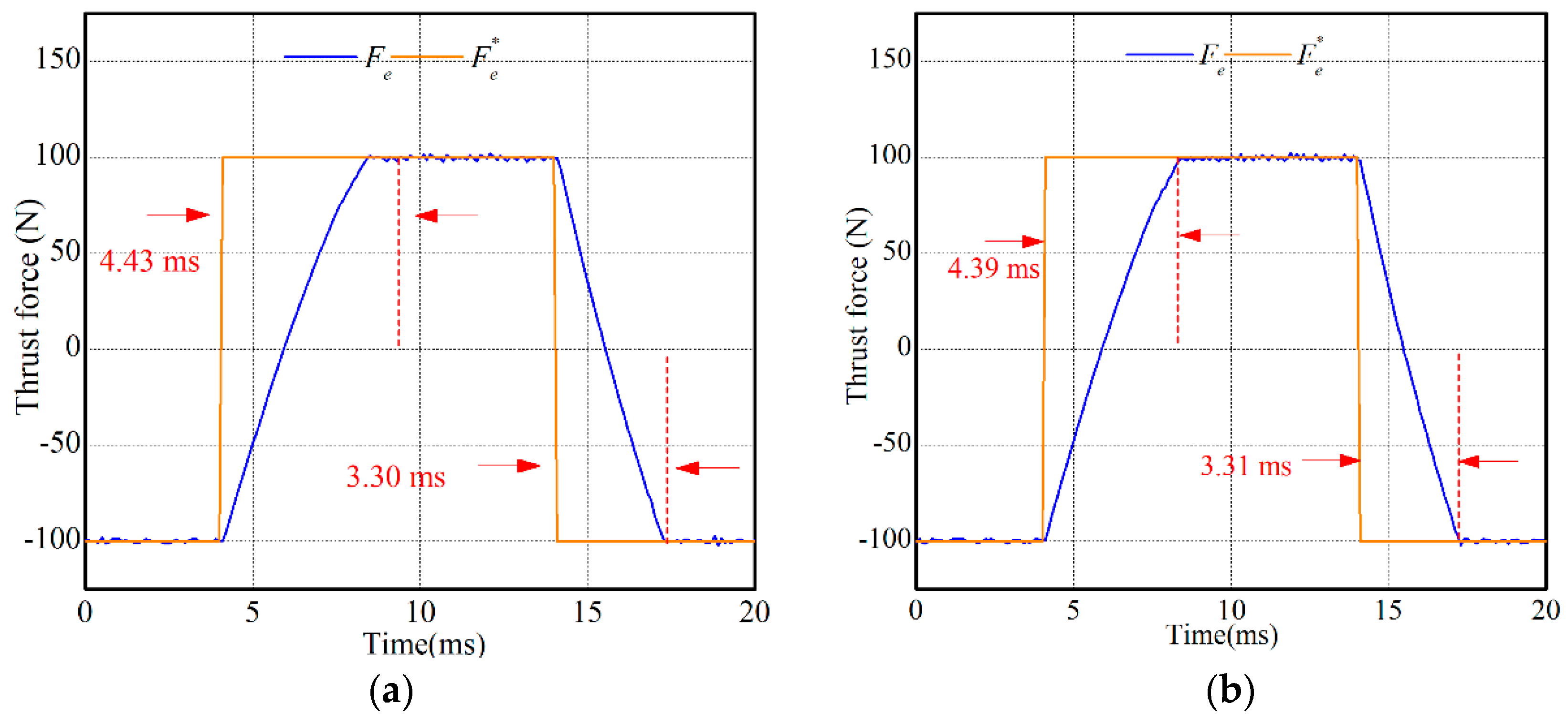
5.3. Thrust Force Response Experiment

In this experiment, the thrust force response performances of both MPCCs were compared. The reference thrust force was increased from −100 N to 100 N, and then returned to −100 N. Figure 11 shows the experimental results. It can be found in Figure 11 that both MPCC-I and MPCC-II had fast thrust force response. The rising and falling time of MPCC-I were respectively 4.43 m·s (ITAE value: 0.00538 N·s²) and 3.30 m·s (ITAE value: 0.00339 N·s²) while those of MPCC-II were respectively 4.39 m·s (ITAE value: 0.00542 N·s²) and 3.31 m·s (ITAE value: 0.00341 N·s²). Hence, MPCC-I and MPCC-II had nearly the same thrust force response.

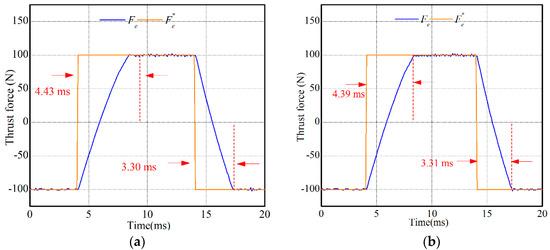
Figure 11. Thrust force response performances: (a) MPCC-I and (b) MPCC-II.

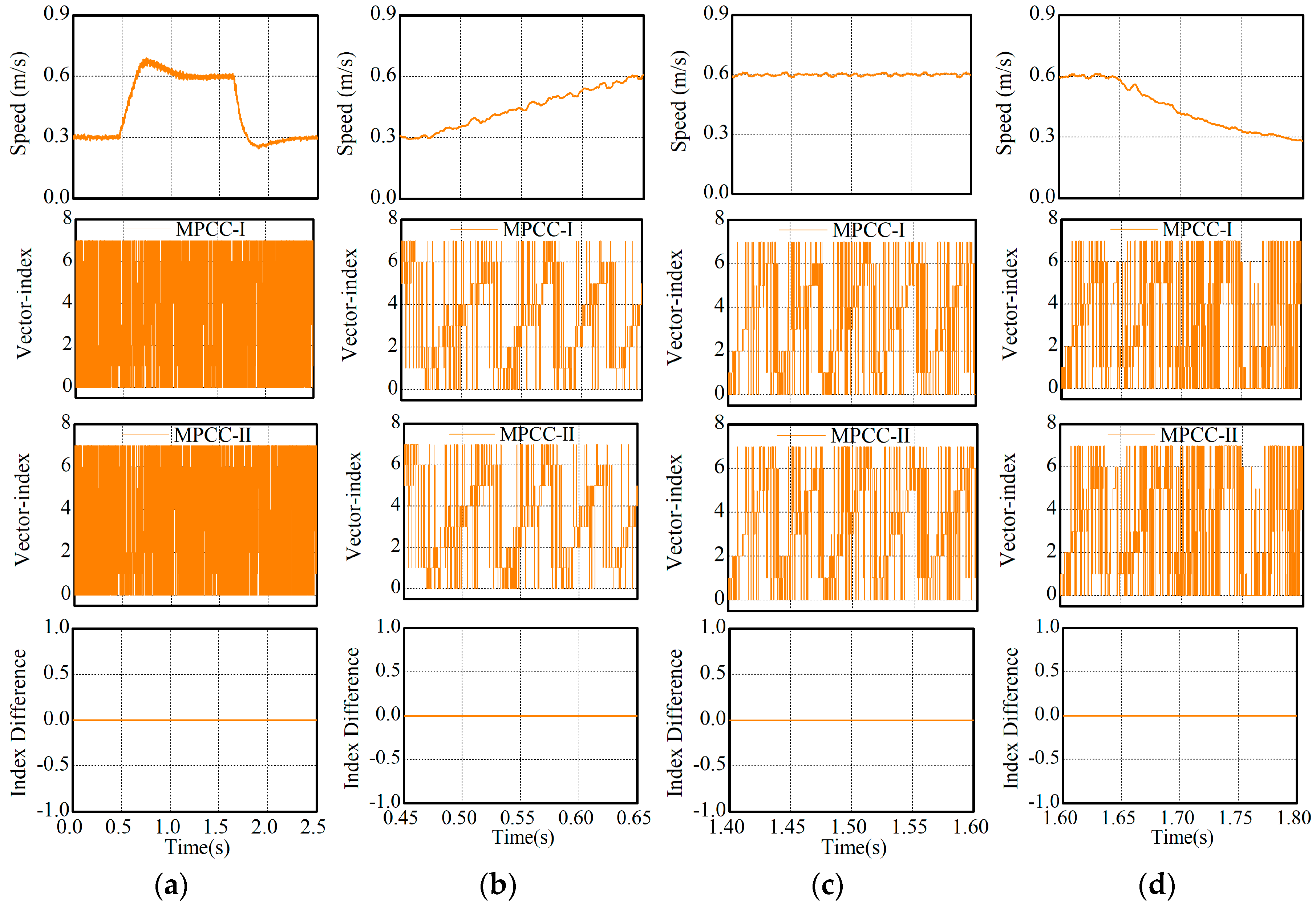
5.4. Comparison of VV Selection

Both MPCCs run at the same time in this experiment but only the command signals of MPCC-II were implemented by the VSI. In other words, the command signals of MPCC-I were generated only for comparison instead of implementation. The reference speed was changed between 0.3 m/s and 0.6 m/s. Experimental results are illustrated in Figure 12, in which the numbers 0–7 respectively represent U₀–U₇. It can be found in Figure 12 that both MPCCs always selected the same VV no matter in transient- or steady-state operations. Therefore, the equivalence of both MPCC was well verified.

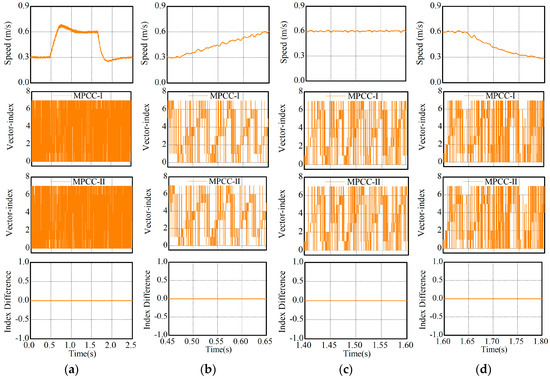
Figure 12. Comparison of VV selection by both MPCCs. (a) t = 0–2.5 s, (b) t = 0.5–0.70 s, (c) t = 1.4–1.6 s, and (d) t = 1.7–1.9 s.

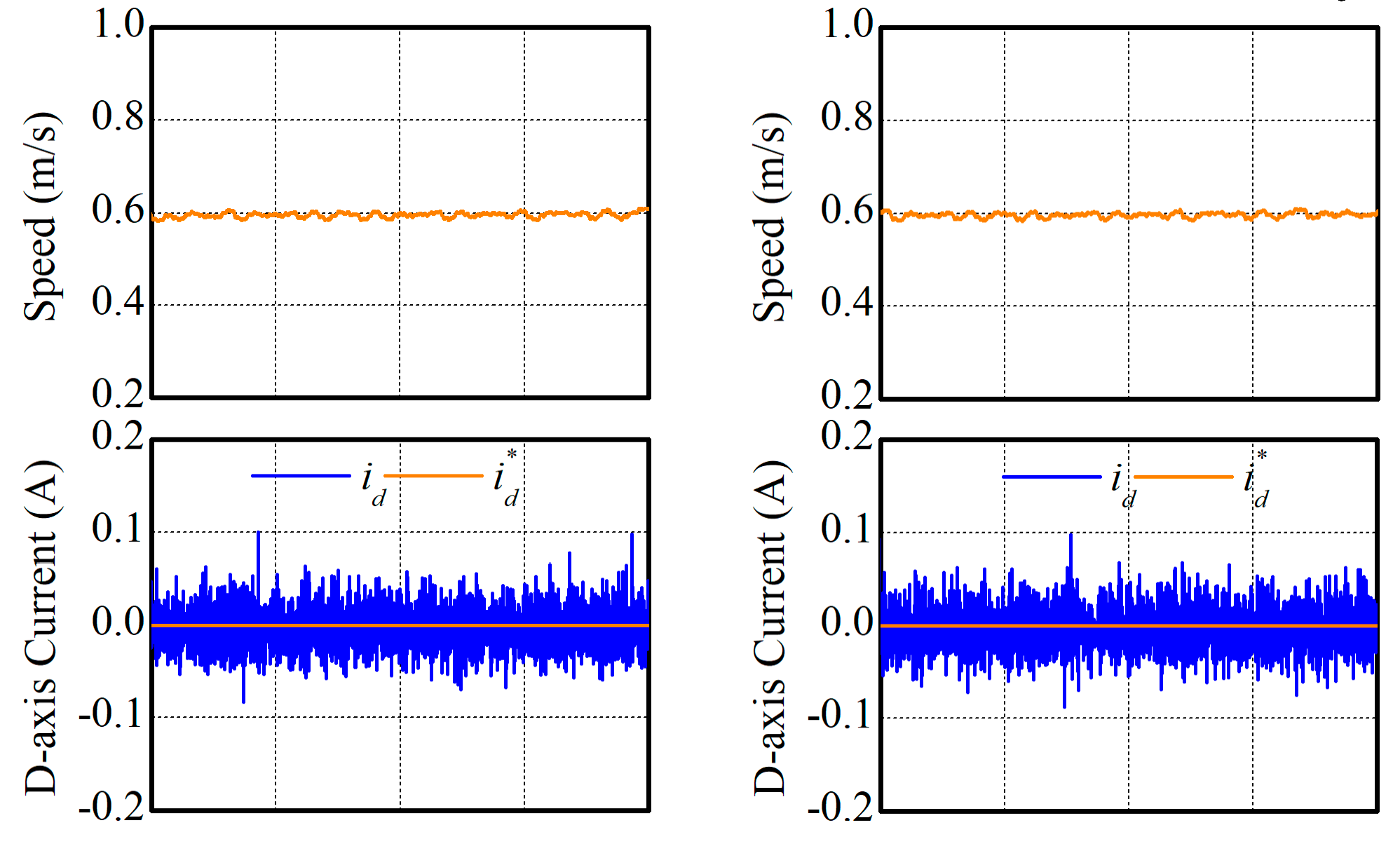
5.5. Motor Parameter Variation

It is well known that MPCC is sensitive to the accuracy of the motor modeling, unmatched parameters, uncertainties, and disturbances. Therefore, compensation actions are usually necessary if high-performances are required. However, the purpose of this paper was to provide a simple but equivalent MPCC. Hence, there were no compensation actions taken in this paper. Some details about parameter compensation of MPCC can be found in [23]. In this subsection, the simplification and equivalence of MPCC-II were evaluated considering the motor parameter variation. As an example, 150% of the rated mover inductance and 50% of the rated mover resistance were considered in this experiment, and the experimental results are illustrated in Figure 13 and Figure 14. According to the experimental results, the performances of both MPCCs are compared in Table 5 and Table 6. It can be found in the two previous tables that MPCC-I and MPCC-II still had nearly the same performances.

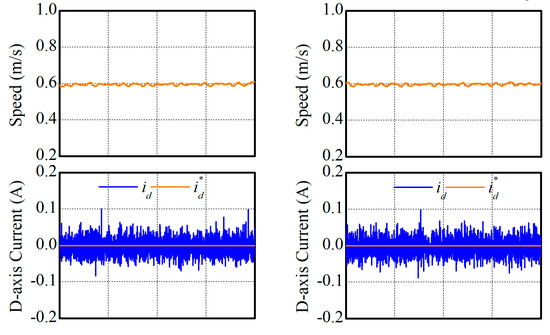
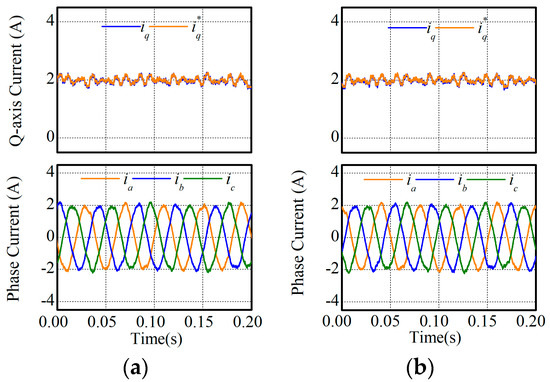
Figure 13. Steady-state performances with inaccurate mover inductance: (a) MPCC-I and (b) MPCC-II.

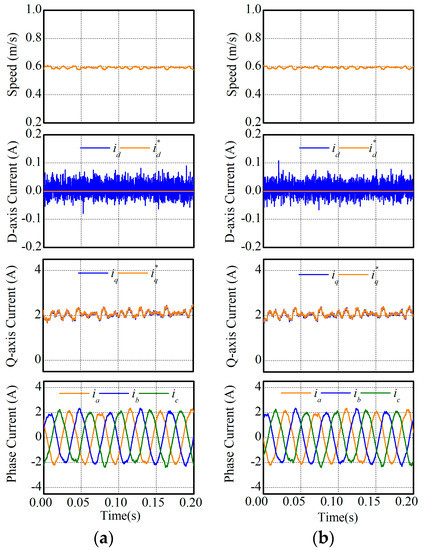
Figure 14. Steady-state performances with inaccurate mover resistance: (a) MPCC-I and (b) MPCC-II.

Table 5. Performance comparison with inaccurate mover inductance.

Operation Condition		Standard Deviation			THD of Phase Currents
Ref. Speed	MPCC	Speed (m/s)	id (A)	iq (A)
0.6 m/s	MPCC-I	0.00553	0.0240	0.110	4.47%
	MPCC-II	0.00549	0.0241	0.111	4.45%

Table 6. Performance comparison with inaccurate mover resistance.

Operation Condition		Standard Deviation			THD of Phase Currents
Ref. Speed	MPCC	Speed (m/s)	id (A)	iq (A)
0.6 m/s	MPCC-I	0.00581	0.0228	0.121	4.35%
	MPCC-II	0.00577	0.0224	0.118	4.36%

6. Conclusions

For the reduction of the computation burden, a simple but equivalent solution was proposed for the MPCC of PPMLM traction systems. In the proposed MPCC, a continuous reference VV was predicted, and the optimal VV was determined according to the shortest distance principle instead of the cost function. Though the performances of the proposed MPCC were not enhanced in terms of precision, robustness, and dynamics, the computation cost could be significantly reduced, which achieved the target of this paper. The simplification and the equivalence of the proposed MPCC were verified by experimental results. Although the proposed MPCC was designed for PPMLM originally, it is also novel for the rotary PMSM. From the viewpoint of the implementation, there is no difference between the PMLM and the rotary PMSM.