Reactive Power Management Considering Stochastic Optimization under the Portuguese Reactive Power Policy Applied to DER in Distribution Networks
Abstract
1. Introduction
- To design a two-stage stochastic reactive power management model considering a full AC-OPF. It has the purpose of aiding the decision-making of the DSO under the uncertain and variable behavior of RES connected in the distribution network;
- To propose a reactive power service provided by the DSO to the TSO in advance of the operating hour. This service can be used by the TSO in the transmission system management, defining a reactive power operation in the TSO/DSO boundary substations. This can help the TSO in different services like the voltage control and congestion management in the transmission system;
- Take into account the Portuguese reactive power policy on distribution grids, assessing the behavior and applicability of the proposed model.
2. Reactive Power Policies
2.1. Portuguese Reactive Power Policy
2.2. Proactive Reactive Power Management
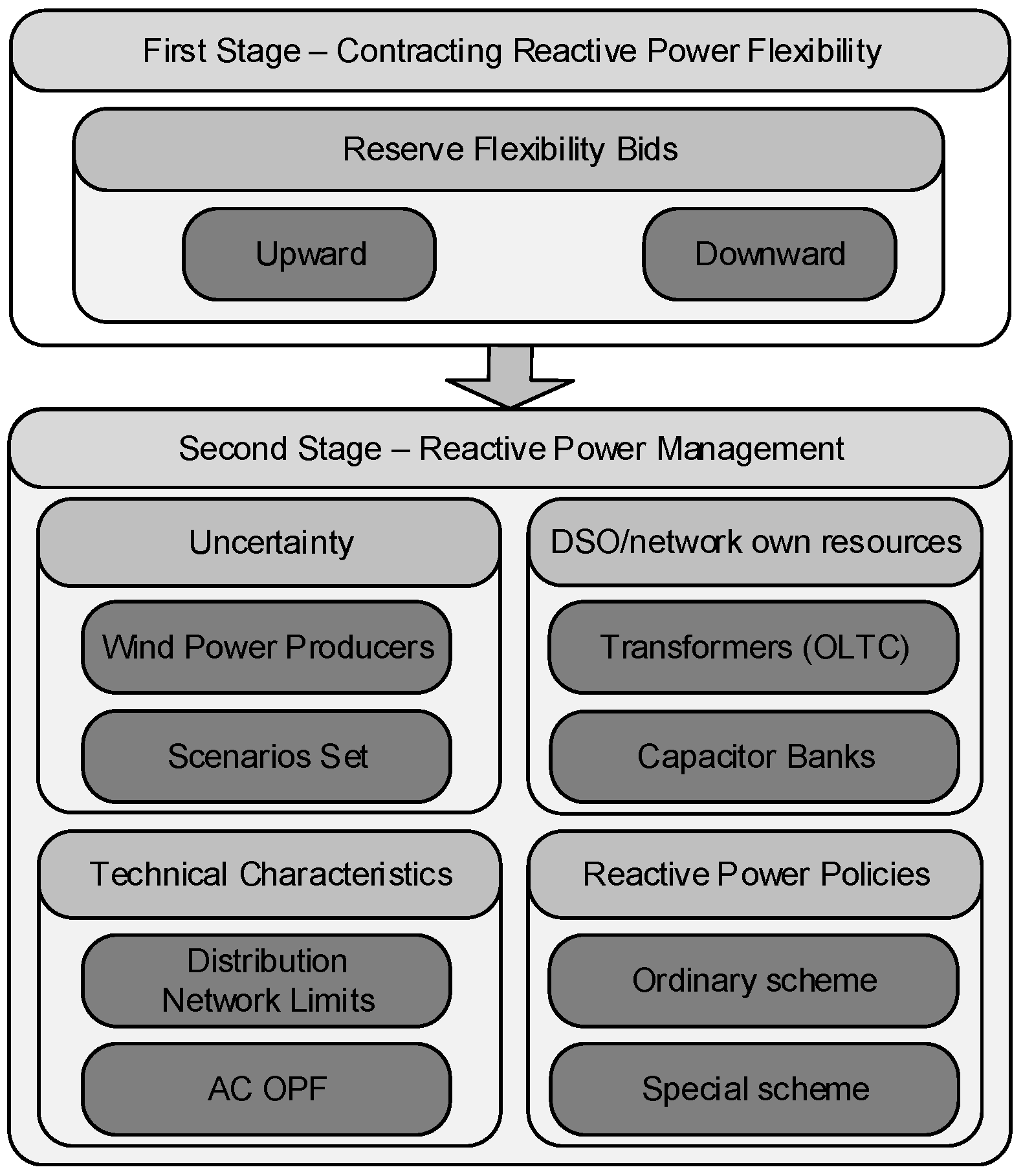
3. Mathematical Formulation
3.1. Objective Function
3.2. First-Stage Constraints
3.3. Second-Stage Constraints
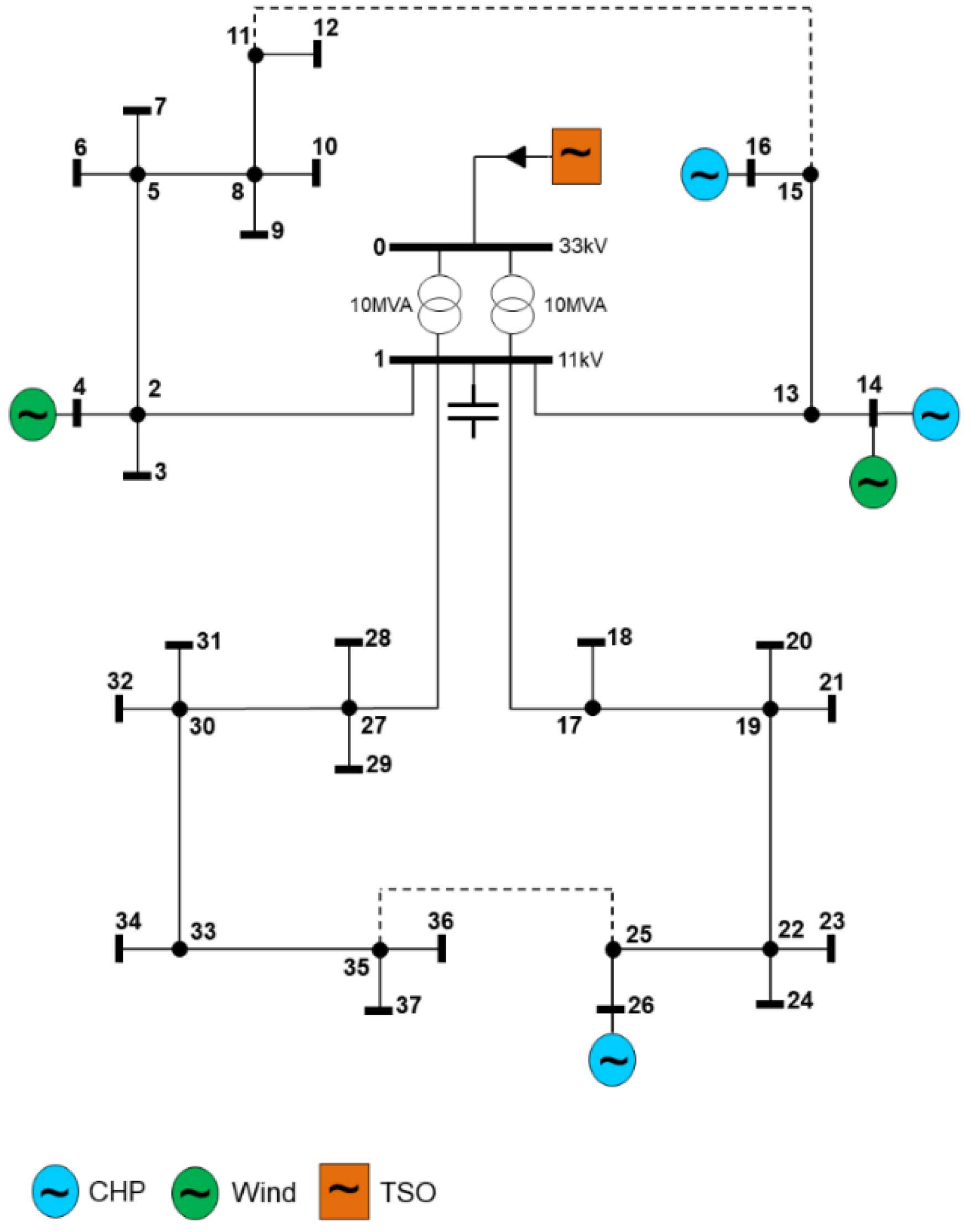
4. Case Study
4.1. 37-Bus Distribution System
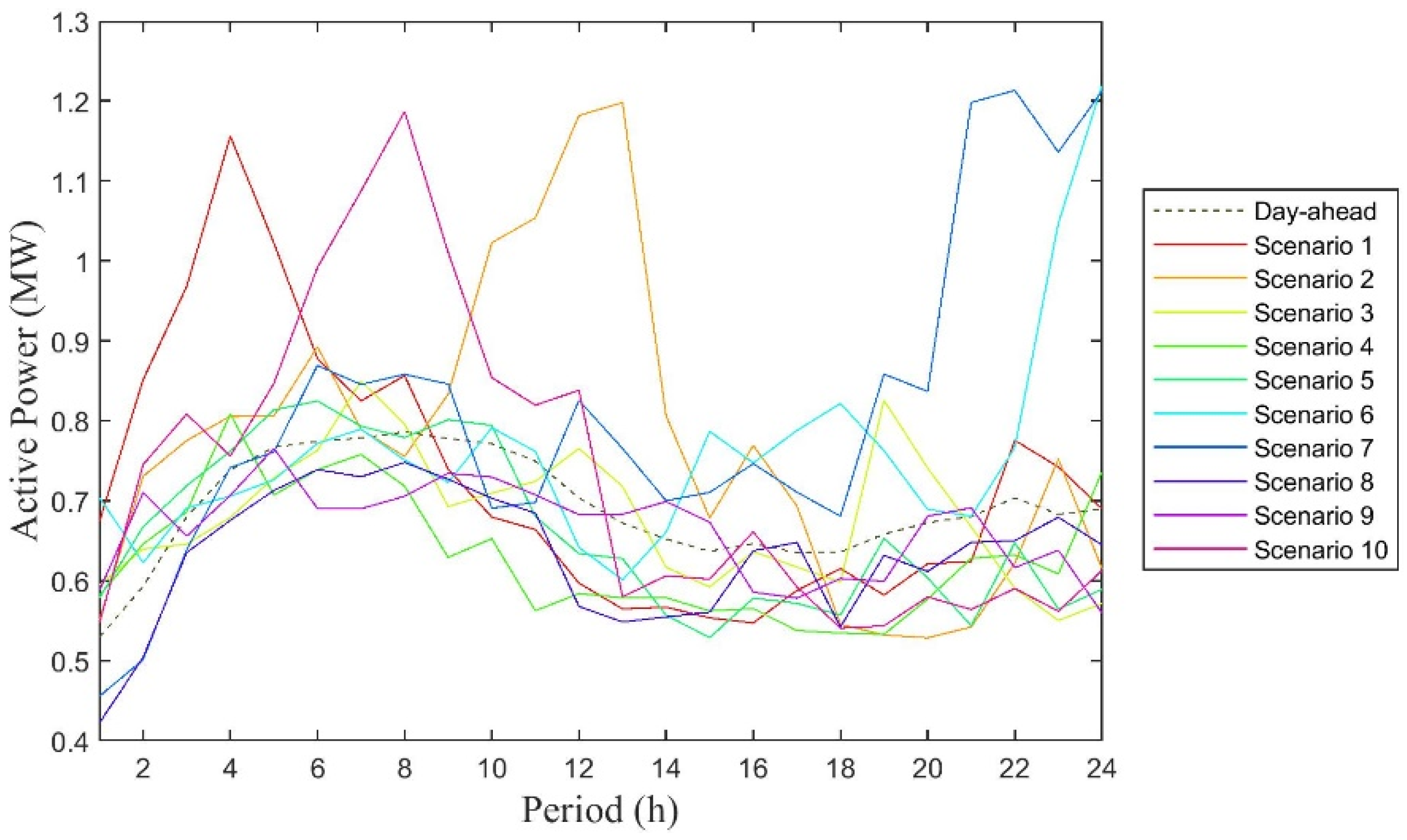
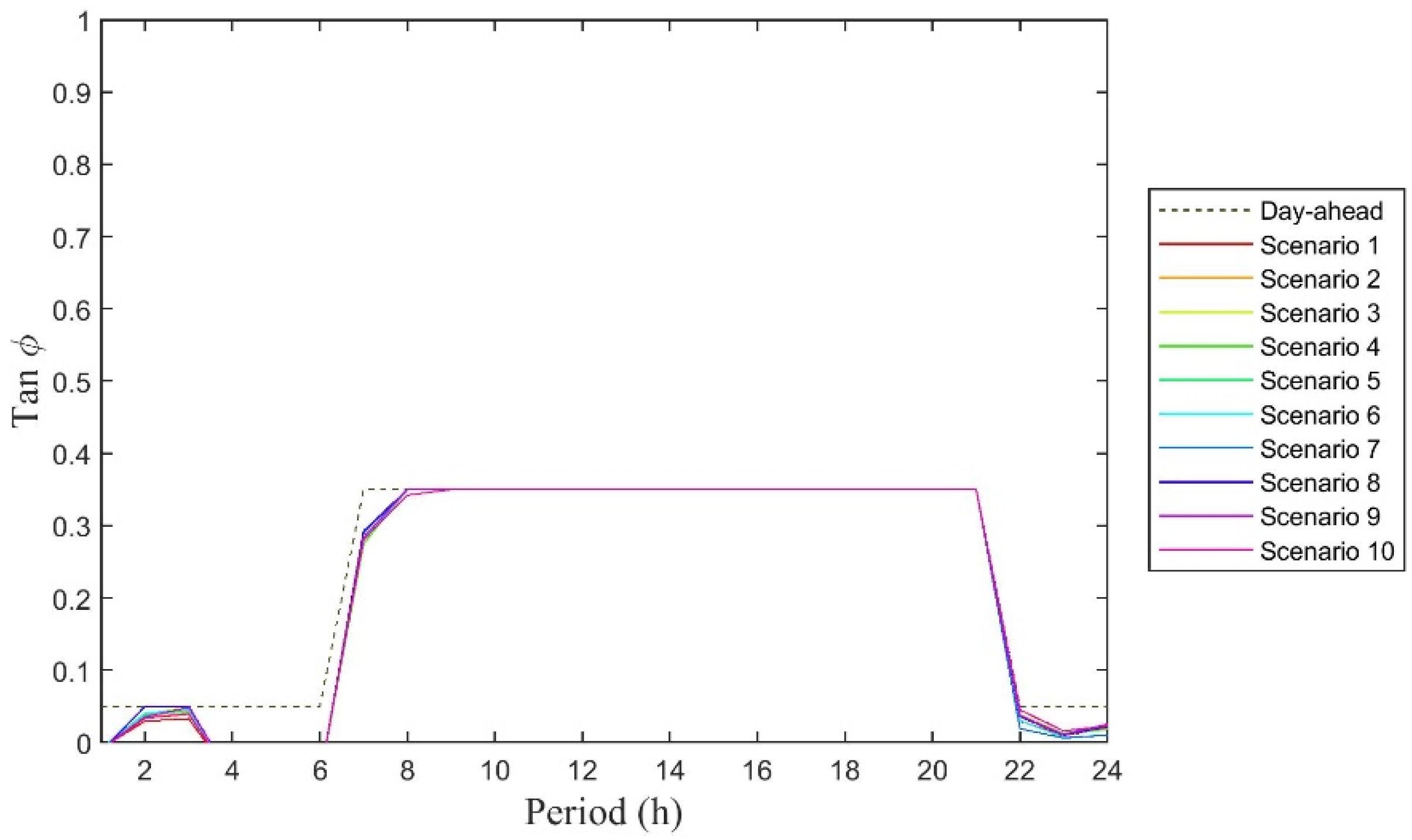
4.2. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Parameters | |
| Power deviation in each scenario | |
| Imaginary part in admittance matrix | |
| Cost | |
| Real part in admittance matrix | |
| Number of unit resources | |
| Penalty for external supplier’s flexibility | |
| Series admittance of line that connects two buses | |
| Shunt admittance of line that connects two buses | |
| Variables | |
| Voltage angle | |
| Active power | |
| Reactive power | |
| Reactive power flexibility used in the operating stage | |
| Reactive power relaxation in the operating stage | |
| Reactive power flexibility contracted at day-ahead stage | |
| Reactive power relaxation at day-ahead stage | |
| Apparent power | |
| Voltage magnitude | |
| Voltage in polar form | |
| Voltage at slack bus | |
| Voltage level activated by the DSO in the transformer | |
| Binary variable | |
| Auxiliary variable for absolute function linearization | |
| Subscripts | |
| Index of scenarios | |
| Index of capacitor bank units | |
| Capacitor bank abbreviation | |
| Index of generators units | |
| Bus index | |
| Index of load consumers | |
| Load consumers abbreviation | |
| Index of levels (tap changing) for capacitor banks and transformers | |
| Transmission system operator | |
| Time index | |
| Index of transformer units | |
| Transformer abbreviation | |
| Superscripts | |
| Activation cost of resources in real-time stage | |
| Generation curtailment | |
| Maximum limit | |
| Minimum limit | |
| Operating point of the power resource | |
| Downward reactive power flexibility | |
| Upward reactive power flexibility | |
| Demand response of consumer l | |
References
- Pérez-Arriaga, I.J.; Ruester, S.; Schwenen, S.; Battle, C.; Glachant, J.-M. From distribution networks to smart distribution systems: Rethinking the regulation of European electricity DSOs. Util. Policy 2014, 31, 229–237. [Google Scholar]
- Eurelectric Active Distribution System Management: A Key Tool for the Smooth Integration of Distributed Generation. Available online: https://www.eurelectric.org/media/1781/asm_full_report_discussion_paper_final-2013-030-0117-01-e.pdf (accessed on 22 October 2019).
- Soares, T.; Bessa, R.J. Proactive management of distribution grids with chance-constrained linearized AC OPF. Int. J. Electr. Power Energy Syst. 2019, 109, 332–342. [Google Scholar] [CrossRef]
- Morais, H. TDX-ASSIST: Agreed Models, Use Case List, and Use Case Description in UML, D1.2. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5bfb19910&appId=PPGMS (accessed on 22 October 2019).
- Gayatri, M.T.L.; Parimi, A.M.; Pavan Kumar, A.V. A review of reactive power compensation techniques in microgrids. Renew. Sustain. Energy Rev. 2018, 81, 1030–1036. [Google Scholar] [CrossRef]
- Parida, S.K.; Srivastava, S.C.; Singh, S.N. A review on reactive power management in electricity markets. Int. J. Energy Sect. Manag. 2011, 5, 201–214. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A. Optimal reactive power dispatch: A review, and a new stochastic voltage stability constrained multi-objective model at the presence of uncertain wind power generation. IET Generation, Transm. Distrib. 2017, 11, 815–829. [Google Scholar] [CrossRef]
- Rabiee, A.; Soroudi, A.; Mohammadi-Ivatloo, B.; Parniani, M. Corrective voltage control scheme considering demand response and stochastic wind power. IEEE Trans. Power Syst. 2014, 29, 2965–2973. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Jiang, C.; Yin, S.; Yang, M. Dynamic coordinated active-reactive power optimization for active distribution network with energy storage systems. Appl. Sci. 2019, 9, 1129. [Google Scholar] [CrossRef]
- Kang, S.J.; Kim, J.; Park, J.W.; Baek, S.M. Reactive power management based on voltage sensitivity analysis of distribution system with high penetration of renewable energies. Energies 2019, 12, 1493. [Google Scholar] [CrossRef]
- Stock, D.S.; Sala, F.; Berizzi, A.; Hofmann, L. Optimal control of wind farms for coordinated TSO-DSO reactive power management. Energies 2018, 11, 173. [Google Scholar] [CrossRef]
- ERSE Regulamento da Rede de distribuição—Portaria 596-2010. Available online: http://www.erse.pt/pt/electricidade/regulamentos/redededistribuicao/Documents/Portaria 596-2010 RRT RRD.pdf (accessed on 22 October 2019).
- ERSE Despacho no3/2010. Available online: http://www.erse.pt/pt/consultaspublicas/consultas/Documents/31_4/Despacho_3_2010.pdf (accessed on 22 October 2019).
- ERSE Informação Sobre Faturação de Energia Reativa: Princípios e Boas Práticas. Available online: http://www.erse.pt/pt/electricidade/regulamentos/relacoescomerciais/Documents/Recomendações/Recomendação de energia reactiva.pdf (accessed on 22 October 2019).
- Simão, T.; Gama, P.; Louro, M.; Carvalho, L.; Gloria, G.; Pestana, R.; Reis, F.; Soares, T.; Silva, J. TDX-ASSIST: Beyond state of art in TSO-DSO interoperability—The Portuguese demonstrator. In Proceedings of the 25th International Conference on Electricity Distribution, Madrid, Spain, 3–6 June 2019; pp. 3–6. [Google Scholar]
- Zhang, Y.J.; Ren, Z. Optimal reactive power dispatch considering costs of adjusting the control devices. IEEE Trans. Power Syst. 2005, 20, 1349–1356. [Google Scholar] [CrossRef]
- ERSE Despacho no 7253/2010. Available online: http://www.erse.pt/pt/legislacao/Legislacao/Attachments/1411/Despacho 7253_2010.pdf (accessed on 22 October 2019).
- Allan, R.N.; Billinton, R.; Sjarief, I.; Goel, L.; So, K.S. A reliability test system for educational purposes—Basic distribution-system data and results. IEEE Trans. Power Syst. 1991, 6, 813–820. [Google Scholar] [CrossRef]
- Morais, H.; Sousa, T.; Soares, J.; Faria, P.; Vale, Z. Distributed energy resources management using plug-in hybrid electric vehicles as a fuel-shifting demand response resource. Energy Convers. Manag. 2015, 97, 78–93. [Google Scholar] [CrossRef]
- Pinson, P. Wind energy: Forecasting challenges for its operational management. Stat. Sci. 2013, 28, 564–585. [Google Scholar] [CrossRef]
- Bukhsh, W.A.; Zhang, C.; Pinson, P. Data for Stochastic Multiperiod OPF Problems. Available online: https://sites.google.com/site/datasmopf/ (accessed on 22 October 2019).
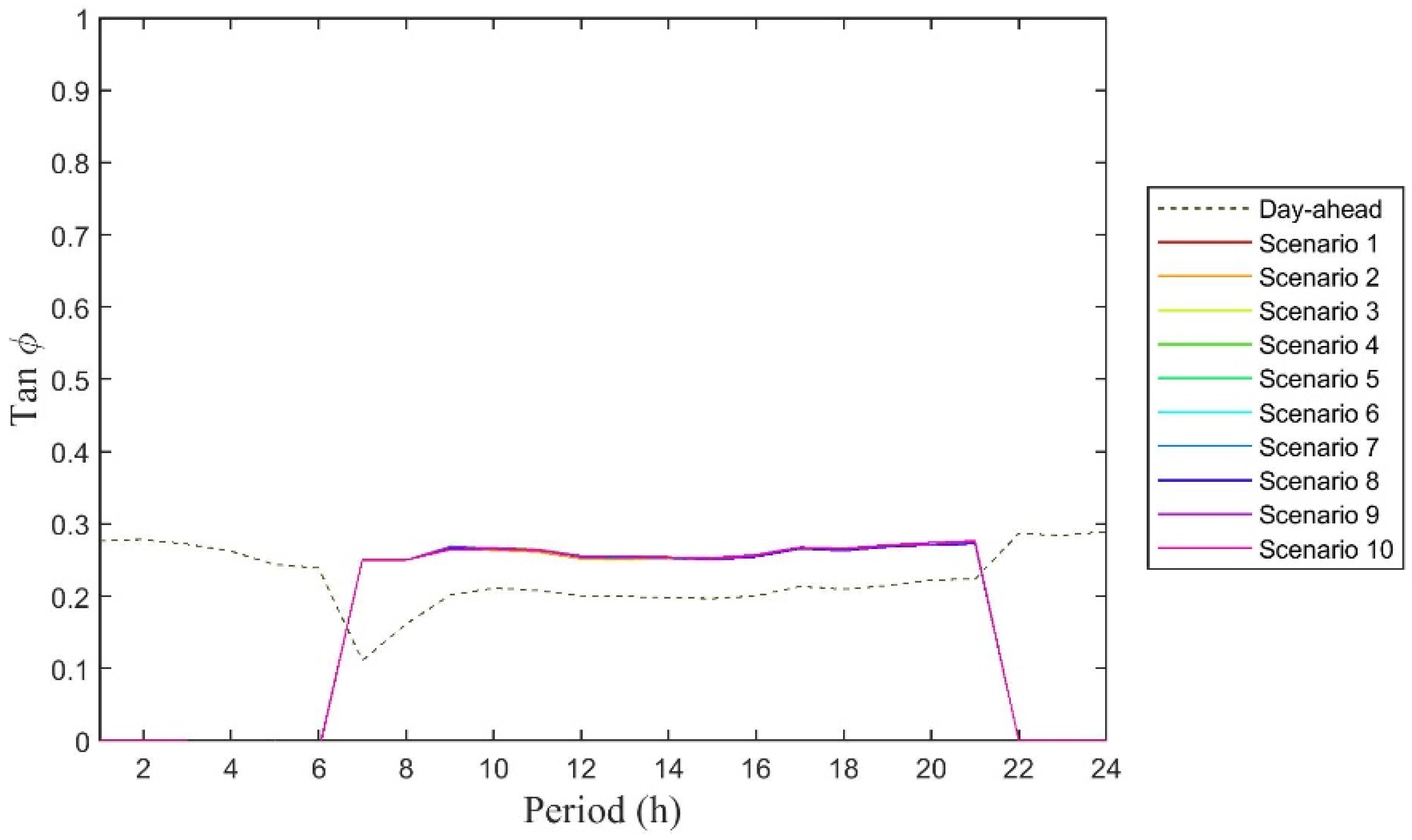
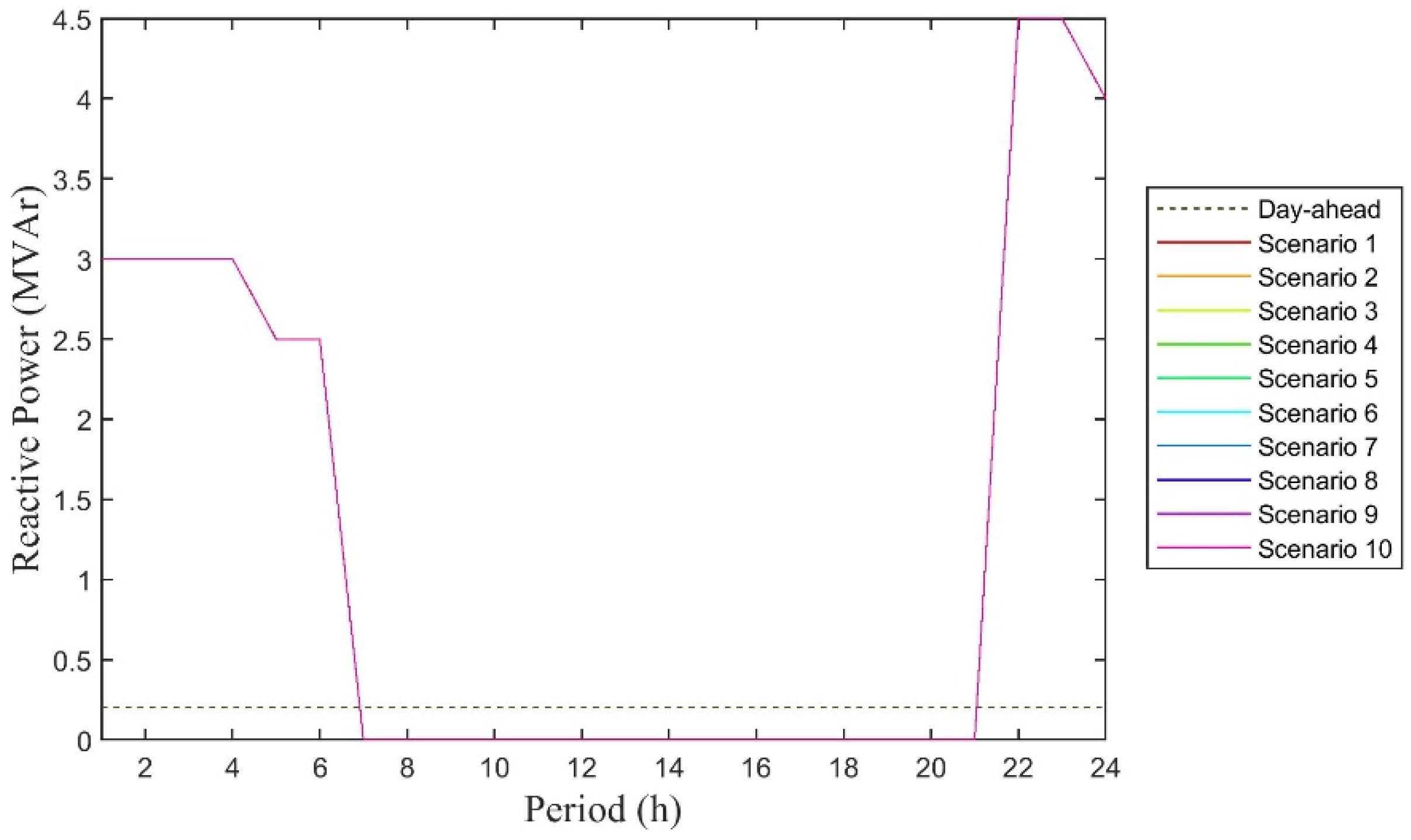
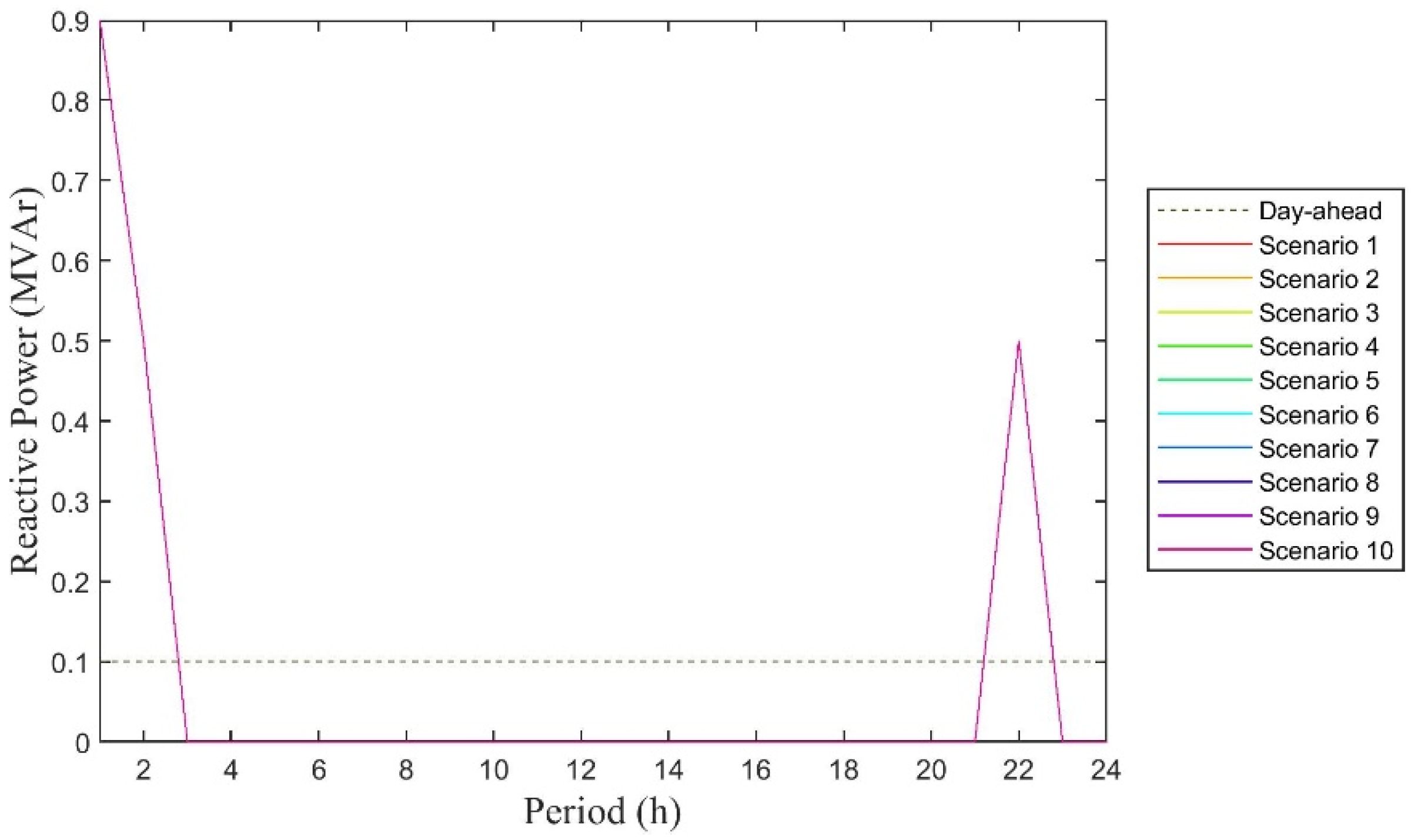
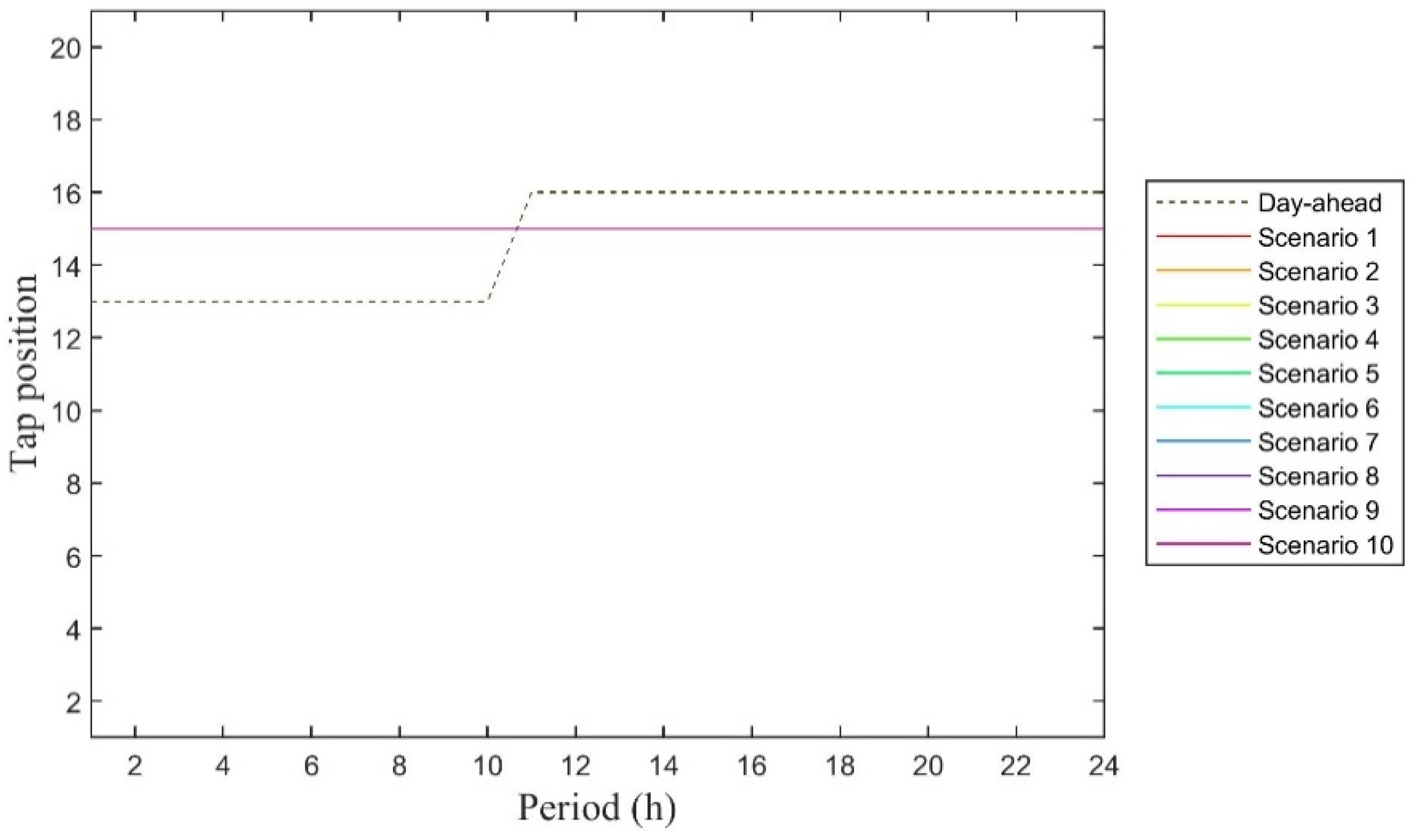
| Voltage Level | tan ϕ | |
|---|---|---|
| Peak Period | Off-Peak Period | |
| High Voltage | 0 | 0 |
| Medium Voltage (P > 6MW) | 0 | 0 |
| Medium Voltage (P ≤ 6MW) | 0.3 | 0 |
| Low Voltage | 0 | 0 |
| Load. | Bus | Active Power Consumption (kW) | Reactive Power Consumption (kVAr) | ||||
|---|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | ||
| 1 | 3 | 373.2 | 677.9 | 1190.5 | 112.0 | 203.4 | 357.2 |
| 2 | 4 | 206.1 | 591.2 | 1015.6 | 61.8 | 177.4 | 304.7 |
| 3 | 6 | 88.4 | 599.0 | 1029.8 | 26.5 | 179.7 | 308.9 |
| 4 | 7 | 394.7 | 716.9 | 1259.1 | 118.4 | 215.1 | 377.7 |
| 5 | 9 | 539.0 | 761.8 | 1089.0 | 161.7 | 228.5 | 326.7 |
| 6 | 10 | 298.7 | 636.6 | 1040.9 | 89.6 | 191.0 | 312.3 |
| 7 | 12 | 323.0 | 586.5 | 1030.1 | 96.9 | 176.0 | 309.0 |
| 8 | 14 | 387.0 | 1110.4 | 1907.4 | 116.1 | 325.4 | 567.1 |
| 9 | 16 | 745.6 | 1589.1 | 2598.3 | 223.7 | 425.6 | 779.5 |
| 10 | 18 | 509.7 | 720.3 | 1029.8 | 152.9 | 169.7 | 308.9 |
| 11 | 20 | 88.4 | 599.0 | 1029.8 | 26.5 | 152.1 | 308.9 |
| 12 | 21 | 373.2 | 677.9 | 1190.5 | 112.0 | 190.9 | 357.2 |
| 13 | 23 | 365.1 | 778.1 | 1272.3 | 109.5 | 208.4 | 381.7 |
| 14 | 24 | 539.0 | 761.8 | 1089.0 | 161.7 | 179.5 | 326.7 |
| 15 | 26 | 323.0 | 586.5 | 1030.1 | 96.9 | 165.1 | 309.0 |
| 16 | 28 | 178.3 | 511.6 | 878.8 | 53.5 | 149.9 | 261.3 |
| 17 | 29 | 74.4 | 503.8 | 866.2 | 22.3 | 128.0 | 259.9 |
| 18 | 31 | 314.0 | 570.2 | 1001.4 | 94.2 | 160.5 | 300.4 |
| 19 | 32 | 290.4 | 618.9 | 1011.9 | 87.1 | 165.8 | 303.6 |
| 20 | 34 | 93.5 | 633.4 | 1089.0 | 28.1 | 160.9 | 326.7 |
| 21 | 36 | 217.9 | 625.3 | 1074.1 | 65.4 | 183.2 | 319.3 |
| 22 | 37 | 323.0 | 586.5 | 1030.1 | 96.9 | 165.1 | 309.0 |
| DER | Number of Units | Total Installed Power | Operating Point Pop (MW) | ||
|---|---|---|---|---|---|
| Min | Mean | Max | |||
| CHP | 3 | 2.5 (MVA) | 1.0 | 1.15 | 1.5 |
| Wind | 2 | 20 (MVA) | 11.31 | 14.01 | 15.34 |
| Transmission system operator (TSO) | 1 | 20 (MVA) | - | - | - |
| DER | Upward Cost Cup (m.u./kVAr) | Downward Cost Cdw (m.u./kVAr) | ||||
|---|---|---|---|---|---|---|
| Min | Mean | Max | Min | Mean | Max | |
| CHP | 0.02 | 0.04 | 0.06 | 0.02 | 0.04 | 0.06 |
| Wind | 0.02 | 0.025 | 0.03 | 0.02 | 0.025 | 0.03 |
| TSO | 1 | 1 | 1 | 1 | 1 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abreu, T.; Soares, T.; Carvalho, L.; Morais, H.; Simão, T.; Louro, M. Reactive Power Management Considering Stochastic Optimization under the Portuguese Reactive Power Policy Applied to DER in Distribution Networks. Energies 2019, 12, 4028. https://doi.org/10.3390/en12214028
Abreu T, Soares T, Carvalho L, Morais H, Simão T, Louro M. Reactive Power Management Considering Stochastic Optimization under the Portuguese Reactive Power Policy Applied to DER in Distribution Networks. Energies. 2019; 12(21):4028. https://doi.org/10.3390/en12214028
Chicago/Turabian StyleAbreu, Tiago, Tiago Soares, Leonel Carvalho, Hugo Morais, Tiago Simão, and Miguel Louro. 2019. "Reactive Power Management Considering Stochastic Optimization under the Portuguese Reactive Power Policy Applied to DER in Distribution Networks" Energies 12, no. 21: 4028. https://doi.org/10.3390/en12214028
APA StyleAbreu, T., Soares, T., Carvalho, L., Morais, H., Simão, T., & Louro, M. (2019). Reactive Power Management Considering Stochastic Optimization under the Portuguese Reactive Power Policy Applied to DER in Distribution Networks. Energies, 12(21), 4028. https://doi.org/10.3390/en12214028






