Appendix A. Robustness Analysis
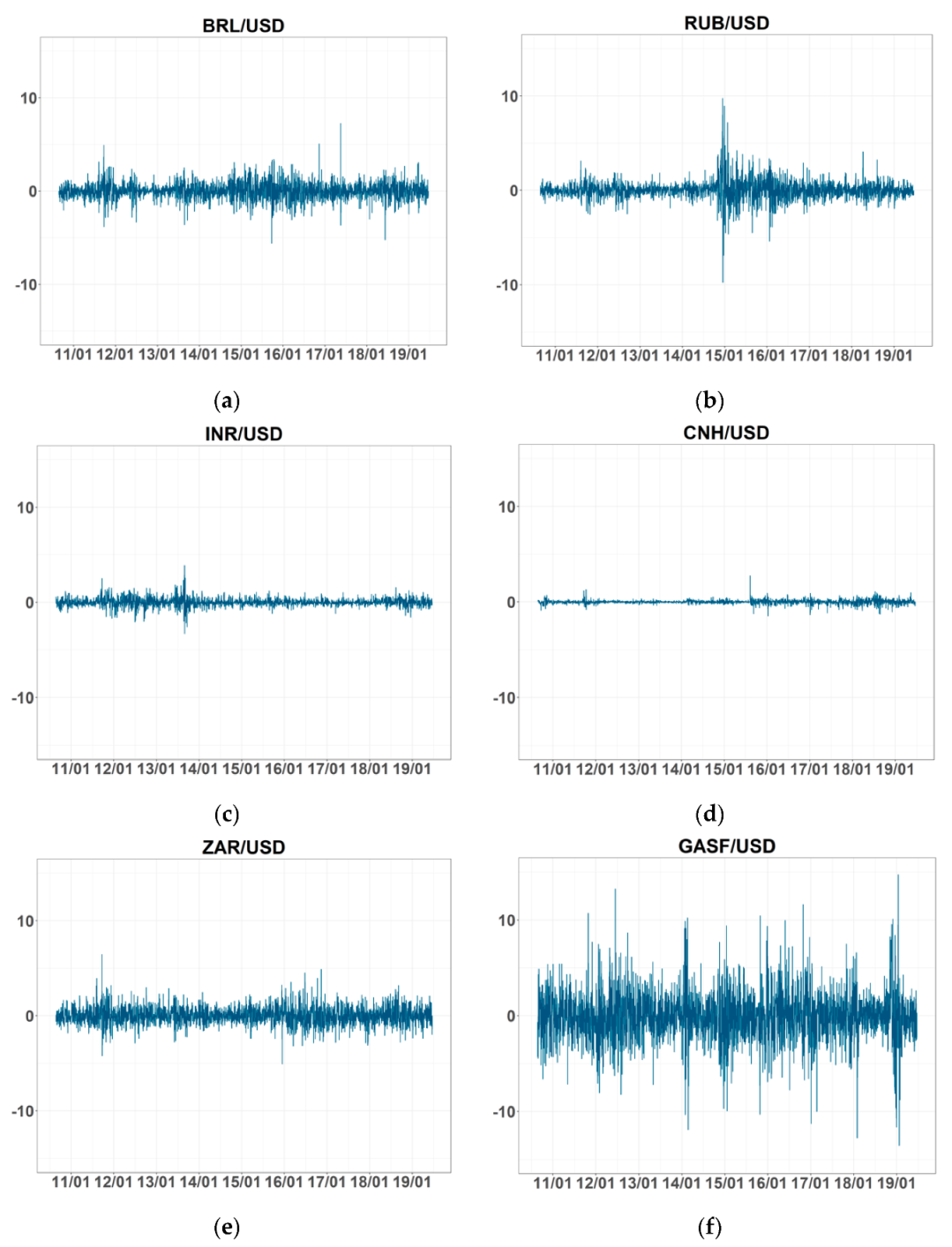
We used the Henry Hub natural gas spot price (GASS) as the natural gas price data to examine the robustness of our results. (The natural gas futures index in the United Kingdom, which is known as the UK National Balancing Point (NBP), was also used to conduct the robustness check, but the results were quite similar to those from GASS, so we only present the connectedness table of NBP and exchange rates (
Table A2) in
Appendix A).
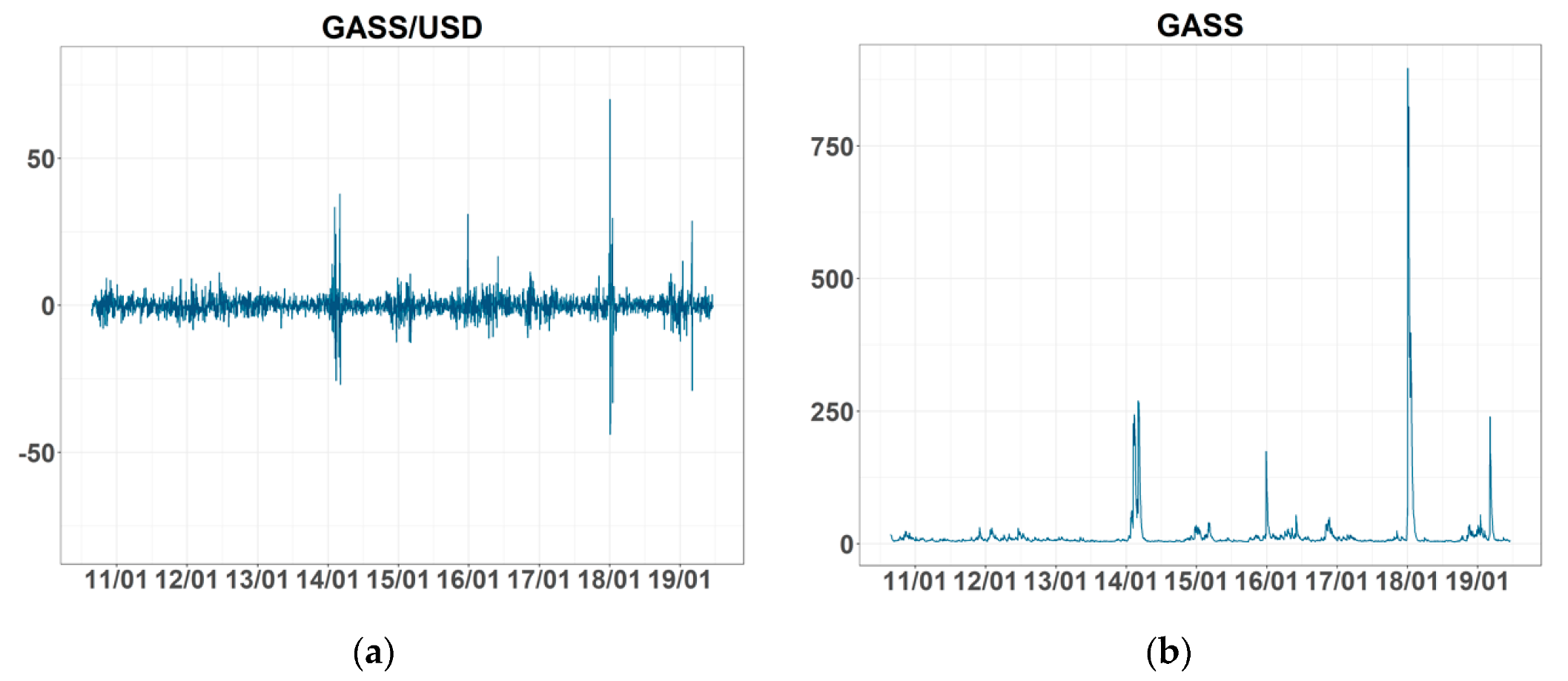
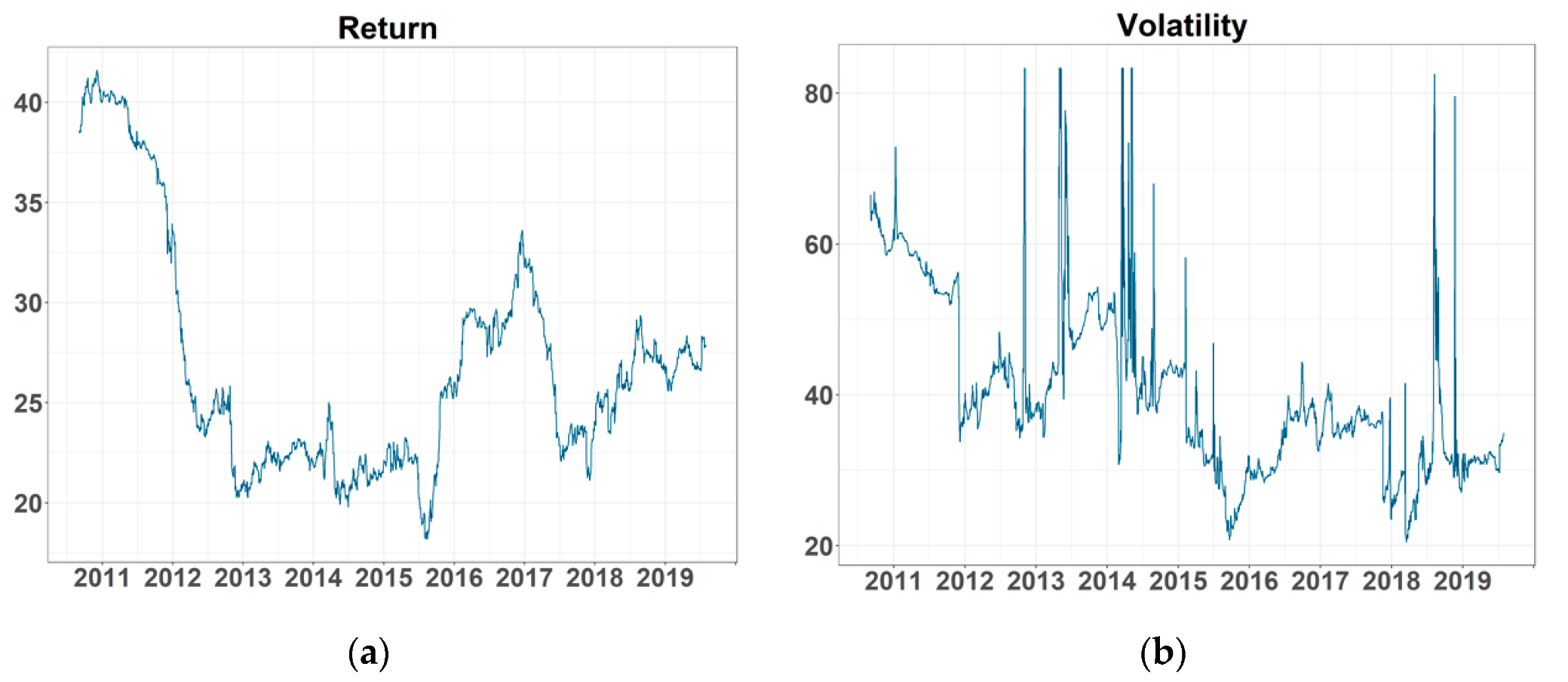
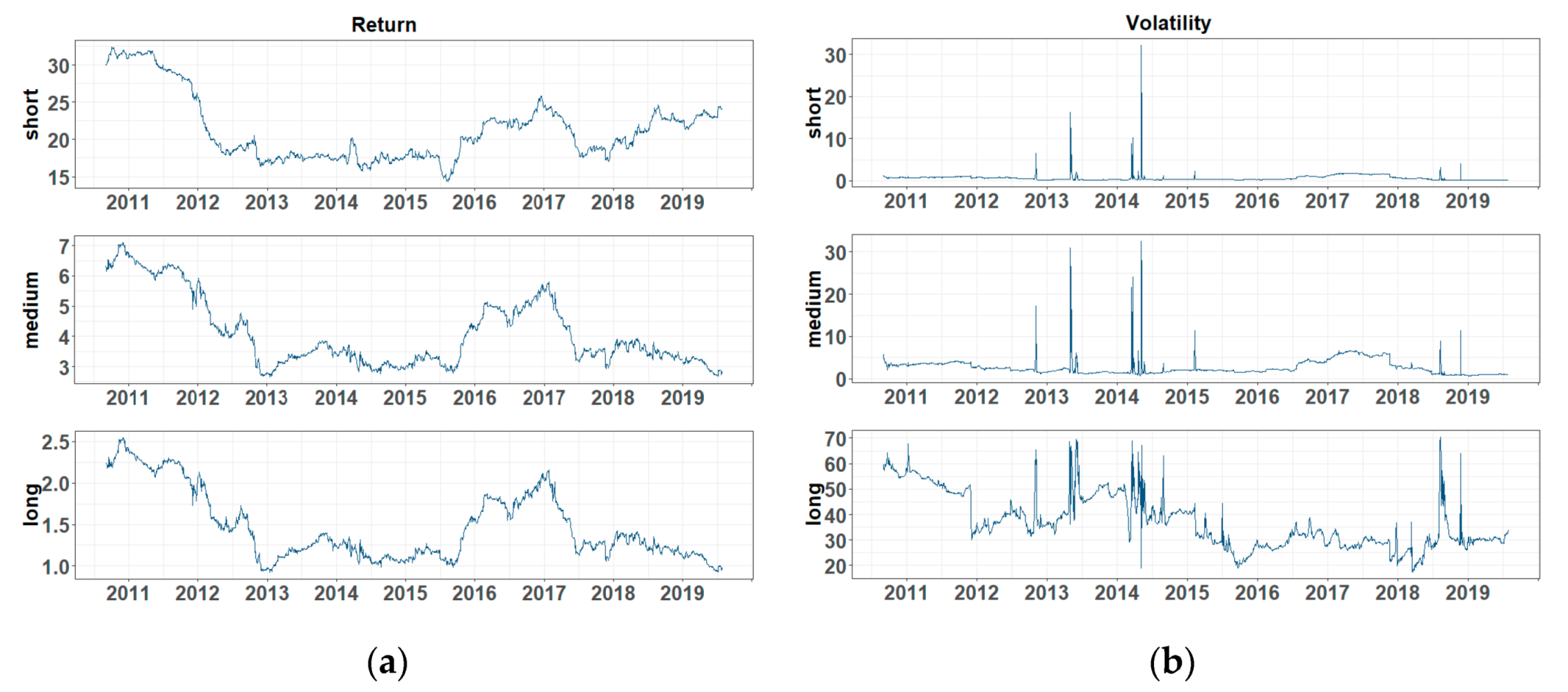
The plot of GASS’s return and volatility series are reported in
Figure A1. We found that some values of volatility were extremely large (the maximum is over 800). We think that the reason for this is that the natural gas spot price was more easily affected by the change of demand and supply than the future price, even though the change was small.
We summarize the results of connectedness and the frequency decomposition of short, medium, and long term in
Table A1,
Table A3,
Table A4,
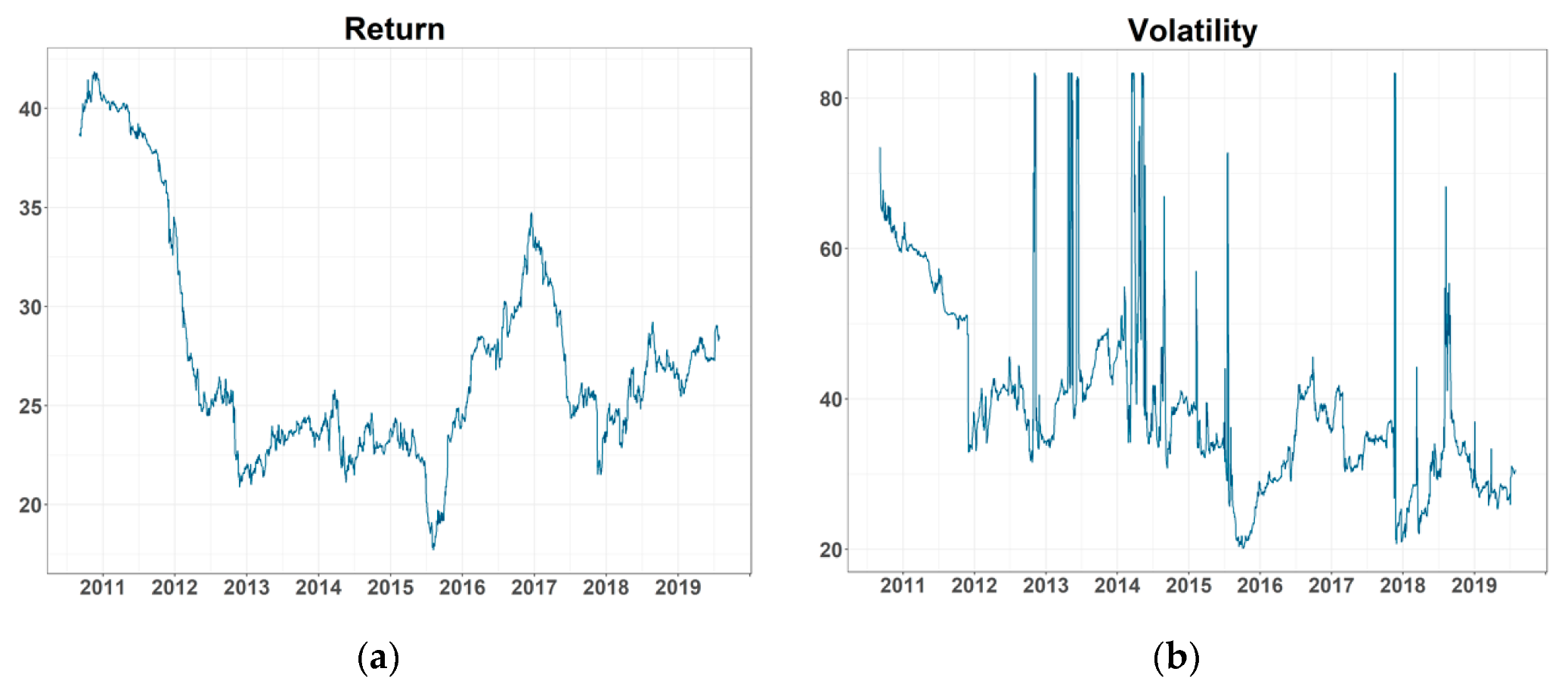
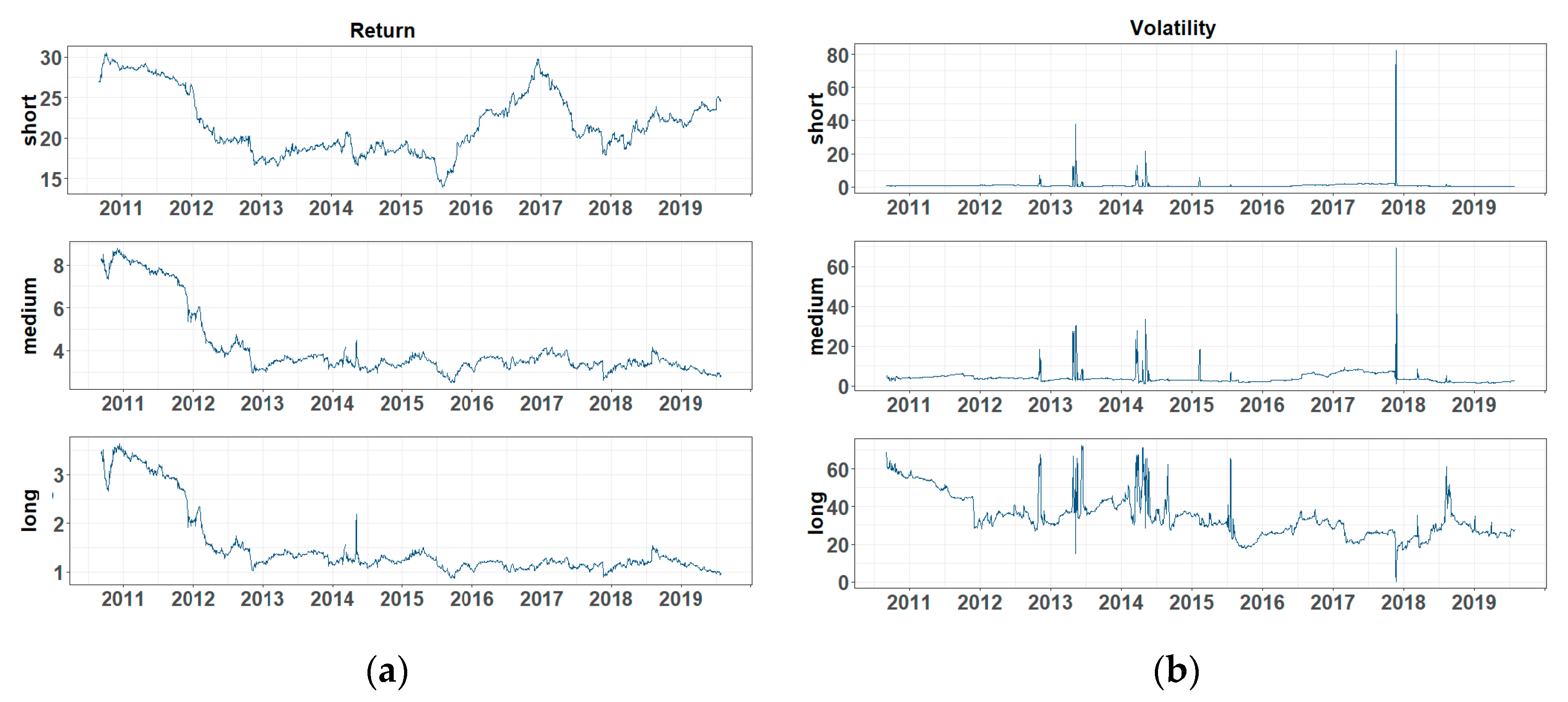
Table A5, respectively. The result is quite similar to that of GASF and exchange rates. We also used a 300 rolling-window to conduct the time-varying analysis. The dynamic connectedness and its spectral representation are plotted in
Figure A2 and
Figure A3, respectively. The net pairwise connectedness of return series and volatilities are illustrated in
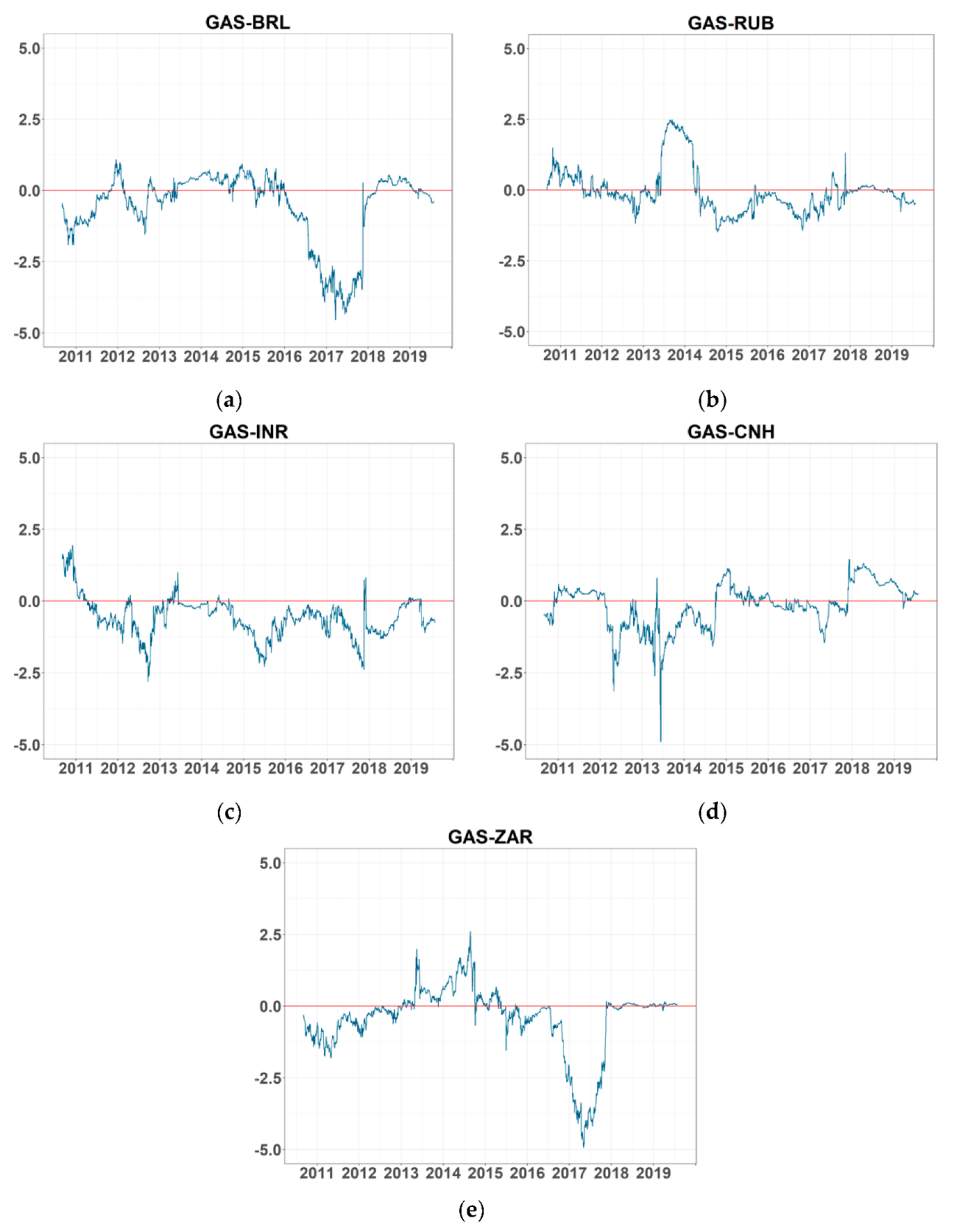
Figure A4 and
Figure A5, respectively. All results are consistent with those from the analysis using the natural gas future price, except for the net pairwise connectedness of return series (
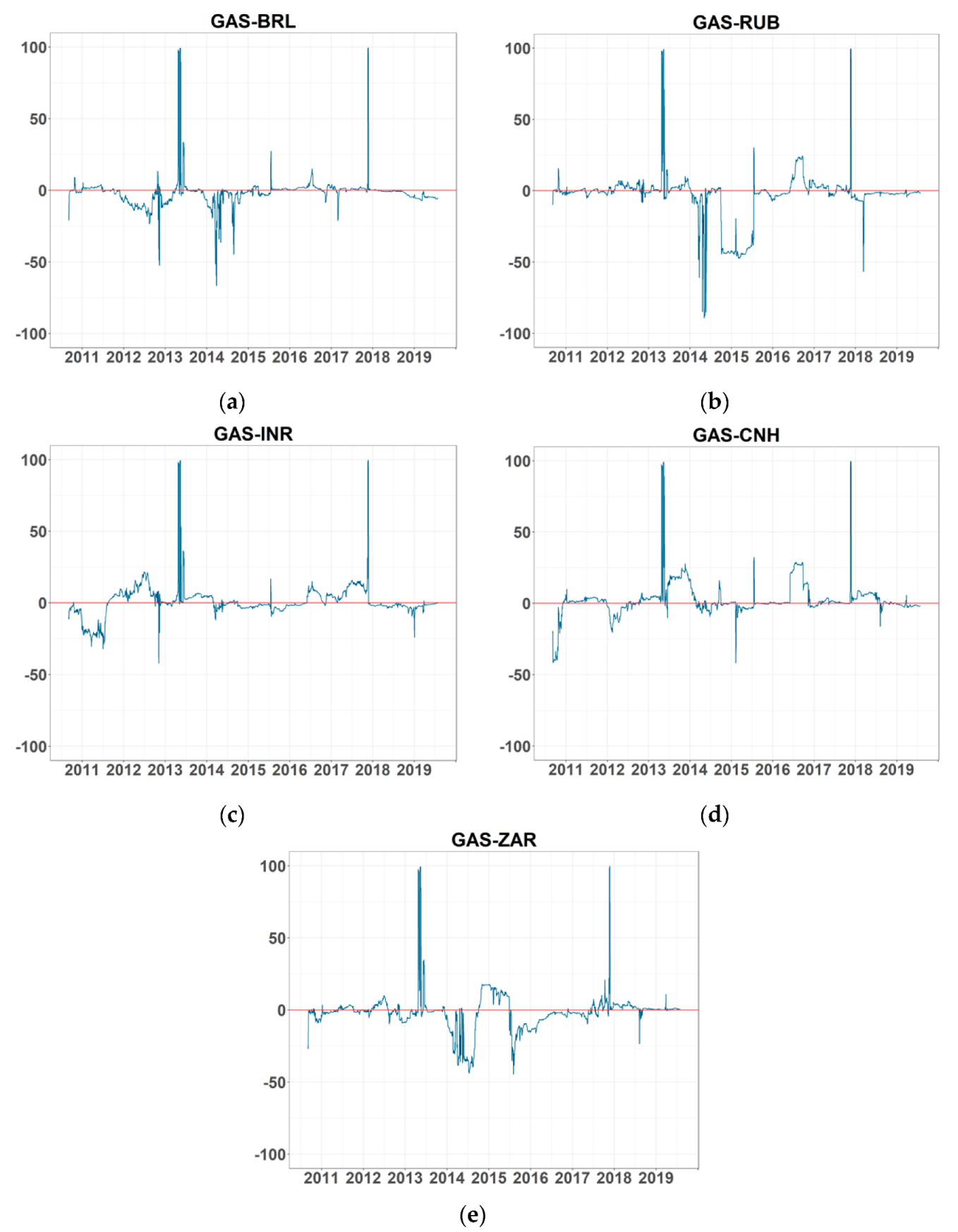
Figure A4). Some values are opposite to the result above, but all of them are low, even the maximum value, which is less than 5% and negligible.
The results of robustness confirm the suitability of our proposed approach, which aimed to capture the relationship between the natural gas price and exchange rates.
Table A1.
Connectedness between the natural gas spot price and BRICS’s exchange rates.
Table A1.
Connectedness between the natural gas spot price and BRICS’s exchange rates.
| | BRL | RUB | INR | CNH | ZAR | GASS | From | GAS-FX |
|---|
| Return |
| BRL | 69.839 | 7.714 | 1.456 | 3.124 | 17.688 | 0.179 | 30.161 | −0.249 |
| RUB | 8.323 | 73.405 | 2.681 | 3.276 | 12.230 | 0.085 | 26.595 | −0.058 |
| INR | 5.571 | 3.833 | 77.727 | 3.652 | 9.066 | 0.152 | 22.273 | 0.040 |
| CNH | 3.588 | 3.648 | 3.378 | 81.296 | 7.953 | 0.137 | 18.704 | 0.136 |
| ZAR | 16.233 | 10.559 | 3.252 | 6.206 | 63.643 | 0.108 | 36.357 | 0.094 |
| GASS | 0.429 | 0.143 | 0.113 | 0.001 | 0.014 | 99.301 | 0.699 | |
| To | 34.143 | 25.896 | 10.879 | 16.259 | 46.951 | 0.660 | 22.465 | |
| Net | 3.983 | −0.699 | −11.394 | −2.444 | 10.593 | −0.039 | | |
| Volatility |
| BRL | 75.533 | 3.660 | 0.288 | 0.354 | 20.138 | 0.025 | 24.467 | −0.377 |
| RUB | 0.890 | 97.569 | 0.750 | 0.298 | 0.479 | 0.014 | 2.431 | −0.006 |
| INR | 3.133 | 0.494 | 92.791 | 0.277 | 3.235 | 0.070 | 7.209 | −0.234 |
| CNH | 3.679 | 0.213 | 2.713 | 85.576 | 7.123 | 0.696 | 14.424 | 0.678 |
| ZAR | 11.251 | 0.282 | 0.801 | 1.067 | 86.363 | 0.236 | 13.637 | 0.208 |
| GASS | 0.402 | 0.020 | 0.304 | 0.018 | 0.028 | 99.229 | 0.771 | |
| To | 19.356 | 4.669 | 4.856 | 2.015 | 31.003 | 1.041 | 10.490 | |
| Net | −5.111 | 2.238 | −2.354 | −12.410 | 17.367 | 0.270 | | |
Table A2.
Connectedness between the UK NBP and BRICS’s exchange rates.
Table A2.
Connectedness between the UK NBP and BRICS’s exchange rates.
| | BRL | RUB | INR | CNH | ZAR | GASS | From | GAS-FX |
|---|
| Return |
| BRL | 69.761 | 7.791 | 1.352 | 3.139 | 17.707 | 0.249 | 30.239 | −0.099 |
| RUB | 8.337 | 73.395 | 2.660 | 3.307 | 12.251 | 0.049 | 26.605 | −0.014 |
| INR | 5.472 | 3.796 | 77.446 | 3.686 | 9.115 | 0.485 | 22.554 | 0.134 |
| CNH | 3.600 | 3.676 | 3.391 | 80.904 | 7.971 | 0.458 | 19.096 | −0.088 |
| ZAR | 16.162 | 10.491 | 3.227 | 6.215 | 63.346 | 0.559 | 36.654 | −0.286 |
| GASS | 0.348 | 0.062 | 0.352 | 0.546 | 0.845 | 97.847 | 2.153 | |
| To | 33.919 | 25.816 | 10.983 | 16.893 | 47.889 | 1.800 | 22.883 | |
| Net | 3.680 | −0.788 | −11.571 | −2.204 | 11.236 | −0.353 | | |
| Volatility |
| BRL | 75.164 | 3.509 | 0.542 | 0.277 | 20.254 | 0.254 | 24.836 | −0.041 |
| RUB | 0.947 | 96.034 | 0.952 | 0.188 | 0.549 | 1.329 | 3.966 | 1.213 |
| INR | 3.494 | 0.244 | 90.752 | 0.328 | 3.404 | 1.778 | 9.248 | −1.243 |
| CNH | 3.879 | 0.269 | 2.684 | 85.577 | 6.804 | 0.788 | 14.423 | 0.611 |
| ZAR | 11.028 | 0.318 | 0.775 | 0.822 | 86.380 | 0.677 | 13.620 | −0.742 |
| GASS | 0.295 | 0.116 | 3.021 | 0.177 | 1.419 | 94.971 | 5.029 | |
| To | 19.643 | 4.456 | 7.974 | 1.792 | 32.430 | 4.827 | 11.854 | |
| Net | −5.193 | 0.491 | −1.274 | −12.631 | 18.810 | −0.202 | | |
Table A3.
Connectedness between the natural gas spot price and exchange rates in the frequency domain (short term).
Table A3.
Connectedness between the natural gas spot price and exchange rates in the frequency domain (short term).
| | BRL | RUB | INR | CNH | ZAR | GASS | From | GAS-FX |
|---|
| Return |
| BRL | 58.953 | 6.079 | 1.107 | 2.772 | 14.530 | 0.118 | 24.606 | −0.295 |
| RUB | 6.713 | 58.808 | 2.160 | 2.705 | 9.511 | 0.057 | 21.146 | −0.060 |
| INR | 4.027 | 2.716 | 64.161 | 2.696 | 6.053 | 0.150 | 15.641 | 0.075 |
| CNH | 2.969 | 3.124 | 2.809 | 66.238 | 6.361 | 0.096 | 15.357 | 0.095 |
| ZAR | 13.475 | 8.616 | 2.769 | 5.042 | 51.620 | 0.089 | 29.991 | 0.081 |
| GASS | 0.414 | 0.118 | 0.075 | 0.001 | 0.008 | 81.932 | 0.615 | |
| To | 27.597 | 20.653 | 8.919 | 13.216 | 36.463 | 0.510 | 17.893 | |
| Net | 2.991 | −0.494 | −6.722 | −2.141 | 6.472 | −0.106 | | |
| Volatility |
| BRL | 2.698 | 0.002 | 0.028 | 0.002 | 0.205 | 0.002 | 0.238 | −0.003 |
| RUB | 0.001 | 1.256 | 0.011 | 0.002 | 0.026 | 0.001 | 0.041 | −0.003 |
| INR | 0.016 | 0.009 | 1.099 | 0.006 | 0.030 | 0.000 | 0.061 | −0.001 |
| CNH | 0.010 | 0.002 | 0.022 | 5.130 | 0.056 | 0.004 | 0.093 | 0.001 |
| ZAR | 0.090 | 0.011 | 0.014 | 0.006 | 1.193 | 0.000 | 0.121 | −0.001 |
| GASS | 0.005 | 0.004 | 0.001 | 0.004 | 0.001 | 8.637 | 0.015 | |
| To | 0.123 | 0.028 | 0.076 | 0.019 | 0.318 | 0.007 | 0.095 | |
| Net | −0.116 | −0.014 | 0.015 | −0.075 | 0.197 | −0.008 | | |
Table A4.
Connectedness between the natural gas spot price and exchange rates in the frequency domain (medium term).
Table A4.
Connectedness between the natural gas spot price and exchange rates in the frequency domain (medium term).
| | BRL | RUB | INR | CNH | ZAR | GASS | From | GAS-FX |
|---|
| Return |
| BRL | 8.061 | 1.197 | 0.254 | 0.265 | 2.325 | 0.045 | 4.086 | 0.032 |
| RUB | 1.195 | 10.750 | 0.382 | 0.423 | 1.997 | 0.020 | 4.018 | 0.001 |
| INR | 1.143 | 0.821 | 10.068 | 0.705 | 2.216 | 0.003 | 4.888 | −0.025 |
| CNH | 0.465 | 0.392 | 0.426 | 11.137 | 1.177 | 0.030 | 2.489 | 0.030 |
| ZAR | 2.045 | 1.423 | 0.359 | 0.856 | 8.868 | 0.014 | 4.697 | 0.010 |
| GASS | 0.013 | 0.019 | 0.028 | 0.000 | 0.004 | 13.017 | 0.065 | |
| To | 4.861 | 3.852 | 1.448 | 2.250 | 7.720 | 0.113 | 3.374 | |
| Net | 0.775 | −0.166 | −3.440 | −0.240 | 3.023 | 0.048 | | |
| Volatility |
| BRL | 9.181 | 0.005 | 0.052 | 0.020 | 1.331 | 0.005 | 1.413 | −0.030 |
| RUB | 0.007 | 3.981 | 0.043 | 0.013 | 0.090 | 0.002 | 0.155 | −0.003 |
| INR | 0.253 | 0.076 | 5.828 | 0.015 | 0.084 | 0.002 | 0.430 | −0.012 |
| CNH | 0.090 | 0.003 | 0.086 | 14.160 | 0.385 | 0.093 | 0.657 | 0.087 |
| ZAR | 0.486 | 0.050 | 0.049 | 0.005 | 4.430 | 0.006 | 0.596 | 0.002 |
| GASS | 0.036 | 0.005 | 0.014 | 0.007 | 0.004 | 35.740 | 0.065 | |
| To | 0.872 | 0.139 | 0.244 | 0.059 | 1.894 | 0.108 | 0.553 | |
| Net | −0.541 | −0.016 | −0.186 | −0.598 | 1.298 | 0.044 | | |
Table A5.
Connectedness between the natural gas spot price and exchange rates in the frequency domain (long term).
Table A5.
Connectedness between the natural gas spot price and exchange rates in the frequency domain (long term).
| | BRL | RUB | INR | CNH | ZAR | GASS | From | GAS-FX |
|---|
| Return |
| BRL | 2.825 | 0.437 | 0.095 | 0.087 | 0.833 | 0.016 | 1.468 | 0.014 |
| RUB | 0.415 | 3.847 | 0.138 | 0.149 | 0.722 | 0.007 | 1.431 | 0.001 |
| INR | 0.401 | 0.296 | 3.498 | 0.250 | 0.797 | 0.000 | 1.744 | −0.010 |
| CNH | 0.155 | 0.132 | 0.144 | 3.921 | 0.415 | 0.010 | 0.857 | 0.010 |
| ZAR | 0.713 | 0.520 | 0.124 | 0.308 | 3.155 | 0.005 | 1.669 | 0.003 |
| GASS | 0.001 | 0.006 | 0.010 | 0.000 | 0.002 | 4.352 | 0.019 | |
| To | 1.685 | 1.391 | 0.512 | 0.793 | 2.769 | 0.038 | 1.198 | |
| Net | 0.217 | −0.040 | −1.232 | −0.063 | 1.099 | 0.019 | | |
| Volatility |
| BRL | 63.654 | 3.654 | 0.208 | 0.333 | 18.603 | 0.018 | 22.815 | −0.343 |
| RUB | 0.882 | 92.332 | 0.696 | 0.283 | 0.362 | 0.011 | 2.234 | 0.001 |
| INR | 2.864 | 0.409 | 85.864 | 0.257 | 3.121 | 0.068 | 6.719 | −0.221 |
| CNH | 3.580 | 0.209 | 2.605 | 66.285 | 6.682 | 0.598 | 13.674 | 0.591 |
| ZAR | 10.675 | 0.220 | 0.738 | 1.056 | 80.740 | 0.230 | 12.919 | 0.207 |
| GASS | 0.361 | 0.011 | 0.289 | 0.008 | 0.023 | 54.851 | 0.691 | |
| To | 18.362 | 4.502 | 4.535 | 1.937 | 28.790 | 0.926 | 9.842 | |
| Net | −4.454 | 2.268 | −2.183 | −11.737 | 15.872 | 0.235 | | |
Figure A1.
Daily return and volatility: (a) return series and (b) volatility.
Figure A1.
Daily return and volatility: (a) return series and (b) volatility.
Figure A2.
Dynamic connectedness: (a) total connectedness of return series and (b) total connectedness of volatilities. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
Figure A2.
Dynamic connectedness: (a) total connectedness of return series and (b) total connectedness of volatilities. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
Figure A3.
Frequency decomposition of dynamic connectedness: (a) frequency decomposition of total connectedness for return series and (b) frequency decomposition of total connectedness for volatilities. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
Figure A3.
Frequency decomposition of dynamic connectedness: (a) frequency decomposition of total connectedness for return series and (b) frequency decomposition of total connectedness for volatilities. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
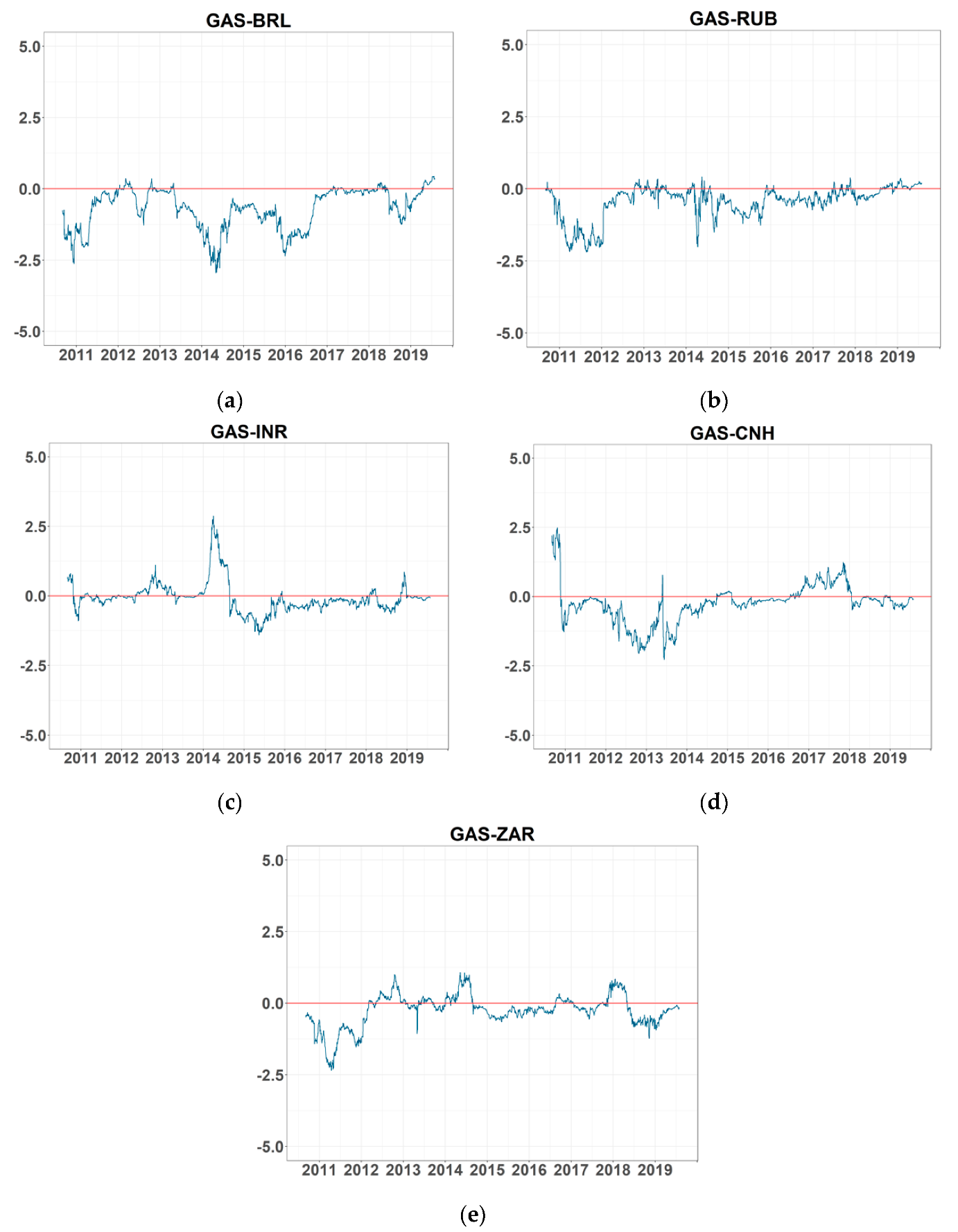
Figure A4.
Net pairwise connectedness of return series: (a–e) refer to the net pairwise connectedness between GASS and BRL, RUB, INR, CNH, and ZAR return series, respectively. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
Figure A4.
Net pairwise connectedness of return series: (a–e) refer to the net pairwise connectedness between GASS and BRL, RUB, INR, CNH, and ZAR return series, respectively. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
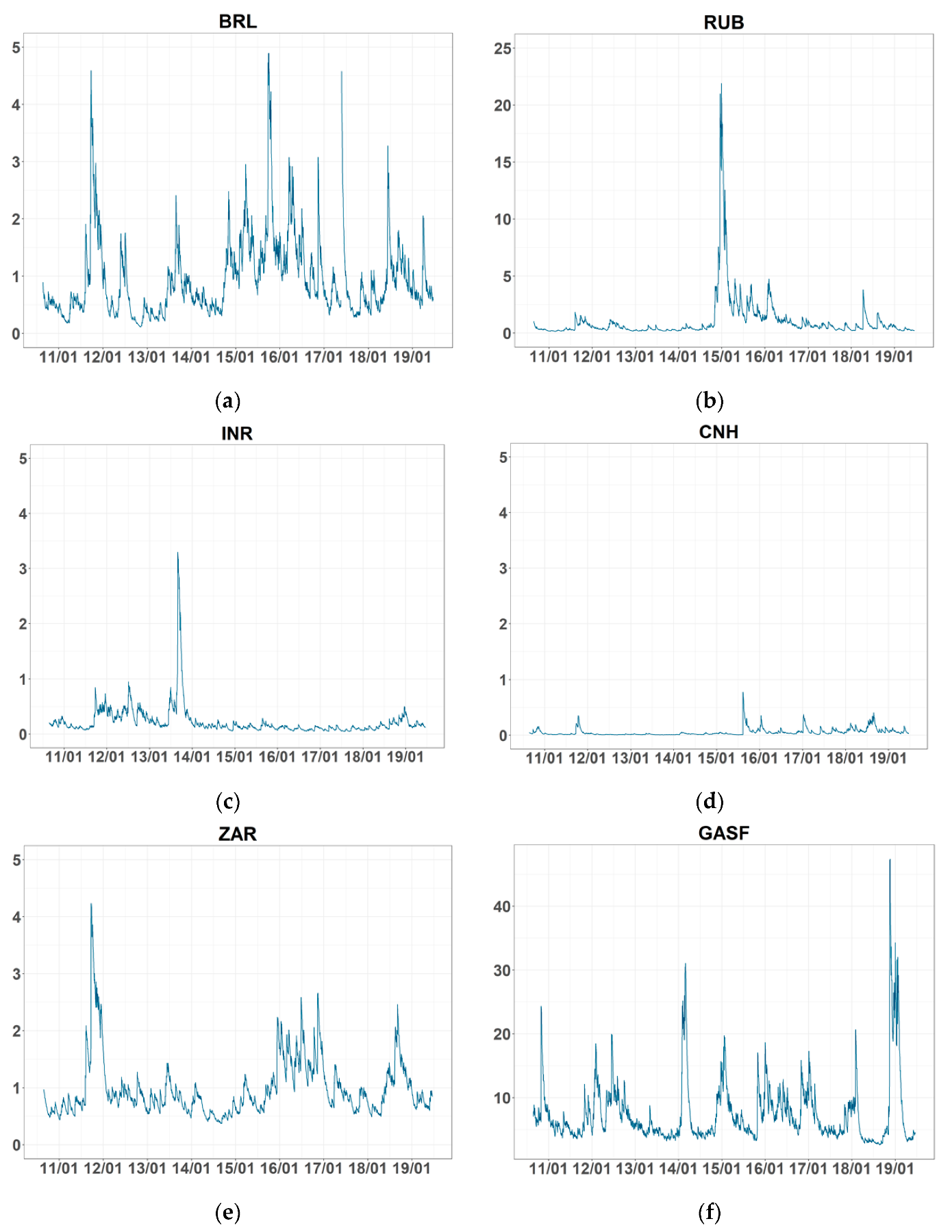
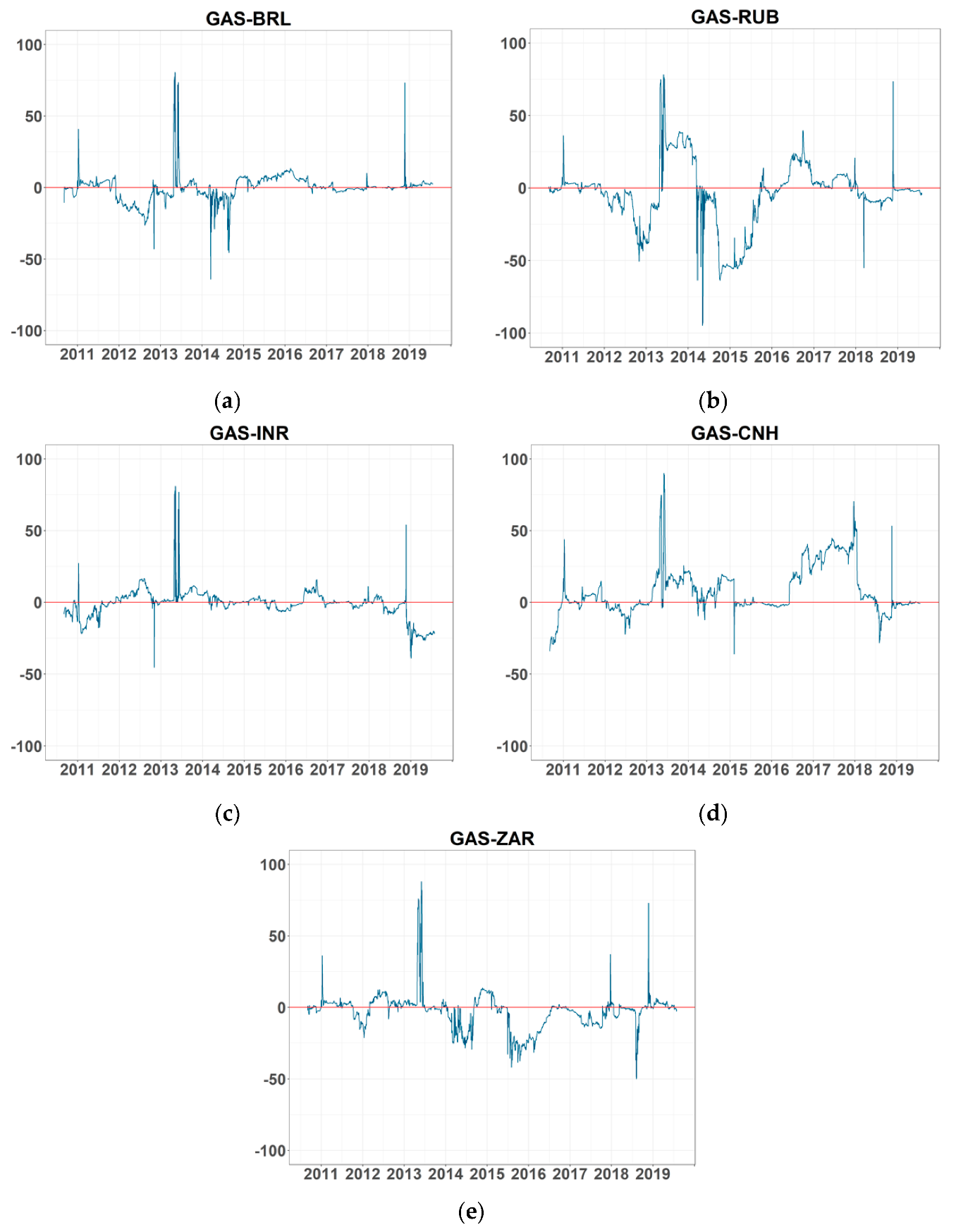
Figure A5.
Net pairwise connectedness of volatility. (a–e) refer to the net pairwise connectedness between the volatility of GASS and BRL, RUB, INR, CNH, and ZAR, respectively. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.
Figure A5.
Net pairwise connectedness of volatility. (a–e) refer to the net pairwise connectedness between the volatility of GASS and BRL, RUB, INR, CNH, and ZAR, respectively. Note: BRL, RUB, INR, CNH, and ZAR are Brazilian Real, Russian Ruble, Indian Rupee, offshore Chinese Yuan, and South African Rand, respectively. GASF is the Henry Hub natural gas futures price.