Calculation of Ion Flow Field of Monopolar Transmission Line in Corona Cage Including the Effect of Wind
Abstract
:1. Introduction
2. Mathematical Description
2.1. Governing Equations and Simplifying Assumption
- b is the ion mobility, 1.5 × 10−4, m2/V/s;
- E is the electric field, V/m;
- ρ is the negative space charge density, C/m3;
- J− is the negative ion current density vector, A/m2;
- W is the wind velocity vector, m/s; and
- ε0 is the permittivity of air equals 8.854 × 10−12, F/m.
- (a)
- The thin ionization layer close to the conductor surface is neglected;
- (b)
- The ion mobility remains unchanged throughout the solution process;
- (c)
- Influence exerted by ion diffusion is ignored;
- (d)
- Kaptzov’s assumption [21] which presumes the electric field on conductor surface remains constant after the applied voltage reaches the onset value is adopted.
2.2. Boundary Conditions
- Vapp is the voltage supplied on the conductor, V;
- ρs refers to the space charge density on the conductor surface, C/m3;
- Eon is the onset electric field, V/m; and
- Eon is assumed to be constant on the conductor surface according to Kaptzov’s assumption, the explicit value is attained using Peek’s empirical formula [22]:
- m is the roughness factor set to 0.65; and
- r is the radius of the conductor, m.
- Eg is the ground level electric field under the conductor, V/m;
- Ec is the nominal electric field on the conductor, V/m;
- Vc is the onset voltage of the conductor, V;
- Vcon is the conductor voltage, V; and
- Hcon is the height of the conductor, m.
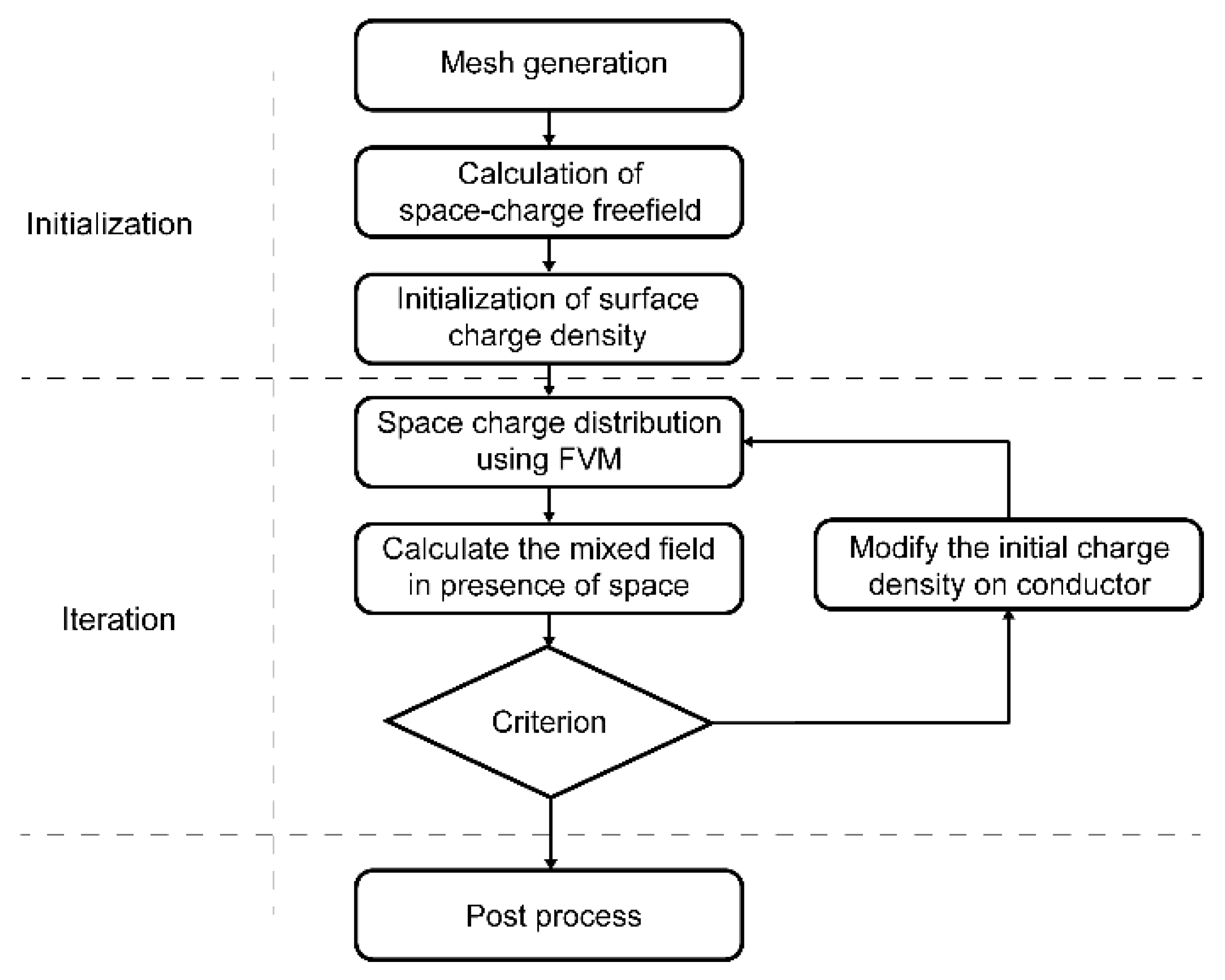
3. Solution Process
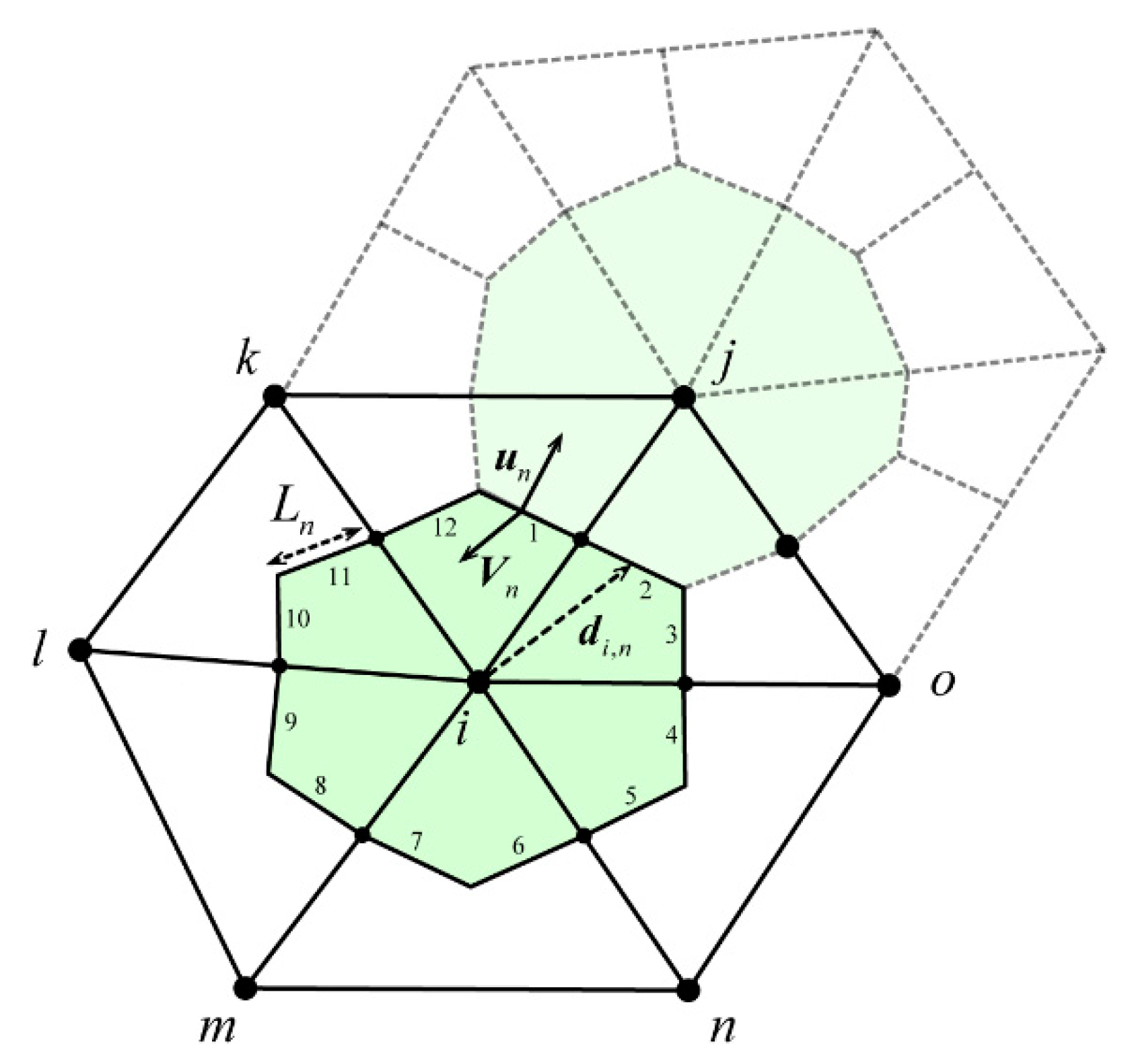
3.1. Discretization of Calculation Domain
3.2. Calculation of Electric Field
- sj is the area of the polygon cell, m3;
- ri and rj are the distances between the observation point to the source, m;
- and are the distances between the observation point to the image points, m;
- Qi are the simulation charges consist of Qcond and Qcage, C; and
- ρj is the charge density on triangulation nodes, C/m3.
3.3. Calculation of Ion Current Density
- s and l are the area and boundary of the cell.
- Vn = bEn + Wn, En and Wn are the outward normal component of electric field and wind speed on cell edges, and
- Ln is the length of the ith cell; and
- n presents the serial number of the edges.
- ρi,n is the charge density on the edge, C/m3;
- di,n is the vector direct from the ith node to the corresponding neighboring nodes; and
- ∇ρi,n and ∇ρn,i are the gradient of corresponding upwind node.
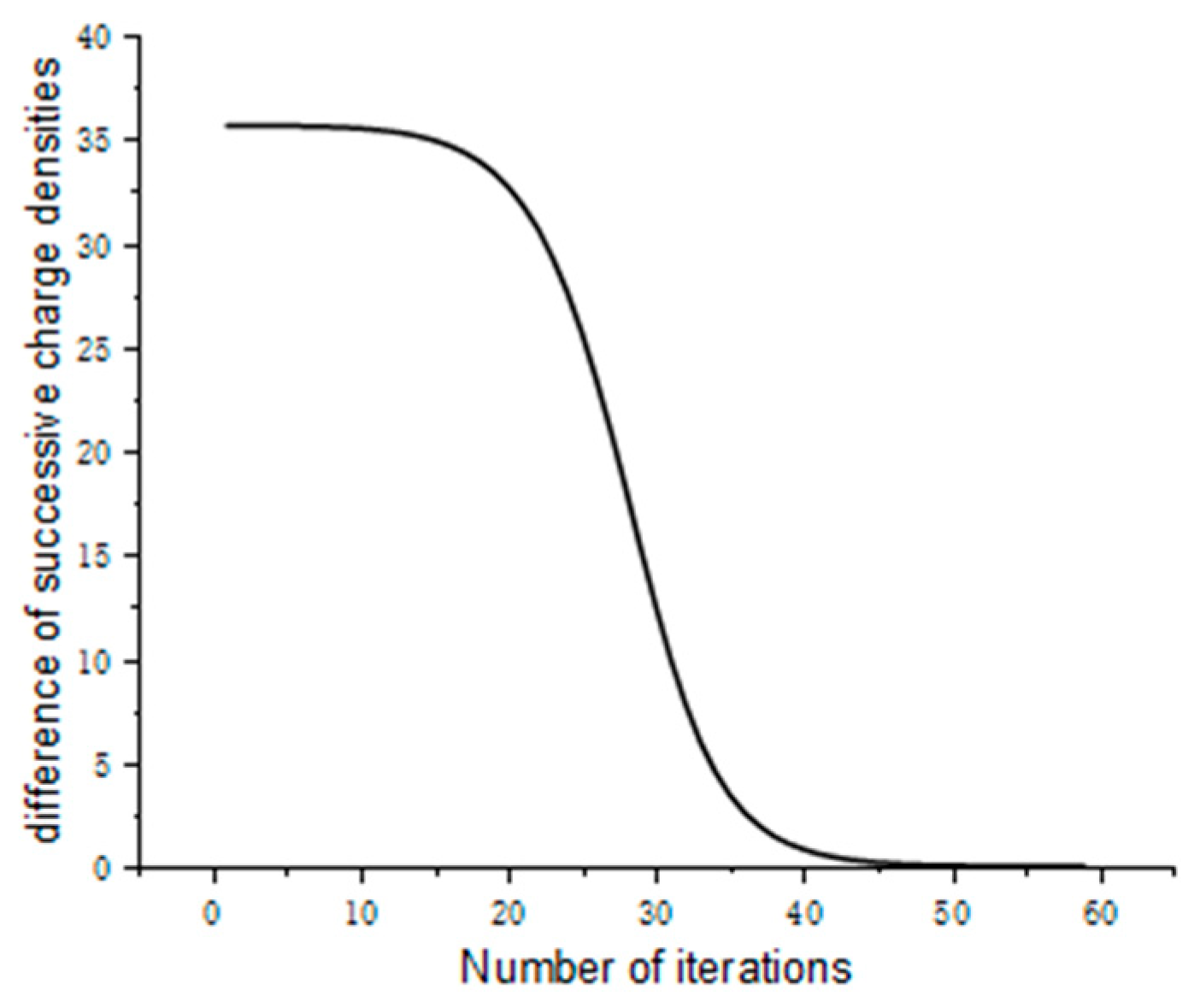
3.4. Terminal Criteria and Initial Charge Density
- δE and δρ are relative terminal criteria;
- Ec is the electric field on conductor surface, V/m; and
- ρm,i and ρm−1,i are consecutive space charge densities of the iteration process in ith cell, C/m3.
- ρm−1, ρm are charge densities of two consecutive iteration on conductor surface, C/m3; and
- μ is the acceleration factor equals to two.
4. Validation
4.1. Design of the Experiment
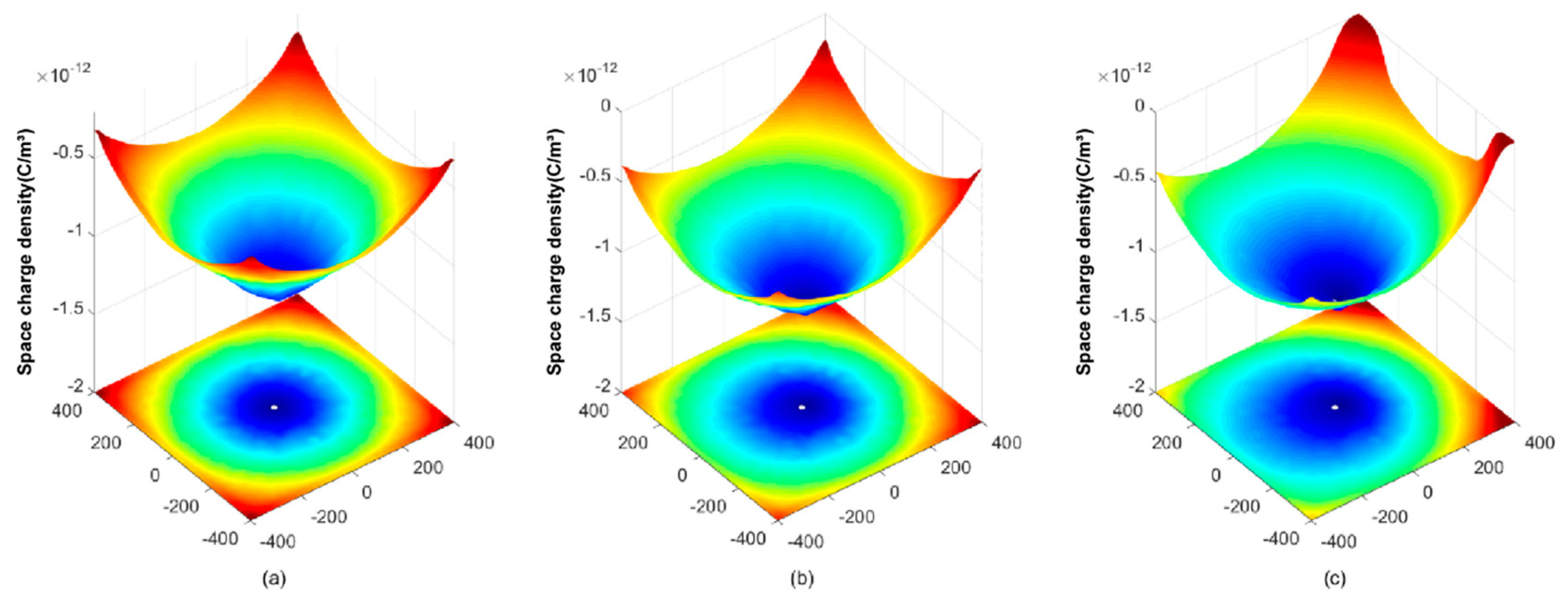
4.2. Discussion of Numerical and Measured Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Maruvada, P.S. Corona Performance of High-Voltage Transmission Lines; Research Studies Press Baldock: Herfordshire, UK, 2000. [Google Scholar]
- Janischewskyj, W.; Cela, G. Finite Element Solution for Electric Fields of Coronating DC Transmission Lines. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 1000–1012. [Google Scholar] [CrossRef]
- Takuma, T.; Ikeda, T.; Kawamoto, T. Calculation of ION Flow Fields of HVDC Transmission Lines By the Finite Element Method. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 4802–4810. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Farghally, M.; Abdel-Sattar, S. Finite element solution of monopolar corona equation. IEEE Trans. Electr. Insul. 1983, EI-18, 110–119. [Google Scholar] [CrossRef]
- Li, X.; Ciric, I.R.; Raghuveer, M.R. Highly stable finite volume based relaxation iterative algorithm for solution of DC line ionized fields in the presence of wind. Int. J. Numer. Model. Electron. Netw. Devices Fields 1997, 10, 355–370. [Google Scholar] [CrossRef]
- Davis, J.L.; Hoburg, J.F. HVDC transmission line computations using finite element and characteristics method. J. Electrost. 1986, 18, 1–22. [Google Scholar] [CrossRef]
- Fortin, S.; Zhao, H.; Ma, J.; Member, S.; Dawalibi, F.P. A New Approach to Calculate the Ionized Field Transmission Lines in the Space and on the Earth Surface. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006. [Google Scholar]
- Zhou, X.; Cui, X.; Lu, T.; Fang, C.; Zhen, Y. Spatial distribution of ion current around HVDC bundle conductors. IEEE Trans. Power Deliv. 2012, 27, 380–390. [Google Scholar] [CrossRef]
- Guillod, T.; Pfeiffer, M.; Franck, C.M. Improved coupled ion-flow field calculation method for AC/DC hybrid overhead power lines. IEEE Trans. Power Deliv. 2014, 29, 2493–2501. [Google Scholar] [CrossRef]
- Zhang, B.; Mo, J.; He, J.; Zhuang, C. A Time-domain Approach of Ion Flow Field around AC-DC hybrid Transmission Lines Based on Method of Characteristics. IEEE Trans. Magn. 2015, 52, 7205004. [Google Scholar] [CrossRef]
- Lu, T.; Feng, H.; Cui, X.; Zhao, Z.; Li, L. Analysis of the ionized field under HVDC transmission lines in the presence of wind based on upstream finite element method. IEEE Trans. Magn. 2010, 46, 2939–2942. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, T.; Cui, X.; Zhen, Y.; Liu, G. Simulation of ion-flow field using fully coupled upwind finite-element method. IEEE Trans. Power Deliv. 2012, 27, 1574–1582. [Google Scholar] [CrossRef]
- Levin, P.L.; Hoburg, J.F. Donor Cell-Finite Element Descriptions of Wire-Duct Precipitator Fields, Charges, and Efficiencies. IEEE Trans. Ind. Appl. 1990, 26, 662–670. [Google Scholar] [CrossRef]
- Zhang, B.; He, J.; Zeng, R.; Gu, S.; Cao, L. Calculation of Ion Flow Field Under HVdc Bipolar Transmission Lines by Integral Equation Method. IEEE Trans. Magn. 2007, 43, 1237–1240. [Google Scholar] [CrossRef]
- Long, Z.; Yao, Q.; Song, Q.; Li, S. A second-order accurate finite volume method for the computation of electrical conditions inside a wire-plate electrostatic precipitator on unstructured meshes. J. Electrost. 2009, 67, 597–604. [Google Scholar] [CrossRef]
- Yin, H.; He, J.; Zhang, B.; Zeng, R. Finite volume-based approach for the hybrid ion-flow field of UHVAC and UHVDC transmission lines in parallel. IEEE Trans. Power Deliv. 2011, 26, 2809–2820. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, B.; He, J.; Zeng, R.; Li, R. Time-domain finite volume method for ion-flow field analysis of bipolar high-voltage direct current transmission lines. IET Gener. Transm. Distrib. 2012, 6, 785–791. [Google Scholar] [CrossRef]
- Yang, F.; Liu, Z.; Luo, H.; Liu, X.; He, W. Calculation of ionized field of HVDC transmission lines by the meshless method. IEEE Trans. Magn. 2014, 50, 7200406. [Google Scholar] [CrossRef]
- Bian, X.; Yu, D.; Meng, X.; Macalpine, M.; Wang, L.; Guan, Z.; Yao, W.; Zhao, S. Corona-generated space charge effects on electric field distribution for an indoor corona cage and a monopolar test line. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1767–1778. [Google Scholar] [CrossRef]
- Lekganyane, M.J.; Ijumba, N.M.; Britten, A.C. A comparative study of space charge effects on corona current using an indoor corona cage and a monopolar test line. In Proceedings of the 2007 IEEE Power Engineering Society Conference and Exposition in Africa, Johannesburg, South Africa, 16–20 July 2007. [Google Scholar]
- Kaptzov, N.A. Elektrische Vorgänge in Gasen und im Vakuum; VEB Deutscher Verlag der Wissenschaften: Berlin, Germany, 1955; pp. 488–491. ISBN 978-3-446-42771-6. [Google Scholar]
- Peek, F.W. Dielectric Phenomena in High Voltage Engineering; McGraw-Hill Book Company, Inc: New York, NY, USA, 1920. [Google Scholar]
- Abdel-salam, M.; Al-hamouz, Z. A finite-element analysis of bipolar ionized field. IEEE Tans. Ind. Appl. 1995, 31, 477–483. [Google Scholar] [CrossRef]
- Zhou, X.; Cui, X.; Lu, T.; Zhen, Y.; Luo, Z. A time-efficient method for the simulation of ion flow field of the AC-DC hybrid transmission lines. IEEE Trans. Magn. 2012, 48, 731–734. [Google Scholar] [CrossRef]
- Li, X. Numerical Analysis of Ionized Fields Associated with HVDC Transmission Lines Including Effect of Wind. Ph.D. Thesis, The University of Manitoba, Winnipeg, MB, USA, 1997. [Google Scholar]
- Urban, R.G.; Reader, H.C.; Holtzhausen, J.P. Small corona cage for wideband HVac radio noise studies: Rationale and critical design. IEEE Trans. Power Deliv. 2008, 23, 1150–1157. [Google Scholar] [CrossRef]


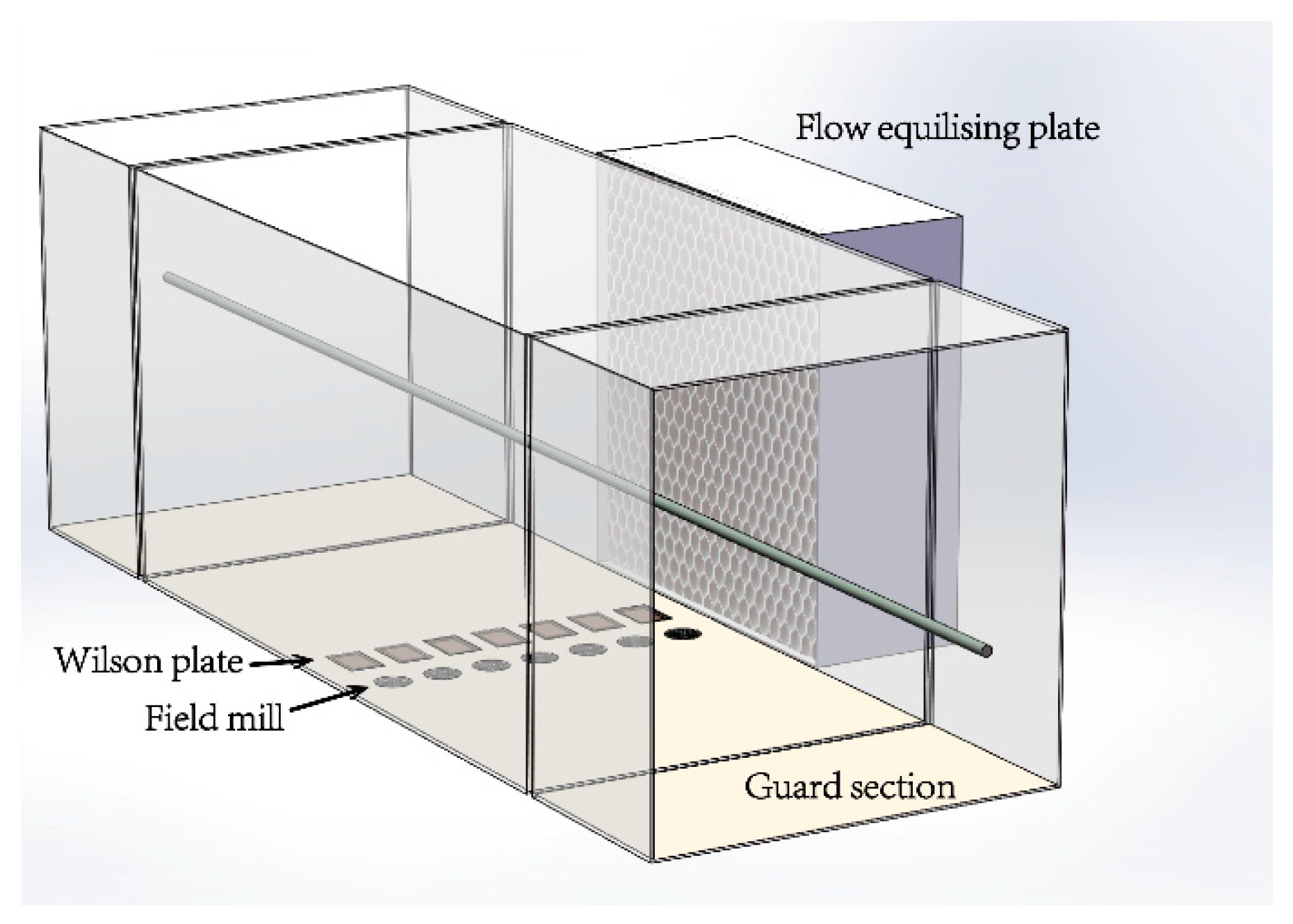

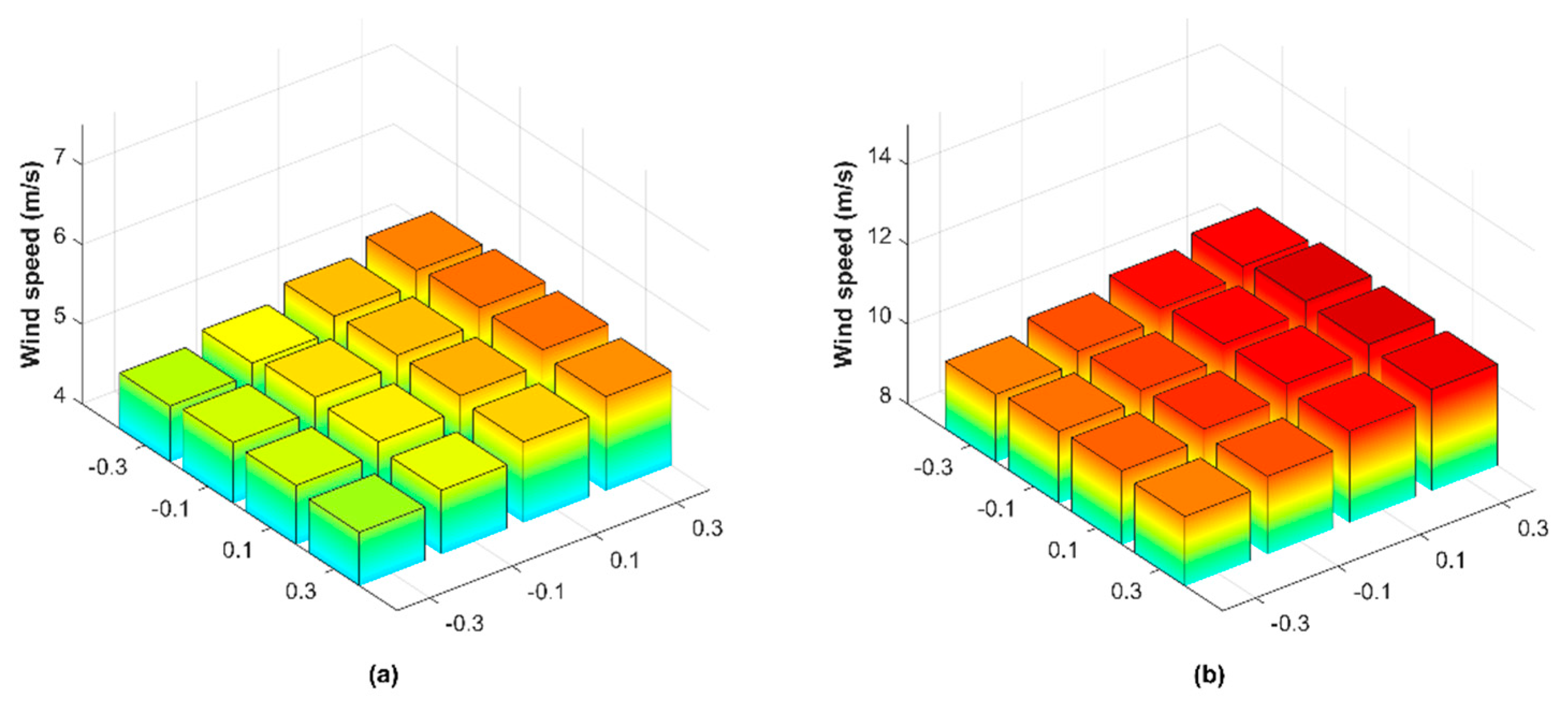
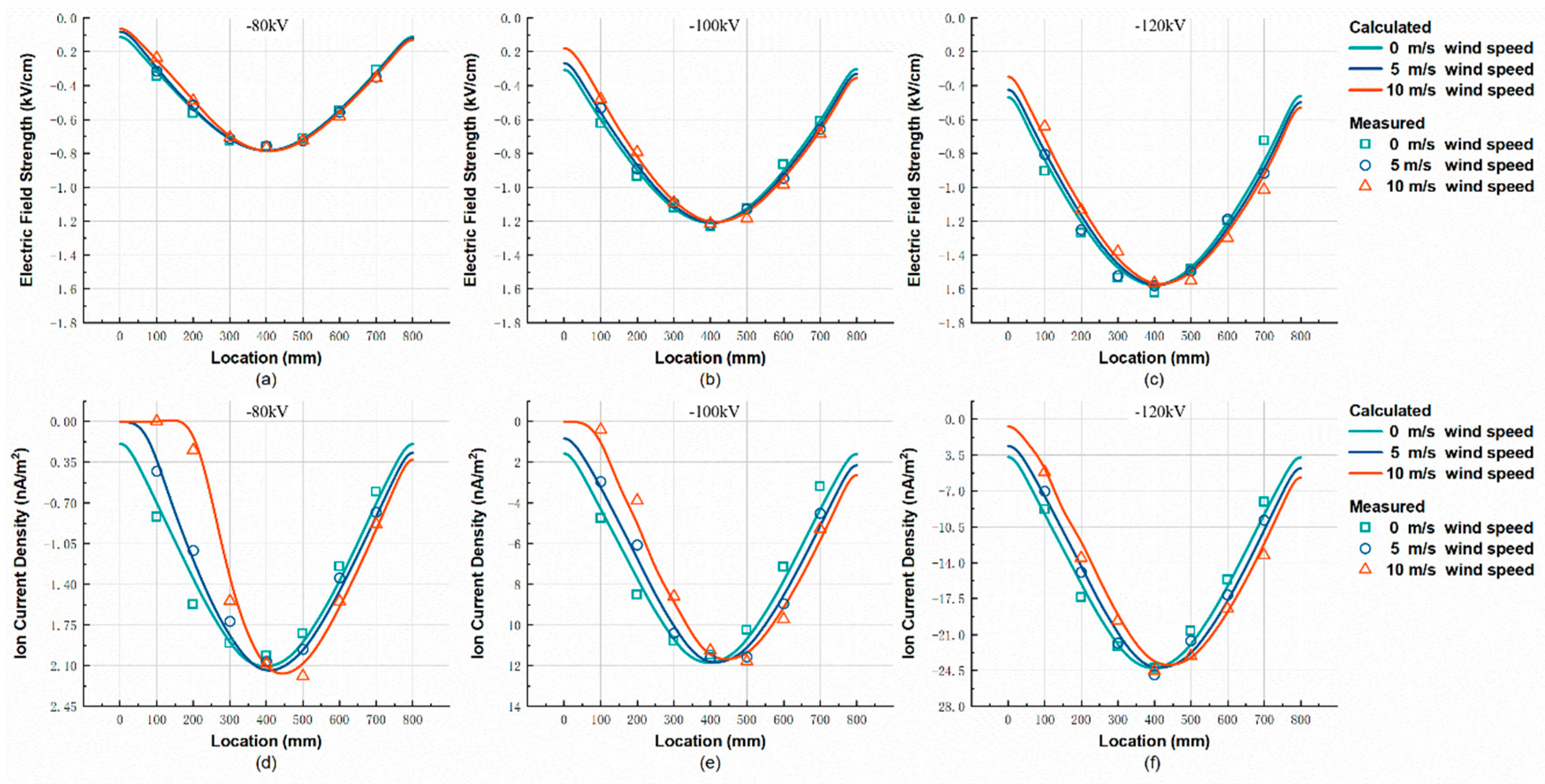

| Distribution Variables | Conductor Surface | Cage Wall |
|---|---|---|
| Electric potential | Vapp | 0 |
| Space-charge density | ρs | |
| Electric field | Eon |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhao, X. Calculation of Ion Flow Field of Monopolar Transmission Line in Corona Cage Including the Effect of Wind. Energies 2019, 12, 3924. https://doi.org/10.3390/en12203924
Li Z, Zhao X. Calculation of Ion Flow Field of Monopolar Transmission Line in Corona Cage Including the Effect of Wind. Energies. 2019; 12(20):3924. https://doi.org/10.3390/en12203924
Chicago/Turabian StyleLi, Zhenyu, and Xuezeng Zhao. 2019. "Calculation of Ion Flow Field of Monopolar Transmission Line in Corona Cage Including the Effect of Wind" Energies 12, no. 20: 3924. https://doi.org/10.3390/en12203924
APA StyleLi, Z., & Zhao, X. (2019). Calculation of Ion Flow Field of Monopolar Transmission Line in Corona Cage Including the Effect of Wind. Energies, 12(20), 3924. https://doi.org/10.3390/en12203924




