Abstract
As new grid codes have been created to permit the integration of large scale photovoltaic power plants into the transmission system, the enhancement of the local control of the photovoltaic (PV) generators is necessary. Thus, the objective of this paper is to present a local controller of active and reactive power to comply the new requirements asked by the transmission system operators despite the variation of ambient conditions without using extra devices. For this purpose, the control considers the instantaneous capability curves of the PV generator which vary due to the change of solar irradiance, temperature, dc voltage and modulation index. To validate the control, the PV generator is modeled in DIgSILENT PowerFactory and tested under different ambient conditions. The results show that the control developed can modify the active and reactive power delivered to the desired value at different solar irradiance and temperature.
1. Introduction
As more large scale photovoltaic power plants (LS-PVPPs) are being installed, the electrical system can face some challenges related to four key areas: (i) active power control, (ii) reactive power control, (iii) voltage support and (iv) frequency support [1]. Thus, many countries have updated their grid codes to permit a smooth interaction between these power plants with the transmission system. For instance, Puerto Rico requires that these PVPPs behaves similar to conventional power plants despite the intermittent conditions [2]. Considering these changes on the grid codes there are two key aspects necessary to approach: active and reactive power control.
According to the grid codes presented by Puerto Rico, Romania, South Africa and Germany, the active power management for LS-PVPPs should consider: power curtailment, ramp rate control and active power reserves (Figure 1) [2,3,4,5]. Power curtailment, also called as absolute control or limiting control, addresses the reduction of the possible active power that the power plant can generate during the day depending on the grid requirements [6]. This requirement prevents overloading at peak generation hours of PVPPs (around midday) or also when the demand is lower than the possible generated active power from the PVPP. However, due to the intermittency of the solar source, ramp rate control is also necessary to be addressed [7]. The aim of these ramp rates is to smooth the change from low to high solar irradiance and vicevesa, so the change does not affect the voltage or the frequency. As more LS-PVPPs are being introduced at the transmission system, the participation on frequency regulation is a new challenge. Thus, power reserve are already being considered in some of the grid codes. The power reserve is the reduction of the output power during some hours of the day. This reduction can oscillate between 10 to 20% of the maximum possible that the PVPP can generate [1,8].
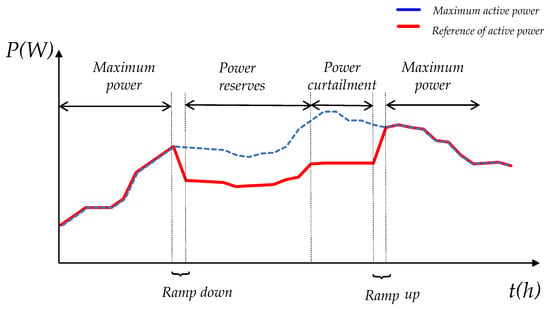
Figure 1.
Active power variation applying the new control functions.
There are two main techniques used to manage the active power: (i) incorporate energy storage, and (ii) new control strategies of the PV generator [1]. In the literature, the main topology proposed is the use of the energy storage together with the PV inverter that are distributed along the PVPP [9,10,11]. For instance, the study developed by Muller et al, proposes the use of ultracapacitors together with a central inverter to manage the power transients due to the variability of solar irradiance. In this study, the output power fluctuations are reduced and it helps to comply the grid code limits [9]. Commonly, the management of the active power relays on the charge of the battery during high solar irradiance and the discharge in high peak demand [12]. This type of control smooths the output power of the single PV generator during the day [11,13,14,15,16,17,18,19]. However, the incorporation of energy storage increases the cost of installation and operation of the LS-PVPP [20]. An alternative solution is the improvement of the control by considering the characteristics of the PV generator. Commonly, the active power is managed by the maximum power point tracker (MPPT) which is part of the overall control of the PV inverter. However, the MPPT cannot withstand the power curtailment, the power reserve or the ramp rates. Therefore, this tracker should not only consider the maximum power point but also the reference of active power given by the transmission system operator (TSO). Some studies propose this method for multistring topologies (two stage inverters) used in small applications [8,21,22]. However, these studies have not been applied for central inverters that are commonly used in LS-PVPPs [23].
In the case of reactive power, the new grid codes require that the LS-PVPP injects or absorbs reactive power according to a predefined relationship between the active and the reactive power (power factor ()) or an specific value of reactive power. The grid codes presented by China, Germany, South Africa, Romania, and Puerto Rico requires that the LS-PVPP works under an specific capability curve (Figure 2). From this curve, it can be seen that Puerto Rico has the strictest requirement ( p.u). Meanwhile, China, Germany, Romania and South Africa require a maximum reactive power close to p.u. To comply these grid codes, commonly STATCOMs or capacitors are added at the point of common coupling (PCC), as it is explained in [24]. However, limited research has been developed regarding the reactive power control of PV generators in LS-PVPPs without using extra equipment. For instance, Rakibuzzaman et al. [25] explain the control of reactive power and how the capability curve could influence in the response, but, the variation of ambient conditions is not considered on this approach. Additionally, R. Varma et al. and L. Luo are working on the control of LS-PVPPs as STATCOM to support the grid when power oscillation occurs [26,27]. However, it considers the remaining inverter capacity and depends on the solar irradiance behavior. From a general point of view without any specific source of energy, new types of reactive power control for grid tied inverters have been presented in [28,29]. These studies do not take into account the variation of solar irradiance during the day or the corresponding capability curves of the PV generator. It is worth to point out that the control of reactive power in a LS-PVPP has not commonly been developed considering the capability curves. There are four main parameters that characterize these curves: (i) modulation index, (ii) dc voltage, (iii) solar irradiance, and (iv) ambient temperature, as it is explained in [30,31]. From this research, it can be understood that the variation of the dc voltage and the modulation index can help to have the complete curve despite the variation of ambient conditions. Although, this can reduce the active power generated by the PV generator.
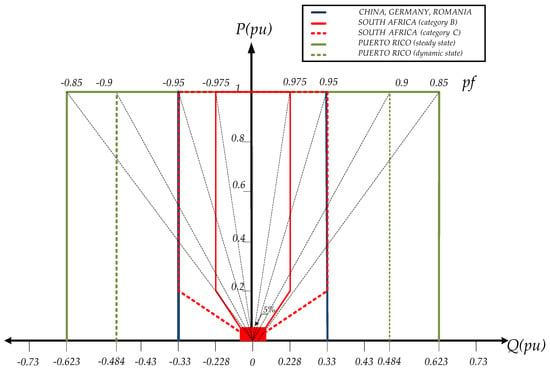
Figure 2.
Reactive power requirements.
Thus, the objective of this paper is to propose a control of active and reactive power for a PV generator applied in LS-PVPPs for grid code compliance. In this paper, the PV generator has a three phase central inverter (one stage of inversion). To control the active power, two main targets are accomplished: (i) Power curtailment, and (ii) Power reserves, by using an adaptation of the Maximum Power Point Tracker (MPPT). For the reactive power control, two considerations are addressed: (i) preference of active over reactive power and (ii) preference of reactive over active power. For this control, the instant capability curves are considered by the adjustment of the dc voltage and the modulation index depending on the solar irradiance and temperature that affects to the production of active power. To validate this study, a LS-PVPP is modeled and simulated in DIgSILENT PowerFactory under different ambient conditions. The paper is structured as follows: Section 2 explains the configuration and the control structure of a PVPP. The active power control is explained in Section 3, meanwhile the reactive power control is detailed in Section 4. Then, the simulations and the results are presented in Section 5. Finally, the discussion and the conclusions are in Section 6 and Section 7 respectively.
2. Configuration and Control Structure
In a LS-PVPP, tens to hundreds of PV generators are interconnected through a collection grid in order to increase the power. ABB, SMA, Danfoss, and First Solar have described some topologies for this distribution as radial, ring and star [23]. The main difference among them is the reliability and the cost [32]. In the current paper, radial configuration is considered as it is the most used topology. In the case of the PV generator, the configuration can be central, string or multistring. The most used configuration is the central one where the PV array is interconnected to a single stage inverter [33,34]. Then, the inverter is connected with a three winding transformer (Figure 3).
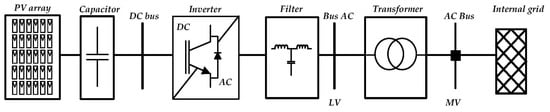
Figure 3.
PV generator in central configuration.
As many PV generators are interconnected in a LS-PVPP, a central controller is necessary. Additionally, each PV generator has to perform its local control. Thus, a hierarchical control architecture is considered, as it is illustrated in (Figure 4), where the first stage is the transmission system operator (TSO) who sends the requirements, then the second stage is the power plant control (PPC) and the third stage is the PV generator’s local control.
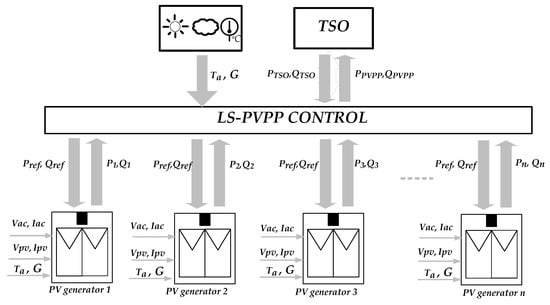
Figure 4.
Proposed control architecture for a large scale photovoltaic power plant (LS-PVPP).
The control of the LS-PVPP is focused in two main tasks: (i) apply grid support actions, for example in case of disturbances, and (ii) coordinate the control of active and reactive power according to TSO’s requirements [11,24]. For the second task, the PPC uses a Proportional-Integral (PI) controller to reduce the error between the reference given by the TSO and the power available in the grid. Then, the total active or reactive power calculated by the controller is divided by the total number of PV generators in the LS-PVPP and this is the reference value under which the PV generators should respond (Figure 5) [24,32]. After these references are calculated, the PV generator develops its corresponding control according to grid code requirements and the behavior of the internal grid to keep ac voltage and frequency constant.
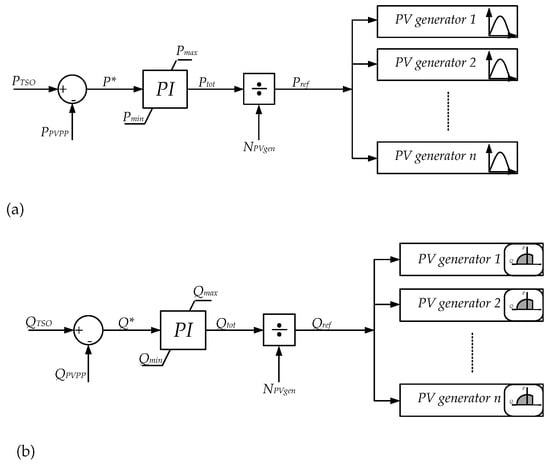
Figure 5.
Power plant control (a) Active power and (b) Reactive power.
A general control structure of a PV generator is illustrated in Figure 6. The PV generator has three main tasks: (i) MPPT, (ii) the inverter control, and (iii) the control of active and reactive power. For the first task, the MPPT, the aim is to look for the at each solar irradiance and temperature according to the P-V curves characteristics. To address this, algorithms as perturb and observe, hill climbing, incremental conductance as the more known and others as fuzzy control and swarm optimization have been developed [35,36].
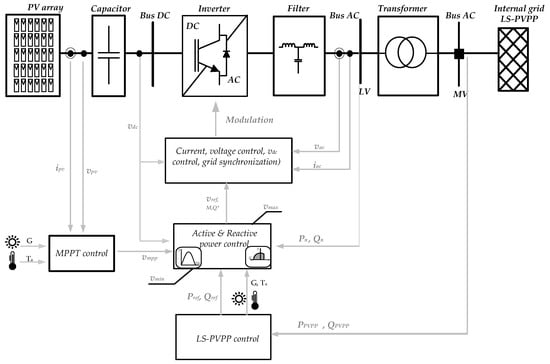
Figure 6.
General control of a PV generator.
The second task, it is the one in charge of the general inverter control to interconnect the PV generator with the internal grid of the PVPP. This control performs the grid synchronization, the voltage modulation, the dc voltage regulation and the current loop. The third task, it is in charge of the delivering of the power demanded by the PPC. This control should consider the PQ capability curves of the PV generator analysed in [30] and the variation of ambient conditions as solar irradiance and ambient temperature.
3. Active Power Control
To address the active power control of a PV generator is nesessary to understand the limitations that it has as a system (PV array and the PV inverter). The active power production capability of a PV generator can be presented by a P-G curve (Figure 7). From the figure, four main regions can be identified. Region I is the starting phase, Region II is the controlling phase, Region III is the clipping phase and Region IV is the shut off phase. To go from one region to other three main points are considered: cut-in, rated and cut out solar irradiance. The solar irradiance at which the PV generator first starts to generate power is named as “cut-in solar irradiance”. As the solar irradiance increases, the PV generator starts to work with the MPPT control. When the rated power is reached, the point of solar irradiance is the one named as “rated solar irradiance”. Eventhough, the PV array can generate more power due to higher solar irradiance, the inverter limits the generation of active power and loses the ability to track the MPP. Thus, in this region the PV generator waste available PV power. As the solar irradiance increases, the cell temperature also does it. The active power is reduced and the system cannot track any longer the active power. When this point is reached (cut out solar irradiance), the PV generator has to shut off.
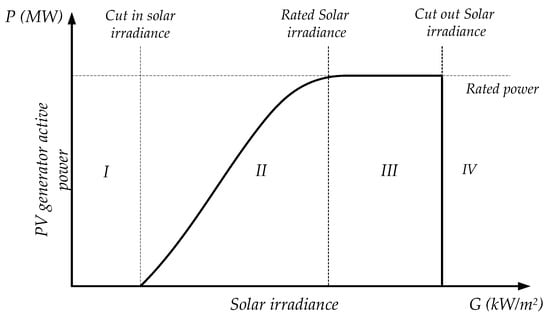
Figure 7.
Control areas of a PV generator in a Power vs Solar irradiance curve (P-G curve).
Taking into consideration this curve, the present section proposes an active power control of a PV generator for power curtailment and active power reserves.
3.1. Power Curtailment
To address the power curtailment, the PV generator cannot be working at the maximum power point. Instead the control works close to the reference of active power () given by the PPC. Thus, a Reference Power Point Tracker (RPPT) is used. Considering the P-G curve, it can be seen that the MPPT control is applied until a point of solar irradiance depending on the power reference. Although, the solar irradiance increases, the PV generator can only supply the reference power by using the RPPT control. In this case, the RPPT control can be applied in Region II and III of the P-G curve (Figure 8a).
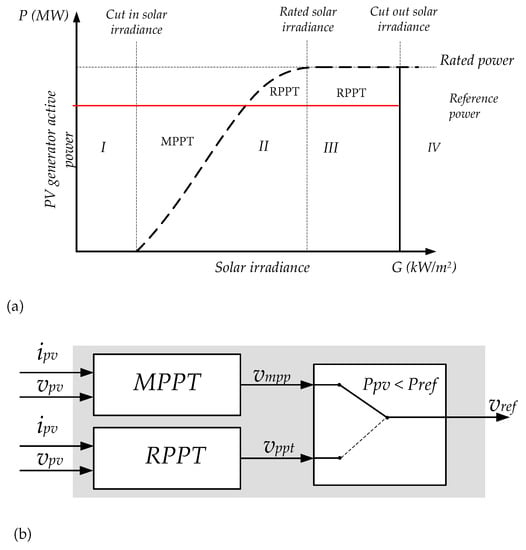
Figure 8.
Active power curtailment (a) P-G curve when a reference is given and (b) logic between maximum power point tracker (MPPT) and Reference Power Point Tracker (RPPT).
The control of active power will be managed according to two variables: dc voltage variation and the active power reference (). For that purpose, any algorithm used for MPPT can also be used in RPPT but the target point is what changes. The most common algorithm is Perturb and Observe, that is used in the present study. In this case, the dc voltage is changed by small steps () until the active power generated by the PV array is the same as the power reference. Each time the solar irradiance changes, the algorithm should only decide if the dc voltage reference should increase or decrease its value. On this control, the dc voltage limits are also considered according to the PV array and the inverter limitations (, ). However, as the solar irradiance changes, the reference of active power could be higher than the maximum possible power that the PV generator can supply. In this case, the algorithm starts to work as a normal MPPT (Figure 8b).
An example of this control is illustrated in Figure 9, where the first point is for a given solar irradiance (blue line) and with a voltage equal to the open circuit voltage (). At this point, the active power that the PV generator can supply is equal to 0. Then, the dc voltage will reduce its value in small steps in order to be close to the reference (2). In the case, the solar irradiance reduces, the new point of operation will be in (3). Then, again the control will change its dc voltage to get close to the reference. As the maximum power at the new solar irradiance is less than the reference, the control will change to MPPT instead of RPPT until it gets the maximum power (4). If the solar irradiance suddenly increases (red line), the PV generator operates in a new point (5). As the dc voltage is equal to , this has to increase in small steps until the active power generated is the same as the reference given by the PPC (6). This algorithm is presented in the block diagram illustrated in Figure 10.
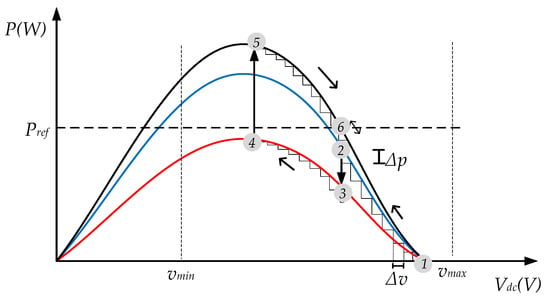
Figure 9.
RPPT operation in a PV generator. (1) Initial point. (2) Point of operation by using the algorithm. (3) Change of point of operation because of solar irradiance. (4) New maximum power point. (5) Reduce of power. (6) Reference of active power.
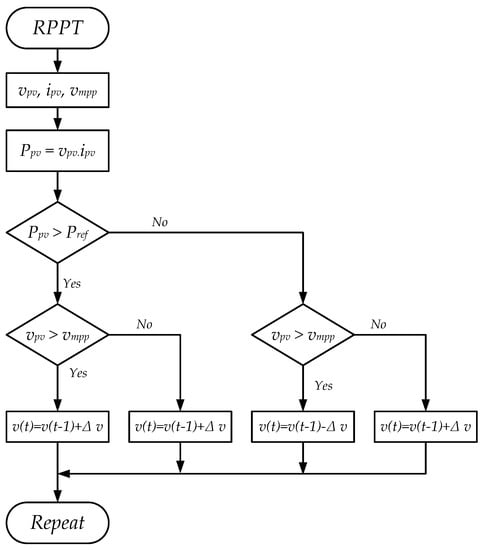
Figure 10.
RPPT control algorithm.
3.2. Active Power Reserves
In this paper, any energy storage is used. So, to approach the active power reserves is necessary to work in deloaded operation. This operation consists that the PV generator supply a reduced output power instead of the maximum power. The reduction can be between 10 or 20% of the maximum power for each solar irradiance as it is illustrated in Figure 11. To obtain the new operation point, the dc voltage is different than the .
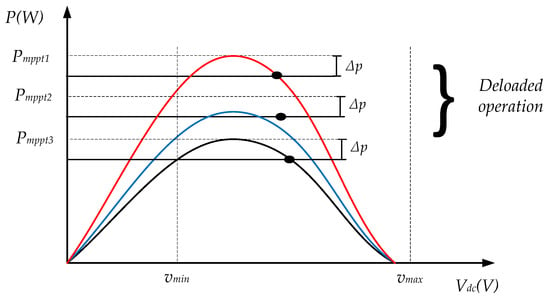
Figure 11.
Deloading operation in PV generators.
To control the PV generator for active power reserves, it is necessary to calculate at each time step the possible maximum active power that the PV generator can supply (). Then, the power reserve is given by the percentage required by the TSO of the maximum possible active power given by the expression:
The new reference for active power can be calculated as follows:
With this new reference, the RPPT control explained in Section 3.1 can be applied. Then, the new P-G curve is presented according to the new performance of the PV generator in Figure 12. In this case, the RPPT can be used in region II and III of the P-G curve.
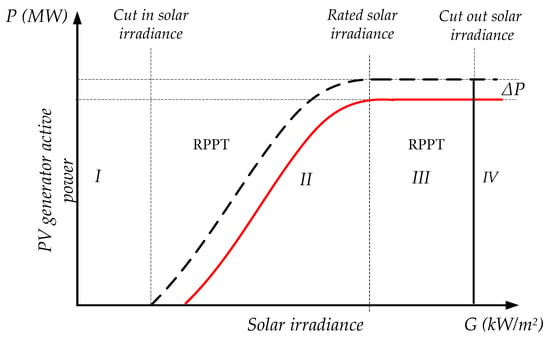
Figure 12.
Control areas of a PV generator in a P-G curve when power reserve is considered.
In summary, the PV generator will be working with MPPT or RPPT depending on the ambient conditions and the PPC ’s requirements. Then, the dc voltage () will vary according to the control chosen until it fulfills the requirements (Figure 13).
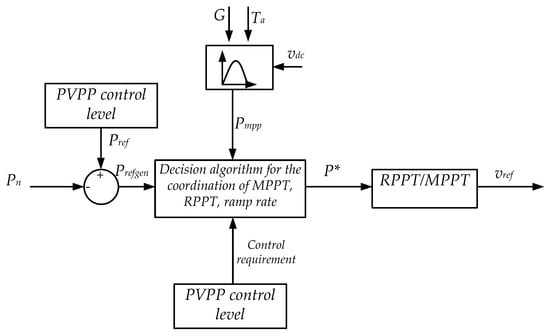
Figure 13.
Control scheme for control of active power in PV generators.
After the active control has been addressed, the reactive power control is explained in the following section.
4. Reactive Power Control
The P-Q curves of a PV generator depends not only on the variation of solar irradiance or temperature but also on the dc voltage applied at the terminals of the PV arrar or the modulation index as part of the internal inverter control. In Figure 14 can be seen the variation of these parameters and how they affect to the P-Q curve.
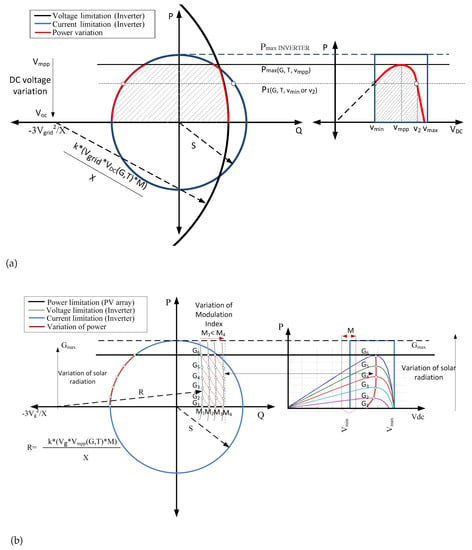
Figure 14.
PQ capability curve of a PV generator (a) Variable dc voltage (b) Variable Modulation index [30] (Reproduced from Solar Energy, Vol 140, Ana Cabrera et al., “Capability curve analysis of photovoltaic generation systems”, Copyright (2016), with permission from Elsevier).
These curves obeys to the following expressions:
Taking into account this P-Q curve, this section presents a novel control to provide reactive power depending on the grid code requirements. In this case, the reactive power control is set as a priority (Figure 15). This control reads the reference of reactive power given by the plant operator. If the reactive power control is not a priority, the control is developed with a conventional reactive power regulation. But if the reactive power is set as a priority, then the PV generator has to calculate the maximum possible reactive power () by taking into account the capability curves studied in [30] and the variation of ambient conditions.
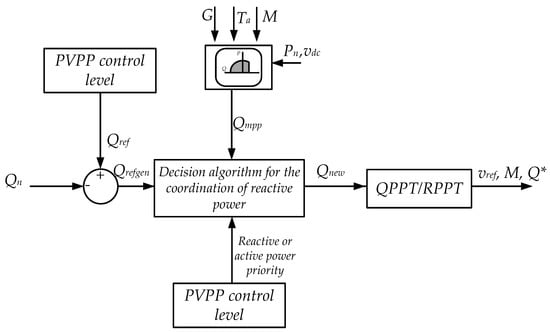
Figure 15.
Control scheme for control of reactive power in PV generators.
The performance of the control will vary depending if it is absorbing or injecting reactive power.
4.1. Absorption of Reactive Power
For the absorption of reactive power, the area of operation is in the fourth quadrant of the PQ capability curve. The maximum limitation of the reactive power varies according to:
where, the is the maximum active power that the PV generator can supply at that instant. For a given reference of absorbed reactive power , the control evaluates if this is higher than the at each instant. If it is higher, then the PV generator has to reduce the injection of active power by the variation of dc voltage. So, the PV generator is not working any longer at MPP instead will be working in other point of operation of active power. The RPPT control should again track the reference of active power calculated due to reactive power reference. Every time the solar irradiance changes, the control has to track the reactive power point by the variation of active power. This control will be called as the reactive power point tracker (QPPT).
This behavior is illustrated in Figure 16, where the first point is for a given solar irradiance (A). At this point, the active power that the PV generator can supply is . On this instant, a reference of reactive power is given to the generator’s control. However, with this power the is lower than the reference. Thus, a new reference of active power is calculated (). To achieve this point, the dc voltage has to change from to so the PV generator starts to work at point B. Then, the generator can supply the value of reactive power equal to the reference (point 3). In the case the solar irradiance changes a new PV curve is generated (blue line), because of the dc voltage value, the new active power is and the PV generator starts to work in point C (PV curve) and 4 (PQ curve). As the RPPT control has to follow the reference of reactive power, then the dc voltage reduces to reach the reference (Point D and point 3).
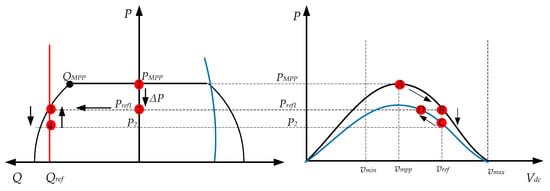
Figure 16.
QPPT operation in a variable PQ and ambient conditions: Absorption of reactive power. (1) MPP at one solar irradiance, (2) Variation of active power reference, (3) Reference of reactive power, (4) New active and reactive power.
4.2. Injection of Reactive Power
For the injection of reactive power, the area of operation is in the first quadrant of the PQ capability curve. The maximum limitation of the reactive power varies according to:
where, the modulation index (M) varies between 0 and 1. The maximum possible reactive power for a given solar irradiance, temperature and is when M is equal to 1. In order to increase this value of reactive power, the modulation index can be higher than 1 but it can cause the increment of harmonics [37].
In the case, the PPC asks a reference higher than , the control should manage in one hand the dc voltage to reduce the active power and on the other hand the modulation index. This behavior is illustrated in Figure 17, where the first point is for a given solar irradiance (A). At this point, the active power that the PV generator can supply is . In this instant, a reference of reactive power is given to the generator’s control. However, with this power the is lower than the reference. Thus, a new point of operation is calculated. First, the maximum modulation index varies to a higher value in order to increase the operation area. So, the maximum possible reactive power that the PV generator can inject increases. Then, to reach this point of operation at the specific reference of reactive power, the generated active power is reduced (). To achieve this point the dc voltage has to change from to and the PV generator starts to work at point B. The corresponding algorithm that follows the logic illustrated in Figure 18.
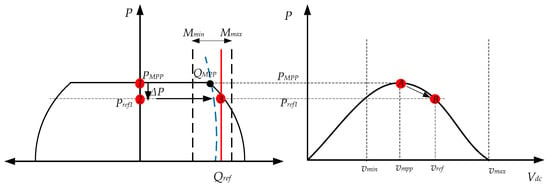
Figure 17.
QPPT operation in a variable PQ and ambient conditions: Injection of reactive power. (1) MPP at one solar irradiance, (2) Variation of active power reference, (3) Reference of reactive power.
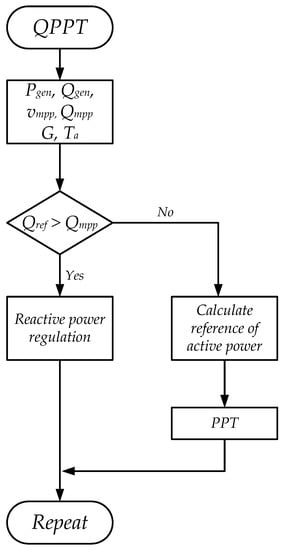
Figure 18.
Logic of control for reactive power in PV generators.
The control of active and reactive power is tested for different scenarios. These tests and the performance of the control are explained in the following section.
5. Simulation and Results
A LS-PVPP of 24 MW is designed and modeled in DIgSILENT PowerFactory and has the configuration presented in Figure 19. For the current study the results for a single PV generator are presented. The main characteristics of the PV generator are summarized in Table 1. The design of this power plant was developed according to the solar irradiance and temperature data taken from Urcuqui-Ecuador in 2014. Besides, the inverter has been oversized 20% of the maximum active power capacity of the PV array. Each PV generator has a nominal power capacity of 0.6 MVA.
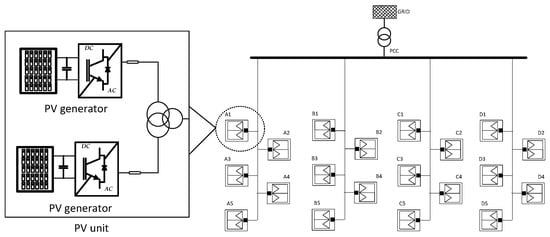
Figure 19.
PVPP diagram under study.

Table 1.
PV panel and array characteristics.
Two cases studies are considered: (i) testing the active power control (case study A) and (ii) testing the reactive power control (case study B). For each type of control, the PPC is the one that sends the references of active or reactive power to the local controller. For these tests, three days are chosen with different solar irradiance and an ambient temperature around 10 °C to 25 °C (Figure 20).
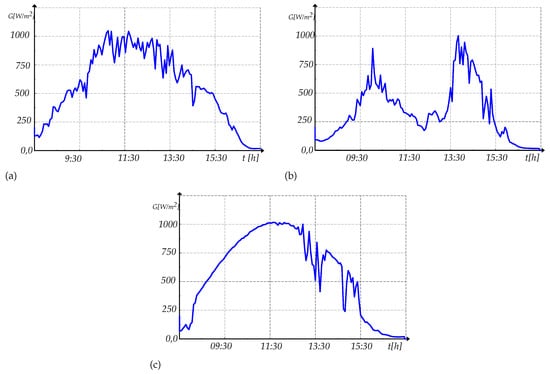
Figure 20.
Solar irradiance data (a) Day 1 (b) Day 2, and (c) Day 3.
5.1. Case Study A
For this case study, three different active power values are set as references during the day:
- Set a power reserve of 20% of the maximum power capacity from 6:00 to 10:00 and from 15:00 to 18:00.
- Set a power curtailment of 50% of the maximum capacity from 10:00 to 15:00.
- Deactivate the power curtailment to reach the maximum power point during 10 min (11:25 to 11:35).
The test is developed for day one and two, and the results are illustrated in Figure 21. For any of the days tested, the control of active power makes possible to keep the power reserve equal to 20% of the maximum power capacity for active power higher than 0.20 p.u. When the generated active power is lower than 0.2 p.u, the power reserve is not reached and instead is equal to the maximum possible.
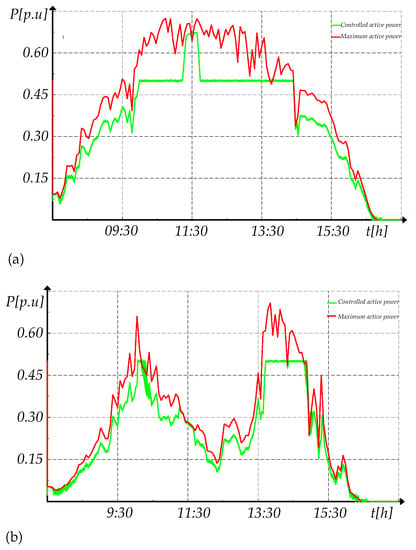
Figure 21.
Control of active power for different power references. (a) Day one, (b) Day two.
However, in the case of power curtailment, there are some differences between the first and the second day. In day 1, the active power reference is reached easily with the control due to the sufficient solar irradiance. On day 2, however, the new reference of power is only reached during ten minutes in the morning and eighty minutes in the afternoon. This behavior is because of the drastic changes of solar irradiance during the day.
The deactivation of the power curtailment in order to get the maximum power during ten minutes is successful in day 1 and day 2. It is important to notice that due to the MPPT control, the ramp rate to get the maximum power is 0.05 MW/min on day 1 and 0.026 MW/min on day 2.
5.2. Case Study B
In this case study, the reactive power control is tested considering the solar irradiance of day 3. To understand the performance of this control, some tests are developed: (a) active power priority and (b) reactive power priority.
5.2.1. Active Power Priority
In this case, the normal MPPT control is used during the day as it is illustrated in Figure 22. Taking into account this control, the maximum reactive power that the PV generator can absorb is illustrated in Figure 23 together with the operational area. It can be seen, that the maximum reactive power that the PV generator can absorb is variable in the time as it is not a priority. The reactive power varies from 0.6 pu to 1 p.u depending on the time of the day.
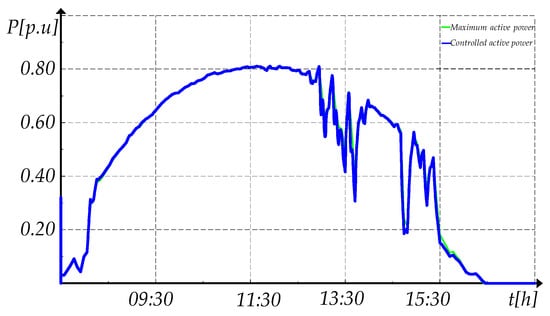
Figure 22.
Active power response for day 3 considering MPPT.
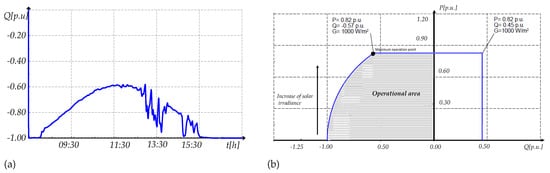
Figure 23.
Absorbed reactive power when MPPT is considered (a) Maximum possible reactive power and (b) Operational area.
In the case that a reference of absorbed reactive power is required ( p.u) by the PV generator and the MPPT is still used, the response of it is illustrated in Figure 24 together with the operational area. With these conditions, the PV generator can follow the reactive power reference between some hours (06:00 to 08:00 and 15:00 to 18:00). However, when the active power exceeds a certain value, the PV generator cannot follow the reference of reactive power.
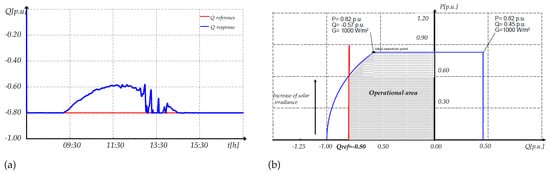
Figure 24.
Absorbed reactive power when a reference of reactive power is considered (a) Response of reactive power (b) Operational area.
For a p.u, the PV generator can inject the reactive power depending on the voltage limitation and the modulation index. A modulation index of 1 and 1.75 is tested and illustrated in Figure 25 and Figure 26 respectively together with their operation area. When the modulation index is 1, the reactive power is equal to 0.45 p.u for any solar irradiance. Meanwhile, when the modulation index is 1.75, the reference of reactive power is reached from 07:00 to 10:00 and from 13:30 to 18:00. However, from 10:00 to 13:00, the reference of reactive power is not reached. Instead, the maximum possible reactive power is injected, which depends on the solar irradiance. The curve that limits its behavior from 10:00 to 13:00 is the current curve, for the rest of the day it is the voltage curve.
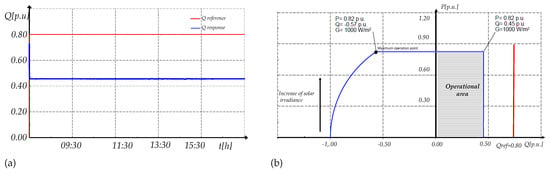
Figure 25.
Injected reactive power with MPPT control and (a) Response of reactive power and (b) Operational area.
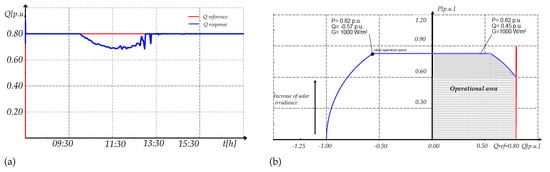
Figure 26.
Injected reactive power with MPPT control and (a) Response of reactive power and (b) Operational area.
5.2.2. Reactive Power Priority
To test this control, two references of reactive power are simulated: (i) p.u and (ii) p.u For the first reference (absorption of reactive power), the results of active and reactive power are illustrated in Figure 27 with the corresponding capability curve. In this case, the PV generator absorbs a value of reactive power equal to its reference almost all the time. Due to the changes of irradiance and the response time of the control, there are specific times where there is an error around 0.05 p.u. Because of the control and the ambient conditions, the active power is limited to 0.6 p.u between the hours 08:00 to 13:00.
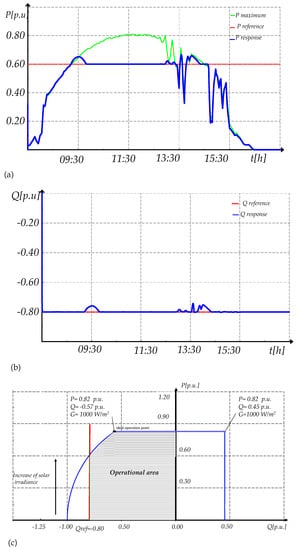
Figure 27.
QPPT response when a reactive power reference is applied (a) Active power, (b) Reactive power, and (c) Operational area.
For the second reference (injection of reactive power), two different modulation index are tested: (i) and (ii) (Figure 28 and Figure 29). When , the reactive power cannot reach the reference of reactive power and stays at the maximum value (0.45 p.u). In the case , the PV generator injects a reactive power equal to the reference during all the time by the reduction of active power from 09:00 to 13:30.
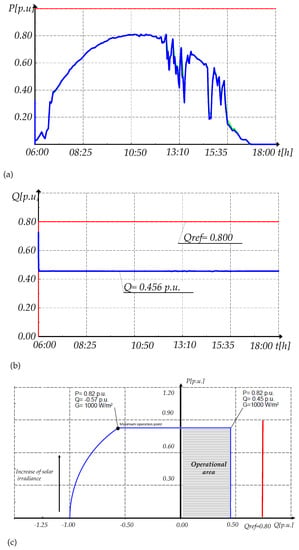
Figure 28.
Power response with QPPT for (a) Active power and (b) Reactive power, and (c) Operational area.
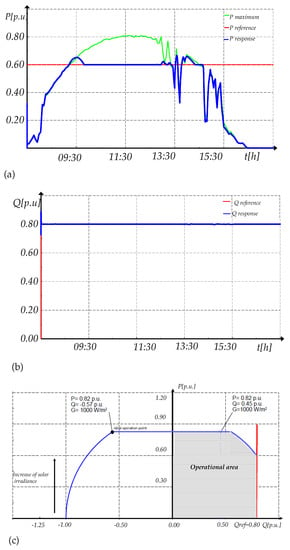
Figure 29.
Power response with QPPC for (a) Active power and (b) Reactive power, and (c) Operational area.
6. Discussion
From the controller presented in this paper and from the obtained results, some important issues are necessary to be addressed:
6.1. Active Power Control
The control of active power in a suboptimal point (lower than the MPP) can be developed with a RPPT control. The PV generator can supply power according to an active power reference. The response, however, depends as well on the solar irradiance fluctuations during the day. For instance, on the second day, between 14:00 to 15:00 quick solar irradiance variations are presented and the control tries to respect the 20% of power reserve but the control does not follow this reference.
6.2. Reactive Power Control
For the injection or absorption of reactive power, the response also depends on the solar irradiance when the active power generation is a priority. It can be stated that with a maximum active power, there will be a maximum reactive power that can be injected or absorbed depending on the capability curves. Because of this, if a reference of reactive power is set and at the same time the active power control is a priority, the reference will be reached only if it is lower than the maximum reactive power point possible at that instant. In the case that the reactive power is a priority and there is high solar irradiance, the reference of reactive power can be reached only if the active power point changes to other point of operation lower than the MPP.
It is important to notice that for injection of reactive power, the variation of this value does not present large fluctuation as it depends on the changes of dc voltage together with the modulation index. If the maximum modulation remains fix, then the reactive power that the PV generator can inject also remains close to a fix value. However, this value could be lower than the reference set by the control. Therefore, a change of modulation index helps to achieve the reference of reactive power asked by the PPC.
6.3. Compliance of Grid Codes
Considering the response of the PV generator for the different scenarios for reactive power, it can be analised if the requirements of the grid codes can be achieved under different scenarios. Figure 30 illustrates the capability curve given by the PV generator together with the capability curve required by Puerto Rico and Germany for steady state conditions.
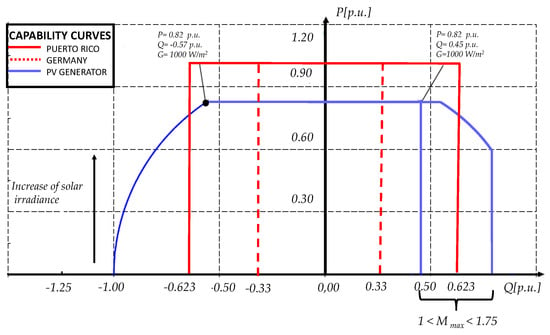
Figure 30.
Capability curves comparison considering the grid codes of Puerto Rico, Germany and the capability curve extracted from the current study case.
When QPPT is utilized, the PV generator can inject or absorb reactive power according to the requirements but the active power generated could be lower than the MPP. For absorbed reactive power, if the reference is 0.623 p.u, then the new reference of active power should be 0.78 p.u. For the injection of reactive power, the modulation index has to be higher than 1 to comply this reference.
However, when the reactive power is not set as a priority then the requirements asked by the grid code of Puerto Rico cannot be accomplished for higher solar irradiance and maximum modulation index of 1. So, new equipment should be installed in order to give reactive power support as STATCOM, capacitor banks, FACTS. However, for the case of Germany, at any irradiance the PV generator can supply or inject the reference of reactive power as it is lower than 0.57 p.u without making any change on the operation of active power or the modulation index.
Additionally, it can be seen that for an active power generated lower than 0.78 p.u (corresponding to G = 900 W/m), the PV generator can absorb or inject reactive power higher than the limitations imposed by the grid codes without reducing the generated active power. Thus, it is necessary that the Grid codes will consider the effect of the PV generator performance at different solar irradiance, temperature, dc voltage and modulation index in order to set higher limitations and improve the performance of the LS-PVPP.
7. Conclusions
This paper has presented the control of active and reactive power for a PV generator considering its capability curves variation applied in a large scale photovoltaic power plant. For this purpose, the current paper has presented the general configuration and control structure used commonly in a LS-PVPP. Then the active power control for a PV generator has been presented considering active power curtailment and active power reserves. Additionally, the control of reactive power was also studied under two different considerations: active power priority or reactive power priority taking into account the corresponding capability curves. Finally, DIgSILENT PowerFactory was used to simulate the control proposed under different conditions. From the control developed and the simulation some conclusions are presented.
The quick variation of solar irradiance affects not only to the active power response but also to the reactive power. When the solar irradiance is high, then the reactive power capability is reduced. Besides, this could disrupt the plant with quick variations of reactive power, this can be reduced with an appropriate control of the reactive power.
The modulation index and the dc voltage value play an important role on the point of operation of the PV generator when reactive power is injected. For an appropriate control the maximum modulation index can vary between 1 to 1.75 to comply grid code requirements.
The capability curves play an important role in the control of the PV generator when active and reactive power control are considered. These curves should be taken into account for each solar irradiance, ambient temperature, dc voltage and modulation index. The reactive power reference can be achieved by the consideration of these capability curves together with the control.
Considering the grid code requirements regarding the management of active power, it can be stated that working with RPPT for a given reference helps to comply the basic requirements as power reserves and power curtailment. However, a deeper study on ramp rate control must be developed considering variable solar irradiance. In the case of reactive power, grid codes should also consider the behavior of the PV generator according to ambient conditions in order to set the limitations.
Author Contributions
Research concepts were proposed by A.C.-T. and O.G.-B. Manuscript preparation and data analysis were conducted by A.C.-T., M.A.-P., E.B.-M. The edition of the manuscript was performed by all the authors.
Funding
The work was conducted in the PVTOOL project. PVTOOL is supported under the umbrella of SOLAR-ERA.NET Cofund by the Ministry of Economy and Competitiveness, the CDTI and the Swedish Energy Agency. SOLAR-ERA.NET is supported by the European Commission within the EU Framework Programme for Research and Innovation HORIZON 2020 (Cofund ERA-NET Action, n° 691664). It also was funded by the National Department of Higher Education, Science, Technology and Innovation of Ecuador (SENESCYT).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| PV | Photovoltaic |
| LS-PVPP | Large Scale Photovoltaic Power Plant |
| PLL | Phase Locked Loop |
| PPC | Power Plant Controller |
| PCC | Point of Common Coupling |
| G | Solar Irradiance |
| Ambient Temperature | |
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracker |
| TSO | Transmission System Operator |
| RPPT | Reference Power Point Tracker |
| , | Active and Reactive Power of the PVPP measured at the PCC |
| P, Q | Active and Reactive Power |
| , | Reference of Active and Reactive Power |
| Power reserve | |
| , | Active and Reactive Power at the maximum power point of operation |
| dc | direct current |
| dc voltage measured at the dc bus of the PV inverter | |
| , | values of voltage and current measured at the terminals of the PV array |
| , | values of voltage and current at the maximum power point of operation |
| M | Modulation Index |
| X | Reactance of the grid |
| Perturb and Observe | |
| VSC ac voltage | |
| Grid voltage |
References
- Cabrera-Tobar, A.; Bullich-Massagué, E.; Aragüés-Peñalba, M.; Gomis-Bellmunt, O. Review of advanced grid requirements for the integration of large scale photovoltaic power plants in the transmission system. Renew. Sustain. Energy Rev. 2016, 62, 971–987. [Google Scholar] [CrossRef]
- Magoro, B.; Khoza, T. Grid Connection Code for Renewable Power Plants Connected to the Electricity Transmission System or the Distribution System in South Africa; Technical Report; NERSA: Pretoria, South Africa, 2012. [Google Scholar]
- BDEW. Technical Guideline Generating Plants Connected to the Medium-Voltage Network; BDEW: Dresden, Germany, 2008. [Google Scholar]
- Liang, J.; Wang, Y.; Fubao, W.; XiaoFang, W.; Chao, A.; Zhen, L.; XiaoGang, K.; Jian, Z.; Zhileir, C.; ChenHui, N.; et al. Comparative Study of Standards for Grid Connected PV System in China, the US and European Countries; Technical Report; National Energy Administration of China: Beijing, China, 2013.
- Gevorgian, V.; Booth, S. Review of PREPA Technical Requirements for Interconnecting Wind and Solar Generation; Technical Report; NREL: Lakewood, CO, USA, 2013.
- Bird, L.; Cochran, J.; Wang, X. Wind and Solar Energy Curtailment: Experience and Practices in the United States; Technical Report; NREL: Lakewood, CO, USA, 2014.
- Cabrera-Tobar, A.; Fernandez, Y.; Huaca, J.; Pozo, M.; Bellmunt, O.G.; Massi Pavan, A. The effect of ambient temperature on the yield of a 3 MWp PV plant installed in Ecuador. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. Development of flexible active power control strategies for grid-connected photovoltaic inverters by modifying MPPT algorithms. In Proceedings of the IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 87–92. [Google Scholar] [CrossRef]
- Muller, N.; Kouro, S.; Renaudineau, H.; Wheeler, P. Energy storage system for global maximum power point tracking on central inverter PV plants. In Proceedings of the IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Li, X.; Hui, D.; Lai, X. Battery Energy Storage Station (BESS)-Based Smoothing Control of Photovoltaic (PV) and Wind Power Generation Fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 464–473. [Google Scholar] [CrossRef]
- Bullich-Massagué, E.; Aragüés-Peñalba, M.; Sumper, A.; Boix-Aragones, O. Active power control in a hybrid PV-storage power plant for frequency support. Sol. Energy 2017, 144, 49–62. [Google Scholar] [CrossRef]
- Ellis, A.; Schoenwald, D.; Hawkins, J.; Willard, S.; Arellano, B. PV output smoothing with energy storage. In Proceedings of the 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 001523–001528. [Google Scholar] [CrossRef]
- Alam, M.; Muttaqi, K.; Sutanto, D. A Novel Approach for Ramp-Rate Control of Solar PV Using Energy Storage to Mitigate Output Fluctuations Caused by Cloud Passing. IEEE Trans. Energy Convers. 2014, 29, 507–518. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T. A Coordinated Control Method for Leveling PV Output Power Fluctuations of PV–Diesel Hybrid Systems Connected to Isolated Power Utility. IEEE Trans. Energy Convers. 2009, 24, 153–162. [Google Scholar] [CrossRef]
- Van Haaren, R.; Morjaria, M.; Fthenakis, V. An energy storage algorithm for ramp rate control of utility scale PV (photovoltaics) plants. Energy 2015, 91, 894–902. [Google Scholar] [CrossRef]
- Beltran, H. Energy Storage Systems Integration into PV Power Plants. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2011. [Google Scholar]
- De la Parra, I.; Marcos, J.; García, M.; Marroyo, L. Control strategies to use the minimum energy storage requirement for PV power ramp-rate control. Sol. Energy 2015, 111, 332–343. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Integration of PV and BES units in commercial distribution systems considering energy loss and voltage stability. Appl. Energy 2014, 113, 1162–1170. [Google Scholar] [CrossRef]
- Galtieri, J.; Krein, P.T. Solar Variability Reduction Using Off-Maximum Power Point Tracking and Battery Storage. In Proceedings of the IEEE 44th Photovoltaic Specialist Conference (PVSC), Washington, DC, USA, 25–30 June 2017; pp. 3214–3219. [Google Scholar] [CrossRef]
- Hoke, A.; Maksimovic, D. Active power control of photovoltaic power systems. In Proceedings of the 1st IEEE Conference on Technologies for Sustainability (SusTech), Portland, OR, USA, 1–2 August 2013; pp. 70–77. [Google Scholar] [CrossRef]
- Yang, Y.; Blaabjerg, F.; Wang, H. Constant power generation of photovoltaic systems considering the distributed grid capacity. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 379–385. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F.; Wang, H. Benchmarking of constant power generation strategies for single-phase grid-connected Photovoltaic systems. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 370–377. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Bullich-Massagué, E.; Aragüés-Peñalba, M.; Gomis-Bellmunt, O. Topologies for large scale photovoltaic power plants. Renew. Sustain. Energy Rev. 2016, 59, 309–319. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Serrano-Salamanca, L.; Ferrer-San-José, R.; Pacheco-Navas, C.; Aragüés-Peñalba, M.; Bullich-Massagué, E. Power plant control in large-scale photovoltaic plants: Design, implementation and validation in a 9.4 MW photovoltaic plant. IET Renew. Power Gener. 2015, 10, 50–62. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R.; Ramachandaramurthy, V. A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 2015, 41, 1423–1436. [Google Scholar] [CrossRef]
- Maleki, H.; Varma, R.K. Coordinated control of PV solar system as STATCOM (PV-STATCOM) and Power System Stabilizers for power oscillation damping. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Luo, L.; Gu, W.; Zhang, X.P.; Cao, G.; Wang, W.; Zhu, G.; You, D.; Wu, Z. Optimal siting and sizing of distributed generation in distribution systems with PV solar farm utilized as STATCOM (PV-STATCOM). Appl. Energy 2018, 210, 1092–1100. [Google Scholar] [CrossRef]
- Sadnan, R.; Khan, M.Z.R. Fast real and reactive power flow control of grid-tie Photovoltaic inverter. In Proceedings of the 9th International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 20–22 December 2016; pp. 570–573. [Google Scholar] [CrossRef]
- Weckx, S.; Gonzalez, C.; Driesen, J. Combined Central and Local Active and Reactive Power Control of PV Inverters. IEEE Trans. Sustain. Energy 2014, 5, 776–784. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Bullich-Massagué, E.; Aragüés-Peñalba, M.; Gomis-Bellmunt, O. Capability curve analysis of photovoltaic generation systems. Sol. Energy 2016, 140, 255–264. [Google Scholar] [CrossRef]
- Cabrera-Tobar, A.; Aragues-Penalba, M.; Gomis-Bellmunt, O. Effect of Variable Solar Irradiance on the Reactive Power Response of Photovoltaic Generators. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Van Hertem, D.; Gomis-Bellmunt, O.; Liang, J. HVDC Grids for Offshore and Supergrid of the Future; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Pavan, A.M.; Castellan, S.; Quaia, S.; Roitti, S.; Sulligoi, G. Power Electronic Conditioning Systems for Industrial Photovoltaic Fields: Centralized or String Inverters? In Proceedings of the International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; pp. 208–214. [Google Scholar] [CrossRef]
- Sánchez Reinoso, C.R.; Milone, D.H.; Buitrago, R.H. Simulation of photovoltaic centrals with dynamic shading. Appl. Energy 2013, 103, 278–289. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. MPPT techniques for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Belkaid, A.; Colak, I.; Isik, O. Photovoltaic maximum power point tracking under fast varying of solar radiation. Appl. Energy 2016, 179, 523–530. [Google Scholar] [CrossRef]
- Rashid, M. Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).