A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics
Abstract
1. Introduction
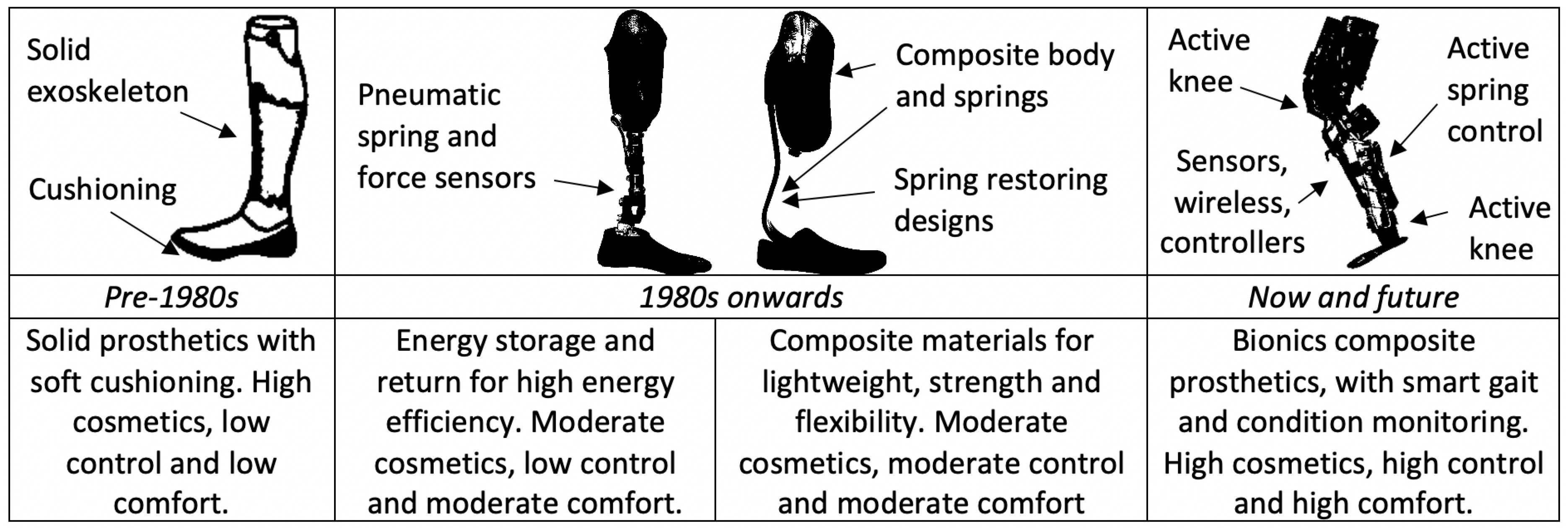
- Conventional Solid Cushioned Prosthetics: They are typically made of solid wood, plastic or metal structures, with some soft cushioning with foam or rubber to provide a degree of comfort and energy efficiency. The basic principle is not too distinct from solid prosthetics reported since antiquity. A key design feature is to mimic human leg and feet from a cosmetic point of view. The primary aim is to enable basic gait functionality to an amputee. However, the non-optimised gait pattern from these prostheses can stress the healthy limbs and joints, causing injury after prolonged use. A classical example is the SACH foot, which has an energy efficiency estimated up to 31% [9]. Users are required to manually control these solid prosthetics, and this is typically described as passive control. The gait is typically unnatural with limping patterns, which can result in repeated stress injuries to other health body parts such as joints, limbs and hip.
- Energy Storage and Return (ESR): They typically contains a spring component acting as a restoring force mechanism, allowing mechanical energy to be momentarily stored and returned to the gait motion while walking and running. The spring can either be a linear mechanical spring or a second-order pneumatic air spring. The use of ESR in prosthetics design since the 1980s has been considered as a crucial milestone towards helping to improve gait pattern and behaviour based on biomechanics research [5]. The ESR mechanism can generally be modelled as a second-order mass–spring–damper system, with a focus on the restoring force term.Key optimisation parameters include minimising damping and synchronising energy return rate to the gait speed. When a runner’s rate of compression of the ESR prosthetics is close to the resonant frequency of the ESR foot, energy efficiency can be maximised. Classic examples include the Flex foot mainly used in sports and the Seattle foot that incorporates springs into a cushioned foot. The springs themselves can either be mechanical spring structures made of metal, plastic or composite materials, or pneumatic springs relying on air or fluidic pressure as the restoring force. Seattle and Flex come in various design embodiments, with energy efficiency estimated up to 52% and 84%, respectively [9].
- Composite Materials: The use of carbon fibre reinforced polymer (CFRP) composites coincided with the developed of the Flex foot and Seatle foot, primarily as part of the employed spring material within the lower limb [10] in contrast to metallic springs due to CFRP’s lightweight, flexibility and high strength [5]. CFRP can be five times lighter than steel while offering either similar or up to an order of magnitude higher tensile strength. This is seen in both as a critical enabling material for professional sports as well as a high performance material in commercial prosthetics.Amputee athletes with CFRP c-shaped flexible lower limb prosthetics are able to attain athletic records that are just about 10% lower than abled-bodied athletic records [5]. Furthermore, in commercial prosthetics, the use of CFRP and ESR prosthetics have been crucial to reduce stress on the joints and hips of the amputees compared to conventional solid cushioned prosthetics [11]. Composite materials are also possible to be integrated with functional materials such as piezoelectric transducers to enable sensing and harvesting capabilities [12].
- Bionics and Active Control: While ESR prosthetics provide a better energy efficiency and comfort than traditional solid cushioned prosthetics, gait behaviour is still far from ideal [7]. Improper gait can result in repeated stress and injury to the healthy parts of the human body. More recently, there has been an increasing trend in prosthetics research to develop towards bionics leg and feet, where motors and actuators [13] integrated with active or semi-active control systems [14] are used to control the motion of ankles and knees. The aim is to mimic the natural human biomechanics and gait pattern, where gait information gathered from sensors are used to control the knee and ankle orientations in order to improve towards the biomechanics of a normal gait [15].The active or semi-active control of these bionic prosthetics involve various integrated sensors along with variable damping, actuation power drive and artificial intelligence [16]. However, some of the design challenges include aiming to achieve high force/torque and power efficiency while minimising weight and size of the drive and power systems [17]. In particular, the weight of the batteries to power the sensors and drive systems can be a key limiting factor while trying to optimise between operation time and weight.A study that assumed a basic system using two motors to control knee and ankle has estimated that a lithium polymer battery pack of reasonable size and weight can attain a range of 5 km [18]. The goal is to extend this range to maximise mobility and life quality for amputees. However, to have full degrees of freedom in control, motor actuators are required on all three axes for both knee and ankle, thus requiring even more power and limiting the practical range further. Fortunately, the motors and actuators used to control prosthetic knee and ankle are not required to continuously operate in active mode and many semi-active strategies have been proposed [19]. The active operation time period of servo motors can be as short as 10 ms to make a minute and precise angular orientation correction. Most of the time, these motors can be put into sleep mode in order to conserve energy. The use of energy harvesting can potentially help to recharge the on-board battery and compensate the intermittent energy drains by the motors.
2. Method
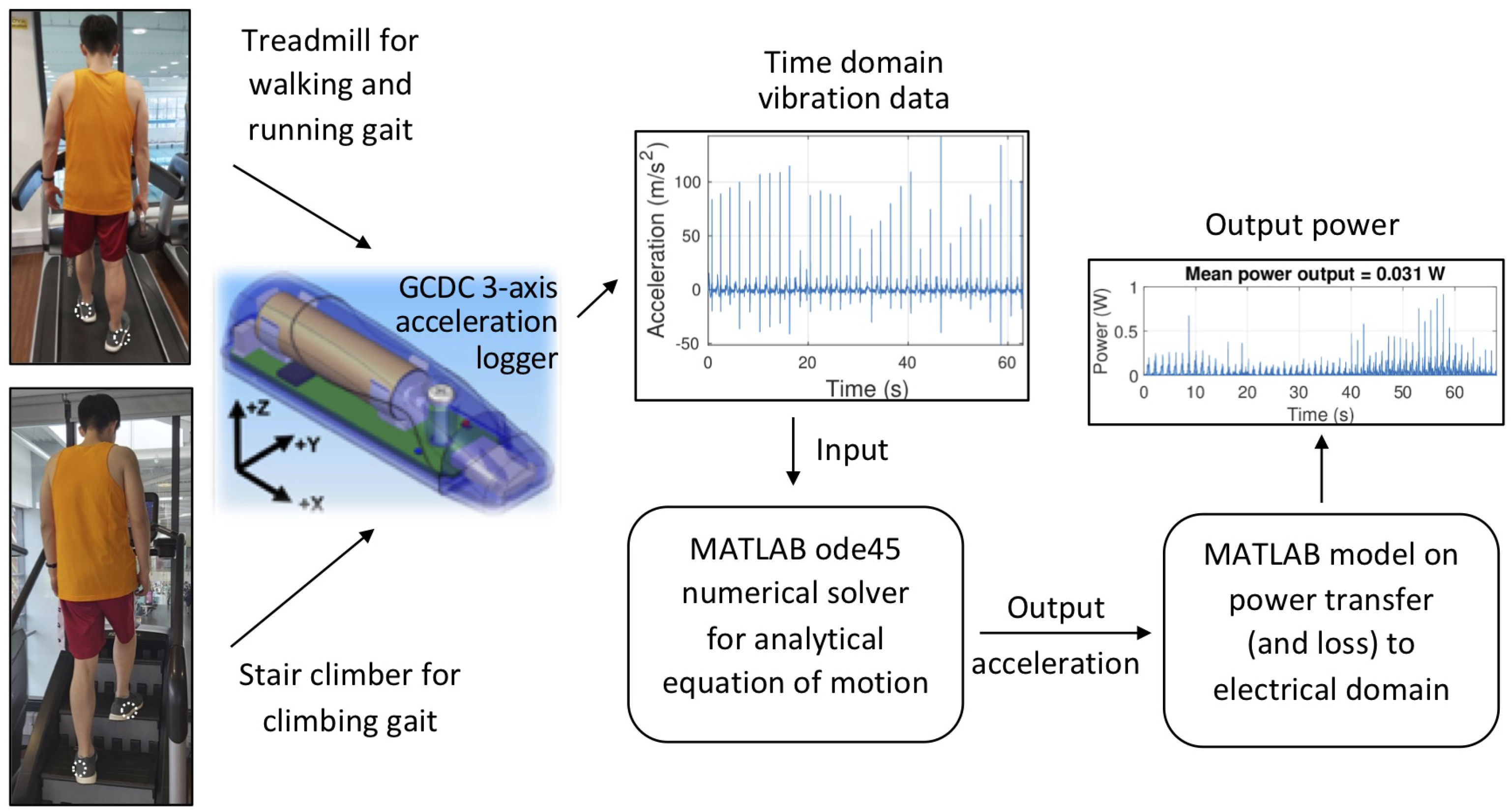
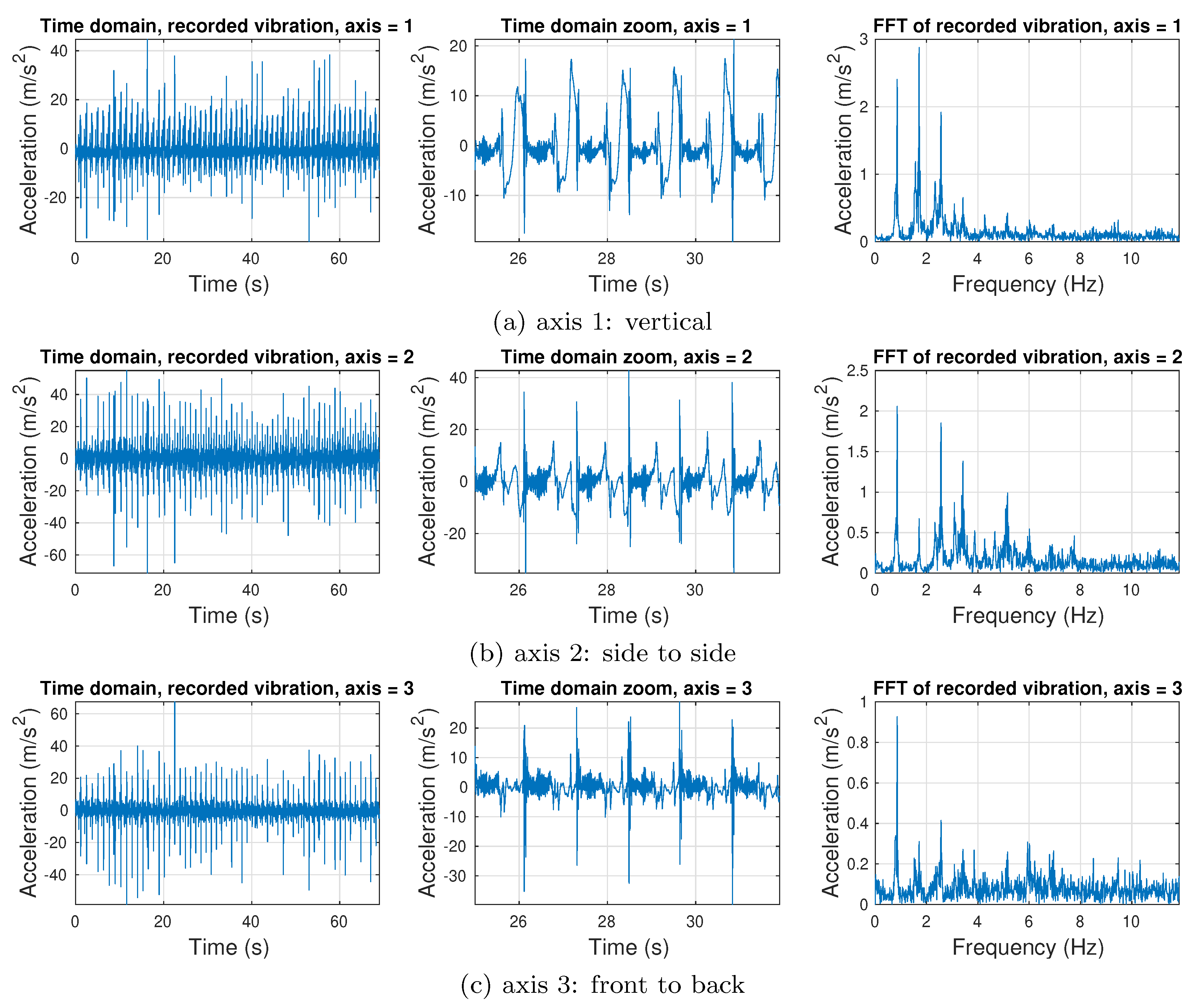
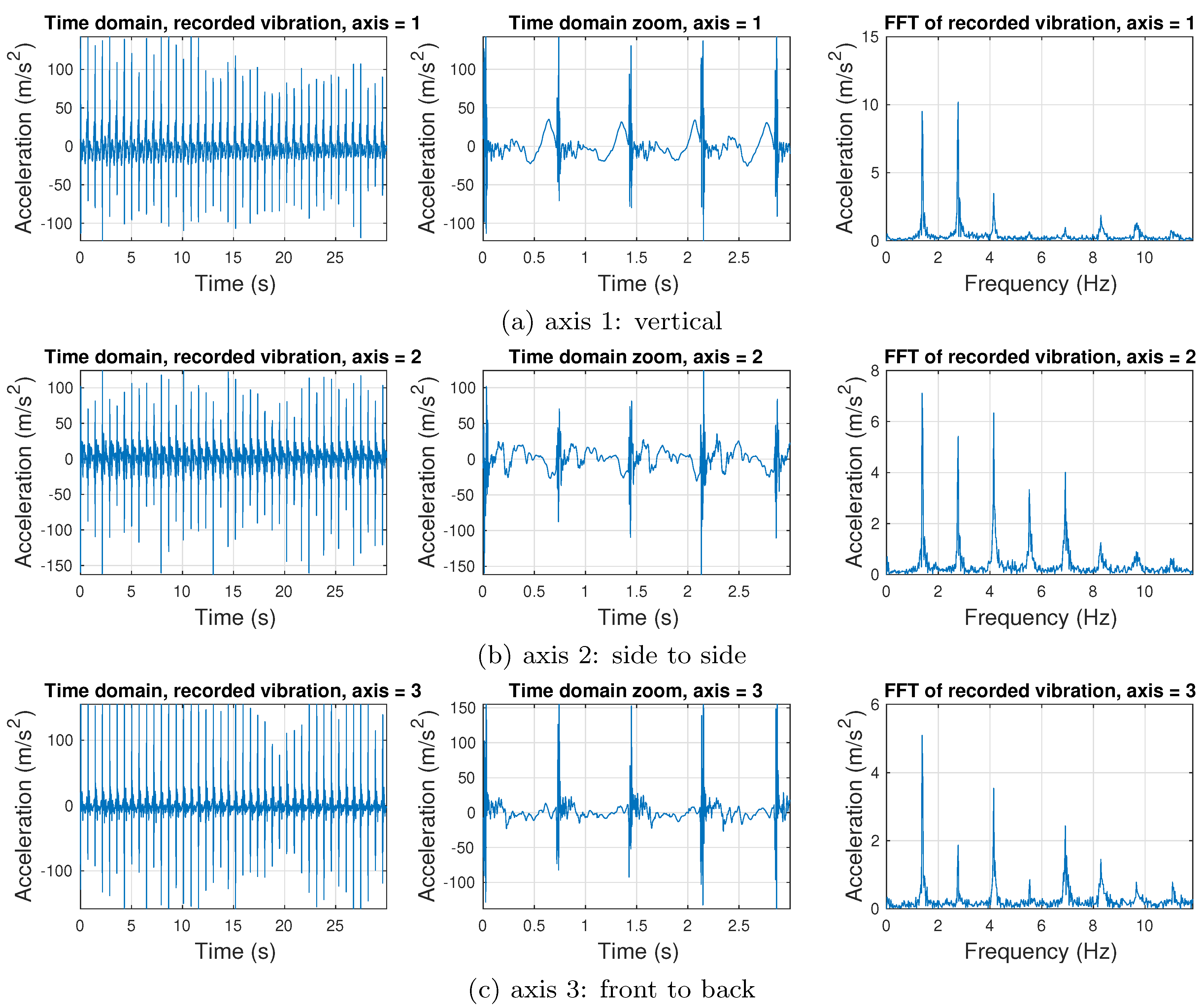
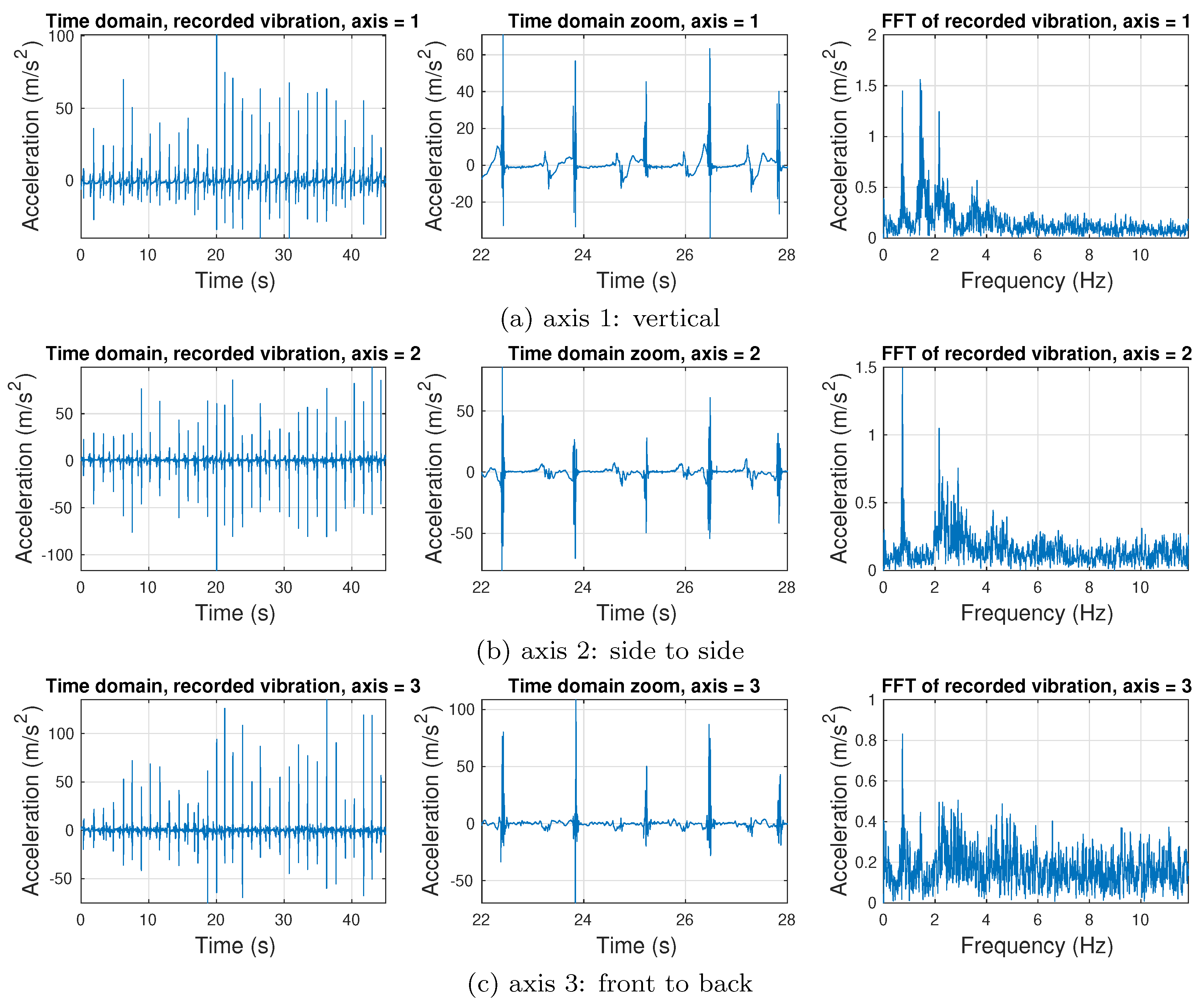
2.1. Gait Measurement and Analysis
- Accelerometer x axis (1): sagittal axis
- Accelerometer y axis (2): longitudinal axis
- Accelerometer z axis (3): frontal axis
- Walking at 3 km/h
- Walking at 6 km/h
- Running at 9 km/h
- Climbing at 30 steps per minute
- Climbing at 40 steps per minute
- Climbing at 60 steps per minute
- Walking at 3 km/h with 20 kg weight in the left hand to simulate limping
- Walking at 3 km/h with 20 kg weight in the right hand to simulate limping
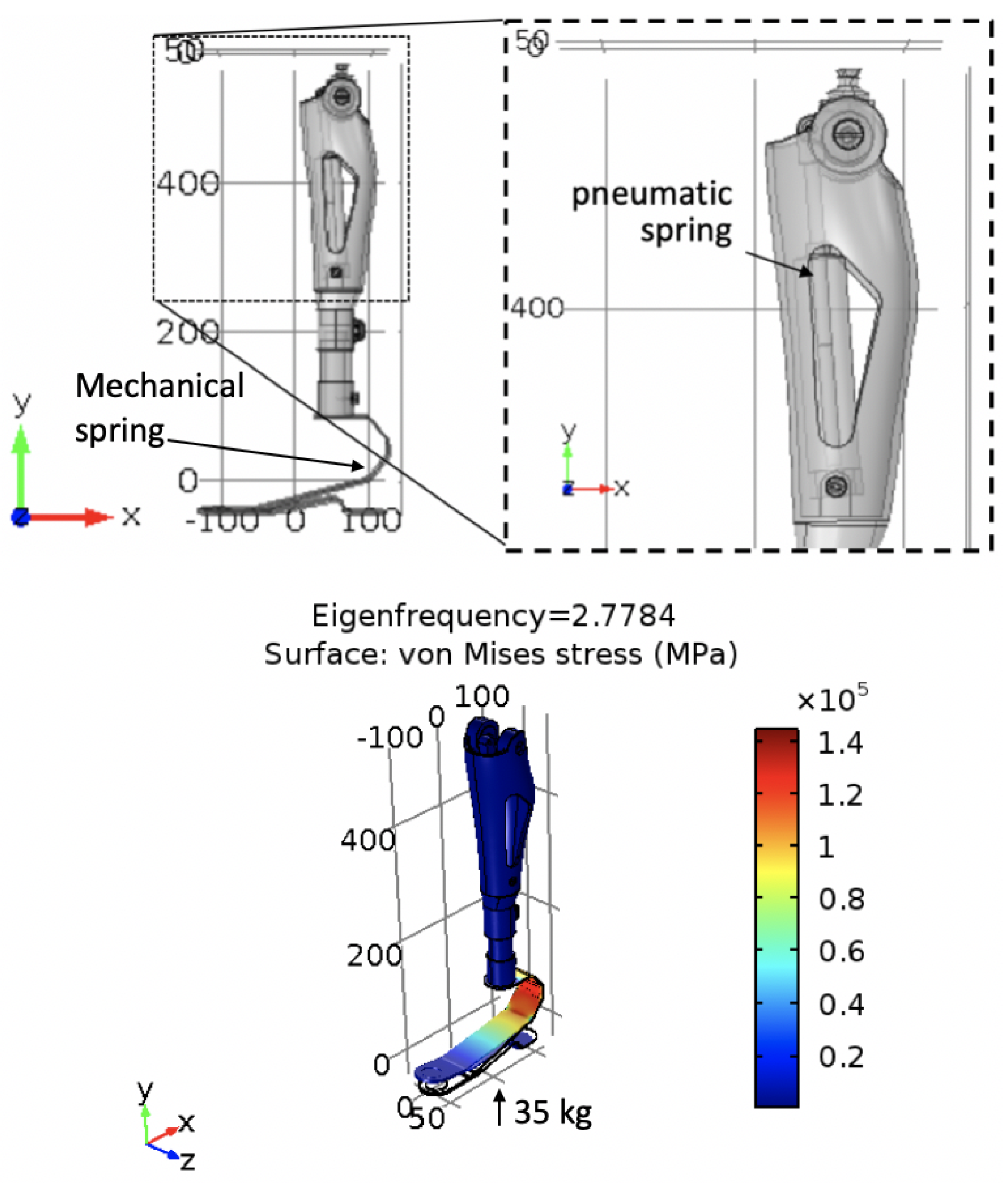
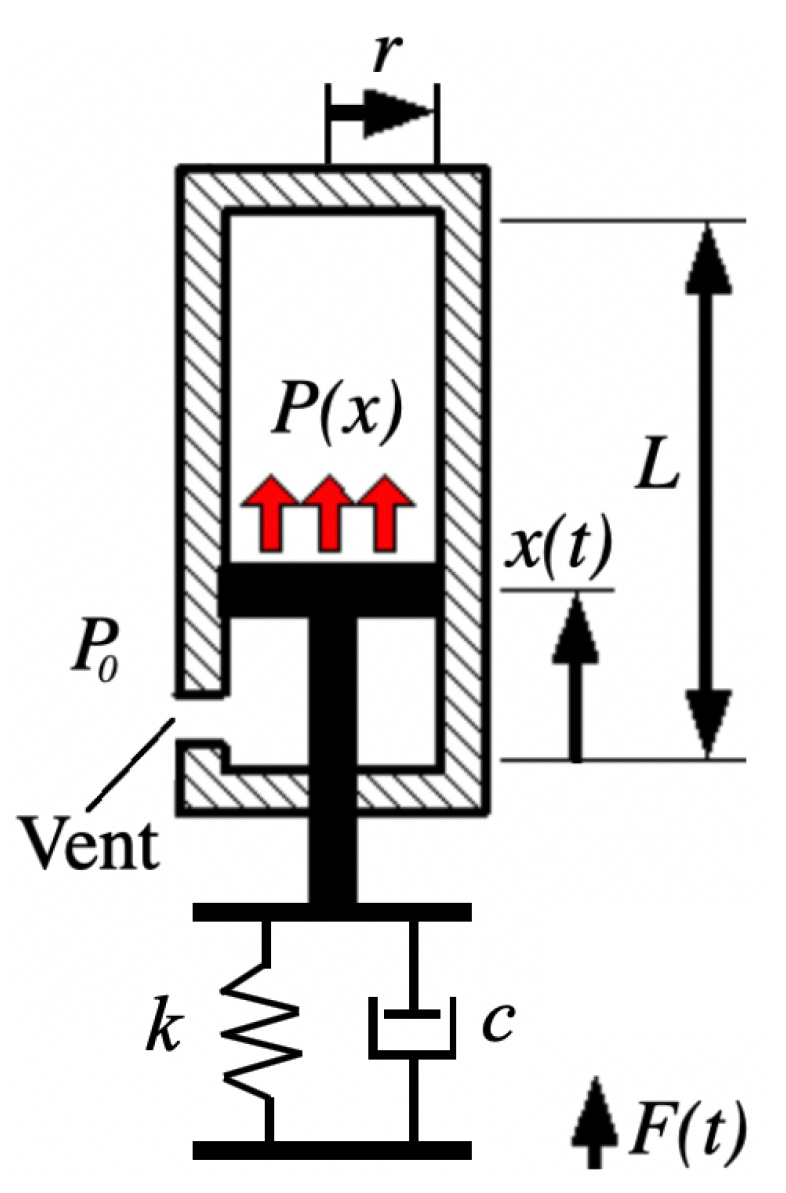
2.2. Analytical and Numerical Model
3. Results
3.1. Analytical and Finite Element Model
3.2. Measured Gait Three-Axis Acceleration Data
3.3. Numerically Simulated Power Predication
4. Discussion
5. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ESR | energy storage and return |
| SACH | solid ankle, cushioned heel |
| MEMS | microelectromechanical systems |
| CFRP | carbon fibre reinforced polymer |
| DOF | degrees of freedom |
References
- Samuelsson, K.A.; Töytäri, O.; Salminen, A.L.; Brandt, Å. Effects of lower limb prosthesis on activity, participation, and quality of life: A systematic review. Prosthetics Orthot. Int. 2012, 36, 145–158. [Google Scholar] [CrossRef]
- Bliquez, L.J. Classical Prosthetics. Archaeology 1983, 36, 25–29. [Google Scholar]
- Staros, A. The SACH (solid-ankle cushion-heel) foot. Orthop. Prosthet. Appl. J. 1957, 2, 23–31. [Google Scholar]
- Lehmann, J.; Price, R.; Boswell-Bessette, S.; Dralle, A.; Questad, K.; deLateur, B. Comprehensive analysis of energy storing prosthetic feet: Flex Foot and Seattle Foot Versus Standard SACH foot. Arch. Phys. Med. Rehabil. 1993, 74, 1225–1231. [Google Scholar] [CrossRef]
- Nolan, L. Carbon fibre prostheses and running in amputees: A review. Foot Ankle Surg. 2008, 14, 125–129. [Google Scholar] [CrossRef] [PubMed]
- South, B.J.; Fey, N.P.; Bosker, G.; Neptune, R.R. Manufacture of Energy Storage and Return Prosthetic Feet Using Selective Laser Sintering. J. Biomech. Eng. 2009, 132, 015001. [Google Scholar] [CrossRef] [PubMed]
- Versluys, R.; Desomer, A.; Lenaerts, G.; Beyl, P.; Van Damme, M.; Vanderborght, B.; Vanderniepen, I.; Van der Perre, G.; Lefeber, D. From conventional prosthetic feet to bionic feet: A review study. In Proceedings of the 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 49–54. [Google Scholar]
- Versluys, R.; Beyl, P.; Damme, M.V.; Desomer, A.; Ham, R.V.; Lefeber, D. Prosthetic feet: State-of-the-art review and the importance of mimicking human ankle–foot biomechanics. Disabil. Rehabil. Assist. Technol. 2009, 4, 65–75. [Google Scholar] [CrossRef]
- Pailler, D.; Sautreuil, P.; Piera, J.; Genty, M.; Goujon, H. Evolution in prostheses for sprinters with lower-limb amputation. Ann. Readapt. Med. Phys. 2004, 47, 374–381. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Scholz, M.S.; Blanchfield, J.; Bloom, L.; Coburn, B.; Elkington, M.; Fuller, J.; Gilbert, M.; Muflahi, S.; Pernice, M.; Rae, S.; et al. The use of composite materials in modern orthopaedic medicine and prosthetic devices: A review. Compos. Sci. Technol. 2011, 71, 1791–1803. [Google Scholar] [CrossRef]
- Highsmith, M.J.; Kahle, J.T.; Bongiorni, D.R.; Sutton, B.S.; Groer, S.; Kaufman, K.R. Safety, energy efficiency, and cost efficacy of the C-Leg for transfemoral amputees: A review of the literature. Prosthetics Orthot. Int. 2010, 34, 362–377. [Google Scholar] [CrossRef] [PubMed]
- Alsaadi, A.; Shi, Y.; Pan, L.; Tao, J.; Jia, Y. Vibration energy harvesting of multifunctional carbon fibre composite laminate structures. Compos. Sci. Technol. 2019, 178, 1–10. [Google Scholar] [CrossRef]
- Liu, M.; Datseris, P.; Huang, H.H. A Prototype for Smart Prosthetic Legs-Analysis and Mechanical Design. Adv. Mater. Res. 2012, 403–408, 1999–2006. [Google Scholar] [CrossRef]
- Park, J.; Yoon, G.H.; Kang, J.W.; Choi, S.B. Design and control of a prosthetic leg for above-knee amputees operated in semi-active and active modes. Smart Mater. Struct. 2016, 25, 085009. [Google Scholar] [CrossRef]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.J.; Goldfarb, M. Self-contained powered knee and ankle prosthesis: Initial evaluation on a transfemoral amputee. In Proceedings of the IEEE International Conference on Rehabilitation Robotics, Kyoto, Japan, 23–26 June 2009. [Google Scholar]
- Ferreira, C.; Reis, L.P.; Santos, C.P. Review of Control Strategies for Lower Limb Prostheses. In Robot 2015: Second Iberian Robotics Conference; Reis, L.P., Moreira, A.P., Lima, P.U., Montano, L., Muñoz-Martinez, V., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 209–220. [Google Scholar]
- Windrich, M.; Grimmer, M.; Christ, O.; Rinderknecht, S.; Beckerle, P. Active lower limb prosthetics: A systematic review of design issues and solutions. Biomed. Eng. Online 2016, 15, 140. [Google Scholar] [CrossRef] [PubMed]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.; Goldfarb, M. Design and control of an active electrical knee and ankle prosthesis. In Proceedings of the 2nd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008. [Google Scholar]
- Pillai, M.V.; Kazerooni, H.; Hurwich, A. Design of a semi-active knee-ankle prosthesis. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Tucker, M.R.; Fite, K.B. Mechanical damping with electrical regeneration for a powered transfemoral prosthesis. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, ON, Canada, 6–9 July 2010; pp. 13–18. [Google Scholar]
- Jia, Y.; Yan, J.; Soga, K.; Seshia, A. A parametrically excited vibration energy harvester. J. Intel. Mater. Syst. Struct. 2013. [Google Scholar] [CrossRef]
- Jia, Y.; Yan, J.; Soga, K.; Seshia, A. Parametric resonance for vibration energy harvesting with design techniques to passively reduce the initiation threshold amplitude. Smart Mater. Struct. 2014, 23, 13. [Google Scholar] [CrossRef]
- Jia, Y.; Seshia, A. Directly and parametrically excited bi-stable vibration energy harvester for broadband operation. Proc. Transducers 2013, 2013, 454–457. [Google Scholar]
- Jia, Y.; Seshia, A.A. Power Optimization by Mass Tuning for MEMS Piezoelectric Cantilever Vibration Energy Harvesting. J. MEMS 2015, 25, 108–117. [Google Scholar] [CrossRef]
- Jia, Y.; Yan, J.; Soga, K.; Seshia, A. Parametrically excited MEMS vibration energy harvesters with design approaches to overcome initiation threshold amplitude. J. Micromech. Microeng. 2013, 23, 10. [Google Scholar] [CrossRef]
- Jia, Y.; Yan, J.; Soga, K.; Seshia, A. Multi-frequency Operation of a MEMS Vibration Energy Harvester by Accessing Five Orders of Parametric Resonance. J. Phys. Conf. Ser. 2013, 476, 607–611. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric Nanogenerators as New Energy Technology for Self-Powered Systems and as Active Mechanical and Chemical Sensors. ACS Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Lin, L.; Chen, J.; Niu, S.; Zi, Y. Triboelectric Nanogenerators; Springer: New York, NY, USA, 2016. [Google Scholar]
- Priya, S.; Inman, D. Energy Harvsting Technologies; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gonzalez, J.; Rubio, A.; Moll, F. Human powered piezoelectric batteries to supply power to wearable electronic devices. Int. J. Soc. Mater. Eng. Resour. 2002, 10, 34–40. [Google Scholar] [CrossRef]
- Mitcheson, P.; Yeatman, E.; Rao, G.; Holmes, A.; Green, T. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Selles, R.W.; Bussmann, J.B.; Wagenaar, R.C.; Stam, H.J. Effects of prosthetic mass and mass distribution on kinematics and energetics of prosthetic gait: A systematic review. Arch. Phys. Med. Rehabil. 1999, 80, 1593–1599. [Google Scholar] [CrossRef]
- Du, S.; Jia, Y.; Zhao, C.; Amaratunga, G.A.J.; Seshia, A.A. A Fully Integrated Split-Electrode SSHC Rectifier for Piezoelectric Energy Harvesting. IEEE J.-Solid-State Circuits 2019, 54, 1733–1743. [Google Scholar] [CrossRef]
- Beeby, S.; Tudor, M.; White, N. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175–R195. [Google Scholar] [CrossRef]
- Jia, Y.; Do, C.D.; Zou, X.; Seshia, A.A. A Hybrid Vibration Powered Microelectromechanical Strain Gauge. IEEE Sens. J. 2015, 16, 235–241. [Google Scholar] [CrossRef]
- Nox, P. Prosthetic Leg; GRABCAD: Cambridge, MA, USA, 2017. [Google Scholar]
- AV, R.; MR, S.; RG, E. Influence of speed and step frequency during walking and running on motion sensor output. Med. Sci. Sport. Exerc. 2007, 39, 716–727. [Google Scholar]
- Jia, Y.; Li, S.; Shi, Y. An Analytical and Numerical Study of Magnetic Spring Suspension with Energy Recovery Capabilities. Energies 2018, 11, 3126. [Google Scholar] [CrossRef]
- STMicroelectronics. STM32L4 Power Control; STMicroelectronics: Geneva, Switzerland, 2019. [Google Scholar]
- Darroudi, S.M.; Caldera-Sànchez, R.; Gomez, C. Bluetooth Mesh Energy Consumption: A Model. Sensors 2019, 19, 1238. [Google Scholar] [CrossRef]
- InvenSense. MPU-9250 Nine-Axis (Gyro + Accelerometer + Compass) MEMS MotionTrackin Device; InvenSense: San Jose, CA, USA, 2019. [Google Scholar]
- Omron. OMRON MEMS Gauge Pressure Sensor 2SMPP-02; Omron: Kyoto, Japan, 2019. [Google Scholar]
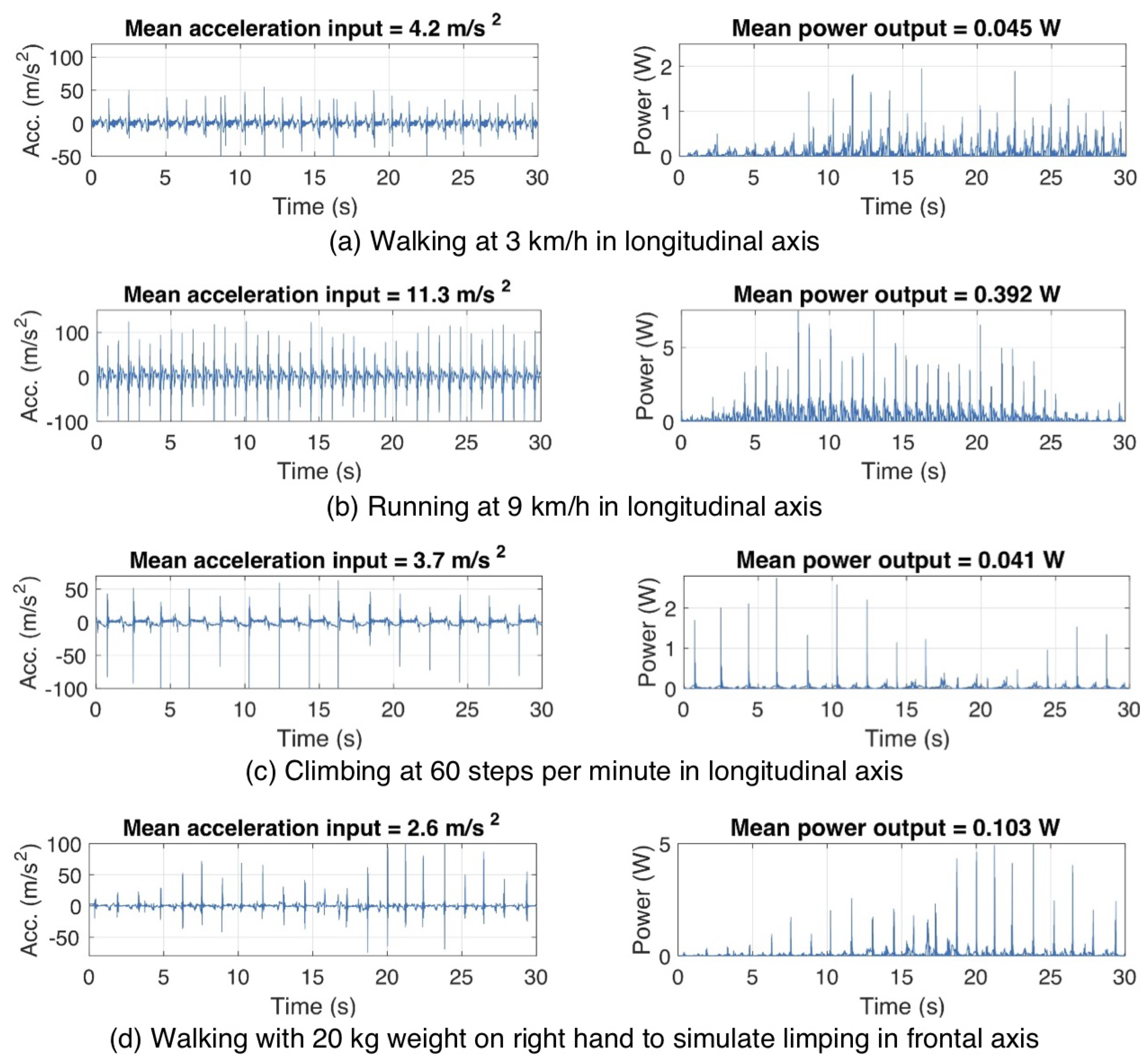
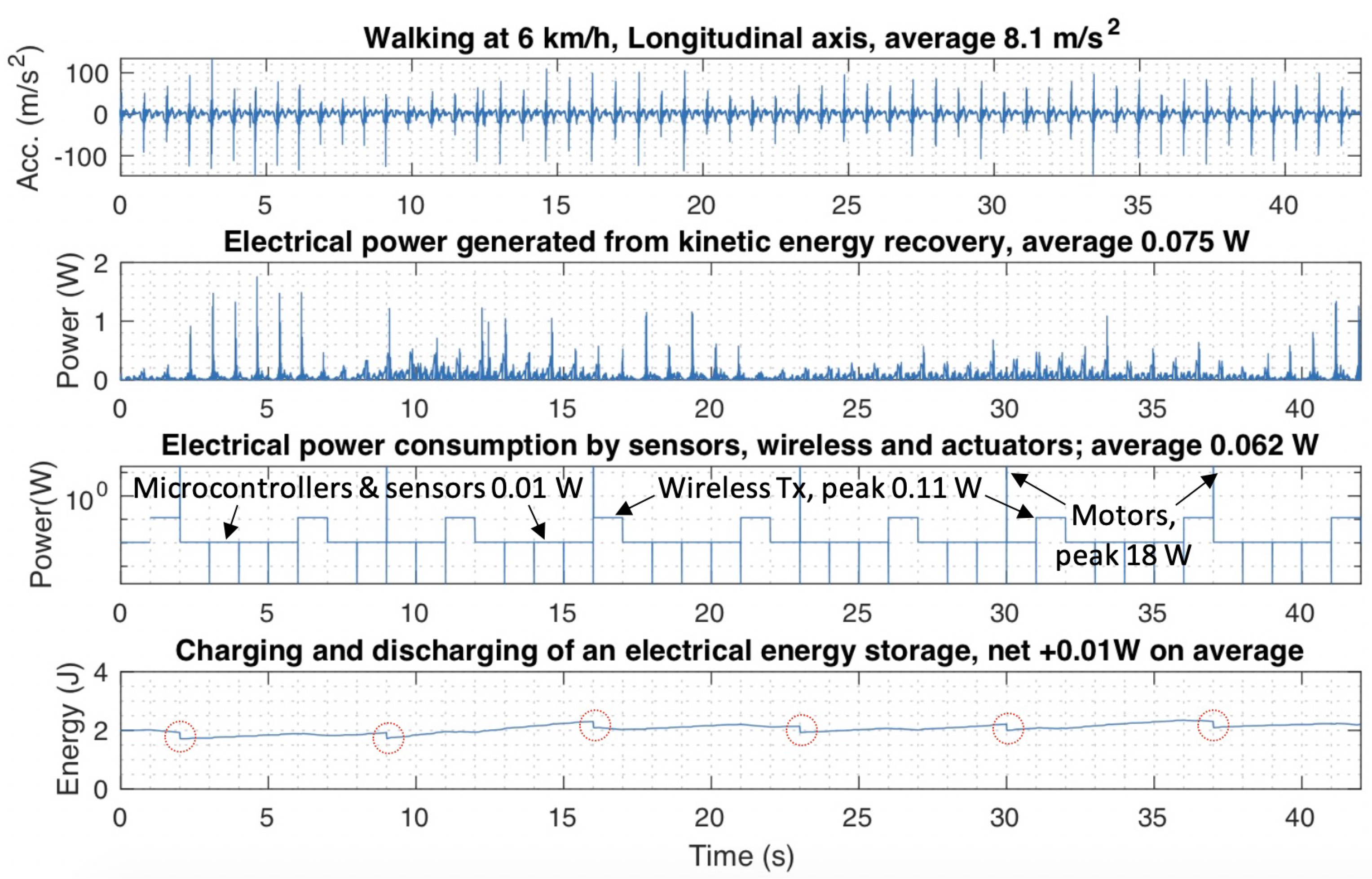
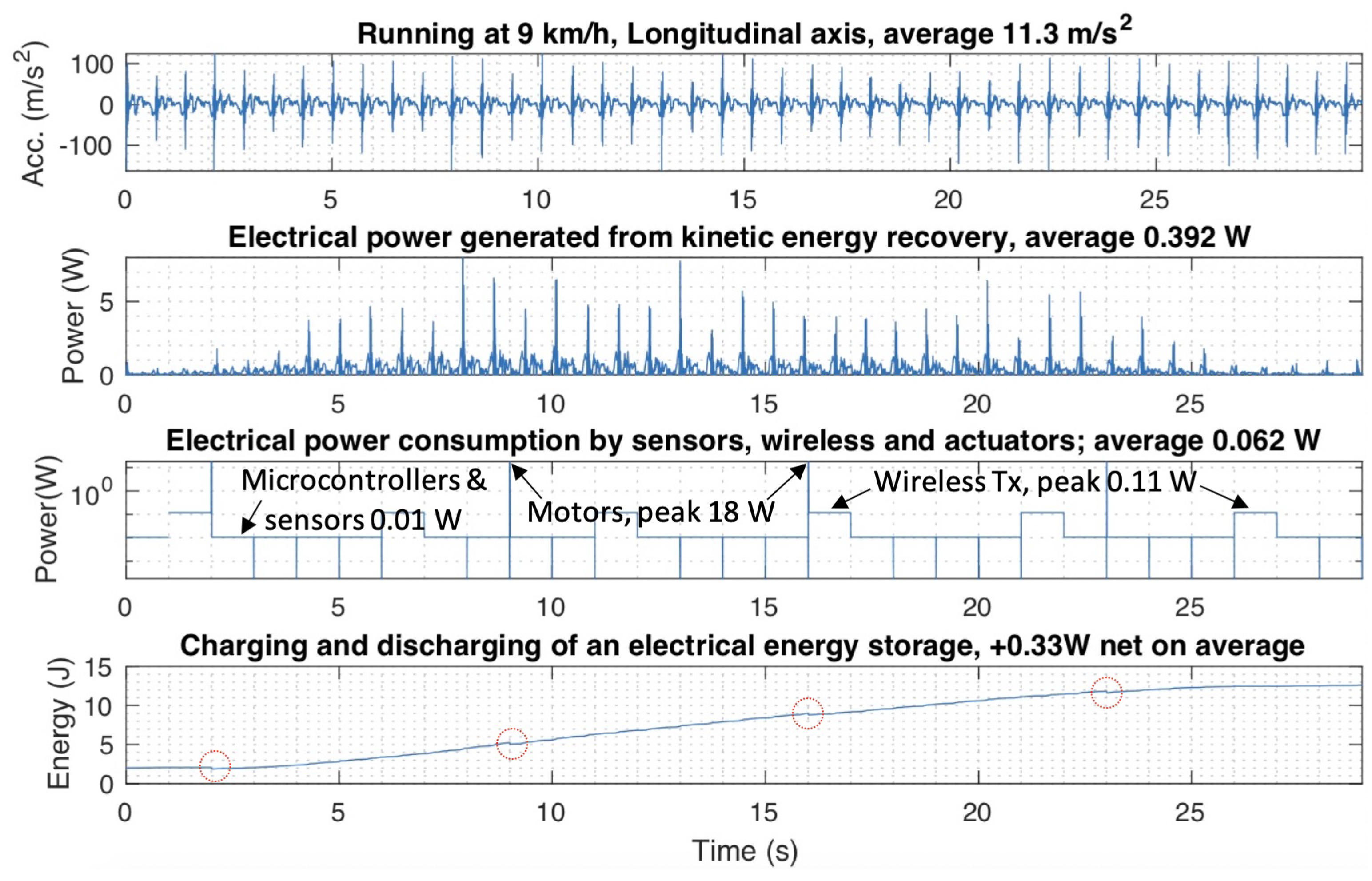
| Gait Condition | Acc. (m/s2) | Power (mW) | Axis |
|---|---|---|---|
| Walking at 3 km/h | 4.2 | 31 | Sagittal |
| 4.2 | 45 | Longitudinal | |
| 2.3 | 34 | Frontal | |
| Walking at 6 km/h | 7.9 | 96 | Sagittal |
| 8.1 | 75 | Longitudinal | |
| 6.1 | 57 | Frontal | |
| Running at 9 km/h | 11.7 | 341 | Sagittal |
| 11.3 | 392 | Longitudinal | |
| 9.4 | 241 | Frontal | |
| Climbing at 60 steps per minute | 2.3 | 29 | Sagittal |
| 3.7 | 41 | Longitudinal | |
| 1.9 | 27 | Frontal | |
| Walking with 20 kg weight in the left hand | 2.3 | 87 | Sagittal |
| 2.4 | 52 | Longitudinal | |
| 2.5 | 62 | Frontal | |
| Walking with 20 kg weight in the right hand | 2.8 | 102 | Sagittal |
| 2.7 | 69 | Longitudinal | |
| 2.6 | 103 | Frontal |
| Device/Operation Mode | (mW) | Notes |
|---|---|---|
| Microproccessing unit (MPU) | 0.36 | active mode [39] |
| 32-bit ARM Cortex | 0.002 | standby mode [39] |
| Bluetooth 5 + RF chip | 27 | transceiver mode [40] |
| 0.045 | sleep mode, clock [40] | |
| MEMS 9 DOF motion sensor + MPU | 0.05 | InvenSense [41] |
| MEMS strain gauge + ASIC | 0.01 | Uni. Cambridge [35] |
| MEMS pressure sensor + ASIC | 0.2 | Omron [42] |
| DC Motor at 0.85 kg f.cm torque | 4500 | 3 units of 1.5 W motor |
| Servo actuator with 5 N starting force | 9000 | 3 units of 3 W motor |
| Power conditioning circuit | 0.1 | switch mode type [33] |
| Other electrical components + leakage | 0.5 | estimate |
| Power Budget Item | Active Power | Period | Active in | Active Time | Average Power |
|---|---|---|---|---|---|
| (W) | (s) | Period (%) | in 1 min. (s) | in 1 min. (W) | |
| MPU, ×4 units | 2.00×10 | 1.0 | 100 | 60 | 2.000×10 |
| Bluetooth 5.0 + RF chip Tx, ×4 units | 1.08×10 | 5.0 | 20 | 12 | 2.160×10 |
| Bluetooth 5.0 + RF chip sleep, ×4 units | 1.80×10 | 5.0 | 80 | 48 | 1.440×10 |
| MEMS 9 DOF, ×4 units | 2.00×10 | 1.0 | 100 | 60 | 2.000×10 |
| MEMS pressure sensor, ×4 units | 2.00×10 | 1.0 | 100 | 60 | 2.000×10 |
| Memory + misc. electric, ×4 units | 2.00×10 | 1.0 | 100 | 60 | 2.000×10 |
| Power conditioning circuit, ×4 units | 4.00×10 | 1.0 | 100 | 60 | 4.000×10 |
| Misc. elec. and leakage, ×4 units | 2.00×10 | 1.0 | 100 | 60 | 2.000×10 |
| DC motor, ×3 units, right ankle | 1.50×10 | 6.0 | 0.17 | 0.1 | 2.501×10 |
| DC motor, ×3 units, left ankle | 1.50×10 | 6.0 | 0.17 | 0.1 | 2.501×10 |
| DC motor, ×3 units, right knee | 1.50×10 | 6.0 | 0.17 | 0.1 | 2.501×10 |
| DC motor, ×3 units, left knee | 1.50×10 | 6.0 | 0.17 | 0.1 | 2.501×10 |
| Servo actuator, ×3 units, right ankle | 3.00×10 | 6.0 | 0.17 | 0.1 | 5.001×10 |
| Servo actuator, ×3 units, left ankle | 3.00×10 | 6.0 | 0.17 | 0.1 | 5.001×10 |
| Servo actuator, ×3 units, right knee | 3.00×10 | 6.0 | 0.17 | 0.1 | 5.001×10 |
| Servo actuator, ×3 units, left knee | 3.00×10 | 6.0 | 0.17 | 0.1 | 5.001×10 |
| Sum | 6.215×10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Wei, X.; Pu, J.; Xie, P.; Wen, T.; Wang, C.; Lian, P.; Xue, S.; Shi, Y. A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics. Energies 2019, 12, 3824. https://doi.org/10.3390/en12203824
Jia Y, Wei X, Pu J, Xie P, Wen T, Wang C, Lian P, Xue S, Shi Y. A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics. Energies. 2019; 12(20):3824. https://doi.org/10.3390/en12203824
Chicago/Turabian StyleJia, Yu, Xueyong Wei, Jie Pu, Pengheng Xie, Tao Wen, Congsi Wang, Peiyuan Lian, Song Xue, and Yu Shi. 2019. "A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics" Energies 12, no. 20: 3824. https://doi.org/10.3390/en12203824
APA StyleJia, Y., Wei, X., Pu, J., Xie, P., Wen, T., Wang, C., Lian, P., Xue, S., & Shi, Y. (2019). A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics. Energies, 12(20), 3824. https://doi.org/10.3390/en12203824









