Abstract
In this paper, we propose a technique to share the licensed spectrums of all mobile network operators (MNOs) of a country with in-building small cells per MNO by exploiting the external wall penetration loss of a building and introducing the time-domain eICIC technique. The proposed technique considers allocating the dedicated spectrum Bop per MNO only its to outdoor macro UEs, whereas the total spectrum of all MNOs of the country Bco to its small cells indoor per building such that technically any small indoor cell of an MNO can have access to Bco instead of merely Bop assigned only to the MNO itself. We develop an interference management strategy as well as an algorithm for the proposed technique. System-level capacity, spectral efficiency, and energy efficiency performance metrics are derived, and a generic model for energy efficiency is presented. An optimal amount of small indoor cell density in terms of the number of buildings L carrying these small cells per MNO to trade-off the spectral efficiency and the energy efficiency is derived. With the system-level numerical and simulation results, we define an optimal value of L for a dense deployment of small indoor cells of an MNO and show that the proposed spectrum sharing technique can achieve massive indoor capacity, spectral efficiency, and energy efficiency for the MNO. Finally, we demonstrate that the proposed spectrum sharing technique could meet both the spectral efficiency and the energy efficiency requirements for 5G mobile networks for numerous traffic arrival rates to small indoor cells per building of an MNO.
Keywords:
spectrum sharing; multiple-operator; eICIC; small cell; nationwide; spectral efficiency; energy efficiency; 5G 1. Introduction
1.1. Background
Usually, each mobile network operator (MNO) of a country is allocated with a dedicated licensed spectrum to serve its users’ traffic. Such static allocations of radio spectra were once sufficient to ensure user demands. To reuse the same dedicated spectrum for an MNO, techniques such as fractional frequency reuse [1] are useful to serve more users with reasonable data rate demands. In the last decade, the demand for mobile communications has grown significantly due to an increase in the number of subscribers as well as the volume of traffic and data rate per user. Since more than 60 percent of data is generated in indoor environments, ensuring high indoor data rates and capacity per user have become crucial demands. Even though the subscriber-base of an MNO has been increased tremendously, the radio spectrum allocated to an MNO has not been increased proportionately. Recently, instead of a static allocation, the dynamic allocation of radio spectrum resources has been found to be more effective. In the dynamic spectrum allocation, the spectrum allocated to user equipments (UEs) of an MNO could be shared by UEs of another MNO such that the overall spectrum availability for an MNO could be increased to address high indoor data rates and capacity demands.
1.2. Existing Literature
Extensive studies have already been carried out on spectrum sharing for both heterogeneous systems [2,3] and homogeneous systems [4]. Typically, in heterogeneous systems, the spectra of a different systems (e.g., space-satellite systems and TV white spaces) is shared with an MNO. On the other hand, for homogeneous systems, spectrum sharing is performed between MNOs. In Reference [5], authors have presented inter-operator Dynamic Spectrum Access (DSA) algorithms based on game theory by formulating a two-players non-zero sum game where the operators are the players. Likewise, authors in [6] have addressed the problem of spectrum sharing where competitive operators coexist in the same frequency band. Following first a strategic non-cooperative game, in a cognitive context, with the presence of primary and secondary operators, the inter-operator spectrum sharing problem is reformulated as a Stackelberg game using a hierarchy where the primary operator is the leader. Further, authors in [7] have shown the potential gain by spectrum sharing between two cellular operators in terms of network efficiency. Furthermore, authors in [8], addressed the problem of spectrum sharing between two operators in a dynamic network where both operators are allowed to share a fraction of their licensed spectrum band with each other by forming a common spectrum band to maximize the gain in profits of both operators while considering the fairness among the operators.
Besides, co-primary shared access (CoPSA) [9] has been proposed as an effective spectrum sharing technique for homogeneous systems. In CoPSA, MNOs share their licensed spectrums through mutual agreements and users of different MNOs have equal access rights. Spectrum pooling and mutual renting are the two major access methods of CoPSA [10]. In spectrum pooling, instead of allocating spectrum exclusively on a dedicated access basis, spectrums of different MNOs are allocated on a shared basis with equal priority to access the whole spectrum. In mutual renting, a part of the spectrum allocated exclusively to an MNO could be rented by another MNO. However, spectrum pooling suffers from ensuring sufficient data rate and capacity during the high data rate and capacity demands when all MNOs want to get access to the spectrum pool simultaneously. Likewise, in mutual renting, the licensed spectrum MNO always has preemptive priority to access its own spectrum [9]. Moreover, a major limitation of these methods is that the spectrum sharing has been considered performing mostly between two MNOs such that only the spectrum of one MNO could be shared with the other.
1.3. Contribution
To overcome the aforementioned problems with homogeneous systems, in this paper, we propose a technique that considers sharing the spectrums allocated to all MNOs, instead of only two or more MNOs, of a country with small indoor cells per building per MNO. More elaborately, the proposed spectrum sharing technique exploits the high external wall penetration loss [9] of energy-efficient modern buildings. This is due to the fact that modern building materials include metallic surface or foil, concrete external wall structure, and windows consisting of low emission glasses that result in increasing outdoor-indoor penetration losses as compared to older buildings. Note that, according to [11], the average outdoor-indoor penetration losses in modern buildings range from 19 dB to 23 dB for the signal frequencies of 900 MHz to 2100 MHz with a peak penetration loss of 35 dB in contrast to 6 dB to 9 dB for older buildings. Hence, by exploiting the high penetration loss of any building, the whole mobile radio spectrum allocated for a country could be assigned to only UEs of small cells per building per MNO, whereas, only the dedicated licensed spectrum of the MNO itself is assigned to outdoor UEs per macrocell. Since small indoor cells can use the entire spectrum of a country, massive capacity, spectral efficiency, and energy efficiency can be achieved. In addition, we present a generic model for energy efficiency and find an optimal density of small cells in terms of the number of buildings per MNO to the trade-off between the spectral efficiency and energy efficiency. Finally, we also show that the proposed spectrum sharing technique can satisfy the spectral efficiency and the energy efficiency requirements for the fifth-generation (5G) mobile networks.
1.4. Organization
The paper is organized as follows. In Section 2, the system model, including system architecture, proposed spectrum sharing technique and its related issues are discussed. In Section 3, the co-channel interference (CCI) scenario and management are discussed as well as traffic arrival rates to small cells per MNO and the corresponding allocated time per almost blank subframe (ABS) pattern period (APP) are deduced. In Section 4, system-level capacity, spectral efficiency, and energy efficiency performance metrics are derived. In Section 5, a generic model of energy efficiency is developed, and the condition for the optimality of the spectral efficiency and energy efficiency is deduced. Scheduling and fairness principles proposed a spectrum sharing algorithm, and default simulation parameters and assumptions are described in Section 6. In Section 7, the performances of the proposed spectrum sharing technique are evaluated as well as compared against the spectral efficiency and the energy efficiency requirements for 5G mobile networks. We conclude the paper in Section 8.
1.5. Declaration
A small part of this paper has been accepted for presentation in the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (IEEE DySPAN), Newark, NJ, USA, 11–14 November 2019 [12]. The conference article has been extended considerably in terms of enhancement of background material, expansion of discussion, and inclusion of new problems and corresponding solutions. Conference materials, whenever used in terms of texts are rewritten, and figures are reproduced with citations. Finally, this paper is written comprehensively such that readers will find it self-contained, detailed, and complete, unlike its conference solutions.
2. System Model
2.1. System Architecture
Figure 1 shows the system architecture for the total number of MNOs xm = 4 of a nation. Each MNO is assumed to consist of a number of outdoor, indoor and offloaded UEs. A certain percentage of total macro UEs of each MNO is considered indoor, and a number of macro UEs are considered offloaded to picocells. Each MNO is assumed to deploy in-building small cells to provide good indoor coverage and the number of small cells per MNO varies from one building to another. Each MNO has a dedicated spectrum of Bop and Bop of each of the xm MNOs are aggregated to become the total spectrum of all MNOs of the country Bco. Bop of each MNO is aggregated to a common pool where a centralized scheduler manages sharing and allocating Bco to all operators. Note that due to the necessity of a new entity to the centralized management of the radio spectrum, such a common spectrum polling could be provided with an additional cost from the deployment, by either the national regulatory authority (NRA), or any third party, or operators under certain common sharing and negotiation among them. In summary, the followings are assumed for the system: (1) Each MNO has a dedicated licensed spectrum Bop, (2) Bop would vary with an operator’s requirement, and (3) There are xm operators, and hence, the xm spectrum bands exist in the system.
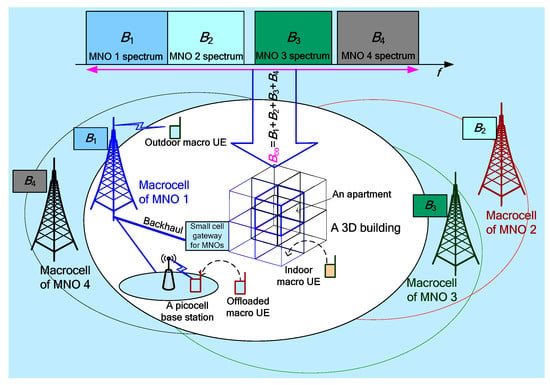
Figure 1.
System architecture for xm = 4 MNOs [12].
2.2. Proposed Spectrum sharing Technique and Related Issues
Spectrum sharing among multiple MNOs is considered as one of the most effective solutions to address the scarcity of spectrum availability of an MNO. Though several spectrum sharing techniques have already been proposed in the literature, most do not address adequately the user demand, particularly when sharing the spectrum Bop of one system with the other, simultaneously. To overcome this problem, in this paper, we propose a novel spectrum sharing technique by considering that the dedicated spectrum Bop per MNO is allocated to outdoor macro UEs of any MNO. However, for small indoor cells, Bco is made accessible by each small cell of all MNOs of the country with an equal priority such that technically any small indoor cell of each MNO could have access to the maximum spectrum of the whole Bco instead of the merely dedicated Bop only for any outdoor UE of the corresponding MNO, as shown in Figure 2. This results in achieving massive indoor capacity by an MNO.
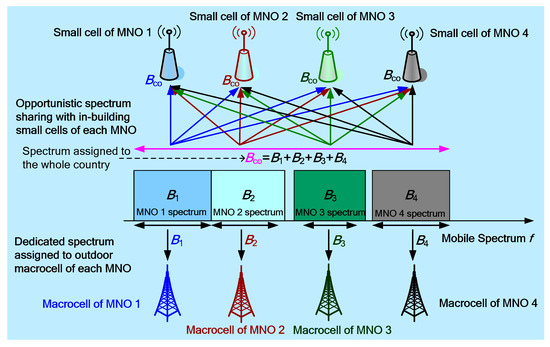
Figure 2.
An abstract view of the proposed spectrum sharing technique for the maximum number of MNOs xm = 4 [12].
Due to the unboundedness for getting access to the whole spectrum Bco anywhere anytime by small indoor cells of any MNO subject to satisfying certain conditions in order to avoid CCI among MNOs, we refer the proposed spectrum sharing scheme as the indoor ubiquitous spectrum sharing technique. By adopting such a technique, each MNO can pay only whatever the amount of spectrum it uses to serve its indoor users over a certain duration of time instead of paying the whole spectrum Bco licensing fee. This can ensure both the fairness in the licensing fee and the improvement in overall spectral utilization.
To enable the proposed spectrum sharing technique among multiple MNOs nationwide, the following major issues are needed to be addressed. In what follows, each issue is stated, followed by the approach to address the corresponding issue in the subsequent sections of this paper.
- (1)
- Issue 1: How to address dynamic resource allocation among MNOs to improve the overall spectrum utilization?How to address: The static allocation of the time resource based on the number of MNOs may cause either underutilization or scarcity of the spectrum of an MNO. To address this issue, we consider allocating the time resource to small cells of an MNO dynamically based on the actual traffic arrival rate in order to improve the spectrum utilization.
- (2)
- Issue 2: How to optimize for the fair allocation of the time resource to each MNO when applying the proposed nationwide spectrum sharing technique?How to address: We consider assigning an optimal number of transmission time intervals (TTIs) to an MNO x in proportion with the ratio of the average number of UEs of the MNO x to the sum of the average number of UEs of all other MNOs that are active during any APP.
- (3)
- Issue 3: How to ensure optimality between the spectral efficiency and the energy efficiency performances of an MNO for the proposed technique?How to address: we consider defining the minimum value of L denoted as Lmin by using the slope of the energy efficiency curve such that choosing any value of L ≥ Lmin results in improving both the spectral efficiency and energy efficiency responses of an MNO. The values of spectral and energy efficiencies corresponding to L ≥ Lmin define the region of optimality for both efficiencies. In other words, depending on the requirements for the spectral and energy efficiencies, an optimal value of L ≥ Lmin is chosen.
- (4)
- Issue 4: How to clarify that the proposed technique is scalable and can meet the spectral and energy efficiencies of the next-generation mobile networks?How to Address: To ensure scalability, we consider sharing the whole spectrum with small cells per building L per MNO such that by increasing the value of L subject to L ≥ Lmin more spectral efficiency and energy efficiency could be achieved. Further, in the paper, we show that by adjusting the value of L corresponding to the varying number of TTIs allocated to an MNO during each APP, the spectral efficiency and the energy efficiency requirements for the 5G mobile network could be achieved.
- (5)
- Issue 5: How to describe and address the CCI scenarios in the proposed technique. Also, how does the CCI affect the point of optimality for spectral and energy efficiencies?How to address: We describe in detail the CCI due to the presence of multiple MNOs operating at the spectrum using the ABS based enhanced intercell interference coordination (eICIC) technique. Since with the change of CCI, the number of TTIs allocated to an MNO change, an optimal number of TTIs is allocated to each MNO based on the actual traffic demand of the MNO as compared to that of the others. In general, since an increase in CCI results in degrading the spectral and efficiency performances, the minimum point of optimality in terms of L, corresponding to which both the spectral and energy efficiencies intersect one another, shifts leftward resulting in a decrease in the minimum optimal point Lmin and vice versa.
3. Co-Channel Interference Scenario and Management
3.1. Co-Channel Interference Scenario
Figure 3 shows numerous CCI scenarios with respect to MNO 1 based on the number of small cells deployed by other MNOs with that of MNO 1. In Figure 3a, small cell UEs of MNO 1 and indoor UEs of MNOs 2, 3, and 4 are served by their respective small cells. In Figure 3b, small cell UEs of MNO 1 and indoor UEs of MNO 4 are served by their own small cells. However, indoor macro UEs of MNO 2 and MNO 3 are served by their respective macrocells. In Figure 3c, only small cell UEs of MNO 1 are present. No UEs of other MNOs’ do exist in the small cell coverage of MNO 1. Further, a macro UE in the outdoor is served by the macrocell of MNO 1. However, when a macro UE of MNO 1 enters the building, the signal quality of it suddenly falls such that it is offloaded to a small cell of MNO 1. Note that the spectrums of all MNOs are pooled and aggregated to a commonplace called common spectrum scheduler, which allocates spectrum resources to small cells of each MNO following the given below principle.
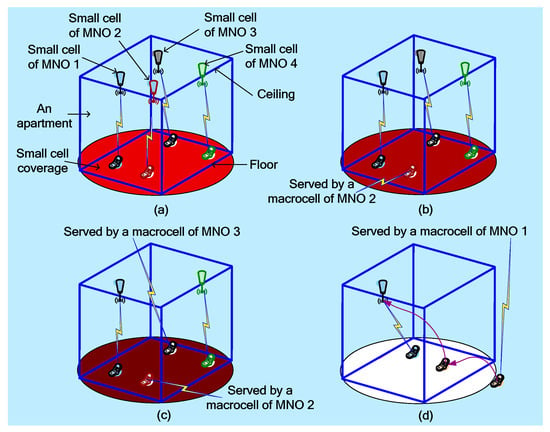
Figure 3.
An illustration of the CCI strength when sharing the spectrum of one MNO (MNO 1) with that of others (MNOs 2, 3, and 4): (a) maximum CCI for xm = 4, (b) CCI for xm = 3, (c) minimum CCI for xm = 2, and (d) no CCI for xm = 1.
Let where xm denotes the maximum number of MNOs of a country. Then, for a given MNO x, if any UE of MNOs other than x exists within the coverage of a small cell of MNO x deployed in any building , any UE within the coverage of is served only during non-ABSs. The allocation of non-ABSs to a UE is defined such that there is a fair allocation of time resources, i.e., TTIs, to UEs of each MNO over an APP, resulting in increasing the number of non-ABSs with an increase in UEs of the MNO x within the coverage of . Note that and vary with MNO x and its corresponding .
The arrival process of small cell UEs of MNO x to its small cell coverages can be modeled by the Poisson process. Let denote respectively the average number of arrivals of UEs of MNOs per building L such that the average duration of time, i.e., the number of non-ABSs, allocated to of any MNO x is found based on a fair time resource allocation strategy, i.e., in proportionate with the ratio of the average number of UEs of any MNO x to the sum of the overall average number of UEs of MNOs present in the coverage of in any APP.
3.2. Defining Call Arrivals of Small Cells per MNO
The sessions or call arrivals can be modeled as a Poisson process [13,14] such that the traffic activity of UEs of an MNO when served by an in-building small cell base station (BS) could be modeled as an exponentially distributed continuous-time Poisson process. Moreover, given the present state, the future state is independent of the past state such that the traffic activity of a UE can be modeled as a two-state Markov chain with an off-state to an on-state transition rate , and an on-state to off-state transition rate . For simplicity, we assume that an in-building small cell BS (SBS) of any MNO could serve the maximum of one UE at a time. Hence, the number of active SBSs is the same as the number of in-building UEs at any time t for any L, i.e., where and .
Let denote the on-state probabilities of SBSs of MNO x that correspond to the number of active UEs of the MNO x per building, which can be found using the Birth-Death process [13] as shown in Figure 4.
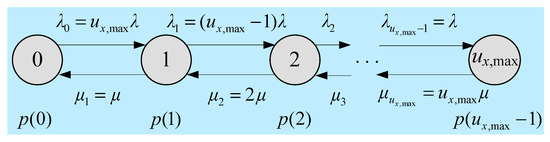
Figure 4.
Traffic in-progress state diagram for UEs of an MNO x per 3-dimensional (3D) building.
Denote and respectively the birth rate and death rate such that the following holds [15,16].
Hence,
Since , using Equation (1), the following could be obtained.
Hence, the probability that the number of UEs, ux of MNO x, is present within a building is given by,
So we can find the expected value of the number of UEs, of MNO x within the building as follows:
Since we assume that a small cell can serve the maximum of one MNO UE at any time t, the maximum number of UEs per 3D building . Since each SBS can serve the maximum of one UE, the number of SBSs is equal to the number of UEs. This, in turn, implies that the probability given by is also the probability that the ux number of SBSs are active to serve UEs simultaneously during any time period.
3.3. Co-Channel Interference Management
We propose an approach for the CCI management to share the whole spectrum per country with small indoor cells per MNO each assigned with a dedicated spectrum, as shown in Figure 5. The eICIC technique [17,18] is employed to share the whole spectrum with indoor UEs of multiple MNOs such that in any TTI of an APP only UEs of at max one MNO could be served. Indoor macro UEs of any MNO are offloaded to its small cells if small indoor cells of the corresponding MNO are available. Hence, in any TTI, all indoor UEs are served by small cells of any MNO and there is no existence of any indoor macro UEs as they are all offloaded to small cells of their MNO’s network. If otherwise, i.e., no small indoor cells exist, all indoor macro UEs are served by their respective MNO’s macrocells. Hence, it is the responsibility of the indoor macro UEs to sense and detect if they have any small indoor cells within their range in any building, once they move into a building.
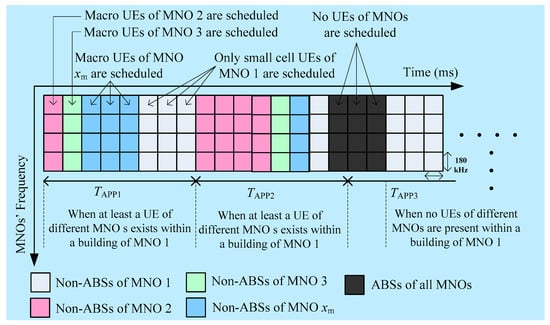
Figure 5.
CCI avoidance using ABS based eICIC technique for small cells of MNO 1 in a building [12].
Since in any TTI only UEs of one MNO are served, UEs of other MNOs do not transmit except some control signals, which are termed as ABS, such that for any MNO x, the following holds.
Also,
However, if no UEs of MNOs but x do exist with traffic in-progress within the coverage of , UEs of MNO x is scheduled in all TTIs per APP. Note that if no UEs of MNOs but x does exist without any traffic in-progress, then no UE of MNO x is scheduled such that the following holds for any MNO x.
The APP TAPP is updated frequently in regular time intervals to update the presence of UEs of other MNOs within the small cell coverage. Further, we assume that if there exists at least a UE of any MNO x, the number of TTIs allocated to that UE must be non-zero to ensure the continuity of services. Hence, using Equations (5)–(7) and above assumptions, by forming and solving the following optimization problem, we can find an optimal value of non-ABSs for the MNO x = 1.
where is the maximum transmit power of any small cell sx of any MNO x. The solution of the above optimization problem for the MNO x = 1 is given by,
Proof:
Using Equation (8a),
Using Equation (8b–d), since a UE of any MNO X/x = 1 in any TTI may not exist in the small cell coverage of MNO 1, can be expressed as , where , and defines that if exists in the set ; otherwise, .
Since ABSs and non-ABSs are strictly integers, applying Equation (8b,e,f), the optimal value of TnABS,x is given by,
Hence, . □
4. Performance Metrics Estimation
4.1. Capacity, Spectral Efficiency, and Energy Efficiency Performance
Let Mco denote the number of resource blocks (RBs) in Bco. Note that the whole spectrum Bco is aggregated to a common pool where a centralized scheduler manages sharing and allocating Mco RBs to all MNOs. Since, in general, the proposed technique may take advantage of the spatial distribution of UEs of different MNOs in small indoor cells, any MNO may get access to as much spectra as needed out of Bco. Likewise, all other MNOs also make use of the necessary spectrums from the common pool of spectrum of Bco Hz, which in turn results in improved spectral utilization of Bco. Such a common poll of spectrums for the indoor coverage can be provided by either the NRA, or any third party, or under certain conditions concerning sharing and negotiations among MNOs.
Since small cells of all MNOs operate at the same spectrum Bco and use the same indoor environment, the system-level performance of small cells of all MNOs would follow the same. Hence, in the following, we evaluate the performance of only one MNO (i.e., MNO 1) operating at the dedicated spectrum B1. The performance of the rest of the MNOs can be evaluated following the same procedure. Assume that there are 4 MNOs, i.e., xm = 4, in the system shown in Figure 1 such that , which are assigned with the dedicated spectrum , respectively such that the following holds.
Now, for L = 1, the received signal-to-interference-plus-noise ratio for a UE at RB = i in TTI = t could be expressed as
where is the transmit power, is the noise power, is the total interference signal power, and is the link loss for a link between a UE and a base station at RB = i in TTI = t. can be expressed in dB as
where and are respectively the total antenna gain and connector loss. , , and , respectively denote large scale shadowing effecst, small scale Rayleigh or Rician fading, and distance-dependent path loss between a base station and a UE at RB = i in TTI = t.
Using Shannon’s capacity formula, a link throughput at RB = i in TTI = t in bps per Hz is given by [19],
where β is considered as the implementation loss factor.
(1) Outdoor capacity: Since outdoor UEs of any MNO must operate at the dedicated spectrum of the MNO; the whole dedicated spectrum can be allocated to its outdoor UEs of each MNO. Further, whenever an outdoor macro UE moves into a building, the macro UE is bound to offload to one of its MNO’s SBS and to disconnect the connection with the macro cell. Once the outdoor UE is offloaded to an SBS, it continues to communicate with the SBS only. However, for UEs of other MNOs when existing within the coverage of SBSs of the MNO 1, these UEs first sense and detect if there is any SBS of the corresponding MNOs x. If the UEs detect their MNOs’ SBSs, like MNO 1, the UEs are also offloaded to their SBSs. On the contrary, if no SBSs are present, the UEs of MNOs are then served by their respective macrocells during the TTIs estimated by in Equation (9). The same explanation is applicable for all UEs of all MNOs.
Hence, for MNO 1, the aggregate capacity of all N macro UEs for M1 RBs corresponding to B1 and Q TTIs can be expressed as
where and are responses over RBs of all outdoor macro UEs of MNO 1 in tT.
(2) Indoor capacity: Since all SBSs of MNO 1 per building operate at the spectrum of Bco in given by (9), the capacity served by an SBS of MNO 1 at RBs corresponding to the spectrum Bco is then given by,
If all SBSs per 3D building serves simultaneously in at RBs, the aggregate capacity per 3D building is then given by,
4.2. System-Level Performance Analysis
(1) Single building small cell deployment (i.e., L = 1): using Equations (14) and (16), the system-level capacity of MNO 1, including the outdoor UEs as well as in-building small cell UEs, for L = 1 is given by,
Remark 1.
Note that, in estimating the spectral efficiency, we consider only the licensed spectrum of an MNO, not the shared or reused spectrum from other MNOs or systems. Hence, the capacity that is achieved by the spectrum of other MNOs = 1 using SBSs of MNO 1 could be interpreted as the capacity achieved because of sharing the same spectrums of MNOs = 1 with MNO 1 such that the effective spectrum of MNO 1 is its licensed spectrum of RBs only.
Now, the average system-level spectral efficiency of MNO 1 after sharing the spectrum Bco with SBSs of MNO 1 is given by,
Similarly, the average system-level energy efficiency of MNO 1 after sharing the spectrum Bco with its SBSs per building in joules/bit (J/b) is given by,
where , and denote transmit powers of a macrocell, picocell, and small cell respectively. Likewise, , , and denote the total number of macrocells, picocells, and small cells of a single building of MNO 1, respectively.
(2) Ultra-dense small cell deployment (i.e., L ≥ 1): For L ≥ 1, we assume that the indoor propagation characteristics and the distance of UEs from their respective SBSs in each of the L buildings do not deviate significantly from one another, such that by linear approximation, the average aggregate capacity for MNO 1 is roughly given by,
Now, the spectral efficiency for L buildings is given by,
Similarly, the energy efficiency for L buildings is given by,
when L >> 1, such that could be approximated as follows:
which leads to the following as well
Using the assumption for Equation (20), for the given values of M1 and Q, the above equations imply that the system-level capacity, and hence, the spectral efficiency for an ultra-dense small indoor cell network are mainly affected by the density of small cells such that both the capacity and spectral efficiency performances could be improved with an increase in small cell density.
Since is very much less in magnitude than that of both and , Equations (20) and (22) can be approximated as follows when the value of L is very small:
Note that the numerator terms in Equation (25) are constant for the fixed values of and . The above equations result in the following.
where is a constant. Hence, for small values of L, the system-level energy efficiency (i.e., energy required per bit transmission) performance is mainly defined by the capacity of outdoor UEs.
However, when L >> 1, surpasses the value of such that Equation (22) could be rewritten as follows.
Now using Equation (23) for L >> 1, we can find the following.
where is a constant for the given values of and and is independent of L. Hence, for an ultra-dense deployment of small cells, the system-level energy efficiency performance gets almost steady, i.e., the energy efficiency does not improve noticeably, even though the density of small cells in terms of L increases. Such steadiness in energy efficiency performance implies the fact that there is an upper limit of density of small cells in terms of L beyond which no considerable improvement in energy efficiency could be achieved, which is contrary to the capacity and spectral efficiency performances that improve without a limit with L.
Since an increase in density of small cells is associated with the complexity and the cost of deployment and maintenance of small cells, and the spectral efficiency and energy efficiency show counter performances to each other, an optimal value of density of small cells in terms of L could be derived that can trade-off both performance requirements. We address this issue in the next section.
5. Modeling Energy Efficiency and the Condition for Optimality
5.1. Modeling Energy Efficiency
Recall that, from Equation (22), the energy efficiency for L ≥ 1 is given by,
where is a time scaling factor for the small cell transmit power with when only small cells of MNO 1 is active. For the existence of at least a UE of other MNOs than MNO 1, . Equation (30) can be rewritten as follows:
where ; ; ; .
For the typical transmit powers of macrocell base station (e.g., 40 W), picocell base station (e.g., 5 W), and femtocell base station (e.g., 0.1 W), the energy efficiency improves with an increase in L when . Hence, energy efficiency can be modeled as given by Equation (30) subject to strictly satisfying the following condition:
Note that for very large values of L, and such that Equation (31) can be approximated as follows:
The above expression clarifies that energy efficiency is non-zero for any value of L (i.e., the density of small cells) and tends to get fixed when L is very large, i.e., as energy efficiency tends to (i.e., ).
Since energy efficiency gets fixed for large values of L, it cannot be improved any further. Saying it another way, the maximum value of energy efficiency is given by,
5.2. Condition for Optimality
We consider using the slope of energy efficiency curve given by Equation (31) to derive an optimal value of L. Note that, from Equation (31), decays exponentially with an increase in L. However, from Equation (24), the spectral efficiency increases linearly with an increase in L. From Equations (24) and (31), since the spectral efficiency and energy efficiency change contrary to one another with an increase in L, the normalized energy efficiency and spectral efficiency curves must intersect one another for a certain value of L = Lmin where the normalized responses of both and are obtained by scaling Equations (31) and (24) by their respective maximum values. Due to the negative exponential decay response of the energy efficiency and the linearly increased response of spectral efficiency, choosing any values of L < Lmin results in less data rate per Hertz and more energy required per bit transmission than that for L = Lmin. On the other hand, choosing any values of L > Lmin results in more data rate per Hertz and less energy required per bit transmission than that for L = Lmin.
Hence, we consider defining an optimal value of L as any value of L such that L ≥ Lmin. Lmin is the minimum value L at which the normalized energy efficiency and spectral efficiency curves versus L intersect one another. Choosing any value of L ≥ Lmin results in improving both the spectral efficiency and energy efficiency performances. The values spectral efficiency and energy efficiency corresponding to L ≥ Lmin define the region of optimality for both efficiencies. Hence, depending on the requirements for the spectral and energy efficiencies, an optimal value of L ≥ Lmin could be chosen. It is to be noted that since the energy efficiency does not vary significantly for large values of L, the point of optimality is mainly driven by the spectral efficiency requirement of an MNO.
We consider finding an optimal value of L denoted as L* by defining a slope on the energy efficiency curve given by Equation (31). Now, to find the slope of Equation (31), let’s take the derivative of the normalized energy efficiency given by Equation (31) as follows:
Solving Equation (36), for different values of L, we can have the followings:
In Equation (37), the value of the slope for L = 0 corresponds to the response of energy efficiency for macrocell UEs only. However, is a non-zero value of given by Equation (36) and is a design parameter that trade-offs both spectral efficiency and energy efficiency requirements set by an MNO. Since L* is defined by L ≥ Lmin, using Equation (37), L* can be found for the slope as follows.
Note that the angle of the slope is strictly , which implies that is always negative. Hence, using Equation (37), is also always negative. Since then is also negative such that in Equation (38), both negatives in the numerator and the denominator cancel each other. Hence, from Equation (38), L* is given by subject to ,
Since, in Equation (39), all other parameters are constant, knowing , the value of L* can be determined using Equation (39). Now, using Equation (39), the optimal values of energy efficiency and spectral efficiency corresponding to are then given respectively by,
6. Proposed Algorithm and Default Parameters and Assumptions
The logical operation of the proposed spectrum sharing technique is given in Algorithm 1. An optimal value of L, spectral efficiency, and energy efficiency of each MNO is calculated. Note that capacity, spectral efficiency, and energy efficiency responses of any MNO x are directly impacted by L, , and Bco. In Table 1, the default parameters and assumptions used for the performance evaluation are given. Since we intend to find an optimal value of small cell density and the corresponding spectral and energy efficiencies by normalizing the actual values of spectral and energy efficiencies for an arbitrary density of small cells, changing the values of bandwidths of MNOs, as shown in Table 1, does not have any impact on the characteristics of any performance responses. Further, since we mainly consider homogeneous systems and focus on showing how to share the licensed spectrums, which are mainly low frequencies of below 3 GHz, of one MNO to another in a country, the performance evaluation with millimeter-wave signals for 5G, which are considered mainly for the small indoor cell coverage and backhauling purposes, is beyond the scope of this paper.

Table 1.
Default parameters and assumptions.
| Algorithm 1 Proposed spectrum sharing technique among all MNOs of a country |
 |
7. Performance Analysis and Comparison
7.1. Impact of on
Referring to Equation (9), it could be found that the number of TTIs over TAPP allocated to in-building small cells of MNO x is a function of the average rate of arrivals of UEs to small cells of other MNOs , as well as the value of xm. Straightforwardly, an increase in the values of either or xm causes the number of TTIs allocated to small cells of MNO x to decrease. Since the number of serving TTIs TnABS, x decreases, the resultant capacity obtained from small cells of MNO x also decreases. From Figure 3, it is to be noted that as the collocated small cells belong to more MNOs, more CCI is generated, resulting in degrading the overall network capacity of any MNO x. Since the probability of simultaneously active small cells of all MNOs xm is low enough, a major portion of the common spectrum Bco in the pool could be used by any MNO x at any time t.
7.2. Impact of on Capacity, Spectral Efficiency, and Energy Efficiency
Recall that for MNOs. We consider four sets of values for the arrival rate of small cell UEs to vary the CCI scenarios, as shown in Figure 3 for the performance evaluation of all four MNOs of a country, which are respectively given by , , , and . Note that these arrival rates, respectively, correspond to the CCI scenarios in Figure 3a for the maximum CCI, Figure 3b for the CCI of xm = 3, Figure 3c for minimum CCI, and Figure 3d for no CCI. According to Equation (9), these arrival rates, in turn, vary the serving period of small cells of MNO 1 . Now applying Equation (9), the optimal number of TTIs per APP allocated to small cells of a building of MNO 1 for these sets of arrival rates is given by respectively. Figure 6 shows that the achievable capacity for each CCI scenario, i.e., , for a single building L = 1.
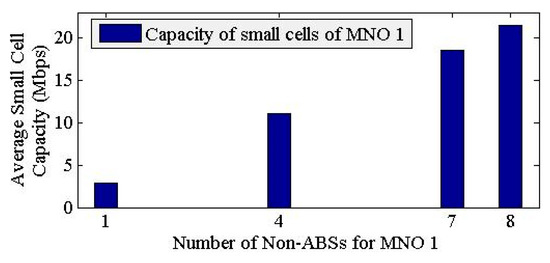
Figure 6.
Capacity performance of small cells of MNO 1 with the variation of for L = 1.
Now using Table 1 for parameters and assumptions for a 3D building and bandwidths of all MNOs, from Figure 6, it can be found that the achievable capacity of small cells of MNO 1 increases as the optimal number of allocated TTIs to them increases. The capacity is the minimum when , whereas it is the maximum when , i.e., when all TTIs in an APP are allocated to small cells. More specifically, when small cells of all MNOs are active simultaneously, they cause to occur the maximum level of CCI since small cells of all MNOs then intend to get access to the whole spectrum Bco. Hence, to avoid this mutual CCI among small cells, based on the traffic arrival rates to small cells of all MNOs, the common resource scheduler (CoRS) allocates an optimal number of TTIs to small cells of each MNO x. That’s why, the minimum number of TTIs of only 1, for the arrival rate as mentioned before, is allocated to small cells of MNO 1 when small cells of all MNOs (i.e., xm = 4) are active. This results in the minimum achievable capacity for small cells of MNO 1, as shown in Figure 6. Likewise, the capacity performance of small cells of MNO 1 is the maximum when no small cells of MNOs, other than MNO 1 are active (i.e., for ) such that no CCI exists and all eight TTIs per APP could be allocated to small cells of MNO 1 only. Note that all these assumed sets of values of arrival rates of UEs to small cells of each MNO are arbitrary, and considering any values other than these will not alter the innate characteristics of the performance shown in Figure 6.
Remark 2.
Note that when no spectrum sharing is considered, irrespective of the rate of arrivals of UEs to small cells of any MNO, the overall achievable capacity should not vary from one MNO to another since small cells of each MNO can operate at only the spectrum of their respective MNOs, i.e., Bop, in all TTIs per APP without exploring the actual capacity demand of users. This may cause underutilization of the spectrum if there is no traffic demand from one MNO at any time, whereas there exists a scarcity of spectrum from other MNOs at the same time. To allow fairness among MNOs, the maximum capacity for an APP is upper limited by twice the capacity per TTI, i.e., approximately 5.8514 Mbps, as shown in Figure 6 for xm = 4, which is one-fourth the maximum capacity that can be achieved when sharing spectrums of all four MNOs with no CCI. This problem is solved by the proposed technique by dynamically adjusting the radio resource allocation to small cells of any MNO x based on the actual traffic demand as shown in Figure 6. Further, the proposed spectrum sharing can improve the achievable capacity of small cells of an MNO x by up to the maximum xm times the capacity that can be achieved without sharing spectrum with small cells of MNO x.
7.3. Spectral Efficiency and Energy Efficiency Performances
Figure 7 shows the overall system-level spectral efficiency and energy efficiency responses of MNO 1 with the variation of small cell density, i.e., the number of buildings, as a function of the number of non-ABSs assigned to small cells of MNO 1, TnABS,1. For any TnABS,1, as the value of L increases, both spectral efficiency and energy efficiency responses improve. More specifically, the overall system-level spectral efficiency varies linearly, whereas energy efficiency varies negatively exponentially. Unlike the spectral efficiency, the improvement in the energy efficiency is noticeable when L is small and gets almost fixed when L tends to very large. Likewise, for any value of L, an increase in the number of non-ABSs (i.e., TTIs) allocated to small cells of MNO 1 improves both spectral efficiency and energy efficiency responses, i.e., increases the average data rate per Hertz and decreases the average required to transmit power per bit.
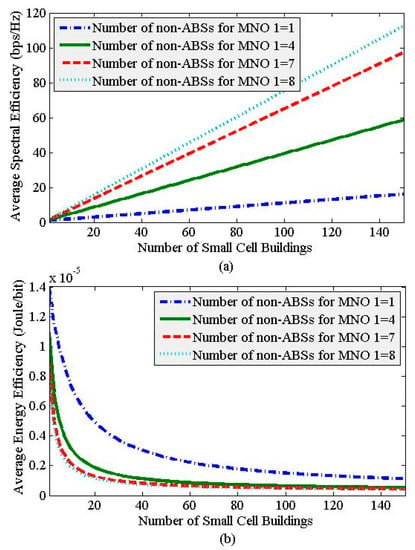
Figure 7.
System-level spectral efficiency (a) and energy efficiency (b) performances of MNO 1 with the density of small cells, i.e., for L ≥ 1.
The normalized spectral efficiency and energy efficiency performances of MNO 1 for TnABS,1 = 4 in Figure 7 are shown in Figure 8. It is found that choosing a slope on the energy efficiency curve that corresponds to the value of L = L1, which is less than the value of L = L2 = 22, results in very poor performances in both the spectral efficiency and energy efficiency. Also, choosing a slope that corresponds to the value of L = L3, which is greater than the value of L = L2, results in an improvement in both spectral efficiency and energy efficiency performances.
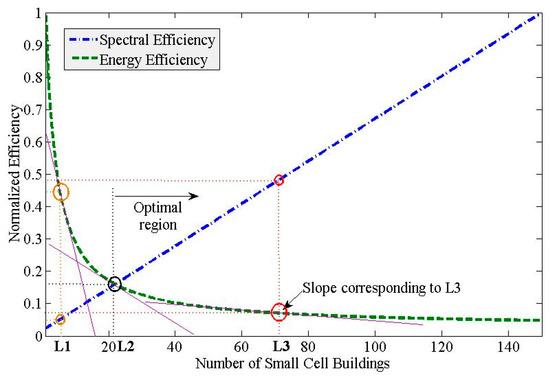
Figure 8.
Normalized spectral efficiency and energy efficiency performances of MNO 1 for L ≥ 1 and TnABS,1 = 4.
However, choosing a slope that corresponds to L = L2 where both spectral efficiency and energy efficiency curves intersect one another each with the normalized value of 0.16 is the minimum value of L = L2 = Lmin that gives a trade-off and ensures optimal performance in both energy and spectral efficiencies. Hence, any values of L ≥ Lmin is an optimal value of L = L* as given by Equation (39) corresponding to the optimal spectral efficiency and energy efficiency requirements set by the MNO 1 for TnABS,1 = 4 as given by Equations (40) and (41). Note that the normalized value of the spectral efficiency and energy efficiency is 0.16 for L = Lmin = 22 (Figure 8). Hence, the actual values of spectral and energy efficiencies corresponding to the values of L ≥ Lmin are the region of optimality. Hence, from Figure 7, for the (minimum) optimal value of L = Lmin = 22, the corresponding optimal (minimum) values of spectral efficiency and energy efficiency are respectively 1.74 µJ/bit (i.e., 0.16 × the maximum value of energy efficiency of 10.93 µJ/bit for L = 1) and 9.3702 bps/Hz (i.e., 0.16 × the maximum value of spectral efficiency of 58.5636 bps/Hz for L = 150). Note that the improvement in energy efficiency performance gets almost steady for L > L3. Moreover, choosing a slope corresponding to L > L3 also causes to increase both the cost and the complexity of the network due to increasing the number of small cells. Hence, it is recommended to choose a slope on the energy efficiency curve that corresponds to a value of L which is not too larger than that of the (minimum) optimal value of L = Lmin = 22 (Figure 8).
7.4. Performance Comparison with 5G Requirements
We consider comparing spectral efficiency and energy efficiency performances of the proposed spectrum sharing technique with that required for 5G mobile networks. In doing so, we intend to find a value of L that can meet both spectral efficiency and energy efficiency requirements for 5G networks. Let and , respectively denote spectral efficiency and energy efficiency for any value of . Let and denote the minimum spectral efficiency and energy efficiency requirements for 5G mobile networks. The value of L that can satisfy both requirements can be found by solving the following problem.
Using Table 2, an optimal (minimum) value of L, i.e., , for numerous values of TnABS,1 can be found as follows.

Table 2.
The minimum value of L to satisfy the spectral efficiency and energy efficiency requirements of 5G systems.
Proof:
For 5G mobile networks, it is expected that an average spectral efficiency of [24] and energy efficiency of [24,25] need to be satisfied. Now, using Figure 7, Table 2 shows the minimum values of L = Lmin required to meet the spectral efficiency and energy efficiency for 5G mobile networks for different values of TnABSs,1, including 1, 4, 7, and 8, as shown in Figure 7.
Hence, from Table 2, it can be found that an optimal (minimum) value of L = Lmin that can satisfy both and for TnABSs,1 = 1, 4, 7, and 8 are given by L* = Lmin = 356, 94, 57, and 49, respectively. Note that with an increase in time resources allocated to small cells of MNO 1, the requirement in terms of L to satisfy spectral and energy efficiencies of 5G mobile networks decreases. Moreover, as mentioned earlier (Figure 7b), energy efficiency does not change significantly for any L > Lmin though spectral efficiency changes proportionately. So, the choice of L is mainly driven by the requirement for spectral efficiency of 5G mobile networks as compared to that for energy efficiency. □
Hence, based on the above solution and proof to find an optimal (minimum) value of L for a number of values of , spectral efficiency and energy efficiency requirements for 5G mobile networks (i.e., [24] and [24,25], respectively) can be easily met for any value of . More specifically, unlike spectral efficiency, energy efficiency requirement for 5G mobile networks can be easily met for a small value of L such that the density of small cells, i.e., an optimal value of L can be defined solely by spectral efficiency requirement to satisfy both spectral efficiency and energy efficiency requirements for 5G mobile networks.
8. Conclusions
In this paper, we have proposed a novel spectrum sharing technique to share the whole spectrum assigned to all mobile network operators (MNOs) of a country with small cells per building per MNO by using the time-domain eICIC technique and by exploiting the high external wall penetration loss of each building. To avoid interference among small cells of different MNOs in each building, only small cells of any MNO have been considered serving in any TTI. Further, the number of TTIs per ABS pattern period (APP) has been considered when allocating to small cells per building of any MNO x in proportion with the average rate of traffic arrivals to small cells of the corresponding MNO x over the total average rate of traffic arrivals to small cells of all MNOs. An algorithm of the proposed technique has been presented, and the system-level capacity, spectral efficiency, and energy efficiency performance metrics have been derived.
A generic energy efficiency model for the dense deployment of small cells in terms of the number of buildings L has been presented, and an optimal value of L has been derived that could trade off both the energy efficiency and spectral efficiency of an MNO. Extensive system-level numerical and simulation analysis has been carried out. It has been shown that by applying the proposed technique, massive indoor capacity, spectral efficiency, and energy efficiency can be achieved. Further, it has been found that spectral efficiency increase linearly, whereas energy efficiency decreases negative exponentially with an increase in L such that a region of optimality in terms of L for both spectral and energy efficiencies has been defined.
Finally, by varying the time resources allocated to small cells of an MNO, it has been shown that the proposed spectrum sharing technique can meet the requirements of spectral and energy efficiencies for 5G mobile networks, irrespective of the number of TTIs allocated per APP to small cells per building. The proposed spectrum sharing technique could help improve the indoor capacity without any further investment in licensing an additional spectrum to operate small cells of an MNO.
Funding
This research received no external funding.
Acknowledgments
A small part of this paper has been accepted for publication at the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (IEEE DySPAN), Newark, NJ, USA, 11–14 November 2019 [12].
Conflicts of Interest
The author declares no conflict of interest.
References
- Saquib, N.; Hossain, E.; Kim, D.I. Fractional frequency reuse for interference management in LTE-advanced hetnets. IEEE Wirel. Commun. 2013, 20, 113–122. [Google Scholar] [CrossRef]
- Guidotti, A.; Vanelli-Coralli, A.; Conti, M.; Andrenacci, S.; Chatzinotas, S.; Maturo, N.; Evans, B.; Awoseyila, A.; Ugolini, A.; Foggi, T.; et al. Architectures and key technical challenges for 5G systems incorporating satellites. IEEE Trans. Veh. Technol. 2019, 68, 2624–2639. [Google Scholar] [CrossRef]
- Saha, R.K. Spectrum Sharing in Satellite-Mobile Multisystem Using 3D In-Building Small Cells for High Spectral and Energy Efficiencies in 5G and Beyond Era. IEEE Access 2019, 7, 43846–43868. [Google Scholar] [CrossRef]
- Saha, R.K. Realization of Licensed/Unlicensed Spectrum Sharing Using eICIC in Indoor Small Cells for High Spectral and Energy Efficiencies of 5G Networks. Energies 2019, 12, 2828. [Google Scholar] [CrossRef]
- Kamal, H.; Coupechoux, M.; Godlewski, P. Inter-operator spectrum sharing for cellular networks using game theory. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 425–429. [Google Scholar]
- Bennis, M.; Debbah, M.; Lasaulce, S. Inter-Operator Spectrum Sharing from a Game Theoretical Perspective. EURASIP J. Adv. Signal Process. 2009, 2009, 295739. [Google Scholar] [CrossRef][Green Version]
- Jorswieck, E.A.; Badia, L.; Fahldieck, T.; Karipidis, E.; Luo, J. Spectrum sharing improves the network efficiency for cellular operators. IEEE Commun. Mag. 2014, 52, 129–136. [Google Scholar] [CrossRef]
- Joshi, S.K.; Manosha, K.B.S.; Codreanu, M.; Latva-aho, M. Dynamic inter-operator spectrum sharing via Lyapunov optimization. IEEE Trans. Wirel. Commun. 2017, 16, 6365–6381. [Google Scholar] [CrossRef]
- Tehrani, R.H.; Vahid, S.; Triantafyllopoulou, D.; Lee, H.; Moessner, K. Licensed Spectrum Sharing Schemes for Mobile Operators: A Survey and Outlook. IEEE Commun. Surv. Tutor. 2016, 18, 2591–2623. [Google Scholar] [CrossRef]
- The Electronic Communications Committee. “Licensed shared access (LSA),” ECC Report 205, The Electronic Communications Committee, Copenhagen, Denmark, 2014. Available online: https://www.ecodocdb.dk/download/baa4087d-e404/ECCREP205.PDF (accessed on 30 June 2019).
- Asp, A.; Sydorov, Y.; Keskikastari, M.; Valkama, M.; Niemela, J. Impact of Modern Construction Materials on Radio Signal Propagation: Practical Measurements and Network Planning Aspects. In Proceedings of the 2014 IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–7. [Google Scholar]
- Saha, R.K. Nationwide spectrum sharing of mobile network operators with indoor small cells. In Proceedings of the IEEE International Symposium on Dynamic Spectrum Access Networks (IEEE DySPAN), Newark, NJ, USA, 11–14 November 2019. [Google Scholar]
- Chimeh, J.D.; Hakkak, M.; Alavian, S.A. Internet Traffic and Capacity Evaluation in UMTS Downlink. In Proceedings of the Future Generation Communication and Networking (FGCN 2007), Jeju, Korea, 6–8 December 2007; pp. 547–552. [Google Scholar]
- European Telecommunications Standards Institute (ETSI); Universal Mobile Telecommunications System (UMTS). Selection Procedures for the Choice of Radio Transmission Technologies of the UMTS. European Telecommunications Standards Institute (ETSI); Sophia Antipolis Valbonne, France, TR 101 112, UMTS 30.03, ver. 3.2.0, 1998–2004. Available online: https://www.etsi.org/deliver/etsi_tr/101100_101199/101112/03.02.00_60/tr_101112v030200p.pdf (accessed on 2 January 2017).
- Kleinrock, L. Queueing Systems, Vol I: Theory; Wiley-Interscience: New York, NY, USA, 1975. [Google Scholar]
- Pérez-Romero, J.; Sallent, O.; Agustí, R.; Díaz-Guerra, M.A. Radio Resource Management Strategies in UMTS; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Saha, R.K. Multiband spectrum sharing with indoor small cells in Hybrid Satellite-Mobile systems. In Proceedings of the 2019 IEEE 90th Veh. Tech. Conf. (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–7. [Google Scholar]
- Saha, R.K. A technique for massive spectrum sharing with ultra-dense in-building small cells in 5G era. In Proceedings of the 2019 IEEE 90th Veh. Tech. Conf. (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–7. [Google Scholar]
- Ellenbeck, J.; Schmidt, J.; Korger, U.; Hartmann, C. A Concept for Efficient System-Level Simulations of OFDMA Systems with Proportional Fair Fast Scheduling. In Proceedings of the 2009 IEEE Globecom Workshops, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- E-UTRA. Radio Frequency (RF) System Scenarios; Document 3GPP TR 36.942; 3rd Generation Partnership Project: Sophia Antipolis Valbonne, France, 2007. [Google Scholar]
- Simulation Assumptions and Parameters for FDD HeNB RF Requirements; Document TSG RAN WG4R4-092042; Alcatel-Lucent, picoChip Designs, Vodafone: San Francisco, CA, USA, 2009.
- Geng, S.; Kivinen, J.; Zhao, X.; Vainikainen, P. Millimeter-wave propagation channel characterization for short-range wireless communications. IEEE Trans. Veh. Technol. 2009, 58, 3–13. [Google Scholar] [CrossRef]
- Saha, R.K.; Saengudomlert, P.; Aswakul, C. Evolution toward 5G mobile networks-A survey on enabling technologies. Eng. J. 2016, 20, 87–119. [Google Scholar] [CrossRef]
- Wang, C.-X.; Haider, F.; Gao, X.; You, X.-H.; Yang, Y.; Yuan, D.; Aggoune, H.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Auer, G.; Giannini, V.; Gódor, I.; Blume, O.; Fehske, A.; Rubio, J.A.; Frenger, P.; Olsson, M.; Sabella, D.; Gonzalez, M.J.; et al. How much energy is needed to run a wireless network? In Green Radio Communication Networks; Cambridge University Press (CUP): Cambridge, UK, 2012; pp. 359–384. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).