A Comprehensive Inverter-BESS Primary Control for AC Microgrids
Abstract
:1. Introduction
- Regulation of frequency and voltage in Grid-Forming mode independently of the number of paralleled generators using the VGM technique in order to mimic the dynamic behavior of synchronous generators;
- Ability to guarantee black-start of the MG in Grid-Forming mode;
- Correct active and reactive power sharing in parallel with other DERs;
- Fast control actions in grid-connected mode to allow providing frequency and voltage support (GSM) as well as power control following the reference signals from the secondary level control;
- Synchronization and connection of the BESS to the external main grid or to other DERs in islanded mode with minimum transients;
- The BESS converter is able to work both in VGM and in GSM guaranteeing the possibility to work in parallel with other DERs or an external main grid;
- The primary control can be switched from Grid-Forming mode to Grid-Support mode and vice versa without converter power interruption;
- Considering the Grid-Support mode, the proposed control is able to provide fast actions to the MG because this functionality is implemented in the primary level and not in the secondary one;
- When the support to the MG is not necessary, the control is able to use control signal coming from the secondary level control in order to satisfy other tasks reported in IEEE Std. 1547 such as State of Charge management, power smoothing, and compliance with power flow constraints imposed at the connection point with the external Main Grid (peak lopping);
- Considering the Grid-Forming operating mode, the proposed VGM technique is a PI-based one, which means that the tuning procedure can be easily manged by operators and not just by control engineers.
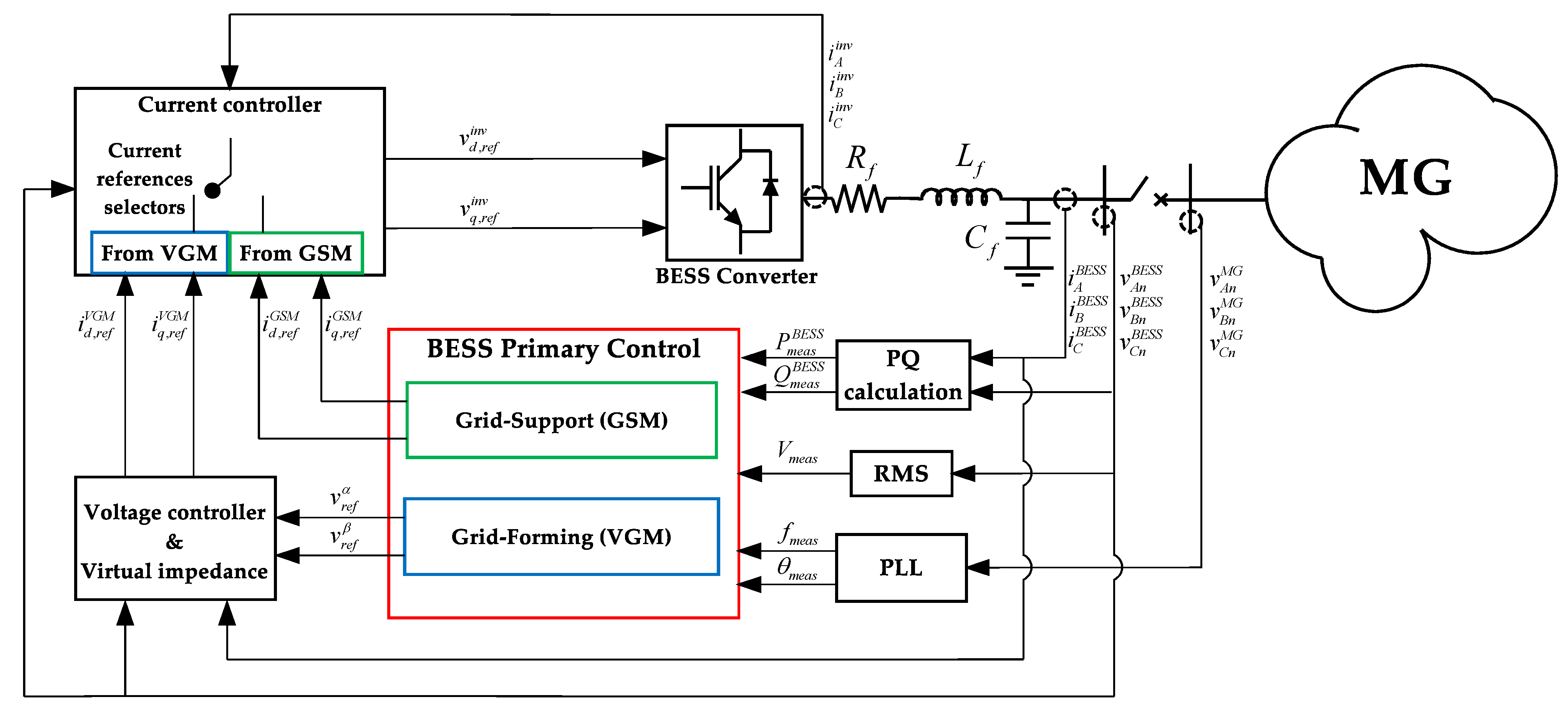
2. Primary Control Method Description
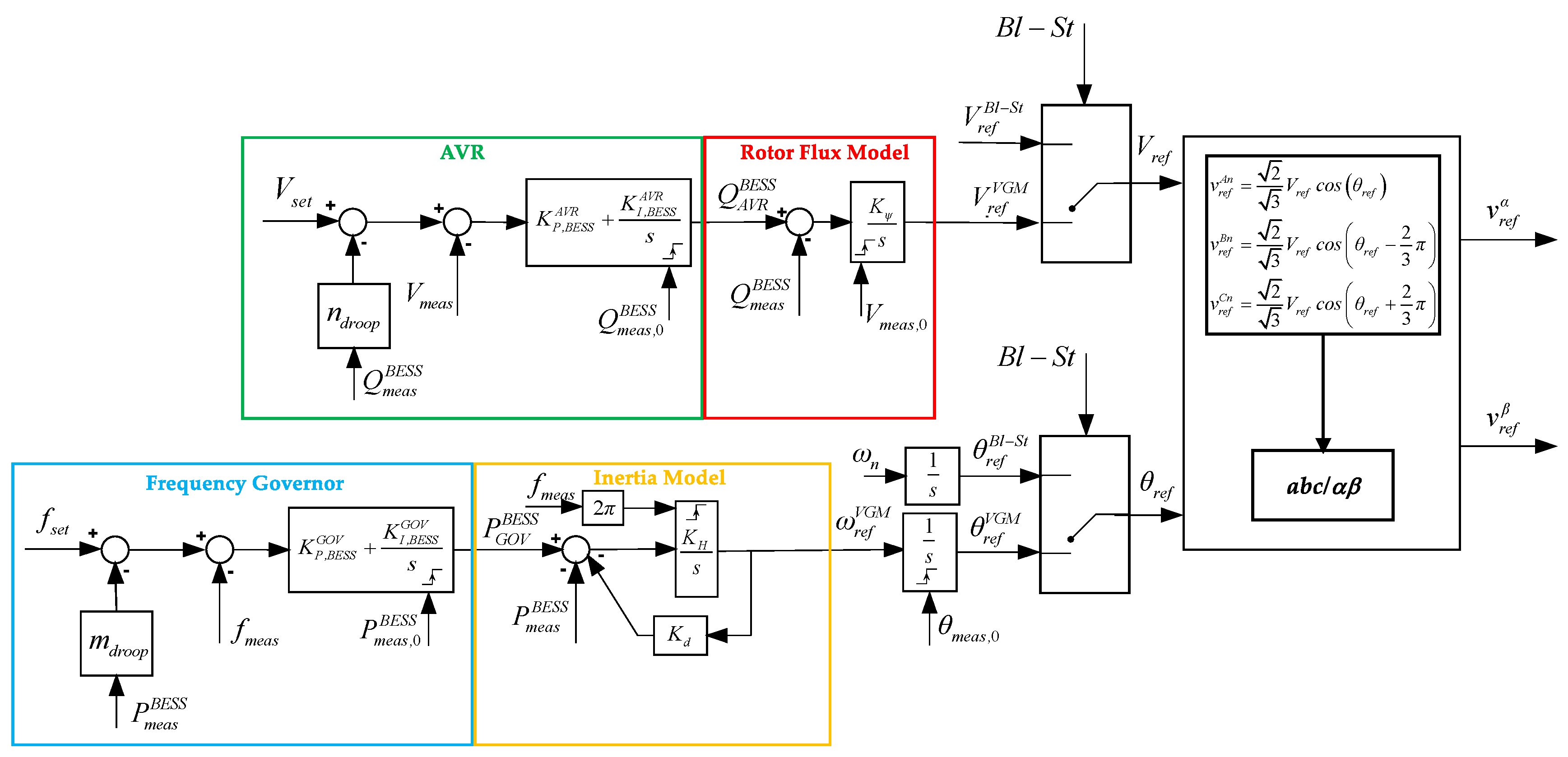
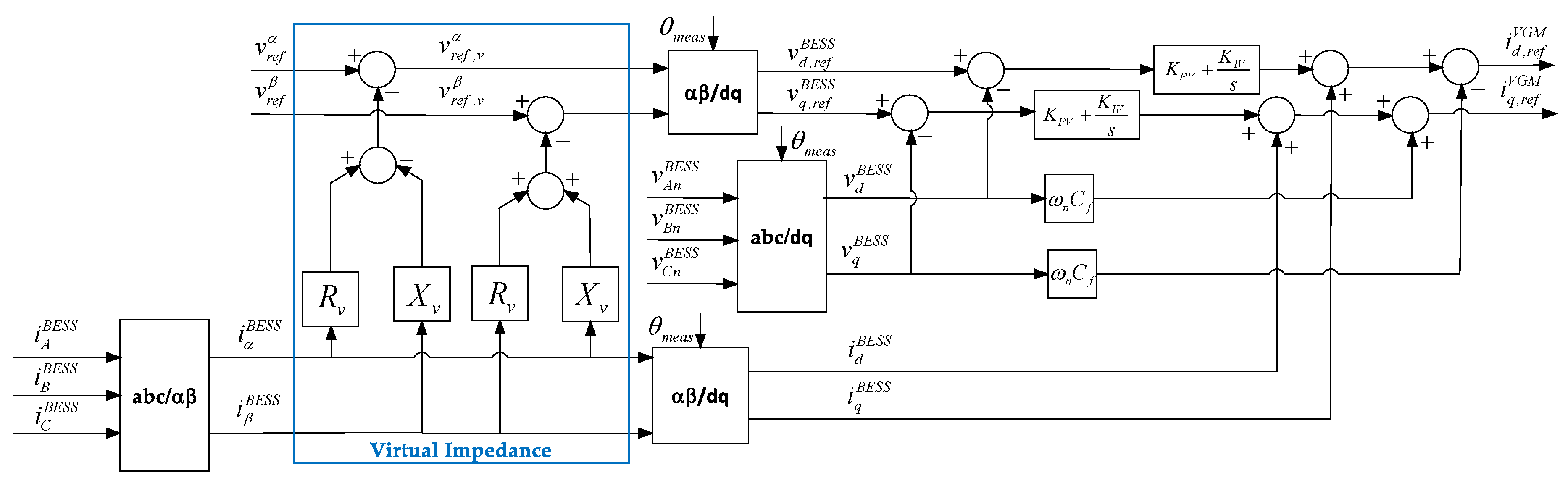
2.1. Grid-Forming Operating Mode: VGM
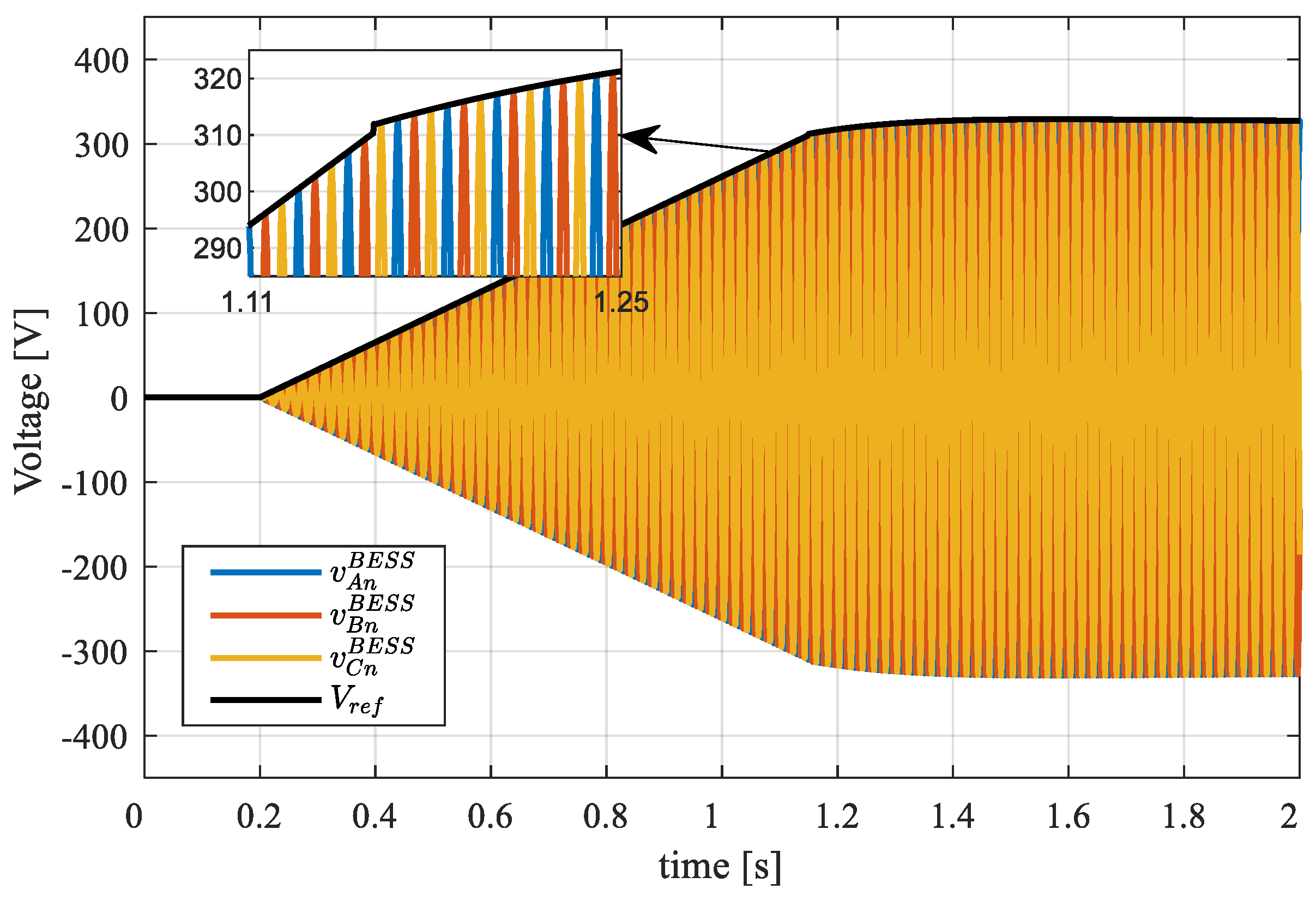
- If the measured RMS voltage is zero, the primary control is able to understand the necessity to provide a black-start procedure; so, imposing the logic signal named Bl-St equal to 1, the VGM channel is bypassed and the MG is energized using a ramp voltage reference and the rated angular frequency .
- When the voltage reaches a specific percentage of the rated voltage , the VGM control channel is activated (reset of the control integrators) and the selectors switch to the VGM control actions and .
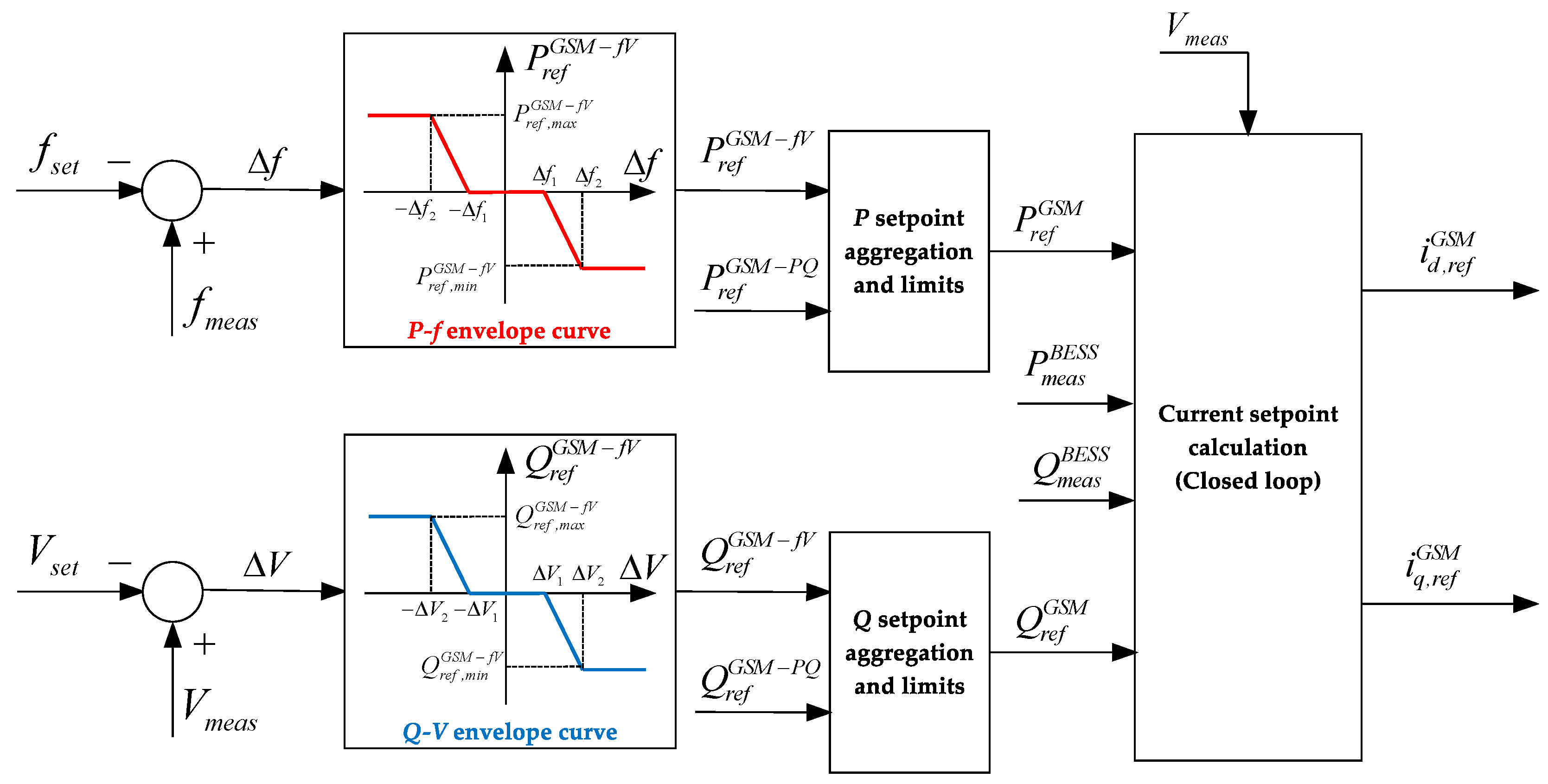
2.2. Grid-Support Operating Mode: GSM
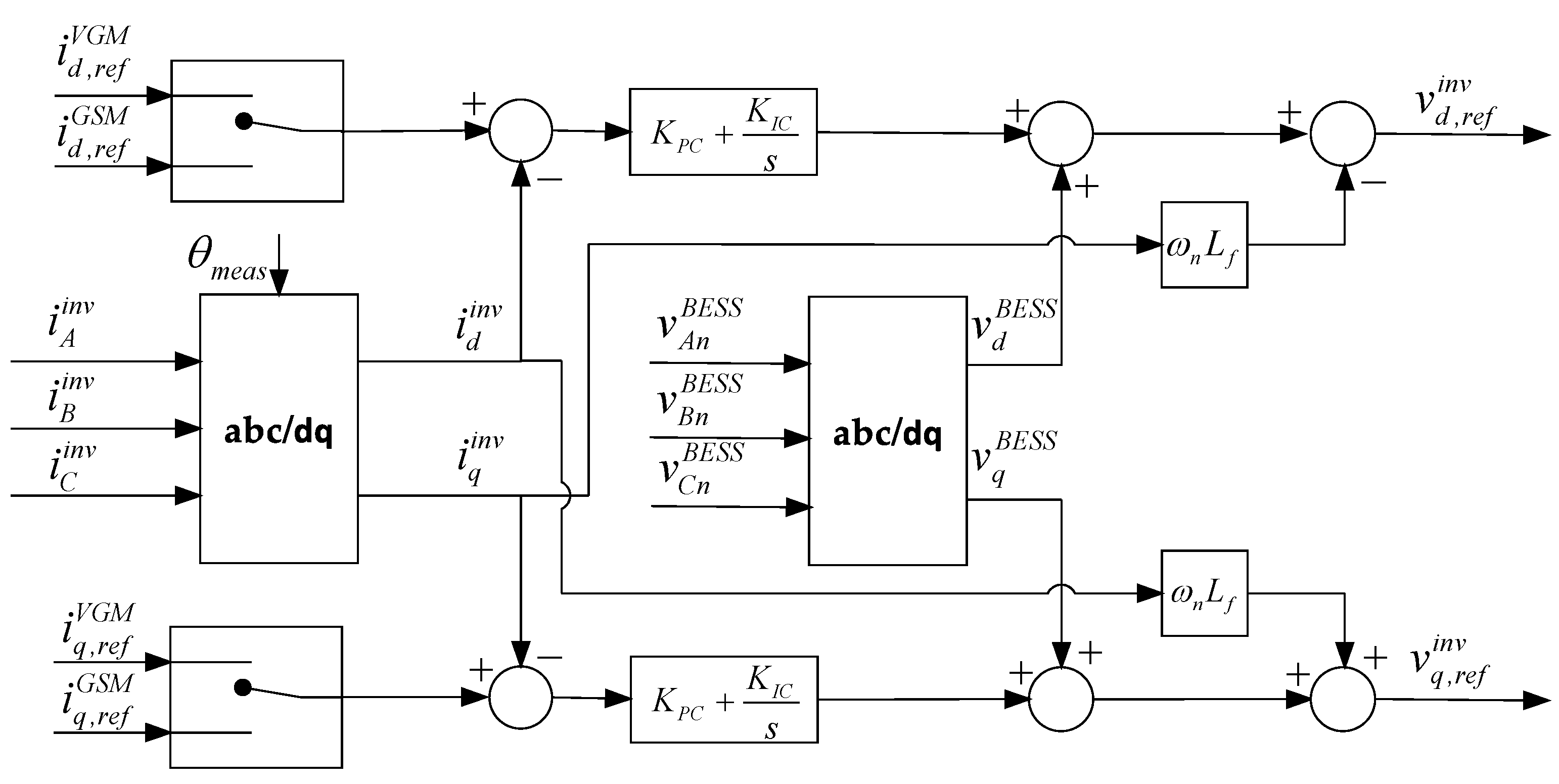
2.3. Voltage and Current Inner Control Loops
3. DIgSILENT PowerFactory® Model for Testing
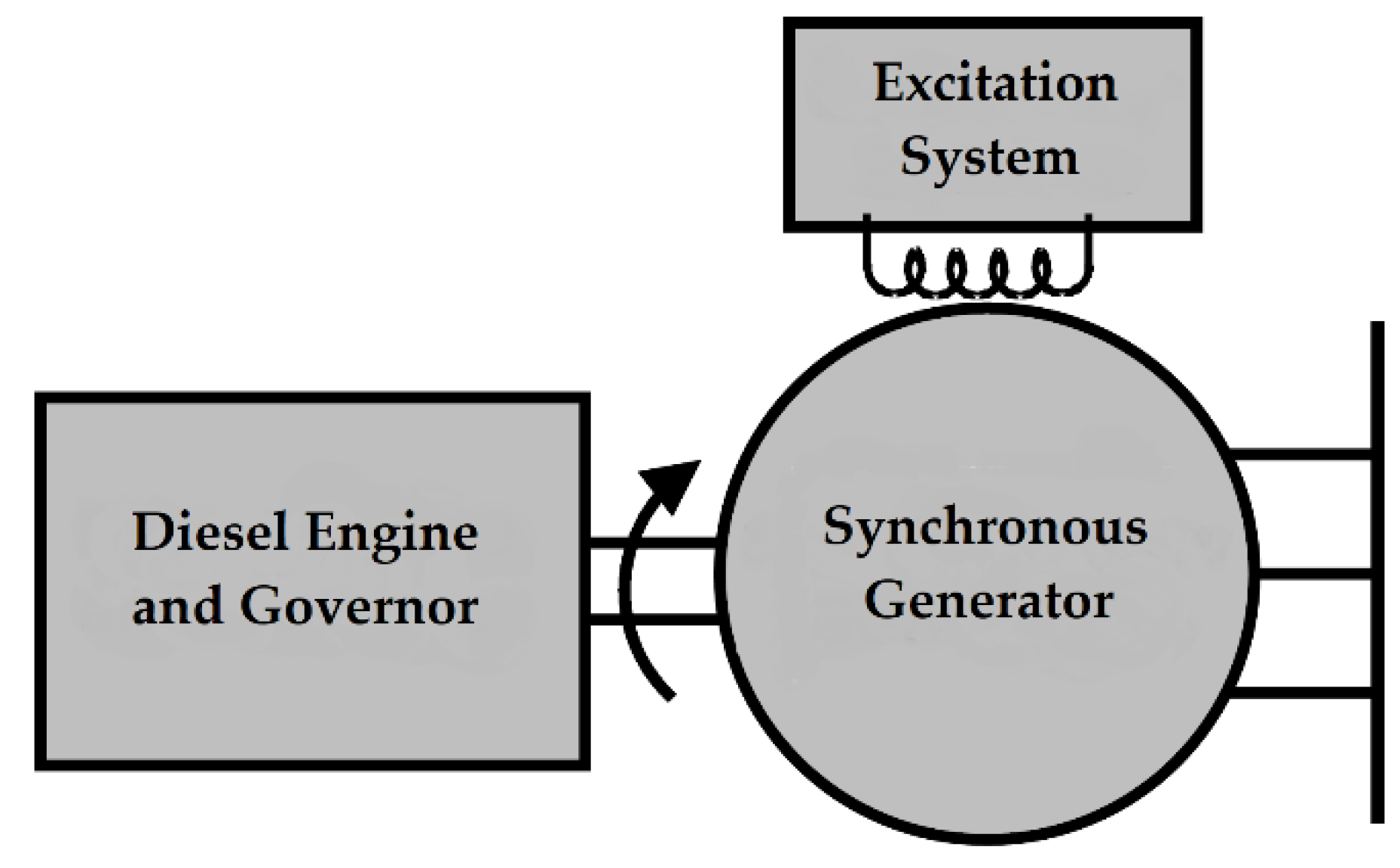
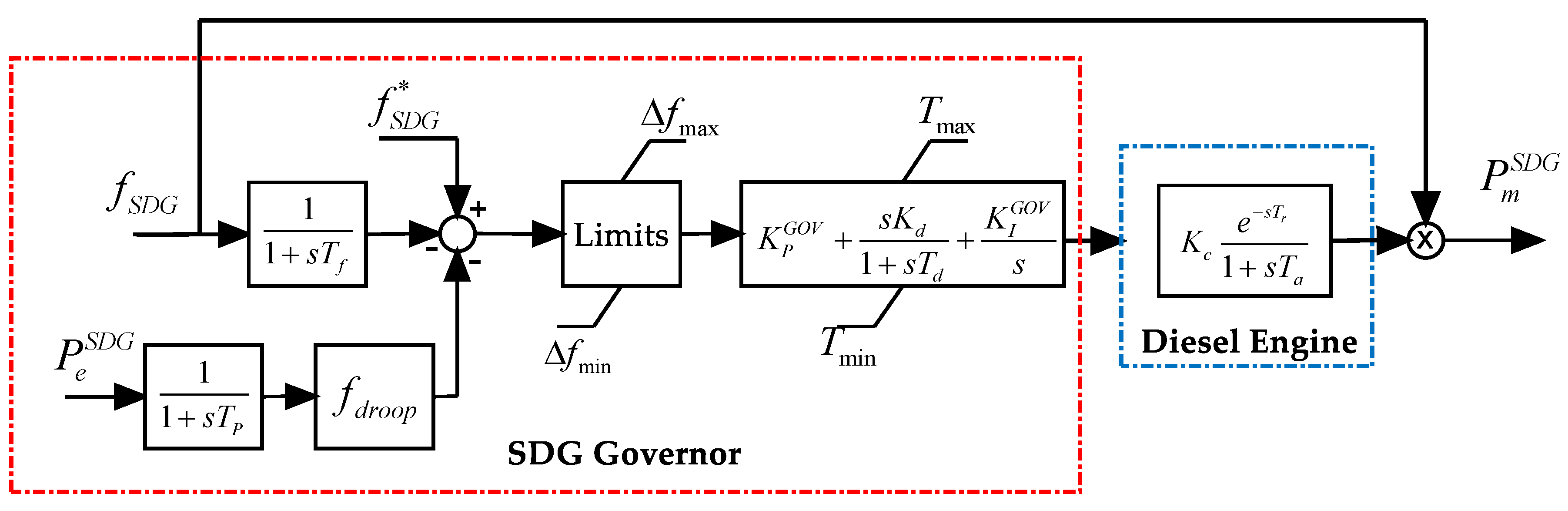
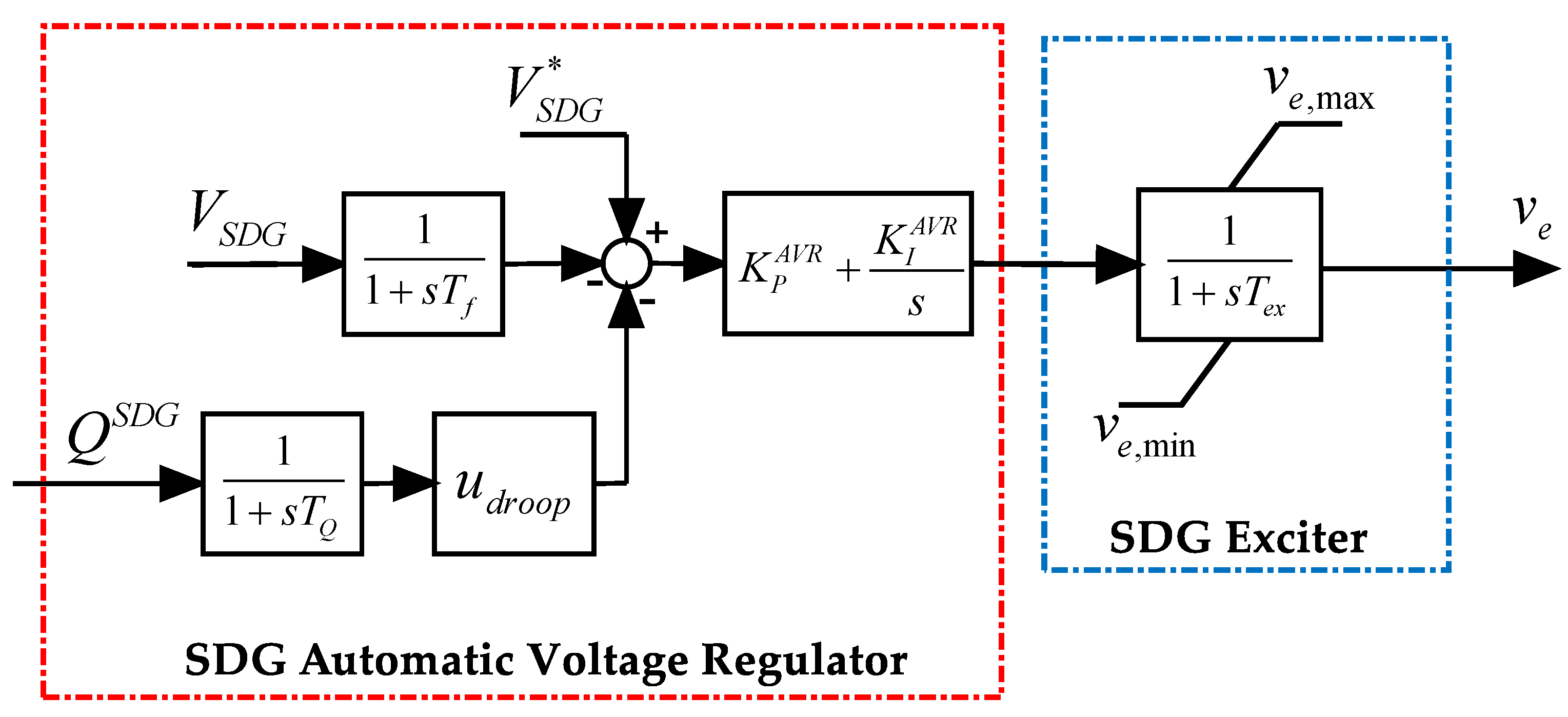
3.1. Synchronous Diesel Generator Model for Paralleling Operation
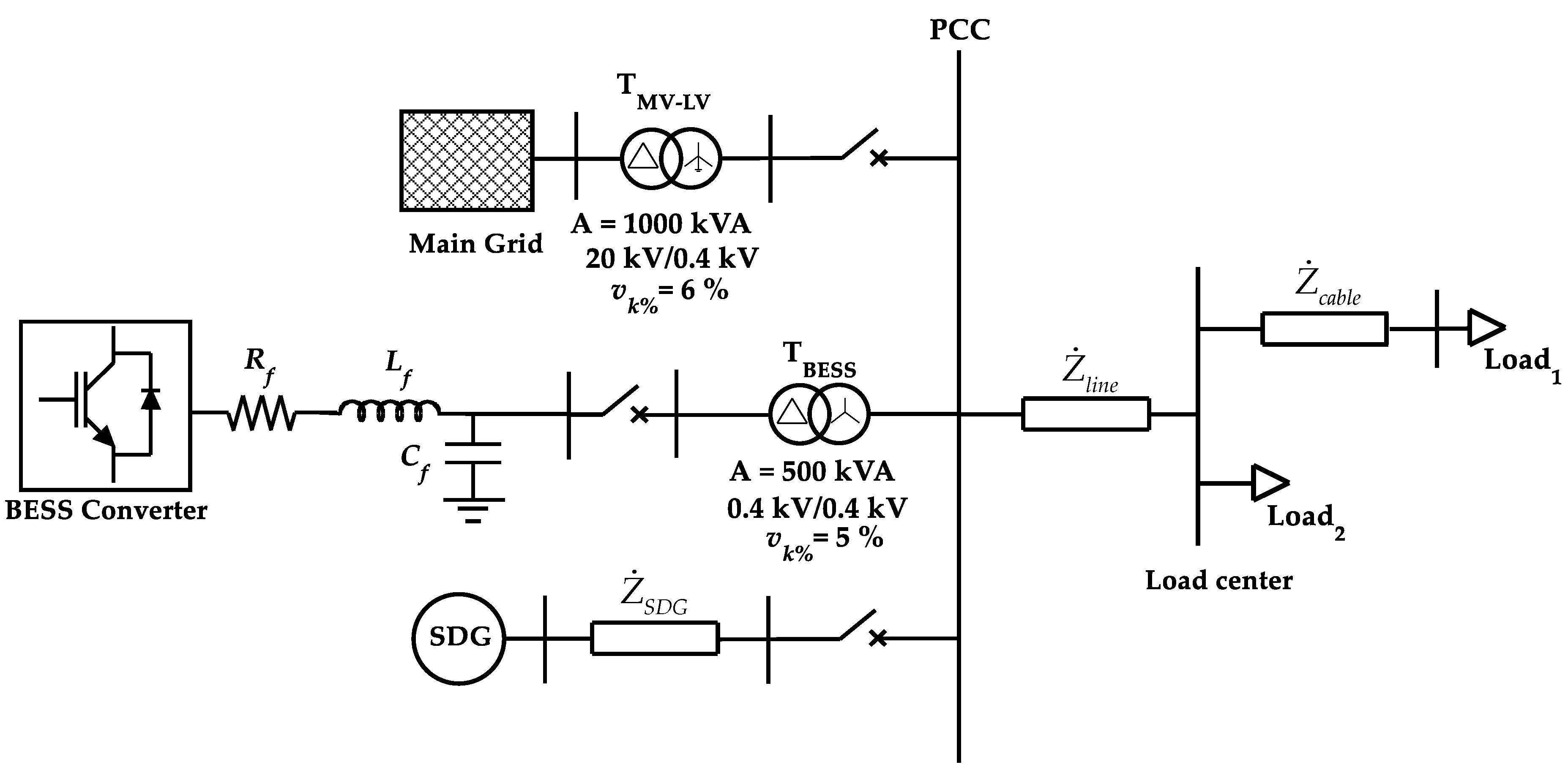
3.2. Test MG Layout and Parameters
4. Simulations Results
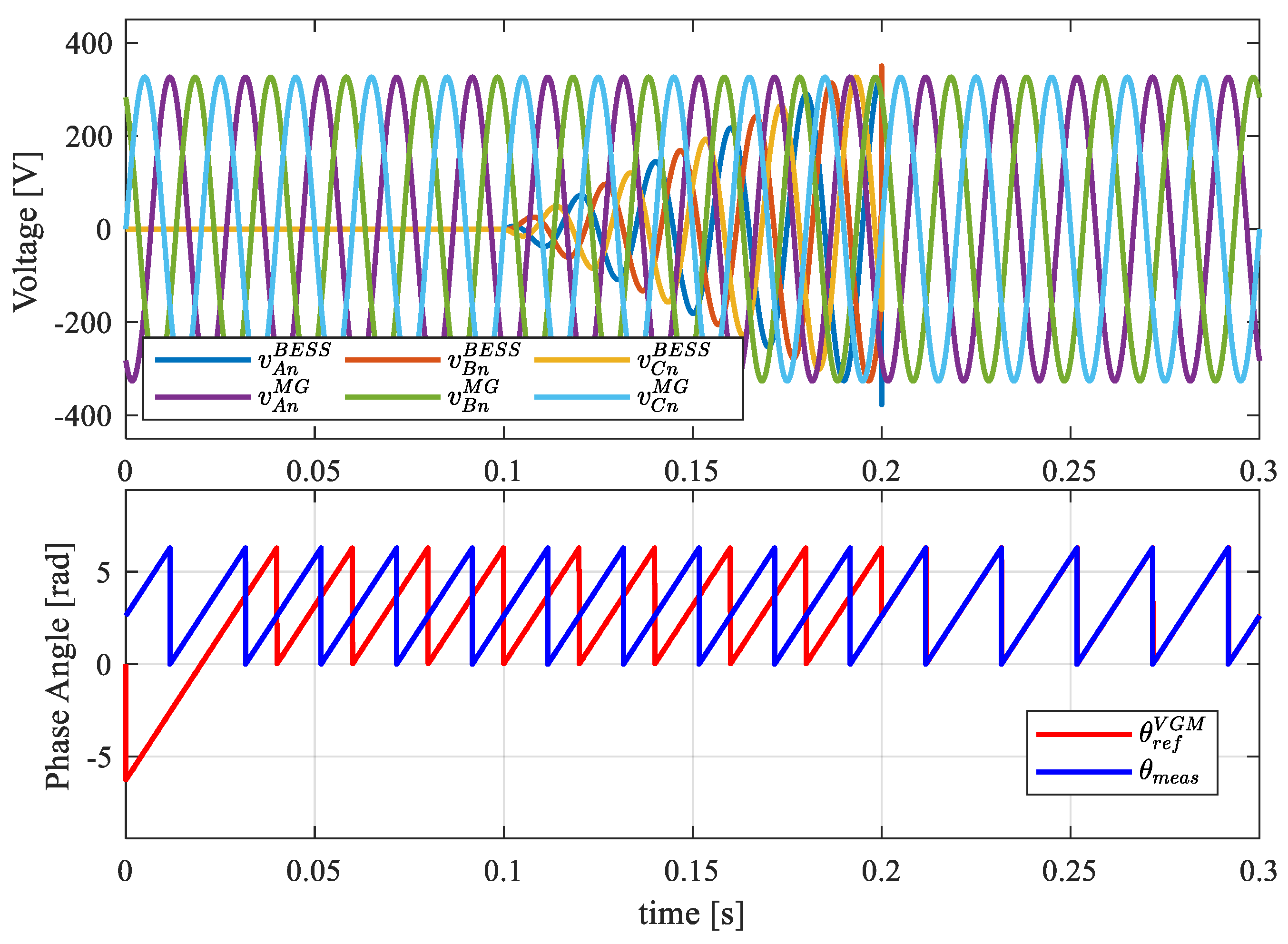
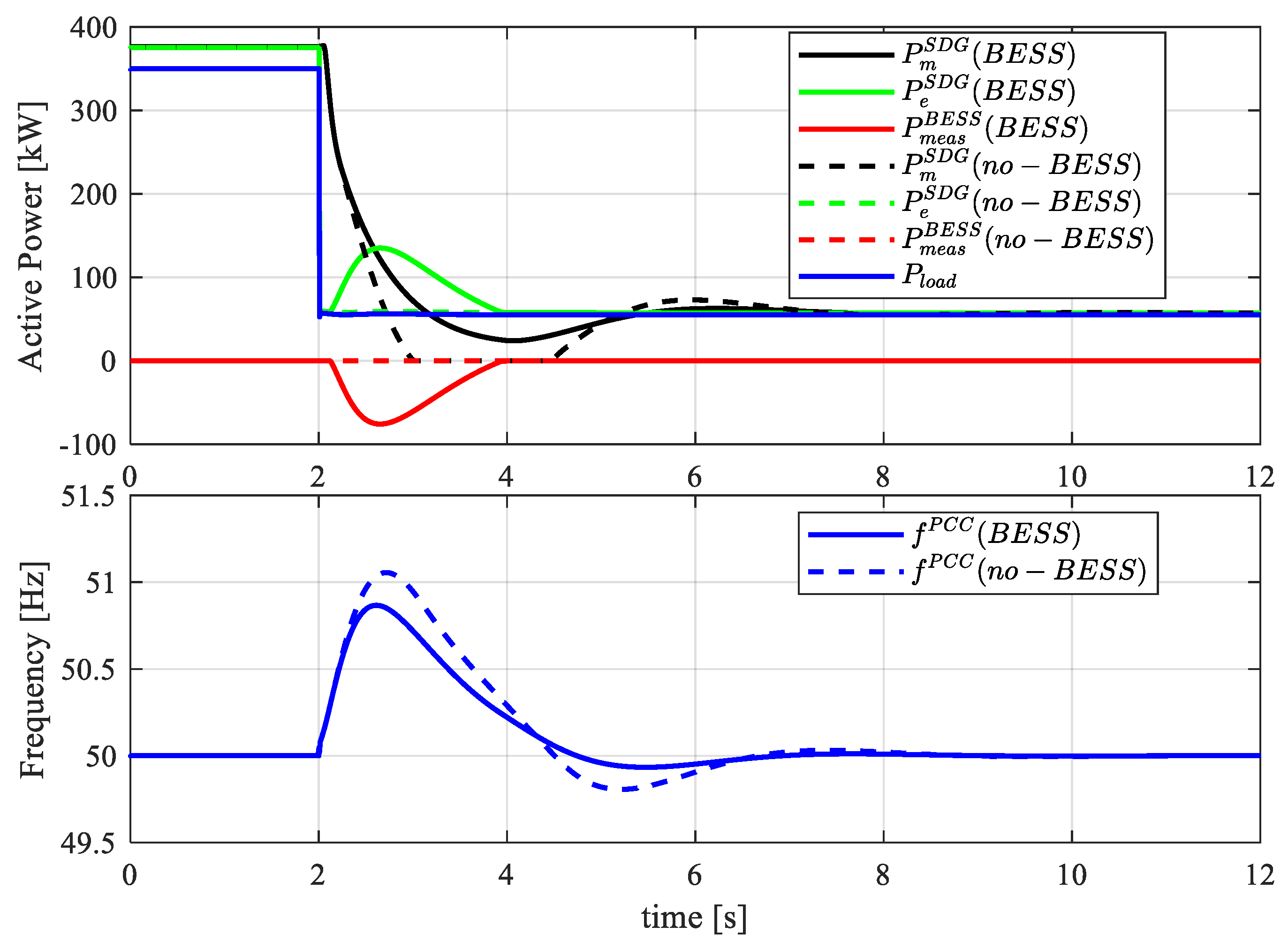
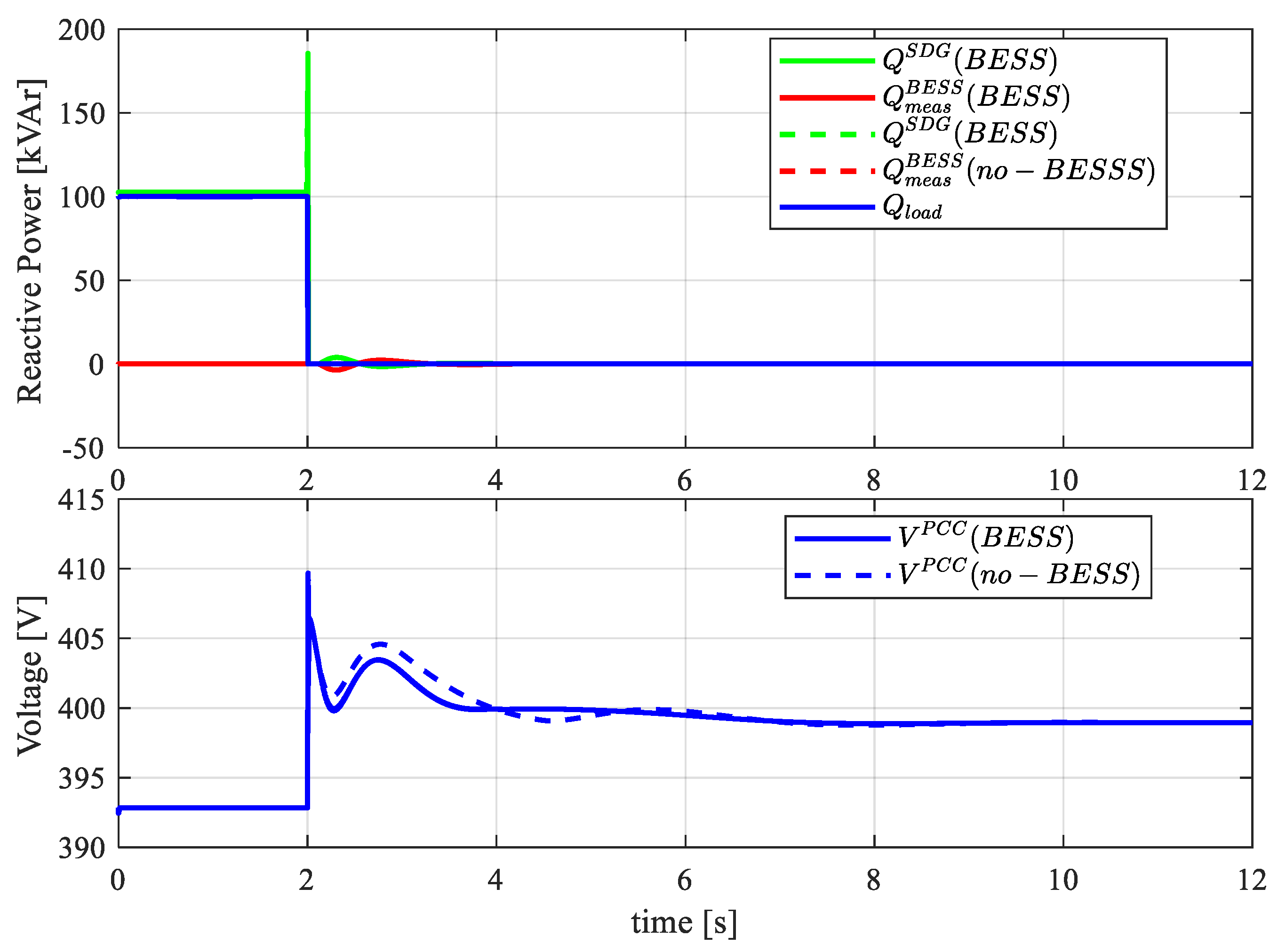
4.1. Black Start and Load Step in a Stand-Alone Configuration
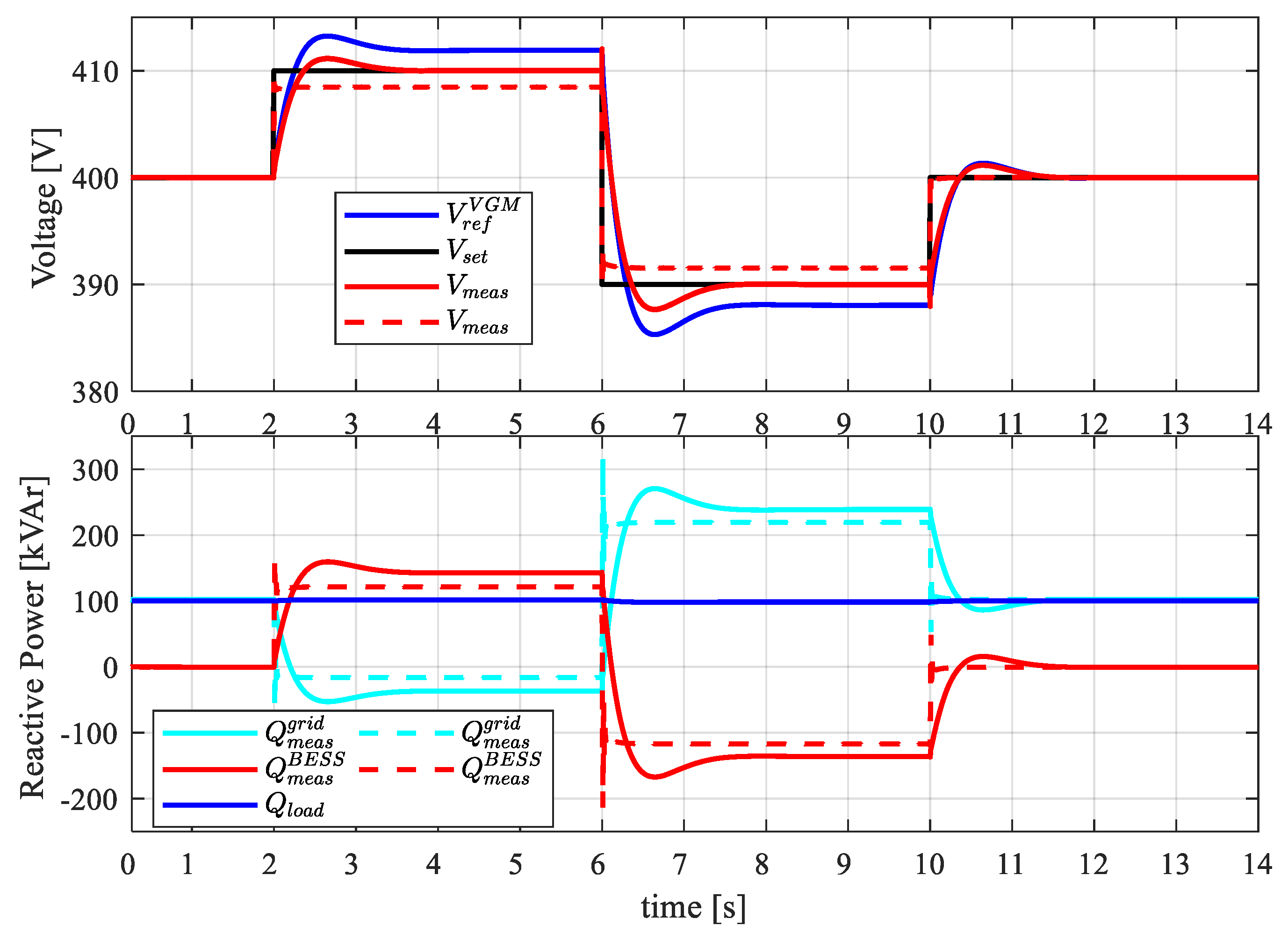
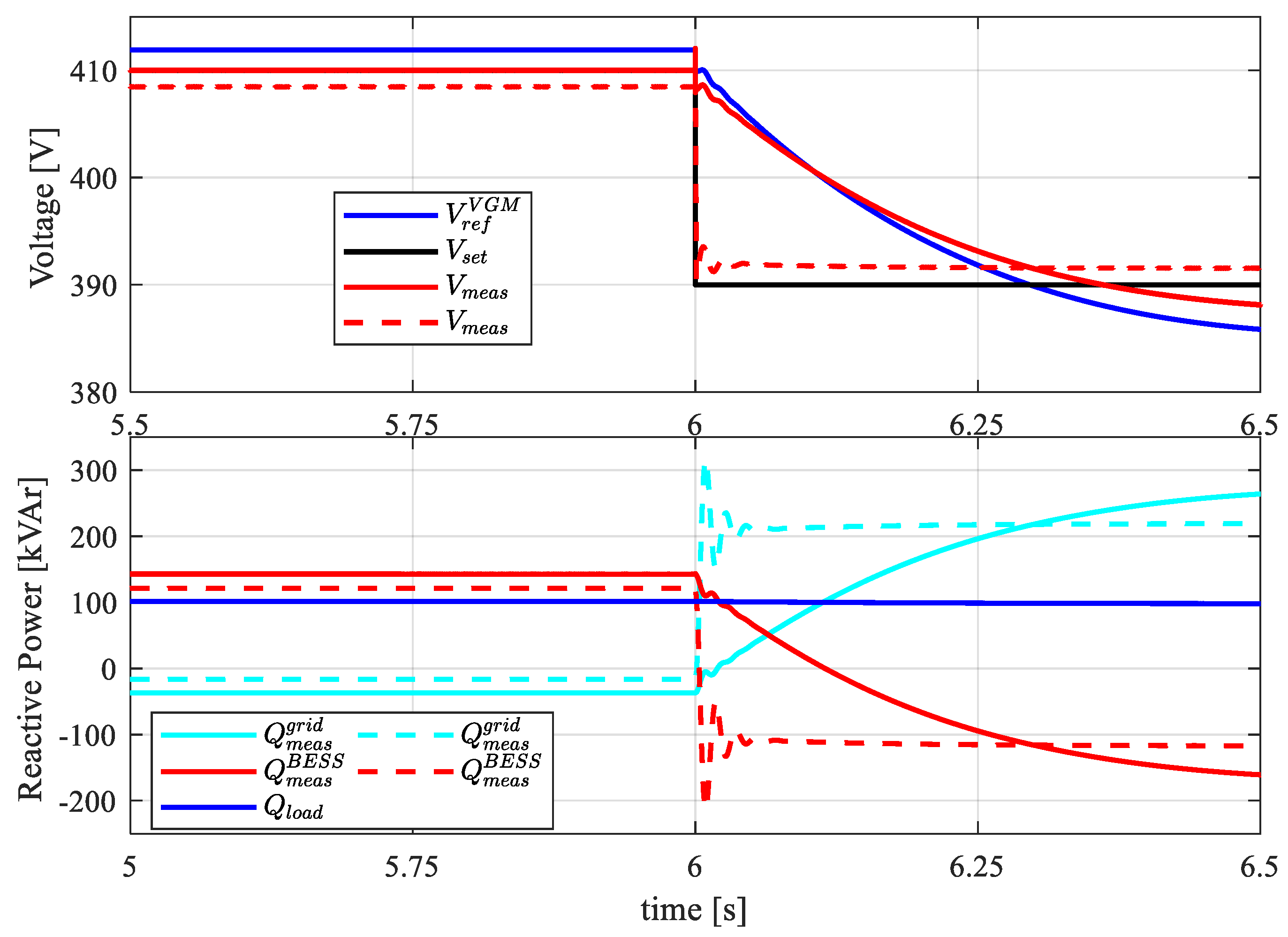
4.2. VGM Operating Mode With Setpoints Variation
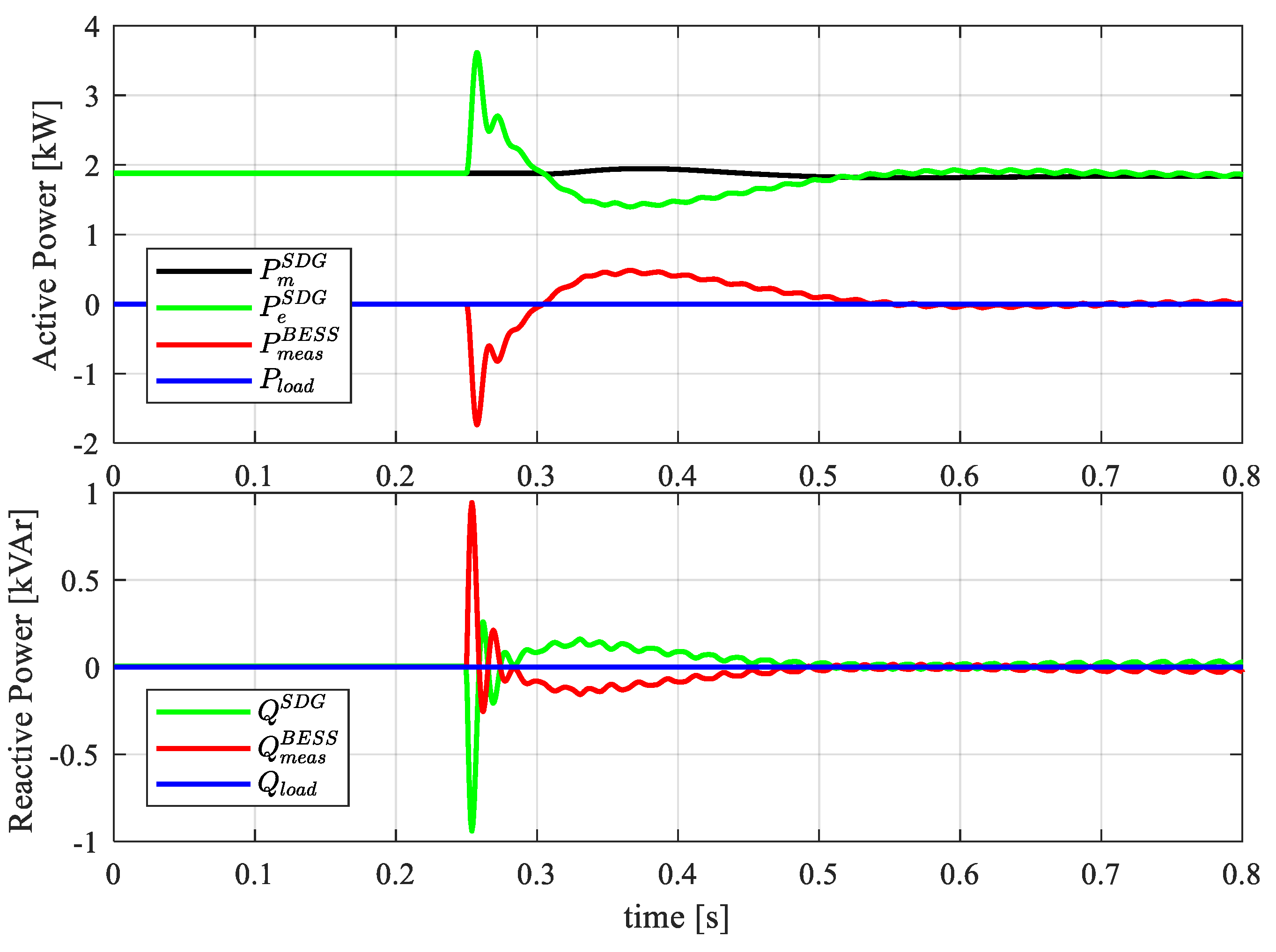
4.3. Paralleling Action and Load Sharing
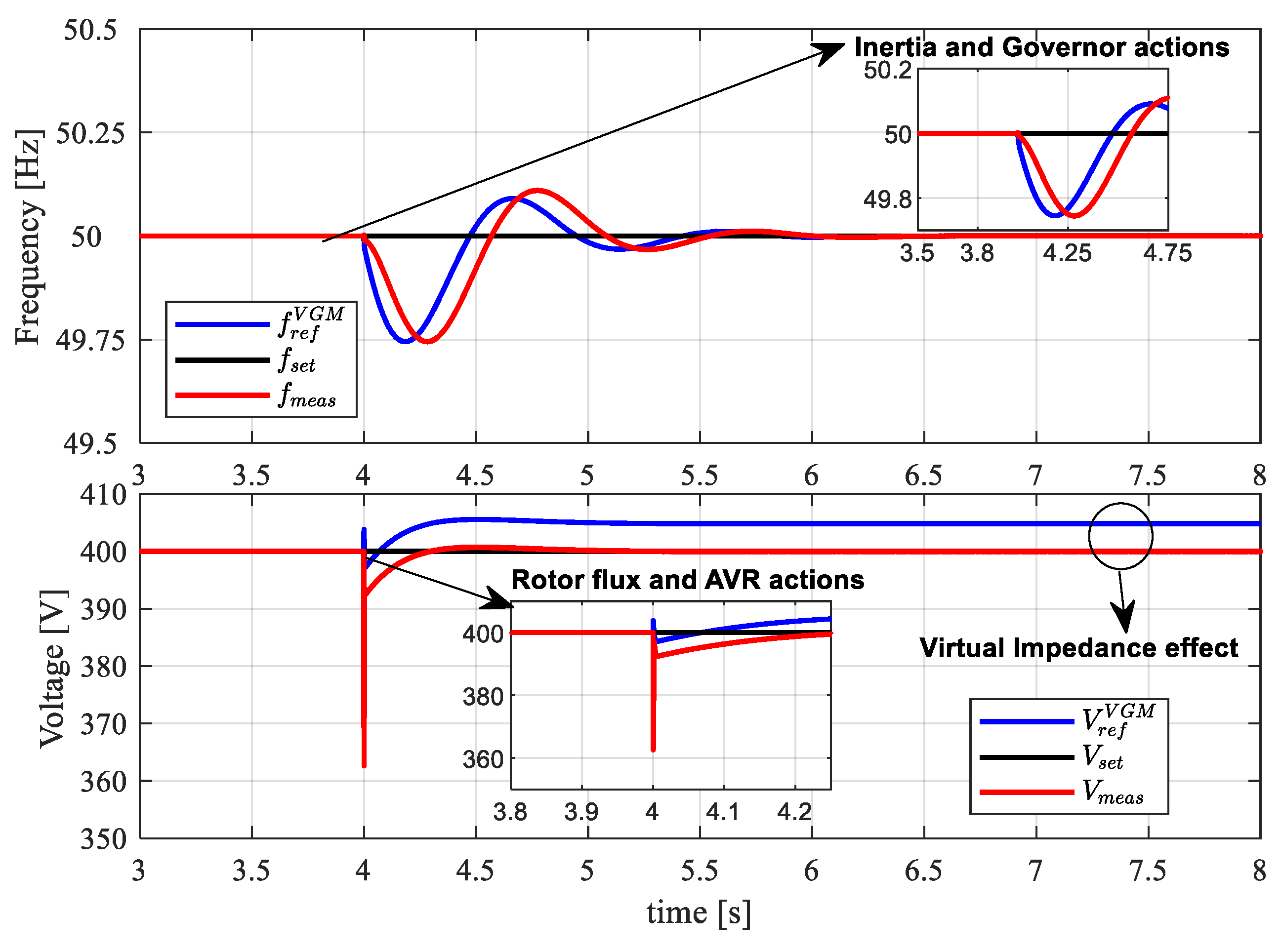
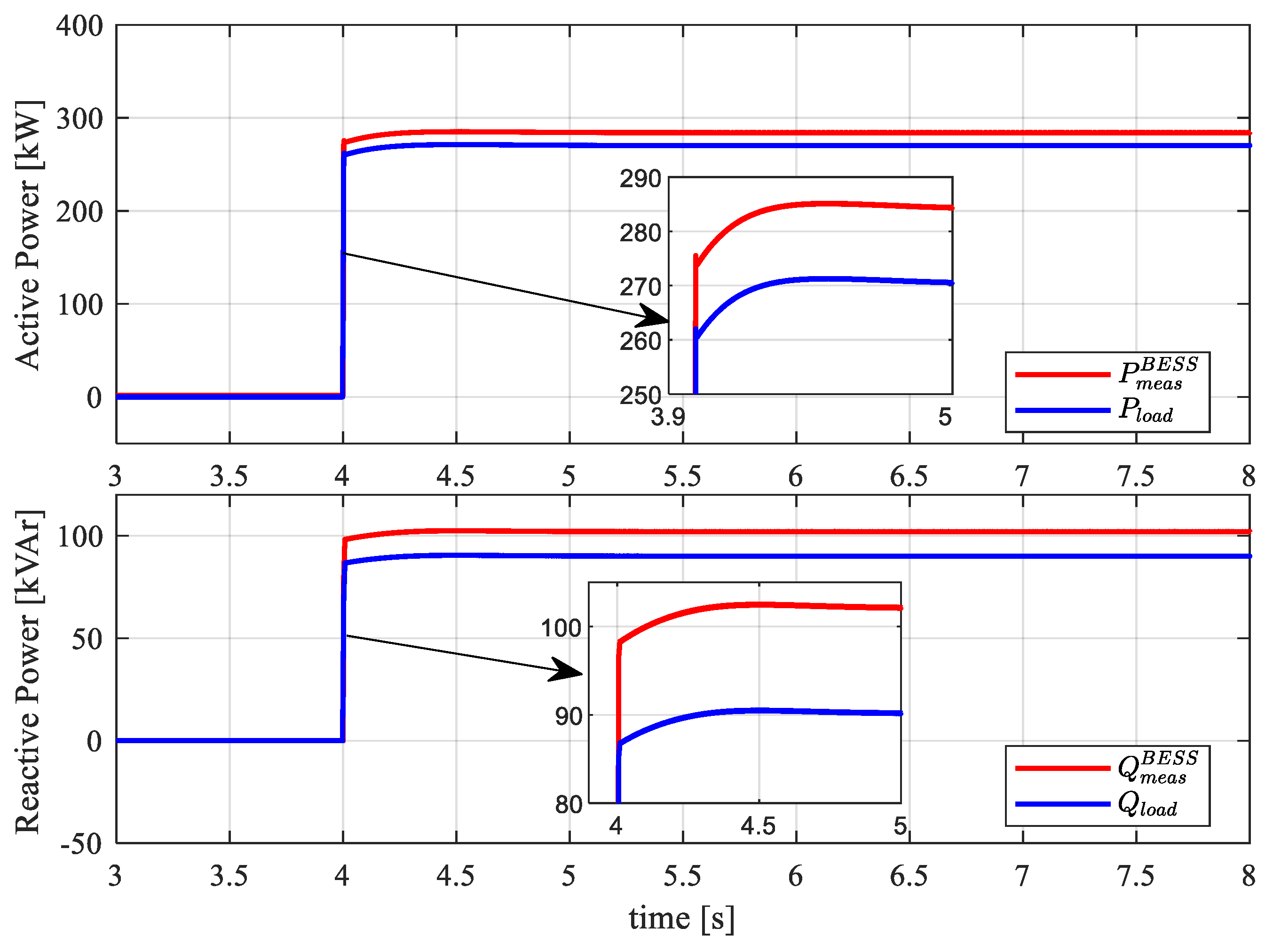
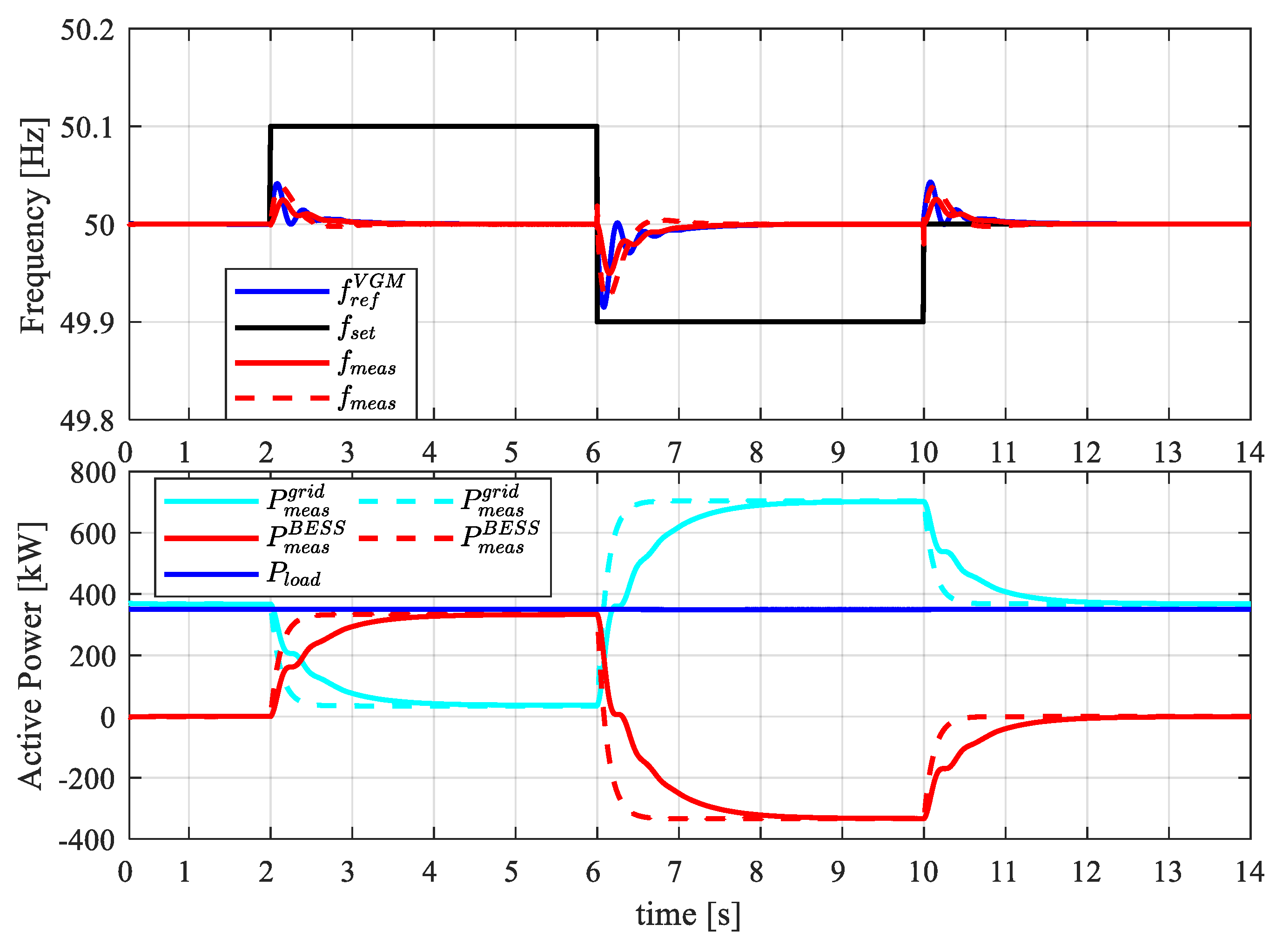
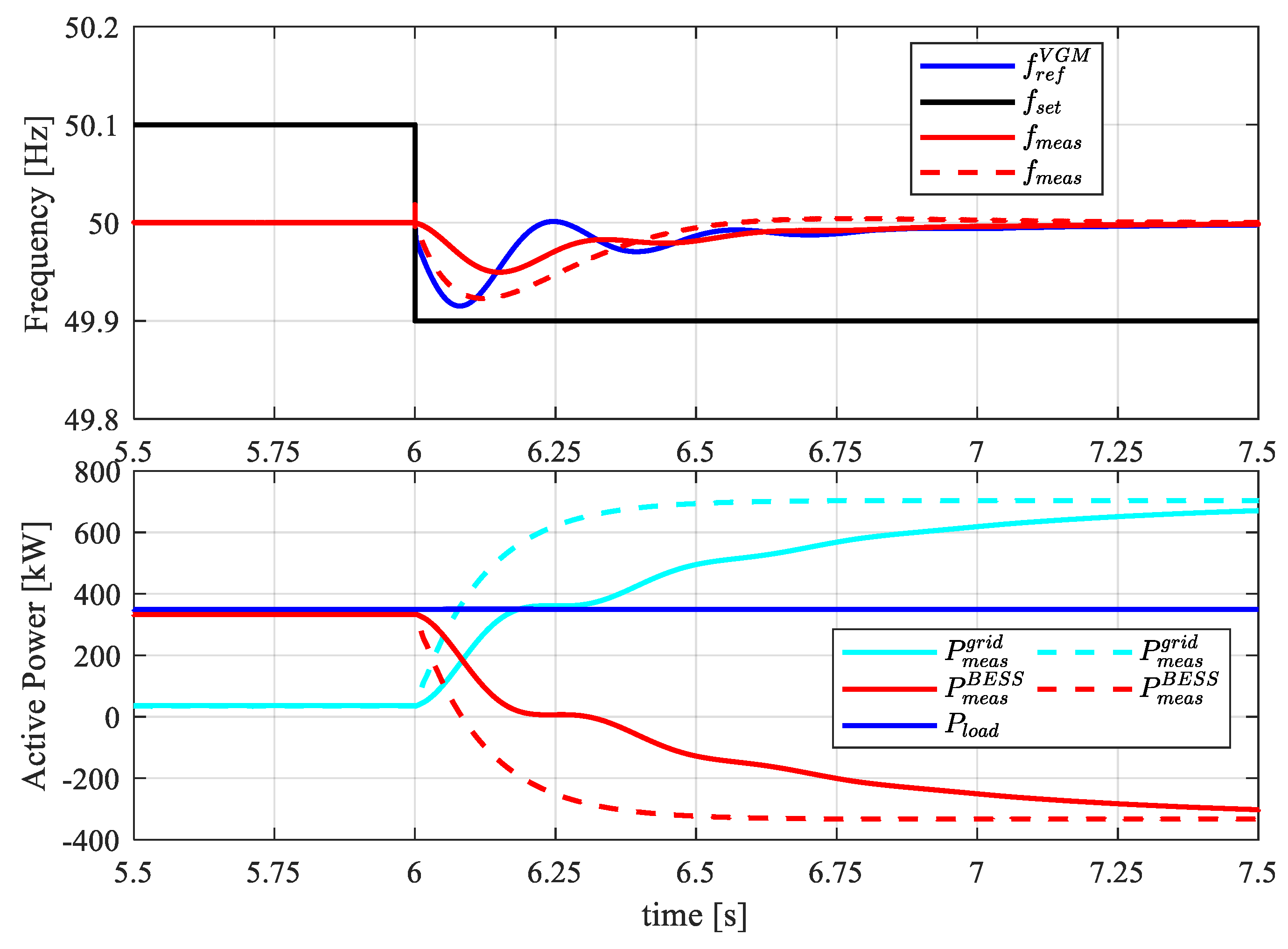
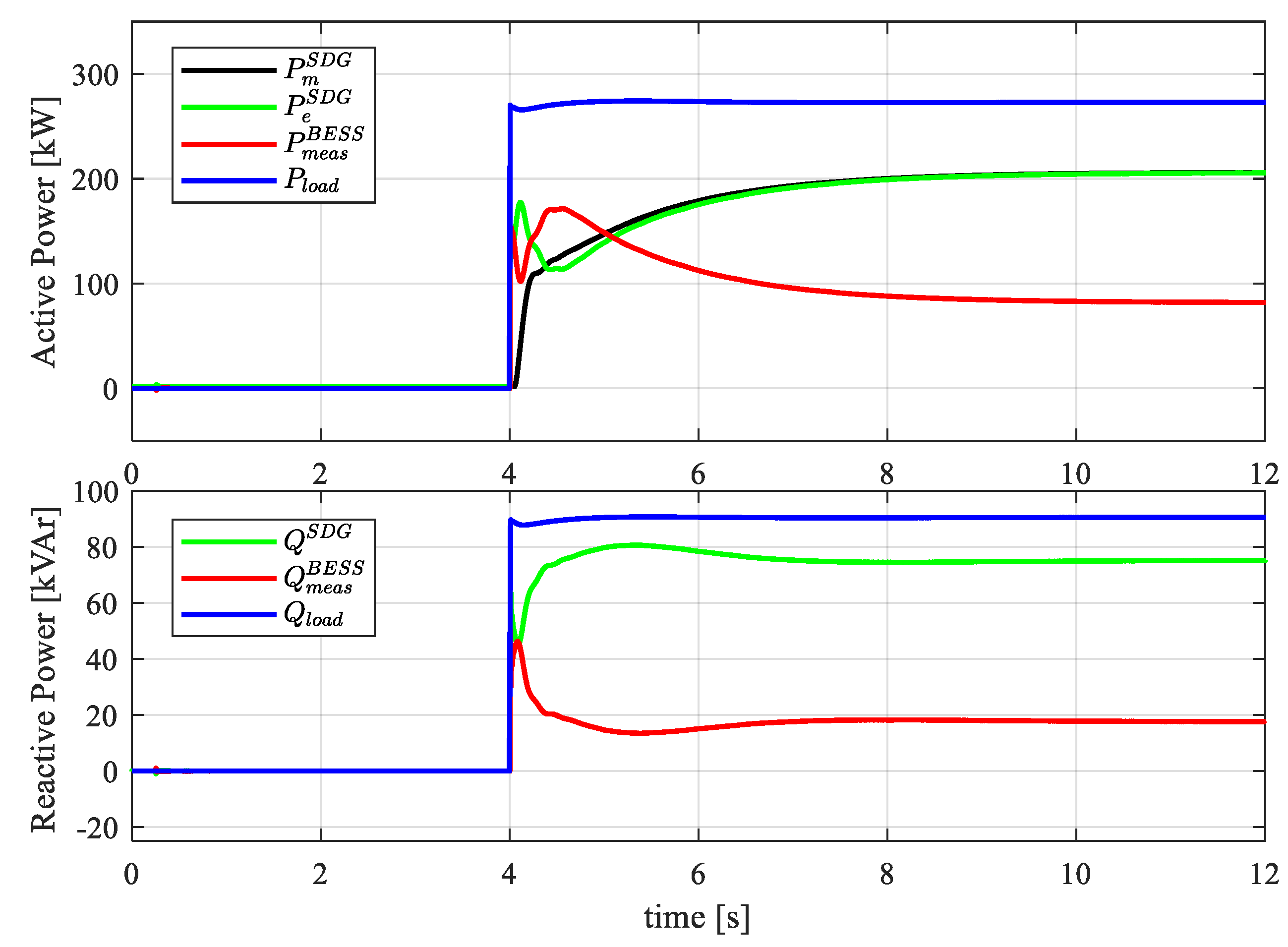
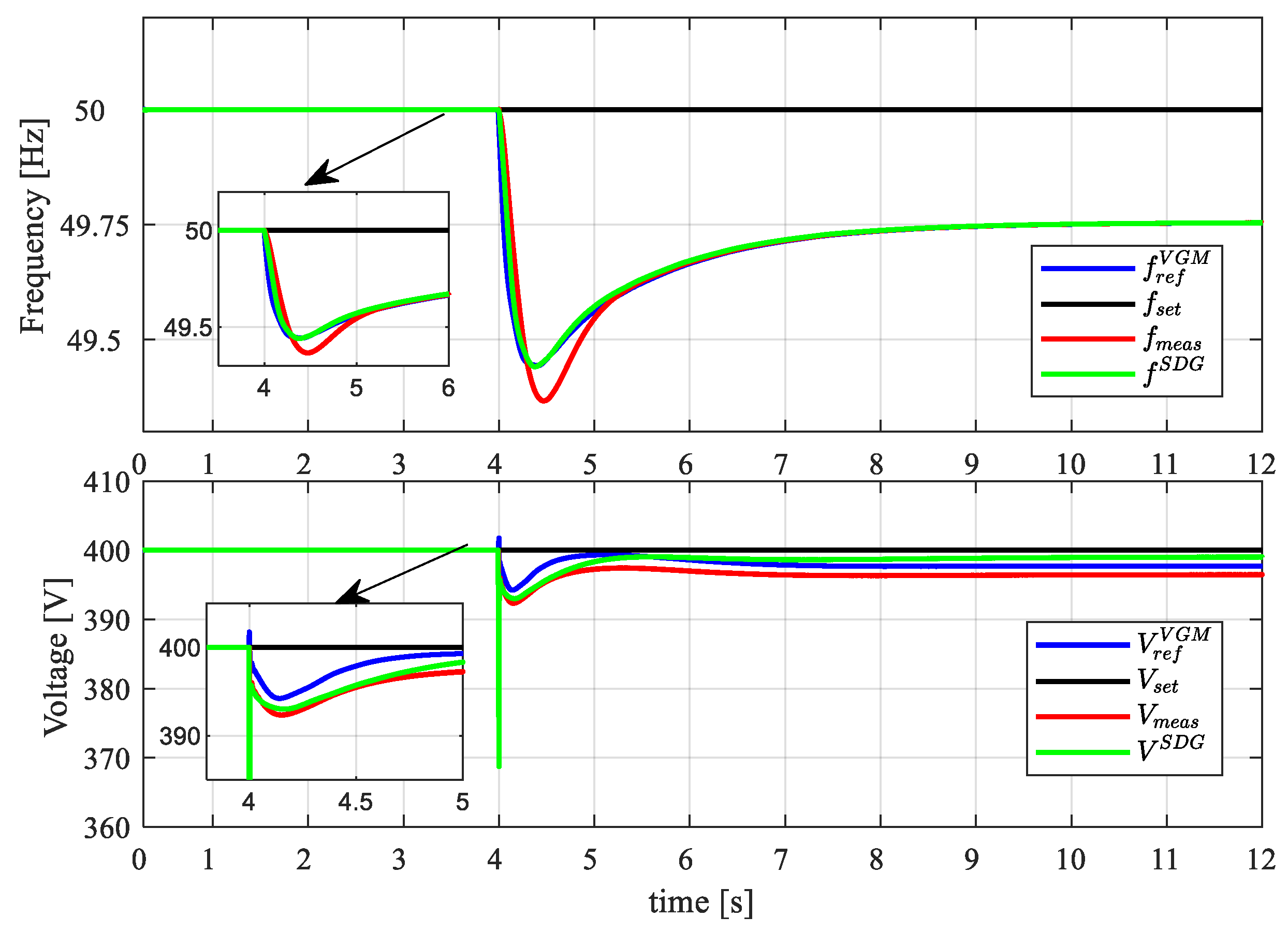
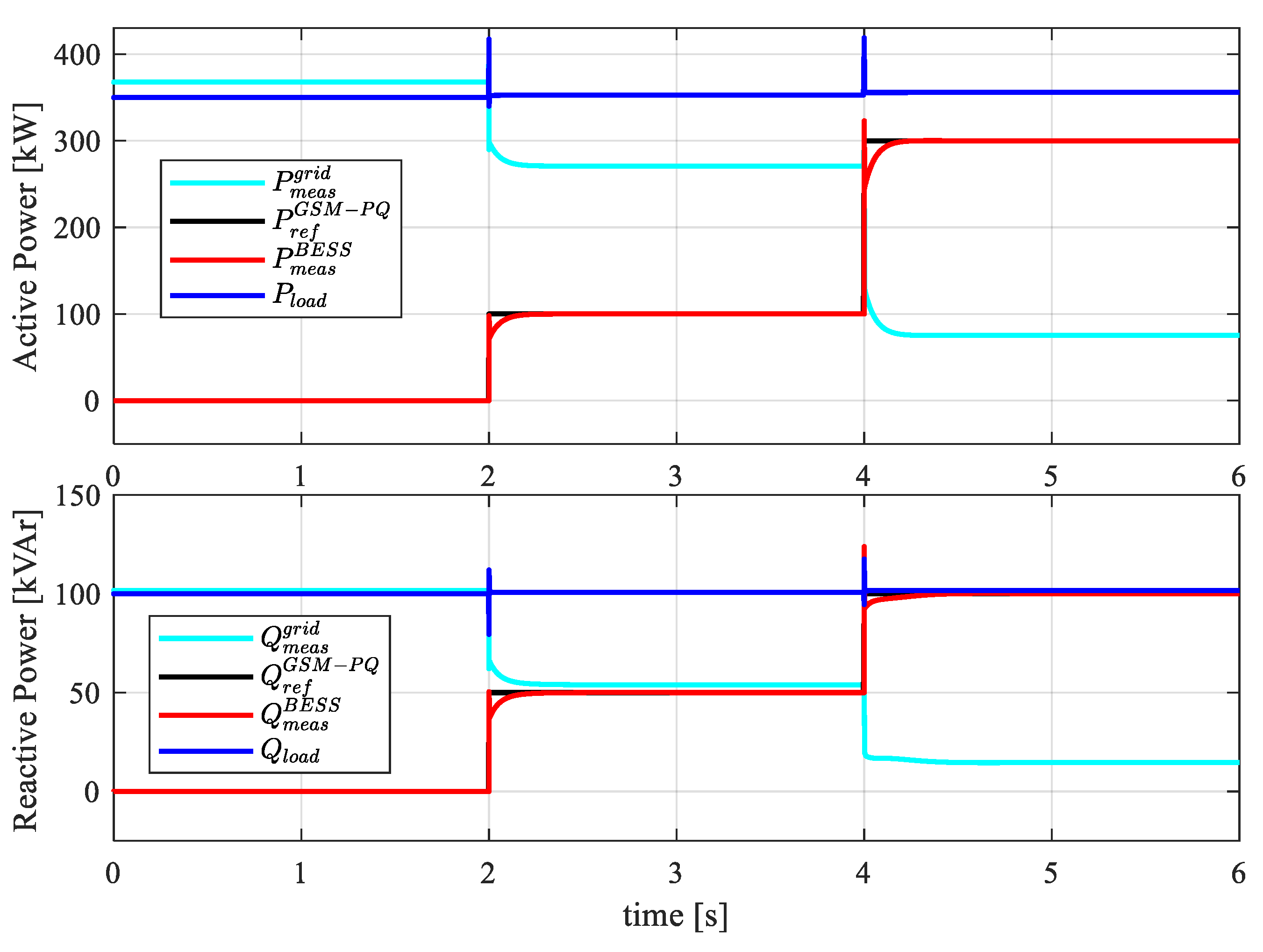
4.4. Grid Support Action
- In the first configuration, the BESS converter is not connected to the MG. Two different loads, namely and , are connected to the MG with , and (pure resistive load). Loads are supplied by the SDG, while the main grid is disconnected.
- In the second configuration, the BESS is connected to the MG in GSM-fV mode ready to provide voltage and frequency support after MG contingencies.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mariam, L.; Basu, M.; Conlon, M.F. Microgrid: Architecture, policy and future trends. Renew. Sustain. Energy Rev. 2016, 64, 477–489. [Google Scholar] [CrossRef]
- U.S.D.O. Energy. DOE Microgrid Workshop Report. Available online: https://www.energy.gov/about-us (accessed on 27 October 2018).
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; de Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Luna, A.C.; Meng, L.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Online Energy Management Systems for Microgrids: Experimental Validation and Assessment Framework. IEEE Trans. Power Electron. 2018, 33, 2201–2215. [Google Scholar] [CrossRef]
- Lu, X.; Yu, X.; Lai, J.; Wang, Y.; Guerrero, J.M. A Novel Distributed Secondary Coordination Control Approach for Islanded Microgrids. IEEE Trans. Smart Grid 2018, 9, 2726–2740. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- IEEE PES Industry Technical Support Task Force. Impact of IEEE 1547 Standard on Smart Inverters; Technical Report PES-TR67; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Zeineldin, H.H. AQ–fDroop Curve for Facilitating Islanding Detection of Inverter-Based Distributed Generation. IEEE Trans. Power Electron. 2009, 24, 665–673. [Google Scholar] [CrossRef]
- Zeineldin, H.H.; El-saadany, E.F.; Salama, M.M.A. Distributed Generation Micro-Grid Operation: Control and Protection. In Proceedings of the 2006 Power Systems Conference: Advanced Metering, Protection, Control, Communication, and Distributed Resources, Clemson, SC, USA, 14–17 March 2006; pp. 105–111. [Google Scholar]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Bevrani, H. Robust Power System Frequency Control; Springer: Berlin/Heidelberg, Germany, 2009; Volume 85. [Google Scholar]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Zhong, Q.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhong, Q.; Nguyen, P.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Zhong, Q.; Konstantopoulos, G.C.; Ren, B.; Krstic, M. Improved Synchronverters with Bounded Frequency and Voltage for Smart Grid Integration. IEEE Trans. Smart Grid 2018, 9, 786–796. [Google Scholar] [CrossRef]
- Arco, S.D.; Suul, J.A. Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers for microgrids. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–7. [Google Scholar]
- Fathi, A.; Shafiee, Q.; Bevrani, H. Robust Frequency Control of Microgrids Using an Extended Virtual Synchronous Generator. IEEE Trans. Power Syst. 2018, 33, 6289–6297. [Google Scholar] [CrossRef]
- Hirase, Y.; Noro, O.; Yoshimura, E.; Nakagawa, H.; Sakimoto, K.; Shindo, Y. Virtual synchronous generator control with double decoupled synchronous reference frame for single-phase inverter. IEEJ J. Ind. Appl. 2015, 4, 143–151. [Google Scholar] [CrossRef]
- Chen, Y.; Hesse, R.; Turschner, D.; Beck, H. Improving the grid power quality using virtual synchronous machines. In Proceedings of the 2011 International Conference on Power Engineering, Energy and Electrical Drives, Torremolinos, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Xiang-zhen, Y.; Jian-hui, S.; Ming, D.; Jin-wei, L.; Yan, D. Control strategy for virtual synchronous generator in microgrid. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, Shandong, China, 6–9 July 2011; pp. 1633–1637. [Google Scholar]
- Sakimoto, K.; Miura, Y.; Ise, T. Stabilization of a power system with a distributed generator by a Virtual Synchronous Generator function. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 29 May–2 June 2011; pp. 1498–1505. [Google Scholar]
- Shintai, T.; Miura, Y.; Ise, T. Reactive power control for load sharing with virtual synchronous generator control. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 Jun 2012; pp. 846–853. [Google Scholar]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation Damping of a Distributed Generator Using a Virtual Synchronous Generator. IEEE Trans. Power Deliv. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator With Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Tuckey, A.; Round, S. Practical application of a complete virtual synchronous generator control method for microgrid and grid-edge applications. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 25–28 June 2018; pp. 1–6. [Google Scholar]
- Lopes, J.P.; Moreira, C.; Resende, F. Control strategies for microgrids black start and islanded operation. Int. J. Distrib. Energy Resour. 2005, 1, 241–261. [Google Scholar]
- D. GmbH. DIgSILENT PowerFactory 2017 User Manual; DIgSILENT: Gomaringen, Germany, 2017. [Google Scholar]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
| BESS Converter Data | SDG Data | Load Data | |||||
|---|---|---|---|---|---|---|---|
| 500 kVA | 1250 kVA | 300 kW | 0.007 + j0.0008 Ω | ||||
| 400 V (AC-side) | 0.8 | 100 kVAr | 0.014 + 0.0016 Ω | ||||
| 50 Hz | 400 V | 50 kW | 0.0037 + j0.0004 Ω | ||||
| 0.044 Ω | 50 Hz | 0 kVAr | |||||
| 0.088 mH | |||||||
| 50 μF | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fusero, M.; Tuckey, A.; Rosini, A.; Serra, P.; Procopio, R.; Bonfiglio, A. A Comprehensive Inverter-BESS Primary Control for AC Microgrids. Energies 2019, 12, 3810. https://doi.org/10.3390/en12203810
Fusero M, Tuckey A, Rosini A, Serra P, Procopio R, Bonfiglio A. A Comprehensive Inverter-BESS Primary Control for AC Microgrids. Energies. 2019; 12(20):3810. https://doi.org/10.3390/en12203810
Chicago/Turabian StyleFusero, Michele, Andrew Tuckey, Alessandro Rosini, Pietro Serra, Renato Procopio, and Andrea Bonfiglio. 2019. "A Comprehensive Inverter-BESS Primary Control for AC Microgrids" Energies 12, no. 20: 3810. https://doi.org/10.3390/en12203810
APA StyleFusero, M., Tuckey, A., Rosini, A., Serra, P., Procopio, R., & Bonfiglio, A. (2019). A Comprehensive Inverter-BESS Primary Control for AC Microgrids. Energies, 12(20), 3810. https://doi.org/10.3390/en12203810







