Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System
Abstract
1. Introduction
2. Methodology and Data
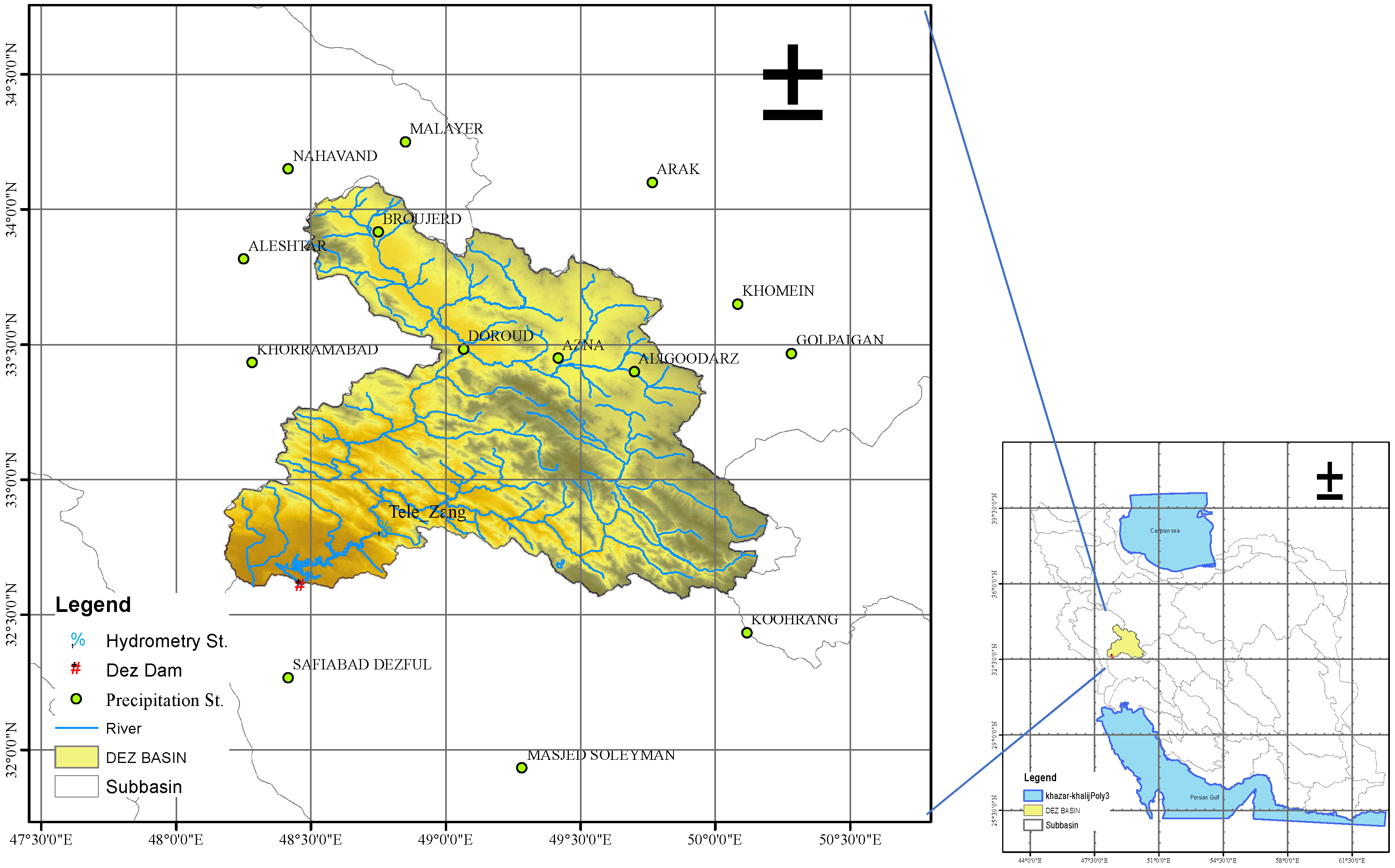
2.1. Study Area
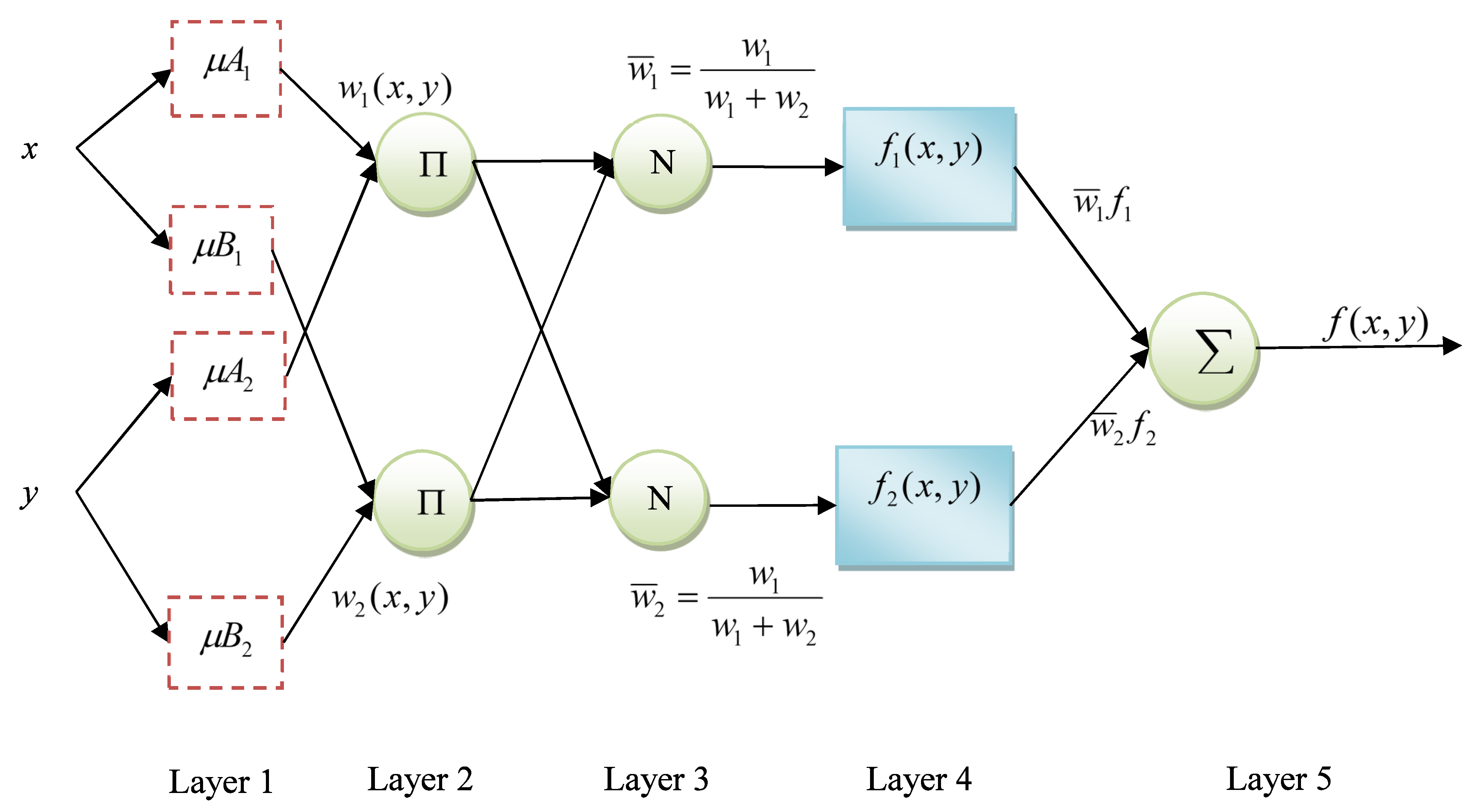
2.2. ANFIS: Adaptive Neuro-Fuzzy Inference System
- Rule one: if x and y = and , respectively, then .
- Rule two: if x and y = and , respectively, then
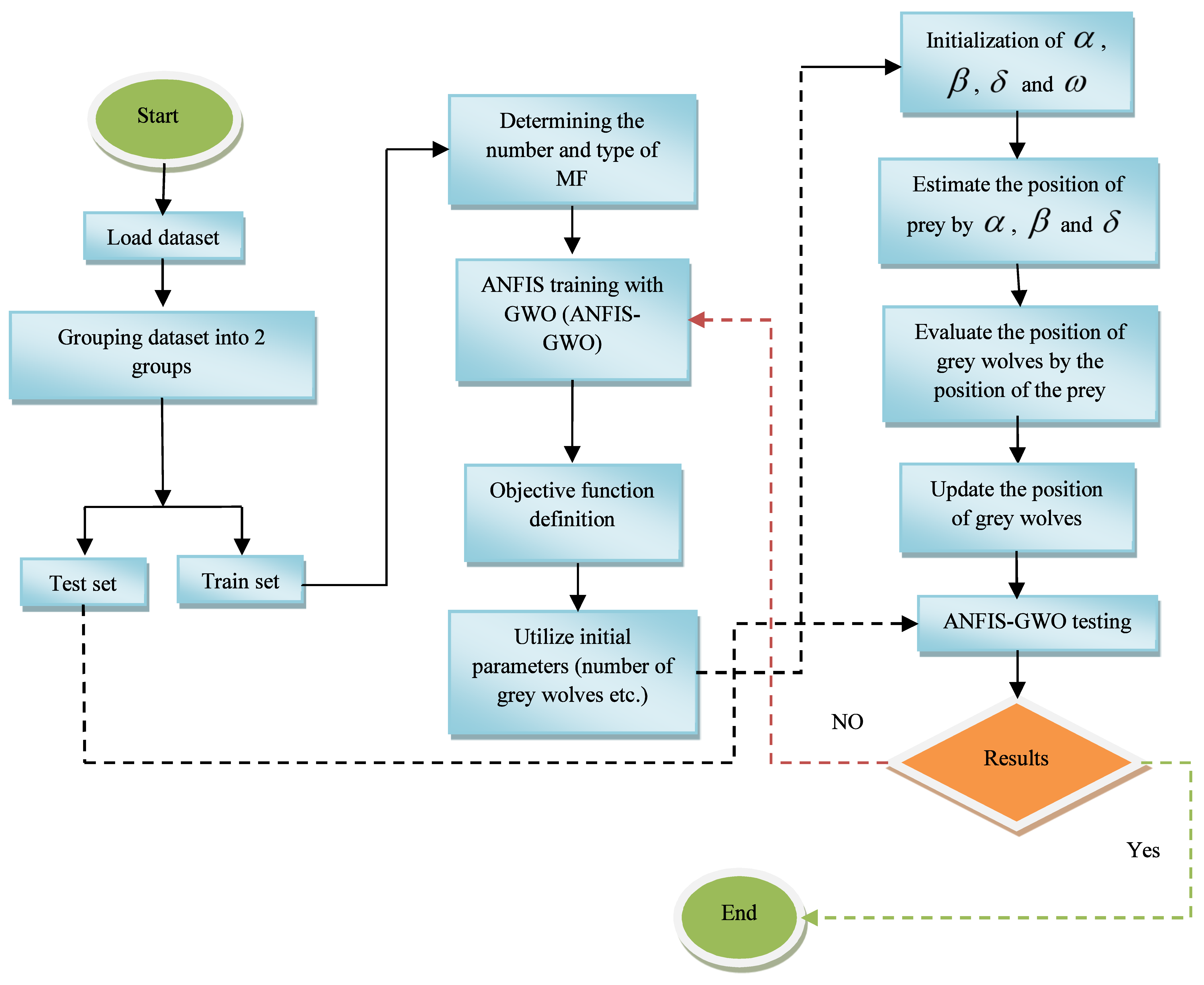
2.3. Grey Wolf Optimization (GWO)
- Identifying, following and approaching the prey;
- Encircling the prey;
- Attacking the prey.
2.4. Performance Criteria
3. Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Hamlet, A.F.; Huppert, D.; Lettenmaier, D.P. Economic value of long-lead streamflow forecasts for Columbia River hydropower. J. Water Resour. Plan. Manag. 2002, 1282, 91–101. [Google Scholar] [CrossRef]
- Tang, G.L.; Zhou, H.C.; Li, N.; Wang, F.; Wang, Y.; Jian, D. Value of medium-range precipitation forecasts in inflow prediction and hydropower optimization. Water Resour. Manag. 2010, 24, 2721–2742. [Google Scholar] [CrossRef]
- Zhou, H.; Tang, G.; Li, N.; Wang, F.; Wang, Y.; Jian, D. Evaluation of precipitation forecasts from NOAA global forecast system in hydropower operation. J. Hydroinform. 2011, 13, 81–95. [Google Scholar] [CrossRef]
- Block, P. Tailoring seasonal climate forecasts for hydropower operations. Hydrol. Earth Syst. Sci. 2011, 15, 1355–1368. [Google Scholar] [CrossRef]
- Rheinheimer, D.E.; Bales, R.C.; Oroza, C.A.; Lund, J.R.; Viers, J.H. Valuing year-to-go hydrologic forecast improvements for a peaking hydropower system in the Sierra Nevada. Water Resour. Res. 2016, 52, 3815–3828. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Xu, W.; Wang, B. An Optimal Operation Model for Hydropower Stations Considering Inflow Forecasts with Different Lead-Times. Water Resour. Manag. 2017. [Google Scholar] [CrossRef]
- Peng, Y.; Xu, W.; Liu, B. Considering precipitation forecasts for real-time decision-making in hydropower operations. Int. J. Water Resour. Dev. 2017, 33, 987–1002. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, R.; Li, A.; Ji, C. Runoff forecast uncertainty considered load adjustment model of cascade hydropower stations and its application. Energy 2018, 158, 693–708. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Hammid, A.T.; Sulaiman, M.H.B.; Abdalla, A.N. Prediction of small hydropower plant power production in Himreen Lake dam (HLD) using artificial neural network. Alexandria Eng. J. 2018, 57, 211–221. [Google Scholar] [CrossRef]
- Boucher, M.A.; Ramos, M.H. Ensemble Streamflow Forecasts for Hydropower Systems. Handb. Hydrometeorol. Ensemble Forecast. 2018, 1–19. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An Ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Shamshirband, S.; Jafari Nodoushan, E.; Adolf, J.E.; Abdul Manaf, A.; Mosavi, A.; Chau, K.W. Ensemble models with uncertainty analysis for multi-day ahead forecasting of chlorophyll a concentration in coastal waters. Eng. Appl. Comput. Fluid Mech. 2019, 13, 91–101. [Google Scholar] [CrossRef]
- Bui, K.T.T.; Bui, D.T.; Zou, J.; Van Doan, C.; Revhaug, I. A novel hybrid artificial intelligent approach based on neural fuzzy inference model and particle swarm optimization for horizontal displacement modeling of hydropower dam. Neural Comput. Appl. 2018, 29, 1495–1506. [Google Scholar]
- Kim, Y.O.; Eum, H.I.; Lee, E.G.; Ko, I.H. Optimizing Operational Policies of a Korean Multireservoir System Using Sampling Stochastic Dynamic Programming with Ensemble Streamflow Prediction. J. Water Resour. Plan Manag. 2007, 133, 4. [Google Scholar] [CrossRef]
- Ch, S.; Anand, N.; Panigrahi, B.K. Streamflow forecasting by SVM with quantum behaved particle swarm optimization. Neurocomputing 2013, 101, 18–23. [Google Scholar] [CrossRef]
- Cote, P.; Leconte, R. Comparison of Stochastic Optimization Algorithms for Hydropower Reservoir Operation with Ensemble Streamflow Prediction. J. Water Resour. Plan Manag. 2016, 142, 04015046. [Google Scholar] [CrossRef]
- Keshtegar, B.; Falah Allawi, M.; Afan, H.A.; El-Shafie, A. Optimized River Stream-Flow Forecasting Model Utilizing High-Order Response Surface Method. Water Resour. Manag. 2016, 30, 3899–3914. [Google Scholar] [CrossRef]
- Paul, M.; Negahban-Azar, M. Sensitivity and uncertainty analysis for streamflow prediction using multiple optimization algorithms and objective functions: San Joaquin Watershed, California. Model. Earth Syst. Environ. 2018, 4, 1509–1525. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Mohammadzadeh, D.; Shamshirband, S.; Hajikhodaverdikhan, P.; Mosavi, A.; Chau, K.W. Prediction of remaining service life of pavement using an optimized support vector machine. Eng. Appl. Comput. Fluid Mech. 2019, 16, 120–144. [Google Scholar]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5 concentration forecasting. Atmos. Environ. 2016, 134, 168–180. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Choubin, B.; Khalighi-Sigaroodi, S.; Malekian, A.; Kişi, O. Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for the prediction of precipitation based on large-scale climate signals. Hydrol. Sci. J. 2016, 61, 1001–1009. [Google Scholar] [CrossRef]
- Firat, M.; Güngör, M. Hydrological time-series modelling using an adaptive neuro-fuzzy inference system. Hydrol. Process. 2007, 22, 2122–2132. [Google Scholar] [CrossRef]
- Shabri, A. A Hybrid Wavelet Analysis and Adaptive Neuro-Fuzzy Inference System for Drought Forecasting. Appl. Math. Sci. 2014, 8, 6909–6918. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. Precipitation forecasting using wavelet genetic programming and wavelet-neuro-fuzzy conjunction models. Water Resour. Manag. 2011, 25, 3135–3152. [Google Scholar] [CrossRef]
- Awan, J.A.; Bae, D.H. Drought prediction over the East Asian monsoon region using the adaptive neuro-fuzzy inference system and the global sea surface temperature anomalies. Int. J. Climatol. 2016, 36, 4767–4777. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O. Advanced Optimization by Nature-Inspired Algorithms; Springer: Singapore, 2017. [Google Scholar]
- Muro, C.; Escobedo, R.; Spector, L.; Coppinger, R. Wolf-pack (Canis Lupus) hunting strategies emerge from simple rules in computational simulations. Behav. Process. 2011, 88, 192–197. [Google Scholar] [CrossRef]
- Amr, H.; El-Shafie, A.; El Mazoghi, H.; Shehata, A.; Taha, M.R. Artificial neural network technique for rainfall forecasting applied to Alexandria, Egypt. Int. J. Phys. Sci. 2011, 6, 1306–1316. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Willmott, C.J. On the evaluation of model performance in physical geography. In Spatial Statistics and Models; Springer: Dordrecht, The Netherlands, 1984; pp. 443–460. [Google Scholar]
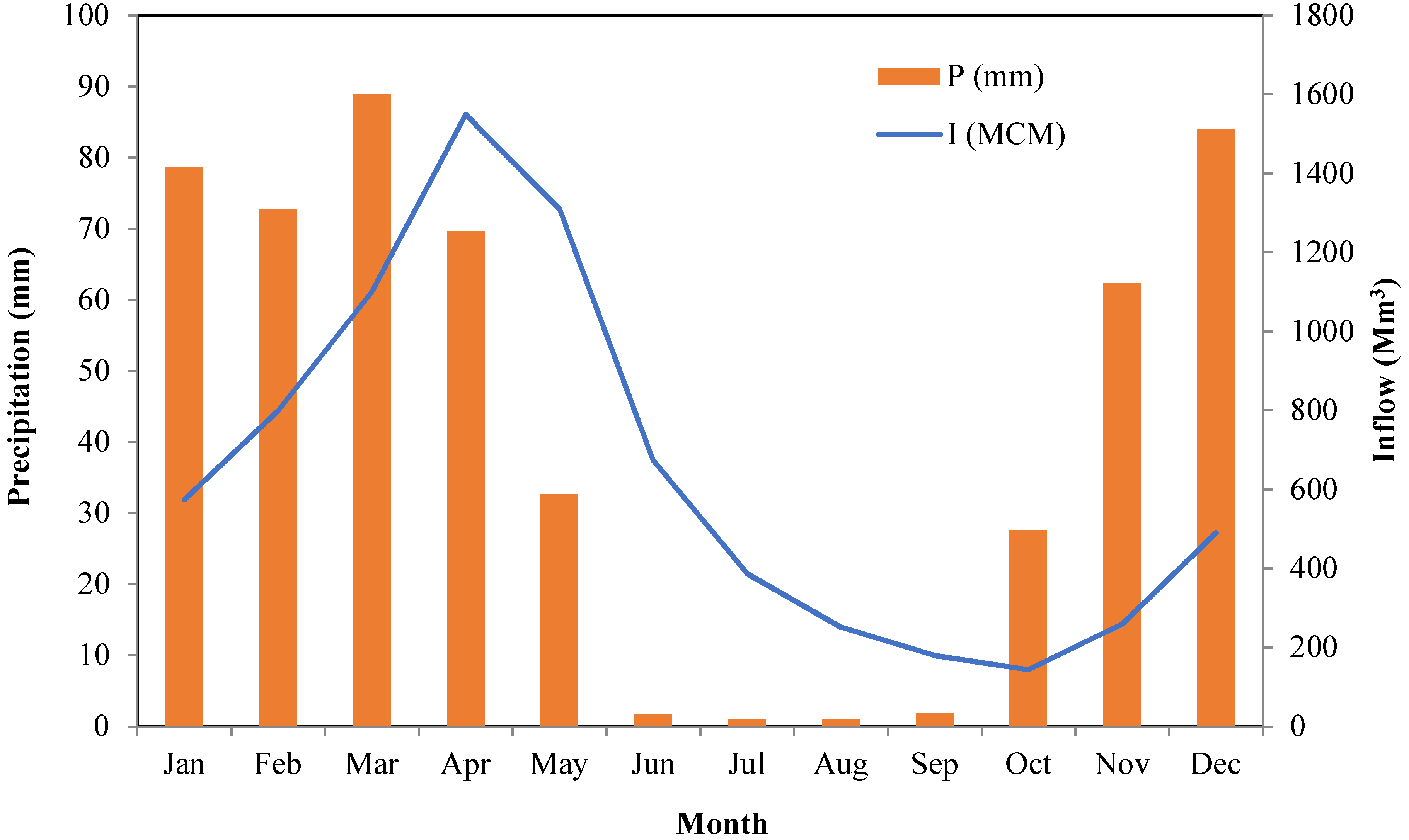


| Parameter | Mode | Mean | Min | S.D. | First Quartile | Median | Third Quartile | Max | Skew. | Kurtosis. |
|---|---|---|---|---|---|---|---|---|---|---|
| Ht | 26,545.98 | 165,297.70 | 26,545.98 | 56,093.06 | 130,338.42 | 168,568.96 | 203,734.07 | 354,879.53 | −0.10 | 2.76 |
| Qt | 63.28 | 651.71 | 63.28 | 615.23 | 209.87 | 430.22 | 842.41 | 3643.84 | 1.86 | 6.91 |
| Pt | 0.00 | 42.82 | 0.00 | 46.91 | 0.47 | 27.97 | 71.81 | 238.47 | 1.10 | 3.69 |
| Model | Input Parameters | Output |
|---|---|---|
| M1 | Qt | Ht |
| M2 | Qt, Pt | Ht |
| M3 | Qt-1, Qt | Ht |
| M4 | Qt-1, Qt, Ht-1 | Ht |
| M5 | Ht-1 | Ht |
| M6 | Qt-1, Qt, Pt, Ht-1 | Ht |
| M7 | Ht-2, Ht-1 | Ht |
| M8 | Qt, Ht-2, Ht-1 | Ht |
| M9 | Qt-1, Qt, Ht-2, Ht-1 | Ht |
| M10 | Ht-12, Ht-2, Ht-1 | Ht |
| M11 | Ht-12, Ht-1 | Ht |
| M12 | Ht-12 | Ht |
| M13 | Qt-4, Qt-3, Qt-2, Qt-1, Qt | Ht |
| M14 | Qt-3, Qt-2, Qt-1, Qt | Ht |
| M15 | Qt-2, Qt-1, Qt | Ht |
| M16 | Qt-3, Qt-2, Ht-12, Ht-1 | Ht |
| M17 | Qt-3, Ht-2, Ht-1 | Ht |
| M18 | Qt-4, Qt-3 | Ht |
| M19 | Pt-5, Pt-4, Qt-4, Qt-3, Qt-2 | Ht |
| M20 | Pt-5, Pt-4, Qt-3, Qt-2 | Ht |
| Ht | Qt | Pt | Ht-1 | Ht-2 | Ht-3 | Ht-4 | Ht-5 | Ht-6 | Ht-12 | Qt-1 | Qt-2 | Qt-3 | Qt-4 | Qt-5 | Qt-6 | Pt-1 | Pt-2 | Pt-3 | Pt-4 | Pt-5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ht | 1 | ||||||||||||||||||||
| Qt | 0.11 | 1 | |||||||||||||||||||
| Pt | 0.05 | 0.13 | 1 | ||||||||||||||||||
| Ht-1 | 0.66 | 0.01 | 0.1 | 1 | |||||||||||||||||
| Ht-2 | 0.34 | 0 | 0.07 | 0.66 | 1 | ||||||||||||||||
| Ht-3 | 0.15 | 0.02 | 0.02 | 0.34 | 0.66 | 1 | |||||||||||||||
| Ht-4 | 0.06 | 0.02 | 0 | 0.16 | 0.35 | 0.66 | 1 | ||||||||||||||
| Ht-5 | 0.02 | 0.01 | 0.02 | 0.06 | 0.16 | 0.35 | 0.67 | 1 | |||||||||||||
| Ht-6 | 0.01 | 0 | 0.08 | 0.02 | 0.06 | 0.16 | 0.35 | 0.66 | 1 | ||||||||||||
| Ht-12 | 0.18 | 0.01 | 0.06 | 0.14 | 0.08 | 0.04 | 0.02 | 0.01 | 0.01 | 1 | |||||||||||
| Qt-1 | 0.27 | 0.46 | 0 | 0.11 | 0.01 | 0 | 0.02 | 0.02 | 0.01 | 0.09 | 1 | ||||||||||
| Qt-2 | 0.31 | 0.14 | 0.09 | 0.27 | 0.11 | 0.01 | 0 | 0.02 | 0.02 | 0.15 | 0.46 | 1 | |||||||||
| Qt-3 | 0.31 | 0 | 0.19 | 0.31 | 0.26 | 0.11 | 0.01 | 0 | 0.02 | 0.17 | 0.14 | 0.46 | 1 | ||||||||
| Qt-4 | 0.24 | 0.02 | 0.24 | 0.31 | 0.31 | 0.26 | 0.11 | 0.01 | 0 | 0.13 | 0 | 0.14 | 0.46 | 1 | |||||||
| Qt-5 | 0.11 | 0.11 | 0.18 | 0.24 | 0.31 | 0.31 | 0.26 | 0.11 | 0.01 | 0.05 | 0.03 | 0 | 0.14 | 0.46 | 1 | ||||||
| Qt-6 | 0.02 | 0.17 | 0.04 | 0.11 | 0.24 | 0.31 | 0.31 | 0.26 | 0.11 | 0 | 0.11 | 0.03 | 0 | 0.14 | 0.46 | 1 | |||||
| Pt-1 | 0 | 0.45 | 0.23 | 0.06 | 0.1 | 0.07 | 0.02 | 0 | 0.02 | 0.01 | 0.13 | 0 | 0.09 | 0.19 | 0.24 | 0.18 | 1 | ||||
| Pt-2 | 0.04 | 0.39 | 0.06 | 0 | 0.06 | 0.1 | 0.07 | 0.02 | 0 | 0 | 0.45 | 0.13 | 0 | 0.09 | 0.19 | 0.24 | 0.23 | 1 | |||
| Pt-3 | 0.11 | 0.29 | 0 | 0.04 | 0 | 0.06 | 0.1 | 0.07 | 0.02 | 0.03 | 0.39 | 0.45 | 0.13 | 0 | 0.09 | 0.19 | 0.06 | 0.23 | 1 | ||
| Pt-4 | 0.2 | 0.14 | 0.06 | 0.1 | 0.04 | 0 | 0.06 | 0.1 | 0.07 | 0.08 | 0.28 | 0.39 | 0.45 | 0.13 | 0 | 0.09 | 0 | 0.06 | 0.23 | 1 | |
| Pt-5 | 0.21 | 0.02 | 0.2 | 0.2 | 0.1 | 0.04 | 0 | 0.06 | 0.1 | 0.12 | 0.14 | 0.28 | 0.39 | 0.45 | 0.13 | 0 | 0.06 | 0 | 0.06 | 0.23 | 1 |
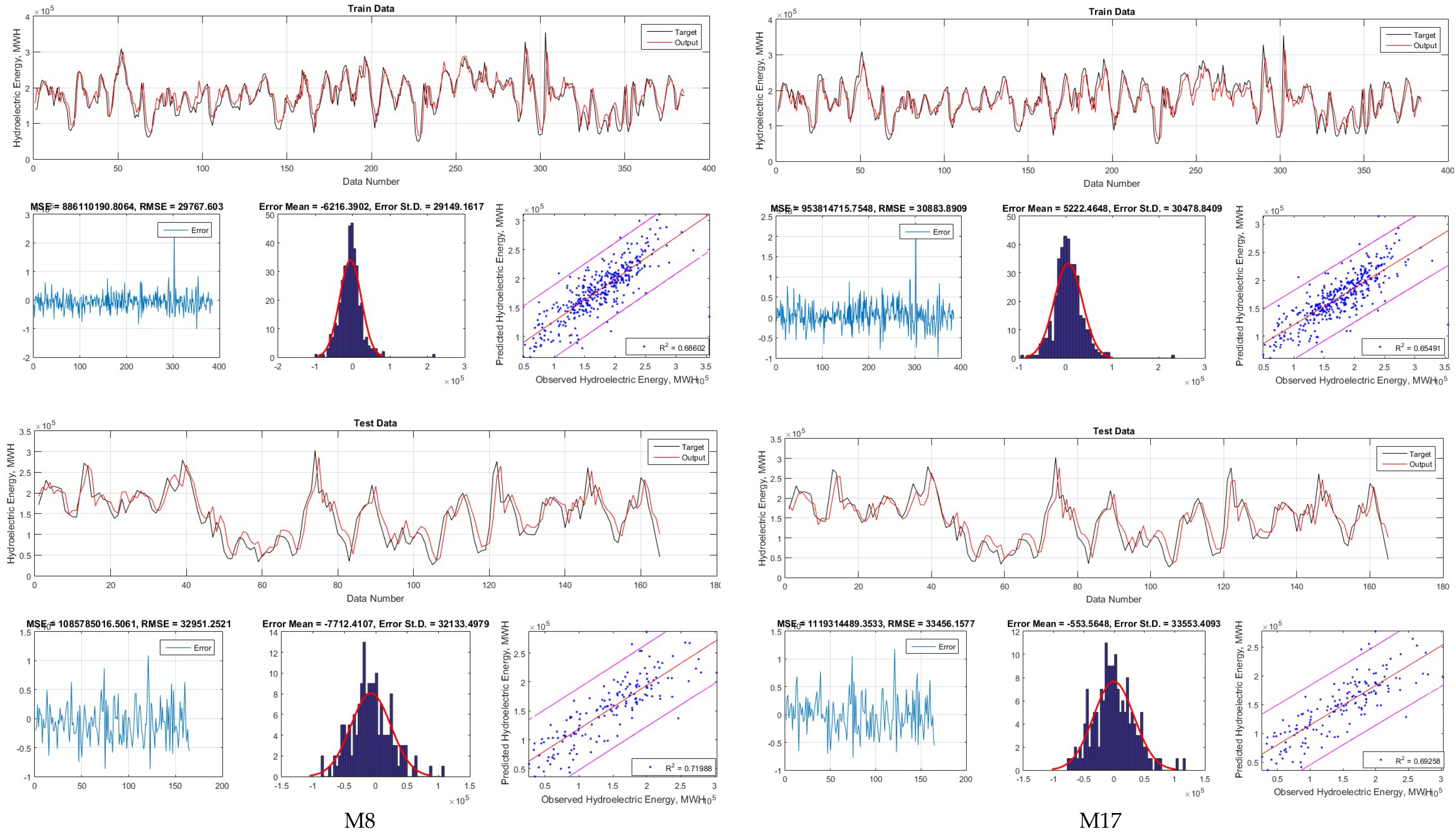
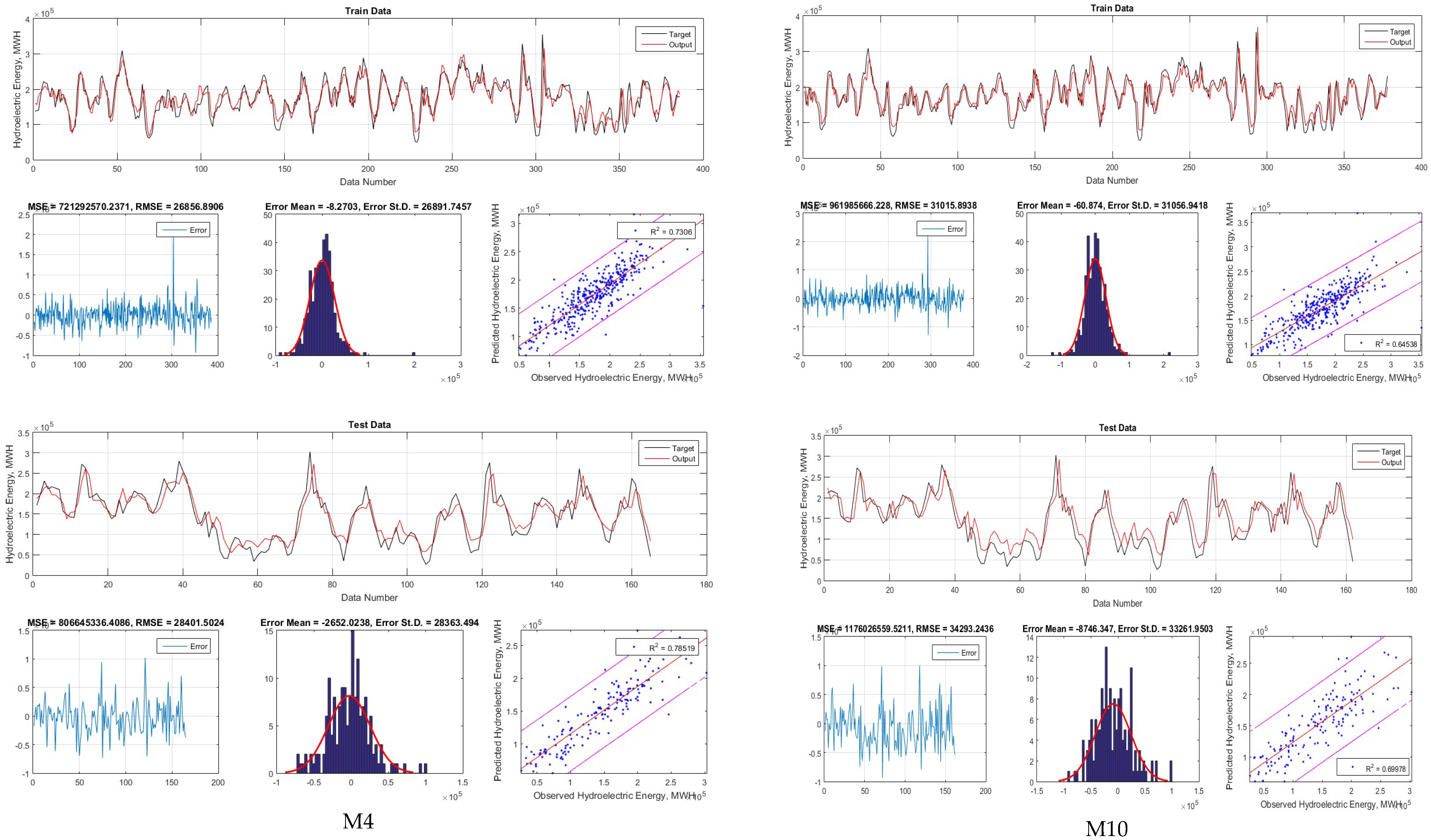
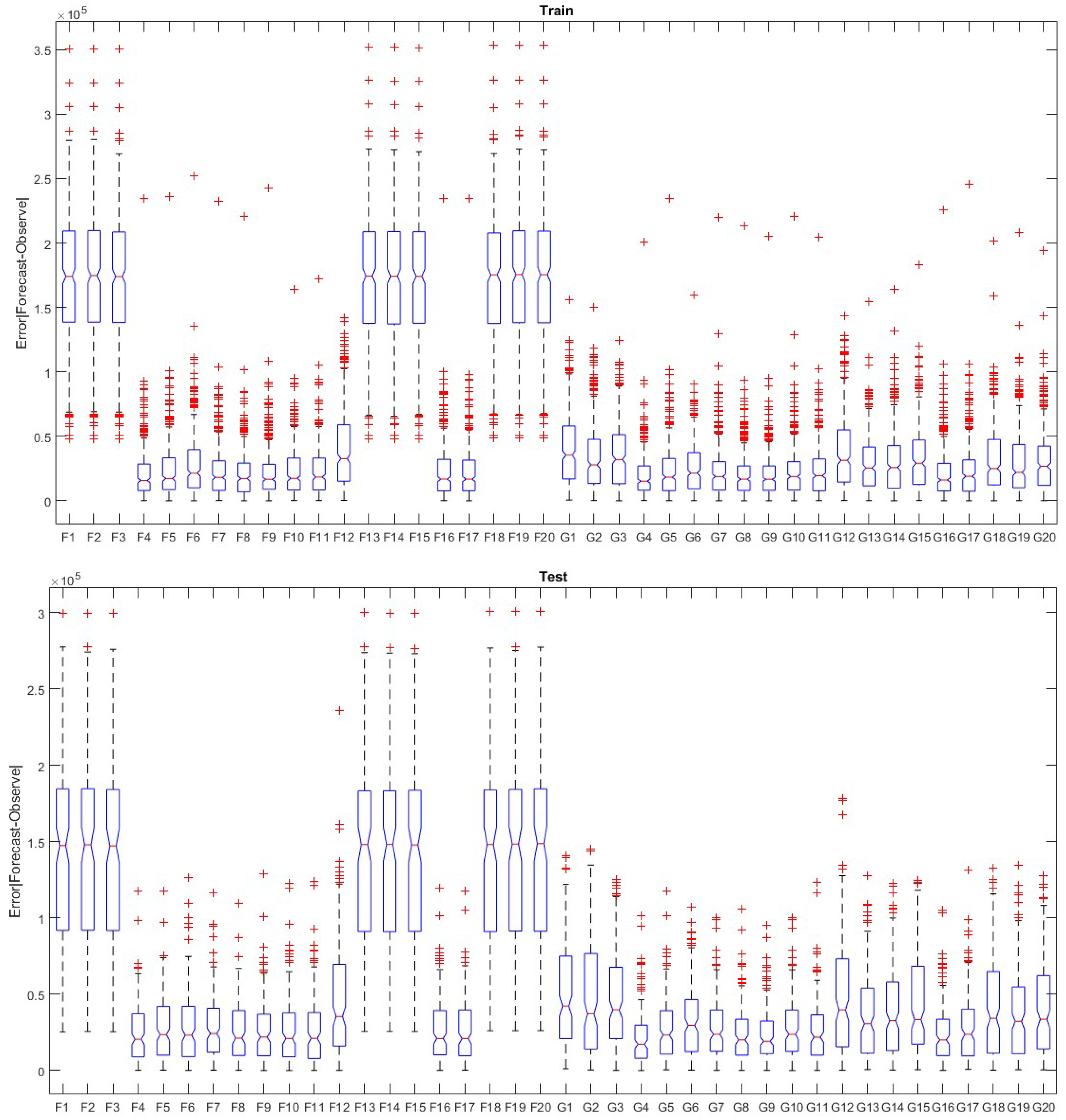
| Train | ANFIS1 | ANFIS2 | ANFIS3 | ANFIS4 | ANFIS5 | ANFIS6 | ANFIS7 | ANFIS8 | ANFIS9 | ANFIS10 | |
| RSQ | 0.08 | 0.12 | 0.17 | 0.68 | 0.62 | 0.51 | 0.63 | 0.69 | 0.66 | 0.67 | |
| RMSE | 179,477 | 179,882 | 179,305 | 29,260 | 32,165 | 38,263 | 31,488 | 29,768 | 30,164 | 29,991 | |
| MAE | 171,981 | 172,397 | 171,840 | 21,000 | 23,451 | 28,172 | 22,869 | 21,539 | 21,599 | 22,521 | |
| RAE | 4.10 | 4.11 | 4.11 | 0.50 | 0.56 | 0.67 | 0.55 | 0.51 | 0.52 | 0.54 | |
| d | 0.31 | 0.31 | 0.31 | 0.90 | 0.88 | 0.83 | 0.88 | 0.90 | 0.89 | 0.89 | |
| NSE | −11.02 | −11.08 | −11.01 | 0.68 | 0.61 | 0.45 | 0.63 | 0.67 | 0.66 | 0.67 | |
| CI | −3.41 | −3.42 | −3.41 | 0.61 | 0.54 | 0.38 | 0.56 | 0.60 | 0.59 | 0.60 | |
| ANFIS11 | ANFIS12 | ANFIS13 | ANFIS14 | ANFIS15 | ANFIS16 | ANFIS17 | ANFIS18 | ANFIS19 | ANFIS20 | ||
| RSQ | 0.66 | 0.12 | 0.22 | 0.26 | 0.23 | 0.64 | 0.65 | 0.35 | 0.22 | 0.32 | |
| RMSE | 30,579 | 51,150 | 179,856 | 179,647 | 179,438 | 31,253 | 30,884 | 179,512 | 180,465 | 180,470 | |
| MAE | 23,091 | 40,660 | 172,323 | 172,134 | 171,954 | 22,451 | 22,071 | 172,115 | 172,932 | 172,973 | |
| RAE | 0.55 | 0.97 | 4.12 | 4.11 | 4.11 | 0.54 | 0.53 | 4.12 | 4.13 | 4.13 | |
| d | 0.89 | 0.54 | 0.31 | 0.31 | 0.31 | 0.88 | 0.89 | 0.31 | 0.31 | 0.31 | |
| NSE | 0.66 | 0.04 | −11.06 | −11.02 | −11.01 | 0.64 | 0.64 | −11.02 | −11.11 | −11.11 | |
| CI | 0.58 | 0.02 | −3.41 | −3.41 | −3.41 | 0.56 | 0.57 | −3.41 | −3.43 | −3.43 | |
| Test | ANFIS1 | ANFIS2 | ANFIS3 | ANFIS4 | ANFIS5 | ANFIS6 | ANFIS7 | ANFIS8 | ANFIS9 | ANFIS10 | |
| RSQ | 0.12 | 0.15 | 0.21 | 0.73 | 0.70 | 0.64 | 0.67 | 0.72 | 0.69 | 0.66 | |
| RMSE | 155,453 | 155,740 | 155,021 | 31,265 | 33,984 | 36,654 | 35,367 | 32,951 | 33,508 | 35,003 | |
| MAE | 143,490 | 143,773 | 143,018 | 24,498 | 26,694 | 28,267 | 28,096 | 25,989 | 25,890 | 26,600 | |
| RAE | 2.85 | 2.85 | 2.83 | 0.49 | 0.53 | 0.56 | 0.56 | 0.51 | 0.51 | 0.53 | |
| d | 0.38 | 0.37 | 0.38 | 0.92 | 0.91 | 0.89 | 0.89 | 0.91 | 0.90 | 0.89 | |
| NSE | −5.67 | −5.69 | −5.60 | 0.73 | 0.68 | 0.63 | 0.66 | 0.70 | 0.69 | 0.66 | |
| CI | −2.13 | −2.13 | −2.11 | 0.67 | 0.62 | 0.56 | 0.59 | 0.64 | 0.62 | 0.59 | |
| ANFIS11 | ANFIS12 | ANFIS13 | ANFIS14 | ANFIS15 | ANFIS16 | ANFIS17 | ANFIS18 | ANFIS19 | ANFIS20 | ||
| RSQ | 0.68 | 0.15 | 0.51 | 0.42 | 0.31 | 0.68 | 0.69 | 0.45 | 0.39 | 0.37 | |
| RMSE | 34,307 | 59,395 | 154,896 | 154,929 | 154,933 | 34,157 | 33,456 | 154,793 | 155,475 | 155,535 | |
| MAE | 25,910 | 45,123 | 142,788 | 142,914 | 142,926 | 26,613 | 25,956 | 142,809 | 143,361 | 143,448 | |
| RAE | 0.51 | 0.89 | 2.82 | 2.83 | 2.83 | 0.53 | 0.51 | 2.82 | 2.83 | 2.83 | |
| d | 0.90 | 0.64 | 0.38 | 0.38 | 0.38 | 0.90 | 0.90 | 0.38 | 0.38 | 0.38 | |
| NSE | 0.68 | 0.03 | −5.56 | −5.60 | −5.60 | 0.68 | 0.69 | −5.55 | −5.61 | −5.61 | |
| CI | 0.61 | 0.02 | −2.10 | −2.11 | −2.11 | 0.61 | 0.62 | −2.10 | −2.11 | −2.11 |
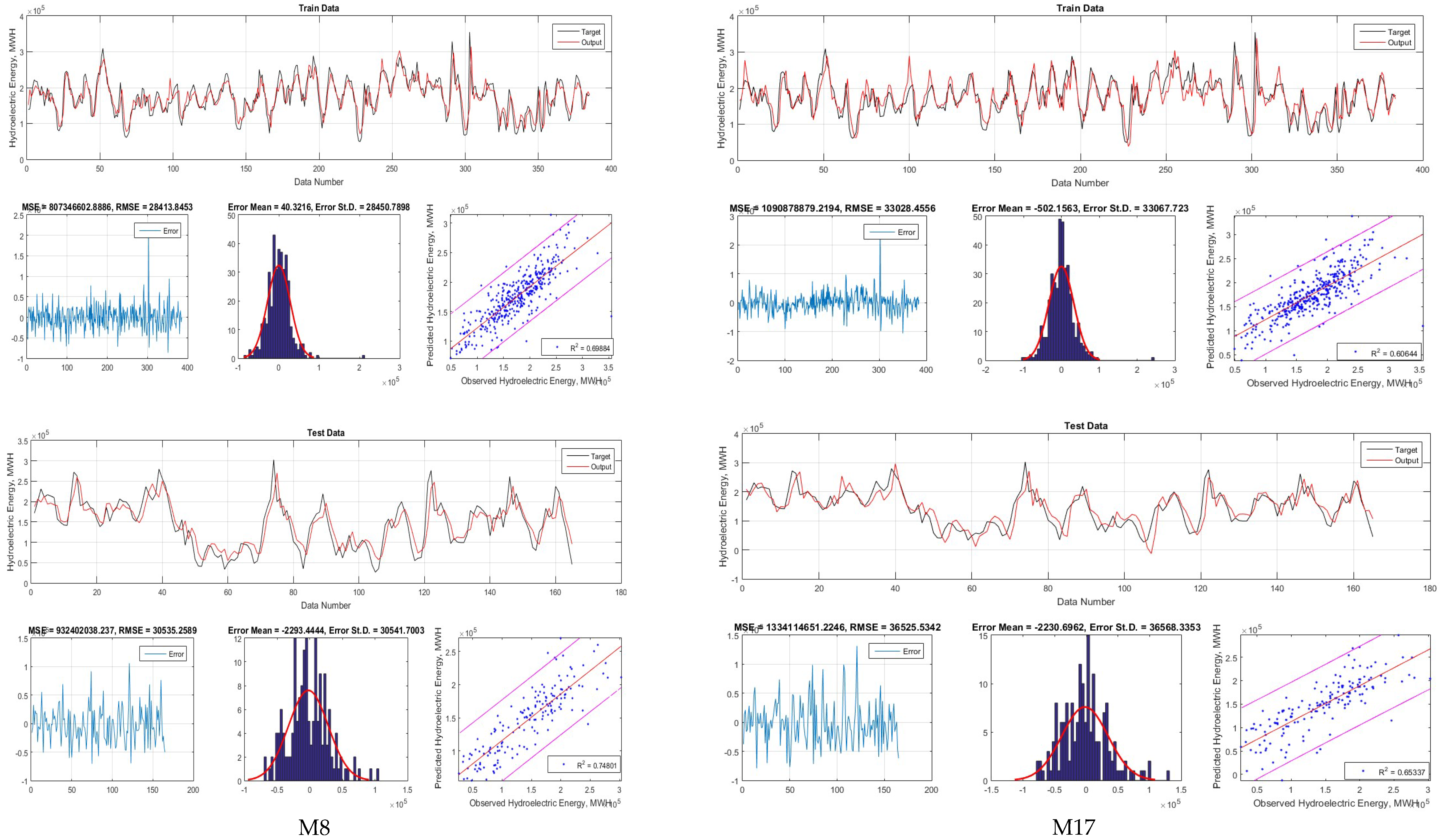
| Train | G-A1 | G-A2 | G-A3 | G-A4 | G-A5 | G-A6 | G-A7 | G-A8 | G-A9 | G-A10 | |
| RSQ | 0.09 | 0.31 | 0.28 | 0.73 | 0.63 | 0.63 | 0.65 | 0.70 | 0.72 | 0.65 | |
| RMSE | 49,503 | 42,889 | 43,809 | 26,857 | 31,477 | 32,559 | 30,770 | 28,414 | 27,482 | 31,016 | |
| MAE | 40,463 | 33,764 | 35,873 | 19,773 | 22,984 | 25,600 | 22,453 | 20,854 | 20,365 | 22,675 | |
| RAE | 0.97 | 0.81 | 0.86 | 0.47 | 0.55 | 0.61 | 0.54 | 0.50 | 0.49 | 0.54 | |
| d | 0.39 | 0.68 | 0.66 | 0.92 | 0.88 | 0.84 | 0.88 | 0.91 | 0.91 | 0.88 | |
| NSE | 0.09 | 0.31 | 0.28 | 0.73 | 0.63 | 0.60 | 0.65 | 0.70 | 0.72 | 0.65 | |
| CI | 0.03 | 0.21 | 0.19 | 0.67 | 0.55 | 0.51 | 0.57 | 0.63 | 0.65 | 0.57 | |
| G-A11 | G-A12 | G-A13 | G-A14 | G-A15 | G-A16 | G-A17 | G-A18 | G-A19 | G-A20 | ||
| RSQ | 0.64 | 0.18 | 0.48 | 0.42 | 0.33 | 0.68 | 0.61 | 0.32 | 0.41 | 0.37 | |
| RMSE | 31,073 | 47,263 | 37,224 | 39,510 | 42,411 | 29,521 | 33,028 | 42,668 | 39,952 | 41,037 | |
| MAE | 23,219 | 37,781 | 29,617 | 30,810 | 33,846 | 21,076 | 23,585 | 32,684 | 30,033 | 31,964 | |
| RAE | 0.55 | 0.90 | 0.71 | 0.74 | 0.81 | 0.50 | 0.56 | 0.78 | 0.72 | 0.76 | |
| d | 0.88 | 0.53 | 0.80 | 0.75 | 0.68 | 0.90 | 0.88 | 0.68 | 0.75 | 0.73 | |
| NSE | 0.64 | 0.18 | 0.48 | 0.42 | 0.33 | 0.68 | 0.59 | 0.32 | 0.41 | 0.37 | |
| CI | 0.57 | 0.09 | 0.39 | 0.32 | 0.22 | 0.61 | 0.52 | 0.22 | 0.30 | 0.27 | |
| Test | G-A1 | G-A2 | G-A3 | G-A4 | G-A5 | G-A6 | G-A7 | G-A8 | G-A9 | G-A10 | |
| RSQ | 0.11 | 0.21 | 0.26 | 0.79 | 0.69 | 0.71 | 0.70 | 0.75 | 0.76 | 0.70 | |
| RMSE | 62,420 | 58,695 | 56,473 | 28,402 | 34,128 | 40,849 | 34,151 | 30,535 | 29,928 | 34,293 | |
| MAE | 50,699 | 45,595 | 46,289 | 21,439 | 27,079 | 32,838 | 27,480 | 24,131 | 23,811 | 27,566 | |
| RAE | 1.01 | 0.90 | 0.92 | 0.42 | 0.54 | 0.65 | 0.54 | 0.48 | 0.47 | 0.55 | |
| d | 0.44 | 0.58 | 0.54 | 0.93 | 0.89 | 0.79 | 0.89 | 0.92 | 0.92 | 0.89 | |
| NSE | −0.07 | 0.05 | 0.12 | 0.78 | 0.68 | 0.54 | 0.68 | 0.74 | 0.75 | 0.68 | |
| CI | −0.03 | 0.03 | 0.07 | 0.72 | 0.61 | 0.43 | 0.61 | 0.68 | 0.69 | 0.60 | |
| G-A11 | G-A12 | G-A13 | G-A14 | G-A15 | G-A16 | G-A17 | G-A18 | G-A19 | G-A20 | ||
| RSQ | 0.69 | 0.13 | 0.51 | 0.48 | 0.35 | 0.73 | 0.65 | 0.35 | 0.45 | 0.43 | |
| RMSE | 33,816 | 59,590 | 47,204 | 49,583 | 54,710 | 31,377 | 36,526 | 54,756 | 48,849 | 52,456 | |
| MAE | 26,205 | 46,902 | 37,185 | 38,988 | 43,489 | 24,547 | 28,006 | 42,243 | 37,949 | 41,320 | |
| RAE | 0.52 | 0.93 | 0.73 | 0.77 | 0.86 | 0.49 | 0.55 | 0.83 | 0.75 | 0.82 | |
| d | 0.90 | 0.51 | 0.68 | 0.64 | 0.56 | 0.92 | 0.89 | 0.55 | 0.68 | 0.61 | |
| NSE | 0.69 | 0.02 | 0.39 | 0.32 | 0.18 | 0.73 | 0.63 | 0.18 | 0.35 | 0.25 | |
| CI | 0.61 | 0.01 | 0.27 | 0.21 | 0.10 | 0.67 | 0.57 | 0.10 | 0.24 | 0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.-w. Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System. Energies 2019, 12, 289. https://doi.org/10.3390/en12020289
Dehghani M, Riahi-Madvar H, Hooshyaripor F, Mosavi A, Shamshirband S, Zavadskas EK, Chau K-w. Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System. Energies. 2019; 12(2):289. https://doi.org/10.3390/en12020289
Chicago/Turabian StyleDehghani, Majid, Hossein Riahi-Madvar, Farhad Hooshyaripor, Amir Mosavi, Shahaboddin Shamshirband, Edmundas Kazimieras Zavadskas, and Kwok-wing Chau. 2019. "Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System" Energies 12, no. 2: 289. https://doi.org/10.3390/en12020289
APA StyleDehghani, M., Riahi-Madvar, H., Hooshyaripor, F., Mosavi, A., Shamshirband, S., Zavadskas, E. K., & Chau, K.-w. (2019). Prediction of Hydropower Generation Using Grey Wolf Optimization Adaptive Neuro-Fuzzy Inference System. Energies, 12(2), 289. https://doi.org/10.3390/en12020289








