Simulating Three-Dimensional Plume Migration of a Radionuclide Decay Chain through Groundwater
Abstract
1. Introduction
2. Mathematical Model
3. Results and Discussion
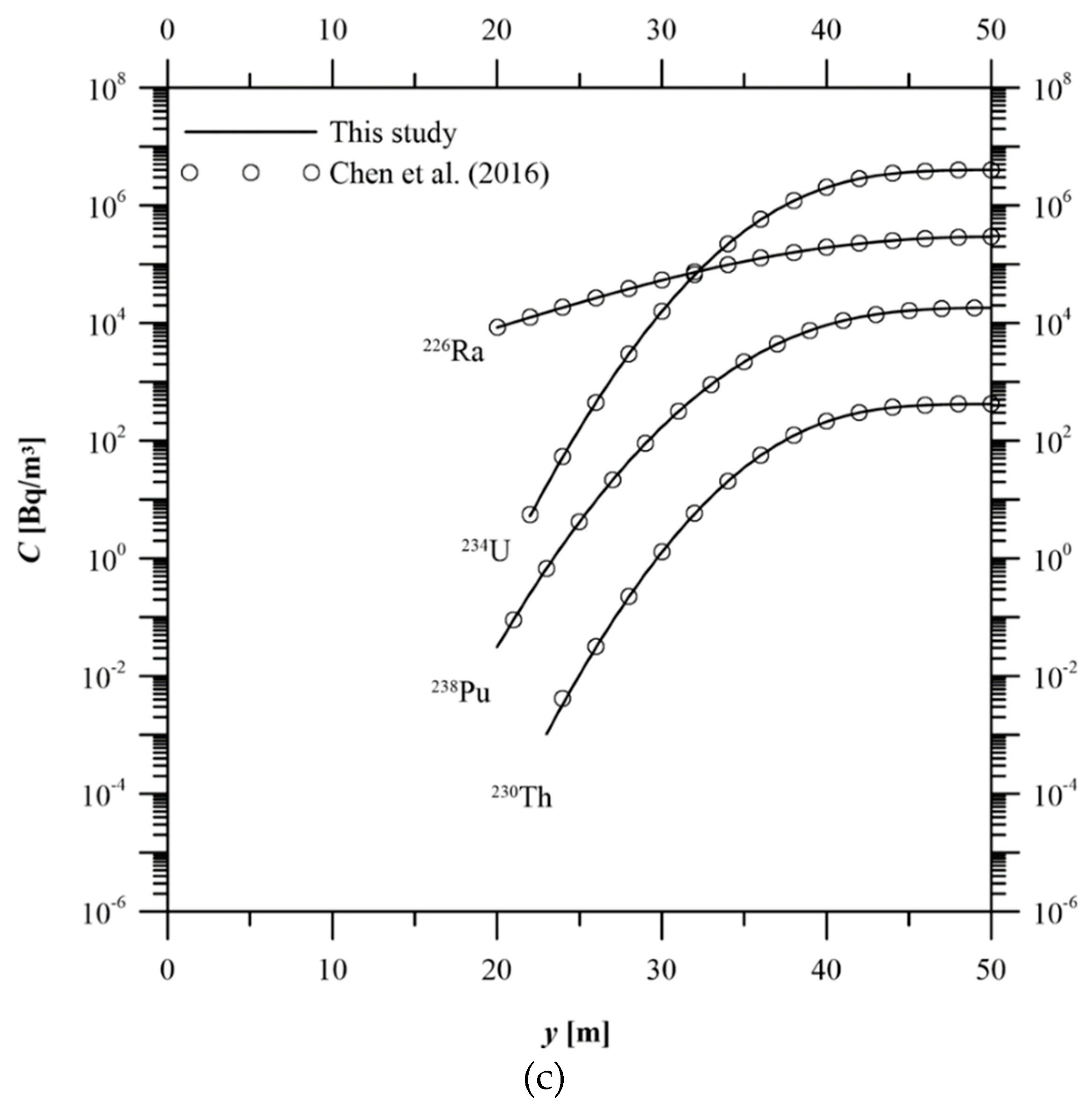
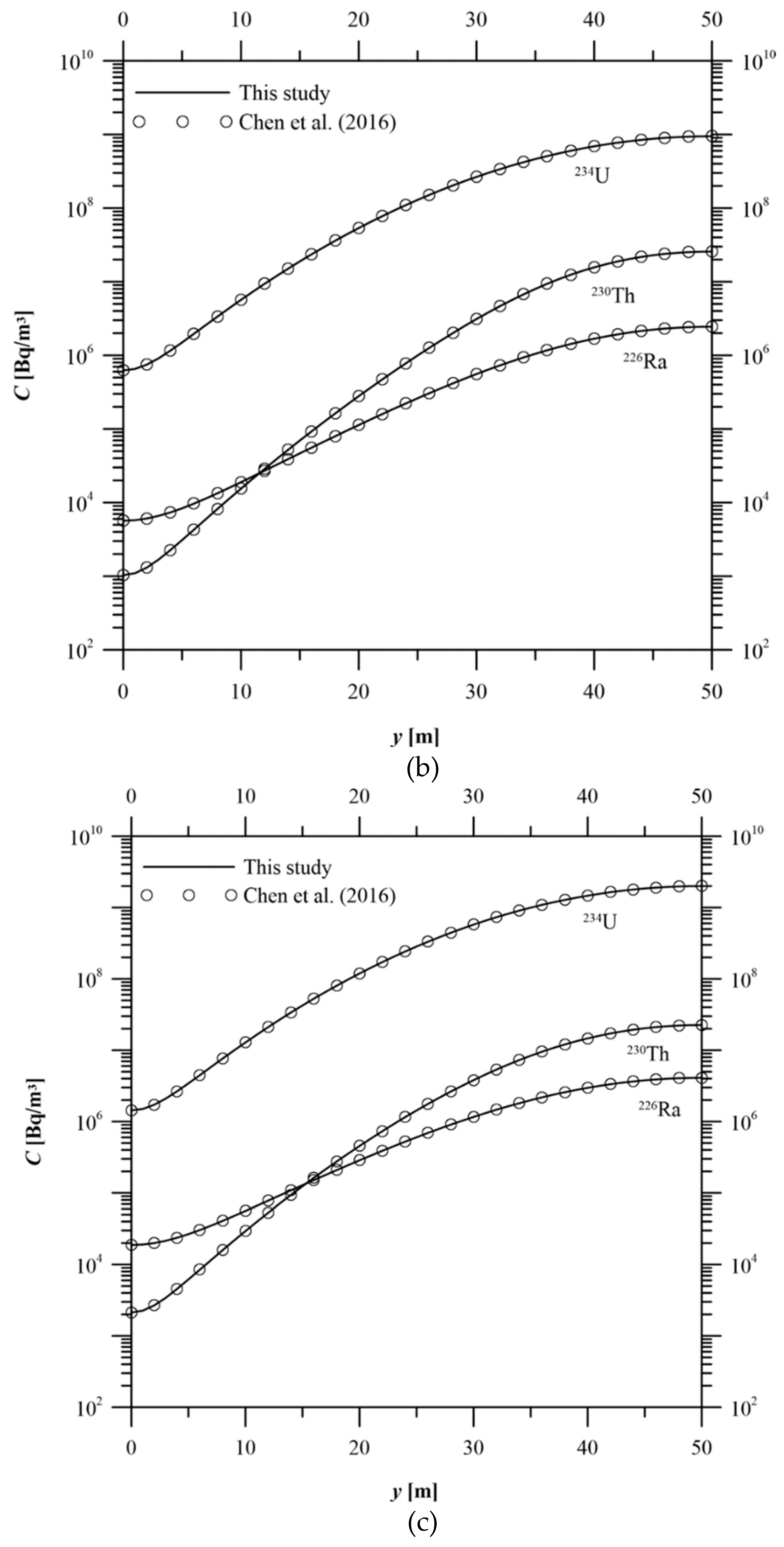
3.1. Verification of the Developed Analytical Solution
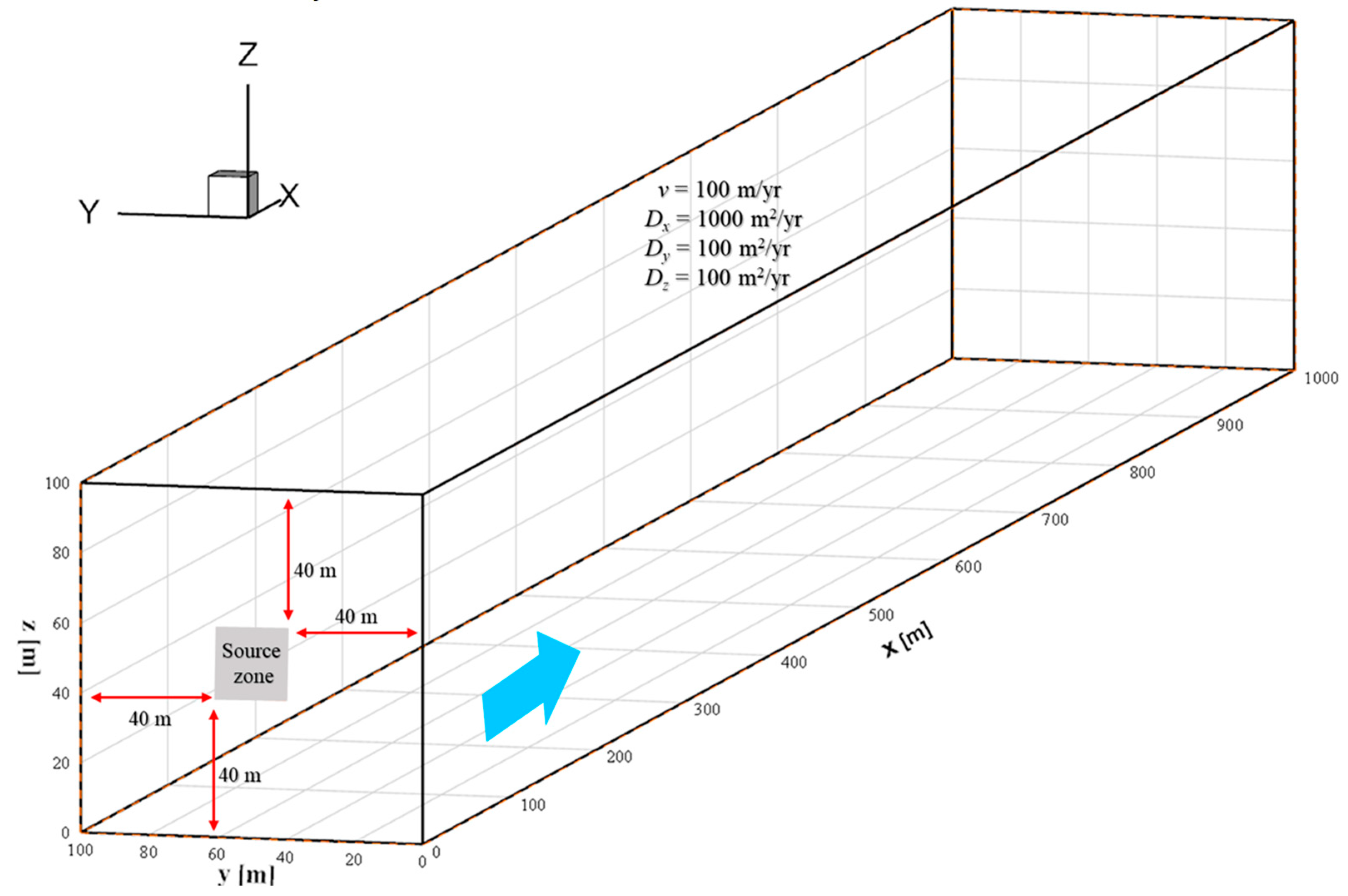
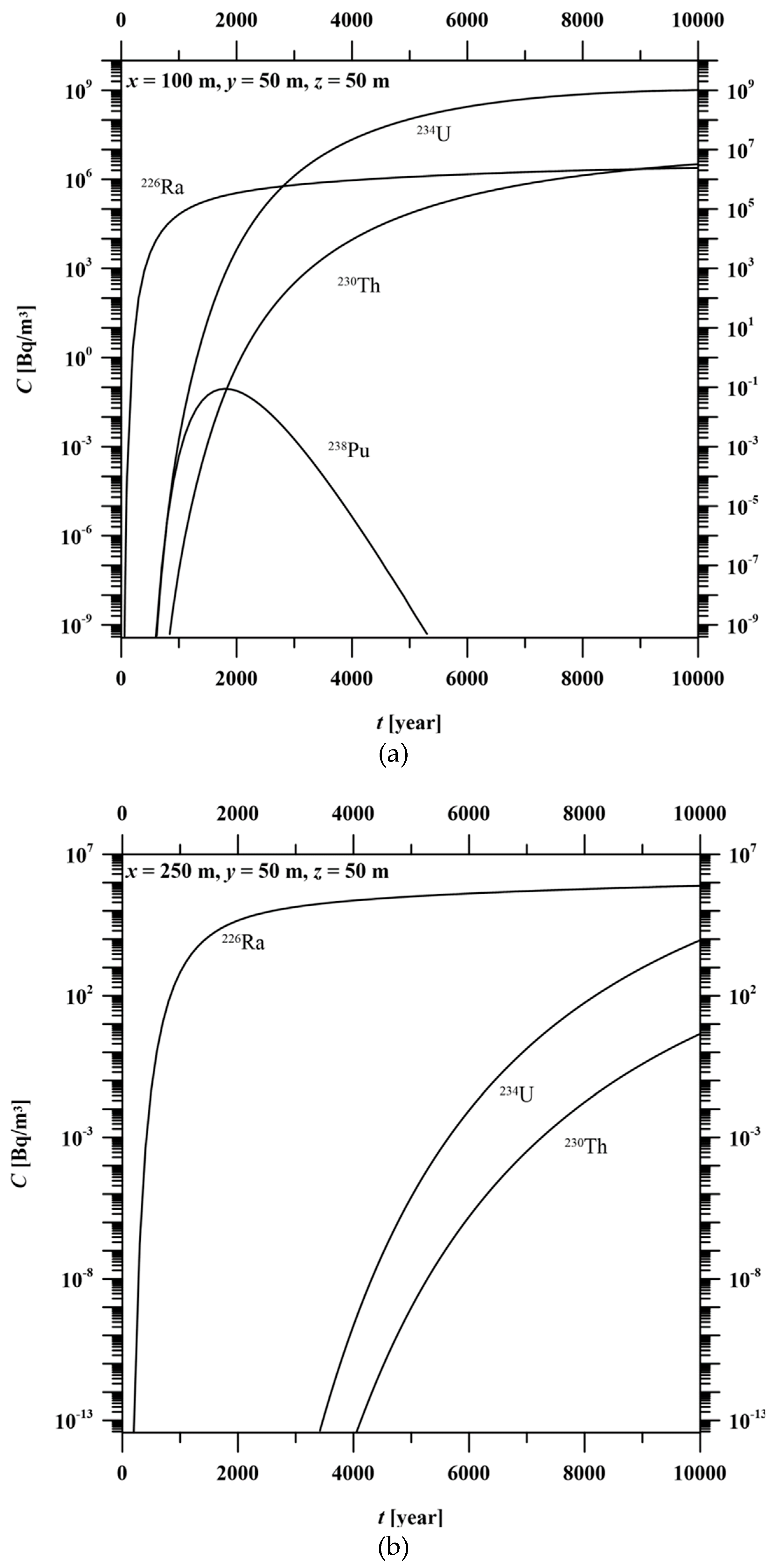
3.2. Application of the Analytical Model
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yeh, G.T. AT123D: Analytical Transient One-, Two-, and Three- Dimensional Simulation of Waste Transport in the Aquifer System, ORNL-5602; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1981. [Google Scholar]
- Van Genuchten, M.T.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation; Technical Bulletin No. 1661; US Department of Agriculture: Washington, DC, USA, 1982. [Google Scholar]
- Batu, V. A generalized two-dimensional analytical solution for hydrodynamic dispersion in bounded media with the first-type boundary condition at the source. Water Resour. Res. 1989, 25, 1125–1132. [Google Scholar] [CrossRef]
- Batu, V. A generalized two-dimensional analytical solute transport model in bounded media for flux-type finite multiple sources. Water Resour. Res. 1993, 29, 2881–2892. [Google Scholar] [CrossRef]
- Batu, V. A generalized three-dimensional analytical solute transport model for multiple rectangular first-type sources. J. Hydrol. 1996, 174, 57–82. [Google Scholar] [CrossRef]
- Leij, F.J.; Skaggs, T.H.; Van Genuchten, M.T. Analytical solution for solute transport in three-dimensional semi-infinite porous media. Water Resour. Res. 1991, 27, 2719–2733. [Google Scholar] [CrossRef]
- Leij, F.J.; Toride, N.; van Genuchten, M.T. Analytical solutions for non-equilibrium solute transport in three-dimensional porous media. J. Hydrol. 1993, 151, 193–228. [Google Scholar] [CrossRef]
- Park, E.; Zhan, H. Analytical solutions of contaminant transport from finite one-, two, three-dimensional sources in a finite thickness aquifer. J. Contam. Hydrol. 2001, 53, 41–61. [Google Scholar] [CrossRef]
- Chen, J.S.; Liu, C.W.; Liao, C.M. A novel analytical power series solution for solute transport in a radially convergent flow field. J. Hydrol. 2002, 266, 120–138. [Google Scholar] [CrossRef]
- Chen, J.S.; Ni, C.F.; Liang, C.P.; Chiang, C.C. Analytical power series solution for contaminant transport with hyperbolic asymptotic distance-dependent dispersivity. J. Hydrol. 2008, 362, 142–149. [Google Scholar] [CrossRef]
- Chen, J.S.; Ni, C.F.; Liang, C.P. Analytical power series solutions to the two-dimensional advection-dispersion equation with distance-dependent dispersivities. Hydrol. Process. 2008, 22, 4670–4678. [Google Scholar] [CrossRef]
- Chen, J.S.; Chen, J.T.; Liu, C.W.; Liang, C.P.; Lin, C.M. Analytical solutions to two-dimensional advection–dispersion equation in cylindrical coordinates in finite domain subject to first- and third-type inlet boundary conditions. J. Hydrol. 2011, 405, 522–531. [Google Scholar] [CrossRef]
- Chen, J.S.; Liu, Y.H.; Liang, C.P.; Liu, C.W.; Lin, C.W. Exact analytical solutions for two-dimensional advection-dispersion equation in cylindrical coordinates subject to third-type inlet boundary condition. Adv. Water Resour. 2011, 34, 365–374. [Google Scholar] [CrossRef]
- Chen, J.S.; Hsu, S.Y.; Li, M.H.; Liu, C.W. Assessing the performance of a permeable reactive barrier-aquifer system using a dual-domain solute transport model. J. Hydrol. 2016, 543, 849–860. [Google Scholar] [CrossRef]
- Chen, J.S.; Li, L.Y.; Lai, K.H.; Liang, C.P. Analytical model for advective-dispersive transport involving flexible boundary inputs, initial distributions and zero-order productions. J. Hydrol. 2017, 554, 187–199. [Google Scholar] [CrossRef]
- Zhan, H.; Wen, Z.; Gao, G. An analytical solution of two-dimensional reactive solute transport in an aquifer-aquitard system. Water Resour. Res. 2009, 45, W10501. [Google Scholar] [CrossRef]
- Pérez Guerrero, J.S.; Skaggs, T.H.; van Genuchten, M.T. Analytical solution for multi-species contaminant transport in finite media with time-varying boundary condition. Transp. Porous Med. 2010, 85, 171–188. [Google Scholar] [CrossRef]
- Gao, G.; Zhan, H.; Feng, S.; Fu, B.; Ma, Y.; Huang, G. A new mobile-immobile model for reactive solute transport with scale-dependent dispersion. Water Resour. Res. 2010, 46, W08533. [Google Scholar] [CrossRef]
- Gao, G.; Zhan, H.; Feng, S.; Huang, G.; Fu, B. A mobile-immobile model with an asymptotic scale-dependent dispersion function. J. Hydrol. 2012, 424, 172–183. [Google Scholar] [CrossRef]
- Gao, G.; Fu, B.; Zhan, H.; Ma, Y. Contaminant transport in soil with depth-dependent reaction coefficients and time-dependent boundary conditions. Water Res. 2013, 47, 2507–2522. [Google Scholar] [CrossRef]
- Chen, J.S.; Liu, C.W. Generalized analytical solution for advection-dispersion equation in finite spatial domain with arbitrary time-dependent inlet boundary condition. Hydrol. Earth Syst. Sci. 2011, 15, 2471–2479. [Google Scholar] [CrossRef]
- Pérez Guerrero, J.S.; Pontedeiro, E.M.; van Genuchten, M.T.; Skaggs, T.H. Analytical solutions of the one-dimensional advection–dispersion solute transport equation subject to time-dependent boundary conditions. Chem. Eng. J. 2013, 221, 487–491. [Google Scholar] [CrossRef]
- Liang, C.P.; Hsu, S.Y.; Chen, J.S. An analytical model for solute transport in an infiltration tracer test in soil with a shallow groundwater table. J. Hydrol. 2016, 540, 129–141. [Google Scholar] [CrossRef]
- Nair, R.N.; Sunny, F.; Manikandan, S.T. Modelling of decay chain transport in groundwater from uranium tailings ponds. Appl. Math. Model. 2010, 34, 2300–2311. [Google Scholar] [CrossRef]
- Cho, C.M. Convective transport of ammonium with nitrification in soil. Can. J. Soil Sci. 1971, 51, 339–350. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. Convective–dispersive transport of solutes involved in sequential first-order decay reactions. Comput. Geosci. 1985, 11, 129–147. [Google Scholar] [CrossRef]
- Lunn, M.; Lunn, R.J.; Mackay, R. Determining analytic solution of multiple species contaminant transport with sorption and decay. J. Hydrol. 1996, 180, 195–210. [Google Scholar] [CrossRef]
- Sun, Y.; Clement, T.P. A decomposition method for solving coupled multi-species reactive transport problems. Transp. Porous Med. 1999, 37, 327–346. [Google Scholar] [CrossRef]
- Sun, Y.; Peterson, J.N.; Clement, T.P. A new analytical solution for multiple species reactive transport in multiple dimensions. J. Contam. Hydrol. 1999, 35, 429–440. [Google Scholar] [CrossRef]
- Sun, Y.; Petersen, J.N.; Clement, T.P.; Skeen, R.S. Development of analytical solutions for multi-species transport with serial and parallel reactions. Water Resour. Res. 1999, 35, 185–190. [Google Scholar] [CrossRef]
- Srinivasan, V.; Clememt, T.P. Analytical solutions for sequentially coupled one-dimensional reactive transport problems-Part I: Mathematical derivations. Adv. Water Res. 2008, 31, 203–218. [Google Scholar] [CrossRef]
- Srinivasan, V.; Clement, T.P. Analytical solutions for sequentially coupled one-dimensional reactive transport problems-Part II: Special cases, implementation and testing. Adv. Water Res. 31, 219–232. [CrossRef]
- Pérez Guerrero, J.S.; Skaggs, T.H.; van Genuchten, M.T. Analytical solution for multi-species contaminant transport subject to sequential first-order decay reactions in finite media. Transp. Porous Med. 2009, 80, 373–387. [Google Scholar] [CrossRef]
- Chen, J.S.; Lai, K.H.; Liu, C.W.; Ni, C.F. A novel method for analytically solving multi-species advective-dispersive transport equations sequentially coupled with first-order decay reactions. J. Hydrol. 2012, 420, 191–204. [Google Scholar] [CrossRef]
- Chen, J.S.; Liu, C.W.; Liang, C.P.; Lai, K.H. Generalized analytical solutions to sequentially coupled multi-species advective-dispersive transport equations in a finite domain subject to an arbitrary time-dependent source boundary condition. J. Hydrol. 2012, 456–457, 101–109. [Google Scholar] [CrossRef]
- Bauer, P.; Attinger, S.; Kinzelbach, W. Transport of a decay chain in homogeneous porous media: Analytical solutions. J. Contam. Hydrol. 2001, 49, 217–239. [Google Scholar] [CrossRef]
- Montas, H.J. An analytical solution of the three-component transport equation with application to third-order transport. Water Resour. Res. 2003, 39, 1036. [Google Scholar] [CrossRef]
- Quezada, C.R.; Clement, T.P.; Lee, K.K. Generalized solution to multi-dimensional multi-species transport equations coupled with a first-order reaction network involving distinct retardation factors. Adv. Water Res. 2004, 27, 507–520. [Google Scholar] [CrossRef]
- Sudicky, E.A.; Hwang, H.T.; Illman, W.A.; Wu, Y.S. A semi-analytical solution for simulating contaminant transport subject to chain-decay reactions. J. Contam. Hydrol. 2013, 144, 20–45. [Google Scholar] [CrossRef]
- Kreft, A.; Zuber, A. Comment on “Flux averaged and volume averaged concentrations in continuum approaches to solute transport”. Water Resour. Res. 1986, 22, 1157–1158. [Google Scholar] [CrossRef]
- Parker, J.C.; van Genuchten, M.T. Flux-averaged and volume-averaged concentrations in continuum approaches to solute transport. Water Resour. Res. 1984, 20, 866–872. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Parker, J.C. Boundary conditions for displacement experiments through short laboratory soil columns. Soil Sci. Soc. Am. J. 1984, 48, 703–708. [Google Scholar] [CrossRef]
- Parlange, J.Y.; Barry, D.A.; Starr, J.L. Comments on “Boundary conditions for displacement experiments through short laboratory soil columns”. Soil Sci. Soc. Am. J. 1985, 49, 1325. [Google Scholar] [CrossRef]
- Chen, J.S.; Liang, C.P.; Liu, C.W.; Li, L.Y. An analytical model for simulating two-dimensional multispecies plume migration. Hydrol. Earth Sys. Sci. 2016, 20, 733–753. [Google Scholar] [CrossRef]
- Huang, J.; Goltz, M.N. Solutions to equations incorporating the effect of rate-limited contaminant mass transfer on vadose zone remediation by soil vapor extraction. Water Resour. Res. 1999, 35, 879–883. [Google Scholar] [CrossRef]
- Lai, K.H.; Liu, C.W.; Liang, C.P.; Chen, J.S.; Sie, B.R. A novel method for analytically solving a radial advection-dispersion equation. J. Hydrol. 2016, 542, 532–540. [Google Scholar] [CrossRef]
- Chen, J.S.; Ho, Y.C.; Liang, C.P.; Wang, S.W.; Liu, C.W. Semi-analytical model for coupled multispecies advective-dispersive transport subject to rate-limited sorption. J. Hydrol. 2019, 579, 124–164. [Google Scholar] [CrossRef]
- Sneddon, I.H. The Use of Integral Transforms; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- De Hoog, F.R.; Knight, J.H.; Stokes, A.N. An improved method for numerical inversion of Laplace transforms. SIAM J. Sci. Stat. Comput. 1982, 3, 357–366. [Google Scholar] [CrossRef]
- Chen, J.S.; Chen, C.S.; Chen, C.Y. Analysis of solute transport in a divergent flow tracer test with scale-dependent dispersion. Hydrol. Process. 2007, 21, 2526–2536. [Google Scholar] [CrossRef]
- Higashi, K.; Pigford, T. Analytical models for migration of radionuclides in geological sorbing media. J. Nucl. Sci. Technol. 1980, 17, 700–709. [Google Scholar] [CrossRef]
- ICRP. Compendium of Dose Coefficients based on ICRP Publication 60; ICRP Publication: Ottawa, ON, Canada, 2012. [Google Scholar]







| Parameter | Unit | Value |
|---|---|---|
| Domain length, | m | 250 |
| Domain width, | m | 100 |
| Domain height, | m | 100 |
| Groundwater velocity, | m/year | 100 |
| Dispersion coefficient, Dx | m2/year | 1000 |
| Dispersion coefficient, Dy | m2/year | 100 |
| Dispersion coefficient, Dz | m2/year | 100 |
| Retardation factor, Ri | ||
| 238Pu | 10,000 | |
| 234U | 14,000 | |
| 230Th | 50,000 | |
| 226Ra | 500 | |
| Radioactive decay constant, λi | ||
| 238Pu | year−1 | 0.0079 |
| 234U | year−1 | 0.0000028 |
| 230Th | year−1 | 0.0000087 |
| 226Ra | year−1 | 0.00043 |
| Initial amount of nuclide, | ||
| 238Pu | Bq/m2 | 1.5×1015 |
| 234U | 0 | |
| 230Th | 0 | |
| 226Ra | 0 | |
| Proportionality constant, γi | ||
| 238Pu | year−1 | 0.001 |
| 234U | year−1 | 0.001 |
| 230Th | year−1 | 0.001 |
| 226Ra | year−1 | 0.001 |
| Ingestion dose coefficient, DFi | ||
| 238Pu | Sv/Bq | 2.3 × 10−7 |
| 234U | Sv/Bq | 4.9 × 10−8 |
| 230Th | Sv/Bq | 2.1 × 10−7 |
| 226Ra | Sv/Bq | 2.8 × 10−7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-S.; Liang, C.-P.; Chang, C.-H.; Wan, M.-H. Simulating Three-Dimensional Plume Migration of a Radionuclide Decay Chain through Groundwater. Energies 2019, 12, 3740. https://doi.org/10.3390/en12193740
Chen J-S, Liang C-P, Chang C-H, Wan M-H. Simulating Three-Dimensional Plume Migration of a Radionuclide Decay Chain through Groundwater. Energies. 2019; 12(19):3740. https://doi.org/10.3390/en12193740
Chicago/Turabian StyleChen, Jui-Sheng, Ching-Ping Liang, Cheng-Hung Chang, and Ming-Hsien Wan. 2019. "Simulating Three-Dimensional Plume Migration of a Radionuclide Decay Chain through Groundwater" Energies 12, no. 19: 3740. https://doi.org/10.3390/en12193740
APA StyleChen, J.-S., Liang, C.-P., Chang, C.-H., & Wan, M.-H. (2019). Simulating Three-Dimensional Plume Migration of a Radionuclide Decay Chain through Groundwater. Energies, 12(19), 3740. https://doi.org/10.3390/en12193740





