Research and Application of a Novel Hybrid Model Based on a Deep Neural Network Combined with Fuzzy Time Series for Energy Forecasting

Abstract

In recent years, although deep learning algorithms have been widely applied to various fields, ranging from translation to time series forecasting, researchers paid limited attention to modelling parameter optimization and the combination of the fuzzy time series. In this paper, a novel hybrid forecasting system, named CFML (complementary ensemble empirical mode decomposition (CEEMD)-fuzzy time series (FTS)-multi-objective grey wolf optimizer (MOGWO)-long short-term memory (LSTM)), is proposed and tested. This model is based on the LSTM model with parameters optimized by MOGWO, before which a fuzzy time series method involving the LEM2 (learning from examples module version two) algorithm is adopted to generate the final input data of the optimized LSTM model. In addition, the CEEMD algorithm is also used to de-noise and decompose the raw data. The CFML model successfully overcomes the nonstationary and irregular features of wind speed data and electrical power load series. Several experimental results covering four wind speed datasets and two electrical power load datasets indicate that our hybrid forecasting system achieves average improvements of 49% and 70% in wind speed and electrical power load, respectively, under the metric MAPE (mean absolute percentage error).

1. Introduction

Effective forecasting plays an essential role in various aspects, such as energy application, economic risk management, standardized management, policy making, and so on. Forecasting helps corporations, governments, and other organizations and institutions to evaluate the market and to make relative predictions to better understand potential relations among entities and to plan for the future, which is a useful way to make policies on both the private and the social levels. As a result, many forecasting methods have been proposed during the past decades. Among these, there are two different categories: time series forecasting and causal forecasting. Since causal forecasting has some inherent limitations, including the reliability and availability of independent variables, time series forecasting has been applied much more widely due to its convenience for data collection and its high accuracy as well as stability. Time series forecasting methods presume that history will repeat itself, which means that the forecasting of future values is based on present values and past observations. Nowadays, time series forecasting has achieved great success in many industries, especially in the energy industry.

With the rapid development of the energy industry and increasing demand for high-level management and application, its infrastructure has been upgraded by a great extent, as a result of which the prices, supply, as well as demand have oscillated to a greater extent and have become more unpredictable than ever before. This has posed a great challenge to the forecasting method in terms of accuracy and stability, since forecasting plays an essential role in qualifying those unfortune features by which people are able to gain more accurate forecasts that can be applied to risk management, energy planning, industry configuration, and so on. In previous years, electrical power load forecasting has been an important part of power system planning and the basis of the economic operation of power systems. Unfortunately, we have to confront several difficulties, such as meteorological factors, development speed, and some cases of unpredictable natural devastation, if we want to take good advantage of power load data. Researchers have focused on exploring nonsymmetrical faults [1], ground faults [2], microgrid distributions [3], etc. For instance, Qu et al. [4] explored and developed an intelligent damping controller which can reduce power fluctuations in hybrid power systems. Ye et al. [5] studied long-term load forecasting based on support vector regression (SVR) and explored nonlinear relationships between economic growth in terms of GDP and power load requirements. On the other hand, with the inadequate implementation of corresponding emission and environmental protection policies [6], wind power has attracted many scientists and researchers [7]. Currently, wind power accounts for roughly 10% of the total consumption of energy in Europe—15% more than that of Spain and Germany [8]. To utilize the wind more effectively and efficiently, we need to get accurate forecasts of the wind speed. Nevertheless, as for wind speed, it has an inherently volatile and irregular quality and is considered a fairly tricky weather element to predict accurately as a result of its randomness and nonlinearity [9]. Numerous researchers and scientists have made great contributions to the development of effective and robust wind speed forecasting models, which can also be used to forecast electrical power load data. According to time horizons, there are four different types of forecasting methods: long-range forecasting, medium-range forecasting, short-time-period forecasting, and very-short-term forecasting. Moreover, it can also be divided into the following four types: artificial intelligence methods, statistical methods, spatial correlation methods, and physical methods [10].

Physical models containing parameters ranging from temperature to topography to pressure are usually used on a massive scale for long-term wind speed prediction with multiple weather parameters [11]. On the contrary, statistical models, such as the autoregressive (AR) model, Auto-Regressive Average (ARMA) [12], Autoregressive Integrated Moving Average (ARIMA) [13], fractional ARIMA (FARIMA) [14], exponential smoothing (ES) [15], and grey prediction (GP) [16], are developed on the basis of the relationships among variables through mathematical statistics to illustrate the potential correlations within the historical data sampled from the observed wind speed data. Spatial correlation methods mainly take into account the other factors, such as the direction of the wind, the terrain roughness, and the height above the horizon. Sometimes, this kind of method achieves high accuracy [17].

With the rapid development of and increasing research on computer science, the performance of complex calculations in less time has become possible. Consequently, in the past few years, a large number of statistical learning models have been recorded, which eventually formed a mature theoretical system. The renowned ANN (artificial neurol network) is widely utilized for wind speed forecasting fields, which have the ability to carry on the parallel processing and to deliver nonlinear maps. This mainly includes back propagation (BP) [18], the radial basis function (RBF) [19], the Elman neural network (ENN) [20], the wavelet neural network (WNN) [21,22], and others. In addition, during the past twenty years, the neural network field has experienced some innovations which have resulted in well-known deep learning (DL) models [23]. Particularly, the large computational cost has been the largest drawback of conventional neural network algorithms. However, greedy layer-wise pretraining is able to train the so-called deep belief network (DBN) more efficiently [24,25]. Following pertinent progresses, scientists are now able to create and train neural networks with not only one hidden layer, which, in turn, has increased generalization capabilities and allowed better outcomes. This field has also been renamed “in-depth learning” to assess the depth of progress made [26]. The success of DL models can be seen in computer science applications, such as image recognition [27], speech recognition [28], and machine translation [29]. Moreover, the benefits have also spread to energy-related fields, such as wind power forecasting, which especially refers to wind speed forecasting. In the same field, Wang et al. [30] proposed the convolutional neural networks (CNNs) to acquire precise probability prediction of wind power. However, there is still relatively less research about the DL-related models being applied in wind speed forecasting fields compared with the most active part of this technology. In Reference [31], a deep autoencoder (DAC) combined with extreme gradient boosting (XGB) was proposed to forecast the building cooling load; A deep neural network (DNN) was also applied to get the forecasting results; this method was more accurate than the other methods presented in the same paper. In Reference [32], the DL model was also shown to discern the islanding highly accurately. Therefore, regarding this point, we considered the application of these kinds of technologies in wind speed forecasting in an effort to get a higher accuracy. Furthermore, the authors of Reference [33] proposed a DL strategy applied to time series forecasting and demonstrated how it can be successfully used in electricity consumption forecasting, which correlates with the wind speed data to some extent. Except for ANNs, fuzzy logic methods [34] as well as support vector machine (SVM) [35]-related methods, such as least-squares support vector machines (LSSVMs) [36], Gaussian processes [37], and others, are also commonly applied in the forecasting of wind speed.

However, each method has different drawbacks and disadvantages as a result of its inherent nature. The drawbacks of the aforementioned models are summarized as follows:

(1)

Because physical algorithms are very sensitive to market information, they need a long run time and a large amount of computing resources. In addition, these models have shortcomings in dealing with short-term forecasting problems and they do not have high accuracy and validity in short-term forecasting.

(2)

Traditional statistical arithmetic methods fail to manage forecasting with fluctuations and high levels of noise, nonlinear and irregular trends, or other inherent characteristics of wind speed data that are primarily confined by the premise of a linear pattern along a time series. Moreover, oftentimes, these methods require a large amount of historical data on which they deeply depend in realistic cases. This means that once there is an abrupt and unexpected change in the original data as a result of social or environmental factors, prediction errors will proliferate all at once [38].

(3)

Spatial correlation arithmetic methods based on vast quantities of information, for example, the wind speed information of many spatially correlated sites which is difficult to collect and analyze, makes it hard to perform perfect wind speed forecasting [39].

(4)

Artificial intelligence arithmetic methods, different from other approaches, are able to deal with nonlinear features which are hidden among historical wind speed data. Although many studies have been carried out and the methods have been successfully applied to address complex data patterns, there are also some defects and drawbacks within artificial intelligence methods, such as showing a relatively low convergence rate and over-fitting, easily getting into a local optimum, etc.

(5)

Individual forecasting models are good at forecasting to some extent, but they rarely focus on the importance and necessity of data preprocessing; therefore, these approaches cannot always get a good forecasting outcome.

Hence, with the objective of combining all the advantages and of avoiding the weaknesses, a number of combined forecasting methods have been proposed [40]. Bates and Granger proposed the combination prediction theory and showed promising outcomes in 1969 [41]. Since then, research on combinatorial forecasting theory has attracted extensive attention [42]. Xiao et al. developed two combined models for wind speed sequence prediction: the AI combination model [43,44,45] and NNCT (no negative constraint theory). The results indicate that more reliable and accurate forecasts are attained when the combined models are applied.

In addition, with the purpose of achieving highly accurate forecasting, some types of time series preprocessing techniques, such as wavelet packet decomposition (WPD) [46], fast ensemble empirical mode decomposition (FEEMD) [47], and singular spectrum analysis (SSA) [48] techniques, have been effectively applied in the data preprocessing stages of time series forecasting fields in an effort to decrease the random disturbance traits of the original windspeed data. Similarly, techniques have been widely used in such hybrid models to get a higher forecasting accuracy. Thus, the complementary ensemble empirical mode decomposition (CEEMD) that is modified from the ensemble empirical mode decomposition (EEMD) is applied in this paper.

Thus, in this study, the CEEMD-FTS (fuzzy time series)-MOGWO (multi-objective grey wolf optimizer)-long short-term memory (LSTM), a combined model with CEEMD as the preprocessing part, is based on LSTM, which belongs to the RNNs (recurrent neurol networks) within the DL field, but a modified version with less disadvantages and more powerful memorizing capability and the meritorious multi-objective optimization algorithm MOGWO is developed. Subsequently, to deal with the uncertain forecasting problems and to dig out more useful and constructive information hidden within the history data to get a better forecasting result, we also combine the aforementioned model with the fuzzy time series analyzing method based on rough set rule induction which contains the LEM2 (learning from examples module version two).

Generally, the innovations of this study can be summarized as follows:

(1).

This study proposes a hybrid forecasting model which can take advantage of deep learning networks as well as the fuzzy time analysis technique based on the LEM2 rule-generating algorithm, which increases the forecasting accuracy obviously. To our knowledge, it has not been found that deep leaning neural networks are combined with the rough set induction theory. Hence, our study develops a hybrid model combining LSTM with the fuzzy time series analysis technique that uses rough sets to generate rules as a replacement for traditional rule-generating methods.

(2).

This study improves the forecasting stability and accuracy simultaneously with the deep learning neural network through the weight-determining method called MOGWO based on the leave-one-out strategy and swarm intelligence, which helps to find best weighting parameters for the LSTM neural network. Most previous studies just paid attention to one aim (stability or accuracy). Therefore, to achieve high accuracy and stability, a multi-objective optimization algorithm, MOGWO, is successfully applied in this study.

(3).

This study provides a scientific and reasonable evaluation of the new hybrid forecasting model made to verify the forecasting performance of the combined forecasting model proposed in this paper. Three experiments are carried out in this paper, including comparisons between different deep learning neutral networks, efficiency and effectiveness tests among various models in four different wind sites, and a contrast experiment in which the proposed hybrid forecasting system is applied to electrical load forecasting with two different electrical power load data series on Wednesday and Sunday. The outcome illustrates that this proposed system performs well.

(4).

This study delivers an insightful discussion about the developed forecasting system, illustrating the improvements brought about by different parts of the proposed forecasting model as well as the multistep forecasting ability. Five discussion topics are presented in this paper, namely statistical significance, association strength, improvement percentage, multistep ahead forecasting, and sensitivity analysis. Through these discussions, the effectiveness of the hybrid forecasting framework is verified.

The remainder of this paper is organized as follows:

Section 2 gives the profile of principles of methods corresponding to the proposed hybrid models, namely the CFML model (CEEMD-FTS-MOGWO-LSTM). Relevant methodology is shown Also, in this section, including the data preprocessing method, the fuzzy time series technique with LEM2, the MOGWO, and the long short-term memory algorithm. Moreover, several evaluations and experiments that help to demonstrate the performance of the CFML model are presented in Section 3. Moreover, Section 4 gives a discussion about different comparison outcomes. Finally, Section 5 concludes this study.

2. Methodology

An innovative hybrid forecasting model is successfully developed and the corresponding components are introduced briefly in this section, including the data preprocessing technique named complementary ensemble empirical mode decomposition (CEEMD), the fuzzy analyzing part based on rough sets induction theory, the forecasting algorithm named LSTM, and the multi-objective optimization algorithm MOGWO.

2.1. Hybrid Forecasting Framework

Figure 1 and Figure 2 shows combined the CFML forecasting model, from which the CFML system can be expounded as follows:

Figure 1. Explicit processes of data input and complementary ensemble empirical mode decomposition (CEEMD) parts of the CEEMD-fuzzy time series (FTS) multi-objective grey wolf optimizer (MOGWO)-LSTM (CFML) model.

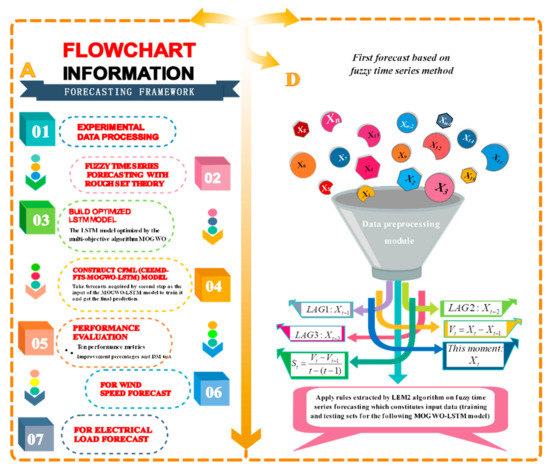
Figure 2. Flowchart of the paper and the input data of the first forecasting.

• The original wind speed data is decomposed by applying the CEEMD method into several subseries named Intrinsic Mode Functions (IMFs).
• The fuzzy analysis method is applied using the rough set induction LEM2 algorithm to generate the forecasting rules, and raw data are applied to these rules to generate preliminary forecasts. These forecasts obtained by fuzzy time series forecasting are not precise enough, but the difference between these forecasts and the actual values can demonstrate potential forecasting biases that are useful for modifying the learning process of the following neural network, namely the LSTM model optimized with MOGWO. As for the raw input data, we accept five dimensions for each forecast, including lag1, lag2, lag3, slope, and the present data, in order to forecast the following one for each subseries (Figure 2).
• The output data generated from the previous steps is used as the input data for the LSTM forecasting module, which is optimized by the multi-objective optimization algorithm called MOGWO for each subseries. Specifically, real values of $X_t$ lag1, and lag2 and their differences, including D1, D2, and D3, are adopted as input data of the LSTM model modified by MOGWO (Table 1).
  Table 1. The selected input variables for long short-term memory (LSTM).

  Factors	Explanation
  $X_t$	The present value
  LAG1	first-order lagged period $X_{t-1}$
  LAG2	second-order lagged period $X_{t-2}$
  D1	difference 1: $D_t=X_t-forecasted X_t$
  D2	difference 2: $D_{t-1}=X_{t-1}-forecasted X_{t-1}$
  D2	difference 3: $D_{t-2}=X_{t-2}-forecasted X_{t-2}$

• The forecasting outcomes of each subseries generated from the preprocessing part named CEEMD are aggregated to obtain the eventual forecasting results of CFML.

2.2. Data Preprocessing Module

The CEEMD algorithm, proposed by Yeh et al. [49], is the modified version of the EEMD and EMD. According to Anbazhagan et al. [50], the primary steps of this algorithm are as follows:

Step 1:

Add white noise pairwise with the identical amplitude and the opposite phase to the raw data sequence $v\left(t\right)$, after which we can obtain a pair of polluted signals:

$$\left\{\begin{array}{c}{P}_{ni}=v\left(t\right)+W_{ni}\left(t\right)\\ N_{ni}=v\left(t\right)-W_{ni}\left(t\right)\end{array}\right.$$

(1)

where $P_{ni}$ denotes the positive noise of i-th trial, $N_{ni}$ is the negative noise of i-th trial, and $W_{ni}$ represents the noise with identical amplitude and phase.

Step 2:

Decompose the polluted signal pairs ($P_{ni},N_{ni}$) into a finite set including IMF components:

$$\left\{\begin{array}{c}{P}_{ni}\left(t\right)={\displaystyle {\displaystyle \sum }_{j=1}^M}{u}_{ij}^{+}\left(t\right)\\ N_{ni}\left(t\right)={\displaystyle {\displaystyle \sum }_{j=1}^M}{u}_{ij}^{-}\left(t\right)\end{array}\right.$$

(2)

where $u_{ij}^{-}$ and $u_{ij}^{+}$ are the j-th intrinsic mode functions of the i-th trial with negative and positive noise. Furthermore, M signifies the number of IMFs.

Step 3:

Two sets of IMF components, i.e., the negative noise set of the first IMF component ${\left\{u_{ij}^{-}\left(t\right)\right\}}_{i=1,j=1}^{T,M}$ and positive noises ${\left\{u_{ij}^{+}\left(t\right)\right\}}_{i=1,j=1}^{T,M}$, are obtained by performing the above two steps T times with different amounts of white noise.

Step 4:

The component of the j-th IMF $u_j\left(t\right)$ can be calculated as follows in order to get the ensemble means of whole IMFs:

$$u_j\left(t\right)= \frac{1}{2T}{\displaystyle \sum }_{i=1}^T\left(u_{ij}^{+}\left(t\right)+u_{ij}^{-}\left(t\right)\right)$$

(3)

2.3. Rough Set Theory (RST) and LEM2

In this part, the fuzzy forecasting module of the proposed new hybrid model CFML which contains the rough set theory and the more detailed rule induction algorithm called LEM2 is introduced in brief.

Pawlak and Skoworn proposed RST [51], and it has been acknowledged as one of the most effective mathematical techniques for dealing with uncertainty as well as vagueness. The premise of Rough Set Philosophy is that, due to the lack of information in the discourse space related to each object, the few information objects distinguished by the same information cannot be distinguished. The set of all indistinguishable objects is regarded as the basic set and creates the basic particles of cosmic knowledge. Any union of elementary sets is accepted as an exact set; otherwise, the set is called a rough set. RST includes the utilization of indiscernibility relations to approximately approach the sets of objects by upper and lower approximations [52]. This rough set theory is widely used to acquire more accurate rules to predict objects, and the LEM2 algorithm is usually adopted as a way of applying rough set theory to the induction of rules.

LEM2 [53], a rough set rule induction algorithm, is most frequently adopted as it has better results in most cases. In this study, the formed rules are generated in an “if-then” manner through composing several fuzzy decision values as well as fuzzy conditional values. Moreover, “supports” indicate how many records are archived in the dataset that matches the generated decision rules. LEM2 computes a local covering and then converts it into a rule set. LEM2 learns a discriminant rule set; it learns the smallest set of minimal rules describing a concept. This algorithm can generate both certain and possible rules from a decision table. The rough set induction LEM2 algorithm has several advantages because of the application of rough set theory, as follows:

1.

Rough sets can discern hidden facts and make it possible for us to understand these facts in natural language, which contributes a great deal to decision making;

2.

Rough sets take the background information of decision makers into account;

3.

Rough sets can deal with both qualitative and quantitative attributes;

4.

Rough sets enable machines to extract certain rules in a relatively short time, which means it reduces the time cost of discovering hidden rules.

The detailed process of how LEM2 works is briefly demonstrated as follows: For an attribute–value pair $(e;u)=o$, a block of n which is signified by $[o]$, is a set of instances belonging to $H$ so that, for an attribute, e has a value u. For a concept represented by the decision–value pair $(n;p)$, B is a nonempty upper or lower approximation of it. Set $K$ consists of a set of attribute–value pairs $o=(e;u)$, which is called set $T$ only under the condition that $\varnothing \ne \left[\mathrm{T}\right]={\cap }_{o\in T}\left[o\right]\subseteq K$, where set $T$ is a minimal complex of $K$ only under the condition that $K$ depends on set $T$ and that there are no subsets of $T$ such that $K$ depends on the subset. Symbol C is a nonempty collection of nonempty attribute–value pair sets, and $L$ is the local covering of $K$. A more detailed explanation can be found in the work of Grzymala-Busse [53].

Figure 3 demonstrates the pseudocode of LEM2 based on the study of Liu et al. [54].

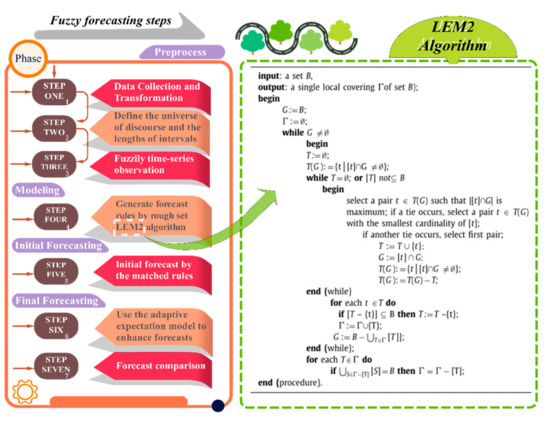
Figure 3. Flowchart of fuzzy time series forecasting.

Step 1.

Compute all attribute–value pair blocks.

Step 2.

Identify attribute–value pairs with the largest $\left|\left[(e;u)\right]\cap G\right|$.

Step 3.

If the cardinality of the set $\left|\left[(e;u)\right]\cap G\right|$ is equal to another one, then select the attribute pair with the smallest block size.

Step 4.

If necessary, we have to go through an additional internal loop in order to find the candidates for the minimal complex.

Step 5.

Then, the following steps are used to find the second minimal complex and so on.

Step 6.

Finally, we can get the local covering of a hidden fact, which may reveal the decision-making process.

2.4. Multi-Objective Grey Wolf Optimizer (MOGWO)

To get more accurate forecasts, we adopt the GWO (grey wolf optimizer) algorithm which is modified to deal with the multi-objective problems to optimize the main forecasting model LSTM. By using the multi-objective optimization theory, we can achieve both an accurate and a stable forecasting quality.

Mirjalili et al. proposed the grey wolf optimization algorithm [55], which was based on grey wolves’ social leadership and hunting skills. In addition, the hunting process is led by three wolves (α, β, and δ). The rest of the wolves follow these three leaders throughout the whole search process to approach the global best solution.

The following formulas were proposed in an effort to emulate the encircling behaviors of grey wolves:

$$K=\left|B\times R^p\left(ite\right)-R\left(ite\right)\right|$$

(4)

$$R(ite+1)=R_p(ite)-M\times K$$

(5)

where K denotes the distance between the prey and the predator, ite refers to the current iteration, $R$ denotes the position vector of wolves, $R_p$ is the prey’s position vector, and $M$ and $B$ are coefficient vectors:

$$M=2c\times e_1-c$$

(6)

$$B =2c\times e_2-c$$

(7)

where $e_1$ and $e_2$ are random vectors in $[0,1]$ and the elements of $c$ decrease linearly from 2 to 0 across all iterations.

The GWO algorithm archives the first three best results gained so far in each iteration and then imposes other agents, namely the rest of the wolves, to update the positions with respect to them. The following formulas are calculated constantly for each search agent [55] in order to mimic the hunting process, and the promising regions of the search space are also found in this process:

$$K_{\alpha }=\left|B_1\times R_{\alpha }-R\right|$$

(8)

$$K_{{}_{\beta }}=\left|B_2\times R_{\beta }-R\right|$$

(9)

$$K_{\delta }=\left|B_3\times R_{\delta }-R\right|$$

(10)

$$R_1=R_{\alpha }-M_1\times (K_{\alpha })$$

(11)

$$R_2=R_{\beta }-M_2\times (K_{\beta })$$

(12)

$$R_3=R_{\delta }-M_3\times (K_{\delta })$$

(13)

$$R(t+1)=\frac{R_1+R_2+R_3}{3}$$

(14)

The $B$ vector produces random values in $[0,2]$. This will help the GWO algorithm show increased behavior in the whole optimization process and help to avoid and explore the local optimum. All these steps are illustrated in Figure 4. R_i is the position of wolf i, which also represents the initial weight and threshold of the LSTM model. That is to say, R_i is a vector and its dimension is determined by the number of initial weights and thresholds of the LSTM model and each element in this vector is a value of a threshold or a weight of LSTM.

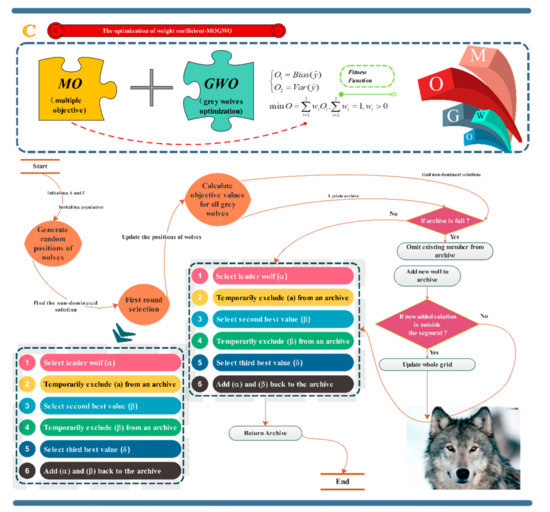
Figure 4. Position updating mechanism of search agents and the effects of A on it.

Attacking is the final stage of hunting, in which the wolf pack catches the prey and the prey stops moving. The process is determined by $D$. Grey wolves will continue to hunt when $\left|D\right|<1$, and the wolves are obliged to leave the prey when $\left|D\right|>1$.

2.5. Long Short-Term Memory (LSTM)

The LSTM model was developed by Schmidhuber and Horchreiter [56]. The harmless gradient in the network is truncated by forcing constant error flow through the constant error turntable in a special multiplication unit. In order to cope with these constant error flows, all of the nonlinear units are able to learn to close or open gates in this network.

The cell state is the key part of the LSTM structure. It runs directly along the entire chain, deleting or adding information to the cell state, carefully adjusted by structures called gates. These gates serve as optional entry points for this information. They consist of a pointwise multiplication operation and a sigmoid neural net layer (Figure 5).

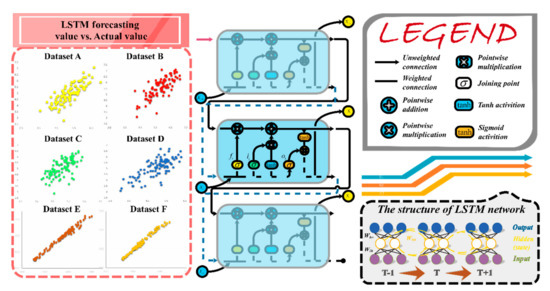
Figure 5. LSTM (long-short-term memory) structure.

An input at time i is ($X_i$), and the following formulas are used to compute the hidden state ($S_i$):

• In the LSTM module, the first step is to determine which information will be discarded from the cell state. The forget gate ($f_i$) is in charge of making decisions, as follows:

  $$f=\sigma (X_i\times T^f+S_{i-1}\times V^i+b_i)$$

  (15)

  where σ is the sigmoid function which turns the input value into an outcome between 0 and 1. T signifies weight parameters, and b denotes bias parameters (i.e., $T^f$, $T^j$, $T^c$, and $T^o$ and $b_i{}_i$,$b_j$, $b_c$, and $b_o$). In this part, the exponents of T and V are not power values; they are just notations used to illustrate which gate the parameters belong to. For instance, $T^f$ represents the weight parameters belonging to the forget gate, namely gate f.
• The next step is to determine which new information will be selected and stored in the cell state. This step has two sub-steps: The first one is the input gate ($Inpu{t}_i$) layer that helps to determine which value is going to be updated. A tanh layer is the second one, which produces a vector composed of new candidate values $C_i$. Calculations are demonstrated as follows:

  $$Inpu{t}_i=\sigma (X_i\cdot T^{input}+S_{i-1}\cdot V^{input}+b_j)$$

  (16)

  $${\tilde{C}}_i=tanh(X_i\cdot T^c+S_{i-1}\cdot V^c+b_c)$$

  (17)

  where ${\tilde{C}}_i$ is a candidate memory cell, which is similar to a memory cell, but uses a tanh function.
• The next step is to update the old cell state $C_{i-1}$ into the new cell state $C_i$, which can be described as follows:

  $$C_i=C_{i-1}\otimes f_i\otimes Inpu{t}_i\otimes {\tilde{C}}_i$$

  (18)

  In Equation (26), the symbol $\otimes$ represents pointwise multiplication.
• The final step is to determine what is about to be generated and selected as the output. This output is a filtered version which is predicated on the cell state, during which the output gate ($o_i$) determines which final output will consist of a specific part of the cell state. After, the cell state runs through the tanh layer, which is multiplied by the output gate as follows:

  $$o_i=\sigma \left(X_i\cdot T^o+S_{i-1}\cdot V^o+b_o\right)$$

  (19)

  $$S_i=o_i\otimes tanh(C_i)$$

  (20)

Algorithm: MOGWO-LSTM
Objective function $\min \left\{\begin{array}{l}fitnes{s}_1=\left|Bias(\widehat{x})\right|\\ fitnes{s}_2=Std(x-\widehat{x})\end{array}\right.$ Input:
Training data: $x_t^{\left(0\right)}=\left(x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\dots ,x^{\left(0\right)}\left(p\right)\right)$
Testing data: $x_f^{\left(0\right)}=\left(x^{\left(0\right)}\left(p+1\right),x^{\left(0\right)}\left(p+2\right),\dots ,x^{\left(0\right)}\left(p+l\right)\right)$
Output:
${\widehat{y}}_f^{\left(0\right)}=\left({\widehat{y}}_f^{\left(0\right)}\left(p+1\right),{\widehat{y}}_f^{\left(0\right)}\left(p+2\right),\dots ,{\widehat{y}}_f^{\left(0\right)}\left(p+l\right)\right)$—a series of forecasting data
Parameters of MOGWO:
Iter—the maximum number of iterations	n—the number of grey wolves
t—the current iteration number	Ri—the position of wolf i
e1—the random vector in [0, 1]	c—the constant vector in [0, 2]
Parameters of LSTM:
Iteration—the maximum number of iterations	Bias_input—the bias vector of the input gate in [0, 1]
Input_num—the knots of the input	Bias_forget—the bias vector of the forget gate in [0, 1]
Cell_num—the knots of the cell	Bias_output—the bias vector of the output gate in [0, 1]
Output_num—the knots of the output Cost_gate—the termination error cost	yita—the rate of adjustment for the weight at each time data_num-the number of columns of training data.
1:/*Set the parameters of MOGWO and LSTM*/
2:/*Initialize the grey wolf population Ri (i = 1, 2, ..., n) randomly*/
3:/*Initialize c, M, and B*/
4:/*Define the archive size*/
5: FOR EACH i: 1 ≤ i ≤ n DO
6: Evaluate the corresponding fitness function Fi for each search agent
7: END FOR
8: /*Find the non-dominated solutions and initialize the archive with them*/
9: Rα, Rβ, Rδ= SelectLeader(archive)
10: WHILE (t < Iter) DO
11: FOR EACH i: 1 ≤ i ≤ n DO
12: /*Update the position of the current search agent*/
13: Kj = |Bi $\cdot$ Rj−R|, i = 1, 2, 3; j = α, β, δ
14: Ri = Rj−Mi $\cdot$ Kj, i = 1, 2, 3; j = α, β, δ
15: R(t + 1) = (R1 + R2 + R3)/3
16: END FOR
17: /*Update c, M, and B*/
18: M = 2 $\cdot$ c $\cdot$ e1−c; B = 2 $\cdot$ c $\cdot$ e2−c
19: /*Evaluate the corresponding fitness function Fi for each search agent*/
20: /*Find the non-dominated solutions*/
21: /*Update the archive with regard to the obtained non-dominated solutions*/
22: IF the archive is full DO
23: /*Delete one solution from the current archive members*/
24: /*Add the new solution to the archive*/
25: END IF
26: IF any newly added solutions to the archive are outside the hypercubes DO
27: /*Update the grids to cover the new solution(s)*/
28: END IF
29: Rα, Rβ, Rδ = SelectLeader(archive)
30: t = t + 1
31: END WHILE
32: RETURN archive
33: OBTAIN R* = SelectLeader(archive)
34: Set R* as the initial weight and threshold of LSTM
35: /*Standardize the training data and testing data*/
36: /*Initialize the structure of the LSTM network*/ 37:/*Initialize cost_gate, bias_input, bias_forget, bias_output and the weight of the LSTM network*/ 38: FOR EACH i: 1 ≤ i ≤ Iteration DO 39: yita=0.01 40: FOR EACH m: 1 ≤ m ≤ data_num DO 41: Equation (15) to Equation (20) 42: /*Calculate the error cost of this round*/ 43: error cost = ${\displaystyle \sum }_{t=1}^l{\left(forecasted {\widehat{x}}_t-actual x_t\right)}^2,$ l is the dimension of testing data 44: IF error cost < cost_gate DO 45: Break 46: END IF 47: /*Update the weight of all gates*/ 48: END FOR 49: IF error cost < cost_gate DO 50: Break 51: END IF 52: END FOR 53: /* Learning process has been done/ 54: Input the standardized historical data into LSTM to forecast the future changes 55: De-normalize the obtained forecasting outcomes and generate the final forecasting results

There are two commonly adopted criteria for verifying forecasting effectiveness, accuracy and stability. Also, we should not just focus on one objective. Both objectives—high accuracy and stability—should be studied simultaneously and implemented in the optimization part. Therefore, based on bias-variance framework, the fitness function should be defined as follows:

$$\begin{array}{l}E{(\widehat{x}-x)}^2=E{\left[\widehat{x}-E(\widehat{x})+E(\widehat{x})-x\right]}^2\\ =E{\left[\widehat{x}-E(\widehat{x})\right]}^2+{\left[E(\widehat{x})-E(x)\right]}^2\\ =Var(\widehat{x})+Bia{s}^2(\widehat{x})\end{array}$$

(21)

where x is the actual value, $\widehat{x}$ is the forecasted value, and E is the expectation value of the corresponding variable.

The bias equals the average difference between the actual and forecasted values, which represents forecasting accuracy. A smaller absolute value of the bias demonstrates a more accurate forecasting accuracy. A smaller variance value indicates a more stable forecasting performance. However, in the conduct of most experiments, it was found that the criteria are not suitable for issues that this paper seeks to address. Thus, the standard deviation of forecasting errors is selected as a substitute for fitness 2. Therefore, the fitness function in this paper is formulated as follows:

$$\min \left\{\begin{array}{l}fitnes{s}_1=\left|Bias(\widehat{x})\right|\\ fitnes{s}_2=Std(x-\widehat{x})\end{array}\right.$$

(22)

Hence, the objectives of multi-objective optimization problems are usually conflicting. In that regard, the Pareto optimal solution set provides an answer since it represents the best trade-offs between different objectives. Our optimization problem in this study is a minimization issue, so the way we choose suitable solutions can be formulated as follows:

Minimize the following:

$$F(x)=\left\{f_1(x),f_2(x),\cdot \cdot \cdot ,f_o(x)\right\}$$

(23)

Subject to the following:

$$g_i(x)\ge 0, i=1,2,\cdot \cdot \cdot ,m$$

(24)

$$h_i(x)\ge 0, i=1,2,\cdot \cdot \cdot ,p$$

(25)

$$L_i\le x_i\le U_i, i=1,2,\cdot \cdot \cdot ,n$$

(26)

where o denotes the number of objectives, m is the number of inequality constraints, p is the number of equality constraints, and Li and Ui are the lower and upper boundaries of the i-th variables, respectively.

Also, several definitions regarding this problem is listed as follows:

Definition 1.

Pareto dominance.

Suppose that there are two vectors: $x=(x_1,x_2,\cdot \cdot \cdot ,x_k)$ and $y=(y_1,y_2,\cdot \cdot \cdot ,y_k)$. Vector x dominates y, denoted as $x\succ y,$ if

$$\forall i\left\{1,2,\cdot \cdot \cdot ,k\right\},\left[f_i(x)\ge f_i(y)\right]\wedge \left[i\in 1,2,\cdot \cdot \cdot ,k:f_i(x)\right]$$

(27)

Definition 2.

Pareto optimality.

The solution $x\in X$ is named a Pareto optimal if

$$\nexists y\in X\left|F(y)\succ F(x)\right.$$

(28)

Two solutions are non-dominated with respect to each other if neither of them dominates the other.

Definition  3.

Pareto optimal set.

The set including all non-dominated solutions is named a Pareto set as follows:

$$P_s:=\left\{x,y\in X\left|\exists F(y)\succ F(x)\right.\right\}$$

(29)

Definition 4.

Pareto optimal front.

A set containing the corresponding values of Pareto optimal solutions in a Pareto optimal set is defined as a Pareto optimal front:

$$P_f:=\left\{F(x)\left|x\in P_s\right.\right\}$$

(30)

2.6. Evaluation Module

This section illustrates reasonable and scientific evaluating modules. In addition, some typical evaluation metric rules that are usually adopted in the relevant research are adopted to verify the forecasting performance; $R^2$ (Pearson’s correlation coefficient) and DM test methods are also exploited in this paper.

2.6.1. Typical Performance Metric

As far as we know, there are no uniform and consistent criteria to test the validity of the prediction results or to compare the results with those of other models. In this study, we adopt lots of multifarious methods and metrics, which are all shown in Table 2. Here, N is the length of the dataset, A denotes the actual value, whereas F represents the forecasting value.

Table 2. Performance metric rules.

Metric	Definition	Equation
AE	Average error of N forecasting results	$AE=\frac{1}{\mathrm{N}}{\displaystyle \sum }_{i=1}^N\left(A_{i-}{F}_i\right)$
MAE	Mean absolute error of N forecasting results	$MAE=\frac{1}{\mathrm{N}}{\displaystyle \sum }_{i=1}^N\left|A_{i-}{F}_i\right|$
RMSE	Square root of average of the error squares	$RMSE=\sqrt{\frac{1}{\mathrm{N}}{\displaystyle \sum }_{i=1}^N{\left(A_{i-}{F}_i\right)}^2}$
NMSE	The normalized average of the squares of the errors	$NMSE=\frac{1}{\mathrm{N}}{\displaystyle \sum }_{i=1}^N\frac{{\left(A_{i-}{F}_i\right)}^2}{F_i{A}_i}$
MAPE	Average of N absolute percentage error	0$MAPE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|\frac{A_i-F_i}{A_i}\right|}\times 100\%$
IA	Index of agreement of the forecasting results	$IA= 1-\frac{{{\displaystyle \sum }}_{i=1}^N{\left(A_{i-}{F}_i\right)}^2}{{{\displaystyle \sum }}_{i=1}^N{\left(\left|F_i-\overline{A}\right|+\left|A_i+\overline{A}\right|\right)}^2}$
FB	Fractional bias of N forecasting results	$FB=2\times \frac{\overline{A}-\overline{F}}{\overline{A}+\overline{F}}$
U1	Theil U statistics 1 of forecasting results	$U1=\frac{\sqrt{\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{\left(A_{i-}{F}_i\right)}^2}}{\sqrt{\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{A}_i{}^2}+\sqrt{\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{F}_i{}^2}}$
U2	Theil U statistics 2 of forecasting results	$U2=\frac{\sqrt{\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{\left(\frac{A_{i+1-}{F}_{i+1}}{A_i}\right)}^2}}{\sqrt{\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{\left(\frac{A_{i+1-}{F}_i}{A_i}\right)}^2}}$
DA	Direction accuracy of the forecasting results	$DA=\frac{1}{l}{\displaystyle \sum }_{i=1}^l{w}_i,w_i=\left\{{}_{0,otherwise}^{1,if(A_{i+1}-A_i)\cdot (F_{i+1}-A_i)>0}\right.$
INDEX	Improvement ratio of the index among different models	$INDEX=\frac{{\left|F_i-A_i\right|}_{compared}-{\left|F_i-A_i\right|}_{proposed}}{{\left|F_i-A_i\right|}_{proposed}}$
R	Pearson’s correlation coefficient	$R=\frac{{{\displaystyle \sum }}_i^N\left(A_i-\overline{A}\right)\left(F_i-\overline{F}\right)}{\sqrt{{{\displaystyle \sum }}_i^N{\left(A_i-\overline{A}\right)}^2{{\displaystyle \sum }}_i^N{\left(F_i-\overline{F}\right)}^2}}$

2.6.2. Diebold–Mariano Test

Considering α as the significance level, the null hypothesis $H_0$ indicates that there are no significant differences between the two different forecasting models. Otherwise, $H_1$ denotes the disagreement with $H_0$. The following formulas indicate the related hypotheses:

$$H_0:E\left[Loss\left(e_i^1\right)\right]=E\left[Loss\left(e_i^2\right)\right]$$

(31)

$$H_1:E\left[Loss\left(e_i^1\right)\right]\ne E\left[Loss\left(e_i^2\right)\right]$$

(32)

where $Loss$ represents the loss function of forecasting errors and $e_i^p$ $(p=1,2)$ are the forecasting errors of two comparison models.

Furthermore, the DM test statistics can be calculated as follows:

$$\mathrm{DM} \mathrm{value}=\frac{{{\displaystyle \sum }}_{i=1}^n\left(Loss\left(e_i^1\right)-Loss\left(e_i^2\right)\right)/n}{\sqrt{S^2/n}}{s}^2$$

(33)

where $s^2$ is an estimation for the variance of $d_i=Loss\left(e_i^1\right)-Loss\left(e_i^2\right)$.

The DM test value is compared with $Z_{\alpha /2}$. $H_0$ will be rejected under the circumstance that the DM statistic falls outside the acceptance interval $[-Z_{\alpha /2},Z_{\alpha /2}]$, which indicates that there is a significant difference between the comparison models and the forecasting performances of the proposed model, meaning we accept $H_1$.

3. Analysis and Experiments

In this part, three different experiments using four different wind speed datasets acquired from Liaotung peninsula and two different electrical power load datasets collected from QLD (Queensland) are carried out to test the proposed hybrid system.

3.1. Raw Data Description

In this study, four different 10-min wind speed datasets were collected from four sites (Figure 6), namely the four wind pour plants in the Liaotung peninsula: the Hengshan site ($40°{\rm N},120°{\rm E}$), Xianren island ($40°{\rm N},122.5°{\rm E}$), the Donggang site ($42.5°{\rm N},122.5°{\rm E}$), and the Danton site ($40°{\rm N},125°{\rm E}$).

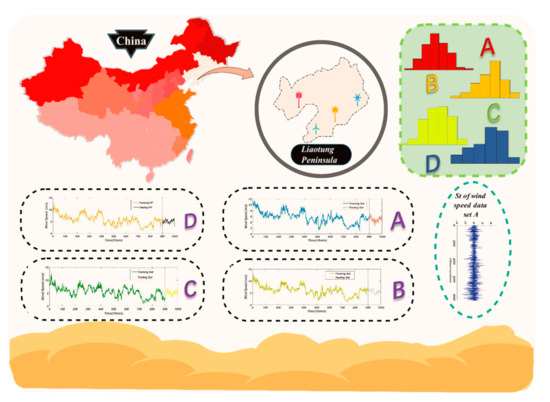
Figure 6. Four wind speed datasets with 10-min time intervals.

Also, two additional electrical load datasets were applied to demonstrate the efficiency of the hybrid forecasting model. The total number of data points in each wind speed dataset was 9488, and that of the electrical load was 2544. Only the first 1000 observations were adopted to verify the model. Of the total 1000 observations, the first 900 observations were used as the training set, while the testing set contained the remaining 100 observations (Figure 6). Furthermore, some basic statistical information, i.e., minimum, average values, as well as maximum values, etc. of the dataset referred to above are demonstrated in Table 3.

Table 3. Statistical values of each experiment dataset.

Data Set	Statistical Indicator					Data Set	Statistical Indicator
	Mid.	Max.	Min.	Std	Mean		Mid.	Max.	Min.	Std	Mean
Dataset A						Dataset D
All samples	4.9391	17.200	0.1000	2.7072	4.6000	All samples	4.8754	17.700	0.1000	2.6413	4.6000
Training	5.7401	11.800	1.2000	2.0136	5.8000	Training	5.6011	12.500	0.9000	1.8937	5.8000
Testing	4.9750	7.1000	2.8000	0.7774	5.0000	Testing	5.1120	6.7000	3.1000	0.7983	5.2500
Dataset B						Dataset E
All samples	5.2674	28.800	0.1000	2.9040	4.9000	All samples	6043.4	8180.7	4488.0	841.07	6189.2
Training	6.1190	12.700	1.3000	2.0481	6.2000	Training	6065.9	8180.7	4488.0	849.28	6214.1
Testing	5.6190	7.1000	3.1000	0.8237	5.7000	Testing	5840.7	7221.2	4515.0	736.47	5981.9
Dataset C						Dataset F
All samples	5.0718	22.100	0.1000	2.9000	4.6000	All samples	5515.5	7780.5	4357.8	684.29	5444.2
Training	5.8262	12.300	1.3000	2.0946	5.8000	Training	5542.3	7780.5	4357.8	693.79	5472.0
Testing	5.0920	6.5000	2.9000	0.7108	5.1000	Testing	5273.9	6416.3	4447.3	537.19	5170.9

3.2. Experiment I: Tests of MOGWO and LSTM

In this experiment, we present two subparts to verify the superiority of the MOGWO and LSTM forecasting algorithm, respectively.

3.2.1. Test of MOGWO

The four typical test functions that are demonstrated in Table 4 are commonly used to verify the superiority of the proposed optimizer and to deal with the multi-objective optimization issues [57,58,59]. NSGA-Ⅱ and multi-objective dragonfly (MODA) were used in this study for comparison. The experimental parameters were as follows: the search agents’ total number was 50, the archive size was 50, and the iteration number was 100. The inverted generational distance (IGD), a widely used metric, was adopted in this paper for the evaluation. Each test function was tested fifty times, and Table 5 shows the statistical values of the IGD. Moreover, Figure 7 demonstrates the Pareto optimal solutions which were acquired by different algorithms.

Table 4. Four test benchmark functions.

Kursawe	ZDT1
Minimize $f_1\left(x\right)={\displaystyle \sum }_{i=1}^2\left[-10\exp \left(-0.2\sqrt{x_1^2+x_2^2}\right)\right]$	Minimize $f_1\left(x\right)=x_i$
Minimize $f_2\left(x\right)={\displaystyle \sum }_{i=1}^3\left[{\left|x_i\right|}^{0.8}+5\sin \left(x_i^3\right)\right]$	Minimize $f_2\left(x\right)=g\left(x\right)\times h\left(f_1\left(x\right),g\left(x\right)\right)$
where $-5\le x_i\le 5,1\le i\le 3$	where $\begin{array}{l}G\left(x\right)=1+\frac{9}{N-1}{\displaystyle \sum }_{i=2}^N{x}_i\\ h\left(f_1\left(x\right),g\left(x\right)\right)=1-\sqrt{\frac{f_1\left(x\right)}{g\left(x\right)}}\\ 0\le x_i\le 1,1\le i\le 30\end{array}$
ZDT2	ZDT3
Minimize $f_1\left(x\right)=x_i$	Minimize $f_1\left(x\right)=x_i$
Minimize $f_2\left(x\right)=g\left(x\right)\times h\left(f_1\left(x\right),g\left(x\right)\right)$	Minimize $f_2\left(x\right)=g\left(x\right)\times h\left(f_1\left(x\right),g\left(x\right)\right)$
where $\begin{array}{l}G\left(x\right)=1+\frac{9}{N-1}{\displaystyle \sum }_{i=2}^N{x}_i\\ h\left(f_1\left(x\right),g\left(x\right)\right)=1-{\left(\frac{f_1\left(x\right)}{g\left(x\right)}\right)}^2\\ 0\le x_i\le 1,1\le i\le 30\end{array}$	where $\begin{array}{l}G\left(x\right)=1+\frac{9}{29}{\displaystyle \sum }_{i=2}^N{x}_i\\ h\left(f_1\left(x\right),g\left(x\right)\right)=1-\sqrt{\frac{f_1\left(x\right)}{g\left(x\right)}}\\ 0\le x_i\le 1,1\le i\le 30\end{array}$

Table 5. Statistical values of the inverted generational distance (IGD) for four test functions.

Test Functions	IGD Values
	Mean	Max.	Min.	Std.	Med.
Kursawe
MODA	0.012500	0.021500	0.008500	0.003600	0.011500
NSGA-Ⅱ	0.006500	0.015500	0.004500	0.002800	0.005900
MOGWO	0.005200	0.005800	0.004900	0.000251	0.005200
ZDT1
MODA	0.014600	0.022300	0.007900	0.004800	0.014400
NSGA-Ⅱ	0.015800	0.036400	0.000375	0.008800	0.013500
MOGWO	0.006800	0.016400	0.002100	0.003800	0.005900
ZDT2
MODA	0.013900	0.022100	0.006900	0.004600	0.012100
NSGA-Ⅱ	0.029200	0.060400	0.003300	0.013500	0.025600
MOGWO	0.009000	0.019400	0.001200	0.005500	0.008100
ZDT3
MODA	0.018700	0.025900	0.007000	0.005200	0.019300
NSGA-Ⅱ	0.011500	0.021500	0.004700	0.004700	0.011000
MOGWO	0.005600	0.015000	0.001000	0.003000	0.005600

The values in bold indicate the best value of each benchmark function.

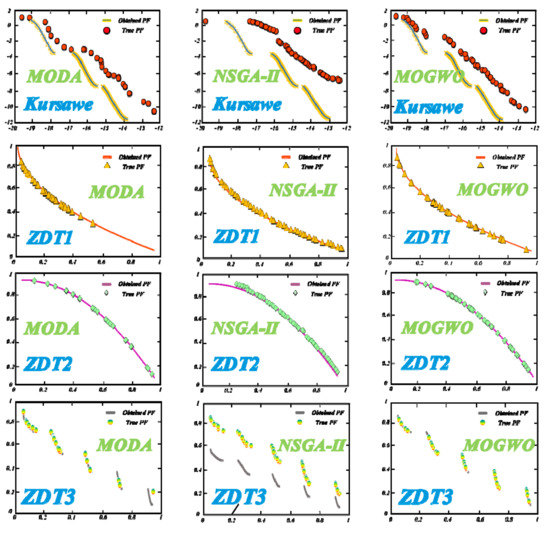
Figure 7. Obtained Pareto optimal solutions by NSGA-II, MODA, and MOGWO for the test functions: Kursawe, ZDT1, ZDT2, and ZDT3.

Based on the outcomes, two conclusions were made as follows:

• The MOGWO algorithm obtained the best IGD outcomes among almost all optimizers for four test functions (Kursawe, ZDT1, ZDT2, and ZDT3) while performing worse than the Kursawe as well as ZDT1 algorithms in terms of the minimum value and worse than MODA regarding the standard deviation. From a whole perspective, these outcomes are strong enough to demonstrate the superior optimization ability of MOGWO algorithms compared with the others.
• Figure 7 shows that the MOGWO algorithm was able to obtain more Pareto optimal solutions. In addition, the solutions found by the MOGWO algorithm were more evenly distributed on the true PF (pareto front) curve and were closer to the real Pareto optimal solutions.

Remark: The optimizing ability of MOGWO has been proven through the results and discussions of the aforementioned experiment comparison. Thus, MOGWO can be widely used to cope with multi-objective problems, thus being adopted as the best optimization model in the proposed CFML system.

3.2.2. Test of LSTM in CEEMD-FTS-MOGWO-LSTM

This subsection aims to compare LSTM, DBN, CNN, and SAE for the four wind speed datasets collected from four different wind farms with 10-min data. We set the parameters for each model based on the error and bias since there are no previous studies on how to set the optimal parameters. Also, to reduce the impact of randomness, we took the mean value of the experiments performed 50 times. The relative results and detailed values are listed in Table 6, and Figure 8 demonstrates the prediction outcomes of the aforementioned four models at the four wind speed sites. From the forecasting data, we drew several conclusions:

Table 6. Forecasting results of the four deep learning algorithms at four sites.

Sites	Models	AE	MAE	RMSE	NMSE	MAPE	IA	FB	r	U1	U2
Dataset A	CNN	−0.1466	0.5558	0.6871	0.0215	0.1143	0.9958	0.0299	0.5871	0.0693	0.845
	DBN	−0.2578	0.4917	0.6105	0.0169	0.0988	0.9967	0.0528	0.7122	0.0618	0.8078
	SAE	−0.2431	0.4891	0.6084	0.0165	0.0982	0.9967	0.0501	0.7083	0.062	0.7952
	LSTM	0.2706	0.4364	0.5462	0.0138	0.0948	0.9973	−0.0530	0.7915	0.0529	0.6470
Dataset B	CNN	0.1251	0.5515	0.7198	0.0191	0.1063	0.9963	−0.0220	0.5558	0.0628	0.8427
	DBN	0.2338	0.4853	0.6111	0.0115	0.0885	0.9974	−0.0402	0.7284	0.0521	0.8130
	SAE	−0.01814	0.5077	0.6337	0.0146	0.0947	0.9971	0.0032	0.6608	0.0560	0.7455
	LSTM	0.2034	0.4448	0.5677	0.0122	0.0863	0.9977	−0.0356	0.7645	0.0492	0.6598
Dataset C	CNN	−0.1974	0.5585	0.7095	0.0221	0.1288	0.9957	0.0394	0.5892	0.0700	0.8672
	DBN	0.1024	0.4765	0.6138	0.0154	0.0981	0.9968	−0.0197	0.5589	0.0587	0.7241
	SAE	−0.0451	0.4538	0.5808	0.0145	0.0936	0.9971	0.0089	0.6481	0.0568	0.6088
	LSTM	0.0131	0.4419	0.5731	0.0146	0.0928	0.9971	−0.0026	0.6241	0.0557	0.6151
Dataset D	CNN	−0.1974	0.5585	0.7095	0.0221	0.1132	0.9957	0.0394	0.5892	0.0700	0.8672
	DBN	−0.3784	0.5490	0.6827	0.0202	0.1077	0.9960	0.0772	0.7419	0.0688	0.8875
	SAE	−0.1586	0.4776	0.6025	0.0154	0.0958	0.9969	0.0315	0.7227	0.0592	0.7510
	LSTM	−0.1168	0.4295	0.5565	0.0131	0.0868	0.9974	0.0231	0.7488	0.0544	0.7198

The values in bold indicate the best values of each benchmark function.

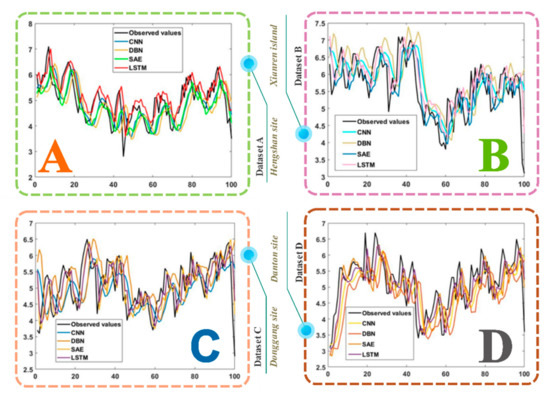
Figure 8. Forecasting results of the four deep learning algorithms.

• The LSTM model achieved almost the best results and the most accurate predictions of all four wind speed datasets with roughly the same run time and identical training and testing datasets. Namely, the adopted LSTM model outperformed the CNN, DBN, and SAE from a whole perspective and provided fairly competitive results.
• For the data collected from the four different wind farms, the LSTM model worked better than the other three deep learning models, which means that the superiority of the LSTM forecasting algorithm remained, regardless of the different geographical distribution, to some extent.
• The forecasting performance of different models was adequately reflected by the error metrics adopted by us in this part. That is to say, error measurement is effective and can be used to accurately evaluate the ability of the prediction models.

Remark: For all four datasets, although the LSTM model performed more poorly than the other models on some metrics, the best values of the majority of error metrics, such as mean absolute error (MAE), square root of average of the error squares (RMSE), mean absolute percentage error (MAPE), index of agreement (IA), and so on, indicate that the adopted LSTM model can achieve excellent forecasting accuracy. That is also the reason why we chose LSTM as the main forecasting model in our proposed hybrid forecasting model.

3.3. Experiment II

The comparisons made in this experiment were conducted to demonstrate the specific improvements brought by the fuzzy time series forecasting part and the optimizer algorithm as well as the combination of MOGWO and FTS. Furthermore, an experiment to prove the enhancement in the forecasting ability of the combined model brought by CEEMD was made as well. Moreover, the comparisons between the proposed hybrid forecasting model and all the other models are also listed and analyzed in this part. Table 7 and Figure 9 demonstrate the relevant error metric values of the models mentioned above.

Table 7. Results of the developed forecasting framework and other models (Experiment II).

Sites	Models	AE	MAE	RMSE	NMSE	MAPE	IA	FB	U1	U2	DA	r2
Dataset A	ARIMA	0.0019	0.3995	0.4941	0.0115	0.0837	0.9978	−0.0004	0.0491	0.6576	0.4242	0.7830
	GRNN	0.1427	0.4650	0.5723	0.0154	0.1004	0.9970	−0.0283	0.0562	0.6984	0.4949	0.7057
	WNN	0.0089	0.4678	0.5812	0.0161	0.0994	0.9969	−0.0018	0.0578	0.7621	0.5152	0.6738
	LSTM	0.2706	0.4364	0.5462	0.0138	0.0948	0.9973	−0.0530	0.0529	0.6470	0.4343	0.7915
	MOGWO-LSTM	0.1142	0.4069	0.5007	0.0117	0.0864	0.9978	−0.0227	0.0492	0.6376	0.5152	0.7848
	FTS-LSTM	0.0599	0.4041	0.4966	0.0115	0.0852	0.9978	−0.0120	0.0491	0.6453	0.4848	0.7822
	FTS-MOGWO-LSTM	−0.0106	0.3962	0.4884	0.0110	0.0822	0.9979	0.0021	0.0483	0.6585	0.4343	0.7828
	CEEMD-FTS-MOGWO-LSTM	−0.0205	0.2314	0.2964	0.0041	0.0487	0.9992	0.0041	0.0296	0.7439	0.7374	0.9359
Dataset B	ARIMA	0.0129	0.4160	0.5344	0.0103	0.0768	0.9980	−0.0023	0.0470	0.6528	0.4848	0.7809
	GRNN	0.1744	0.4548	0.5907	0.0136	0.0889	0.9975	−0.0306	0.0514	0.7058	0.5859	0.7252
	WNN	0.1796	0.4394	0.5510	0.0118	0.0858	0.9978	−0.0315	0.0479	0.6692	0.4949	0.7726
	LSTM	−0.2642	0.4271	0.5487	0.0138	0.0863	0.9973	0.0545	0.0560	0.7711	0.5152	0.7855
	MOGWO-LSTM	−0.0291	0.4338	0.5521	0.0114	0.0803	0.9978	0.0052	0.0488	0.6926	0.5152	0.7519
	FTS-LSTM	−0.2094	0.4398	0.5700	0.0116	0.0791	0.9977	0.0380	0.0512	0.7650	0.5455	0.7632
	FTS-MOGWO-LSTM	−0.0980	0.4204	0.5356	0.0105	0.0773	0.9979	0.0176	0.0477	0.7189	0.5253	0.7663
	CEEMD-FTS-MOGWO-LSTM	−0.0532	0.2345	0.2850	0.0032	0.0439	0.9994	0.0095	0.0253	0.6145	0.7677	0.9737
Dataset C	ARIMA	−0.0031	0.4313	0.5485	0.0130	0.0893	0.9974	−0.0006	0.0534	0.5905	0.4343	0.6835
	GRNN	0.0932	0.4836	0.6393	0.0185	0.1038	0.9964	−0.0181	0.0617	0.6799	0.5051	0.5105
	WNN	0.0199	0.4727	0.6438	0.0186	0.1005	0.9964	−0.0039	0.0625	0.7127	0.4343	0.5528
	LSTM	0.0131	0.4419	0.5731	0.0146	0.0928	0.9971	−0.0026	0.0557	0.6151	0.5556	0.6241
	MOGWO-LSTM	0.1206	0.4315	0.5739	0.0146	0.0919	0.9971	−0.0234	0.0553	0.5997	0.5253	0.6341
	FTS-LSTM	−0.0550	0.4181	0.5416	0.0129	0.0868	0.9974	0.0109	0.0531	0.6260	0.5758	0.6515
	FTS-MOGWO-LSTM	0.0929	0.3892	0.5201	0.0121	0.0826	0.9976	−0.0181	0.0503	0.6044	0.6061	0.6905
	CEEMD-FTS-MOGWO-LSTM	−0.0189	0.2432	0.3085	0.0039	0.0488	0.9992	0.0037	0.0301	0.5552	0.7677	0.9154
Dataset D	ARIMA	−0.0415	0.4194	0.5416	0.0121	0.0846	0.9975	0.0081	0.0525	0.6718	0.4242	0.7712
	GRNN	−0.1744	0.4986	0.6308	0.0173	0.1008	0.9966	0.0347	0.0621	0.7936	0.5051	0.6845
	WNN	−0.2658	0.4778	0.5979	0.0150	0.0943	0.9969	0.0534	0.0594	0.7732	0.4242	0.7516
	LSTM	−0.1168	0.4295	0.5565	0.0131	0.0868	0.9974	0.0231	0.0544	0.7198	0.4848	0.7488
	MOGWO-LSTM	−0.0652	0.4094	0.5411	0.0122	0.0831	0.9975	0.0128	0.0527	0.7009	0.5455	0.7516
	FTS-LSTM	−0.0447	0.4075	0.5263	0.0114	0.0825	0.9976	0.0088	0.0512	0.6954	0.5859	0.7582
	FTS-MOGWO-LSTM	0.0151	0.3825	0.5031	0.0106	0.0787	0.9978	−0.0030	0.0487	0.6923	0.5859	0.7740
	CEEMD-FTS-MOGWO-LSTM	−0.1282	0.2569	0.3272	0.0039	0.0491	0.9993	0.9991	0.0254	0.5921	0.7179	0.9280

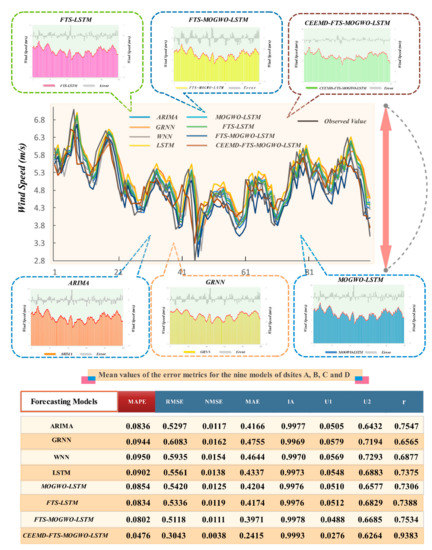
Figure 9. Forecasting results of the developed forecasting system and the other compared models (Experiment II).

(1)

For the first comparison, WNN, GRNN, ARIMA, and the LSTM models were built and compared with each other in order to determine the best one for performing wind speed forecasting, which was found to be the ARIMA. However, of all the neural network algorithms, LSTM was shown to be the best one, and Experiment I proved that LSTM is better than the other three deep learning models as well. Hence, the following steps and comparisons are all based on the basic and regular forecasting model—LSTM.

(2)

In terms of R (Pearson’s correlation coefficient), ARIMA failed to outdo LSTM in datasets A and B. In addition, we tried AR, MA, ARMA, and ARIMA with different parameters each, and we found that of all these settings, ARMA(2,1), ARIMA(3,1,2), and ARIMA(3,2,2), achieved almost the same forecasting accuracy at about 8% MAPE, which is apparently better than that of the other neural networks. The reason for this phenomenon is that the moving-average model that includes AR requires clear rhythm patterns and fairly linear data series trends, whereas wind speed datasets are neither seasonal nor regular, so all of these irregular features were almost removed by the moving-average method as a result of the differencing operation.

(3)

From Table 7, for example, the MOGWO-LSTM achieved a MAPE value of 8.64%, while the basic LSTM model only achieved a MAPE value of 9.48% in the case of site A. Moreover, we tested the effectiveness of the fuzzy time series forecasting part. For example, in the case of site B, the MAPE value of FTS-LSTM was 7.91%, 8.34% lower than that of the LSTM model.

(4)

According to Figure 8, the FTS-MOGWO-LSTM model achieved 8.02% in MAPE and 75.34% in r² from a mean perspective, although it failed to reach the highest r² value in datasets A and B. Next, the separate improvement on the forecasting ability brought by FTS or MOGWO varied in different datasets. For example, in the case of dataset A, FTS-LSTM was higher than MOGWO-LSTM, which means that MOGWO contributes more to forecasting.

(5)

Apart from these comparisons, the decomposition algorithm was also tested in this part. In this paper, we tested several parameter configurations regarding the Nstd (signal noise ratio), NR (noise addition number), Maxiter (maximum number of iterations), and modes (number of IMFs) in the CEEMD algorithm. We tested the Nstd (0.05–0.4), NR (10–500), Maxiter (100–1000), and modes (9–13) to find the best configuration. Detailed parameter settings vary from dataset to dataset, so settings should be changed at any time when the dataset is changed. In this part, for instance, the best settings for dataset A were as follows: an Nstd of 0.2, an NR of 50, and a Maxiter of 500. The total IMF number was 12, and the best accuracy is acquired by 11 IMFs. Also, Table 8 shows that the CFML model achieved the highest r² value and the lowest MAPE in all four data sites, which demonstrates the improvements brought by CEEMD.

Table 8. Experimental outcomes of the proposed forecasting system and other models (Experiment III, Wednesday).

Models	AE	MAE	RMSE	NMSE	MAPE	IA	FB	U1	U2	DA	R
GRNN	45.5683	196.0143	241.4824	0.0018	0.0347	0.9996	−0.0078	0.0204	0.7029	0.3535	0.9478
WNN	20.7296	168.5709	205.6567	0.0014	0.0302	0.9997	−0.0035	0.0174	0.7651	0.6667	0.9604
CNN	137.5887	229.2342	239.6551	0.0025	0.0403	0.9994	−0.0233	0.0247	0.7953	0.444	0.9362
DBN	19.7873	191.6701	243.2305	0.0019	0.0341	0.9996	−0.0034	0.0206	0.7248	0.2727	0.9444
SAE	101.5634	175.8553	214.9376	0.0013	0.0304	0.9997	−0.0173	0.0181	0.7351	0.4343	0.9652
LSTM	−161.6647	172.3742	205.9165	0.0011	0.0281	0.9997	0.0281	0.0177	0.7425	0.7576	0.9916
FTS-LSTM	47.6418	96.6102	115.9360	0.0004	0.0171	0.9999	−0.0081	0.0098	0.5328	0.7071	0.9904
MOGWO-LSTM	−83.5761	106.2048	129.7533	0.0004	0.0176	0.9999	0.0144	0.0111	0.5570	0.7677	0.9918
FTS-MOGWO-LSTM	26.9179	84.9093	104.1058	0.0003	0.0146	0.9999	−0.0046	0.0088	0.4629	0.7677	0.9903
EMD-FTS-MOGWO-LSTM	52.6362	67.7765	79.8200	0.0002	0.0116	1.0000	−0.0090	0.0068	0.4940	0.7374	0.9968
EEMD-FTS-MOGWO-LSTM	11.3961	55.9408	69.4255	0.0001	0.0096	1.0000	−0.0020	0.0059	0.4142	0.8283	0.9957
CEEMD-FTS-MOGWO-LSTM	−29.7311	47.5537	64.3627	0.0001	0.0083	1.0000	0.0051	0.0055	0.4030	0.9293	0.9970

The values in bold indicate the best values of each benchmark function.

Remark: Through the aforementioned comparisons and conclusions, it is apparent that the proposed hybrid forecasting model achieves the best values in all the applied error metrics. Moreover, the outcomes prove that the adopted multi-objective optimizer MOGWO, the data decomposition approach CEEMD, and the fuzzy time series part can improve the forecasting ability of the original forecasting model LSTM to a great extent.

3.4. Experiment III: Tested with Electrical Load Data

The third experiment aims to verify the performance of the proposed CFML forecasting model in QLD (Queensland) electrical power load forecasting (Figure 10). Due to the similarity in weekdays or weekends and the noticeable differences between the load data from weekdays and weekends, the data from Wednesday was randomly selected as a representative of weekdays and the data from Sunday was chosen to represent weekends [60]. Table 8 and Table 9 list the experimental outcomes. All forecasting results from Wednesday and Sunday are depicted in Figure 10. In addition, the basic datasets from Wednesday and Sunday in QLD are shown in Figure 10, and both of these datasets were collected from Queensland in Australia. The specific results of electrical load forecasts are presented and shown clearly in this subsection, from which the following conclusions were drawn:

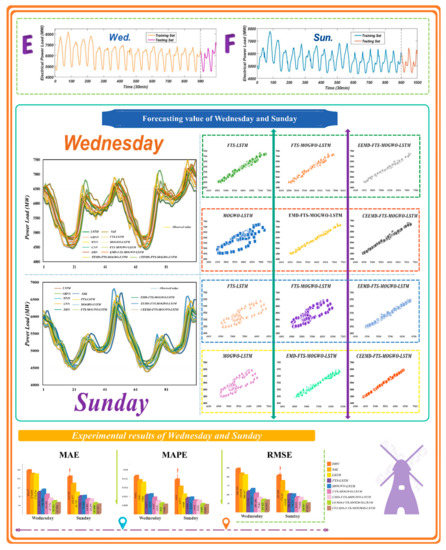
Figure 10. The forecasting results from Wednesday and Sunday as well as the basic data descriptions.

Table 9. Experimental outcomes of the proposed forecasting system and other models (Experiment III, Sunday).

Models	AE	MAE	RMSE	NMSE	MAPE	IA	FB	U1	U2	DA	R
GRNN	17.5396	149.6115	190.1444	0.0013	0.0284	0.9997	−0.0033	0.0179	0.6929	0.3838	0.9376
WNN	38.7488	103.6095	137.2156	0.0006	0.0194	0.9998	−0.0073	0.0129	0.6450	0.7071	0.9711
CNN	16.6657	162.4187	200.3068	0.0013	0.0302	0.9997	−0.0032	0.0189	0.7094	0.3737	0.9308
DBN	8.2873	163.9351	205.5054	0.0015	0.0310	0.9996	−0.0016	0.0194	0.7268	0.3232	0.9234
SAE	6.4847	132.5766	173.3199	0.0010	0.0244	0.9998	−0.0012	0.0163	0.6732	0.4949	0.9487
LSTM	−2.8595	92.739	113.8205	0.0004	0.0175	0.9999	0.0005	0.0107	0.6788	0.8081	0.9916
FTS-LSTM	−20.6497	77.1604	100.2723	0.0003	0.0143	0.9999	0.0039	0.0095	0.5844	0.8485	0.9910
MOGWO-LSTM	−4.2641	78.6017	98.7397	0.0003	0.0148	0.9999	0.0008	0.0093	0.6091	0.8485	0.9917
FTS-MOGWO-LSTM	1.9840	64.8811	82.8495	0.0002	0.0122	0.9999	−0.0004	0.0078	0.5073	0.8586	0.9907
EMD-FTS-MOGWO-LSTM	−6.8800	62.4585	79.6677	−0.0002	0.0118	0.9999	0.0013	0.0075	0.5218	0.7778	0.9904
EEMD-FTS-MOGWO-LSTM	−8.9363	47.3082	60.5872	0.0001	0.0088	1.0000	0.0017	0.0057	0.4453	0.8586	0.9960
CEEMD-FTS-MOGWO-LSTM	−40.7260	41.1810	47.4667	0.00008	0.0079	1.0000	0.0078	0.0045	0.3802	0.8687	0.9990

The values in bold indicates the best values of each benchmark function.

(1)

Regarding the electrical power load data from Wednesday and all forecasting steps, the proposed hybrid forecasting system performed the best among all the other models. Moreover, among all the single models involved in this experiment, the single model that performed best was the WNN algorithm, while the worst was the CNN model. However, this may be a result of the data features, which does not mean that the CNN constantly performs more poorly than the WNN model. Since the regular form of the CNN model is designed to deal with figure data, to perform unidimensional time series forecasting, it should be first transformed into a matrix in which each row contains many observations, such as 128 or 256, just like the grey scale image data to some extent. Otherwise, it is also reasonable and practical to let each row represent the number you would like to use as input data, but a compromise in the accuracy may arise on some occasions.

(2)

For the test of the optimization part and the verification of the fuzzy forecasting part, comparisons between MOGWO-LSTM and LSTM and comparisons between FTS-LSTM and LSTM are obviously shown in the aforementioned tables and figures, respectively. For instance, on Wednesday, the regular LSTM model achieved a MAPE of 2.81%, which is higher than the MAPE of FTS-LSTM by 39.14%. Moreover, the MOGWO-LSTM increased by 37.36% in terms of the MAPE of 1.76%. Also, the FTS-MOGWO-LSTM model possessed a MAPE of 1.46%, lower than that of the single LSTM combined with FTS or MOGWO. Noticeably, although this combined model did not have that highest r², it was not obviously lower than that of other compared models. Moreover, it was apparently higher than that of regular networks such as GRNN, WNN, DBN, SAE, and so on.

(3)

All comparisons for the electrical power load data on Wednesday and Sunday demonstrate that the decomposition methods achieved the best forecasting results. In this study, we tested different parameter settings regarding the Nstd, NR, Maxiter, and modes for EMD, EEMD, and CEEMD. The following outcomes were all acquired based on the best parameter settings for each decomposition algorithm. Table 9 and Table 10 show that the CEEMD method apparently outweighs the EEMD and EMD methods, which explains why the CEEMD was selected by us and employed in this research. Also, from Figure 10, the forecasts gained by the CEEMD model corresponded most to the real data on both Wednesday and Sunday.

Table 10. Results for the Diebold–Mariano (DM) test.

Models	Dataset A	Dataset B	Dataset C	Dataset D	Dataset E	Dataset F	Average
GRNN	3.9575	3.6231 *	4.0912 *	5.1216 *	6.8446 *	6.3102 *	7.4871 *
WNN	4.2354 *	3.8835 *	4.0655 *	5.3478 *	7.0481 *	5.5907 *	5.0285 *
CNN	6.4340 *	4.4792 *	5.4704 *	5.1895 *	6.6125 *	6.8757 *	5.8436 *
DBN	5.8905 *	5.1538 *	4.0607 *	5.7001 *	5.7287 *	6.2989 *	5.4721 *
SAE	5.9415 *	4.7566 *	4.7852 *	5.5428 *	7.7388 *	6.3725 *	5.8563 *
LSTM	4.0334 *	3.8478 *	4.3132 *	4.4067 *	7.9982 *	6.4910 *	5.1817 *
FTS-LSTM	4.9204 *	4.6690 *	5.3686 *	4.1885 *	5.1504 *	4.8412 *	4.8064 *
MOGWO-LSTM	3.6338 *	3.8032 *	3.9883 *	4.0228 *	5.4912 *	5.5515 *	4.4151 *
FTS-MOGWO-LSTM	4.4712 *	4.1507 *	3.8489 *	3.8727 *	4.0104 *	4.5032 *	4.1429 *
EMD-FTS-MOGWO-LSTM	-	-	-	-	1.9867 *	4.7634 *	3.3751 *
EEMD-FTS-MOGWO-LSTM	-	-	-	-	0.8353	2.5458 *	1.6901 *
CEEMD-FTS-MOGWO-LSTM	-	-	-	-	-	-	-

* Indicates the 1% significance level.

Remark: Based on the three experiments mentioned above, the strong applicability of the developed model in these two electrical power load signals and in different wind data sites, which feature different characteristics, reasonably and convincingly demonstrates that the CEEMD-FTS-MOGWO-LSTM model has universal applicability. Also, the CFML model performs better than all other compared benchmark models.

4. Discussion

In this section, based on the Diebold–Mariano test (DM test), we discuss and analyze the forecasting model’s statistical significance, after which we adopt the Pearson’s correlation coefficient to discuss the association strength. Then, to verify the contributions of our CFML model, the improvement percentages between different combinations of basic models are also discussed in this section. Also, the multistep-ahead forecasting of the developed model and a sensitivity analysis are conducted.

4.1. Discussion I: Statistical Significance

The DM test is widely used to demonstrate the significance of the improvement brought by the developed CFML forecasting system compared with other algorithms. Table 10 lists the specific DM test outcomes, which demonstrates that we are able to reject the null hypothesis at the 1% significance level because all of the compared models’ DM test outcomes were greater than the critical 1% significance value for all four wind speed datasets and the two electrical power load data series. Hence, we are convinced that the proposed CFML forecasting system obviously outweighs the other compared algorithms. According to this, we are able to conclude reasonably that the hybrid forecasting framework displays a significant difference in terms of the statistical level. Furthermore, this proves that the proposed CFML model is superior to the other models mentioned above and involved in wind speed forecasting.

4.2. Discussion II: Association Strength

The Pearson test can reveal the correlation strength between the predicted and actual values, which was proposed by scientist Karl Pearson. In this section, the correlation strength is discussed based on the Pearson test to prove the superiority of the proposed hybrid prediction model and all other comparative models. Specifically, if the Pearson’s correlation coefficient is equal to 0, there is no linear relationship between the two sets of data and, if the Pearson’s correlation coefficient is equal to 1, there is a linear relationship between the actual value and the predicted value. Table 11 demonstrates the outcomes of the Pearson’s test, from which we were able to obtain the conclusion that the values of all other comparative models were lower than that of the proposed CFML forecasting model, which shows that the forecasting values of the CFML model possess higher association strengths to some extent.

Table 11. Results for the Pearson’s test.

Models	Dataset A	Dataset B	Dataset C	Dataset D	Dataset E	Dataset F	Average
GRNN	0.7830	0.7252	0.5105	0.6845	0.9478	0.9376	0.7648
WNN	0.6738	0.7726	0.5528	0.7516	0.9504	0.9711	0.7787
CNN	0.5871	0.5558	0.2078	0.5892	0.9362	0.9308	0.6345
DBN	0.7122	0.7284	0.5589	0.7419	0.9444	0.9234	0.7682
SAE	0.7083	0.6608	0.6481	0.7227	0.9652	0.9487	0.7756
LSTM	0.7915	0.7855	0.6241	0.7488	0.9916	0.9916	0.8221
FTS-LSTM	0.7822	0.7632	0.6515	0.7582	0.9904	0.9910	0.8228
MOGWO-LSTM	0.7848	0.7663	0.6341	0.7515	0.9918	0.9917	0.8200
FTS-MOGWO-LSTM	0.7828	0.7663	0.6905	0.7740	0.9903	0.9907	0.8324
EMD-FTS-MOGWO-LSTM	-	-	-	-	0.9968	0.9904	0.9936
EEMD-FTS-MOGWO-LSTM	-	-	-	-	0.9957	0.9960	0.9959
CEEMD-FTS-MOGWO-LSTM	0.9369	0.9737	0.9154	0.928	0.9970	0.9990	0.9583

The values in bold indicate the best values of each benchmark function.

4.3. Discussion III: Improvement Percentage

In order to fully and clearly demonstrate the superiority of the proposed hybrid prediction system, this section discusses the percentage improvements in MAPE, RMSE, MAE, and direction accuracy (DA) between the developed system and other comparative models. These comparisons analyze and quantify how each component works in the overall prediction framework. Table 12 demonstrates the outcomes of the improvement percentages, taking dataset B and the electrical load power on Wednesday as examples, which shows the following conclusions:

Table 12. Results for the discussion of improvement percentages.

Improvement Percentages	Dataset B	Wednesday	Average	Dataset B	Wednesday	Average
	MOGWO-LSTM vs. LSTM			FTS-LSTM vs. LSTM
MAE	−1.568719	38.387067	18.409174	−2.973542	43.953213	20.489836
RMSE	−0.619646	36.98742	18.183887	−3.881903	43.697567	19.907832
MAPE	6.952491	37.366548	22.15952	8.34299	39.145907	23.744449
U2	10.180262	24.983165	17.581714	0.791078	28.242424	14.516751
Improvement Percentages	FTS-MOGWO-LSTM vs. LSTM			FTS-MOGWO-LSTM vs. MOGWO-LSTM
MAE	1.568719	50.741294	26.155007	3.088981	20.051354	11.570168
RMSE	2.387461	49.442711	25.915086	2.988589	19.766357	11.377473
MAPE	10.428737	48.042705	29.235721	3.73599	17.045455	10.390723
U2	6.76955	37.656566	22.213058	−3.797286	16.894075	6.5483945
Improvement Percentages	FTS-MOGWO-LSTM vs. FTS-LSTM			CEEMD-FTS-MOGWO-LSTM vs. MOGWO-LSTM
MAE	4.411096	12.111454	8.261275	45.94283	55.224528	50.58368
RMSE	6.035088	10.204078	8.119583	48.37892	50.396098	49.387508
MAPE	2.275601	14.619883	8.447742	45.33001	52.840909	49.085461
U2	5.804507	13.119369	9.461938	11.27635	27.648115	19.462233
Improvement Percentages	CEEMD-FTS-MOGWO-LSTM vs. FTS-MOGWO-LSTM			CEEMD-FTS-MOGWO-LSTM vs. LSTM
MAE	44.219791	43.99471	44.107251	45.09483	72.412519	58.753673
RMSE	46.788648	38.175683	42.482166	48.05905	68.743301	58.401175
MAPE	43.208279	43.150685	43.179482	49.13094	70.462633	59.796786
U2	14.522187	12.94016	13.731174	20.30865	45.723906	33.016278

(1)

By contrasting the improvement percentage between FTS-MOGWO-LSTM with FTS-LSTM and MOGWO-LSTM, we drew the conclusion that the combination of MOGWO and FTS contributes more than either FTS-LSTM or MOGWO-LSTM to the forecasting ability of the whole presented hybrid CFML forecasting model.

(2)

The comparison between the CEEMD-FTS-MOGWO-LSTM and the FTS-MOGWO-LSTM models obviously revealed the improvement brought by the addition of the decomposition approach CEEMD.

(3)

On average, all improvement percentages were positive and significant, except for the percentages of FTS-MOGWO-LSTM, as it fluctuated according to different datasets with different features. This can be studied in the future. Regardless of the fluctuations, all values revealed that FTS-MOGWO-LSTM does perform better than the regular one.

4.4. Discussion Ⅳ: Multistep-Ahead Forecasting

Now, we consider that the one-step forecasting model is sometimes insufficient to ensure the controllability and reliability of the electrical power load or wind speed forecasting system. Therefore, to test the multistep performance of the developed CFML system, the multistep prediction in this study used the two datasets listed in Table 3 (i.e., dataset A and the electrical power load on Sunday as representatives).

Table 13 illustrates the forecasting outcomes of those comparative models (i.e., GRNN, LSTM, and EEMD-FTS-MOGWO-LSTM) and the proposed CEEMD-FTS-MOGWO-LSTM forecasting model. It can be observed that for one-step, two-step, and three-step predictions using electrical power load data or wind speed data, the proposed model always achieved the lowest MAPE value in the test models. That is to say, the developed framework effectively carried out multistep-ahead forecasting in electrical power load prediction or wind speed prediction (through effective error index measurements).

Table 13. Results for the multistep-ahead forecasting.

Data	Multistep Ahead	Forecasting Models	MAE	RMSE	NMSE	MAPE	IA	FB	U1	U2	DA	r
Dataset A	One-step ahead	GRNN	0.4650	0.5723	0.0154	0.1004	0.9970	−0.0283	0.0562	0.6984	0.4949	0.7057
		LSTM	0.4364	0.5462	0.0138	0.0948	0.9973	−0.0530	0.0529	0.6470	0.4343	0.7915
		EEMD-FTS-MOGWO-LSTM	0.2513	0.3215	0.0048	0.0524	0.9990	0.0101	0.0322	0.7000	0.7778	0.9478
		CEEMD-FTS-MOGWO-LSTM	0.2314	0.2964	0.0041	0.0487	0.9992	0.0041	0.0296	0.7439	0.7374	0.9359
	Two-step ahead	GRNN	0.5546	0.6748	0.0203	0.1170	0.9959	−0.0149	0.0666	0.8160	0.3232	0.5548
		LSTM	0.4980	0.6034	0.0175	0.1058	0.9967	0.0023	0.0600	0.8169	0.4545	0.6754
		EEMD-FTS-MOGWO-LSTM	0.3725	0.4655	0.0090	0.0730	0.9980	0.0586	0.0477	0.7563	0.6263	0.8897
		CEEMD-FTS-MOGWO-LSTM	0.3121	0.3930	0.0072	0.0667	0.9986	−0.0169	0.0387	0.5739	0.6566	0.8691
	Three-step ahead	GRNN	0.5688	0.7183	0.0239	0.1262	0.9954	−0.0601	0.0694	0.8542	0.4545	0.5725
		LSTM	0.5449	0.6986	0.0213	0.1076	0.9956	0.0716	0.0719	0.8715	0.3535	0.6332
		EEMD-FTS-MOGWO-LSTM	0.4327	0.5276	0.0122	0.0877	0.9975	0.0546	0.0539	0.7566	0.6162	0.8082
		CEEMD-FTS-MOGWO-LSTM	0.3818	0.4891	0.0116	0.0840	0.9978	−0.0405	0.0478	0.7496	0.5859	0.8332
Dataset F	One-step ahead	GRNN	149.6115	190.1444	0.0013	0.0284	0.9997	−0.0033	0.0179	0.6929	0.3838	0.9376
		LSTM	92.7390	113.8205	0.0004	0.0175	0.9999	0.0005	0.0107	0.6788	0.8081	0.9916
		EEMD-FTS-MOGWO-LSTM	47.3082	60.5872	0.0001	0.0088	1.0000	0.0017	0.0057	0.4453	0.8586	0.996
		CEEMD-FTS-MOGWO-LSTM	41.1810	47.4667	0.00008	0.0079	1.0000	0.0078	0.0045	0.3802	0.8687	0.999
	Two-step ahead	GRNN	192.6101	244.0532	0.0021	0.0368	0.9995	−0.0069	0.0230	0.7653	0.3535	0.8958
		LSTM	137.3114	171.6678	0.0010	0.0258	0.9998	0.0032	0.0162	0.6710	0.4848	0.9708
		EEMD-FTS-MOGWO-LSTM	109.3356	151.5123	0.0007	0.0202	0.9998	−0.0096	0.0142	0.6495	0.6061	0.9685
		CEEMD-FTS-MOGWO-LSTM	56.0655	72.4324	0.0002	0.0105	1.0000	−0.0010	0.0068	0.4913	0.7879	0.9909
	Three-step ahead	GRNN	225.4602	287.1460	0.0029	0.0429	0.9993	−0.0092	0.0270	0.8026	0.2525	0.8480
		LSTM	225.4602	287.1460	0.0029	0.0429	0.9993	−0.0092	0.0270	0.8026	0.2525	0.8480
		EEMD-FTS-MOGWO-LSTM	139.4634	177.1613	0.0012	0.0272	0.9997	−0.0209	0.0165	0.7375	0.5859	0.9673
		CEEMD-FTS-MOGWO-LSTM	107.3264	133.4660	0.0007	0.0208	0.9999	−0.0120	0.0125	0.6643	0.6364	0.9779

4.5. Discussion V: Sensitivity Analysis

The hybrid forecasting model has two essential parameters, namely the number of iterations and the number of search agents. Hence, in this subsection, we explore the effects of these two parameters on the prediction performance of wind speed dataset A. That is, the other parameters’ values were unchanged, while the number of search agents and iterations changed. Specifically, we set the search agents as 5, 10, 15, 20, 25, and 30, and then, we kept the search agent at the value of 10, changing the values of iterations to 5, 10, 20, 30, 40, and 50. Table 14 and Table 15 illustrate the experimental outcomes of dataset A. The following conclusions were drawn:

Table 14. Sensitivity analysis of different search agent numbers based on MOGWO.

Metrics	The Value of Search Agent Number
	5	10	15	20	25	30
AE	−0.583443	−0.020492	−0.480544	−1.462529	−0.670987	−1.334932
MAE	0.613591	0.231376	0.492307	1.462529	0.680333	1.334932
RMSE	0.680007	0.296408	0.540443	1.483524	0.730494	1.349639
NMSE	0.019238	0.004058	0.011898	0.127156	0.022886	0.105523
MAPE	0.119743	0.048723	0.096181	0.294995	0.133244	0.271309
IA	0.995908	0.999202	0.997397	0.983123	0.995343	0.985745
FB	0.124580	0.004128	0.101493	0.344632	0.144625	0.309906
U1	0.071900	0.029562	0.056484	0.172524	0.077915	0.154459
U2	0.974610	0.743881	0.851054	1.010876	0.974186	1.003426
DA	0.575758	0.737374	0.626263	0.484848	0.565657	0.484848
r	0.925713	0.935871	0.969081	0.964314	0.955029	0.970766

The values in bold indicate the best values of each benchmark function.

Table 15. Sensitivity analysis of the different iteration numbers based on MOGWO.

Metrics	The Value of Iteration Number
	5	10	20	30	40	50
AE	−0.372790	−0.020492	0.288276	0.091318	0.133480	−0.398180
MAE	0.40222	0.231376	0.310034	0.350980	0.355459	0.409639
RMSE	0.474841	0.296408	0.362281	0.419625	0.438289	0.464493
NMSE	0.008926	0.004058	0.006453	0.008568	0.009241	0.009084
MAPE	0.077856	0.048723	0.068445	0.076189	0.077642	0.080769
IA	0.997962	0.999202	0.998823	0.998390	0.998213	0.998088
FB	0.077850	0.004128	−0.05631	−0.01819	−0.02647	0.083373
U1	0.049091	0.029562	0.035048	0.041391	0.043116	0.048082
U2	0.767918	0.743881	0.716270	0.726236	0.744410	0.779216
DA	0.656566	0.737374	0.666667	0.666667	0.646465	0.676768
r	0.947467	0.935871	0.969309	0.850194	0.883903	0.955046

The values in bold indicate the best values of each benchmark function.

(1)

The value of MAPE first decreased as the number of search agents increased. Then, it declined to the minimum value with 10 search agents, after which it started increasing and fluctuated at a high level except for a decrease at 25 search agents. Overall, we can see that the proposed hybrid CFML forecasting model performed the best with 10 search agents.

(2)

Keeping the number of search agents at the best value of 10, we changed the number of iterations in order to check the influence caused by the iterations on the performance of the presented model. We almost drew a similar conclusion to that of the search agents to some degree. We can see that, as the number of iterations increased from 5 to 30, the accuracy measured by various metrics, especially MAPE, first fell to the minimum value with 10 iterations and then rose gradually as the number of iteration increased. According to these two conclusions, we set the number of search agents and the number of iterations to 10 in our experiment.

(3)

It was found through the comparisons that the number of those two parameters would worsen the performance of the CEEMD-FTS-MOGWO-LSTM system proposed in this study if either they were too small or too big. In addition, different prediction conditions were shown to depend to a large extent on the decision-making process. Therefore, it is important to figure out the optimal parameters under different application conditions.

Remark: According to Discussions I to V, we can draw the conclusion that the proposed hybrid forecasting system, namely CEEMD-FTS-MOGWO-LSTM, possesses a more effective and stable forecasting ability, regarding not only the wind speed but also the electrical power load, than other models in terms of a lot of aspects, such as the correlation strength, statistical significance, and forecasting accuracy. Also, the small number of iterations and search agents demonstrates the superiority and convenience of the proposed model.

5. Conclusions

Accurate wind speed electrical power load forecasting is crucial for power grid safety management, power system operation, and the power market. However, due to the nonlinearity and randomness of wind speed data and electrical power load series, it is still a difficult and challenging task to establish an effective forecasting framework to deal with this problem. In this study, a new hybrid prediction system was developed in order to obtain stability and accuracy simultaneously. Four wind speed datasets and two electrical power load datasets were adopted to test the effectiveness of the hybrid forecasting framework. The outcomes show that our proposed system outperformed all other comparative benchmark models on many indicators. Firstly, a data preprocessing decomposition approach, named CEEMD, was successfully applied in this study to enhance the forecasting ability of the CFML forecasting model. Secondly, an effective multi-objective optimization algorithm, MOGWO, was successfully combined and used to find out the optimal initial parameters. It not only achieved better results in testing functions than the other two optimization models (NSGA-II and MODA) but also showed the best optimization capability. Moreover, fuzzy time series forecasting with the rough set induction rule, which is based on the LEM2 algorithm to build rule sets, was successfully combined with MOGWO and the deep learning algorithm, called LSTM, in this paper. It was shown that the addition of the FTS part, the MOGWO part, and the data decomposition part all bring improvements in the performance of the hybrid forecasting framework. Also, a similar method can be applied in other fields, for example, the electrical power load, which was verified in this paper. Finally, the forecasting models CEEMD, FTS, and MOGWO showed the ability to carry the strength of each component and to effectively improve the forecasting ability of the CFML forecasting model in terms of stability and accuracy.