Cost Forecasting Model of Transformer Substation Projects Based on Data Inconsistency Rate and Modified Deep Convolutional Neural Network
Abstract
:1. Introduction
2. Methodology
2.1. Modified FOA
2.1.1. FOA
- (1)
- Initialize the location of the fruit fly swarm according to Equation (1).
- (2)
- For an individual fruit fly, set the random direction and distance for food finding, as shown in Equations (2) and (3):
- (3)
- Estimate the distance between the origin point and the smell concentration of each individual fruit fly as follows:
- (4)
- Take the value of smell concentration into its judgement function; then, in light of Equation (6), obtain the smell concentration at each location
- (5)
- Find out the optimal smell concentration among the fruit fly swarm:
- (6)
- Keep a record of the optimal smell concentration as well as its , coordinates. Afterwards, the fruit flies can fly to the destination by the use of vision.
- (7)
- The iterative optimization is carried out by a repeat of Step (2) to Step (5). At each iteration, determine whether the smell concentration shows an advantage over the former one. If so, follow Step (6).
2.1.2. MFOA
2.2. DIR
- (1)
- Initialize the best subset as , namely an empty set.
- (2)
- Estimate the DIR of that are made up of subset with each residual feature.
- (3)
- Select the feature with minimum inconsistency rate as the optimal one. Then, update it in the light of .
- (4)
- Make a list of the inconsistency rates of the feature subsets. After that, sort them in ascending order.
- (5)
- Choose the feature subset with fewer characteristics. If or is the minimum ratio of all the adjacent feature subsets, is able to be screened as the optimal one, where represents the adjacent previous subset.
2.3. DCNN
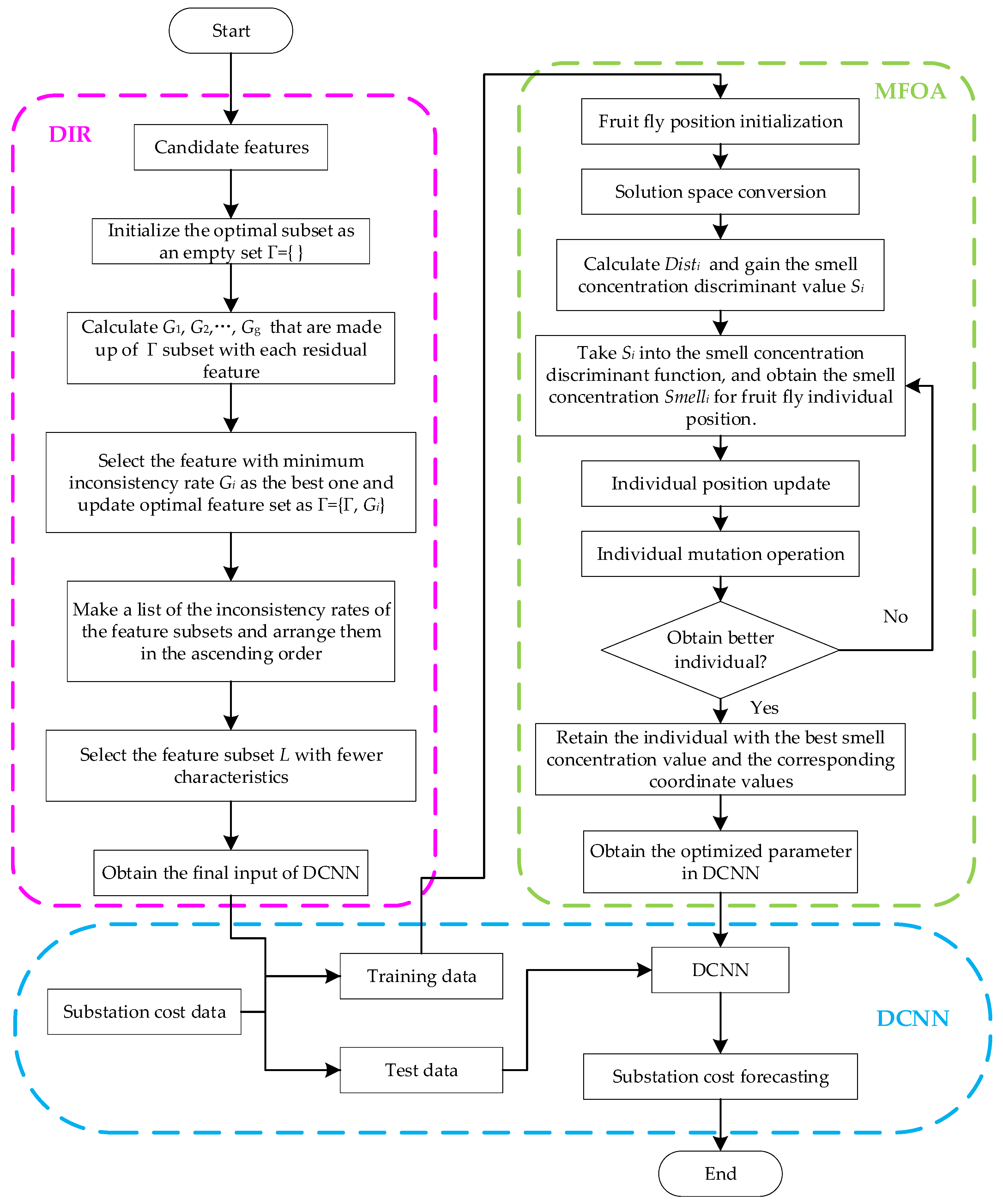
2.4. Approach of MFOA–DIR–DCNN
- (1)
- Determine the initial candidate features of substation project cost. In the DIR, initialize the optimal subset as an empty set .
- (2)
- Complete parameter initialization in the MFOA. By trying a combination of multiple parameter settings, the best parameter initialization supposes that the maximum iteration number equals 200; the scope of the fruit fly position and random flight distance are set as [0, 10] and [−1, 1], respectively.
- (3)
- Calculate inconsistency. Compute the inconsistency of that is made up of subsets with each residual feature. The feature with minimum inconsistency rate is selected as the best one, and the updated optimal feature is set as .
- (4)
- Derive the optimal feature subset along with the best values of parameters in the DCNN. The feature subset at current iteration is brought into the DCNN, and both prediction accuracy and fitness value can be calculated for this training process. Then, determine whether each iteration satisfies the termination requirements (reach the target error value or the maximum number of iterations). If not, reinitialize the feature subset and repeat the above steps until the conditions are met. It is noteworthy that the parameters in the DCNN also need to be optimized, and the initial values of weight and threshold are randomly assigned. Therefore, a fitness function based on both forecasting precision and feature selection quantity is set up, as shown in Equation (36):where represents the quantity of selected best characteristics in each iteration, and and equal the constants in [0, 1].
- (5)
- Forecast via the DCNN. When the iterative number reaches the maximum, the estimation stops. Here, the optimal feature subset, the best values of , and are taken into the DCNN model for substation project cost forecasting.
3. Case Study
3.1. Data Processing
3.2. Model Performance Evaluation
- (1)
- Relative error (RE)
- (2)
- Root mean square error (RMSE)
- (3)
- Mean absolute percentage error (MAPE)
- (4)
- Average absolute error (AAE)where is the number of testing samples, while and represent the actual value and predictive value of substation project cost, respectively. The aforementioned indicators are negatively correlated with forecasting precision.
3.3. Feature Selection
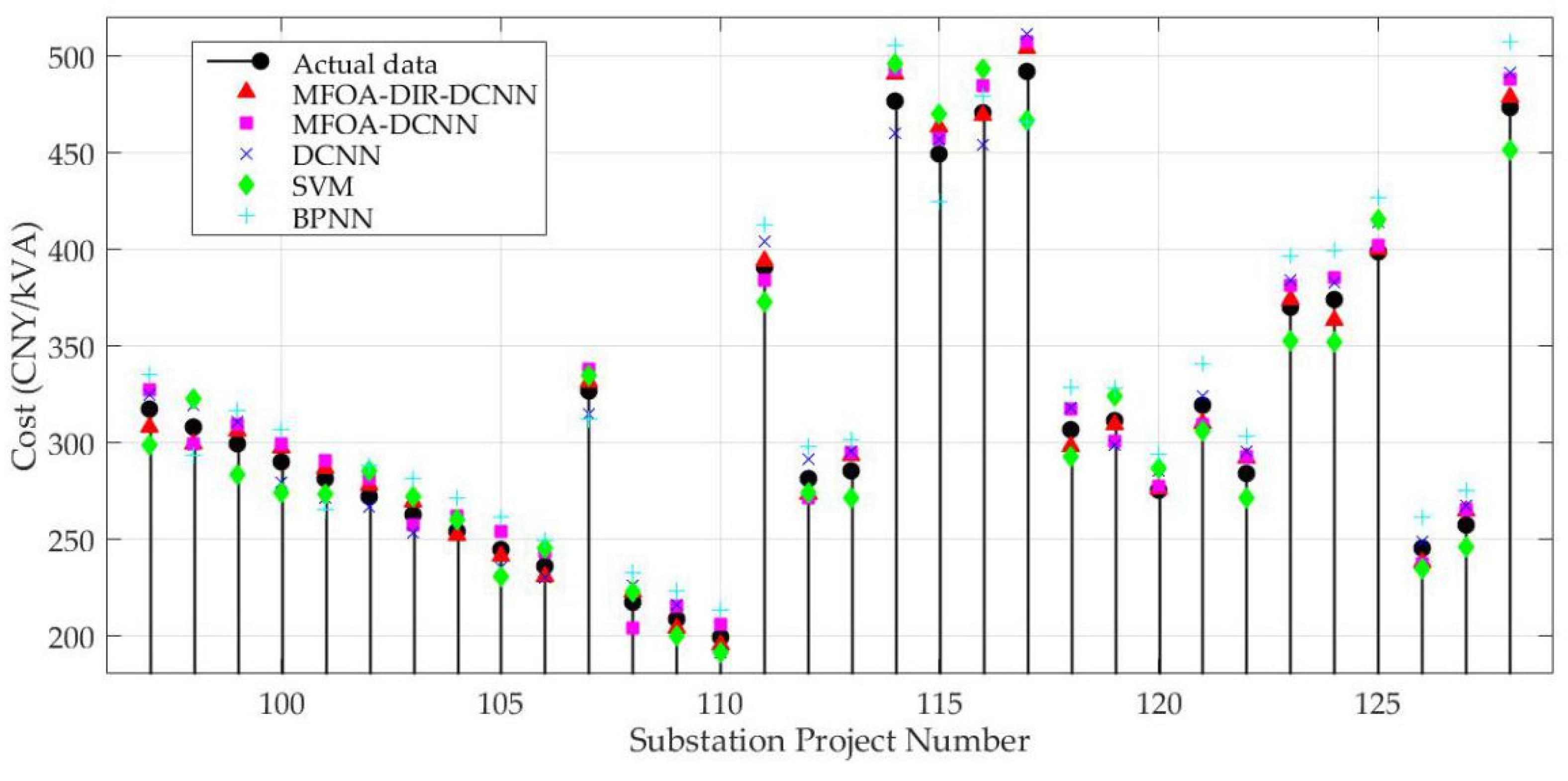
3.4. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| MFOA | modified fruit fly optimization algorithm |
| FOA | fruit fly optimization algorithm |
| DIR | data inconsistency rate |
| DCNN | deep convolutional neural network |
| ANNs | artificial neural networks |
| SVM | support vector machine |
| BPNN | back propagation neural network |
| ELM | extreme learning machine |
| RBFNN | radial basis function neural network |
| GRNN | general regression neural network |
| APSO | adaptive particle swarm optimization |
| CS | cuckoo search algorithm |
| DNN | deep neural network |
| CNN | convolutional neural network |
| RE | relative error |
| RMSE | root mean square error |
| MAPE | mean absolute percentage error |
| AAE | average absolute error |
Appendix A
| Candidate Features | Statistic Information | ||||
|---|---|---|---|---|---|
| Area | Type | <2000 m2 | >2000 m2 and <4000 m2 | >4000 m2 | |
| Statistics | 26 | 78 | 24 | ||
| Construction type | Type | New substation | Extended main transformer | Extended interval engineering | |
| Statistics | 56 | 48 | 24 | ||
| Voltage level | Type | 35 kV | 110 kV | 220 kV | |
| Statistics | 27 | 82 | 19 | ||
| Main transformer capacity | Type | <30 MVA | >30 MVA and <50 MVA | >50 MVA | |
| Statistics | 32 | 78 | 18 | ||
| High-voltage side outlet number | Type | <4 | >4 | ||
| Statistics | 64 | 64 | |||
| Low-voltage side outlet number | Type | <4 | >4 | ||
| Statistics | 86 | 42 | |||
| Topography | Type | Hillock, hillside field and flat | Plain, paddy field and rainfed cropland | mountainous region and depression | |
| Statistics | 64 | 52 | 10 | ||
| Schedule | Type | <90 days | >90 days and <180 days | >180 days | |
| Statistics | 57 | 35 | 36 | ||
| Substation type | Type | Indoor | Semi-indoor | Outdoor | |
| Statistics | 82 | 20 | 26 | ||
| Number of transformers | Type | 1 | 2 | ||
| Statistics | 27 | 101 | |||
| Economic development level | Type | <200 billion CNY | >200 billion CNY and <400 billion CNY | >400 billion CNY | |
| Statistics | 16 | 92 | 20 | ||
| Inflation rate | Type | <2% | <2% and >4% | >4% | |
| Statistics | 11 | 111 | 6 | ||
| Main transformer price | Type | <100,000 CNY | >100,000 CNY | ||
| Statistics | 26 | 102 | |||
| High-voltage side circuit breaker price | Type | <10,000 CNY | >10,000 CNY | ||
| Statistics | 45 | 83 | |||
| Number of high-voltage side breakers | Type | <2 | >2 | ||
| Statistics | 68 | 60 | |||
| Number of low voltage capacitors | Type | 1 | >1 | ||
| Statistics | 56 | 72 | |||
| High voltage fuse price | Type | <500 CNY | >500 CNY | ||
| Statistics | 59 | 69 | |||
| Current transformer price | Type | <10,000 CNY | >10,000 CNY | ||
| Statistics | 23 | 105 | |||
| Power capacitor price | Type | <100,000 CNY | >100,000 CNY | ||
| Statistics | 89 | 39 | |||
| Reactor price | Type | <5000 CNY | >5000 CNY | ||
| Statistics | 57 | 71 | |||
| Power bus price | Type | <2000 CNY/m | >2000 CNY/m | ||
| Statistics | 69 | 59 | |||
| Arrester price | Type | <2000 CNY | >2000 CNY | ||
| Statistics | 76 | 52 | |||
| Measuring instrument price | Type | <10,000 CNY | >10,000 CNY | ||
| Statistics | 39 | 89 | |||
| Relay protection device price | Type | <10,000 CNY | >10,000 CNY | ||
| Statistics | 40 | 88 | |||
| Signal system price | Type | <100,000 CNY | >100,000 CNY | ||
| Statistics | 44 | 84 | |||
| Automatic device price | Type | <20,000 CNY | >20,000 CNY | ||
| Statistics | 90 | 38 | |||
| Site leveling cost | Type | <500,000 CNY | >500,000 CNY | ||
| Statistics | 65 | 63 | |||
| Foundation treatment cost | Type | <1,000,000 CNY | >1,000,000 CNY | ||
| Statistics | 76 | 52 | |||
| Technical level of the designers | Type | <50% | >50% and >80% | >80% | |
| Statistics | 19 | 83 | 26 | ||
| Number of accidents | Type | 0 | >0 | ||
| Statistics | 122 | 6 | |||
| Engineering deviation rate | Type | <15% | >15% | ||
| Statistics | 107 | 21 | |||
| Construction progress level | Type | 0 day | >0 day and <15 days | >15 days | |
| Statistics | 96 | 15 | 17 | ||
| Rainy and snowy days | Type | <7 days | >7 days and <14 days | >14 days | |
| Statistics | 48 | 67 | 13 | ||
References
- Pal, A.; Vullikanti, A.K.S.; Ravi, S.S. A PMU Placement Scheme Considering Realistic Costs and Modern Trends in Relaying. IEEE Trans. Power Syst. 2017, 32, 552–561. [Google Scholar] [CrossRef]
- Heydt, G.T. A Probabilistic Cost/Benefit Analysis of Transmission and Distribution Asset Expansion Projects. IEEE Trans. Power Syst. 2017, 32, 4151–4152. [Google Scholar] [CrossRef]
- Hu, L.X. Research on Prediction of Architectural Engineering Cost based on the Time Series Method. J. Taiyuan Univ. Technol. 2012, 43, 706–709. [Google Scholar]
- Wei, L.; Yuan, Y.-n.; Dong, W.-d.; Zhang, B. Study on engineering cost forecasting of electric power construction based on time response function optimization grey model. In Proceedings of the IEEE, International Conference on Communication Software and Networks, Xi’an, China, 27–29 May 2011; pp. 58–61. [Google Scholar]
- Wei, L. A Model of Building Project Cost Estimation Based on Multiple Structur Integral Linear Regression. Archit. Technol. 2015, 46, 846–849. [Google Scholar]
- Li, J.; Wang, R.; Wang, J.; Li, Y. Analysis and forecasting of the oil consumption in China based on combination models optimized by artificial intelligence algorithms. Energy 2018, 144, 243–264. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, L.; Du, R.; Wang, C.; Chen, L.; Tian, L.; Stanley, H.E. A novel hybrid method of forecasting crude oil prices using complex network science and artificial intelligence algorithms. Appl. Energy 2018, 220, 480–495. [Google Scholar] [CrossRef]
- Ling, Y.P.; Yan, P.F.; Han, C.Z.; Yang, C.G. BP Neural Network Based Cost Prediction Model for Transmission Projects. Electr. Power 2012, 45, 95–99. [Google Scholar]
- Liang, Y.; Niu, D.; Cao, Y.; Hong, W.C. Analysis and Modeling for China’s Electricity Demand Forecasting Using a Hybrid Method Based on Multiple Regression and Extreme Learning Machine: A View from Carbon Emission. Energies 2016, 9, 941. [Google Scholar] [CrossRef]
- Liu, J.; Qing, Y.E. Project Cost Prediction Model Based on BP and RBP Neural Networks in Xiamen City. J. Huaqiao Univ. 2013, 34, 576–580. [Google Scholar]
- Niu, D.; Liang, Y.; Hong, W.C. Wind Speed Forecasting Based on EMD and GRNN Optimized by FOA. Energies 2017, 10, 2001. [Google Scholar] [CrossRef]
- Nieto, P.G.; Lasheras, F.S.; García-Gonzalo, E.; de Cos Juez, F.J. PM 10, concentration forecasting in the metropolitan area of Oviedo (Northern Spain) using models based on SVM, MLP, VARMA and ARIMA: A case study. Sci. Total Environ. 2018, 621, 753–761. [Google Scholar] [CrossRef]
- Peng, G.; Si, H.; Yu, J.; Yang, Y.; Li, S.; Tan, K. Modification and application of SVM algorithm. Comput. Eng. Appl. 2011, 47, 218–221. [Google Scholar]
- Niu, D.; Zhao, W.; Li, S.; Chen, R. Cost Forecasting of Substation Projects Based on Cuckoo Search Algorithm and Support Vector Machines. Sustainability 2018, 10, 118. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, Q.; Tang, M.; Nie, W.; Ma, S.; Xu, Z. Comparison of two optimized machine learning models for predicting displacement of rainfall-induced landslide: A case study in Sichuan Province, China. Eng. Geol. 2017, 218, 213–222. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Larson, D.B.; Chen, M.C.; Lungren, M.P.; Halabi, S.S.; Stence, N.V.; Langlotz, C.P. Performance of a Deep-Learning Neural Network Model in Assessing Skeletal Maturity on Pediatric Hand Radiographs. Radiology 2017, 287, 313–322. [Google Scholar] [CrossRef]
- Siddiqui, S.A.; Salman, A.; Malik, M.I.; Shafait, F.; Mian, A.; Shortis, M.R.; Harvey, E.S. Automatic fish species classification in underwater videos: Exploiting pretrained deep neural network models to compensate for limited labelled data. Ices J. Mar. Sci. 2018, 75, 374–389. [Google Scholar] [CrossRef]
- Yu, X.; Dong, H. PTL-CFS based deep convolutional neural network model for remote sensing classification. Computing 2018, 100, 773–785. [Google Scholar] [CrossRef]
- Chen, Y.H.; Krishna, T.; Emer, J.S.; Sze, V. Eyeriss: An Energy-Efficient Reconfigurable Accelerator for Deep Convolutional Neural Networks. IEEE J. Solid State Circuits 2017, 52, 127–138. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Wang, H.; Yi, H.; Peng, J.; Wang, G.; Liu, Y.; Jiang, H.; Liu, W. Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network. Energy Convers. Manag. 2017, 153, 409–422. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, G.Q.; Wang, G.B.; Peng, J.C.; Jiang, H.; Liu, Y.T. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart deep learning based wind speed prediction model using wavelet packet decomposition, convolutional neural network and convolutional long short term memory network. Energy Convers. Manag. 2018, 166, 120–131. [Google Scholar] [CrossRef]
- Gunduz, H.; Yaslan, Y.; Cataltepe, Z. Intraday prediction of Borsa Istanbul using convolutional neural networks and feature correlations. Knowl. Based Syst. 2017, 137, 138–148. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep Convolutional Neural Network for Inverse Problems in Imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Pan, W.T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl. Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, W.N.; Yu, Z.; Gu, T.; Li, Y.; Zhang, H.; Zhang, J. Adaptive Multimodal Continuous Ant Colony Optimization. IEEE Trans. Evol. Comput. 2017, 21, 191–205. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Lin, J.; Sheng, G.; Yan, Y.; Dai, J.; Jiang, X. Prediction of Dissolved Gas Concentrations in Transformer Oil Based on the KPCA-FFOA-GRNN Model. Energies 2018, 11, 225. [Google Scholar] [CrossRef]
- Niu, D.; Ma, T.; Liu, B. Power load forecasting by wavelet least squares support vector machine with improved fruit fly optimization algorithm. J. Comb. Optim. 2016, 33, 1122–1143. [Google Scholar]
- Hu, R.; Wen, S.; Zeng, Z.; Huang, T. A short-term power load forecasting model based on the generalized regression neural network with decreasing step fruit fly optimization algorithm. Neurocomputing 2017, 221, 24–31. [Google Scholar] [CrossRef]
- Cao, G.; Wu, L. Support vector regression with fruit fly optimization algorithm for seasonal electricity consumption forecasting. Energy 2016, 115, 734–745. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, K.; Wang, J.; Zhang, W.; Leng, W. A Hybrid Model Based on Ensemble Empirical Mode Decomposition and Fruit Fly Optimization Algorithm for Wind Speed Forecasting. Adv. Meteorol. 2016, 2016, 3768242. [Google Scholar] [CrossRef]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl. Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Song, Z.; Niu, D.; Xiao, X.; Zhu, L. Substation Engineering Cost Forecasting Method Based on Modified Firefly Algorithm and Support Vector Machine. Electr. Power 2017, 50, 168–178. [Google Scholar]
- Zhang, C.; Kumar, A.; Ré, C. Materialization Optimizations for Feature Selection Workloads. ACM Trans. Database Syst. 2016, 41, 2. [Google Scholar] [CrossRef]
- Niu, D.; Wang, H.; Chen, H.; Liang, Y. The General Regression Neural Network Based on the Fruit Fly Optimization Algorithm and the Data Inconsistency Rate for Transmission Line Icing Prediction. Energies 2017, 10, 2066. [Google Scholar]
- Chen, T.; Ma, J.; Huang, S.H.; Cai, A. Novel and efficient method on feature selection and data classification. J. Comput. Res. Dev. 2012, 49, 735–745. [Google Scholar]
- Liu, J.P.; Li, C.L. The Short-Term Power Load Forecasting Based on Sperm Whale Algorithm and Wavelet Least Square Support Vector Machine with DWT-IR for Feature Selection. Sustainability 2017, 9, 1188. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Liu, Y. A least squares support vector machine model optimized by moth-flame optimization algorithm for annual power load forecasting. Appl. Intell. 2016, 45, 1166–1178. [Google Scholar] [CrossRef]
- Wu, L.; Cao, G. Seasonal SVR with FOA algorithm for single-step and multi-step ahead forecasting in monthly inbound tourist flow. Knowl. Based Syst. 2016, 110, 157–166. [Google Scholar]
- Iscan, H.; Gunduz, M. A Survey on Fruit Fly Optimization Algorithm. In Proceedings of the International Conference on Signal-Image Technology & Internet-Based Systems. IEEE Computer Society, Bangkok, Thailand, 23–27 November 2015; pp. 520–527. [Google Scholar]
- Zhang, F.; Cai, N.; Wu, J.; Cen, G.; Wang, H.; Chen, X. Image denoising method based on a deep convolution neural network. IET Image Process. 2018, 12, 485–493. [Google Scholar] [CrossRef]
- Lu, Y.; Niu, D.; Qiu, J.; Liu, W. Prediction Technology of Power Transmission and Transformation Project Cost Based on the Decomposition-Integration. Math. Probl. Eng. 2015, 2015, 651878. [Google Scholar] [CrossRef]
- Kang, J.X.; Ai, L.S.; Zhang, X.R.; LIU, S.M.; CAO, Y.; MA, L.; CHENG, Z.H. Analysis of Substation Project Cost Influence Factors. J. Northeast Dianli Univ. 2011, 31, 131–136. (In Chinese) [Google Scholar]
- Zhang, L.; Zhou, W.; Jiao, L. Wavelet support vector machine. IEEE Trans. Syst. Man Cybern. Soc. 2004, 34, 34–39. [Google Scholar] [CrossRef]





| Serial Number | Cost | Serial Number | Cost | Serial Number | Cost | Serial Number | Cost |
|---|---|---|---|---|---|---|---|
| 1 | 358.3 | 33 | 980.6 | 65 | 336.8 | 97 | 317.1 |
| 2 | 324.2 | 34 | 286.8 | 66 | 339.5 | 98 | 308.0 |
| 3 | 368.9 | 35 | 279.5 | 67 | 342.1 | 99 | 298.9 |
| 4 | 370.2 | 36 | 308.6 | 68 | 344.7 | 100 | 289.9 |
| 5 | 450.1 | 37 | 312.8 | 69 | 244.2 | 101 | 280.8 |
| 6 | 266.5 | 38 | 315.9 | 70 | 346.8 | 102 | 271.7 |
| 7 | 301.6 | 39 | 364.2 | 71 | 349.5 | 103 | 262.6 |
| 8 | 325.8 | 40 | 361.3 | 72 | 352.1 | 104 | 253.5 |
| 9 | 310.3 | 41 | 375.6 | 73 | 394.7 | 105 | 244.5 |
| 10 | 405.6 | 42 | 389.9 | 74 | 405.6 | 106 | 235.4 |
| 11 | 392.5 | 43 | 372.5 | 75 | 428.2 | 107 | 326.3 |
| 12 | 448.2 | 44 | 383.9 | 76 | 443.0 | 108 | 217.2 |
| 13 | 305.8 | 45 | 295.6 | 77 | 459.8 | 109 | 208.1 |
| 14 | 356.9 | 46 | 270.2 | 78 | 493.3 | 110 | 199.1 |
| 15 | 1058.6 | 47 | 260.8 | 79 | 289.4 | 111 | 390.0 |
| 16 | 501.2 | 48 | 240.7 | 80 | 293.7 | 112 | 280.9 |
| 17 | 337.1 | 49 | 223.3 | 81 | 297.9 | 113 | 285.1 |
| 18 | 304.5 | 50 | 239.3 | 82 | 402.2 | 114 | 476.5 |
| 19 | 291.8 | 51 | 381.7 | 83 | 491.5 | 115 | 449.3 |
| 20 | 279.2 | 52 | 406.9 | 84 | 491.3 | 116 | 470.4 |
| 21 | 299.3 | 53 | 315.6 | 85 | 212.6 | 117 | 491.8 |
| 22 | 285.6 | 54 | 285.5 | 86 | 452.6 | 118 | 306.4 |
| 23 | 305.5 | 55 | 252.5 | 87 | 353.7 | 119 | 310.7 |
| 24 | 208.6 | 56 | 214.5 | 88 | 254.8 | 120 | 274.9 |
| 25 | 356.2 | 57 | 325.8 | 89 | 155.9 | 121 | 319.2 |
| 26 | 401.5 | 58 | 328.4 | 90 | 375.9 | 122 | 283.4 |
| 27 | 378.6 | 59 | 311.1 | 91 | 375.9 | 123 | 369.5 |
| 28 | 369.5 | 60 | 333.7 | 92 | 397.0 | 124 | 373.8 |
| 29 | 253.8 | 61 | 336.3 | 93 | 418.1 | 125 | 398.6 |
| 30 | 300.5 | 62 | 309.0 | 94 | 344.3 | 126 | 244.8 |
| 31 | 272.7 | 63 | 341.6 | 95 | 335.3 | 127 | 256.9 |
| 32 | 423.4 | 64 | 334.2 | 96 | 326.2 | 128 | 472.9 |
| Serial Number | Actual Value | BPNN | SVM | DCNN | MFOA–DCNN | MFOA–DIR–DCNN |
|---|---|---|---|---|---|---|
| 97 | 317.1 | 335.3 | 298.3 | 324.3 | 326.7 | 308.0 |
| 98 | 308.0 | 292.9 | 322.4 | 318.8 | 298.7 | 298.8 |
| 99 | 298.9 | 316.3 | 283.1 | 310.5 | 308.7 | 305.9 |
| 100 | 289.9 | 306.6 | 273.4 | 278.8 | 298.9 | 297.2 |
| 101 | 280.8 | 265.2 | 273.0 | 270.9 | 290.1 | 286.5 |
| 102 | 271.7 | 288.0 | 284.7 | 266.1 | 281.1 | 278.0 |
| 103 | 262.6 | 281.0 | 271.5 | 253.2 | 257.3 | 269.0 |
| 104 | 253.5 | 270.9 | 259.8 | 257.5 | 261.9 | 251.6 |
| 105 | 244.5 | 261.1 | 230.3 | 234.7 | 253.5 | 240.9 |
| 106 | 235.4 | 248.7 | 244.8 | 229.6 | 243.1 | 230.2 |
| 107 | 326.3 | 312.0 | 334.1 | 314.3 | 337.9 | 330.8 |
| 108 | 217.2 | 232.5 | 222.4 | 225.9 | 203.9 | 222.5 |
| 109 | 208.1 | 222.8 | 199.6 | 216.0 | 215.1 | 203.8 |
| 110 | 199.1 | 212.8 | 191.0 | 191.2 | 205.4 | 194.7 |
| 111 | 390.0 | 412.0 | 372.3 | 403.8 | 383.8 | 393.9 |
| 112 | 280.9 | 297.5 | 273.8 | 290.7 | 271.2 | 273.3 |
| 113 | 285.1 | 300.8 | 271.1 | 295.3 | 294.6 | 293.1 |
| 114 | 476.5 | 504.8 | 495.9 | 459.6 | 492.4 | 490.0 |
| 115 | 449.3 | 424.1 | 469.9 | 456.0 | 456.9 | 462.7 |
| 116 | 470.4 | 479.0 | 493.3 | 453.7 | 484.6 | 468.8 |
| 117 | 491.8 | 465.7 | 466.3 | 511.1 | 507.0 | 503.6 |
| 118 | 306.4 | 328.1 | 292.3 | 317.4 | 316.8 | 298.0 |
| 119 | 310.7 | 328.0 | 323.9 | 298.3 | 300.6 | 309.1 |
| 120 | 274.9 | 294.0 | 286.4 | 285.3 | 277.1 | 275.6 |
| 121 | 319.2 | 340.2 | 305.5 | 323.8 | 308.8 | 309.7 |
| 122 | 283.4 | 303.3 | 271.2 | 294.7 | 292.6 | 291.4 |
| 123 | 369.5 | 396.0 | 352.3 | 383.5 | 381.0 | 373.7 |
| 124 | 373.8 | 399.2 | 351.6 | 382.3 | 385.1 | 363.1 |
| 125 | 398.6 | 426.2 | 415.1 | 413.6 | 401.8 | 399.5 |
| 126 | 244.8 | 260.9 | 234.3 | 248.3 | 236.9 | 237.5 |
| 127 | 256.9 | 274.9 | 245.8 | 267.2 | 265.2 | 264.2 |
| 128 | 472.9 | 506.9 | 451.0 | 490.8 | 487.6 | 478.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Huang, Y.; Gao, C.; Jiang, Y. Cost Forecasting Model of Transformer Substation Projects Based on Data Inconsistency Rate and Modified Deep Convolutional Neural Network. Energies 2019, 12, 3043. https://doi.org/10.3390/en12163043
Wang H, Huang Y, Gao C, Jiang Y. Cost Forecasting Model of Transformer Substation Projects Based on Data Inconsistency Rate and Modified Deep Convolutional Neural Network. Energies. 2019; 12(16):3043. https://doi.org/10.3390/en12163043
Chicago/Turabian StyleWang, Hongwei, Yuansheng Huang, Chong Gao, and Yuqing Jiang. 2019. "Cost Forecasting Model of Transformer Substation Projects Based on Data Inconsistency Rate and Modified Deep Convolutional Neural Network" Energies 12, no. 16: 3043. https://doi.org/10.3390/en12163043
APA StyleWang, H., Huang, Y., Gao, C., & Jiang, Y. (2019). Cost Forecasting Model of Transformer Substation Projects Based on Data Inconsistency Rate and Modified Deep Convolutional Neural Network. Energies, 12(16), 3043. https://doi.org/10.3390/en12163043




