Transient Stress Distribution and Failure Response of a Wellbore Drilled by a Periodic Load
Abstract
:1. Introduction
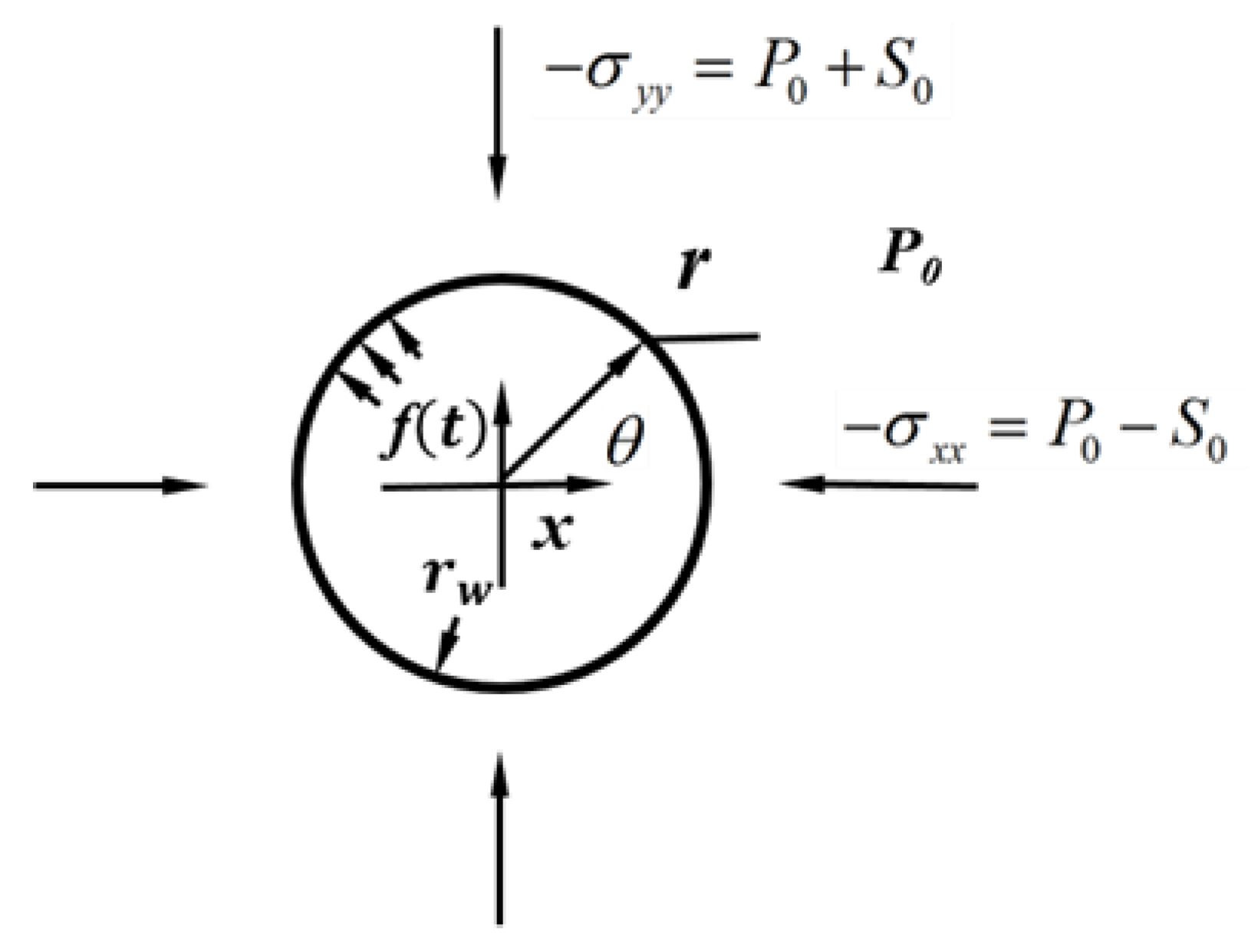
2. Mathematical Formulation
2.1. Constitutive and Dynamic Equations
2.2. Fluid Flow Equation
2.3. Dimensionless Governing Equations
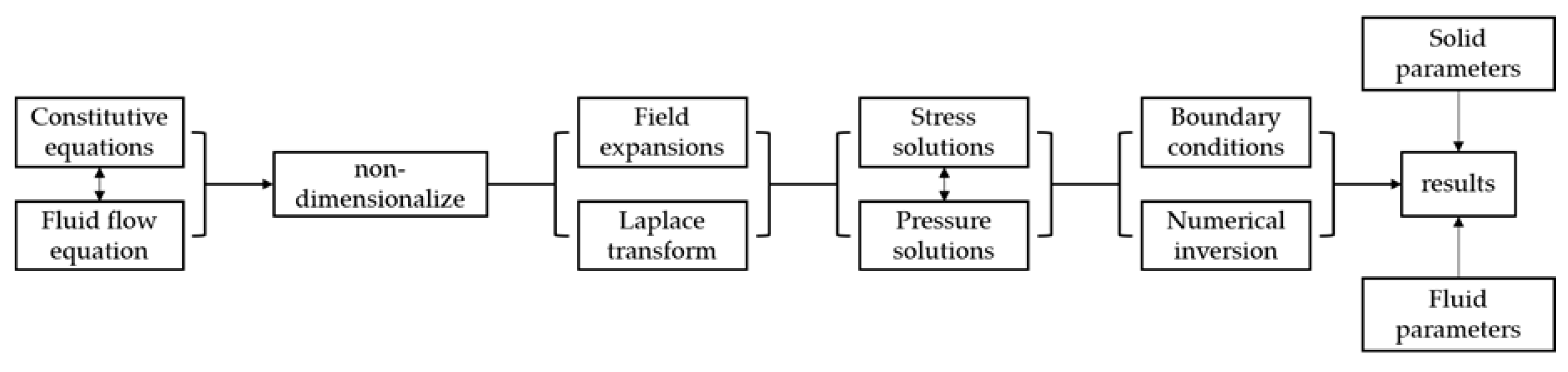
3. Solution Strategy
3.1. Field Expansions
3.2. Solutions in the Laplace Domain
3.3. Boundary Conditions
3.4. Numerical Method
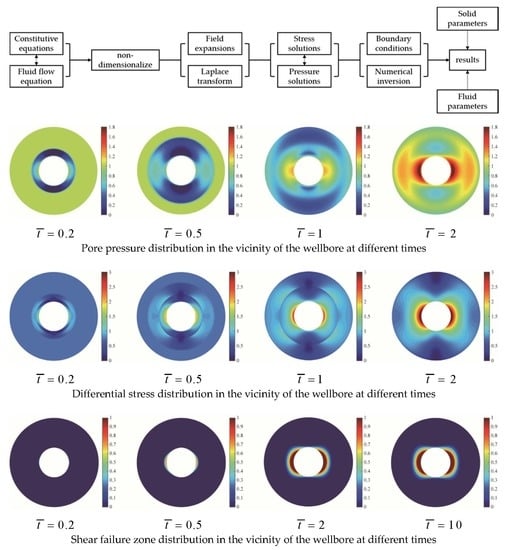
4. Stress Distribution and Failure Responses
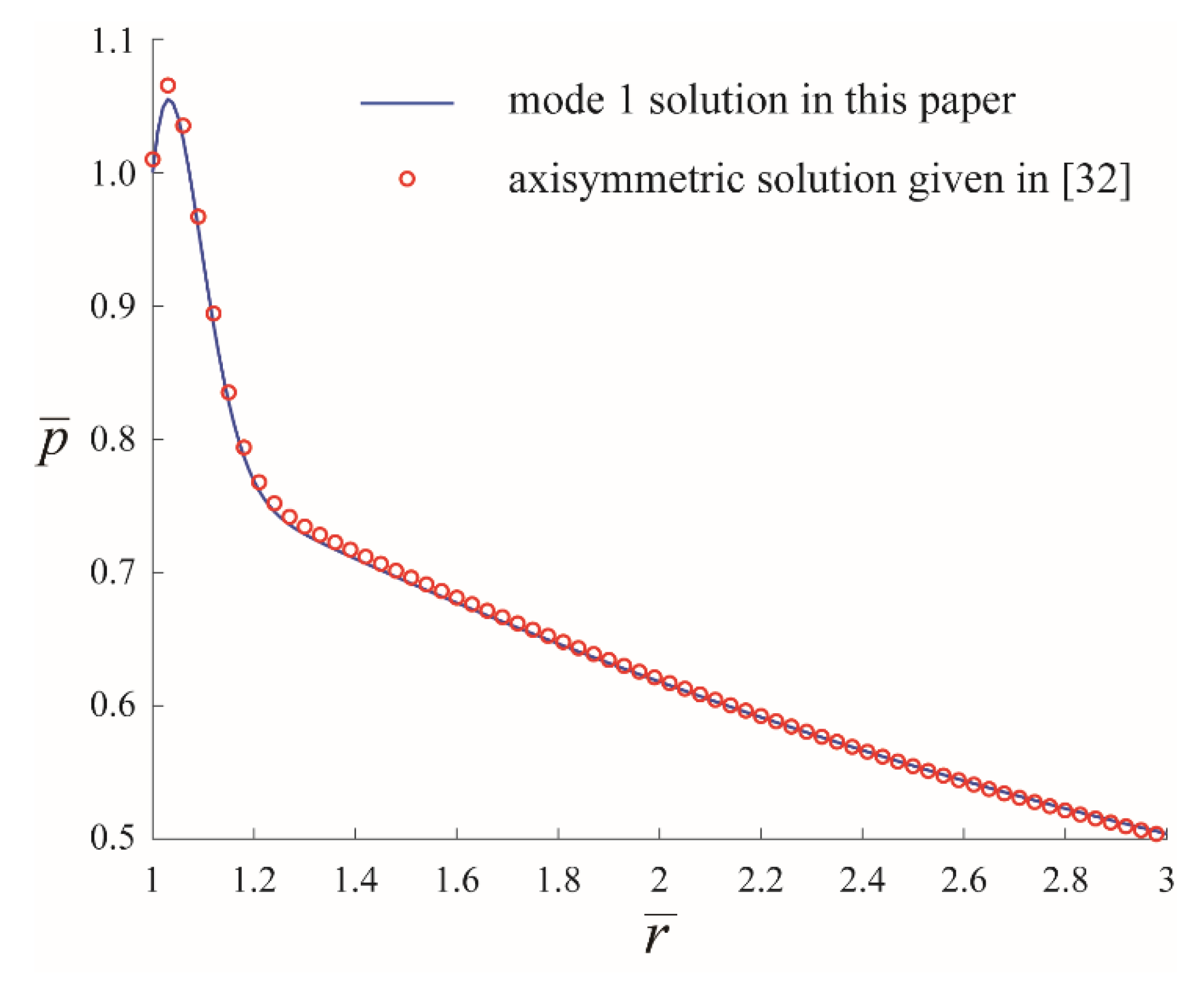
4.1. Model Verification
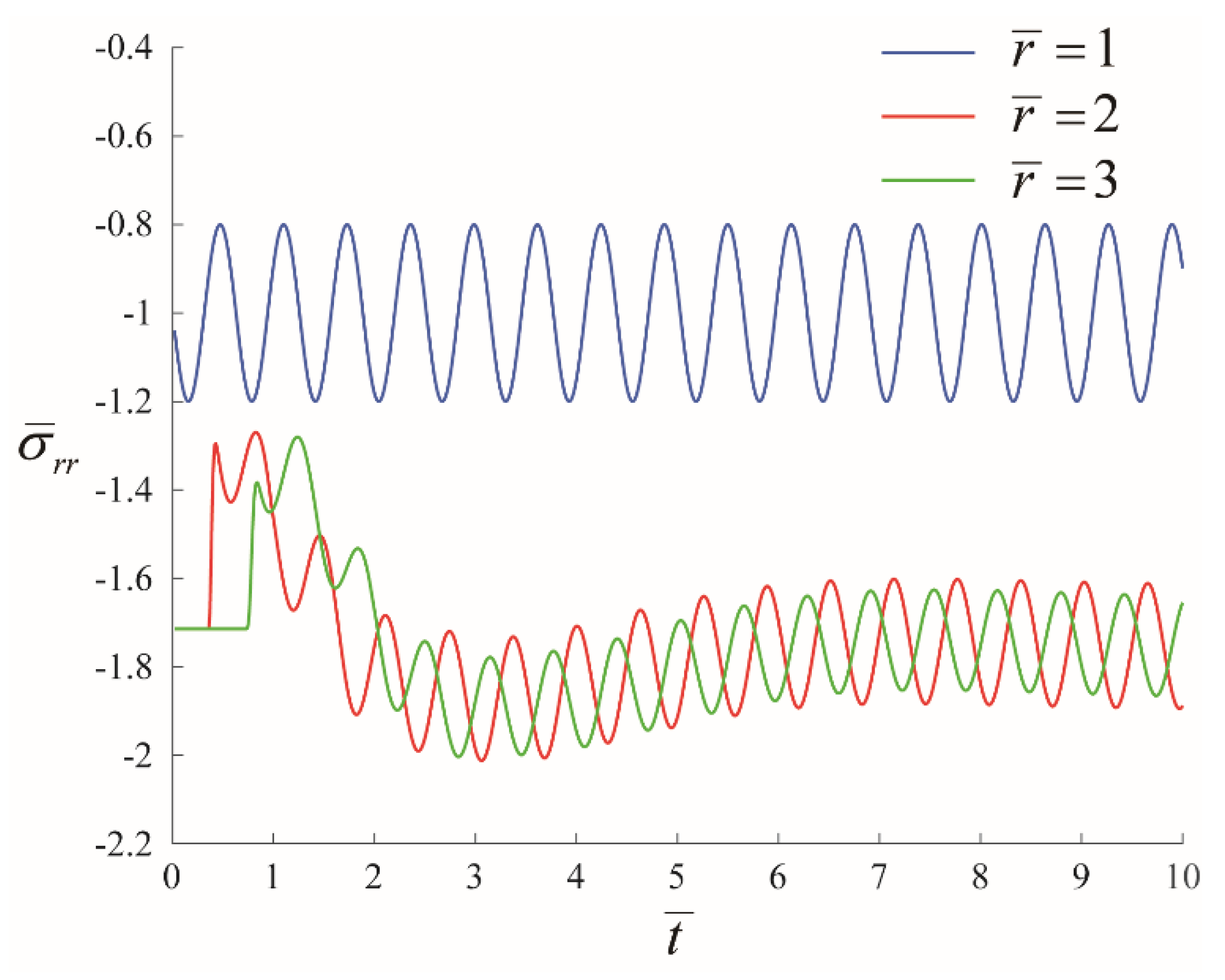
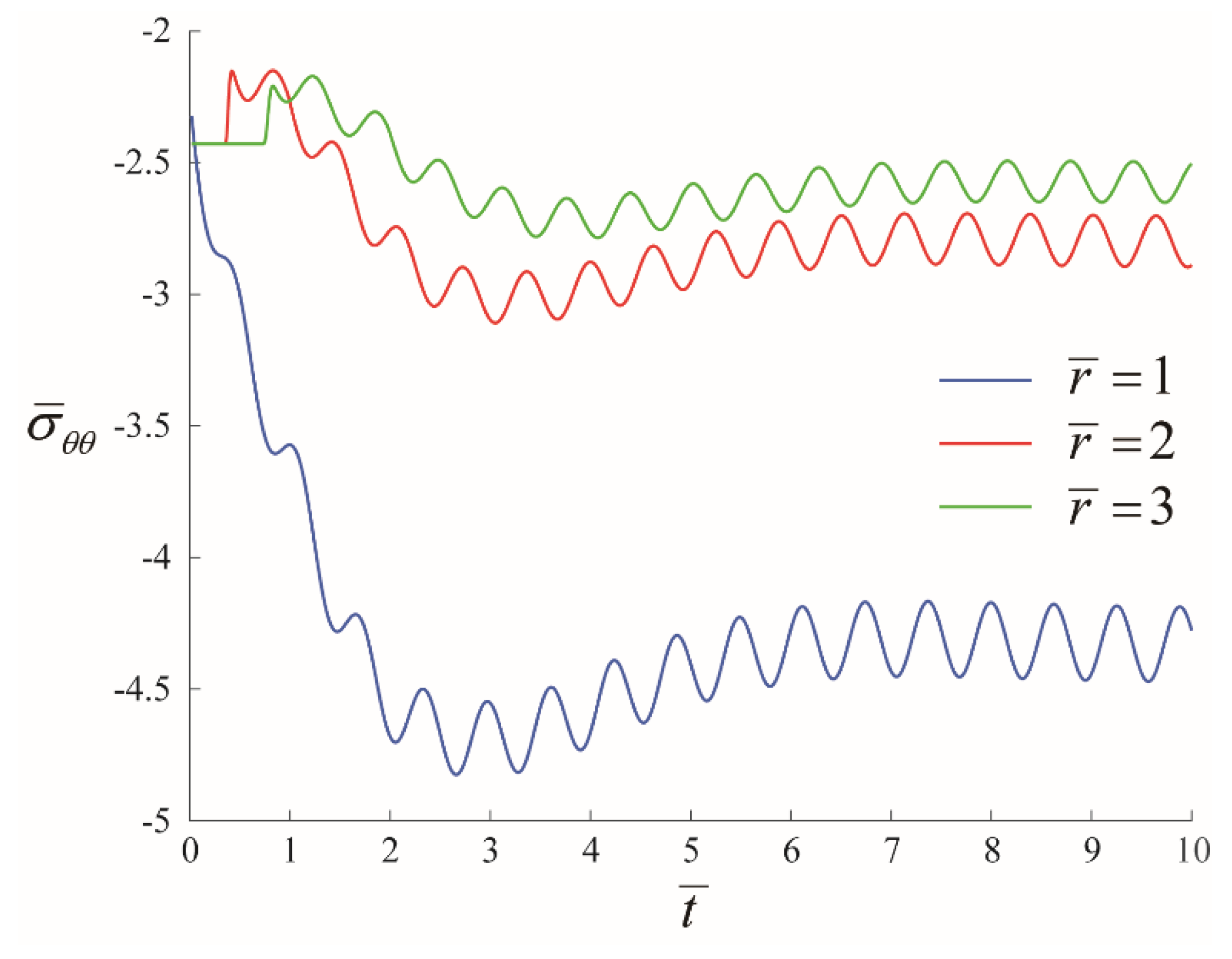
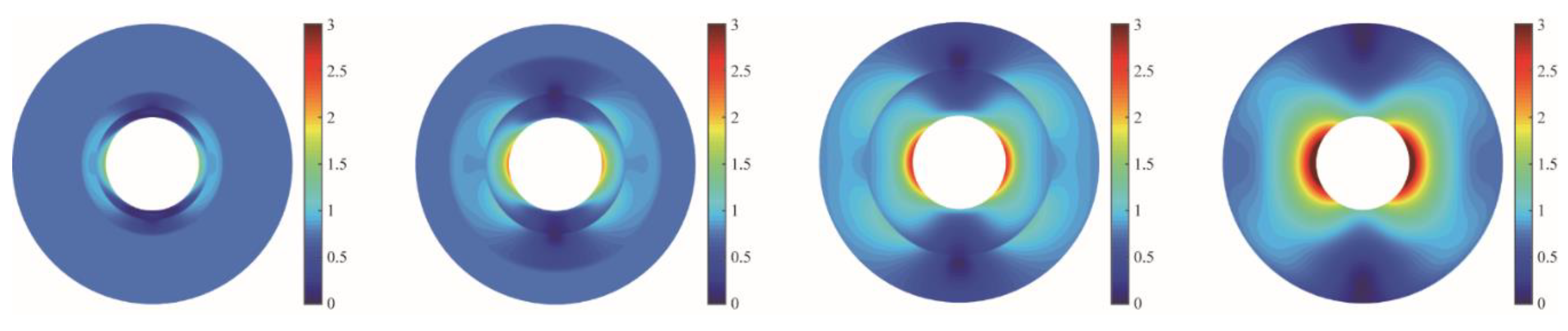
4.2. Dynamic Distributions of Stress Components and Pressure
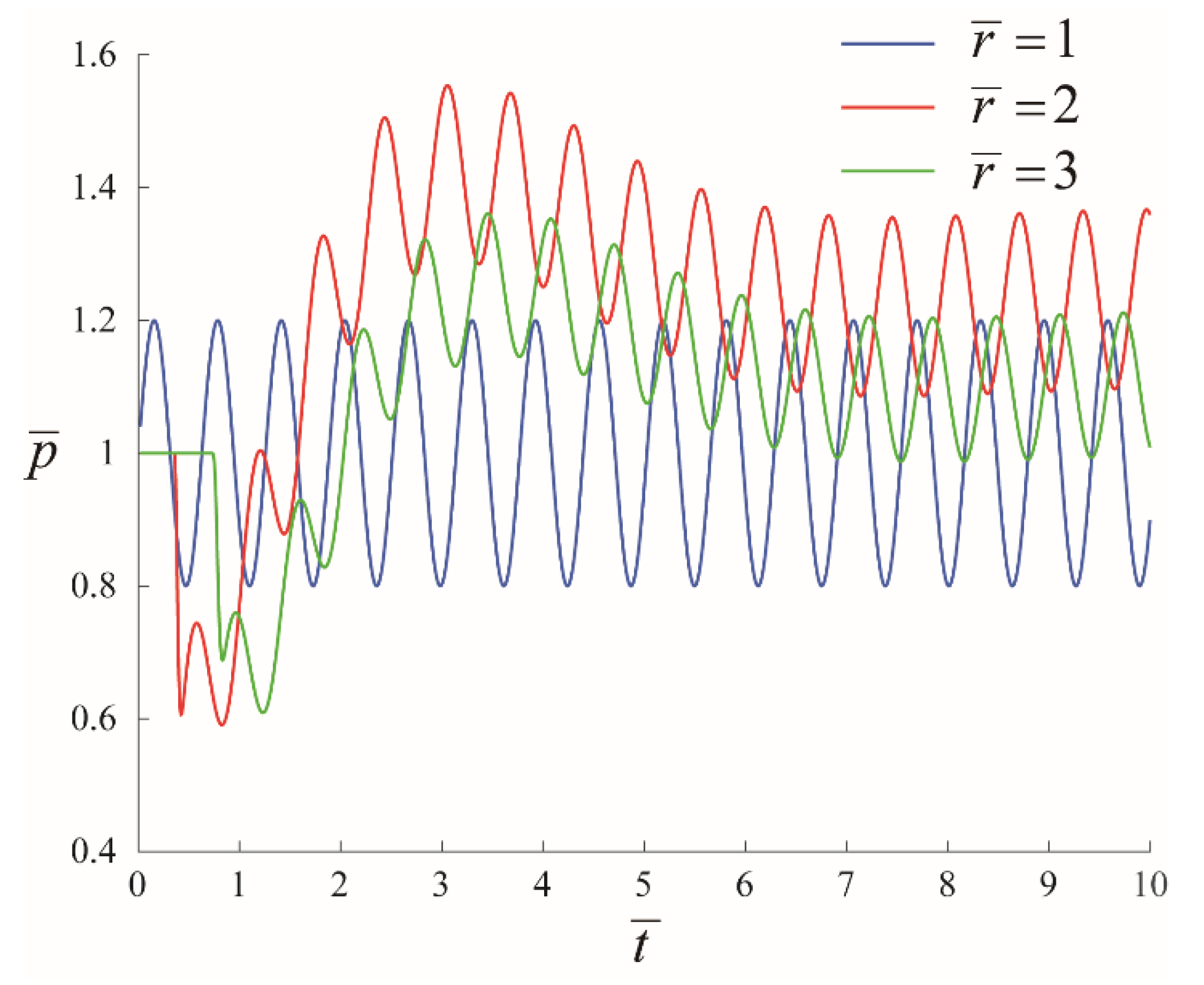
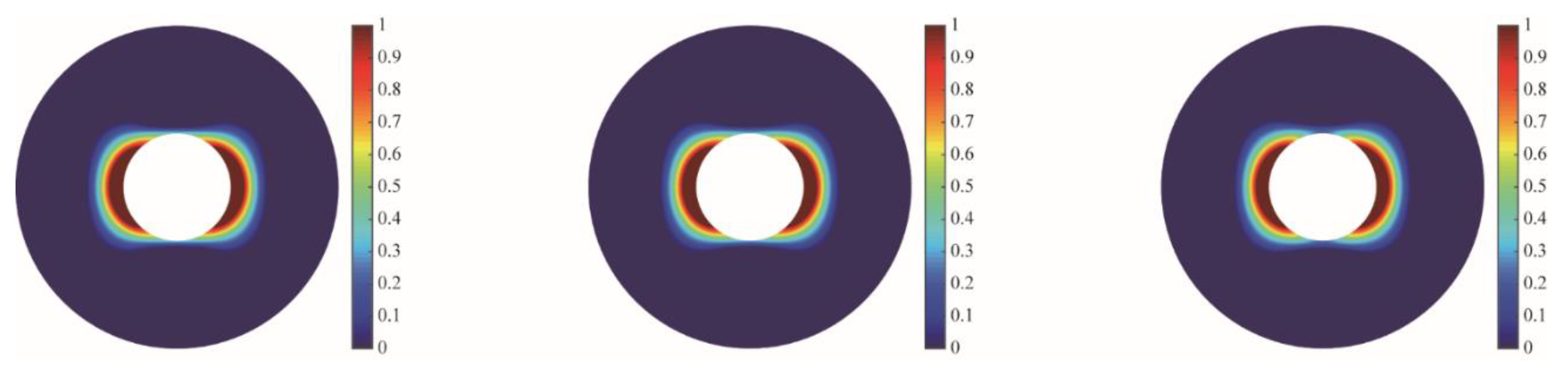
4.3. Failure Responses
4.3.1. Effect of Poroelastic Parameters
4.3.2. Effect of In-Situ Stress
4.3.3. Effect of Periodic Loads
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Unit | Definition |
|---|---|---|
| m | Radius defined in Figure 1 | |
| Angle defined in Figure 1 | ||
| m | Radius of the borehole | |
| , | MPa | Far-field mean and deviatoric parts of the stress |
| , | m | Displacement components of the solid |
| , | m | Displacement components of the fluid |
| MPa | Stress component | |
| , , | MPa | Radial stress, hoop stress and shear stress |
| Strain component | ||
| Volumetric strain | ||
| MPa | Excess pore water pressure | |
| MPa | Constant bottom-hole pressure | |
| MPa | Transient bottom-hole pressure | |
| Kronecker delta. when and when | ||
| GPa | Lame constant of the bulk material | |
| GPa | Shear modulus of the bulk material | |
| Increment of pore fluid per unit volume | ||
| Biot effective stress coefficient | ||
| GPa | Biot modulus | |
| GPa | Bulk modulus of solid grains | |
| GPa | Bulk modulus of pore fluid | |
| GPa | Drained bulk modulus of the porous medium | |
| Kg·m−3 | Density of porous medium | |
| Kg·m−3 | Density of porous fluid | |
| s | Time | |
| , , | m3 | Volumes of the porous medium, solid grains and pores |
| MPa | Effective stress vector of the porous medium | |
| m3·s−1·m−2 | Volumetric flux of pore fluid | |
| Kg·m−3 | Mass density of the fluid added into the porous medium | |
| Porosity of the porous medium | ||
| mD(10−15m2) | Permeability of the porous medium | |
| mPa·s | Viscosity of the porous fluid | |
| MPa | Unperturbed pore pressure | |
| MPa | Amplitude of stress wave | |
| s−1 | Angular frequency of stress wave | |
| ° | Internal friction angle | |
| MPa | Cohesion | |
| MPa | Maximum principal stress | |
| MPa | Minimum principal stress | |
| Non-dimensional tortuosity factor | ||
| , | Dimensionless quantities | |
| , , | Constants in different mode solutions |
References
- Fjar, E.; Holt, R.M.; Raaen, A.M.; Risnes, R.; Horsrud, P. Petroleum Related Rock Mechanics; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Kirsch, C. Die theorie der elastizitat und die bedurfnisse der festigkeitslehre. Zeitschrift des Vereines Deutscher Ingenieure 1898, 42, 797–807. [Google Scholar]
- Bradley, W.B. Failure of inclined boreholes. J. Energy Resour. Technol. 1979, 101, 232–239. [Google Scholar] [CrossRef]
- Aadnoy, B.S.; Chenevert, M.E. Stability of highly inclined boreholes (includes associated papers 18596 and 18736). SPE Drill. Eng. 1987, 2, 364–374. [Google Scholar] [CrossRef]
- Zoback, M.D. Reservoir Geomechanics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Meng, M.; Zamanipour, Z.; Miska, S.; Yu, M.; Ozbayoglu, E.M. Dynamic stress distribution around the wellbore influenced by surge/swab pressure. J. Pet. Sci. Eng. 2019, 172, 1077–1091. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.H.D. Poroelastic response of a borehole in a non-hydrostatic stress field. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 171–182. [Google Scholar] [CrossRef]
- Zamanipour, Z.; Miska, S.Z.; Hariharan, P.R. Effect of transient surge pressure on stress distribution around directional wellbores. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 1–3 March 2016. [Google Scholar]
- Zhang, F.; Kang, Y.; Wang, Z.; Miska, S.; Yu, M.; Zamanipour, Z. Transient coupling of swab/surge pressure and in-situ stress for wellbore-stability evaluation during tripping. SPE J. 2018, 23, 1019–1038. [Google Scholar] [CrossRef]
- Meng, M.; Zamanipour, Z.; Miska, S.; Yu, M.; Ozbayoglu, E.M. Dynamic Wellbore Stability Analysis Under Tripping Operations. Rock Mech. Rock Eng. 2019, 1–21. [Google Scholar] [CrossRef]
- Feng, Y.; Li, X.; Gray, K.E. An easy-to-implement numerical method for quantifying time-dependent mudcake effects on near-wellbore stresses. J. Pet. Sci. Eng. 2018, 164, 501–514. [Google Scholar] [CrossRef]
- Chen, P.; Miska, S.Z.; Ren, R.; Yu, M.; Ozbayoglu, E.; Takach, N. Poroelastic modeling of cutting rock in pressurized condition. J. Pet. Sci. Eng. 2018, 169, 623–635. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I: Low-frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid, II: Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Rasolofosaon, P.N.J. Importance of interface hydraulic condition on the generation of second bulk compressional wave in porous media. Appl. Phys. Lett. 1988, 52, 780–782. [Google Scholar] [CrossRef]
- Kelder, O.; Smeulders, D.M.J. Propagation and damping of compressional waves in porous rocks: Theory and experiments. SEG Technical Program Expanded Abstracts 1995. Soc. Explor. Geophys. 1995, 675–678. [Google Scholar] [CrossRef]
- Gurevich, B.; Kelder, O.; Smeulders, D.M.J. Validation of the slow compressional wave in porous media: Comparison of experiments and numerical simulations. Transp. Porous Media 1999, 36, 149–160. [Google Scholar] [CrossRef]
- Schanz, M. Poroelastodynamics: Linear models, analytical solutions, and numerical methods. Appl. Mech. Rev. 2009, 62, 030803. [Google Scholar] [CrossRef]
- Schanz, M.; Cheng, A.H.D. Transient wave propagation in a one-dimensional poroelastic column. Acta Mech. 2000, 145, 1–18. [Google Scholar] [CrossRef]
- Xie, K.; Liu, G.; Shi, Z. Dynamic response of partially sealed circular tunnel in viscoelastic saturated soil. Soil Dyn. Earthq. Eng. 2004, 24, 1003–1011. [Google Scholar] [CrossRef]
- Gao, M.; Wang, Y.; Gao, G.Y.; Yang, J. An analytical solution for the transient response of a cylindrical lined cavity in a poroelastic medium. Soil Dyn. Earthq. Eng. 2013, 46, 30–40. [Google Scholar] [CrossRef]
- Liu, G.B.; Xie, K.H.; Yao, H.L. Scattering of elastic wave by a partially sealed cylindrical shell embedded in poroelastic medium. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 1109–1126. [Google Scholar]
- Hasheminejad, S.M.; Kazemirad, S. Dynamic response of an eccentrically lined circular tunnel in poroelastic soil under seismic excitation. Soil Dyn. Earthq. Eng. 2008, 28, 277–292. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Chen, M.; Chen, K. Poroelastodynamic response of a borehole in a non-hydrostatic stress field. Int. J. Numer. Anal. Methods Geomech. 2017, 93, 82–93. [Google Scholar] [CrossRef]
- Senjuntichai, T.; Keawsawasvong, S.; Plangmal, R. Three-dimensional dynamic response of multilayered poroelastic media. Mar. Georesour. Geotechnol. 2018, 37, 424–437. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Senjuntichai, T. Poroelastodynamic fundamental solutions of transversely isotropic half-plane. Comput. Geotech. 2019, 106, 52–67. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Wei, S.M.; Chen, M.; Zhang, Y.Y.; Lu, Y.H. Transient failure of a borehole excavated in a poroelastic continuum. Mech. Res. Commun. 2019. [Google Scholar] [CrossRef]
- Mehrabian, A.; Abousleiman, Y.N. Generalized poroelastic wellbore problem. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2727–2754. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Hosseini, H. Dynamic stress concentration near a fluid-filled permeable borehole induced by general modal vibrations of an internal cylindrical radiator. Soil Dyn. Earthq. Eng. 2002, 22, 441–458. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M. Comparison of different numerical Laplace inversion methods for engineering applications. Appl. Math. Comput. 2007, 189, 1966–1981. [Google Scholar] [CrossRef]
- Senjuntichai, T.; Rajapakse, R.K.N.D. Transient response of a circular cavity in a poroelastic medium. Int. J. Numer. Anal. Methods Geomech. 1993, 17, 357–383. [Google Scholar] [CrossRef]



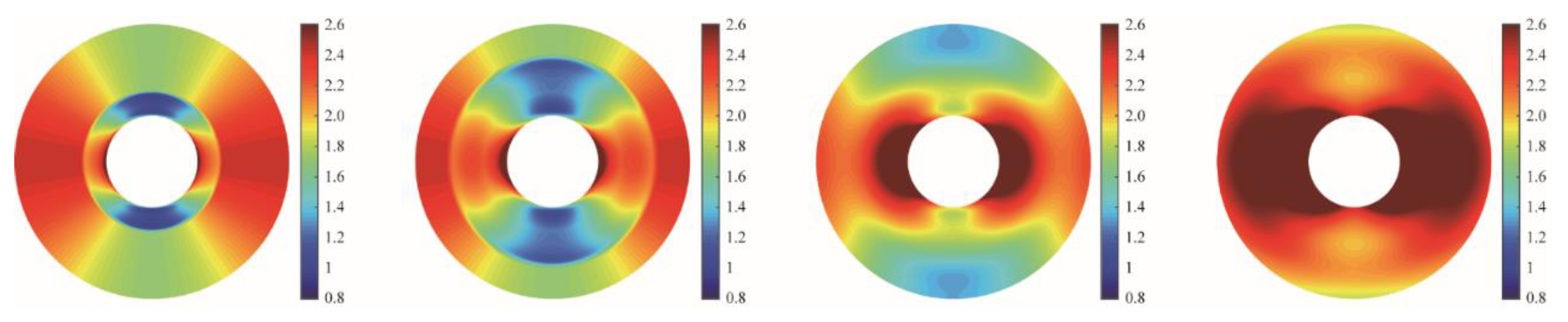
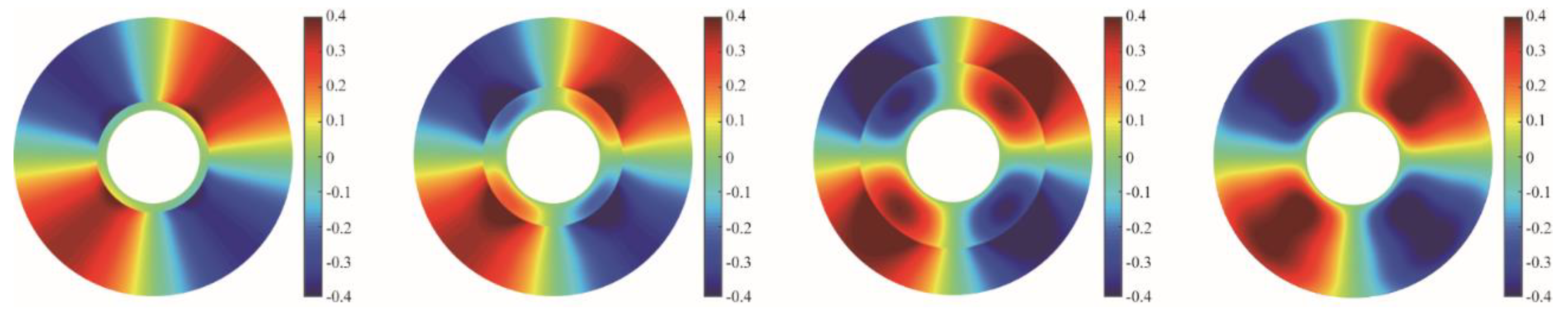
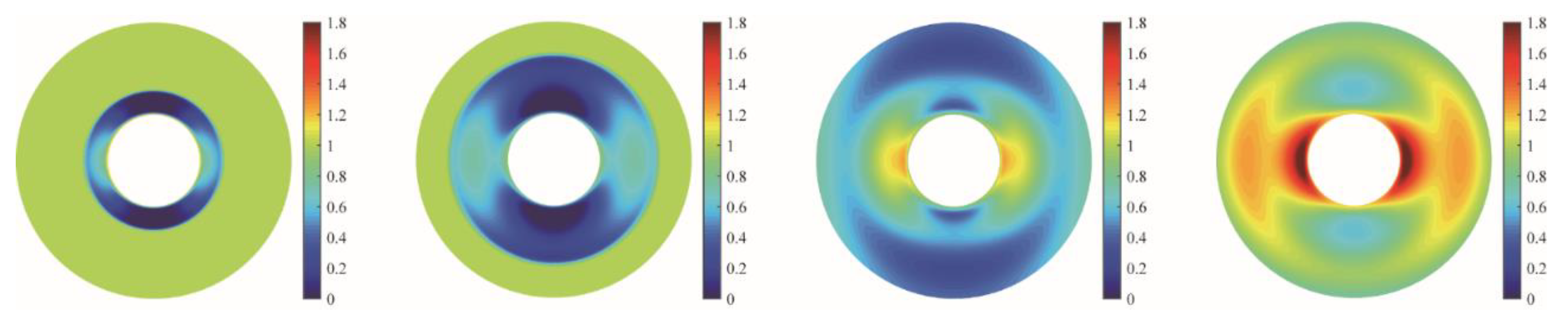


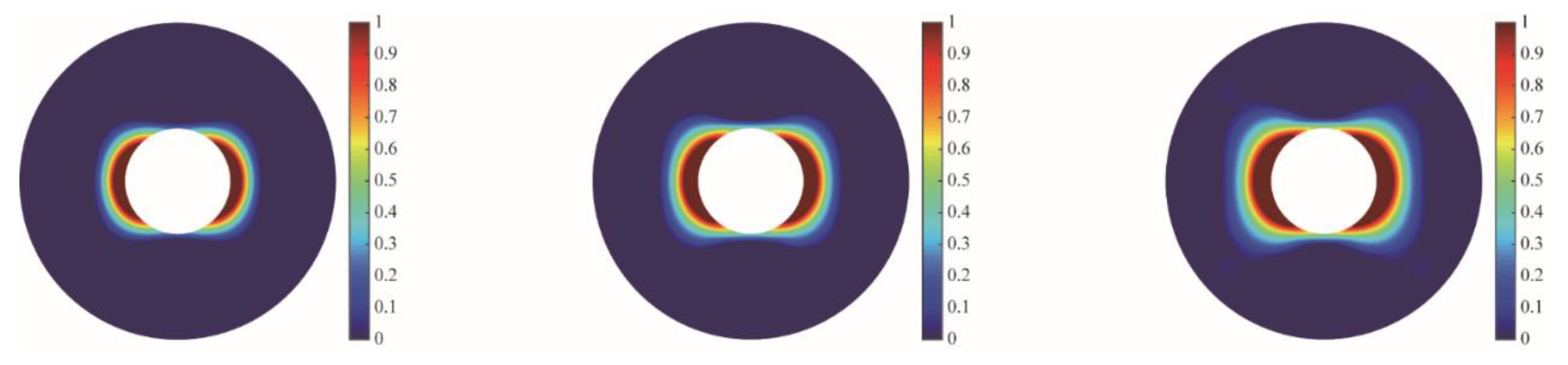
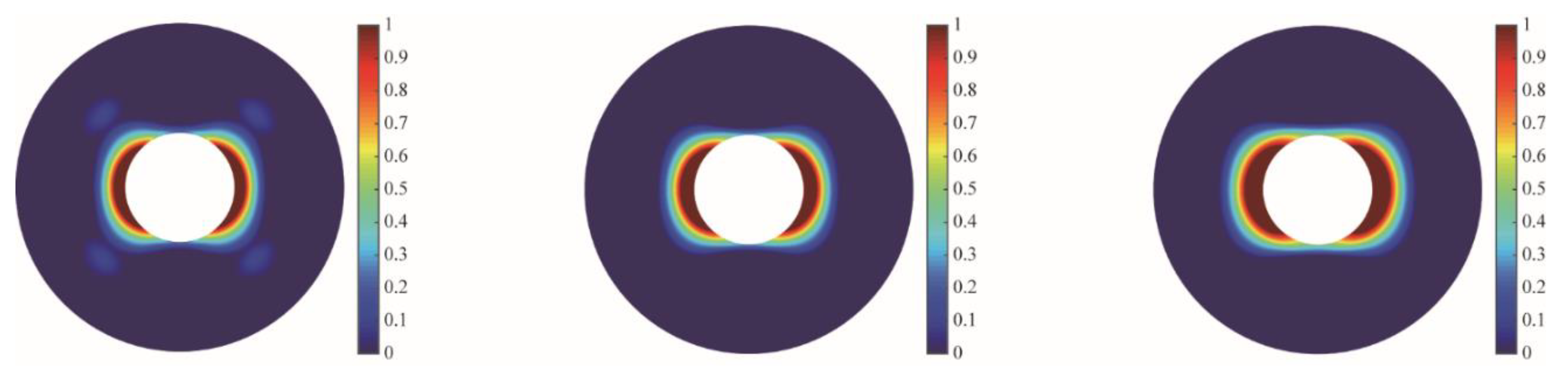

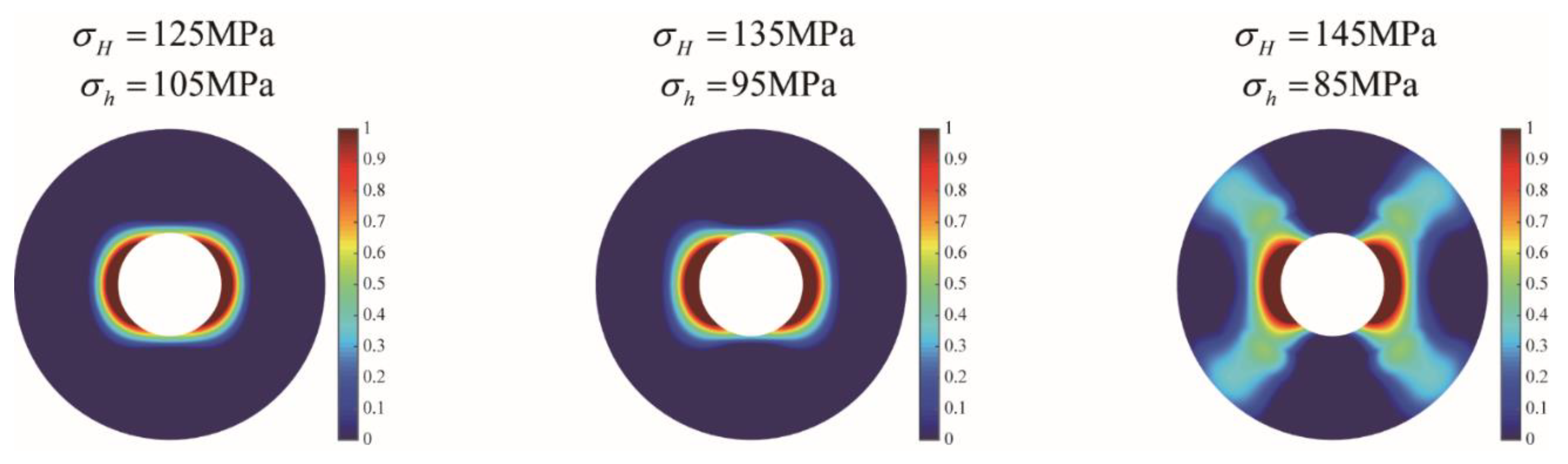
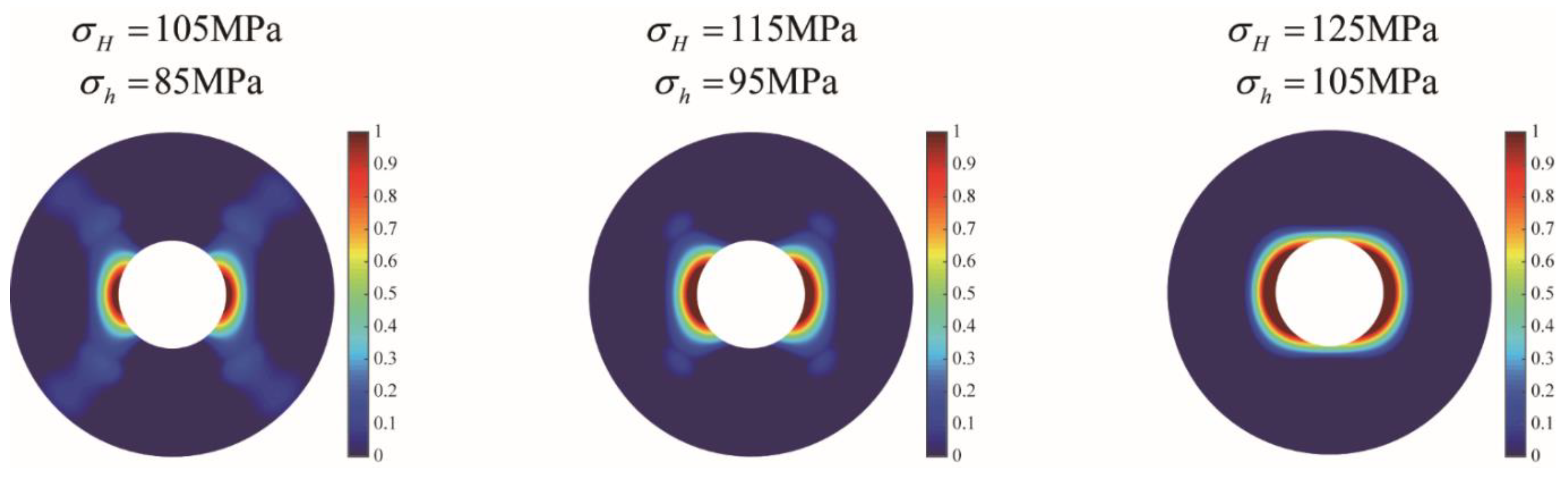

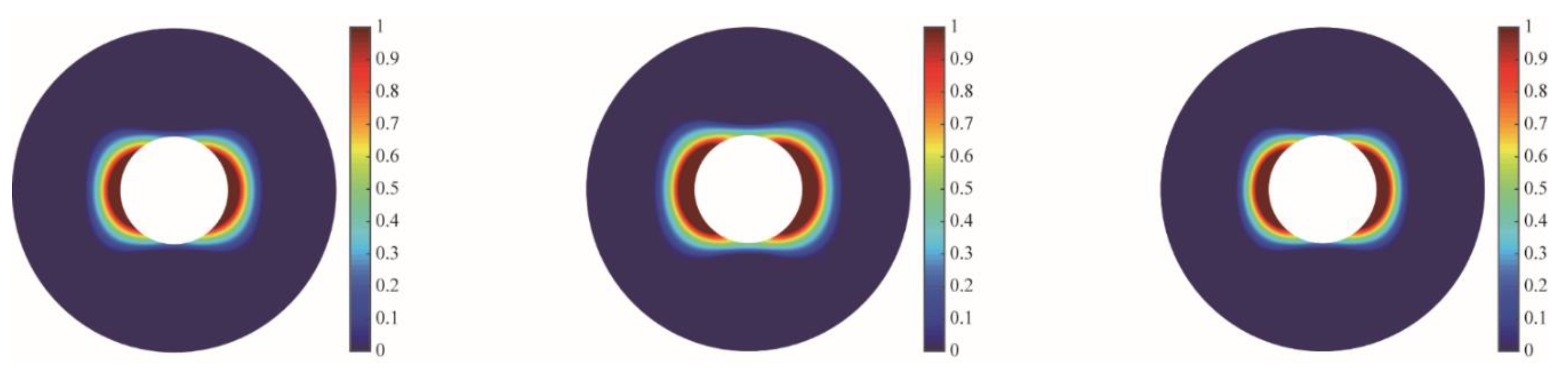
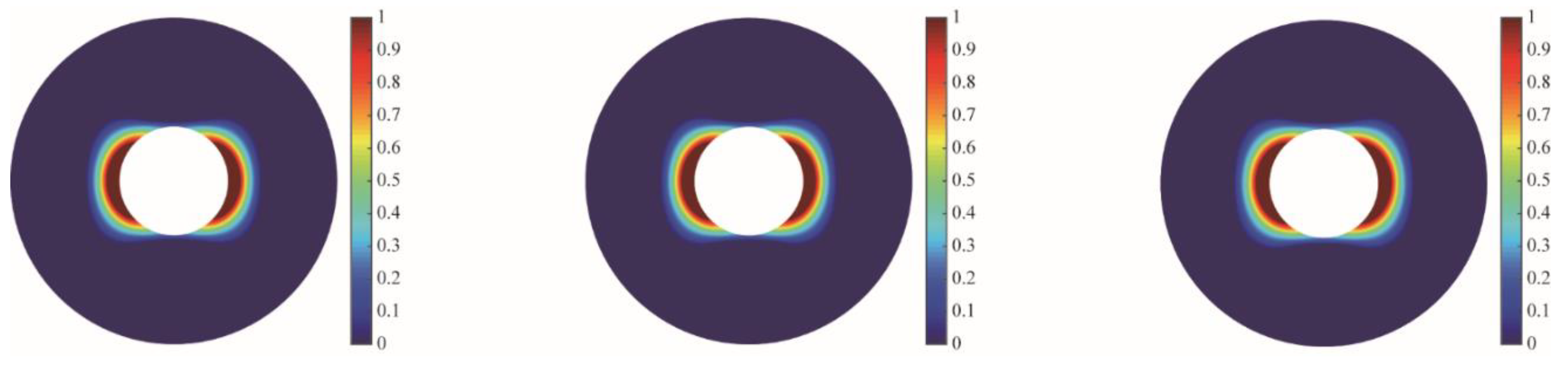

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Shear modulus [GPa] | 10 | Lame constant [GPa] | 7 |
| Biot coefficient | 0.6 | Biot modulus [GPa] | 10 |
| Pore fluid density [kg·m−3] | 300 | Rock density [kg·m−3] | 2800 |
| Rock permeability [mD] | 0.8 | Pore fluid viscosity [Pa·s] | 3 × 10−5 |
| Tortuosity factor | 1.6 | Rock porosity | 0.06 |
| Maximum principal stress [MPa] | 130 | Minimum principal stress [MPa] | 100 |
| Initial pore pressure [MPa] | 50 | Wellbore radius [m] | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, M.; Xia, Y.; Jin, Y.; Yin, S. Transient Stress Distribution and Failure Response of a Wellbore Drilled by a Periodic Load. Energies 2019, 12, 3486. https://doi.org/10.3390/en12183486
Wang X, Chen M, Xia Y, Jin Y, Yin S. Transient Stress Distribution and Failure Response of a Wellbore Drilled by a Periodic Load. Energies. 2019; 12(18):3486. https://doi.org/10.3390/en12183486
Chicago/Turabian StyleWang, Xiaoyang, Mian Chen, Yang Xia, Yan Jin, and Shunde Yin. 2019. "Transient Stress Distribution and Failure Response of a Wellbore Drilled by a Periodic Load" Energies 12, no. 18: 3486. https://doi.org/10.3390/en12183486
APA StyleWang, X., Chen, M., Xia, Y., Jin, Y., & Yin, S. (2019). Transient Stress Distribution and Failure Response of a Wellbore Drilled by a Periodic Load. Energies, 12(18), 3486. https://doi.org/10.3390/en12183486