An Investigation into the Effects of Weak Interfaces on Fracture Height Containment in Hydraulic Fracturing
Abstract
:1. Introduction
2. Method and Model
2.1. Block Discrete Element Method
2.1.1. Constitutive Model of Joints
2.1.2. Contact Friction Joint Model
2.1.3. Fluid Flow in Fracture
2.1.4. Motion Equation of Blocks
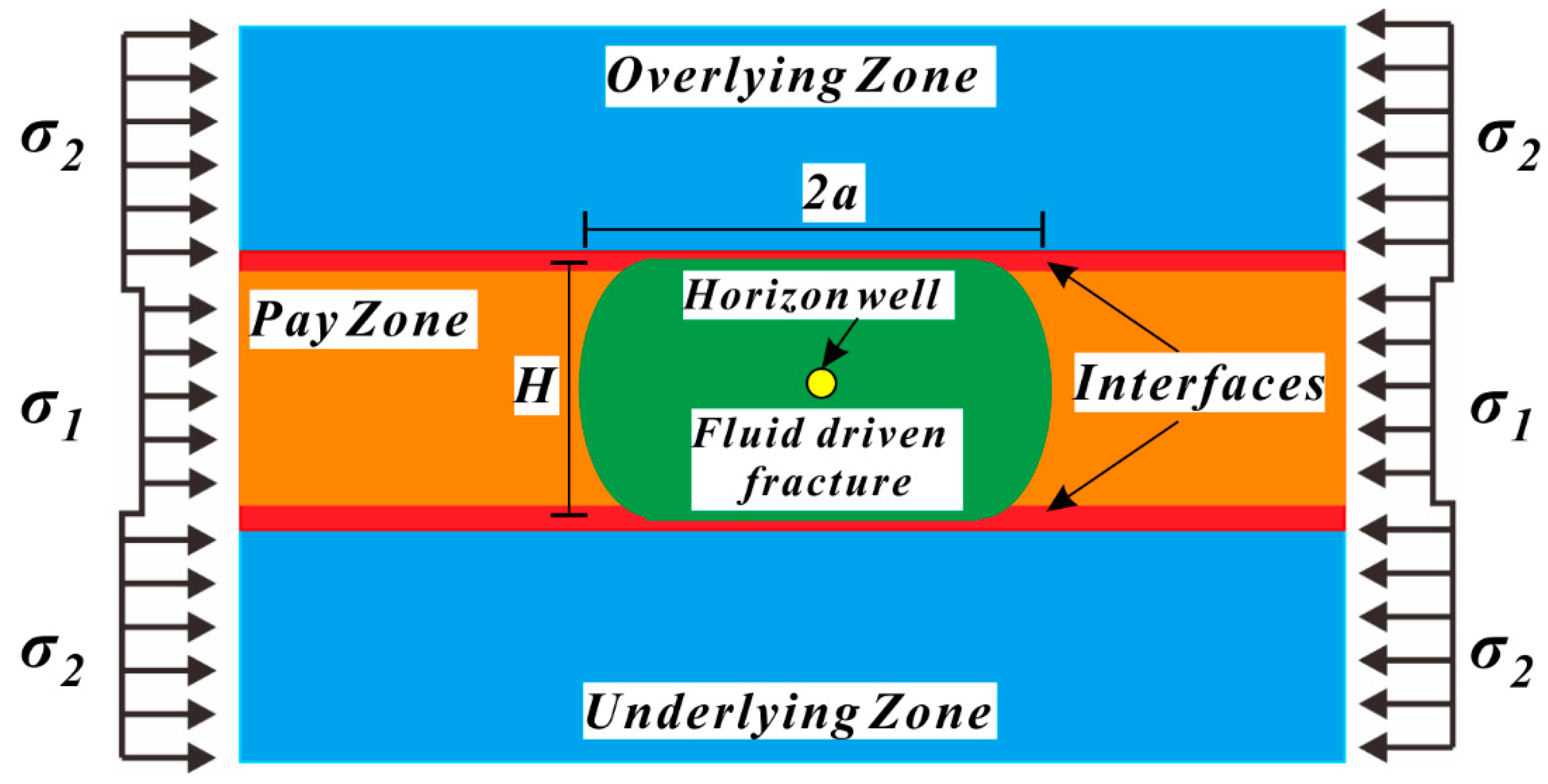
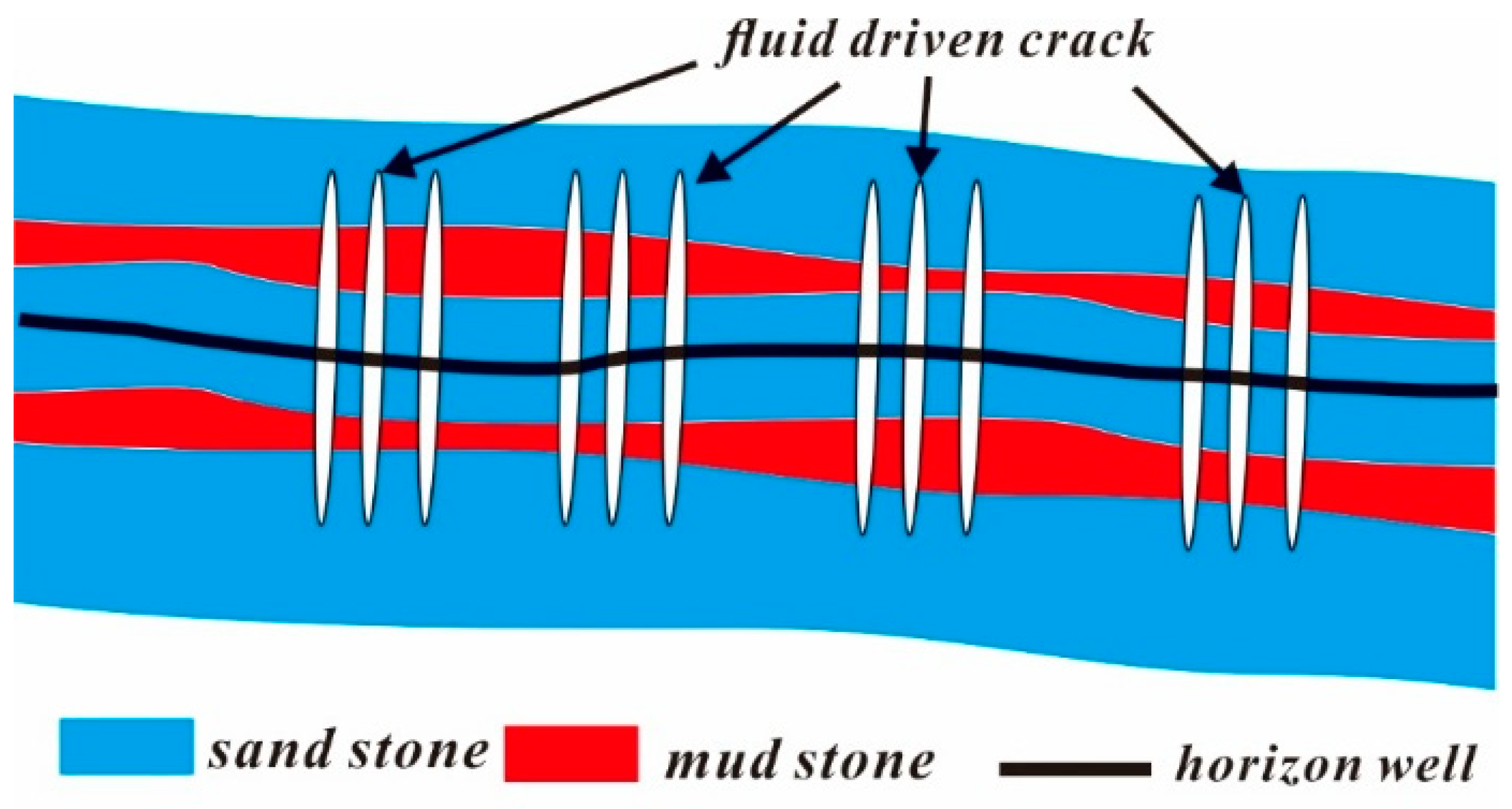
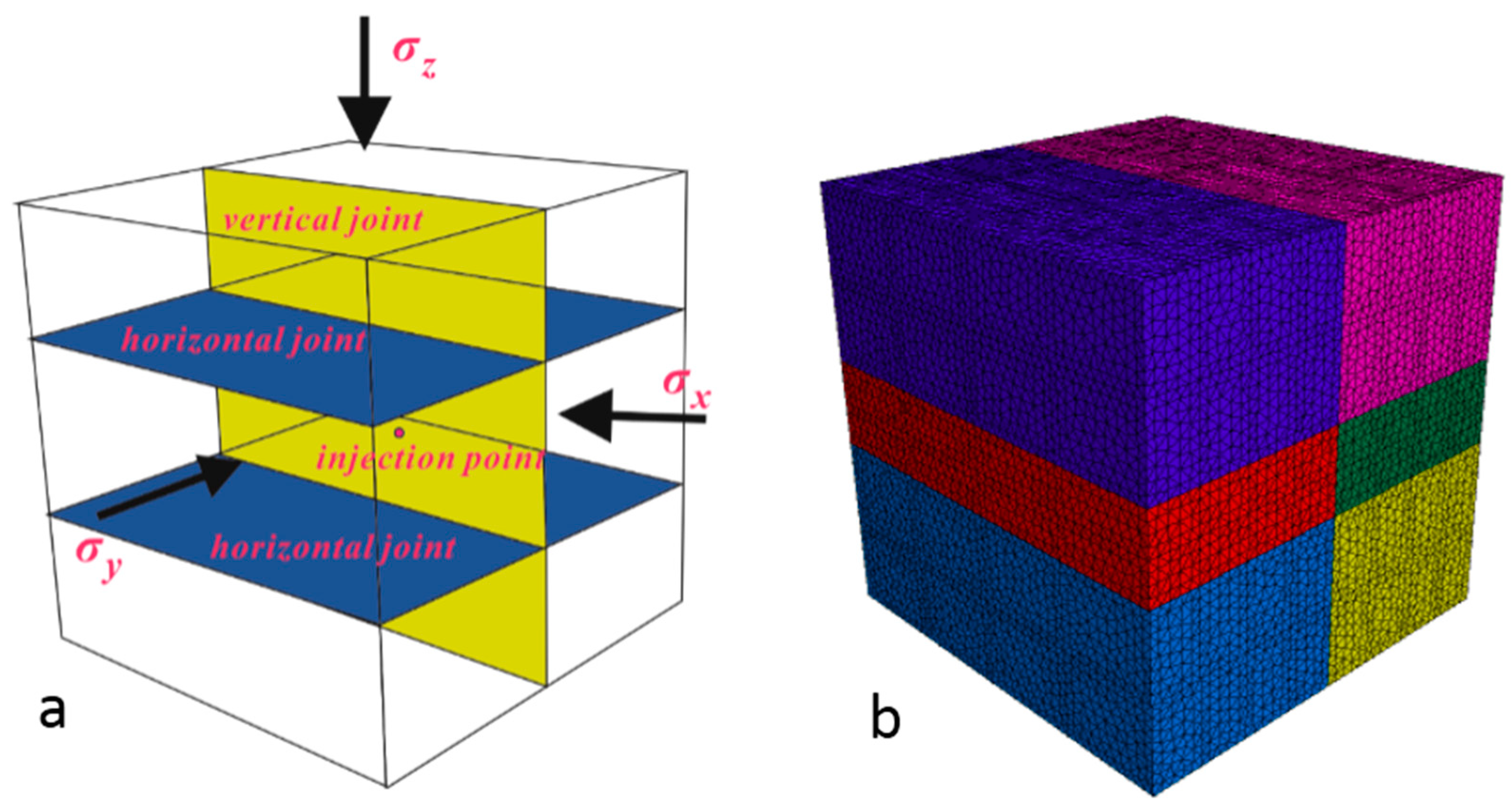
2.2. Numerical Model Description
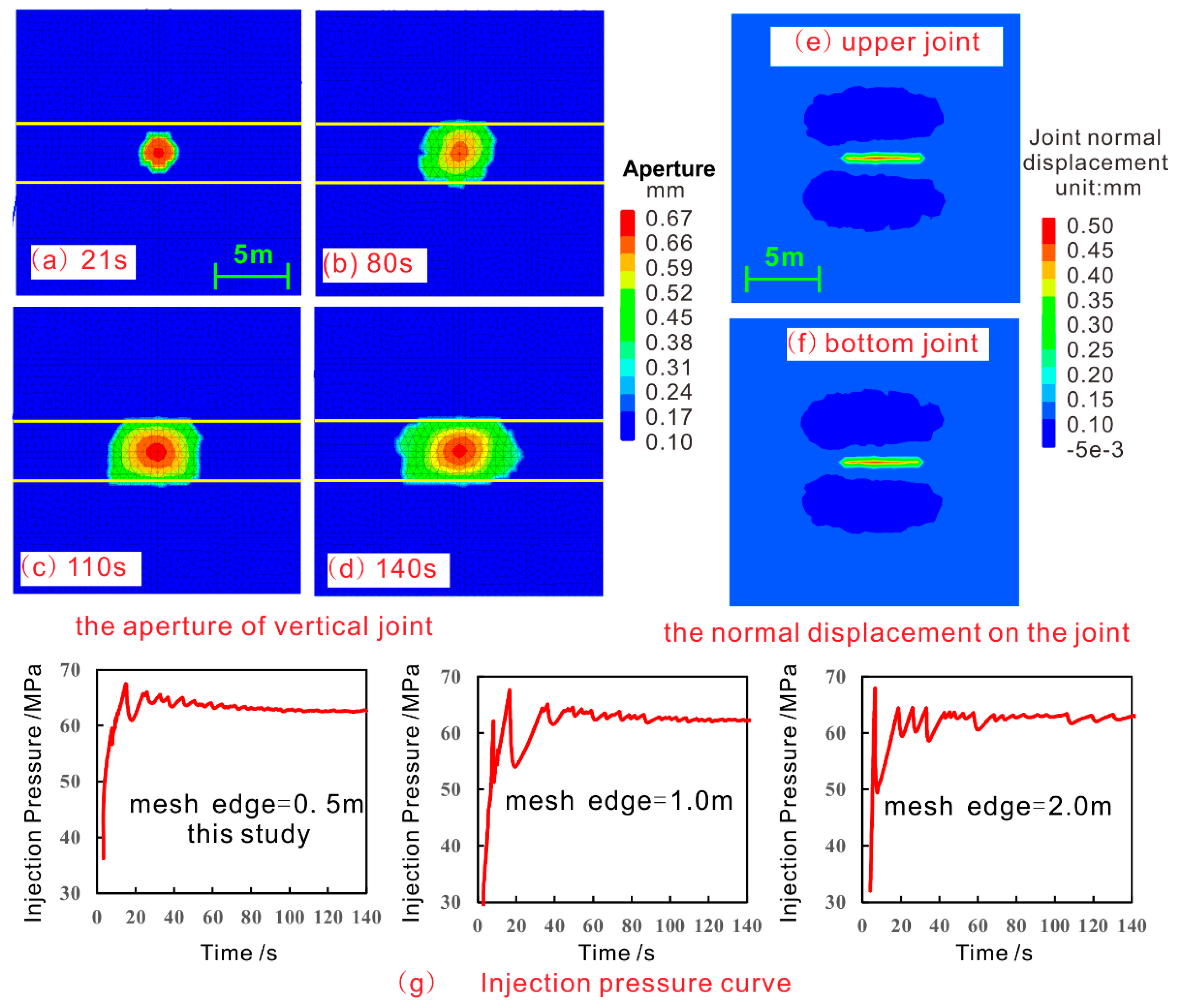
3. Results
4. Discussion and Analysis
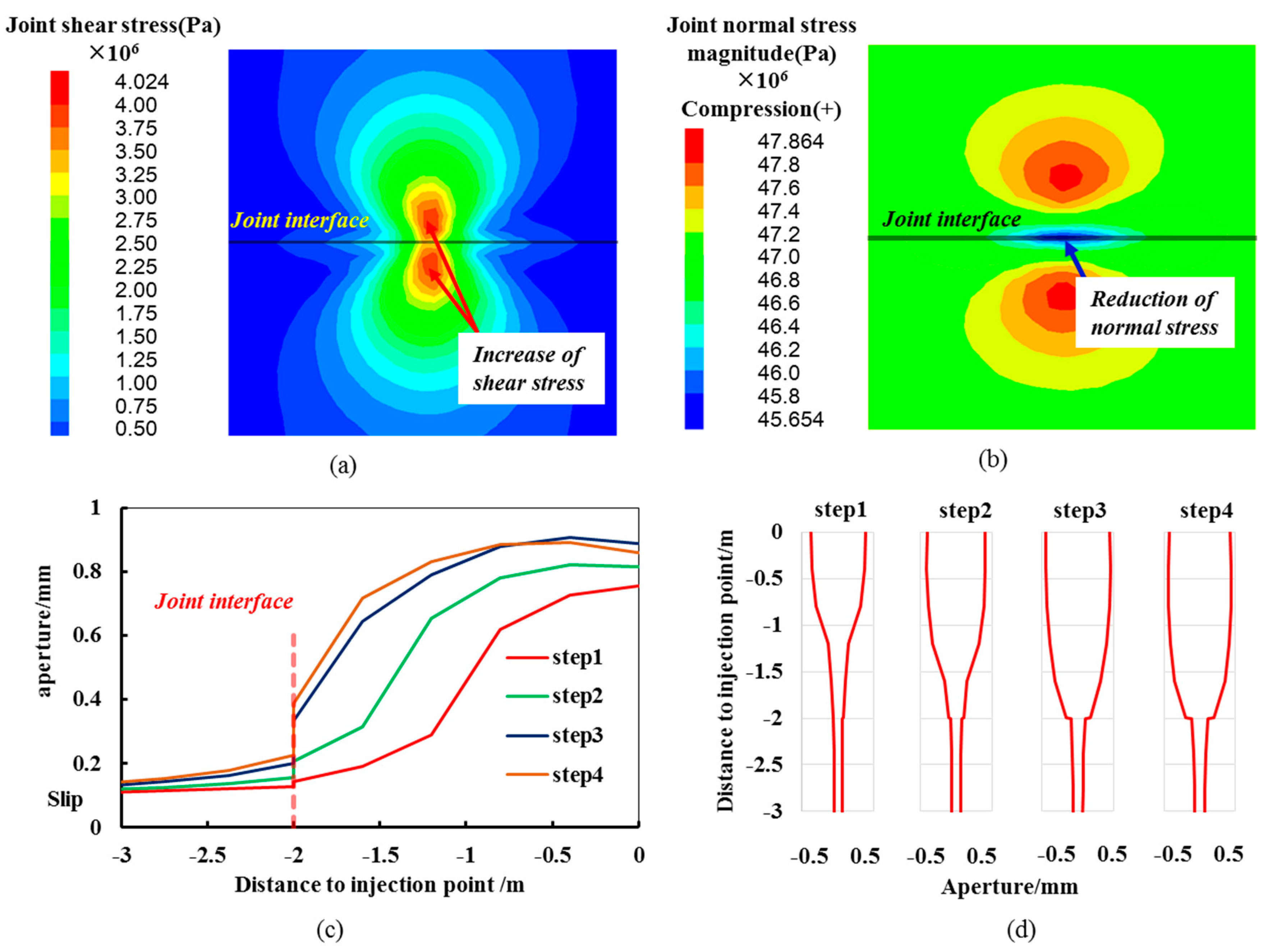
4.1. Stress State of the Interface
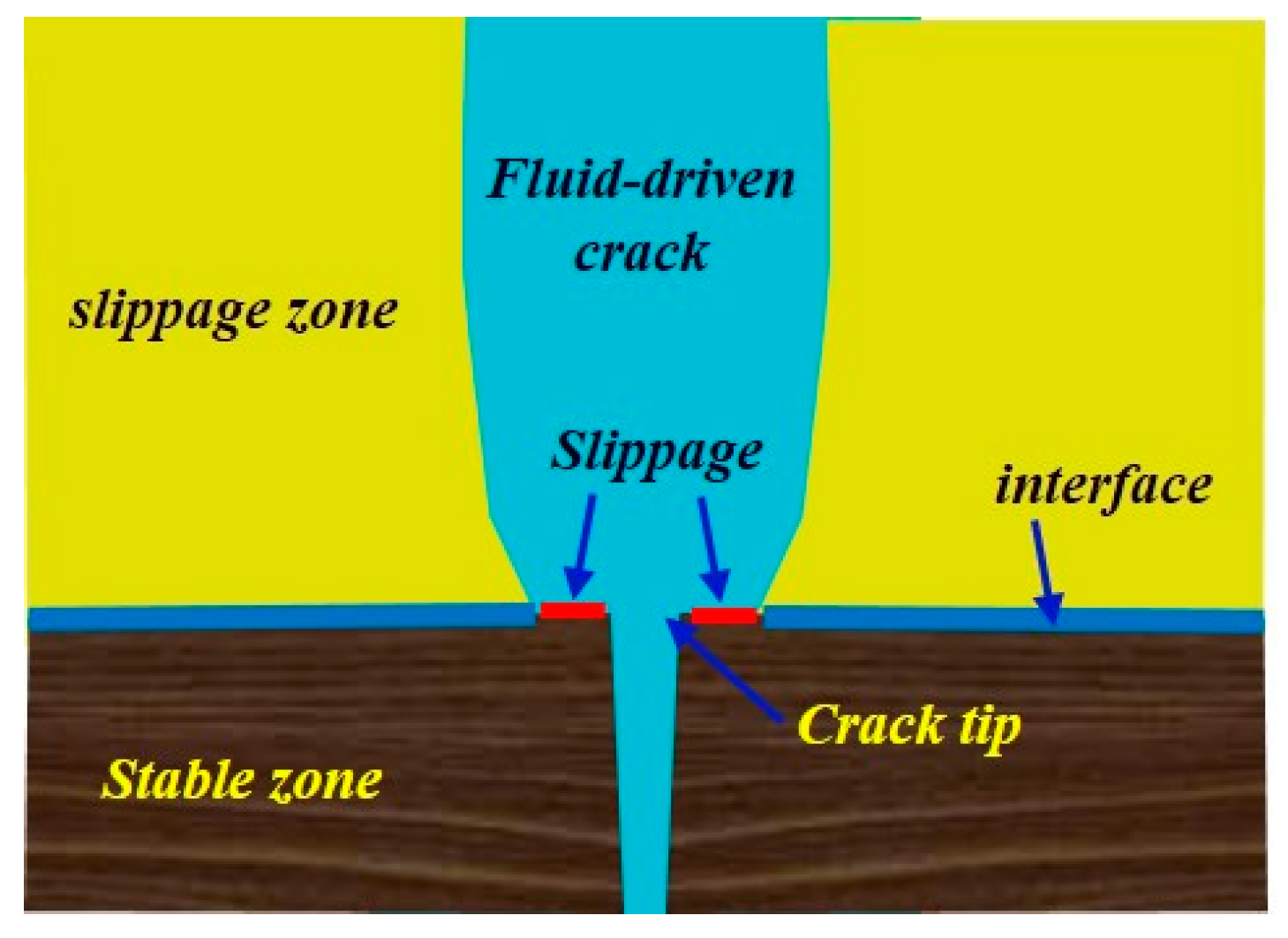
4.2. Slippage Forms on Interface
4.2.1. Shear Failure on Interface
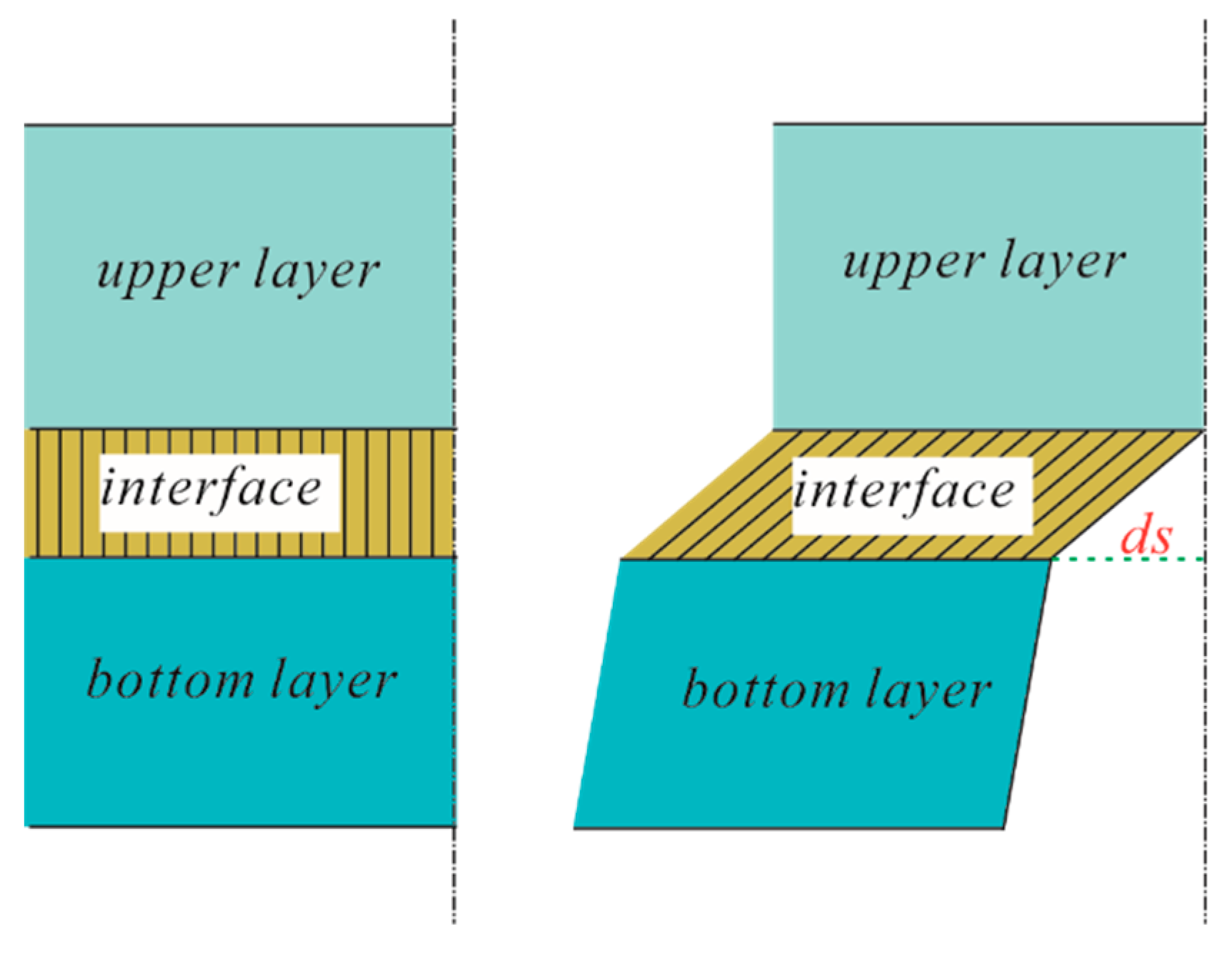
4.2.2. Discontinuous Deformation Caused by Interface
4.3. Manual Intervention of Interface Slippage in Hydraulic Fracture Containment
5. Conclusions
- (1)
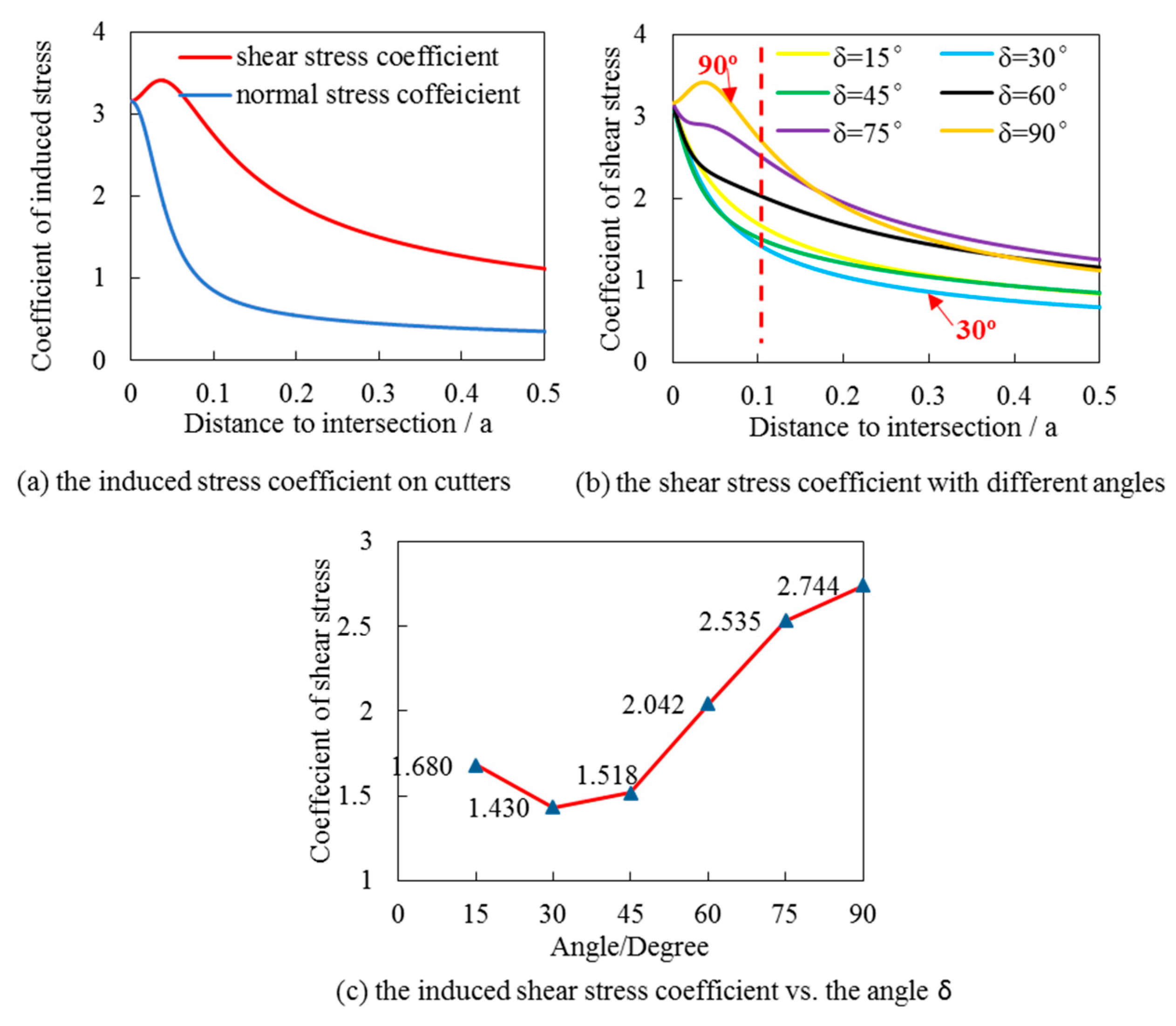
- Interface slippage is one reason for fracture containment besides stress contrast and rock properties. Fracture containment still exists in the situation of the same stress state and rock properties, which means that fracture height containment still exists in one layer with a weak interface. Fracture tip blunting is the key factor that hinders fracture propagation. The mechanism of interface slippage is critical for fracture containment. The slippage forms on the interface include shear failure on the interface and discontinuous deformation caused by the interface.
- (2)
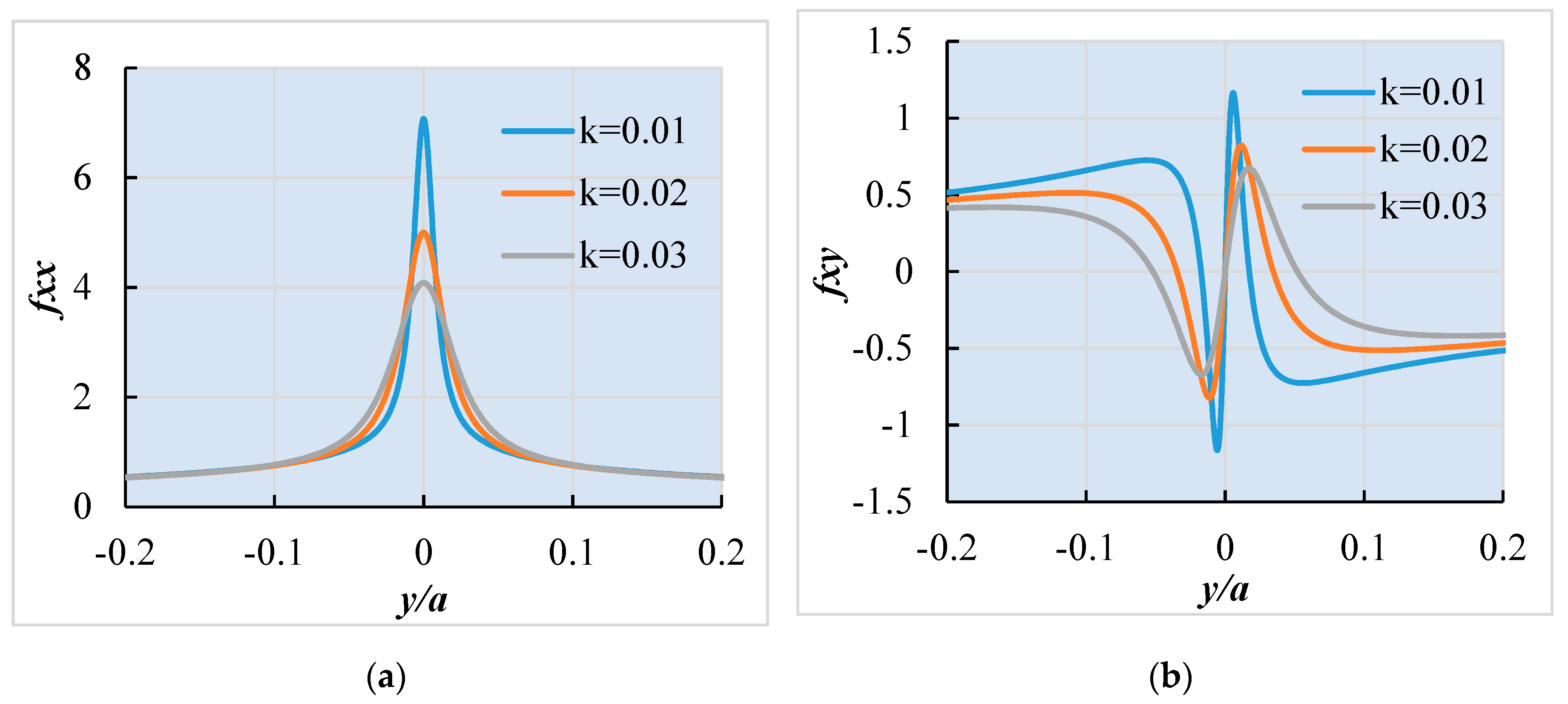
- The coefficients of induced normal and shear stress were derived. The results show that induced stress can offset the original compressive stress and reduce the normal stress on joints, and shear stress in the range of 0.05 a is larger than the initial state. This indicates that hydraulic fracture will cause a reduction of normal stress and an increase of shear stress on joints.
- (3)
- According to the intended purpose, for hydraulic fracturing in pay zones or along multilayers, different measures, including manual intervention of stress, perforation angle, and fracturing fluid viscosity, are expected. For multilayer fracturing, fluid-driven fractures should be positioned at 30° to the interfaces by stress intervention and perforation angle, and shear stress should be increased, and normal stress reduced. Higher viscosity is appropriate. On the contrary, for pay zone fracturing, fluid-driven fractures should be adjusted to 90° to the interfaces by stress intervention and perforation angle, and shear stress should be decreased, and normal stress increased. Lower viscosity is appropriate.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
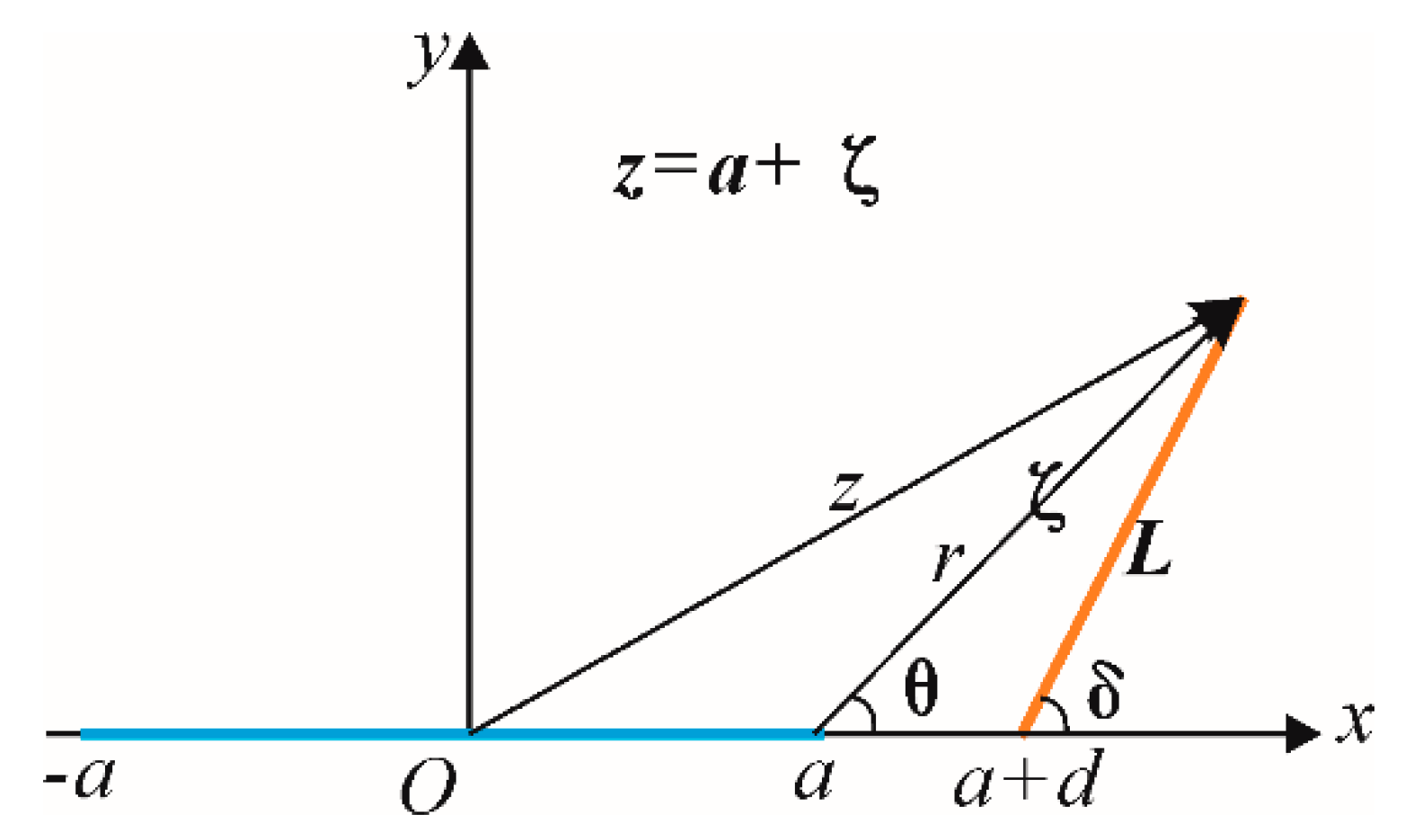
Appendix A. Stress State on the Interfaces for Orthogonal Joint Conditions
Appendix B. Stress State on the Interfaces for Nonorthogonal Joint Conditions
References
- Chuprakov, D.A.; Prioul, R. Hydraulic fracture height containment by weak horizontal interfaces. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, Woodland, TX, USA, 3–5 February 2015; pp. 1–17. [Google Scholar]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Xing, P.; Bunger, A.; Yoshioka, K.; Adachi, K.; El-Fayoumi, A. Experimental study of hydraulic fracture containment in layered reservoirs. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Weng, X.; Chuprakov, D.; Kresse, O.; Prioul, R.; Wang, H. Hydraulic fracture-height containment by permeable weak bedding interfaces. Geophysics 2018, 83, MR137–MR152. [Google Scholar] [CrossRef]
- Xiangjun, C.; Langfeng, M.; Zhongbao, W.; Yiqun, Y.; Yang, Z.; Linlin, S. Calculating method of the productivity for the trans-layer fractured horizontal well. Pet. Geol. Oilfield Dev. Daqing 2019, 3, 65–72. [Google Scholar] [CrossRef]
- Simonson, E.; Abou-Sayed, A.; Clifton, R. Containment of massive hydraulic fractures. Soc. Pet. Eng. J. 1978, 18, 27–32. [Google Scholar] [CrossRef]
- Van Eekelen, H. Hydraulic fracture geometry: fracture containment in layered formations. Soc. Pet. Eng. J. 1982, 22, 341–349. [Google Scholar] [CrossRef]
- Fung, R.; Vilayakumar, S.; Cormack, D.E. Calculation of vertical fracture containment in layered formations. SPE Form. Eval. 1987, 2, 518–522. [Google Scholar] [CrossRef]
- Daneshy, A. Hydraulic fracture propagation in layered formations. Soc. Pet. Eng. J. 1978, 18, 33–41. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Schmidt, R.A.; Northrop, D.A. In-situ stresses: The predominant influence on hydraulic fracture containment. J. Pet. Technol. 1982, 34, 653–664. [Google Scholar] [CrossRef]
- Warpinski, N.R.; Clark, J.A.; Schmidt, R.A.; Huddle, C.W. Laboratory investigation on the effect of in situ stresses on hydraulic fracture containment. Soc. Pet. Eng. J. 1982, 22. [Google Scholar] [CrossRef]
- Teufel, L.W.; Clark, J.A. Hydraulic-fracture propagation in layered rock: Experimental studies of fracture containment. Soc. Pet. Eng. J. 1981. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E. Modeling hydraulic fracture propagation and proppant transport in a two-layer formation with stress drop. Eng. Fract. Mech. 2018, 199, 705–720. [Google Scholar] [CrossRef]
- Wasantha, P.; Konietzky, H.; Xu, C. Effect of in-situ stress contrast on fracture containment during single-and multi-stage hydraulic fracturing. Eng. Fract. Mech. 2019, 205, 175–189. [Google Scholar] [CrossRef]
- Huang, J.; Ma, X.; Shahri, M.; Safari, R.; Yue, K.; Mutlu, U. Hydraulic fracture growth and containment design in unconventional reservoirs. In Proceedings of the 50th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Xu, W.; Prioul, R.; Berard, T.; Weng, X.; Kresse, O. Barriers to hydraulic fracture height growth: A new model for sliding interfaces. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Woodlands, TX, USA, 5–7 February 2019. [Google Scholar]
- Xing, P.; Yoshioka, K.; Adachi, J.; El-Fayoumi, A.; Bunger, A.P. Laboratory demonstration of hydraulic fracture height growth across weak discontinuitiesHF height growth with weak interfaces. Geophysics 2018, 83, MR93–MR105. [Google Scholar] [CrossRef]
- Wang, H.; Liu, H.; Wu, H.A.; Wang, X.X. A 3D numerical model for studying the effect of interface shear failure on hydraulic fracture height containment. J. Pet. Sci. Eng. 2015, 133, 280–284. [Google Scholar] [CrossRef]
- Tang, J.; Wu, K. A 3-D model for simulation of weak interface slippage for fracture height containment in shale reservoirs. Int. J. Solids Struct. 2018, 144, 248–264. [Google Scholar] [CrossRef]
- Gil, I.; Nagel, N.; Sanchez-Nagel, M.; Damjanac, B. The effect of operational parameters on hydraulic fracture propagation in naturally fractured reservoirs-getting control of the fracture optimization process. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011. [Google Scholar]
- Cundall, P.A. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 107–116. [Google Scholar] [CrossRef]
- Hart, R.; Cundall, P.; Lemos, J. Formulation of a three-dimensional distinct element model—Part II. Mechanical calculations for motion and interaction of a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 117–125. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, F.; Li, N.; He, M. Influence of fault on the surrounding rock stability for a mining tunnel: Distance and tectonic stress. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Zhu, J.B.; Liao, Z.Y.; Tang, C.A. Numerical SHPB tests of rocks under combined static and dynamic loading conditions with application to dynamic behavior of rocks under in situ stresses. Rock Mech. Rock Eng. 2016, 49, 3935–3946. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, J.; Lei, Y. The propagation behavior of hydraulic fracture in rock mass with cemented joints. Geofluids 2019, 2019. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 1968, 94, 637–660. [Google Scholar]
- Deng, C.; Kong, W.; Zheng, Y. Analysis of the ultimate bearing capacity of jointed rock foundations by fem. Ind. Constr. 2005, 35, 51–54. [Google Scholar]
- Youjun, J.; Jie, W.; Liuke, H. Analysis on inflowing of the injecting water in faulted formation. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. Available online: https://www.itascacg.com/software/3dec (accessed on 1 June 2019).
- Zhao, Z.; Kim, H.; Haimson, B. Hydraulic fracturing initiation in granite. In Proceedings of the 2nd North American Rock Mechanics Symposium, Montreal, QC, Canada, 19–21 June 1996. [Google Scholar]
- Bai, M.; Green, S.; Casas, L.; Miskimins, J. 3-D simulation of large-scale hydraulic fracturing tests. In Proceedings of the 41st US Rock Mechanics Symposium, Golden, CO, USA, 17–21 June 2006. [Google Scholar]
- Kim, G.H.; Wang, J.Y. Interpretation of hydraulic fracturing pressure in low-permeability gas formations. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 27–29 March 2011. [Google Scholar]
- Shiyu, L. , Taiming, H., Xiangchu, Y. Fracture Mechanics of Rock; Science Press: Beijing, China, 2016. [Google Scholar]
- Zheng, Y.; Liu, J.; Zhang, B. Artificial interference of stress field in a near-fracture zone by water injection in a preexisting crack. Adv. Civil Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Chen, M. Dynamic fracture propagation in hydraulic re-fracturing. J. Pet. Sci. Eng. 2010, 70, 266–272. [Google Scholar] [CrossRef]
- Gao, Q.; Cheng, Y.; Han, S.; Yan, C.; Jiang, L. Numerical modeling of hydraulic fracture propagation behaviors influenced by pre-existing injection and production wells. J. Pet. Sci. Eng. 2019, 172, 976–987. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Q.; Song, Z. Changes of ground stress field and development policy in later half period of water injection for the extremely low permeability reservoirs with fractures. Geoscience 2008, 4, 647–654. [Google Scholar]
- Wright, C.; Conant, R.; Golich, G.M.; Bondor, P.L.; Murer, A.S.; Dobie, C.A. Hydraulic fracture orientation and production/injection induced reservoir stress changes in diatomite waterfloods. Poceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 8–10 March 1995. [Google Scholar]
- Manríquez, A.L. Stress behavior in the near fracture region between adjacent horizontal wells during multistage fracturing using a coupled stress-displacement to hydraulic diffusivity model. J. Pet. Sci. Eng. 2018, 162, 822–834. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Han, K.; Hou, B.; Chen, M.; Gou, J. Analysis of hydraulic fracture initiation and vertical propagation behavior in laminated shale formation. Fuel 2017, 206, 482–493. [Google Scholar] [CrossRef]
- Beugelsdijk, L.J.L.; de Pater, C.J.; Sato, K. Experimental hydraulic fracture propagation in a multi-fractured medium. In Proceedings of the SPE Asia Pacific Conference on Integrated Modelling for Asset Management, Yokohama, Japan, 25–26 April 2000. [Google Scholar]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modulus | 20 GPa | Fluid viscosity | 0.0015 Pa.s |
| Poisson’s ratio | 0.25 | Fluid density | 1000 kg/m3 |
| Density of rock (ρ) | 2600 kg/m3 | Depth (h) | 3000 m |
| Joint friction | 20° | Injection rate | 0.01 m3/s |
| Joint cohesion | 0 MPa | Initial vertical stress | 76.518 MPa |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Liu, J.; Zhang, B. An Investigation into the Effects of Weak Interfaces on Fracture Height Containment in Hydraulic Fracturing. Energies 2019, 12, 3245. https://doi.org/10.3390/en12173245
Zheng Y, Liu J, Zhang B. An Investigation into the Effects of Weak Interfaces on Fracture Height Containment in Hydraulic Fracturing. Energies. 2019; 12(17):3245. https://doi.org/10.3390/en12173245
Chicago/Turabian StyleZheng, Yongxiang, Jianjun Liu, and Bohu Zhang. 2019. "An Investigation into the Effects of Weak Interfaces on Fracture Height Containment in Hydraulic Fracturing" Energies 12, no. 17: 3245. https://doi.org/10.3390/en12173245
APA StyleZheng, Y., Liu, J., & Zhang, B. (2019). An Investigation into the Effects of Weak Interfaces on Fracture Height Containment in Hydraulic Fracturing. Energies, 12(17), 3245. https://doi.org/10.3390/en12173245






