The Effect of Collector Shading and Masking on Optimized PV Field Designs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Diffuse Radiation Models
2.2. Isotropic Diffuse Model
2.3. Anisotropic Diffuse Model
2.4. Formulation of the Optimal Design of a PV Field
2.4.1. Maximum Annual Incident Energy-Horizontal Field
2.4.2. Maximum Annual Incident Energy-Inclined Field
3. Results
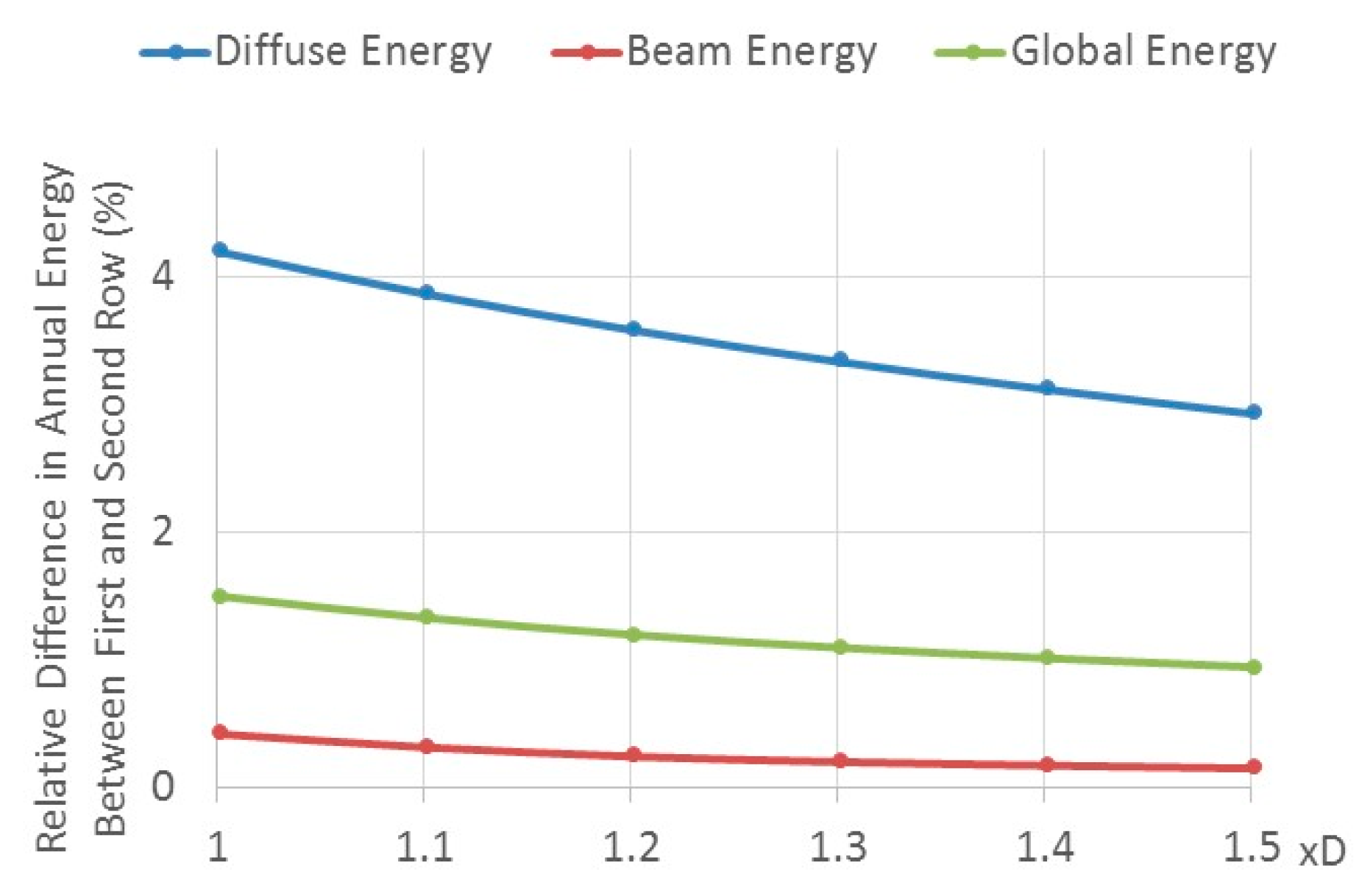
3.1. Optimization Results: Horizontal Field–Isotropic Model—Tel Aviv
- The percentage annual energy loss due to shading (beam) on the second row (cast by the collector in front) amounts to 0.42%.
- The percentage annual energy loss due to masking (diffuse) on the second row (caused by the collector in front) amounts to 4.2%.
- The percentage annual global energy loss due to shading and masking on the second row (caused by the collector in front) amounts to 1.49%.
- The incident diffuse radiation on the second and subsequent collector rows dominates the energy loss of the whole PV field.
3.2. Optimization Results: Horizontal Field–Anisotropic Model—Tel Aviv
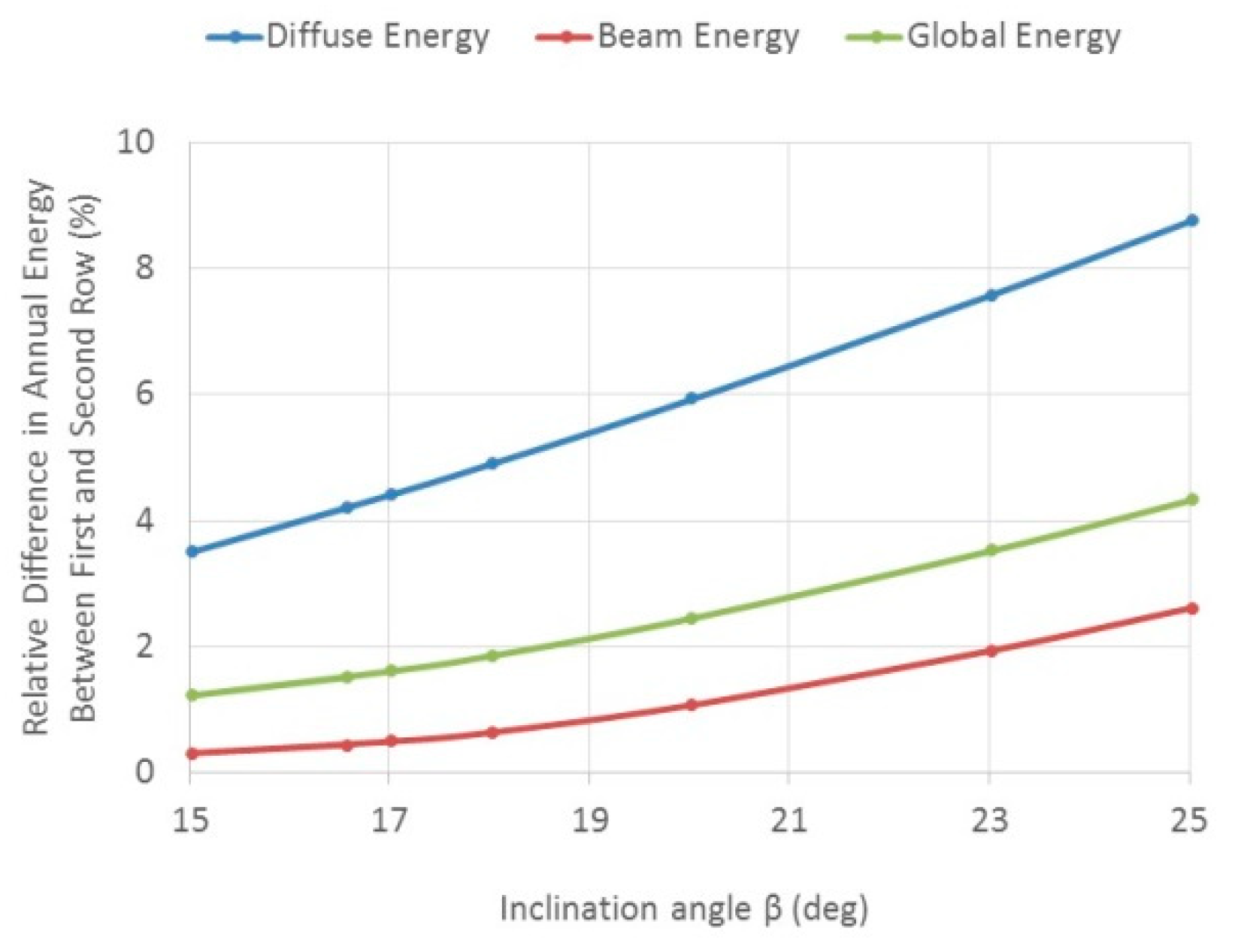
3.3. Optimization Results: Inclined Field–Isotropic Model—Tel Aviv
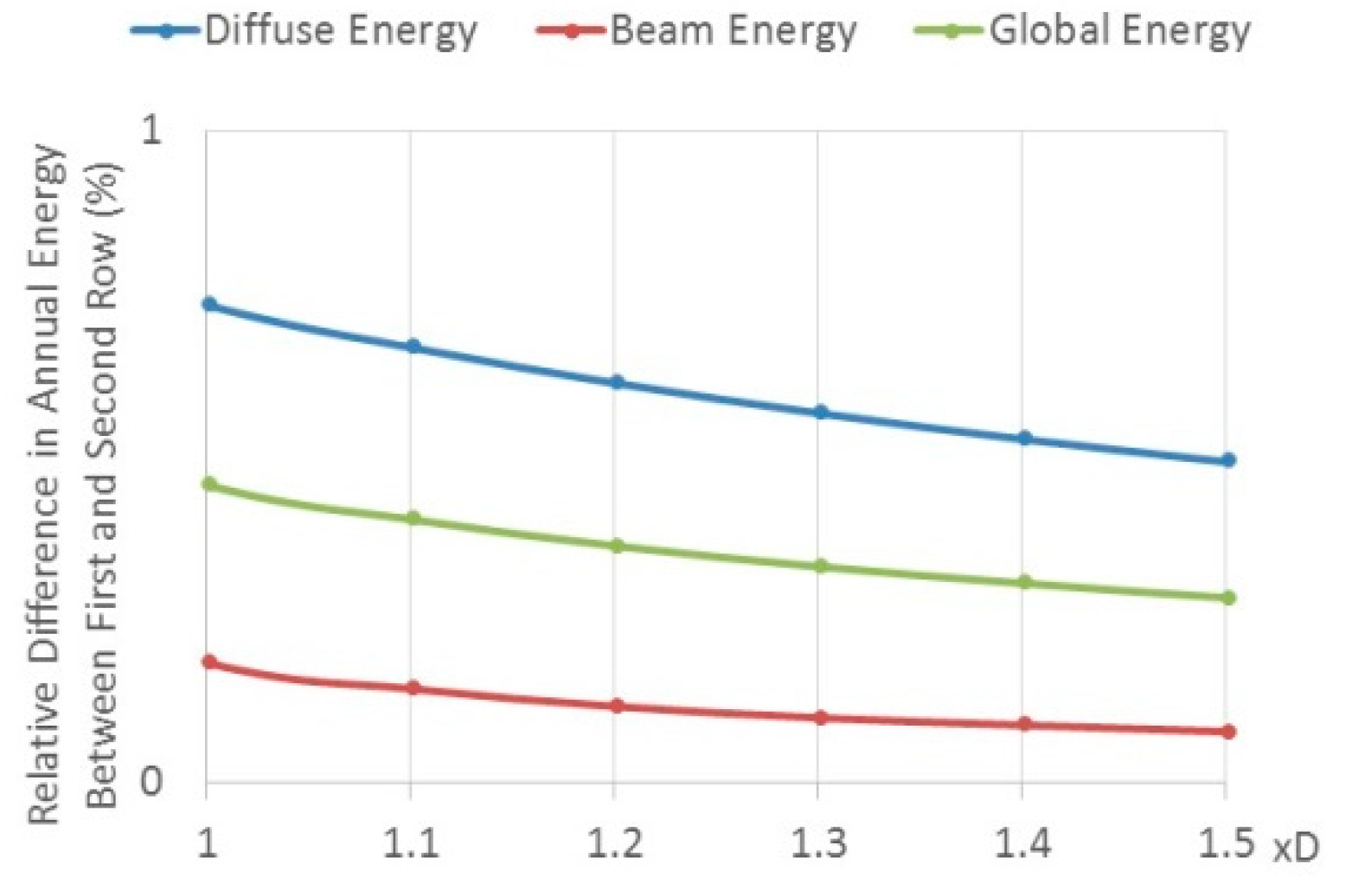
3.4. Optimization Results: Horizontal Field–Isotropic Model—Lindenberg
3.5. Optimization Results: Horizontal Field–Anisotropic Model—Lindenberg
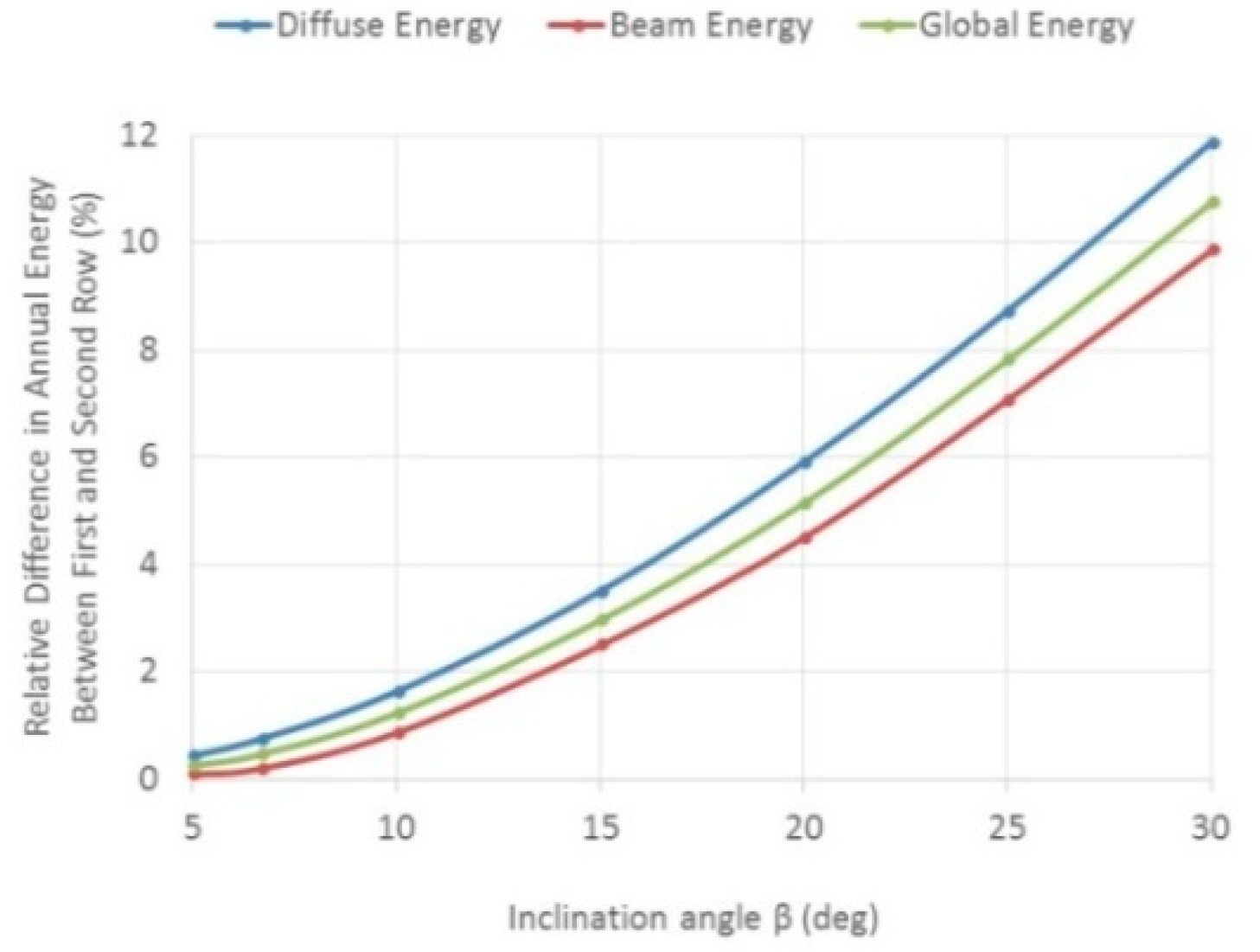
3.6. Optimization Results: Inclined Field–Isotropic Model—Lindenberg
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Patel, J.; Agarwal, V. MATLAB-Based Modeling to Study the Effect of Partial Shading on PV Array Characteristics. IEEE Trans. Energy Convers. 2008, 23, 302–310. [Google Scholar] [CrossRef]
- Diaz-Dorado, E.; Suarez-Garcia, A.; Carrillo, C.; Cidras, J. Influence of the Shadows in Photovoltaic Systems with different configurations of bypass diodes. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2010, Pisa, Italy, 14–16 June 2010. [Google Scholar]
- Peled, A.; Appelbaum, J. The view-factor effect shaping of I–V chatacteristics. Prog. Photovolt. 2018, 26, 273–280. [Google Scholar] [CrossRef]
- Coleman, T.F.; Branch, M.A.; Grace, A. Optimization Toolbox for Use with Matlab; The MathWorks, Inc.: Natick, MA, USA, 1999. [Google Scholar]
- Bhatti, M. Asghar, Practical Optimization Methods; Springer: Berlin, Germany, 2000. [Google Scholar]
- Appelbaum, J.; Weinstock, D. Optimal Solar Field Design of Stationary Collectors. J. Sol. Energy Eng. 2004, 126, 363–371. [Google Scholar]
- Aronescu, A.; Appelbaum, J. Design optimization of photovoltaic solar fields-insight and methodology. Renew. Sustain. Energy Rev. 2017, 76, 882–893. [Google Scholar] [CrossRef]
- Bourennani, F.; Rizvi, R.; Rahnamayan, S. Optimization of photovoltaic array using the differential evolution algorithm. In Proceedings of the 10th International Conference on Clean Energy (ICCE-2010), Famagusta, Northern Cyprus, 15–17 September 2010. [Google Scholar]
- Liu, B.Y.H.; Jordan, R.C. The long-term average performance of flat-plate solar energy collectors. Sol. Energy 1963, 7, 53–74. [Google Scholar] [CrossRef]
- Klucher, T.M. Evaluation of models to predict insolation on tilted surfaces. Sol. Energy 1979, 23, 111–114. [Google Scholar] [CrossRef]
- Hottel, H.C.; Sarofin, A.F. Radiative Transfer; McGraw-Hill: New York, NY, USA, 1967; pp. 31–39. [Google Scholar]
- Srinivasan, J.; (Radiation Heat Transfer Professor J.). Srinivasan Centre for Atmospheric and Oceanic Sciences Indian Institute of Science, Bangalore Lecture-6 Triangular-Enclosure; Srinivasan Centre for Atmospheric and Oceanic Sciences Indian Institute of Science: Bangalore, India, 2013. [Google Scholar]


| 102,975 | 260,285 | 363,260 | 98,646 | 259,190 | 357,837 | 13,603,213 |
| 112,432 | 258,289 | 370,721 | 107,187 | 257,617 | 364,804 | 13,868,453 |
| K | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 102,975 | 260,285 | 363,260 | 98,646 | 259,190 | 357,837 | 13,603,213 | 0 | 16.55 | 0.85 | 38 |
| 102,305 | 257,610 | 359,915 | 96,228 | 256,163 | 352,391 | 14,103,168 | 5 | 23.95 | 0.80 | 40 |
| 102,522 | 256,465 | 358,987 | 96,595 | 256,465 | 353,060 | 14,482,083 | 10 | 28.20 | 0.80 | 41 |
| 105,349 | 107,103 | 212,452 | 104,575 | 106,906 | 211,481 | 7,825,754 |
| 109,492 | 107,107 | 216,599 | 108,594 | 106,910 | 215,504 | 7,974,748 |
| K | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 105,349 | 107,103 | 212,452 | 104,575 | 106,906 | 211,481 | 7,825,754 | 0 | 6.68 | 0.86 | 37 |
| 105,112 | 114,648 | 219,760 | 103,764 | 114,457 | 218,221 | 8,293,949 | 5 | 13.61 | 0.82 | 38 |
| 104,787 | 120,665 | 225,451 | 102,675 | 120,477 | 223,152 | 8,705,237 | 10 | 20.71 | 0.82 | 39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aronescu, A.; Appelbaum, J. The Effect of Collector Shading and Masking on Optimized PV Field Designs. Energies 2019, 12, 3471. https://doi.org/10.3390/en12183471
Aronescu A, Appelbaum J. The Effect of Collector Shading and Masking on Optimized PV Field Designs. Energies. 2019; 12(18):3471. https://doi.org/10.3390/en12183471
Chicago/Turabian StyleAronescu, Avi, and Joseph Appelbaum. 2019. "The Effect of Collector Shading and Masking on Optimized PV Field Designs" Energies 12, no. 18: 3471. https://doi.org/10.3390/en12183471
APA StyleAronescu, A., & Appelbaum, J. (2019). The Effect of Collector Shading and Masking on Optimized PV Field Designs. Energies, 12(18), 3471. https://doi.org/10.3390/en12183471





