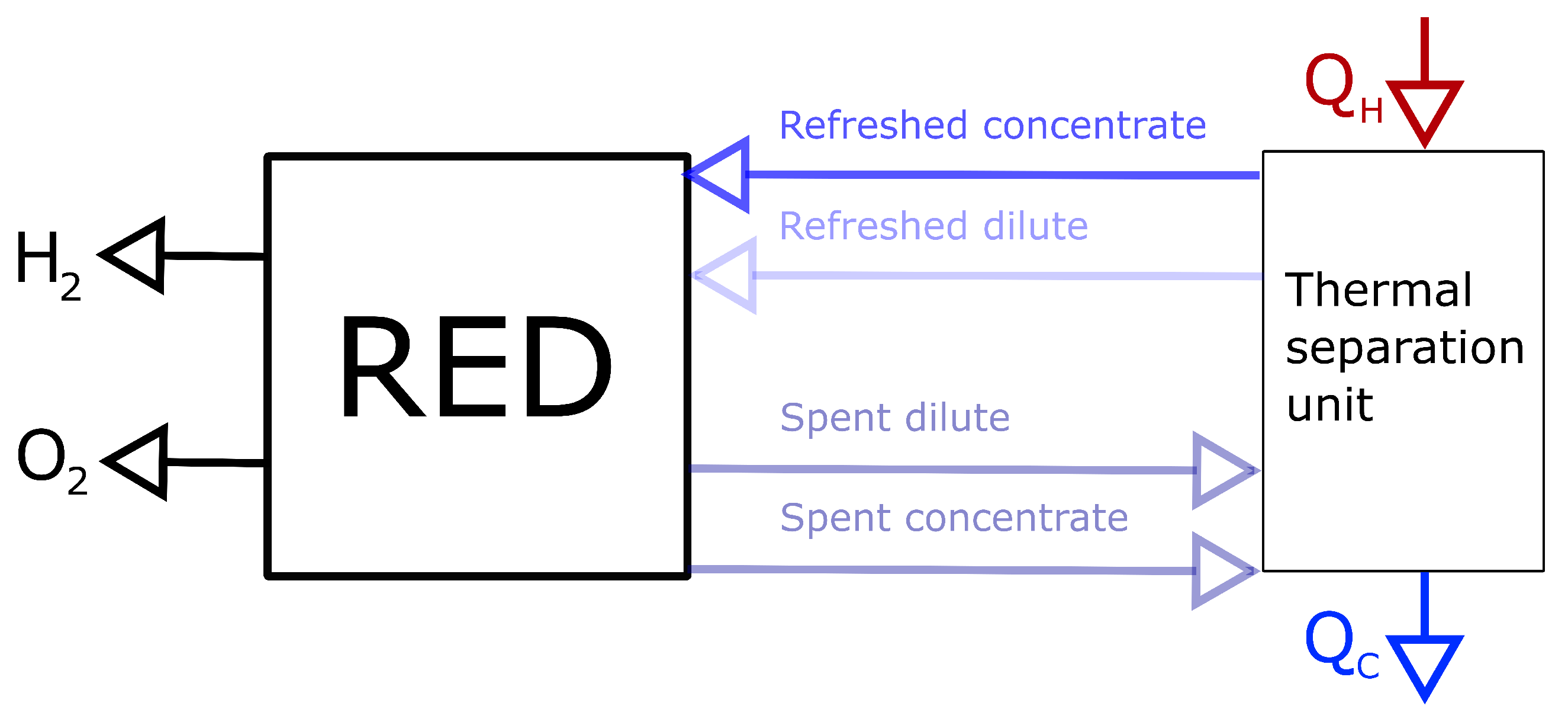
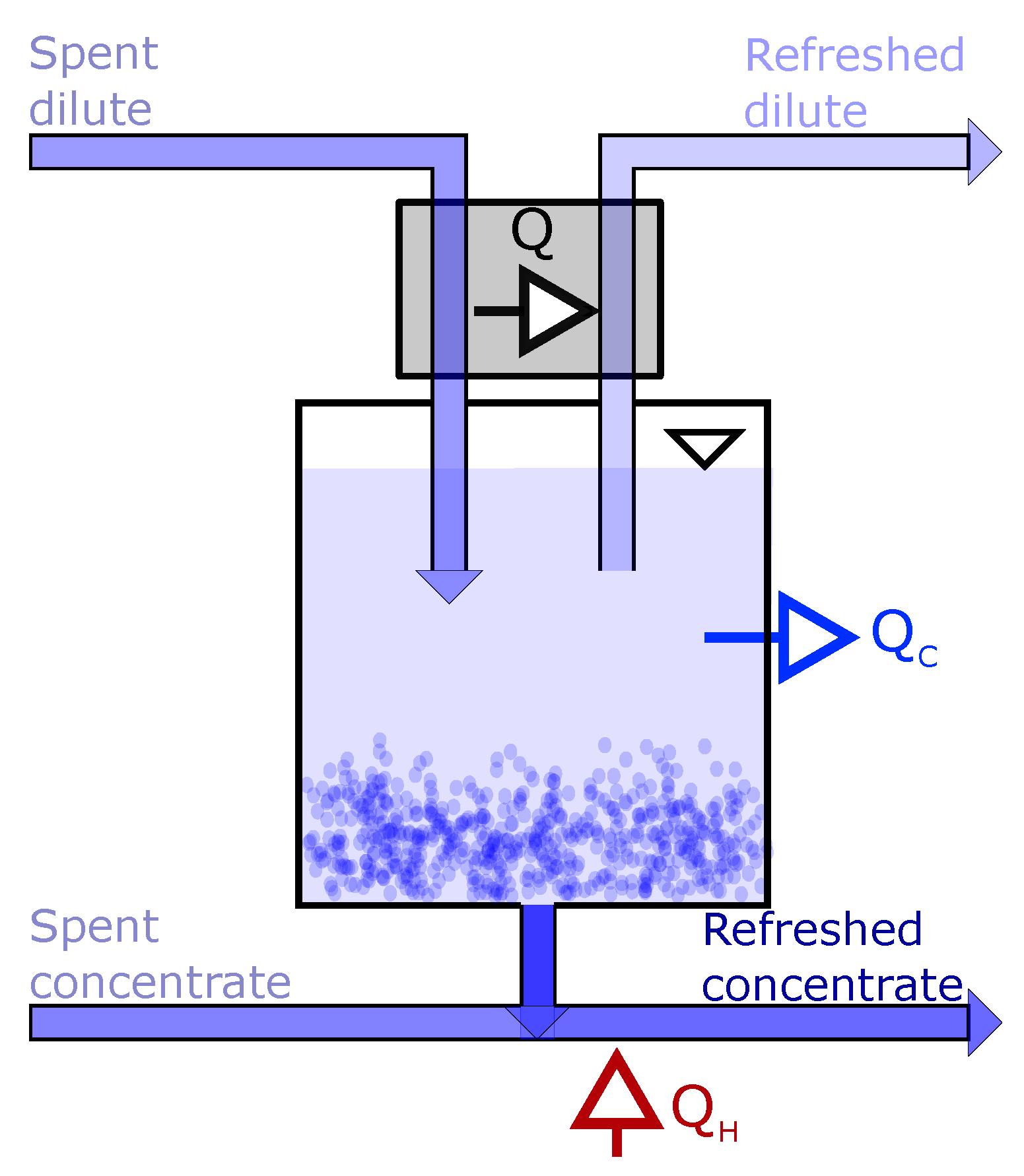
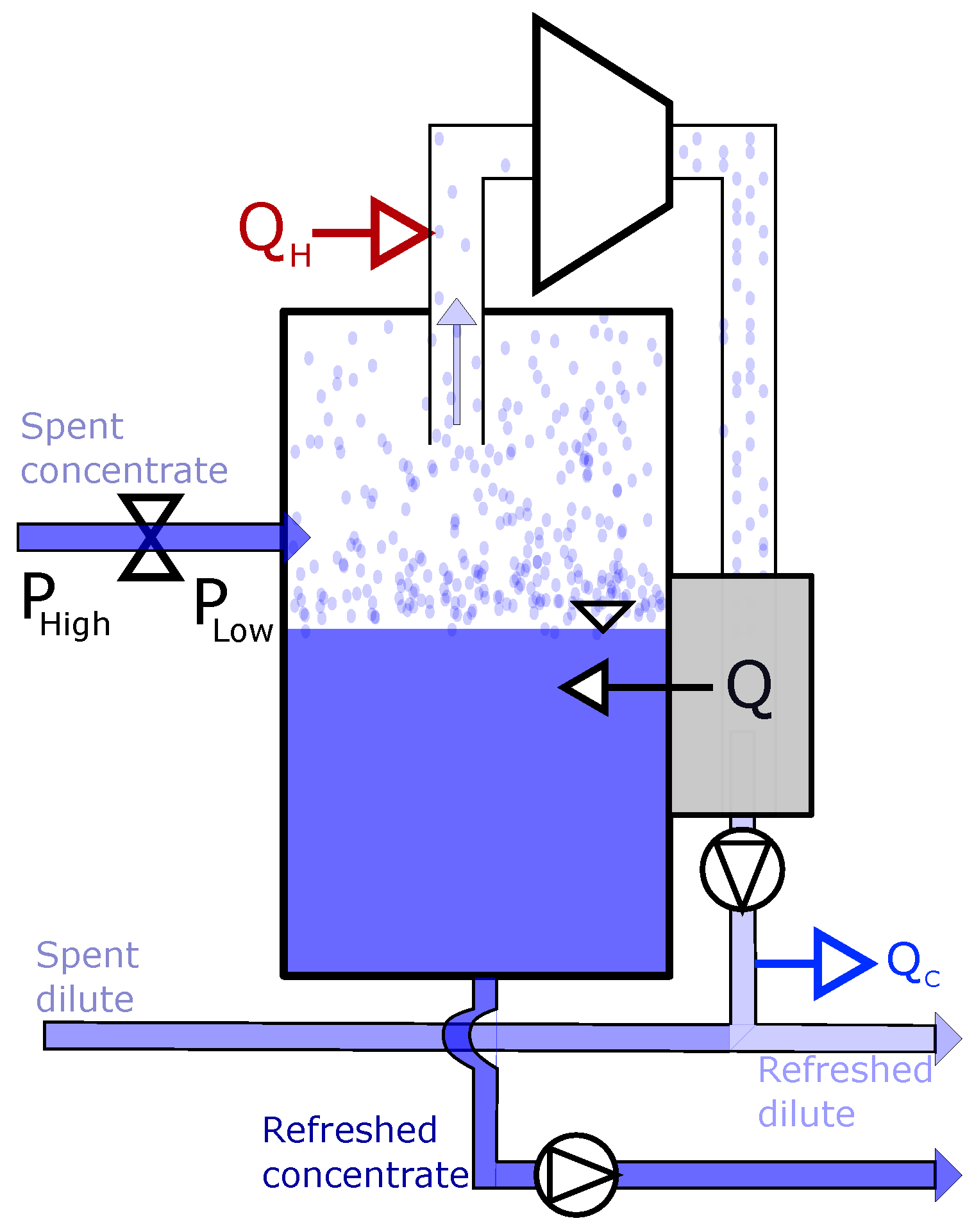
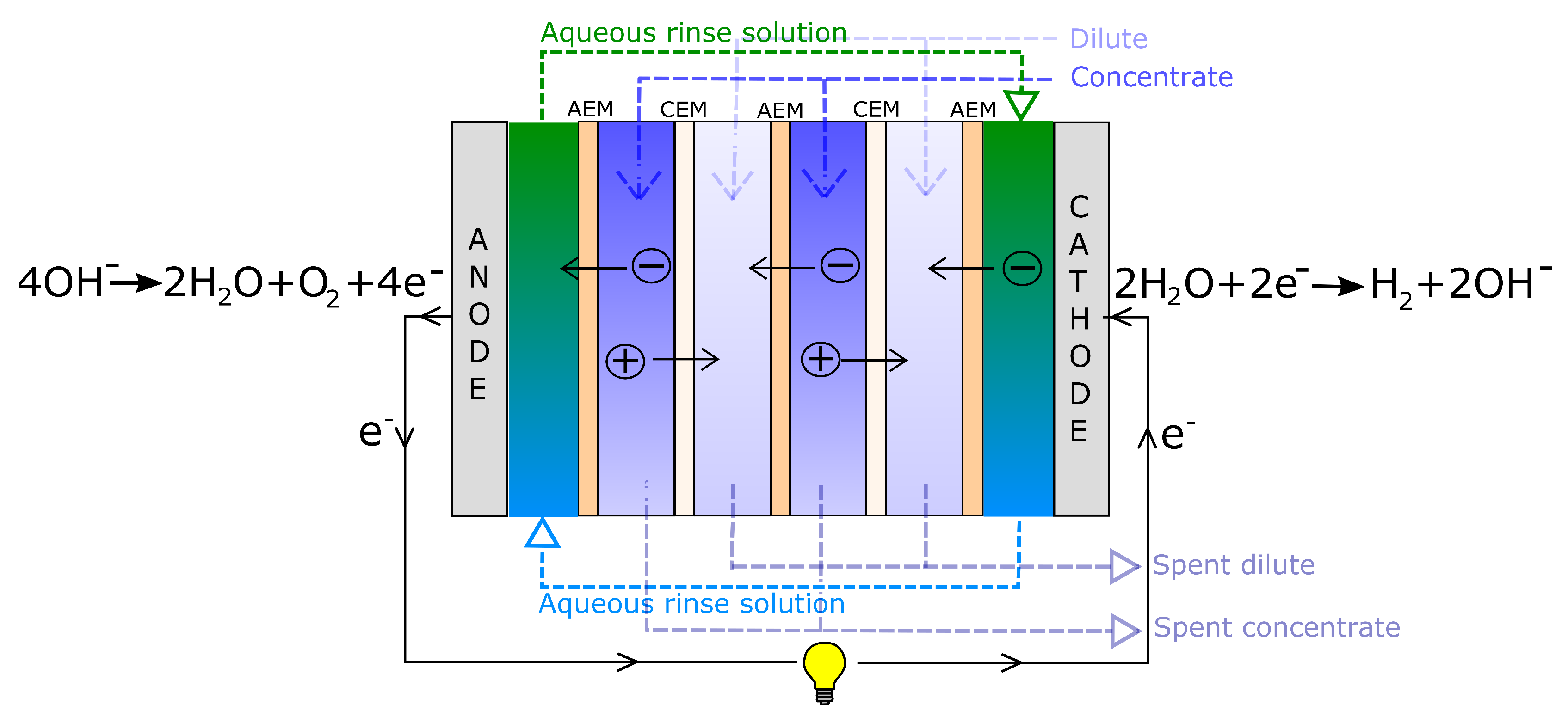
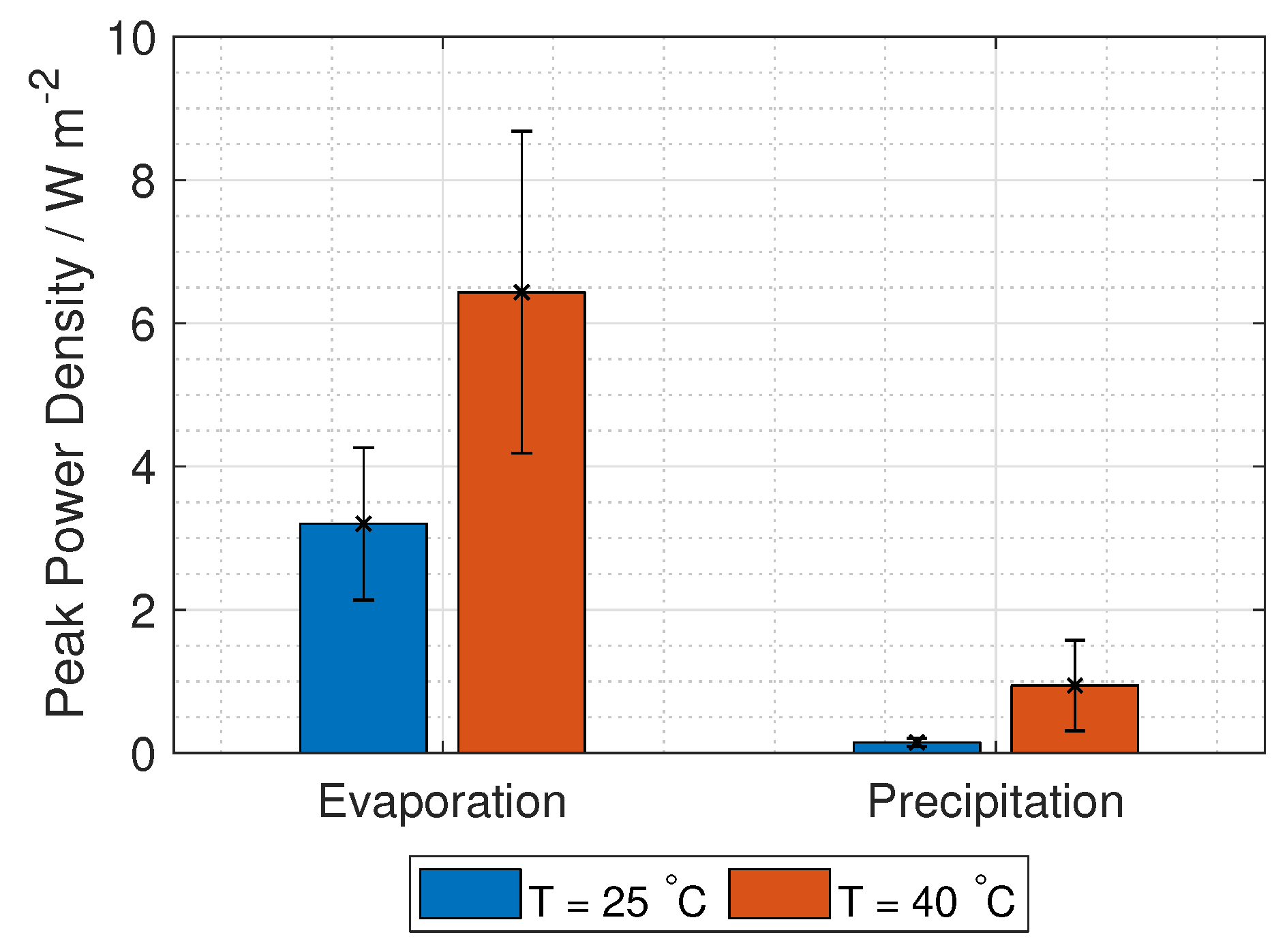
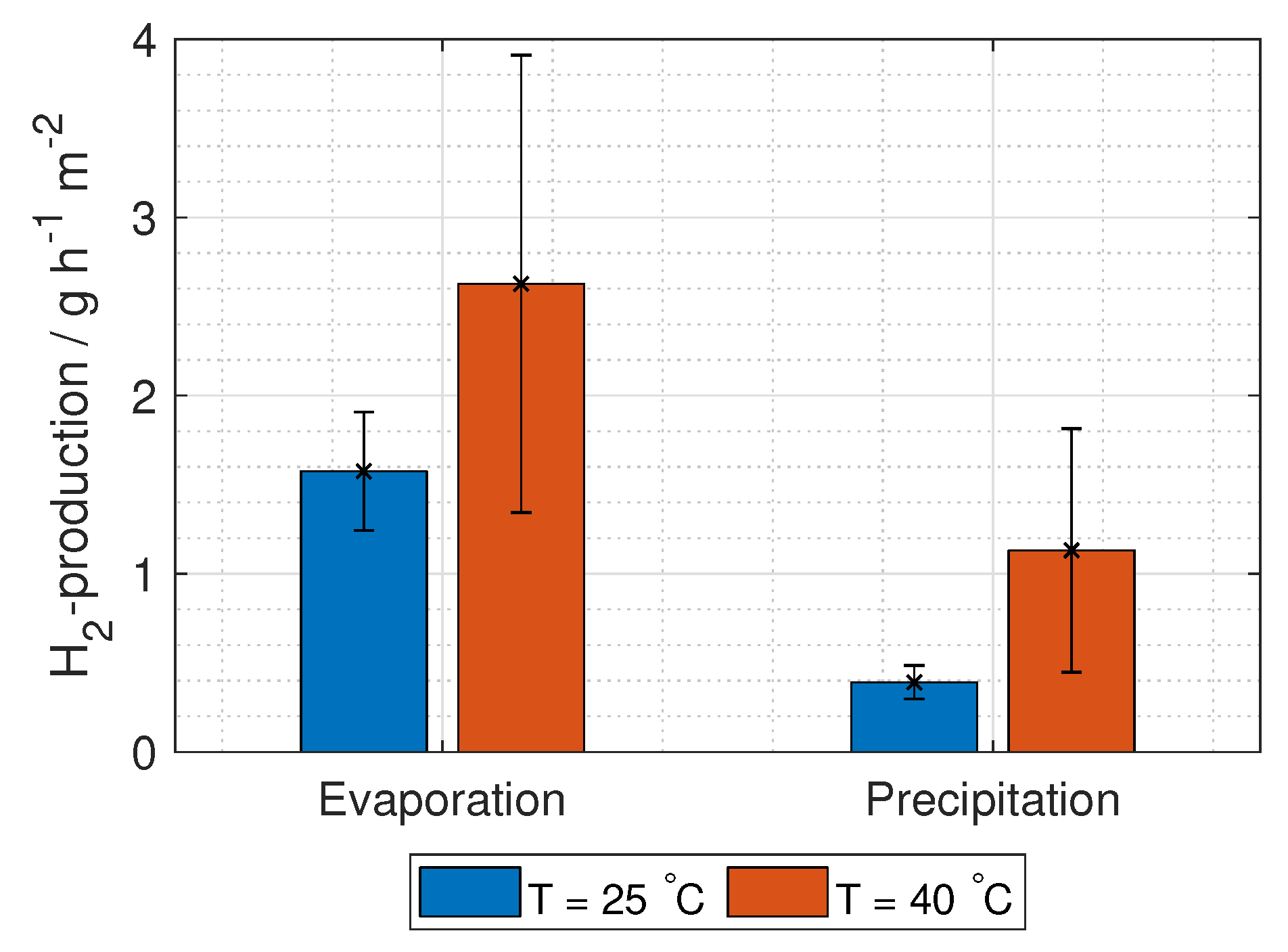
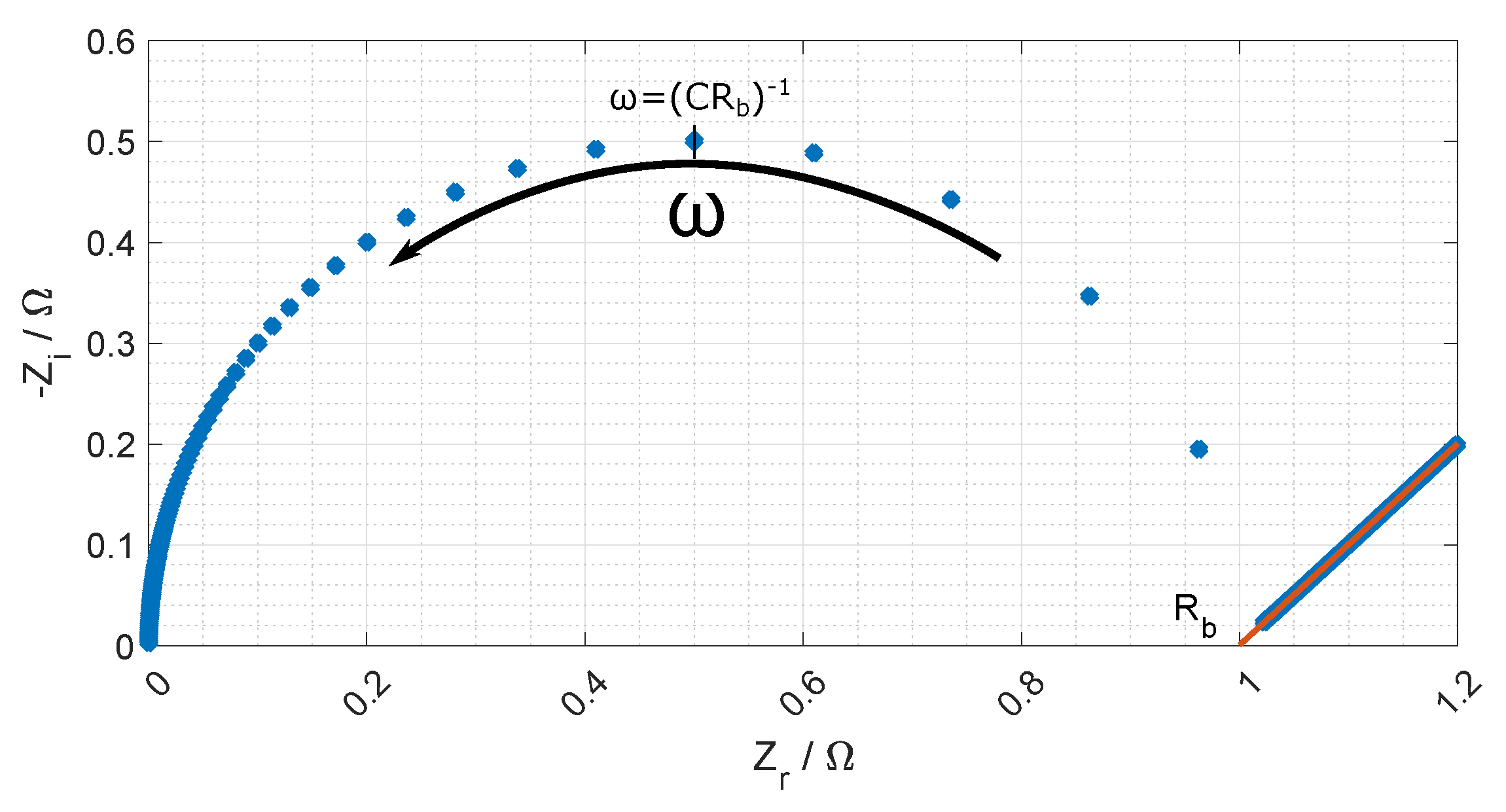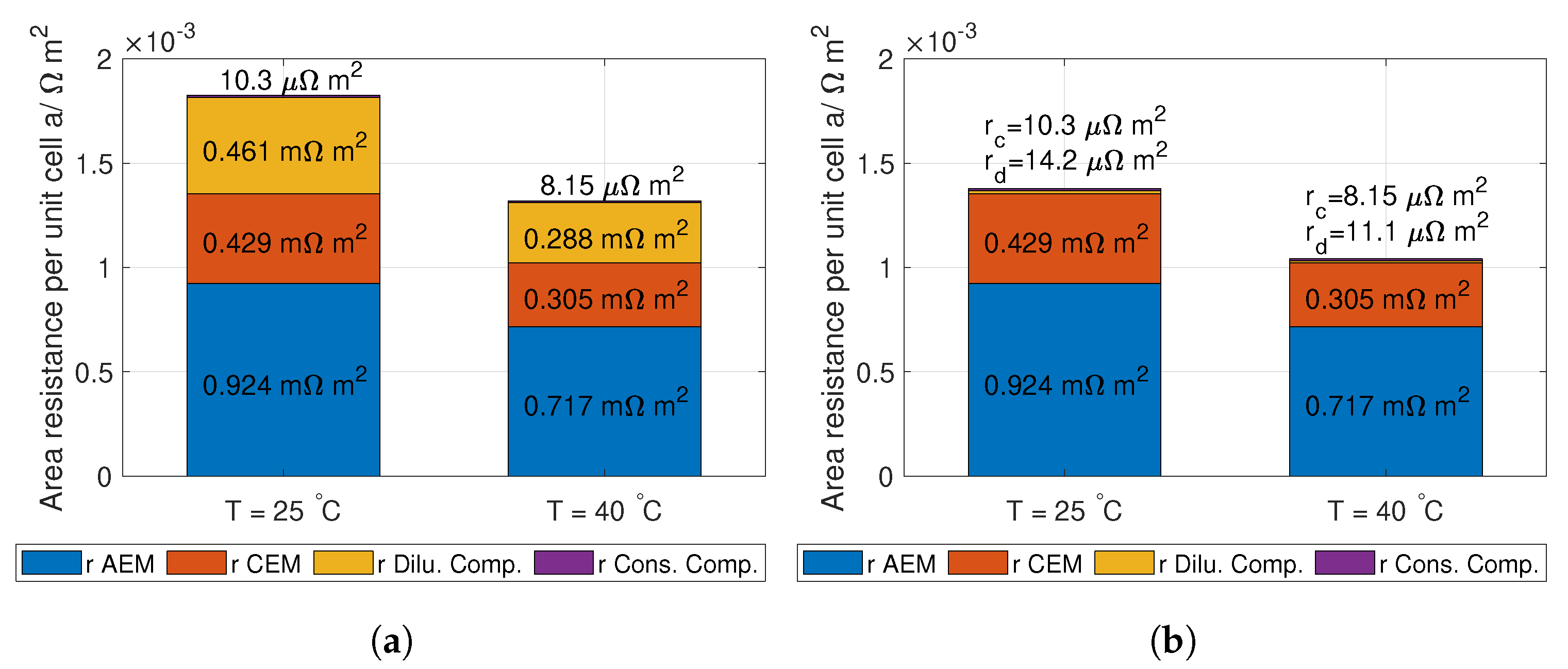3.1. Driving Voltage
The open-circuit voltage (OCV) or the Donnan voltage,
, over a RED unit cell is given by the Nernst equation:
where
is the mean permselectivity of the AEM and CEM in the unit cell,
R is the ideal gas constant,
T is the temperature in Kelvin,
z is the valence number of the ions transported,
F is Faraday’s constant, and
/
and
/
are the concentration and activity coefficients of the concentrated/dilute solution, respectively [
24].
The ratio of the activity coefficients are often assumed unity. However, due to concentrations close to the salt saturation point, the Stokes–Robinson equation is used for the calculation of the solution activity coefficient [
25,
26]:
where
I is the ionic strength (reference: 1 mole salt per kg solvent).
is the mean of the valence of the cation and anion (1 for KNO
),
is the molar mass of water (0.018 kg mol
),
is the number of ions per molecule (2 for KNO
) and
is the distance of the closest approach, which is dependent on the kinetic energy of the ions, thereby also the concentration and temperature of the solution. For simplicity,
is set constant with temperature and concentration, and found from curve fitting of data from Dash et al. and Marcos-Arroyo et al. [
27,
28] to Equation (
4), and found to be 1.1 Å. The hydration number,
h, is found to have a dependence on temperature and concentration [
29]. Afanasiev et al. [
30] suggest an exponential dependence on concentration and negligible dependence on temperature, while Onori [
31] gives a linear dependence on concentration and states that the hydration number is dependent on temperature. For simplicity,
h for KNO
is set constant with temperature and concentration and taken to be the mean value from Lu et al. [
32]: 5.
In Equation (
4),
A and
B are temperature dependent constants given in Equation (
5) (at 25
C
(kg mol
)
and
(kg mol
)
m
[
33]).
where
is Avogadro constant,
is the density of the solvent (here water and set to constant 1000 kg m
for simplicity),
is the elementary charge,
is permittivity of vacuum,
is Boltzmann constant, and
T is the temperature in Kelvin.
is the dielectric constant of the solvent [
34] (here water) and given in Equation (
6) (rewritten to use temperature in Kelvin instead of Celsius):
In Equation (
4),
is the water activity as a function of the salt concentration. Sangster et al. [
35] measured the water activity in KNO
solutions above 3 M and extrapolated the data for concentrations down to 0 M, giving a linear trend of the water activity. An approximation of the linear equation for the water activity in a KNO
solution with molality
b is given in Equation (
7):
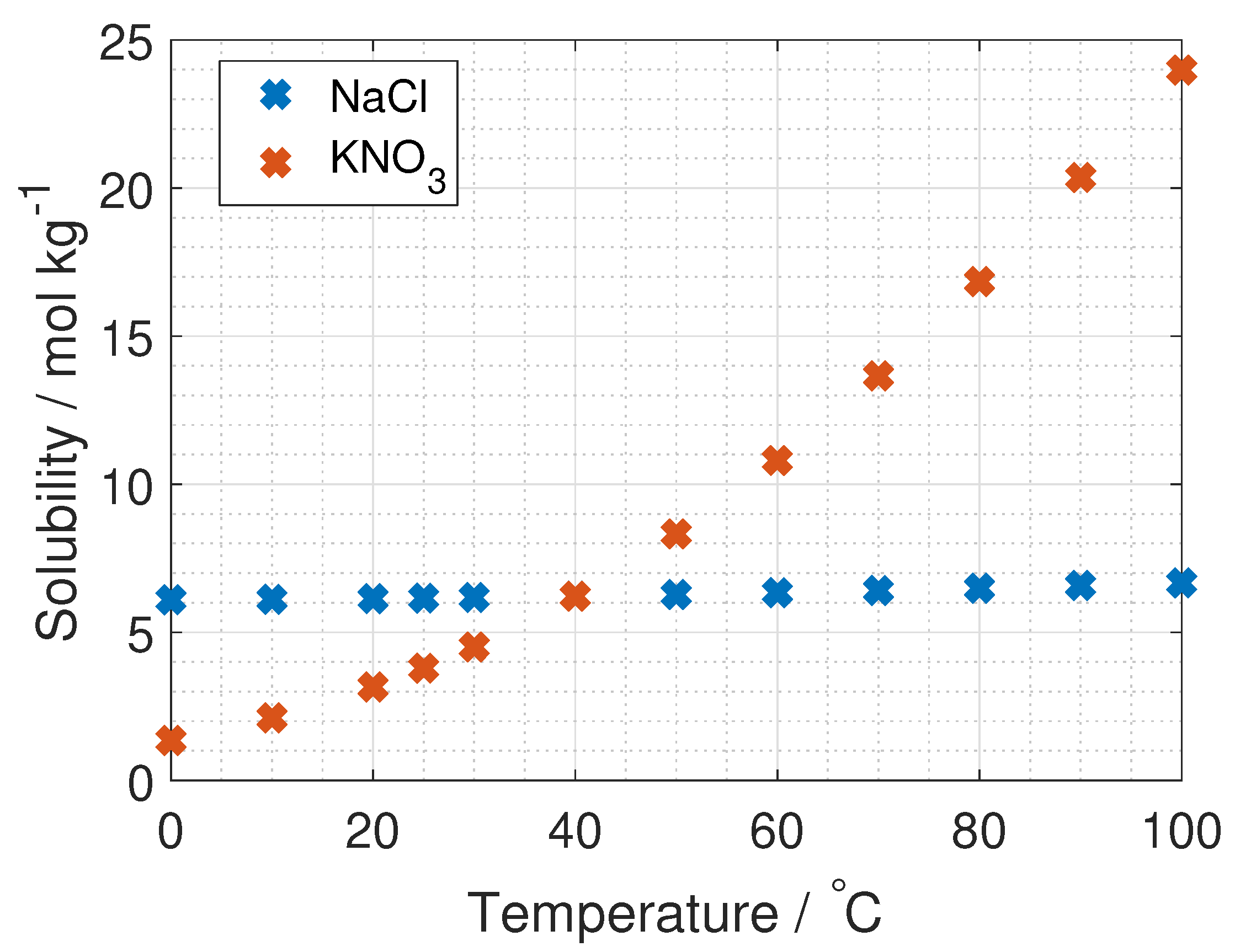
To the author’s knowledge, the activity coefficient of KNO
is only measured at 25
C and up to salt concentrations of 3.5 mol kg
, by Dash et al. and Marcos-Arroyo et al. [
27,
28]. Their experiments were similar, but Dash et al. used double junction reference electrode, while Marcos-Arroyo et al. used single junction. The modeled activity coefficient from Stokes–Robinson equation (Equation (
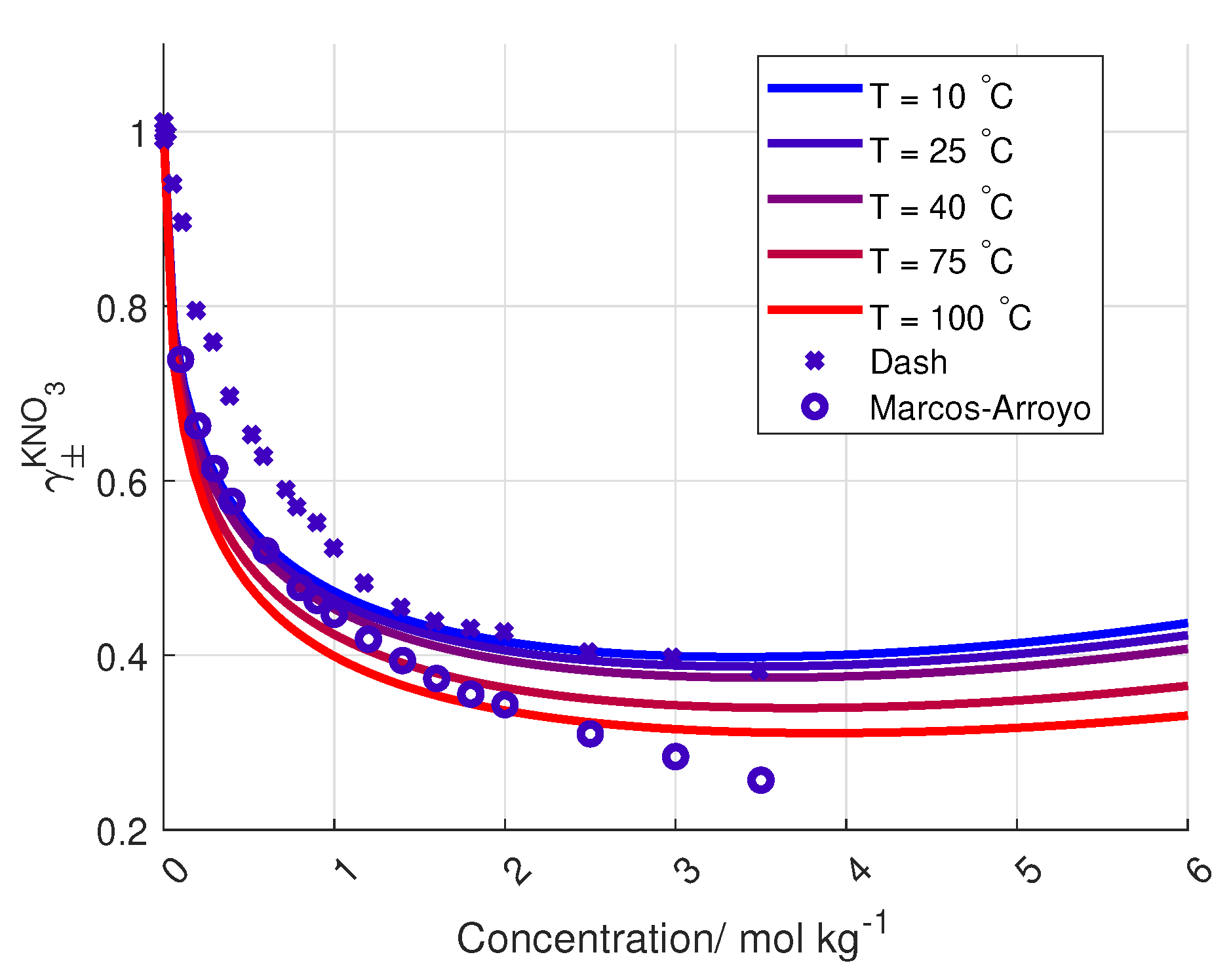
4)) is plotted in
Figure 6 together with the data from Dash and Marcos-Arroyo.
A reason for the deviation between the Stokes–Robinson equation and the measured activity coefficient of KNO
from Dash et al. and Marcos-Arroyo et al. [
27,
28] is the assumption of no temperature or concentration dependency in the hydration number and the distance of closest approach in the model.
The apparent permselectivity,
from Equation (
3), increases with increasing concentration difference [
36]. Krakhella et al. [
37] measured FAS-50 and FKS-50 from Fumatech [
18,
19] at elevated NaCl concentrations, and found the permselectivity to vary (with concentrations) from 0.5 to 0.8. Ji and Geise [
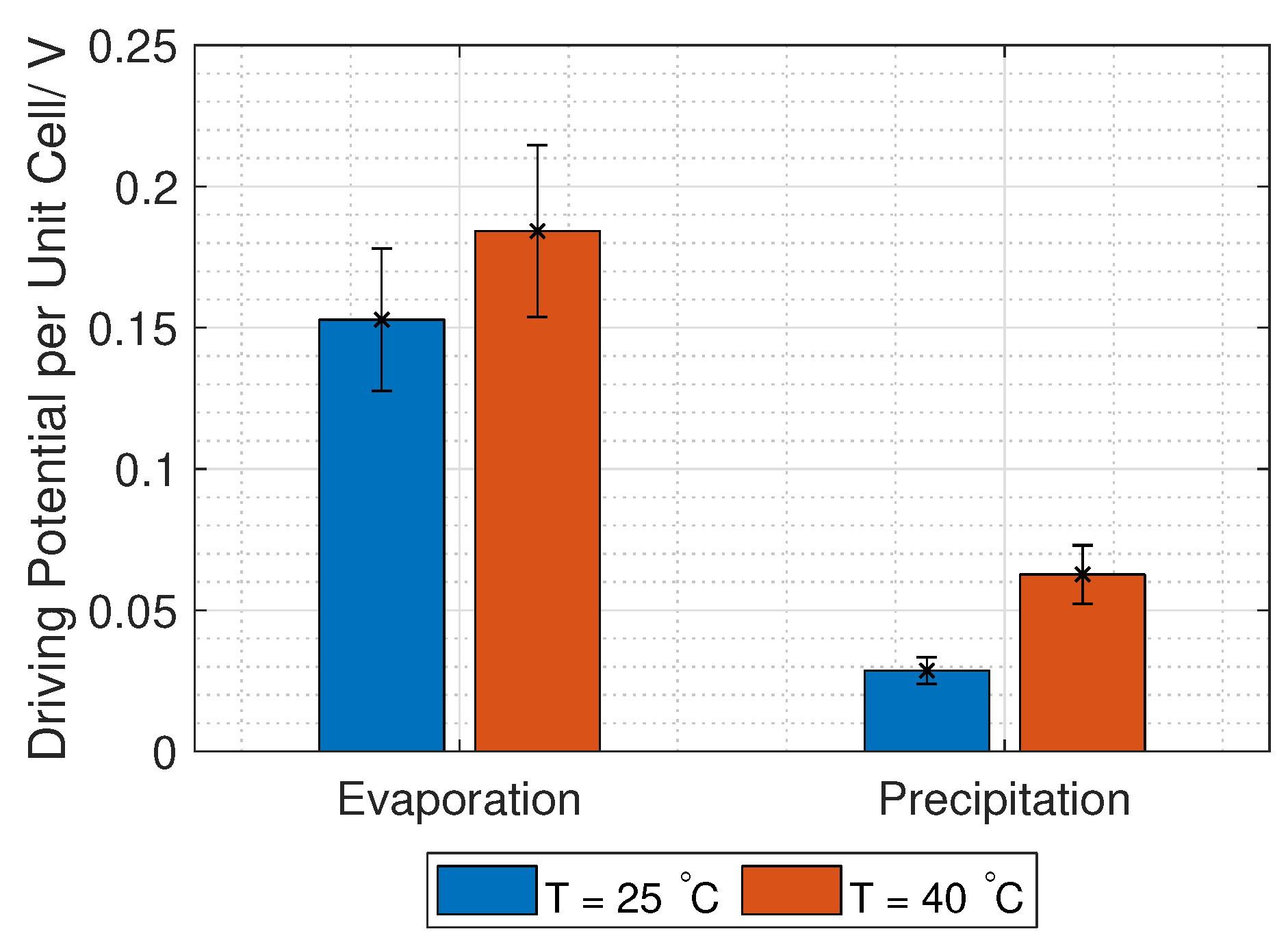
38] found that the permselectivity of two membranes dropped by approximately 2% when the temperature increased from 14 to 31
C. However, the Donnan voltage increases with increased temperature (Equation (
3)), which was confirmed experimentally by Długołȩcki et al. and Van Egmond et al. [
39,
40], among others.
The total voltage in a RED stack is given in Equation (
8):
where
is the number of unit cells,
i is the current density per cross-section area and
r is the unit cell area resistance given in Equation (
14).
represents lumped electrode losses, including the activation overpotential losses and the ohmic losses at the electrodes. The power density gained from the RED stack is the stack voltage times the current, given in Equation (
9):
The voltage needed for hydrogen production is 1.23 V, while the current density is found at maximum power density, where the derivative of Equation (
9) with respect to current density is zero. Using these two limitations, gives two equations with two unknowns (current and number of unit cells):
Solving Equation (
10) gives the operating current density per unit cell area,
and the number of unit cells needed:
The hydrogen production in grams per hour per cross-section area is
where
M is the molar mass of hydrogen gas (2.02 g mol
).
It is important to highlight that the total ohmic losses of the RED stack,
, need to be (1.23 V + E
) for all current densities and number of unit cells. This can be seen by solving Equation (
10).
3.2. Losses
The losses considered in this work is the lumped electrode losses at the electrodes and the ohmic losses per unit cell. The Tafel losses are here considered to be a lumped loss of the activation potential and ohmic losses at the electrodes [
24]. The operational current density for the RED stack is assumed small (<100 A m
), where the activation and ohmic losses at the electrodes are approximately 0.10 V (see [
24], p. 156).
The ohimc losses are given in Equation (
14):
where
and
are the conductivity of the AEM and CEM [S m
] respectively,
and
is the thickness of the AEM and CEM, and
is the spacer shadow (dimensionless) [
39].
d is the thickness of the spacer,
(dimensionless) is the volume factor occupied by the spacer or the porosity (for no spacer:
= 1. For definition, see [
41]).
and
are the conductivities of the dilute and concentrated solution respectively (S m
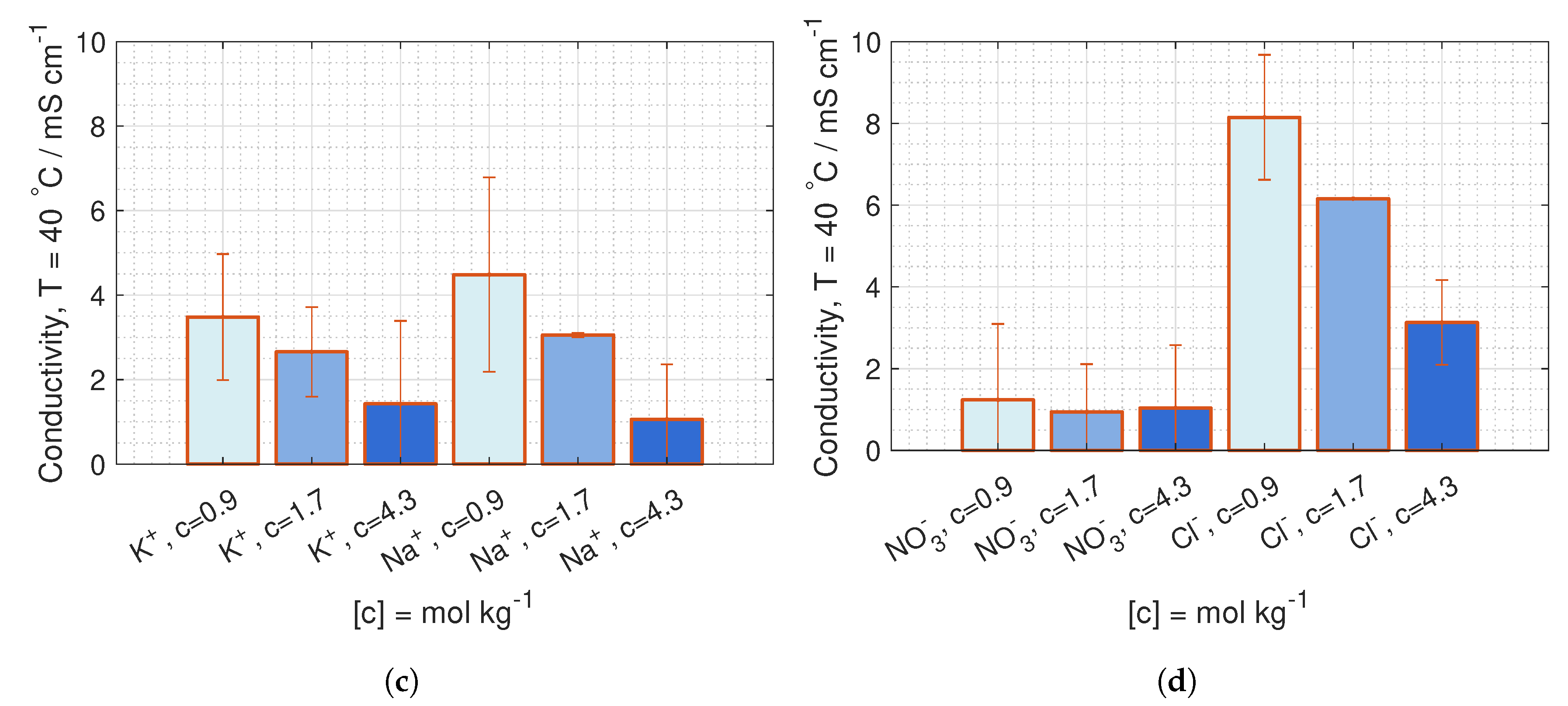
). Theoretical values for
and
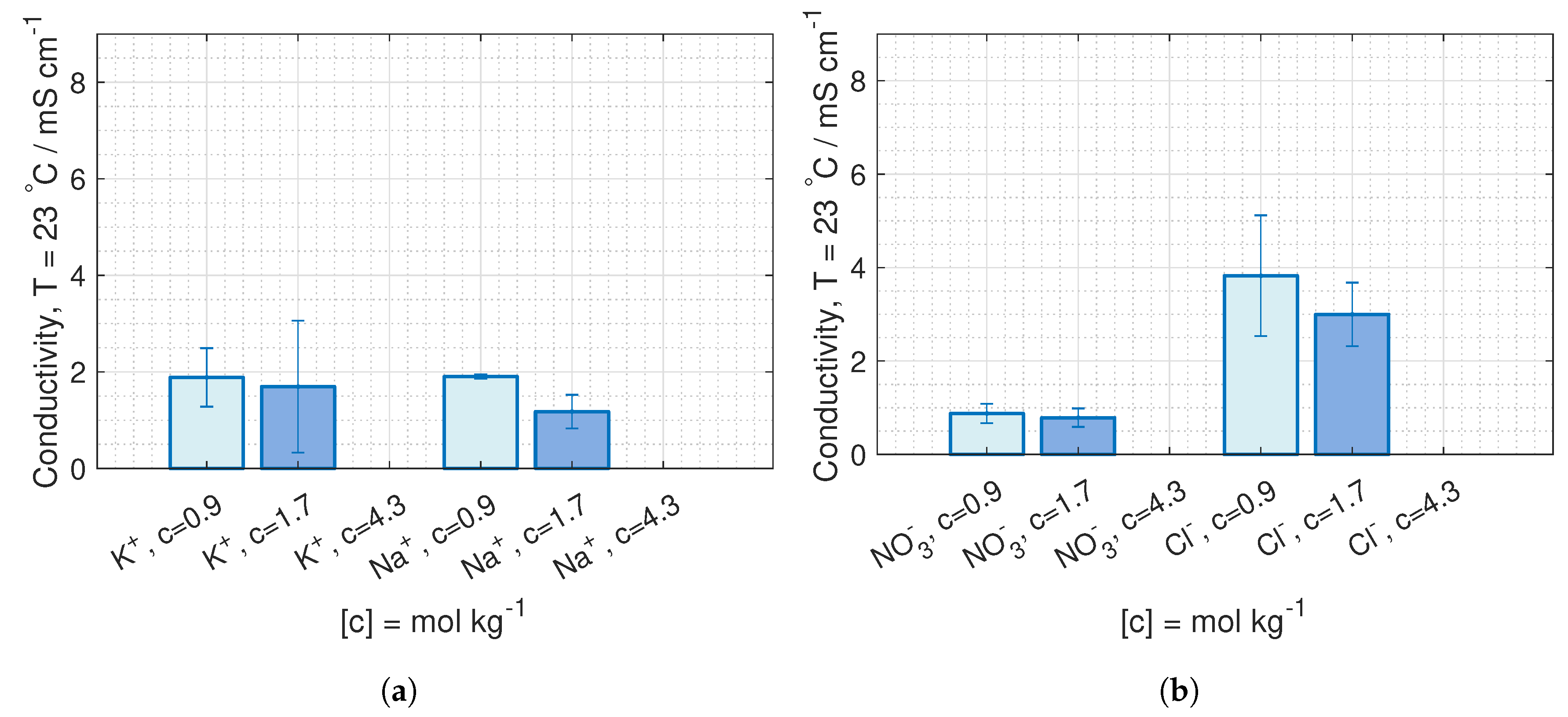
are deduced from conductivity measurement from [
42], where the data is fitted to Kohlrausch’s equation (given in Hamann [
43], p. 22) for 23
C and 40
C:
where
b is the molality, and the coefficients,
and
, are given in
Table 1.
is equivalent to the molar conductivity of infinite dilute solution,
, and
is a coefficient related to the stoichiometry of the electrolyte.
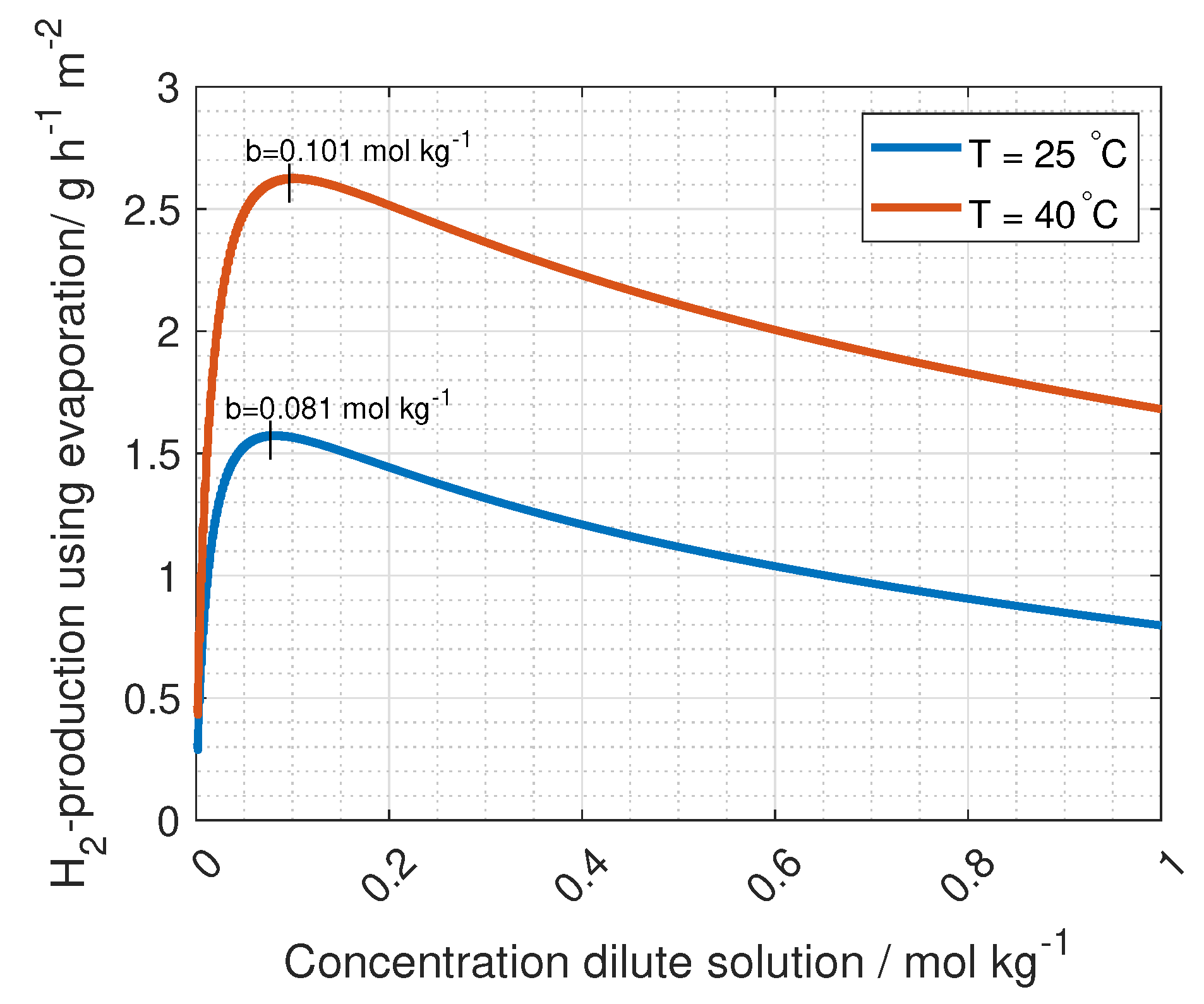
The ohmic losses in the flow compartment should be optimised with respect to hydrogen production (see Equation (
13)). For wider compartments, the ohmic resistance increases, while pumping energy decreases. The ideal compartment width was found to be approximately 100 µm [
44]. However, the compartment thickness in the simulations in this article is taken from Fumatechs ED-stack (given in Table 4). The solution concentration also contributes to the ohmic losses of the flow compartment, where a lower salt concentration increases the resistance (see Equation (
15)). This would suggest higher concentrations on both sides of the membrane. However, a higher salt concentration gradient between the compartments enhances the RED driving potential (see Equation (
3)). Optimising the solution resistance is needed for highest possible power density and hydrogen production, and varies with cell geometry and solution flow. When these factors are accounted for, the ionic resistance in the membranes is the main contributor to ohmic losses [
8,
45].
The energy losses in the RED-stack can be calculate from (unit Wh m
(hydrogen)):
where
is the voltage loss over the RED-stack and
p is the pressure (1 atm = 101,325 Pa).
3.3. Ionic Membrane Conductivity
The ionic conductivity in the membrane in Equation (
14), depends on the concentration and diffusion coefficient for both the counterions and co-ions [
46] (Equation (
8)). The concentration of counterions in the membranes is dependent on the fixed charges, and the amount of salt and water absorbed in the membrane pores [
46,
47]. The fixed charges are quantified by the ion exchange capacity (IEC) and are given as mmol g
, and are constant (per membrane weight) with concentration. By increasing the IEC, the hydrophilicity of the polymer chains in the membrane increases and with it the water uptake. Water makes the membrane swell, reducing the density of the fixed charges in the membrane and increasing the adsorption of ions in the membrane. For the two membranes used in the experiments in this article, the IEC is 1.2–1.4 for CEM and 1.6–2.0 mmol g
for AEM [
18,
19], indicating a slightly better conductivity in AEM than CEM.
The swelling of the membrane is also affected by the difference between the membrane concentration and the external concentration. The water uptake in the membrane does not change much with the external concentration, but if the external concentration exceeds a certain limit (the Donnan concentration of the membrane), water can diffuse from the membrane to the solution, due to osmotic forces [
46], decreasing the water and salt content inside the membrane. This concentration limit is around 0.07 M for Nafion 117 [
48]. The result of the swelling and de-swelling, is a flux of water and dissolved salt into the membrane at low external concentration, and a flux of water from the membrane to the external solution at high external concentration, resulting in a strictly increasing concentration of both counterion concentration and co-ions in the membrane pores with external concentration [
46].
The concentration of co-ions is also affected by the Donnan voltage over the membrane/solution interface, where a lower Donnan voltage between membrane and external solution leads to higher co-ion adsorption in the membrane [
46].
The other factor affecting the ion conductivity in the membrane is the diffusion coefficient [
46]. For NaCl the diffusion coefficient of the counterion is reported to decrease slightly with external concentration in CEM, while in AEM, the reported data showed no effect on the concentration [
47]. However, the reported data from [
47] is only conducted up to 1 M NaCl. For higher concentrations, the diffusion coefficient is believed to decrease with external concentrations, due to deswelling of the membrane. Kamcev et al. found the diffusion coefficient of the counterion always to exceed the co-ion, regardless of anionic or cationic membrane [
46]. This indicates a faster transport at the fixed groups than in the pores.
Smaller particles should theoretically have a higher diffusion coefficient [
49]. However, a smaller ionic radius has more charges per area on the surface of the ion, bringing more water molecules with it [
49], increasing the hydraulic diameter. This results in two effects on the conductivity. The first effect is increased membrane wetting, where more water increases the conductivity. The second effect is that the physically larger ion will lower the diffusion coefficient. The crystalline and the hydrated radius of Na
, K
, Cl
and NO
are found from [
49] and given in
Table 2.
3.4. Electrochemical Impedance Spectrocopy
In electrochemical impedance spectroscopy (EIS), an oscillating current (or potential) is applied to the system at a specific frequency, and the amplitude and phase shift of the voltage (or current) is measured. From this, the impedance of the system can be obtained.
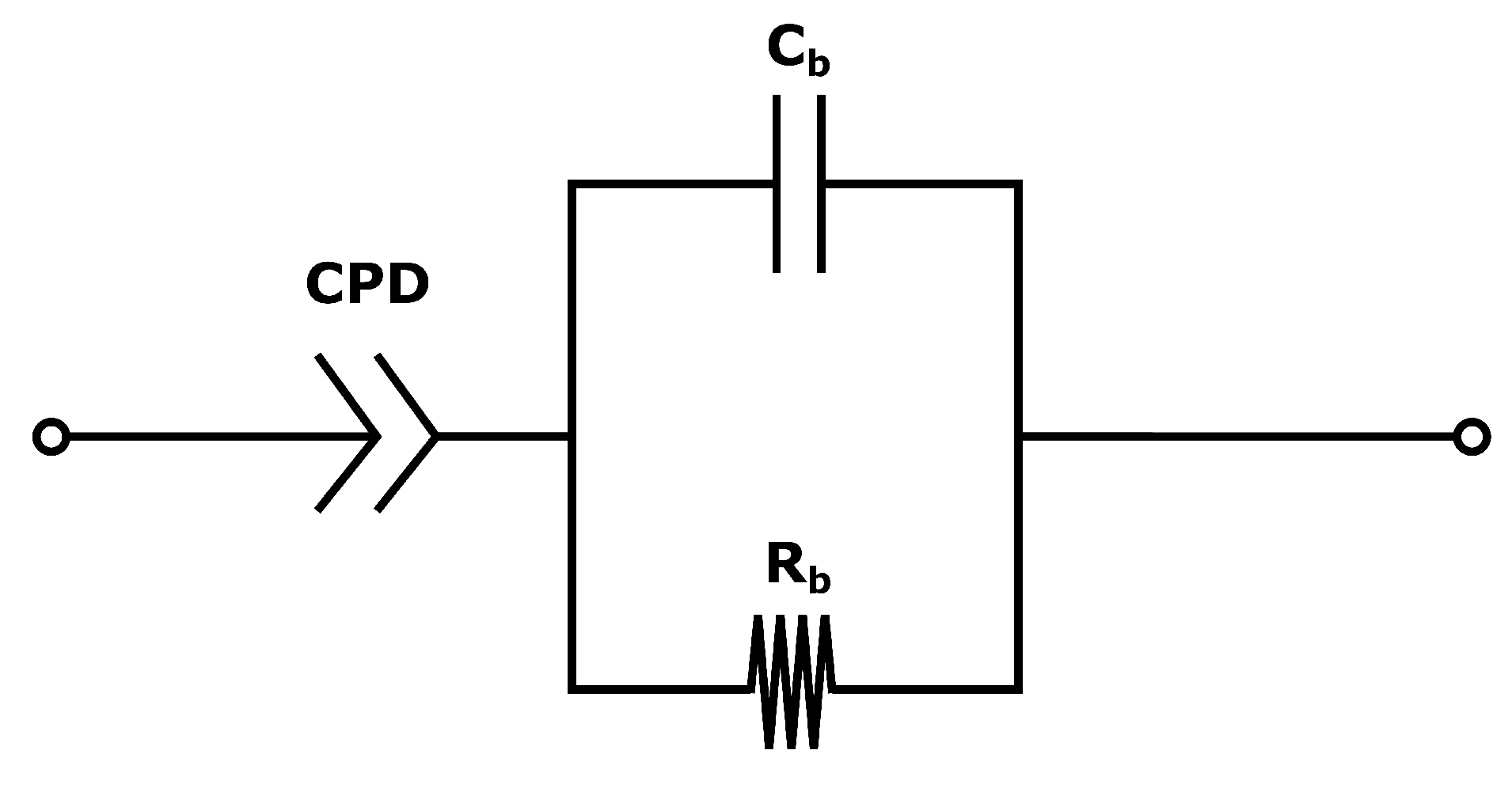
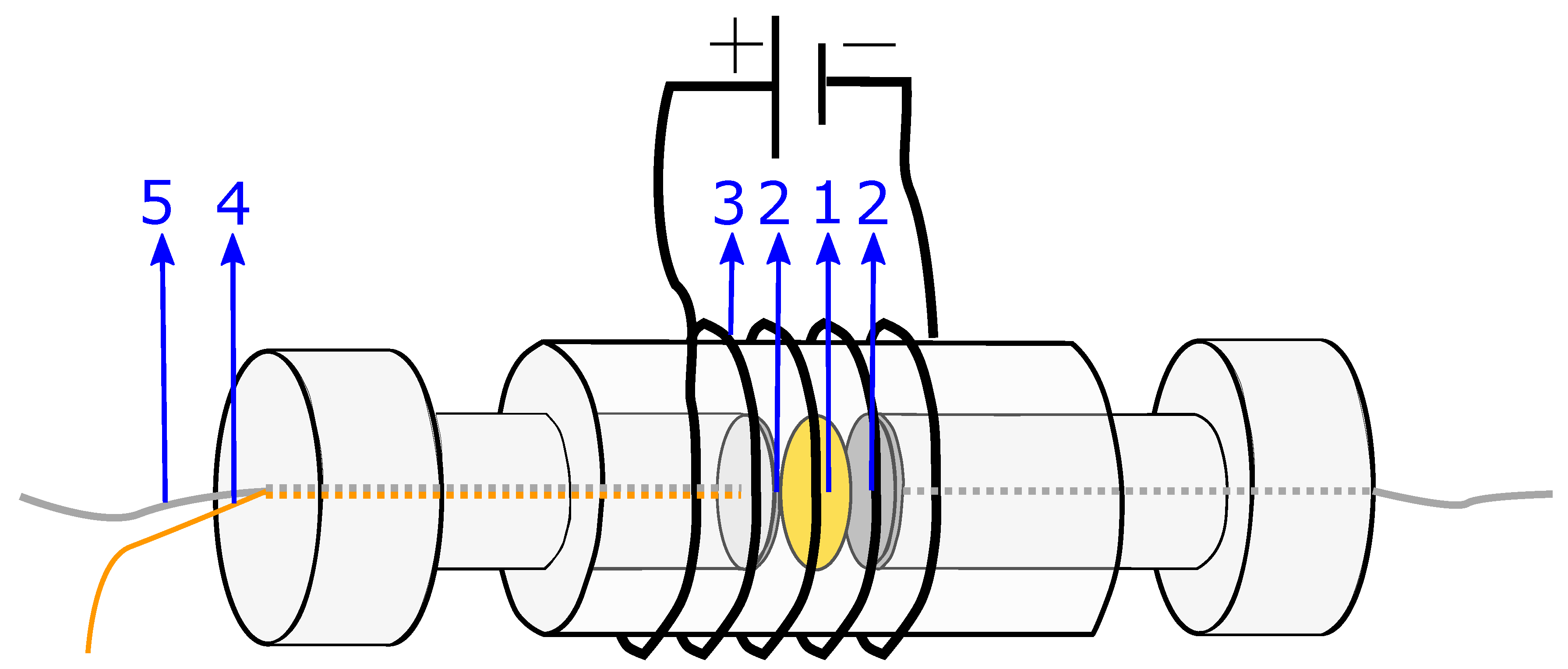
The system used for the present measurements is a membrane compressed between two electrodes (more details in
Section 4.2). The equivalent circuit is therefore a series of the three components: the two electrode-membrane interfaces, and one membrane bulk impedance. The interface impedance between the membrane and the electrodes consists of a capacitive impedance (
), due to the double layer, in parallel with a resistance (
) representing the blocking interface. The membrane impedance is a bulk resistance (
) in parallel with a capacitor (
) due to the double layers building up in the pores in the membrane [
50]. The total impedance is given in:
Since no charge can pass the electrode/membrane interface, the interface impedance is merely capacitive [
50]. Electrodes with a perfectly flat surface purely have a capacitive behaviour, although small irregularities in most electrodes lead to the use of a constant phase element (CPE) instead of a capacitor when analysing the impedance. The total impedance in Equation (
17) can be simplified to:
The equivalent circuit for the electrode membrane system is given in
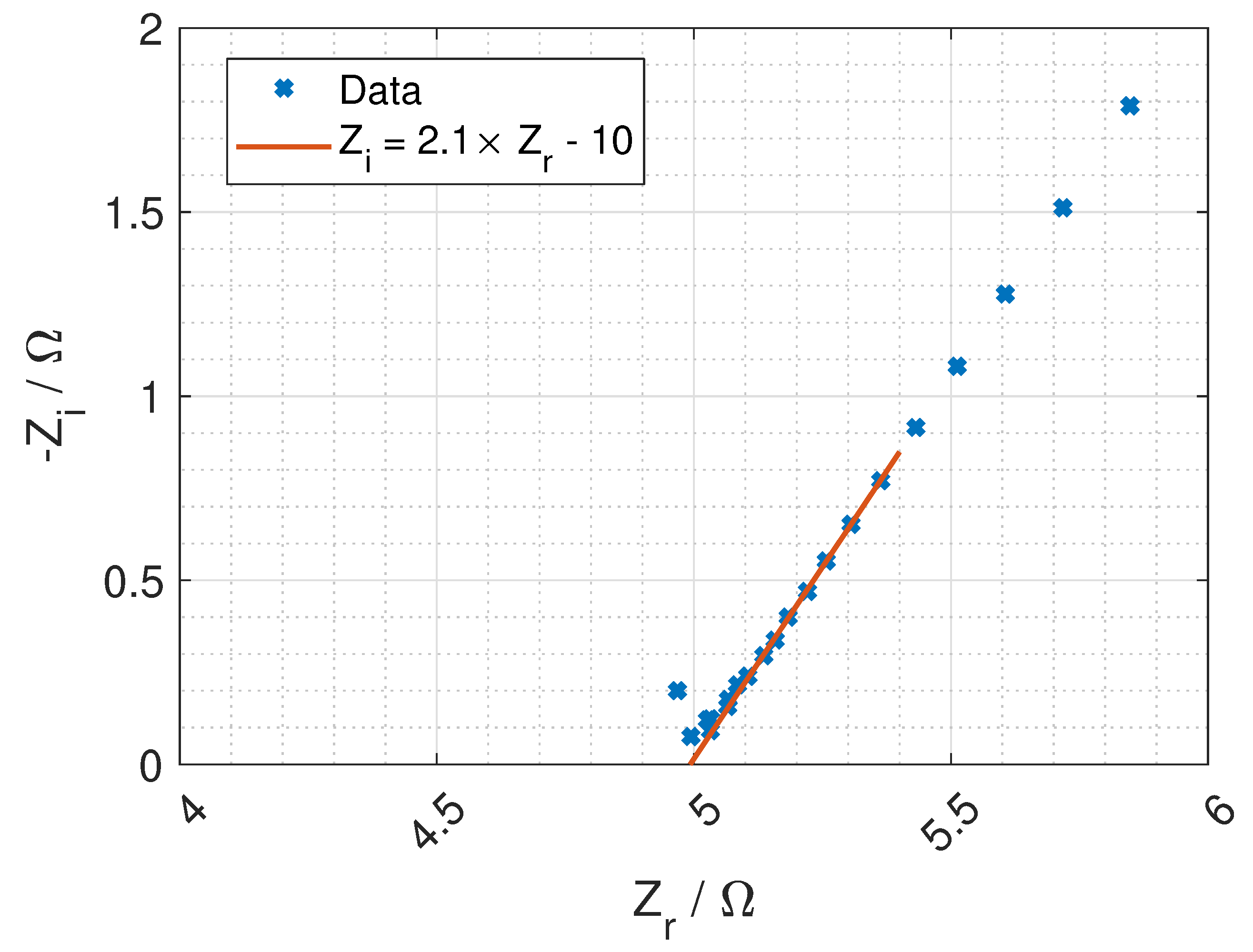
Figure 7 and a typical Nyquist plot of the resistance is given in
Figure 8 where the bulk resistance in the membrane is marked.
When the frequency increases the contribution from the CPE decreases, and the contribution from the membrane increases. At a given frequency (≈1 MHz), the majority of the impedance is from the membrane resistance, and the ohmic membrane resistance can be found from the Nyquist plot (see
Figure 8).