Abstract
Condition monitoring of bearings is an open issue. The use of the stator current to monitor induction motors has been validated as a very advantageous and practical way to detect several types of faults. Nevertheless, for bearing faults, the use of vibrations or sound generally offers better results in the accuracy of the detection, although with some disadvantages related to the sensors used for monitoring. To improve the performance of bearing monitoring, it is proposed to take advantage of more information available in the current spectra, beyond the usually employed, incorporating the amplitude of a significant number of sidebands around the first eleven harmonics, growing exponentially the number of fault signatures. This is especially interesting for inverter-fed motors. But, in turn, this leads to the problem of overfitting when applying a classifier to perform the fault diagnosis. To overcome this problem, and still exploit all the useful information available in the spectra, it is proposed to use shrinkage methods, which have been lately proposed in machine learning to solve the overfitting issue when the problem has many more variables than examples to classify. A case study with a motor is shown to prove the validity of the proposal.
1. Introduction
Induction motors are a fundamental part of many production processes due to their inherent robustness, low cost, and reliability, among other advantages. However, they are not fault-free, with bearings being the component that accounts for the greatest percentage of total failures [1].
The signals that are most frequently used for bearing fault detection are vibration and acoustic noise [2]. However, the use of the stator current to monitor the motor provides some practical advantages related to the simplicity and noninvasive characteristics of the sensors. These advantages are especially relevant in industrial facilities, where some motors can run simultaneously [3,4]. The use of current has proven its effectiveness in detecting faults such as broken bars and eccentricity [2], but in the case of faulty bearings, it faces technical difficulties that hinder its successful implementation. Mainly, the low energy of the vibrations are associated to the fault, which makes it difficult to distinguish in the current spectrum the frequency components related to the fault that may be buried in the noise [1,5,6]. Besides, for inverter-fed motors, the noise is higher and there are other harmonics present in the spectrum, which complicates even more the detection of the faulty related components [7]. Consistently, in [8], denoising techniques are applied to highlight the faulty components in the current spectrum. Other advanced spectral techniques have also been proposed, such as wavelets [9,10], Short-Time Fourier Transform [11], Gabor spectrogram [11] Hilbert–Huang Transform [12,13], Empirical Mode Decomposition [14], Ensemble Empirical Mode Decomposition [15], Modulation Signal Bispectrum [16], Spectral Kurtosis [17], Spectral Subtraction [18], and space vector angular fluctuation method [19]. These techniques have the drawback of a high computational cost. Parametric methods that assume that the signal fits a particular model have also been proposed such as MUSIC (Multiple Signal Classification) [14,20] and maximum likelihood estimation [21]. These methods yield good results as long as the signal really follows the assumed model. Besides, when analyzing inverter-fed motors, the spectra are noisier and the harmonics injected by the inverter have to be considered too, what makes it difficult to apply the mentioned techniques.
The first stage related to the detection of the fault provides with some fault signatures that will feed the second stage of the process, the diagnosis. A wide variety of algorithms have been proposed to diagnose faulty bearings, such as Artificial Neural Networks [22,23], Support Vector Machines [12,24,25], K-nearest neighbors [26,27], supervised fuzzy-neighborhood density-based clustering [28], random forest [29], bagging, boosting, and stacking methods [30], Common Vector Approach [31], Decision Trees [32,33], maximum margin classification [34], Bayes classifier [35], Euclidean Distance Minimization [36], and Bayesian inference [37]. The aforementioned algorithms were mostly applied making use of the known fault signatures related to bearing faults, limited to just a few signatures (usually just the sideband around the main harmonic, as it will be shown in Section 2). However, for challenging cases, this is a restricted use of the information available in the spectra. In the case of inverter-fed motors, the information related to sidebands around the harmonics introduced by the supply can be used [3]. In [38], it is shown how the effects of different types of bearing faults are spread over the spectrum, being for some cases more notorious for the 3rd and 7th harmonics and, in other cases, for high-frequency odd harmonics; besides, these effects are different depending on the operating characteristics of the motor. In [39], the cases of excessive and defective lubrication are analyzed, showing how these situations produce changes in the amplitudes of different sidebands around different harmonics, showing also a variation depending on the load.
Consequently, in this paper, it is proposed to take advantage of the information available over the spectrum, considering not only the main frequency, but also different odd and even harmonics (up to the 11th one) and including many more sidebands than is usual in literature. This way, instead of using just a few signatures to feed the algorithm, as is usual in literature, almost one thousand signatures are used in this proposal.
The drawback of feeding the classifier with a high number of signatures is a clear risk of overfitting. Overfittings arises when the model has learned the data too well, leading to a small error in the training set (used to build the model) but poor prediction ability. Besides, overfitting is intensified by the presence of noise in the data [40] and, precisely, when dealing with motors fed from inverters, a significant presence of noise is to be expected. A solution to minimize the overfitting problem is to apply shrinkage techniques. These techniques perform shrinking on the values of the coefficients in the trained model. There are several versions of shrinkage techniques, depending on the degree of shrinkage of each coefficient. If some of them can be set to zero, then the method is known as Lasso (Least Absolute Shrinkage and Selection Operator), and consequently the number of signatures in the classifier is reduced, obtaining simpler models. If the value of the coefficients is reduced, but all the signatures are included in the model, the method is known as Ridge Regression. The technique known as Elastic Nets is a way of combining both Lasso and Ridge Regression.
To monitor correctly the state of the bearings and be really useful for maintenance purposes, it is essential to be able to distinguish between different states of deterioration and detect incipient faults before they develop into critical ones. With this purpose, it has been simulated in the laboratory a progressive deterioration of an induction motor bearing via the contamination of the lubrication, introducing particles of silicon carbide in the bearing grease. This process tries to emulate conditions usually present in the industry that produce bearing wear related to the use, to inadequate lubrication, or to the proper contamination of the grease in open ball bearings.
In this paper, it is proposed the use of a large number of fault signatures, obtained from the current spectra to monitor bearing failures. A case study is presented, where five states of deterioration of the bearing are considered, giving rise to a problem of multiclassification. The improvement in the performance of different classifiers when using such fault signatures is shown by comparing with the performance of the usual signatures used in these studies. Then, to deal with the problem of overfitting, shrinkage techniques are applied, comparing the performance of Lasso, Ridge Regression, and Elastic Nets, proving their validity to diagnose bearing failures.
2. Fault Signatures
When a bearing defect appears, a radial motion between rotor and stator will occur, modifying the airgap of the motor, thus changing the airgap field. These modifications in the airgap can be interpreted as a combination of bidirectional rotating eccentricities [41], which implies that the defect affects the stator current and, therefore, it is possible to monitor it in the current spectra. The radial motion generates harmonics in the stator current at frequencies given by Equation (1)
where f1 is the main supply frequency, n is an entire number, and fv is the vibration characteristic frequency. fv depends on the type of bearing fault (outer or inner race, balls and train defect), with expressions that are a function of the geometry and composition of the bearing [7].
The fault frequencies given by Equation (1) are the result of taking into account the deviations in the main component of the airgap field. When the motor is fed by a power converter, the harmonics level is increased and so is the noise level, hampering the detection of the fault signatures. Nevertheless, the presence of these harmonics can be used to increase the available information, also considering the deviations produced in the fields as a consequence of these harmonics. Even when the motor is directly fed from the line, since the supply is hardly ever perfectly sinusoidal, the number of fault signatures can be increased too, considering the harmonic introduced by the supply. Therefore, Equation (1) can be generalized by Equation (2), where k is the order of the current harmonic.
Considering Equation (2), the number of fault signatures can be increased, resulting in a smaller or larger number of variables depending on the value of k and n. In [7,38], the first sideband around the 5th and 7th harmonics is employed. In this paper, it is proposed to use a larger number of signatures, considering more harmonics, and other sidebands in addition to the first one. In the case study of Section 4, the first eleven current harmonics are used to feed the classifier, considering the first eleven sidebands around those harmonics. As each sideband is composed of two values, and eleven sidebands around eleven harmonics are considered, there are 242 signatures for each characteristic bearing fault frequency, resulting in 968 signatures. Table 1 summarizes the information regarding the proposed fault signatures and the comparison with the traditional approach.

Table 1.
Bearing fault signatures considered in the traditional and in the proposed approach.
3. Diagnosis
The next step after selecting the candidate fault signatures is to choose and train the classifier. Many classification algorithms are available, with a wide variety of them already proposed to perform diagnosis tasks in induction motors. With the purpose of analyzing the improvement in the performance of the classifier when using the fault signatures presented in the previous section, the MATLAB 2019a (Mathworks, Natick, Massachusetts, U.S.A.) Classification learner App has been used. In this app, there are available different types of classifiers: decision trees, discriminant analysis, logistic regression classifiers, Naïve Bayes classifiers, support vector machines, nearest neighbor classifiers, and ensemble classifiers. In each group, there are several classifiers available. Using these classifiers, it has been proved (as shown in the results section) the huge increase in performance of all the classifiers when using the 968 fault signatures instead of the usual eight signatures.
However, when using such a high number of signatures, and with a reduced number of tests, the risk of overfitting is certain. Shrinkage techniques allow to make use of all the predictors by shrinking the coefficients towards zero, hence, reducing variance [42]. If applied in linear models (which has the advantage in terms of interpretability of the model), it performs as follows: let xi be the m predictors (or fault signatures in the context of condition monitoring) and yi the response for the n cases of the problem. A linear model tries to estimate the m + 1 coefficients (b0, …, bm). Using a least squares fitting approach, bi are selected to minimize (a).
To perform the shrinkage, a second term is added to (a), , which acts as shrinkage penalty. Its influence depends on the value of λ, which is a tuning parameter that increases or decreases the penalty. For higher values of λ, the penalty grows and the coefficient estimated will tend to zero, which implies that the estimation is somehow penalized, sacrificing some of the performance on the training set but with the aim of improving its predictive capacity with future observations. The penalty applies to all the coefficients but the intercept, b0, since this term is just an estimation of the mean when the predictors are zero [42].
This way of applying the penalty, so performing the shrinkage on the estimated coefficients is known as Ridge Regression. It has the disadvantage that the shrinkage is applied to all the coefficients but none of them are set to zero, so all the predictors are included in the solution, which for problems with a large number of predictors (as in the problem dealt in this paper) leads to a loss of the interpretability of the model. A way of tackling this problem is to change the penalty term into , or in statistical terms, to change an l2 penalty for an l1 one [42]. The use of an l1 norm has the inconvenience of turning the function to minimize into one that is nondifferentiable, although there are available methods to proceed with the minimization, such as proximal gradient ones [43]. This way of considering the penalty gives rise to the method known as Lasso. As opposed to Ridge Regression, with Lasso, some variables are canceled, so perform as variable selection, depending the number of the variables to be selected on the value of λ (as λ grows, less variables are selected).
Lasso was first applied to linear regressions and lately is receiving much attention, being proposed to regularize a wide variety of statistical models [44]. In accordance with Occam’s razor principle, simpler models are preferable, as long as they predict well the training data, since they are more likely to generalize well to unseen data [45]. With this principle in mind, Logistic Regression has been chosen as base model in which to apply the shrinkage technique. Logistic regression is adapted to classification problems since has a discrete outcome. It is based on the logistic function given by Equation (4), which is suitable to be used in classification since its outcome can be inferred as a probability since it runs between 0 and 1, and its elongated S-shape offers the advantage that the same additional input influences less the outcome for values near zero or one [46,47]. For binary classification, a threshold value of 0.5 is defined to assign the outcome to one class or the other, which in condition monitoring would be healthy or faulty. When the aim is to distinguish among different states of failure, there are several classes into which the outcome can be classified. This multiclassification is performed via the one-versus-all approach, as represented in the flow chart in Figure 1. This way, several binary classifiers are trained (as many as classes), where each classifier confronts one class against the rest. Finally, the outcome is assigned to the class where the probability is highest.
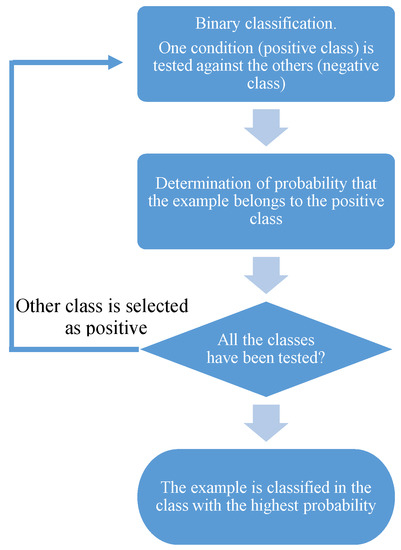
Figure 1.
Methodology for multiclass classification.
4. Results
4.1. Test Bench
The tested induction motor is a two pole pair squirrel cage motor, star connected, with a rated power of 0.75 kW at 400 V and a rated current of 1.9 A at a rated speed of 1395 RPM. The tests were performed at two load levels, low (almost no load) and high (rated speed), using a magnetic powder brake. The data were collected using a DAC PCI-6250 M model (16 analogue inputs—16-bit 1 MS/s) of National Instruments and Hall effect sensors of LEM (LEM, Fribourg, Germany). The sampling frequency was 25 kHz, with a sampling time of 10 s (steady state).
Four different supply conditions were considered (Table 2). The first one (S1) represents the motor directly fed from a 400 V utility supply. Supply S2 is the motor fed by an inverter (ABB) at 50 Hz and with a switching frequency of 4 kHz. For S3, the operating frequency was changed to 25 Hz, and for S4 the switching frequency was established at 5 kHz. The converter operated with an open-loop scalar V/Hz control.

Table 2.
Supplies tested.
To initiate the tests, a new SKF Explorer 6004 bearing (SKF; Göteborg; Sweden) was used, performing the corresponding tests to represent the healthy condition. Then, to provoke the progressive wear of the bearing, the lubricant grease was contaminated using silicon carbide, a ceramic material with high resistance to erosion and corrosion, and high thermal cycling. This process was established to simulate industrial environment conditions that lead to the degradation of the bearing, such as inadequate lubrication, overloads, or lubricant contamination (especially relevant to open bearings). During this process, five condition states were defined according to the degradation of the bearing, as summarized in Table 3. After assembling the new bearing, 20 tests per supply were run, corresponding to the healthy state (C1). Then, the bearing was first contaminated, and the motor run unloaded for 12 hours to lead the bearing to the “incipient fault” condition (C2). In this condition, 15 tests were performed for each supply. The process of running the motor unloaded and contaminating the grease was repeated, giving way to “intermediate fault” condition (C3), with 15 tests per supply, “developed fault”, with 10 tests (C4), and “complete breakdown” (C5), with 10 tests for each supply. Figure 2 presents pictures of the bearing in each of the conditions, showing the evolution of the fault along the tests.

Table 3.
Bearing conditions tested.

Figure 2.
Evolution of the condition states of the bearing (see Table 3): (a) C1; (b) C2; (c) C3; (d) C4; (e) C5.
4.2. Classification with 968 Fault Signatures
In order to show the improvement in the classification when using the whole of the fault signatures, as proposed in Section 2, next the results obtained using the MATLAB 2019a Classification learner App are presented. Five-fold cross validation was used. Table 4 summarizes the results obtained with the App with the accuracy for the classification in each of the five bearing conditions at low and high load. All the algorithms included in the App have been tested, showing the one that has the best performance for each tested case (depending on the load and the supply) and its accuracy. The same procedure has been applied, feeding the algorithms with eight inputs, following the traditional procedure of considering just the first sideband around the vibration characteristics frequencies, according to Equation (2).

Table 4.
Comparison between the traditional (eight fault signatures) and proposed approach (968 fault signatures) with the algorithms included in the MATLAB 2019a Classification learner App.
According to the results shown in Table 4, it is very clear that the use of the fault signatures related to a bigger number of sidebands around more harmonics outperformed the use of just eight fault signatures. The huge improvement in the performance was observable in all the cases for the different supplies, operating frequencies, switching frequencies, and loads. The results were in general better for high load, since the energy associated to the harmonics was higher. It is also remarkable that there was a variety of selected algorithms, with Support Vector Machines the most repeated, although, in some cases, Gaussian Naive Bayes, Linear Discriminant, Fine k-Nearest Neighbor and Bagged Trees performed better. This discrepancy added difficulty to the selection of a classifier valid for all the operating conditions. An algorithm that performs well for all the cases would be desirable. Besides, as it was stated earlier, the use of a big number of signatures (much bigger than the number of tests) may lead to overfitting, losing from the trained algorithms the ability to generalize when classifying new observations. To take into account this situation, shrinkage was applied, as explained in Section 3.
4.3. Classification with 968 Fault Signatures by Applying Shrinkage
The previous section has shown that the classification improves hugely when more information available in the spectra is considered. In this section, shrinkage methods are applied, with the double purpose of selecting an algorithm with good performance independently of the operating conditions and of avoiding the problem of overfitting (prone to appear due to the high number of fault signatures, much higher than the number of tests). As explained in Section 3, two different types of shrinkage methods were considered: Ridge regression where all the inputs are considered in the classification, and Lasso that performs variable selection (considering a higher or lower number of inputs in the classification, depending on the value of the penalty parameter). A third method was included in the comparison, Elastic nets, which can be considered as a mixture between Lasso and Ridge regression.
To build the algorithms and measure their performance, the data sets for each case study were divided into two different sets, the training set consisting of 70% of the cases, and the test set with the other 30% of the data. Table 5 shows the performance, measured in terms of accuracy, for the three shrinkage methods, for each supply and load. It can be observed that the results were very good for all the cases, although with some differences in the performance among the cases analyzed, as it also happened for the algorithms considered in the previous section. The three shrinkage methods performed well, although in general, Lasso obtained the best accuracy, therefore, if a single method were to be selected, Lasso would be the candidate. In this selection, it has also been taken into account that, since Lasso eliminated variables from the classifier, the model obtained gains in interpretability and computational cost. For that reason, next, a deeper analysis on the performance of Lasso is presented, taking especially into consideration the influence of the penalty parameter, since the number of variables selected (and, consequently, the characteristics of the model) depend on this parameter.

Table 5.
Accuracy (%) obtained using different methods of shrinkage with 968 fault signatures.
As it was stated in Section 3, the main way in which Lasso avoids overfitting is by feature selection, which is controlled by adjusting the regularization parameter λ. The bigger λ, the more parameters bj in Equation (3) will be zero, that is, the corresponding predictors will not be considered when designing the classifier. Therefore, if a high value of λ is chosen, it is much less likely to result in overfitting, besides, the computational cost is highly reduced. The drawback is that, if less predictors are considered, the performance of the classifier will be reduced. Therefore, a trade-off must be reached to select the best value for the regularization parameter, to obtain a good classifier performance with less computational cost. The selection of the value of the regularization parameter has been performed, considering the train set. No additional validation set has been considered, since the number of tests per case study was low and this would have led to training, validating, and test sets with very few data in each one. Figure 3 shows the evolution of the accuracy, depending on the regularization parameter for the test set, and Table 6 shows the selected value for each supply and load condition. The value chosen for the classifier was the highest one that achieved the best accuracy for that supply and load, since for smaller values of λ, the computational cost would be higher. If a unique value were to be chosen for all the supplies, 0.05 could be selected when operating at high load, and 0.02 at low load. If the common value of 0.02 were to be chosen, the performance of the algorithm in this case would be decreased around 5%, although the computational cost would be decreased. The number of variables selected varied approximately between 10 and 20 for the different cases tested, decreasing the number as lambda increased. This selection is the main difference with the other two shrinkage methods; for Ridge regression, as no selection was performed, the number was the starting 968, while for Elastic nets, the number was approximately the intermediate between lasso and Ridge regression.
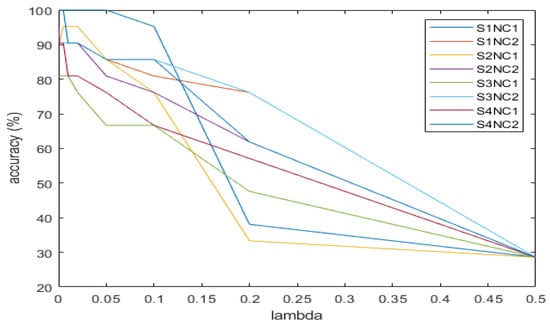
Figure 3.
Performance of Lasso classifier, depending on the value of the regularization parameter for different supplies (S1–S6) and loads (HL: high load; LL: low load).

Table 6.
Regularization parameter selected for different supplies and level of load.
So far, accuracy has been used to measure the performance of the classifier. Obviously, from an algorithmic point of view, it is important to classify all the states correctly, and therefore to achieve the highest possible accuracy. However, from a condition monitoring point of view, some misclassifications are more relevant than others, being especially relevant to predict the first and fifth states correctly, that is, the healthy and completely faulty conditions. With this purpose, Table 7, Table 8, Table 9 and Table 10 show the confusion matrices resulting from applying Lasso classifier for the four supplies and two load conditions. It can be observed how for the healthy state, for 48 instances (there were six true healthy states in each of the eight cases) only one case (S3, low load) was misclassified. And even if this case can be considered as a false negative, this instance was classified as an incipient fault, not as a more developed one. In the same way, for the 24 complete faulty cases (three for each of the eight cases) only one was misclassified (again, S3 at low load), being predicted as an intermediate fault. Finally, it is relevant to point out that for all the 168 cases classified, 13 were not correctly classified, but just four of them were classified more than one class away from the true class.

Table 7.
Confusion matrices for supply S1 applying lasso classifier.

Table 8.
Confusion matrices for supply S2 applying lasso classifier.

Table 9.
Confusion matrices for supply S3 applying lasso classifier.

Table 10.
Confusion matrices for supply S4 applying lasso classifier.
5. Discussion
A procedure for the diagnosis of induction motor bearings has been presented. The main purpose of the proposal is to maintain the good performance of existing methods that use vibrations or sound as inputs, but using the stator current. So far, the monitoring of the current has not achieved as good a performance as the use of the other variables mentioned, but since it has some clear advantages related to the necessary sensors, it is advisable to have a procedure that allows the use of the current. To achieve this goal, it has been proposed to take advantage of more information that can be extracted from the spectra beyond what is commonly used, but without the extra computational cost that other techniques, including parametric and non-parametric methods, usually require. Besides, the proposed method is particularly adequate for inverter-fed induction motors where noisier spectra and significant harmonics and interharmonics are present.
It has been shown that the use of much more information greatly improved the performance of the diagnosis, which has been proved by means of 24 classifiers (available in the Matlab Classification learner app). However, it must be taken into account that detection and diagnosis are interlinked. There is no use in expecting a good diagnosis performance if the fault signatures obtained during the detection process are of a bad quality. Conversely, although there were high informative fault signatures, if the diagnosis stage is badly designed, the whole process will suffer. Besides, the chosen algorithm must be in accordance with the available variables. Therefore, it has been selected a type of classifier that can perform well with the particular conditions of the problem, where there were many more fault signatures than cases to classify. Shrinkage methods have been chosen since they allow to perform in those condition, avoiding the problem of overfitting.
Three shrinkage methods have been compared, Lasso, Ridge regression, and Elastic nets, and all of them have proved to achieve a very good performance in the cases analyzed. Although all three meet the expectations, Lasso has been chosen to analyze its results in greater depth, since this method selects variables, providing simpler and more interpretable models. For the analysis of the performance of Lasso, the confusion matrices for eight different scenarios have been provided and analyzed. Although from an algorithmic point of view it is important to classify all the states correctly, from a maintenance perspective it is especially relevant the presence of false positives or false negatives concerning the healthy and complete fault conditions. That is, some misclassifications are more relevant than others are. For example, wrong predictions between conditions corresponding to intermediate and incipient faults are not likely to have important repercussions but, on the contrary, a misclassification between states healthy and complete fault will surely have further implications. It has been shown that the predictions obtained with the proposed method matched the expectations from a condition monitoring perspective.
Author Contributions
Conceptualization, O.D.-P., D.M.-S. and W.F.G.; Data curation, W.F.G.; Methodology, O.D.-P.; Software, C.D.P.-G.; Validation, D.M.-S.; Writing—original draft, O.D.-P.; Writing—review & editing, D.M.-S.
Funding
This research was partly funded by CAPES (process BEX552269/2011-5).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Immovilli, F.; Bellini, A.; Rubini, R.; Tassoni, C. Diagnosis of bearing faults in induction machines by vibration or current signals: A critical comparison. IEEE Trans. Ind. Appl. 2010, 46, 1350–1359. [Google Scholar] [CrossRef]
- Henao, H.; Capolino, G.A.; Fernandez-Cabanas, M.; Filippetti, F.; Bruzzese, C.; Strangas, E.; Pusca, R.; Estima, J.; Riera-Guasp, M.; Hedayati-Kia, S. Trends in fault diagnosis for electrical machines. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Akin, B.; Toliyat, H.A.; Orguner, U.; Rayner, M. PWM Inverter Harmonics Contributions to the Inverter-Fed Induction Machine Bearing Fault Diagnosis. In Proceedings of the IEEE Applied Power Electronics Conference, APEC 2007—Twenty Second Annual, Anaheim, CA, USA, 25 February–1 March 2007; pp. 1393–1399. [Google Scholar]
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G.-A. Advances in diagnostic techniques for induction machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Zarei, J.; Poshtan, J. An advanced Park’s vectors approach for bearing fault detection. Tribol. Int. 2009, 42, 213–219. [Google Scholar] [CrossRef]
- Blodt, M.; Granjon, P.; Raison, B.; Rostaing, G. Models for bearing damage detection in induction motors using stator current monitoring. IEEE Trans. Ind. Electron. 2008, 55, 1813–1822. [Google Scholar] [CrossRef]
- Duque, O.; Pérez, M.; Moríñigo, D. Detection of bearing faults in cage induction motors fed by frequency converter using spectral analysis of line current. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 17–22. [Google Scholar]
- Zhou, W.; Habetler, T.G.; Harley, R.G. Bearing Fault Detection Via Stator Current Noise Cancellation and Statistical Control. IEEE Trans. Ind. Electron. 2008, 55, 4260–4269. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, A.; Kumar, N. Motor Current Signature Analysis for Bearing Fault Detection in Mechanical Systems. Procedia Mater. Sci. 2014, 6, 171–177. [Google Scholar] [CrossRef]
- Deekshit Kompella, K.C.; Venu Gopala Rao, M.; Srinivasa Rao, R. DWT based bearing fault detection in induction motor using noise cancellation. J. Electr. Syst. Inf. Technol. 2016, 3, 411–427. [Google Scholar]
- Rosero, J.; Cusido, J.; Garcia Espinosa, A.; Ortega, J.A.; Romeral, L. Broken Bearings Fault Detection for a Permanent Magnet Synchronous Motor under non-constant working conditions by means of a Joint Time Frequency Analysis. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 3415–3419. [Google Scholar]
- Kablaa, A.; Mokrani, K. Bearing fault diagnosis using Hilbert-Huang transform (HHT) and support vector machine (SVM). Mech. Ind. 2016, 17, 308. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H.; Turri, S. An Efficient Hilbert-Huang Transform-Based Bearing Faults Detection in Induction Machines. IEEE Trans. Energy Convers. 2017, 32, 401–413. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Osornio-Rios, R.; Romero-Troncoso, R.J.; Garcia-Perez, A. Fused Empirical Mode Decomposition and MUSIC Algorithms for Detecting Multiple Combined Faults in Induction Motors. J. Appl. Res. Technol. 2015, 13, 160–167. [Google Scholar] [CrossRef]
- Amirata, Y.; Benbouzidb, M.E.H.; Wang, T.; Bachad, K.; Felda, G. EEMD-based notch filter for induction machine bearing faults detection. Appl. Acous. 2018, 133, 202–209. [Google Scholar] [CrossRef]
- Alwodai, A.; Wang, T.; Chen, Z.; Gu, F.; Cattley, R.; Ball, A. A Study of Motor Bearing Fault Diagnosis using Modulation Signal Bispectrum Analysis of Motor Current Signals. J. Sign. and Inform. Proc. 2013, 4, 72–79. [Google Scholar] [CrossRef]
- Leite, V.C.M.N.; Borges da Silva, J.G.; Veloso, G.F.C.; Borges da Silva, L.E.; Lambert-Torres, G.; Bonaldi, E.L.; de Oliveira, L.E.L. Detection of Localized Bearing Faults in Induction Machines by Spectral Kurtosis and Envelope Analysis of Stator Current. IEEE Trans. Ind. Electron. 2015, 62, 1855–1865. [Google Scholar] [CrossRef]
- El Bouchikhi, E.H.; Choqueuse, V.; Benbouzid, M.E.H. Current Frequency Spectral Subtraction and Its Contribution to Induction Machines’ Bearings Condition Monitoring. IEEE Trans. Energy Convers. 2013, 28, 135–144. [Google Scholar] [CrossRef]
- Arkan, M.; Çaliş, H.; Tağluk, M.E. Bearing and misalignment fault detection in induction motors by using the space vector angular fluctuation signal. Electr. Eng. 2005, 87, 197–206. [Google Scholar] [CrossRef]
- Boudinar, A.H.; Benouzza, N.; Bendiabdellah, A.; Khodja, A. Induction Motor Bearing Fault Analysis Using a Root-MUSIC Method. IEEE Trans. Ind. Appl. 2016, 52, 3851–3860. [Google Scholar] [CrossRef]
- El Bouchikhi, E.H.; Choqueuse, V.; Benbouzid, M.E.H. Induction machine bearing faults detection based on a multi-dimensional MUSIC algorithm and maximum likelihood estimation. ISA Trans. 2016, 63, 413–424. [Google Scholar] [CrossRef]
- Godoy, W.F.; da Silva, I.N.; Goedtel, A.; Palácios, R.H.C.; Gongora, W.S. Neural approach for bearing fault classification in induction motors by using motor current and voltage. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 2087–2092. [Google Scholar]
- Ballal, M.S.; Khan, Z.J.; Suryawanshi, H.M.; Sonolikar, R.L. Adaptive Neural Fuzzy Inference System for the Detection of Inter-Turn Insulation and Bearing Wear Faults in Induction Motor. IEEE Trans. Ind. Electron. 2007, 54, 250–258. [Google Scholar] [CrossRef]
- Zarei, J.; Arefi, M.M.; Hassani, H. Bearing fault detection based on interval type-2 fuzzy logic systems for support vector machines. In Proceedings of the 6th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO), Istanbul, Turkey, 27–29 May 2015; pp. 1–6. [Google Scholar]
- Salem, S.B.; Bacha, K.; Chaari, A. Support vector machine based decision for mechanical fault condition monitoring in induction motor using an advanced Hilbert-Park transform. ISA Trans. 2012, 51–55, 566–572. [Google Scholar] [CrossRef]
- Bouguerne, A.; Lebaroud, A.; Medoued, A.; Boukadoum, A. Classification of induction machine faults by K-nearest neighbor. In Proceedings of the 7th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 1–4 December 2011; pp. I-363–I-366. [Google Scholar]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled with K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803. [Google Scholar] [CrossRef]
- Farajzadeh-Zanjani, M.; Razavi-Far, R.; Saif, M. Diagnosis of Bearing Defects in Induction Motors by Fuzzy-Neighborhood Density-Based Clustering. In Proceedings of the IEEE 14th International Conference on Machine Learning and Applications, Miami, FL, USA, 9–11 December 2015; pp. 935–940. [Google Scholar]
- Peng, H.-W.; Chiang, P.-J. Control of mechatronics systems: Ball bearing fault diagnosis using machine learning techniques. In Proceedings of the 8th Asian Control Conference (ASCC), Kaohsiung, Taiwan, 15–18 May 2011; pp. 175–180. [Google Scholar]
- Santos, S.P.; Costa, J.A.F. A Comparison between Hybrid and Non-hybrid Classifiers in Diagnosis of Induction Motor Faults. In Proceedings of the 11th IEEE International Conference on Computational Science and Engineering, Sao Paulo, Brazil, 16–18 July 2008; pp. 301–306. [Google Scholar]
- Ergin, S.; Tezel, S.; Gulmezoglu, M.B. DWT-based fault diagnosis in induction motors by using CVA. In Proceedings of the International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Istanbul, Turkey, 15–18 June 2011; pp. 129–132. [Google Scholar]
- Cunha Palácios, R.H.; da Silva, I.N.; Goedtel, A.; Godoy, W.F. A comprehensive evaluation of intelligent classifiers for fault identification in three-phase induction motors. Electr. Power Syst. Res. 2015, 127, 249–258. [Google Scholar] [CrossRef]
- Sugumaran, V.; Ramachandran, K.I. Automatic rule learning using decision tree for fuzzy classifier in fault diagnosis of roller bearing. Mech. Syst. Signal Process. 2007, 21, 2237–2247. [Google Scholar] [CrossRef]
- Zeng, M.; Yang, Y.; Zheng, J.; Cheng, J. Maximum margin classification based on flexible convex hulls for fault diagnosis of roller bearings. Mech. Syst. Signal Process. 2016, 66–67, 533–545. [Google Scholar] [CrossRef]
- Mbo’o, C.P.; Hameyer, K. Fault Diagnosis of Bearing Damage by Means of the Linear Discriminant Analysis of Stator Current Features from the Frequency Selection. IEEE Trans. Ind. Appl. 2016, 52, 3861–3868. [Google Scholar]
- Montechiesi, L.; Cocconcelli, M.; Rubini, R. Artificial immune system via Euclidean Distance Minimization for anomaly detection in bearings. Mech. Syst. Signal Process. 2016, 76, 380–393. [Google Scholar] [CrossRef]
- Wang, D. An extension of the infograms to novel Bayesian inference for bearing fault feature identification. Mech. Syst. Signal Process. 2016, 80, 19–30. [Google Scholar] [CrossRef]
- Frosini, L.; Bassi, E.; Fazzi, A.; Gazzaniga, C. Use of the stator current for condition monitoring of bearings in induction motors. In Proceedings of the 2008 International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–6. [Google Scholar]
- Morinigo-Sotelo, D.; Duque-Perez, O.; Perez-Alonso, M. Assessment of the lubrication condition of a bearing using spectral analysis of the stator current. In Proceedings of the International Symposium on Power Electronics Electrical Drives Automation and Motion (SPEEDAM), Pisa, Italy, 14–16 June 2010; pp. 1160–1165. [Google Scholar]
- Domingos, P. The Master Algorithm; Basic Books: New York, NY, USA, 2015. [Google Scholar]
- Benbouzid, M.E.H.; Kliman, G.B. What stator current processing based technique to use for induction motor rotor faults diagnosis? IEEE Trans. Energy Convers. 2003, 18, 238–244. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Tibshirani, T.H.R. An Introduction to Statistical Learning; Springer: Berlin, Germany, 2013. [Google Scholar]
- Amaral Santos, P.L.; Imangaliyev, S.; Schutte, K.; Levin, E. Feature selection via co-regularized sparse-group Lasso. In Machine Learning, Optimization and Big Data; Pardalos, P.M., Conca, P., Giuffrida, G., Nicosi, G., Eds.; Springer: Berlin, Germany, 2016; pp. 118–131. [Google Scholar]
- Tibshirani, D.R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Statist. Soc. B 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Zhang, X. Regularization. In Encyclopedia of Machine Learning, 2010 ed.; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010. [Google Scholar]
- Kleinbaum, G.; Klein, M. Logistic Regression, 3rd ed.; Spinger Science+Business Media: New York, NY, USA, 2010. [Google Scholar]
- Pampel, F.C. Logistic Regression. A Primer; Sage Publications: Thousand Oaks, CA, USA, 2000. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).