Multi-Band Frequency Window for Time-Frequency Fault Diagnosis of Induction Machines
Abstract
1. Introduction
- Performing the STFT with a wide range of windows with different lengths, and selecting, for each point in the TF domain, the best result obtained at that point among the complete set of windows.
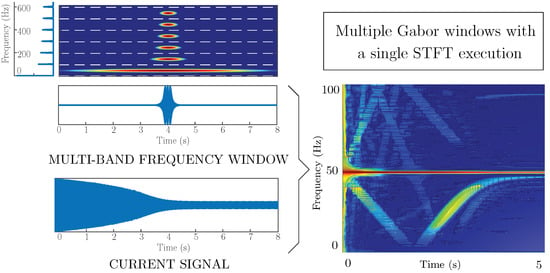
- Instead of running a separate STFT for each of the windows used in the analysis, a single, multi-band window is built by stacking all the desired analysing windows in consecutive frequency bands. This approach obtains in parallel the spectrograms corresponding to several hundreds of different analysis windows with the computing cost of a single one, which makes it suitable for fast, online diagnostic systems in transient regime.
2. Time-Frequency Analysis of the Machine’s Current via STFT with a Multi-Band Window
2.1. Spectrogram of Machine’s Current
- For each instant , the current signal is multiplied element by element by the conjugate of a suitable time window centered at ,that emphasizes the content of the current signal at time and attenuates it at other times
- The Fourier transform if applied to the time-windowed signal , which gives the frequency content of the current signal around timewhere and f stands for the frequency, in Hz.
- The energy density spectrum at time is obtained as
2.2. Frequency Shifting of the Gaussian Analysing Window
3. Proposed Multi-Band Analysing Window
3.1. Steps for Applying the Proposed Multi-Band Window
- The analysis window (15) is built:
- first, the bandwidth of diagnostic interest [0–] is established ([0–100 Hz] in this case), which gives the maximum number of elementary Gaussian windows from (14) (). The current signal is low-pass filtered with a cut-off frequency equal to . In this work, a spectral filter which zeroes all the spectrum bins with a frequency greater than has been used, as in Reference [45].
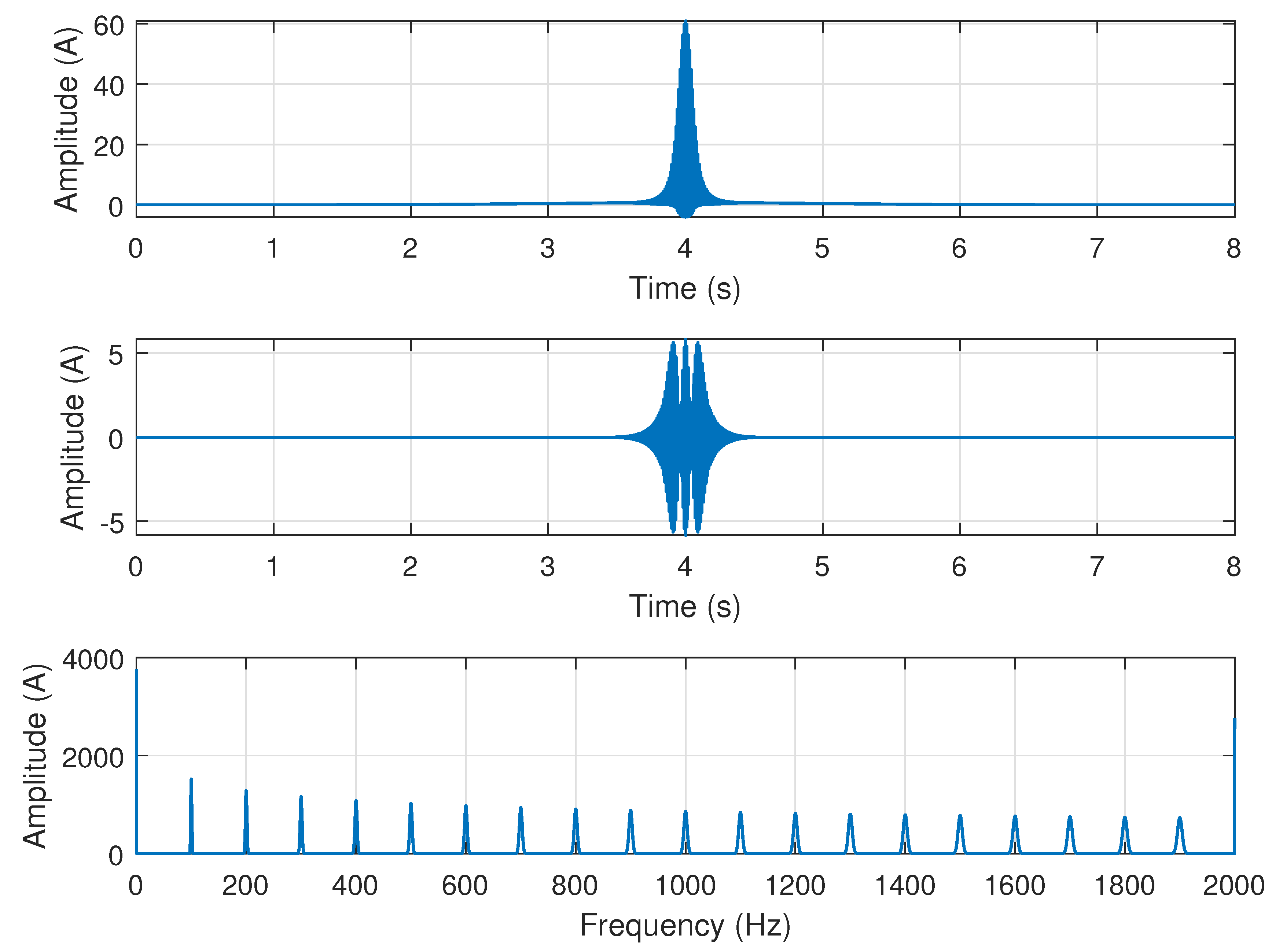
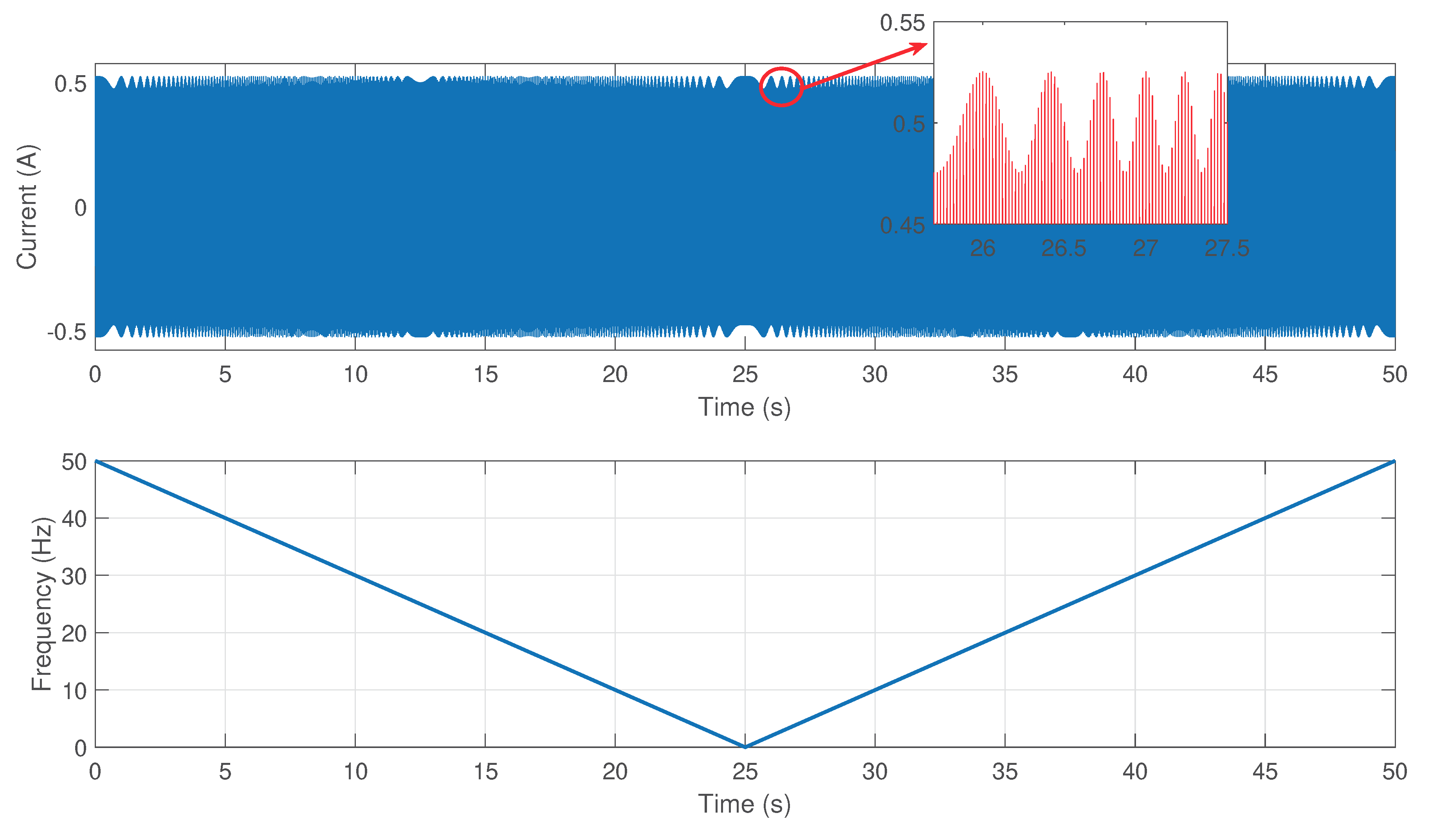
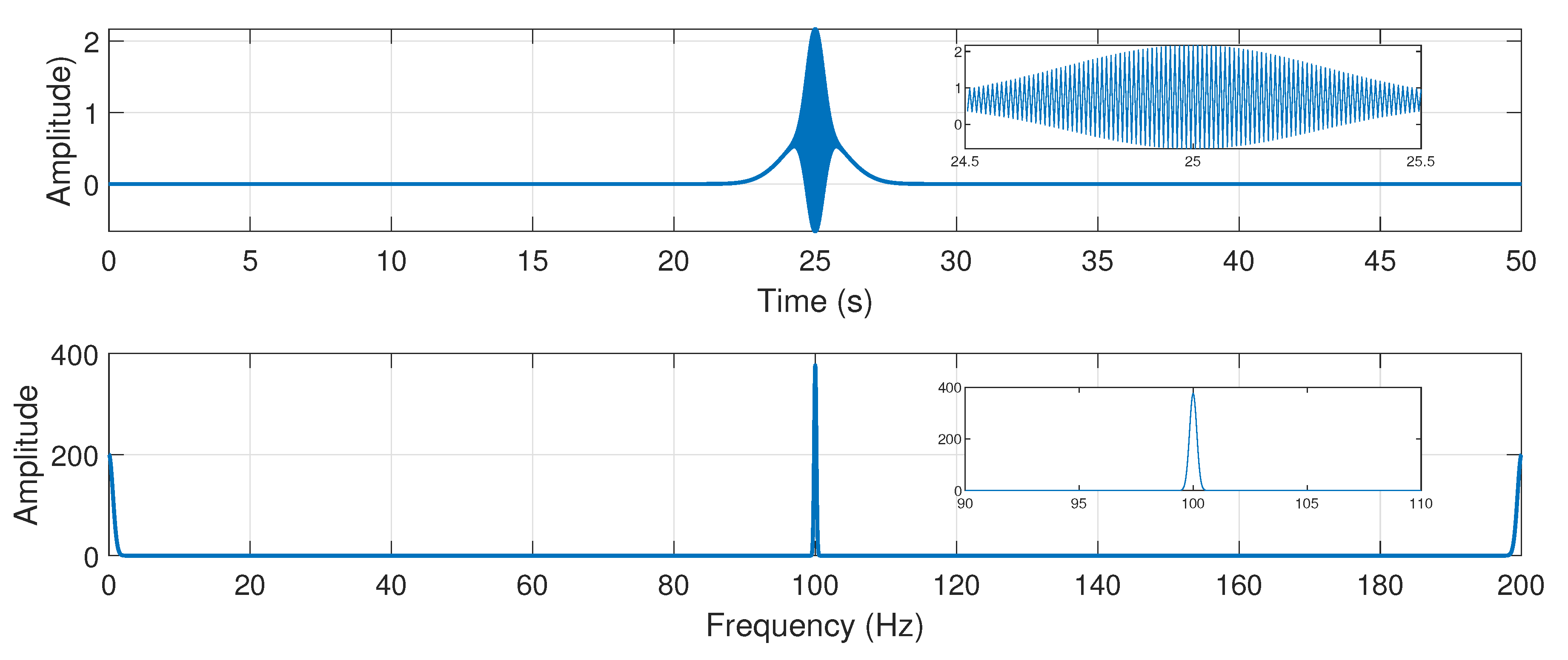
- second, the parameters of each of these windows in (15) must be selected. For an actual application of the method, a high number of parameters would be automatically generated, as was explained in Section 3, applying an expression similar to (22) in Section 4. For the simple signal (17), only two values of are used, (a long window) and , tailored to the chirp component according to Reference [35].
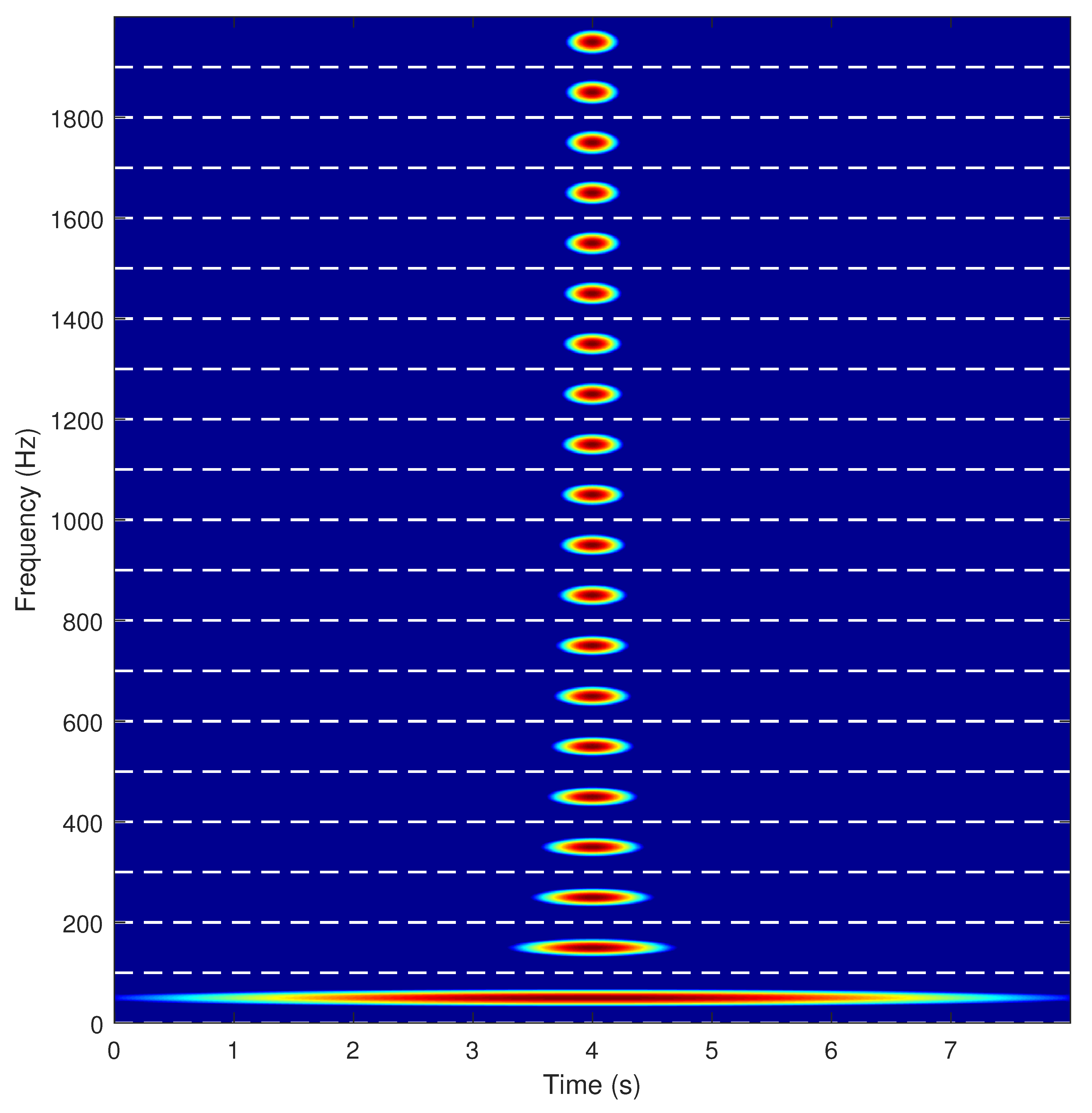
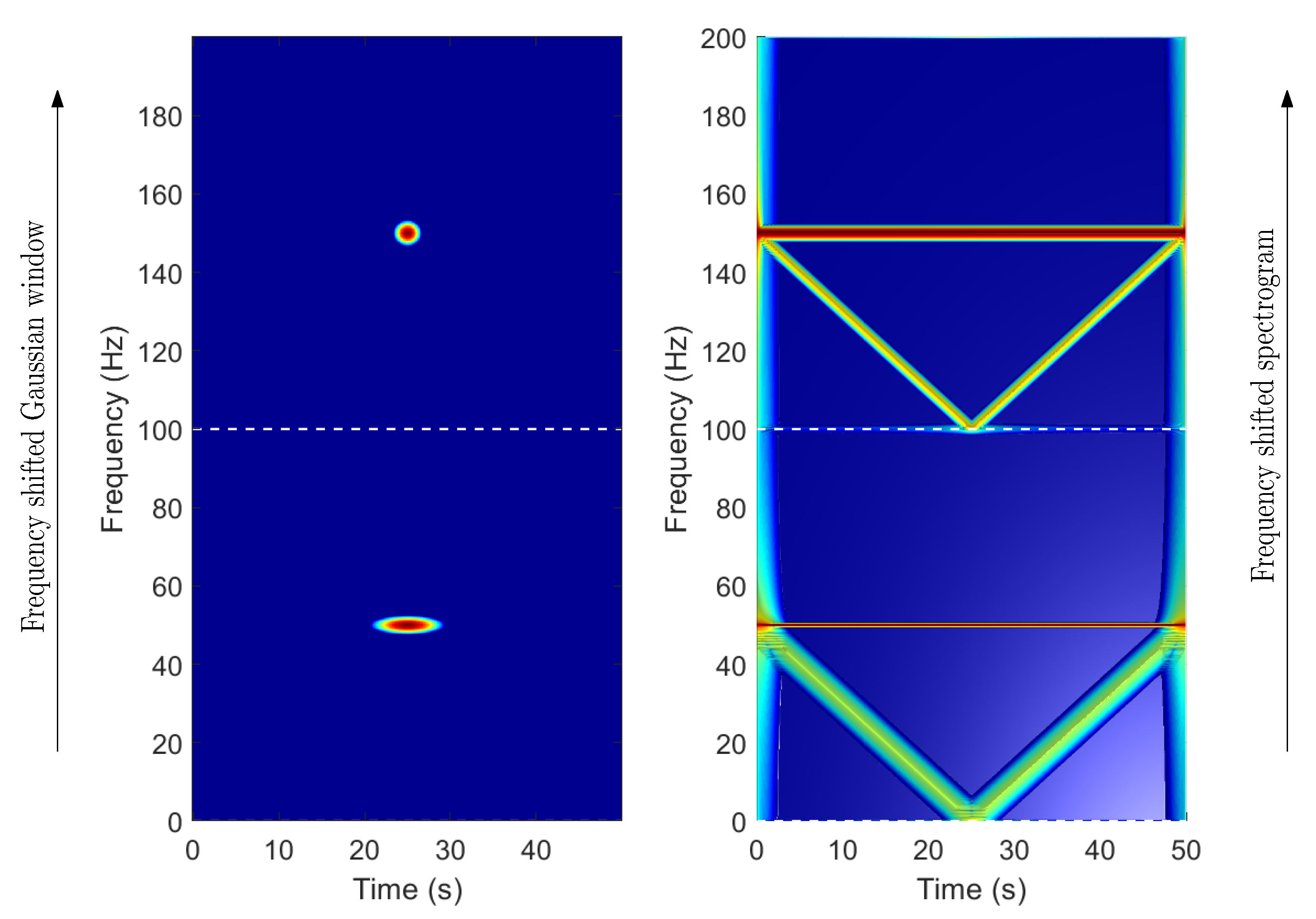
- The spectrogram of the current signal (17) is built, using the multi-band window (18) as sliding window (Figure 5). It shows two elementary spectrograms in adjacent TF regions, obtained with a single run of the STFT algorithm. The bottom one () locates the sinusoidal component at 50 Hz but blurs the chirp component. On the contrary, the top one () locates the chirp component but widens the sinusoidal component. This second Gaussian window, and the spectrogram that it generates, have been shifted to the frequency band [100–200 Hz].
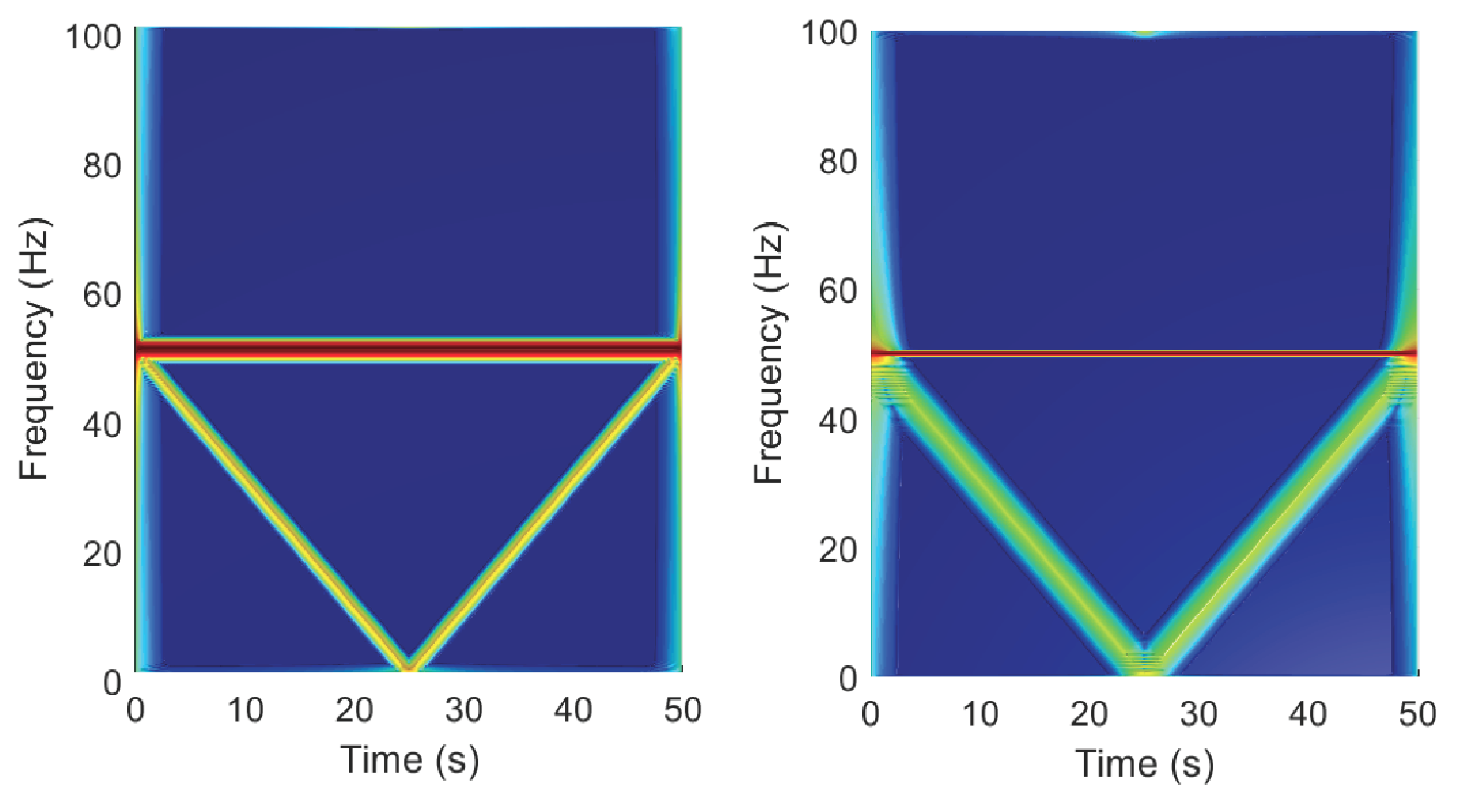
- All the stacked, elementary spectrograms obtained in step 2 are shifted back to the frequency band [0–], as shown in Figure 6. This process has a negligible computational cost, just the renumbering of the frequency axis of each elementary spectrogram.
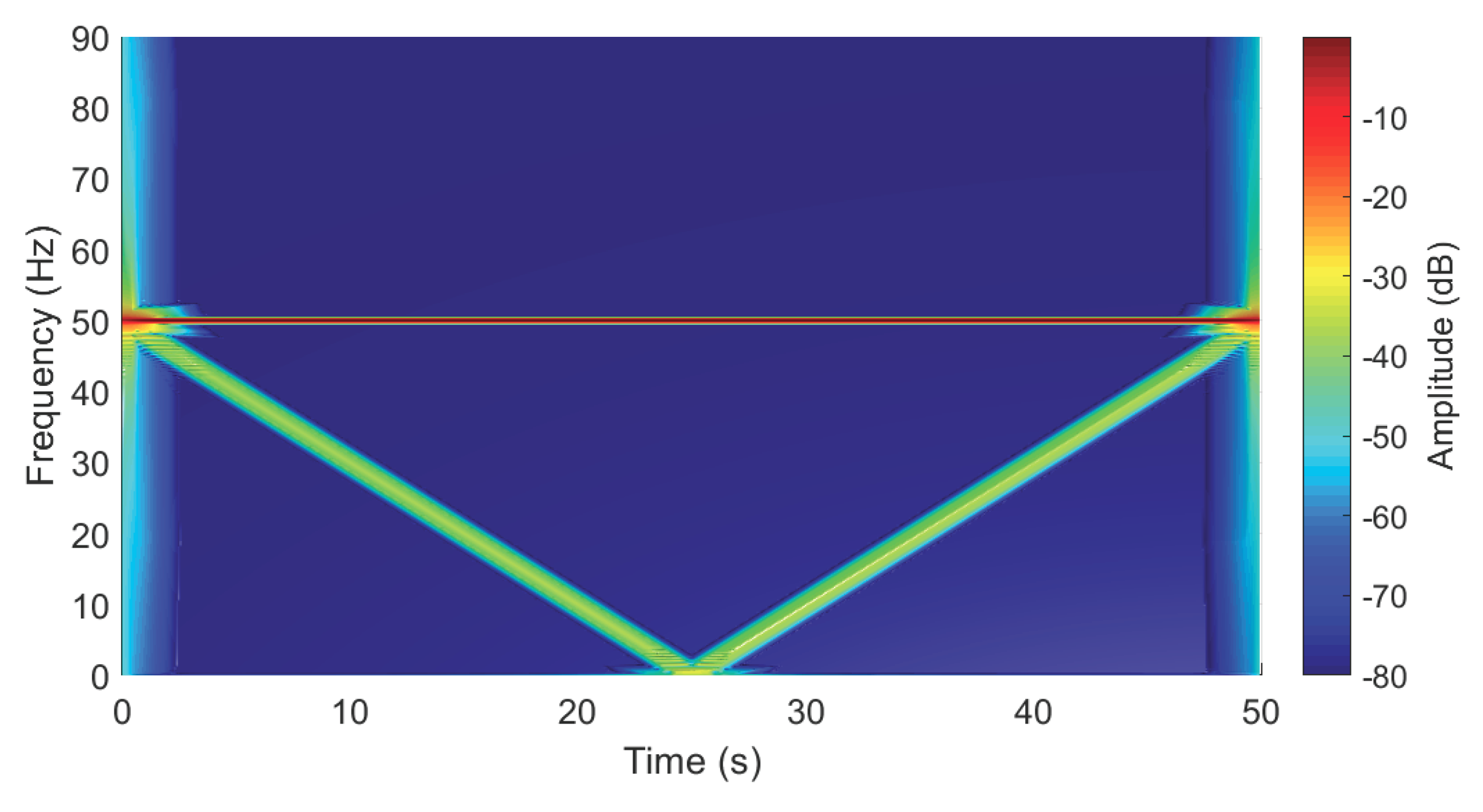
- The points with the same time-frequency coordinates in all the relocated spectrograms obtained in step 3 (Figure 6) are combined to give a single high resolution spectrogram of the TF region of diagnostic interest, in the frequency band [0–] (Figure 7). The combination process used in this work consists in selecting, for each point of this region, the minimum value obtained among all the relocated spectrograms. The final result shows with a high resolution both the sinusoidal component at 50 Hz and the chirp component.
4. Experimental Validation
- The analysis window (15) is built:
- first, the bandwidth of diagnostic interest is established. In this case, from (20), the frequency band of interest is the [0–50 Hz] band. Due to the presence of higher order harmonics in the current spectrum, apart form the LSH, a wider band [0–125 Hz] has been selected, in order to better assess the strength of the LSH compared with them. In this way, with a sampling frequency of 5000 Hz, the maximum number of elementary Gaussian windows from (14) is windows.
- second, the parameter of each of these windows in (15) is selected. In this case, a linear range of the parameter is used, covering the range [ – ].
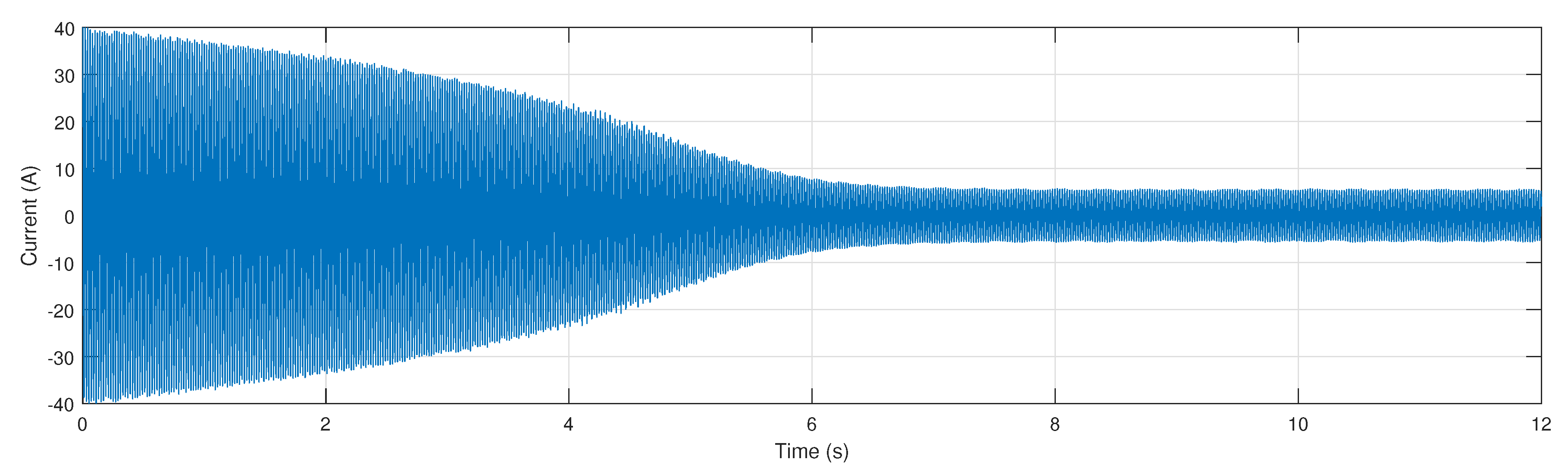
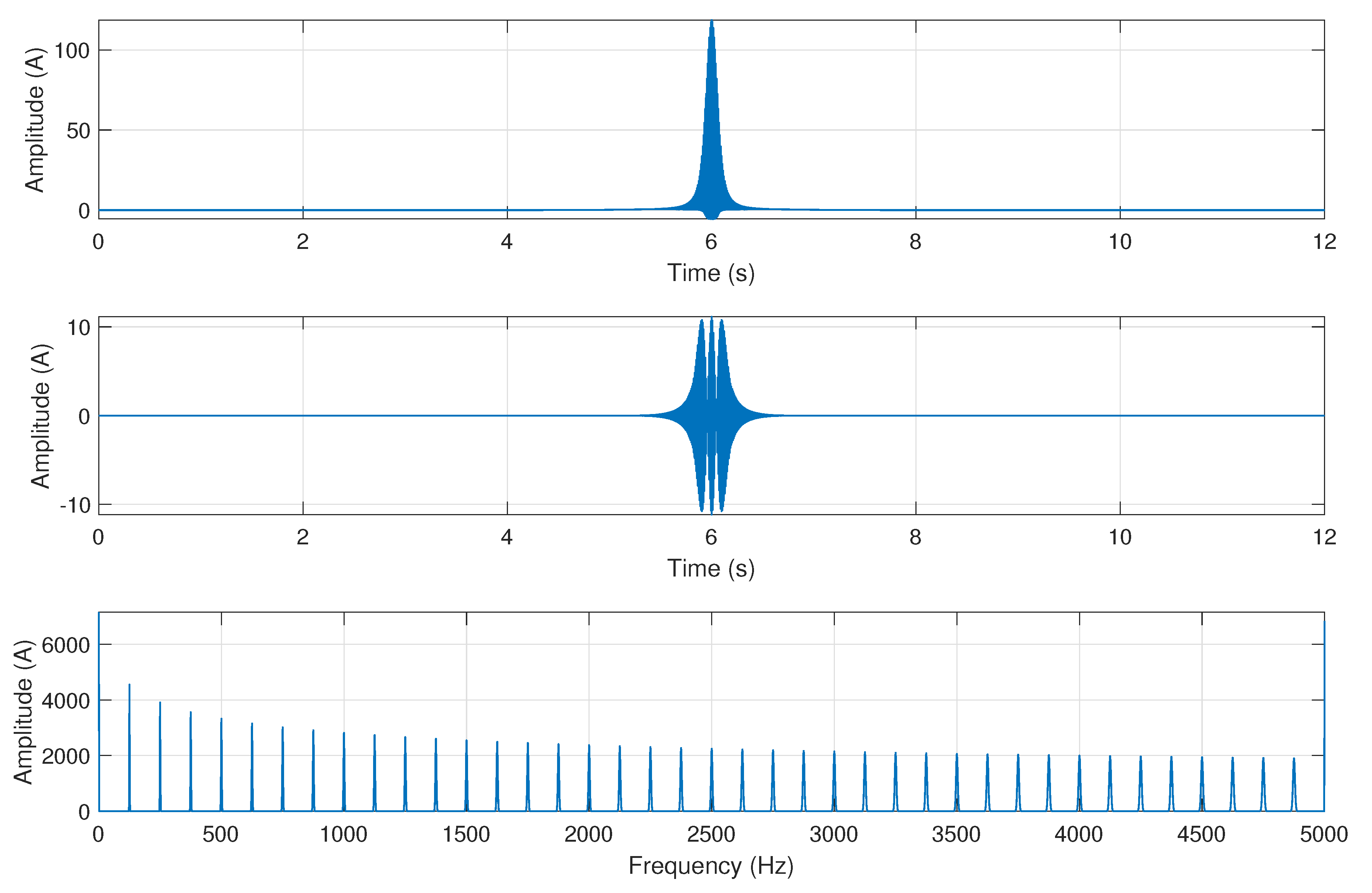
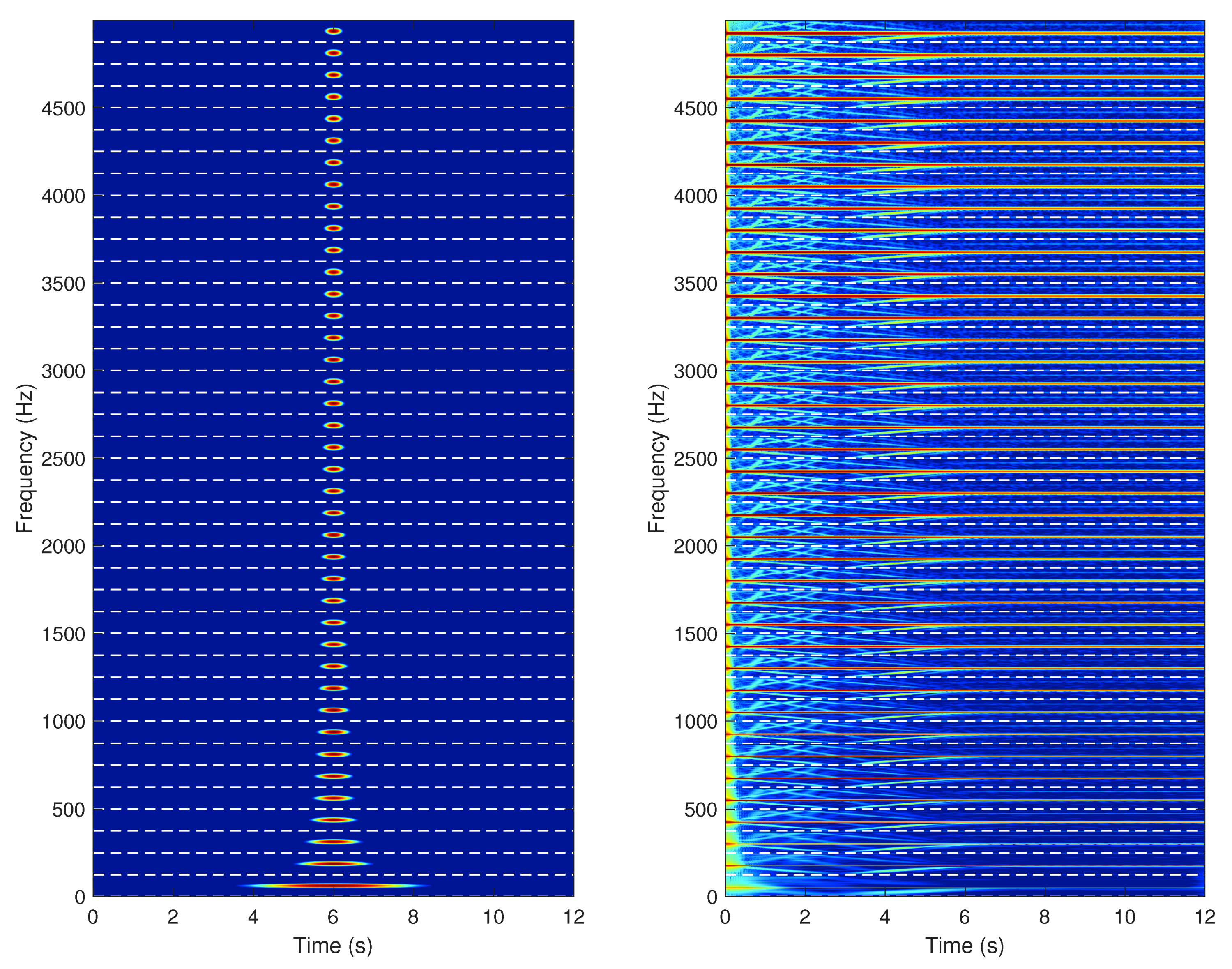
- The spectrogram of the current signal of Figure 8 is built. First, the current signal is low-pass filtered, keeping only the frequency bins of its spectrum lower than 125 Hz. After, and using the multi-band window (21) as sliding window, the STFT algorithm (4) is applied, which generates the spectrogram shown in Figure 10. This spectrogram contains 40 elementary spectrograms in adjacent TF regions (Figure 10, right), obtained with 40 different Gaussian windows (Figure 10, left), at the cost of a single run of the STFT algorithm (6 seconds with the computer of Appendix C). This computation time is not compatible with real-time applications but this is not important for the diagnosis of faults that develop progressively along hours, days or months, such as rotor asymmetries, eccentricities or bearing faults.Two of the 40 individual Gaussian windows shown in Figure 10 are displayed in Figure 11, left, along with their corresponding current spectra (Figure 11, right). The two zoomed bands corresponds to the spectrogram located in the base frequency band [0–125 Hz] (Figure 11, bottom), which defines clearly the fundamental component but blurs the fault harmonics, and to the spectrogram shifted to the frequency band [1500–1625 Hz] (Figure 11, top), which defines clearly the fault harmonics but widens the fundamental component.
- All the stacked, elementary spectrograms obtained in step 2 (Figure 10, right), are relocated in the base frequency band [0–125 Hz], by renumbering their frequency axis.
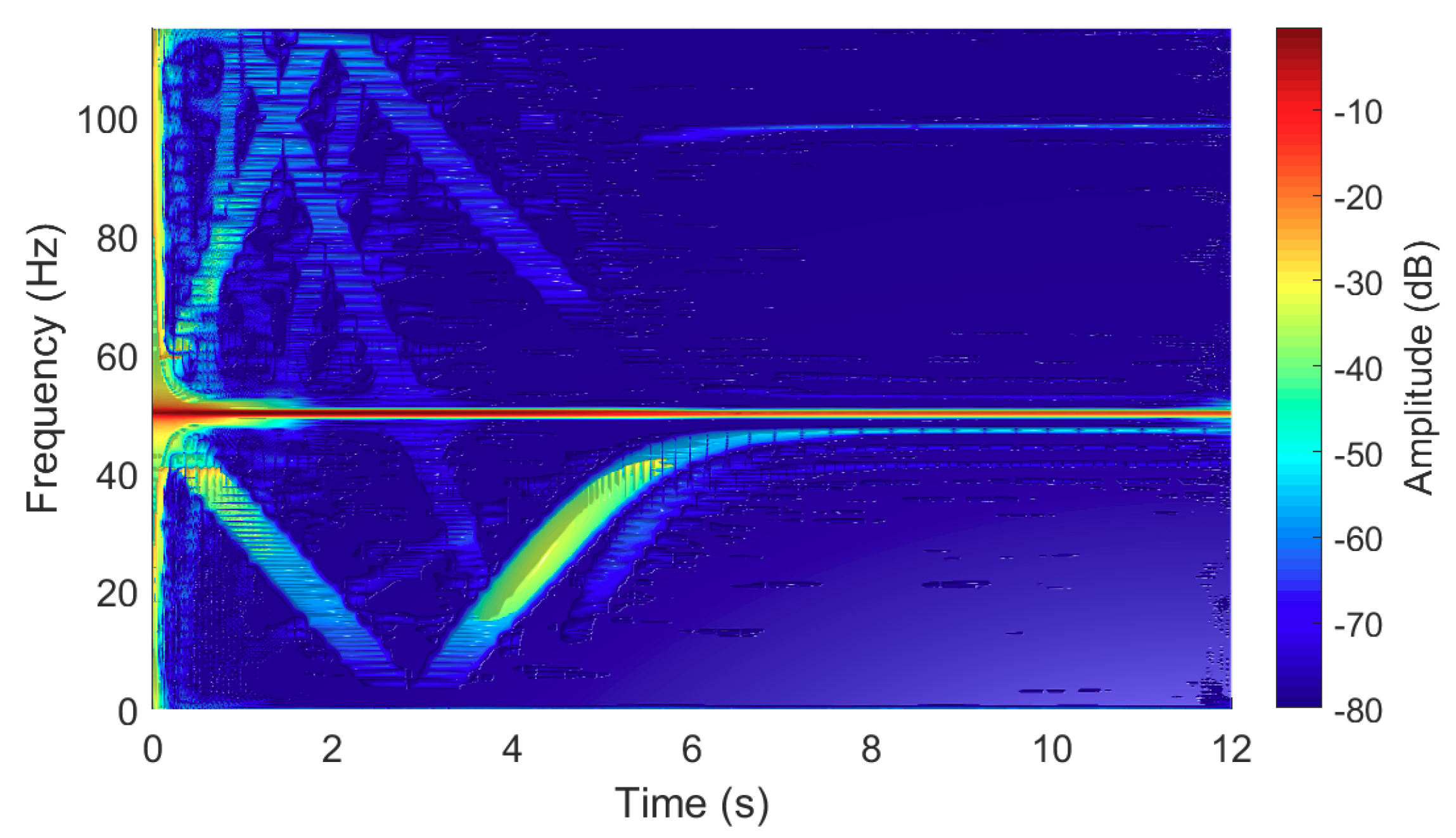
- All the relocated, elementary spectrograms obtained in step 3 (Figure 10, right), are combined to give a high resolution spectrogram of the TF region of diagnostic interest (Figure 12). The combination process used in this work consists in selecting, for each point of this [0–125 Hz] region, the minimum value obtained among all the relocated spectrograms. The final result shows with a high resolution both the sinusoidal component at 50 Hz and the LSH fault component. Unlike the individual spectrograms, the optimized spectrogram clearly shows the LSH not only during the transient period but also when the steady state is reached; it is also remarkable the set of fault-related second-order components that are revealed, which helps to get a more reliable diagnostic.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Motor Characteristics
Appendix B. Current Clamp
Appendix C. Computer Features
References
- Chang, H.C.; Jheng, Y.M.; Kuo, C.C.; Hsueh, Y.M. Induction Motors Condition Monitoring System with Fault Diagnosis Using a Hybrid Approach. Energies 2019, 12, 1471. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, D. A Survey of Condition Monitoring and Fault Diagnosis toward Integrated O&M for Wind Turbines. Energies 2019, 12, 2801. [Google Scholar]
- Bandyopadhyay, I.; Purkait, P.; Koley, C. Performance of a Classifier Based on Time-Domain Features for Incipient Fault Detection in Inverter Drives. IEEE Trans. Ind. Inform. 2019, 15, 3–14. [Google Scholar] [CrossRef]
- Artigao, E.; Honrubia-Escribano, A.; Gomez, E. In-Service Wind Turbine DFIG Diagnosis using Current Signature Analysis. IEEE Trans. Ind. Electron. 2019, 1. [Google Scholar] [CrossRef]
- Swana, E.F.; Doorsamy, W. Investigation of Combined Electrical Modalities for Fault Diagnosis on a Wound-Rotor Induction Generator. IEEE Access 2019, 7, 32333–32342. [Google Scholar] [CrossRef]
- Esakimuthu Pandarakone, S.; Mizuno, Y.; Nakamura, H. A Comparative Study between Machine Learning Algorithm and Artificial Intelligence Neural Network in Detecting Minor Bearing Fault of Induction Motors. Energies 2019, 12, 2105. [Google Scholar] [CrossRef]
- Huang, B.; Feng, G.; Tang, X.; Gu, J.X.; Xu, G.; Cattley, R.; Gu, F.; Ball, A.D. A Performance Evaluation of Two Bispectrum Analysis Methods Applied to Electrical Current Signals for Monitoring Induction Motor-Driven Systems. Energies 2019, 12, 1438. [Google Scholar] [CrossRef]
- Bo, L.; Xu, G.; Liu, X.; Lin, J. Bearing Fault Diagnosis Based on Subband Time-Frequency Texture Tensor. IEEE Access 2019, 7, 37611–37619. [Google Scholar] [CrossRef]
- Yu, G. A Concentrated Time-Frequency Analysis Tool for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 1–11. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Shi, J.; Shen, C.; Huang, W.; Zhu, Z. A coarse-to-fine decomposing strategy of VMD for extraction of weak repetitive transients in fault diagnosis of rotating machines. Mech. Syst. Signal Process. 2019, 116, 668–692. [Google Scholar] [CrossRef]
- Irhoumah, M.; Pusca, R.; Lefevre, E.; Mercier, D.; Romary, R. Detection of the Stator Winding Inter-Turn Faults in Asynchronous and Synchronous Machines Through the Correlation Between Harmonics of the Voltage of Two Magnetic Flux Sensors. IEEE Trans. Ind. Appl. 2019, 55, 2682–2689. [Google Scholar] [CrossRef]
- Skowron, M.; Wolkiewicz, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Effectiveness of Selected Neural Network Structures Based on Axial Flux Analysis in Stator and Rotor Winding Incipient Fault Detection of Inverter-fed Induction Motors. Energies 2019, 12, 2392. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, Z.; Vong, C.M.; Pecht, M. A Rotating Machinery Fault Diagnosis Method Based on Feature Learning of Thermal Images. IEEE Access 2019, 7, 12348–12359. [Google Scholar] [CrossRef]
- Parvathi Sangeetha, B.; Hemamalini, S. Rational-Dilation Wavelet Transform based Torque Estimation from Acoustic signals for Fault Diagnosis in a Three Phase Induction Motor. IEEE Trans. Ind. Inform. 2019, 15, 3492–3501. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Tarchała, G.; Wolkiewicz, M. Performance of the Stator Winding Fault Diagnosis in Sensorless Induction Motor Drive. Energies 2019, 12, 1507. [Google Scholar] [CrossRef]
- Abdi Monfared, O.; Doroudi, A.; Darvishi, A. Diagnosis of rotor broken bars faults in squirrel cage induction motor using continuous wavelet transform. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 167–182. [Google Scholar] [CrossRef]
- Nemec, M.; Ambrožič, V.; Fišer, R.; Nedeljković, D.; Drobnič, K. Induction Motor Broken Rotor Bar Detection Based on Rotor Flux Angle Monitoring. Energies 2019, 12, 794. [Google Scholar] [CrossRef]
- Zappalá, D.; Sarma, N.; Djurović, S.; Crabtree, C.; Mohammad, A.; Tavner, P. Electrical & mechanical diagnostic indicators of wind turbine induction generator rotor faults. Renew. Energy 2019, 131, 14–24. [Google Scholar] [CrossRef]
- Salah, A.A.; Dorrell, D.G.; Guo, Y. A Review of the Monitoring and Damping Unbalanced Magnetic Pull in Induction Machines Due to Rotor Eccentricity. IEEE Trans. Ind. Appl. 2019, 55, 2569–2580. [Google Scholar] [CrossRef]
- Wang, T.; Lu, G.; Yan, P. A Novel Statistical Time-Frequency Analysis for Rotating Machine Condition Monitoring. IEEE Trans. Ind. Electron. 2019, 1. [Google Scholar] [CrossRef]
- Jiang, X.; Shi, J.; Huang, W.; Zhu, Z. Non-dominated solution set based on time–frequency infograms for local damage detection of rotating machines. ISA Trans. 2019. [Google Scholar] [CrossRef] [PubMed]
- Faiz, J.; Moosavi, S. Eccentricity fault detection—From induction machines to DFIG—A review. Renew. Sustain. Energy Rev. 2016, 55, 169–179. [Google Scholar] [CrossRef]
- Kumar, D.; Basit, A.; Saleem, A.; Abbas, E.G. PLC Based Monitoring & Protection of 3-Phase Induction Motors against Various Abnormal Conditions. In Proceedings of the 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 30–31 January 2019; pp. 1–6. [Google Scholar]
- Guven, Y.; Atis, S. Implementation of an embedded system for real-time detection of rotor bar failures in induction motors. ISA Trans. 2018, 81, 210–221. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Bracamonte, J.E.; Ramirez-Cortes, J.M.; de Jesus Rangel-Magdaleno, J.; Gomez-Gil, P.; Peregrina-Barreto, H.; Alarcon-Aquino, V. An Approach on MCSA-Based Fault Detection Using Independent Component Analysis and Neural Networks. IEEE Trans. Instrum. Meas. 2019, 68, 1353–1361. [Google Scholar] [CrossRef]
- Pilloni, A.; Pisano, A.; Riera-Guasp, M.; Puche-Panadero, R.; Pineda-Sanchez, M. Fault Detection in Induction Motors. In AC Electric Motors Control; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2013; pp. 275–309. [Google Scholar]
- Abd-el Malek, M.B.; Abdelsalam, A.K.; Hassan, O.E. Novel approach using Hilbert Transform for multiple broken rotor bars fault location detection for three phase induction motor. ISA Trans. 2018, 80, 439–457. [Google Scholar] [CrossRef] [PubMed]
- Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M.; Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; et al. Automatic Fault Diagnostic System for Induction Motors under Transient Regime Optimized with Expert Systems. Electronics 2018, 8, 6. [Google Scholar] [CrossRef]
- Rivera-Guillen, J.R.; De Santiago-Perez, J.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Romero-Troncoso, R.J. Enhanced FFT-based method for incipient broken rotor bar detection in induction motors during the startup transient. Measurement 2018, 124, 277–285. [Google Scholar] [CrossRef]
- Gröchenig, K. Foundations of Time-Frequency Analysis; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Pineda-Sanchez, M. Short-Frequency Fourier Transform for Fault Diagnosis of Induction Machines Working in Transient Regime. IEEE Trans. Instrum. Meas. 2017, 66, 432–440. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inform. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Yang, B.; Liu, R.; Chen, X. Fault Diagnosis for a Wind Turbine Generator Bearing via Sparse Representation and Shift-Invariant K-SVD. IEEE Trans. Ind. Inform. 2017, 13, 1321–1331. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Pineda-Sanchez, M.; Perez-Cruz, J.; Puche-Panadero, R.; Roger-Folch, J.; Antonino-Daviu, J.A. Diagnosis of Induction Motor Faults via Gabor Analysis of the Current in Transient Regime. IEEE Trans. Instrum. Meas. 2012, 61, 1583–1596. [Google Scholar] [CrossRef]
- Fernandez-Cavero, V.; Morinigo-Sotelo, D.; Duque-Perez, O.; Pons-Llinares, J. A Comparison of Techniques for Fault Detection in Inverter-Fed Induction Motors in Transient Regime. IEEE Access 2017, 5, 8048–8063. [Google Scholar] [CrossRef]
- Daubechies, I.; Planchon, F. Adaptive Gabor transforms. Appl. Comput. Harmon. Anal. 2002, 13, 1–21. [Google Scholar] [CrossRef][Green Version]
- Dörfler, M.; Velasco, G.A. Adaptive Gabor frames by projection onto time-frequency subspaces. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 3097–3101. [Google Scholar]
- He, D.; Cao, H.; Wang, S.; Chen, X. Time-reassigned synchrosqueezing transform: The algorithm and its applications in mechanical signal processing. Mech. Syst. Signal Process. 2019, 117, 255–279. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Z.; Zhao, P.; Li, Z. Local maximum synchrosqueezing transform: An energy-concentrated time-frequency analysis tool. Mech. Syst. Signal Process. 2019, 117, 537–552. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, M.N.S.K.; Liang, X.; Zhang, Y.; Hu, T. Machine Learning based Fault Diagnosis for Single- and Multi-Faults in Induction Motors Using Measured Stator Currents and Vibration Signals. IEEE Trans. Ind. Appl. 2019, 55, 2378–2391. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching Pursuits with Time-Trequency Dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Qin, Y.; Zou, J.; Tang, B.; Wang, Y.; Chen, H. Transient feature extraction by the improved orthogonal matching pursuit and K-SVD algorithm with adaptive transient dictionary. IEEE Trans. Ind. Inform. 2019, 1. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. Part 1: The analysis of information. J. Inst. Electr. Eng. Part III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Matic, D. Fault Diagnosis of Rotating Electrical Machines in Transient Regime Using a Single Stator Current’s FFT. IEEE Trans. Instrum. Meas. 2015, 64, 3137–3146. [Google Scholar] [CrossRef]
- Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Pineda-Sanchez, M. Fault Diagnosis of Induction Machines in a Transient Regime Using Current Sensors with an Optimized Slepian Window. Sensors 2018, 18, 146. [Google Scholar] [CrossRef] [PubMed]

| Type of Fault | Fault Harmonics Frequency | |
|---|---|---|
| Shorted coils | ||
| Rotor asymmetries | ||
| Mixed eccentricity | ||
| Bearing (outer race) | ||
| Bearing (inner race) | ||
| Bearing (balls) | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Baño, A.; Riera-Guasp, M.; Pineda-Sánchez, M. Multi-Band Frequency Window for Time-Frequency Fault Diagnosis of Induction Machines. Energies 2019, 12, 3361. https://doi.org/10.3390/en12173361
Burriel-Valencia J, Puche-Panadero R, Martinez-Roman J, Sapena-Baño A, Riera-Guasp M, Pineda-Sánchez M. Multi-Band Frequency Window for Time-Frequency Fault Diagnosis of Induction Machines. Energies. 2019; 12(17):3361. https://doi.org/10.3390/en12173361
Chicago/Turabian StyleBurriel-Valencia, Jordi, Ruben Puche-Panadero, Javier Martinez-Roman, Angel Sapena-Baño, Martin Riera-Guasp, and Manuel Pineda-Sánchez. 2019. "Multi-Band Frequency Window for Time-Frequency Fault Diagnosis of Induction Machines" Energies 12, no. 17: 3361. https://doi.org/10.3390/en12173361
APA StyleBurriel-Valencia, J., Puche-Panadero, R., Martinez-Roman, J., Sapena-Baño, A., Riera-Guasp, M., & Pineda-Sánchez, M. (2019). Multi-Band Frequency Window for Time-Frequency Fault Diagnosis of Induction Machines. Energies, 12(17), 3361. https://doi.org/10.3390/en12173361