1. Introduction
The concept of “nearly zero energy” is usually associated with nearly zero-energy building (nZEB), which is a building with very high energy performance whose very low energy needs are significantly covered by energy produced locally or nearby from renewable energy sources (RES). In EU, the European Directives 2010/31/EU (Energy Performance of Buildings Directive or EPBD) and 2012/27/EU (Energy Efficiency Directive) provide a general framework of objectives in terms of building performance and energy efficiency, and assign the definition of the modalities for their achievement and implementation directly to member states [
1,
2]. The EPBD requires that all new buildings must be nearly zero-energy buildings (nZEB) as of 31 December 2020.
This concept can also be extended to the definition of a net zero-energy building (NZEB)–or house–if the energy systems installed can convert energy from RES to generate at least as much primary energy as the one consumed by the building over the course of the year [
3]. A more detailed definition and classification of NZEBs, based on an RES supply hierarchy, was proposed in Ref. [
4], suggesting that systems with higher rank are the ones that consume renewable energy produced within the building footprint. However, the definition of NZEB does not imply that this system must be autonomous and isolated from the grid. As remarked in Ref. [
5], one of the main assumptions is that an energy-producing low-energy building must interact with other similar buildings and/or with the energy infrastructure. This interaction guarantees to sell renewable energy surplus and buy energy during shortage periods, without the need of over-sizing storage or curtailing load.
Following this principle, it can be noticed that there are many advantages in approaching large-scale zer-energy designs. Examples of such an approach include the possibility of designing an energy management system at the district level, which exploits the differences in load between buildings with different end-users (for example residences and commercial and tertiary buildings) and optimizes the use of RES differently from what is obtainable through the optimal management of each individual buildings. The work in Ref. [
6] showed that the district approach can yield a 10% improvement in energy efficiency with respect to the individual nZEB approach. In Ref. [
7], the principle of a nearly zero-energy district (nZED), applied at urban scale, is studied from an architectural and urban planning perspective, showing the need to consider the relationships between climatic and morphological indicators. The high number of possible alternative strategies in the construction of nZED or NZED net zero-energy district) constitutes a multidimensional problem that is often tackled through multi-criteria analysis [
8] and meta-heuristics approaches [
9]. In Ref. [
10], multiple options for planning a net zero-energy community are explored through life cycle assessment and multi-attribute decision making. The authors showed how a sustainable energy community must be based on the exploitation of locally available resources, but no reference to storage options is given.
In particular contexts, such as isolated and rural areas, or small islands, where energy supply from conventional sources (diesel, gas, etc.) is problematic and expensive and electrification by the public network is economically unjustified, the use of locally available resources such as biomasses [
11], solar [
12], and wind [
13] can improve reliability, environmental impacts, and energy costs. Further efficiencies can be also reached integrating energy carriers such as electricity and thermal energy [
14]. The scheme of a net zero multi energy system (NZMES) is proposed in Ref. [
15], considering the application to a rural village in Poland and observing that a multi-energy system (MES) structure [
16] can allow the integration of multiple energy infrastructures, also including heat and transportation, and reach higher objectives in terms of sustainability and efficiency [
17].
An NZMES is an energy system based on the use of large amounts of RES, where sustainable and environmentally friendly electricity is converted into other forms of energy in order to satisfy the multiple energy needs of a community without the use of conventional fuels. According to the net zero principle, the total energy production must be roughly equal to the overall energy demand within a specific time horizon (e.g., one year). Since the most commonly available RES technologies are photovoltaic (PV) and wind turbines, a NZMES must be suitably controlled in order to balance electricity demand and production. The electrical loads are powered directly whereas the thermal loads are efficiently supplied by converting electricity into heat through heat pumps in order to eliminate boilers. Due to the volatility of energy production from wind and sun, electrical and thermal energy storage systems (BESS and TESS) should be integrated in the NZMES so that higher levels of self-sufficiency can be reached. In an isolated system, storage will also be needed in order to avoid load curtailments or the use of back-up fossil fuel-fired resources. Obviously, a large energy storage system would increase the levels of self-sufficiency and self-consumption [
18], but because of high capital costs of batteries, an optimal sizing of the energy storage systems and a smart management of the energy infrastructure are unavoidable [
19].
The integration of multi-carrier energy systems and storage implies a more complex design and requires the use of optimal operational control strategies. The complexity in optimizing energy resources is due to the concomitant presence of intermittent renewable energy generation, multiple storage systems, dispatchable energy loads, and the need to balance multiple energy equations simultaneously at a minimum cost. The modeling of interdependencies between different energy systems and cost optimization requires special methods for planning and operation. For example:
- ▪
Optimal sizing and control of the power plants (wind turbine, photovoltaic, and heat pump) and energy storage systems (battery, thermal storage) have to be adopted;
- ▪
A dispatchable load allows batteries to charge even when renewable energy production is low;
- ▪
When energy is available for storage, it must be decided which type of storage must be charged based on next load requirements;
- ▪
Storage systems have a different time response due to storage capacity and charge/discharge rates.
Generally, a multiple storage system requires investigating different control strategies and rules for adopting the right operating mode, taking into account, for example, different time responses of different energy carriers. A methodology, based on economic, technical, and social criteria, is essential to optimally manage the generation capacity and size the energy storage units. An important concept was introduced in Ref. [
20] where a short-term operation in a long-term planning approach is proposed. Based on a representation of short-term system operations within a long-term planning framework, the role of electricity storage in future RES-based systems has been developed according to the following scheme:
- ▪
Short-term-operation: A predictive control is executed at definite times (daily or several times in the same day); it allows a better exploitation of storage resources optimizing their use while increasing the level of self-consumption;
- ▪
Long-term planning based on a short-term optimization allows to avoid the oversizing of the storage equipment and to maximize the capacity of the RES.
This same principle was also adopted in Ref. [
21], where a predictive control problem based on load and renewable generation forecasts is part of a two-stage optimization problem aimed at the optimal sizing of a multi-energy system. The use of predictive control along system operation allows it to optimize the use of storage in the short-term and avoid storage over-sizing in the long-term. The use of predictive control in managing hybrid systems with storage and RES is often suggested. Although the management of a system composed only by renewable generation and BESS is relatively simple, the use of optimal control strategies is recommended in the presence of other dispatchable resources and competing technologies [
22]. In fact, simple pre-defined rules and operating modes [
23,
24] cannot be adopted whenever the number of possible operational solutions grows appreciably or if multiple storage systems that differ in structure, dynamics, time responses, costs, and capacities are installed. In order to decide which storage system must be charged (or discharged), it is necessary to optimize the storage resources according to their different time responses, storage capacity, and charge/discharge speeds. For example, in Ref. [
25], a daily optimization strategy for optimizing both electric and thermal storage at microgrid level was proposed. Similarly, in Refs. [
26,
27], it was shown how multiple storage devices and competing generation resources can be conveniently managed through an optimal control strategy that exploits load and RES forecasts according to typical model predictive control schemes
In this paper, the optimal sizing of electric and thermal storage is applied to the novel definition of an NZMES. Possible storage sizing choices are examined considering the solution of a predictive control problem aimed at optimizing daily operation. For each day of the year, an optimal control problem is solved, aiming at minimizing operating costs. This kind of control problem reproduces the preventive dispatch problem that can be run daily, or several times in the same day according to the typical rolling horizon structure of model predictive control, by the energy management system that controls the NZMES.
The adoption of optimal control techniques permits, during system operation, the optimization of the use of storage and increase in the overall level of self-consumption, making the most of the functional features of each storage resource. The proposed predictive control algorithm is based on the definition of a nonlinear optimal control problem in the discrete time domain that is linearized and then solved through mixed integer linear programming (MILP) in order to speed up calculations and increase its robustness.
The proposed approach is tested considering the sizing problem of a NZMES for a Polish rural village. An energetic model that includes environmental parameters to assess electric, thermal, and (electric) transportation loads is adopted, overcoming the use of Monte Carlo simulations [
28]. Test results will be aimed at assessing the expected technical-economic performance of different sizing options, considering the detailed simulation of a full year of operation. The role of two competing storage options (BESS and TESS) is studied in both terms of self-sufficiency and expected energy costs.
2. Mathematical Model for Optimal Sizing and Operation of a NZMES
In this paper, the technical-economic performances of different NZMES sizing options are assessed simulating a full year of operation. For each day of the year, a predictive control problem is formulated and solved, aimed at optimally dispatching all available energy resources and minimizing variable operating costs. This preventive dispatch problem reproduces the functions that can be run during daily operation by the energy management system that controls the NZMES. The predictive control problem can be solved on a daily basis or more often in order to generate infra-day refinements, as in typical model predictive control (MPC) and rolling horizon approaches. This type of control permits the tracking of optimality even in the presence of stochastic variables such as the intermittent energy production from solar and wind energy, and the full exploitation of storage resources by optimally regulating their charge and discharge.
The use of optimal control tools is also recommended in the presence of two competing storage technologies, such as BESS and TESS, that can be difficult to treat with simple rule-based control. In a multi-energy system, the dispatch of these two resources is, in fact, mutually dependent due to the coupling of electrical and thermal energy. Usually, the adoption of optimal control techniques permits, during system operation, the optimization of the use of storage and increase in the overall level of self-consumption. Integrating short-term optimization in the planning phase permits one to avoid oversizing of storage equipment and, whenever dispatchable energy sources such as conventional fuel generators are also to be installed, maximize the capacity of intermittent generating sources (typically PV and wind turbines).
In the following section, the mathematical model used to simulate daily operations and estimate the long-term performances of an NZMES is described. Although the mathematical formulation will be tailored on a specific NZMES structure, the overall approach is general enough to be applied to any MES.
2.1. Short-Term Optimization Model
The operational problem solved for each day of operation assumes that good forecasts of loads and generation are available at the beginning of the day. If forecasts are known, optimal predictive control can be applied, formulating a nonlinear dynamic problem in the continuous time domain. Assuming that energy variables do not change significantly, in a fixed time interval (for example, one hour), the problem can be discretized and transformed in a nonlinear static problem in the discrete time domain [
26]. The problem to be solved minimized a generically nonlinear function of all system variables
subject to inequality and equality constraints
where vector
collects all dispatchable resources at the
i-th interval and
all the energy inputs and outputs that are considered not dispatchable;
u and
p collect, respectively, all
and
in the selected optimization window (e.g., a single day);
nstep is the number of discrete intervals contained in the optimization window (e.g.,
nstep is 24 if a daily optimization window is divided into 1-h discrete time intervals):
Equations
represent the energy balancing equations for each energy carrier at the
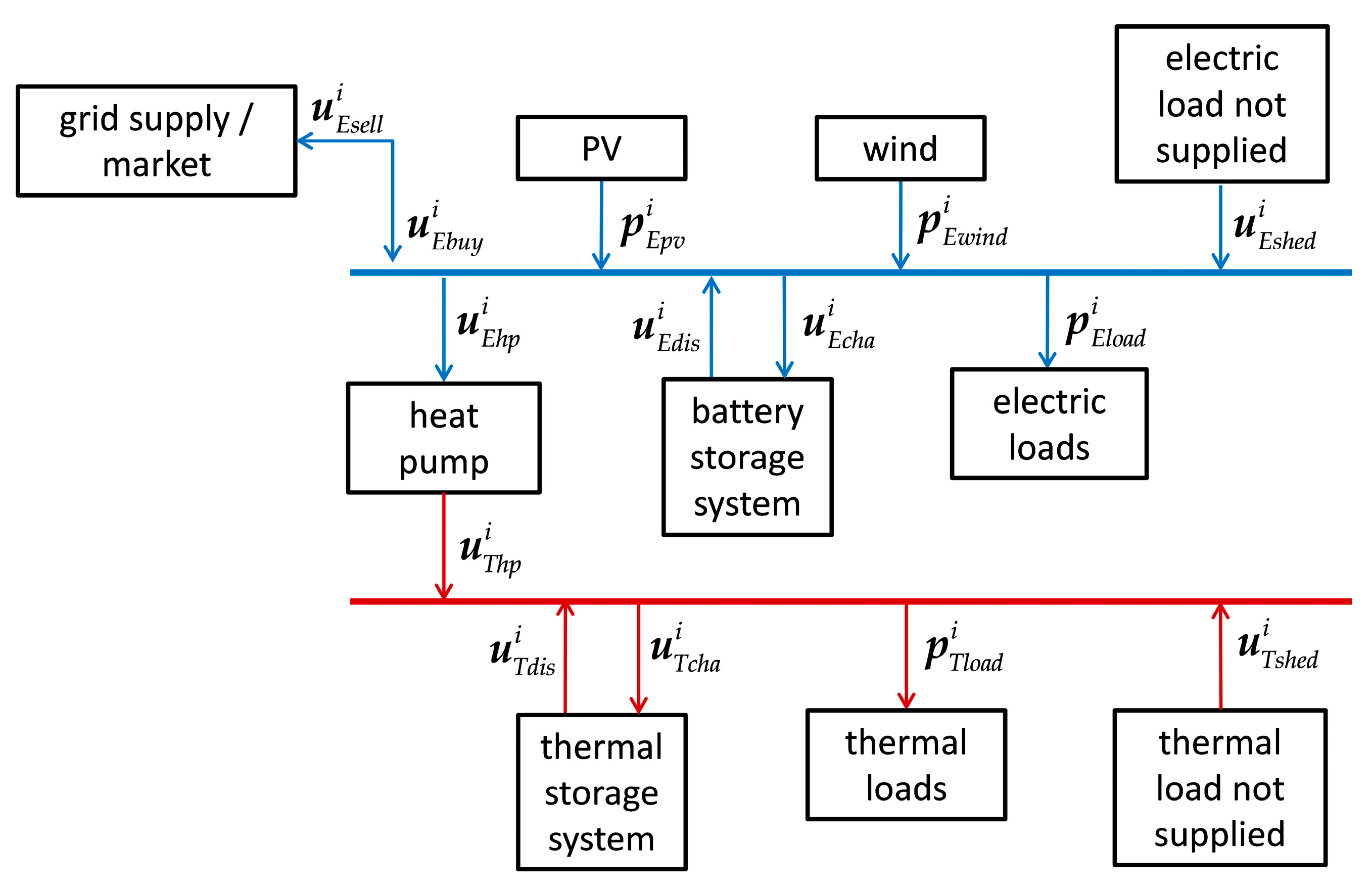
i-th step. In the case of the system under study, represented in
Figure 1, there are two energy vectors (electricity and heat) and therefore the equality equations are 2 ×
nstep. Each equation formulated for the specific
i-th time interval is a function of the sole variables and parameters at this same
i-th time interval.
Equations represent all physical constraints on variables at each time interval. These constraints include the minimum and maximum capacity constraints on storage. As shown in the following, each storage unit at each time step introduces two inequality constraints; therefore, in the modelled system, storage capacity limits are represented by 4 × nstep inequality constraints. Differently from what assumed for equality constraints, these equations at a generic i-th step depend on previous variables, since the current storage state is determined by previous charge and discharge.
In the proposed approach, load and generation forecasts, as well as other environmental parameters, are represented by the chronological profiles obtained by an energetic model of the system that includes weather conditions, number of inhabitants, specific annual consumption, and other environmental parameters. These time-varying profiles are considered deterministically known and, therefore, the solution obtained at the beginning of each day will reproduce what, in MPC theory, is usually regarded as the ideal open-loop optimal control solution [
29]. In actual short-term operation, quantization errors, deviations from forecasted profiles, and other uncertainties will be compensated by the control law updates provided by the closed-loop MPC control. In Ref. [
30], it was shown how the actual MPC solution deviates slightly from the ideal open-loop one, even in the presence of significant forecast errors. In this paper, where a sizing problem is studied, having also considered the level of approximation for assuming the annual chronological curves, the ideal open-loop solution is considered detailed enough to represent the daily response of the NZMES energy management system in a long-term evaluation.
2.1.1. Linearization of the Problem
The optimization problem was generically formulated in the previous section as a nonlinear problem. However, linearization can be obtained introducing a set of integer variables
s that will allow one to more easily treat the discontinuities and nonlinearities introduced by storage and other variables, and to solve the problem by means of typical MILP routines. The MILP problem can be solved with very efficient solvers based on branch and bound methods such as CPLEX, Xpress, or Gurobi. Theses solvers can deal with millions of constraints and several thousands of variables, thanks also to the capabilities of presolvers that can drastically reduce the number of constraints [
31]. In the test results, the Gurobi optimizer was adopted.
The problem linearized problem can be generically formulated as:
subject to inequality and equality constraints
with Equation (3), and with
s collecting all integer variables
2.1.2. Problem Variables and Inputs
The set of continuous and integer variables was chosen according to the structure of the system under study, represented in
Figure 1. It was supposed that renewable energy is never curtailed; consequently, the energy inputs from PV and wind generators are considered non-dispatchable resources and, therefore, they are just inputs of the optimal problem formulation. This hypothesis can be restrictive in the operation of net-zero systems where negative prices can be applied to energy exported at the point of common coupling. However, negative prices are not allowed in any market structure and it is a general belief that renewable production should never be curtailed to exploit their potential in preserving environment. However, since net-zero systems are supposed to limit energy exchanges with neighboring systems as much as possible, it was later assumed that the price paid for selling the excess of energy is null.
Considering the system represented in
Figure 1, at each
i-th time step, the set of continuous control variables is given by the vector
whose elements represent, respectively, the electrical power exported at the point of common coupling (PCC)
, the electrical power imported at the PCC
, the BESS charging power
, the BESS discharging power
, the electrical power consumed by the heat pump
, the electrical load shedding
, the thermal power produced by the heat pump
, the TESS charging power
, the TESS discharging power
, and the thermal load shedding
.
Integer control variables are used to represent variables that introduce discontinuities in the formulation of objective functions or constraints. In general, they can be introduced to transform nonlinear responses into piecewise linear ones. In this simplified problem, the integer variables are
with
being 1 if the system is exporting energy (0 if importing);
being 1 if the BESS is charging (0 if discharging), and
being 1 if the TESS is charging (0 if discharging). As specified earlier, other integer variables can be introduced to consider nonlinear behaviors or discontinuities such as in the case of varying efficiencies, technical minimum power output, variable energy prices, etc. However, for the proposed planning study, linear hypotheses can hold in most cases.
The last vector used to describe the system is given by the non-dispatchable inputs
:
where
is the power generated by the PV units,
is the power generated by the wind turbines,
is the electric load (heat-pump not included), and
is the thermal load.
2.1.3. Equality Constraints
The two main equality constraints are given by the electric and thermal energy balance that, having assumed the power injected in the NZMES is positive, can be written respectively
A further equality constraint can consider heat pump and the transformation of electric energy into thermal:
where
represents the time-varying coefficient of performance (COP) of the heat pump at the
i-th time interval. In the proposed approach, a time-varying COP is assumed, considering an hourly model of how heat source and sink temperatures will vary across one year. The system under study assumes the installation of an air to water heat pump. For such heat pumps, the COP depends on the ambient temperature and on the temperature of the supply water, which was assumed to not vary significantly in a one h time interval. For the sake of simplicity and considering the overall level of approximation for estimating environmental parameters along an entire year, this efficiency has been assumed to not be dependent on the power input/output. However, more detailed nonlinear models can be easily introduced and linearized using a piecewise linear approximation (with each added linear segment requiring the introduction of a new integer variable).
If the linear hypothesis stands, Equation (12) can be included in Equation (11) that, hence, becomes:
2.1.4. Inequality Constraints
A first set of inequality constraints considers the physical limitation of dispatchable units. Since Equation (7) is composed by intrinsically positive variables, these limits are generically formulated through linear expressions in the form:
In detail, they assume the following expressions
The last set of linearized inequality constraints considers the maximum and minimum capacity of storage systems. Having defined for the BESS
,
, and
respectively as the minimum charge, maximum charge, and initial charge, having called
the length of each time interval, and having assumed constant charging and discharging efficiencies
and
, these limits can be written in linear form as:
Equivalent assumptions and definitions can be made for the TESS leading to the definition of the inequality constraints
2.2. Long-Term Optimal Sizing
The proposed approach uses the outputs of the daily optimization described in
Section 2.1 to provide an estimation of the annual technical and economic performances of different NZMES sizing options. Although numerous indices can be introduced [
15], in this paper, the focus was made on self-sufficiency and (levelized) cost of energy so that sizing options can be easily weighted. Moreover, this simplifying assumption allows to have a straightforward perception of how much self-sufficiency weights on energy cost.
Two numerical indices are used to compare NZMES performances in terms of self-sufficiency. The system self-consumption index (
SSCI) estimates the ratio between the amount of load (including battery charge) instantly matching the generated power and the entire amount of generated RES power. The system self-sufficiency index (
SSSI) represents, instead, the amount of load instantly matching the generated power (including the battery discharge) and the entire amount of required load. These indices are used to have a metric of the autonomy level reached by the system under study. Both indices can be calculated according to the following equations:
In order to compare different sizing solutions, the use of levelized costs of energy (
LCOE) is proposed:
where
k represents the generic
k-th year of the investment, CC are annual capital costs, O&M are annual costs including the fixed operation and maintenance costs and the variable operating costs minimized on a daily base through the solution of the optimal problem in
Section 2. MWH is the annual total consumed electric energy. In test results, the discount rate
r was set to 4%.
Please note that in the proposed NZMES scheme, both electric and thermal energy are produced and consumed. The concurrent optimization of combined heat and power generation is problematic, because the cost of energy supply should be allocated partly to the electric and partly to the thermal production. There is not a univocal rule for this allocation, however, a possible option is to introduce a heat credit that represents the equivalent cost for producing thermal energy through high-efficiency natural gas-fired boilers. Adopting this approach, the heat credit is then deducted from the overall operating costs (OP). According to Ref. [
32] the heat credit was set to 0.040 € per each kWht of supplied thermal energy.
3. Model of a NZMES
This study is focused on finding the optimal sizing of a NZMES, as the one schematized in
Figure 1, for a small Polish rural village. The methodology used for assessing the annual energy demand for electric, thermal, and (electric) transportation loads is described in Ref. [
15]. Heat and electricity demands related to the building component are calculated according to a model that includes weather conditions, buildings’ typology and geometry, number of living persons, specific annual consumption, and room temperatures. Space cooling has been neglected because of the high latitude of the village under study. Transportation requirements were calculated considering seven different types of electric vehicles (city cars) and different transportation profiles.
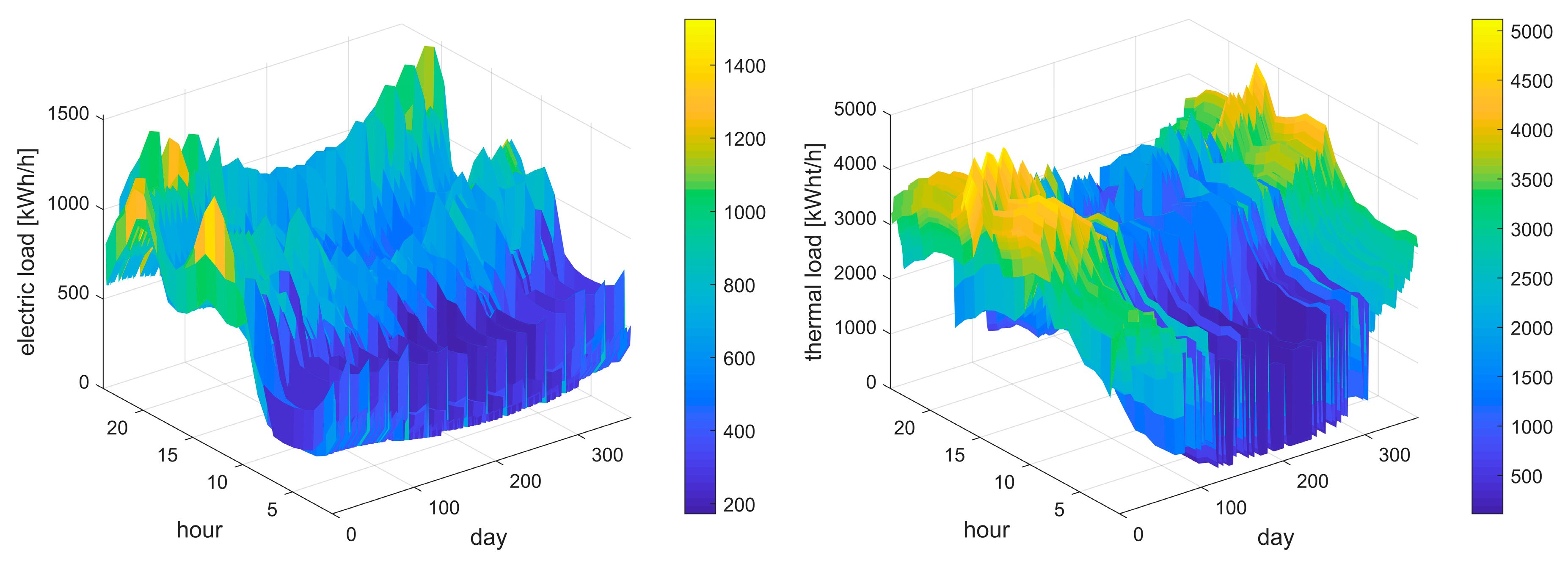
In
Figure 2, the annual electric and thermal load profiles are shown in a 3D-plot. The maximum electric demand is about 1220 kW for buildings and 460 kW for transportation, with an overall maximum of 1530 kW (20 January at 19:00) and an overall annual demand of about 4960 MWh. The maximum thermal demand (23 January at 15:00) is 5120 kWt, with an overall annual request of 19,650 MWht. In terms of electric consumption, this thermal request corresponds to annual 6030 MWh, with a maximum of 2870 kW. The overall annual electric energy need, which according to the net zero principle has to be provided by RES production, is about 10,990 MWh.
PV and wind turbines annual performances were obtained considering measured weather data on an annual basis. The annual expected production of RES was assessed in around 1700 full-load hours for wind and 1000 full-load hours for PV generators. Weather and environmental data were also used to evaluate the expected annual load of both electric and thermal energy.
The main economic parameters used for the study are presented in
Table 1. For technical-economic analysis, the lifetime was set at 20-years for all components. The wear costs of BESS were calculated considering the possibility to have 15,000 cycles with a 70% depth of discharge. The cost of imported energy was set constant at 20 c€/kWh, whereas the price of exported energy at 5 c€/kWh. Curtailment costs were assumed 2.5 €/kWh and 1 €/kWht for electric and thermal energy, respectively.
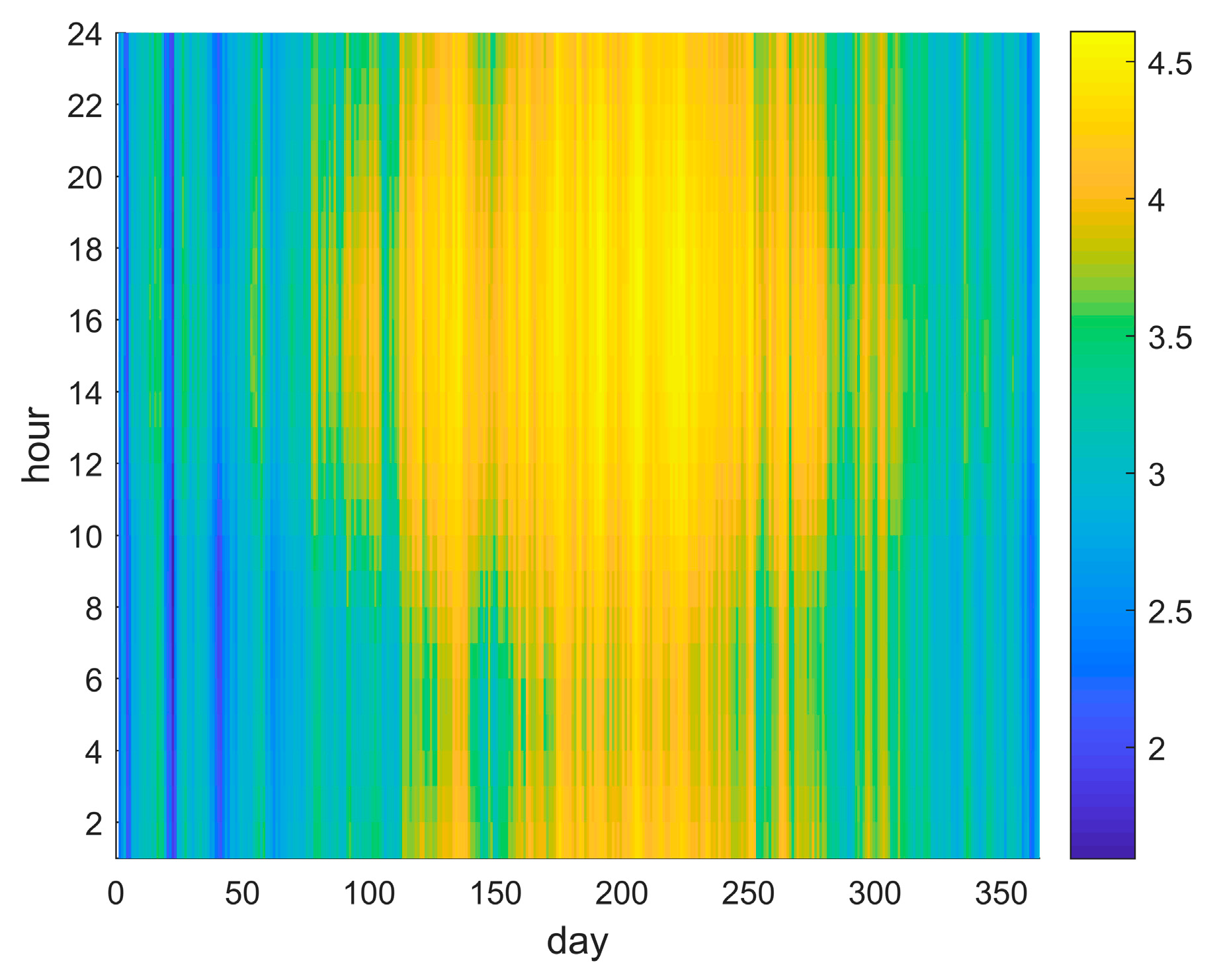
Charge and discharge efficiencies of storage systems were assumed equal to the root square of a constant round-trip efficiency. The round-trip efficiency was set to 80% for BESS and 90% for TESS. The efficiency of the heat-pump was calculated modelling the hourly variation of the expected heat source and sink temperatures along one year. A contour plot of the expected coefficient of performance (COP) is given in
Figure 3 for a whole year.
4. Test Results
The test results were obtained considering different compositions of generation from renewable sources. In order to benchmark different renewable mixes, the installed capacity of photovoltaics and wind generators were chosen in such a way that, having considered the expected full-load hours of both technologies, the total annual production is constant. According to the basic principle of the net zero-energy paradigm, the total annual production from RES covers the expected total electric consumption due to electric, thermal (heat pump), and electric transportation loads. This means that the NZMES can reach unitary self-sufficiency indices only in ideal conditions (i.e., if and only if the renewable production follows consumption exactly at any time).
For each renewable mix, test results were generated considering the availability of electric and thermal storage, in variable sizes. In order to map the mutual influence of storage resources in terms of self-sufficiency and cost of energy, for each configuration of storage, an annual optimization problem is carried out, considering that all energy resources are optimized daily. This means that for each day of the year, an optimization problem, such as the one previously formulated in
Section 2, is solved. The daily optimization allows one to evaluate expected operation costs that also include the costs of interruptions and the wear cost of batteries.
4.1. Case A
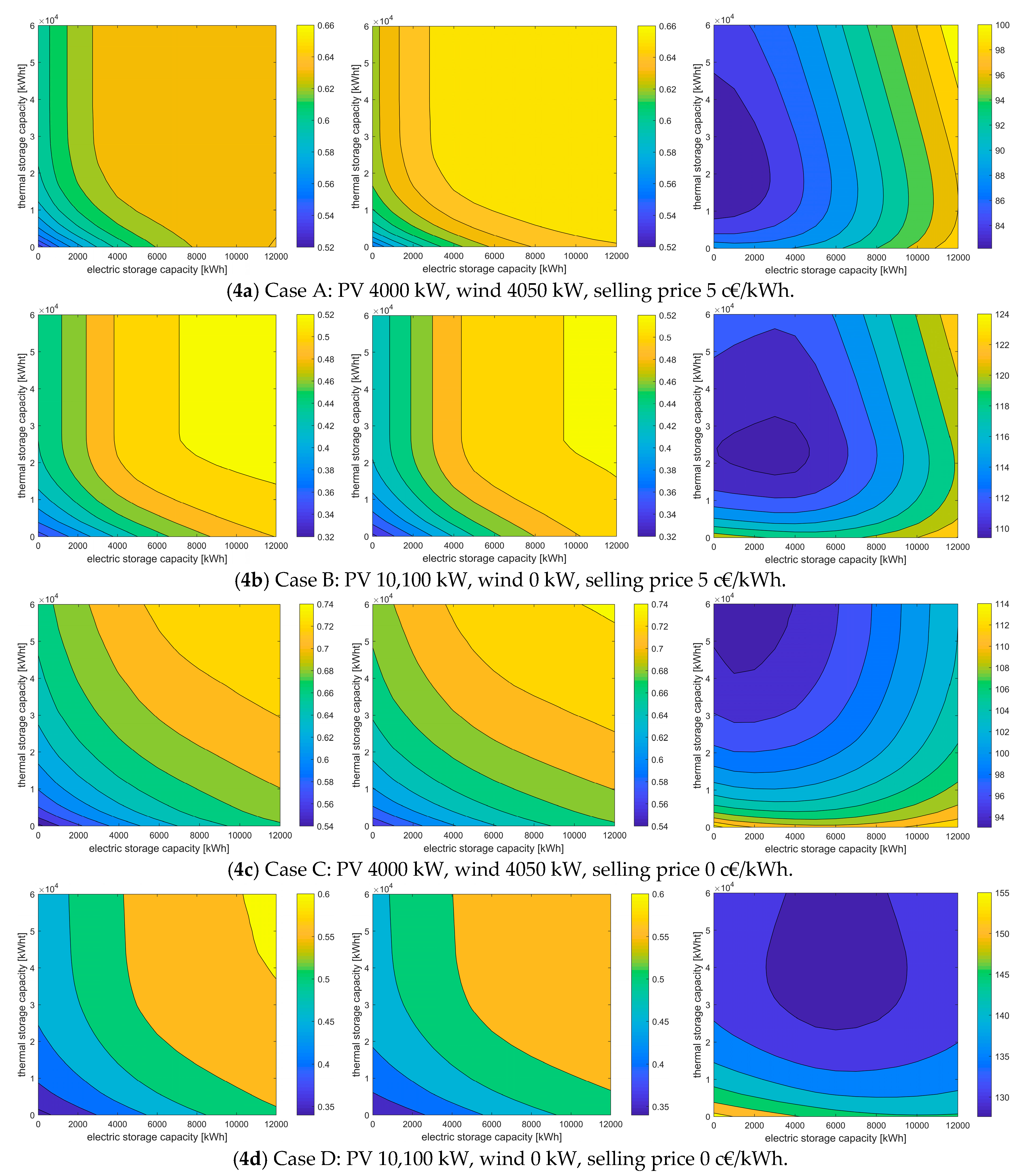
In this first case, photovoltaic and wind generator capacities were set respectively to 4000 kW and 4050 kW, and the selling price is set to 5 c€/kWh. The results of the annual optimization are shown in
Figure 4a, which represents how self-sufficiency indices and the expected levelized cost of energy vary with the sizing of storage. As expected, the ratio between
SSCI and
SSSI is close to one (it ranges from about 0.95 to 0.99). Self-sufficiency grows with an increase of size of any type of storage. However, it can be observed how thermal storage capacities higher than 30,000 kWht do not yield any increase of
SSCI or
SSSI. This is due to the fact that, especially in summer days when RES production is highest, operating costs cannot be minimized further with increased thermal storage. On such days, the daily optimal solution tends to sell the excess electric energy rather than use it for charging thermal storage.
As for the energy cost, it can be observed that the two storage systems (electrical and thermal) will compete in such a way that, having fixed the size of BESS, energy cost will first be reduced by an increase of size of TESS until minimum is reached. After that minimum, any increase of size will result in higher costs because the increase capital expenditures are not justified by a decrease of operating costs. The minimum levelized cost of energy is 82.2 €/MWh and is found in correspondence of a thermal storage capacity of about 20,000 kWht and a null BESS capacity. These results are reported in
Table 2 for all test cases. Self-sufficiency is around 60%, however if higher
SSCI and
SSSI indices are sought, other solutions that include also a BESS can be adopted, accepting a levelized cost only slightly higher than this minimum. Using these charts, the designer can choose the desired level of self-sufficiency knowing the associated costs of energy.
4.2. Case B
In this second case, the presence of the sole PV generation, with a capacity of about 10,100 kW, was assumed (i.e., no wind turbines are installed). Results are shown in
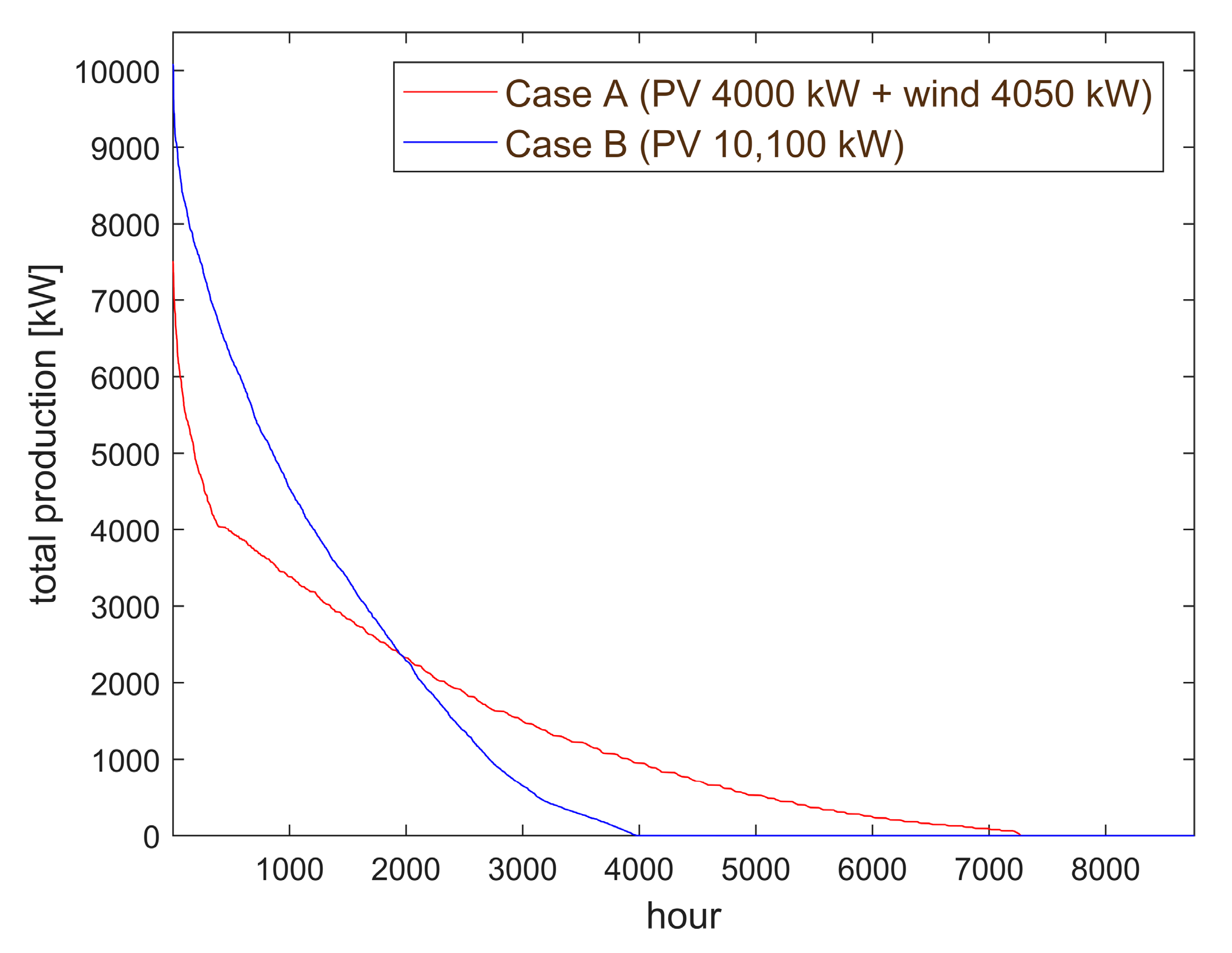
Figure 4b. Due to the presence of a single intermittent source, self-sufficiency cannot reach the same values reached in the previous case. This is clearly due to the fact that PV will only produce in a few hours of the day whereas wind generation is able to produce also in nighttime and on cloudy days. The energy production mix of Case A is therefore characterized by a capacity factor higher than Case B. The production duration curves relative to Case A and B are compared in
Figure 5.
The expected costs are higher in general, due to the necessity of importing more energy. A minimum of 109.4 €/MWh was found in correspondence of a thermal storage capacity of about 24,000 kWht and a 3000 kWh BESS capacity. Self-sufficiency is around 48% (
Table 2). As in the previous case, the TESS is more competitive than BESS, however it can be noticed how the contour lines are more stretched in the direction of BESS capacity. This means that, in the presence of higher electric production intermittence, the electrical storage resource is starting to assume a role complementary to the one of the TESS.
4.3. Case C
This third case is equivalent to Case A (PV and wind respectively at 4000 and 4050 kW), however it was assumed that no revenues from selling energy can be obtained, representing the case where energy “autarky” is highly encouraged by new potential regulatory schemes aimed at sustainable development [
33]. This means that the optimization algorithm will always try to maximize self-consumption and exploit the use of storage. The produced RES energy, which is not consumed or stored, does not contribute to the evaluation of the variable operating costs. Results are shown in
Figure 4c. By comparing
Figure 4a,c, it can be noticed how, considering a same sizing solution, a much higher level of self-sufficiency is reached in Case C. This is due, of course, to a more intensive use of storage resources. Differently from Case A, where a sort of saturation in the use of thermal storage was noticeable for capacities higher than 30,000 kWh, in Case C, an increase of TESS capacity always yields a decrease of variable operating costs and an increase of self-sufficiency.
As for the energy costs, in the studied range of capacities, a minimum is found at 93.0 €/MWh in correspondence to the maximum TESS capacity (about 60,000 kWht) and a 1000 kWh BESS capacity. Self-sufficiency is around 69% (
Table 2). However, as previously remarked, other sizing choices can be made accepting a higher expected cost in exchange of a higher self-sufficiency. Expected costs are higher because there is no remuneration from energy sales.
4.4. Case D
This fourth case considers a null selling price to the system in Case B (only PV production). Results are shown in
Figure 4d. The minimum cost of about 127.6 €/MWh is obtained using a 40,000 kWht TESS and a 6000 kW BESS, with a self-sufficiency around 57% (
Table 2). Self-sufficiency is higher than in Case B, due to the fact that self-consumption is maximized, but still lower than Case C because of the high volatility of PV production. In this case, the use of both competing storage resources is needed in order to reduce energy costs and increase self-sufficiency.
4.5. Discussion
Test results have been aimed at studying the roles that two storage competing resources assume in improving the self-sufficiency and expected energy costs of a NZMES. Even though both storage units can concur to improve the overall level of self-sufficiency, in cases A and C, the installation of the more expensive storage resource (BESS) can be avoided if a minimum expected cost of energy is sought. This is due either to the possibility of receiving a remuneration from energy sales or to a more continuous profile of RES production. In Case B and, especially, in Case D (where both conditions cannot be satisfied), the system is characterized by a higher need of flexibility, and both BESS and TESS can complementary contribute to the optimal operation of the system.
A general observation is that, apart from restricted areas in the chart of possible sizing choices, higher levels of self-sufficiency entail higher energy costs. A total self-sufficiency, as the one reachable in an isolated system, will always have a significant impact on energy costs due to the higher storage needs and to the arise of energy curtailment costs. In the studied NZMES, it was assumed that an interconnection to the electric grid is available. However, in the case of a rural electrification project where the possibility to buy/sell energy from/to the electrical grid will come with a cost, the planning problem should also include the capital costs associated with the building (or renovating) the energy transportation infrastructure. In such cases, the adoption of local storage options can be preferred to the building or the reinforcement of the electrical system.
Higher levels of self-sufficiency can always be reached if, contrarily from the NZMES configuration assumed in this paper, dispatchable generating resources are available. However, unless biomass or biogas fuels are available, dispatchable generation is usually associated with the use of fossil fuel-fired generation plants. In this case, reaching higher self-sufficiency will come with cost in terms of emissions and sustainability. The use of biomasses, unless produced locally, can also affect the “class” of sustainability as suggested in Ref. [
4]. Although this classification difficulty applies to systems larger than buildings, the proposed NZMES can be considered high ranking (at least B) because all energy is produced locally only by PV and wind turbines. The use of lower classified renewable sources such as biomasses would instead affect this rank and overall sustainability. Clearly, in the context of net zero-energy systems, energy sustainability should assume a more significant role with respect to self-sufficiency, since sustainability is the reason that such system was proposed in the first place.
Following these observations, the introduction of dispatchable generation planning options will require a more structured approach for long-term evaluations. Although minimizing the energy cost is always a relevant goal of MES planning, more indices should be introduced in order to take into account environmental impacts, energy supply reliability, and financial sustainability, requiring a multi-criteria approach for the solution of the planning problem. The short-term optimization problem used in this paper can easily accommodate more flexible resources, multiple energy carriers, and detailed components’ models. However, the introduction of grid models and constraints, in case the planning problem also included an assessment of required modifications to the energy transportation infrastructure, will require a different formulation of the short-term optimization problem.
5. Conclusions
In this paper, it was shown how an optimal sizing problem can be coupled to an operational short-term problem aimed at optimizing RES, loads, and storage on a daily basis in a multi energy system. This kind of approach is suggested whenever, due to the presence of several flexible resources, rule-based strategies are difficult to apply to the energy management system. The proposed linearized approach is fast, robust, and allows one to simulate the short-term response of MPC-based control strategies in a long-term framework. Timing is compatible with planning time requirements with each annual simulation, which solves 365 daily optimization problems, employing less than 2 min on a common desktop PC.
The case under study, based on the novel definition of a net zero multi energy system, assumes the presence of an energy management systems that coordinates electrical, thermal, and transportation energy needs of a small village. The overall annual energy demand is satisfied by PV and wind generators, which produce electric energy to be consumed or converted into thermal energy by a heat pump. The problem of optimal sizing of two competing storage resources was studied considering different project hypotheses, showing how minimum costs and self-sufficiency can be mutually exclusive. As suggested in some test cases, energy policies oriented to improve the autarky of energy districts or communities can motivate the use of larger storage systems to pursue higher aims in terms of system self-sufficiency.
In summary, the main findings are:
Integrating predictive control algorithms in long-term evaluation is feasible in terms of computational effort using a time resolution and horizon compatible with practical planning purposes;
The method allows one to optimize competing storage resources such as BESS and TESS;
High self-sufficiency targets entail costs for storage, which may result as unfeasible, driving the planner to choose dispatchable generation and lower classified renewable sources.
Future work will be aimed to provide more extensive studies of the NZMES planning problem, introducing a larger number of variables, possible technologies, and sizing choices. More complex nonlinear models of heat pumps and other components, grid models, and constraints will be studied and integrated. Multi-criteria analysis and meta-heuristics methods can also be used to explore a much wider range of planning options and sizing criteria.