Multi-User AF Relay Networks with Power Allocation and Transfer: A Joint Approach
Abstract
:1. Introduction
2. Preliminaries
2.1. System Model
2.2. Energy Harvesting and Power Transfer Model
2.3. Problem Formulation and Transformation
3. Proposed Power Allocation and Transfer Algorithm
3.1. Subproblem Solution
3.2. Master Problem
| Algorithm 1: Proposed algorithm for given values of and . |
| 1: Set as the maximum number of iterations with step sizes 2: Initialize , and ; 3: Initialize , , , , , , , and . 4: repeat 5: repeat(Solving (P4)) 6: Compute and and ; 7: Compute , , , , , and using (30)–(35). 8: until convergence; 9: Compute and using (26) and (27) 10: Set , , and and . 11: until convergence or . |
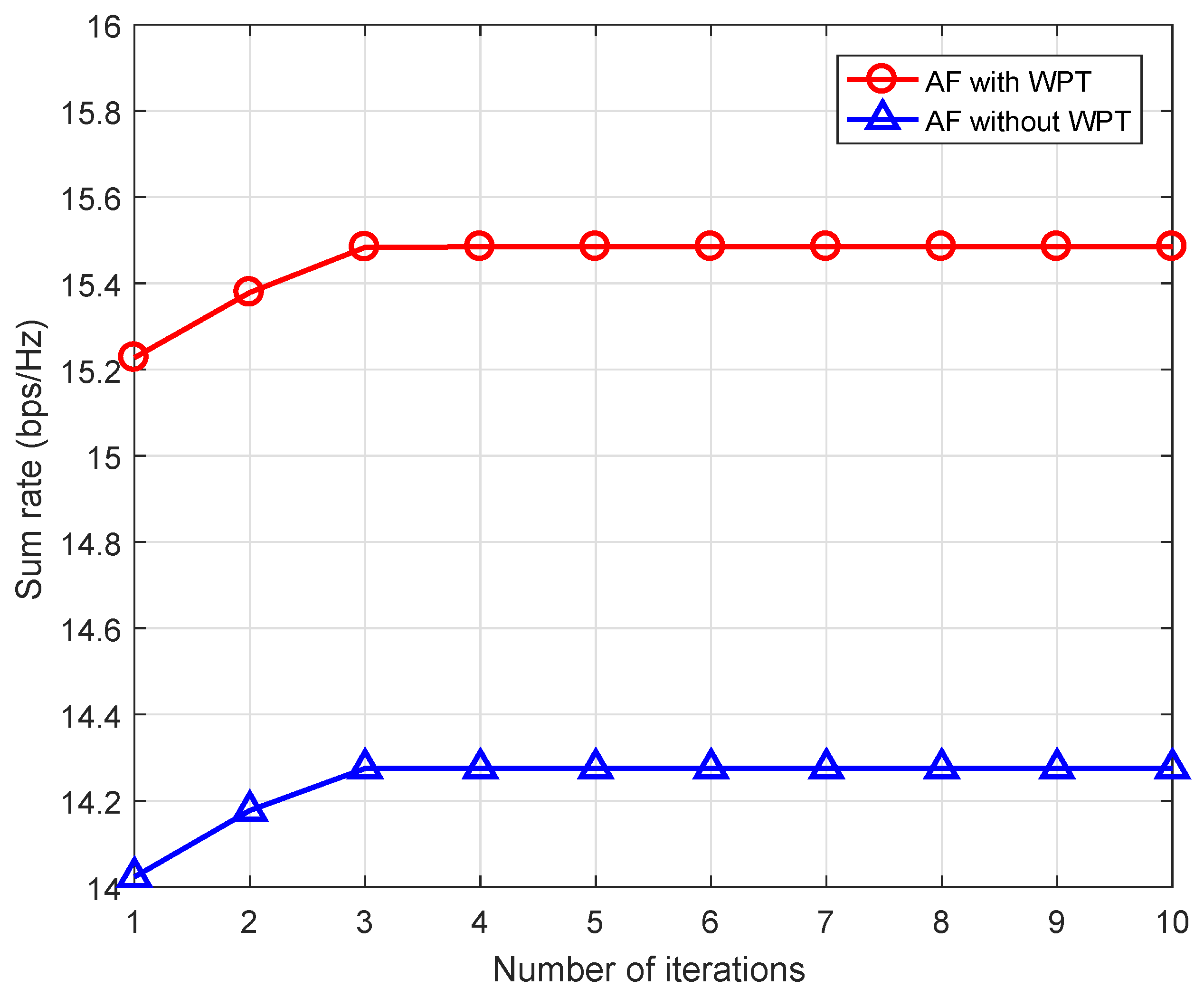
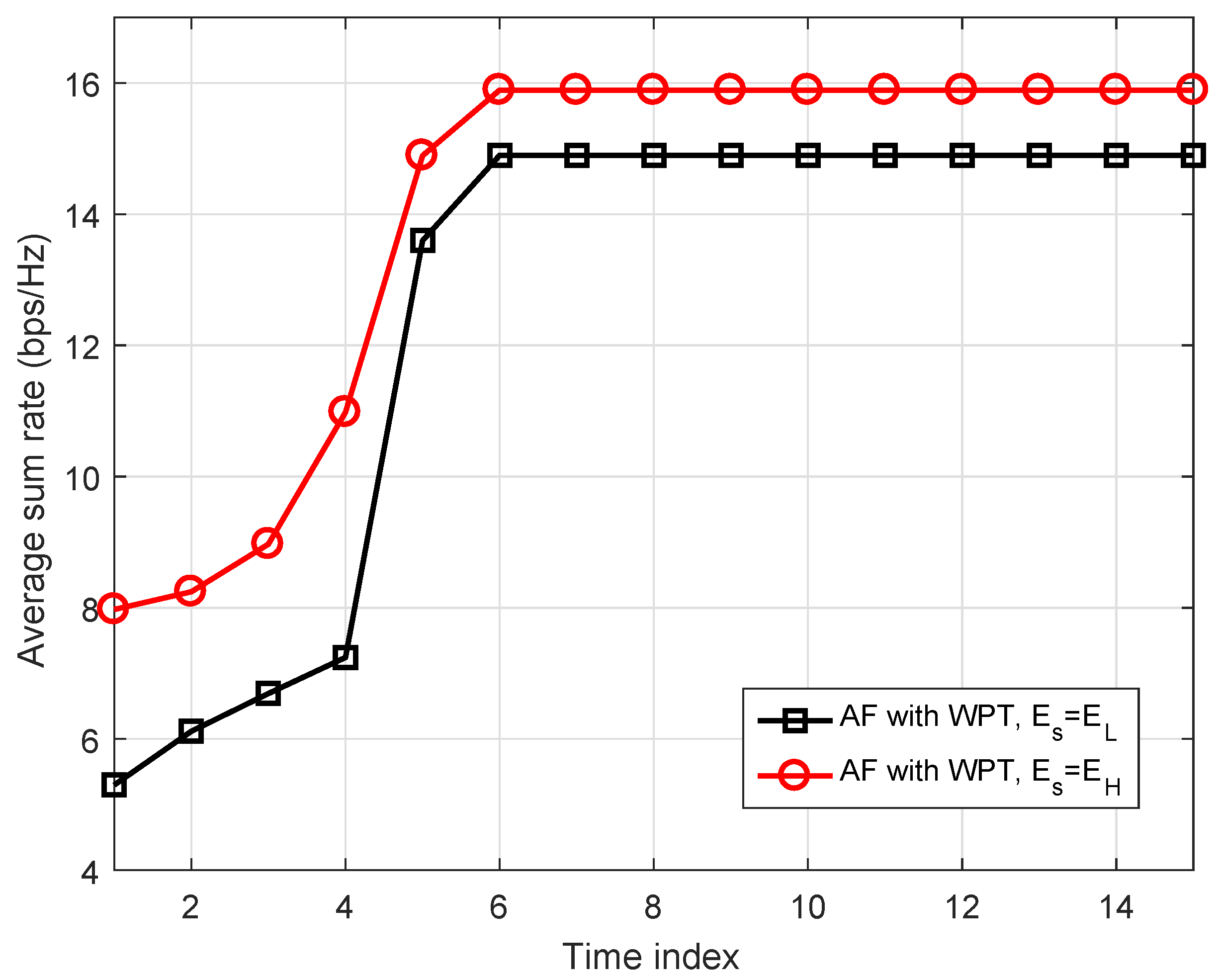
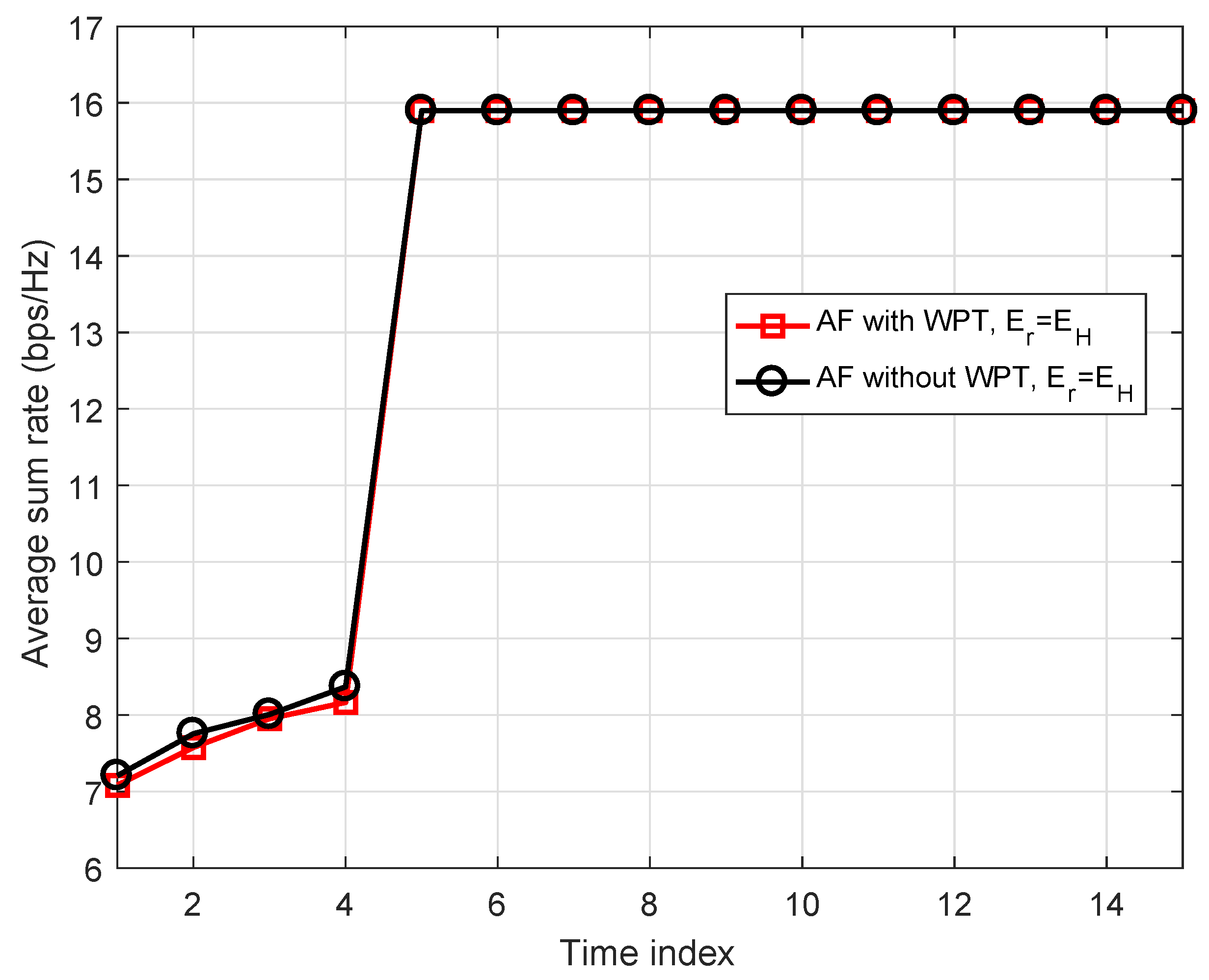
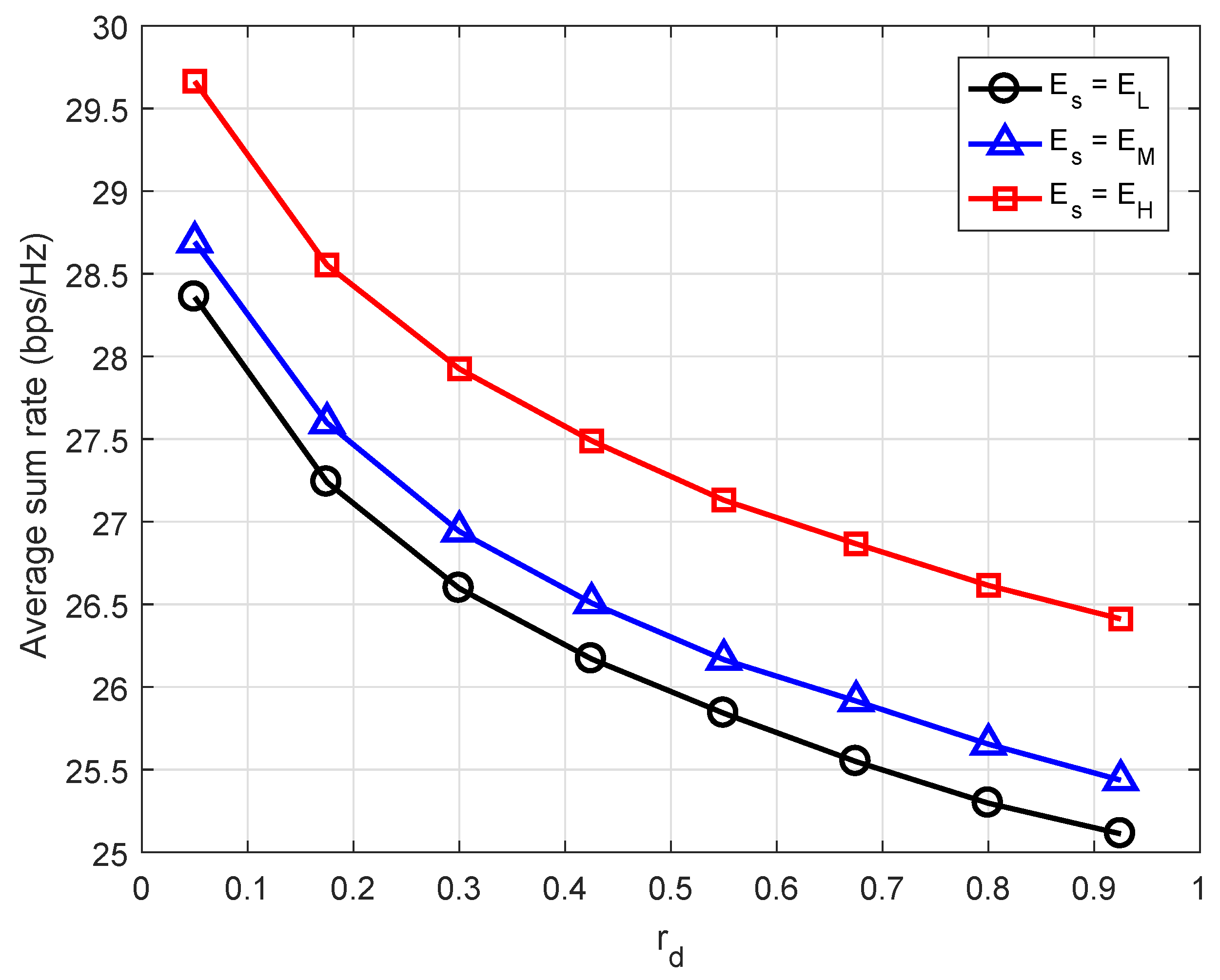
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of Things for smart cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Zhu, C.; Leung, V.C.M.; Shu, L.; Ngai, E.C.H. Green Internet of Things for smart world. IEEE Access 2015, 3, 2151–2162. [Google Scholar] [CrossRef]
- Medepally, B.; Mehta, N.B. Voluntary energy harvesting relays and selection in cooperative wireless networks. IEEE Trans. Wirel. Commun. 2010, 9, 3543–3553. [Google Scholar] [CrossRef]
- Kang, J. Toward secure energy harvesting cooperative networks. IEEE Commun. Mag. 2015, 53, 114–121. [Google Scholar] [CrossRef]
- Gunduz, D.; Michelusi, S.K.N.; Zorzi, M. Designing intelligent energy harvesting communication systems. IEEE Commun. Mag. 2014, 52, 210–216. [Google Scholar] [CrossRef]
- Gupta, A.; Singh, K.; Sellathurai, M. Time-switching EH-based joint relay selection and resource allocation algorithms for multi-user multi-carrier AF relay networks. IEEE Trans. Green Commun. Netw. 2019, 3, 505–522. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Yang, J.; Ulukus, S. Optimal packet scheduling in an energy harvesting communication system. IEEE Trans. Commun. 2012, 60, 220–230. [Google Scholar] [CrossRef]
- Tutuncuoglu, K.; Yener, A. Optimum transmission policies for battery limited energy harvesting nodes. IEEE Trans. Wirel. Commun. 2012, 11, 1180–1189. [Google Scholar] [CrossRef]
- Ho, C.K.; Zhang, R. Optimal energy allocation for wireless communications with energy harvesting constraints. IEEE Trans. Signal Process. 2012, 60, 4808–4818. [Google Scholar] [CrossRef]
- Ozel, O.; Tutuncuoglu, K.; Yang, J.; Ulukus, S.; Yener, A. Transmission with energy harvesting nodes in fading wireless channels: Optimal policies. IEEE J. Sel. Areas Commun. 2011, 29, 1732–1743. [Google Scholar] [CrossRef]
- Singh, K.; Ku, M.; Lin, J. Joint power control and energy transfer for energy harvesting relay networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Singh, K.; Ku, M.; Lin, J.; Ratnarajah, T. Toward optimal power control and transfer for energy harvesting amplify-and-forward relay networks. IEEE Trans. Wirel. Commun. 2018, 17, 4971–4986. [Google Scholar] [CrossRef]
- Gurakan, B.; Ozel, O.; Yang, J.; Ulukus, S. Energy cooperation in energy harvesting communications. IEEE Trans. Commun. 2013, 61, 4884–4898. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R.; Cui, S. Throughput maximization for the gaussian relay channel with energy harvesting constraints. IEEE J. Sel. Areas Commun. 2013, 31, 1469–1479. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, J.; Letaief, K.B. Optimal scheduling and power allocation for two-hop energy harvesting communication systems. IEEE Trans. Wirel. Commun. 2013, 12, 4729–4741. [Google Scholar] [CrossRef]
- Minasian, A.; ShahbazPanahi, S.; Adve, R.S. Energy harvesting cooperative communication systems. IEEE Trans. Wirel. Commun. 2014, 13, 6118–6131. [Google Scholar] [CrossRef]
- Ding, Z.; Perlaza, S.M.; Esnaola, I.; Poor, H.V. Power allocation strategies in energy harvesting wireless cooperative networks. IEEE Trans. Wirel. Commun. 2014, 13, 846–860. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Jiang, Y.; Ma, Y.; Vucetic, B. Distributed power splitting for SWIPT in relay interference channels using game theory. IEEE Trans. Wirel. Commun. 2015, 14, 410–420. [Google Scholar] [CrossRef]
- Huang, K.; Lau, V.K.N. Enabling wireless power transfer in cellular networks: Architecture modeling and deployment. IEEE Trans. Wirel. Commun. 2014, 13, 902–912. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting information and energy simultaneously. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1612–1616. [Google Scholar]
- Grover, P.; Sahai, A. Shannon meets Tesla: Wireless information and power transfer. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 2363–2367. [Google Scholar]
- Zhang, R.; Ho, C.K. MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Singh, K.; Gupta, A.; Ratnarajah, T. Energy efficient resource allocation for multiuser relay networks. IEEE Trans. Wirel. Commun. 2017, 16, 1218–1235. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Visser, H.J.; Vullers, R.J.M. RF energy harvesting and transport for wireless sensor network applications: Principles and requirements. Proc. IEEE 2013, 101, 1410–1423. [Google Scholar] [CrossRef]
- Percy, S.; Knight, C.; Cooray, F.; Smart, K. Supplying the power requirements to a sensor network using radio frequency power transfer. Sensors 2012, 12, 18571–18585. [Google Scholar] [CrossRef] [PubMed]
- Naderi, M.Y.; Chowdhury, K.R.; Basagni, S. Experimental study of concurrent data and wireless energy transfer for sensor networks. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2543–2549. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, R.; Singh, K.; Biswas, S.; Kumar, A. Multi-User AF Relay Networks with Power Allocation and Transfer: A Joint Approach. Energies 2019, 12, 3157. https://doi.org/10.3390/en12163157
Yadav R, Singh K, Biswas S, Kumar A. Multi-User AF Relay Networks with Power Allocation and Transfer: A Joint Approach. Energies. 2019; 12(16):3157. https://doi.org/10.3390/en12163157
Chicago/Turabian StyleYadav, Ramnaresh, Keshav Singh, Sudip Biswas, and Ashwani Kumar. 2019. "Multi-User AF Relay Networks with Power Allocation and Transfer: A Joint Approach" Energies 12, no. 16: 3157. https://doi.org/10.3390/en12163157
APA StyleYadav, R., Singh, K., Biswas, S., & Kumar, A. (2019). Multi-User AF Relay Networks with Power Allocation and Transfer: A Joint Approach. Energies, 12(16), 3157. https://doi.org/10.3390/en12163157



