A Regional Economy-Energy-Transport Model of the EU for Assessing Decarbonization in Transport
Abstract
1. Introduction
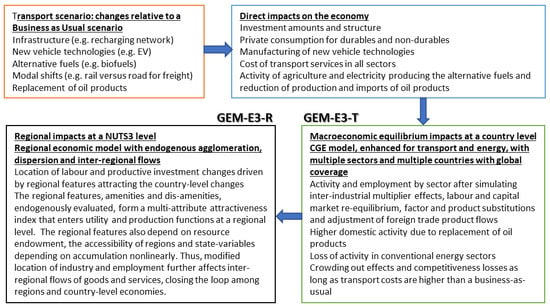
2. Spatial General Equilibrium Modelling
2.1. Literature Survey
2.2. Overview of the GEM-E3-R Model
2.2.1. The Country-Wide Economic Equilibrium Model
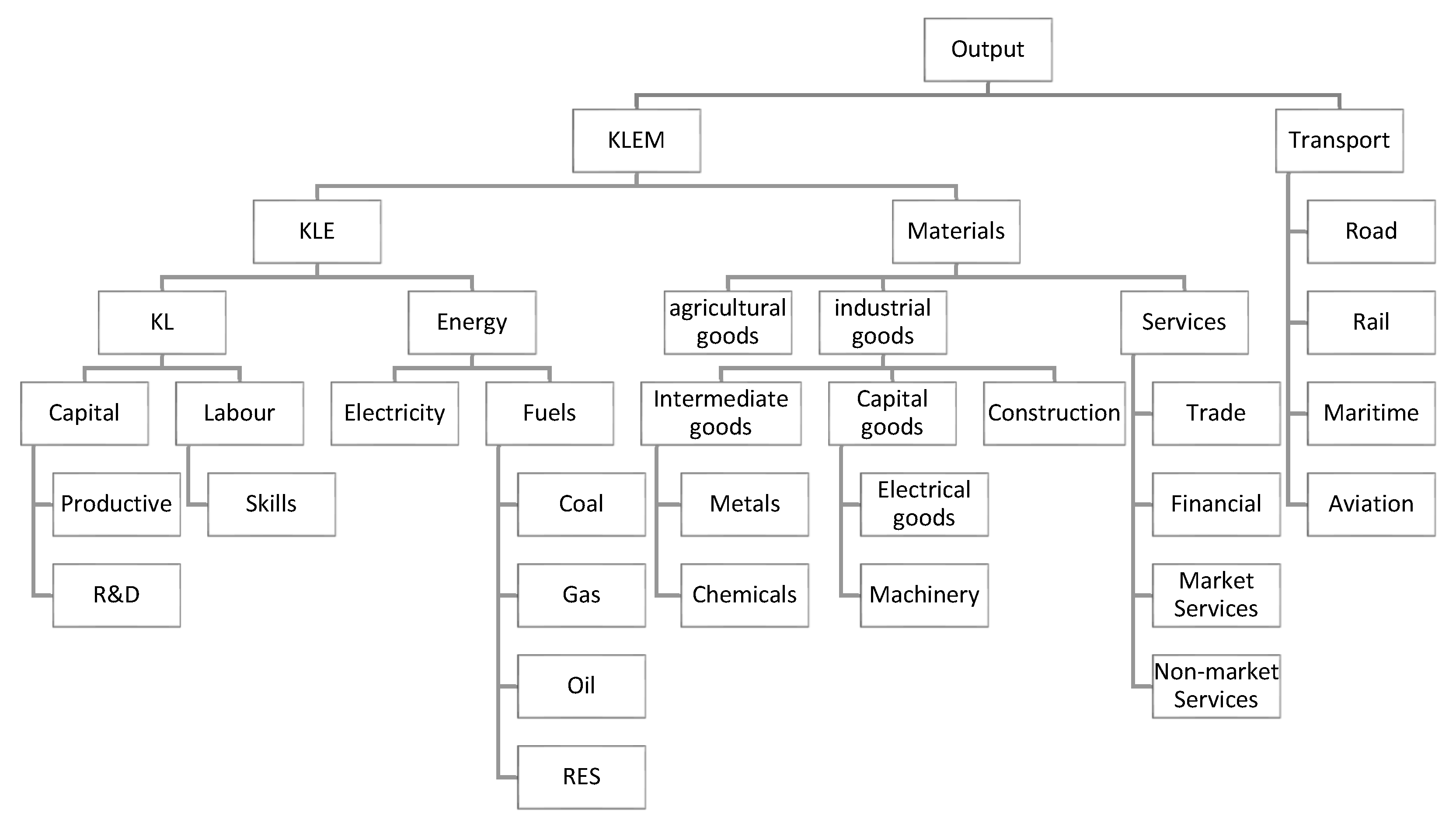
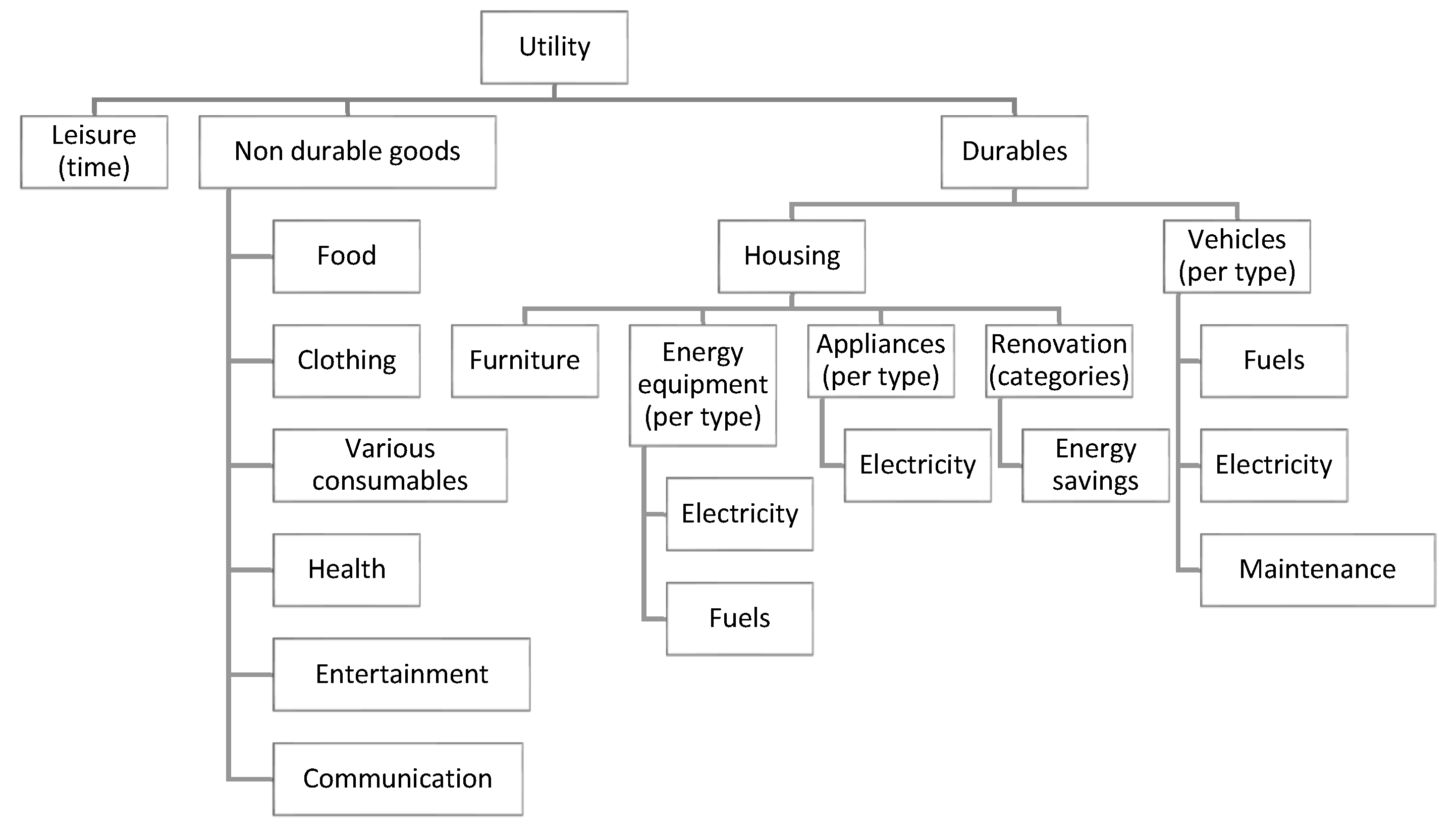
2.2.2. Overview of Functional Forms Used in the Model
2.2.3. The Regional Economic Equilibrium Model
- The human capital availability which is approximated by skilled labour;
- Physical capital availability;
- Capital profitability which is approximated by the ratio of the investment cost to the rental price of capital;
- Natural resources (the model maps the resource-based activities to the location of the natural resources);
- Vertical integration which simulates the incentive of certain industries to form clusters;
- The market size, which is often mentioned as the home market effect in the New Trade theory.
- At the first stage, imports are differentiated by country of origin (i.e., intra-national imports versus international imports);
- At the second stage, the consumption of imported goods is further disaggregated into consumption by region of origin.
3. Model Application
3.1. Base Case Scenario
3.2. Policy Scenario for the Transport Sector
3.3. Results of the Country-Wide Economic Equilibrium Model
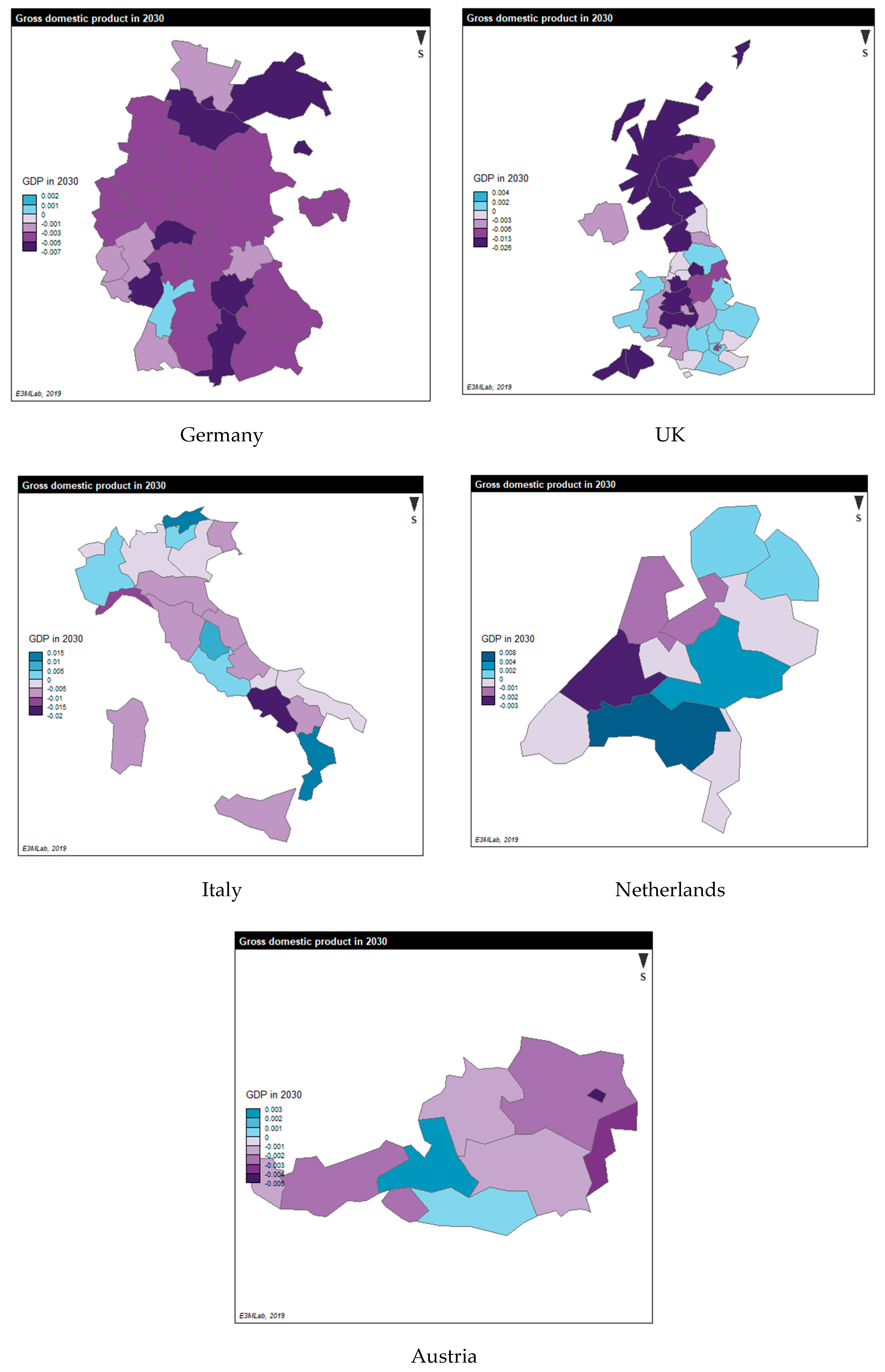
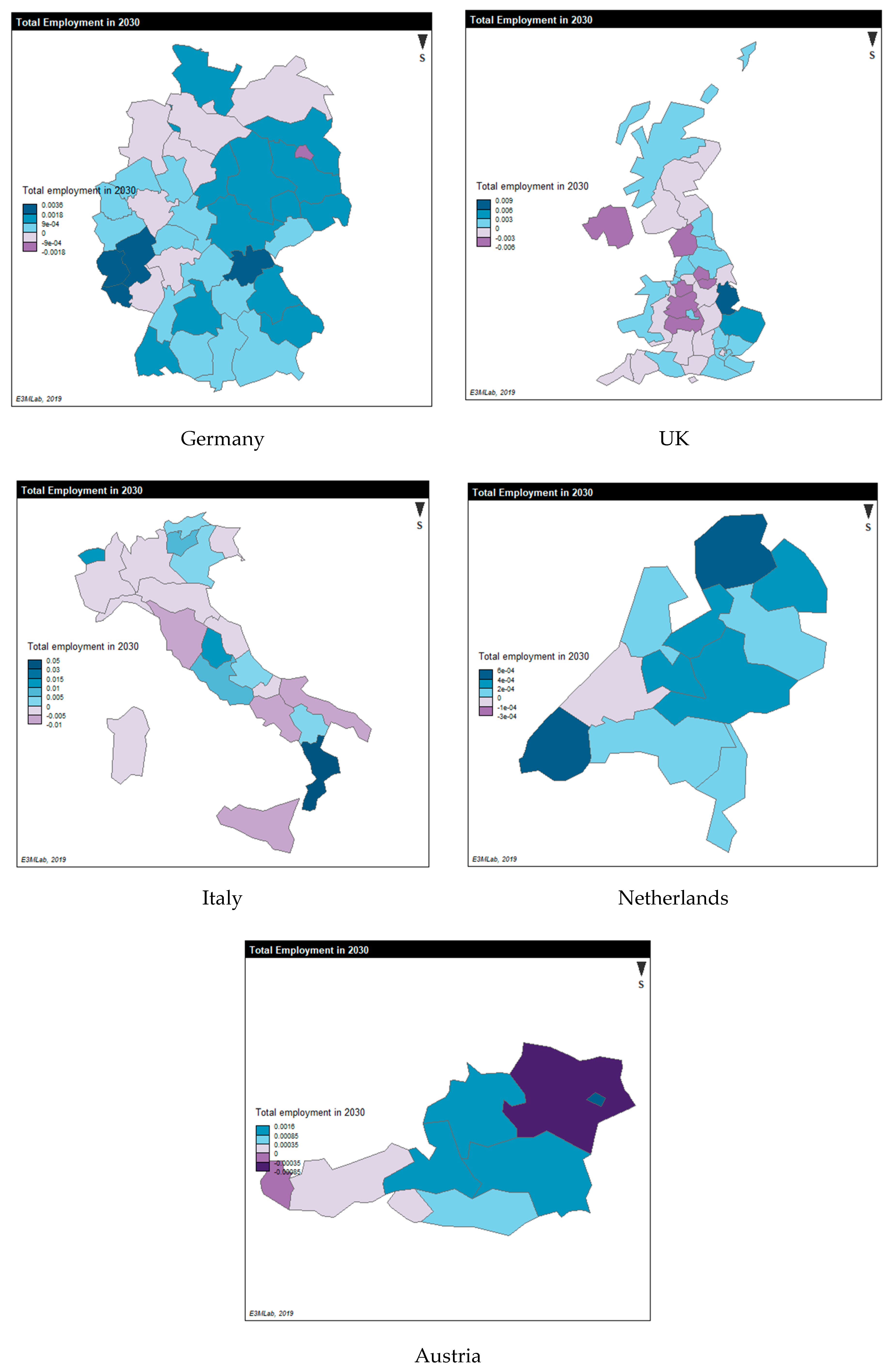
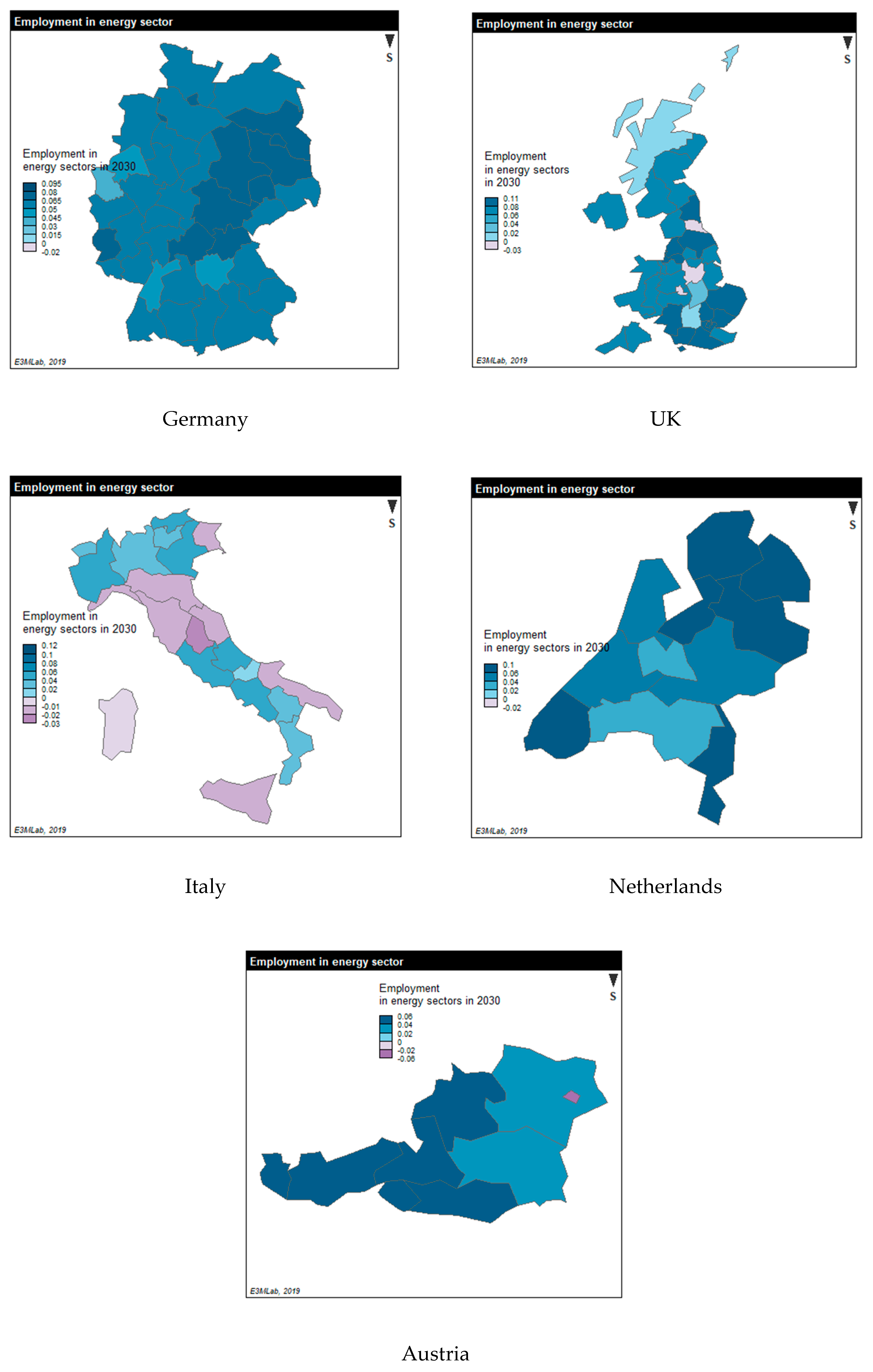
3.4. Results of the Regional Economic Equilibrium Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- European Environmental Agency. Greenhouse gas emissions from transport. Available online: https://www.eea.europa.eu/data-and-maps/indicators/transport-emissions-of-greenhouse-gases/transport-emissions-of-greenhouse-gases-11 (accessed on 15 May 2019).
- European Commission, EU Science Hub. Available online: https://ec.europa.eu/jrc/en/research-topic/transport-sector-economic-analysis (accessed on 15 May 2019).
- White Paper 2011—Roadmap to a Single European Transport Area; European Commission: Brussels, Belgium, 2011; Available online: https://ec.europa.eu/transport/themes/strategies/2011_white_paper_en (accessed on 15 June 2019).
- European Commission. Clean Planet for All a European Long-Term Strategic Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy, In-Depth Analysis in Support of the Commission Communication; COM/2018/773 A; European Commission: Brussels, Belgium, 2018. [Google Scholar]
- Capros, P.; Siskos, P. PRIMES-TREMOVE Transport Model. Available online: https://ec.europa.eu/clima/sites/clima/files/strategies/analysis/models/docs/primes_tremove_en.pdf (accessed on 15 May 2019).
- Bröcker, J.; Mercenier, J. General equilibrium models for transportation economics. In A Handbook of Transport Economics; Palma, D.A., Lindsey, R., Quinet, E., Vickerman, R., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2011; pp. 21–45. [Google Scholar] [CrossRef]
- Robson, E.N.; Wijayaratna, K.P.; Dixit, V.V. A review of computable general equilibrium models for transport and their applications in appraisal. Transp. Res. Part A Policy Pract. 2018, 116, 31–53. [Google Scholar] [CrossRef]
- Rietveld, P. Spatial economic impacts of transport infrastructure supply. Transp. Res. Part A Policy Pract. 1994, 28, 329–341. [Google Scholar] [CrossRef]
- Oosterhaven, J.; Knaap, T. Spatial Economic Impacts of Transport Infrastructure Investments. In Transport Projects, Programmes and Policies; Nellthorp, J., Mackie, P., Pearman, A., Eds.; Routledge: Abingdon, UK, 2003. [Google Scholar] [CrossRef]
- Donaldson, D. Railroads of the Raj: Estimating the Impact of Transportation Infrastructure. Am. Econ. Rev. 2018, 108, 899–934. [Google Scholar] [CrossRef]
- Redding, S.J.; Matthew, A.T. Transportation costs and the spatial organization of economic activity. In Handbook of Regional and Urban Economics; Duranton, G., Henderson, J.V., Strange, W.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 5, pp. 1339–1398. [Google Scholar] [CrossRef]
- Partridge, M.D.; Rickman, D.S. Regional Computable General Equilibrium Modeling: A Survey and Critical Appraisal. Int. Reg. Sci. Rev. 1998, 21, 205–248. [Google Scholar] [CrossRef]
- Bradley, J.; Gács, J.; Kangur, A.; Lubenets, N. HERMIN: A macro model framework for the study of cohesion and transition. In Integration, Growth and Cohesion in an Enlarged European Union; Bradley, J., Petrakos, G., Traistaru, I., Eds.; Springer: New York, NY, USA, 2007; pp. 207–242. [Google Scholar]
- Ivanova, O.; Heyndrickx, C.; Spitaels, K.; Tavasszy, L.; Manshanden, W.; Snelder, M.; Koops, O. RAEM: Version 3.0; Final Report; Transport & Mobility: Leuven, Belgium, 2007; p. 77. [Google Scholar]
- Donaghy, K. CGE Modelling in space. In Handbook of Regional Growth and Development Theories; Capello, R., Nijkamp, P., Eds.; Edward Elgar: Cheltenham, London, UK, 2009; pp. 389–422. [Google Scholar]
- Ivanova, O.; Kancs, D. Rhomolo: A Dynamic General Equilibrium Modelling Approach to the Evaluation of the EU’s Regional Policies. In EERI Research Paper Series 2010/28; Economics and Econometrics Research Institute (EERI): Brussels, Belgium, 2010. [Google Scholar]
- Varga, A.; Jarosi, P.; Sebestuen, T. Modelling the economic impacts of regional R&D subsidies: The GMR-Europe model and its application for EU Framework Program policy impact simulations. In Proceedings of the 6th Regional Innovation Policy Seminar, Circle, Lund, Sweden, 13–14 October 2011. [Google Scholar]
- Di Comite, F.; Kancs, D. Modelling of Agglomeration and Dispersion in RHOMOLO; No. JRC81349; Joint Research Centre (Seville Site): Sevilla, Spain, 2014. [Google Scholar]
- Brandsma, A.; Kancs, D.; Monfort, P.; Rillaers, A. RHOMOLO: A dynamic spatial general equilibrium model for assessing the impact of cohesion policy. Pap. Reg. Sci. 2015, 94, 197–221. [Google Scholar] [CrossRef]
- Giesecke, J.A.; Madden, J.R. Regional Computable General Equilibrium Modeling. In Handbook of Computable General Equilibrium Modeling; Dixon, P.B., Jorgenson, D.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 379–475. [Google Scholar] [CrossRef]
- Partridge, M.D.; Rickman, D.S. Computable General Equilibrium (CGE) Modelling for Regional Economic Development Analysis. Reg. Stud. 2010, 44, 1311–1328. [Google Scholar] [CrossRef]
- Tavasszy, L.A.; Thissen, M.J.P.M.; Oosterhaven, J. Challenges in the application of spatial computable general equilibrium models for transport appraisal. Res. Transp. Econ. 2011, 31, 12–18. [Google Scholar] [CrossRef]
- Leontief, W.; Morgan, A.; Polenske, K.; Simpson, D.; Tower, E. The Economic Impact--Industrial and Regional—Of an Arms Cut. Rev. Econ. Stat. 1965, 47, 217–241. [Google Scholar] [CrossRef]
- Dixon, P.B.; Parmenter, B.R.; Sutton, J. Spatial Disaggregation of Orani Results: A Preliminary Analysis of the Impact of Protection at the State Level. Econ. Anal. Policy 1978, 8, 35–86. [Google Scholar] [CrossRef]
- Dixon, P.B.; Rimmer, M.T.; Tsigas, M.E. Regionalising results from a detailed CGE model: Macro, industry and state effects in the U.S. of removing major tariffs and quotas. Pap. Reg. Sci. 2007, 86, 31–55. [Google Scholar] [CrossRef]
- Horridge, M.; Madden, J.; Wittwer, G. The impact of the 2002–2003 drought on Australia. J. Policy Modeling 2005, 27, 285–308. [Google Scholar] [CrossRef]
- Muth, R. Migration: Chicken or Egg? South. Econ. J. 1971, 37, 295–306. [Google Scholar] [CrossRef]
- Polinsky, M.A.; Shavell, S. Amenities and property values in a model of an urban area. J. Public Econ. 1976, 5, 119–129. [Google Scholar] [CrossRef]
- Rosen, S. Wage-based indexes of urban quality of life. In Current Issues in Urban Economics; Mieszkowski, P., Straszheim, M., Eds.; Johns Hopkins University Press: Baltimore, MD, USA, 1979; pp. 74–104. [Google Scholar]
- Greenwood, M.J. Research on Internal Migration in the United States: A Survey. J. Econ. Lit. 1975, 13, 397–433. [Google Scholar]
- Greenwood, M.J.; Hunt, G.L. Econometrically accounting for identities and restrictions in models of interregional migration. Reg. Sci. Urban Econ. 1984, 14, 113–128. [Google Scholar] [CrossRef]
- Graves, P.E.; Mueser, P.R. The role of equilibrium and disequilibrium in modelling regional growth and decline: A critical reassessment. J. Reg. Sci. 1993, 33, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Partridge, M.D.; Rickman, D.S.; Ali, K.; Olfert, M.R. The geographic diversity of U.S. nonmetropolitan growth dynamics: A geographically weighted regression approach. Land Econ. 2008, 84, 241–266. [Google Scholar] [CrossRef]
- Roback, J. Wages, rents, and the quality of life. J. Political Econ. 1982, 90, 1257–1278. [Google Scholar] [CrossRef]
- Roback, J. Wages, rents, and amenities—Differences among workers and regions. Econ. Inq. 1988, 26, 23–41. [Google Scholar] [CrossRef]
- Redding, J.S.; Rossi-Hansberg, E. Quantitative Spatial Economics. Annu. Rev. Econ. 2016, 9, 21–58. [Google Scholar] [CrossRef]
- Monte, F.; Redding, J.S.; Rossi-Hansberg, E. Commuting, migration, and local employment elasticities. Am. Econ. Rev. 2018, 108, 3855–3890. [Google Scholar] [CrossRef]
- Brueckner, J.K.; Thisse, J.-F.; Zenou, Y. Why is central Paris rich and downtown Detroit poor? An amenity-based theory. Eur. Econ. Rev. 1999, 43, 91–107. [Google Scholar] [CrossRef]
- Judson, D.H.; Reynolds-Scanlon, S.; Popoff, C.L. Migrants to Oregon in the 1990’s: Working age, near-retirees, and retirees make different destination choices. Rural Dev. Perspect. 1999, 14, 24–31. [Google Scholar]
- Beyers, W.B.; Lindahl, D.P. Lone eagles and high fliers in rural producer services. Rural Dev. Perspect. 1996, 11, 2–10. [Google Scholar]
- Johnson, J.D.; Rasker, R. Local government: Local business climate and quality of life. Mont. Policy Rev. 1993, 3, 11–19. [Google Scholar]
- Clark, D.E.; Hunter, W.J. The impact of economic opportunity, amenities and fiscal factors on age-specific migration rates. J. Reg. Sci. 1992, 32, 349–365. [Google Scholar] [CrossRef]
- Poudyal, N.C.; Hodges, D.G.; Cordell, H.K. The role of natural resource amenities in attracting retirees: Implications for economic growth policy. Ecol. Econ. 2008, 68, 240–248. [Google Scholar] [CrossRef]
- McGregor, P.G.; Swales, J.K.; Yin, Y.P. A long-run interpretation of regional input-output analysis. J. Reg. Sci. 1996, 36, 479–501. [Google Scholar] [CrossRef]
- Kim, E.; Kim, K. Impacts of the development of large cities on economic growth and income distribution in Korea: A multiregional CGE model. Pap. Reg. Sci. 2003, 82, 101–122. [Google Scholar] [CrossRef]
- Bröcker, J.; Korzhenevych, A. Forward looking dynamics in spatial CGE modelling. Econ. Model. 2013, 31, 389–400. [Google Scholar] [CrossRef]
- Capros, P.; Van Regemorter, D.; Paroussos, L.; Karkatsoulis, P.; Fragkiadakis, C.; Tsani, S.; Charalampidis, I.; Revesz, T. GEM-E3 Model Documentation; JRC Working Papers JRC83177 2013; Joint Research Centre (Seville Site): Sevilla, Spain, 2013. [Google Scholar] [CrossRef]
- Karkatsoulis, P.; Siskos, P.; Paroussos, L.; Capros, P. Simulating deep CO2 emission reduction in transport in a general equilibrium framework: The GEM-E3T model. Transp. Res. Part D Transp. Environ. 2017, 55, 343–358. [Google Scholar] [CrossRef]
- Fragkos, P.; Tasios, N.; Paroussos, L.; Capros, P.; Tsani, S. Energy system impacts and policy implications of the European Intended Nationally Determined Contribution and low-carbon pathway to 2050. Energy Policy 2017, 100, 216–226. [Google Scholar] [CrossRef]
- Capros, P.; Paroussos, L.; Charalampidis, I.; Fragkiadakis, K.; Karkatsoulis, P.; Tsani, S. Assessment of the macroeconomic and sectoral effects of higher electricity and gas prices in the EU: A general equilibrium modeling approach. Energy Strategy Rev. 2016, 9, 18–27. [Google Scholar] [CrossRef]
- Karkatsoulis, P.; Capros, P.; Fragkos, P.; Paroussos, L.; Tsani, S. First-mover advantages of the European Union’s climate change mitigation strategy. Int. J. Energy Res. 2016, 40, 814–830. [Google Scholar] [CrossRef]
- Shahrokhi Shahraki, H.; Bachmann, C. Designing computable general equilibrium models for transportation applications. Transp. Rev. 2018, 1–28. [Google Scholar] [CrossRef]
- Blanchflower, D.G.; Oswald, A.J. The Wage Curve; The MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Armington, P. A Theory of Demand for Products Distinguished by Place of Production. Staff Pap. Int. Monet. Fund 1969, 16, 159–178. [Google Scholar] [CrossRef]
- Booth, D.E. Spatial patterns in the economic development of the Mountain West. Growth Chang. 1999, 30, 384–405. [Google Scholar] [CrossRef]
- Geurs, K.T. Transport Planning with Accessibility Indices in The Netherlands; Discussion Paper; International Transport Forum: Paris, France, 2018. [Google Scholar]
- Davis, D.R.; Dingel, J.I. The Comparative Advantage of Cities; Working Paper Series; National Bureau of Economic Research: Cambridge, MA, USA, 2014. [Google Scholar] [CrossRef]
- Gaubert, C. Firm Sorting and Agglomeration. National Bureau of Economic Research 2018; Working Paper Series; NBER, 1050 Massachusetts Ave.: Cambridge, MA, USA, 2018. [Google Scholar] [CrossRef]
- Redding, J.S. Estimating Neighborhood Effects: Evidence from War-Time Destruction in London. Available online: https://www.semanticscholar.org/paper/Estimating-Neighborhood-Effects-%3A-Evidence-from-in-Redding/30ac196f987a47e087697bc2e2daba43ab73a95b (accessed on 12 July 2019).
- Nesticò, A.; Sica, F. The sustainability of urban renewal projects: A model for economic multi-criteria analysis. J. Prop. Invest. Financ. 2017, 35, 397–409. [Google Scholar] [CrossRef]
- Dixit, A.K.; Stiglitz, J.E. Monopolistic Competition and Optimum Product Diversity. Am. Economic Review 1977, 67, 297–308. [Google Scholar]
- The 2018 Ageing Report: Underlying Assumptions and Projection Methodologies; European Commission: Brussels, Belgium, 2017.
- European Commission. Eurostat. Regional Statistics Database. Available online: https://ec.europa.eu/eurostat/web/regions/data/database (accessed on 15 May 2019).

| Number | Country/Region | Number | Country/Region |
|---|---|---|---|
| 1 | Austria | 26 | Sweden |
| 2 | Belgium | 27 | Romania |
| 3 | Bulgaria | 28 | Switzerland |
| 4 | Cyprus | 29 | Norway |
| 5 | Czech Republic | 30 | Albania |
| 6 | Croatia | 31 | North Macedonia |
| 7 | Germany | 32 | Serbia |
| 8 | Denmark | 33 | Bosnia and Herzegovina |
| 9 | Spain | 34 | Montenegro |
| 10 | Estonia | 35 | Turkey |
| 11 | Finland | 36 | Russia and Caspian |
| 12 | France | 37 | Belarus |
| 13 | United Kingdom | 38 | Ukraine |
| 14 | Greece | 39 | Moldova |
| 15 | Hungary | 40 | North Africa |
| 16 | Ireland | 41 | Middle East and Persian Gulf |
| 17 | Italy | 42 | USA and Canada |
| 18 | Luxembourg | 43 | Japan and South Korea |
| 19 | Latvia | 44 | Oceania |
| 20 | Malta | 45 | China |
| 21 | Netherlands | 46 | India |
| 22 | Poland | 47 | Other Asian countries |
| 23 | Portugal | 48 | South and Central America |
| 24 | Slovakia | 49 | sub-Saharan Africa |
| 25 | Slovenia | 50 | Rest of the world |
| Number | Category | Number | Category |
|---|---|---|---|
| 1 | Agriculture (other than wheat, cereal grains, etc., and oil seeds) | 20 | Textile and leather products |
| 2 | Wheat, cereal grains, sugarcane, sugar beet | 21 | Mining and quarrying |
| 3 | Oil seeds | 22 | Other industries |
| 4 | Coal | 23 | Construction |
| 5 | Crude oil | 24 | Freight road transport |
| 6 | Oil refinery | 25 | Freight rail transport |
| 7 | Gas | 26 | Freight maritime transport |
| 8 | Electricity generation | 27 | Freight aviation |
| 9 | Electricity networks | 27 | Passengers rail transport |
| 10 | Ferrous metals | 28 | Passengers public road transport |
| 11 | Non-ferrous metals | 29 | Passengers maritime |
| 12 | Chemical products | 30 | Passengers aviation |
| 13 | Paper and pulp | 31 | Wholesale and retail trade; repair of motor vehicles and motorcycles |
| 14 | Non-metallic minerals | 32 | Accommodation and food service activities |
| 15 | Electric goods | 33 | Information and communication |
| 16 | Car manufacturing | 34 | Financial and insurance activities |
| 17 | Other transport equipment | 35 | Real estate activities |
| 18 | Other equipment goods and fabricated metals | 36 | Other market services |
| 19 | Food, beverages, and tobacco | 37 | Non-market services |
| Austria | Germany | UK | Italy | Netherlands | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Base Case | Scenario | Base Case | Base Case | Scenario | Scenario | Base Case | Scenario | Base Case | Scenario | ||
| Passenger Rail | Fuels | 9.4% | 7.0% | 7.2% | 5.4% | 27.5% | 20.6% | 7.2% | 5.4% | 6.9% | 5.2% |
| Electricity | 90.5% | 93.0% | 92.8% | 94.6% | 72.5% | 79.4% | 92.8% | 94.6% | 93.1% | 94.8% | |
| Public Road Transport | Fuels | 98.5% | 90.1% | 97.7% | 89.7% | 99.1% | 89.0% | 97.7% | 89.7% | 98.9% | 89.9% |
| Electricity | 1.5% | 9.9% | 2.3% | 10.3% | 0.9% | 11.0% | 2.3% | 10.3% | 1.1% | 10.1% | |
| Austria | Germany | UK | Italy | Netherlands | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base Case | Scenario | Base Case | Scenario | Base Case | Scenario | Base Case | Scenario | Base Case | Scenario | |
| Electric Vehicle | 1.0% | 21.0% | 3.2% | 19.2% | 0.038 | 23.8% | 0.8% | 20.8% | 2.6% | 22.6% |
| Plug-in Hybrid | 8.2% | 28.2% | 10.0% | 30.0% | 0.08 | 28.0% | 6.6% | 26.6% | 6.3% | 26.3% |
| Hybrid not plug-in | 18.9% | 38.9% | 30.2% | 46.2% | 0.252 | 45.2% | 15.2% | 35.2% | 21.1% | 41.1% |
| Internal Combustion Engine | 71.9% | 11.9% | 56.6% | 4.6% | 0.63 | 3.0% | 77.4% | 17.4% | 70.0% | 10.0% |
| Austria | Germany | UK | Italy | Netherlands | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base Case | Scenario | Base Case | Scenario | Base Case | Scenario | Base Case | Scenario | Base Case | Scenario | |
| 2025 | 8.5% | 13.5% | 7.0% | 12.0% | 5.1% | 8.1% | 5.1% | 10.1% | 5.0% | 10.0% |
| 2030 | 8.8% | 18.8% | 7.0% | 17.0% | 5.3% | 13.1% | 5.3% | 15.3% | 5.2% | 15.2% |
| Country | Variable | 2025 | 2030 | Variable | 2025 | 2030 |
|---|---|---|---|---|---|---|
| Austria | % change of GDP from the Base Case | −0.05% | −0.11% | % change of Private Consumption from the Base Case | 0.09% | 0.16% |
| Germany | 0.07% | 0.10% | 0.10% | 0.18% | ||
| UK | −0.07% | −0.10% | 0.02% | 0.05% | ||
| Italy | −0.06% | −0.11% | 0.00% | 0.01% | ||
| Netherlands | 0.04% | 0.05% | 0.05% | 0.10% | ||
| Austria | % change of Investment from the Base Case | −0.03% | −0.06% | % change of Employment from the Base Case | 0.02% | 0.04% |
| Germany | −0.06% | −0.09% | 0.03% | 0.06% | ||
| UK | −0.04% | −0.09% | 0.01% | 0.02% | ||
| Italy | −0.04% | −0.08% | −0.01% | −0.01% | ||
| Netherlands | 0.03% | 0.04% | 0.01% | 0.02% | ||
| Austria | % change of Exports from the Base Case | 0.25% | 0.21% | % change of Imports from the Base Case | 0.49% | 0.65% |
| Germany | 0.86% | 1.21% | 0.92% | 1.37% | ||
| UK | 0.34% | 0.46% | 0.54% | 0.80% | ||
| Italy | 0.38% | 0.53% | 0.59% | 0.93% | ||
| Netherlands | 0.18% | 0.22% | −0.06% | −0.16% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charalampidis, I.; Karkatsoulis, P.; Capros, P. A Regional Economy-Energy-Transport Model of the EU for Assessing Decarbonization in Transport. Energies 2019, 12, 3128. https://doi.org/10.3390/en12163128
Charalampidis I, Karkatsoulis P, Capros P. A Regional Economy-Energy-Transport Model of the EU for Assessing Decarbonization in Transport. Energies. 2019; 12(16):3128. https://doi.org/10.3390/en12163128
Chicago/Turabian StyleCharalampidis, Ioannis, Panagiotis Karkatsoulis, and Pantelis Capros. 2019. "A Regional Economy-Energy-Transport Model of the EU for Assessing Decarbonization in Transport" Energies 12, no. 16: 3128. https://doi.org/10.3390/en12163128
APA StyleCharalampidis, I., Karkatsoulis, P., & Capros, P. (2019). A Regional Economy-Energy-Transport Model of the EU for Assessing Decarbonization in Transport. Energies, 12(16), 3128. https://doi.org/10.3390/en12163128