Modeling and Stability Analysis of Model Predictive Control Dual Active Bridge Converter
Abstract
:1. Introduction
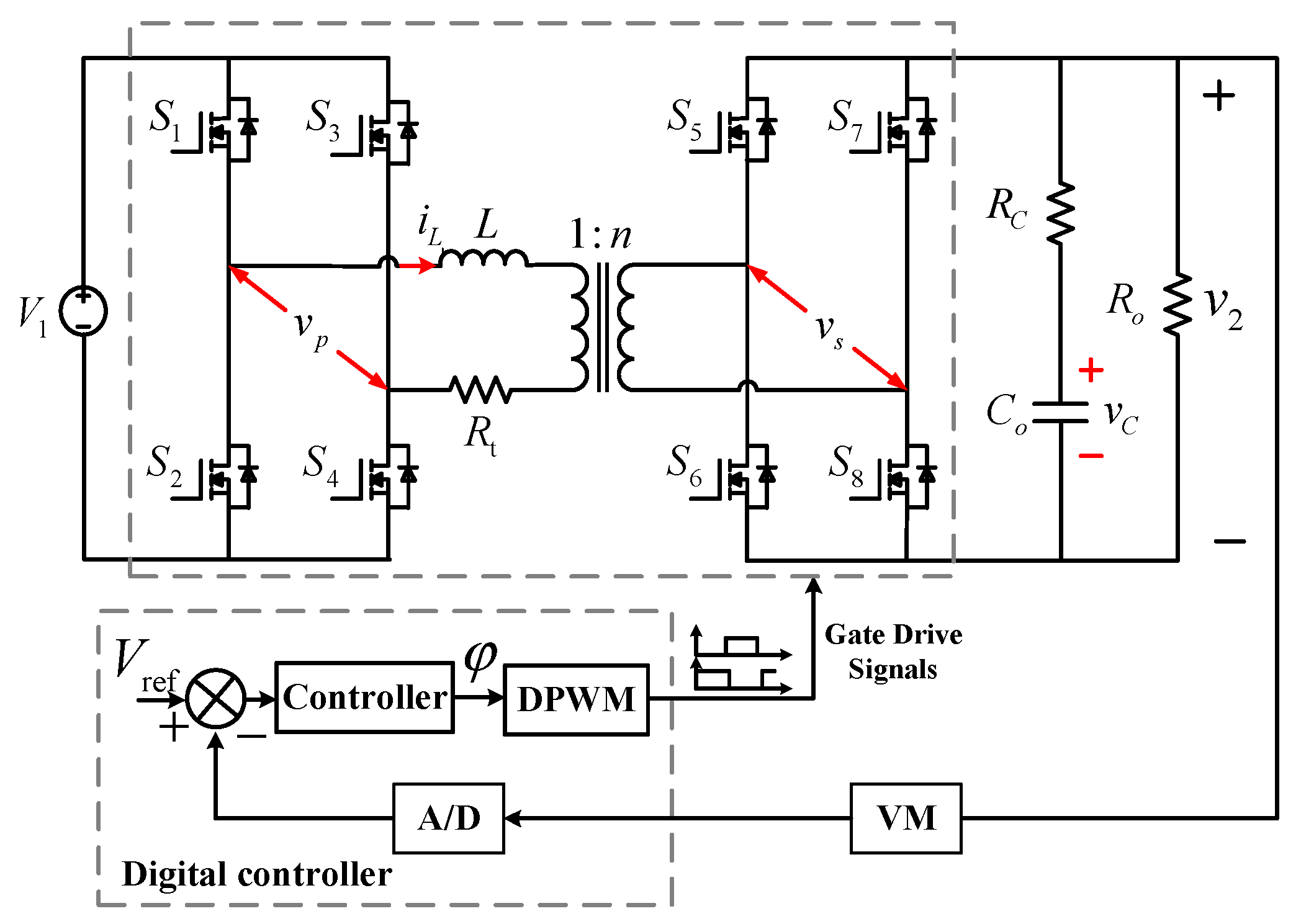
2. System Description
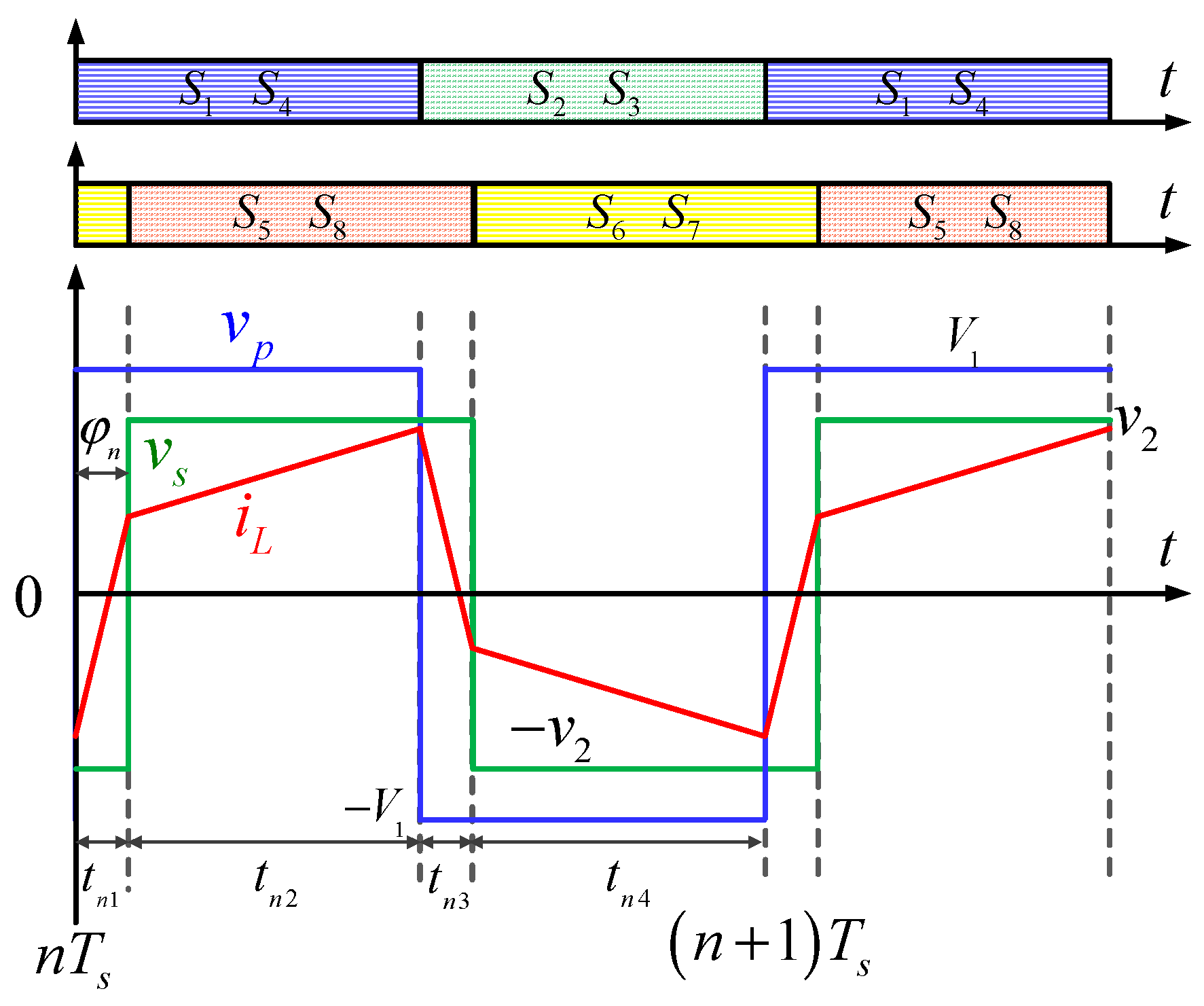
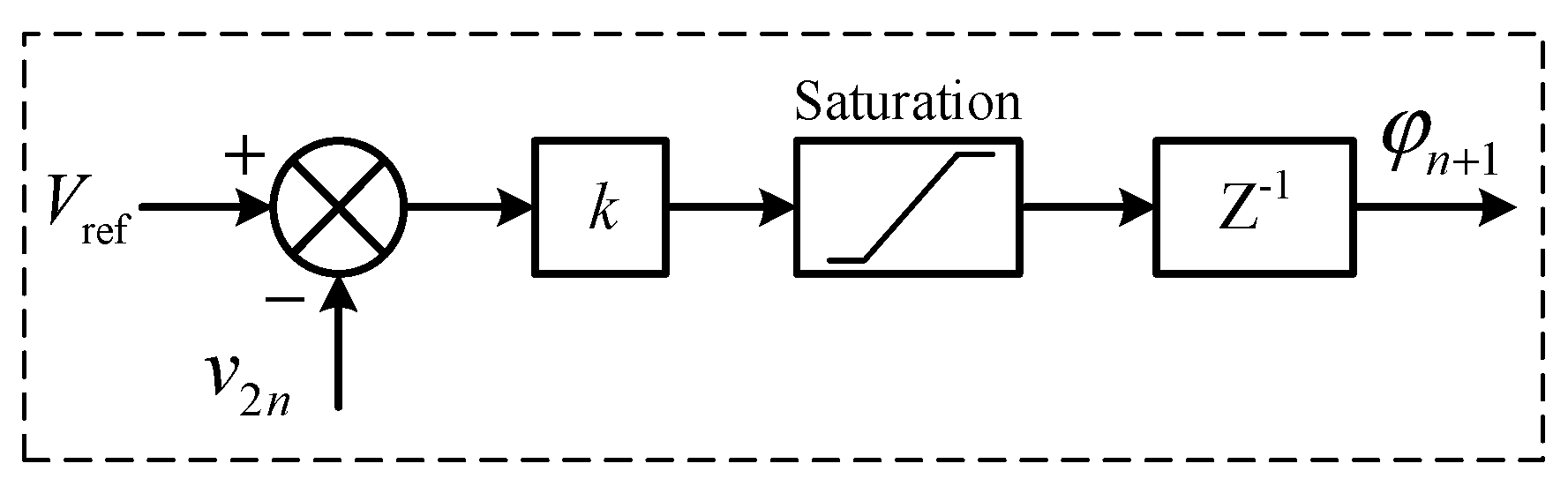
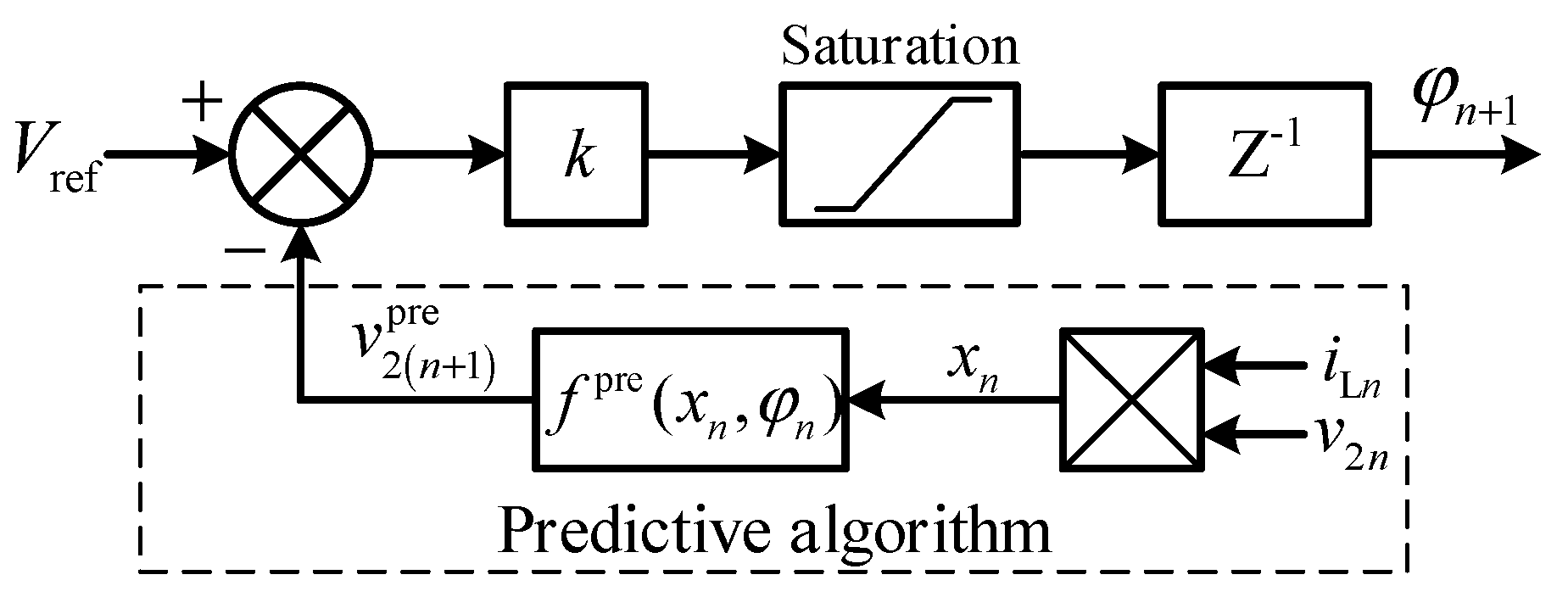
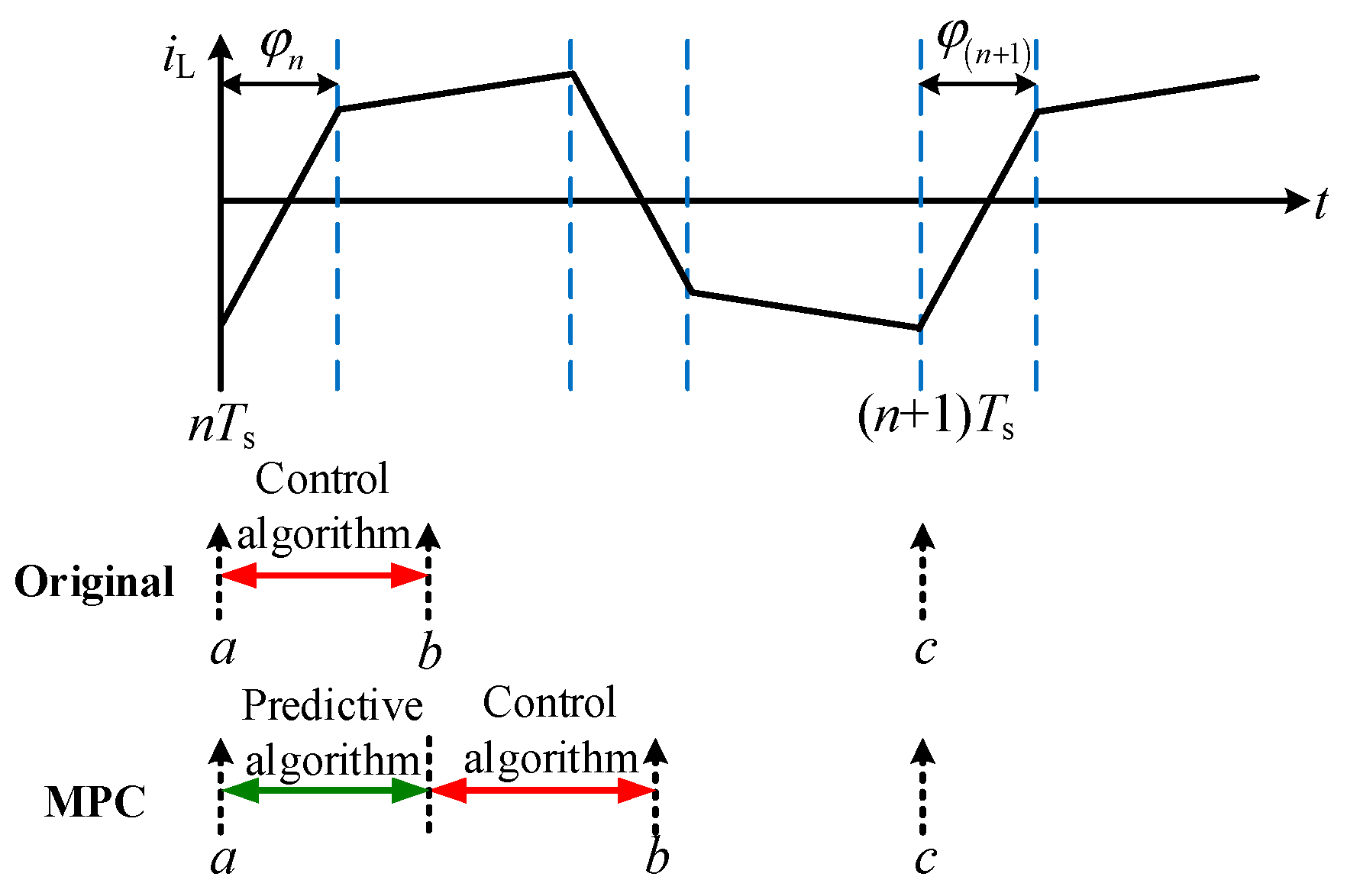
3. Model Predictive Control and Modeling
4. Stability Analysis of the MPC DAB Converter
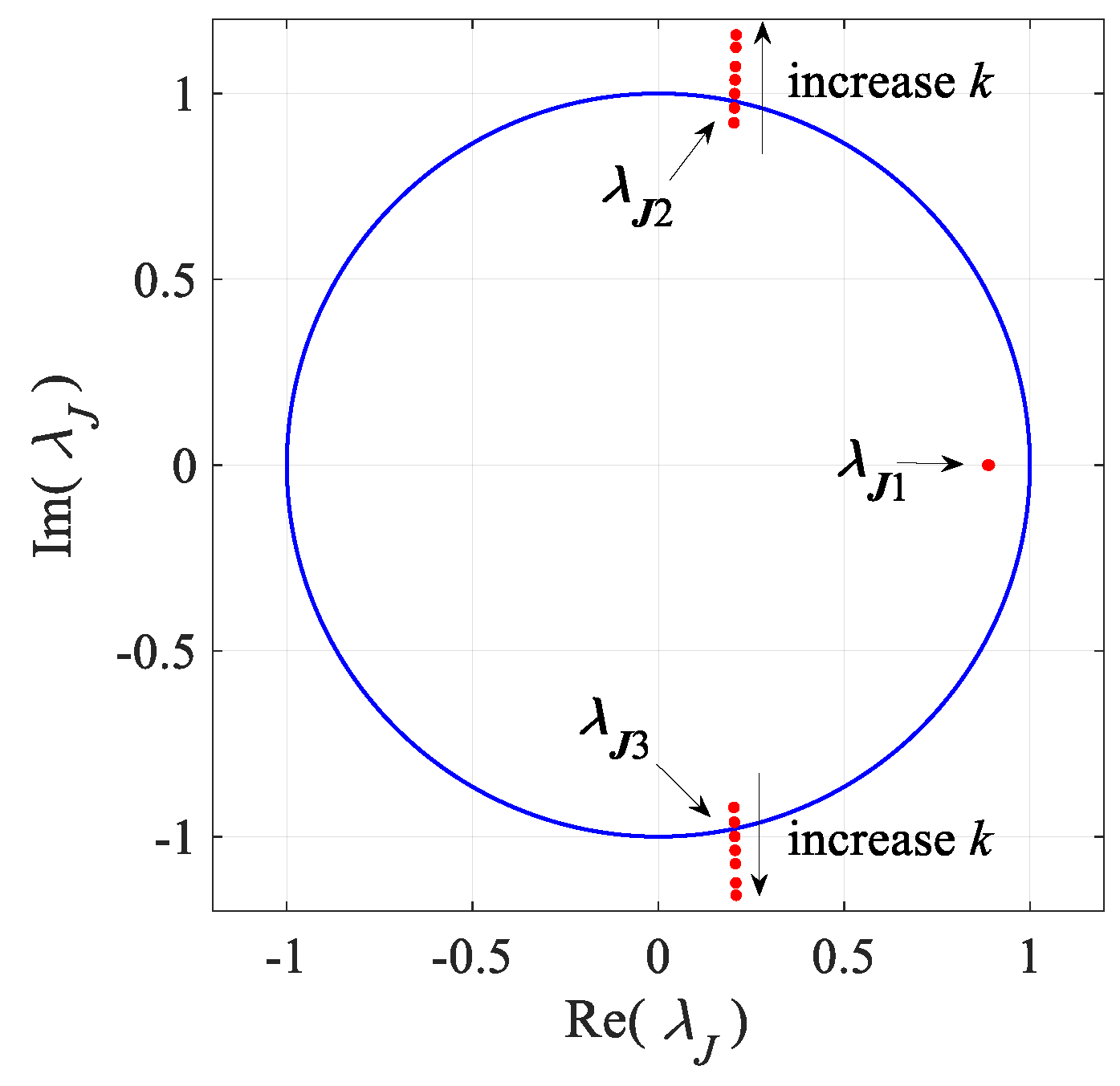
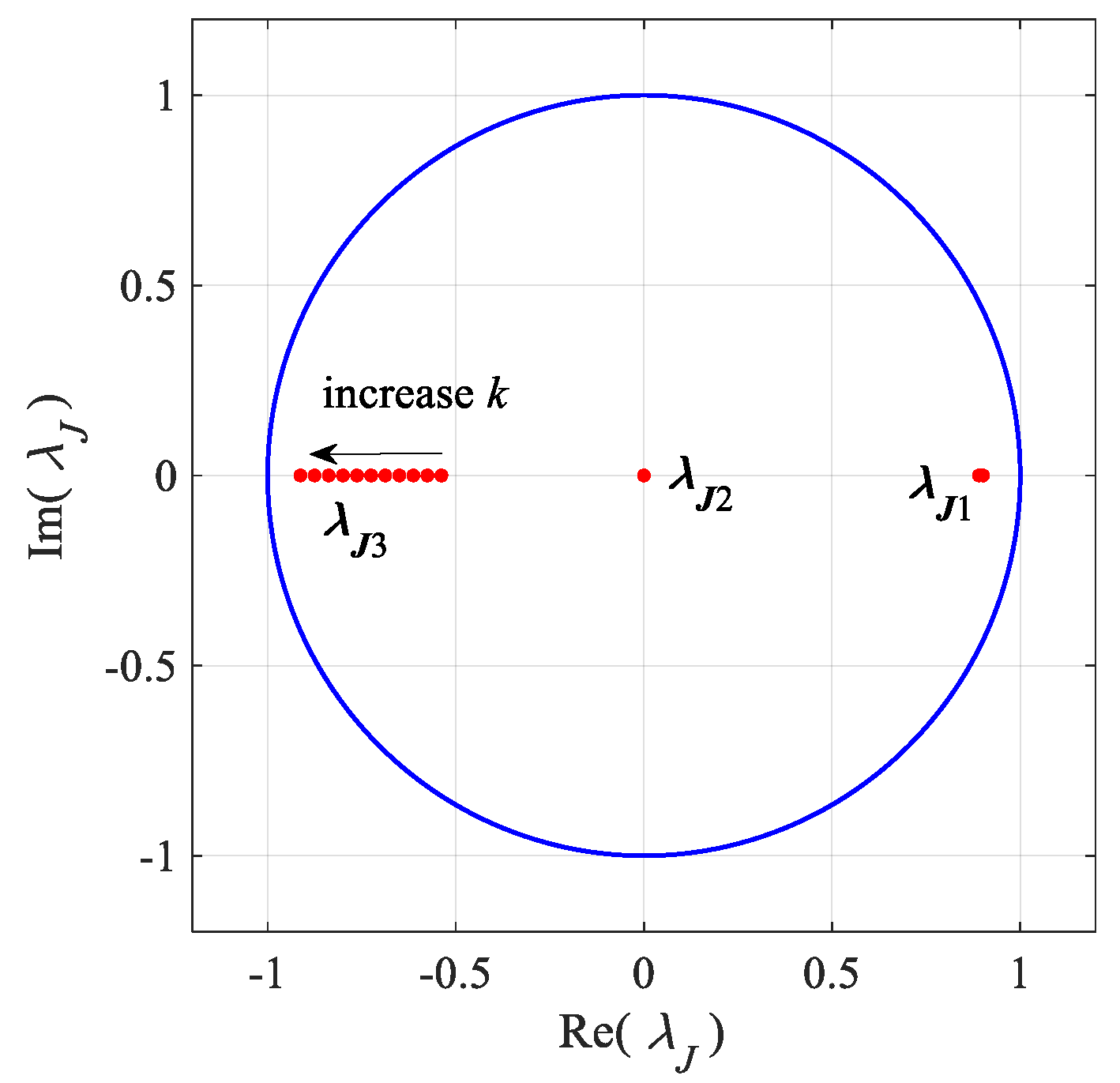
4.1. Calculation of Jacobian Matrix and Floquet Multipliers
4.2. Stability Analysis via the Floquet Multipliers
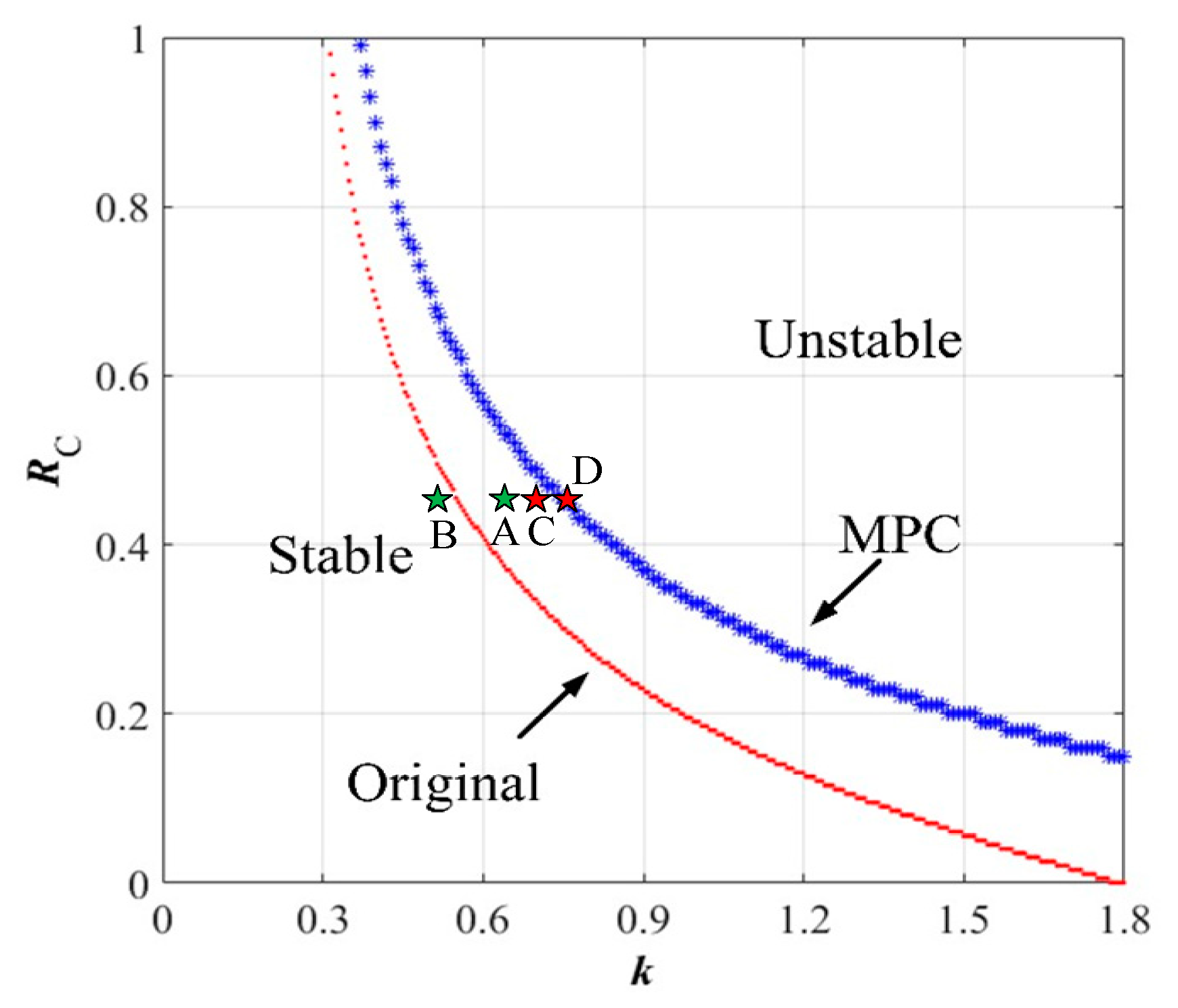
4.3. Stability Boundaries of the System
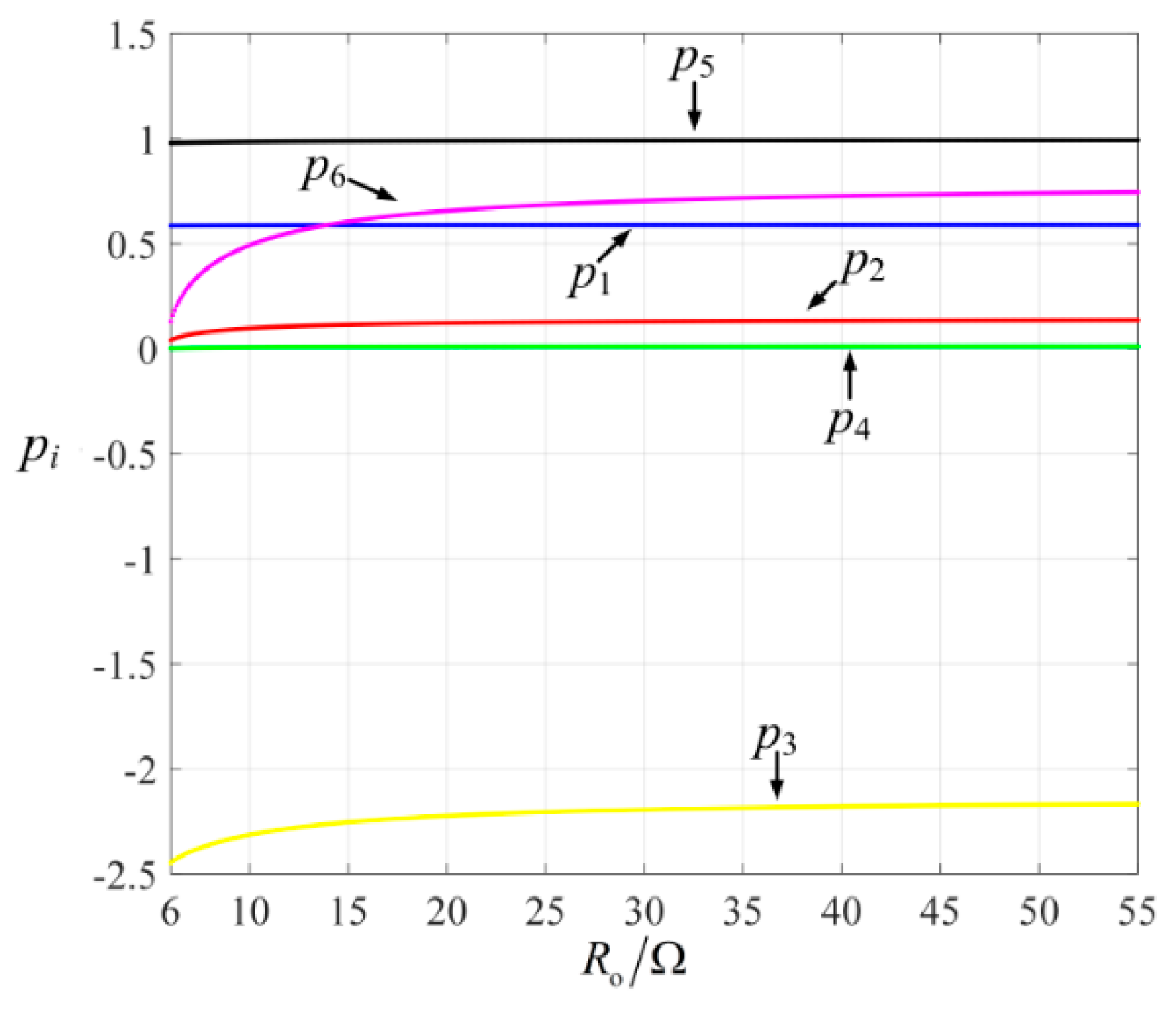
4.4. Sensitivity Analysis
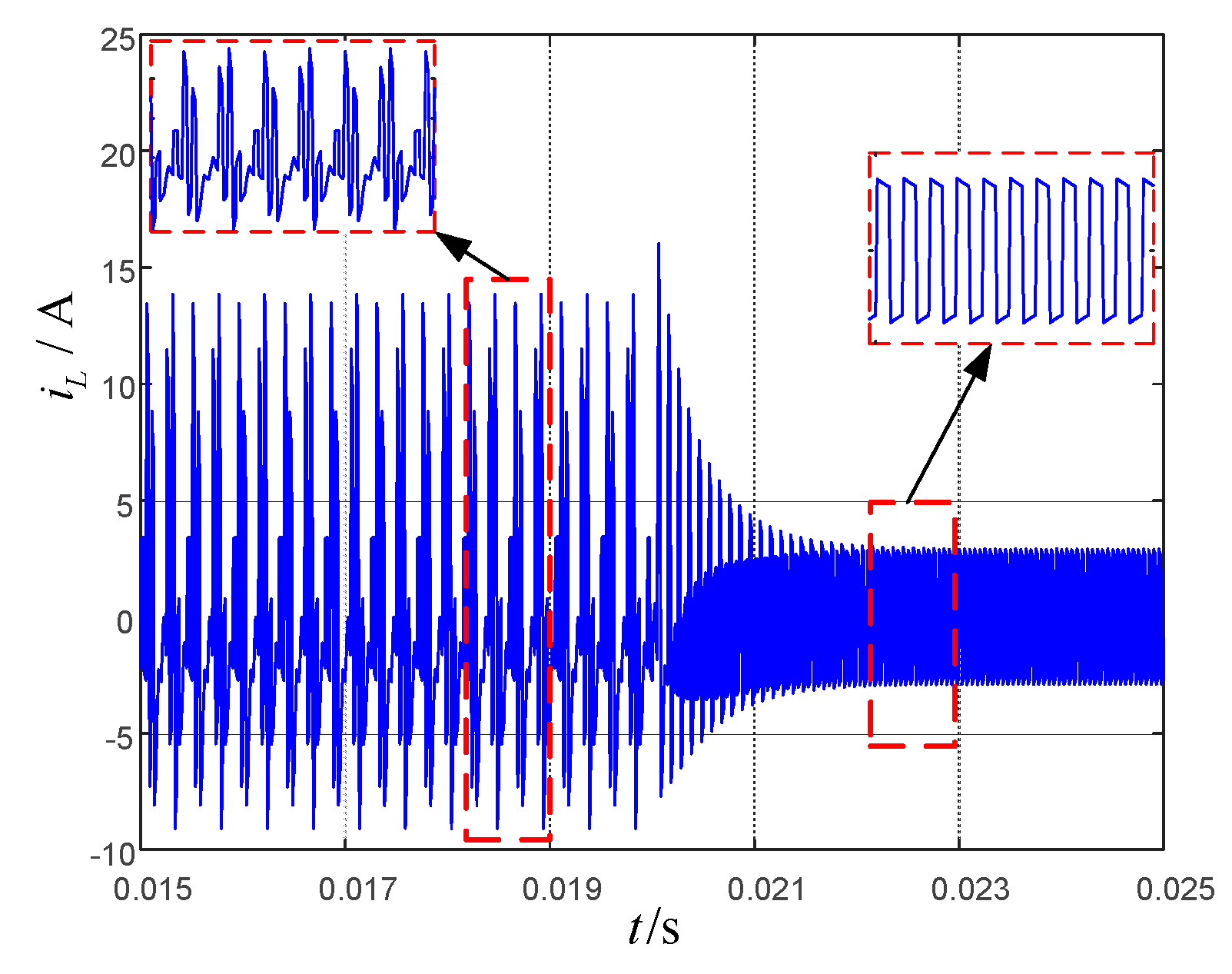
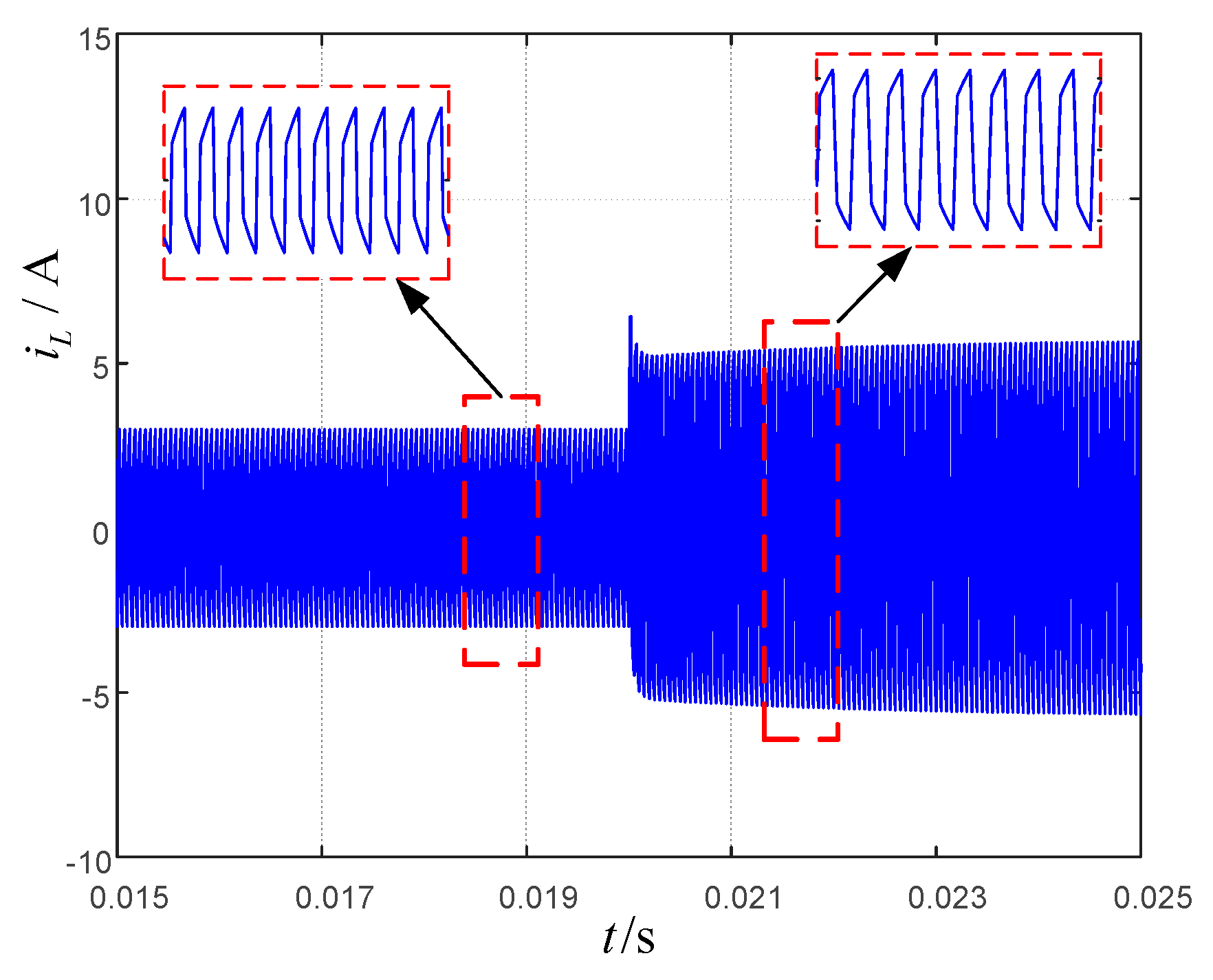
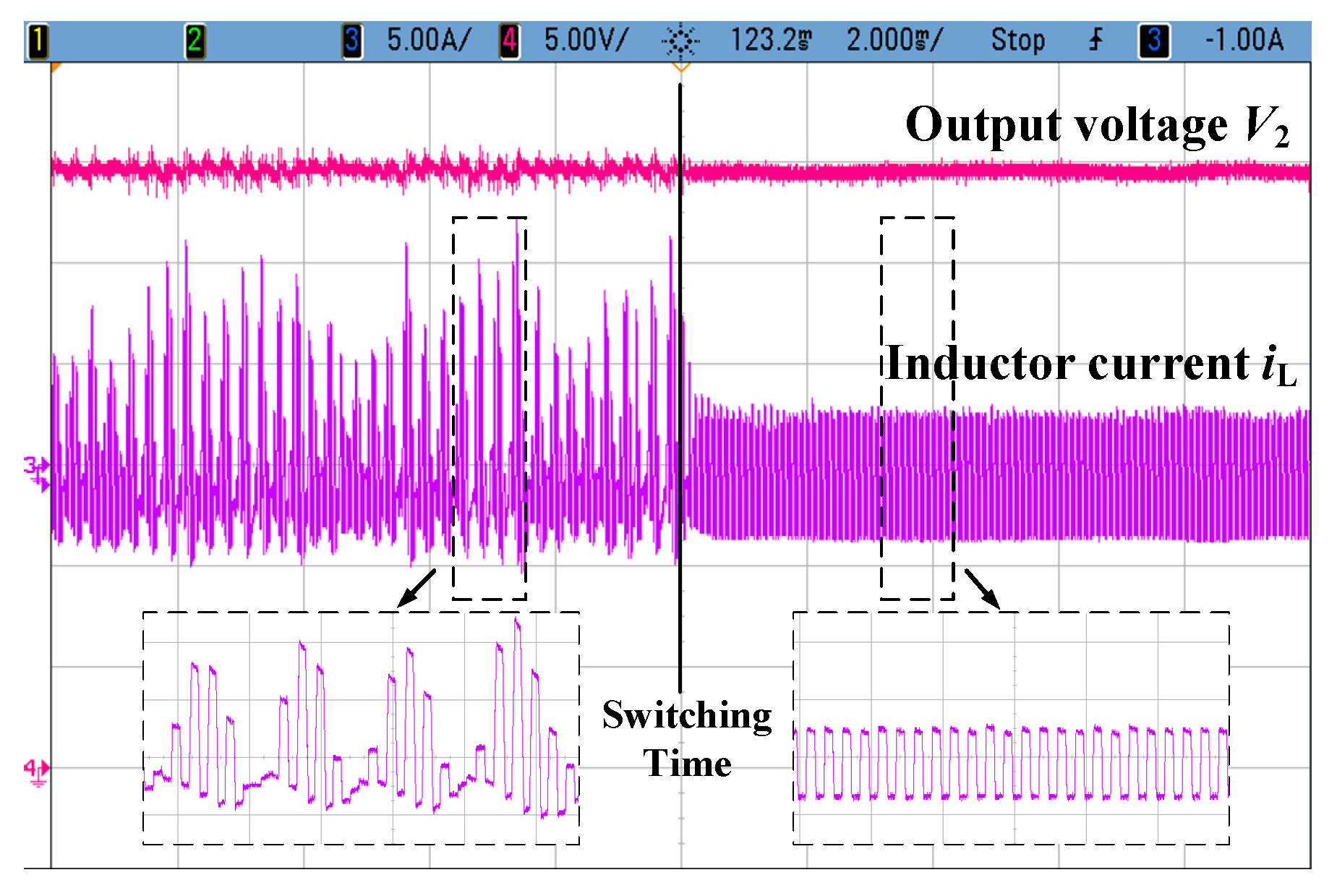
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jang, S.-J.; Lee, T.-W.; Lee, W.-C.; Won, C.-Y. Bi-directional dc-dc converter for fuel cell generation system. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 4722–4728. [Google Scholar]
- Profumo, F.; Tenconi, A.; Cerchio, M.; Bojoi, R.; Gianolio, G. Fuel cells for electric power generation: Peculiarities and dedicated solutions for power electronic conditioning systems. EPE J. 2006, 16, 44–51. [Google Scholar] [CrossRef]
- Samosir, A.S.; Yatim, A.H.M. Implementation of Dynamic Evolution Control of Bidirectional DC-DC Converter for Interfacing Ultracapacitor Energy Storage to Fuel-Cell System. IEEE Trans. Ind. Electron. 2010, 57, 3468–3473. [Google Scholar] [CrossRef]
- Engel, S.P.; Stieneker, M.; Soltau, N.; Rabiee, S.; Stagge, H.; De Doncker, R.W. Comparison of the Modular Multilevel DC Converter and the Dual-Active Bridge Converter for Power Conversion in HVDC and MVDC Grids. IEEE Trans. Power Electron. 2015, 30, 124–137. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Cho, J.; Cho, Y. High-Efficiency Bi-Directional Single-Phase AC/DC Converter Design and Field Application for LVDC Distribution. Energies 2019, 12, 2191. [Google Scholar] [CrossRef]
- Moonem, M.A.; Krishnaswami, H. Analysis of dual active bridge based power electronic transformer as a three-phase inverter. In Proceedings of the IECON 2012 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 238–243. [Google Scholar]
- Zhao, B.; Song, Q.; Liu, W.H.; Sun, Y.D. Overview of Dual-Active-Bridge Isolated Bidirectional DC-DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Takagi, K.; Fujita, H. Dynamic Control and Performance of a Dual-Active-Bridge DC-DC Converter. IEEE Trans. Power Electron. 2018, 33, 7858–7866. [Google Scholar] [CrossRef]
- Feng, B.; Wang, Y.; Man, J. A novel dual-phase-shift control strategy for dual-active-bridge DC-DC converter. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics SocietyIndustrial Electronics Society, Dallas, TX, USA, 29 October–1 Novmber 2014; pp. 4140–4145. [Google Scholar]
- Oggier, G.G.; Garcia, G.O.; Oliva, A.R. Switching Control Strategy to Minimize Dual Active Bridge Converter Losses. IEEE Trans. Power Electron. 2009, 24, 1826–1838. [Google Scholar] [CrossRef]
- Rodriguez, A.; Vazquez, A.; Lamar, D.G.; Hernando, M.M.; Sebastian, J. Different Purpose Design Strategies and Techniques to Improve the Performance of a Dual Active Bridge With Phase-Shift Control. IEEE Trans. Power Electron. 2015, 30, 790–804. [Google Scholar] [CrossRef]
- Oggier, G.G.; Garcia, G.O.; Oliva, A.R. Modulation Strategy to Operate the Dual Active Bridge DC-DC Converter Under Soft Switching in the Whole Operating Range. IEEE Trans. Power Electron. 2011, 26, 1228–1236. [Google Scholar] [CrossRef]
- Krismer, F.; Kolar, J.W. Accurate Small-Signal Model for the Digital Control of an Automotive Bidirectional Dual Active Bridge. IEEE Trans. Power Electron. 2009, 24, 2756–2768. [Google Scholar] [CrossRef]
- Buccella, C.; Cecati, C.; Latafat, H. Digital control of power converters—A survey. IEEE Trans. Ind. Inform. 2012, 8, 437–447. [Google Scholar] [CrossRef]
- Liu, Y.-F.; Meyer, E.; Liu, X. Recent developments in digital control strategies for DC/DC switching power converters. IEEE Trans. Power Electron. 2009, 24, 2567–2577. [Google Scholar]
- Aguilera, R.P.; Acuna, P.; Konstantinou, G.; Vazquez, S.; Leon, J.I. Basic Control Principles in Power Electronics: Analog and Digital Control Design. In Control of Power Electronic Converters and Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 31–68. [Google Scholar]
- Maksimovic, D.; Zane, R.; Erickson, R. Impact of digital control in power electronics. In Proceedings of the the 16th International Symposium on Power Semiconductor Devices & Ics (ISPSD ’04), Kitakyushu, Japan, 24–27 May 2004; pp. 13–22. [Google Scholar]
- Lu, M.H.; Wang, X.F.; Loh, P.C.; Blaabjerg, F.; Dragicevic, T. Graphical Evaluation of Time-Delay Compensation Techniques for Digitally Controlled Converters. IEEE Trans. Power Electron. 2018, 33, 2601–2614. [Google Scholar] [CrossRef]
- Debbat, M.B.; El Aroudi, A.; Giral, R.; Martinez-Salamero, L. Stability analysis and bifurcations of SEPIC DC-DC converter using a discrete-time model. In Proceedings of the 2002 IEEE International Conference on Industrial Technology (ICIT’ 02), Vols I and Ii, Bankok, Thailand, 11–14 December 2002; pp. 1055–1060. [Google Scholar]
- Yu, D.S.; Iu, H.H.C.; Chen, H.; Rodriguez, E.; Alarcon, E.; El Aroudi, A. Instabilities in Digitally Controlled Voltage-Mode Synchronous Buck Converter. Int. J. Bifurc. Chaos 2012, 22, 1250012. [Google Scholar] [CrossRef]
- Shankar, D.P.; Govindarajan, U.; Karunakaran, K. Period-bubbling and mode-locking instabilities in a full-bridge DC-AC buck inverter. IET Power Electron. 2013, 6, 1956–1970. [Google Scholar] [CrossRef]
- Xiong, X.L.; Tse, C.K.; Ruan, X.B. Bifurcation Analysis of Standalone Photovoltaic-Battery Hybrid Power System. IEEE Trans. Circuits Syst. I 2013, 60, 1354–1365. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Kouro, S.; Perez, M.A.; Rodriguez, J.; Llor, A.M.; Young, H.A. Model Predictive Control MPC’s Role in the Evolution of Power Electronics. IEEE Ind. Electron. Mag. 2015, 9, 8–21. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive Control in Power Electronics and Drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Bakeer, A.; Ismeil, M.A.; Orabi, M. Modified finite control set-model predictive controller (MFCS-MPC) for quasi Z-source inverters based on a current observer. J. Power Electron. 2017, 17, 610–620. [Google Scholar] [CrossRef]
- Pawar, D.N.; Singh, N.M. MPC based controller for dual active bidirectional DC-DC converter driving inverter using dynamic phasor approach. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 661–666. [Google Scholar]
- An, F.; Song, W.; Yang, K.; Hou, N.; Ma, J. Improved dynamic performance of dual active bridge dc–dc converters using MPC scheme. IET Power Electron. 2018, 11, 1756–1765. [Google Scholar] [CrossRef]
- Wen, H.Q. Determination of the Optimal Sub-mode for Bidirectional Dual-Active-Bridge DC-DC Converter with Multi-Phase-Shift Control. In Proceedings of the 2013 IEEE ECCE Asia Downunder (ECCE Asia), Melbourne, Australia, 3–6 June 2013; pp. 596–600. [Google Scholar]
- Tariq, M.; Maswood, A.I.; Gajanayake, C.J.; Gupta, A.K.; Sasongko, F. Battery Energy Storage System Integration to the More Electric Aircraft 270 V DC Power Distribution Bus using Peak Current Controlled Dual Active Bridge Converter. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2068–2073. [Google Scholar]
- Wu, K.Y.; de Silva, C.W.; Dunford, W.G. Stability Analysis of Isolated Bidirectional Dual Active Full-Bridge DC-DC Converter With Triple Phase-Shift Control. IEEE Trans. Power Electron. 2012, 27, 2007–2017. [Google Scholar] [CrossRef]
- Shi, L.; Lei, W.J.; Li, Z.Q.; Huang, J.; Cui, Y.; Wang, Y. Bilinear Discrete-Time Modeling and Stability Analysis of the Digitally Controlled Dual Active Bridge Converter. IEEE Trans. Power Electron. 2017, 32, 8787–8799. [Google Scholar] [CrossRef]
- Costinett, D.; Zane, R.; Maksimović, D. Discrete-time small-signal modeling of a 1 MHz efficiency-optimized dual active bridge converter with varying load. In Proceedings of the 2012 IEEE 13th Workshop on Control and Modeling for Power Electronics (COMPEL), Kyoto, Japan, 10–13 June 2012; pp. 1–7. [Google Scholar]
- Mazumder, S.; Alfayyoummi, M.; Nayfeh, A.H.; Borojevic, D. A theoretical and experimental investigation of the nonlinear dynamics of DC-DC converters. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference. Conference Proceedings (Cat. No.00CH37018), Galway, Ireland, 23 June 2000; Volume 2, pp. 729–734. [Google Scholar]
- Shi, L.; Lei, W.J.; Huang, J.; Li, Z.Q.; Cui, Y.; Wang, Y. Full Discrete-Time Modeling and Stability Analysis of the Digital Controlled Dual Active Bridge Converter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar]




| Parameters | Value | Parameters | Value |
|---|---|---|---|
| V1 | 30 V | Ro | 12.5 Ω |
| L | 35.49 μH | fs | 20 kHz |
| Rt | 0.38 Ω | n | 1 |
| Co | 455 μF | Vref | 30 V |
| RC | 0.45 Ω | k | 0.1–0.65 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, G.; Lei, W.; Cui, Y.; Li, K.; Shi, L.; Yin, S. Modeling and Stability Analysis of Model Predictive Control Dual Active Bridge Converter. Energies 2019, 12, 3103. https://doi.org/10.3390/en12163103
Gao G, Lei W, Cui Y, Li K, Shi L, Yin S. Modeling and Stability Analysis of Model Predictive Control Dual Active Bridge Converter. Energies. 2019; 12(16):3103. https://doi.org/10.3390/en12163103
Chicago/Turabian StyleGao, Guoqing, Wanjun Lei, Yao Cui, Kai Li, Ling Shi, and Shiyuan Yin. 2019. "Modeling and Stability Analysis of Model Predictive Control Dual Active Bridge Converter" Energies 12, no. 16: 3103. https://doi.org/10.3390/en12163103
APA StyleGao, G., Lei, W., Cui, Y., Li, K., Shi, L., & Yin, S. (2019). Modeling and Stability Analysis of Model Predictive Control Dual Active Bridge Converter. Energies, 12(16), 3103. https://doi.org/10.3390/en12163103





