An Improved Signal Processing Approach Based on Analysis Mode Decomposition and Empirical Mode Decomposition
Abstract
:1. Introduction
2. Basic Principles of EMD
3. The Sifting Stop Criteria Based on the Valid Data Segment
4. AEMD Method
4.1. Analytical Mode Decomposition (AMD) Method
4.2. Steps of the AEMD Method
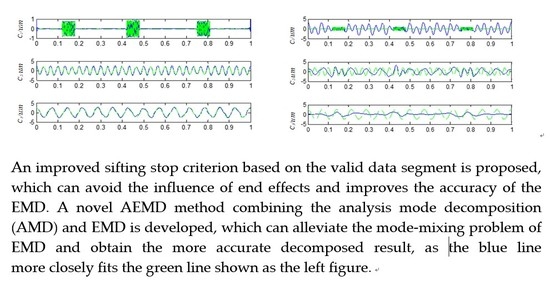
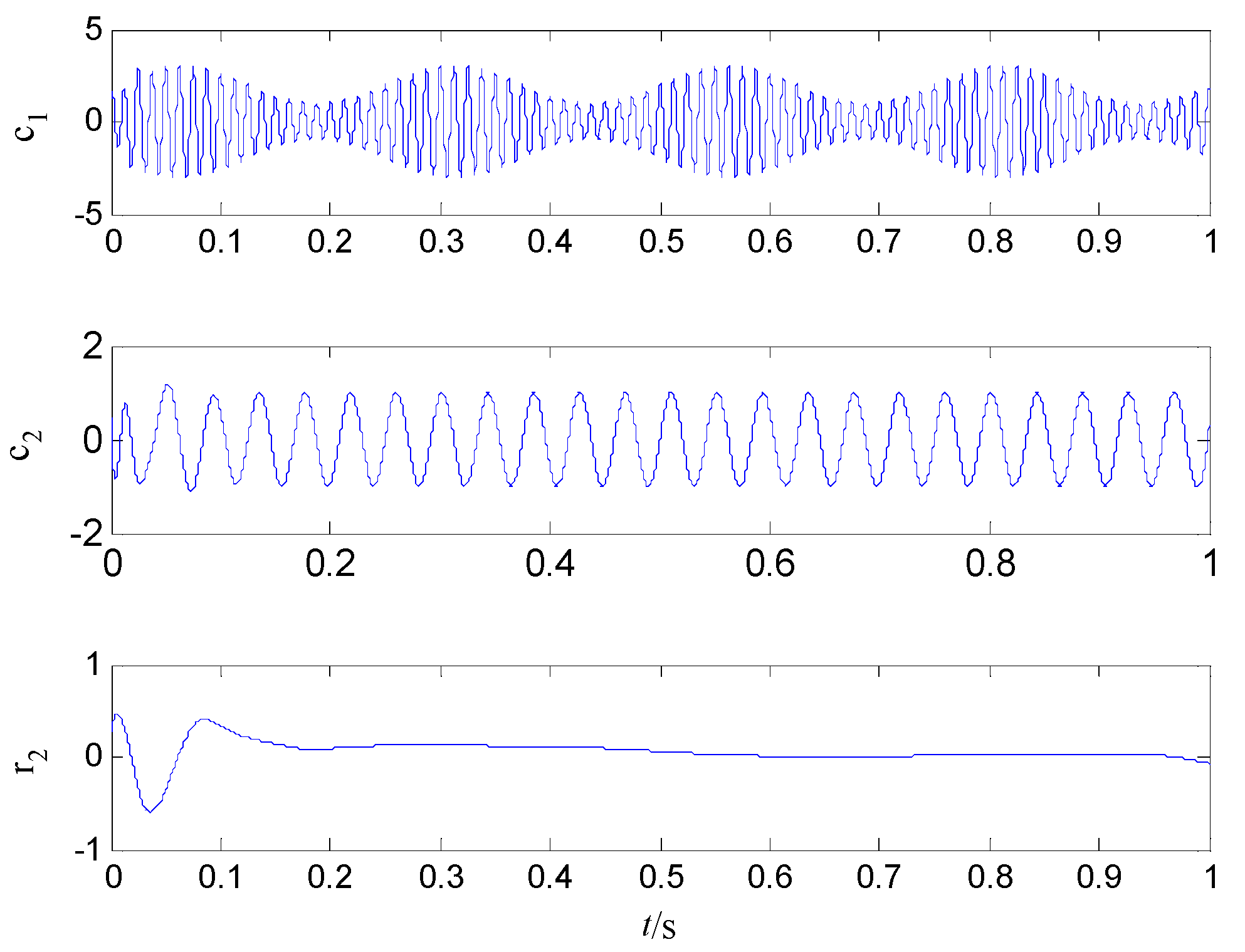
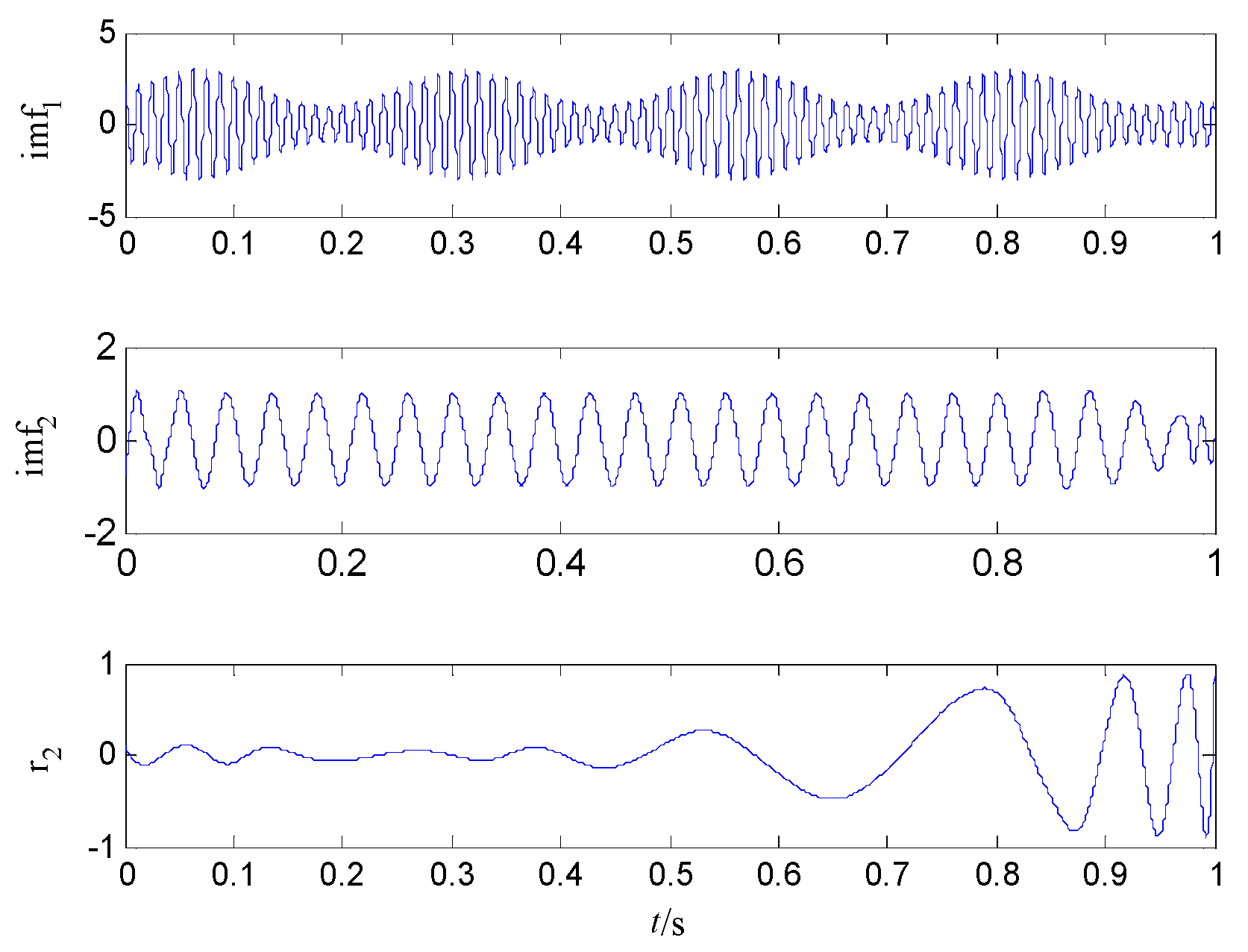
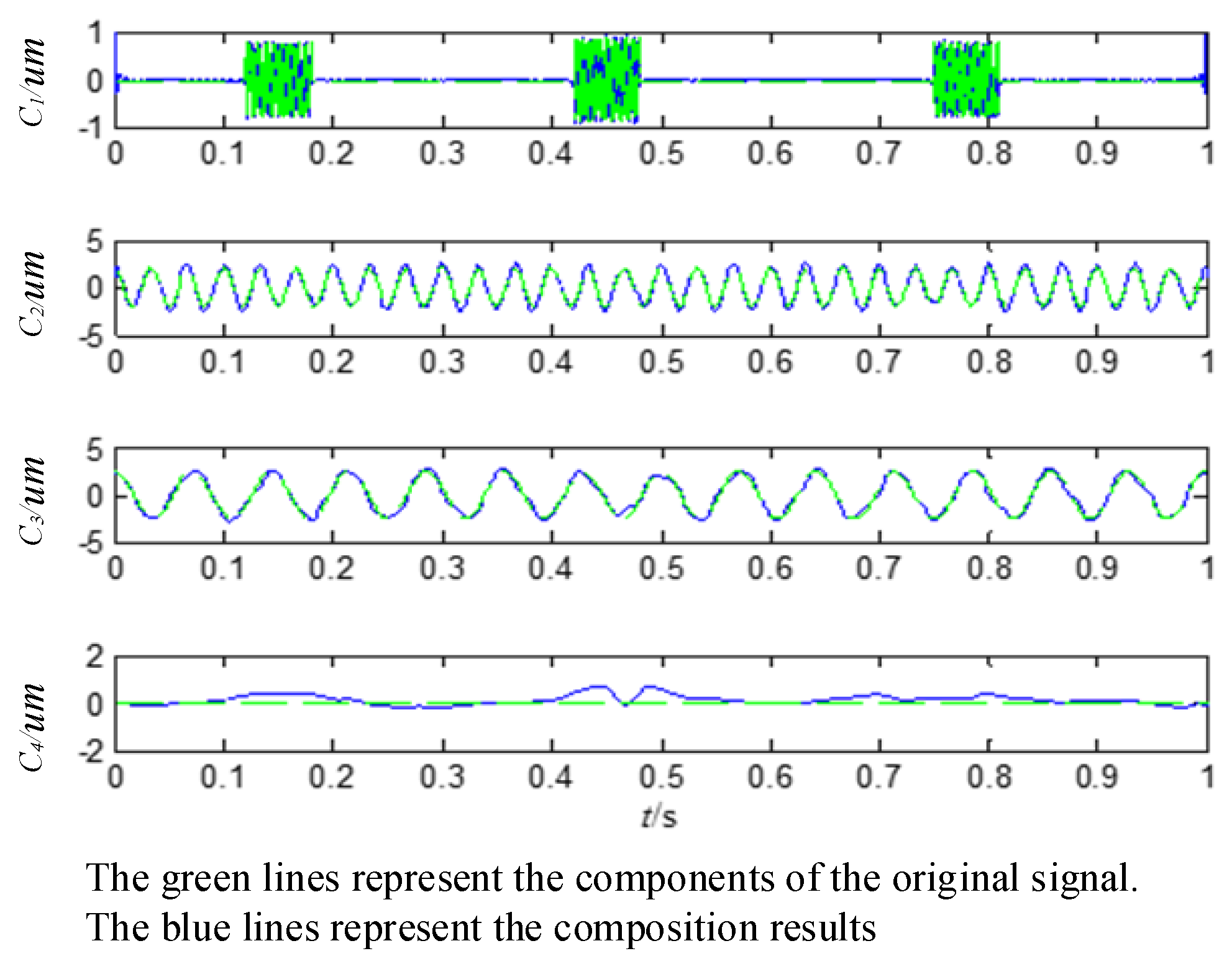
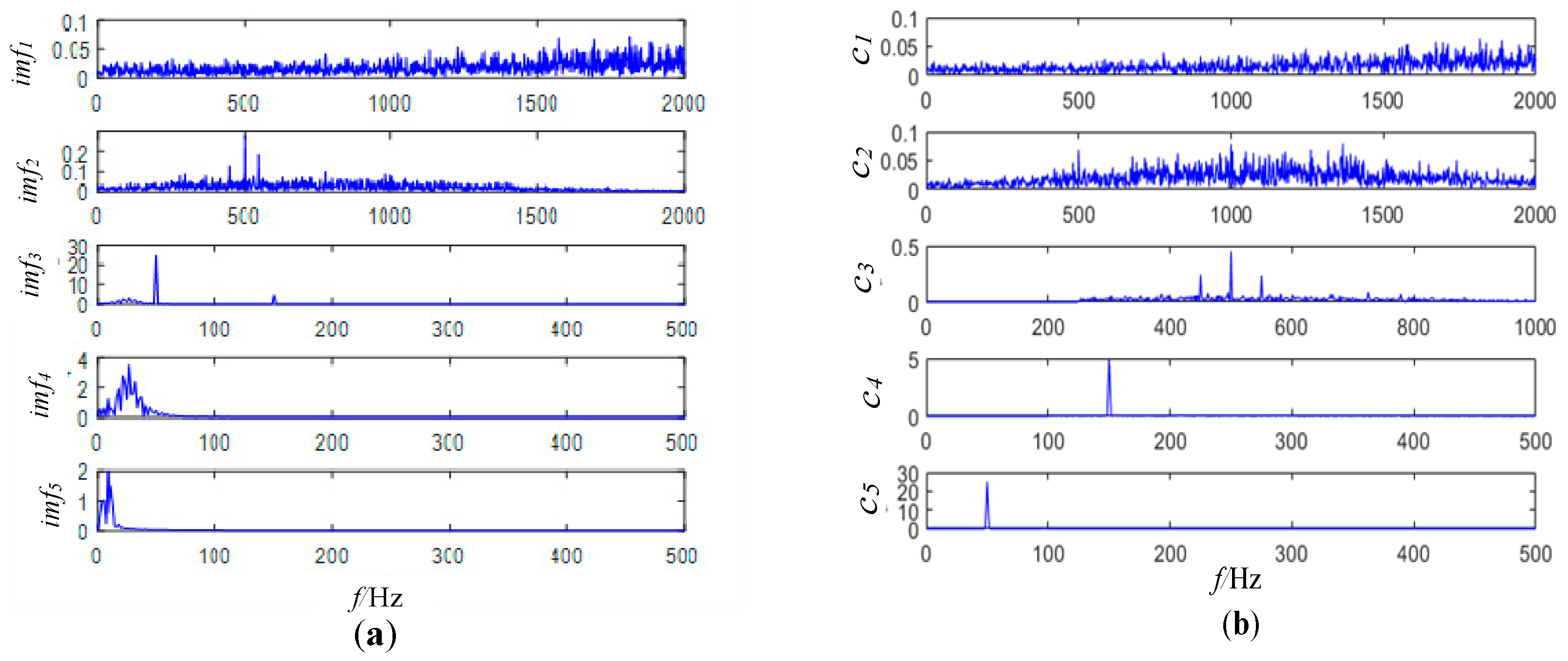
4.3. The Comparison of Simulation Signal Analysis by Different Methods
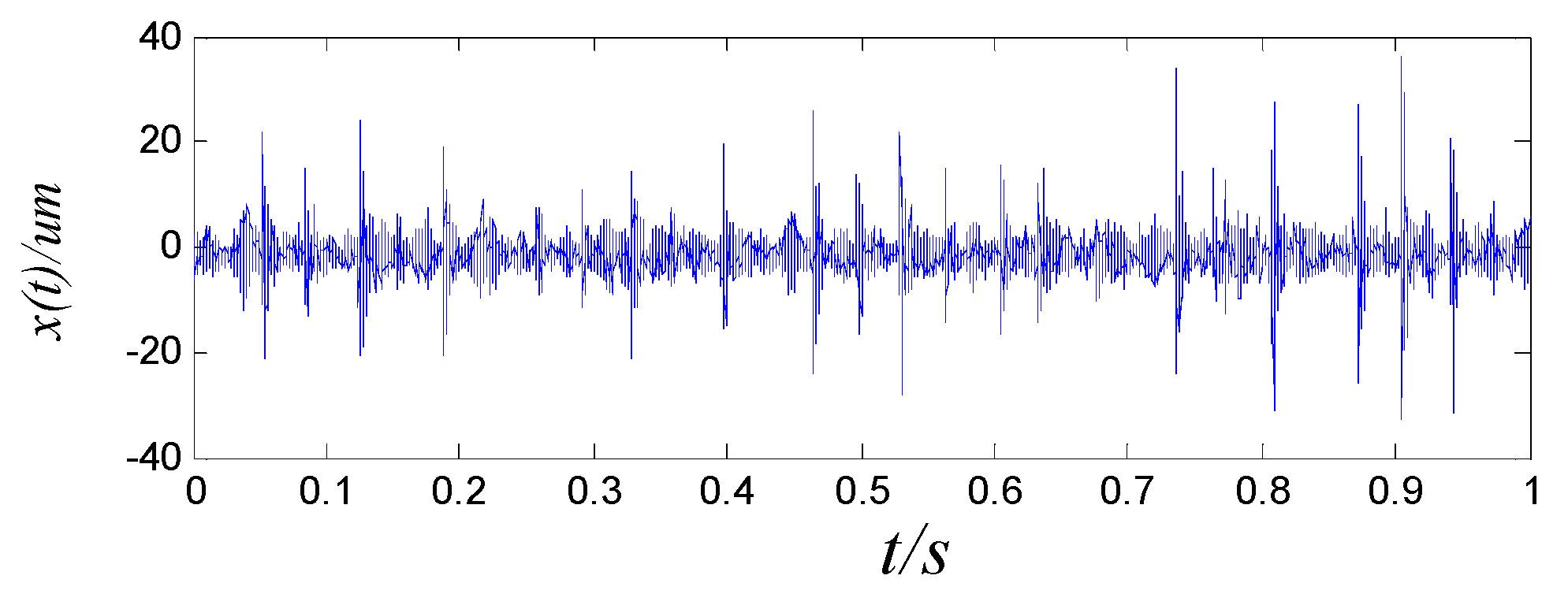
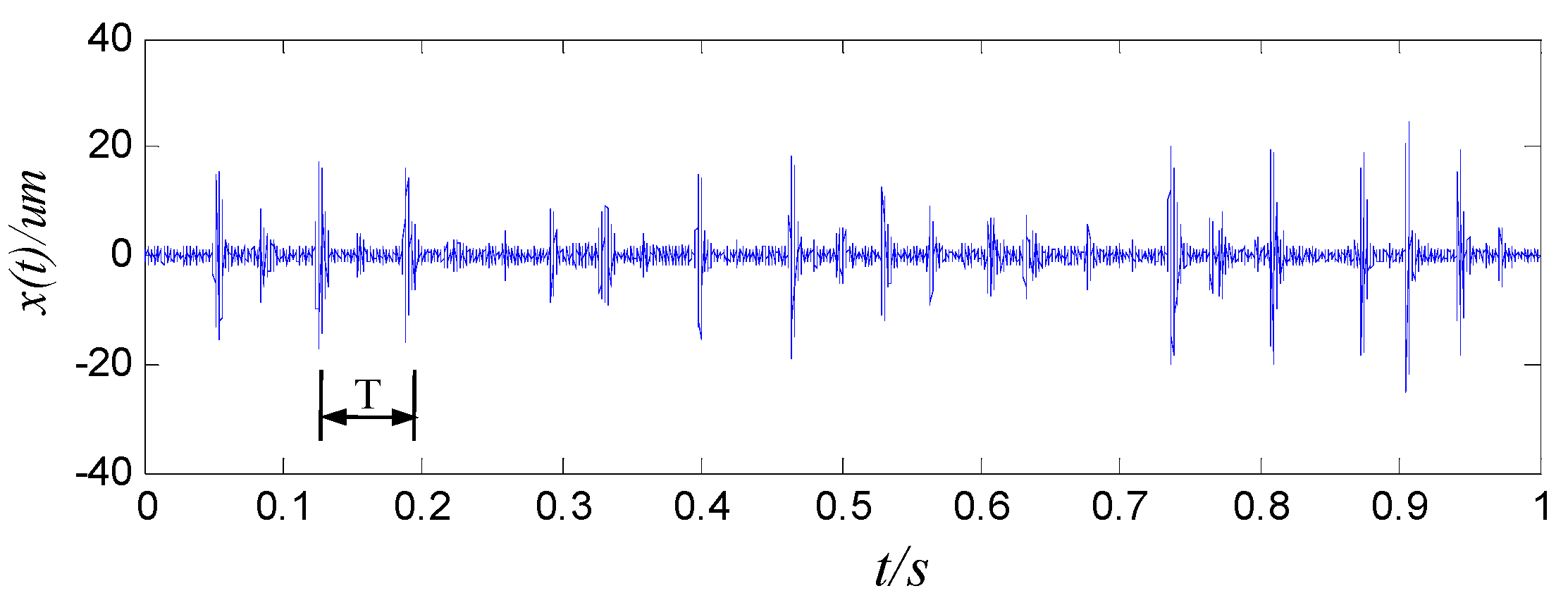
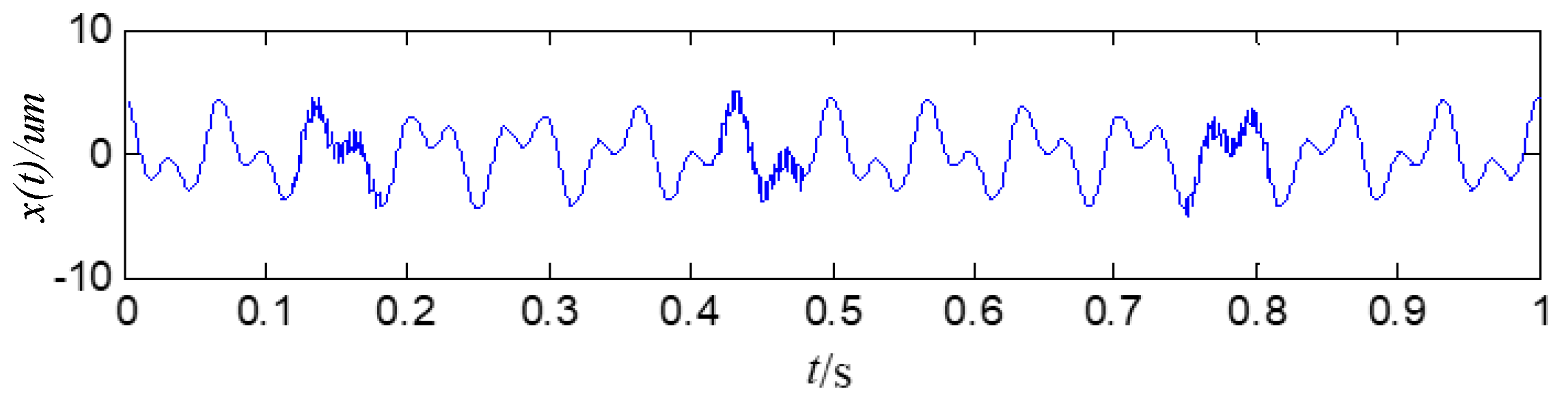
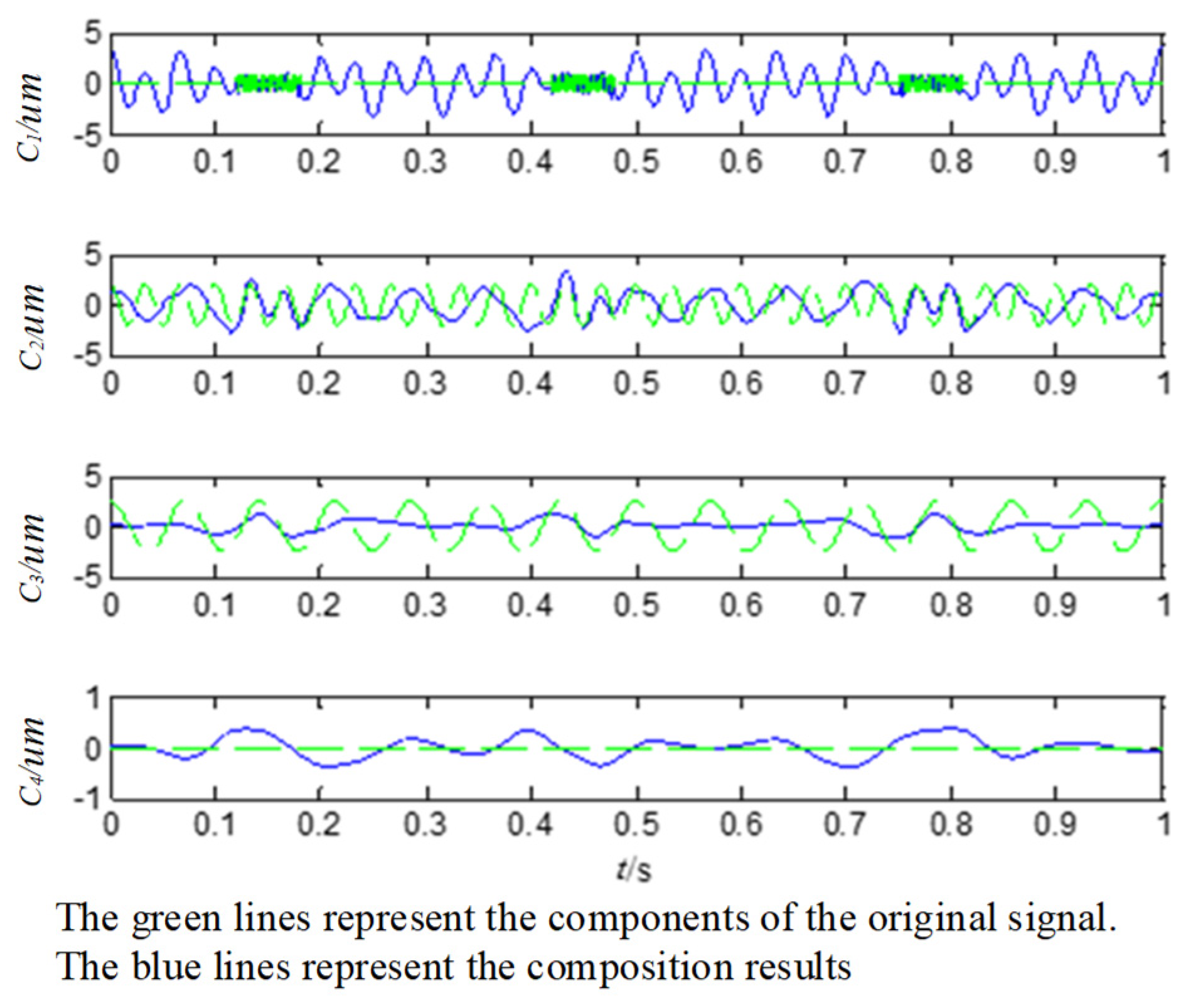
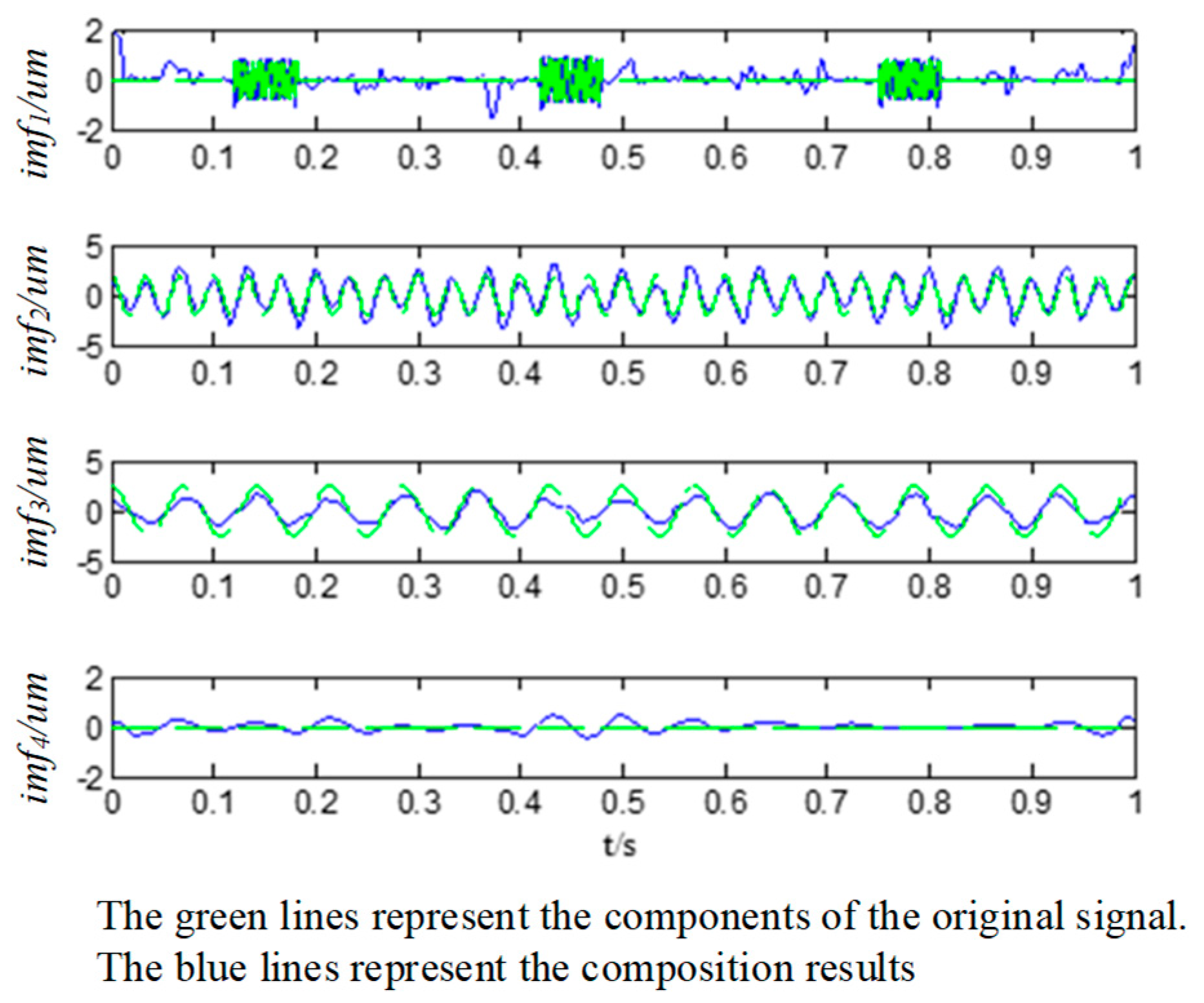
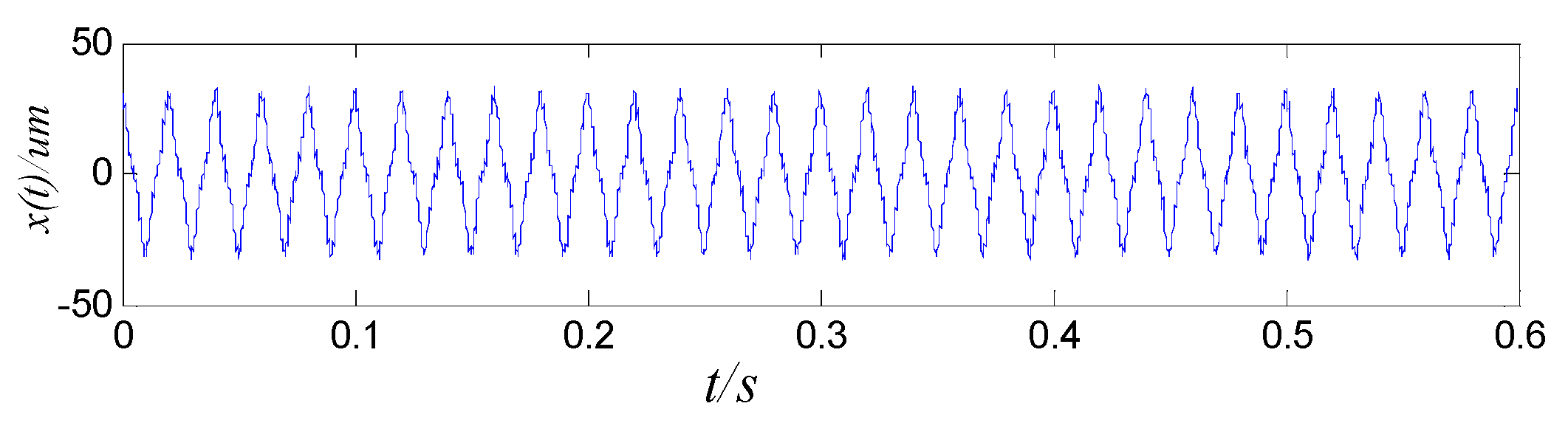
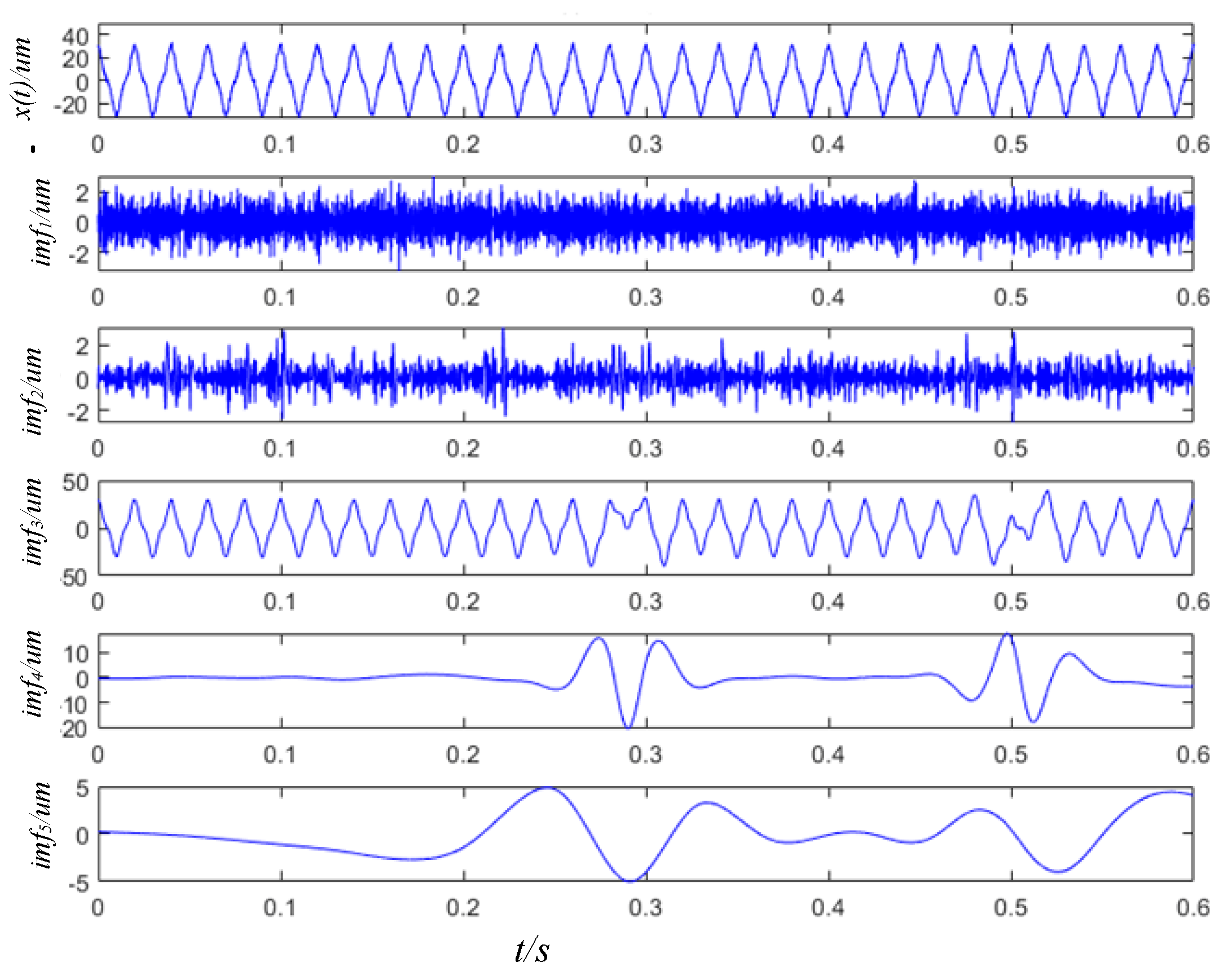
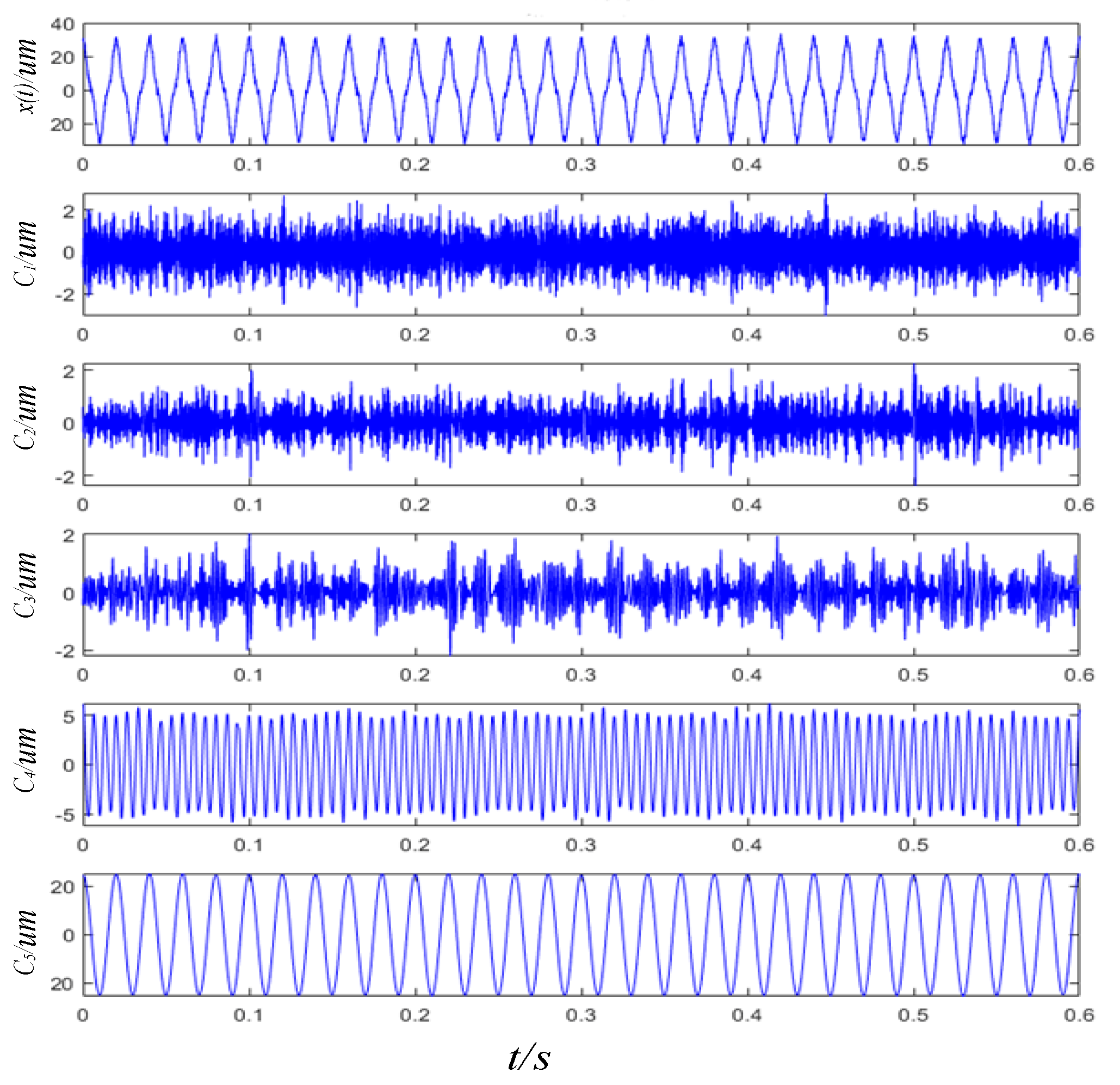
4.4. Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Z.; Cao, S.; Mao, Z. Remaining useful life estimation of aircraft engines using a modified similarity and supporting vector machine (SVM) approach. Energies 2017, 11, 28. [Google Scholar] [CrossRef]
- Han, J.; Ji, G.Y. Gear Fault Diagnosis Based on Improved EMD Method and the Energy Operator Demodulation Approach. J. Changsha Univ. Sci. Technol. 2015, 12, 66–71. [Google Scholar]
- Yang, Y.F.; Wu, Y.F. Application of Empirical Mode Decomposition in the Analysis of Vibration; National Defence of Industry Press: Beijing, China, 2013; pp. 17–45. [Google Scholar]
- Huang, D.S. The Method of False Modal Component Elimination in Empirical Mode Decomposition. Vibration. Meas. Diagn. 2011, 31, 381–384. [Google Scholar]
- Wang, L. Fault Diagnosis of Rotor System Based on EMD-Fuzzy Entropy and SVM. Noise Vib. Control 2012, 6, 172–173. [Google Scholar]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Xue, X.; Zhou, J.; Xu, Y.; Zhu, W.; Li, C. An Adaptively Fast Ensemble Empirical Mode Decomposition Method and Its Applications to Rolling Element Bearing Fault Diagnosis. Mech. Syst. Sig. Process. 2015, 62–63, 444–459. [Google Scholar] [CrossRef]
- Yu, D.J.; Cheng, J.S. The Hilbert-Huang Transform Method in Mechanical Fault Diagnosis; Science Press: Beijing, China, 2006; pp. 179–190. [Google Scholar]
- Cheng, J.; Xu, Y.L. Application of HHT Method in Structural Modal Parameter Identification. J. Vib. Eng. 2003, 16, 383–387. [Google Scholar]
- Cheng, J.; Yang, Y. The application of EMD Method in Local Touch Friction Fault Diagnosis of Rotor. Vibration. Meas. Diagn. 2006, 26, 24–27. [Google Scholar]
- Rilling, G.; Flandrin, P. One or Two Frequencies? The Empirical Mode Decomposition Answers. IEEE Trans. Signal Process. 2008, 56, 85–95. [Google Scholar] [CrossRef]
- Dou, D.Y.; Zhao, Y.K. Application of Ensemble Empirical Mode Decomposition in Failure Analysis of Rotating Machinery. Trans. Chin. Soc. Agric. Eng. 2010, 26, 190–196. [Google Scholar]
- Pustelnik, N.; Borgnat, P.; Flandrin, P. Empirical mode decomposition revisited by multicomponent non-smooth convex optimization. Signal Process. 2014, 102, 313–331. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J.; Zi, Y.Y. Application of the EEMD Method to Rotor Fault Diagnosis of Rotating Machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Zhao, J.P. Study on the Effects of Abnormal Events to Empirical Mode Decomposition Method and the Removal Method for Abnormal Signal. J. Ocean Univ. Qingdao 2001, 31, 805–814. [Google Scholar]
- Deering, R.; Kaiser, J.F. The Use of a Masking Signal to Improve Empirical Mode Decomposition. Acoust. Speech Signal Process. ICASSP 2005, 4, 485–488. [Google Scholar]
- Hu, A.J. Research on the Application of Hilbert-Huang Transform in Vibration Signal Analysis of Rotating Machinery; North China Electric Power University: Bao Ding, Hebei, China, 2008. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Chen, G.D.; Wang, Z.C. A Signal Decomposition Theorem with Hilbert Transform and Its Application to Narrow Band Time Series with Closely Spaced Frequency Components. Mech. Syst. Signal Process. 2012, 28, 258–279. [Google Scholar] [CrossRef]
- Lei, Y.G.; Kong, D.T. Adaptive Ensemble Empirical Mode Decomposition and Application to Fault Detection of Planetary Gear Boxes. J. Mech. Eng. 2014, 50, 64–70. [Google Scholar] [CrossRef]
- Zheng, J.D.; Cheng, J.S.; Yang, Y. Partly Ensemble Empirical Mode Decomposition: An Improved Noise-Assisted Method for Eliminating Mode Mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]
- Hu, J.S.; Yang, S.X. Energy-Based Stop Condition of Empirical Mode Decomposition of Vibration Signal. J. Vib. Meas. Diagn. 2009, 29, 19–22. [Google Scholar]
- Mohammad, S.H.; Siamak, E.K.; Mohammad, S.S. Quantitative diagnosis for bearing faults by improving ensemble empirical mode decomposition. ISA Trans. 2018, 83, 261–275. [Google Scholar]
- Yang, Y.; Yu, D.J.; Cheng, J.S. A Roller Bearing Fault Diagnosis Method Based on EMD Energy Entropy and ANN. J. Sound Vib. 2006, 294, 269–277. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]


| Method | First | Second | Third | Fourth | Fifth | Sixth |
|---|---|---|---|---|---|---|
| EMD | 1.3988 | 1.3860 | 1.3930 | 1.3846 | 1.3820 | 1.3940 |
| EEMD | 41.4875 | 44.8383 | 44.1800 | 42.8480 | 43.2321 | 44.024 |
| AEMD | 1.4027 | 1.3832 | 1.3843 | 1.3934 | 1.3880 | 1.3848 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Liu, B.; Yan, X.; Yang, H. An Improved Signal Processing Approach Based on Analysis Mode Decomposition and Empirical Mode Decomposition. Energies 2019, 12, 3077. https://doi.org/10.3390/en12163077
Chen Z, Liu B, Yan X, Yang H. An Improved Signal Processing Approach Based on Analysis Mode Decomposition and Empirical Mode Decomposition. Energies. 2019; 12(16):3077. https://doi.org/10.3390/en12163077
Chicago/Turabian StyleChen, Zhongzhe, Baqiao Liu, Xiaogang Yan, and Hongquan Yang. 2019. "An Improved Signal Processing Approach Based on Analysis Mode Decomposition and Empirical Mode Decomposition" Energies 12, no. 16: 3077. https://doi.org/10.3390/en12163077
APA StyleChen, Z., Liu, B., Yan, X., & Yang, H. (2019). An Improved Signal Processing Approach Based on Analysis Mode Decomposition and Empirical Mode Decomposition. Energies, 12(16), 3077. https://doi.org/10.3390/en12163077