Characteristic Analysis of the Peak Braking Force and the Critical Speed of Eddy Current Braking in a High-Speed Maglev
Abstract
:1. Introduction
2. Analytical Models and Calculation
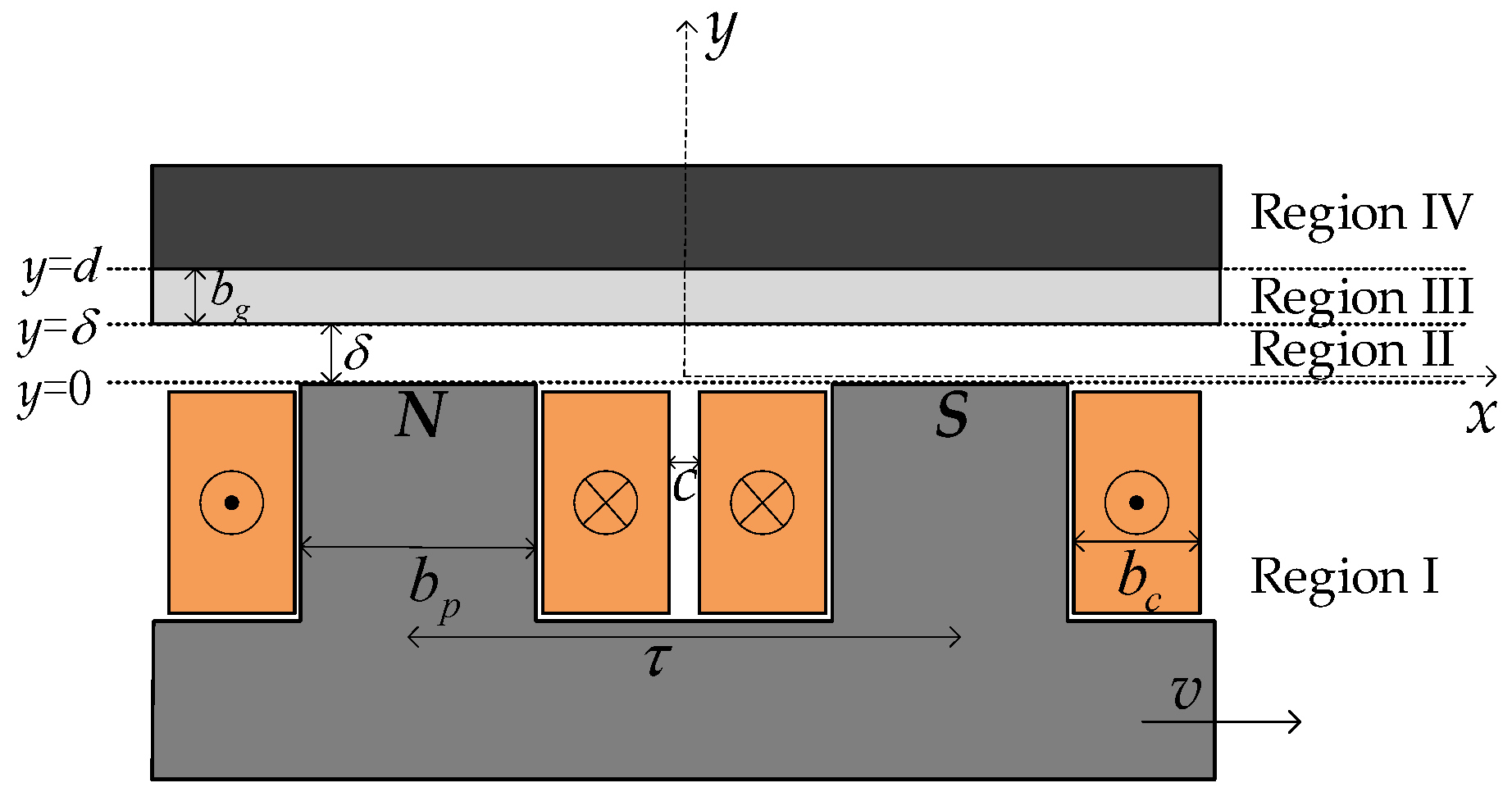
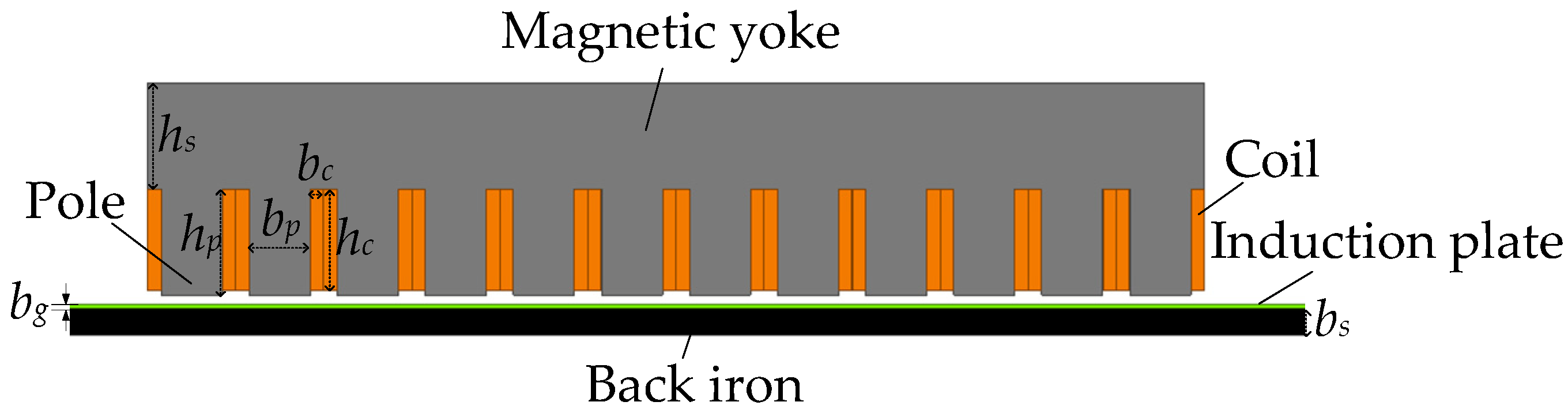
2.1. D Simplified Model of Eddy Current Brake
- (1)
- The relative permeability μr of region I and region IV is infinite (regardless of magnetic saturation);
- (2)
- The relative permeability μr of the induction plate material in region III is 1, which is consistent with vacuum permeability.
2.2. Expressions of Magnetic Vector Potential
2.3. Magnetic Field Boundary Condition
2.4. Eddy Current Braking Force
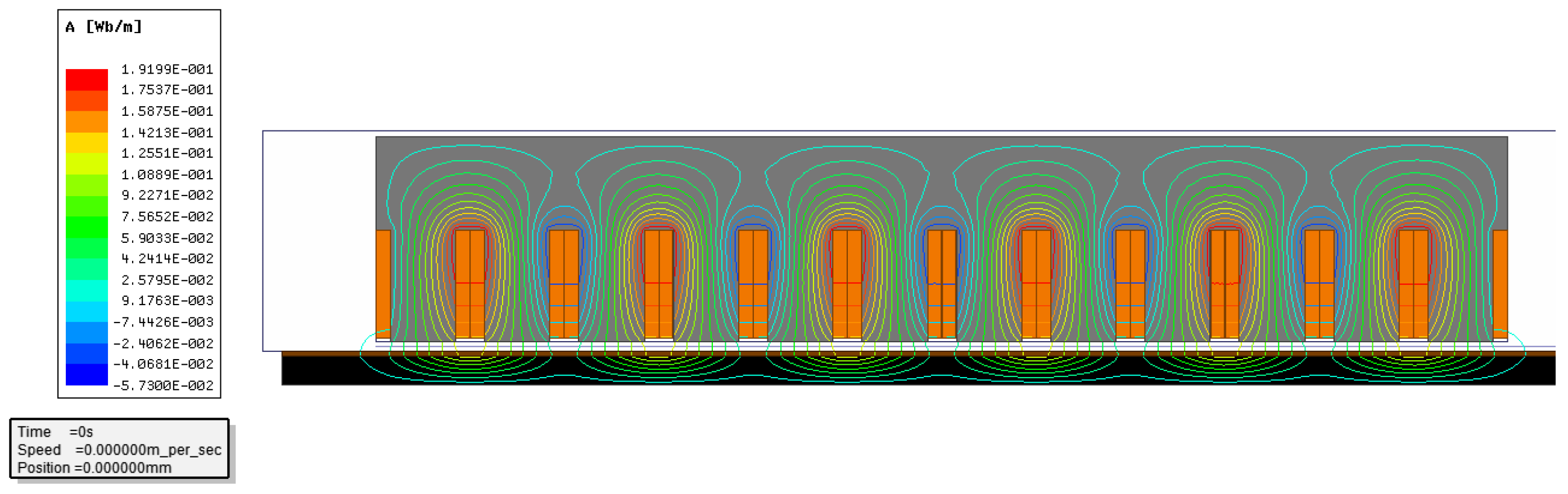
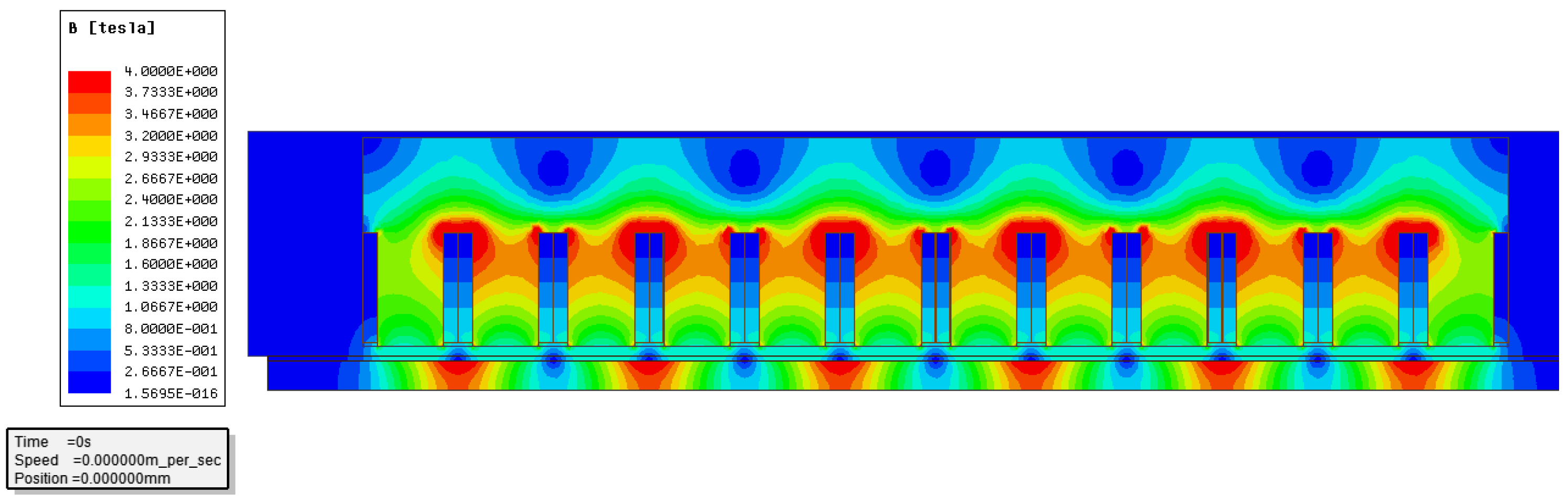
3. Finite Element Verification
- (1)
- The magnetic field is simulated in 2D, and the Cartesian coordinate system and the International Unit System are used;
- (2)
- The lateral end effect has been neglected. The magnetic field distributes uniformly along the z-axis. The current density vector J and the magnetic potential vector A have only z-axis components.
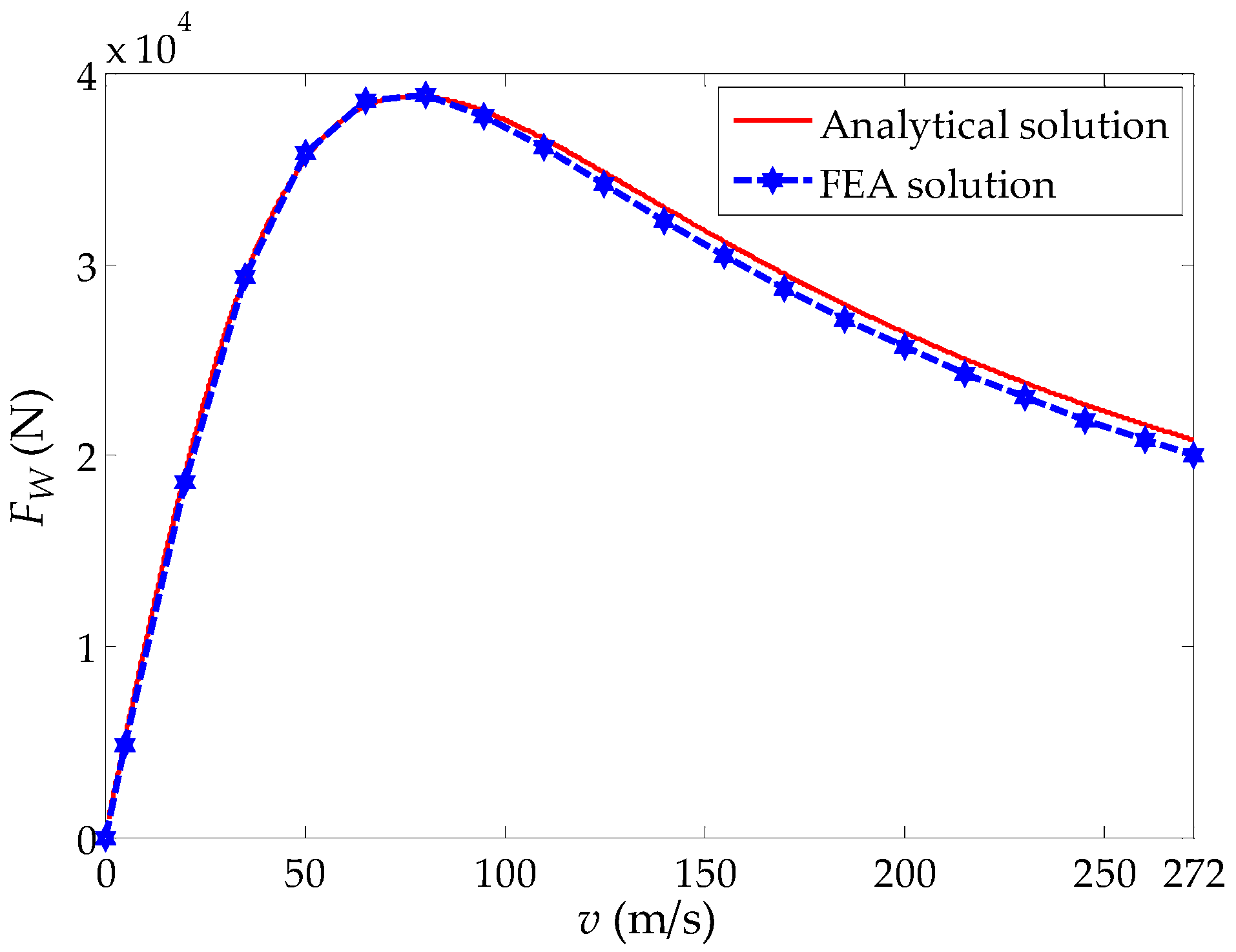
4. Parameter Analysis
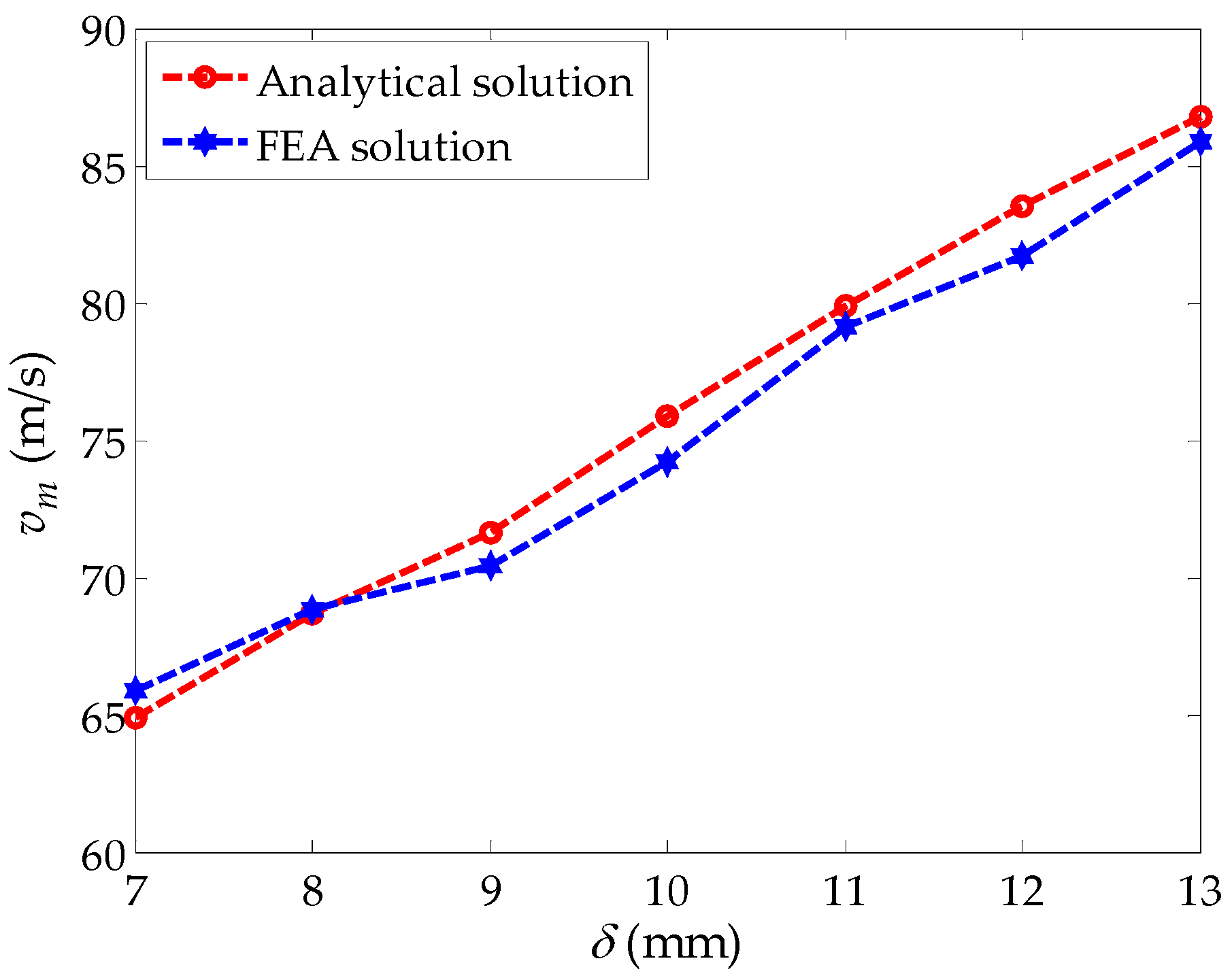
4.1. Effect of the Air Gap Length on the Peak Braking Force and the Critical Speed
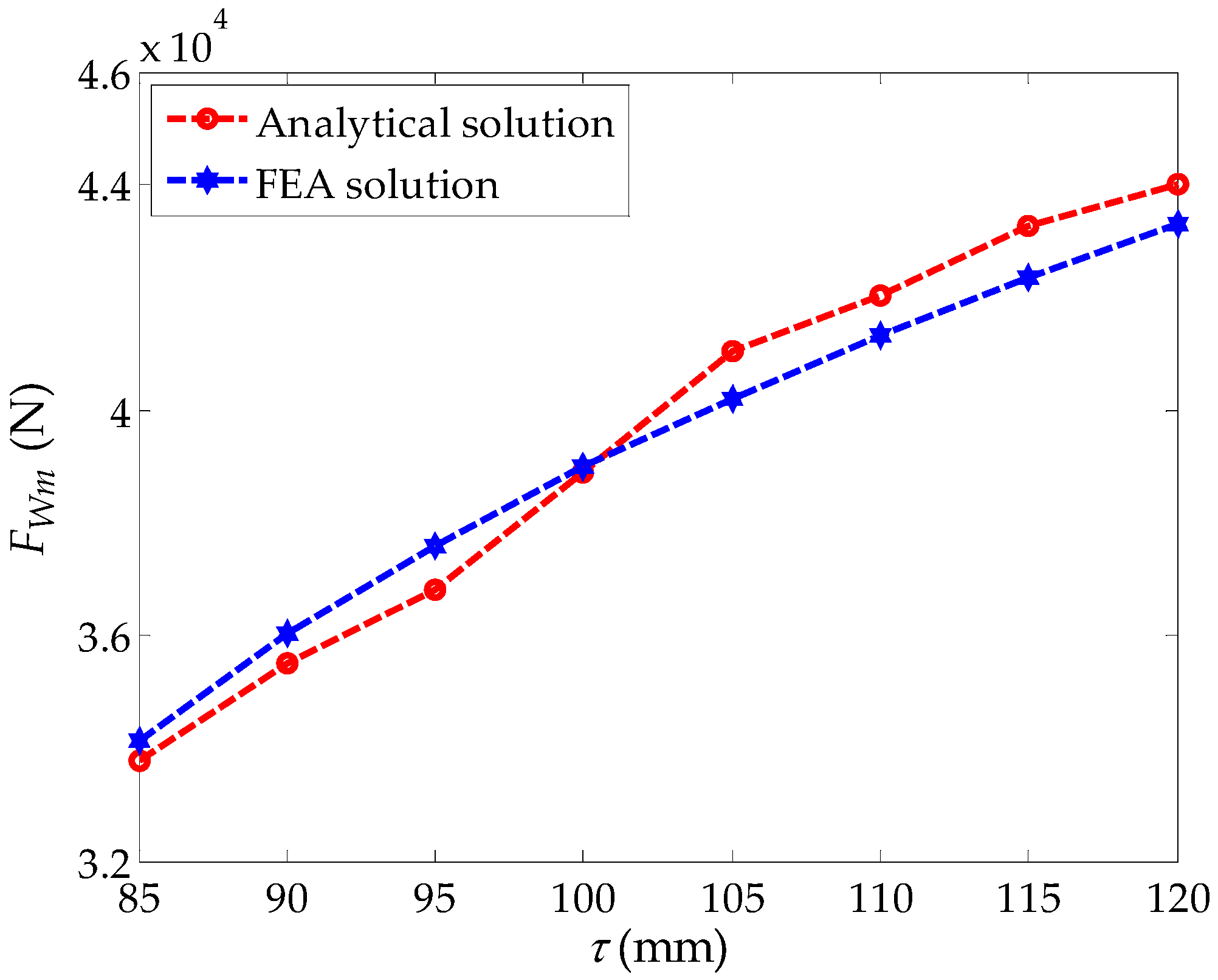
4.2. Effect of the Pole Pitch on the Peak Braking Force and the Critical Speed
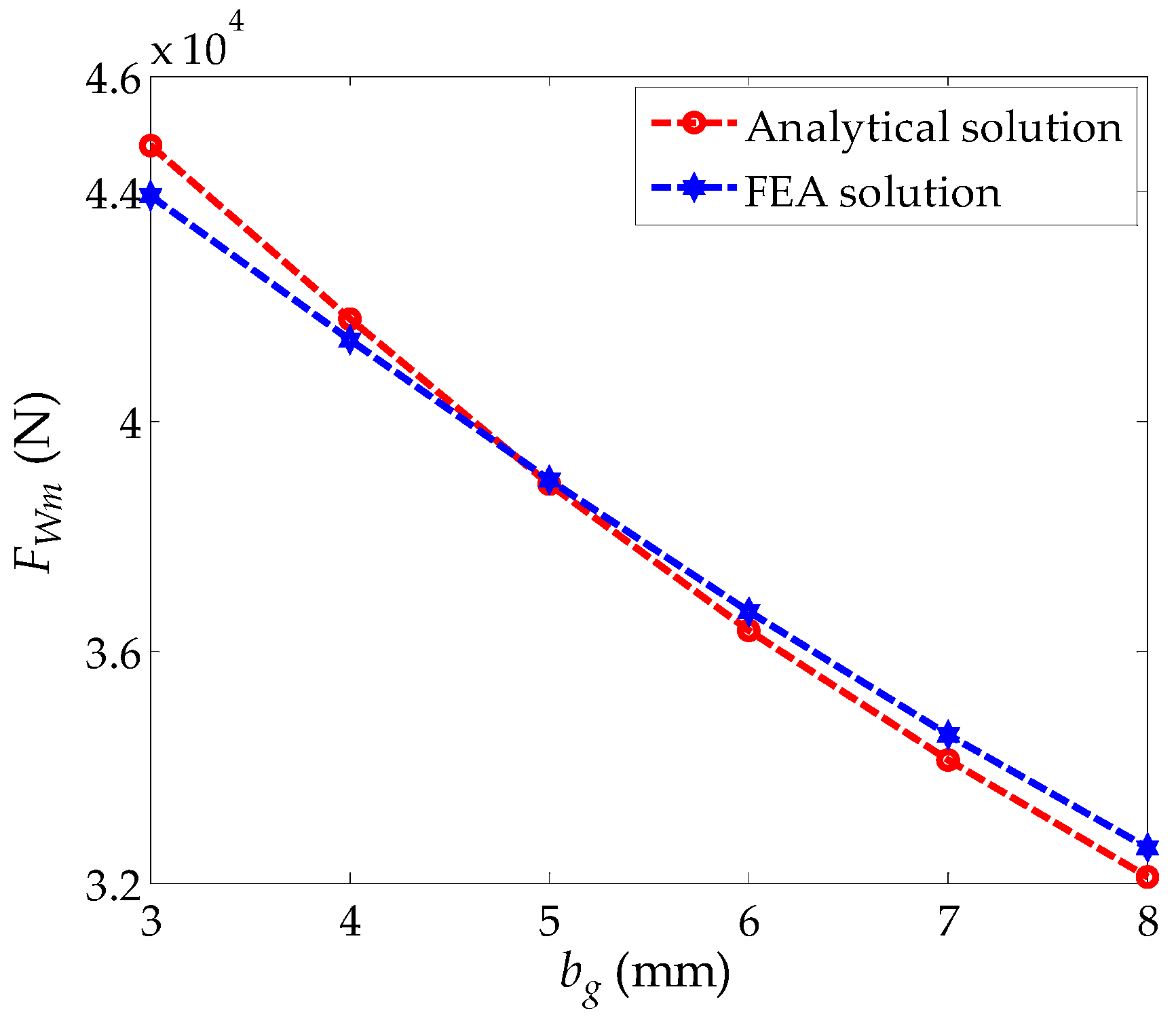
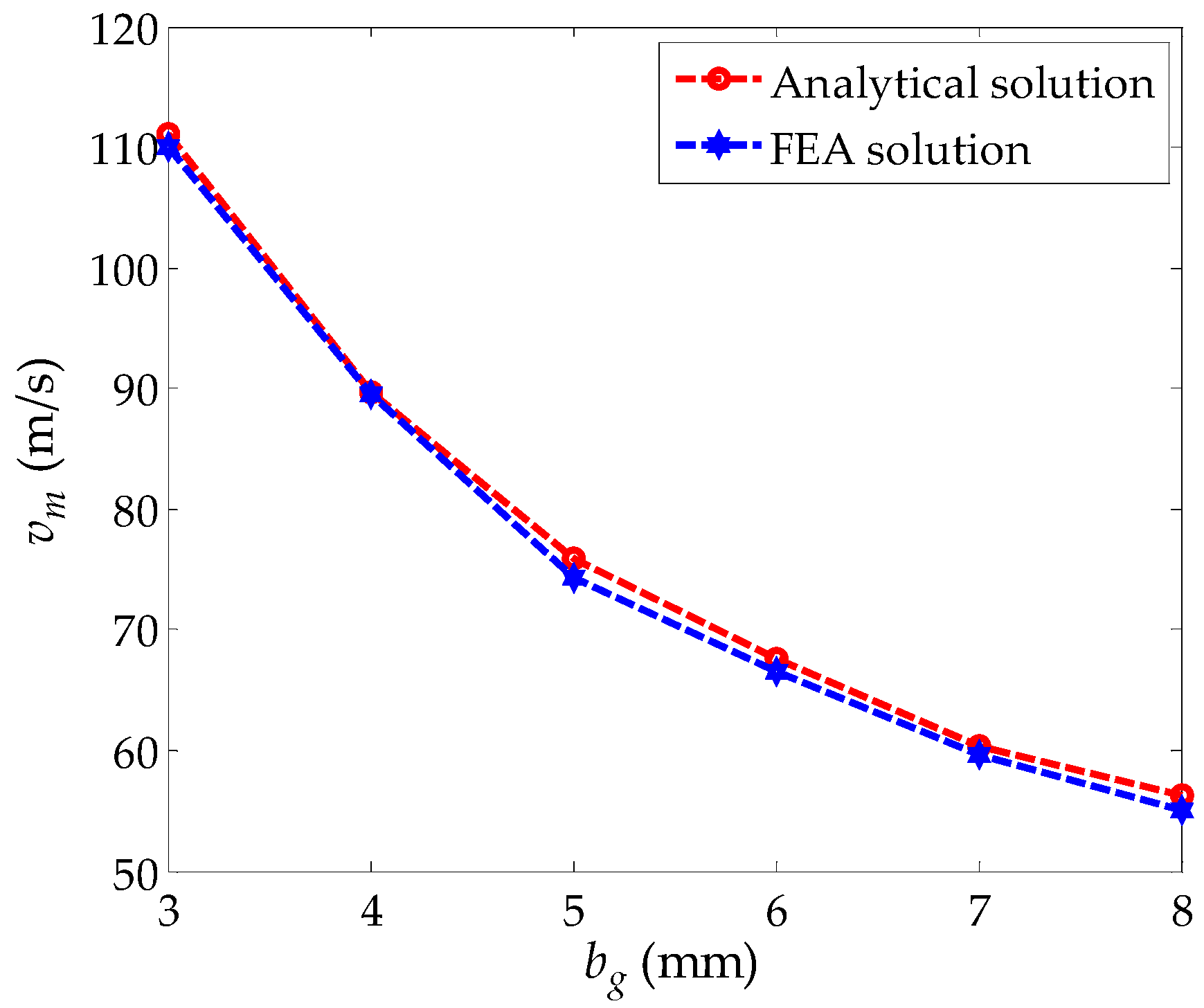
4.3. Effect of the Thickness of the Induction Plate on Peak Braking Force and Critical Speed
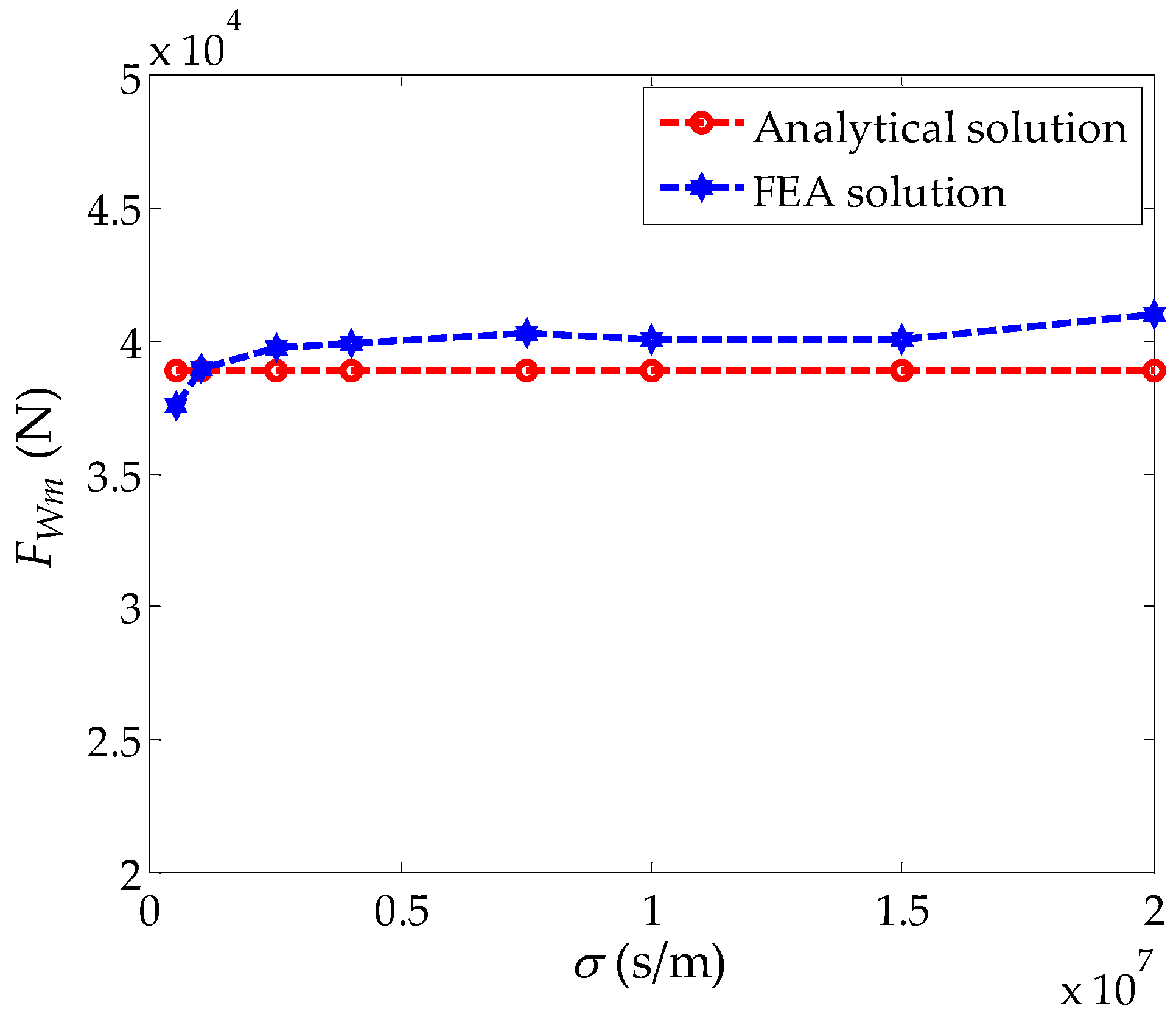
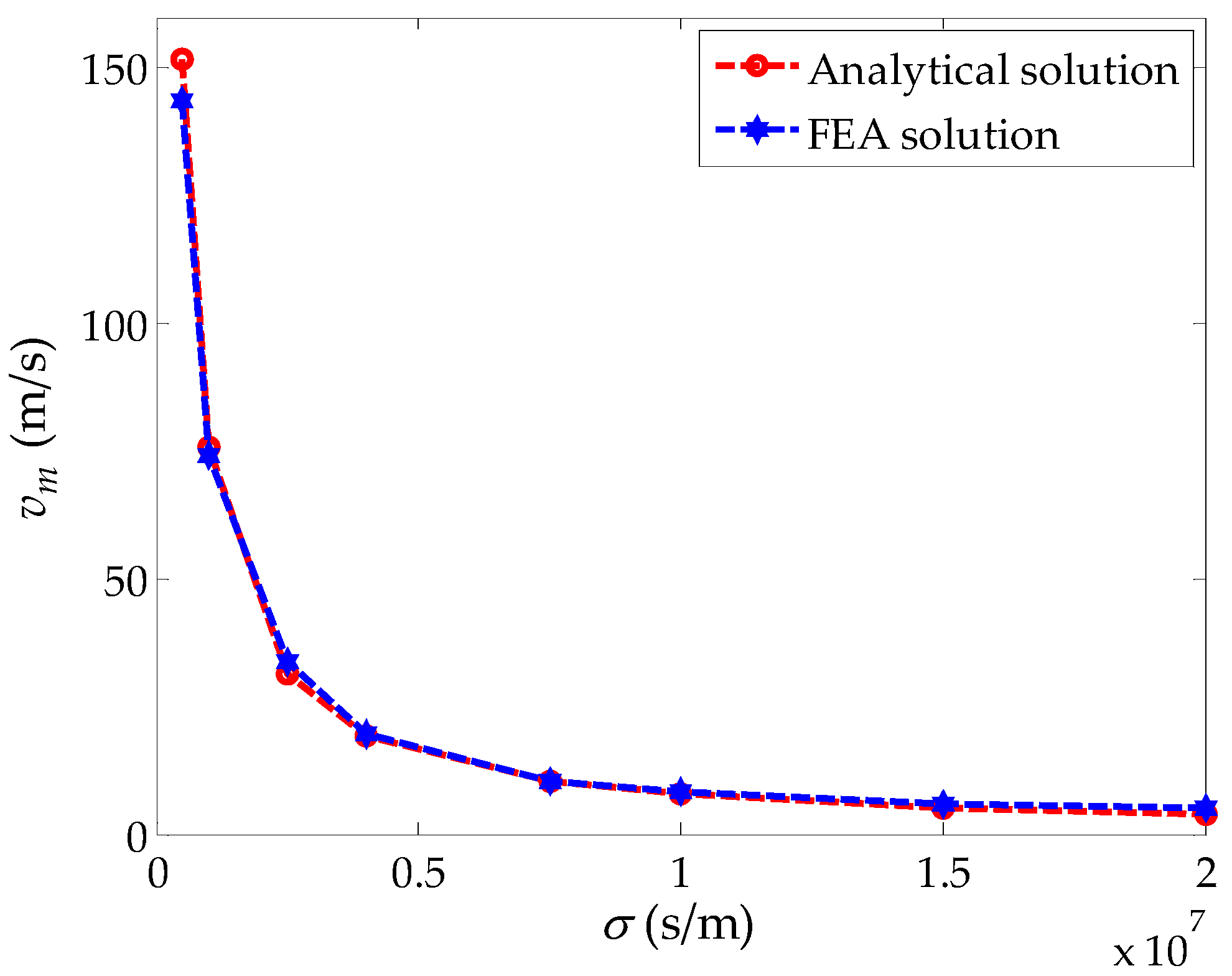
4.4. Effect of Induction Plate Conductivity on Peak Braking Force and Critical Speed
5. Error Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thompson, M.T. Practical issues in the use of NdFeB permanent magnets in maglev, motors, bearings and eddy current brakes. Proc. IEEE 2009, 97, 1758–1767. [Google Scholar] [CrossRef]
- Wang, P.J.; Chiueh, S.J. Analysis of eddy-current brakes for high speed railway. IEEE Trans. Magn. 1998, 34, 1237–1239. [Google Scholar] [CrossRef]
- Kou, B.; Jin, Y.; Lu, Z.; He, Z. Characteristic analysis and control of a hybrid excitation linear eddy current brake. Energies 2015, 8, 7441–7464. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Kumar, S. An alternative approach for calculation of braking force of an eddy-current brake. IEEE Trans. Magn. 2009, 45, 150–154. [Google Scholar] [CrossRef]
- Cho, S.; Liu, H.; Han, W.A.; Ju, L.; Lee, H.W. Eddy current brake with a two-layer structure: Calculation and characterization of braking performance. IEEE Trans. Magn. 2017, 53, 8110205. [Google Scholar] [CrossRef]
- Edwards, J.D.; Jayawant, B.V.; Dawson, W.R.C.; Wright, D.T. Permanent-magnet linear eddy-current brake with a nonmagnetic reaction plate. IEE Proc. Electr. Power Appl. 1999, 146, 627–631. [Google Scholar] [CrossRef]
- Yazdanpanah, R.; Mirsalim, M. Axial-flux wound-excitation eddy-current brakes: Analytical study and parametric modeling. IEEE Trans. Magn. 2014, 50, 1–10. [Google Scholar]
- Xue, Z.; Li, H.; Zhou, Y.; Ren, N.; Wen, W. Analytical prediction and optimization of cogging torque in surface-mounted permanent magnet machines with modified particle swarm optimization. IEEE Trans. Ind. Electron. 2017, 64, 9795–9805. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Meng, G.; Zhou, S.; Cao, Q. Analytical calculation of magnetic field and cogging torque in surface-mounted permanent-magnet machines accounting for any eccentric rotor shape. IEEE Trans. Ind. Electron. 2015, 62, 3438–3447. [Google Scholar] [CrossRef]
- Shin, H.J.; Choi, J.Y.; Cho, H.W.; Jang, S.M. Analytical torque calculations and experimental testing of permanent magnet axial eddy current brake. IEEE Trans. Magn. 2013, 49, 4152–4155. [Google Scholar] [CrossRef]
- Yazdanpanah, R.; Mirsalim, M. Analytical study of axial-flux hybrid excitation eddy current brakes. Int. J. Appl. Electromagn. Mech. 2015, 47, 885–896. [Google Scholar] [CrossRef]
- Canova, A.; Vusini, B. Design of axial eddy-current couplers. IEEE Trans. Ind. Appl. 2003, 39, 725–733. [Google Scholar] [CrossRef]
- Paudel, N.; Bird, J.Z. General 2-D steady-state force and power equations for a traveling time-varying magnetic source above a conductive plate. IEEE Trans. Magn. 2012, 48, 95–100. [Google Scholar] [CrossRef]
- Jin, Y.; Kou, B.; Li, L.; Pan, D. Thermal analysis of a hybrid excitation linear eddy current brake. IEEE Trans. Ind. Electron. 2019, 66, 2987–2997. [Google Scholar] [CrossRef]
- Jiao, Z.; Wang, T.; Liang, Y. Design of a tubular linear oscillating motor with novel compound halbach magnet array. IEEE/ASME Trans. Mechatron. 2017, 22, 498–508. [Google Scholar] [CrossRef]
- Gysen, B.L.J.; Meessen, K.J.; Paulides, J.J.H.; Lomonova, E.A. General formulation of the electromagnetic field distribution in machines and devices using fourier analysis. IEEE Trans. Magn. 2010, 46, 39–52. [Google Scholar] [CrossRef]
- Liu, Z.J.; Vourdas, A.; Binns, K.J. Magnetic field and eddy current losses in linear and rotating permanent magnet machines with a large number of poles. Sci. Meas. Technol. IEE Proc. A 1991, 138, 289–294. [Google Scholar] [CrossRef]
- Kou, B.; Jin, Y.; Zhang, H.; Lu, Z. Analysis and design of hybrid excitation linear eddy current brake. IEEE Trans. Energy Convers. 2014, 29, 496–506. [Google Scholar]
- Kou, B.; Jin, Y.; Zhang, H.; Zhang, L. Nonlinear analytical modeling of hybrid-excitation double-sided linear eddy-current brake. IEEE Trans. Magn. 2015, 51, 8003404. [Google Scholar] [CrossRef]
- Kawai, T.; Inamori, T.; Hori, K. Analytical lorentz force model between 1-D linear currents in arbitrary relative positions and directions. IEEE Trans. Magn. 2018, 54, 1–16. [Google Scholar] [CrossRef]
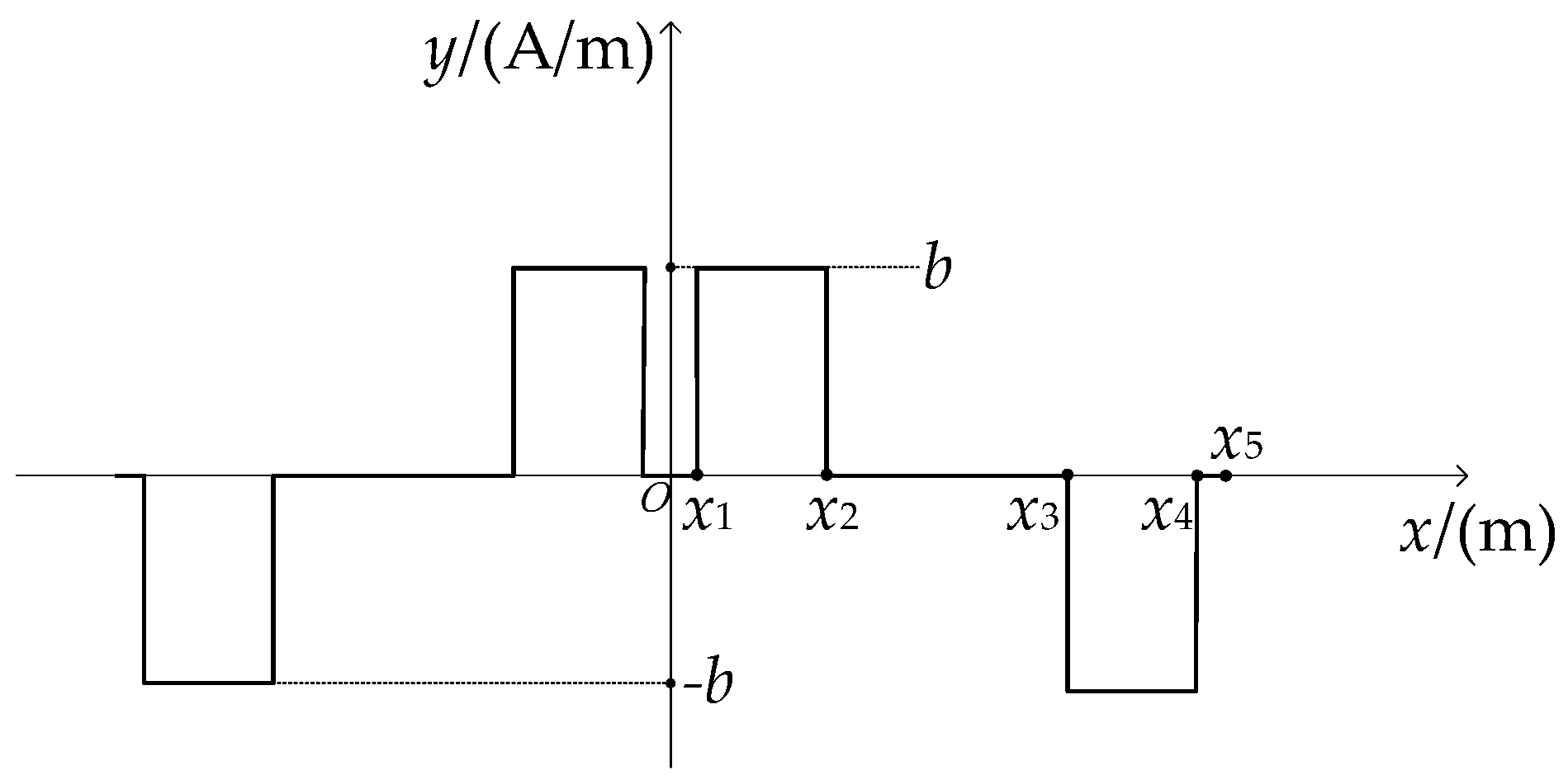


| Parameter | Value |
|---|---|
| x1 | c/2 |
| x2 | c/2 + bc |
| x3 | τ − (c/2 + bc) |
| x4 | τ − c/2 |
| x5 | τ |
| Parameter | Value |
|---|---|
| number of pole pairs p | 6 |
| maximum operating speed vmax | 272 m/s |
| exciting current density J | 12 A/mm2 |
| static air gap magnetic density B0 | 1.5 T |
| the fill factor kf | 0.687 |
| height of exciting coil hc | 115 mm |
| width of exciting coil bc | 15.3 mm |
| pole pitch τ | 100 mm |
| air gap length δ | 10 mm |
| height of yoke hs | 120 mm |
| height of pole hp | 120 mm |
| width pole bp | 69.2 mm |
| thickness of induction plate bg | 5 mm |
| thickness of back iron bs | 30 mm |
| model depth w | 200 mm |
| induction plate conductivity σ | 106 S·m−1 |
| setting simulation time | 6 ms |
| Variable | Peak Braking Force | Critical Speed |
|---|---|---|
| air gap length | 1.89% | 2.25% |
| pole pitch | 2.17% | 2.25% |
| induction plate thickness | 2.01% | 2.16% |
| induction plate conductivity | 5.09% | 21.4% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Xu, J.; Yuan, X.; Wu, X. Characteristic Analysis of the Peak Braking Force and the Critical Speed of Eddy Current Braking in a High-Speed Maglev. Energies 2019, 12, 2622. https://doi.org/10.3390/en12132622
Chen C, Xu J, Yuan X, Wu X. Characteristic Analysis of the Peak Braking Force and the Critical Speed of Eddy Current Braking in a High-Speed Maglev. Energies. 2019; 12(13):2622. https://doi.org/10.3390/en12132622
Chicago/Turabian StyleChen, Chuntao, Jie Xu, Xibo Yuan, and Xinzhen Wu. 2019. "Characteristic Analysis of the Peak Braking Force and the Critical Speed of Eddy Current Braking in a High-Speed Maglev" Energies 12, no. 13: 2622. https://doi.org/10.3390/en12132622
APA StyleChen, C., Xu, J., Yuan, X., & Wu, X. (2019). Characteristic Analysis of the Peak Braking Force and the Critical Speed of Eddy Current Braking in a High-Speed Maglev. Energies, 12(13), 2622. https://doi.org/10.3390/en12132622






