Numerical Investigation of Flow through a Valve during Charge Intake in a DISI -Engine Using Large Eddy Simulation
Abstract
1. Introduction
2. LES Methodology
3. Engine Configuration and Numerical Setup
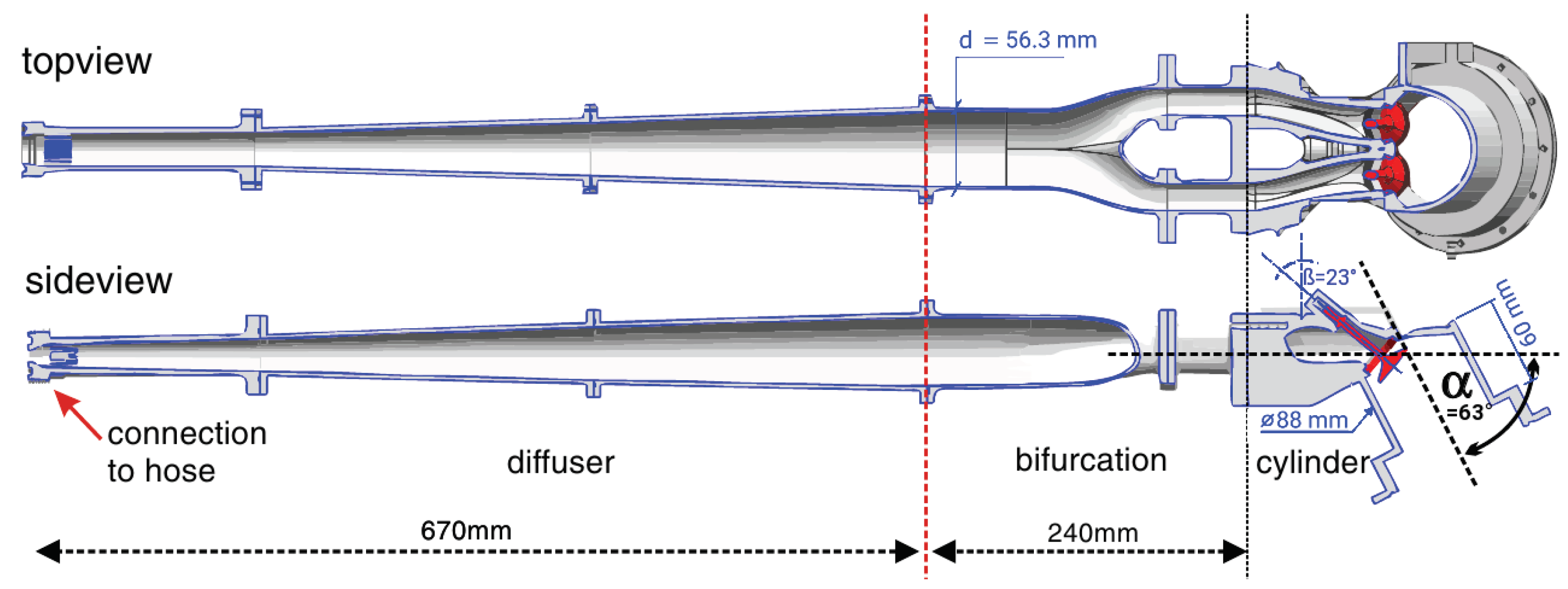
3.1. Engine Configuration
3.2. Numerical Setup: Inlet and Initial Conditions
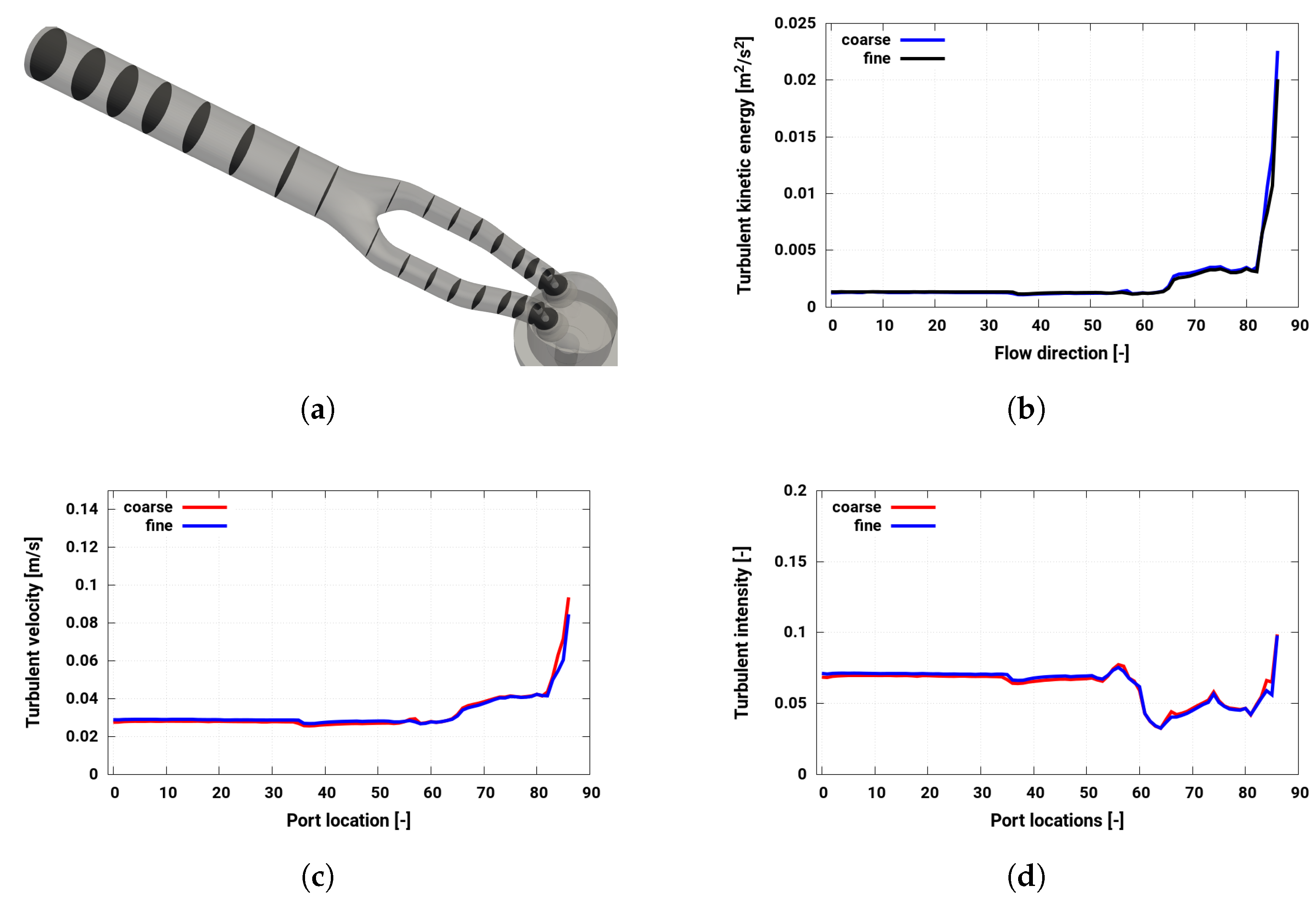
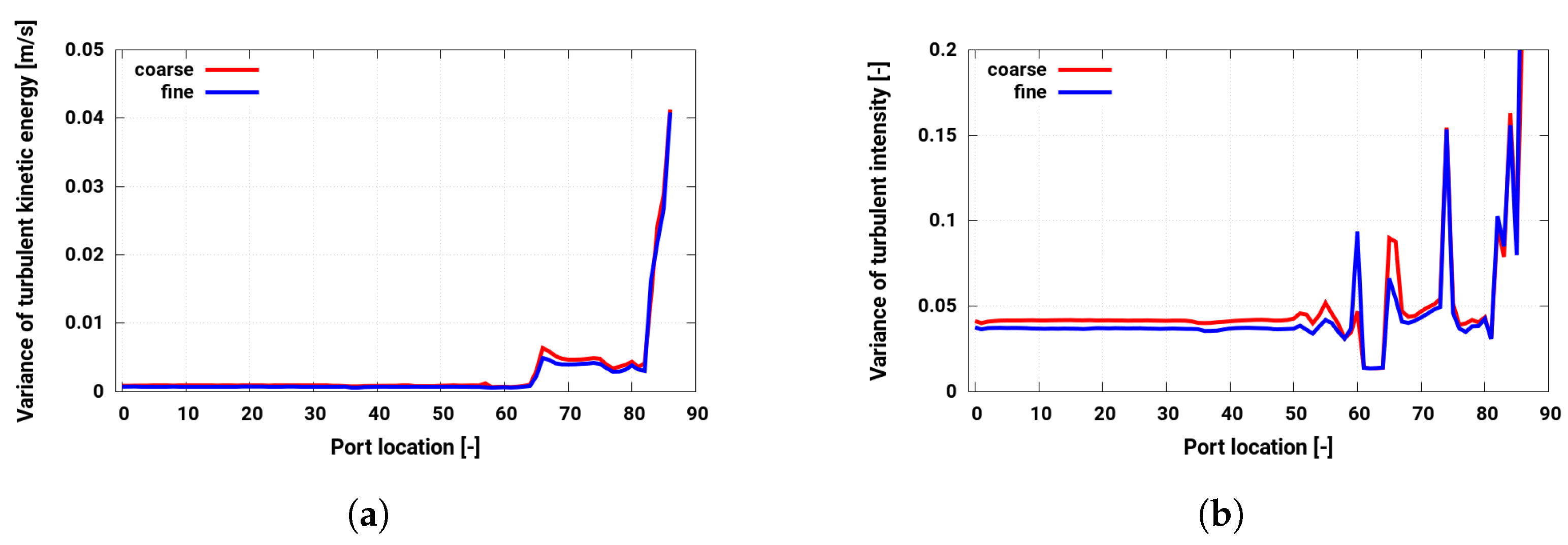
3.3. Numerical Setup: Prior Evaluation of Simulation Measures
4. Results and Discussion
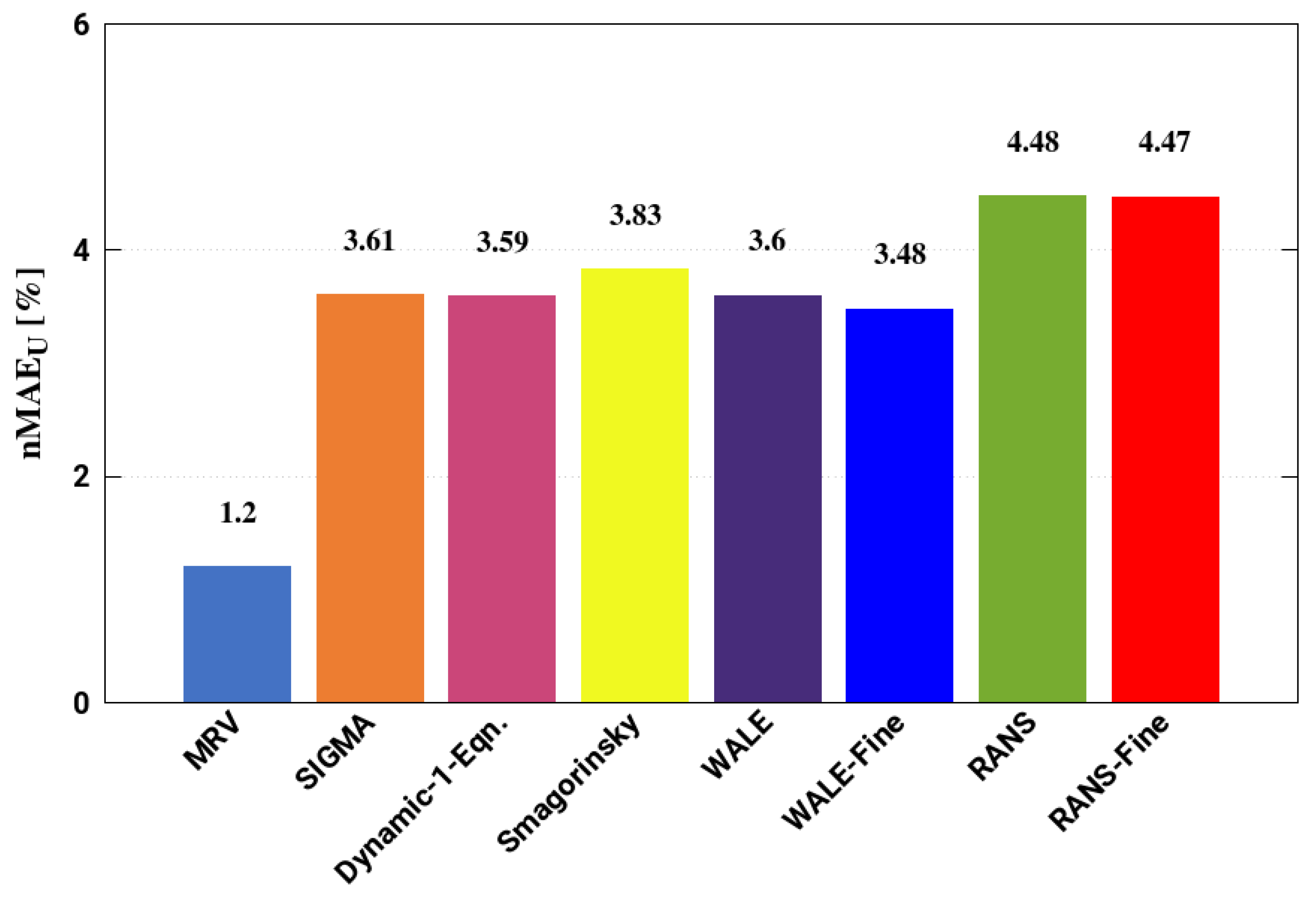
4.1. Evaluation of SGS/Turbulence Models Based on Error Analysis
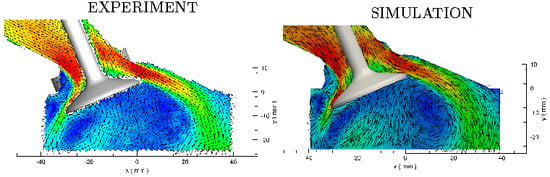
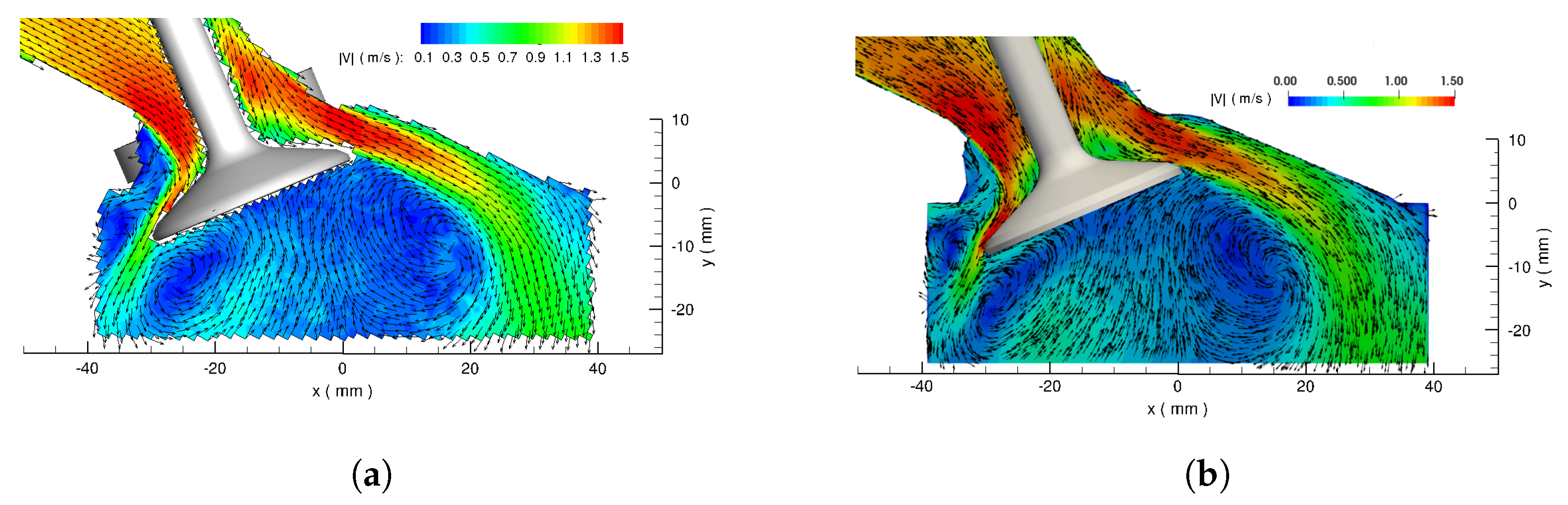
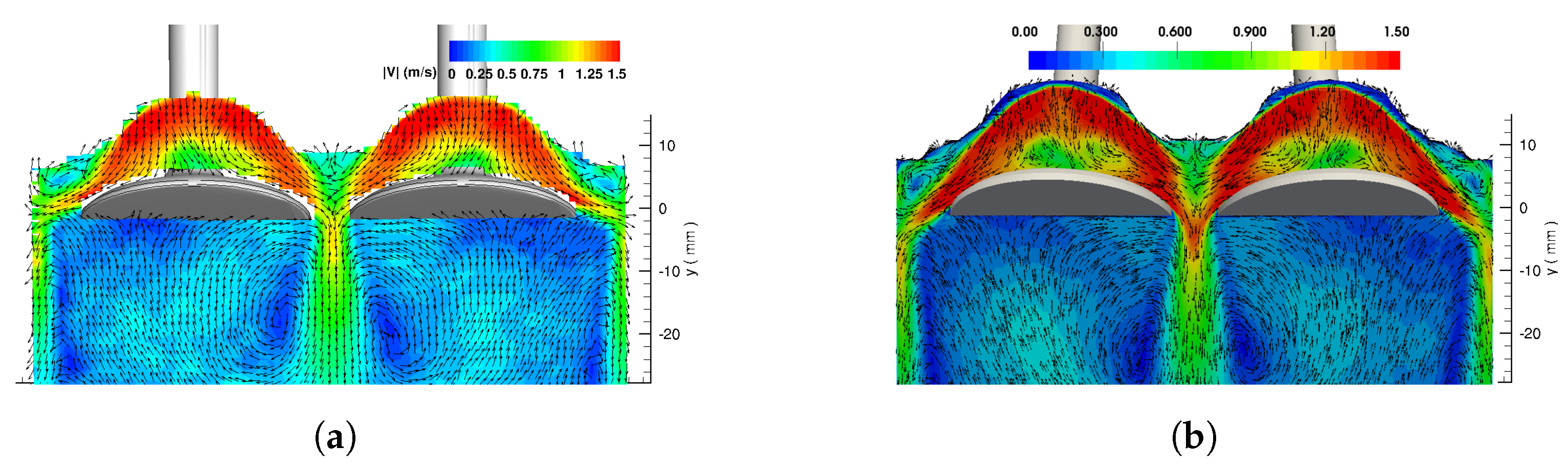
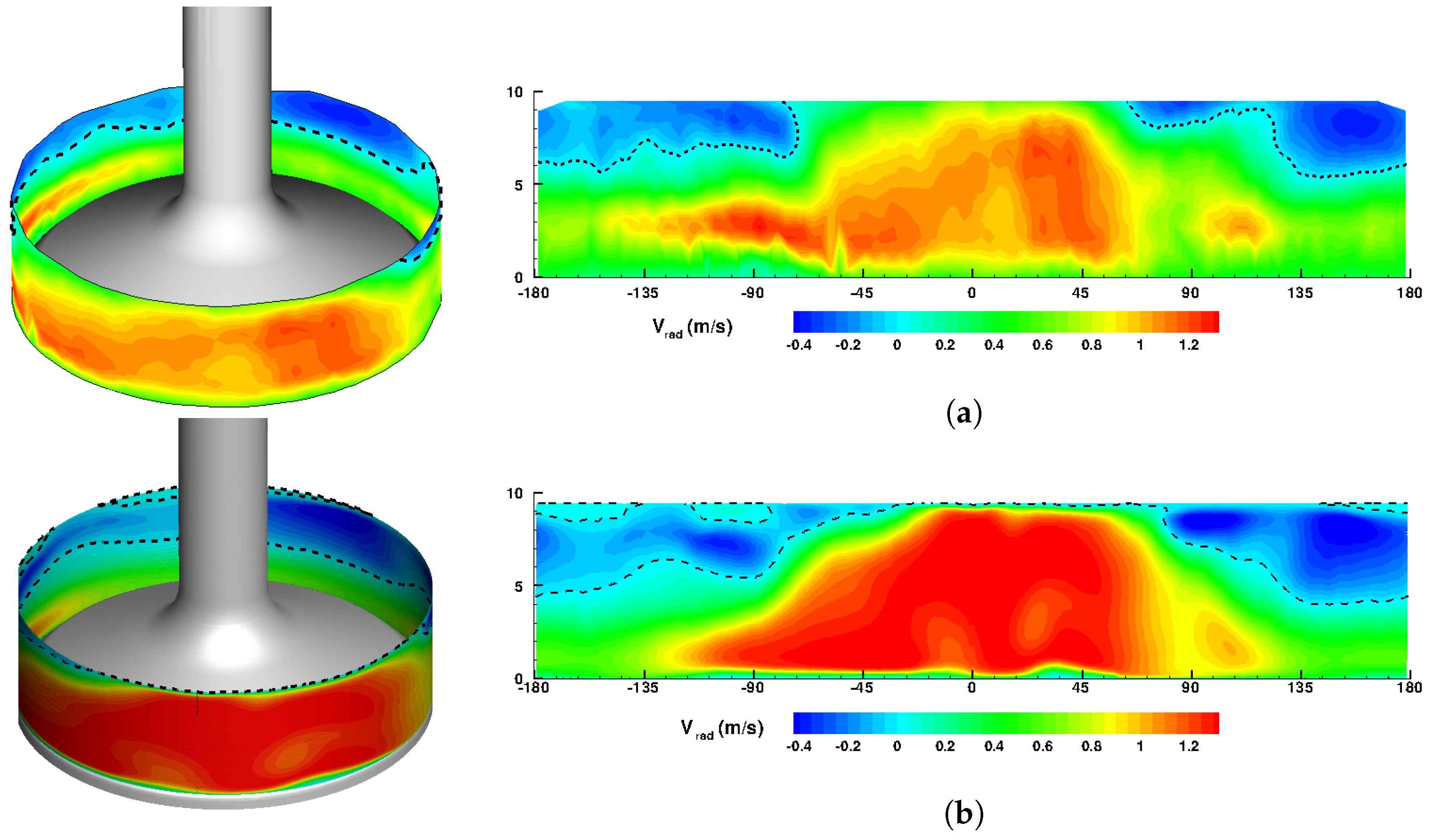
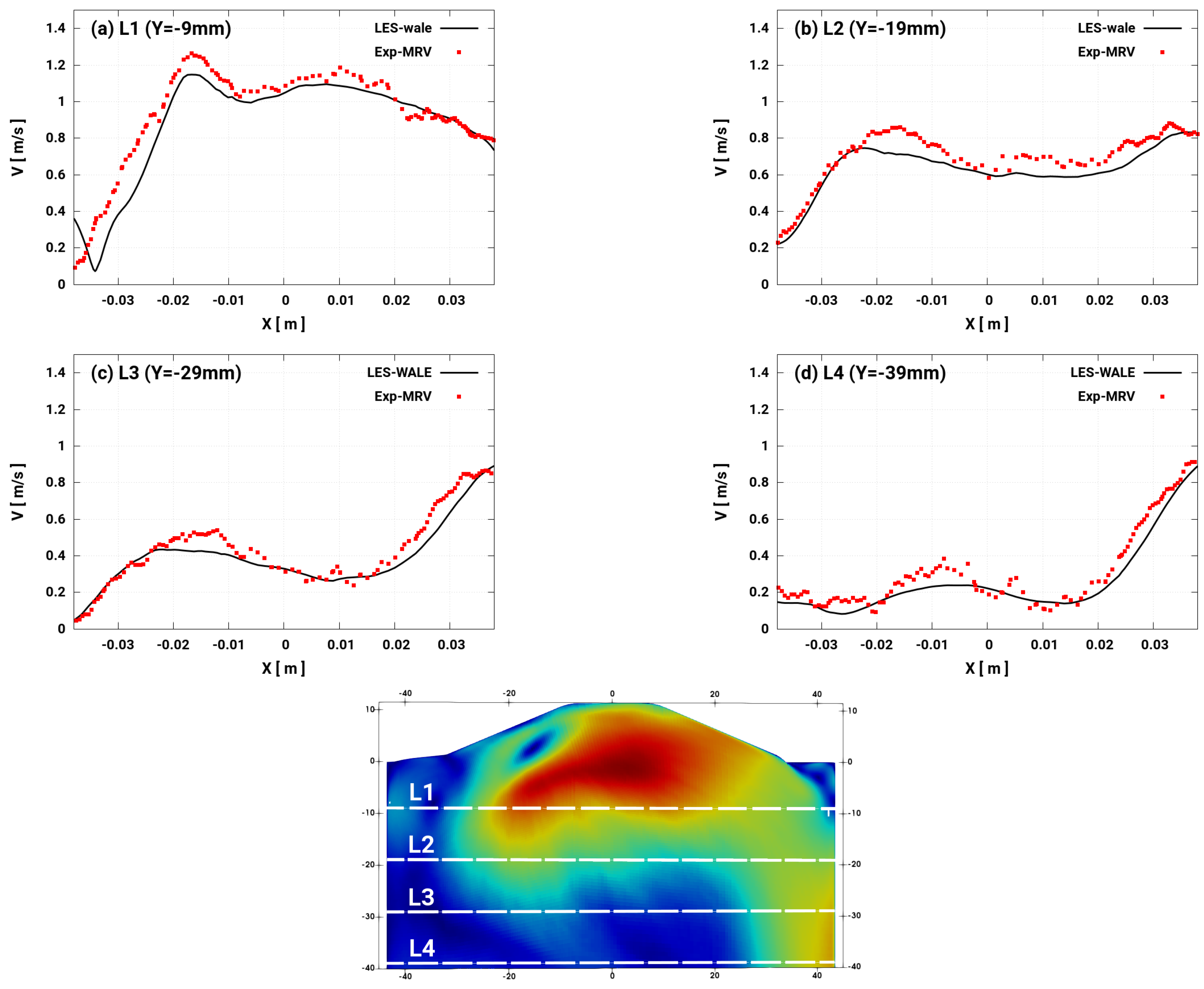
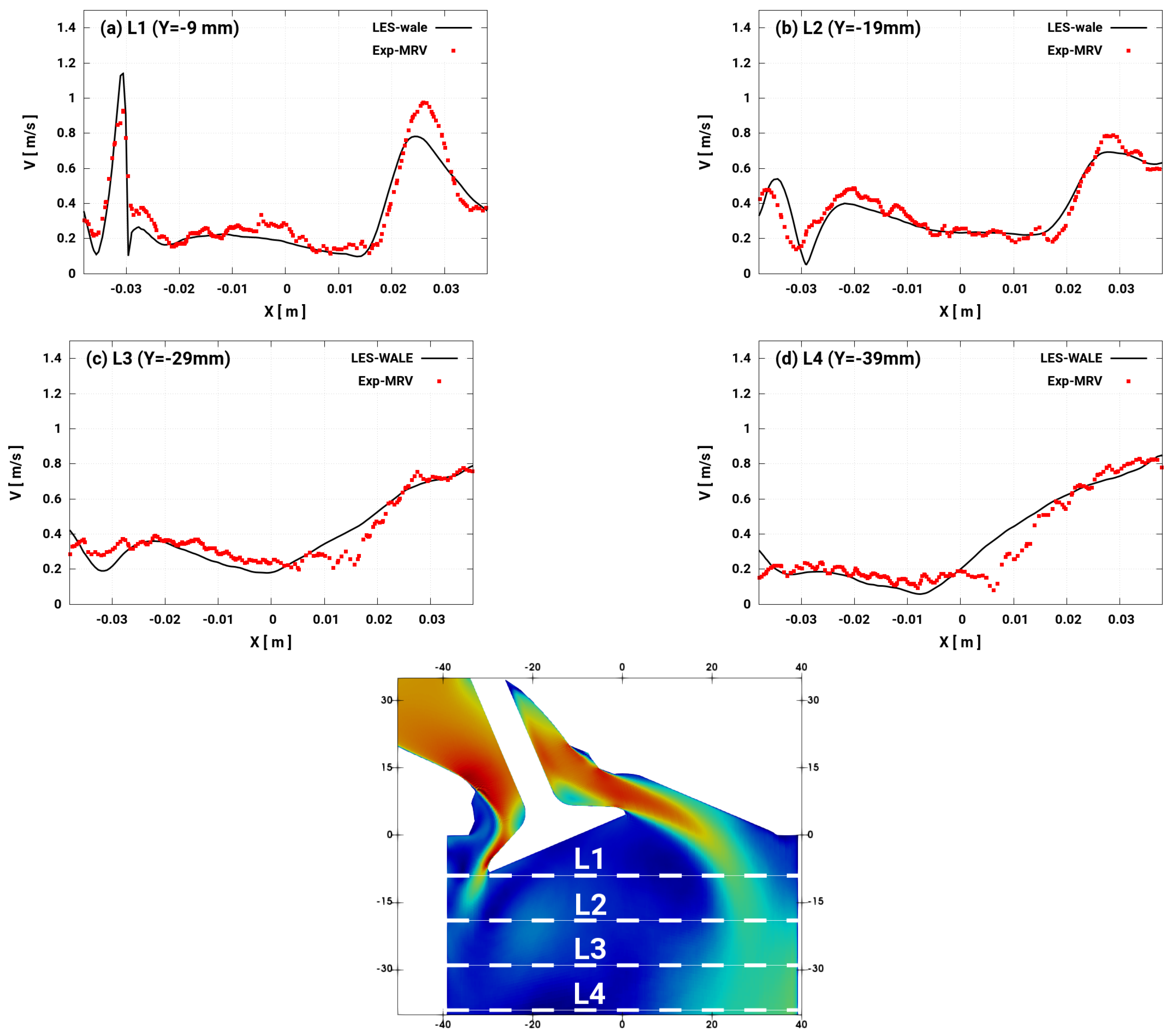
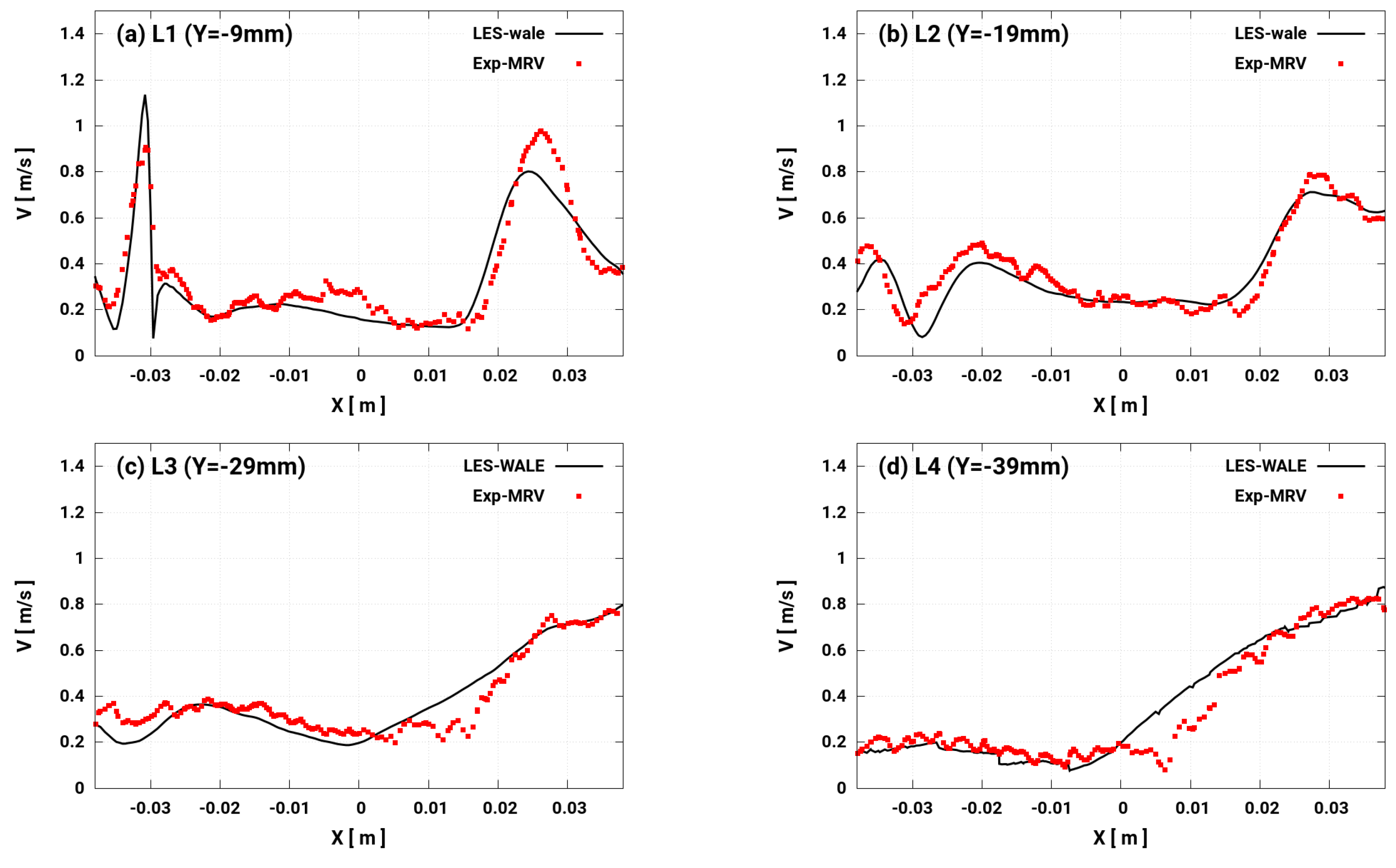
4.2. Validation: Comparisons of LES Results with MRV Data
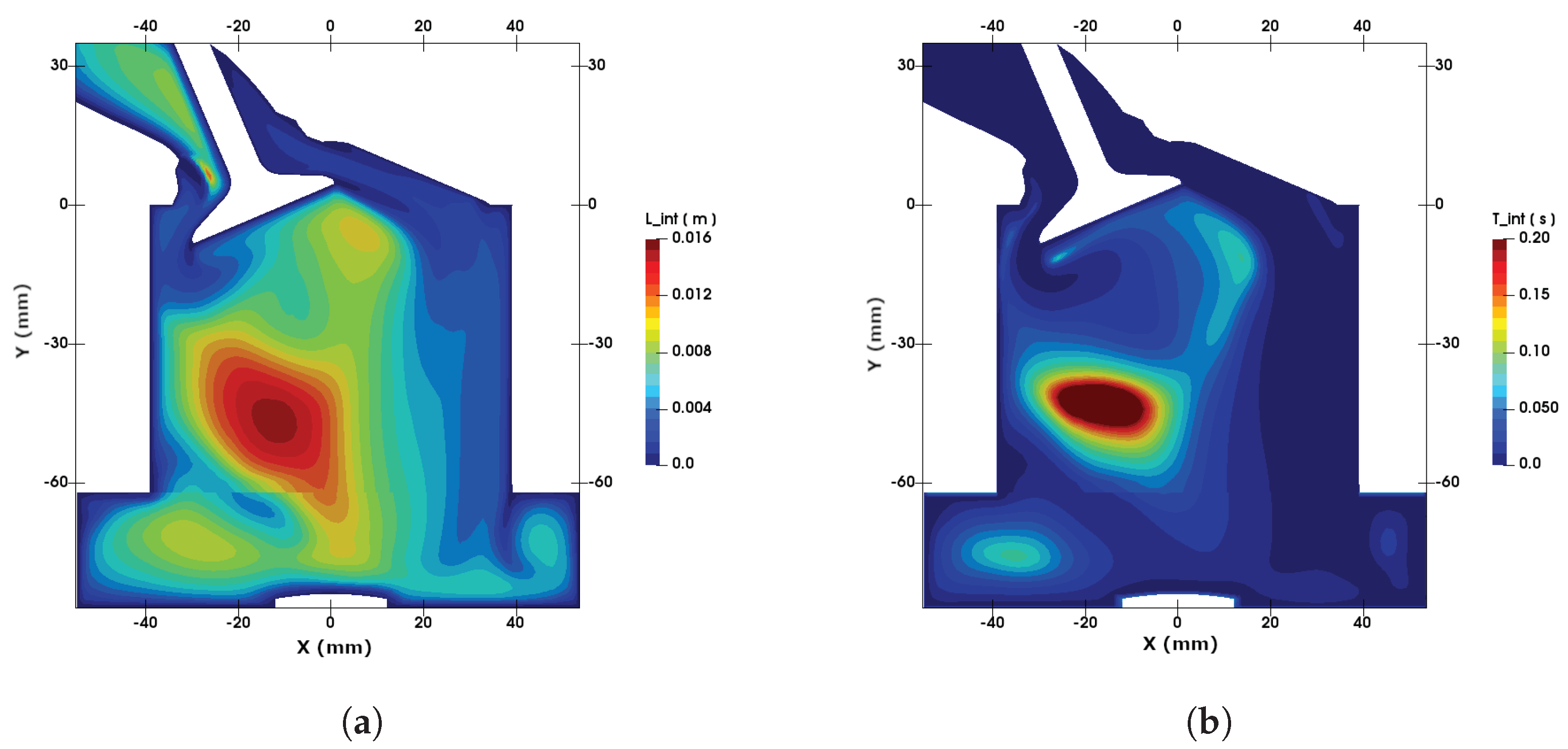
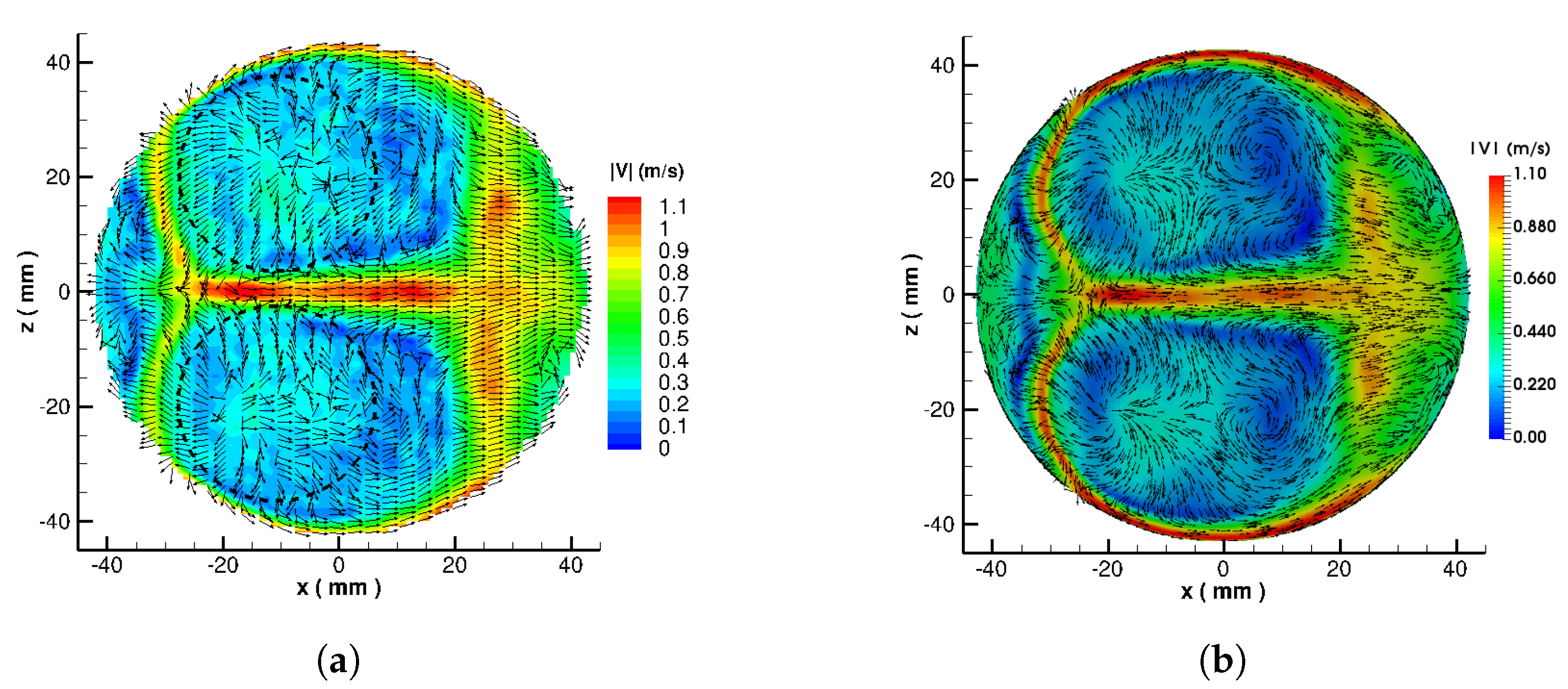
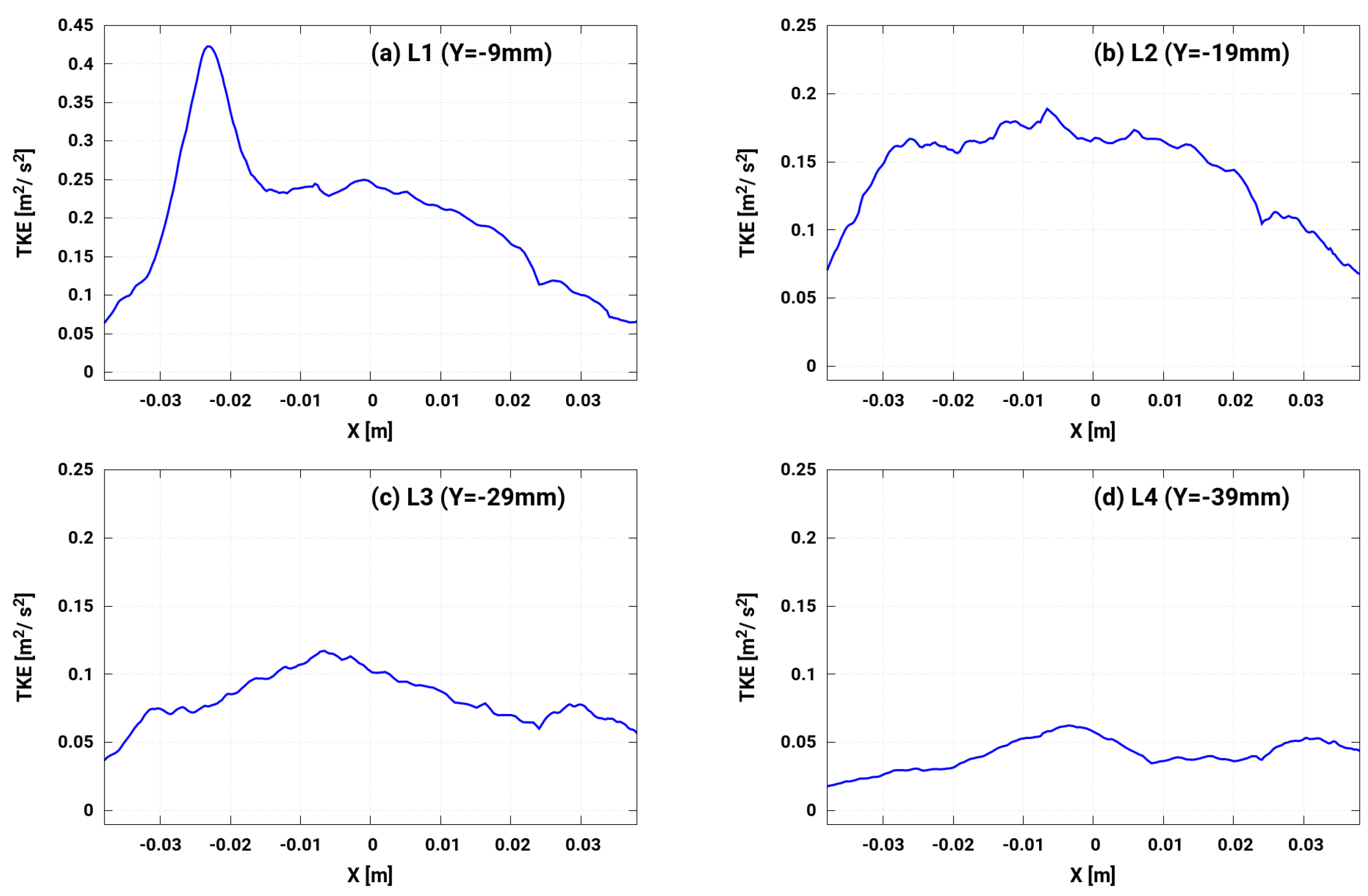
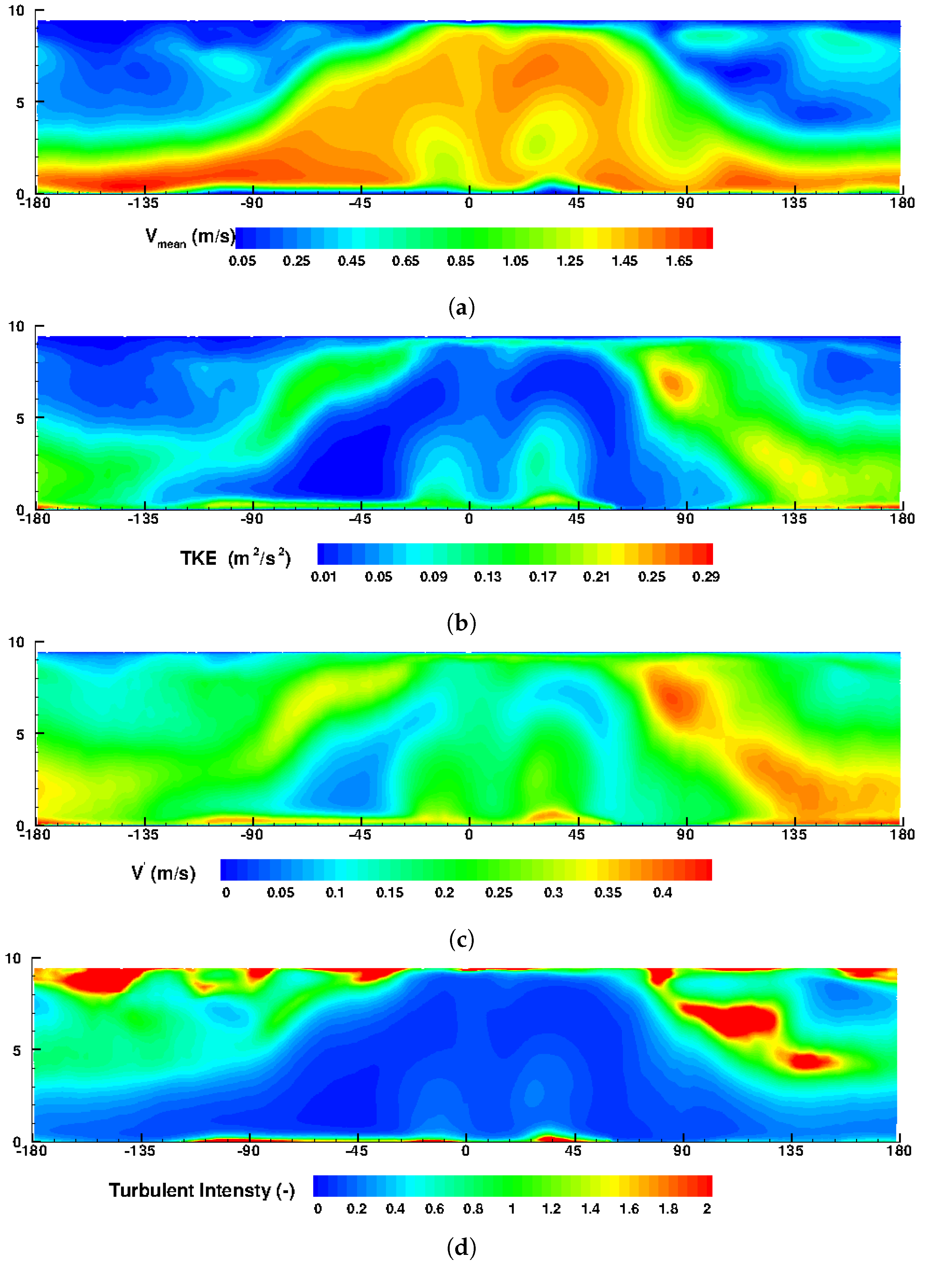
4.3. Turbulence and Statistical Analysis in the Engine Cylinder Chamber and the Intake Port
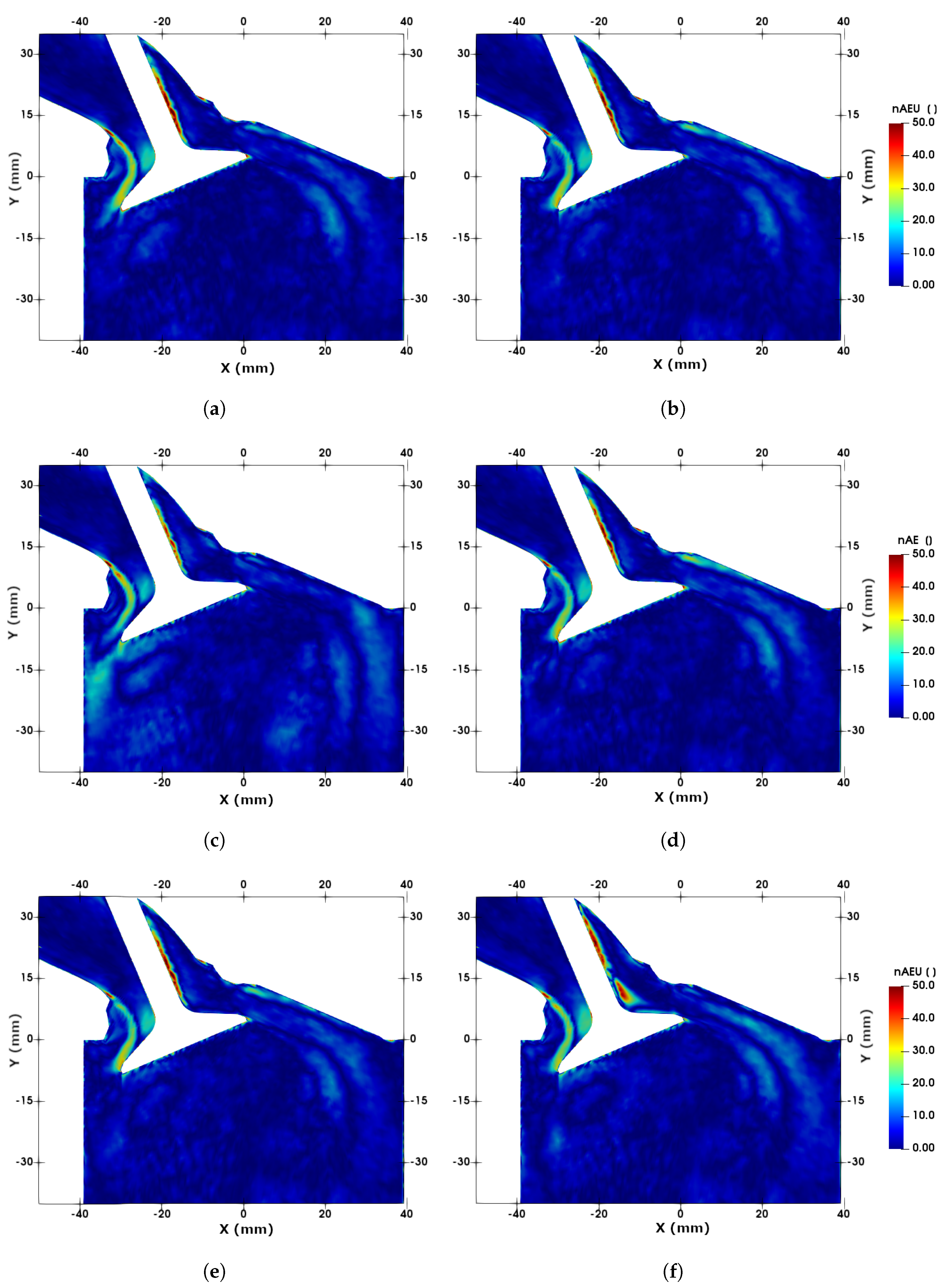
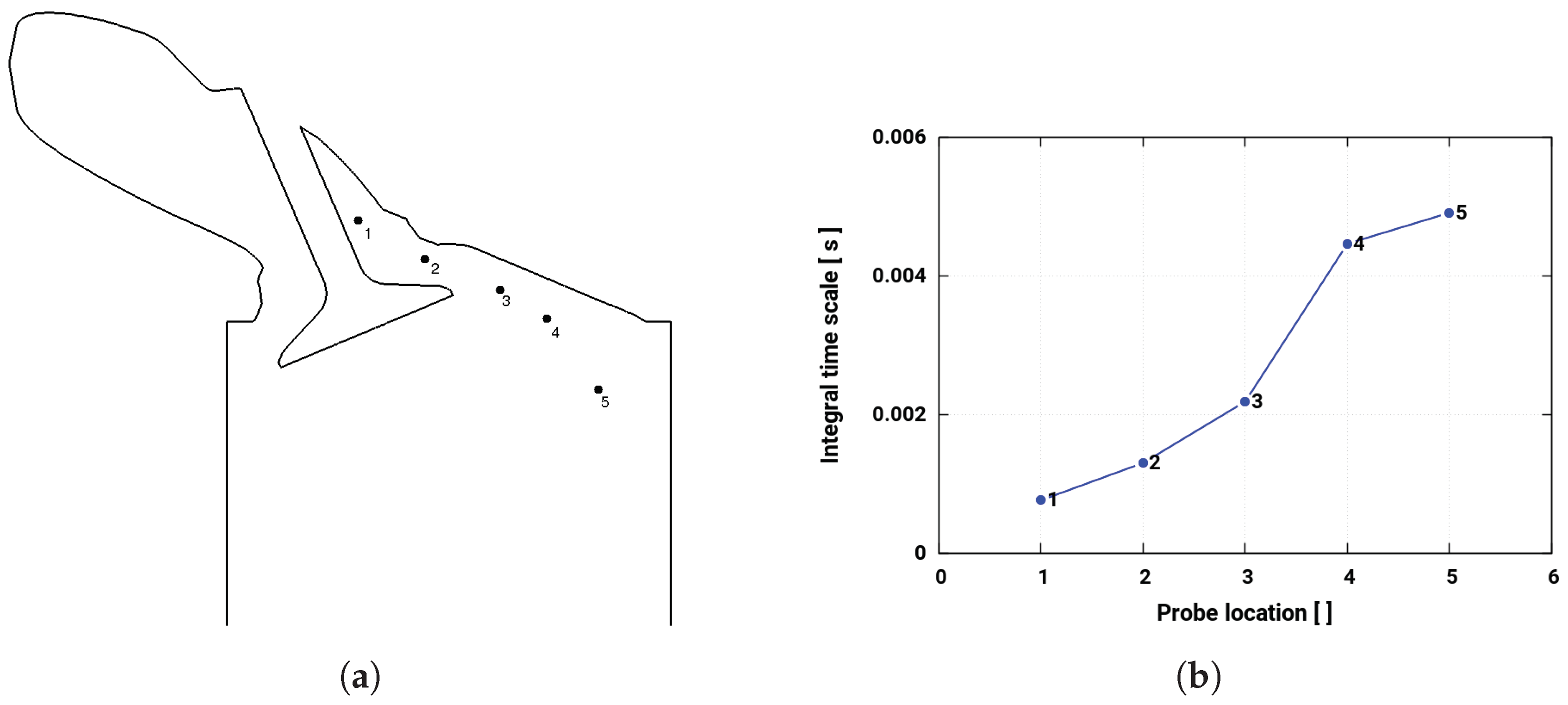
4.4. Turbulence Evolution along the Intake Port
5. Summary
- the WALE model featured relatively a less normalized absolute error relying on the velocity field and emerged as the suitable choice among all the models applied. The standard RANS k- model has proven to be less accurate.
- using the WALE model based on the cost-accuracy criteria, the turbulent flow across the valve curtain clearly featured a back flow resulting in high speed intake jet at the middle. The averaged velocity results showed excellent agreement between LES and MRV measurement revealing the high prediction capability of the suggested LES tool for valve flows.
- physically, for the in-cylinder turbulent flow and for the intake port part, the turbulence and statistical analysis provided by LES led to some additional valuable findings. First, the flow anisotropy along the intake valve has been detected by means of an anisotropy map. Next, the integral turbulent scales along the intake-charge stream suggested a gradual increment of turbulent length scale downstream. Third, the evolution of turbulence properties along the port length showed that the most of the turbulence are generated across the valve passage and are mainly responsible for in-cylinder turbulence.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heywood, J.B. Internal Combustion Engines Fundamentals; McGraw-Hill Publications: Hoboken, NJ, USA, 1989. [Google Scholar]
- Bicen, A.; Vafidis, C.; Whitelaw, J. Steady and unsteady airflow through the intake valve of a reciprocating engine. J. Fluids Eng. 1985, 107, 413–420. [Google Scholar] [CrossRef]
- Desantes, J.M.; Benajes, J.; Urchueguia, J. Evaluation of the non-steady flow produced by intake ports of direct injection Diesel engines. Exp. Fluids 1995, 19, 51–60. [Google Scholar]
- Fukutani, I.; Watanabe, E. Air Flow through Poppet Inlet Valves—Analysis of Static and Dynamic Flow Coefficients; SAE Technical Paper; SAE International: Troy, MI, USA, 1982; p. 820154. [Google Scholar]
- Towers, D.P.; Towers, C.E. Cyclic variability measurements of in-cylinder engine flows using high-speed particle image velocimetry. Meas. Sci. Technol. 2004, 15, 1917–1925. [Google Scholar] [CrossRef]
- Drake, M.; Fansler, T.D.; Lippert, A.M. Stratified-charge combustion: Modeling and imaging of a spray-guided direct-injection spark-ignition engine. Int. J. Engine Res. 2005, 30, 2683–2691. [Google Scholar] [CrossRef]
- Drake, M.; Haworth, D. Advanced gasoline engine development using optical diagnostics and numerical modeling. Proc. Combust. Inst. 2007, 32, 99–124. [Google Scholar] [CrossRef]
- Fansler, T.D.; Reuss, D.L.; Sick, V.; Dahms, R.N. Invited Review: Combustion instability in spray-guided stratified-charge engines: A review. Int. J. Engine Res. 2015, 16, 260–305. [Google Scholar] [CrossRef]
- Stiehl, R.; Bode, J.; Schorr, J.; Krüger, C.; Dreizler, A.; Böhm, B. Influence of intake geometry variations on in-cylinder flow and flow–spray interactions in a stratified direct-injection spark-ignition engine captured by time-resolved particle image velocimetry. Int. J. Engine Res. 2016, 17, 983–997. [Google Scholar] [CrossRef]
- Church, W.; Farrell, P. Effects of Intake Port Geometry on Large Scale In-Cylinder Flows; SAE Technical Paper; lSAE International: Troy, MI, USA, 1998; p. 980484. [Google Scholar]
- Justham, T.; Jarvis, S.; Clarke, A.; Garner, C.; Hargrave, G.K.; Halliwell, N. Simultaneous study of intake and in-cylinder IC engine flow fields to provide an insight into intake induced cyclic variations. J. Phys. Conf. Ser. 2006, 45, 146–153. [Google Scholar]
- Freudenhammer, D.; Peterson, B.; Ding, C.; Böhm, B.; Jung, B.; Grundmann, S. The influence of cylinder head geometry variations on the volumetric intake flow captured by magnetic resonance velocimetry. SAE Int. 2015, 8, 1826–1836. [Google Scholar] [CrossRef]
- Hartmann, F.; Buhl, S.; Gleiss, F.; Barth, P.; Schild, M.; Kaiser, S.A.; Haase, C. Spatially resolved experimental and numerical investigation of the flow through the intake port of an internal combustion engine. Oil Gas Sci. Technol. Rev. IFP Energies Nouvelles 2016, 71, 1–15. [Google Scholar] [CrossRef]
- Freudenhammer, D.; Baum, E.; Peterson, B.; Böhm, B.; Jung, B.; Grundmann, S. Volumetric intake flow measurement of an IC engine using magnetic resonance velocimetry. Exp. Fluids 2014, 55, 1724. [Google Scholar] [CrossRef]
- Freudenhammer, D.; Baum, E.; Peterson, B.; Böhm, B.; Grundmann, S. Towards time-resolved magnetic resonance velocimetry for IC-engine intake flows. In Proceedings of the 17th International Symposium of Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 7–10 July 2014. [Google Scholar]
- Baum, E.; Peterson, B.; Böhm, B.; Dreizler, A. On the validation of LES applied to internal combustion engine flows: Part 1: Comprehensive experimental database. Flow Turbul. Combust. 2014, 92, 269–299. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, Z.; Sun, Y.; Sun, T.; Zhang, R. Steady and unsteady airflow through the intake valve of a reciprocating engine. Eng. Appl. Comput. Fluid Mech. 2016, 10, 312–330. [Google Scholar]
- Nishad, K. Modeling and Unsteady Simulation of Turbulent Multi-Phase Turbulent Flow Including Fuel Injection in IC-Engines. Ph.D. Thesis, Darmstadt University of Technology, Darmstadt, Germany, 2013. [Google Scholar]
- Schmitt, M.; Frouzakis, C.E.; Tomboulides, A.G.; Wright, Y.M.; Boulouchos, K. Direct numerical simulation of multiple cycles in a valve/piston assembly. Phys. Fluids 2014, 26, 1–26. [Google Scholar]
- Vermorel, O.; Richard, S.; Colin, O.; Angelberger, C.; Benkenida, A.; Veynante, D. Towards the understanding of cyclic variability in a spark ignited engine using multi-cycle LES. Combust. Flame 2007, 156, 1525–1541. [Google Scholar] [CrossRef]
- Goryntsev, D.; Sadiki, A.; Klein, M.; Janicka, J. Large eddy simulation based analysis of the effects of cycle-to-cycle variations on air-fuel mixing in realistic DISI engines. Proc. Combust. Inst. 2009, 32, 2759–2766. [Google Scholar] [CrossRef]
- Enaux, B.; Granet, V.; Vermorel, O.; Lacour, C.; Thobois, L.; Dugué, V.; Poinsot, T. Large eddy simulation of a motored single-cylinder piston engine: numerical strategies and validation. Flow Turbul. Combust. 2010, 86, 153–177. [Google Scholar]
- Granet, V.; Vermorel, O.; Lacour, C.; Enaux, B.; Dugué, V.; Poinsot, T. Large-Eddy Simulation and experimental study of cycle-to-cycle variations of stable and unstable operating points in a spark ignition engine. Combust. Flame 2012, 159, 562–1575. [Google Scholar] [CrossRef]
- Goryntsev, D.; Nishad, K.; Sadiki, A.M.; Janicka, J. Application of LES for analysis of unsteady effects on combustion processes and misfires in DISI engine. Oil Gas Sci. Technol. Revue d’IFP Energies Nouvelles 2014, 69, 129–140. [Google Scholar] [CrossRef]
- Sadiki, A.; Di Mare, F.; Nishad, K.; Keller, P.; Stefan, B.; Hartmannand, F.; Hasse, C. Internal Combustion Engine. In Ercoftac best Practice Guidlines: Computational Fluid Dynamics of Turbulent Combustion; Chapter 5; Vervisch, L., Roekaerts, D., Eds.; Ercoftac: European Research Community on Flow, Turbulence and Combustion: London, UK, 2015. [Google Scholar]
- Smagorinsky, J. General circulation experiments with primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Janicka, J.; Sadiki, A. Large eddy simulation of turbulent combustion systems. Proc. Combust. Inst. 2005, 30, 537–547. [Google Scholar] [CrossRef]
- Pitsch, H. Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 1999, 38, 453–482. [Google Scholar] [CrossRef]
- Rutland, C. Large eddy simulations for internal combustion engines - a review. Int. J. Engine Res. 2011, 12, 421–451. [Google Scholar] [CrossRef]
- Keskinen, J.; Vuorinen, V.; Larmi, M. Large Eddy Simulation of the Intake Flow in a Realistic Single Cylinder Configuration; SAE Technical Paper; SAE International: Troy, MI, USA, 2012. [Google Scholar]
- Thobois, L.; Rymer, G.; Souleres, T.; Poinsot, T.; Van den Heuvel, B. Large-Eddy Simulation for the Prediction of Aerodynamics in IC Engines. Int. J. Veh. Des. 2005, 39, 368–382. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. OpenFOAM Programmer’s Guide, 2.4.0 ed.; The OpenFOAM Foundation: London, UK, 2015. [Google Scholar]
- Ries, F.; Nishad, K.; Dressler, L.; Janicka, J.; Sadiki, A. Evaluating large eddy simulation results based on error analysis. Theor. Comput. Fluid Dyn. 2018, 1–20. [Google Scholar] [CrossRef]
- Spalding, D.B. A single formula for the “law of the wall”. J. Appl. Mech. 1961, 28, 455–458. [Google Scholar] [CrossRef]
- Klein, M.; Sadiki, A.; Janicka, J. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 2003, 186, 652–665. [Google Scholar] [CrossRef]
- Kempf, A.; Klein, M.; Janicka, J. Efficient generation of initial- and inflow-conditions for transient turbulent flows in arbitrary geometries. Flow Turbul. Combust. 2005, 74, 67–84. [Google Scholar] [CrossRef]
- Zagarola, M.; Perry, A.; Smits, A. Log laws or power laws: The scaling in the overlap region. Phys. Fluids 1997, 9, 2094–2100. [Google Scholar] [CrossRef]
- Lund, T.; Wu, X.; Squires, K. Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 1998, 140, 233–258. [Google Scholar] [CrossRef]
- Launder, B.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Oberkampf, W.; Roy, C.J. Verification and Validation in Scientific Computing; Cambridge University Press: Camnridge, UK, 2010. [Google Scholar]
- Lumley, J.; Newman, G. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 1977, 82, 161–178. [Google Scholar] [CrossRef]



| LES Models | Operator | Model Coefficient |
|---|---|---|
| Smagorinsky | = 0.18 | |
| WALE | = 0.5 | |
| SIGMA | = 1.5 | |
| one-equation | = 0.18, = 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishad, K.; Ries, F.; Li, Y.; Sadiki, A. Numerical Investigation of Flow through a Valve during Charge Intake in a DISI -Engine Using Large Eddy Simulation. Energies 2019, 12, 2620. https://doi.org/10.3390/en12132620
Nishad K, Ries F, Li Y, Sadiki A. Numerical Investigation of Flow through a Valve during Charge Intake in a DISI -Engine Using Large Eddy Simulation. Energies. 2019; 12(13):2620. https://doi.org/10.3390/en12132620
Chicago/Turabian StyleNishad, Kaushal, Florian Ries, Yongxiang Li, and Amsini Sadiki. 2019. "Numerical Investigation of Flow through a Valve during Charge Intake in a DISI -Engine Using Large Eddy Simulation" Energies 12, no. 13: 2620. https://doi.org/10.3390/en12132620
APA StyleNishad, K., Ries, F., Li, Y., & Sadiki, A. (2019). Numerical Investigation of Flow through a Valve during Charge Intake in a DISI -Engine Using Large Eddy Simulation. Energies, 12(13), 2620. https://doi.org/10.3390/en12132620