Robust Optimization of Energy Hubs Operation Based on Extended Affine Arithmetic
Abstract
:1. Introduction
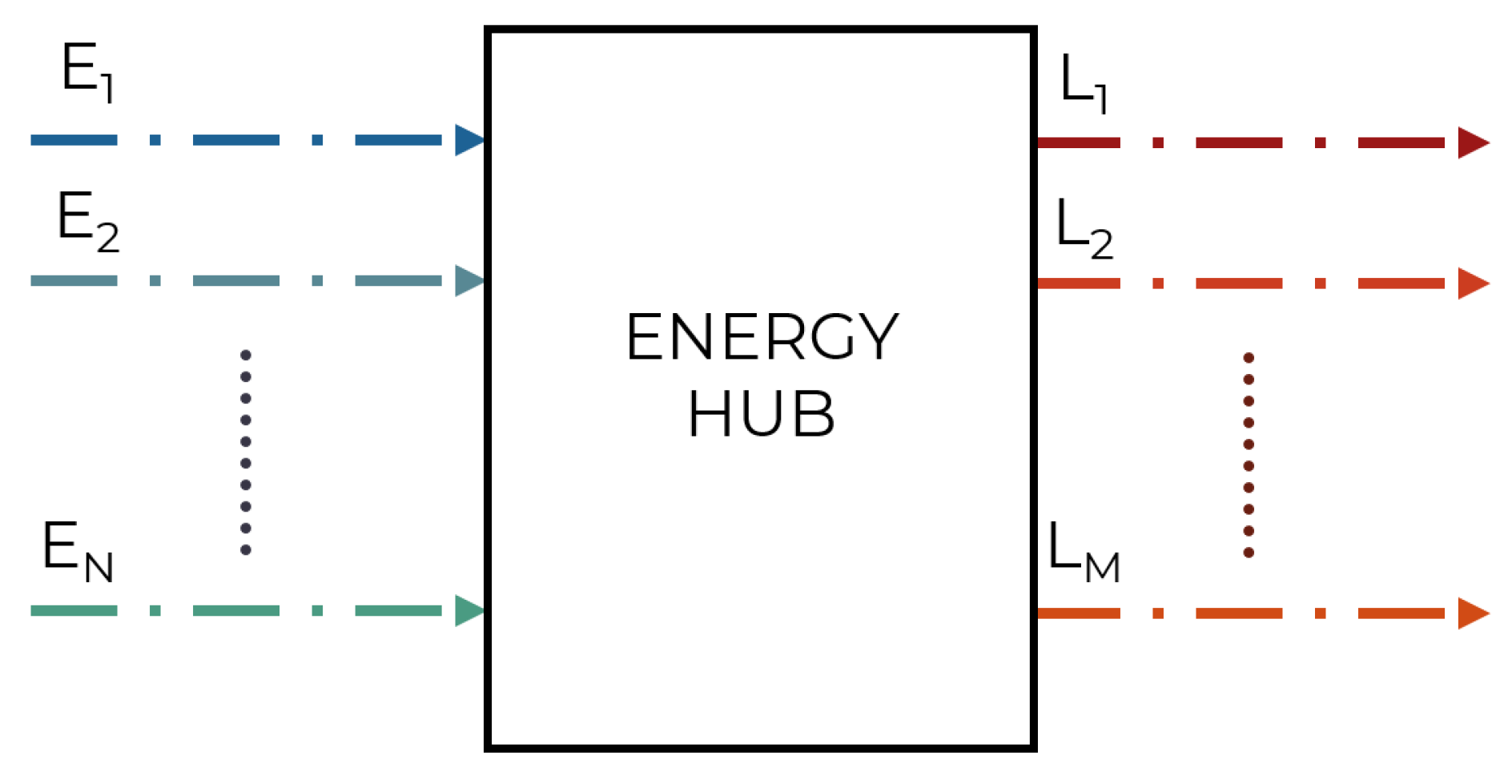
2. The Energy Hub and the Optimal Dispatch Problem
2.1. Energy Hub
2.2. Deterministic Optimal Dispatch
- Energy prices: Electricity and natural gas prices are uncertain. Depending on the considered energy system, they are characterized by different degrees of volatility, which can be estimated [34].
- Load dynamics: Loads are predictable only with a certain degree of accuracy. Different external factors, such as economic, weather and social aspects, affect their dynamics, thus their behaviour is uncertain.
- Renewable energy generation: Production from solar and wind power are intrinsically uncertain [35].
3. Affine Arithmetic
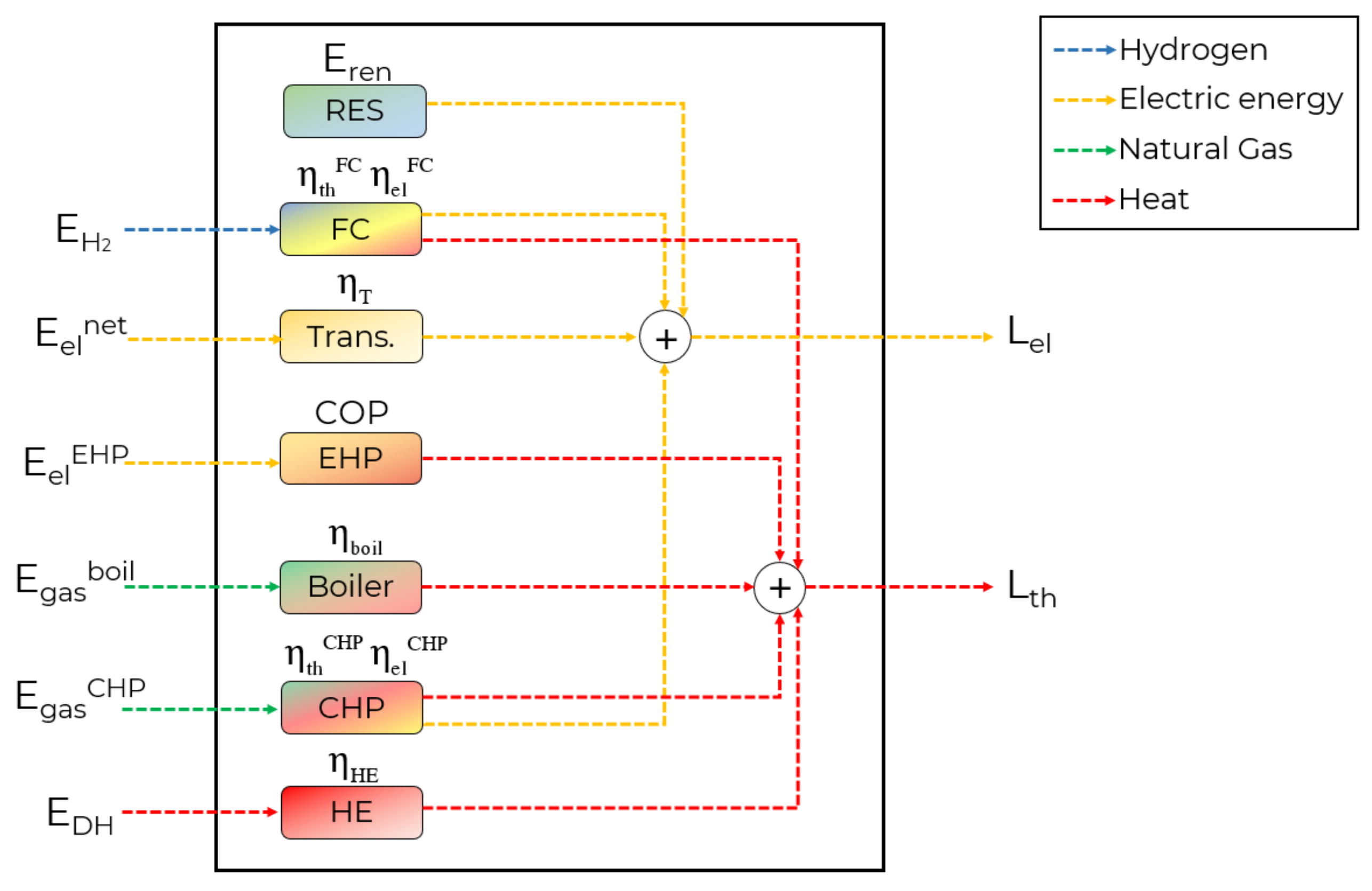
4. Case Study
- Transformer: it connects the electric energy input from the grid to the electric load, .
- Electric Heat Pumps (EHP): they serve the thermal load by efficiently converting input electric energy, the coefficient of performance (COP) is set to .
- Boilers: they simply work by burning natural gas and serving thermal load, .
- Combined Heat and Power (CHP): such elements serve both loads, and they are fed by natural gas. The efficiencies for electric and thermal conversion are: , .
- Fuel Cells (FC): they can produce both electric energy and heat by converting hydrogen , .
- Heat Exchangers (HE): thermal load can be served by district heating, through the heat exchangers, whose heat transfer efficiency is set to .
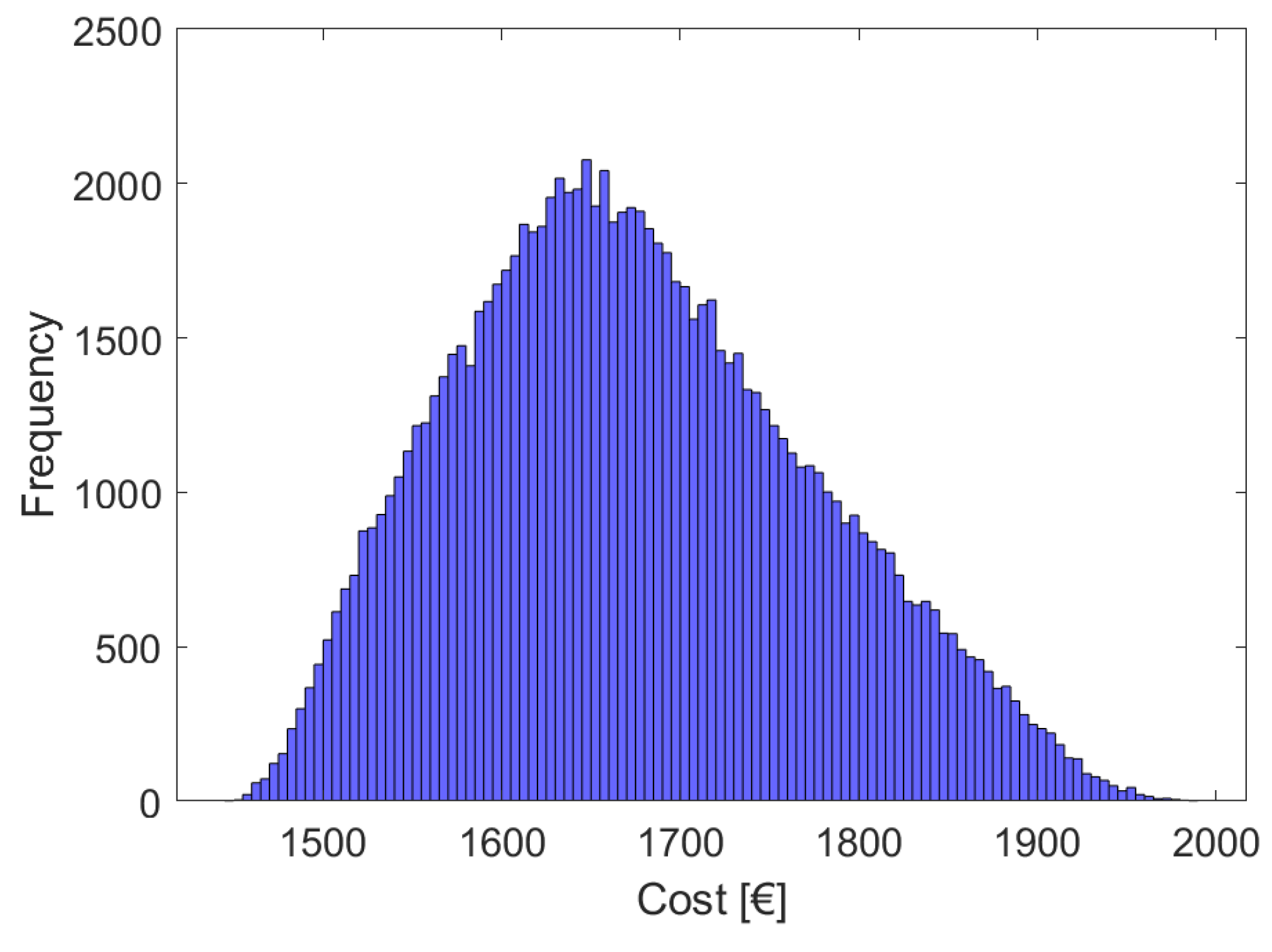
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2006, 5, 24–30. [Google Scholar] [CrossRef]
- Krause, T.; Andersson, G.; Frohlich, K.; Vaccaro, A. Multiple-energy carriers: Modeling of production, delivery, and consumption. Proc. IEEE 2010, 99, 15–27. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept—A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Ma, T.; Wu, J.; Hao, L.; Yan, H.; Li, D. A real time pricing scheme for energy management in integrated energy systems: A stackelberg game approach. Energies 2018, 11, 2858. [Google Scholar] [CrossRef]
- Qi, F.; Wen, F.; Liu, X.; Salam, M. A residential energy hub model with a concentrating solar power plant and electric vehicles. Energies 2017, 10, 1159. [Google Scholar] [CrossRef]
- Brahman, F.; Honarmand, M.; Jadid, S. Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 2015, 90, 65–75. [Google Scholar] [CrossRef]
- Moghaddam, I.G.; Saniei, M.; Mashhour, E. A comprehensive model for self-scheduling an energy hub to supply cooling, heating and electrical demands of a building. Energy 2016, 94, 157–170. [Google Scholar] [CrossRef]
- Wu, R.; Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Multiobjective optimisation of energy systems and building envelope retrofit in a residential community. Appl. Energy 2017, 190, 634–649. [Google Scholar] [CrossRef]
- Orehounig, K.; Evins, R.; Dorer, V. Integration of decentralized energy systems in neighbourhoods using the energy hub approach. Appl. Energy 2015, 154, 277–289. [Google Scholar] [CrossRef]
- Almassalkhi, M.; Hiskens, I. Optimization framework for the analysis of large-scale networks of energy hubs. In Proceedings of the Power Systems Computation Conference, Stockholm, Sweden, 22–26 August 2011. [Google Scholar]
- Ha, T.; Zhang, Y.; Hao, J.; Thang, V.; Li, C.; Cai, Z. Energy hub’s structural and operational optimization for minimal energy usage costs in energy systems. Energies 2018, 11, 707. [Google Scholar] [CrossRef]
- Zhong, Y.; Xie, D.; Zhai, S.; Sun, Y. Day-ahead hierarchical steady state optimal operation for integrated energy system based on energy hub. Energies 2018, 11, 2765. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Ma, J. Multi-objective optimal energy management for the integrated electrical and natural gas network with combined cooling, heat and power plants. Energies 2018, 11, 734. [Google Scholar] [CrossRef]
- Parisio, A.; Del Vecchio, C.; Vaccaro, A. A robust optimization approach to energy hub management. Int. J. Electr. Power Energy Syst. 2012, 42, 98–104. [Google Scholar] [CrossRef]
- Pazouki, S.; Haghifam, M.R.; Moser, A. Uncertainty modeling in optimal operation of energy hub in presence of wind, storage and demand response. Int. J. Electr. Power Energy Syst. 2014, 61, 335–345. [Google Scholar] [CrossRef]
- Canfora, G.; Troiano, L. The importance of dealing with uncertainty in the evaluation of software engineering methods and tools. In Proceedings of the 14th International Conference on Software Engineering and Knowledge Engineering, Ischia, Italy, 15–19 July 2002; ACM: New York, NY, USA, 2002; pp. 691–698. [Google Scholar]
- Vahid-Pakdel, M.; Nojavan, S.; Mohammadi-Ivatloo, B.; Zare, K. Stochastic optimization of energy hub operation with consideration of thermal energy market and demand response. Energy Convers. Manag. 2017, 145, 117–128. [Google Scholar] [CrossRef]
- Najafi, A.; Marzband, M.; Mohamadi-Ivatloo, B.; Contreras, J.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Godina, R. Uncertainty-based models for optimal management of energy hubs considering demand response. Energies 2019, 12, 1413. [Google Scholar] [CrossRef]
- Rakipour, D.; Barati, H. Probabilistic optimization in operation of energy hub with participation of renewable energy resources and demand response. Energy 2019, 173, 384–399. [Google Scholar] [CrossRef]
- Sanjani, K.; Vahabzad, N.; Nazari-Heris, M.; Mohammadi-ivatloo, B. A robust-stochastic approach for energy transaction in energy hub under uncertainty. In Robust Optimal Planning and Operation of Electrical Energy Systems; Springer: Cham, Switzerland, 2019; pp. 219–232. [Google Scholar]
- Najafi-Ghalelou, A.; Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Robust scheduling of thermal, cooling and electrical hub energy system under market price uncertainty. Appl. Therm. Eng. 2019, 149, 862–880. [Google Scholar] [CrossRef]
- Mukherjee, U.; Maroufmashat, A.; Narayan, A.; Elkamel, A.; Fowler, M. A stochastic programming approach for the planning and operation of a power to gas energy hub with multiple energy recovery pathways. Energies 2017, 10, 868. [Google Scholar] [CrossRef]
- Fouskakis, D.; Draper, D. Stochastic optimization: A review. Int. Stat. Rev. 2002, 70, 315–349. [Google Scholar] [CrossRef]
- La Scala, M.; Vaccaro, A.; Zobaa, A. A goal programming methodology for multiobjective optimization of distributed energy hubs operation. Appl. Therm. Eng. 2014, 71, 658–666. [Google Scholar] [CrossRef] [Green Version]
- Vaccaro, A.; Pisani, C.; Zobaa, A.F. Affine arithmetic-based methodology for energy hub operation-scheduling in the presence of data uncertainty. IET Gener. Transm. Distrib. 2015, 9, 1544–1552. [Google Scholar] [CrossRef]
- De Figueiredo, L.H.; Stolfi, J. Affine arithmetic: Concepts and applications. Numer. Algorithms 2004, 37, 147–158. [Google Scholar] [CrossRef]
- Krämer, W. Generalized Intervals and the Dependency Problem. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/pamm.200610322 (accessed on 23 June 2019).
- Neumaier, A. The wrapping effect, ellipsoid arithmetic, stability and confidence regions. In Validation Numerics; Springer: Vienna, Austria, 1993; pp. 175–190. [Google Scholar]
- Bilotta, G. Self-verified extension of affine arithmetic to arbitrary order. Le Matematiche 2008, 63, 15–30. [Google Scholar]
- Soroudi, A.; Amraee, T. Decision making under uncertainty in energy systems: State of the art. Renew. Sustain. Energy Rev. 2013, 28, 376–384. [Google Scholar] [CrossRef]
- Ghasemi, A.; Banejad, M.; Rahimiyan, M. Integrated energy scheduling under uncertainty in a micro energy grid. IET Gener. Transm. Distrib. 2018, 12, 2887–2896. [Google Scholar] [CrossRef]
- Troiano, L.; Mejuto, E.; Kriplani, P. An alternative estimation of market volatility based on fuzzy transform. In Proceedings of the 2017 Joint 17th World Congress of International Fuzzy Systems Association, Otsu, Japan, 27–30 June 2017; In Proceedings of the 9th International Conference on Soft Computing and Intelligent Systems (IFSA-SCIS), Otsu, Japan, 27–30 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar] [Green Version]
- Daryani, N.; Tohidi, S. Economic dispatch of multi-carrier energy systems considering intermittent resources. Energy Environ. 2019. [Google Scholar] [CrossRef]
- Stolfi, J.; de Figueiredo, L.H. An introduction to affine arithmetic. Trends Appl. Comput. Math. 2003, 4, 297–312. [Google Scholar] [CrossRef]
- Vaccaro, A.; Canizares, C.A.; Villacci, D. An affine arithmetic-based methodology for reliable power flow analysis in the presence of data uncertainty. IEEE Trans. Power Syst. 2009, 25, 624–632. [Google Scholar] [CrossRef]
- Gu, W.; Luo, L.; Ding, T.; Meng, X.; Sheng, W. An affine arithmetic-based algorithm for radial distribution system power flow with uncertainties. Int. J. Electr. Power Energy Syst. 2014, 58, 242–245. [Google Scholar] [CrossRef]
| Affine Form Values | x | y |
|---|---|---|
| Central value | 10.04 | 9.96 |
| P. dev. 1 | 2.51 | 2.5 |
| P. dev. 2 | 3.52 | 3.48 |
| Affine Form Values | (€/MWh) | (€/MWh) | (MWh) | (MWh) | (MWh) |
|---|---|---|---|---|---|
| Central value | 60 | 44 | 20 | 20 | 0 |
| Uncertainty | 8 | 4.4 | 0.5 | 0.9 | 2 |
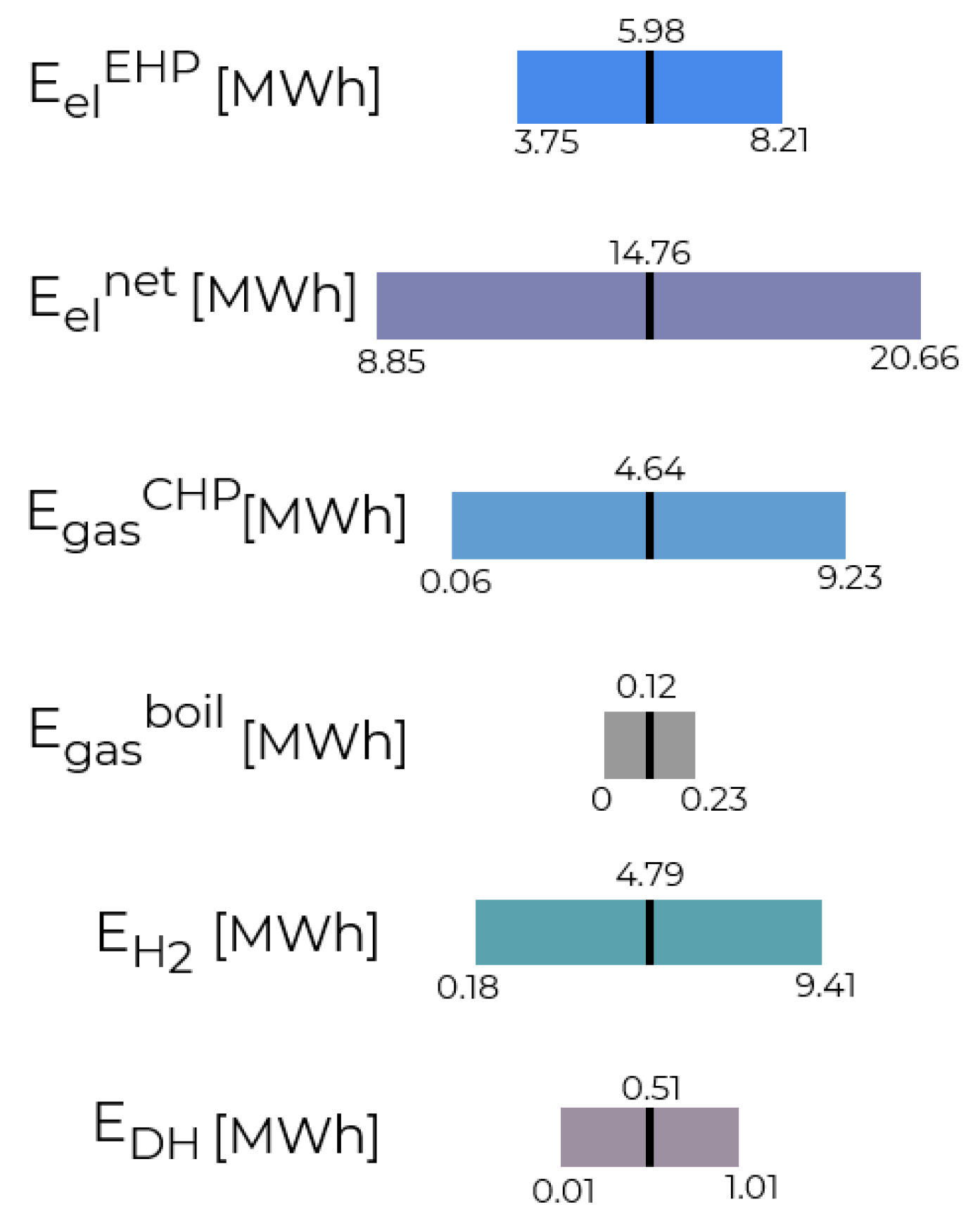
| Affine Form Values | (MWh) | (MWh) | (MWh) | (MWh) | (MWh) | (MWh) |
|---|---|---|---|---|---|---|
| Central value | 5.98 | 14.76 | 4.65 | 0.122 | 4.79 | 0.51 |
| P. dev. 1 | 0.03 | 0.57 | 0.211 | −0.04 | −0.37 | 0 |
| P. dev. 2 | 0.64 | 0.58 | −1.31 | 0 | −0.13 | 0.01 |
| P. dev. 3 | 0.79 | 1.29 | −1.18 | −0.07 | −2.27 | −0.36 |
| P. dev. 4 | 0.44 | 0.84 | −1.85 | 0 | −0.25 | −0.08 |
| P. dev. 5 | −0.31 | −2.62 | 0.03 | 0 | 1.59 | 0.04 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pepiciello, A.; Vaccaro, A.; Mañana, M. Robust Optimization of Energy Hubs Operation Based on Extended Affine Arithmetic. Energies 2019, 12, 2420. https://doi.org/10.3390/en12122420
Pepiciello A, Vaccaro A, Mañana M. Robust Optimization of Energy Hubs Operation Based on Extended Affine Arithmetic. Energies. 2019; 12(12):2420. https://doi.org/10.3390/en12122420
Chicago/Turabian StylePepiciello, Antonio, Alfredo Vaccaro, and Mario Mañana. 2019. "Robust Optimization of Energy Hubs Operation Based on Extended Affine Arithmetic" Energies 12, no. 12: 2420. https://doi.org/10.3390/en12122420
APA StylePepiciello, A., Vaccaro, A., & Mañana, M. (2019). Robust Optimization of Energy Hubs Operation Based on Extended Affine Arithmetic. Energies, 12(12), 2420. https://doi.org/10.3390/en12122420







