Energy and Exergy Analysis of Different Exhaust Waste Heat Recovery Systems for Natural Gas Engine Based on ORC
Abstract
:1. Introduction
2. Methodology
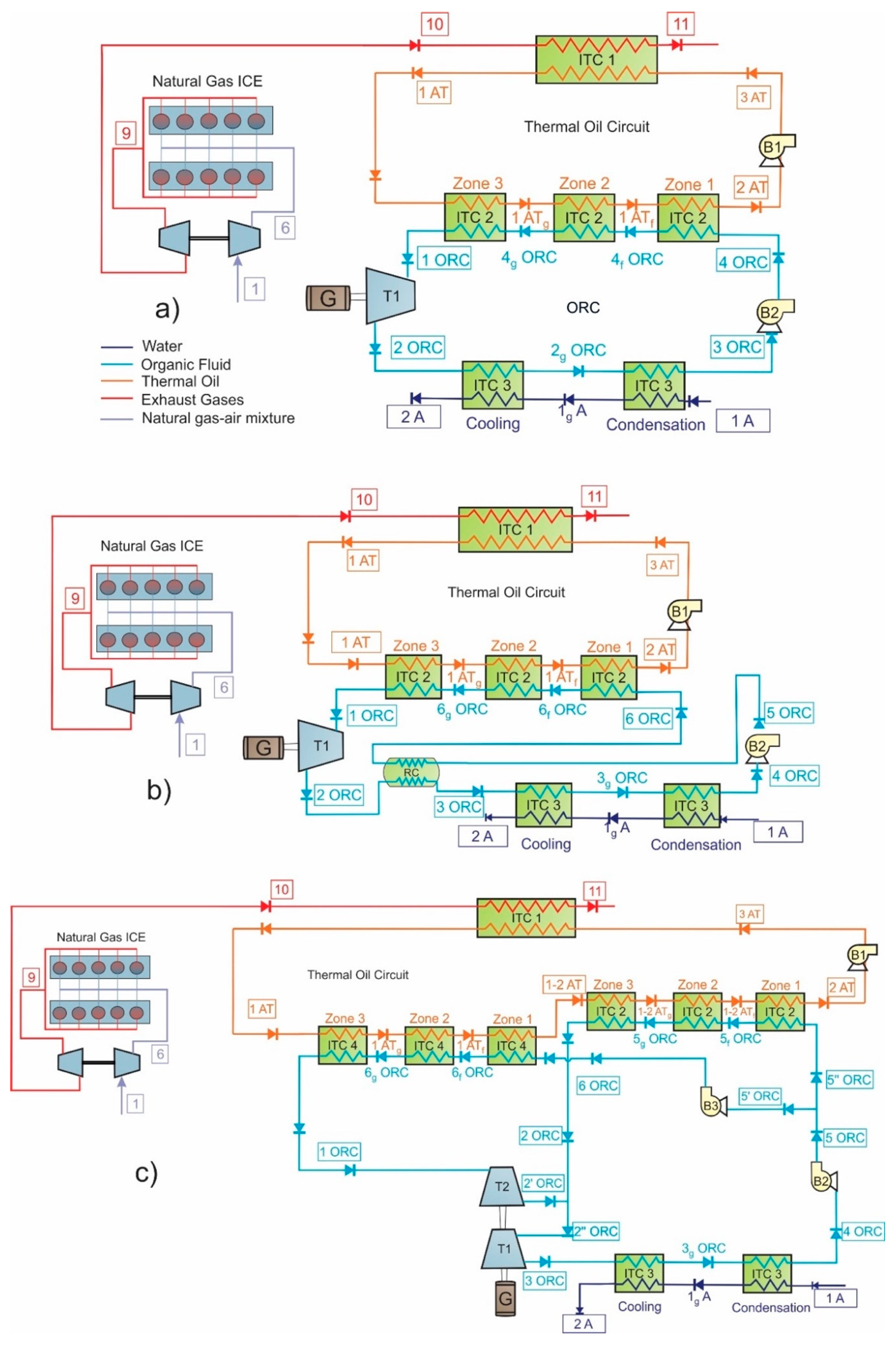
2.1. Description of the System
2.2. Description of the SORC, RORC, and DORC
3. Thermodynamic Modeling
3.1. Energy Analysis
3.2. Exergy Analysis
- Pressure drops in pipelines are neglected.
- Pressure drops in heat exchangers are calculated as a function of the equipment geometry and the hydraulic flow characteristics.
- All the WHR–ORC components of the cycle are thermally insulated.
- The thermal oil circuit absorbs temperature variations in exhaust gases to obtain steady-state operation in each ORC configuration.
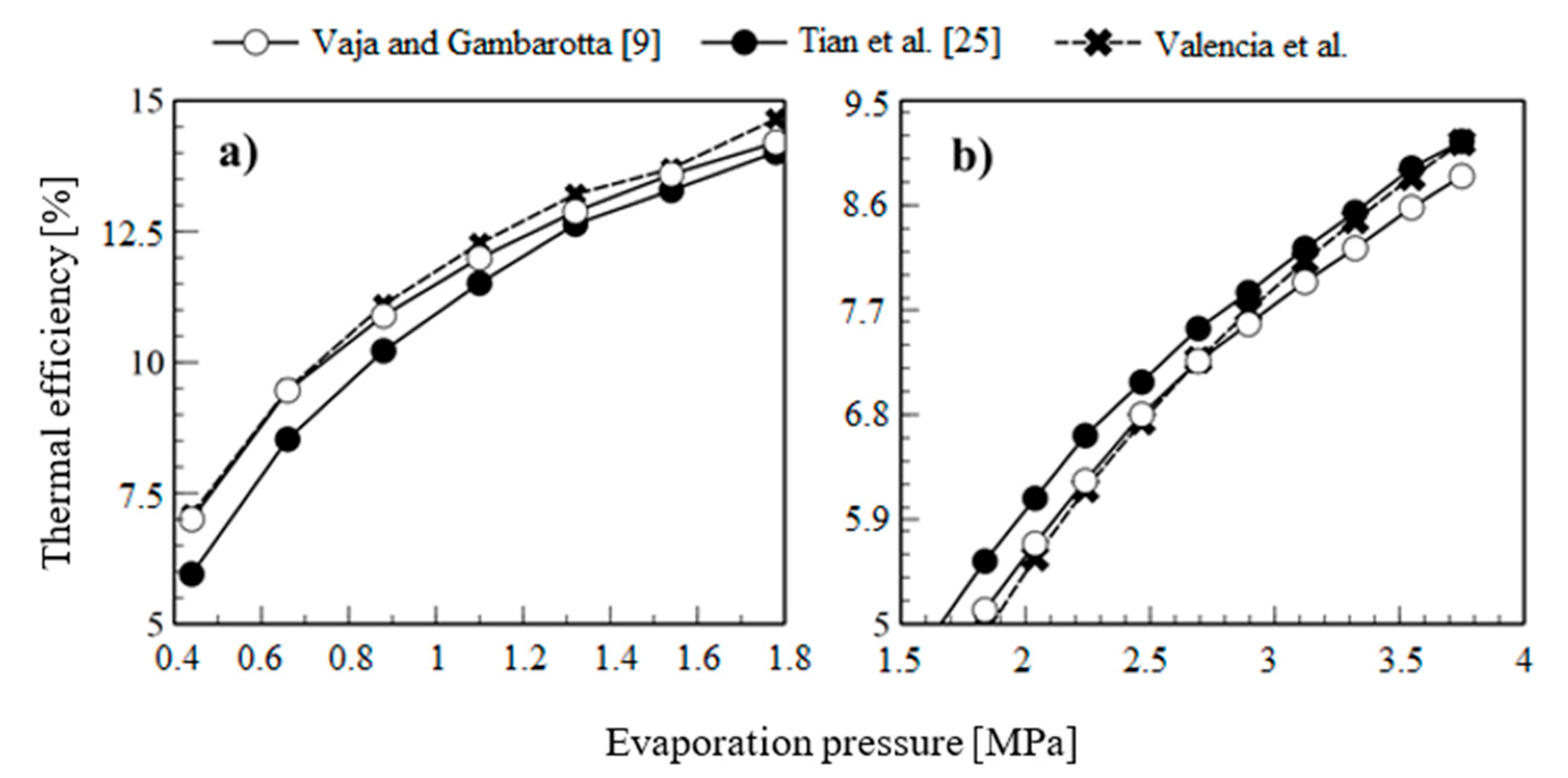
3.3. Validation
- The processes and subsystems are assumed to be in steady state.
- All devices were considered in adiabatic conditions.
- Pressure drops in ORC devices and pipelines are neglected.
- The reference temperature for exergy calculations is 288 K.
4. Results and Discussions
4.1. Sensitivity Analysis
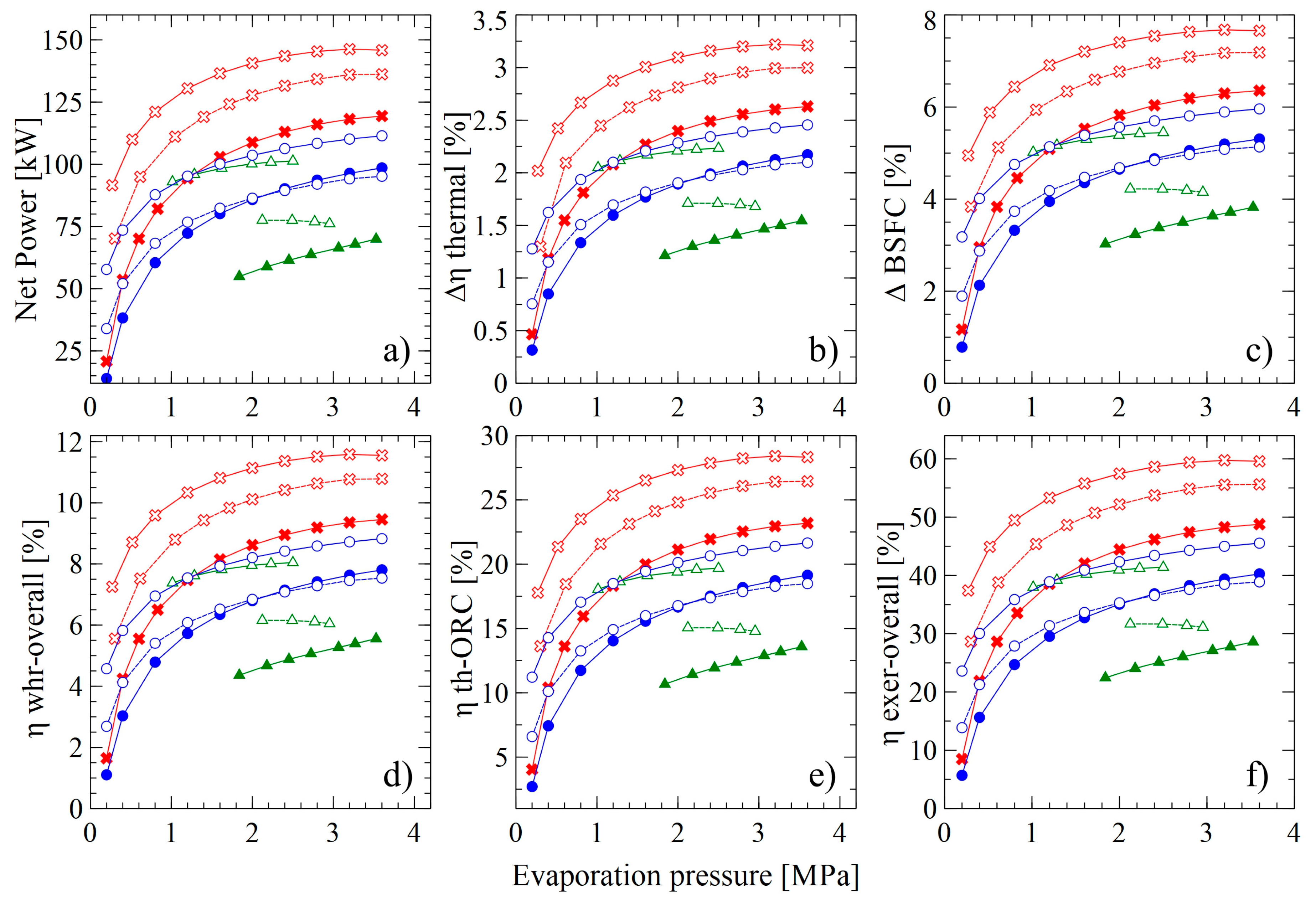
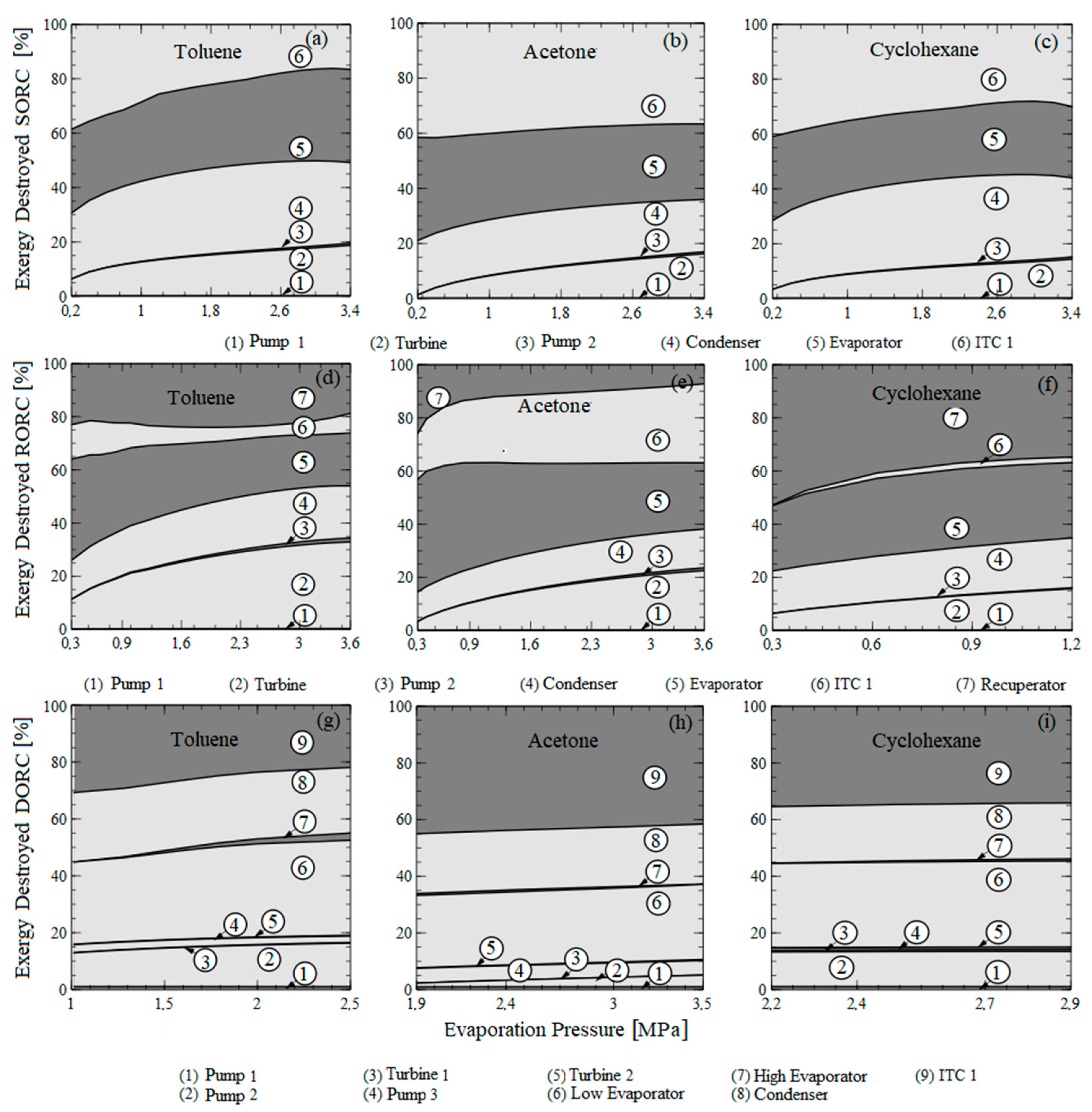
4.1.1. Effect of Evaporation Pressure
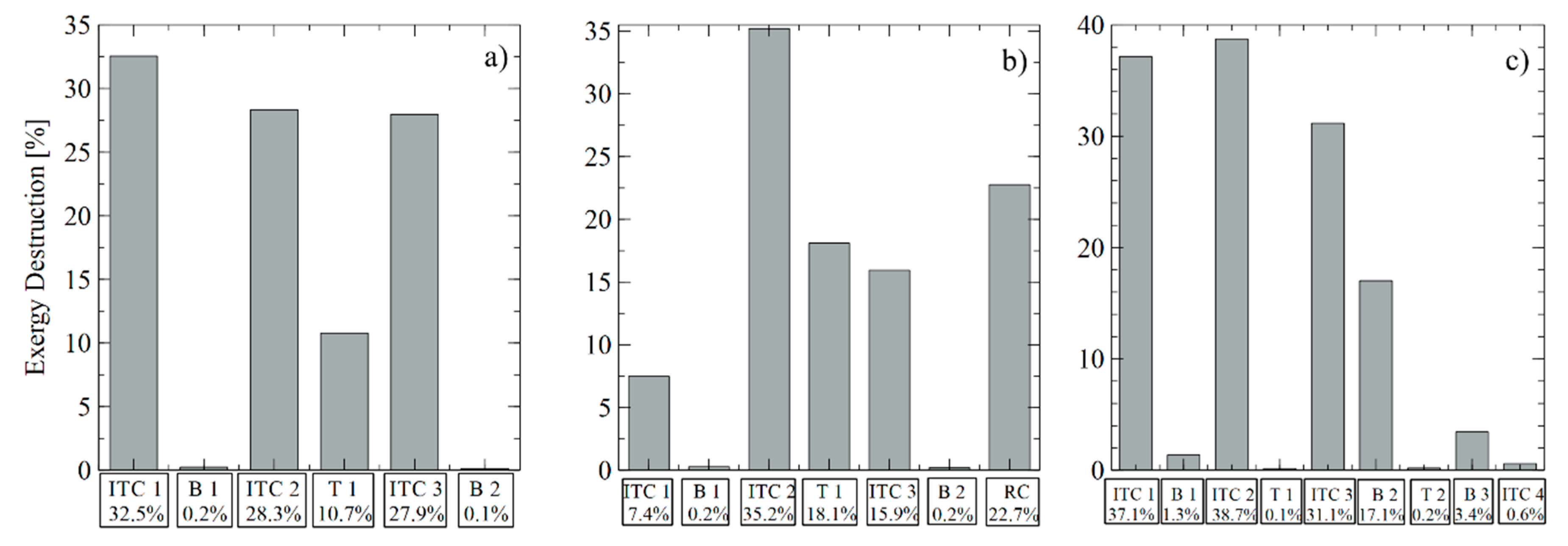
4.1.2. Analysis of the Influence of Evaporation Pressure on the Destruction of Exergy Configurations
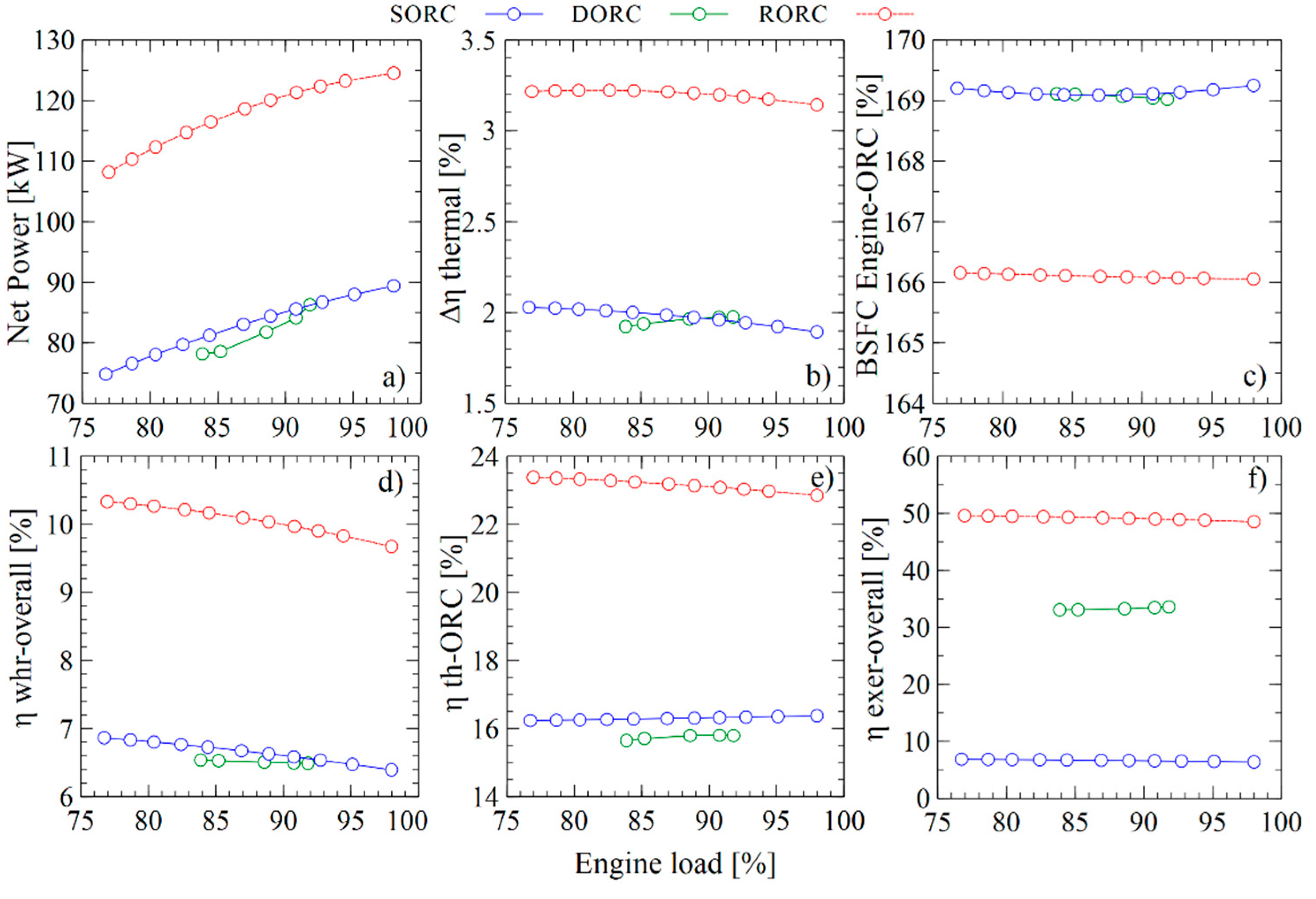
4.1.3. Analysis of the Influence of Engine Load on Energy Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BSFC | Brake-specific fuel consumption |
| DORC | Double pressure organic Rankine cycle |
| GHG | Greenhouse gases |
| GWP | Global warming potential |
| ICE | Internal combustion engine |
| ORC | Organic Rankine cycle |
| RORC | Recuperator organic Rankine cycle |
| SORC | Simple organic Rankine Cycle |
| WHR | Waste heat recovery |
| Nomenclature | |
| Specific heat at constant pressure | |
| Energy (J) | |
| Specific exergy | |
| Specific enthalpy | |
| Heating power | |
| Mass | |
| Mass flow rate | |
| Heat | |
| Universal gas constant . | |
| Rotational engine speed (rpm) | |
| Temperature | |
| Time | |
| Power (kW) | |
| Molar gas fraction | |
| Greek Letters | |
| Thermal efficiency of the cycle | |
| Overall energy conversion efficiency | |
| Exergetic efficiency | |
| Heat recovery efficiency | |
| Subscripts | |
| Destroyed | |
| in | Input |
| out | Output |
| G | Gases |
| VC | Control volume |
| o | Reference condition |
Appendix A
| Component | Different Configurations of Residual Heat Recovery Systems Using ORC | ||
|---|---|---|---|
| SORC | RORC | DORC | |
| Heat Exchanger 1 (ITC1) | (A1) | (A1) | (A1) |
| Pump 1 (B1) | (A2) (A3) | (A2) | (A2) |
| Heat Exchanger (ITC2) | Zone 1 (Preheating) (A4) Zone 2 (Evaporation) (A5) Zone 3 (Overheating) (A6) | (A13) Zone 2 (A5) (A14) | (A21) Zone 2 (A5) (A22) |
| Turbine 1 (T1) | (A7) (A8) | (A7) (A8) | (A29) (A30) |
| Heat Exchanger (ITC3) | (A9) Condenser (A10) | (A15) (A16) | (A15) (A16) |
| Pump 2 (B2) | (A11) (A12) | (A18) | (A27) (A28) |
| RC | - | (A19) (A20) | - |
| Turbine 2 (T2) | - | - | (A25) (A26) |
| Pump 3 (B3) | - | - | (A31) (A32) |
| Heat Exchanger (ITC4) | - | - | (A23) Zone 2 (A5) (A24) |
Appendix B
| Stream | Flow (kg/s) | P (kPa) | T (°C) | Enthalpy (kJ/kg) | Entropy(S-S0) (kJ/kg K) | Exergy (kW) |
|---|---|---|---|---|---|---|
| 10 | 2.77 | 102.30 | 435.07 | −1960.35 | 0.90 | 541.20 |
| 11 | 2.77 | 101.30 | 270.00 | −2143.67 | 0.59 | 296.45 |
| 1 AT | 1.64 | 101.43 | 307.84 | 461.66 | 0.94 | 208.75 |
| 1 ATg | 1.64 | 91.42 | 246.29 | 324.52 | 0.73 | 106.76 |
| 1 ATf | 1.64 | 81.01 | 178.30 | 183.24 | 0.47 | 29.12 |
| 2 AT | 1.64 | 68.15 | 142.65 | 113.96 | 0.31 | 5.90 |
| 3 AT | 1.64 | 170.38 | 142.77 | 114.19 | 0.31 | 5.96 |
| 1 ORC | 0.72 | 675.85 | 272.84 | 633.29 | 1.80 | 169.27 |
| 2 ORC | 0.72 | 22.53 | 202.37 | 513.72 | 1.87 | 69.79 |
| 2 gORC | 0.72 | 22.53 | 65.00 | 301.64 | 1.34 | 31.18 |
| 3 ORC | 0.72 | 22.53 | 65.00 | −87.53 | 0.19 | 2.35 |
| 4 ORC | 0.72 | 675.85 | 65.31 | −86.47 | 0.19 | 2.93 |
| 4 fORC | 0.72 | 675.85 | 194.20 | 181.72 | 0.86 | 50.17 |
| 4 gORC | 0.72 | 675.85 | 194.20 | 477.95 | 1.50 | 124.68 |
| 1 A | 13.32 | 101.30 | 50.00 | 209.42 | 0.27 | 35.20 |
| 1 gA | 13.32 | 101.30 | 55.00 | 230.33 | 0.33 | 54.44 |
| 2 A | 13.32 | 101.30 | 57.72 | 241.72 | 0.37 | 66.59 |
| Stream | Flow (kg/s) | P (kPa) | T (°C) | Enthalpy (kJ/kg) | Entropy(S-S0) (kJ/kg K) | Exergy (kW) |
|---|---|---|---|---|---|---|
| 10 | 2.77 | 102.30 | 435.07 | −1960.35 | 0.90 | 541.20 |
| 11 | 2.77 | 101.30 | 270.00 | −2143.67 | 0.59 | 296.45 |
| 1 AT | 1.51 | 101.43 | 374.47 | 618.96 | 1.25 | 263.92 |
| 1 ATg | 1.51 | 92.78 | 379.55 | 631.30 | 1.27 | 273.93 |
| 1 ATf | 1.51 | 83.89 | 294.56 | 431.40 | 0.98 | 126.19 |
| 2 AT | 1.51 | 68.15 | 209.28 | 246.22 | 0.65 | 26.27 |
| 3 AT | 1.51 | 170.38 | 209.40 | 246.46 | 0.65 | 26.37 |
| 1 ORC | 0.89 | 675.85 | 339.47 | 775.16 | 2.05 | 272.11 |
| 2 ORC | 0.89 | 22.53 | 268.70 | 638.39 | 2.11 | 132.31 |
| 3 ORC | 0.89 | 22.53 | 102.23 | 352.50 | 1.49 | 45.82 |
| 3 gORC | 0.89 | 22.53 | 65.00 | 301.64 | 1.34 | 38.98 |
| 4 ORC | 0.89 | 22.53 | 65.00 | −87.53 | 0.19 | 2.93 |
| 5 ORC | 0.89 | 675.85 | 65.31 | −86.47 | 0.19 | 3.67 |
| 6 ORC | 0.89 | 675.85 | 194.20 | 199.42 | 0.90 | 68.29 |
| 6 fORC | 0.89 | 675.85 | 194.20 | 181.72 | 0.86 | 62.72 |
| 6 gORC | 0.89 | 675.85 | 194.20 | 477.95 | 1.50 | 155.86 |
| 1 A | 16.65 | 101.30 | 50.00 | 209.42 | 0.27 | 44.00 |
| 1 gA | 16.65 | 101.30 | 55.00 | 230.33 | 0.33 | 68.06 |
| 2 A | 16.65 | 101.30 | 55.65 | 233.06 | 0.34 | 71.57 |
| Stream | Flow (kg/s) | T (°C) | P (kPa) | Enthalpy (kJ/kg) | Entropy (S-S0) (kJ/kg K) | Exergy (kW) |
|---|---|---|---|---|---|---|
| 10 | 2.77 | 435.07 | 102.30 | −1960.35 | 0.90 | 541.20 |
| 11 | 2.77 | 270.00 | 101.30 | −2143.67 | 0.59 | 296.45 |
| 1 AT | 1.62 | 316.58 | 686.83 | 481.81 | 0.99 | 215.40 |
| 1 ATg | 1.62 | 296.48 | 676.43 | 435.75 | 0.92 | 178.88 |
| 1 ATf | 1.62 | 245.76 | 666.37 | 323.37 | 0.74 | 99.29 |
| 1-2 AT | 1.62 | 171.41 | 656.79 | 169.58 | 0.44 | 20.13 |
| 1-2 ATg | 1.62 | 228.96 | 647.85 | 287.41 | 0.68 | 77.18 |
| 1-2 Atf | 1.62 | 183.04 | 638.85 | 192.71 | 0.49 | 29.19 |
| 2 AT | 1.62 | 150.98 | 630.14 | 129.89 | 0.35 | 7.53 |
| 3 AT | 1.62 | 151.51 | 755.78 | 130.91 | 0.35 | 7.80 |
| 1A | 8.40 | 50.00 | 101.30 | 209.42 | 0.27 | 27.60 |
| 1g A | 8.40 | 55.00 | 101.30 | 230.33 | 0.33 | 42.69 |
| 2A | 8.40 | 55.00 | 101.30 | 234.54 | 0.34 | 46.10 |
| 1 ORC | 0.45 | 281.58 | 1351.69 | 635.64 | 1.75 | 159.64 |
| 2 ORC | 0.62 | 136.41 | 450.56 | 53.17 | 0.57 | 13.75 |
| 2’ ORC | 0.45 | 252.65 | 450.56 | 597.65 | 1.77 | 132.33 |
| 2” ORC | 1.08 | 173.03 | 450.56 | 368.93 | 1.28 | 139.83 |
| 3 ORC | 1.08 | 65.00 | 22.53 | 298.79 | 1.34 | 46.85 |
| 3g ORC | 1.08 | 65.00 | 22.53 | 301.64 | 1.34 | 47.17 |
| 4 ORC | 1.08 | 65.00 | 22.53 | −87.53 | 0.19 | 3.55 |
| 5 ORC | 1.08 | 65.21 | 450.56 | −86.84 | 0.19 | 4.13 |
| 5’ ORC | 0.45 | 65.21 | 450.56 | −86.84 | 0.19 | 2.40 |
| 5” ORC | 0.62 | 65.21 | 450.56 | −86.84 | 0.19 | 1.74 |
| 5f ORC | 0.62 | 173.04 | 450.56 | 132.93 | 0.76 | 24.32 |
| 5g ORC | 0.62 | 173.04 | 450.56 | 447.79 | 1.46 | 70.24 |
| 6 ORC | 0.45 | 65.64 | 1351.69 | −85.38 | 0.20 | 3.10 |
| 6f ORC | 0.45 | 235.75 | 1351.69 | 283.87 | 1.07 | 68.73 |
| 6g ORC | 0.45 | 235.75 | 1351.69 | 535.81 | 1.56 | 132.70 |
References
- Nawi, Z.M.; Kamarudin, S.; Abdullah, S.S.; Lam, S. The potential of exhaust waste heat recovery (WHR) from marine diesel engines via organic rankine cycle. Energy 2019, 166, 17–31. [Google Scholar] [CrossRef]
- Alshammari, F.; Pesyridis, A.; Karvountzis-Kontakiotis, A.; Franchetti, B.; Pesmazoglou, Y. Experimental study of a small scale organic Rankine cycle waste heat recovery system for a heavy duty diesel engine with focus on the radial inflow turbine expander performance. Appl. Energy 2018, 215, 543–555. [Google Scholar] [CrossRef]
- Liu, P.; Shu, G.; Tian, H.; Wang, X.; Yu, Z. Alkanes based two-stage expansion with interheating Organic Rankine cycle for multi-waste heat recovery of truck diesel engine. Energy 2018, 147, 337–350. [Google Scholar] [CrossRef]
- Michos, C.N.; Lion, S.; Vlaskos, I.; Taccani, R. Analysis of the backpressure effect of an Organic Rankine Cycle (ORC) evaporator on the exhaust line of a turbocharged heavy duty diesel power generator for marine applications. Energy Convers. Manag. 2017, 132, 347–360. [Google Scholar] [CrossRef]
- Patel, P.S.; Doyle, E.F. Compounding the Truck Diesel Engine with an Organic Rankine-Cycle System; SAE International: Warrendale, PA, USA, 1976. [Google Scholar]
- Peris, B.; Navarro-Esbrí, J.; Molés, F. Bottoming organic Rankine cycle configurations to increase Internal Combustion Engines power output from cooling water waste heat recovery. Appl. Therm. Eng. 2013, 61, 364–371. [Google Scholar] [CrossRef]
- Yu, G.; Shu, G.; Tian, H.; Wei, H.; Liu, L. Simulation and thermodynamic analysis of a bottoming Organic Rankine Cycle (ORC) of diesel engine (DE). Energy 2013, 51, 281–290. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Y.; Dong, C.; Wang, L.; Roskilly, A.P. Design and assessment on a novel integrated system for power and refrigeration using waste heat from diesel engine. Appl. Therm. Eng. 2015, 91, 591–599. [Google Scholar] [CrossRef]
- Vaja, I.; Gambarotta, A. Internal Combustion Engine (ICE) bottoming with Organic Rankine Cycles (ORCs). Energy 2010, 35, 1084–1093. [Google Scholar] [CrossRef]
- Kalina, J. Integrated biomass gasification combined cycle distributed generation plant with reciprocating gas engine and ORC. Appl. Therm. Eng. 2011, 31, 2829–2840. [Google Scholar] [CrossRef] [Green Version]
- Mingshan, W.; Jinli, F.; Chaochen, M.; Noman, D.S. Waste heat recovery from heavy-duty diesel engine exhaust gases by medium temperature ORC system. Sci. China Technol. Sci. 2011, 54, 2746–2753. [Google Scholar]
- Yao, B.; Yang, F.; Zhang, H.; Wang, E.; Yang, K. Analyzing the Performance of a Dual Loop Organic Rankine Cycle System for Waste Heat Recovery of a Heavy-Duty Compressed Natural Gas Engine. Energies 2014, 7, 7794–7815. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Zhang, H.; Yu, Z.; Wang, E.; Meng, F.; Liu, H.; Wang, J. Parametric optimization and heat transfer analysis of a dual loop ORC (organic Rankine cycle) system for CNG engine waste heat recovery. Energy 2017, 118, 753–775. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Cho, H.; Zhang, H.; Zhang, J. Thermoeconomic multi-objective optimization of a dual loop organic Rankine cycle (ORC) for CNG engine waste heat recovery. Appl. Energy 2017, 205, 1100–1118. [Google Scholar] [CrossRef]
- Wang, E.; Yu, Z.; Zhang, H.; Yang, F. A regenerative supercritical-subcritical dual-loop organic Rankine cycle system for energy recovery from the waste heat of internal combustion engines. Appl. Energy 2017, 190, 574–590. [Google Scholar] [CrossRef]
- Han, Y.; Kang, J.; Wang, X.; Liu, Z.; Tian, J.; Wang, Y. Modelling and simulation analysis of an ORC-FPC waste heat recovery system for the stationary CNG-fuelled compressor. Appl. Therm. Eng. 2015, 87, 481–490. [Google Scholar] [CrossRef]
- Song, S.; Zhang, H.; Zhao, R.; Meng, F.; Liu, H.; Wang, J.; Yao, B. Simulation and Performance Analysis of Organic Rankine Systems for Stationary Compressed Natural Gas Engine. Energies 2017, 10, 544. [Google Scholar] [CrossRef]
- Liu, P.; Shu, G.; Tian, H.; Wang, X. Engine Load Effects on the Energy and Exergy Performance of a Medium Cycle/Organic Rankine Cycle for Exhaust Waste Heat Recovery. Entropy 2018, 20, 137. [Google Scholar]
- Chacartegui, R.; Sánchez, D.; Múñoz, J.; Sánchez, T. Alternative ORC bottoming cycles FOR combined cycle power plants. Appl. Energy 2009, 86, 2162–2170. [Google Scholar] [CrossRef]
- Qiu, K.; Hayden, A. Integrated thermoelectric and organic Rankine cycles for micro-CHP systems. Appl. Energy 2012, 97, 667–672. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggemann, D. Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Mago, P.J.; Chamra, L.M.; Srinivasan, K.; Somayaji, C. An examination of regenerative organic Rankine cycles using dry fluids. Appl. Therm. Eng. 2008, 28, 998–1007. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Manolakos, D.; Kyritsis, S.; Papadakis, G. Comparative thermodynamic study of refrigerants to select the best for use in the high-temperature stage of a two-stage organic Rankine cycle for RO desalination. Desalination 2009, 243, 74–94. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Papadakis, G.; Lambrinos, G.; Frangoudakis, A. Fluid selection for a low-temperature solar organic Rankine cycle. Appl. Therm. Eng. 2009, 29, 2468–2476. [Google Scholar] [CrossRef] [Green Version]
- Tian, H.; Shu, G.; Wei, H.; Liang, X.; Liu, L. Fluids and parameters optimization for the organic Rankine cycles (ORCs) used in exhaust heat recovery of Internal Combustion Engine (ICE). Energy 2012, 47, 125–136. [Google Scholar] [CrossRef]
- Hung, T.-C.; Lee, D.-S.; Lin, J.-R. An Innovative Application of a Solar Storage Wall Combined with the Low-Temperature Organic Rankine Cycle. Int. J. Photoenergy 2014, 2014, 1–12. [Google Scholar] [CrossRef]
- Zare, V. A comparative exergoeconomic analysis of different ORC configurations for binary geothermal power plants. Energy Convers. Manag. 2015, 105, 127–138. [Google Scholar] [CrossRef]
- Fontalvo, A.; Solano, J.; Pedraza, C.; Bula, A.; Quiroga, A.G.; Padilla, R.V. Energy, Exergy and Economic Evaluation Comparison of Small-Scale Single and Dual Pressure Organic Rankine Cycles Integrated with Low-Grade Heat Sources. Entropy 2017, 19, 476. [Google Scholar] [CrossRef]
- Calise, F.; D’Accadia, M.D.; Macaluso, A.; Piacentino, A.; Vanoli, L. Exergetic and exergoeconomic analysis of a novel hybrid solar–geothermal polygeneration system producing energy and water. Energy Convers. Manag. 2016, 115, 200–220. [Google Scholar] [CrossRef]
- Kerme, E.D.; Orfi, J. Exergy-based thermodynamic analysis of solar driven organic Rankine cycle. J. Therm. Eng. 2015, 1, 192–202. [Google Scholar] [CrossRef]
- Jouhara, H.; Sayegh, M.A. Energy efficient thermal systems and processes. Therm. Sci. Eng. Prog. 2018, 7, e1–e2. [Google Scholar] [CrossRef]
- Chen, T.; Zhuge, W.; Zhang, Y.; Zhang, L. A novel cascade organic Rankine cycle (ORC) system for waste heat recovery of truck diesel engines. Energy Convers. Manag. 2017, 138, 210–223. [Google Scholar] [CrossRef]
- Moran, M.J.; Saphiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Quoilin, S.; Aumann, R.; Grill, A.; Schuster, A.; Lemort, V.; Spliethoff, H. Dynamic modeling and optimal control strategy of waste heat recovery Organic Rankine Cycles. Appl. Energy 2011, 88, 2183–2190. [Google Scholar] [CrossRef]
- Mathworks. Matlab: Computer Program; The MatlabWorks Inc.: Denver, CO, USA, 2018. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.1.; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Trindade, A.B.; Palacio, J.C.E.; González, A.M.; Orozco, D.J.R.; Lora, E.E.S.; Renó, M.L.G.; Del Olmo, O.A. Advanced exergy analysis and environmental assesment of the steam cycle of an incineration system of municipal solid waste with energy recovery. Energy Convers. Manag. 2018, 157, 195–214. [Google Scholar] [CrossRef]
- Val, C.G.F.; De Oliveira, S., Jr. Deep Water Cooled ORC for Offshore Floating Oil Platform Applications. Int. J. Thermodyn. 2017, 20, 229–237. [Google Scholar] [CrossRef]
- El-Emam, R.S.; Dincer, I. Exergy and exergoeconomic analyses and optimization of geothermal organic Rankine cycle. Appl. Therm. Eng. 2013, 59, 435–444. [Google Scholar] [CrossRef]
- Uusitalo, A.; Honkatukia, J.; Turunen-Saaresti, T.; Larjola, J. A thermodynamic analysis of waste heat recovery from reciprocating engine power plants by means of Organic Rankine Cycles. Appl. Therm. Eng. 2014, 70, 33–41. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Comparison between regenerative organic Rankine cycle (RORC) and basic organic Rankine cycle (BORC) based on thermoeconomic multi-objective optimization considering exergy efficiency and levelized energy cost (LEC). Energy Convers. Manag. 2015, 96, 58–71. [Google Scholar] [CrossRef]
- Lai, N.A.; Wendland, M.; Fischer, J. Working fluids for high-temperature organic Rankine cycles. Energy 2011, 36, 199–211. [Google Scholar] [CrossRef]
- Desai, N.B.; Bandyopadhyay, S. Process integration of organic Rankine cycle. Energy 2009, 34, 1674–1686. [Google Scholar] [CrossRef]
- Rayegan, R.; Tao, Y.X. A procedure to select working fl uids for Solar Organic Rankine Cycles (ORCs). Renew. Energy 2011, 36, 659–670. [Google Scholar] [CrossRef]
- Guzovi, Z. The comparision of a basic and a dual-pressure ORC (Organic Rankine Cycle): Geothermal Power Plant Velika Ciglena case study. Energy 2015, 76, 175–186. [Google Scholar] [CrossRef]
- Minea, V. Power generation with ORC machines using low-grade waste heat or renewable energy. Appl. Therm. Eng. 2014, 69, 143–154. [Google Scholar] [CrossRef]
- Nami, H.; Mohammadkhani, F.; Ranjbar, F. Utilization of waste heat from GTMHR for hydrogen generation via combination of organic Rankine cycles and PEM electrolysis. Energy Convers. Manag. 2016, 127, 589–598. [Google Scholar] [CrossRef]

| Description | Value | Units |
|---|---|---|
| Cylinder capacity | 74.852 | L |
| Compression ratio | 10.5 | – |
| Number of cylinders (In V–60°) | 12 | – |
| Stroke length | 220 | mm |
| Diameter in chamber | 190 | mm |
| Maximum torque | 60.66 | kN⋅m |
| Power at nominal speed | 1820 | kW |
| Nominal speed | 1500 | rpm |
| Ignition system | Spark ignition | – |
| Minimum load capacity | 1000 | kW |
| Maximum load capacity | 1982 | kW |
| at minimum load | 1.79 | – |
| at maximum load | 1.97 | – |
| Exhaust gases O2 concentration | 9.45–10.52 | % volume |
| Exhaust gases CO concentration | 588–731 | mg/m3 |
| Exhaust gases NOx concentration | 461–468 | mg/m3 |
| Exhaust gases NO2 concentration | 317–368 | mg/m3 |
| Exhaust gases NO concentration | 65–95 | mg/m3 |
| Description | Value | Units |
| Methane (CH4) | 97.97 | % |
| Nitrogen (N2) | 1.50 | % |
| Ethane (C2H6) | 0.25 | % |
| Carbon dioxide (CO2) | 0.16 | % |
| Fuel–air mixture supply pressure | 1.15–1.25 | bar |
| Uncorrected volumetric ratio | 110–140 | L/s |
| Parameter | Value | Units |
|---|---|---|
| Gas flow | 120 | L/min |
| 1.784 | - | |
| 1482 | rpm | |
| Gas pressure | 1163.6 | mbar |
| Throttle valve | 80.0 | |
| Turbo bypass valve | 9.1 | |
| Gas temperature | 389 | °C |
| Engine coolant temperature | 63.9 | °C |
| Performance Indicators | Value | Units |
|---|---|---|
| Mechanical engine power | 1758.77 | kW |
| Effective engine efficiency | 38.59 | % |
| Heat recovery efficiency | 40.78 | % |
| Heat removed from exhaust gases | 514.85 | kW |
| Specific engine fuel consumption | 177.65 | g/kWh |
| Configuration | Parameter | Value | Units | Reference |
|---|---|---|---|---|
| S/R/DP | Isentropic efficiency turbines | 80 | % | [38] |
| S/R/DP | Isentropic efficiency pumps | 75 | % | [38] |
| S/R/DP | Cooling water temperature (T1A) | 50 | °C | |
| S/R/DP | Pinch Point condenser (ITC3) | 15 | °C | |
| S/R | Pressure Ratio B1 | 2.5 | ||
| DP | Pressure Ratio B1 | 11.09 | ||
| S/R/DP | Pinch Point evaporators (ITC2) (ITC4) | 35 | °C | |
| R | Recovery Effectiveness (RC) | 85 | % | [38] |
| DP | Pressure Ratio B2 | 20 | ||
| DP | Pressure Ratio B3 | 9 | ||
| S/R | Pressure Ratio B2 | 30 |
| Component | Different Configurations of Waste Heat Recovery Systems Using ORC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SORC | RORC | DORC | |||||||
| Fuel | Product | Lost | Fuel | Product | Lost | Fuel | Product | Lost | |
| I1 | . − | ||||||||
| B1 | . | - | - | - | |||||
| ITC2 | − | - | - | - | |||||
| T1 | - | - | - | ||||||
| ITC3 | - | . | - | - | - | - | |||
| B2 | - | - | - | ||||||
| RC | - | - | - | - | - | - | - | ||
| T2 | - | - | - | - | - | - | - | ||
| B3 | - | - | - | - | - | - | − | - | |
| ITC4 | - | - | - | - | - | - | - | ||
| Cycle | Tsource (°C) | F (kg/s) | (°C) | Pinch Point (°C) | (MPa) | ||
|---|---|---|---|---|---|---|---|
| SORC | 0.8 | 0.7 | 250 | 2.737 | 35 | 30 | 0.8–5.5 |
| RORC | 0.95 | 0.89 | 165 | 84.36 | 15 | 10 | 0.31 |
| Parameters | Valencia et al. | Emam et al. [39] | Zare et al. [27] |
|---|---|---|---|
| 165 | 165 | 165 | |
| 84.36 | 84.36 | 82.16 | |
| 75.22 | 78.06 | 76.09 | |
| 394.21 | 399.30 | 390.60 | |
| 809.52 | 810.10 | 808.70 | |
| 124.58 | 124.80 | 124.20 | |
| 16.25 | 16.37 | 16.15 | |
| 48.71 | 48.80 | 48.54 |
| Parameters | SORC | RORC | DORC | Units |
|---|---|---|---|---|
| Thermal efficiency engine–ORC | 40.45 | 41.25 | 40.72 | % |
| Increased thermal efficiency | 1.86 | 2.66 | 2.13 | % |
| Thermal efficiency ORC | 16.40 | 23.51 | 18.74 | % |
| Global energy conversion efficiency | 6.68 | 9.59 | 7.66 | % |
| Global exergetic efficiency | 34.5 | 49.47 | 39.43 | % |
| BSFC engine–ORC | 169.5 | 166.21 | 168.42 | g/kWh |
| Component | Input (kW) | Product (kW) | (kW) | Lost (kW) |
|---|---|---|---|---|
| ITC1 | 541.202051 | 202.794262 | 41.9535673 | 296.454222 |
| B1 | 0.37472727 | 0.05848531 | 0.31624196 | – |
| ITC2 | 202.852748 | 166.340104 | 36.5126437 | – |
| T1 | 99.4808146 | 85.5899807 | 13.8908338 | – |
| ITC3 | – | – | 36.0581887 | 66.5877282 |
| B2 | 0.75619324 | 0.58683347 | 0.16935977 | – |
| Component | Input (kW) | Product (kW) | (kW) | Lost (kW) |
|---|---|---|---|---|
| ITC1 | 541.202051 | 237.549898 | 7.197931 | 296.454222 |
| B1 | 0.36222219 | 0.09598314 | 0.26623905 | – |
| ITC2 | 237.645881 | 203.818309 | 33.827572 | – |
| T1 | 139.797975 | 122.396844 | 17.40113113 | – |
| ITC3 | – | – | 15.3197 | 71.5691491 |
| B2 | 0.94533621 | 0.7336153 | 0.21172091 | – |
| RC | 86.4902041 | 64.620999 | 21.8692051 | – |
| Component | Input (kW) | Product (kW) | (kW) | Lost (kW) |
|---|---|---|---|---|
| ITC1 | 541.20 | 203.57 | 31.15 | 296.45 |
| B1 | 1.66 | 0.26 | 1.40 | – |
| ITC2 | 113.18 | 101.93 | 11.26 | – |
| T1 | 95.39 | 79.75 | 15.63 | – |
| ITC3 | – | – | 31.01 | 6.00 |
| B2 | 0.63 | 0.49 | 0.14 | – |
| T2 | 10.27 | 8.77 | 1.49 | – |
| B3 | 2.09 | 1.63 | 0.47 | – |
| ITC4 | 90.64 | 52.66 | 37.99 | – |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valencia, G.; Fontalvo, A.; Cárdenas, Y.; Duarte, J.; Isaza, C. Energy and Exergy Analysis of Different Exhaust Waste Heat Recovery Systems for Natural Gas Engine Based on ORC. Energies 2019, 12, 2378. https://doi.org/10.3390/en12122378
Valencia G, Fontalvo A, Cárdenas Y, Duarte J, Isaza C. Energy and Exergy Analysis of Different Exhaust Waste Heat Recovery Systems for Natural Gas Engine Based on ORC. Energies. 2019; 12(12):2378. https://doi.org/10.3390/en12122378
Chicago/Turabian StyleValencia, Guillermo, Armando Fontalvo, Yulineth Cárdenas, Jorge Duarte, and Cesar Isaza. 2019. "Energy and Exergy Analysis of Different Exhaust Waste Heat Recovery Systems for Natural Gas Engine Based on ORC" Energies 12, no. 12: 2378. https://doi.org/10.3390/en12122378





