Forecast Horizon and Solar Variability Influences on the Performances of Multiscale Hybrid Forecast Model
Abstract
1. Introduction
2. Material and Methods
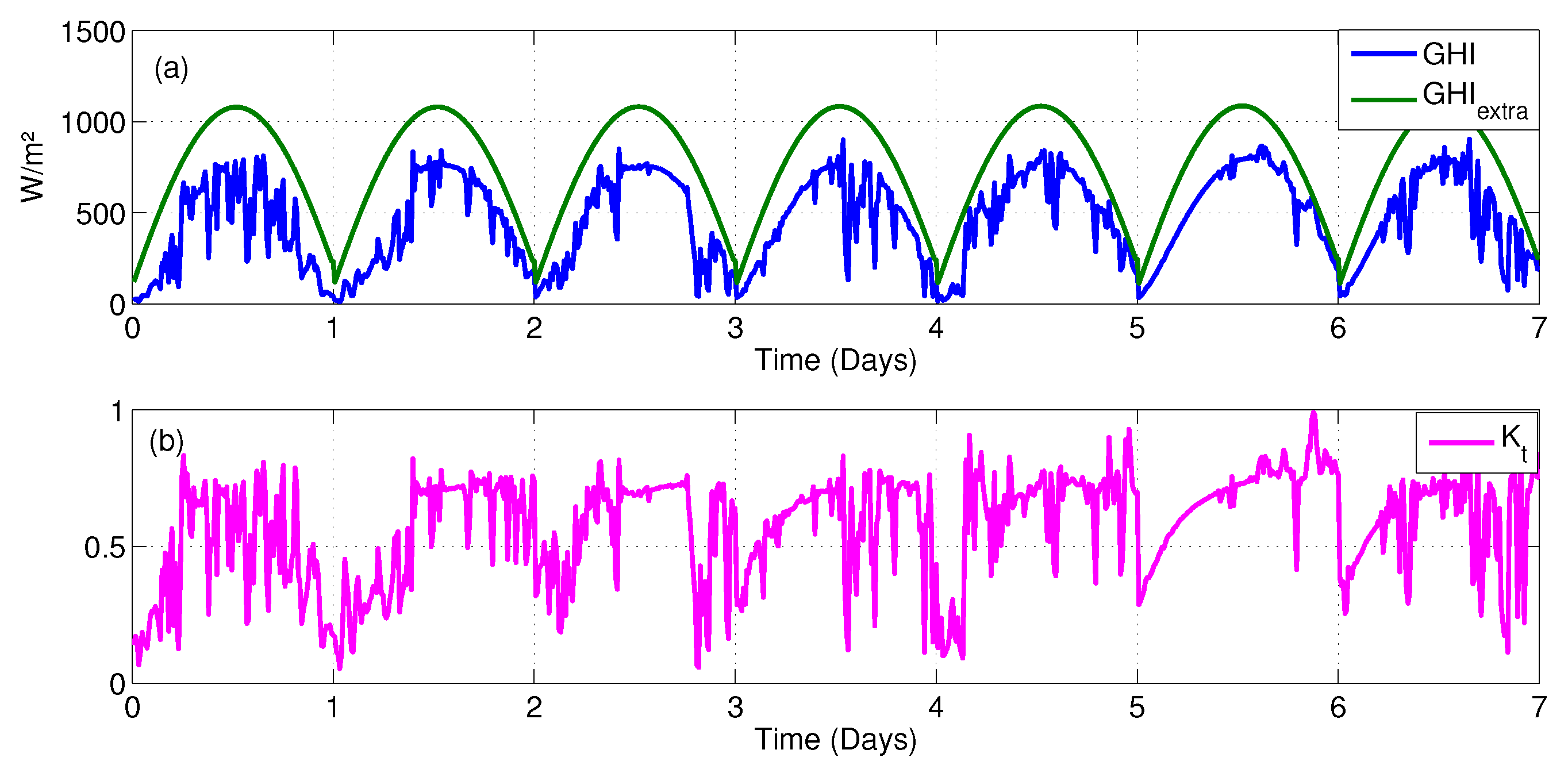
2.1. Data Pre-Processing
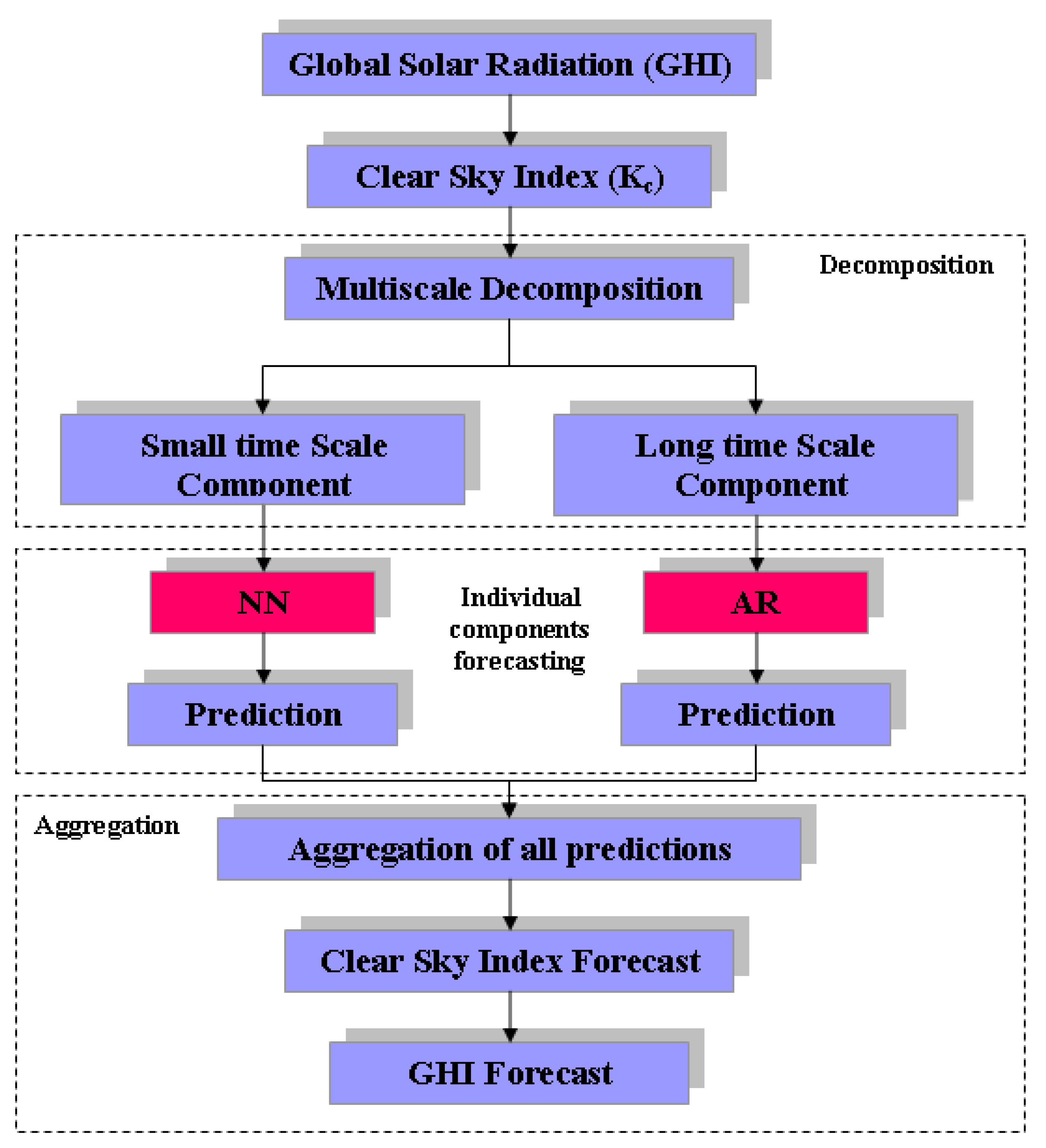
2.2. Forecast Model Method
- Step 1: Detrend the data estimating the clear sky index.
- Step 2: Decompose the signal using a multiscale decomposition method (Empirical Mode Decomposition, Ensemble Empirical Mode Decomposition or Wavelet Decomposition). The choice of forecasting method is adaptive to the characteristic of each component.
- Step 3: Forecast each multiscale decomposition component. The short time scales components are forecasted by NN model (non linear process) and the long time scales components are forecasted by the AR model (linear process).
- Step 4: Sum all the component forecasts to obtain the final predicted time series.
- Step 5: Rebuild the Global solar radiation signal from the predicted by using the Kasten Clear sky model.
2.3. Validation Metrics
- Relative Mean Biais Error
- Relative Mean Absolute Error
- Relative Root Mean Square Errorwhere is the observed value of GHI, is the forecast value of GHI and N the number of point in the dataset for the considered period.
- Skill s: Compare the model performance with a reference model [39]. In this study, the proposed model was compared with the persistence model applying the skill parameter proposed by Coimbra et al. [40]:where index refers to the scaled persistence reference model defined by Equation (7).The corresponding GHI forecast was obtained using Equation (8):
2.4. Methods of MHFM Predictive Performance Analysis according to Forecast Horizons Parameters and Insolation Conditions Parameters
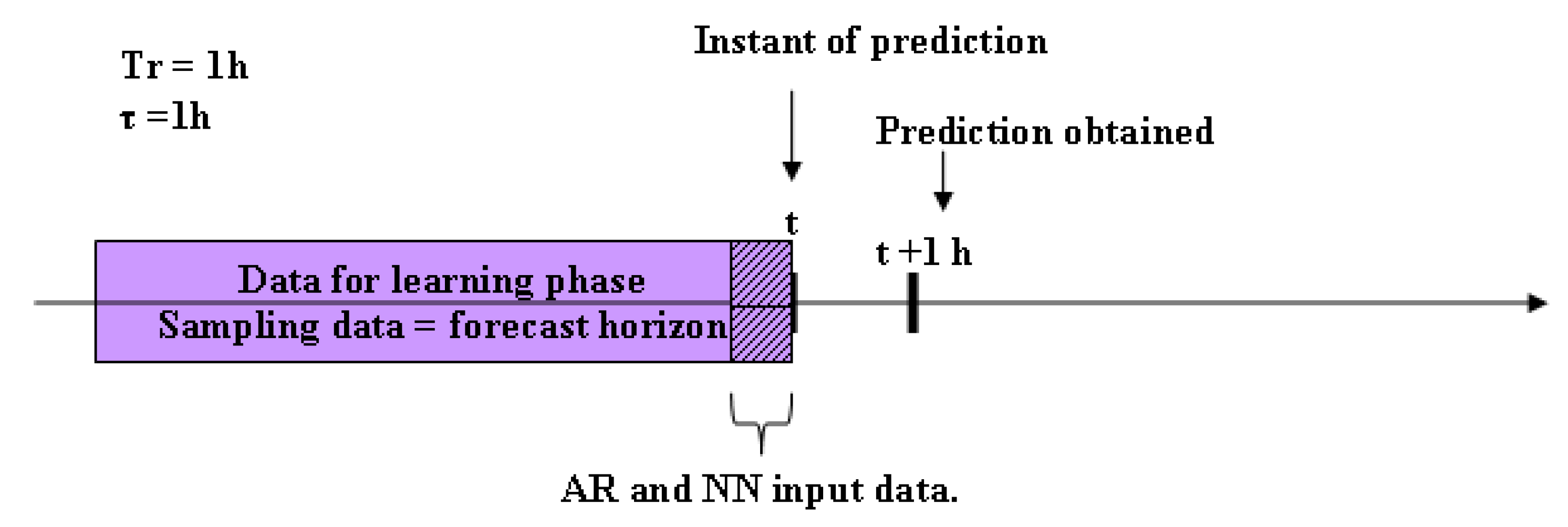
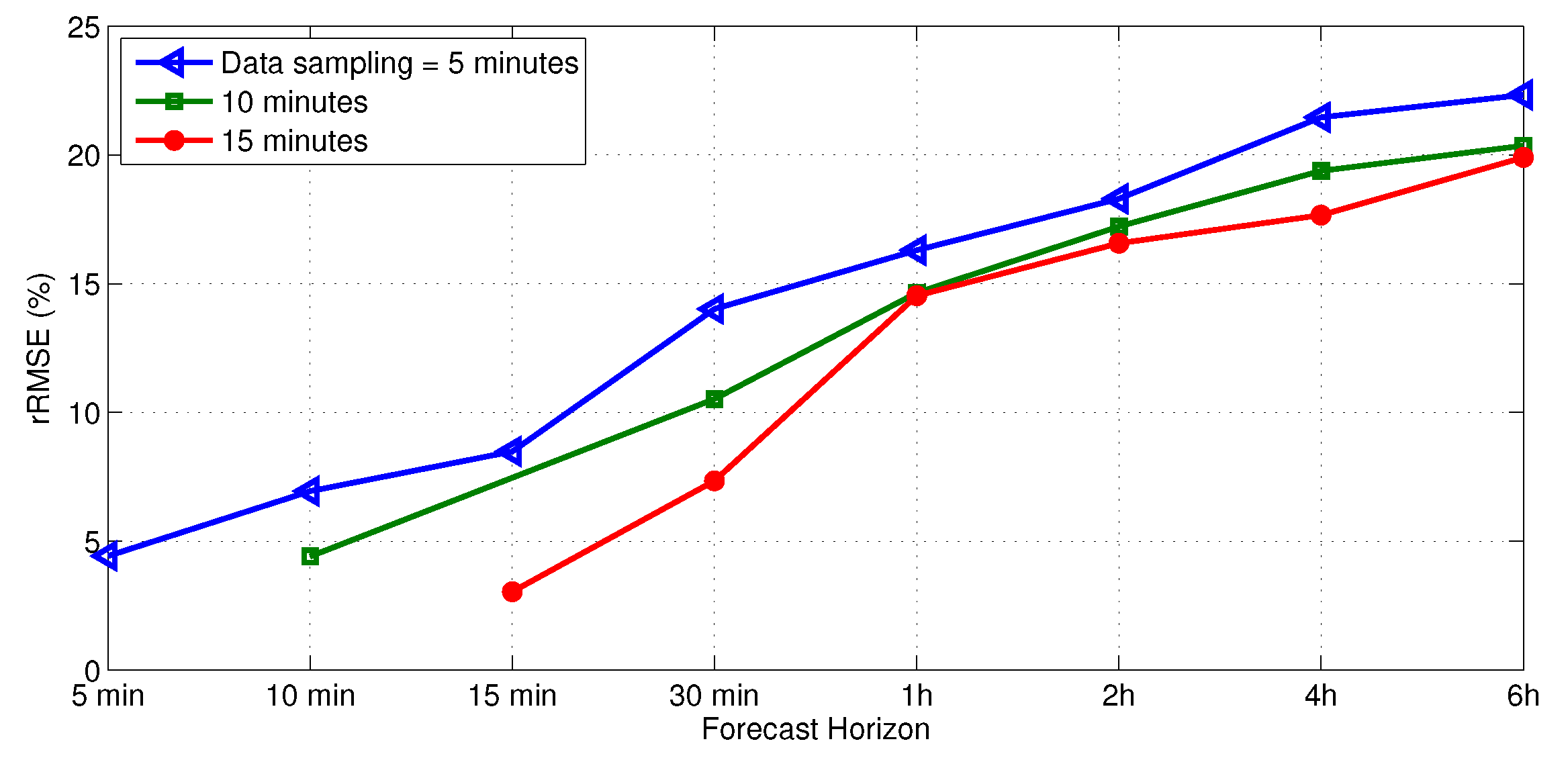
2.4.1. Methods of Forecast Horizon Modeling Process
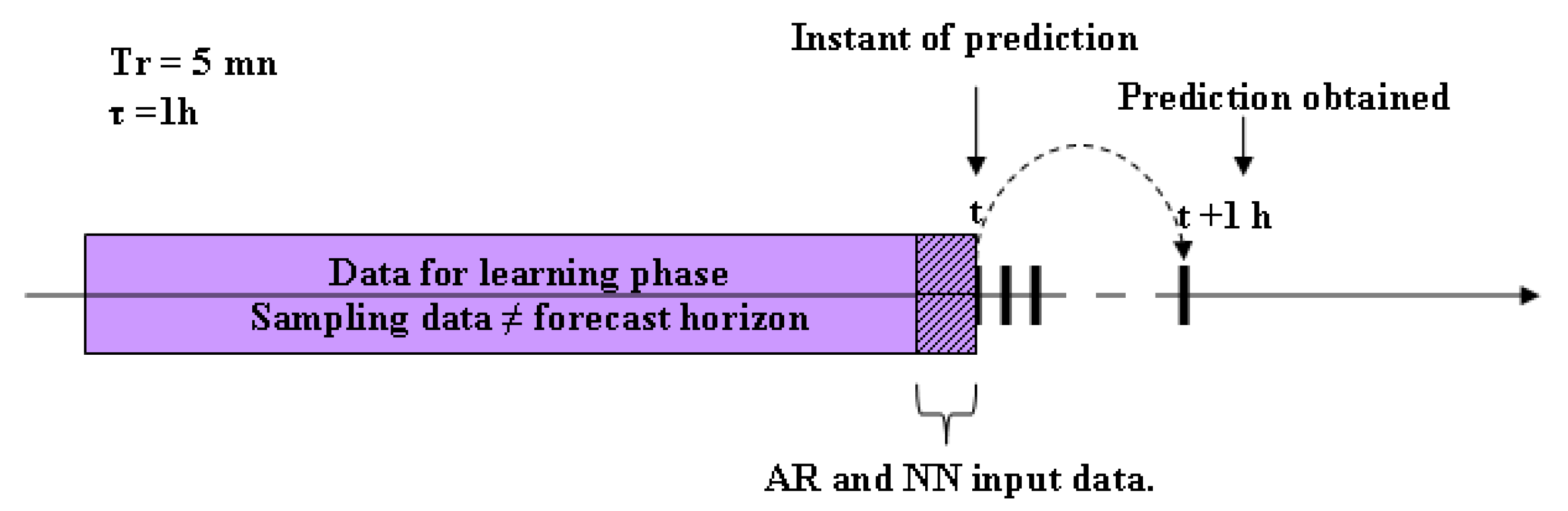
- To provide a forecasting at with a six-month data test, the data test sampling time is also 5 min and the model allows us to obtain every 5 min the forecast at .
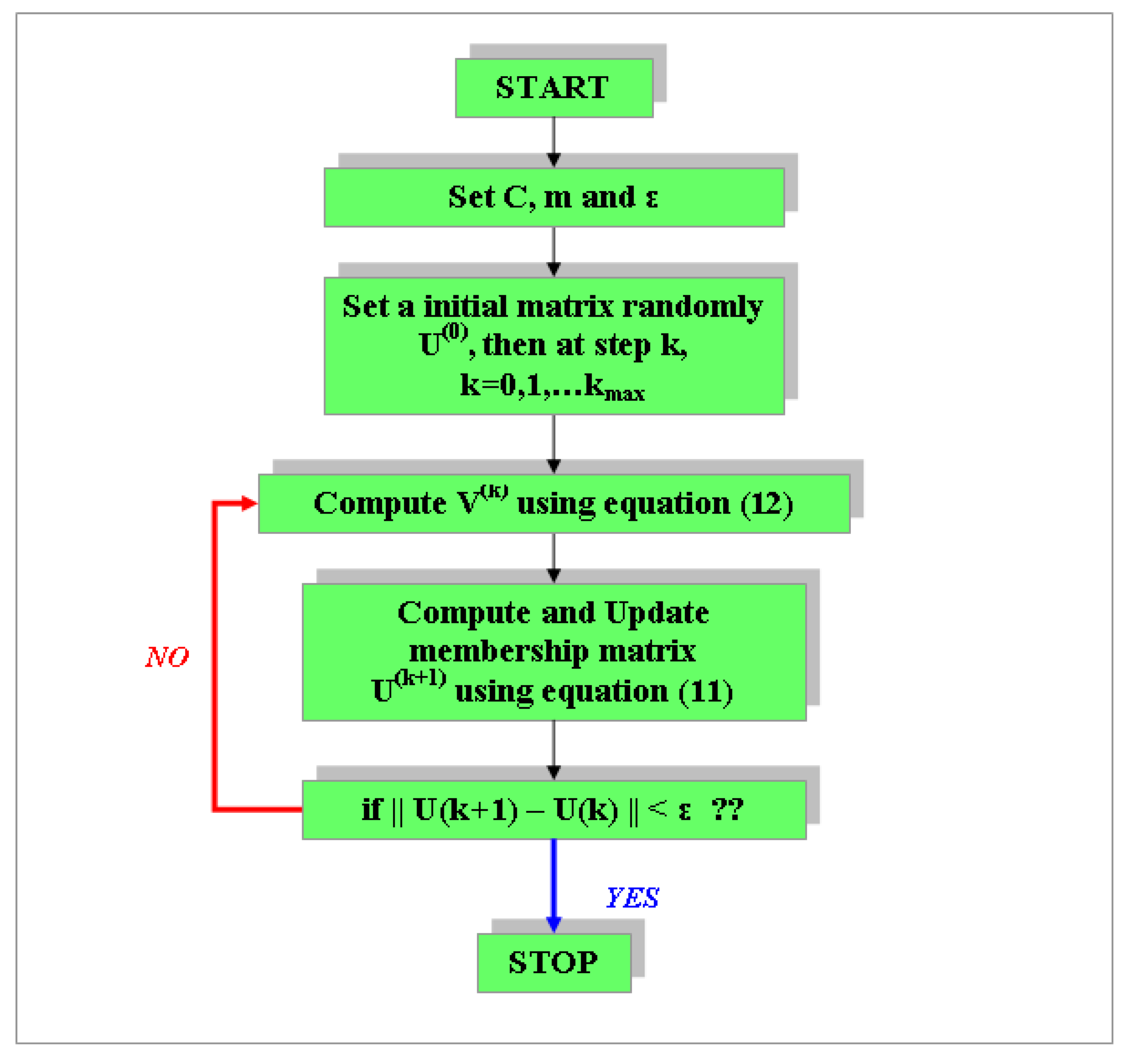
2.4.2. Method of Insolation Conditions Classification
Validity Criterion
3. Results
3.1. Influence of the Forecast Horizons Strategy on Performance Model
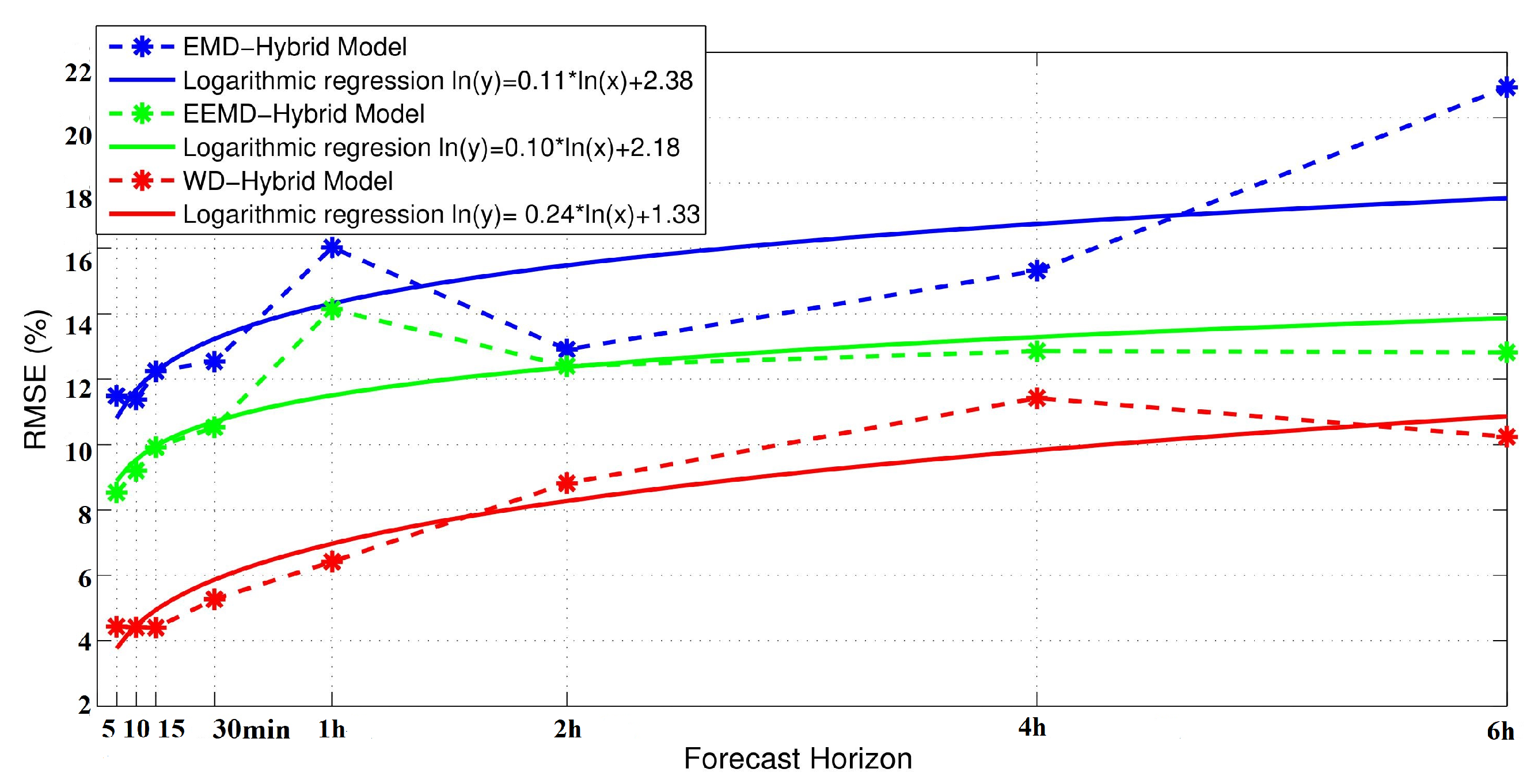
3.1.1. Results: Strategy 1: Sampling Data = Forecast Horizon
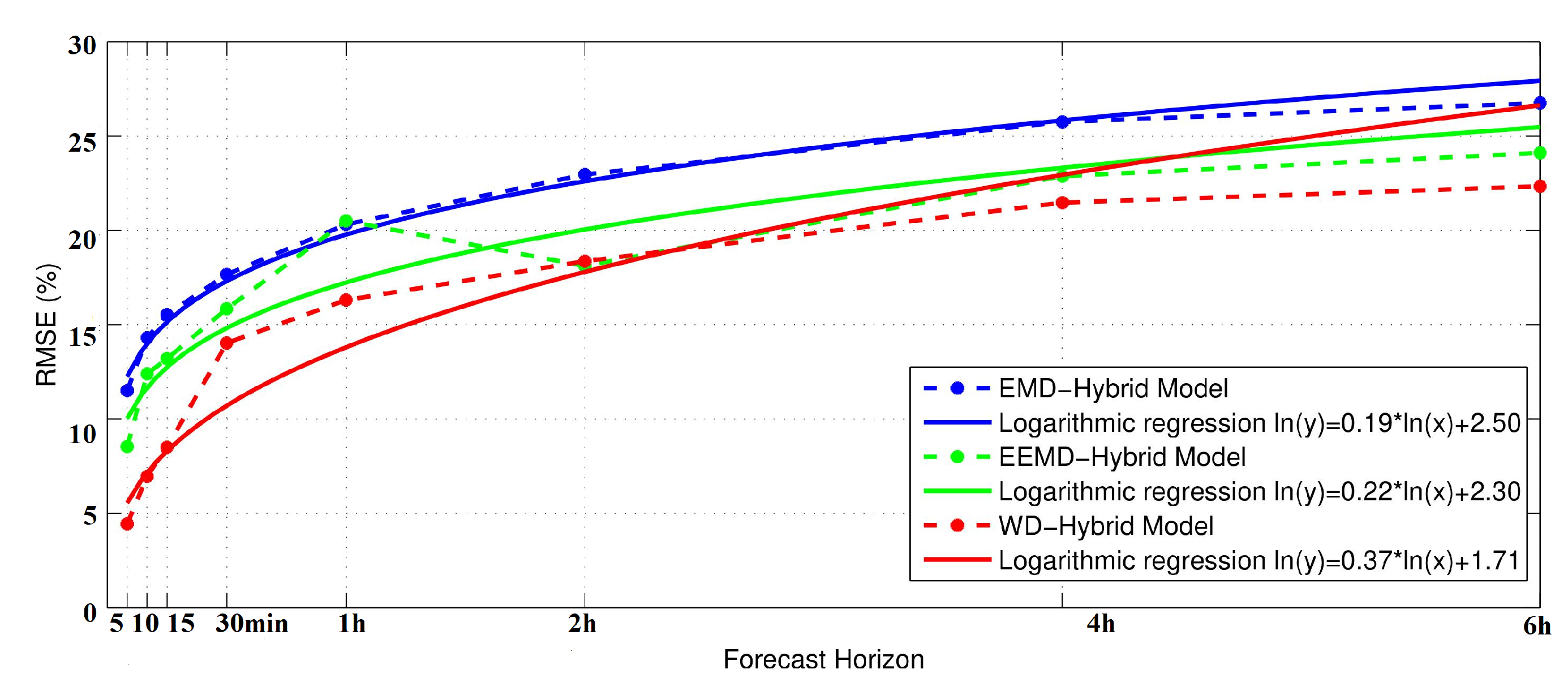
3.1.2. Results: Strategy 2: Sampling Data ≠ Forecast Horizon
3.2. Solar Variability Influence on MHFM Performance
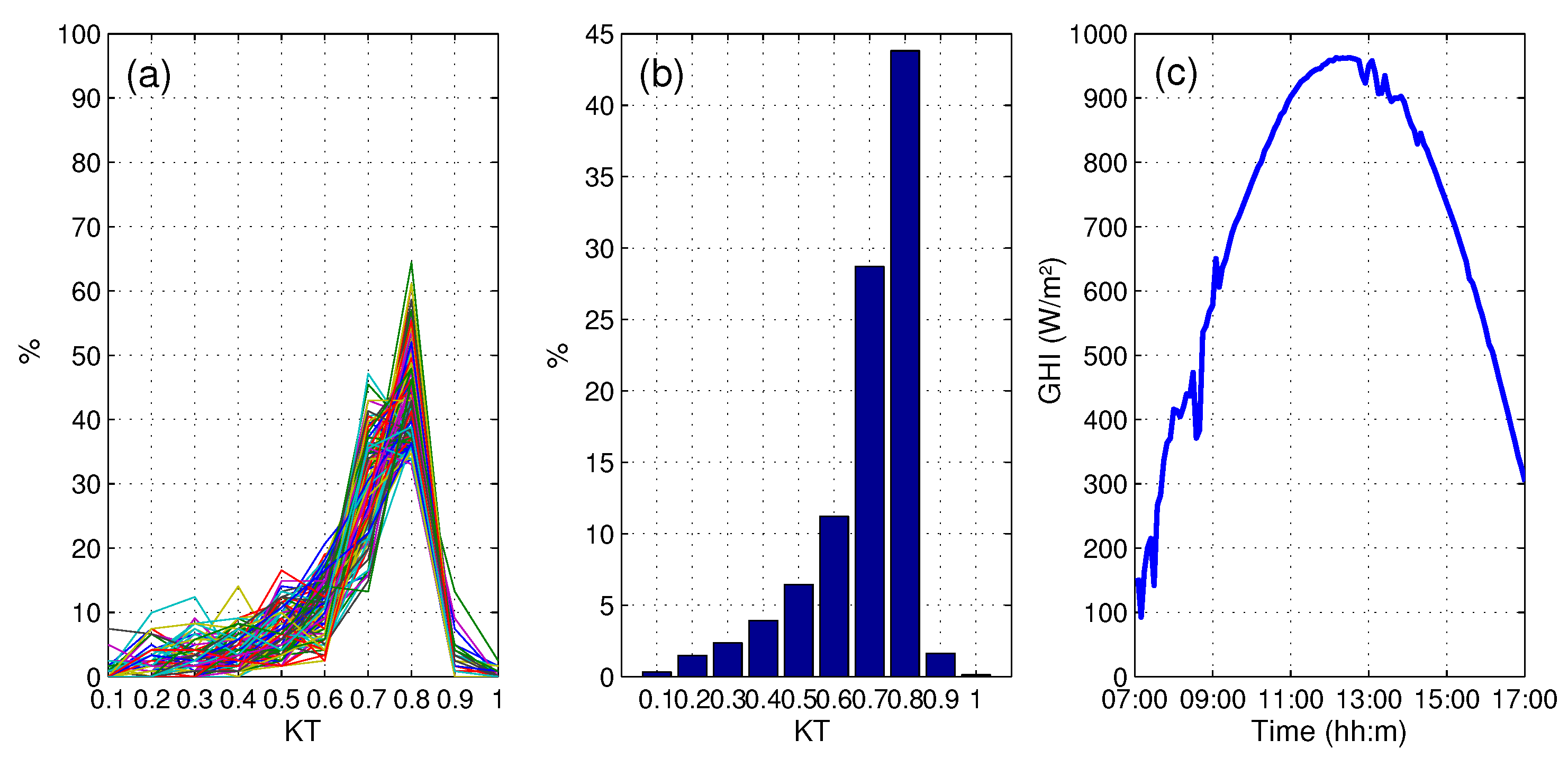
3.2.1. Results of Daily Irradiance Classification
- Clear sky day (CS)
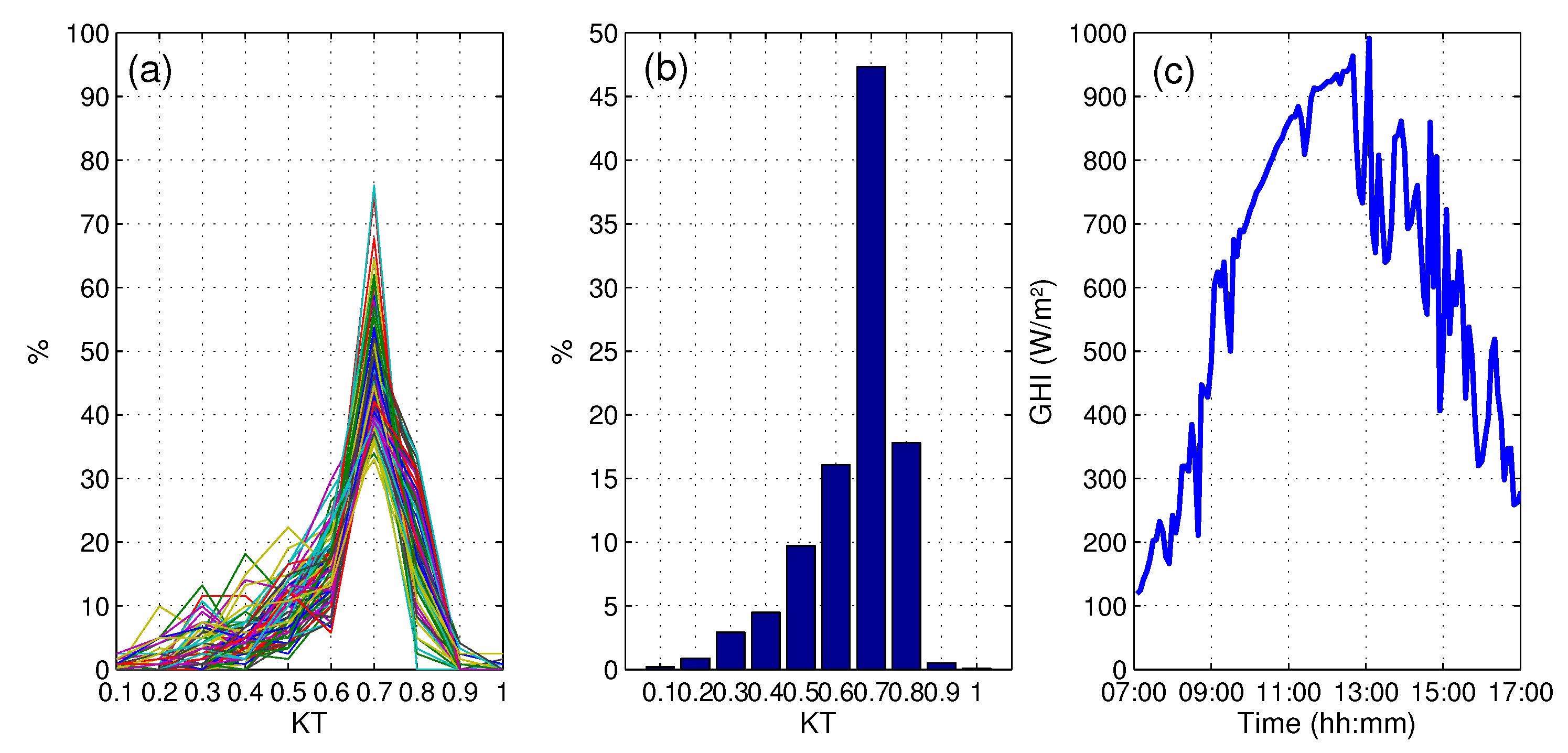
- Intermittent clear sky day (ICS)
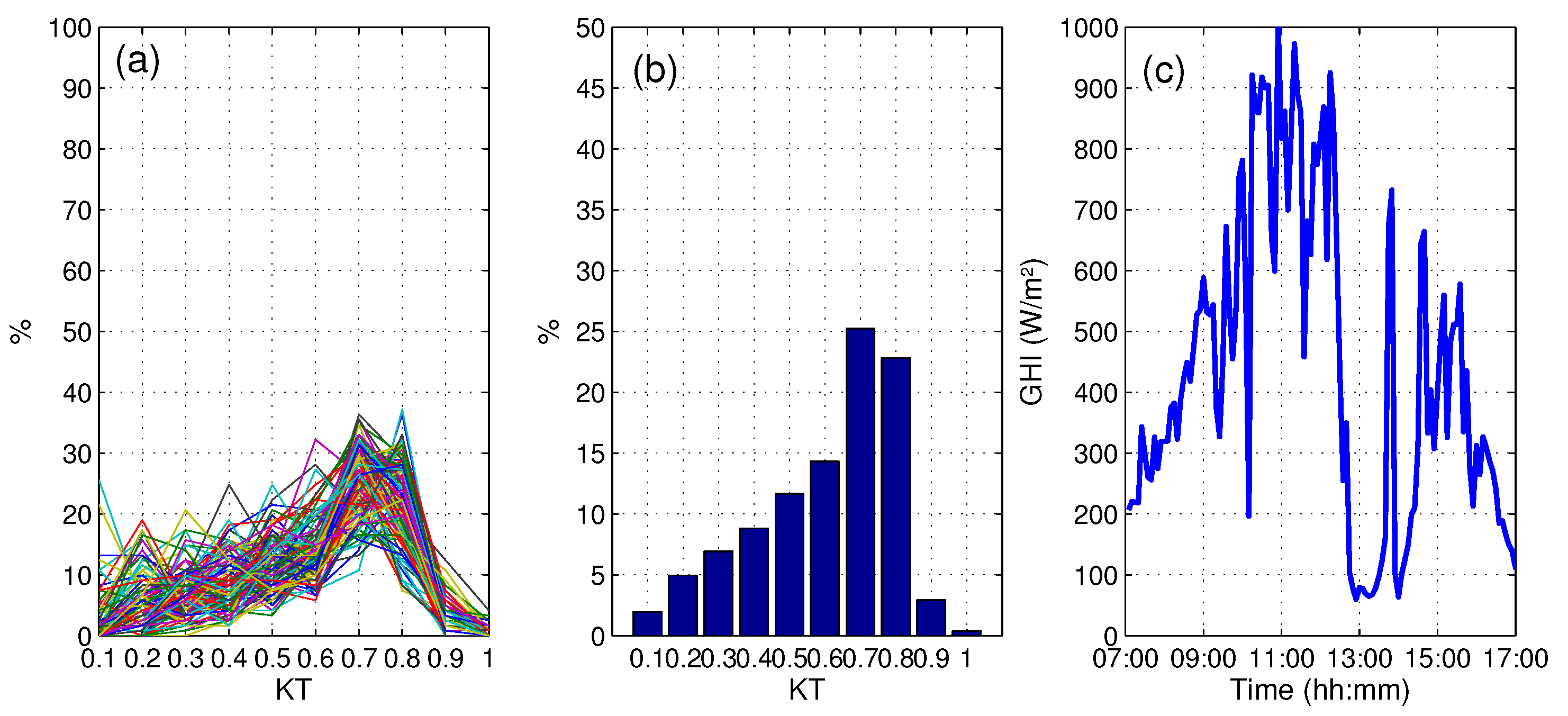
- Cloudy Sky day(ClS)
- Intermittent cloudy sky day(IClS)
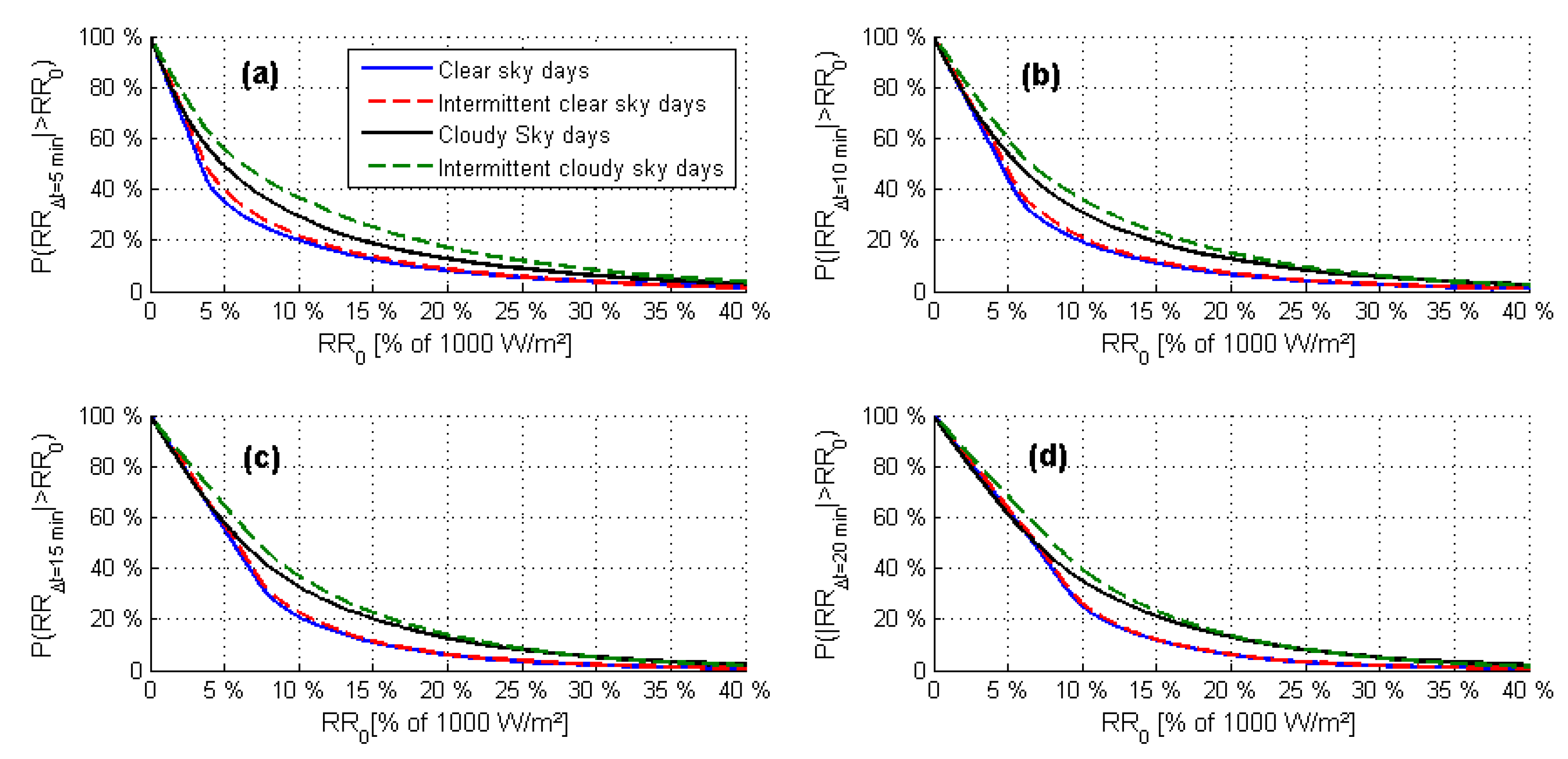
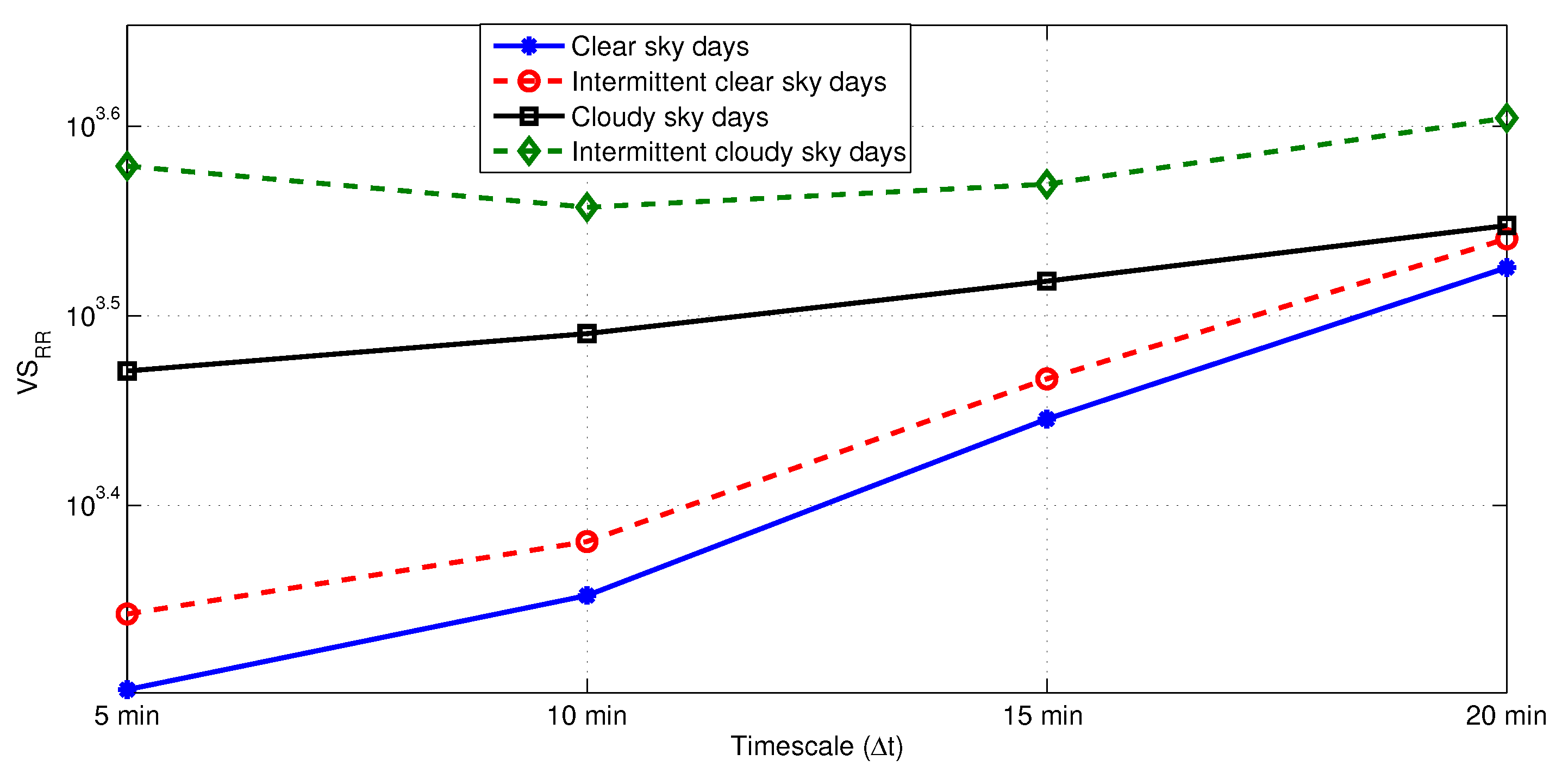
3.2.2. Variability Characterization of Each Day Class
3.2.3. Variability Influence on Hybrid Forecast Model Performances
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.; Coimbra, C.F. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Solar Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A power prediction method for photovoltaic power plan based on wavelet decomposition and artificial neural networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
- Ogliari, E.; Grimaccia, F.; Leva, S.; Musetta, M. Hybrid Predictive Models for Accurate Forecasting in PV Systems. Energies 2013, 6, 1918–1929. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of solar energy modeling techniques. Renew. Sustain. Energy Rev. 2012, 16, 2864–2869. [Google Scholar] [CrossRef]
- Ahmed, O.; Driss, Z.; Hanane, D.; Rachid, B. Artificial neural network analysis of Moroccan solar potential. Renew. Sustain. Energy Rev. 2012, 16, 4876–4889. [Google Scholar]
- Mellit, A.; Kalogirou, S.; Hontoria, L.; Shaari, S. Artificial intelligence techniques for sizing photovoltaic systems: a review. Renew. Sustain. Energy Rev. 2009, 13, 406–419. [Google Scholar] [CrossRef]
- Sharma, V.; Yang, D.; Walsh, W.; Reindl, T. Short term solar irradiance forecasting using a mixed wavelet neural network. Renew. Energy 2016, 90, 481–492. [Google Scholar] [CrossRef]
- Gutierrez-Corea, F.V.; Manso-Callejo, M.A.; Moreno-Regidor, M.P.; Manrique-Sancho, M.T. Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations. Solar Energy 2016, 134, 119–131. [Google Scholar] [CrossRef]
- Kashyap, Y.; Bansal, A.; Sao, A.K. Solar radiation forecasting with multiple parameters neural networks. Renew. Sustain. Energy Rev. 2015, 49, 825–835. [Google Scholar] [CrossRef]
- Huang, J.; Korolkiewicz, M.; Agrawal, M.; Bol, J. Forecasting solar radiation on an hourly time scale using a Coupled AutoRegressive and Dynamical System (CARDS) model. Solar Energy 2013, 87, 136–149. [Google Scholar] [CrossRef]
- Sun, H.; Yan, D.; Zhao, N.; Zhou, J. Empirical investigation on modeling solar radiation series with ARMA–GARCH models. Energy Convers. Manag. 2015, 92, 385–395. [Google Scholar] [CrossRef]
- André, M.; Dabo-Niang, S.; Soubdhan, T.; Ould-Baba, H. Predictive spatio-temporal model for spatially sparse global solar radiation data. Energy 2016, 111, 599–608. [Google Scholar] [CrossRef]
- André, M.; Perez, R.; Soubdhan, T.; Schlemmer, J.; Calif, R.; Monjoly, S. Preliminary assessment of two spatio-temporal forecasting technics for hourly satellite-derived irradiance in a complex meteorological context. Solar Energy 2019, 177, 703–712. [Google Scholar] [CrossRef]
- Reikard, G.; Hansen, C. Forecasting solar irradiance at short horizons: Frequency and time domain models. Renew. Energy 2019, 135, 1270–1290. [Google Scholar] [CrossRef]
- Zhang, G. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Monjoly, S.; André, M.; Calif, R.; Soubdhan, T. Hourly forecasting Global Solar radiation based on Multiscale decomposition methods—A hybrid Approach. Energy 2017, 119, 288–298. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform time-frequency localization and signal analysis. IEEE Trans. Inform. Theory 1990, 36, 961–1004. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert sprectrum for nonlinear and non-stationnary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Solar Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Lauret, P.; Voyant, C.; Soubdhan, T.; Mathieu, D.; Poggi, P. A benchmarking of machine learning technique for solar radiation forecasting in an insular context. Solar Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- Dobbs, A.; Elgindy, T.; Hodge, B.M.; Florita, A. Short-Term Solar Forecasting Performance of Popular Machine Learning Algorithms. In Proceedings of the International Workshop on the Integration of Solar Power into Power Systems (Solar Integration Workshop), Berlin, Germany, 24–25 October 2017. [Google Scholar]
- Sakshi, M.; Praveen, P. Multi-time-horizon Solar Forecasting Using Recurrent Neural Network. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 18–24. [Google Scholar] [CrossRef]
- Reikard, G.; Haupt, S.E.; Jensen, T. Forecasting ground-level irradiance over short horizons: Time series, meteorological, and time-varying parameter models. Renew. Energy 2017, 112, 474–485. [Google Scholar] [CrossRef]
- Soubdhan, T.; Emilion, R.; Calif, R. Classification of daily solar radiation distributions using a mixture of Dirichlet distributions. Solar Energy 2009, 83, 1056–1063. [Google Scholar] [CrossRef]
- Muselli, M.; Poggi, P.; Notton, G.; Louche, A. Classification of typical Meteorological Days from Global Irradiation Records ad Comparison Between Two Mediterranean Coastal Sites in Corsica Island. Energy Convers. Manag. 2000, 41, 1043–1063. [Google Scholar] [CrossRef]
- Soubdhan, T.; Abadi, M.; Emilion, R. Time Dependent Classification of Solar Radiation Sequences Using Best Information Criterion. Energy Procedia 2014, 57, 1309–1316. [Google Scholar] [CrossRef][Green Version]
- Benmouiza, K.; Tadj, M.; Cheknane, A. Classification of Hourly Solar Radiation using Fuzzy-C means algorithm for optimal stand-alone PV system sizing. Electr. Power Energy Syst. 2016, 82, 233–241. [Google Scholar] [CrossRef]
- Johnson, J.; Schenkman, B.; Ellis, A.; Quiroz, J.; Lenox, C. Initial operating experience of the 1.2-MW La Ola photovoltaic system. In Proceedings of the 38th IEEE Photovoltaic Specialists Conference (PVSC), Austin, TX, USA, 3–8 June 2012; Volume 2, pp. 1–6. [Google Scholar]
- Hansen, C.; Stein, J.; Ellis, A. Statistical Criteria for Characterizing Irradiance Time Series; Sandia National Laboratories: Albuquerque, NM, USA, 2010.
- Lave, M.; Reno, M.J.; Broderick, R.J. Characterizing local High-frequency solar variability and its impact to distribution studies. Solar Energy 2015, 118, 327–337. [Google Scholar] [CrossRef]
- Gagné, A.; Turcotte, D.; Goswamy, N.; Poissant, Y. High resolution characterisation of solar variability for two sites in Eastern Canada. Solar Energy 2016, 137, 46–54. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K.; Hoff, T.E. Short-term irradiance variability: Preliminary estimation of station pair correlation as a function of distance. Solar Energy 2012, 86, 2170–2176. [Google Scholar] [CrossRef]
- Dambreville, R.; Blanc, P.; Chanussot, J.; Boldo, D. Very short term forecasting of the global horizontal irradiance using a spatio-temporal autoregressive model. Renew. Energy 2014, 72, 291–300. [Google Scholar] [CrossRef]
- Kasten, F. A simple parametrization of two pyrheliometric formulae for detremining the linke turbidity factor. Meteorol. Rundsch. 1980, 33, 124–127. [Google Scholar]
- Badosa, J.; Haeffelin, M.; Chepfer, H. Scales of spatial and temporal variation of solar irradiance on Reunion tropical island. Solar Energy 2013, 88, 42–56. [Google Scholar] [CrossRef]
- Jiménez-Pérez, P.; Mora-López, L. Modelling and Forecasting hourly Global Solar Radiation using Clustering and Classification techniques. Solar Energy 2016, 135, 682–691. [Google Scholar] [CrossRef]
- Kasten, F. The link Turbidity Factor Based on Improved Values of integral Rayleigh Optical thickness. Solar Energy 1996, 56, 239–244. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H.; Nielsen, H.A. Online short-term solar power forecasting. Solar Energy 2009, 83, 1772–1783. [Google Scholar] [CrossRef]
- Coimbra, C.F.M.; Kleissl, J.; Marquez, R. Overview of Solar Forecasting Method and a metric for accuracy evaluation. In Solar Energy Forecasting and Resource Assessment; Kleissl, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 171–194. [Google Scholar]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of Solar irradiance forecasting methods and a proposition for small scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Panapakidis, I.; Asimopoulos, N.; Dagoumas, A.; Christoforidis, G.C. An Improved Fuzzy C-Means Algorithm for the Implementation of Demand Side Management Measures. Energies 2017, 10, 1407. [Google Scholar] [CrossRef]
- Ruspini, E.H. Numerical Methods for fuzzy clustering. Inf. Sci. 1970, 2, 319–350. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of ISODATA process and its use in clustering compact and well separated cluster. J. Cybern. 1974, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Kluwer Academic Publishers: Norwell, MA, USA, 1981. [Google Scholar]
- Bezdek, J.; Ehrlich, R. Numerical Methods for fuzzy clustering. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Xie, X.; Beni, G. A validity measure for fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 8, 841–847. [Google Scholar] [CrossRef]
- Kleissl, J. Solar Energy Forecasting and Resource Assessment; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Cécé, R.; Bernard, D.; Brioude, J.; Zahibo, N. Microscale anthropogenic pollution modelling in a small tropical island during weak trade winds: Lagrangian particle dispersion simulations using real nested LES meteorological fields. Atmos. Environ. 2016, 139, 98–112. [Google Scholar] [CrossRef]
- Aryaputera, A.W.; Yang, D.; Zhao, L.; Walsh, W.M. Very short-term irradiance forecasting at unobserved locations using spatio-temporal kriging. Solar Energy 2015, 122, 1266–1278. [Google Scholar] [CrossRef]
- Tato, J.H.; Brito, M.C. Using Smart Persistence and Random Forests to Predict Photovoltaic Energy Production. Energies 2019, 12, 100. [Google Scholar] [CrossRef]
- Du, J.; Min, Q.; Zhang, P.; Guo, J.; Yang, J.; Yin, B. Short-Term Solar Irradiance Forecasts Using Sky Images and Radiative Transfer Model. Energies 2018, 11, 1107. [Google Scholar] [CrossRef]


| Models | Forecast Horizon | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 min | 10 min | 15 min | 30 min | 1 h | 2 h | 4 h | 6 h | ||
| EMD-Hybrid Model | rMBE (%) | 0.17 | −0.25 | 0.23 | 0.12 | −0.32 | 1.36 | 1.03 | 1.99 |
| rMAE (%) | 7.42 | 7.73 | 8.30 | 8.54 | 11.43 | 9.00 | 9.87 | 13.16 | |
| rRMSE (%) | 11.49 | 11.38 | 12.24 | 12.54 | 16.03 | 12.91 | 15.32 | 20.93 | |
| Skill (%) | 44.54 | 50.22 | 46.82 | 51.43 | 56.30 | 77.24 | 79.43 | 70.45 | |
| EEMD-Hybrid Model | rMBE (%) | −0.02 | −0.12 | −0.27 | 0.25 | −0.60 | 0.23 | 0.63 | 0.12 |
| rMAE (%) | 5.14 | 5.80 | 6.42 | 7.21 | 8.90 | 8.20 | 8.56 | 8.45 | |
| rRMSE (%) | 8.53 | 9.20 | 9.92 | 10.53 | 14.14 | 12.40 | 12.86 | 12.82 | |
| Skill (%) | 58.83 | 59.72 | 57.10 | 59.21 | 61.45 | 78.15 | 83.31 | 81.91 | |
| WD-Hybrid Model | rMBE (%) | 0.12 | 0.01 | −0.04 | 0.11 | 0.074 | 0.38 | 0.29 | 0.42 |
| rMAE (%) | 2.84 | 3.02 | 3.04 | 3.62 | 4.17 | 6.11 | 8.14 | 7.37 | |
| rRMSE (%) | 4.43 | 4.41 | 3.04 | 5.27 | 6.42 | 8.82 | 11.42 | 10.24 | |
| Skill (%) | 78.58 | 80.69 | 80.73 | 79.57 | 82.50 | 84.45 | 85.18 | 85.54 | |
| Models | Forecast Horizon | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 min | 10 min | 15 min | 30 min | 1 h | 2 h | 4 h | 6 h | ||
| rMBE (%) | 0.17 | 0.013 | 0.07 | −0.33 | 0.48 | −0.14 | 1.36 | −0.14 | |
| rMAE (%) | 7.12 | 9.39 | 10.12 | 11.52 | 13.51 | 15.66 | 17.61 | 18.88 | |
| rRMSE (%) | 11.49 | 14.30 | 15.53 | 17.65 | 20.30 | 22.95 | 25.74 | 26.75 | |
| Skill (%) | 44.54 | 30.85 | 24.91 | 14.68 | 1.86 | −10.95 | −24.29 | −29.13 | |
| EEMD-Hybrid Model | rMBE (%) | −0.02 | −0.38 | −0.53 | 0.31 | −1.15 | −0.49 | 0.27 | 0.33 |
| rMAE (%) | 5.174 | 7.59 | 8.20 | 9.92 | 11.78 | 13.61 | 15.61 | 16.71 | |
| rRMSE (%) | 8.53 | 12.38 | 13.19 | 15.84 | 18.10 | 20.49 | 22.87 | 24.10 | |
| Skill (%) | 58.83 | 40.16 | 36.23 | 23.40 | 12.49 | 0.96 | −10.64 | −16.54 | |
| WD-Hybrid Model | rMBE (%) | 0.12 | 0.18 | 0.12 | 0.24 | −0.22 | 0.17 | 0.26 | 0.15 |
| rMAE (%) | 2.84 | 4.63 | 5.79 | 8.82 | 10.64 | 12.06 | 14.48 | 15.14 | |
| rRMSE (%) | 4.43 | 6.95 | 8.49 | 14.02 | 16.30 | 18.36 | 21.46 | 22.33 | |
| Skill (%) | 78.58 | 66.38 | 58.98 | 32.20 | 21.20 | 11.24 | −3.67 | −7.81 | |
| Number of Cluster C | 2 | 3 | 4 | 5 | 6 |
| Validity Criteria S | 0.43 | 0.37 | 0.33 | 0.51 | 0.57 |
| Clear Sky | Intermittent Clear Sky | Cloudy Sky | Intermittent Cloudy Sky | |
|---|---|---|---|---|
| Number of day | 109 | 84 | 62 | 111 |
| In percentage | 29 | 24 | 17 | 30 |
| EMD-Hybrid Model | EEMD-Hybrid Model | WD-Hybrid Model | ||
|---|---|---|---|---|
| Clear Sky | rMBE (%) | 0.21 | −0.20 | 0.02 |
| rMAE (%) | 5.14 | 3.70 | 2.00 | |
| rRMSE (%) | 7.47 | 5.84 | 2.91 | |
| CIntermittent Clear Sky | rMBE (%) | 0.07 | −0.51 | 0.08 |
| rMAE (%) | 6.00 | 4.39 | 2.35 | |
| rRMSE (%) | 8.76 | 6.95 | 3.35 | |
| CCloudy Sky | rMBE (%) | 0.11 | −0.21 | 0.32 |
| rMAE (%) | 10.14 | 7.71 | 4.72 | |
| rRMSE (%) | 14.81 | 11.76 | 6.73 | |
| CIntermittent Cloudy Sky | rMBE (%) | 0.15 | −0.19 | 0.17 |
| rMAE (%) | 9.32 | 7.42 | 3.81 | |
| rRMSE (%) | 13.36 | 11.16 | 5.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monjoly, S.; André, M.; Calif, R.; Soubdhan, T. Forecast Horizon and Solar Variability Influences on the Performances of Multiscale Hybrid Forecast Model. Energies 2019, 12, 2264. https://doi.org/10.3390/en12122264
Monjoly S, André M, Calif R, Soubdhan T. Forecast Horizon and Solar Variability Influences on the Performances of Multiscale Hybrid Forecast Model. Energies. 2019; 12(12):2264. https://doi.org/10.3390/en12122264
Chicago/Turabian StyleMonjoly, Stéphanie, Maina André, Rudy Calif, and Ted Soubdhan. 2019. "Forecast Horizon and Solar Variability Influences on the Performances of Multiscale Hybrid Forecast Model" Energies 12, no. 12: 2264. https://doi.org/10.3390/en12122264
APA StyleMonjoly, S., André, M., Calif, R., & Soubdhan, T. (2019). Forecast Horizon and Solar Variability Influences on the Performances of Multiscale Hybrid Forecast Model. Energies, 12(12), 2264. https://doi.org/10.3390/en12122264






