Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile
Abstract
1. Introduction
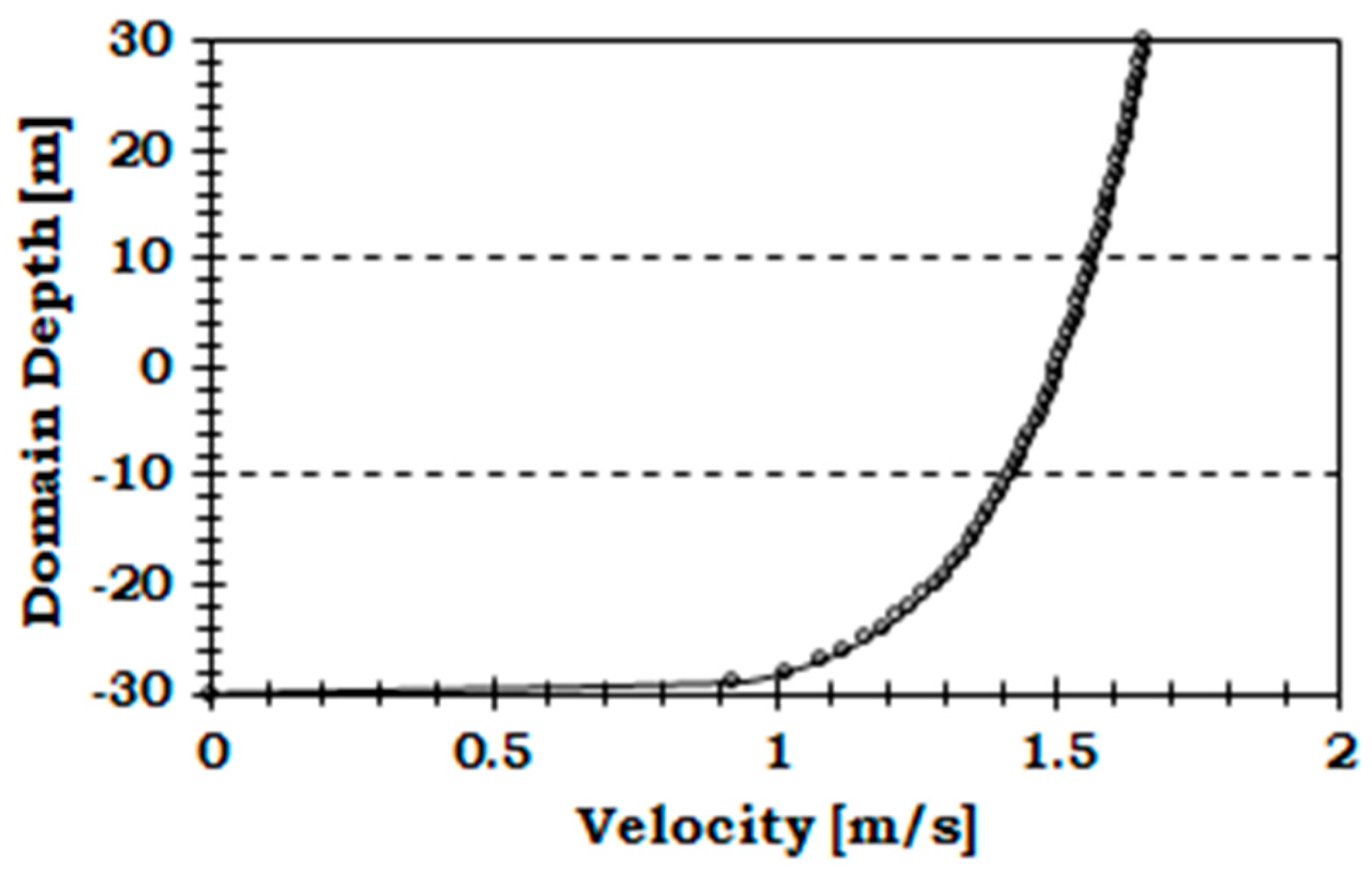
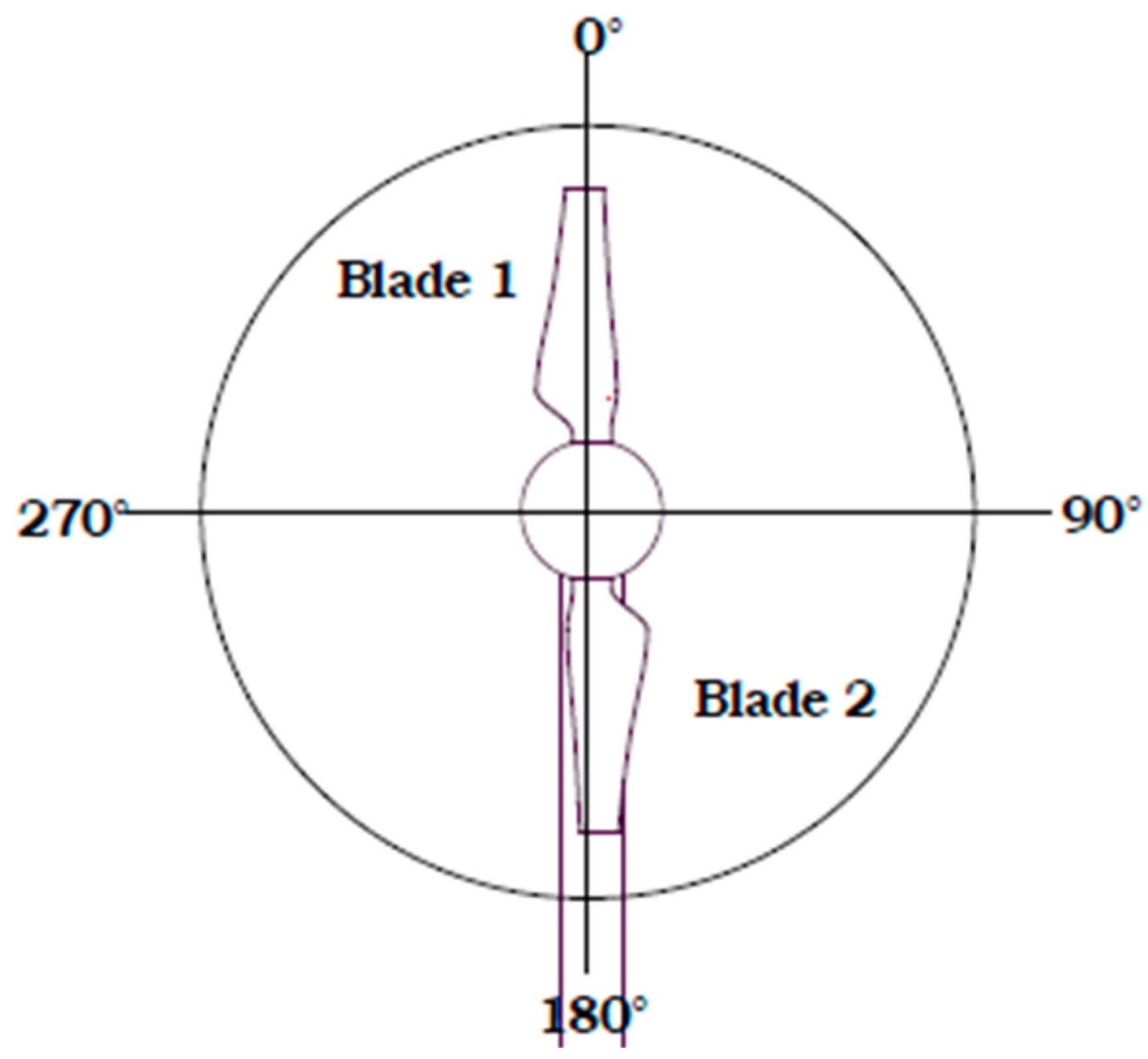
2. Simulation Conditions and Load Parameters
3. Computational Method
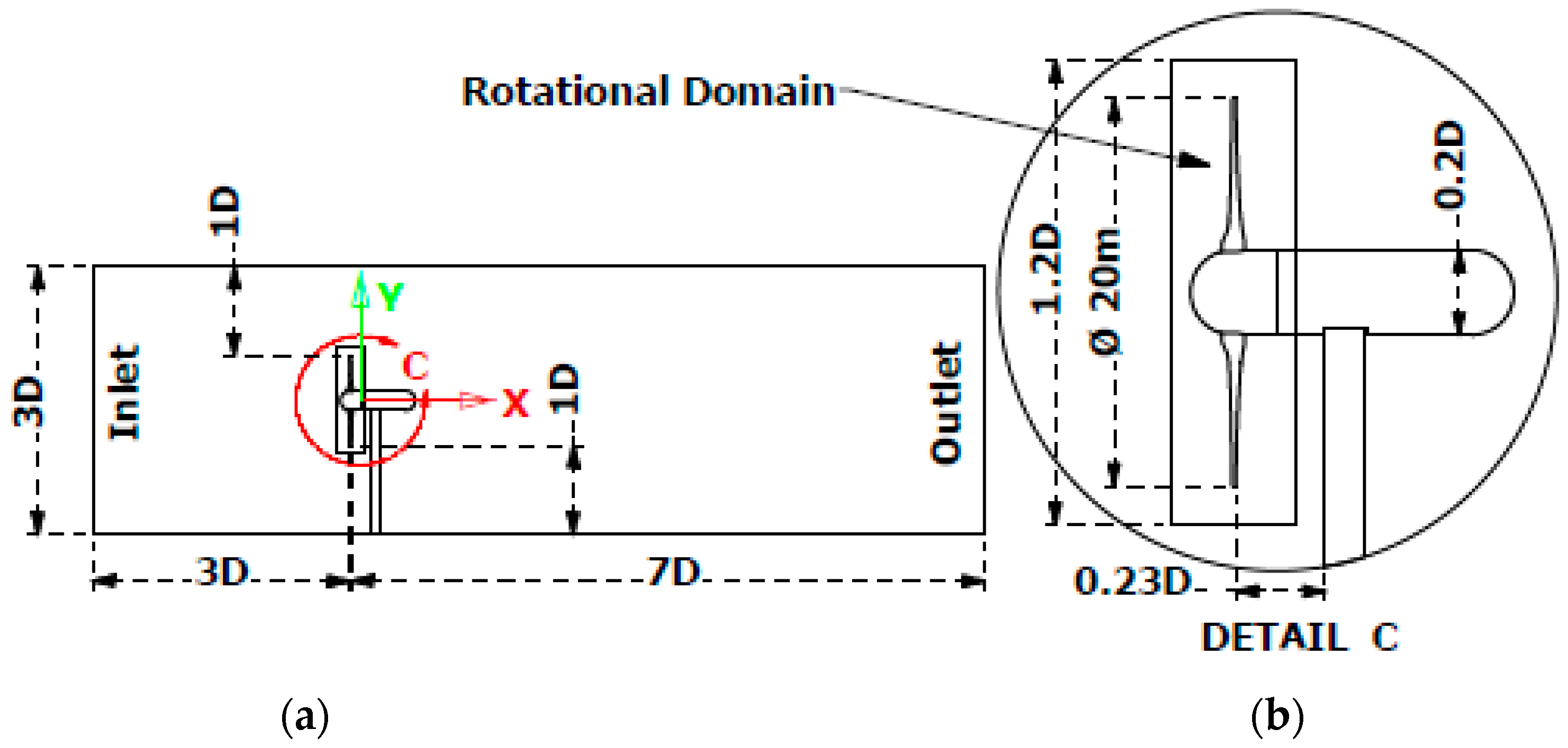
3.1. Computational Fluid Dynamics Model
3.2. Coupled Fluid Structure Interaction Model
3.3. Computational Mesh
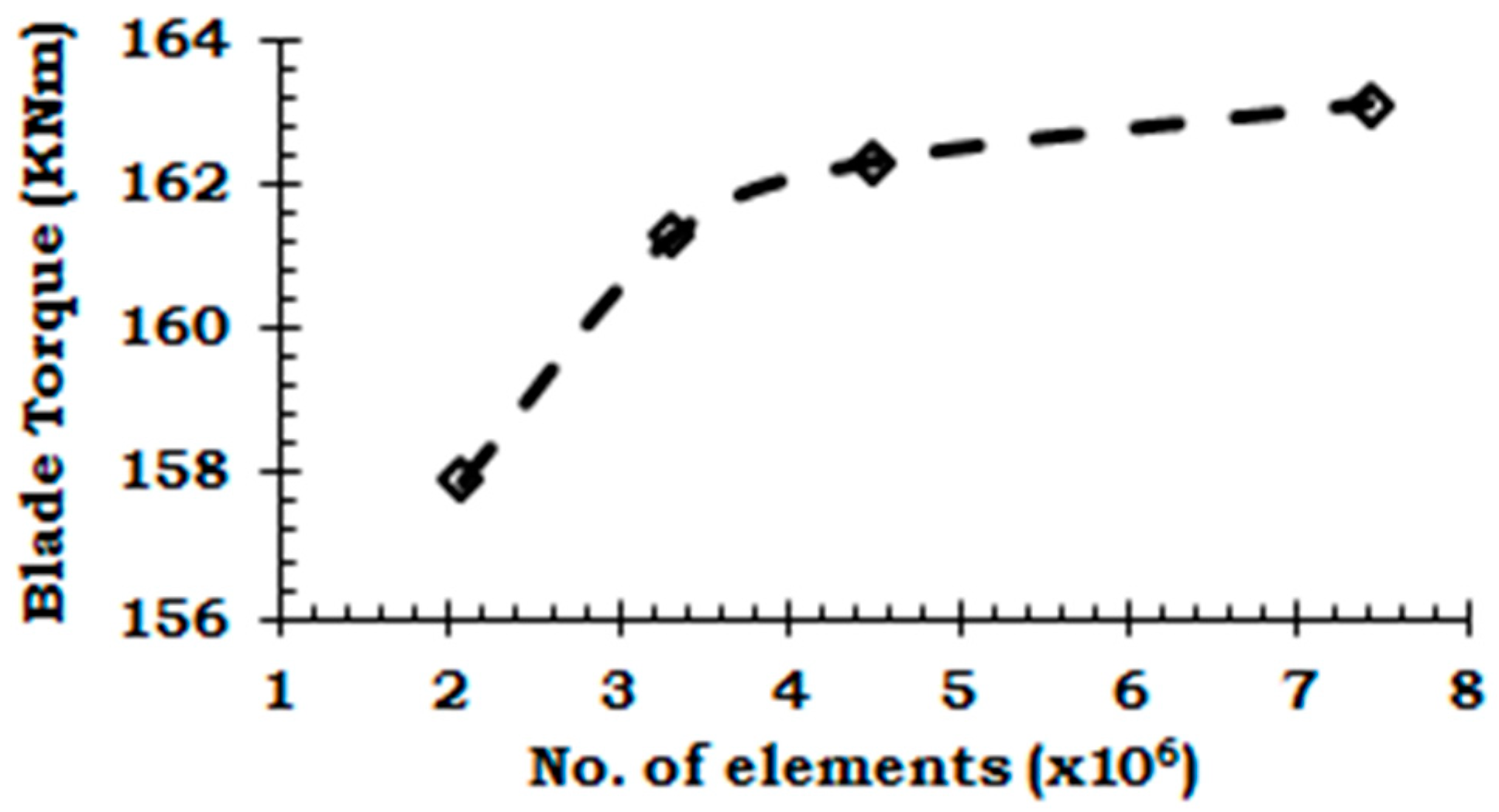
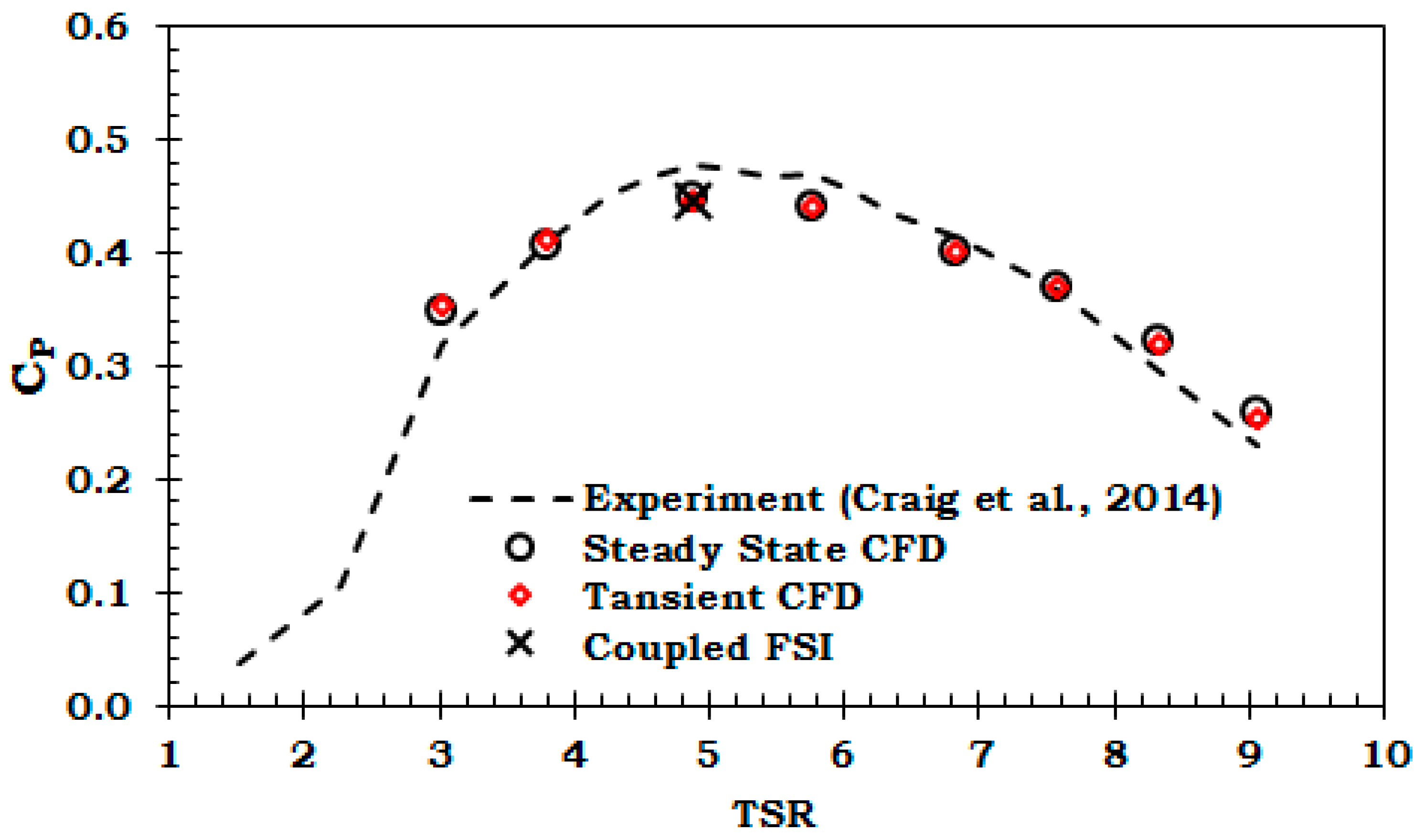
4. Verification and Validation of the Numerical Method
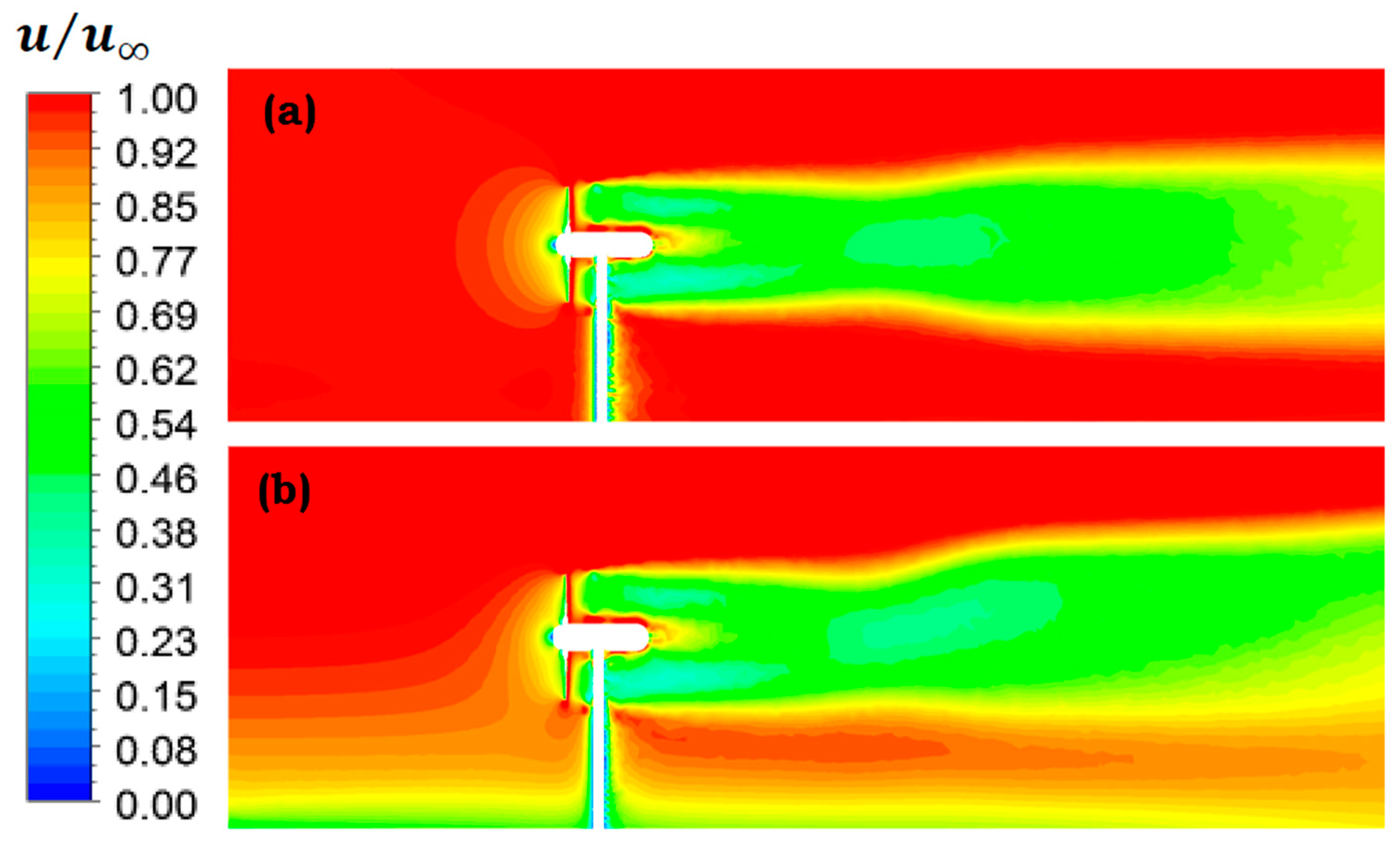
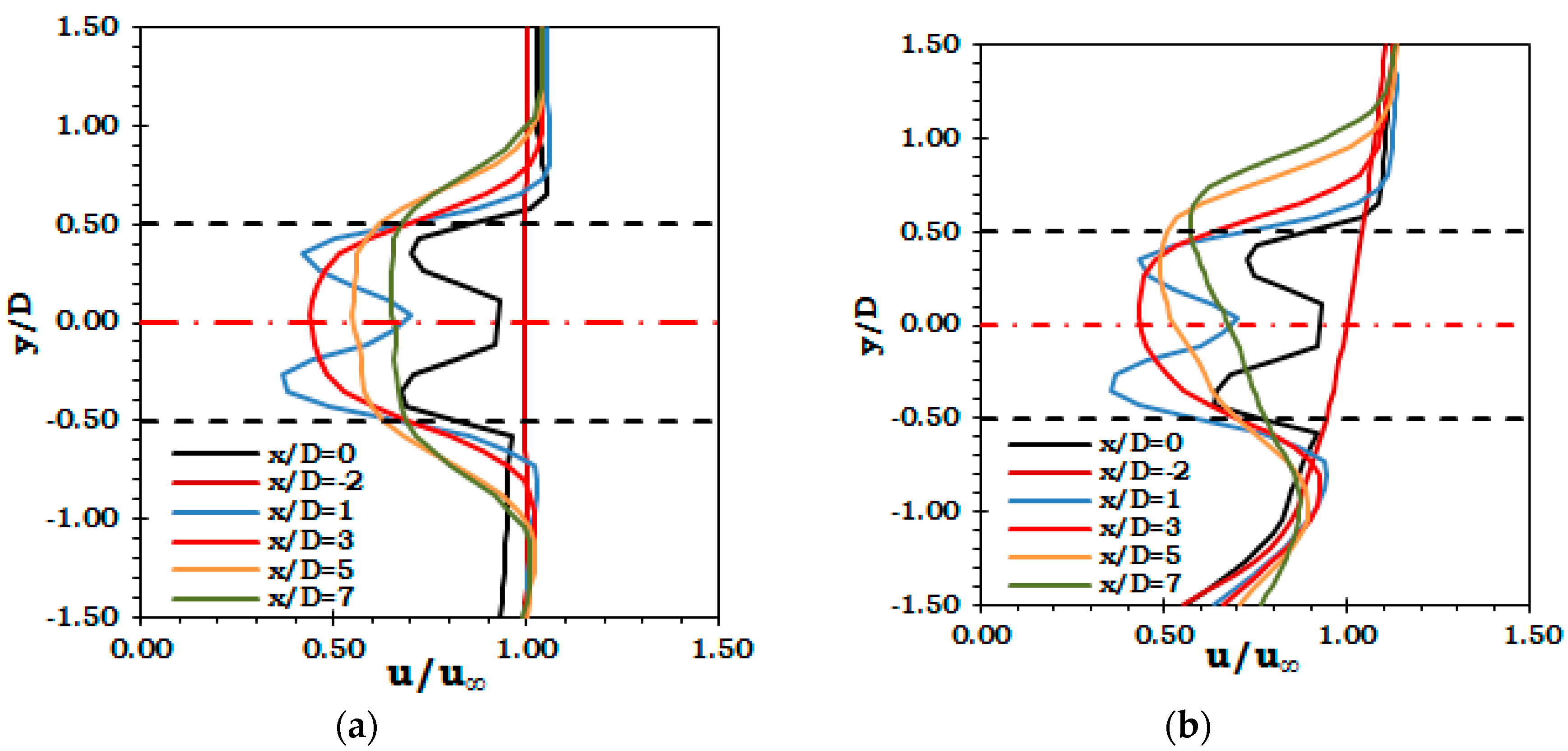
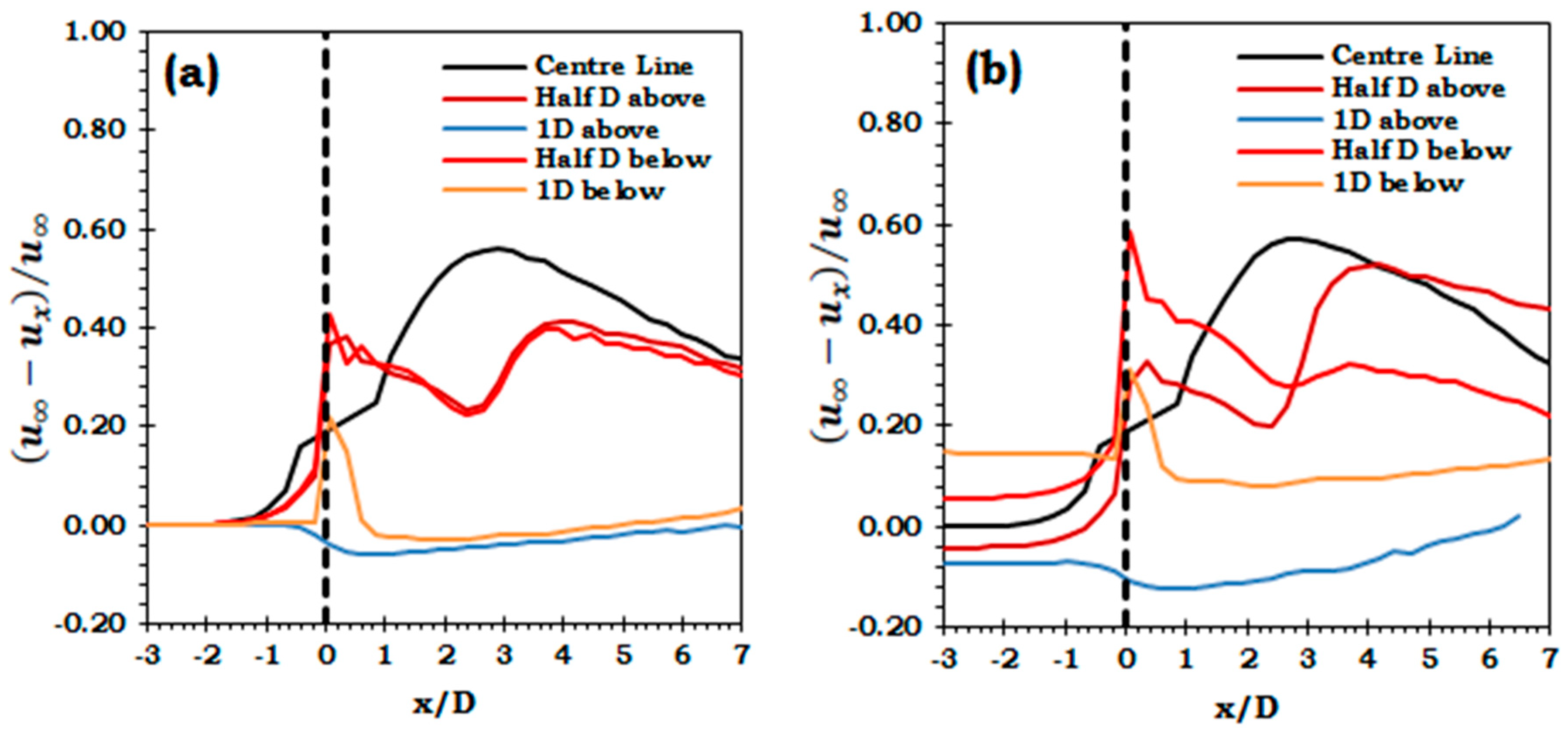
5. Results and Discussion
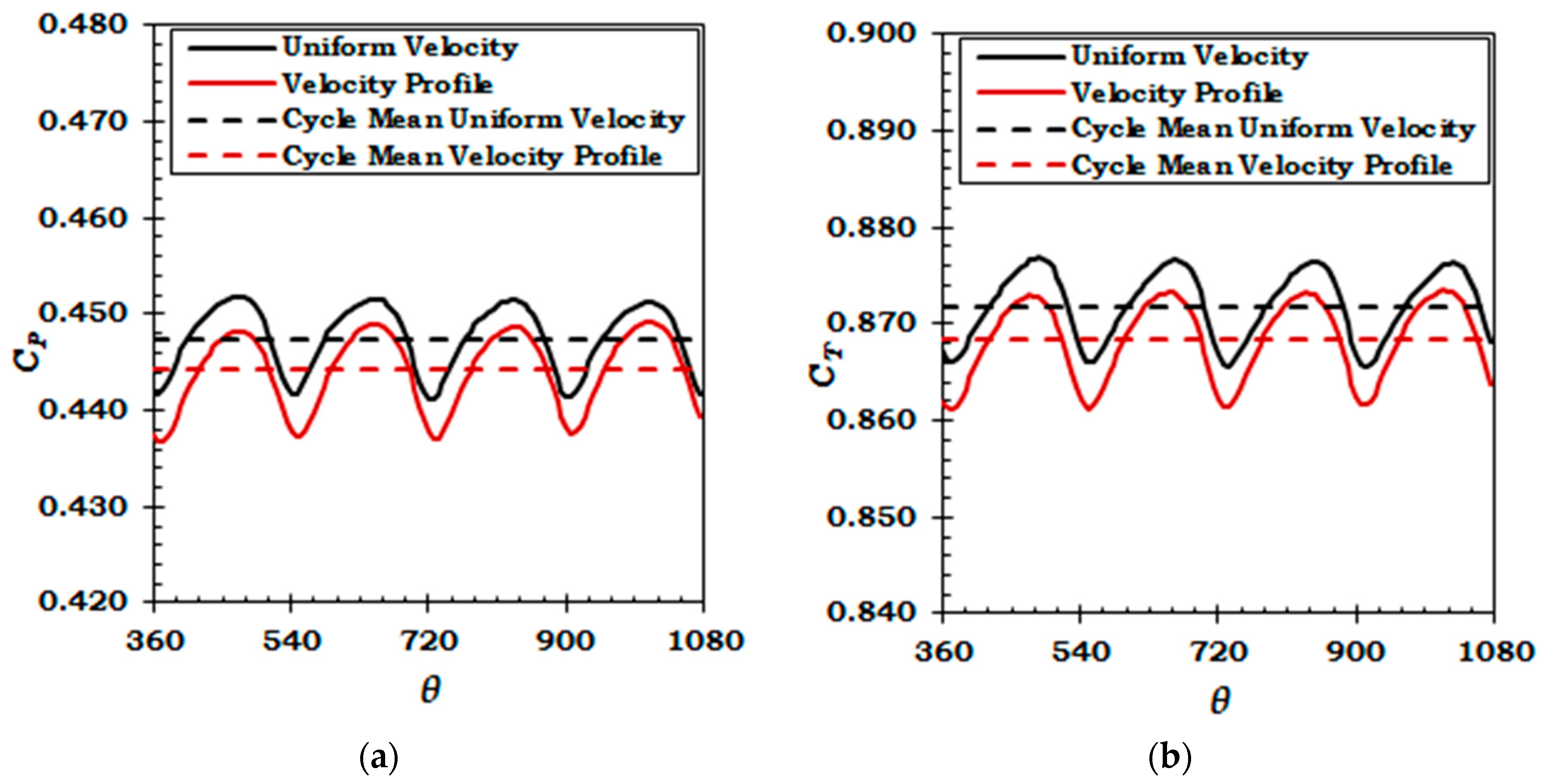
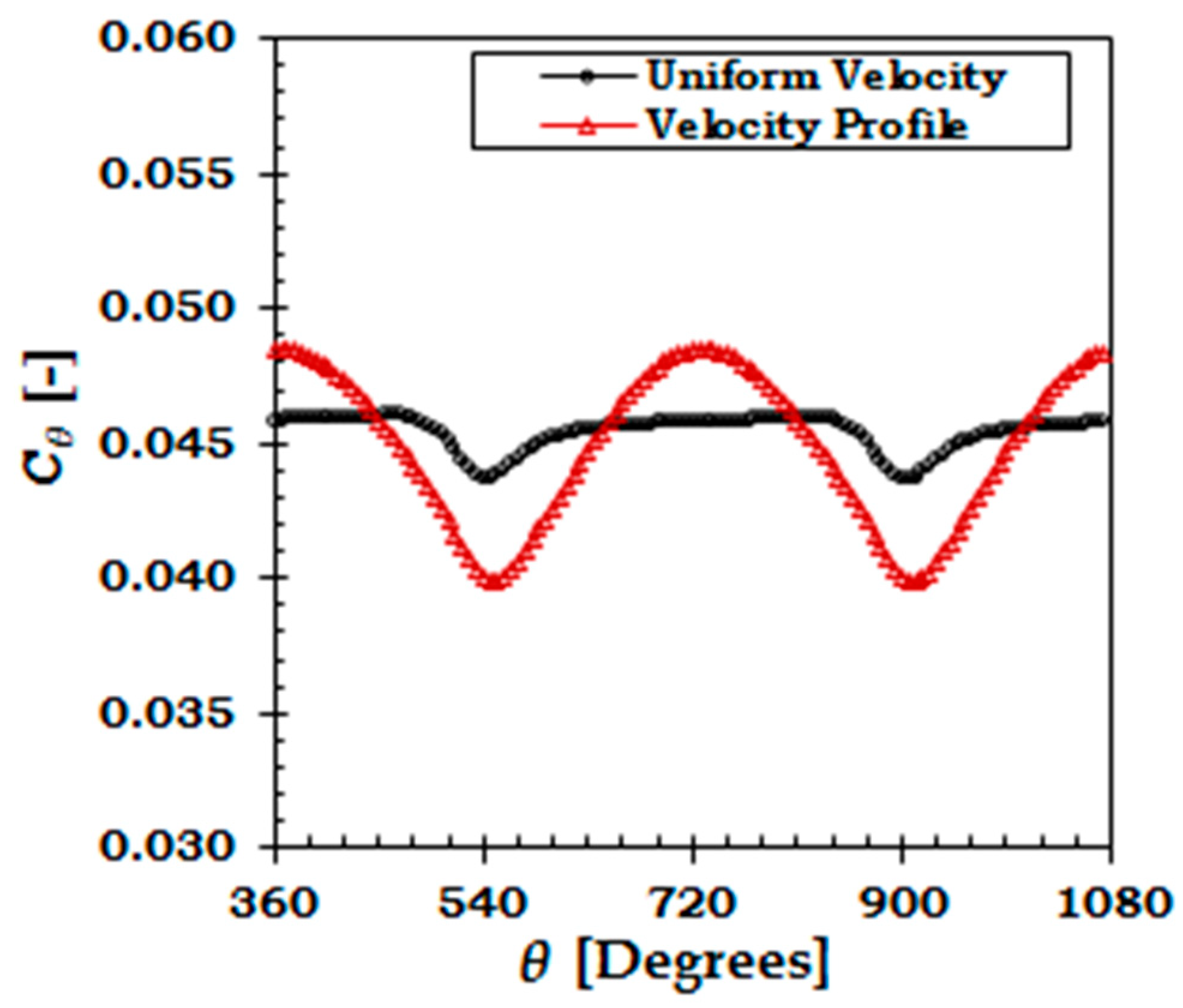
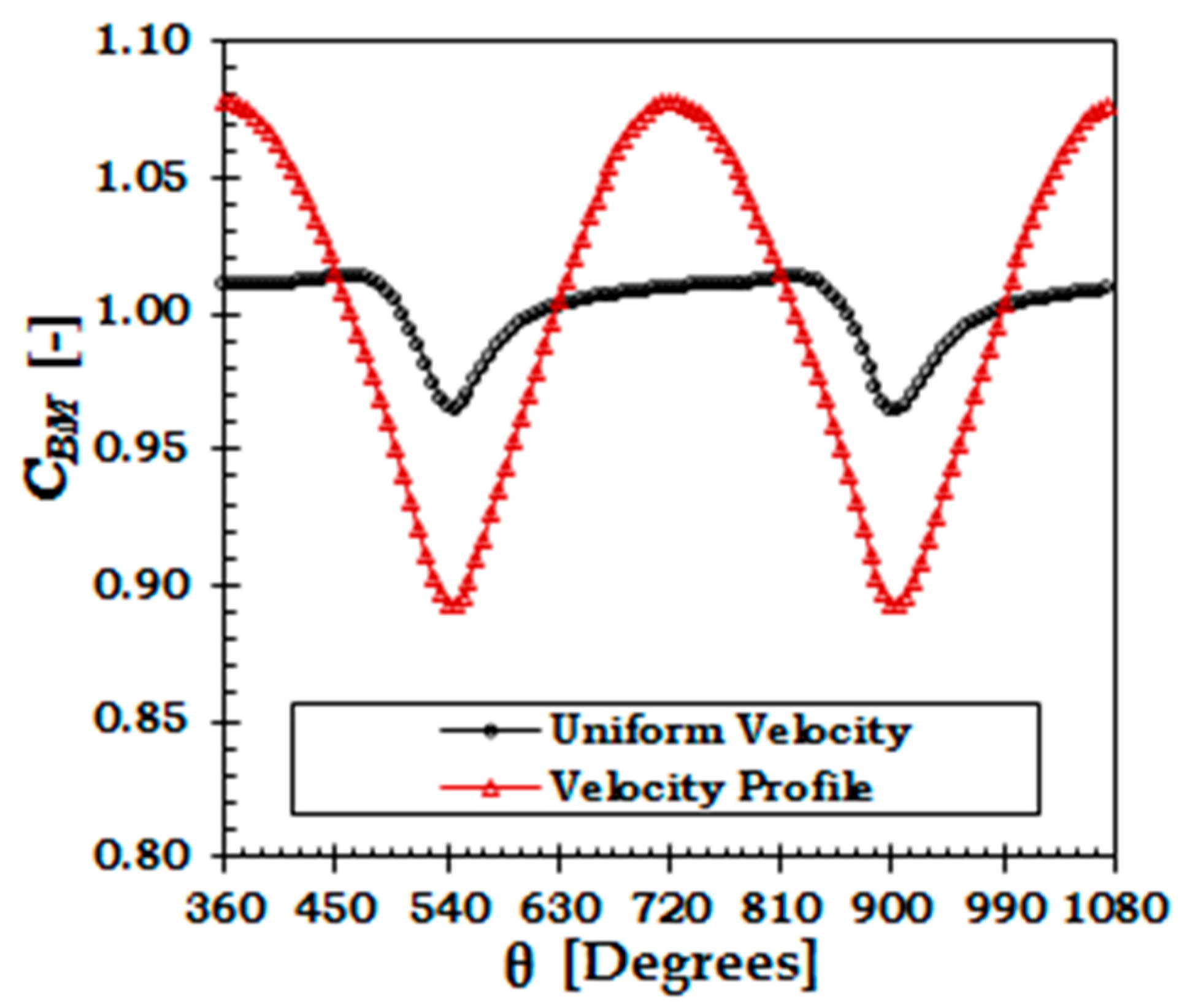
5.1. Effect of Velocity Profile on Variation of Structural Loads
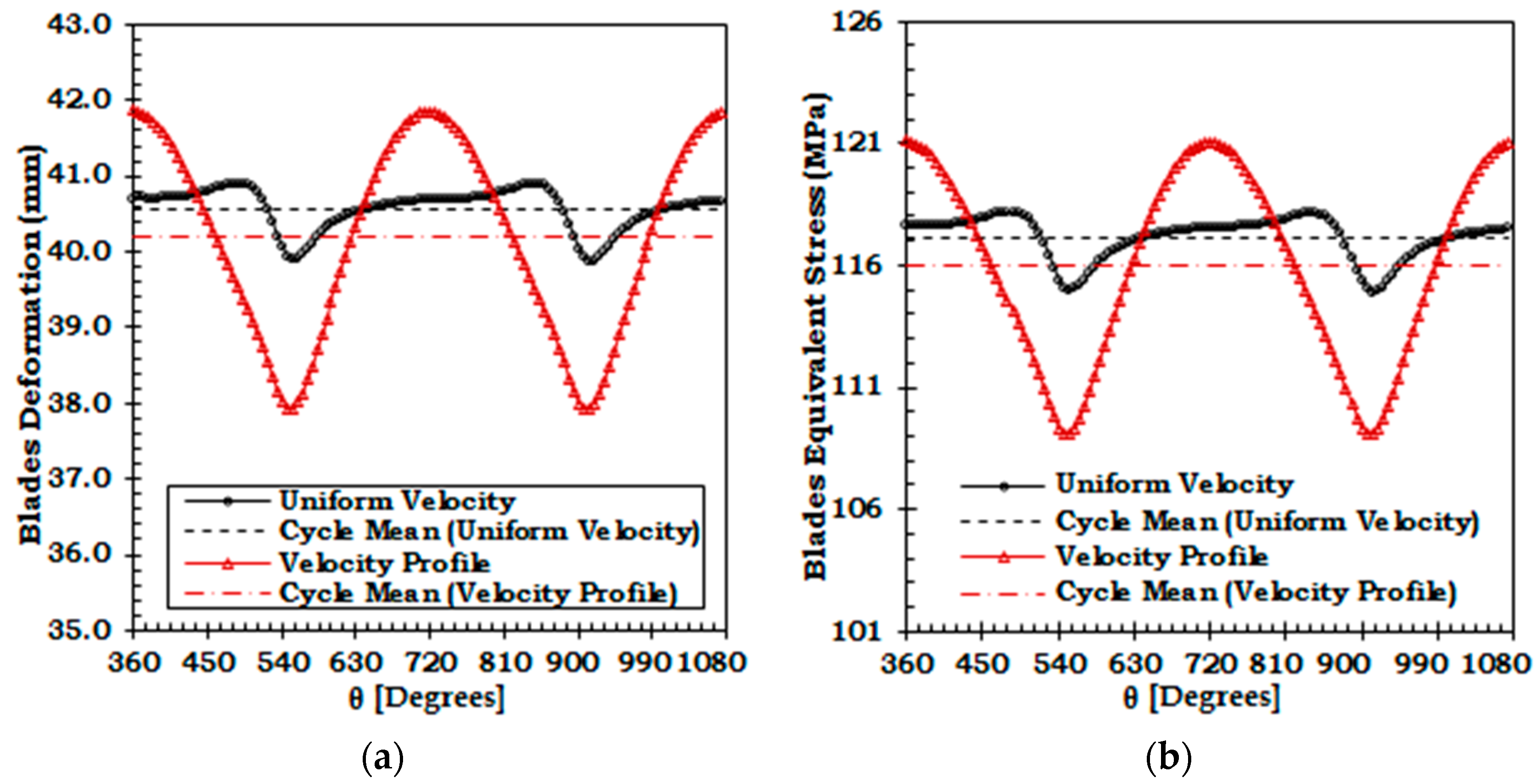
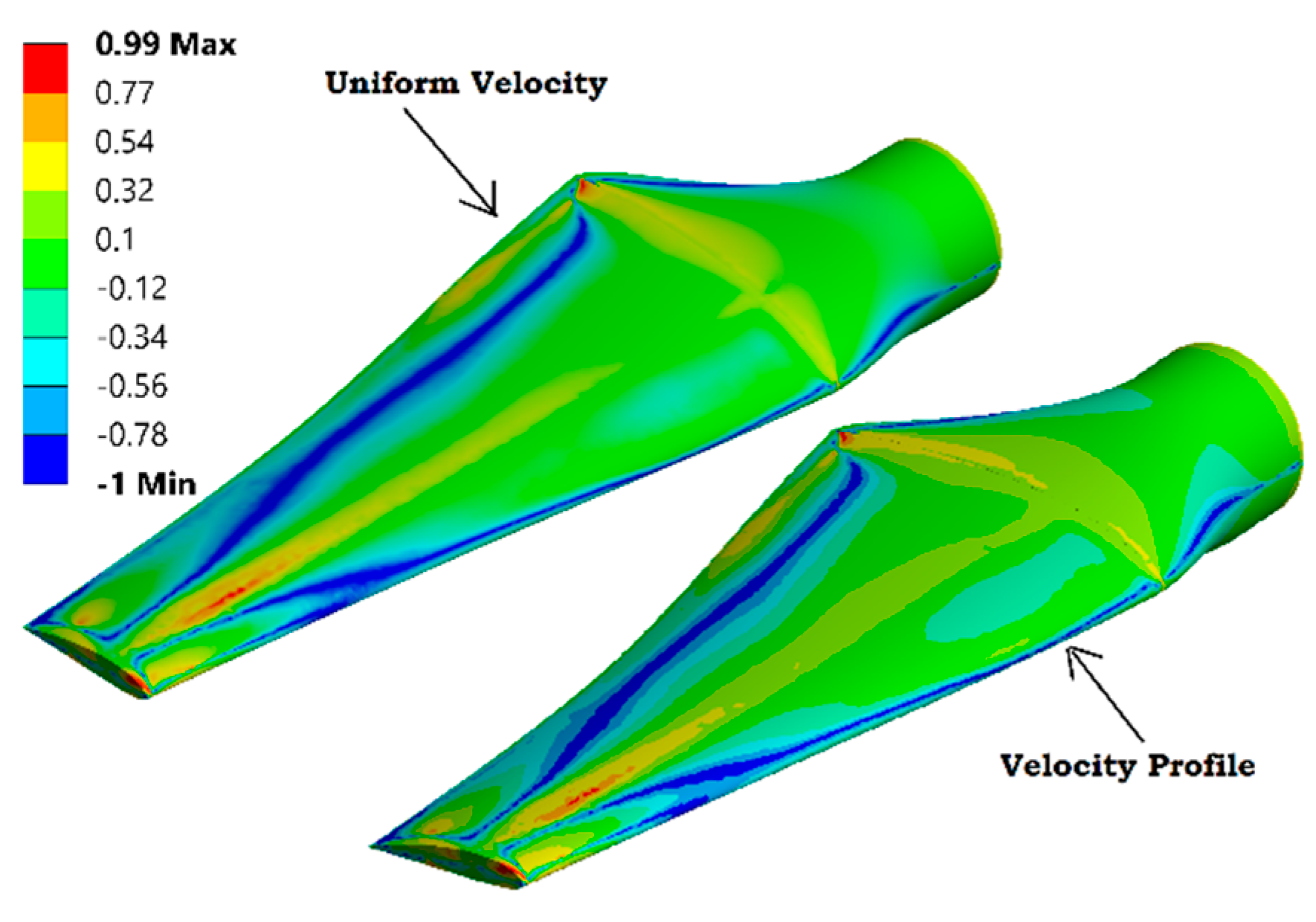
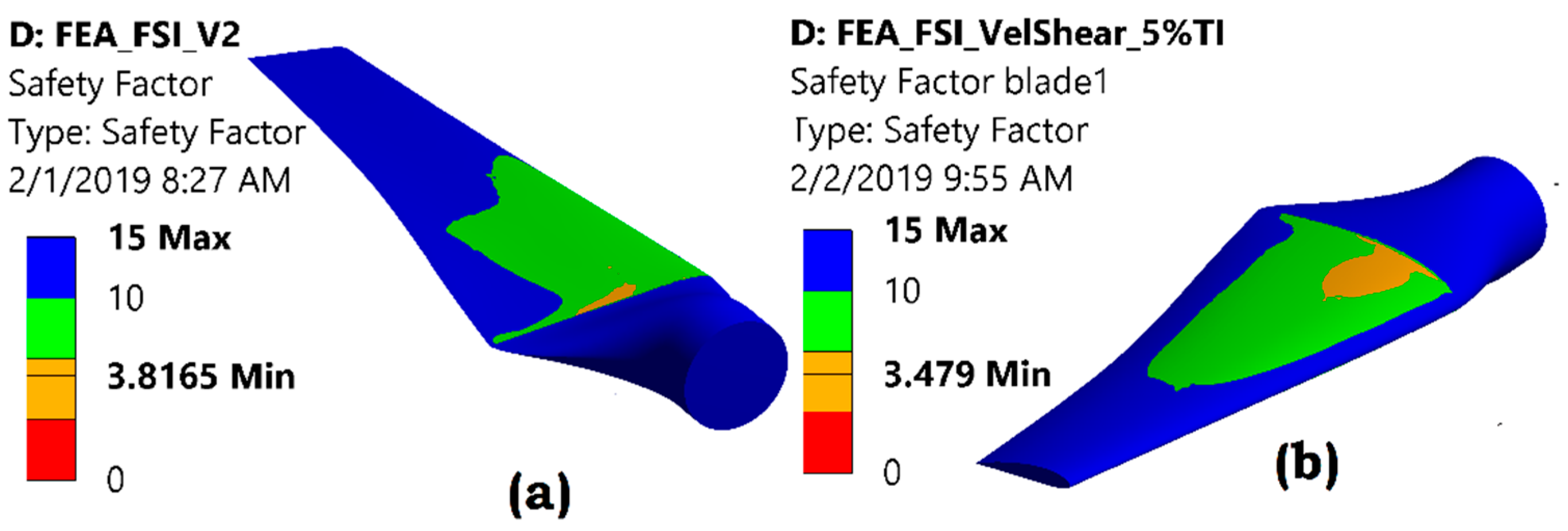
5.2. Effect of Velocity Profile on Variation of Stresses and Implications to Fatigue Life
6. Conclusions and Prospects
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Milne, I.A.; Sharma, R.N.; Flay, R.G.; Bickerton, S. Characteristics of the turbulence in the flow at a tidal stream power site. Philos. Trans. R. Soc. A 2013, 371, 20120196. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.; Davies, A. Influence of wave-current interaction, and high frequency forcing upon storm induced currents and elevations. Estuar. Coast. Shelf Sci. 2001, 53, 397–413. [Google Scholar] [CrossRef]
- Zeiner-Gundersen, D.H. Turbine design and field development concepts for tidal, ocean, and river applications. Energy Sci. Eng. 2015, 3, 27–42. [Google Scholar] [CrossRef]
- Maganga, F.; Germain, G.; King, J.; Pinon, G.; Rivoalen, E. Experimental characterisation of flow effects on marine current turbine behaviour and on its wake properties. IET Renew. Power Gen. 2010, 4, 498–509. [Google Scholar] [CrossRef]
- Barltrop, N.; Varyani, K.; Grant, A.; Clelland, D.; Pham, X. Investigation into wave—Current interactions in marine current turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 233–242. [Google Scholar] [CrossRef]
- Luznik, L.; Flack, K.A.; Lust, E.E.; Taylor, K. The effect of surface waves on the performance characteristics of a model tidal turbine. Renew. Energy 2013, 58, 108–114. [Google Scholar] [CrossRef]
- Blackmore, T.; Myers, L.E.; Bahaj, A.S. Effects of turbulence on tidal turbines: Implications to performance, blade loads, and condition monitoring. Int. J. Mar. Energy 2016, 14, 1–26. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- Mason-Jones, A.; O’doherty, D.; Morris, C.; O’doherty, T.; Byrne, C.; Prickett, P.; Grosvenor, R.; Owen, I.; Tedds, S.; Poole, R. Non-dimensional scaling of tidal stream turbines. Energy 2012, 44, 820–829. [Google Scholar] [CrossRef]
- Draper, S.; Nishino, T.; Adcock, T.; Taylor, P. Performance of an ideal turbine in an inviscid shear flow. J. Fluid Mech. 2016, 796, 86–112. [Google Scholar] [CrossRef]
- Batten, W.; Bahaj, A.; Molland, A.; Chaplin, J. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
- Lewis, M.; Neill, S.; Robins, P.; Hashemi, M. Resource assessment for future generations of tidal-stream energy arrays. Energy 2015, 83, 403–415. [Google Scholar] [CrossRef]
- Blunden, L.; Bahaj, A. Tidal energy resource assessment for tidal stream generators. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 137–146. [Google Scholar] [CrossRef]
- Mason-Jones, A.; O’doherty, D.; Morris, C.; O’doherty, T. Influence of a velocity profile & support structure on tidal stream turbine performance. Renew. Energy 2013, 52, 23–30. [Google Scholar]
- Tatum, S.; Allmark, M.; Frost, C.; O’Doherty, D.; Mason-Jones, A.; O’Doherty, T. CFD modelling of a tidal stream turbine subjected to profiled flow and surface gravity waves. Int. J. Mar. Energy 2016, 15, 156–174. [Google Scholar] [CrossRef]
- Yahagi, K.; Takagi, K. Moment loads acting on a blade of an ocean current turbine in shear flow. Ocean Eng. 2019, 172, 446–455. [Google Scholar] [CrossRef]
- Muchala, S.; Willden, R.H. Influence of support structures on tidal turbine power output. J. Fluids Struct. 2018, 83, 27–39. [Google Scholar] [CrossRef]
- Li, H.; Hu, Z.; Chandrashekhara, K.; Du, X.; Mishra, R. Reliability-based fatigue life investigation for a medium-scale composite hydrokinetic turbine blade. Ocean Eng. 2014, 89, 230–242. [Google Scholar] [CrossRef]
- McCann, G. Tidal current turbine fatigue loading sensitivity to waves and turbulence—A parametric study. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007. [Google Scholar]
- Bahaj, A.; Molland, A.; Chaplin, J.; Batten, W. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Stallard, T.J.; Feng, T.; Stansby, P.K. Experimental study of the mean wake of a tidal stream rotor in a shallow turbulent flow. J. Fluids Struct. 2015, 54, 235–246. [Google Scholar] [CrossRef]
- Draycott, S.; Payne, G.; Steynor, J.; Nambiar, A.; Sellar, B.; Venugopal, V. An experimental investigation into non-linear wave loading on horizontal axis tidal turbines. J. Fluids Struct. 2019, 84, 199–217. [Google Scholar] [CrossRef]
- Fernandez-Rodriguez, E.; Stallard, T.J.; Stansby, P.K. Experimental study of extreme thrust on a tidal stream rotor due to turbulent flow and with opposing waves. J. Fluids Struct. 2014, 51, 354–361. [Google Scholar] [CrossRef]
- Gaurier, B.; Davies, P.; Deuff, A.; Germain, G. Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renew. Energy 2013, 59, 1–12. [Google Scholar] [CrossRef]
- Milne, I.; Day, A.; Sharma, R.; Flay, R. Blade loading on tidal turbines for uniform unsteady flow. Renew. Energy 2015, 77, 338–350. [Google Scholar] [CrossRef]
- Milne, I.; Day, A.; Sharma, R.; Flay, R. The characterisation of the hydrodynamic loads on tidal turbines due to turbulence. Renew. Sustain. Energy Rev. 2016, 56, 851–864. [Google Scholar] [CrossRef]
- Payne, G.S.; Stallard, T.; Martinez, R.; Bruce, T. Variation of loads on a three-bladed horizontal axis tidal turbine with frequency and blade position. J. Fluids Struct. 2018, 83, 156–170. [Google Scholar] [CrossRef]
- Xia, Y.; Takagi, K. Effect of shear flow on a marine current turbine. In Proceedings of the Oceans, Shanghai, China, 10–13 April 2016; pp. 1–5. [Google Scholar]
- Kang, S.; Borazjani, I.; Colby, J.A.; Sotiropoulos, F. Numerical simulation of 3D flow past a real-life marine hydrokinetic turbine. Adv. Water Resour. 2012, 39, 33–43. [Google Scholar] [CrossRef]
- Tedds, S.; Owen, I.; Poole, R. Near-wake characteristics of a model horizontal axis tidal stream turbine. Renew. Energy 2014, 63, 222–235. [Google Scholar] [CrossRef]
- Ahmed, U.; Apsley, D.; Afgan, I.; Stallard, T.J.; Stansby, P.K. Fluctuating loads on a tidal turbine due to velocity shear and turbulence: Comparison of CFD with field data. Renew. Energy 2017, 112, 235–246. [Google Scholar] [CrossRef]
- Ouro, P.; Harrold, M.; Stoesser, T.; Bromley, P. Hydrodynamic loadings on a horizontal axis tidal turbine prototype. J. Fluids Struct. 2017, 71, 78–95. [Google Scholar] [CrossRef]
- Ouro, P.; Stoesser, T. Impact of Environmental Turbulence on the Performance and Loadings of a Tidal Stream Turbine. Flow Turbul. Combust. 2018, 102, 613–639. [Google Scholar] [CrossRef]
- Grogan, D.M.; Leen, S.B.; Kennedy, C.; Brádaigh, C.Ó. Design of composite tidal turbine blades. Renew. Energy 2013, 57, 151–162. [Google Scholar] [CrossRef]
- Suzuki, T.; Mahfuz, H. Analysis of large-scale ocean current turbine blades using Fluid–Structure Interaction and blade element momentum theory. Ships Off Shore Struct. 2018, 13, 451–458. [Google Scholar] [CrossRef]
- Nicholls-Lee, R.; Turnock, S.; Boyd, S. Application of bend-twist coupled blades for horizontal axis tidal turbines. Renew. Energy 2013, 50, 541–550. [Google Scholar] [CrossRef]
- Tatum, S.; Frost, C.; Allmark, M.; O’Doherty, D.; Mason-Jones, A.; Prickett, P.; Grosvenor, R.; Byrne, C.; O’Doherty, T. Wave-current interaction effects on tidal stream turbine performance and loading characteristics. Int. J. Mar. Energy 2016, 14, 161–179. [Google Scholar] [CrossRef]
- Badshah, M.; Badshah, S.; Kadir, K. Fluid Structure Interaction Modelling of Tidal Turbine Performance and Structural Loads in a Velocity Shear Environment. Energies 2018, 11, 1837. [Google Scholar] [CrossRef]
- Craig, H.; Vincent, S.N.; Budi, G.; Michele, G.; Fotis, S.U.S. Department of energy reference model program RM1: Experimental results. Dynamic Pose test, 2 December 2014. [Google Scholar]
- Hagerman, G.; Polagye, B. Methodology for estimating tidal current energy resources and power production by tidal in-stream energy conversion (TISEC) devices, EPRI North American Tidal In Stream Power Feasibility Demonstration Project. EPRI-TP-001 NA Rev 2. 2006. Available online: http://www.pstidalenergy.org/Tidal_Energy_Projects/Misc/EPRI_Reports_and_Presentations/EPRI-TP-001_Guidlines_Est_Power_Production_14Jun06.pdf (accessed on 11 June 2019).
- ANSYS Inc. ANSYS CFX-Solver Modelling Guide; ANSYS, Inc.: Southpointe 2600 ANSYS Drive Canonsburg, PA, USA, 2016. [Google Scholar]
- ANSYS Inc. ANSYS CFX-Solver Theory Guide; ANSYS, Inc.: Southpointe 2600 ANSYS Drive Canonsburg, PA, USA, 2016. [Google Scholar]
- Badshah, M.; VanZwieten, J.; Badshah, S.; Jan, S. CFD study of blockage ratio and boundary proximity effects on the performance of a tidal turbine. IET Renew. Power Gen. 2019. [Google Scholar] [CrossRef]
- Sufian, S.F.; Li, M.; O’Connor, B.A. 3D modelling of impacts from waves on tidal turbine wake characteristics and energy output. Renew. Energy 2017, 114, 308–322. [Google Scholar] [CrossRef]
- Tian, W.; VanZwieten, J.H.; Pyakurel, P.; Li, Y. Influences of yaw angle and turbulence intensity on the performance of a 20 kW in-stream hydrokinetic turbine. Energy 2016, 111, 104–116. [Google Scholar] [CrossRef]
- O’Doherty, T.; Mason-Jones, A.; O’Doherty, D.; Byrne, C.; Owen, I.; Wang, Y. Experimental and computational analysis of a model horizontal axis tidal turbine. In Proceedings of the 8th European Wave and Tidal Energy Conference (EWTEC), Uppsala, Sweden, 7–10 September 2009. [Google Scholar]
- Nitin, K.; Arindam, B. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Davide, M.; Andreas, U. 2014 JRC Ocean Energy Status Report; Publications Office of the European Union: Luxembourg, Luxembourg, 2015; Available online: https://setis.ec.europa.eu/sites/default/files/reports/2014-JRC-Ocean-Energy-Status-Report.pdf (accessed on 11 June 2019).
- Lawson, M.J.; Li, Y.; Sale, D.C. Development and verification of a computational fluid dynamics model of a horizontal-axis tidal current turbine. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; American Society of Mechanical Engineers: Rotterdam, The Netherlands, 2011; pp. 711–720. [Google Scholar]
- Zahle, F.; Sørensen, N. Overset grid flow simulation on a modern wind turbine. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008; p. 6727. [Google Scholar]
- Zahle, F.; Sørensen, N.N.; Johansen, J. Wind turbine rotor-tower interaction using an incompressible overset grid method. Wind Energy 2009, 12, 594–619. [Google Scholar] [CrossRef]
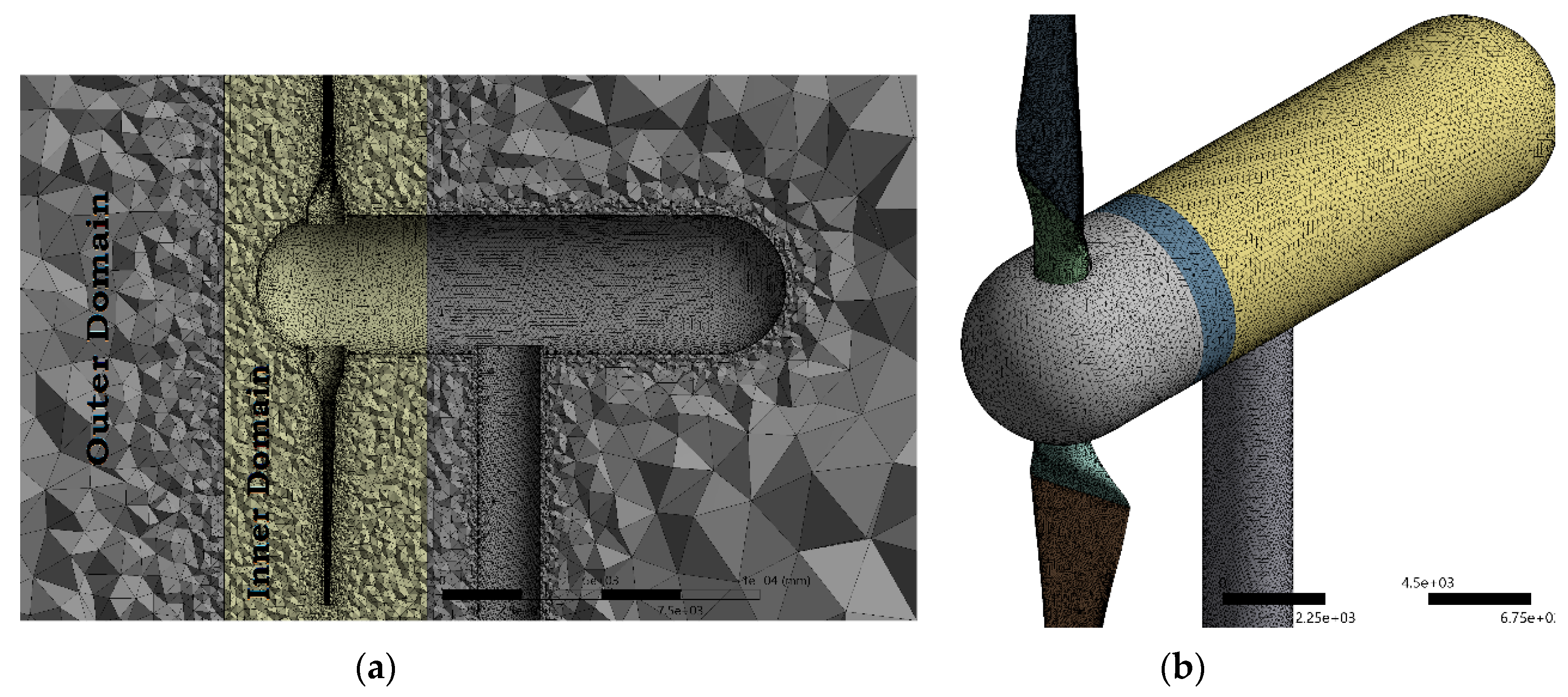
| Density | 7850 | Kg/m3 |
|---|---|---|
| Young Modulus | 2 × 1011 | Pa |
| Poisson’s Ratio | 0.3 | (-) |
| Tensile Yield Strength | 2.5 × 108 | Pa |
| Compressive Yield Strength | 2.5 × 108 | Pa |
| Tensile Ultimate Strength | 4.60 × 108 | Pa |
| Grid | No. of Elements (× 106) | Torque Difference 1 | ||
|---|---|---|---|---|
| Inner Domain | Outer Domain | Total | (%) | |
| 1 | 1.34 | 0.72 | 2.07 | −3.2 |
| 2 | 2.23 | 1.07 | 3.30 | −1.1 |
| 3 | 3.10 | 1.40 | 4.50 | −0.5 |
| 4 | 5.02 | 2.39 | 7.42 | - |
| TSR | Experiment | Steady State CFD | Transient CFD | Coupled FSI | |||
|---|---|---|---|---|---|---|---|
| CP [39] | CP | % Difference 1 | CP | % Difference 1 | CP | % Difference 1 | |
| 3.02 | 0.320 | 0.347 | 8.5 | 0.354 | 10.7 | - | - |
| 3.79 | 0.408 | 0.406 | 0.4 | 0.411 | 0.8 | - | - |
| 4.87 | 0.477 | 0.449 | 5.8 | 0.447 | 6.3 | 0.447 | 6.2 |
| 5.76 | 0.471 | 0.440 | 6.6 | 0.442 | 6.2 | - | - |
| 6.82 | 0.414 | 0.401 | 3.2 | 0.402 | 2.8 | - | - |
| 7.57 | 0.368 | 0.369 | 0.4 | 0.368 | 0.1 | - | - |
| 8.32 | 0.295 | 0.322 | 9.2 | 0.319 | 8.2 | - | - |
| 9.05 | 0.230 | 0.260 | 13.0 | 0.254 | 10.4 | - | - |
| Parameter | Value | Uniform Velocity | Velocity Shear | ||
|---|---|---|---|---|---|
| Single Blade | Rotor | Single Blade | Rotor | ||
| Thrust Coefficient | Peak | 0.437 | 0.877 | 0.445 | 0.869 |
| Mean | 0.433 | 0.872 | 0.429 | 0.864 | |
| Range | 0.012 | 0.011 | 0.039 | 0.012 | |
| % Variation 1 | 2.8 | 1.3 | 9.0 | 1.4 | |
| Torque Coefficient | Peak | 0.046 | 0.093 | 0.048 | 0.092 |
| Mean | 0.045 | 0.092 | 0.045 | 0.091 | |
| Range | 0.002 | 0.002 | 0.009 | 0.002 | |
| % Variation 1 | 5.2 | 2.3 | 19.3 | 2.7 | |
| Flap Wise Bending Moment Coefficient | Peak | 1.013 | - | 1.078 | - |
| Mean | 1.0 | - | 1.0 | - | |
| Range | 0.049 | - | 0.185 | - | |
| % Variation 1 | 4.9 | - | 18.5 | - | |
| Parameter | Value | Uniform Velocity | Velocity Profile |
|---|---|---|---|
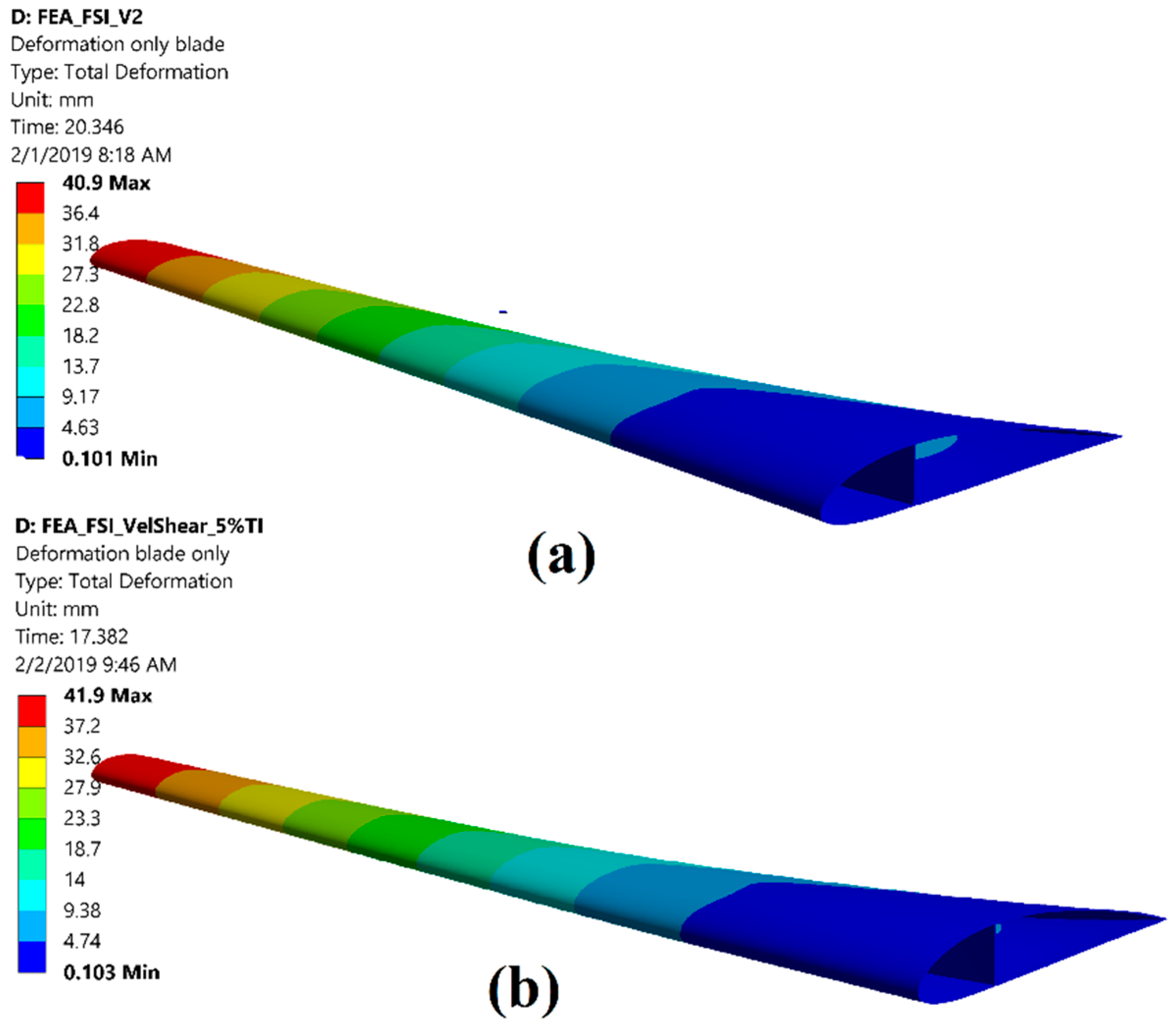
| Deformation [mm] | Peak | 40.9 | 41.9 |
| Mean | 40.6 | 40.2 | |
| Range | 1.0 | 3.9 | |
| % Variation 1 | 2.5 | 9.8 | |
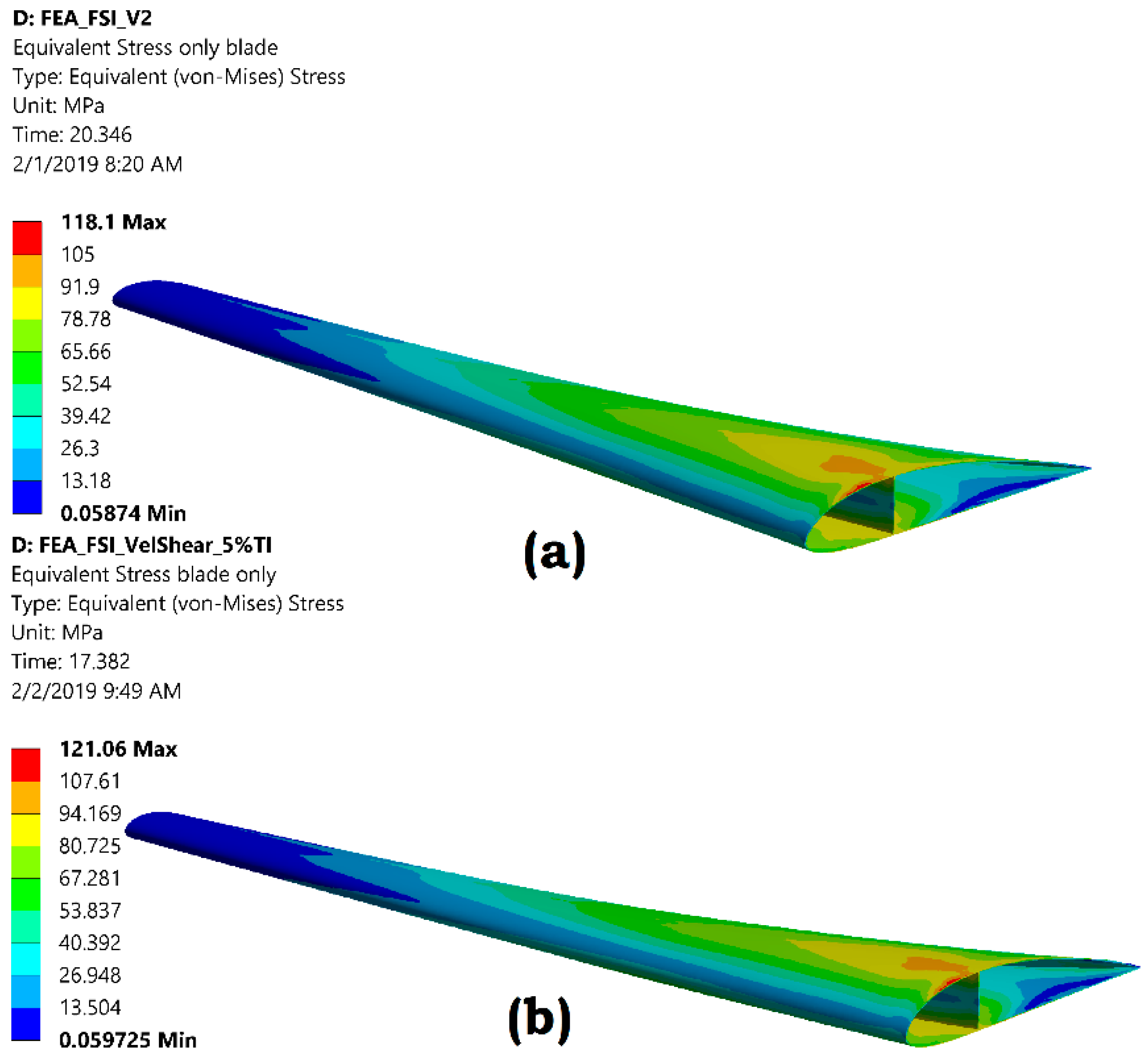
| Stress [MPa] | Peak | 118.1 | 121.1 |
| Mean | 117.1 | 116.0 | |
| Range | 3.2 | 12.0 | |
| % Variation 1 | 2.8 | 10.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badshah, M.; Badshah, S.; VanZwieten, J.; Jan, S.; Amir, M.; Malik, S.A. Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile. Energies 2019, 12, 2217. https://doi.org/10.3390/en12112217
Badshah M, Badshah S, VanZwieten J, Jan S, Amir M, Malik SA. Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile. Energies. 2019; 12(11):2217. https://doi.org/10.3390/en12112217
Chicago/Turabian StyleBadshah, Mujahid, Saeed Badshah, James VanZwieten, Sakhi Jan, Muhammad Amir, and Suheel Abdullah Malik. 2019. "Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile" Energies 12, no. 11: 2217. https://doi.org/10.3390/en12112217
APA StyleBadshah, M., Badshah, S., VanZwieten, J., Jan, S., Amir, M., & Malik, S. A. (2019). Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile. Energies, 12(11), 2217. https://doi.org/10.3390/en12112217






