Optimal Power Flow of Integrated Renewable Energy System using a Thyristor Controlled SeriesCompensator and a Grey-Wolf Algorithm
Abstract
1. Introduction
2. Problem Design
2.1. Objective Function
2.1.1. Real Power Generation Cost
2.1.2. Real Power Generation Cost with Valve-Point Effect
2.1.3. Active Power Loss
2.1.4. Voltage Deviation
2.1.5. Emission
2.2. Modeling of Installed TCSC
2.3. Equality Constraints
2.4. Inequality Constraints
2.4.1. Voltage Limits for Generator Buses
2.4.2. Real Power Generation Limits
2.4.3. Reactive Power Generated Limits
2.4.4. TCSC Limits
2.4.5. Wind Power Constraint
2.4.6. Solar PV Power Constraint
3. Index Based on Optimal Placement of TCSC
3.1. RapidVoltage Stability Index
3.2. Novel Line Stability Index
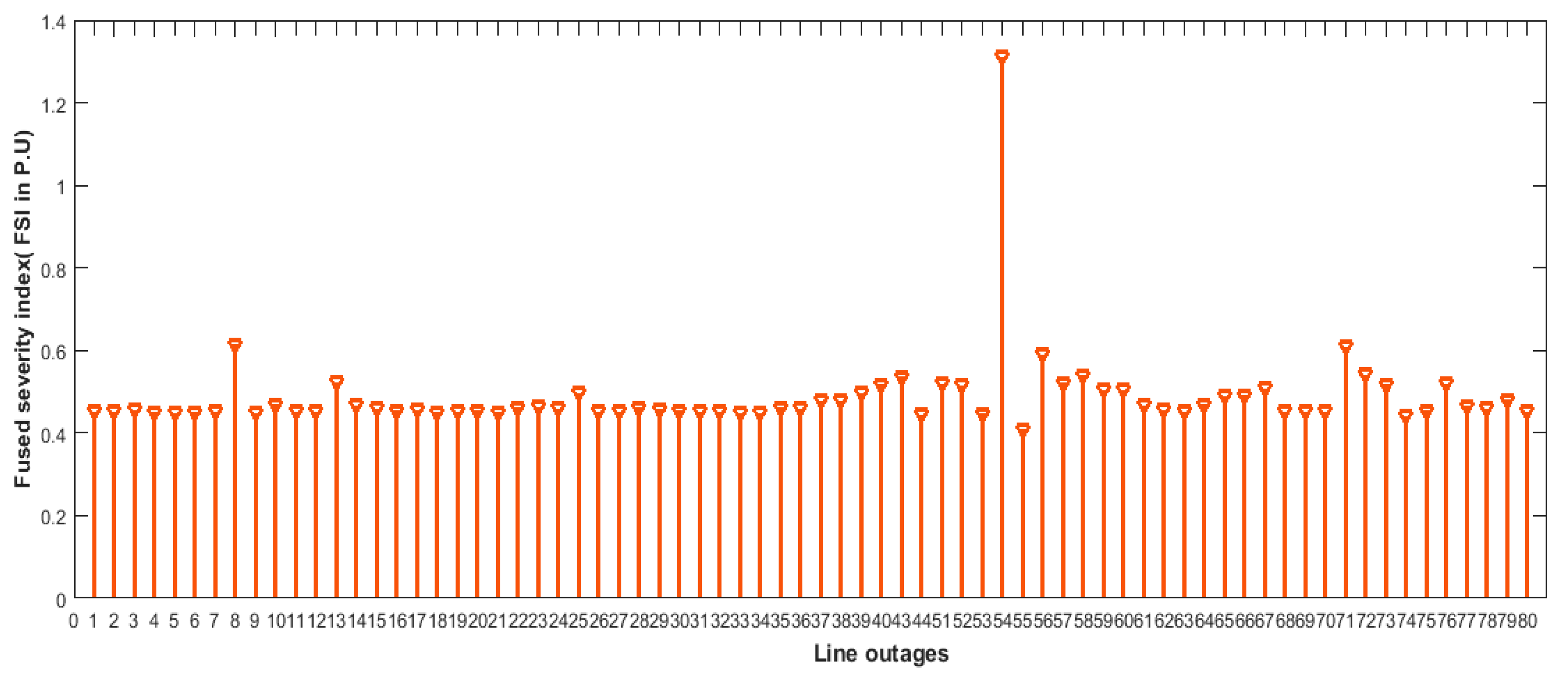
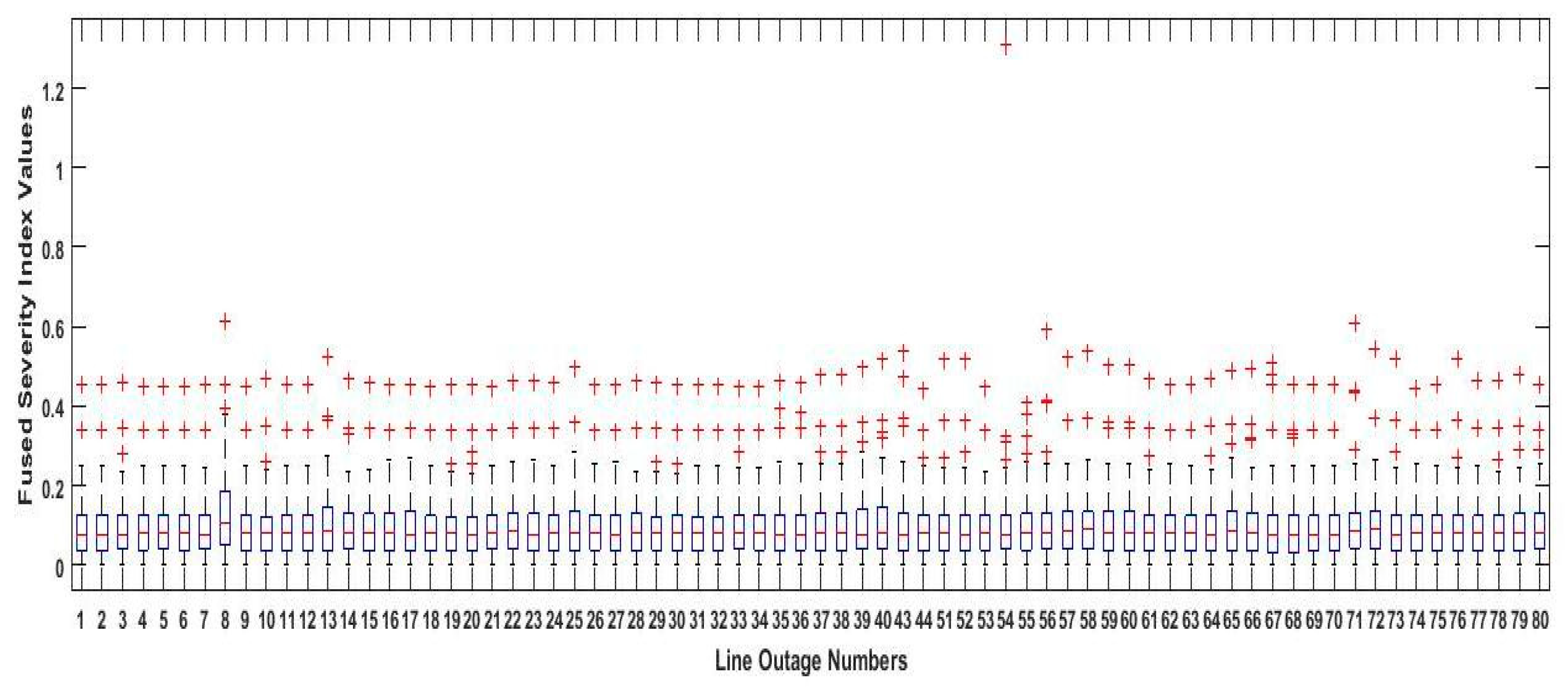
3.3. FusedSeverity Index
3.4. Intermittent Severity Index
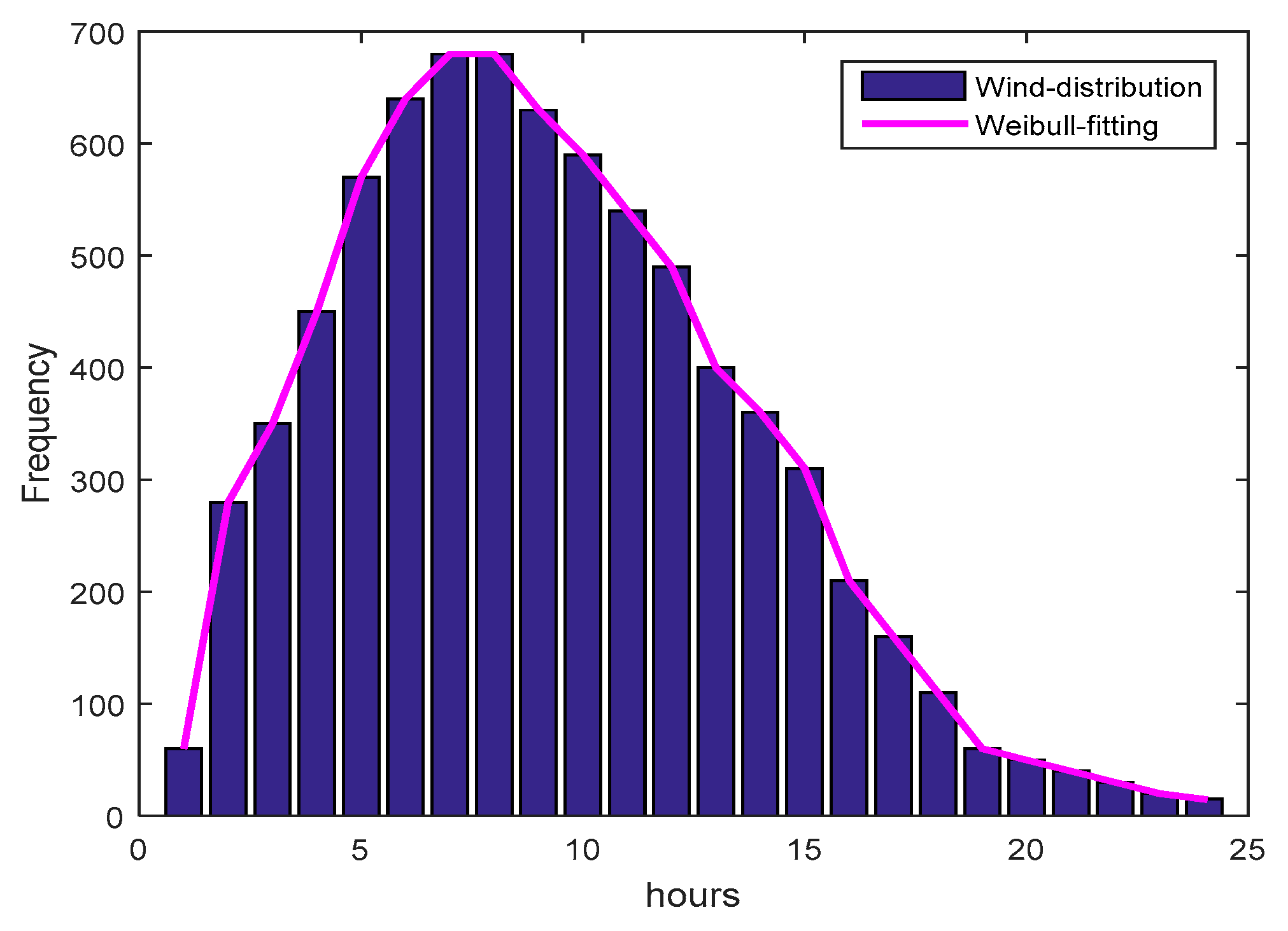
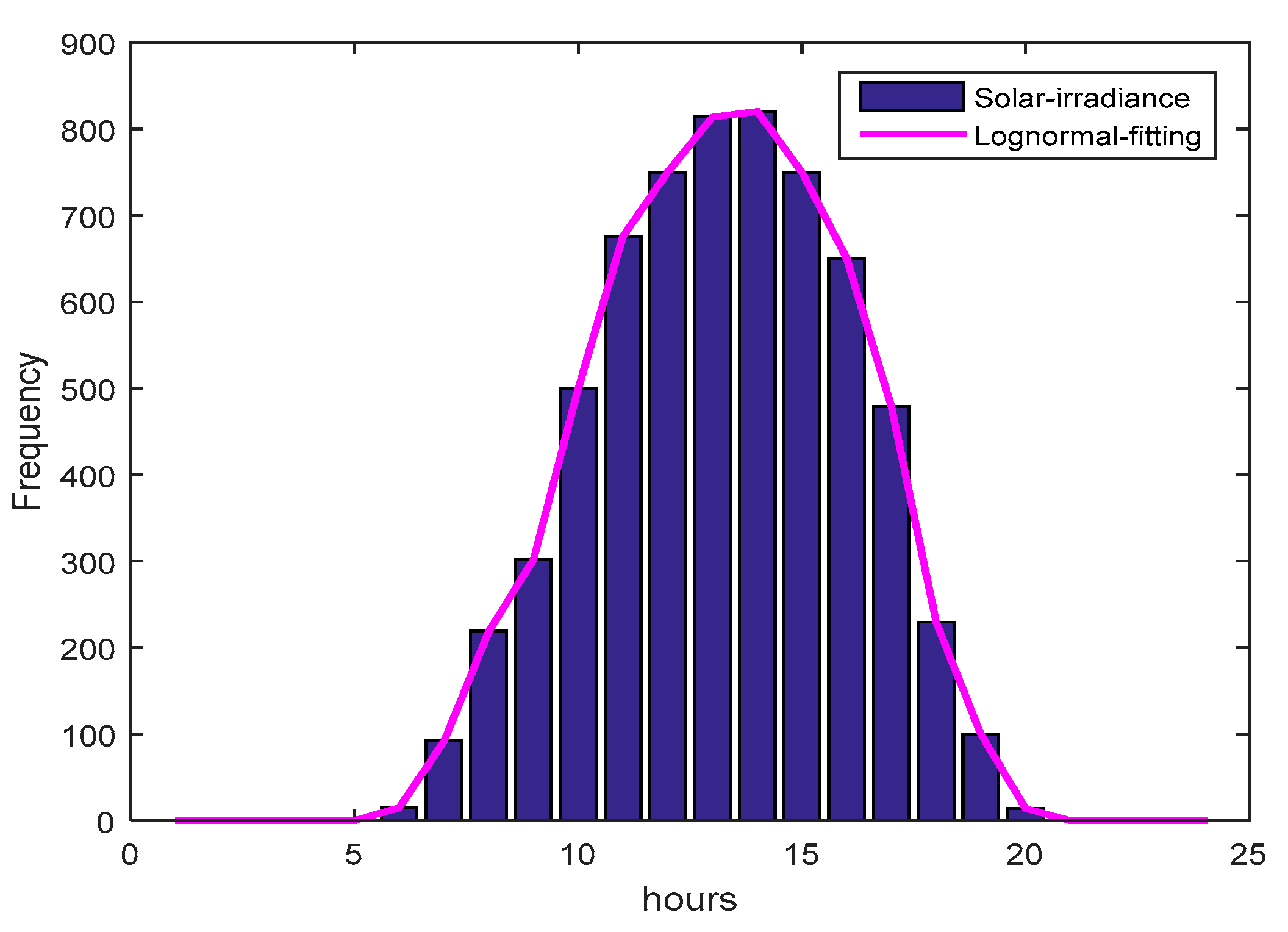
4. Weibull and Lognormal for Wind/PV
4.1. Weibull PDF
4.2. Lognormal PDF
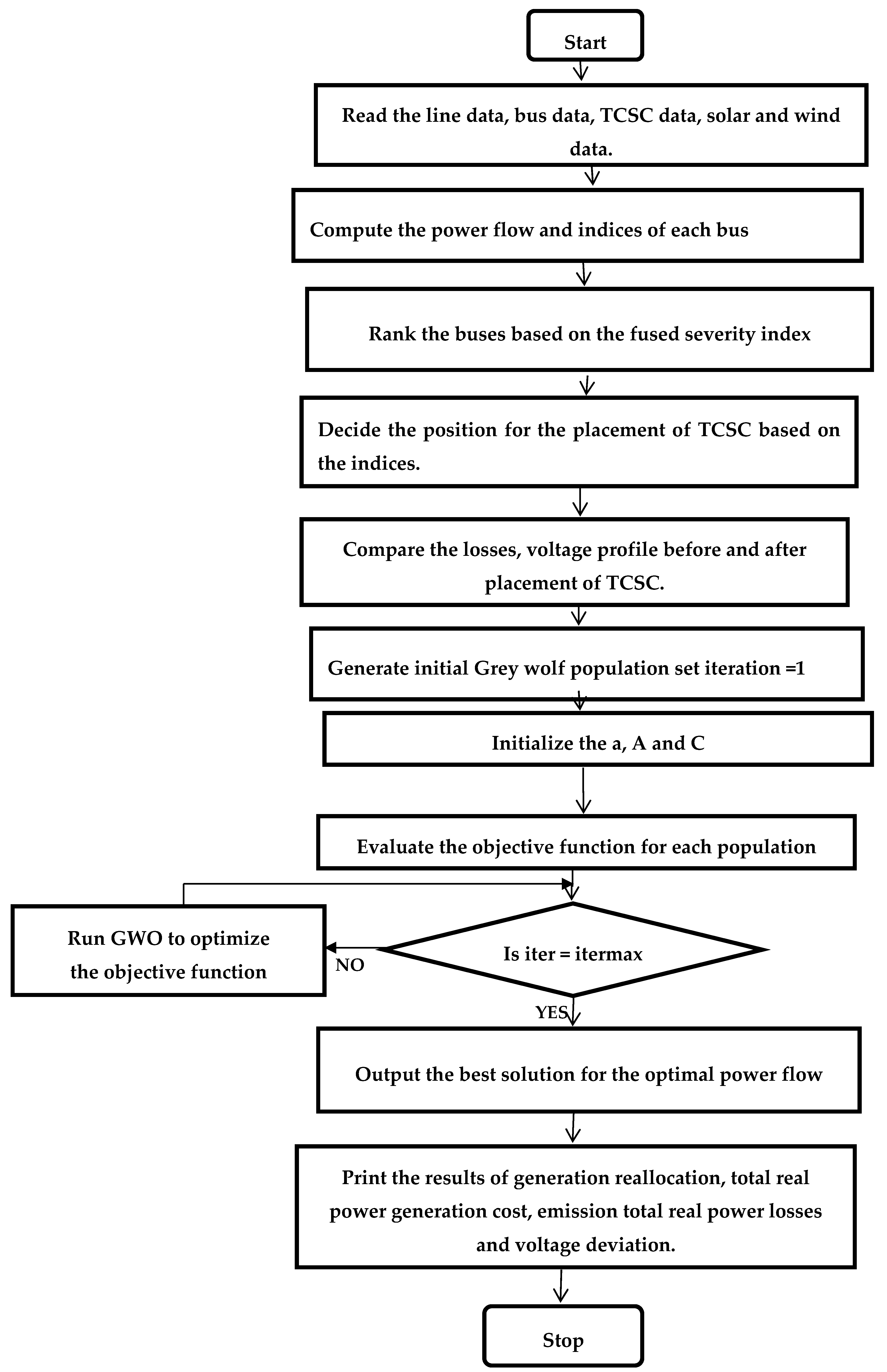
5. Optimal Tuning of TCSC using Grey Wolf Optimization
| Algorithm 1. Grey Wolf Optimizer (GWO) Algorithms |
| 1. Generate the initial prey wolf population/search agents |
| Yj (where j = 1, 2 ….n) |
| 2. Initialize a, A and C |
| 3. Compute the fitness value of each search agent |
| Yα = the best seek after an authority |
| Yβ = the second best seek after an authority |
| Yδ = the third best seek after an authority |
| 4. Initialize Iteration = 1 |
| 5. Repeat the steps |
| 6. For j = 1: Ys (size of Grey wolf) |
| For each chase agent |
| Invigorate the location of the current chase agent by using the equation |
| Y (k+1) = Y1 + Y2 + Y3/3 |
| End for |
| 7. Compute the fitness values of all chase agents |
| 8. Renew the vectors of a, A and C |
| 9. Renew the values of Yα, Yβ, Yδ |
| 10. Increment the Iteration (k = k+1) |
| 11. While (iterations< max number of iterations) |
| 12. Get the output Yα |
| End |
6. Simulation Results
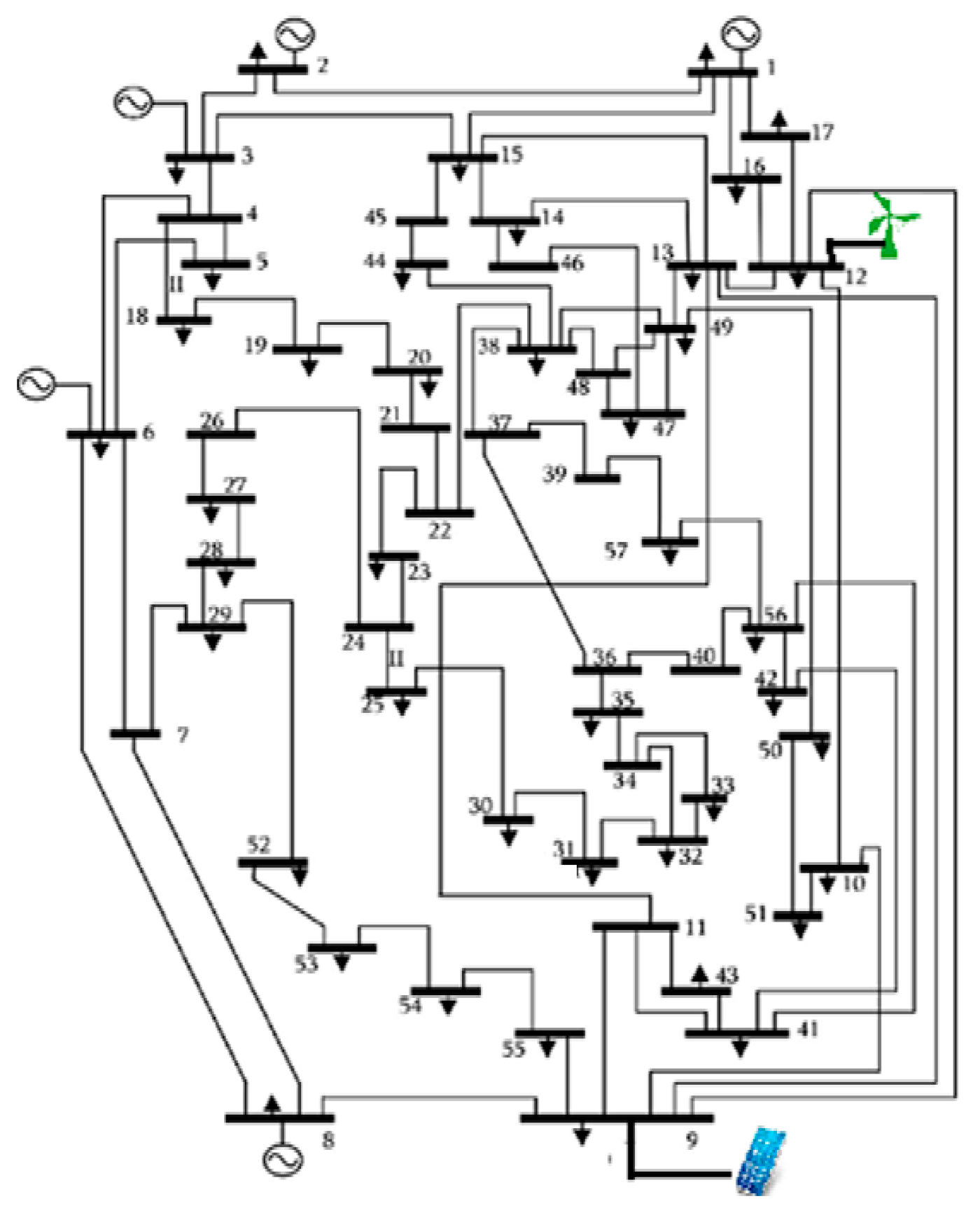
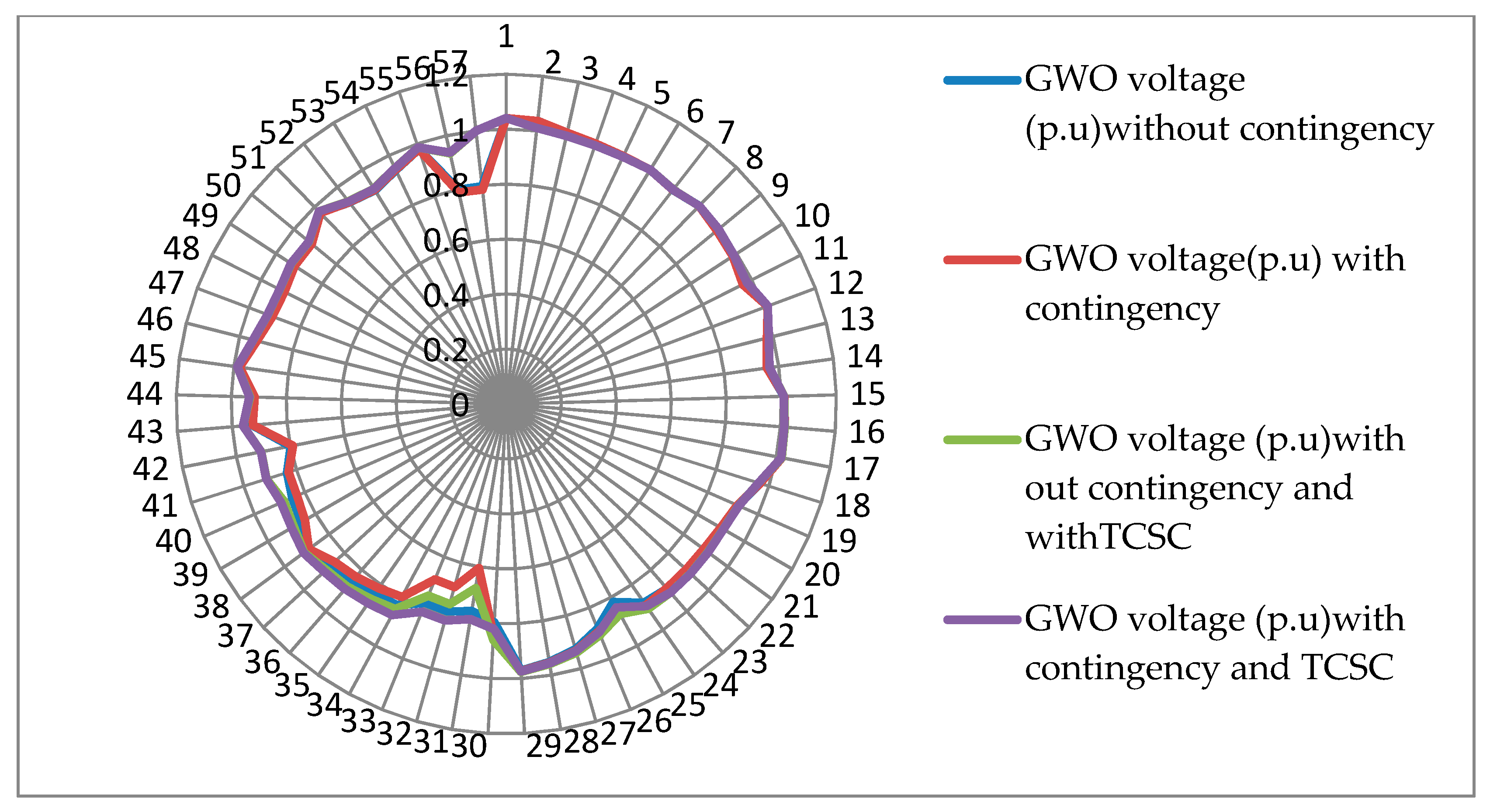
6.1. IEEE57 BusTest System
6.2. Normal Loading Condition
6.3. Contingency Condition using Intermittent Approach
7. Conclusions
- A fused severity index has been implemented for finding out the most stressed line of the transmission system.The weak lines are recognized based on the rank and arranged in descending order of fused severity index for the lines associated between the buses.
- Uncertainties of solar and wind are demonstrated as lognormal and Weibull probabilistic distribution functions and their interconnectionsto the traditional grid are explained.
- The TCSC and output of generators are additionally tuned by limiting a multi-objective function comprising of active power loss, fuel cost with valve-point effect, carbon dischargesutilizing grey wolf algorithm and the best global ideal values are achieved.
- A reduction in the losses, carbon discharges, fuel cost with valve-point effect has been obtained with an improvement in the voltage profile of the integrated system. The reduction in active power loss helps in contingency management. Improvement of voltage deviation helps in protectingthe system against line outages.
- Finally, it can be inferred that the explored strategy is more capable in decreasing the losses, carbon emission and improving the voltage profile.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| TCSC | Thyristor-Controlled Series Compensator |
| SB | Sending end bus |
| RB | Receiving end bus |
| RVSI | Rapid Voltage Stability Index |
| NLSI | Novel Line Stability Index |
| FSI | Fused Severity Index. |
| Probability Density Function | |
| GWO | Grey Wolf Optimizer |
| FACTS | Flexible AC Transmission System |
| VD | Voltage Deviation |
| VPE | Valve Point Effect |
| CE | Carbon Emissions |
| IMSI | Intermittent Severity Index |
| OPF | Optimal Power Flow |
| PV | Photo Voltaic |
| SVC | Static VAR Compensator |
| Symbols | |
| Pwe | Wind power generation from eth bus |
| Psf | Power output from the fth PV plant |
| PL | Overall real power loss |
| QL | Overall reactive power loss, |
| PGi | Real power generated in ith bus |
| PDi | Real power demanded in ithbus |
| The minimum power of the ith thermal unit | |
| Pj | Active power at receiving at jth bus |
| Qj | Reactive power at receiving at jth bus |
| NTG | Number of generator buses |
| a, b, c | Fuel cost coefficients |
| Vk | Magnitude of voltage at bus k |
| X | Reactance of line |
| XTCSC | Reactance of the TCSC |
| Vin | Wind Speed (Cut-in) |
| VCO | Wind Speed (Cut-out) |
| Vr | Wind Speed (Rated) |
| Pr | Rated Power |
| ntl | No. of lines for transmission |
| N | no of buses |
| Z | impedance of line in ohms |
| ge | Direct cost coefficient of the eth wind farm |
| hf | Direct cost coefficient of the fth solar plant |
| The resistance of the line | |
| Sij | Apparent power flowing in the line |
| Vkref | Magnitude of the Reference voltage at the busk |
| di,ei | Valve-Point Effect Coefficient |
| δi, φi, λi, ψi, σi | Emission coefficients |
| c | Scale Parameter |
| k | Shape Parameter |
| PBij | Probability occurring of line ij for all contingencies of the system |
| Β | variance of the lognormal distribution |
| µ | Mean of the lognormal distribution |
| w1,w2, w3, w4, w5, m1, m2 | Weighted factors |
Appendix A
| Generator Bus No. | a ($/MW2/h) | b ($/MW/h) | c ($/h) | δi | φi | λi | ψi | σi | di | ei | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0775 | 20 | 0 | 0 | 1975 | 4.091 | −5.55 | 0.549 | 0.0002 | 0.286 | 18 | 0.037 |
| 2 | 0.01 | 40 | 0 | 0 | 100 | 2.543 | −6.04 | 0.4638 | 0.0005 | 0.333 | 16 | 0.038 |
| 3 | 0.25 | 20 | 0 | 0 | 140 | 6.131 | −5.55 | 0.4151 | 0.00001 | 0.667 | 13.5 | 0.041 |
| 6 | 0.1 | 40 | 0 | 0 | 100 | 3.491 | −5.75 | 0.539 | 0.0003 | 0.266 | 18 | 0.037 |
| 8 | 0.02222 | 20 | 0 | 0 | 550 | 4.258 | −5.09 | 0.3586 | 0.000001 | 0.8 | 14 | 0.04 |
References
- Ogunjuyigbe, A.S.O.; Ayodele, T.R.; Akinola, O.A. Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of the remote residential building. Appl. Energy 2016, 171, 153–171. [Google Scholar] [CrossRef]
- Kusakana, K. Optimal scheduled power flow for distributed photovoltaic/wind/diesel generators with battery storage system. IET Renew Power Gener. 2015, 9, 916–924. [Google Scholar] [CrossRef]
- Sanseverino, E.R.; Di Silvestre, M.L.; Badalamenti, R.; Nguyen, N.Q.; Guerrero, J.M.; Meng, L. Optimal power flow in islanded microgrids using a simple distributed algorithm. Energies 2015, 8, 11493–11514. [Google Scholar] [CrossRef]
- Erdinc, O.; Uzunoglu, M. Optimum design of hybrid renewable energy systems: Overview of different approaches. Renew Sustain. Energy Rev. 2012, 16, 1412–1425. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B.; Ding, H.; Li, H. Risk-based probabilistic voltage stability assessment in an uncertain power system. Energies 2017, 10, 180. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Balog, R.S. Multi-objective optimization and design of a photovoltaic-wind hybrid system for community smart DC microgrid. IEEE Trans. Smart Grid 2014, 5. [Google Scholar] [CrossRef]
- Rambabu, M.; Nagesh Kumar, G.V.; Siva Nagaraju, S. Energy management of microgrid using support vector machine (SVM) model. IIOAB J. 2016, 7, 116–132. [Google Scholar]
- Carvallo, J.P.; Shaw, B.J.; Avila, N.I.; Kammen, D.M. Sustainable Low-Carbon Expansion for the Power Sector of an Emerging Economy: The Case of Kenya. Environ. Sci. Technol. 2017, 51, 10232–10242. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential search algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2016, 79, 1–10. [Google Scholar] [CrossRef]
- Shi, L.; Wang, C.; Yao, L.; Ni, Y.; Bazargan, M. Optimal power flow solution incorporating wind power. IEEE Syst. J. 2012, 6, 233–241. [Google Scholar] [CrossRef]
- Sichilalu, S.; Mathaba, T.; Xia, X. Optimal control of a wind–PV-hybrid powered heat pump water heater. Appl. Energy 2017, 185, 1173–1184. [Google Scholar] [CrossRef]
- Levron, Y.; Guerrero, J.M.; Beck, Y. Optimal Power Flow in MicrogridsWith Energy Storage. Power Syst. IEEE Trans. 2013, PP, 1–9. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, G.A.J. Optimal power flow solutions incorporating stochastic wind and solar power. Energy Convers. Manag. 2017, 148, 1194–1207. [Google Scholar] [CrossRef]
- HamzehAghdam, F.; Salehi, J.; Ghaemi, S. Contingency based energy management of multi-microgrid based distribution network. Sustain. Cities Soc. 2018, 41, 265–274. [Google Scholar] [CrossRef]
- Rao, V.B.; Engineering, E.; Kumar, G.V.N.; Engineering, E. A Comparative Study of BAT and Firefly Algorithms for Optimal Placement and Sizing of Static VAR Compensator for Enhancement of Voltage Stability. Int. J. Energy Optim. Eng. 2015, 4, 68–84. [Google Scholar] [CrossRef]
- Hingorani, N.G.; Gyugyi, L.; El-Hawary, M. Understanding FACTS—Concepts and Technology of Flexible AC Transmission Systems; Wiley-IEEE Press: Hoboken, NJ, USA, December 1999. [Google Scholar]
- Bali, S.K.; Munagala, S.; Gundavarapu, V.N.K. Harmony search algorithm and combined index-based optimal reallocation of generators in a deregulated power system. Neural Comput. Appl. 2017, 1–9. [Google Scholar] [CrossRef]
- Kumar Gundavarapu, V.N.; Mishra, A. Line utilization factor-based optimal allocation of IPFC and sizing using firefly algorithm for congestion management. IET Gener. Transm. Distrib. 2016, 10, 115–122. [Google Scholar] [CrossRef]
- Modarresi, J.; Gholipour, E.; Khodabakhshian, A. A comprehensive review of the voltage stability indices. Renew Sustain. Energy Rev. 2016, 63, 1–12. [Google Scholar] [CrossRef]
- Kim, S.S.; Kim, M.K.; Park, J.K. Consideration of multiple uncertainties for evaluation of available transfer capability using fuzzy continuation power flow. Int. J. Electr. Power Energy Syst. 2008, 30, 581–593. [Google Scholar] [CrossRef]
- Nireekshana, T.; KesavaRao, G.; SivanagaRaju, S. Available transfer capability enhancement with FACTS using Cat Swarm Optimization. Ain Shams Eng. J. 2016, 7, 159–167. [Google Scholar] [CrossRef]
- Samimi, A.; Naderi, P. A New Method for Optimal Placement of TCSC Based on Sensitivity Analysis for Congestion Management. Smart Grid Renew. Energy 2012, 2012, 10–16. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Gupta, V.K. SVC & TCSC for Minimum Operational Cost Under Different Loading Condition. 2012, pp. 1–6. Available online: www.iitk.ac.in/npsc/Papers/NPSC2012/papers/12055.pdf. (accessed on 26 June 2018).
- Mukherjee, A.; Mukherjee, V. Solution of optimal power flow using chaotic krill herd algorithm. Chaos Solit. Fract. 2015, 78. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. A comparative study on particle swarm optimization for optimal steady-state performance of power systems. IEEE Trans. Power Syst. 2006, 21, 1718–1728. [Google Scholar] [CrossRef]
- Daryani, N.; Hagh, M.T.; Teimourzadeh, S. Adaptive group search optimization algorithm for multi-objective optimal power flow problem. Appl. Soft Comput. J. 2016, 38, 1012–1024. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Murty, V.V.S.N.; Kumar, A. Optimal placement of DG in radial distribution systems based on new voltage stability index under load growth. Int. J. Electr. Power Energy Syst. 2015, 69, 246–256. [Google Scholar] [CrossRef]
- Yazdanpanah-Goharrizi, A.; Asghari, R. A Novel Line Stability Index (NLSI) for Voltage Stability assessment of Power Systems. In Proceedings of the 7th WSEAS e 7th WSEAS International Conference on Power Systems, Beijing, China, 15–17 September 2007; pp. 164–167. [Google Scholar]
- Fort Collins Data Access: Results. Available online: http://climate.colostate.edu/~autowx/fclwx_results.php (accessed on 26 June 2018).
| Serial Number. | Parameters | Quantity |
|---|---|---|
| 1 | Grey wolf size | 20 |
| 2 | Number of iterations | 50 |
| 3 | a vector | 2 |
| m1(NLSI) | m2(NVSI) | Total FSI |
|---|---|---|
| 0.5 | 0.5 | 7.3884 |
| 0.6 | 0.4 | 7.5503 |
| 0.7 | 0.3 | 7.7122 |
| 0.8 | 0.2 | 7.8741 |
| 0.9 | 0.1 | 8.036 |
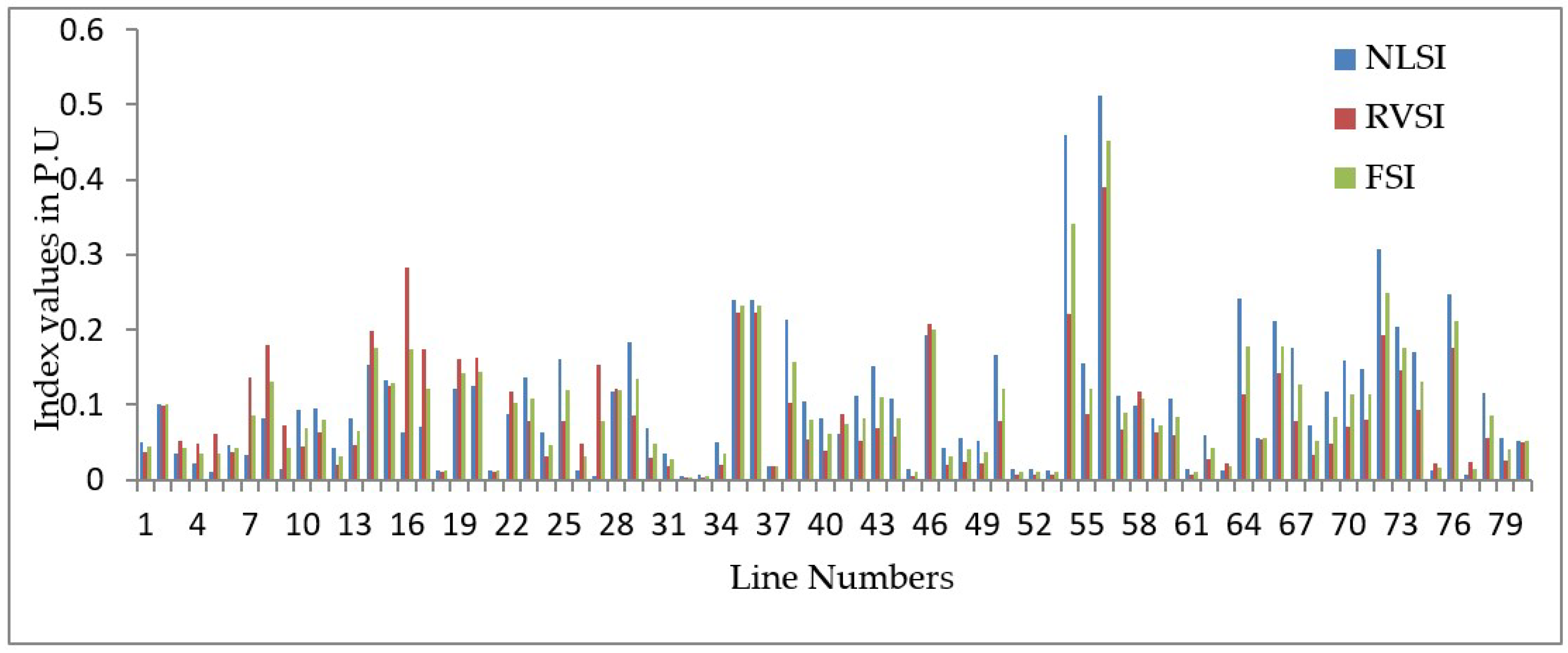
| LINE Numbers | SB Number | RB Number | NLSI (p.u.) | RVSI(p.u.) | FSI(p.u.) |
|---|---|---|---|---|---|
| 56 | 41 | 43 | 0.5123 | 0.3905 | 0.4514 |
| 16 | 1 | 16 | 0.0633 | 0.2836 | 0.3404 |
| 35 | 24 | 25 | 0.2393 | 0.2235 | 0.2494 |
| 36 | 24 | 25 | 0.2393 | 0.2235 | 0.2314 |
| 54 | 11 | 41 | 0.4593 | 0.2214 | 0.2314 |
| 46 | 34 | 32 | 0.1923 | 0.2079 | 0.2119 |
| 14 | 13 | 15 | 0.154 | 0.1984 | 0.2001 |
| 72 | 44 | 45 | 0.3066 | 0.1922 | 0.1777 |
| 8 | 8 | 9 | 0.0812 | 0.1802 | 0.177 |
| 76 | 39 | 57 | 0.2469 | 0.1768 | 0.1762 |
| 17 | 1 | 17 | 0.071 | 0.1735 | 0.175 |
| 20 | 4 | 18 | 0.1249 | 0.162 | 0.1734 |
| 19 | 4 | 18 | 0.1223 | 0.1618 | 0.1575 |
| 27 | 12 | 17 | 0.0041 | 0.1535 | 0.1435 |
| 73 | 40 | 56 | 0.2046 | 0.1453 | 0.1421 |
| 66 | 13 | 49 | 0.2116 | 0.1423 | 0.1349 |
| 7 | 6 | 8 | 0.0339 | 0.1359 | 0.1313 |
| 15 | 1 | 15 | 0.1322 | 0.1244 | 0.1307 |
| 28 | 1 | 15 | 0.1169 | 0.1213 | 0.1283 |
| 58 | 15 | 45 | 0.0984 | 0.1181 | 0.1267 |
| 22 | 7 | 8 | 0.0881 | 0.117 | 0.1223 |
| 64 | 50 | 51 | 0.2413 | 0.1141 | 0.1223 |
| 38 | 26 | 27 | 0.2128 | 0.1023 | 0.1221 |
| 2 | 2 | 3 | 0.1011 | 0.0991 | 0.1194 |
| SB Number | RB Number | Total Power Generation (MW) | Fuel Cost ($/h) | Active Power Losses(MW) | Emission(t/h) | Voltage Deviation in p.u | Valve Point Effect ($/h) | Multi-Objective Function |
|---|---|---|---|---|---|---|---|---|
| 41 | 43 | 1227.2 | 27487 | 31.41 | 1.0064 | 4.852 | 27534 | 11012 |
| 11 | 41 | 12274 | 27521 | 31.5975 | 1.0457 | 4.8338 | 27558 | 11023 |
| 13 | 15 | 12279 | 27515 | 32.0767 | 1.0593 | 4.912 | 27557 | 11022 |
| 44 | 45 | 12278 | 27485 | 31.955 | 1.0276 | 4.9304 | 27540 | 11013 |
| 50 | 51 | 1227.3 | 27489 | 31.1877 | 1.0065 | 4.8526 | 27537 | 11014 |
| Parameter | OF1 | OF2 | OF3 | OF4 | OF5 | OF6 | |
|---|---|---|---|---|---|---|---|
| Real power generation (MW) | PG1(MW) | 158.0297 | 265.076 | 163.4177 | 179.0372 | 170.1787 | 165.5765 |
| PG2(MW) | 100 | 12.8868 | 100 | 100 | 100 | 100 | |
| PG3(MW) | 49.4902 | 125.903 | 49.9138 | 140 | 140 | 51.4046 | |
| PG6(MW) | 18.184 | 106.128 | 15.7625 | 150 | 150 | 14.9543 | |
| PG8(MW) | 490.8169 | 301.122 | 487.1829 | 243.1543 | 251.931 | 484.1597 | |
| PGs(MW) | 200 | 200 | 200 | 200 | 200 | 200 | |
| PGw(MW) | 210 | 210 | 210 | 210 | 210 | 210 | |
| Total Active power generation (MW) | 1226.521 | 1221.12 | 1226.2769 | 1222.192 | 1222.11 | 1226.095 | |
| Total real power generation cost ($/h) | 27343 | 31769 | 27347 | 32907 | 32762 | 27352 | |
| Active power Loss (MW) | 30.72 | 25.316 | 30.47 | 26.39 | 26.31 | 30.29 | |
| Valve point effect cost ($/h) | 27393 | 31815 | 27391 | 32946 | 32799 | 27393 | |
| Voltage deviation (p.u.) | 4.9058 | 4.7912 | 4.8996 | 4.76 | 4.8 | 4.8951 | |
| Carbon Emission(ton/h) | 1.0159 | 0.7945 | 1.0124 | 0.5924 | 0.5911 | 1.0479 | |
| Objective function | 27343 | 25.316 | 27391 | 4.76 | 0.5911 | 10956 | |
| Computation time | 27.99 | 26.99 | 23.68 | 23.98 | 22.76 | 23.44 | |
| Parameter | OF1 | OF2 | OF3 | OF4 | OF5 | OF6 | |
|---|---|---|---|---|---|---|---|
| Real power generation (MW) | PG1(MW) | 171.6265 | 265.1003 | 176.1099 | 324.9398 | 174.6181 | 184.4858 |
| PG2(MW) | 100 | 29.0587 | 100 | 100 | 100 | 100 | |
| PG3(MW) | 47.3295 | 92.2253 | 47.8758 | 22.3223 | 140 | 48.5226 | |
| PG6(MW) | 16.8781 | 114.2285 | 12.0639 | 52.221 | 158.7316 | 6.2416 | |
| PG8(MW) | 479.7787 | 309.8535 | 479.4983 | 314.4824 | 239.0236 | 476.0984 | |
| PGs(MW) | 200 | 200 | 200 | 200 | 200 | 200 | |
| PGw(MW) | 210 | 210 | 210 | 210 | 210 | 210 | |
| Total Active power generation (MW) | 1225.613 | 1220.466 | 1225.548 | 1223.966 | 1222.373 | 1225.348 | |
| Total real power generation cost ($/h) | 26580 | 30032 | 26582 | 30423 | 32409 | 26603 | |
| Active power Loss (MW) | 29.812 | 24.66 | 29.74 | 28.165 | 26.57 | 29.5484 | |
| Valve point effect($/h) | 26629 | 30070 | 26626 | 30461 | 32444 | 26635 | |
| Voltage deviation (p.u.) | 4.8267 | 4.794 | 4.8247 | 4.7794 | 4.808 | 4.8206 | |
| Carbon Emission(ton/h) | 0.9666 | 0.7936 | 0.9727 | 0.9524 | 0.5562 | 0.9755 | |
| Objective function | 26580 | 24.66 | 26626 | 4.7794 | 0.5562 | 10655 | |
| Computation time(secs) | 26.76 | 25.84 | 24.43 | 21.64 | 25.26 | 27.41 | |
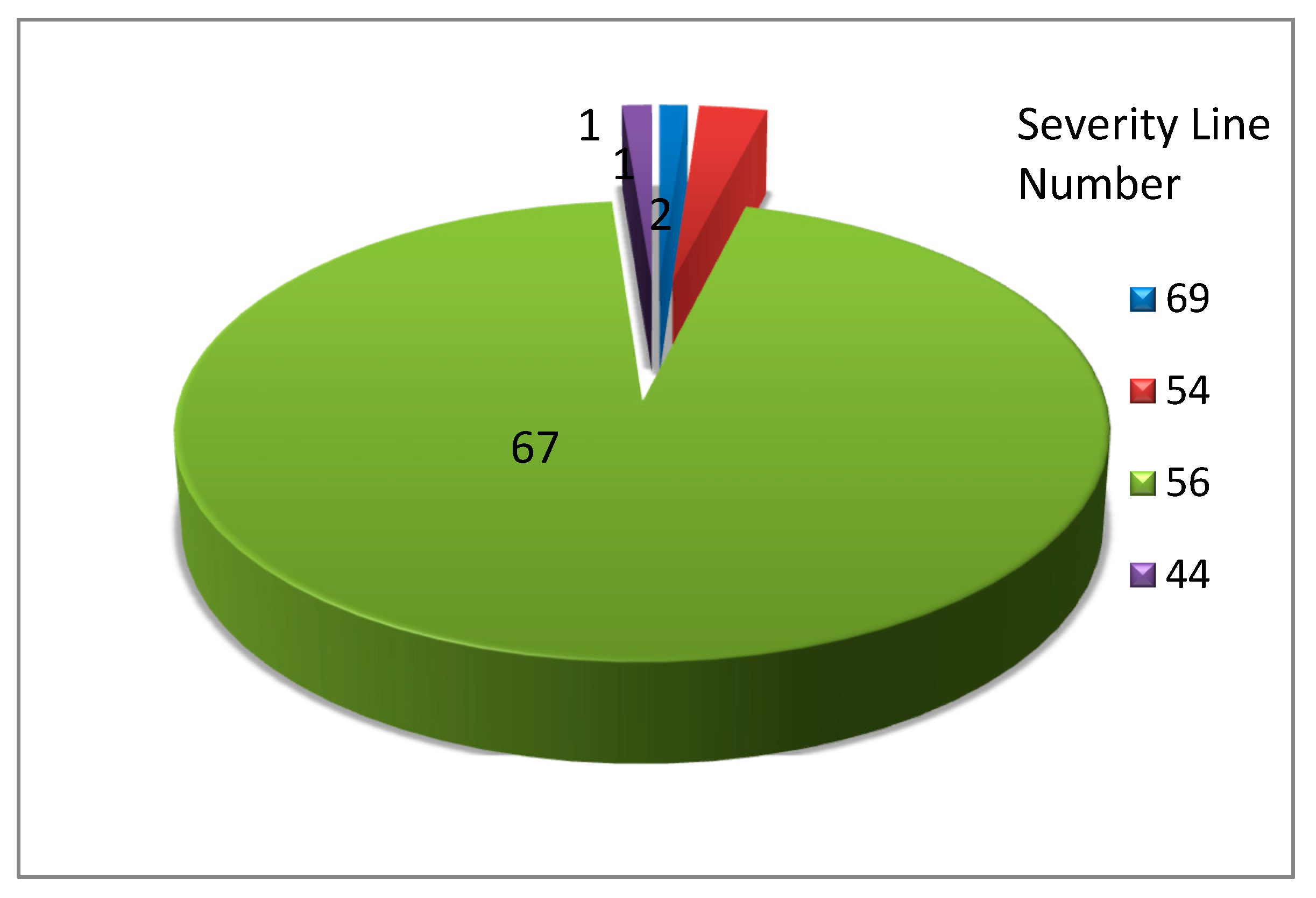
| (Max FSI) x(No of Times the Severity of the Line) | Intermittent Index Value(p.u) | Severity Line No. | SB | RB |
|---|---|---|---|---|
| 0.508323 | 0.508323 | 69 | 53 | 54 |
| 0.6100*2 | 1.22 | 54 | 11 | 41 |
| 0.614*67 | 41.138 | 56 | 41 | 43 |
| 0.537543 | 0.537543 | 44 | 31 | 32 |
| Quantity | Tuned Without Contingency and TCSC | Tuned Without Contingency and with TCSC | Tuned with Contingency and without TCSC | Tuned with Contingency and TCSC | |
|---|---|---|---|---|---|
| Real power generation (MW) | PG1(MW) | 165.576 | 184.4858 | 152.2136 | 192.0006 |
| PG2(MW) | 100 | 100 | 100 | 100 | |
| PG3(MW) | 51.4046 | 48.5226 | 49.3313 | 47.9692 | |
| PG6(MW) | 14.9543 | 6.2416 | 16.5164 | 13.7667 | |
| PG8(MW) | 484.159 | 476.0984 | 501.8825 | 464.311 | |
| PGs(MW) | 200 | 200 | 200 | 200 | |
| PGw(MW) | 210 | 210 | 210 | 210 | |
| Total power generation (MW) | 1226.09 | 1225.35 | 1229.944 | 1228.048 | |
| Total Load(MW) | 1195.8 | 1195.8 | 1195.8 | 1195.8 | |
| Active power Loss (MW) | 30.29 | 25.62 | 34.1438 | 32.2475 | |
| Voltage deviation (p.u.) | 4.8951 | 4.77 | 6.1709 | 6.1562 | |
| Parameter | OF1 | OF2 | OF3 | OF4 | OF5 | OF6 | |
|---|---|---|---|---|---|---|---|
| Real power generation (MW) | PG1(MW) | 160.8007 | 253.576 | 164.1703 | 236.6245 | 164.3258 | 152.2136 |
| PG2(MW) | 100 | 9.0711 | 100 | 100 | 100 | 100 | |
| PG3(MW) | 50.0324 | 140 | 51.0861 | 140 | 140 | 49.3313 | |
| PG6(MW) | 16.8994 | 103.6872 | 17.9614 | 3.989 | 150 | 16.5164 | |
| PG8(MW) | 491.5837 | 307.4762 | 485.7775 | 335.7361 | 260.4213 | 501.8825 | |
| PGs(MW) | 200 | 200 | 200 | 200 | 200 | 200 | |
| PGw(MW) | 210 | 210 | 210 | 210 | 210 | 210 | |
| TotalActivepowergeneration (MW) | 1229.316 | 1223.811 | 1228.995 | 1226.35 | 1224.747 | 1229.944 | |
| Total real power generation cost ($/h) | 27467 | 32206 | 27471 | 30867 | 3276 | 27472 | |
| Active power Loss (MW) | 33.51 | 28.01 | 33.19 | 30.54 | 28.94 | 34.1438 | |
| Valve point effect($/h) | 27516 | 32235 | 27515 | 30909 | 32804 | 27529 | |
| Voltage deviation (p.u.) | 6.097 | 5.962 | 6.09 | 5.9411 | 5.9456 | 6.1109 | |
| Carbon Emission(t/h) | 1.0233 | 0.7879 | 1.0096 | 0.7953 | 0.5958 | 1.0449 | |
| Objective function | 27467 | 28.01 | 27515 | 5.9411 | 0.5958 | 11008 | |
| Computation time(s) | 26.13 | 27.7 | 29.2 | 26.89 | 27.01 | 24.01 | |
| Parameter | OF1 | OF2 | OF3 | OF4 | OF5 | OF6 | |
|---|---|---|---|---|---|---|---|
| Real power generation (MW) | PG1(MW) | 154.0963 | 269.203 | 156.1643 | 329.2276 | 158.5345 | 172.0006 |
| PG2(MW) | 100 | 29.692 | 100 | 100 | 100 | 100 | |
| PG3(MW) | 47.7644 | 95.2386 | 48.1194 | 21.1564 | 140 | 47.9692 | |
| PG6(MW) | 36.5722 | 115.8249 | 34.2858 | 52.4674 | 158.6377 | 13.7667 | |
| PG8(MW) | 480.4047 | 303.6558 | 480.2326 | 314.3568 | 238.3618 | 464.311 | |
| PGs(MW) | 200 | 200 | 200 | 200 | 200 | 200 | |
| PGw(MW) | 210 | 210 | 210 | 210 | 230 | 230 | |
| Total active power generation (MW) | 1228.838 | 1223.614 | 1228.802 | 1227.208 | 1225.534 | 1228.048 | |
| Total real power generation cost ($/h) | 26719 | 30403 | 26721 | 30710 | 32555 | 26759 | |
| Active power Loss (MW) | 33.03 | 27.814 | 33.0021 | 31.4082 | 29.73 | 32.2475 | |
| Valve point effect($/h) | 26767 | 30449 | 26765 | 30744 | 32588 | 26795 | |
| Voltage deviation (p.u.) | 6.1681 | 6.1303 | 6.167 | 6.1143 | 6.1474 | 6.1562 | |
| Carbon emission(ton/h) | 0.9728 | 0.7962 | 0.9755 | 0.9674 | 0.5614 | 0.95 | |
| Objective function | 26719 | 27.814 | 26765 | 6.1143 | 0.5614 | 10719 | |
| Computation time(secs) | 27.68 | 23.92 | 26.104 | 25.09 | 25.98 | 22.89 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rambabu, M.; Nagesh Kumar, G.V.; Sivanagaraju, S. Optimal Power Flow of Integrated Renewable Energy System using a Thyristor Controlled SeriesCompensator and a Grey-Wolf Algorithm. Energies 2019, 12, 2215. https://doi.org/10.3390/en12112215
Rambabu M, Nagesh Kumar GV, Sivanagaraju S. Optimal Power Flow of Integrated Renewable Energy System using a Thyristor Controlled SeriesCompensator and a Grey-Wolf Algorithm. Energies. 2019; 12(11):2215. https://doi.org/10.3390/en12112215
Chicago/Turabian StyleRambabu, M., G. V. Nagesh Kumar, and S. Sivanagaraju. 2019. "Optimal Power Flow of Integrated Renewable Energy System using a Thyristor Controlled SeriesCompensator and a Grey-Wolf Algorithm" Energies 12, no. 11: 2215. https://doi.org/10.3390/en12112215
APA StyleRambabu, M., Nagesh Kumar, G. V., & Sivanagaraju, S. (2019). Optimal Power Flow of Integrated Renewable Energy System using a Thyristor Controlled SeriesCompensator and a Grey-Wolf Algorithm. Energies, 12(11), 2215. https://doi.org/10.3390/en12112215




