Coupled Motion Characteristics of Offshore Wind Turbines during the Integrated Transportation Process
Abstract
:1. Introduction
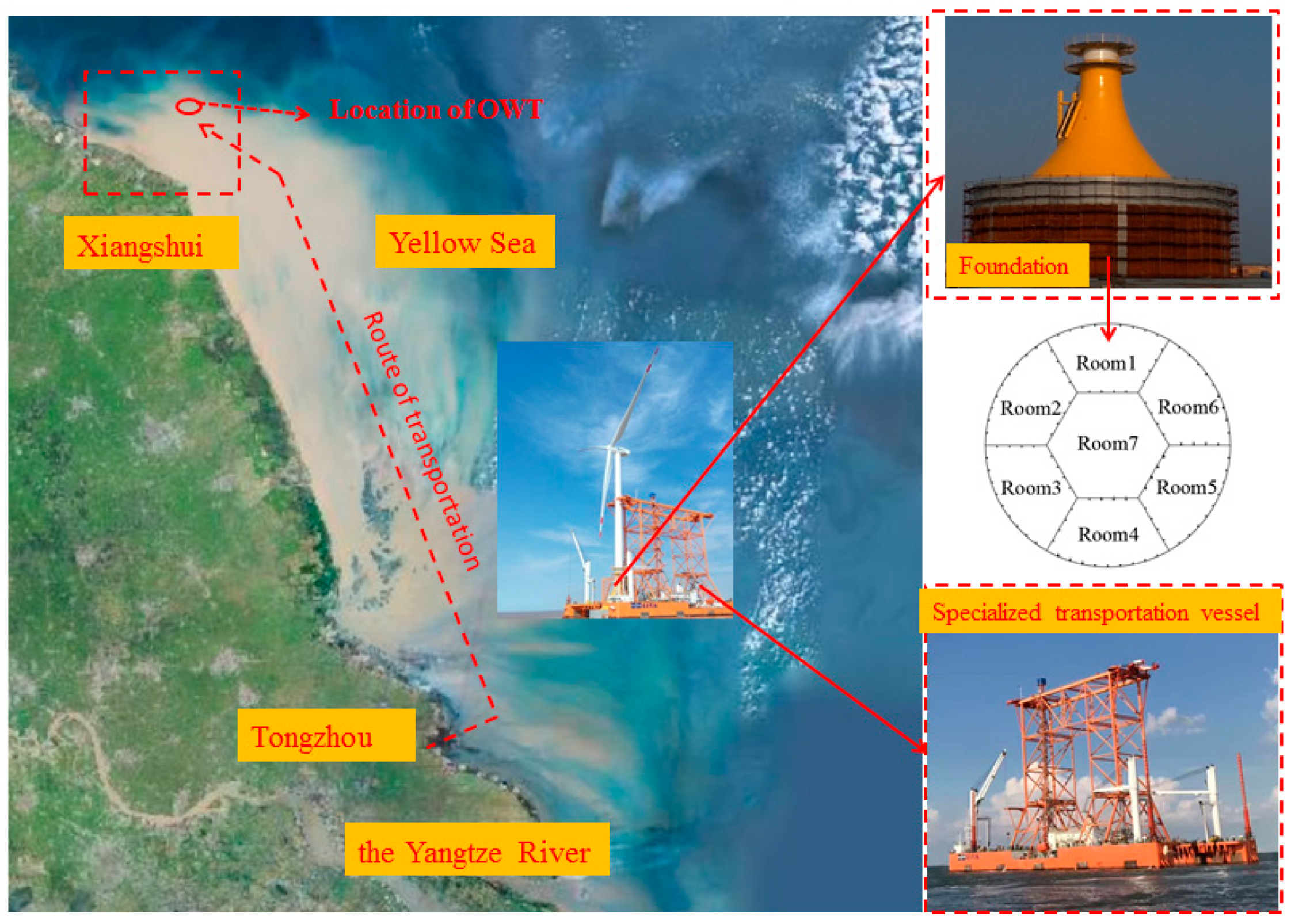
2. Prototype Observation of the Integrated Transportation
2.1. The Dedicated Transportation Vessel
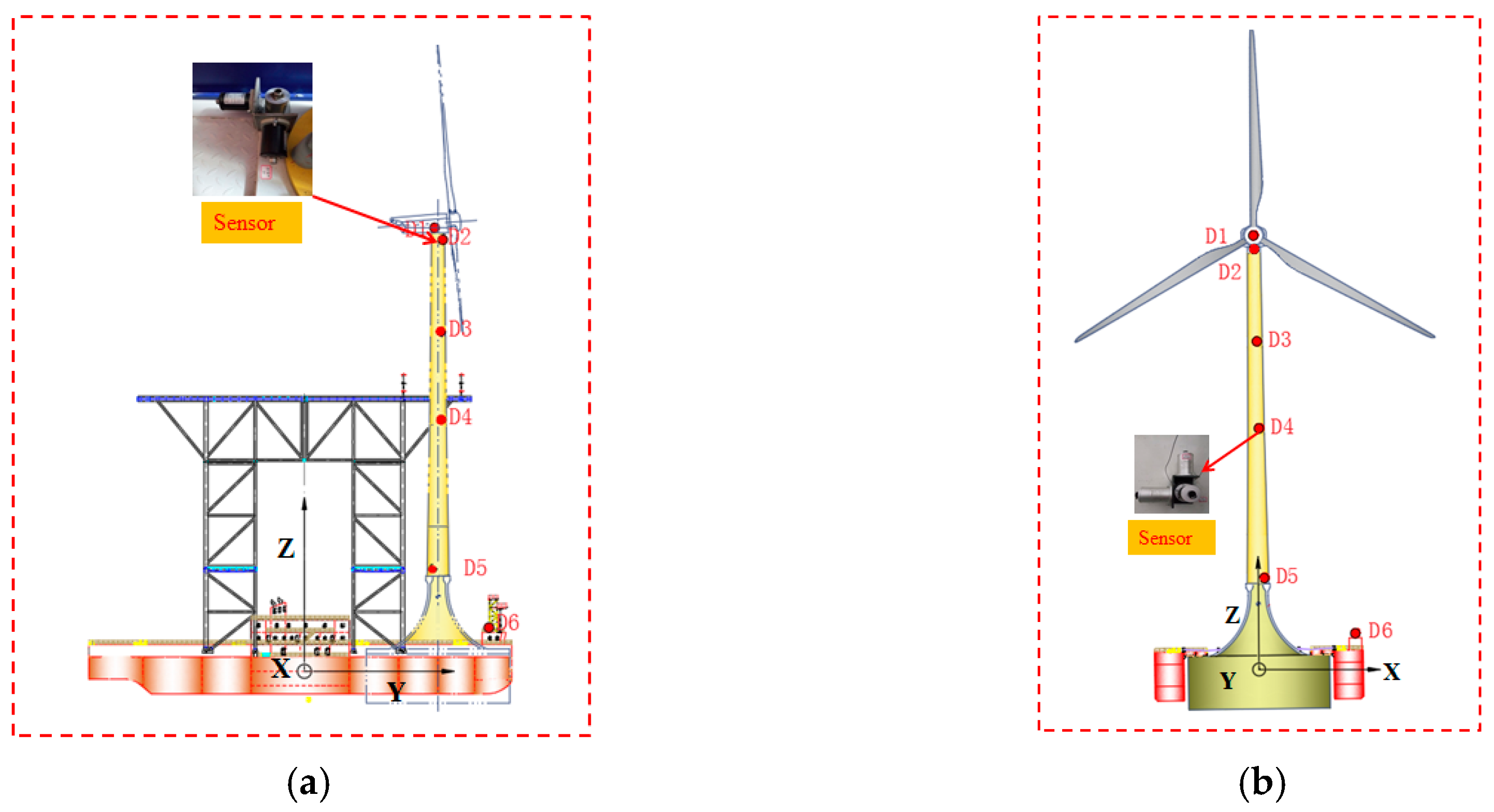
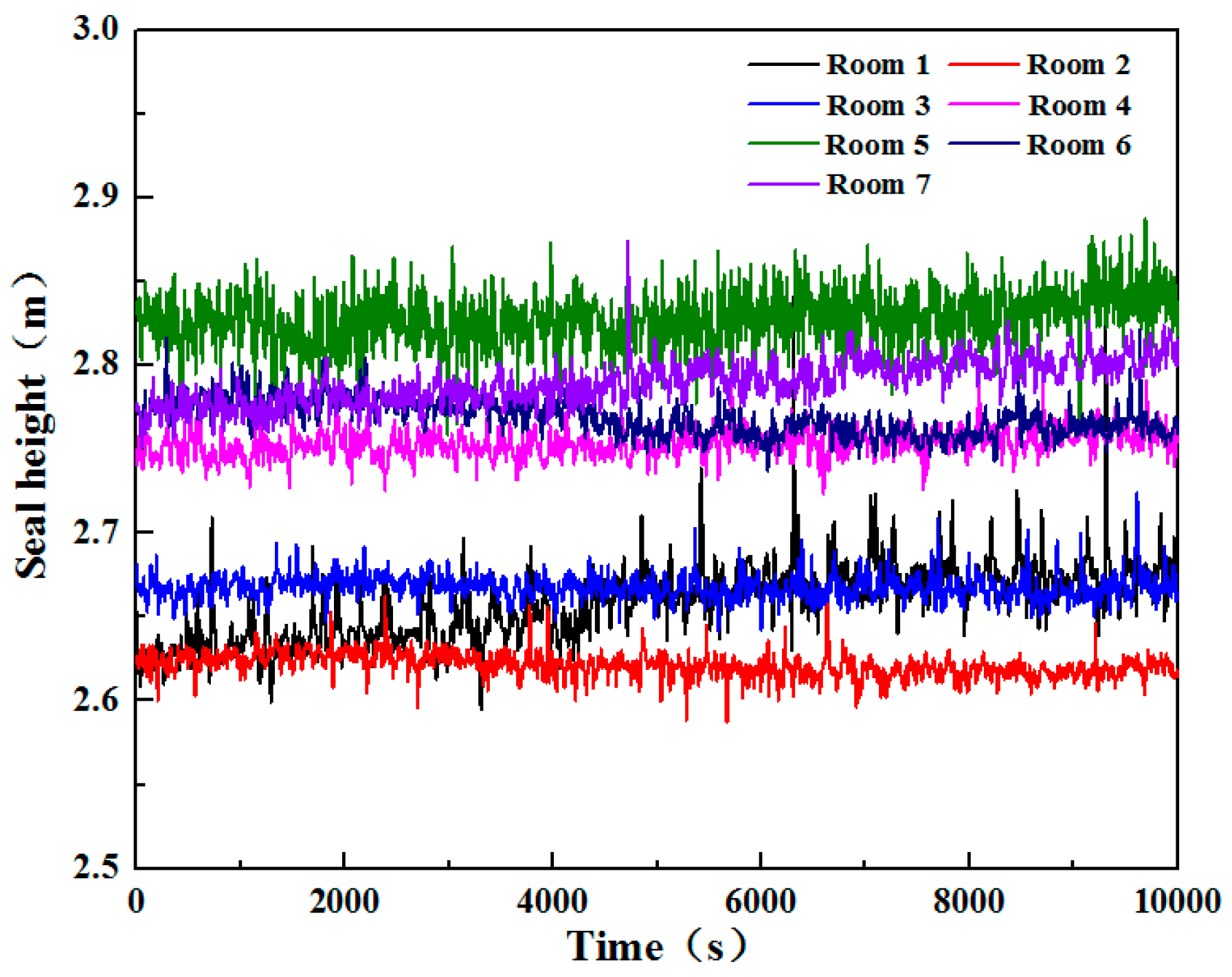
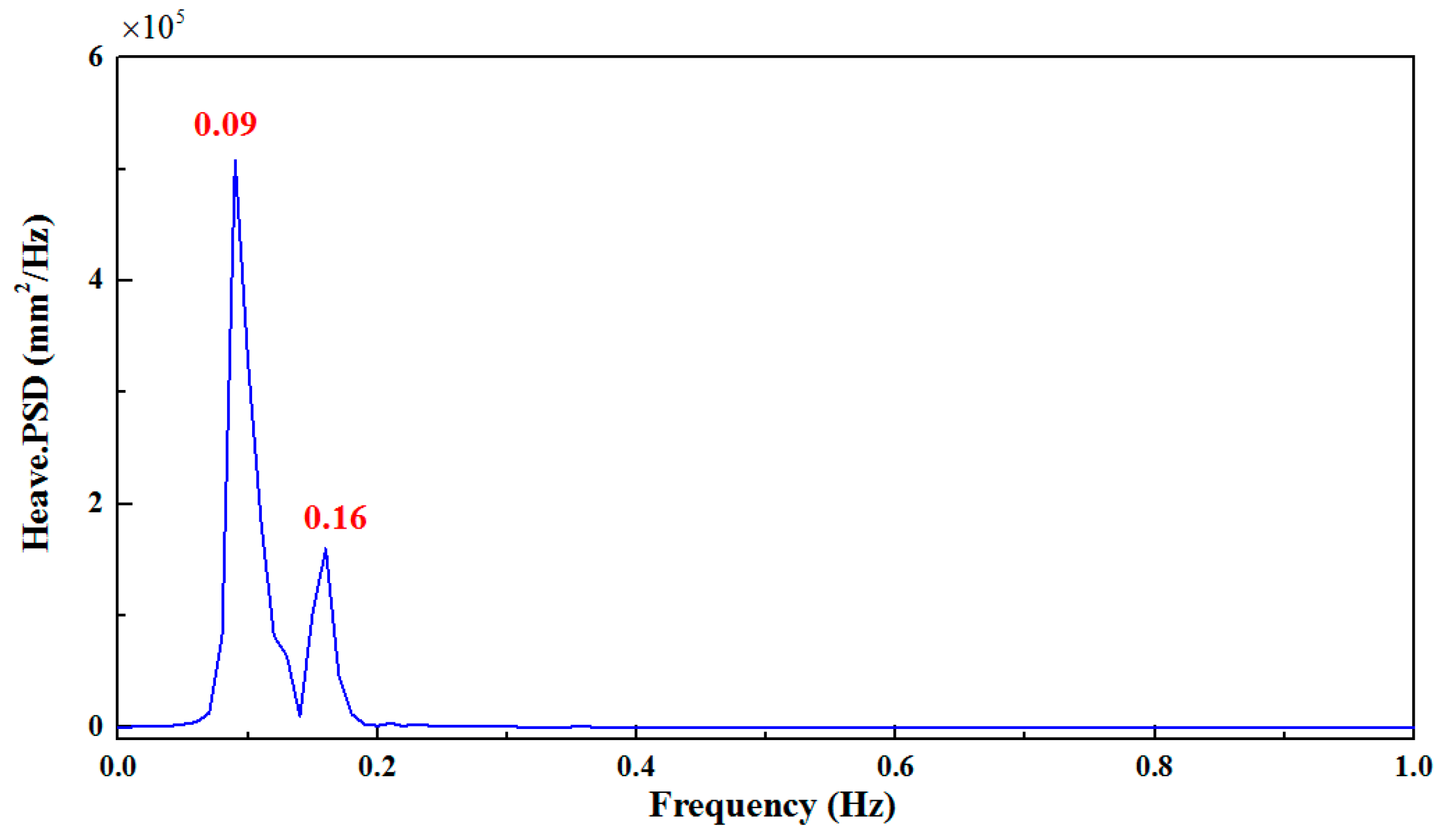
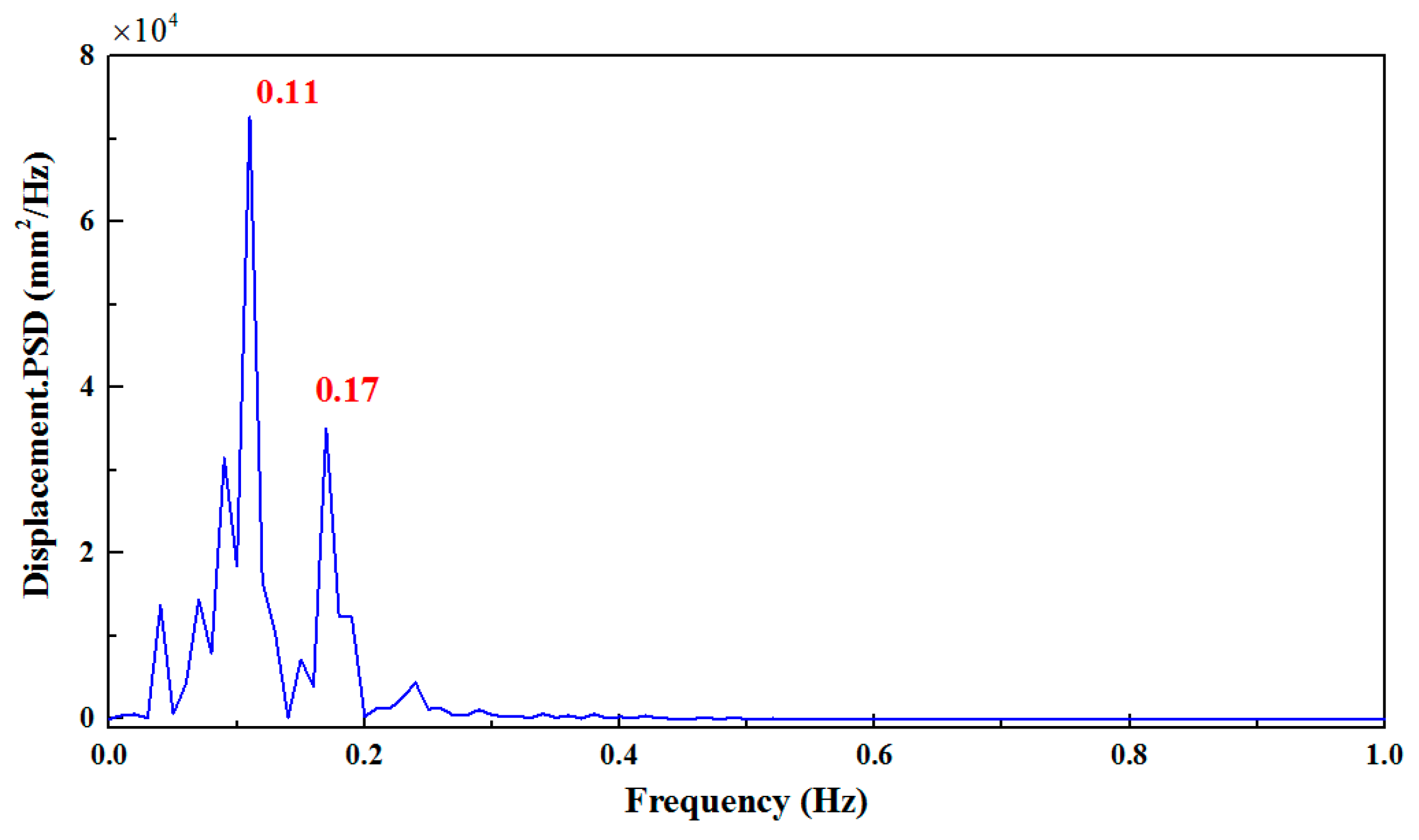
2.2. Arrangement of the Field Measurement
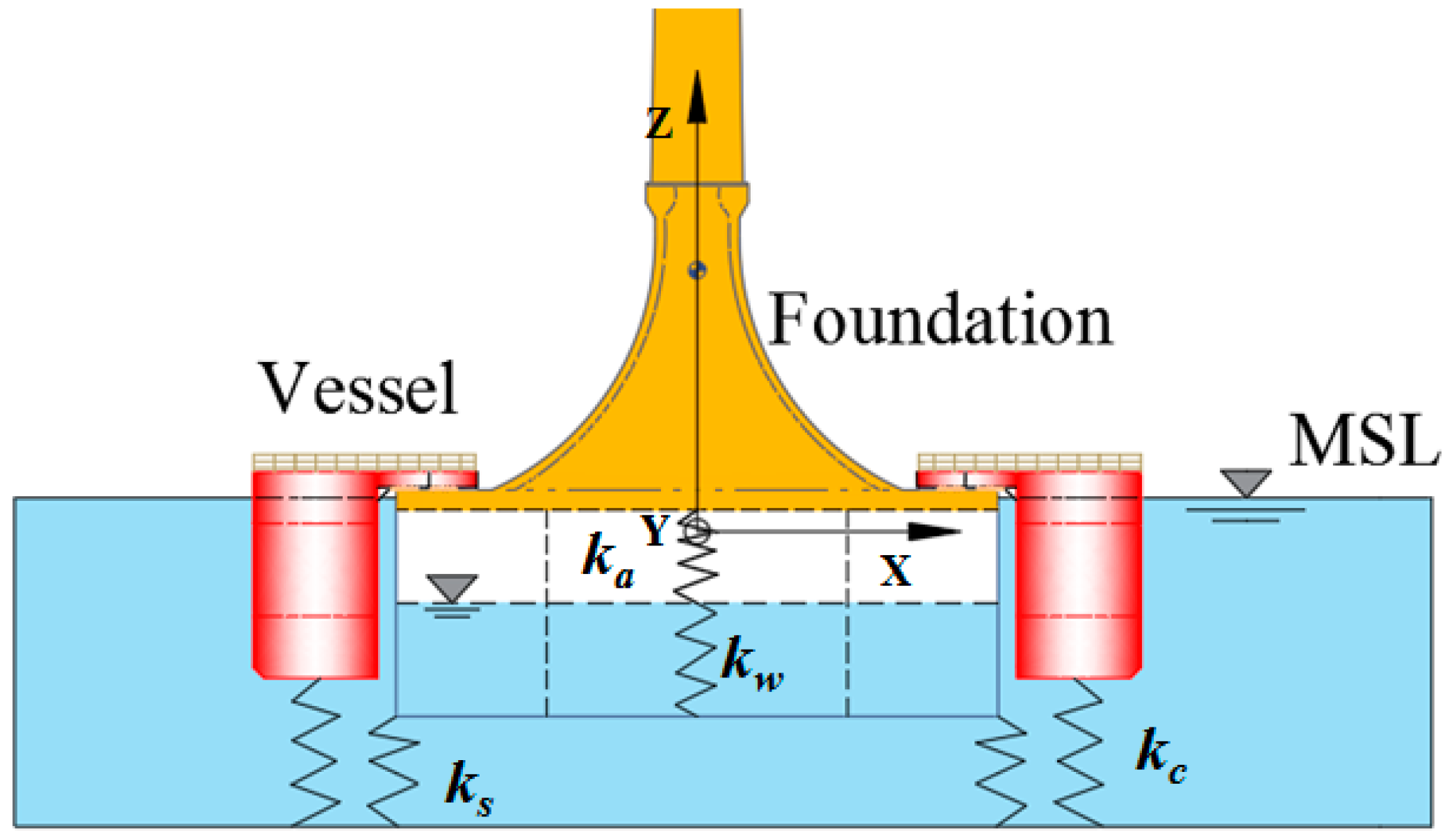
3. Motion Model of the Coupling System Considering Regular Wave Effect
3.1. Elastic Stiffness of the Coupling System
3.1.1. Heave Elastic Stiffness
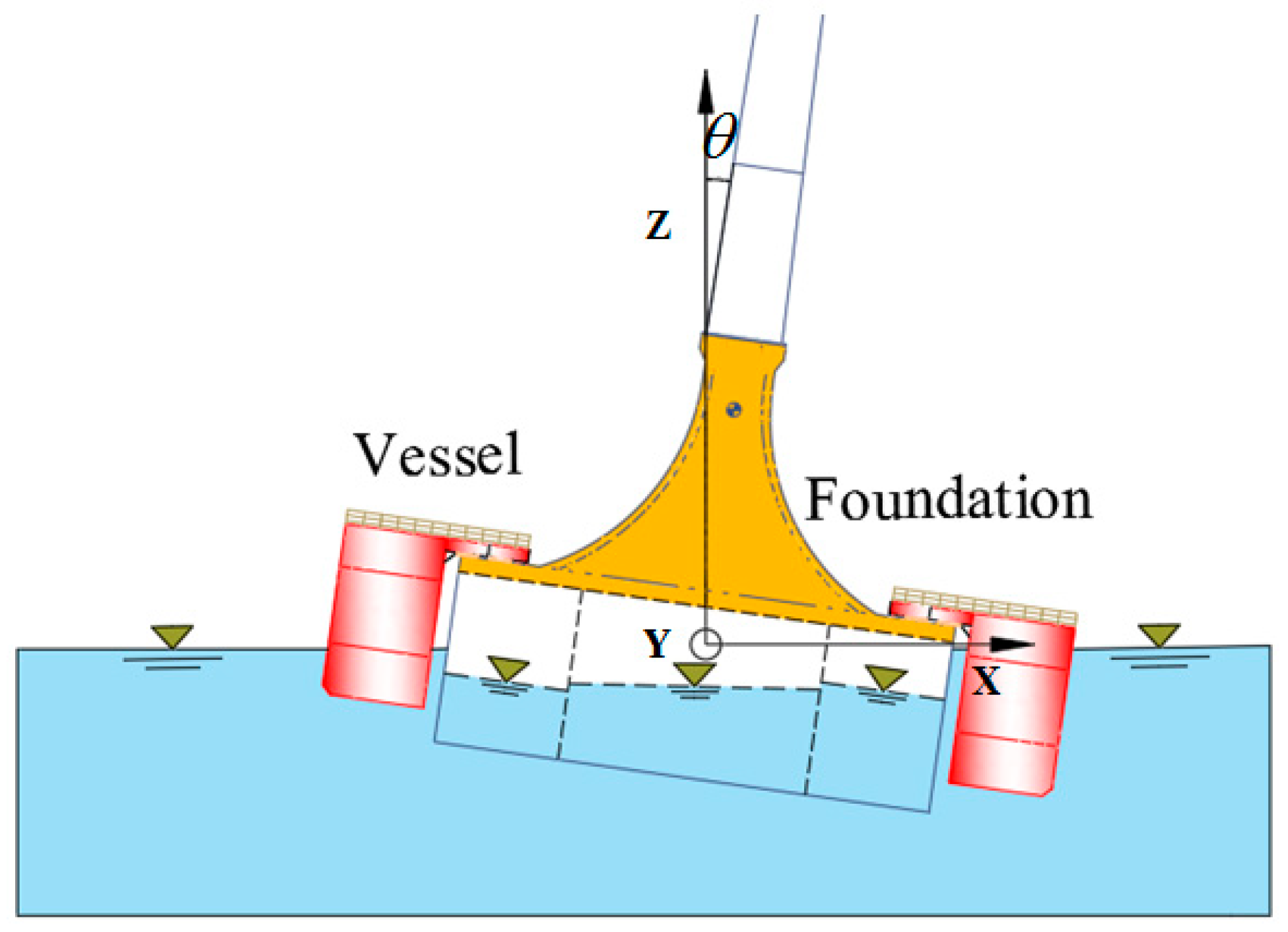
3.1.2. Rock Elastic Stiffness
3.2. Additional Water Correction Coefficient of the Coupling Floating System
3.2.1. Additional Water Correction Coefficient for Heaving
3.2.2. Additional Water Correction Coefficient for Rocking
3.3. The Motion Equation of the Coupling System during the Integrated Transportation Process
- Inertia force. Considering the influence of the additional water correction coefficient of the system, the inertial force at the i-th degree of freedom can be expressed as:where, is the additional water correction coefficient, and is the mass inertial force coefficient of the system.
- Damping force. It is generally considered to be proportional to the speed and can be expressed as:where, is generalized damping coefficient.
- Resilience. Considering the influence of air cushion inside the bucket foundation, its restoring force can be written as:where, is the stiffness coefficient of restoring force.
- Wave disturbance force. The wave disturbance force during the transportation process is related to the amplitude of the incident wave . The whole system can be simplified into a box-shaped floating body with a rectangular cross-section to calculate the wave force and moment. Thus, the wave force of the entire system can be obtained as:where, is the disturbance force generated by the unit incident wave, which is influenced by wavelength, wave direction, vessel shape and speed, and can be calculated by the slice method, and is the wave encounter frequency.
- Wind load. Due to the high height of the structure, the wind effect on the entire system should be considered during the transportation process. The wind load and wind moments of the coupling system are:where, is the air density, is the surface area of wind load, is the instantaneous wind speed, which can be simulated by the Davenport spectral model, is the wind pressure coefficient, is the wind chord angle, and is the arm of wind moments.
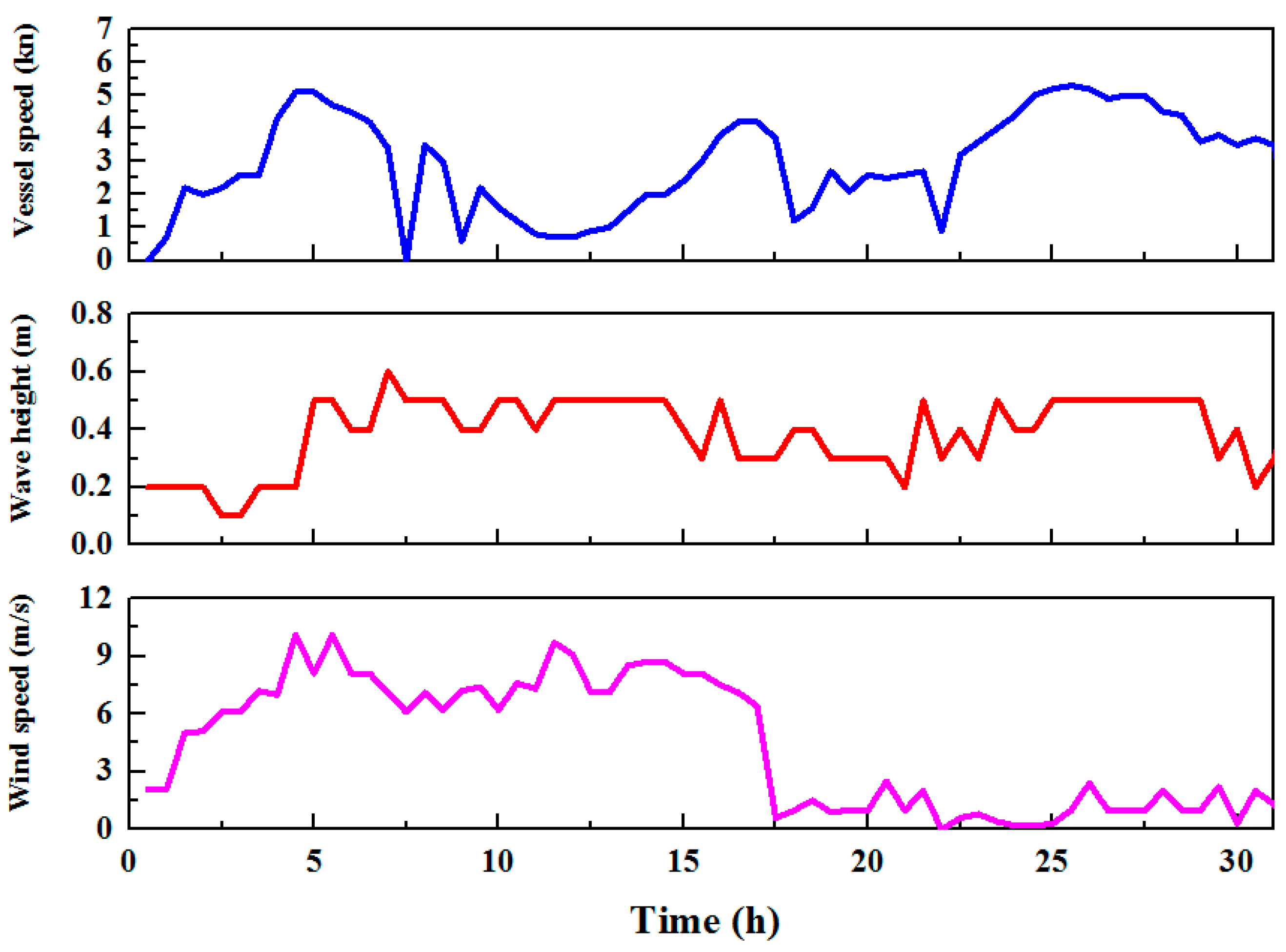
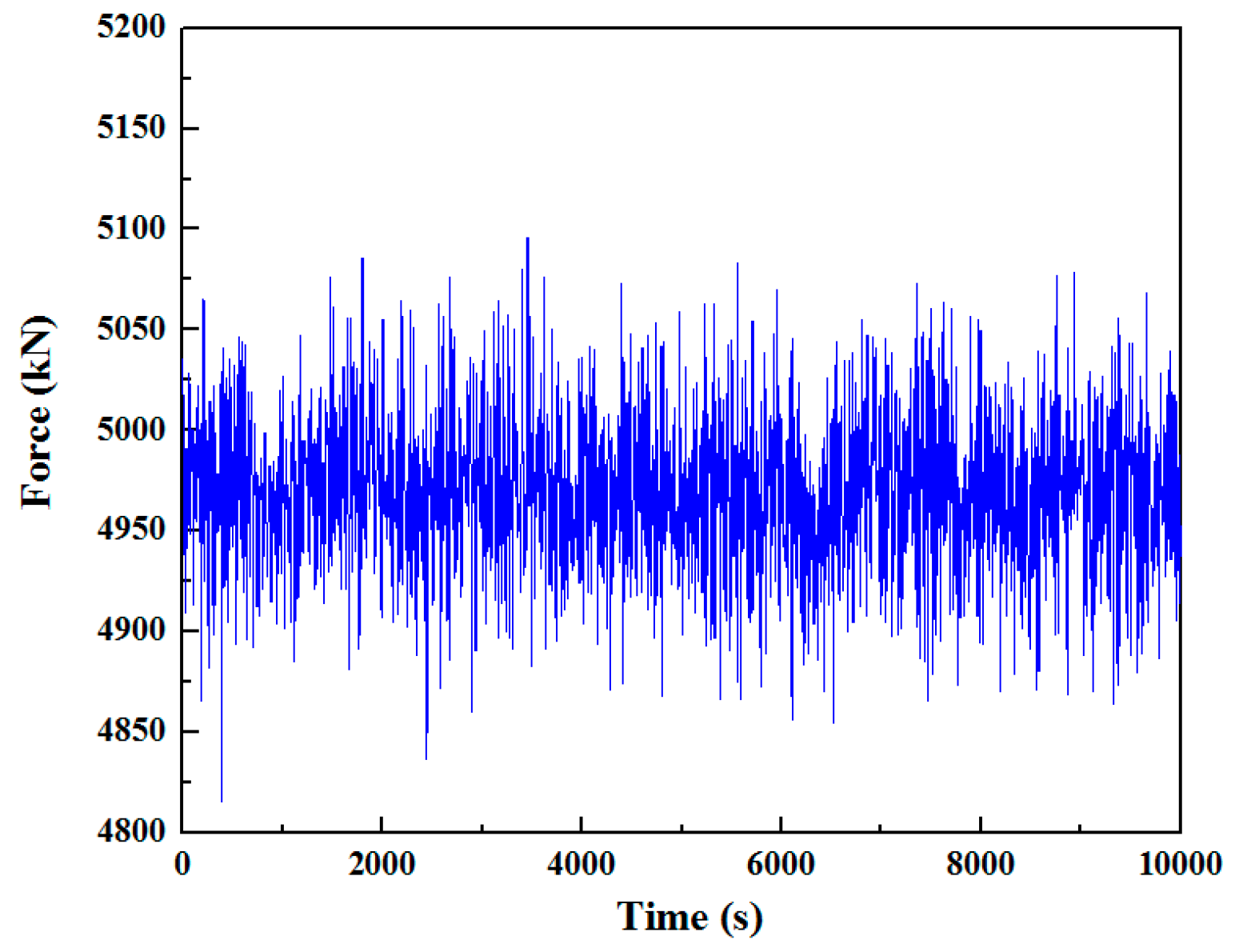
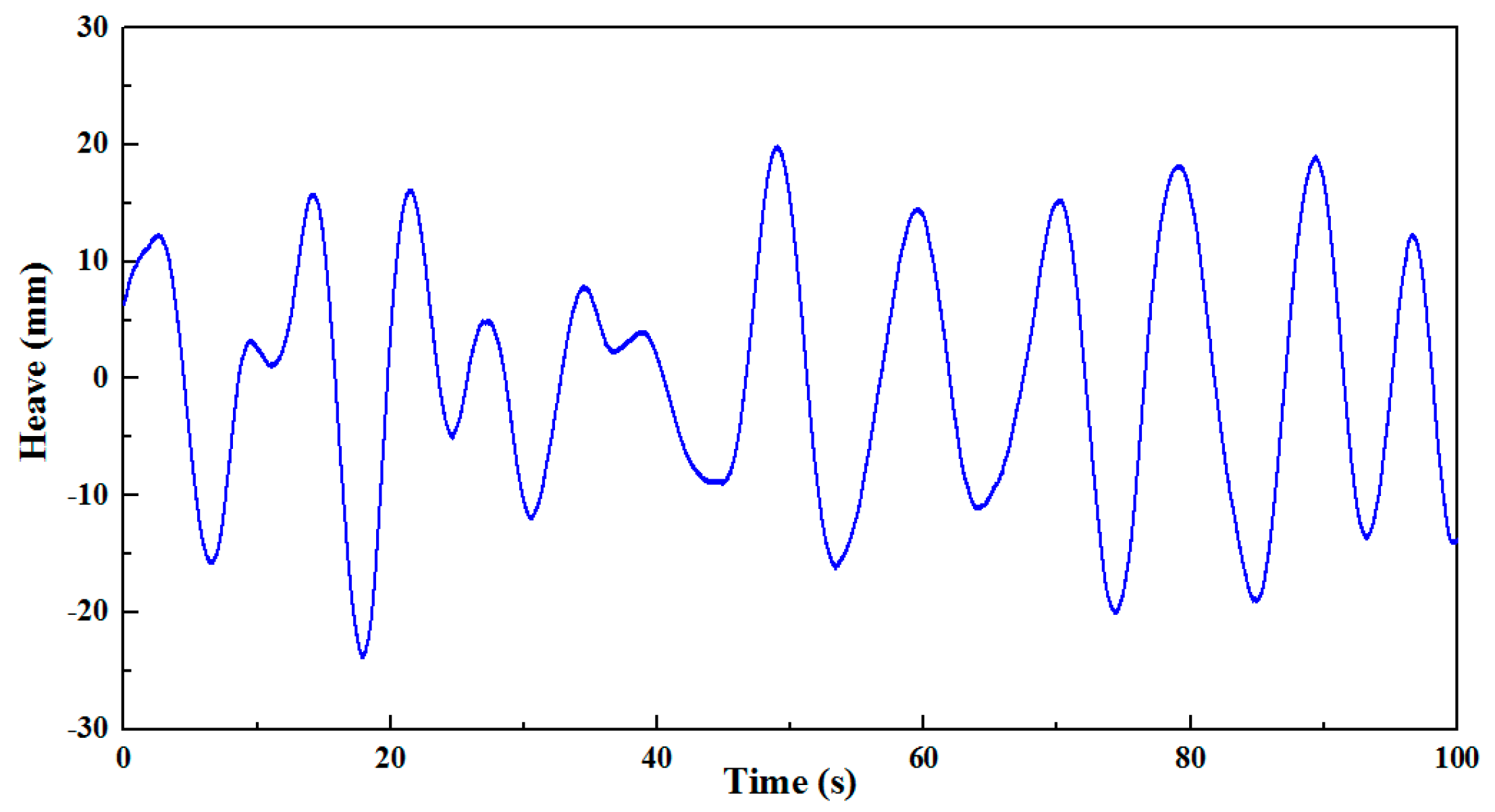
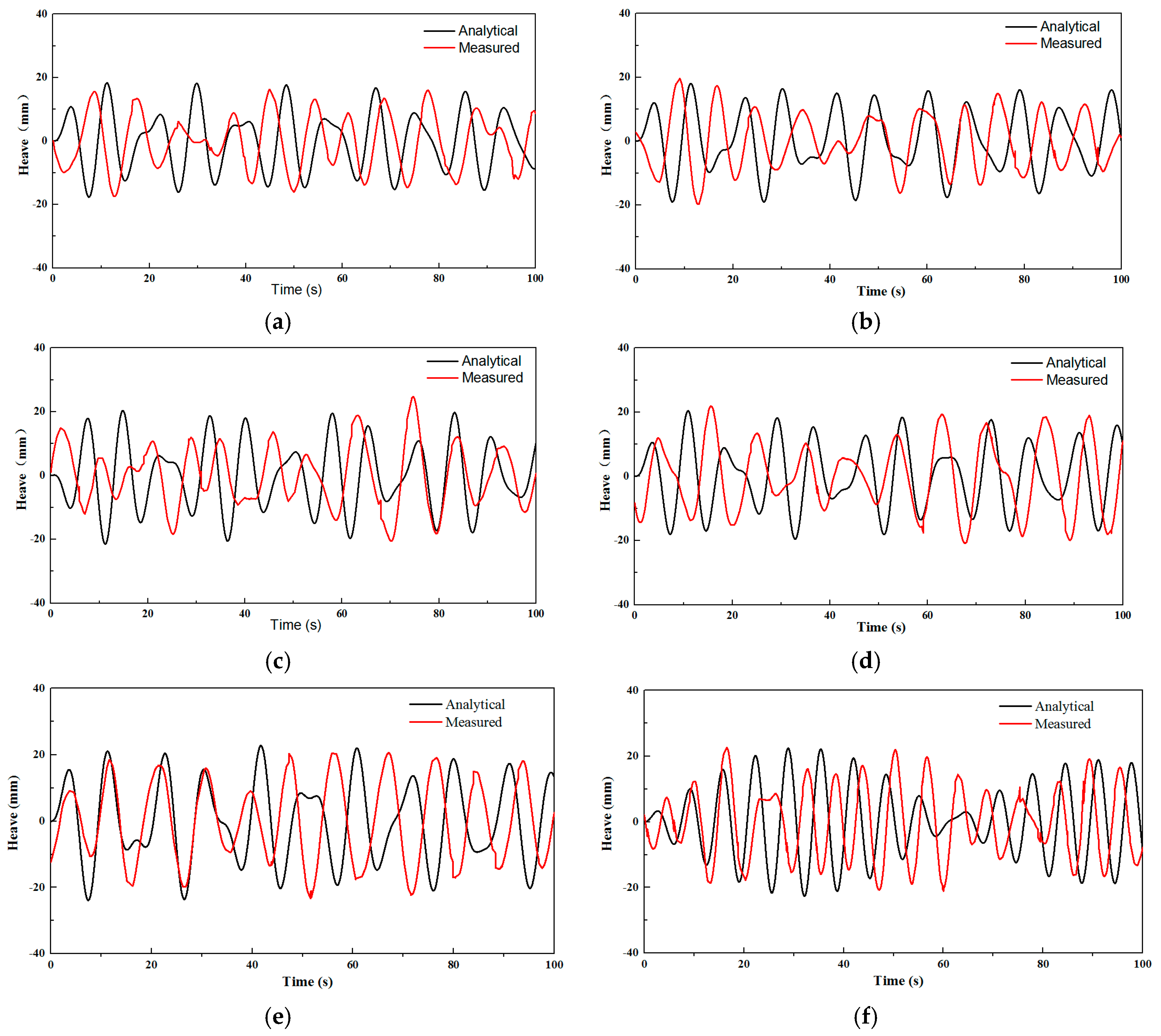
3.4. Verification of Analytical Motion Model Considering Regular Wave Effect
4. Factor Influence on the Motion of the Whole Transport System
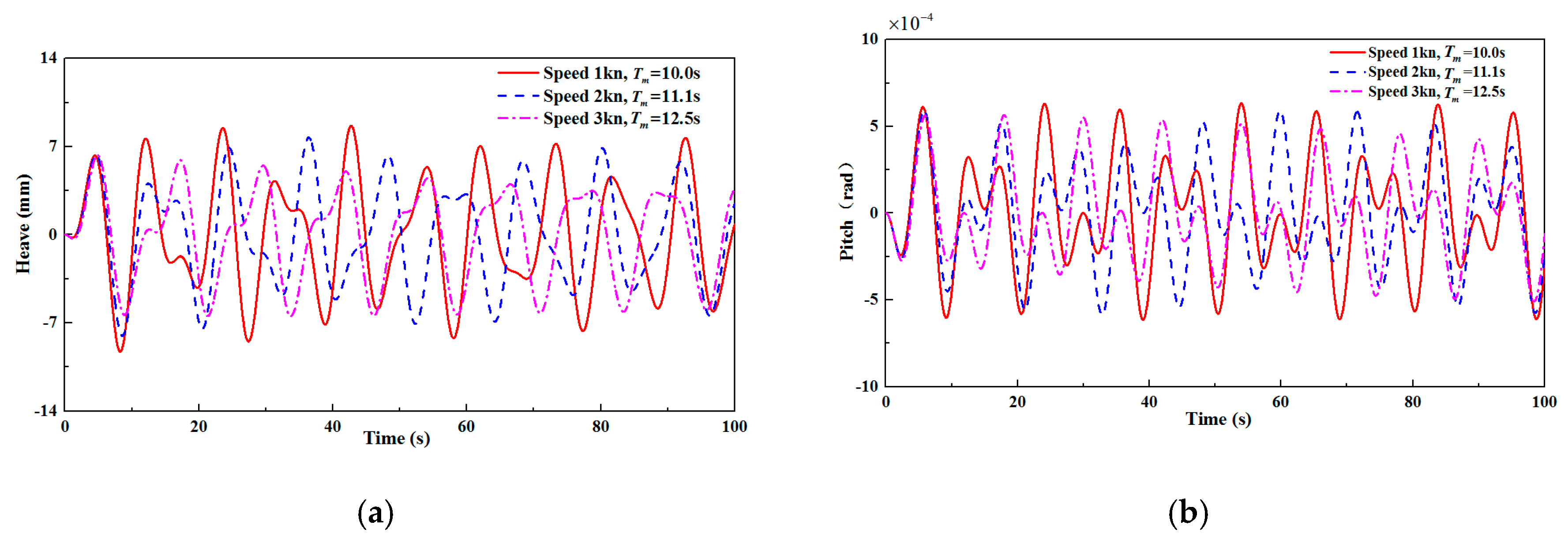
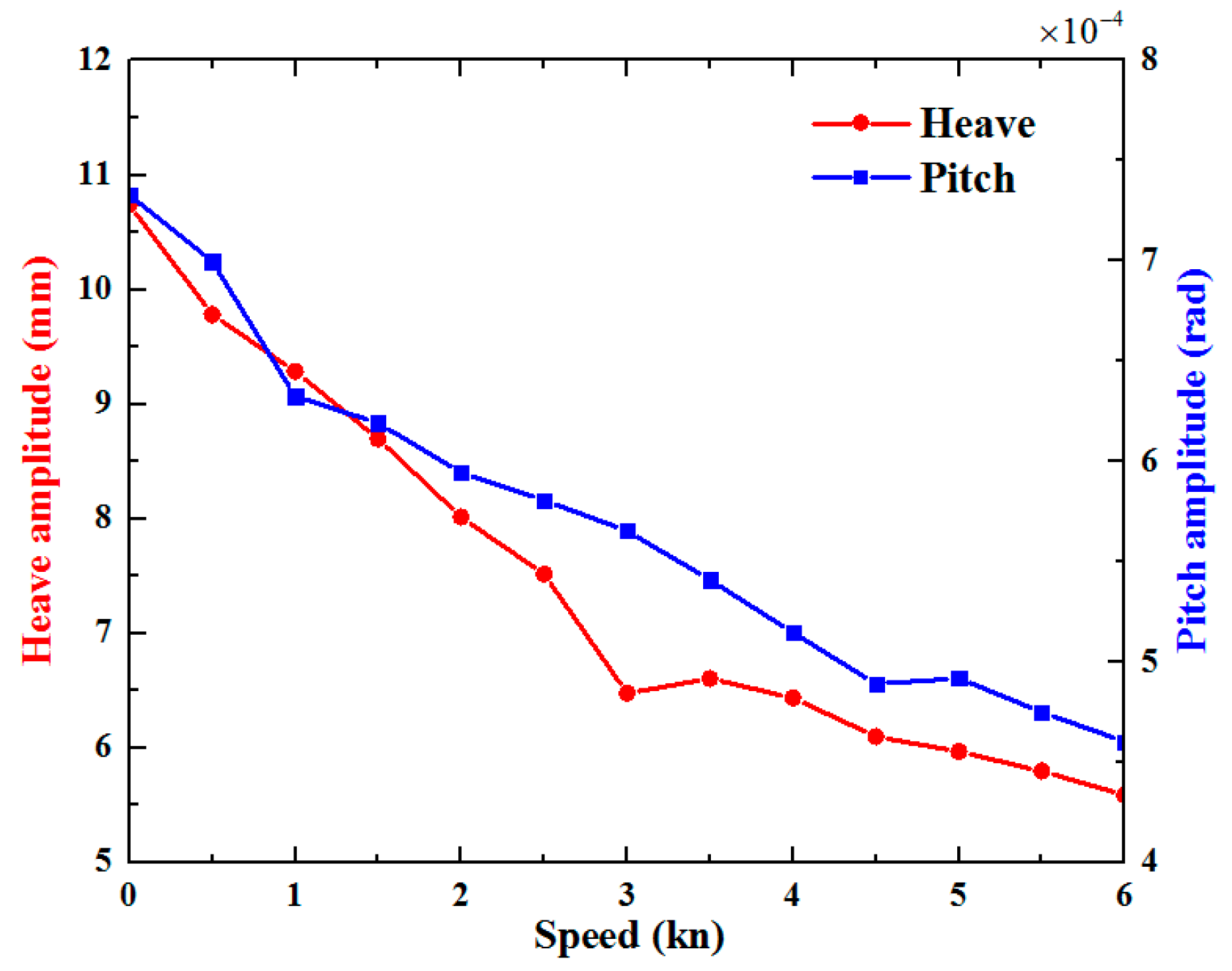
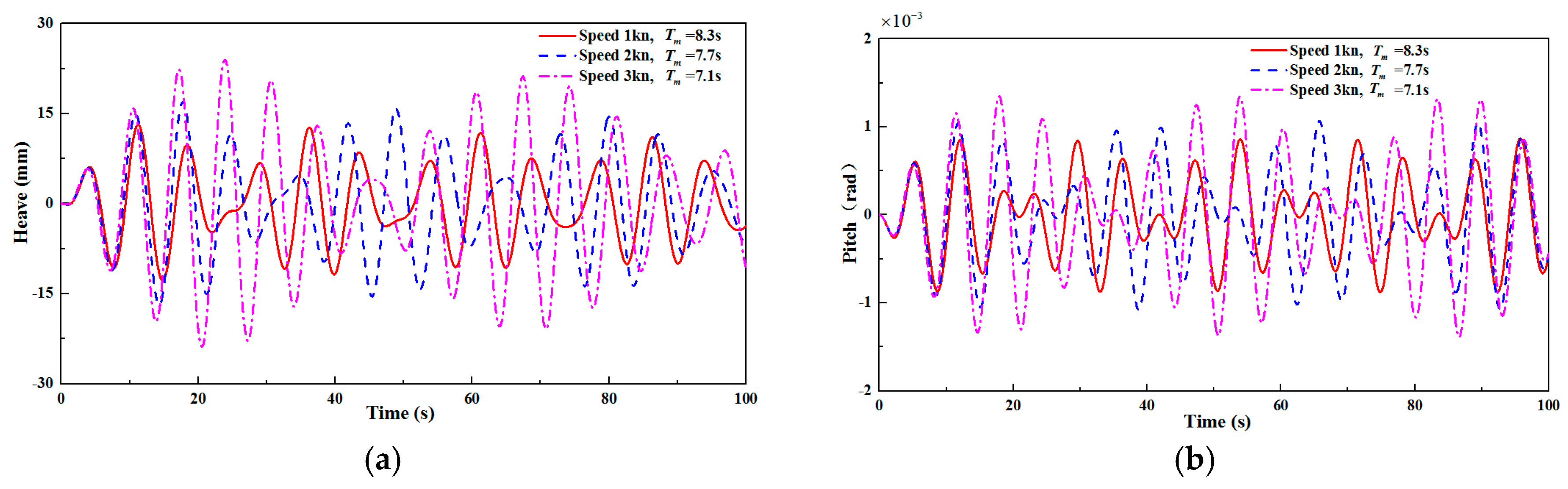
4.1. Vessel Speed Influence
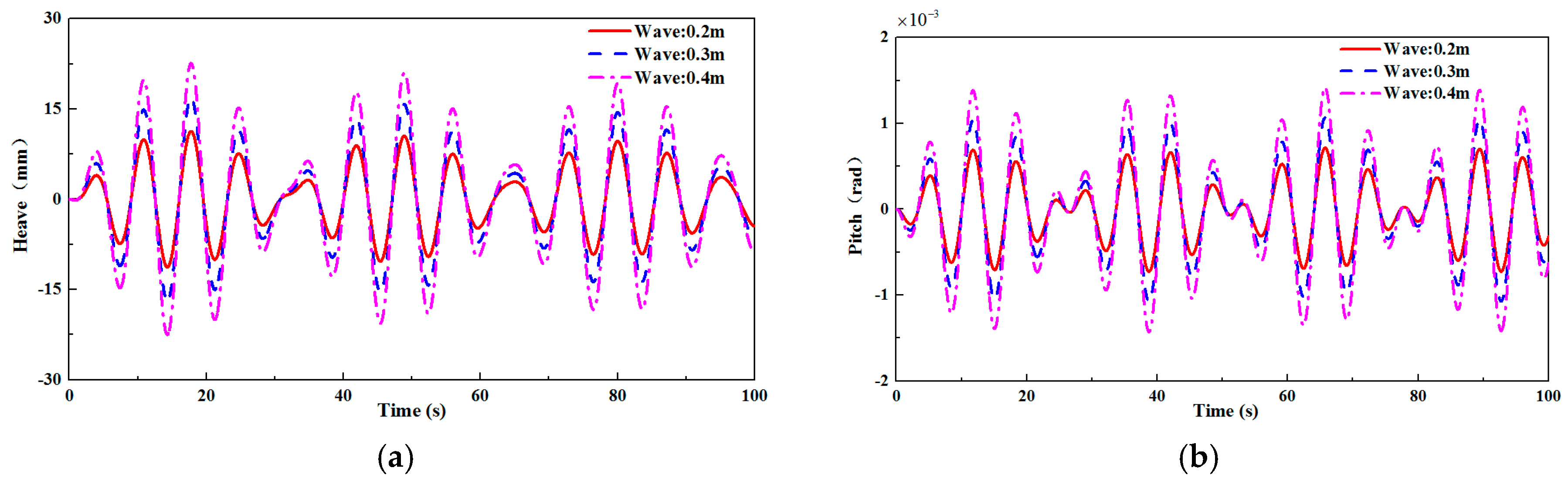
4.2. Wave Height Influence
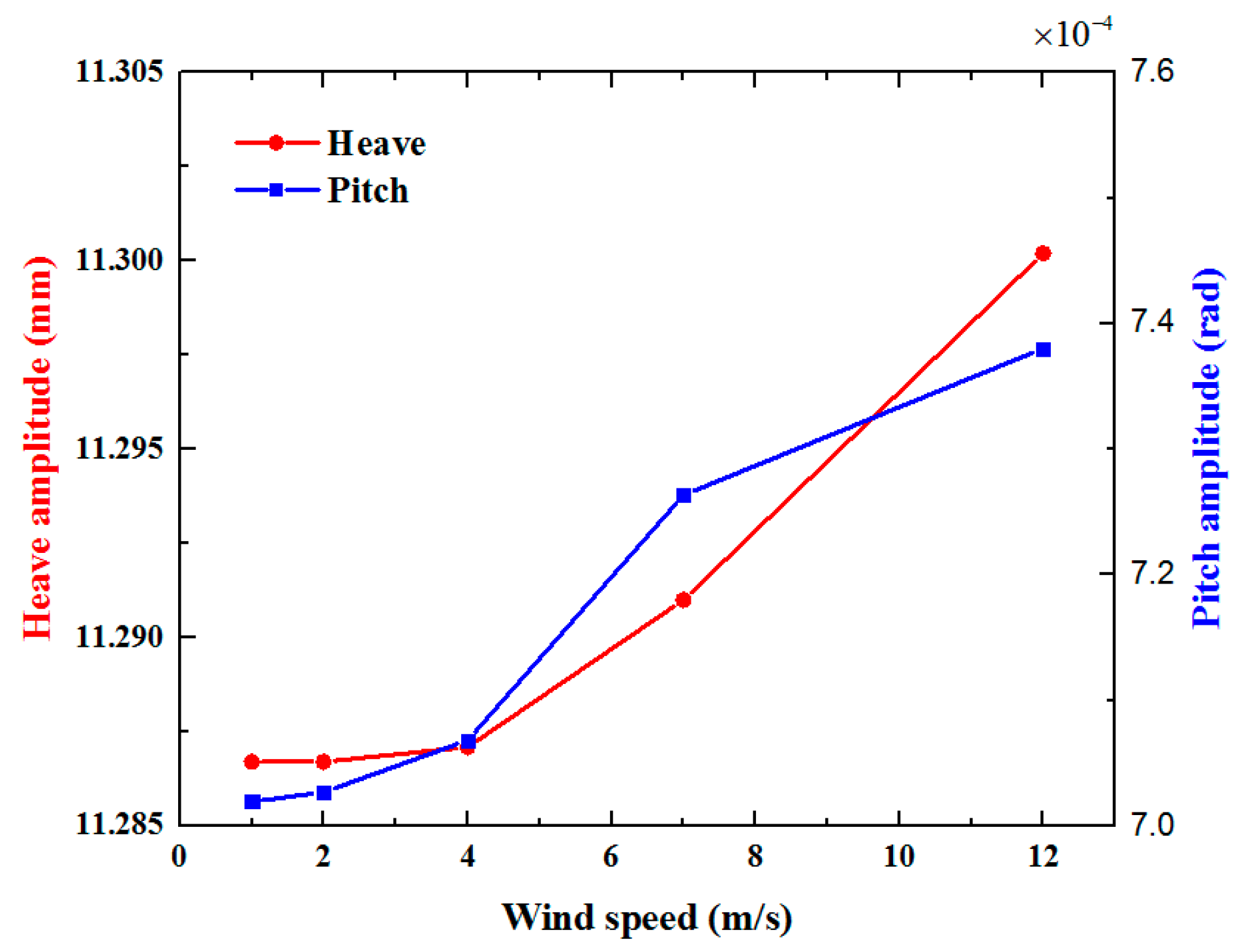
4.3. Wind Speed Influence
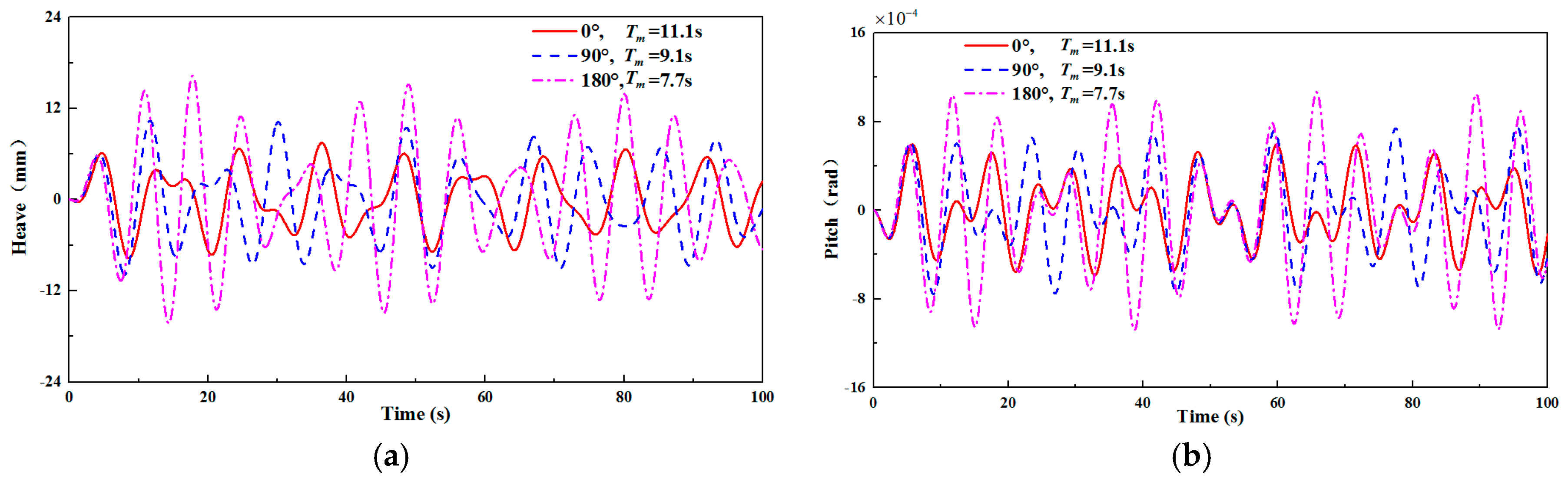
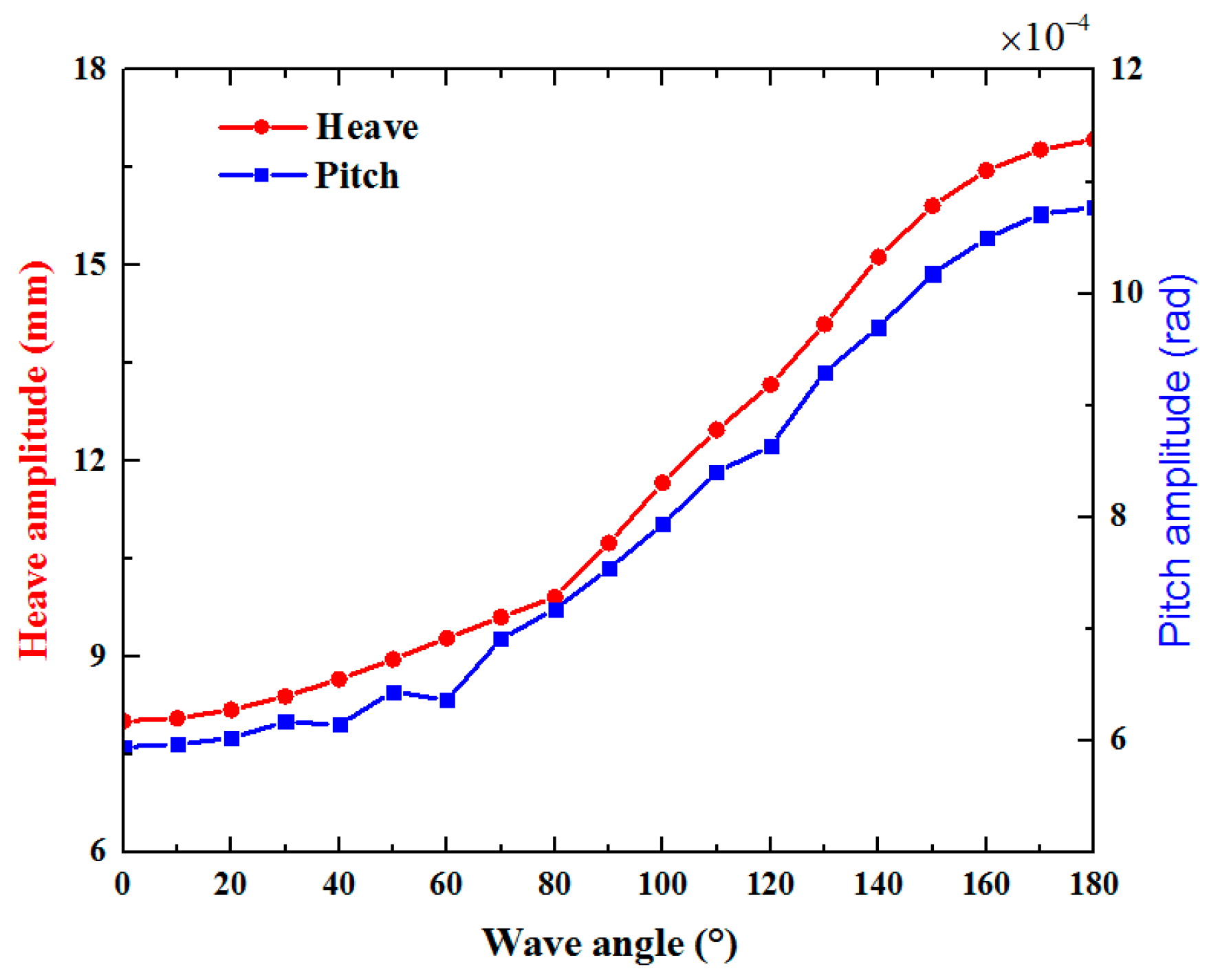
4.4. Wave Angle Influence
5. Factor Sensitivity Analysis
5.1. Grey Relational Analysis (GRA)
- Reference sequence definition
- 2.
- Range change of sequence
- 3.
- Grey relational coefficient and grade calculation
5.2. Results of Sensitivity Analysis
6. Conclusions
- (1)
- The proposed analytical model and motion equations were verified to have a good rationality compared with the measured data obtained from one field measurement on the integrated transportation process of the entire OWT structure. The average deviation of the response amplitude and RMS between measurements and analysis results are 5.21% and 6.08%.
- (2)
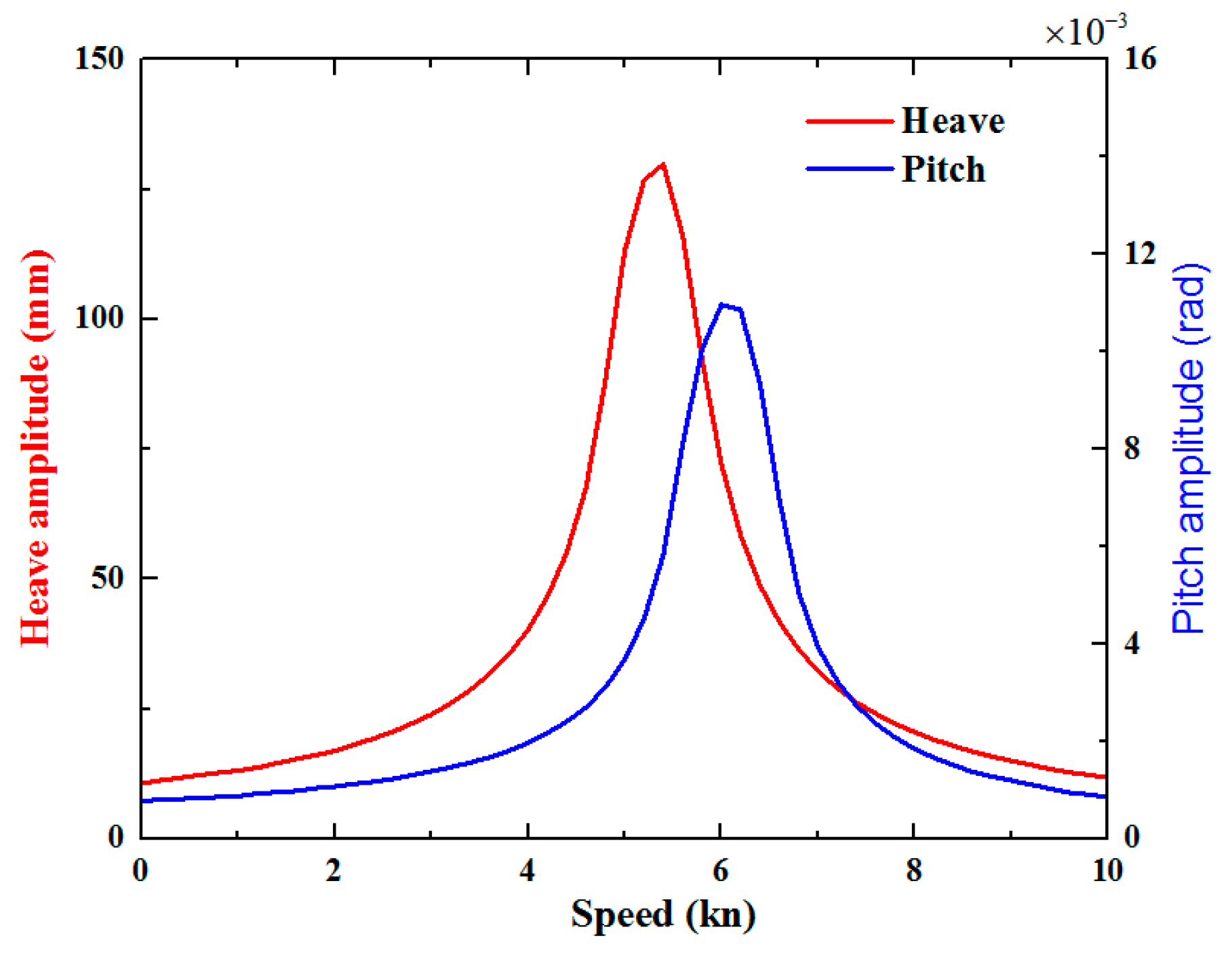
- In the case of sailing along the waves, the amplitudes of the heave and pitch motion responses of the entire system decrease as the vessel speed increases, while the response period increases. On the contrary, in the case of the top wave sailing, the amplitudes of the heave and pitch responses have obvious increasing tends with the increase of the vessel speed, while the response period decreases. In addition, there is a risk of harmonic resonance motion in the entire system at high vessel speeds. Therefore, the vessel speed should be reasonably controlled, and the vessel should consider sailing along the waves, to avoid the occurrence of the harmonic resonance phenomenon.
- (3)
- The analytical motion model was derived based on regular waves and was suitable for shallow water area with small wave height. As the wave height increases, the amplitudes of the pitch and heave response of the entire system also increase. Although the heave and pitch motion responses increase with the increase of wind speed, the wind speed has less influence on the response of the entire system than other factors such as vessel speed and wave height. Moreover, with the increase of the wave angle, the heave and pitch motion response also shows an increasing trend, while the response period decreases. Therefore, the sea condition with smaller wave height is suitable for the integrated transportation.
- (4)
- The sensitivity of the main factors (vessel speed , wave height , and wave angle ) affecting the heave and pitch motion responses was discussed by gray relational analysis method. The results show that the wave height has the greatest influence on the motion, and the sensitivity of each factor is ranked as: wave height > vessel speed > wave angle.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OWT | offshore wind turbine |
| MSL | mean sea level |
| RMS | root mean square |
References
- Global Wind Energy Council (GWEC). Global Wind Report; GWEC: Brussels, Belgium, 2018. [Google Scholar]
- Wang, Y.; Bai, Y. Investigation on installation of offshore wind turbines. J. Mar. Sci. Appl. 2010, 9, 175–180. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Han, Y.; Ding, H.; Zhang, S. Field experiments on wet tows of an integrated transportation and installation vessel with two bucket foundations for offshore wind turbines. Ocean Eng. 2015, 108, 769–777. [Google Scholar] [CrossRef]
- Lian, J.J.; Chen, F.; Wang, H.J. Laboratory tests on soil–skirt interaction and penetration resistance of suction caissons during installation in sand. Ocean Eng. 2014, 84, 1–13. [Google Scholar] [CrossRef]
- Le, C.H.; Ding, H.Y.; Zhang, P.Y. Air-floating towing behaviors of multi-bucket foundation platform. China Ocean Eng. 2013, 27, 645–658. [Google Scholar] [CrossRef]
- Ding, H.Y.; Lian, J.; Li, A.; Zhang, P. One-step-installation of offshore wind turbine on large-scale bucket-top-bearing bucket foundation. Trans. Tianjin Univ. 2013, 3, 188–194. [Google Scholar] [CrossRef]
- Ding, H.Y.; Zhang, P.Y.; Le, C.H.; Liu, X. Construction and installation technique of large-scale top-bearing bucket foundation for offshore wind turbine. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 7234–7237. [Google Scholar]
- Zhang, P.Y.; Ding, H.Y. Towing characteristics of large-scale composite bucket foundation for offshore wind turbines. J. Southeast Univ. 2013, 29, 300–304. [Google Scholar]
- Zhang, P.Y.; Ding, H.Y.; Le, C.H. Hydrodynamic motion of a large prestressed concrete bucket foundation for offshore wind turbines. J. Renew. Sustain. Energy 2013, 5, 477–488. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Ding, H.Y.; Le, C.H.; Huang, X. Motion analysis on integrated transportation technique for offshore wind turbines. J. Renew. Sustain. Energy 2013, 5, 1567–1578. [Google Scholar] [CrossRef]
- Huang, X. Floating Analysis of Integrated Installation Technology with Offshore Wind-Power Structure. Master’s Thesis, Tianjin University, Tianjin, China, 2012. (In Chinese). [Google Scholar]
- Liu, X.Q. Study on Stability and Dynamic Response in Towing of Air-floating Bucket Foundation. Ph.D. Thesis, Tianjin University, Tianjin, China, 2012. (In Chinese). [Google Scholar]
- Sheng, Z.B.; Liu, Y.Z. Principle of Ship, 1st ed.; Shanghai Jiao Tong University Press: Shanghai, China, 2004. (In Chinese) [Google Scholar]
- Wu, X.H.; Zhang, L.W.; Wang, R.K. Ship Maneuverability and Seakeeping, 2nd ed.; China Communications Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Shen, D.H.; Du, J.C. Application of gray relational analysis to evaluate HMA with reclaimed building materials. J. Mater. Civ. Eng. 2005, 17, 400–406. [Google Scholar] [CrossRef]
- Morán, J.; Granada, E.; Míguez, J.L.; Porteiro, J. Use of grey relational analysis to assess and optimize small biomass boilers. Fuel Process. Technol. 2006, 87, 123–127. [Google Scholar] [CrossRef]
- Kuo, Y.; Yang, T.; Huang, G.W. The use of grey relational analysis in solving multiple attribute decision-making problems. Comput. Ind. Eng. 2008, 55, 80–93. [Google Scholar] [CrossRef]



| Vessel Property | Values | Wind Turbine Property | Values |
|---|---|---|---|
| Length | 103.2 m | Tower mass | 207.0 t |
| Molded depth | 9.0 m | Rotor-nacelle mass | 196.0 t |
| Molded breadth | 51.6 m | Tower height | 78.5 m |
| Designed draft | 6.0 m | Hub height | 90.0 m |
| Deck load | 20.0 t/m2 | Tower wall thickness | 48.0~22.0 mm |
| Tower diameter base, top | 4.3~3.2 m | ||
| Rotor diameter | 120.0 m |
| Conditions | Speed (kn) | Wave Height (m) | Wind Speed (m/s) | Wave Angle (°) |
|---|---|---|---|---|
| Condition 1 | 5.0 | 0.2 | 1.0 | 0 |
| Condition 2 | 5.3 | 0.3 | 1.0 | 0 |
| Condition 3 | 3.5 | 0.4 | 1.3 | 0 |
| Condition 4 | 4.4 | 0.3 | 1.0 | 0 |
| Condition 5 | 5.5 | 0.6 | 1.3 | 0 |
| Condition 6 | 0.9 | 0.5 | 7.1 | 0 |
| Conditions | Analytical Amplitude (mm) | Measured Amplitude (mm) | Amplitude Deviation (%) | Analytical RMS (mm) | Measured RMS (mm) | RMS Deviation (%) |
|---|---|---|---|---|---|---|
| Condition 1 | 18.321 | 17.451 | 4.99 | 9.128 | 8.550 | 6.76 |
| Condition 2 | 19.013 | 19.768 | 3.82 | 9.611 | 8.572 | 12.12 |
| Condition 3 | 21.504 | 24.725 | 13.03 | 10.376 | 9.467 | 9.60 |
| Condition 4 | 20.382 | 21.895 | 6.91 | 10.000 | 10.598 | 5.64 |
| Condition 5 | 23.872 | 23.343 | 2.23 | 12.004 | 12.061 | 0.47 |
| Condition 6 | 22.645 | 22.712 | 0.29 | 11.010 | 10.804 | 1.91 |
| Conditions | Analytical (Hz) | Measured (Hz) | Deviation (%) |
|---|---|---|---|
| Condition 1 | 0.1087 | 0.1300 | 16.38 |
| Condition 2 | 0.1049 | 0.1200 | 12.58 |
| Condition 3 | 0.1179 | 0.1100 | 7.18 |
| Condition 4 | 0.1134 | 0.1000 | 13.40 |
| Condition 5 | 0.1022 | 0.1100 | 7.09 |
| Condition 6 | 0.1445 | 0.1500 | 3.67 |
| Factors | Wave Height (m) | Wave Period (s) | Wind Speed (m/s) | Wave Angle (°) |
|---|---|---|---|---|
| Value | 0.3 | 9.05 | 7 | 0 |
| Factors | Vessel Speed (kn) | Wave Period (s) | Wind Speed (m/s) | Wave Angle (°) |
|---|---|---|---|---|
| Value | 2 | 9.05 | 7 | 180 |
| Factors | Vessel Speed (kn) | Wave Period (s) | Wave Height (m) | Wave Angle (°) |
|---|---|---|---|---|
| Value | 2 | 9.05 | 0.2 | 180 |
| Factors | Vessel Speed (kn) | Wave Period (s) | Wave Height (m) | Wind Speed (m/s) |
|---|---|---|---|---|
| Value | 2 | 9.05 | 0.3 | 7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, J.; Jiang, J.; Dong, X.; Wang, H.; Zhou, H.; Wang, P. Coupled Motion Characteristics of Offshore Wind Turbines during the Integrated Transportation Process. Energies 2019, 12, 2023. https://doi.org/10.3390/en12102023
Lian J, Jiang J, Dong X, Wang H, Zhou H, Wang P. Coupled Motion Characteristics of Offshore Wind Turbines during the Integrated Transportation Process. Energies. 2019; 12(10):2023. https://doi.org/10.3390/en12102023
Chicago/Turabian StyleLian, Jijian, Junni Jiang, Xiaofeng Dong, Haijun Wang, Huan Zhou, and Pengwen Wang. 2019. "Coupled Motion Characteristics of Offshore Wind Turbines during the Integrated Transportation Process" Energies 12, no. 10: 2023. https://doi.org/10.3390/en12102023
APA StyleLian, J., Jiang, J., Dong, X., Wang, H., Zhou, H., & Wang, P. (2019). Coupled Motion Characteristics of Offshore Wind Turbines during the Integrated Transportation Process. Energies, 12(10), 2023. https://doi.org/10.3390/en12102023





