Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires
Abstract
:1. Introduction
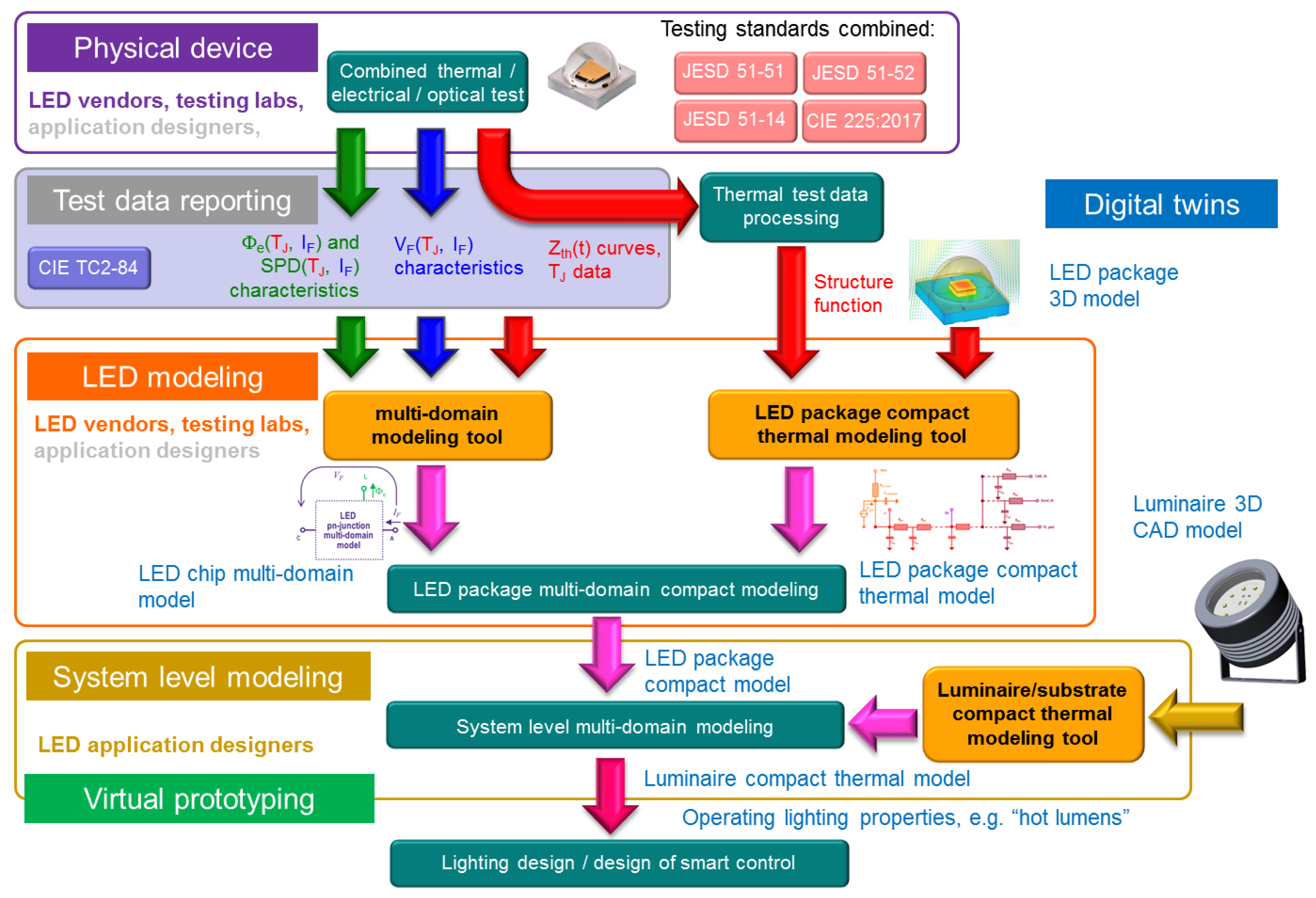
1.1. The Context of this Work
1.2. The Wider Background
1.3. Overall Considerations Regarding Multi-Domain Chip Level Modelling of LEDs Aimed at Use in Industrial Application Design Flows
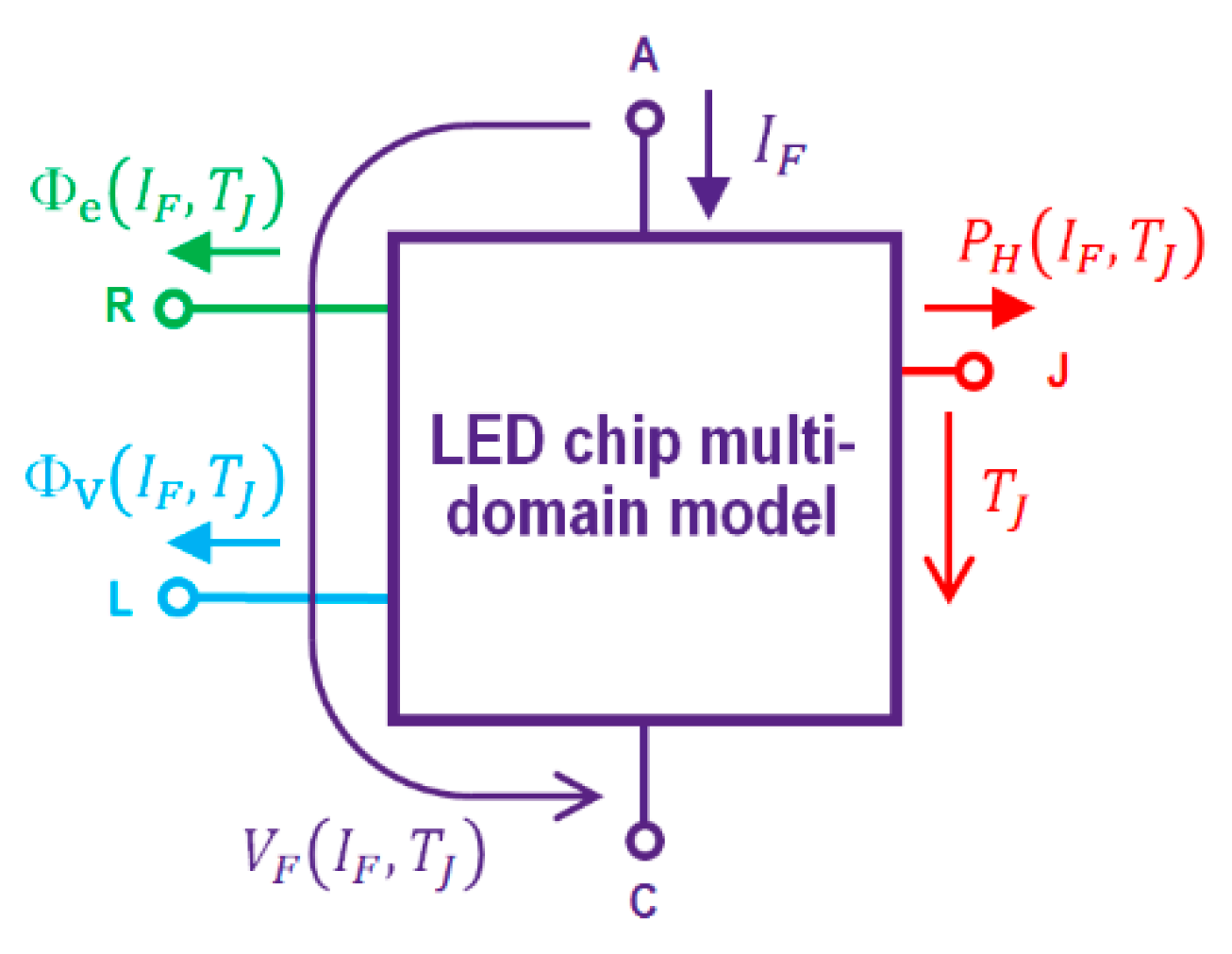
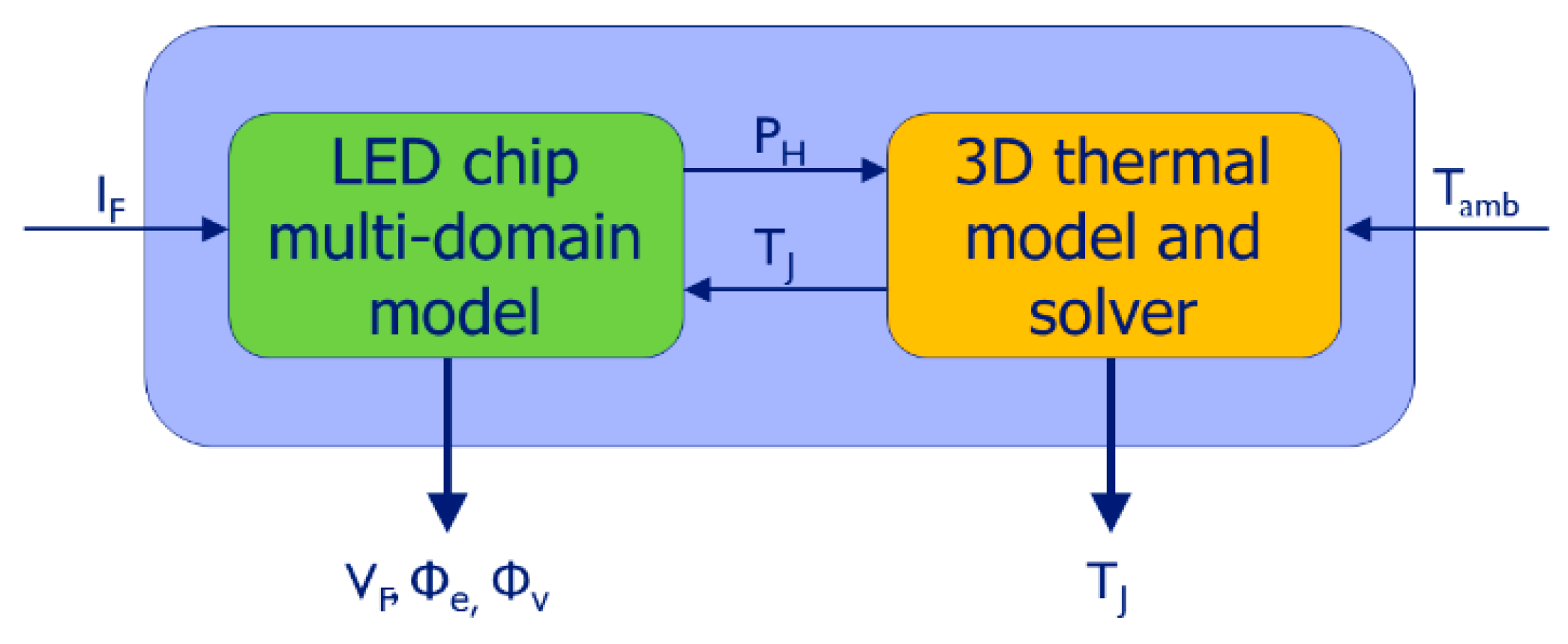
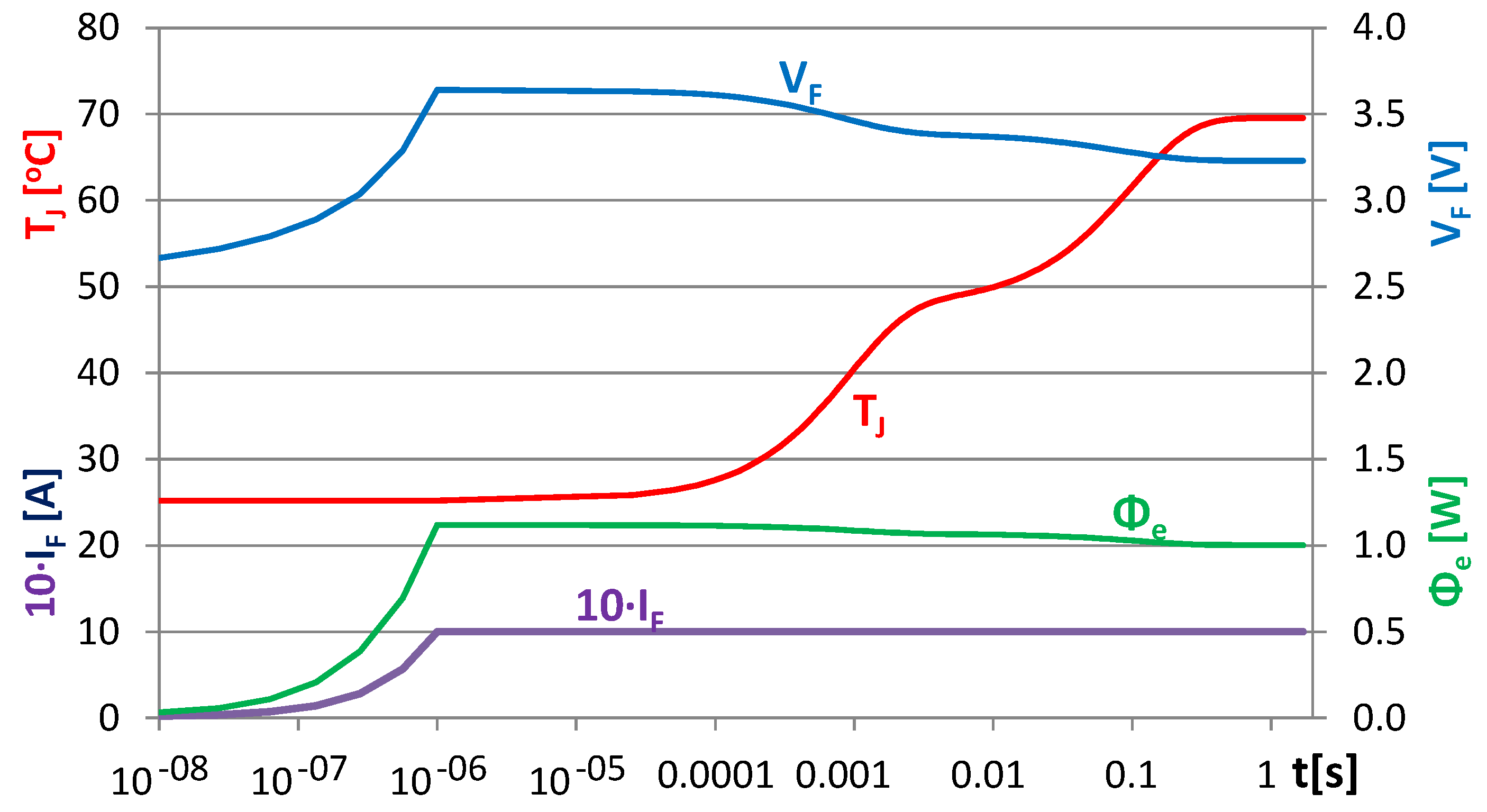
1.4. Expectations for a Chip Level Multi-Domain LED Model
- The heat-flux (also known as the real heating power, leaving the device through the thermal junction node denoted by J.
- The total emitted radiant flux, [36] (also known as the optical power, ), leaving the device through the optical port of the model denoted by R.
- The total emitted luminous flux, [12], leaving the device through the optical port of the model denoted by L.
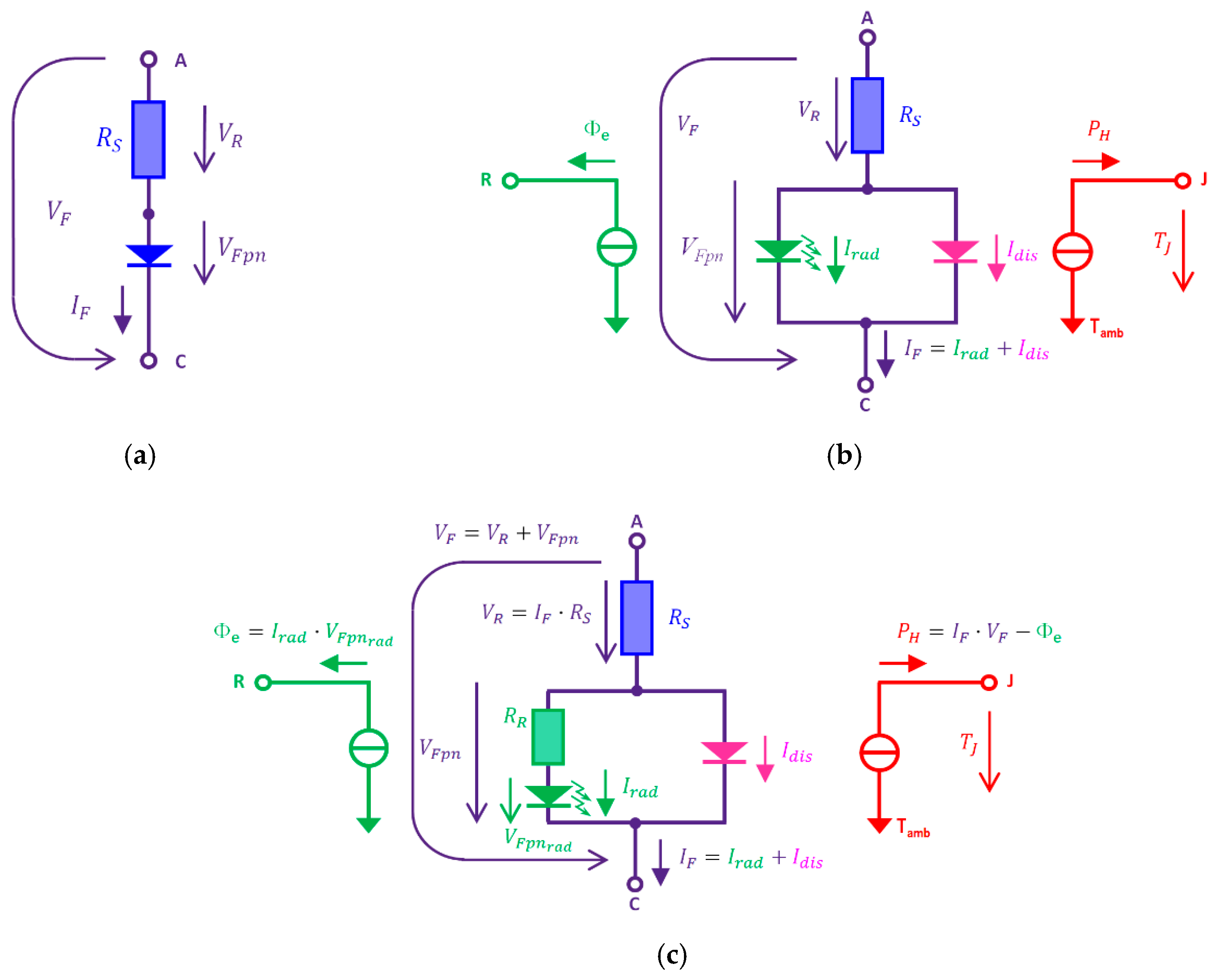
2. The Starting Point: Basic Spice Model
3. An Analytical, Quasi Black-Box Multi-Domain Model of an LED Chip
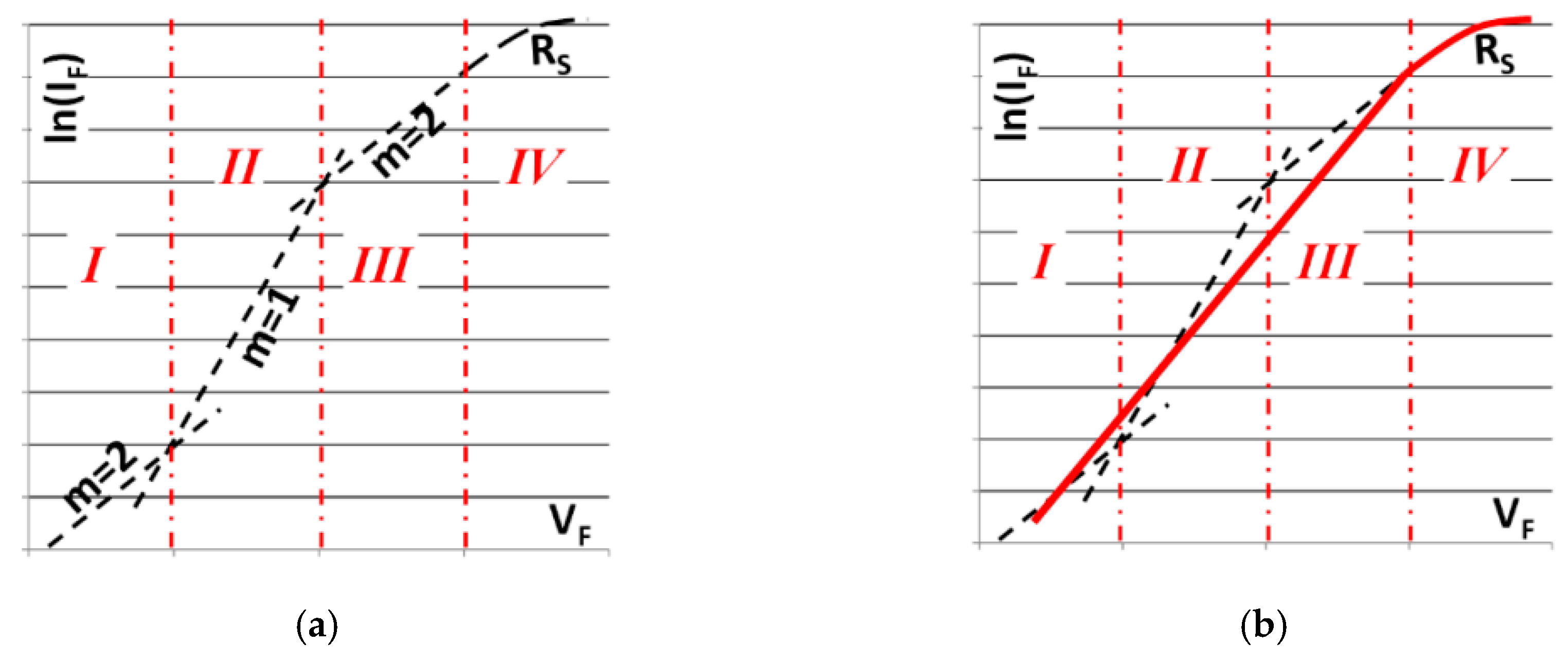
3.1. The Basic Concept: Splitting the Total Forward Current into Two Components
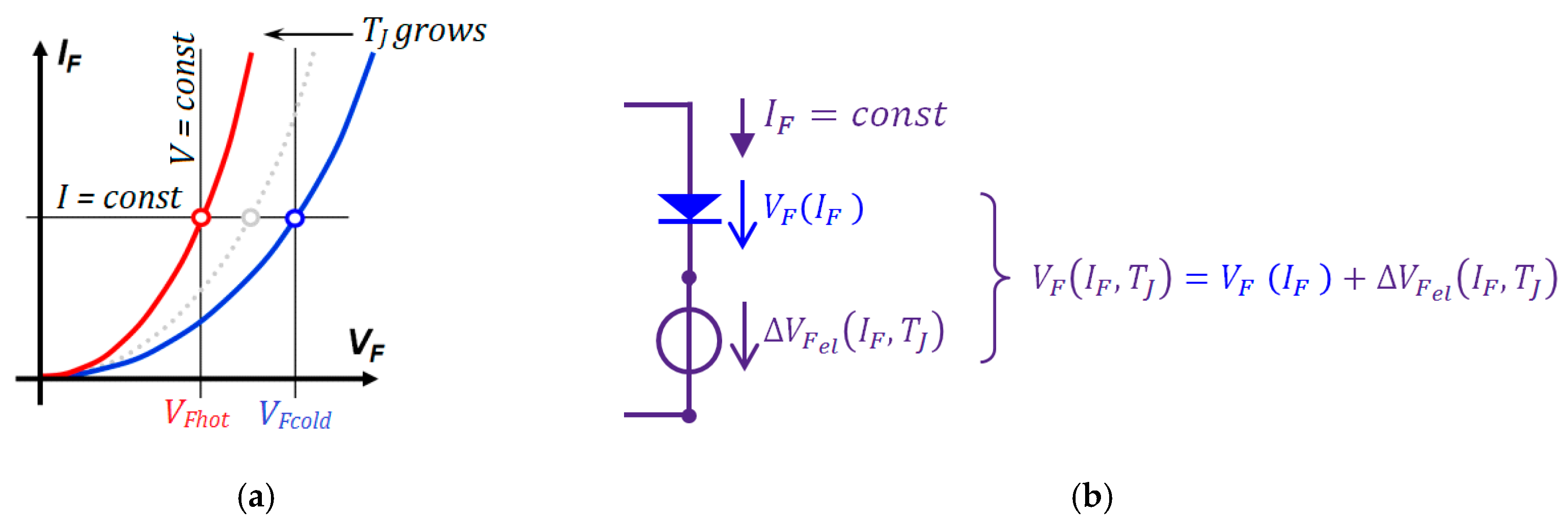
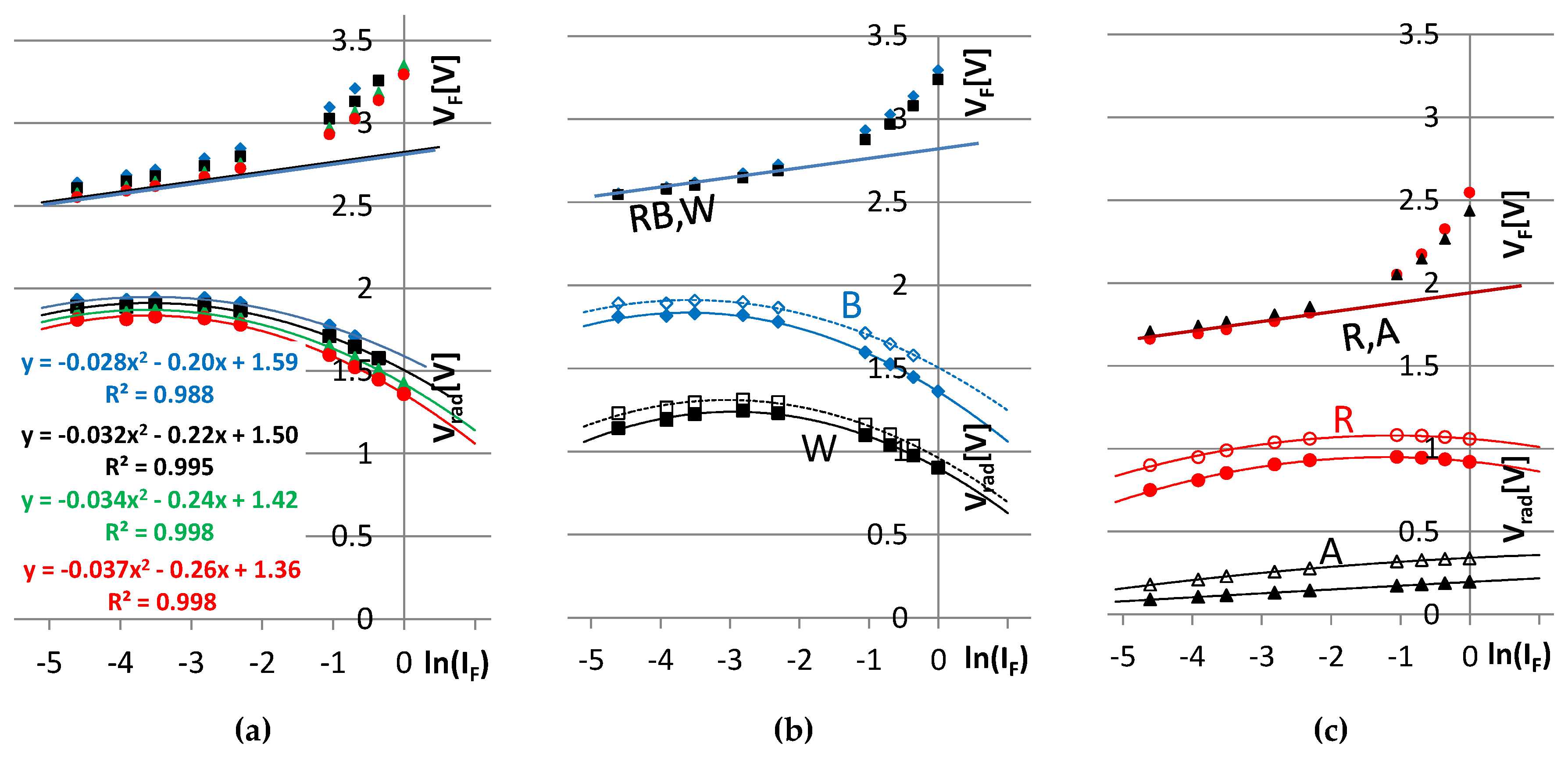
3.2. Model Equations at a Fixed Reference Temperature, , in the Current Driven Mode
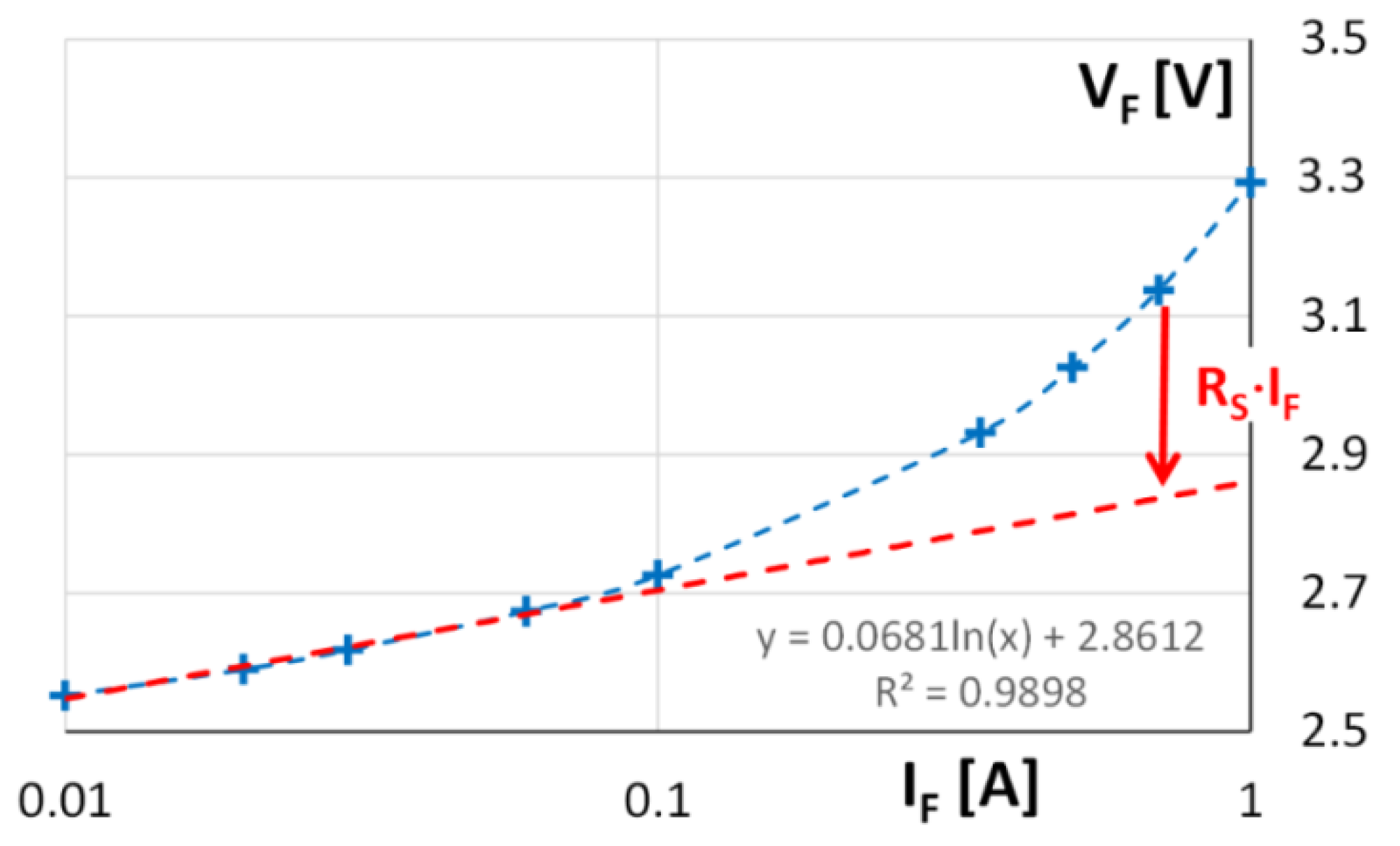
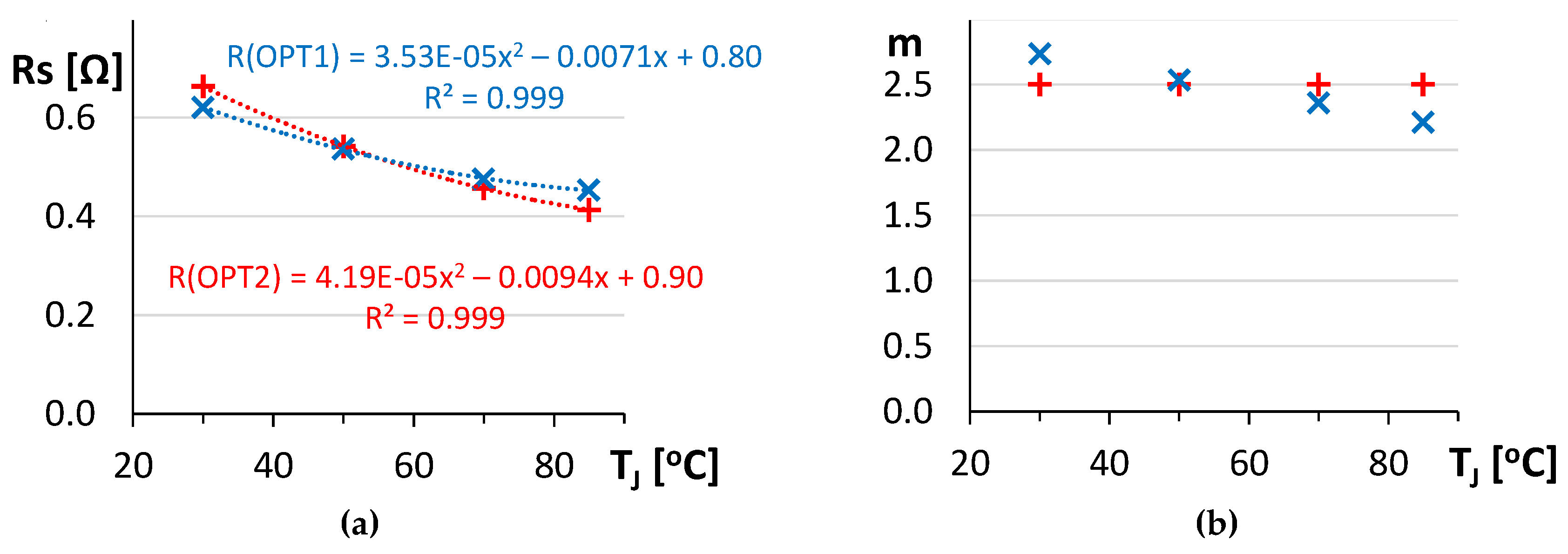
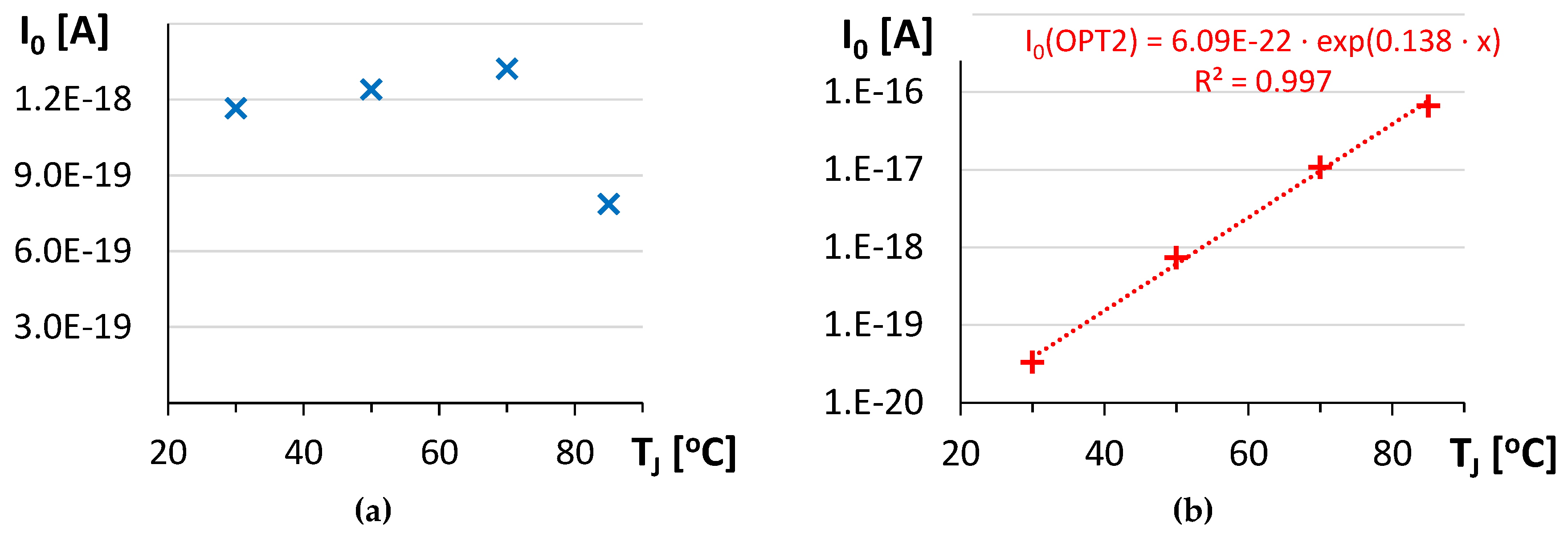
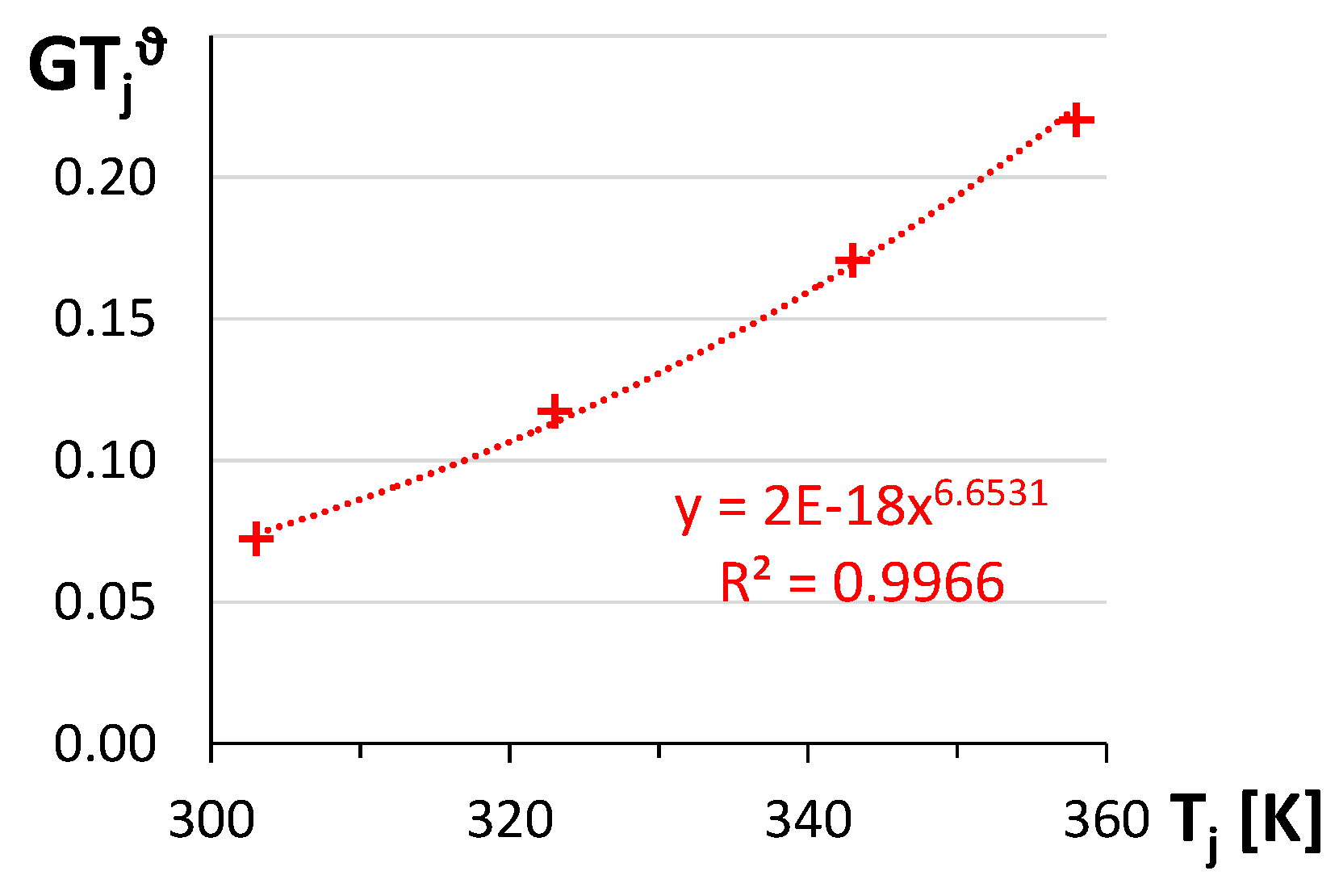
3.3. Implementation of the Temperature Dependence of the LED Chip Model
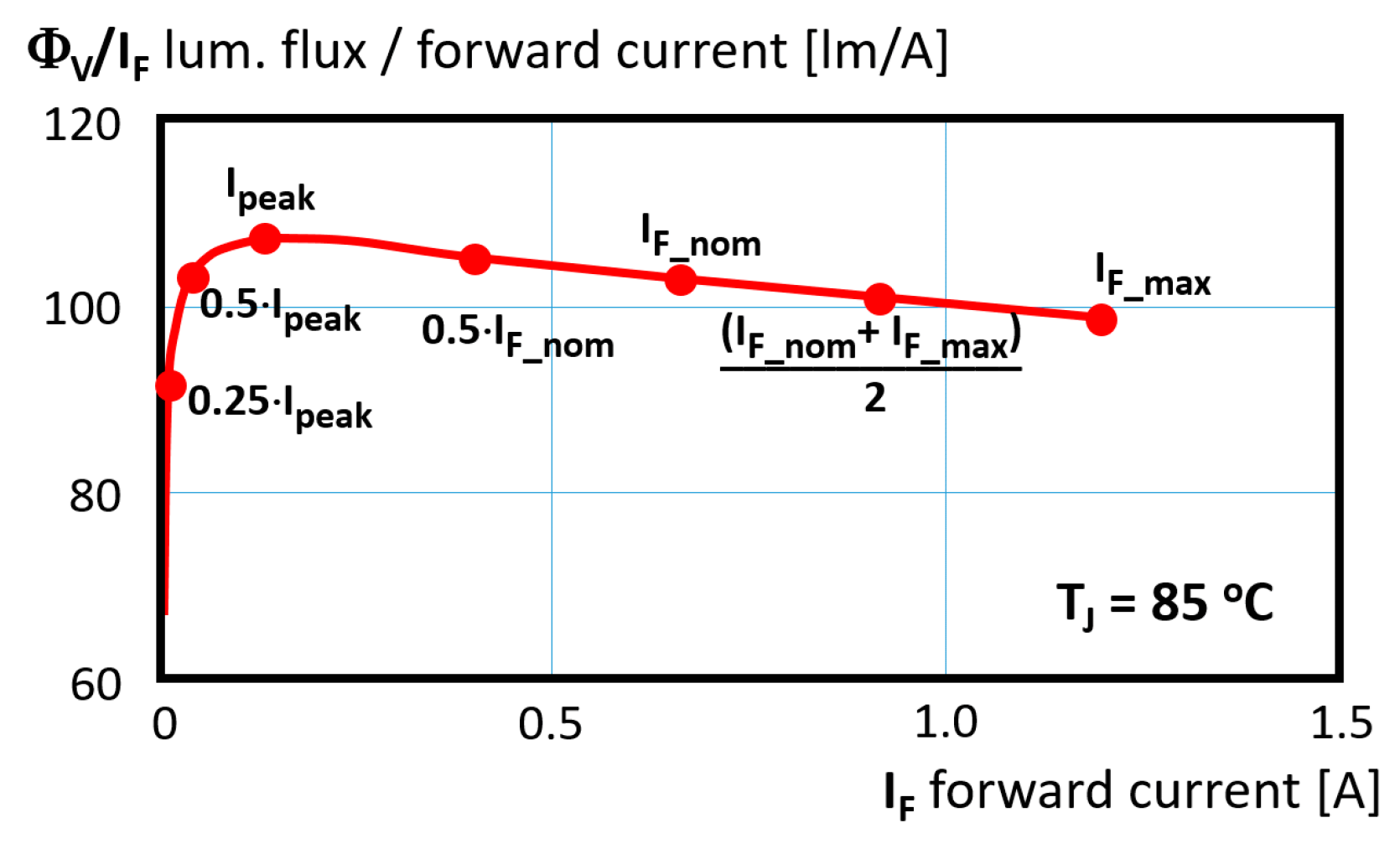
3.4. Modelling the Emitted Luminous Flux
4. An LED Chip Multi-Domain Model Closer to Physics
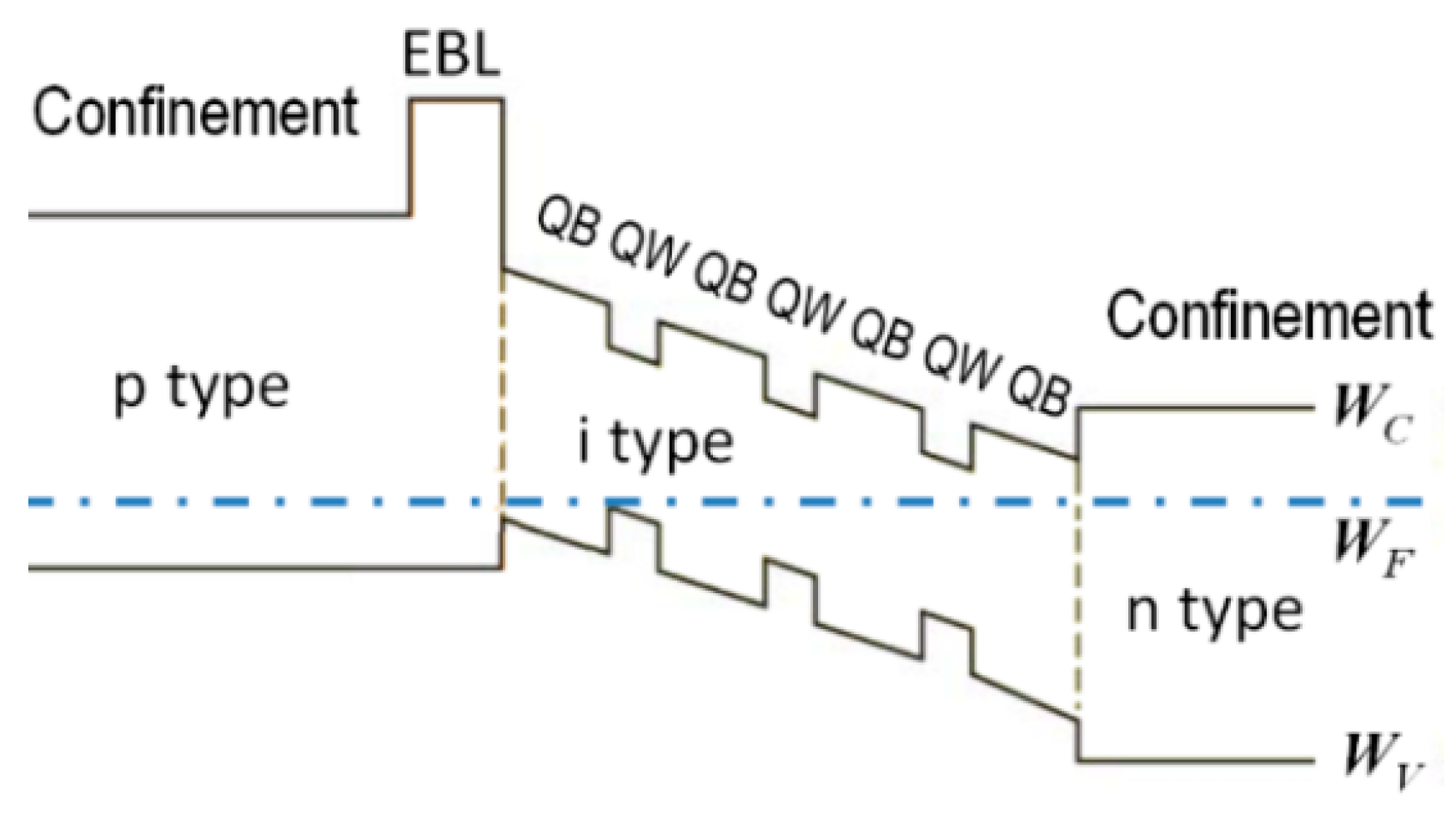
4.1. The Physical Roots
- Number of generated electrons/holes and their recombination through different mechanisms within the section. These effects can be thoroughly treated by the collision theory, but a simplified quantity called the generation and recombination rate can be used in the treatment of the statistical mechanics, too.
- Injection from the adjacent sections, determined by the band structure near the interface.
- Diffusion of minority carriers at low concentrations, that is, in low numbers compared to the density of the majority carriers. This yields , corresponding to Equation (1) with .
- Diffusion of both types of carriers at high concentrations, when the quasi-neutrality principle makes the density of both carriers equal. This yields a current constituent in an form.
4.2. Modeling the Electrical Characteristics
4.3. Modeling the Light Output Characteristics
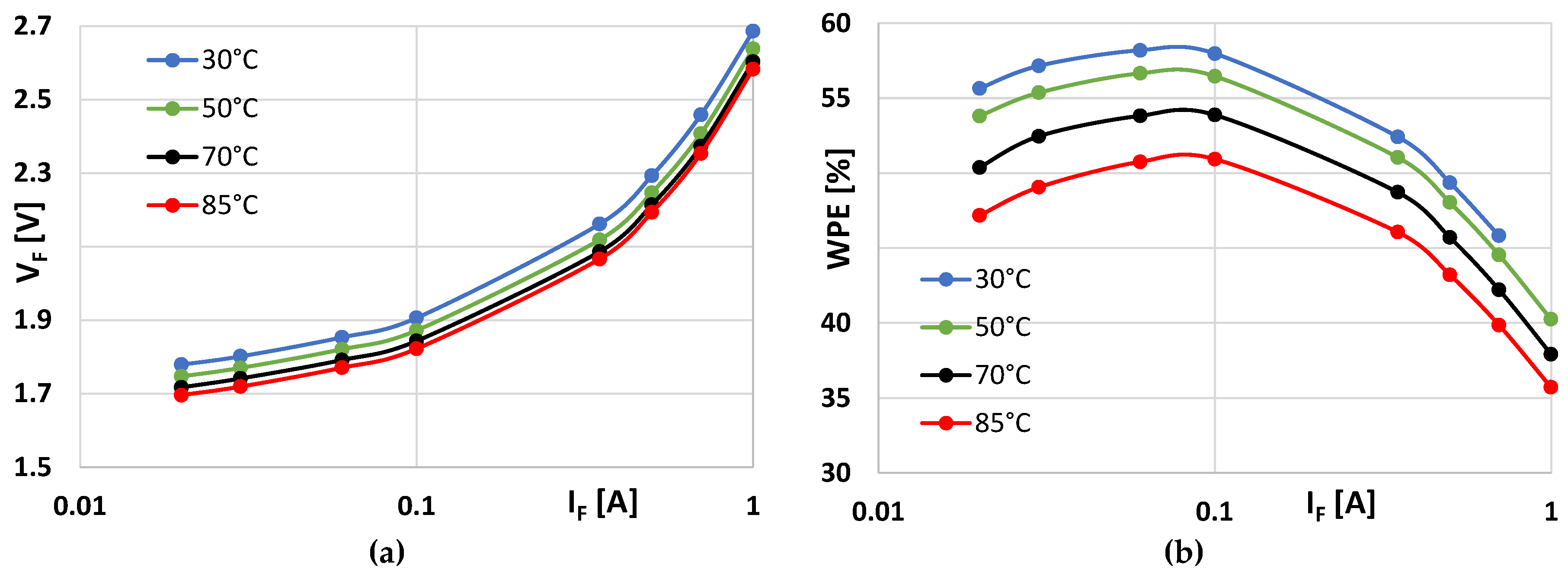
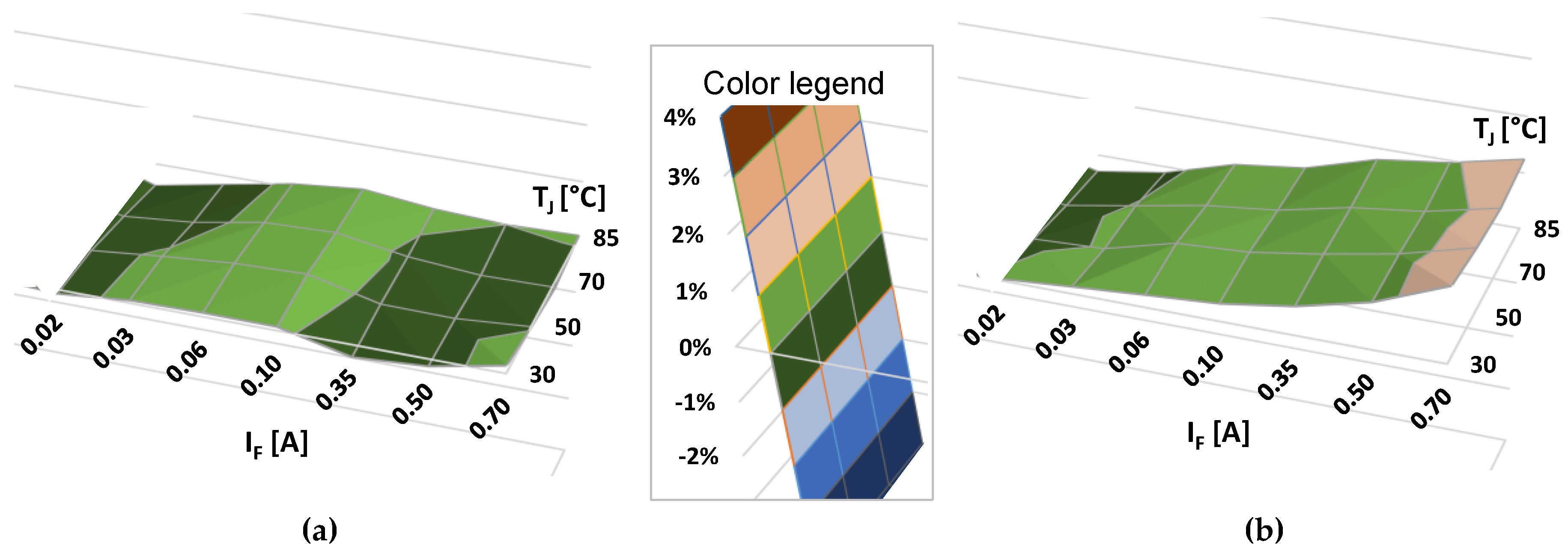
4.4. The Predictive Power of the Physics Based Model
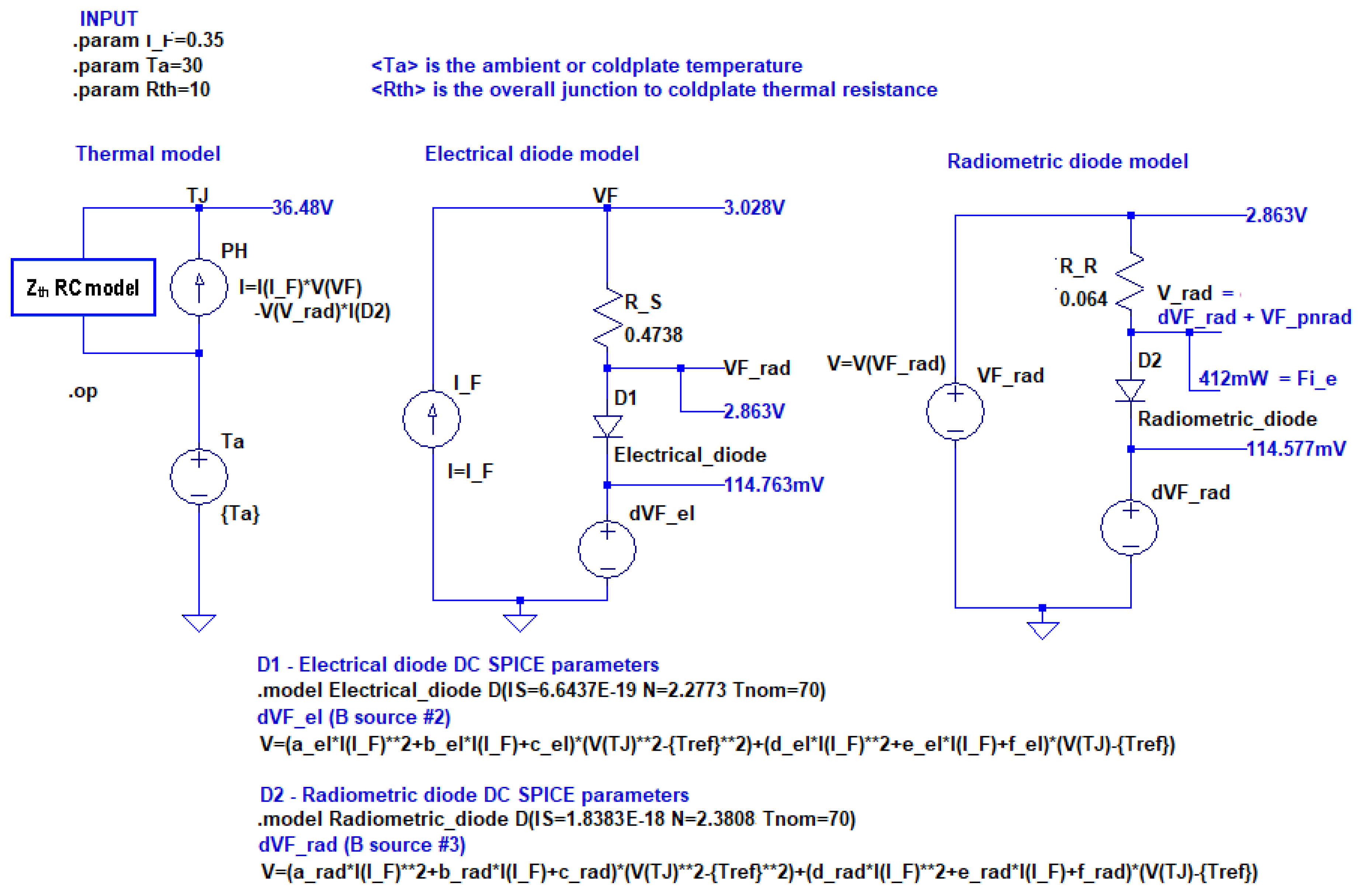
4.5. The Actual Implementation of the Physics Based Model
5. Multi-Domain Modelling of LEDs for Real Design Tasks
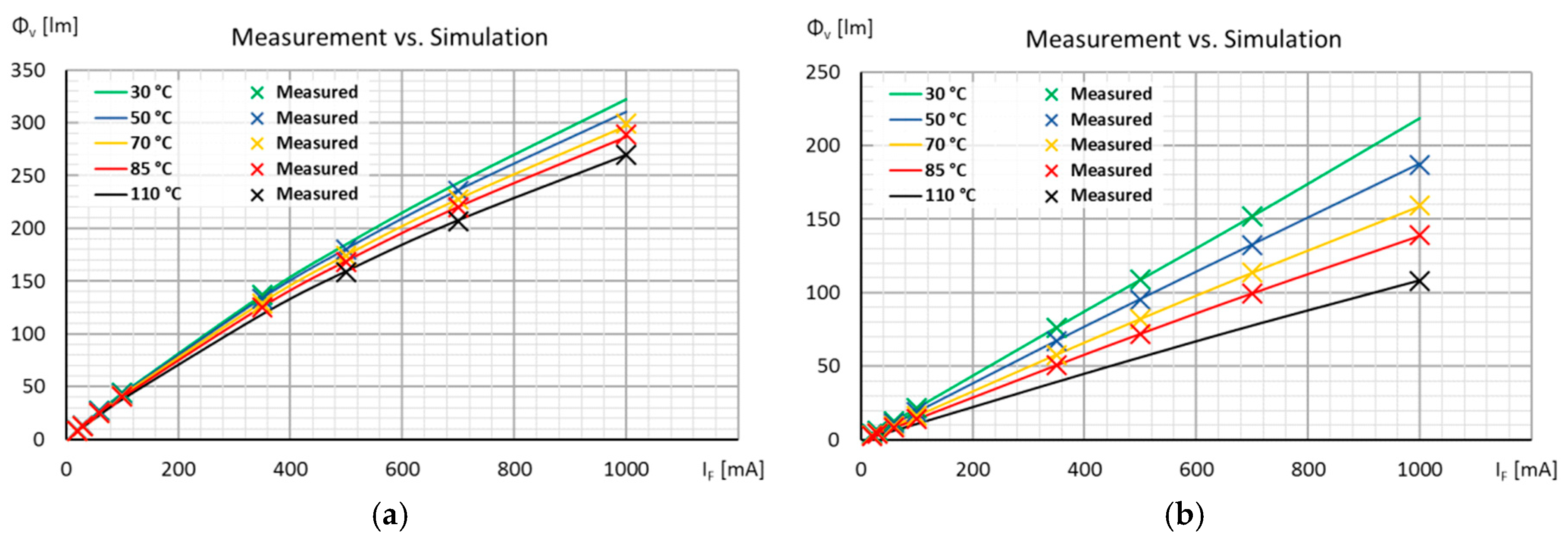
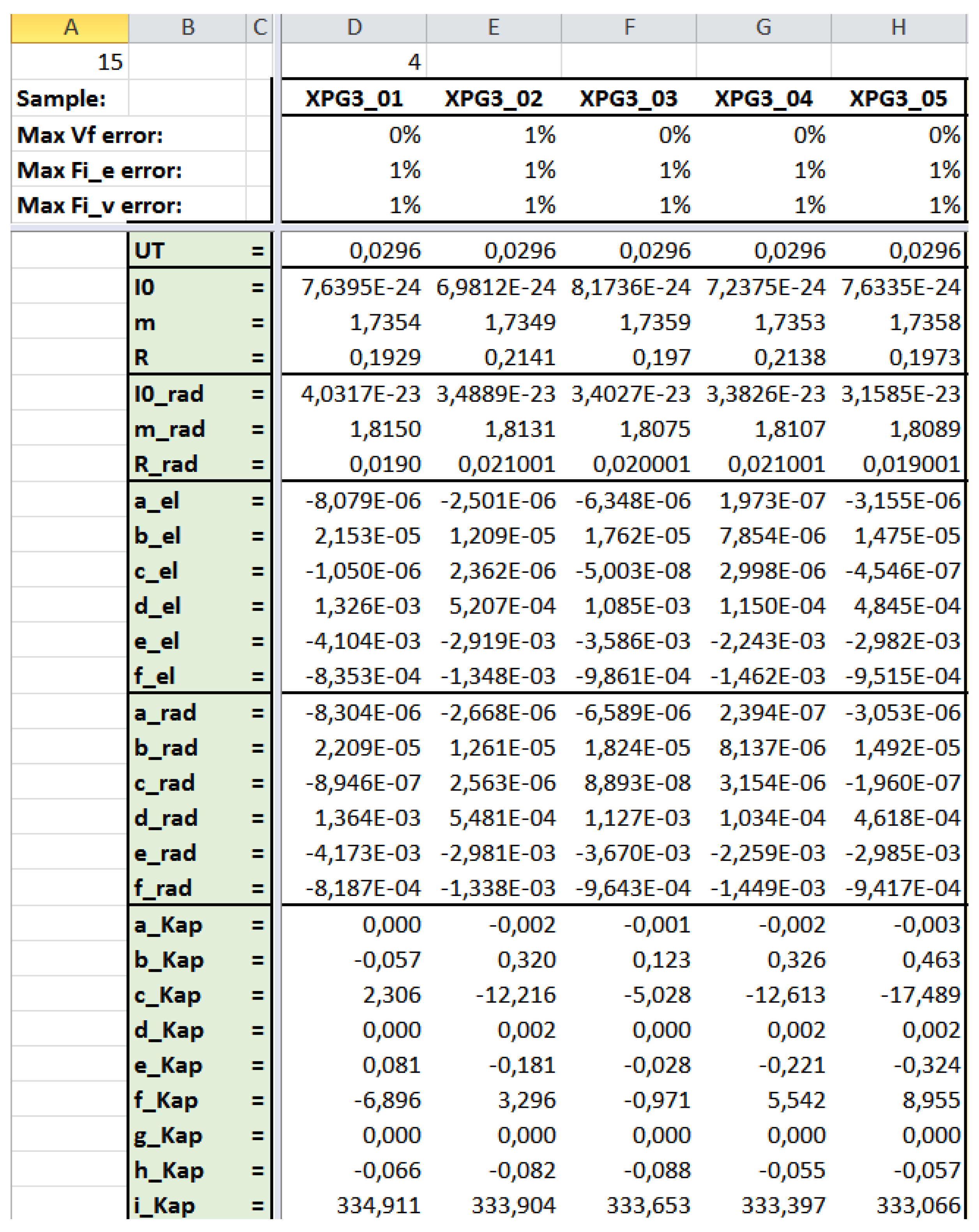
5.1. Modeling an “LED type” and Parameter Extraction
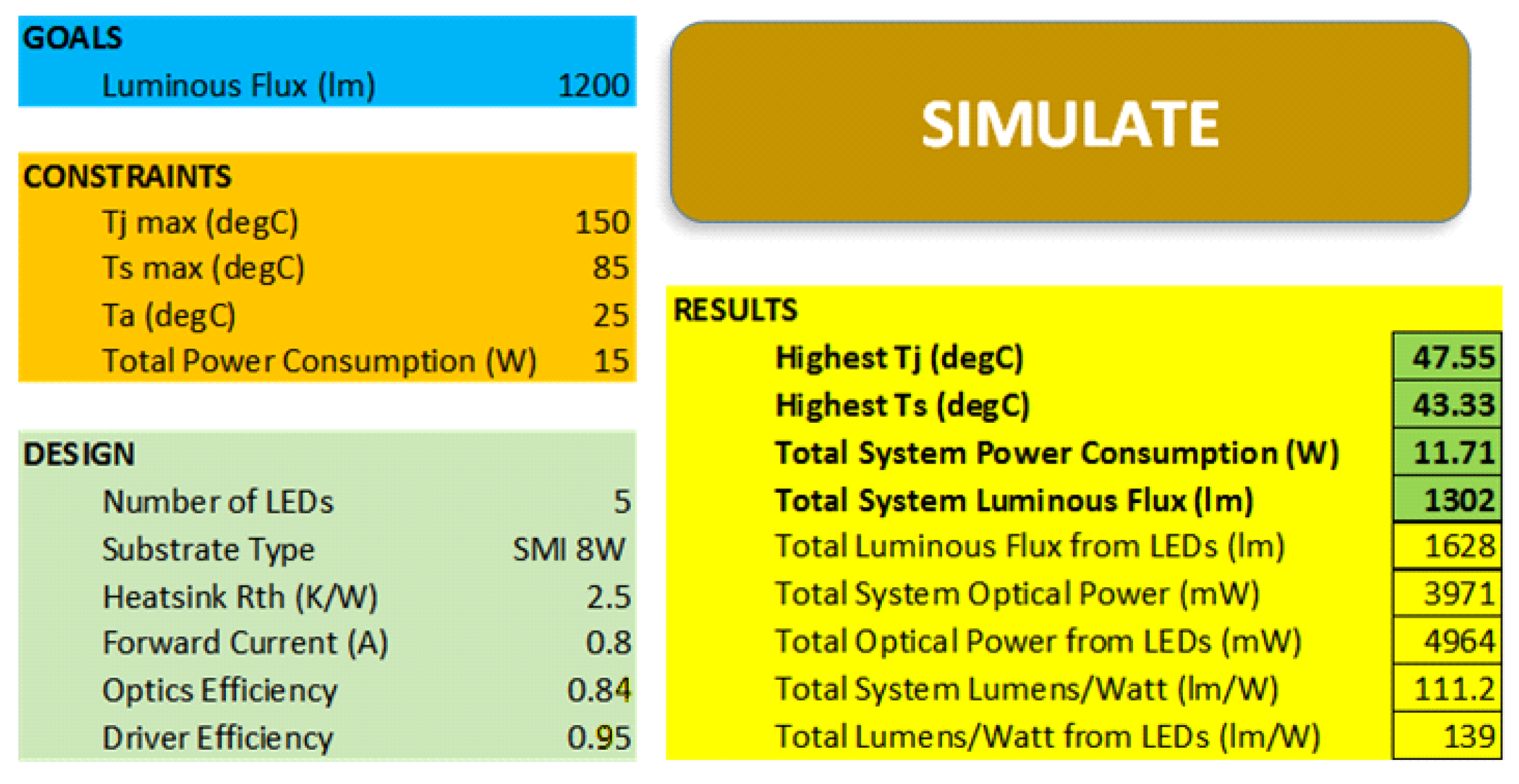
5.2. Applying the Quasi Black-Box Model for a Real Luminaire Design Task
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martin, G.; Poppe, A.; Lungten, S.; Heikkinen, V.; Yu, J.; Rencz, M.; Bornoff, R. Delphi4LED—From measurements to standardized multi-domain compact models of light emitting diodes (LED). Electronics Cooling Magazine, 4 August 2017; 20–23. [Google Scholar]
- Delphi4LED Project Website. Available online: https://delphi4led.org (accessed on 27 March 2019).
- Marty, C.; Yu, J.; Martin, G.; Bornoff, R.; Poppe, A.; Fournier, D.; Morard, E. Design flow for the development of optimized LED luminaires using multi-domain compact model simulations. In Proceedings of the 24th International Workshop on Thermal Investigation of ICs and Systems (THERMINIC’18), Stockholm, Sweden, 26–28 September 2018. [Google Scholar] [CrossRef]
- Martin, G.; Marty, C.; Bornoff, R.; Poppe, A.; Onushkin, G.; Rencz, M.; Yu, J. Luminaire Digital Design Flow with Multi-Domain Digital Twins of LEDs. Energies 2019. submitted to the Special Issue on Thermal and Electro-thermal System Simulation. [Google Scholar]
- Poppe, A. Multi-Domain Compact Modeling of LEDs: An Overview of Models and Experimental Data. Microelectron. J. 2015, 46, 1138–1151. [Google Scholar] [CrossRef]
- Hantos, G.; Hegedüs, J.; Bein, M.C.; Gaál, L.; Farkas, G.; Sárkány, Z.; Ress, S.; Poppe, A.; Rencz, M. Measurement issues in LED characterization for Delphi4LED style combined electrical-optical-thermal LED modeling. In Proceedings of the 19th IEEE Electronics Packaging Technology Conference (EPTC’17), Singapore, 6–9 December 2017. [Google Scholar] [CrossRef]
- Farkas, G.; Gaál, L.; Bein, M.; Poppe, A.; Ress, S.; Rencz, M. LED characterization within the Delphi-4LED Project. In Proceedings of the 17th Intersociety Conference on Thermomechanical Phenomena in Electronic Systems (ITHERM’18), San Diego, CA, USA, 29 May–1 June 2018. [Google Scholar] [CrossRef]
- Poppe, A. Simulation of LED Based Luminaires by Using Multi-Domain Compact Models of LEDs and Compact Thermal Models of their Thermal Environment. Microelectron. Reliab. 2017, 72, 65–74. [Google Scholar] [CrossRef]
- Poppe, A.; Hegedüs, J.; Szalai, A.; Bornoff, R.; Dyson, J. Creating multi-port thermal network models of LED luminaires for application in system level multi-domain simulation using Spice-like solvers. In Proceedings of the 32nd IEEE Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM’16), San Jose, CA, USA, 14–17 March 2016; pp. 44–49. [Google Scholar] [CrossRef]
- Bornoff, R.; Farkas, G.; Gaál, L.; Rencz, M.; Poppe, A. LED 3D Thermal Model Calibration against Measurement. In Proceedings of the 19th International Conference on Thermal, Mechanical and Multiphysics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE’18), Toulouse, France, 15–18 April 2018. [Google Scholar] [CrossRef]
- Bornoff, R. Extraction of Boundary Condition Independent Dynamic Compact Thermal Models of LEDs—A Delphi4LED Methodology. Energies 2019, 12, 1628. [Google Scholar] [CrossRef]
- CIE e-ILV Term 17-738 (Luminous Flux). Available online: http://eilv.cie.co.at/term/738 (accessed on 25 April 2019).
- Titkov, I.E.; Karpov, S.Y.; Yadav, A.; Zerova, V.L.; Zulonas, M.; Galler, B.; Strassburg, M.; Pietzonka, I.; Lugauer, H.-J.; Rafailov, E.U. Temperature-Dependent Internal Quantum Efficiency of Blue High-Brightness Light-Emitting Diodes. IEEE J. Quantum Electron. 2014, 50, 911–920. [Google Scholar] [CrossRef]
- Chies, L.; Dalla Costa, M.A.; Bender, V.C. Improved design methodology for LED Lamps. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Buzios, Brazil, 3–5 June 2015; pp. 1196–1201. [Google Scholar] [CrossRef]
- Tao, X. Study of Junction Temperature Effect on Electrical Power of Light-Emitting Diode (LED) Devices. In Proceedings of the 2015 IEEE 22nd International Symposium on the Physical and Failure Analysis of Integrated Circuits, Hsinchu, Taiwan, 29 June–2 July 2015; pp. 430–433. [Google Scholar] [CrossRef]
- Tao, X.; Yang, B. An Estimation Method for Efficiency of Light-Emitting Diode (LED) Devices. J. Power Electron. 2016, 16, 815–822. [Google Scholar] [CrossRef]
- Raypah, M.E.; Sodipo, B.K.; Devarajan, M.; Sulaiman, F. Estimation of Luminous Flux and Luminous Efficacy of Low-Power SMD LED as a Function of Injection Current and Ambient Temperature. IEEE Trans. Electron. Devices 2016, 63, 2790–2795. [Google Scholar] [CrossRef]
- Farkas, G.; van Voorst Vader, Q.; Poppe, A.; Bognár, G.Y. Thermal Investigation of High Power Optical Devices by Transient Testing. IEEE Trans. Compon. Packag. Technol. 2005, 28, 45–50. [Google Scholar] [CrossRef]
- Poppe, A.; Farkas, G.; Székely, V.; Horváth, G.Y.; Rencz, M. Multi-domain simulation and measurement of power LED-s and power LED assemblies. In Proceedings of the 22nd IEEE Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM’06), Dallas, TX, USA, 14–16 March 2006; pp. 191–198. [Google Scholar] [CrossRef]
- Osram LED PSpice Libraries. Available online: https://www.osram.com/apps/downloadcenter/os/?path=/os-files/Electrical+Simulation/LED/PSpice+Libraries/ (accessed on 25 February 2019).
- Lumileds LWS LTSpice Libraries. Available online: https://www.lumileds.com/support/design-resources/electrical (accessed on 25 February 2019).
- Raynaud, P. Single Kernel Electro-Thermal IC Simulator. In Proceedings of the 19th International Workshop on Thermal Investigation of ICs and Systems (THERMINIC’13), Berlin, Germany, 25–27 September 2013; pp. 356–358. [Google Scholar] [CrossRef]
- Keppens, A. Modeling and Evaluation of High-Power Light-Emitting Diodes for General Lighting. Ph.D. Thesis, Katholeieke Universiteit Leuven, Leuven, Belgium, 2010. D/2010/7515/9. Available online: https://lirias.kuleuven.be/bitstream/123456789/274568/1/PhD+text+AK.pdf (accessed on 25 April 2019).
- Negrea, C.; Svasta, P.; Rangu, M. Electro-Thermal Modeling of Power LED Using Spice Circuit Solver. In Proceedings of the 35th International Spring Seminar on Electronics Technology (ISSE 2012), Bad Aussee, Austria, 9–13 May 2012; pp. 329–334. [Google Scholar] [CrossRef]
- Górecki, K. Electrothermal model of a power LED for SPICE. Int. J. Numer. Model. 2012, 25, 39–45. [Google Scholar] [CrossRef]
- Górecki, K. The Influence of Mutual Thermal Interactions Between Power LEDs on Their Characteristics. In Proceedings of the 20th International Workshop on Thermal Investigation of ICs and Systems (THERMINIC’13), Berlin, Germany, 25–27 September 2013; pp. 188–193. [Google Scholar] [CrossRef]
- Górecki, K. Modelling mutual thermal interactions between power LEDs in SPICE. Microelectron. Reliab. 2015, 55, 389–395. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. Modelling Power LEDs with Thermal Phenomena Taken into Account. In Proceedings of the 22nd International Conference on Mixed Design of Integrated Circuits and Systems, Toruń, Poland, 25–27 June 2015; pp. 432–435. [Google Scholar] [CrossRef]
- Górecki, K.; Ptak, P. New dynamic electro-thermo-optical model of power LEDs. Microelectron. Reliab. 2018, 91, 1–7. [Google Scholar] [CrossRef]
- Farkas, G.; Poppe, A. Thermal testing of LEDs. In Thermal Management for LED Applications; Lasance, C.J.M., Poppe, A., Eds.; Springer: New York, NY, USA; Heidelberg, Germany; Dordrecht, The Netherlands; London, UK, 2014; pp. 73–165. [Google Scholar] [CrossRef]
- Bein, M.C.; Hegedüs, J.; Hantos, G.; Gaál, L.; Farkas, G.; Rencz, M.; Poppe, A. Comparison of two alternative junction temperature setting methods aimed for thermal and optical testing of high power LEDs. In Proceedings of the 23rd International Workshop on Thermal Investigation of ICs and Systems (THERMINIC’17), Amsterdam, The Netherlands, 27–29 September 2017. [Google Scholar] [CrossRef]
- CIE Technical Report 225: 2017. Optical Measurement of High-Power LEDs; CIE: Vienna, Austria, 2017; ISBN 978-3-902842-12-1. [CrossRef]
- JEDEC Standard JESD51-14. Transient Dual Interface Test Method for the Measurement of the Thermal Resistance Junction-To-Case of Semiconductor Devices with Heat Flow Through a Single Path; JEDEC: Arlington, VA, USA, 2010. [Google Scholar]
- T3Ster-TeraLED Product Website. Available online: https://www.mentor.com/products/mechanical/micred/teraled/ (accessed on 27 March 2019).
- Poppe, A.; Farkas, G.; Szabó, F.; Joly, J.; Thomé, J.; Yu, J.; Bosschaartl, K.; Juntunen, E.; Vaumorin, E.; di Bucchianico, A.; et al. Inter Laboratory Comparison of LED Measurements Aimed as Input for Multi-Domain Compact Model Development within a European-wide R&D Project. In Proceedings of the Conference on “Smarter Lighting for Better Life” at the CIE Midterm Meeting 2017, Jeju, Korea, 23–25 October 2017; pp. 569–579. [Google Scholar] [CrossRef]
- CIE e-ILV Terms 17-1025 (Radiant Flux) and 17-1027 (Radiant Power). Available online: http://eilv.cie.co.at/term/1025 and http://eilv.cie.co.at/term/1027, respectively (accessed on 25 April 2019).
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 0-471-14323-5. [Google Scholar]
- Schubert, E.F. Light-Emitting Diodes, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006; ISBN 0-511-34476-7. [Google Scholar]
- JEDEC JESD51-51 Standard. Implementation of the Electrical Test Method for the Measurement of the Real Thermal Resistance and Impedance of Light-Emitting Diodes with Exposed Cooling Surface; JEDEC: Arlington, VA, USA, 2012. [Google Scholar]
- Hantos, G.; Hegedüs, J.; Poppe, A. Different questions of today’s LED thermal testing procedures. In Proceedings of the 34th IEEE Semiconductor Thermal Management Symposium (SEMI-THERM’18), San Jose, CA, USA, 19–23 March 2018; pp. 63–70. [Google Scholar] [CrossRef]
- CIE e-ILV Term 17-730 (Luminous Efficacy of Radiation). Available online: http://eilv.cie.co.at/term/730 (accessed on 27 March 2019).
- Van Zeghbroeck, B. Principles of Semiconductor Devices. Available online: http://ecee.colorado.edu/~bart/book (accessed on 27 March 2019).
- Tansu, N.; Mawst, L.J. Current injection efficiency of InGaAsN quantum-well lasers. J. Appl. Phys. 2005, 97, 054502. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, G.; Zhang, J.; Arif, R.A.; Tansu, N. Analysis of Internal Quantum Efficiency and Current Injection Efficiency in III-Nitride Light-Emitting Diodes. J. Disp. Technol. 2013, 9, 212–225. [Google Scholar] [CrossRef]
- JEDEC JESD51-52 Standard. Guidelines for Combining CIE 127-2007 Total Flux Measurements with Thermal Measurements of LEDs with Exposed Cooling Surface; JEDEC: Arlington, VA, USA, 2012. [Google Scholar]
- Bornoff, R.; Mérelle, T.; Sari, J.; Di Bucchianico, A.; Farkas, G. Quantified Insights into LED Variability. In Proceedings of the 24th International Workshop on Thermal Investigation of ICs and Systems (THERMINIC’18), Stockholm, Sweden, 26–28 September 2018. [Google Scholar] [CrossRef]
- Mérelle, T.; Bornoff, R.; Onushkin, G.; Gaál, L.; Farkas, G.; Poppe, A.; Hantos, G.; Sari, J.; Di Bucchianico, A. Modeling and quantifying LED variability. In Proceedings of the 2018 LED Professional Symposium (LpS2018), Bregenz, Austria, 25–27 September 2018; pp. 194–206, ISBN 978-3-9503209-9-2. [Google Scholar]
- Farkas, G.; Poppe, A.; Gaál, L.; Hantos, G.; Berényi, C.S.; Rencz, M. Structural analysis and modelling of packaged light emitting devices by thermal transient measurements at multiple boundaries. In Proceedings of the 24th International Workshop on Thermal Investigation of ICs and Systems (THERMINIC’18), Stockholm, Sweden, 26–28 September 2018. [Google Scholar] [CrossRef]
- Mérelle, T.; Sari, J.; Di Bucchianico, A.; Onushkin, G.; Bornoff, R.; Farkas, G.; Gaál, L.; Hantos, G.; Hegedüs, J.; Martin, G.; et al. Does a single LED bin really represent a single LED type? In Proceedings of the CIE 2019 29th Quadrennial Session, Washington, DC, USA, 14–22 June 2019. [Google Scholar]

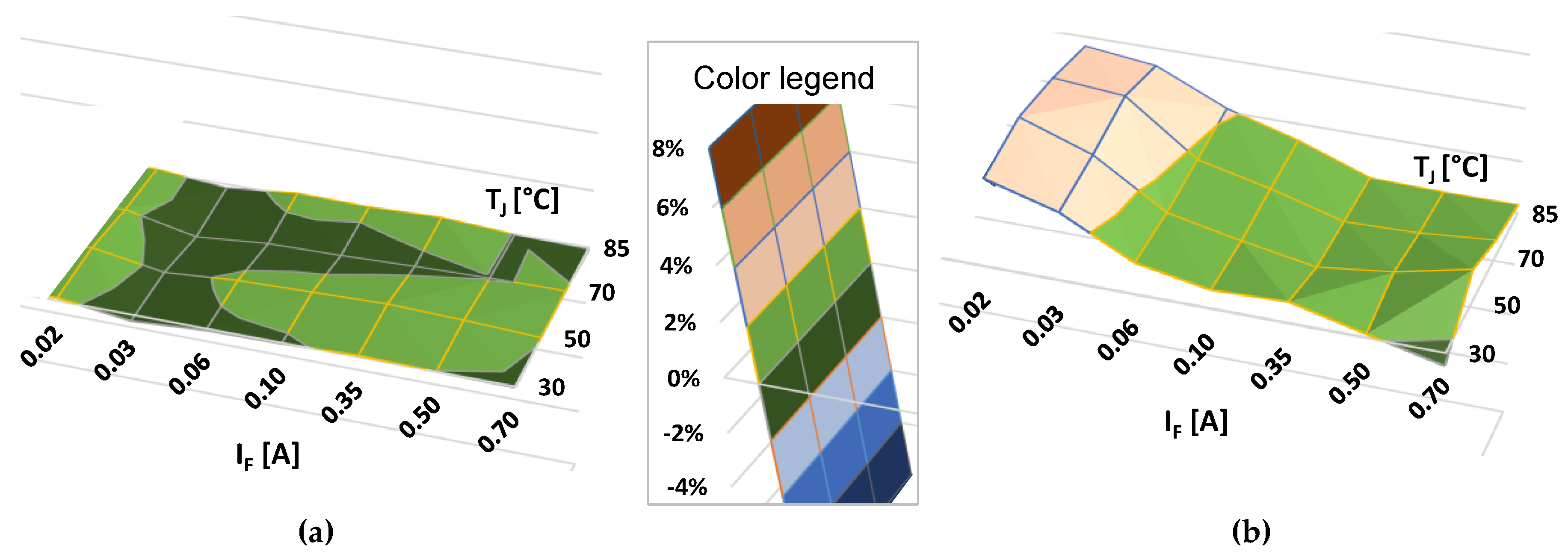
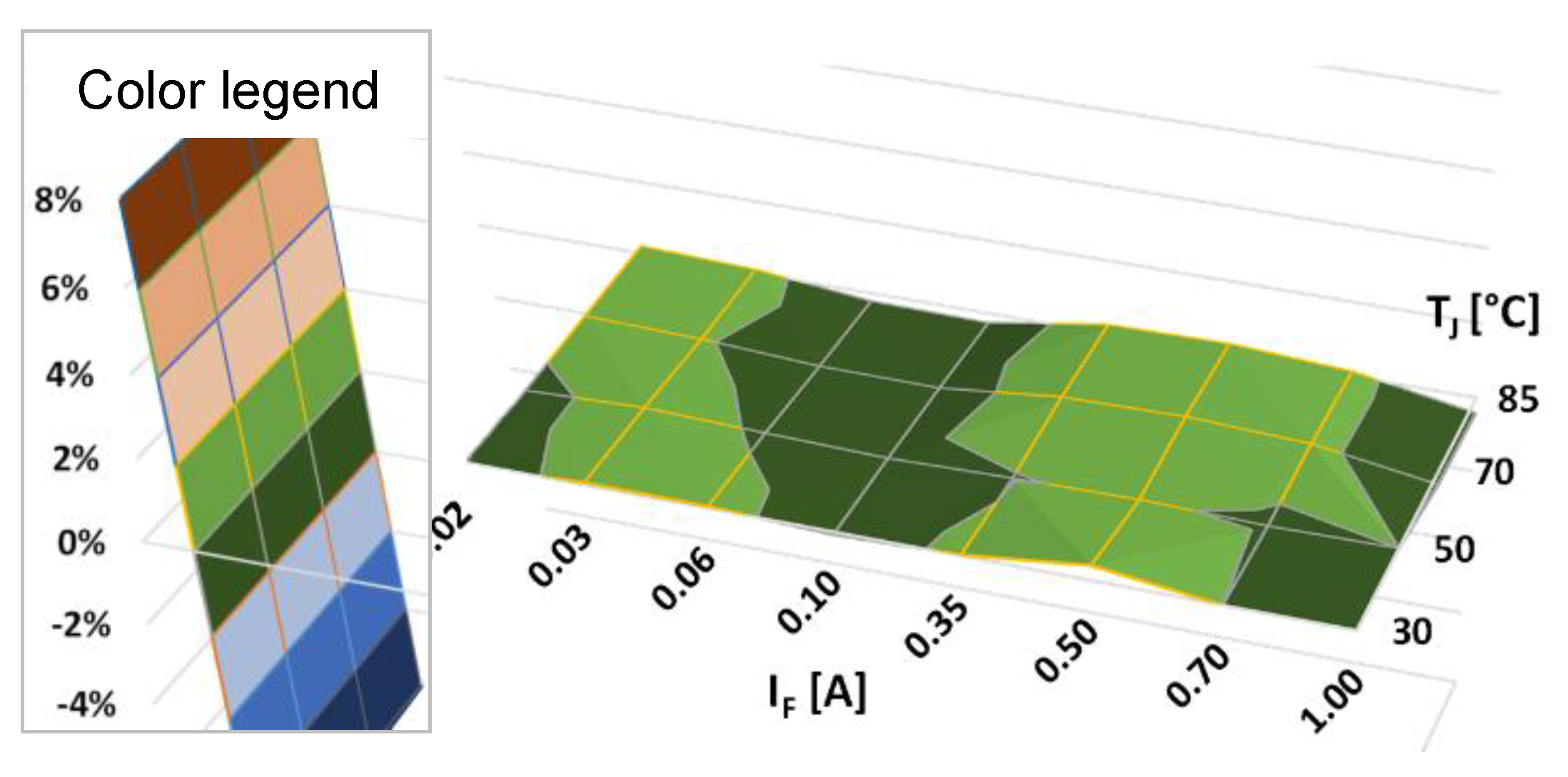
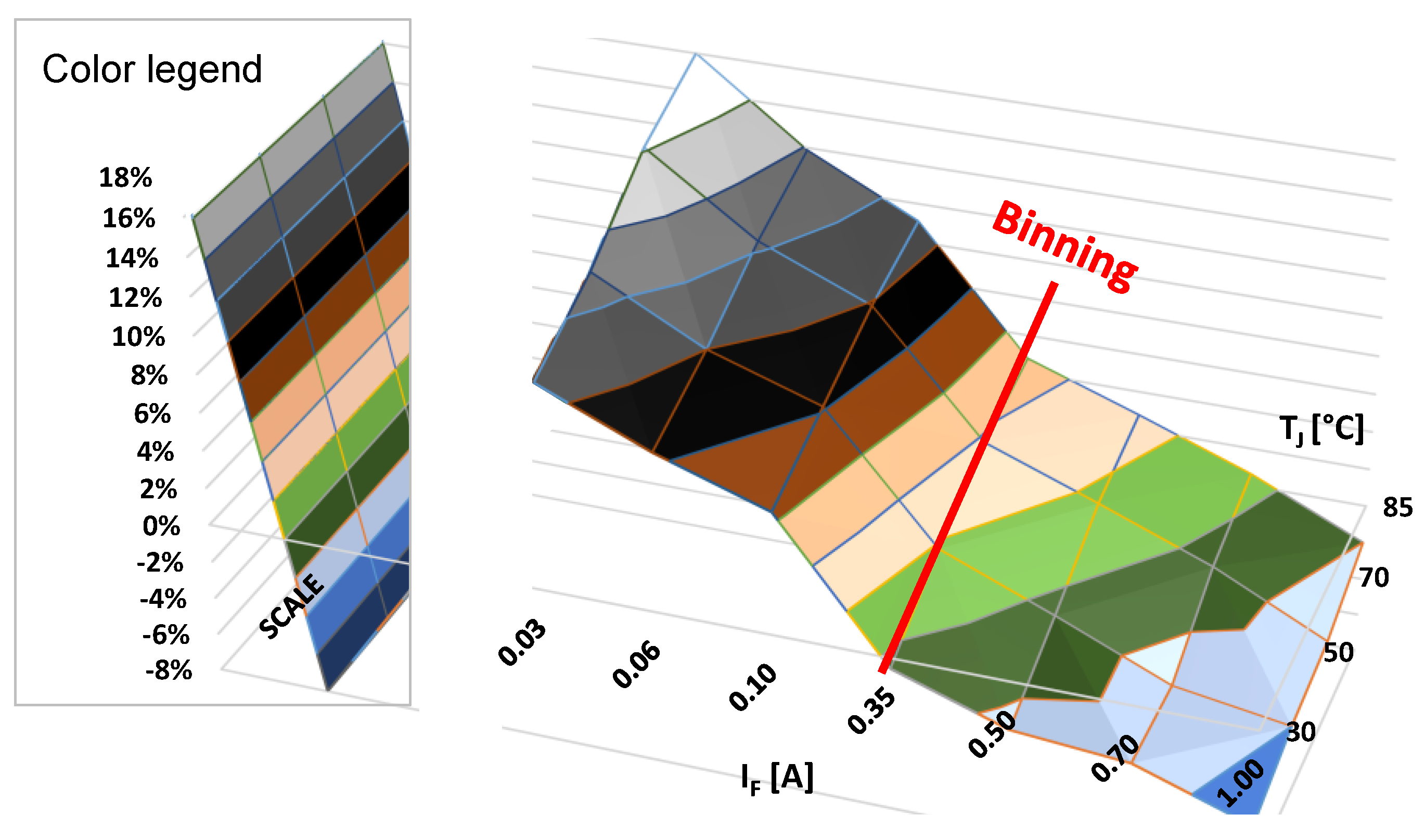
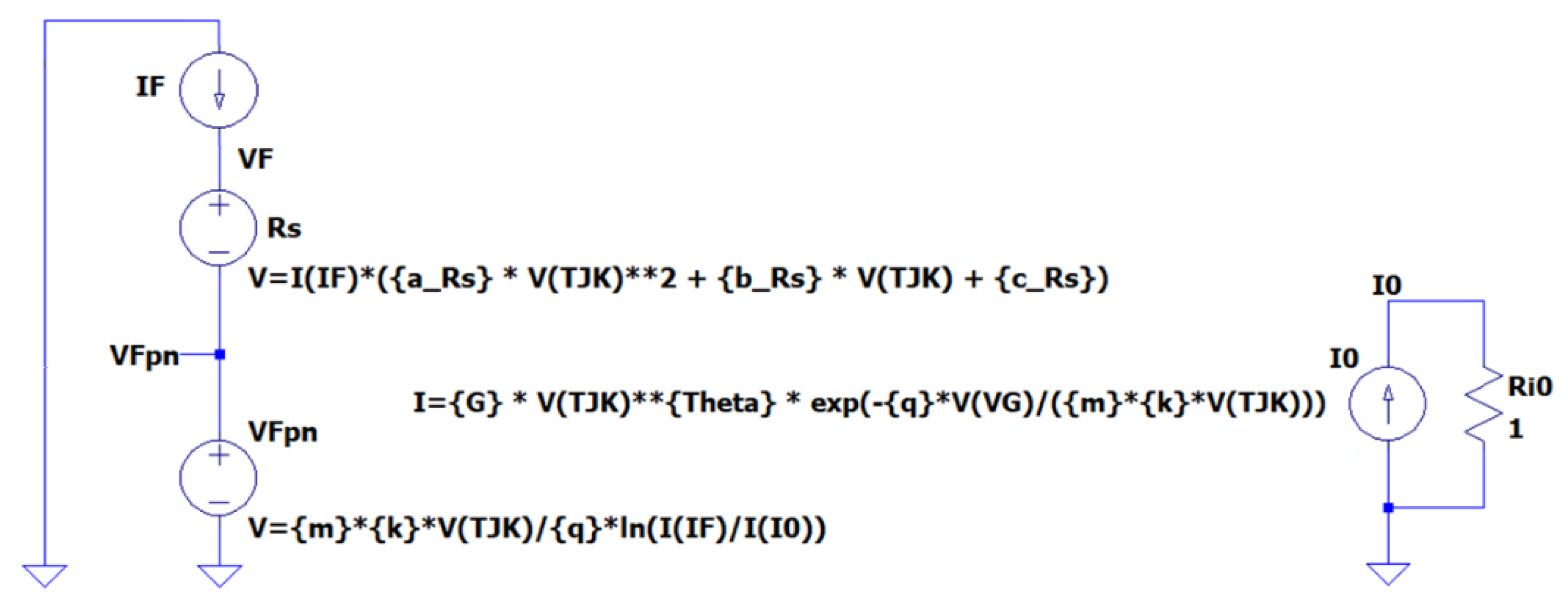


| Input quantities: | |||
| Output quantities:VF, PH, Φe, ΦV | |||
| Model parameters | Symbol in Spice diode model | ||
| Thermal | , | , | |
| Electrical | entire LED | radiative branch only | |
| diode internal pn-junctions at | , | , | , |
| resistors at | to switch of Spice’s model of the series resistance | ||
| Coefficients of the model of the “generators” | , , , , , | , , , , , | - |
| Coefficients of the efficacy of radiation model | , , , , , , , , | - | |
| Color | Code | ||
|---|---|---|---|
| Royal Blue, White | W, RB | 450 | 2.76 |
| Blue | B | 470 | 2.64 |
| Green | G | 515 | 2.41 |
| Amber | A | 600 | 2.07 |
| Red | R | 640 | 1.94 |
| Code | ||||
|---|---|---|---|---|
| RB | 0.662 | 0.413 | 2.5 | 6.6531 |
| W | 0.824 | 0.453 | 1.8 | 5.8421 |
| B | 0.610 | 0.277 | 3.0 | 7.7791 |
| G | 0.553 | 0.298 | 4.0 | 11.1289 |
| A | 0.508 | 0.525 | 1.5 | 8.8466 |
| R | 0.773 | 0.688 | 1.5 | 6.5855 |
| Property | Simulated | Measured |
|---|---|---|
| Total input electric power | 11.71 W | 10.7 W |
| Total emitted luminous flux | 1302 lm | 1339 lm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poppe, A.; Farkas, G.; Gaál, L.; Hantos, G.; Hegedüs, J.; Rencz, M. Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires. Energies 2019, 12, 1909. https://doi.org/10.3390/en12101909
Poppe A, Farkas G, Gaál L, Hantos G, Hegedüs J, Rencz M. Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires. Energies. 2019; 12(10):1909. https://doi.org/10.3390/en12101909
Chicago/Turabian StylePoppe, András, Gábor Farkas, Lajos Gaál, Gusztáv Hantos, János Hegedüs, and Márta Rencz. 2019. "Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires" Energies 12, no. 10: 1909. https://doi.org/10.3390/en12101909
APA StylePoppe, A., Farkas, G., Gaál, L., Hantos, G., Hegedüs, J., & Rencz, M. (2019). Multi-Domain Modelling of LEDs for Supporting Virtual Prototyping of Luminaires. Energies, 12(10), 1909. https://doi.org/10.3390/en12101909