Analytical Modeling and Comparison of Two Consequent-Pole Magnetic-Geared Machines for Hybrid Electric Vehicles
Abstract
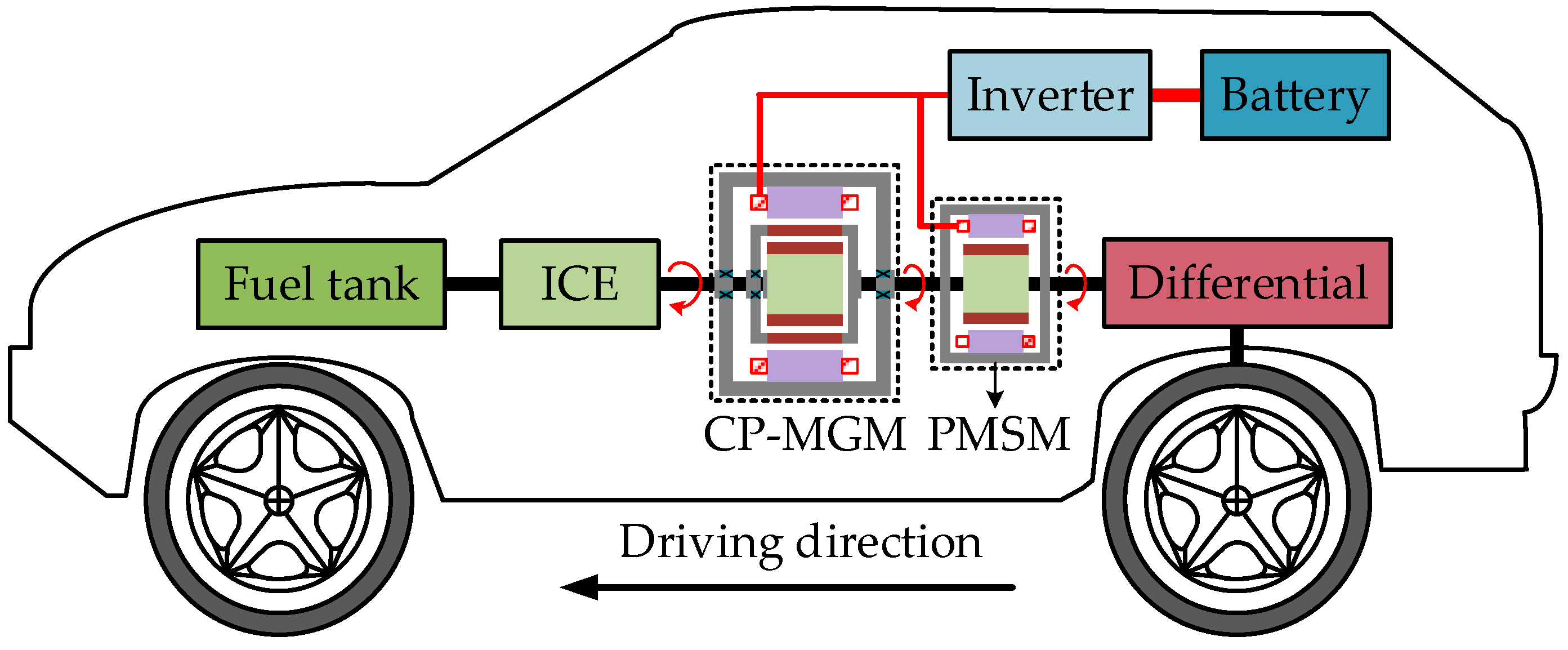
:1. Introduction
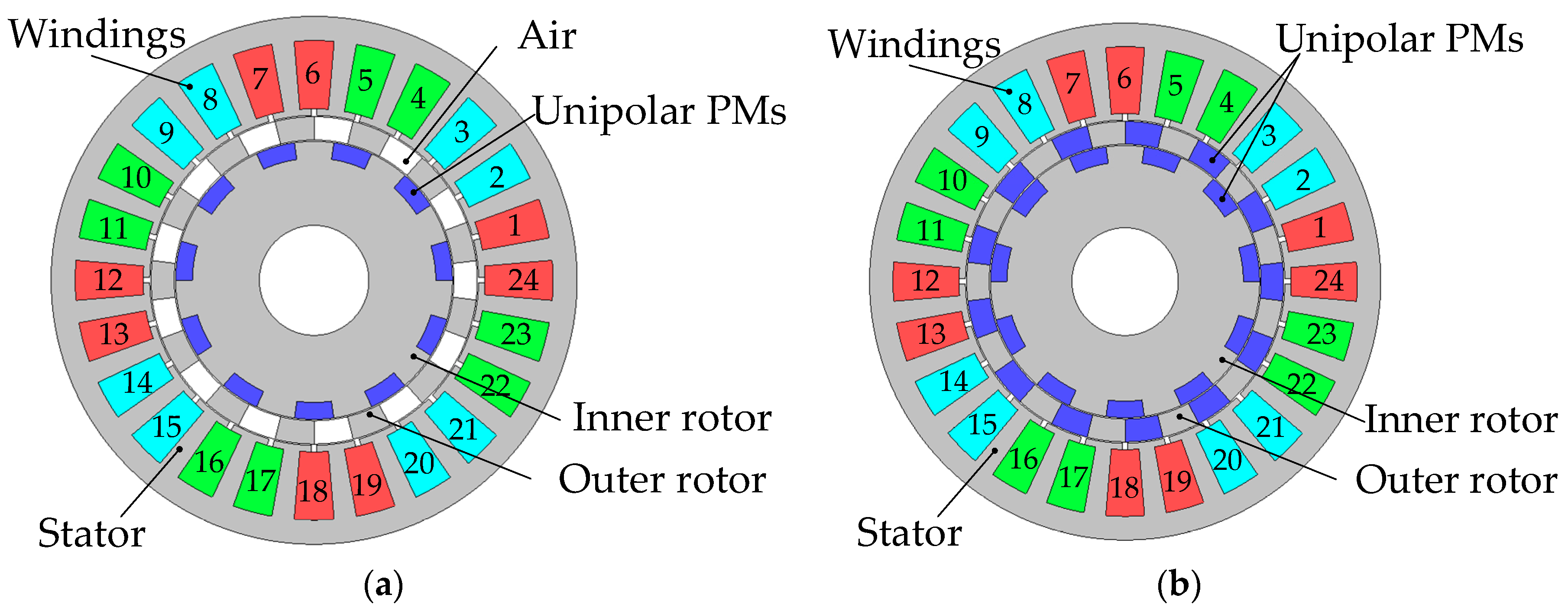
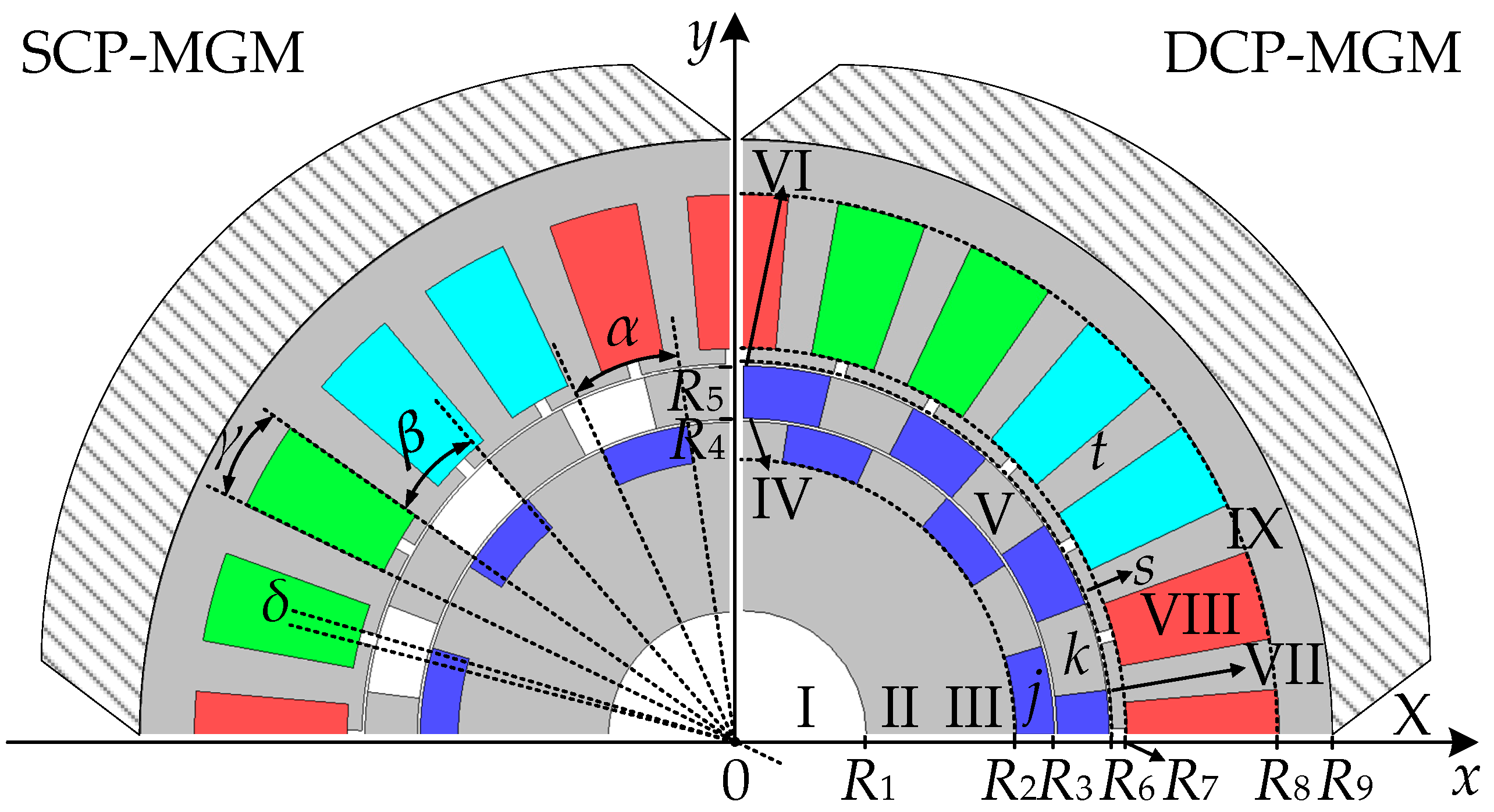
2. Configurations and Operating Principles of SCP-MGM and DCP-MGM
3. Mathematical Modeling of SCP-MGMs and DCP-MGMs
3.1. Assumption and Parameter Definition
- The geometrical shape of the machine has a radial side and a tangential side;
- The magnetic field distribution is constrained in the 2D plane: the axial component is ignored;
- The machine has infinite axial length, so the end effect is ignored;
- The radial component of the permeability of SMM within a certain region is regarded as a constant;
- Eddy–current effects within SMM and PMs are ignored.
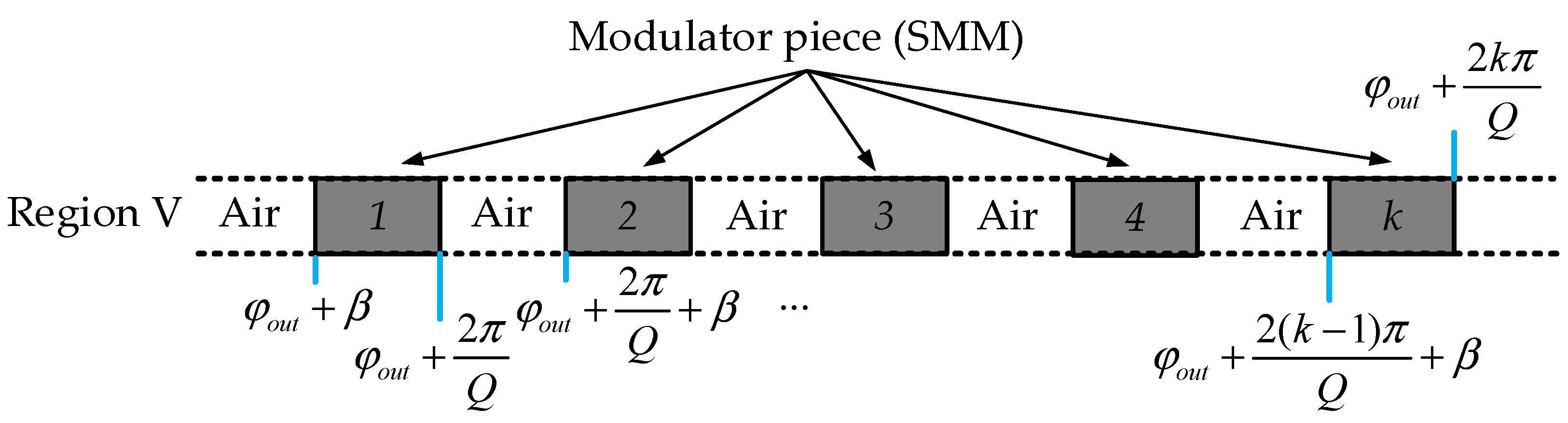
3.2. Partical Differential Equation Solution
3.3. Bondary Condition Application
3.4. Saturation Consideration of Soft-Magnetic Material
3.5. Electromagnetic Parameters Calculation
4. Validation and Comparison
4.1. Simulation Environment and Machine Parameters
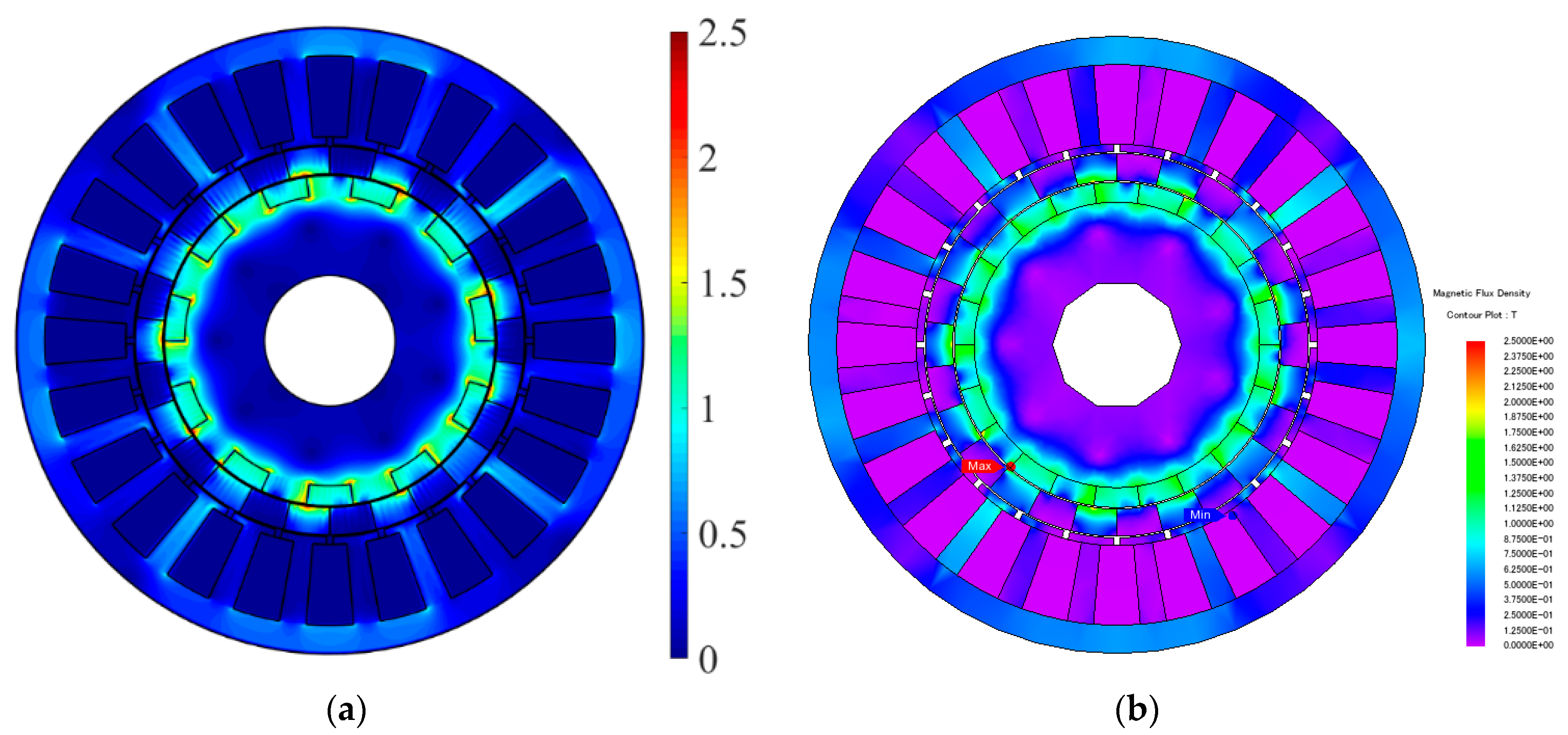
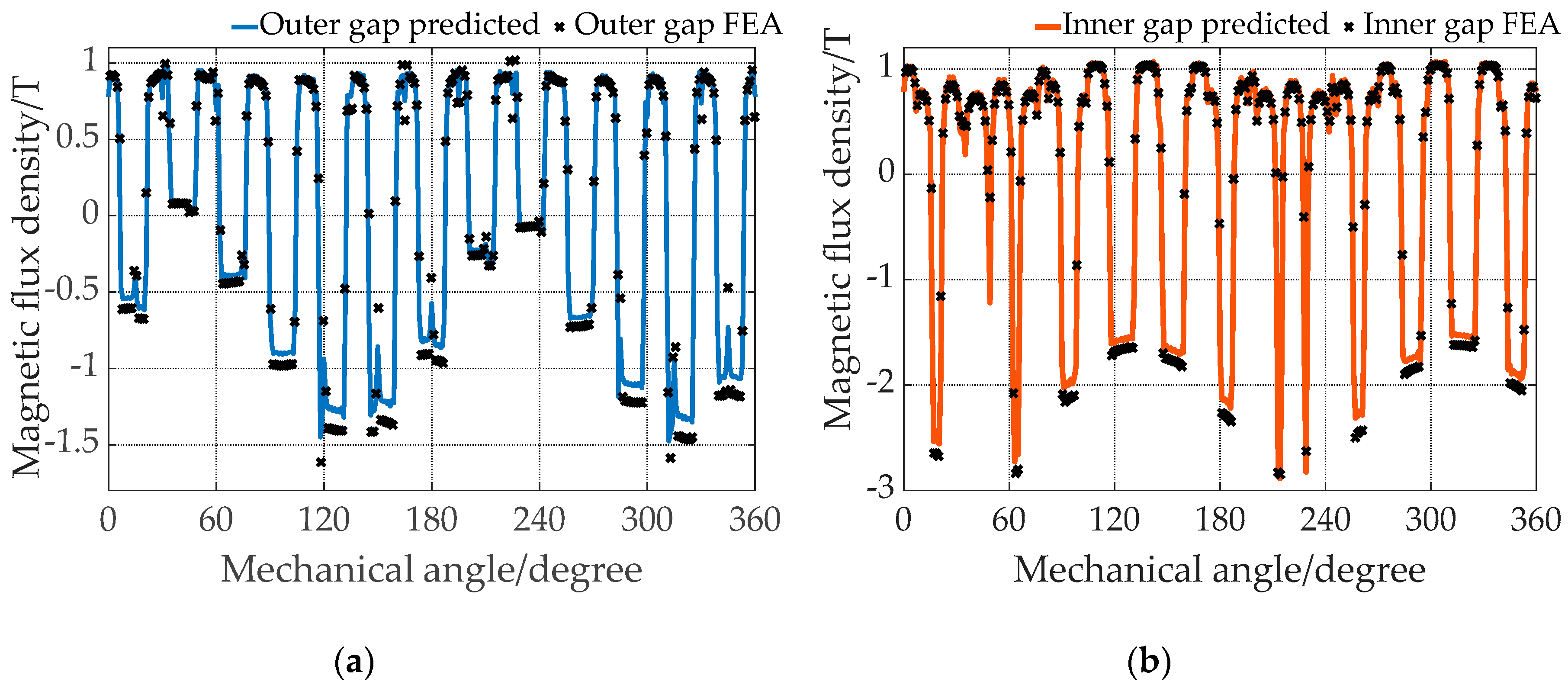
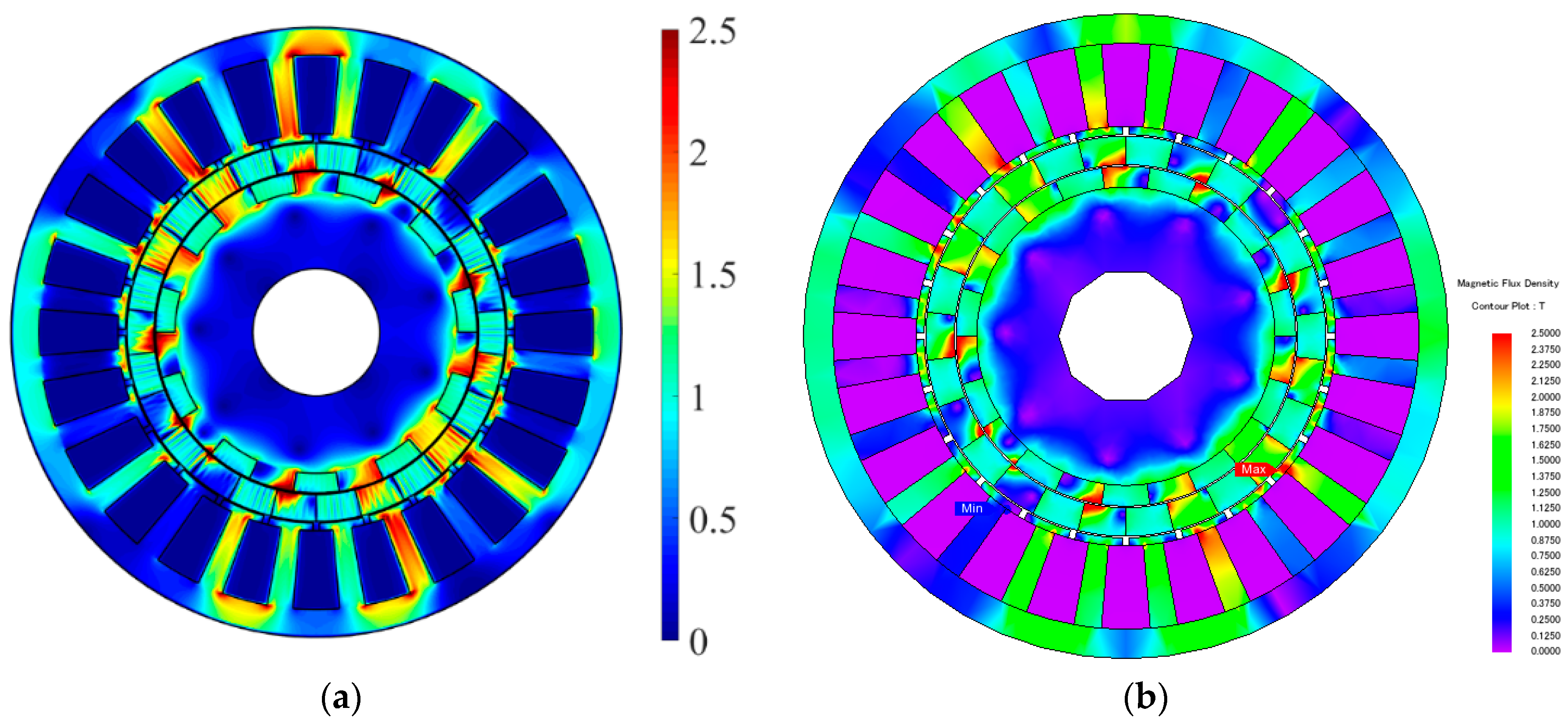
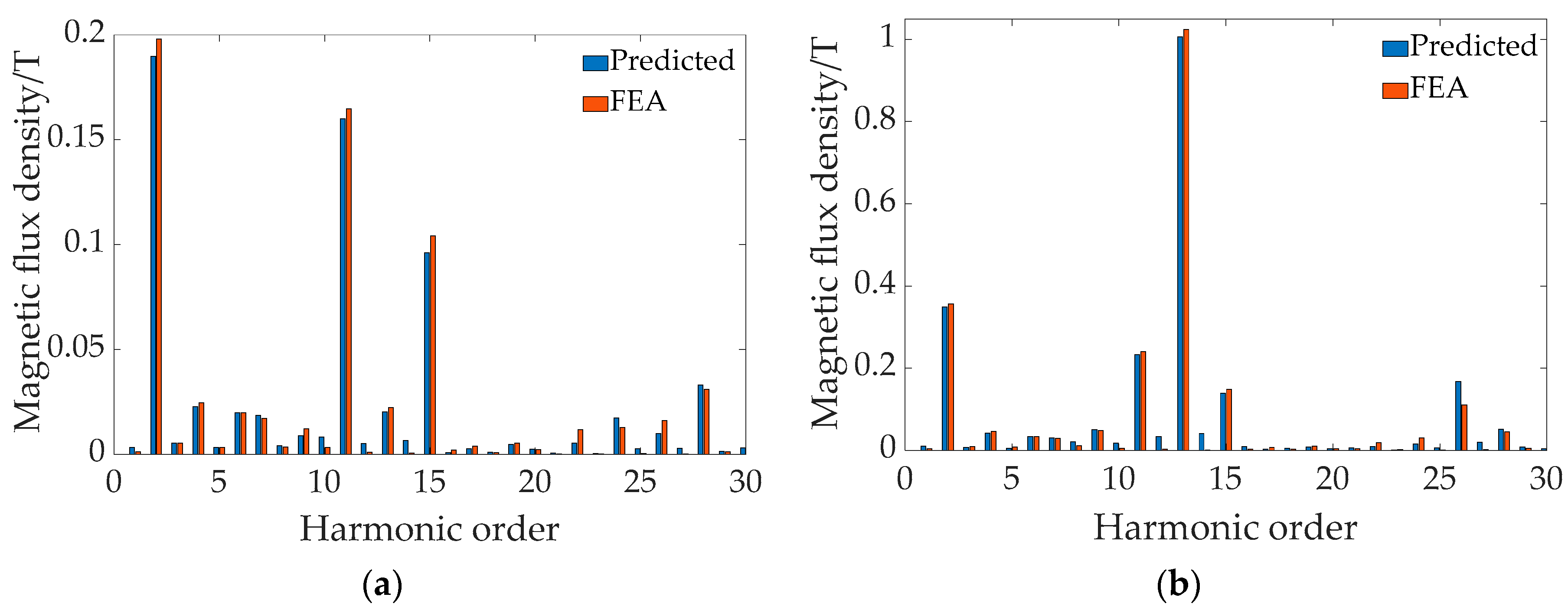
4.2. Comparison between HMM and FEA
4.3. Electromagnetic Performance Analysis under Different Working Conditions
4.3.1. Back EMF under No-Load Condition
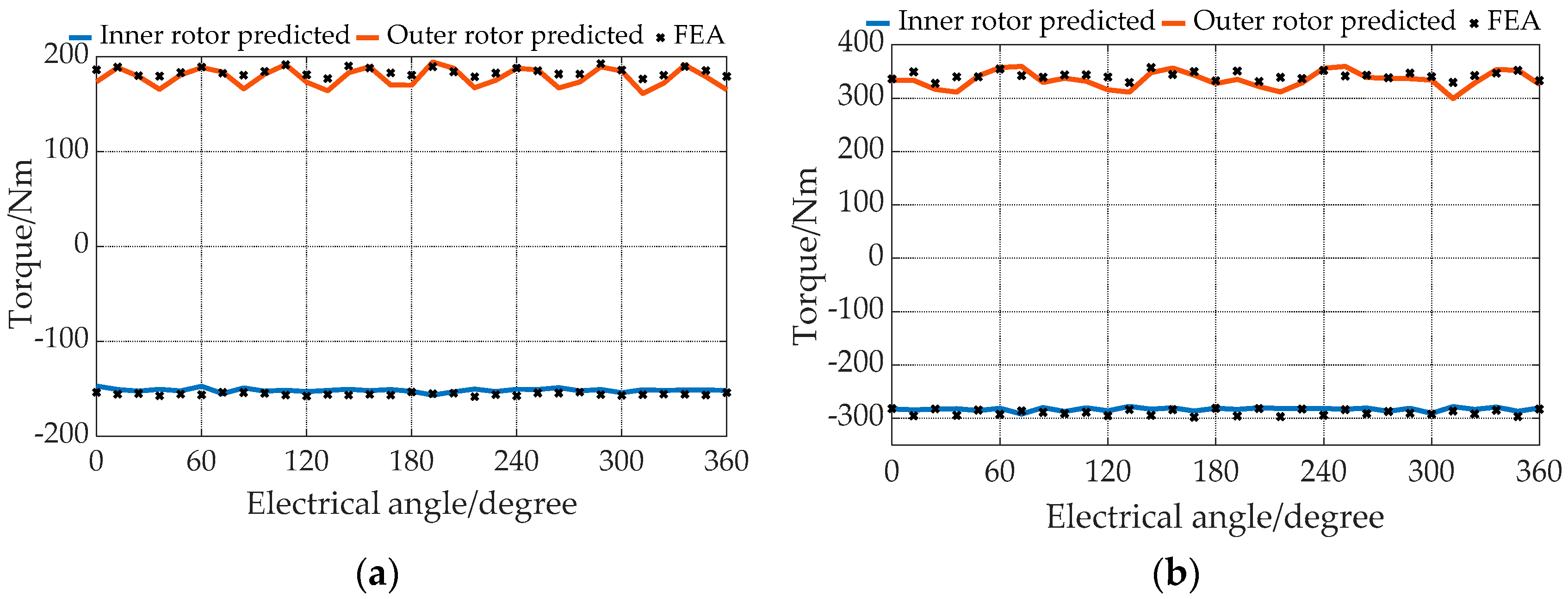
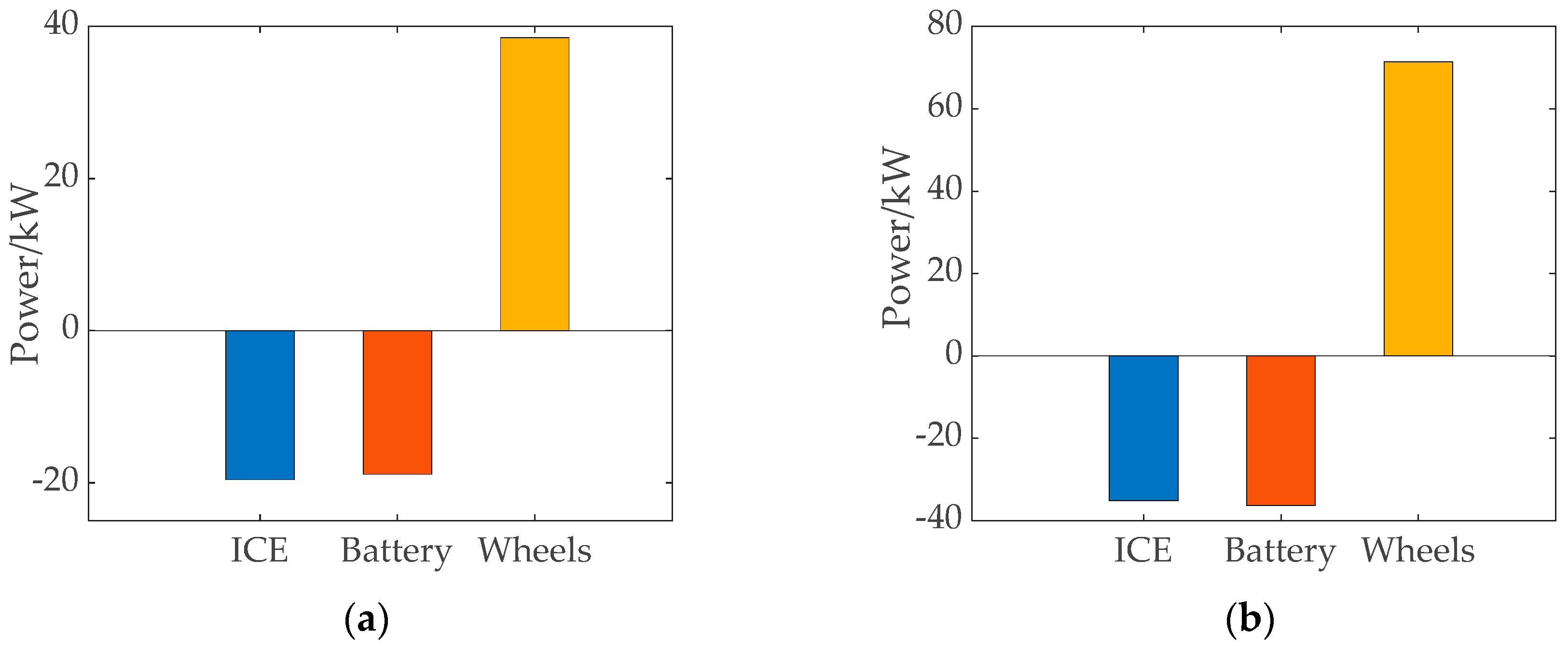
4.3.2. Pure Electric Mode (Mode 1)
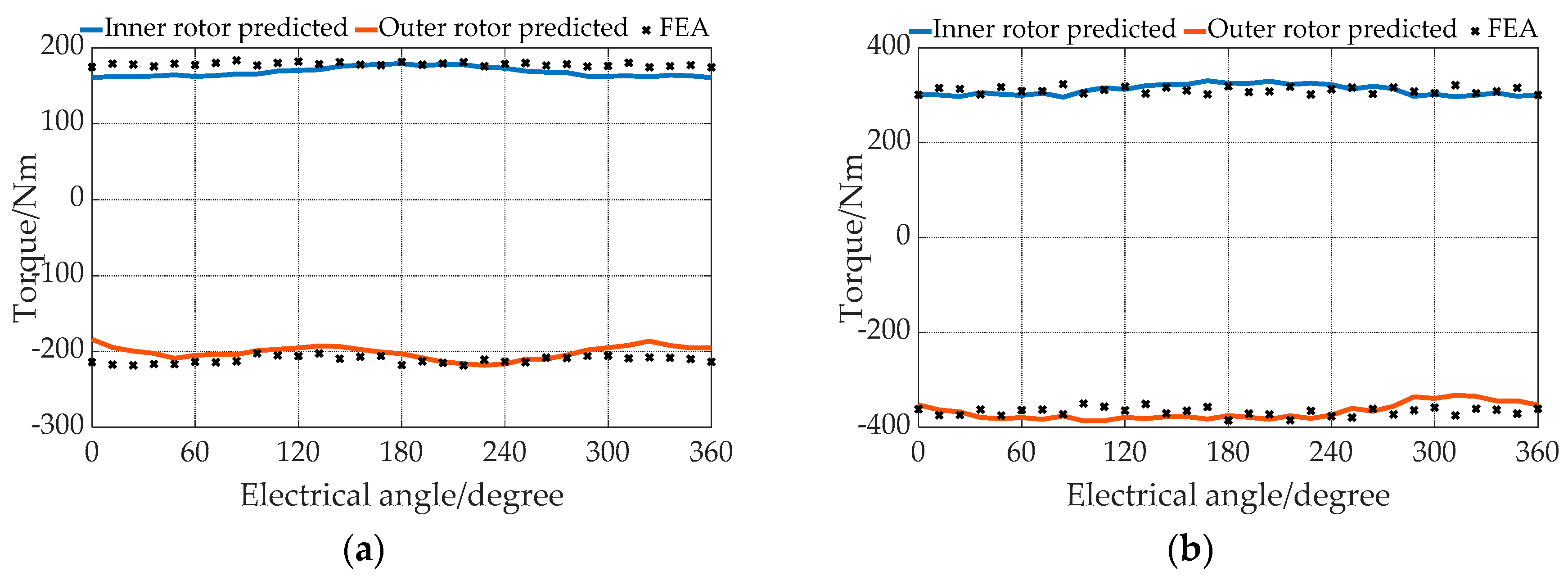
4.3.3. Pure Mechanical Mode (Mode 2)
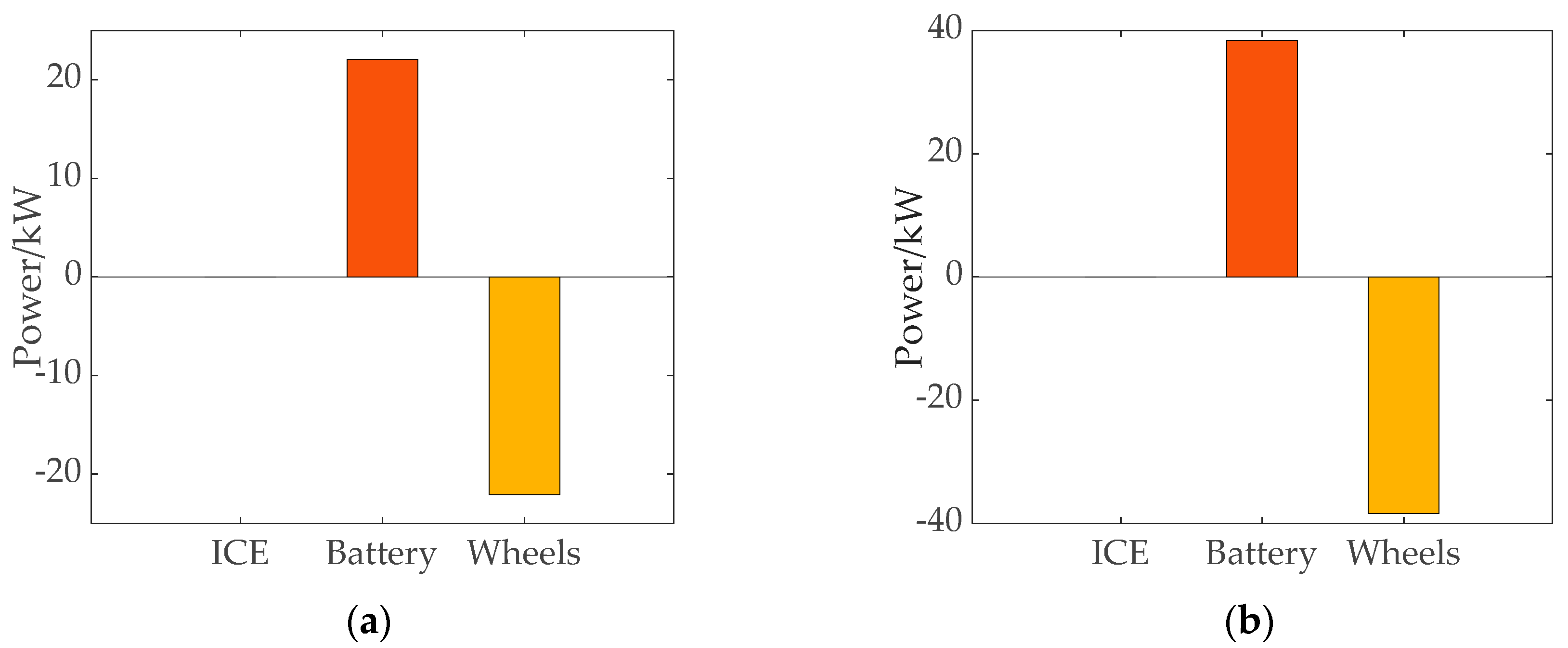
4.3.4. Hybrid Mode (Mode 3)
4.3.5. Regenerative Braking Mode (Mode 4)
4.3.6. Quantitative comparison between HMM and FEA
4.3.7. Discussion of HMM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Region | VMP Expression | Region | VMP Expression |
|---|---|---|---|
| I | II | ||
| III | IV | ||
| V | VI | ||
| VII | VIII | ||
| IX | X |
References
- Liu, C. Emerging Electric Machines and Drives—An Overview. IEEE Trans. Energy Convers. 2018, 33, 2270–2280. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Liu, Y. Analysis of Air-Gap Field Modulation and Magnetic Gearing Effect in Fractional-Slot Concentrated-Winding Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2018, 65, 3688–3698. [Google Scholar] [CrossRef] [Green Version]
- Atallah, K.; Rens, J.; Mezani, S.; Howe, D. A Novel “Pseudo” Direct-Drive Brushless Permanent Magnet Machine. IEEE Trans. Magn. 2008, 44, 4349–4352. [Google Scholar] [CrossRef]
- Atallah, K.; Howe, D. A novel high-performance magnetic gear. IEEE Trans. Magn. 2001, 37, 2844–2846. [Google Scholar] [CrossRef]
- Acharya, V.M.; Bird, J.Z.; Calvin, M. A Flux Focusing Axial Magnetic Gear. IEEE Trans. Magn. 2013, 49, 4092–4095. [Google Scholar] [CrossRef]
- Linni, J.; Chau, K.T.; Gong, Y.; Jiang, J.Z.; Chuang, Y.; Wenlong, L. Comparison of Coaxial Magnetic Gears With Different Topologies. IEEE Trans. Magn. 2009, 45, 4526–4529. [Google Scholar] [CrossRef] [Green Version]
- Holehouse, R.C.; Atallah, K.; Wang, J.B. Design and Realization of a Linear Magnetic Gear. IEEE Trans. Magn. 2011, 47, 4171–4174. [Google Scholar] [CrossRef]
- Liu, C.T.; Chung, H.Y.; Hwang, C.C. Design Assessments of a Magnetic-Geared Double-Rotor Permanent Magnet Generator. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Wang, L.L.; Shen, J.X.; Luk, P.C.K.; Fei, W.Z.; Wang, C.F.; Hao, H. Development of a Magnetic-Geared Permanent-Magnet Brushless Motor. IEEE Trans. Magn. 2009, 45, 4578–4581. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Chen, L.; Quan, L.; Sun, Y.; Hua, W.; Wang, Z. A New Magnetic-Planetary-Geared Permanent Magnet Brushless Machine for Hybrid Electric Vehicle. IEEE Trans. Magn. 2012, 48, 4642–4645. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.T. Electromagnetic Design of a New Electrically Controlled Magnetic Variable-Speed Gearing Machine. Energies 2014, 7, 1539–1554. [Google Scholar] [CrossRef] [Green Version]
- Ho, S.L.; Wang, Q.; Niu, S.; Fu, W.N. A Novel Magnetic-Geared Tubular Linear Machine With Halbach Permanent-Magnet Arrays for Tidal Energy Conversion. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Liu, C.; Yu, J.C.; Lee, C.H.T. A New Electric Magnetic-Geared Machine for Electric Unmanned Aerial Vehicles. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Song, Z.; Liu, S. A Consequent-Pole PM Magnetic-Geared Double-Rotor Machine With Flux-Weakening Ability for Hybrid Electric Vehicle Application. IEEE Trans. Magn. 2019, 1–7. [Google Scholar] [CrossRef]
- Sun, L.; Cheng, M.; Zhang, J.W.; Song, L.H. Analysis and Control of Complementary Magnetic-Geared Dual-Rotor Motor. IEEE Trans. Ind. Electron. 2016, 63, 6715–6725. [Google Scholar] [CrossRef]
- Bai, J.; Liu, J.; Zheng, P.; Tong, C. Design and Analysis of a Magnetic-Field Modulated Brushless Double-Rotor Machine—Part I: Pole Pair Combination of Stator, PM Rotor and Magnetic Blocks. IEEE Trans. Ind. Electron. 2019, 66, 2540–2549. [Google Scholar] [CrossRef]
- Chan, C.C. The state of the art of electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Miller, J.M. Hybrid electric vehicle propulsion system architectures of the e-CVT type. IEEE Trans. Power Electron. 2006, 21, 756–767. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Chau, K.T.; Zhang, Z. Novel Design of Double-Stator Single-Rotor Magnetic-Geared Machines. IEEE Trans. Magn. 2012, 48, 4180–4183. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.L.; Tsai, M.C. Kinematic and Dynamic Analysis of Magnetic Gear With Dual-Mechanical Port Using Block Diagrams. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Chen, L.; Hopkinson, D.; Wang, J.; Cockburn, A.; Sparkes, M.; O’Neill, W. Reduced Dysprosium Permanent Magnets and Their Applications in Electric Vehicle Traction Motors. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Baloch, N.; Kwon, B.I.; Gao, Y.T. Low-Cost High-Torque-Density Dual-Stator Consequent-Pole Permanent Magnet Vernier Machine. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, R.; Li, D.; Li, J.; Zhou, G. Consequent-Pole Flux-Reversal Permanent-Magnet Machine for Electric Vehicle Propulsion. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Wang, H.T.; Fang, S.H.; Yang, H.; Lin, H.Y.; Wang, D.; Li, Y.B.; Jiu, C.X. A Novel Consequent-Pole Hybrid Excited Vernier Machine. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Wang, Q.S.; Niu, S.X.; Yang, S.Y. Design Optimization and Comparative Study of Novel Magnetic-Geared Permanent Magnet Machines. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhang, X.X.; Liu, X.; Chen, Z. Investigation of Unbalanced Magnetic Force in Magnetic Geared Machine Using Analytical Methods. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Shin, K.H.; Cho, H.W.; Kim, K.H.; Hong, K.; Choi, J.Y. Analytical Investigation of the On-Load Electromagnetic Performance of Magnetic-Geared Permanent-Magnet Machines. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Djelloul-Khedda, Z.; Boughrara, K.; Dubas, F.; Kechroud, A.; Tikellaline, A. Analytical Prediction of Iron-Core Losses in Flux-Modulated Permanent-Magnet Synchronous Machines. IEEE Trans. Magn. 2019, 55, 1–12. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Two-Dimensional Analytical Calculation of Magnetic Field and Electromagnetic Torque for Surface-Inset Permanent-Magnet Motors. IEEE Trans. Magn. 2012, 48, 2080–2091. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Analytical Computation of the Magnetic Field Distribution in a Magnetic Gear. IEEE Trans. Magn. 2010, 46, 2611–2621. [Google Scholar] [CrossRef]
- Sprangers, R.L.J.; Paulides, J.J.H.; Gysen, B.L.J.; Lomonova, E.A. Magnetic Saturation in Semi-Analytical Harmonic Modeling for Electric Machine Analysis. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Bai, J.G.; Zheng, P.; Tong, C.D.; Song, Z.Y.; Zhao, Q.B. Characteristic Analysis and Verification of the Magnetic-Field-Modulated Brushless Double-Rotor Machine. IEEE Trans. Ind. Electron. 2015, 62, 4023–4033. [Google Scholar] [CrossRef]
- Chung, C.-T.; Wu, C.-H.; Hung, Y.-H. Effects of Electric Circulation on the Energy Efficiency of the Power Split e-CVT Hybrid Systems. Energies 2018, 11, 2342. [Google Scholar] [CrossRef]
- Li, L. Use of Fourier series in the analysis of discontinuous periodic structures. JOSA A 1996, 13, 1870–1876. [Google Scholar] [CrossRef]
- Articolo, G.A. Partial Differential Equations and Boundary Value Problems with Maple, 2nd ed.; Elsevier: Burlington, MA, USA, 2009; pp. 29–30. [Google Scholar]
- Djelloul-Khedda, Z.; Boughrara, K.; Dubas, F.; Ibtiouen, R. Nonlinear Analytical Prediction of Magnetic Field and Electromagnetic Performances in Switched Reluctance Machines. IEEE Trans. Magn. 2017, 53, 1–11. [Google Scholar] [CrossRef]
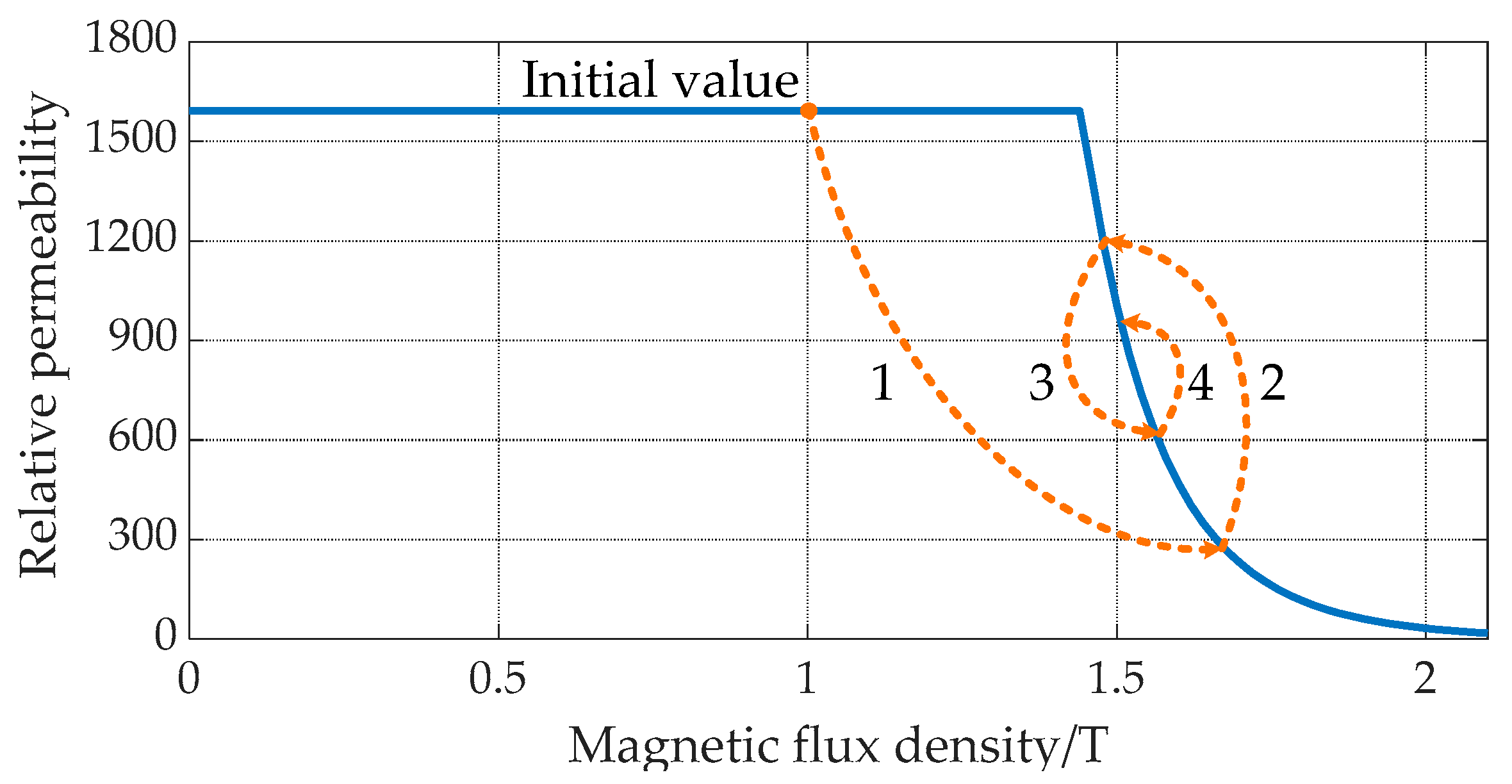
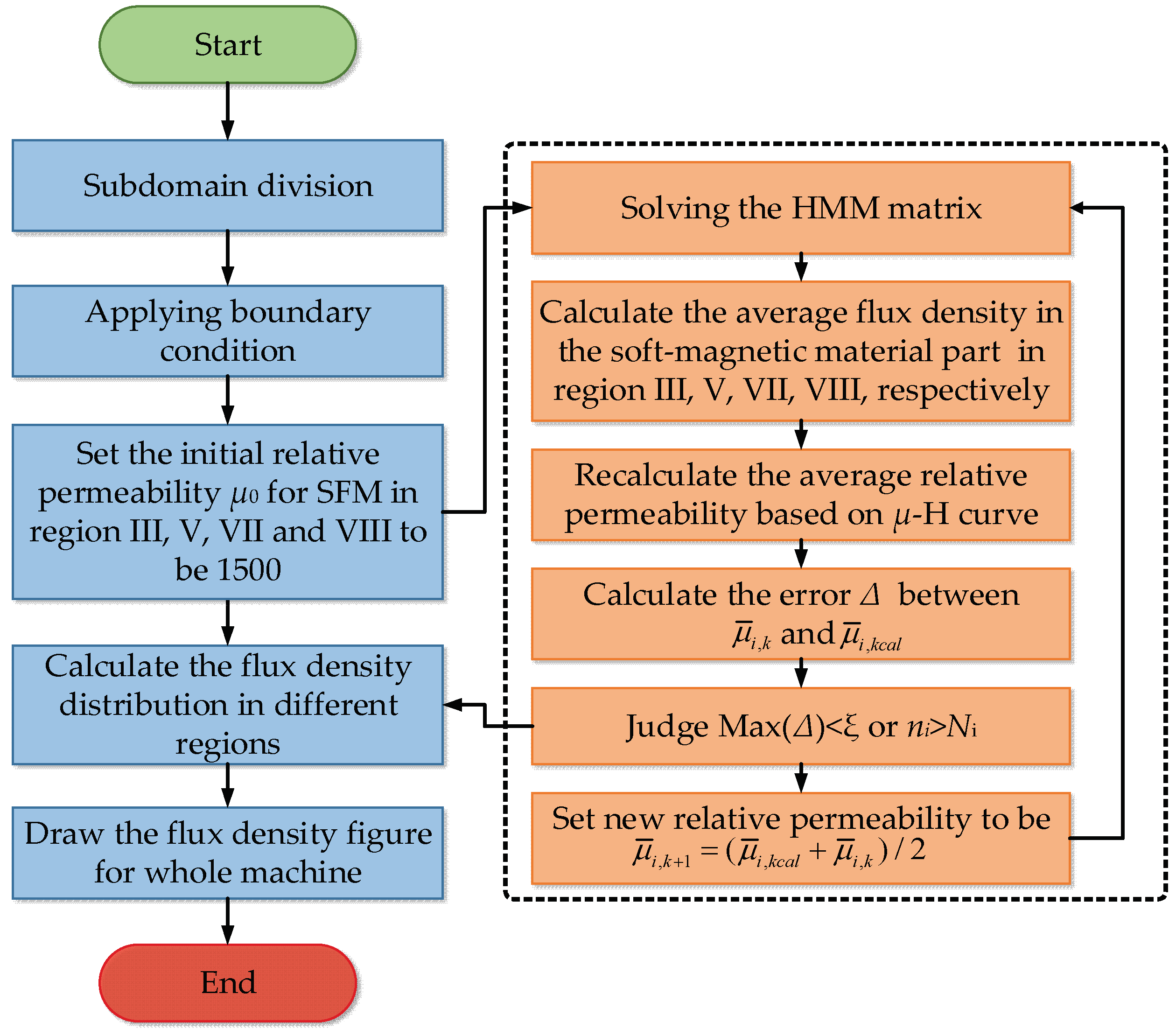
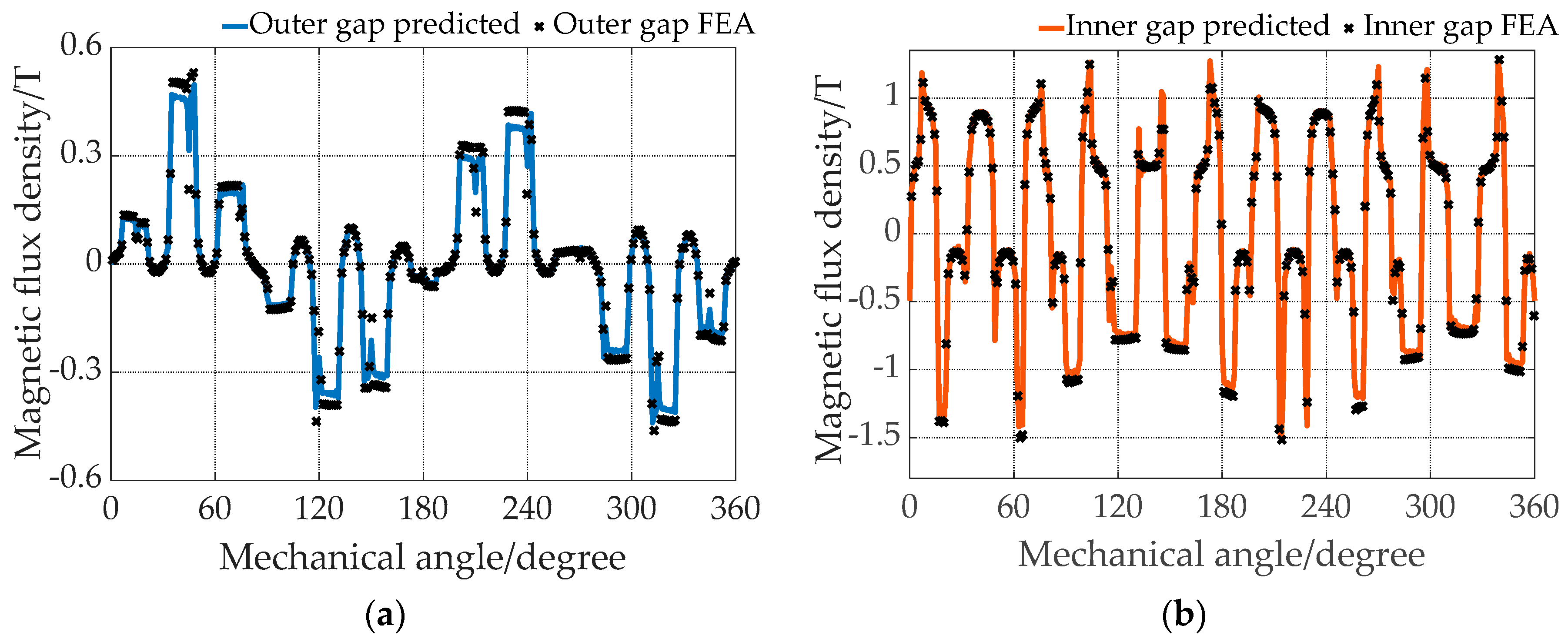
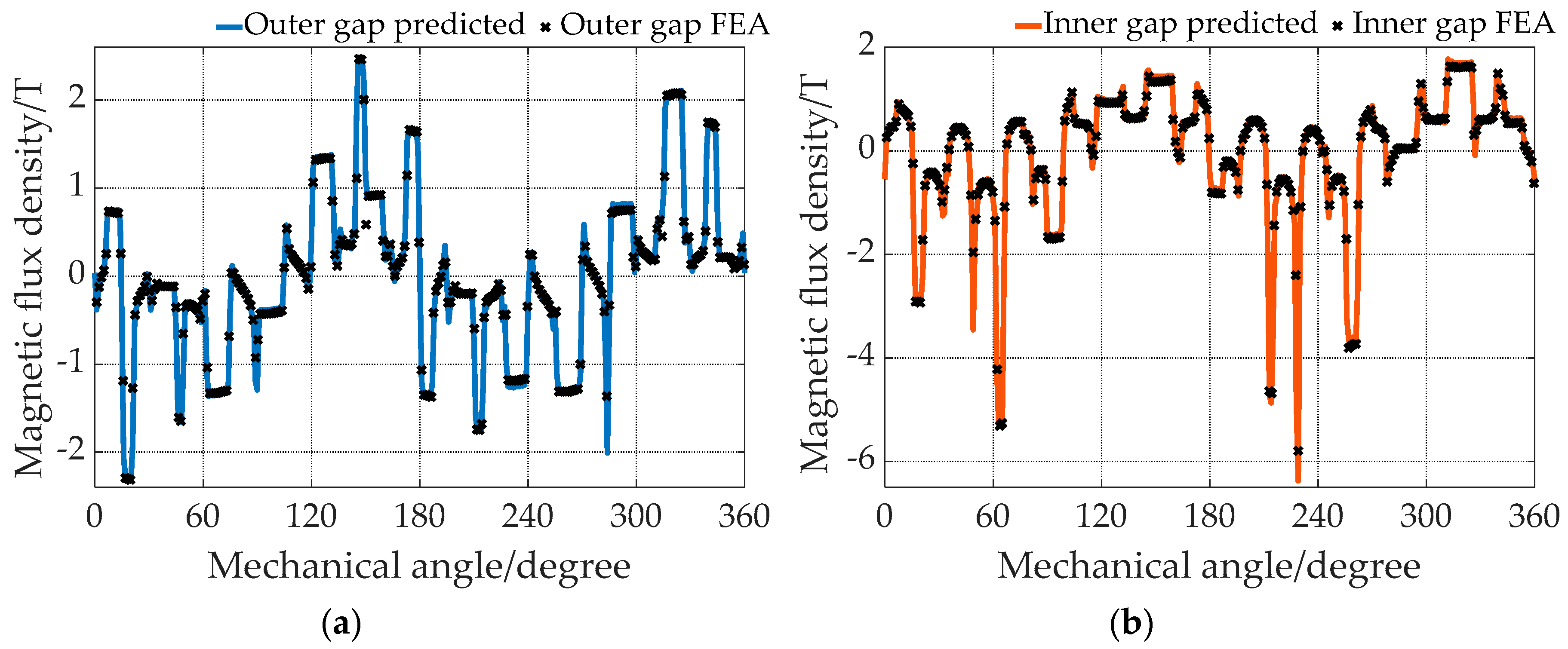

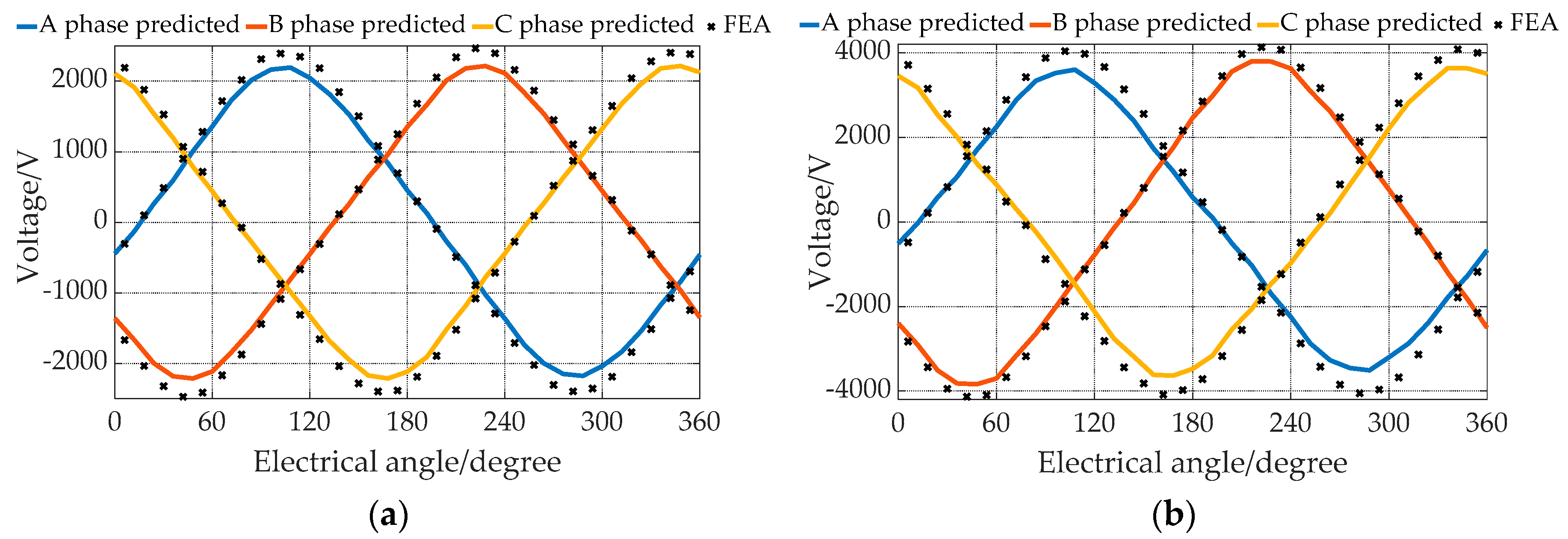

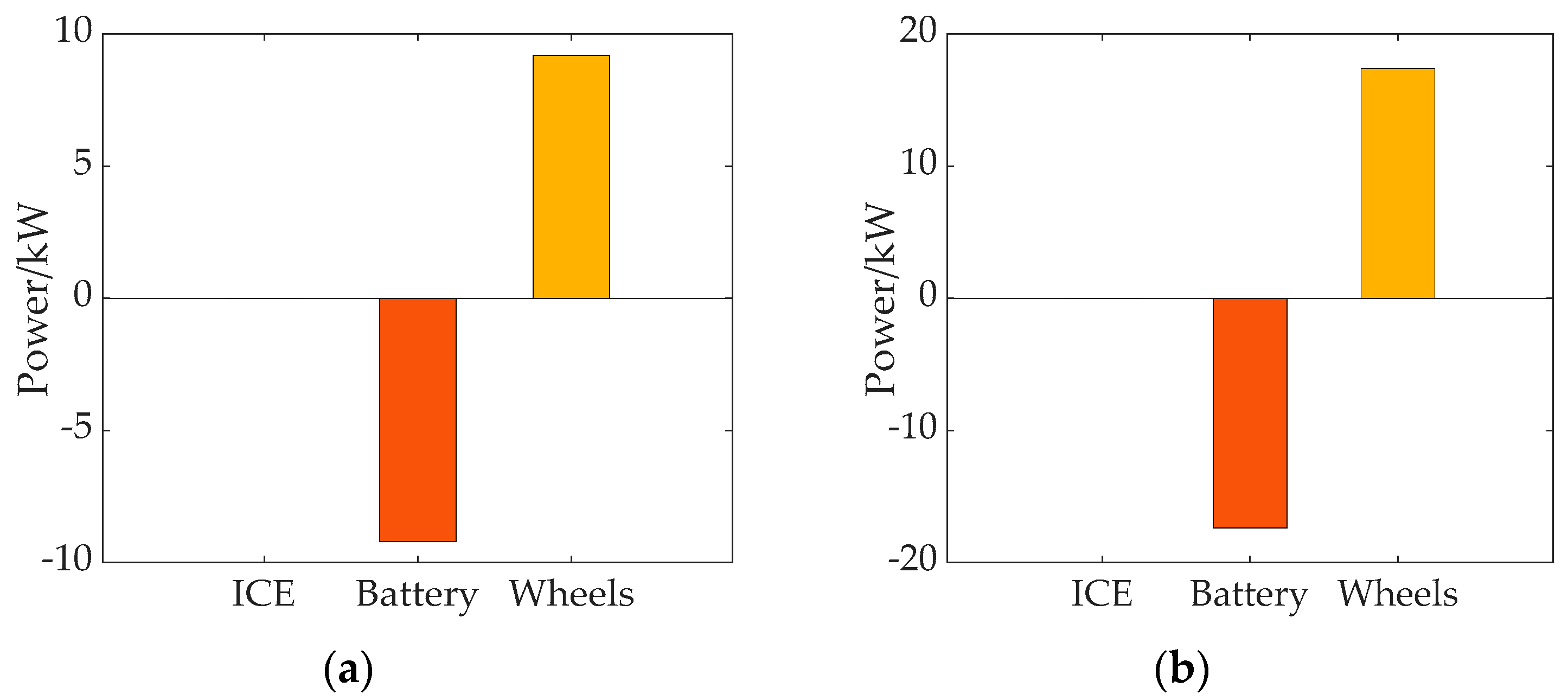
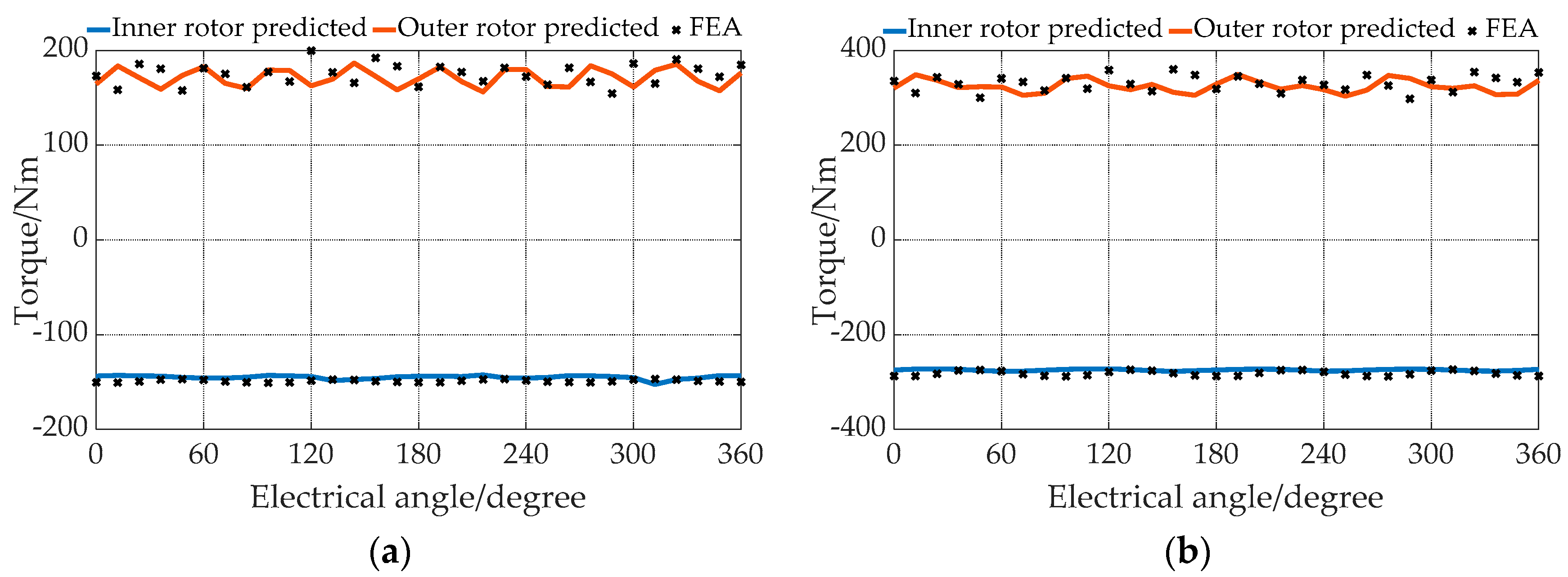
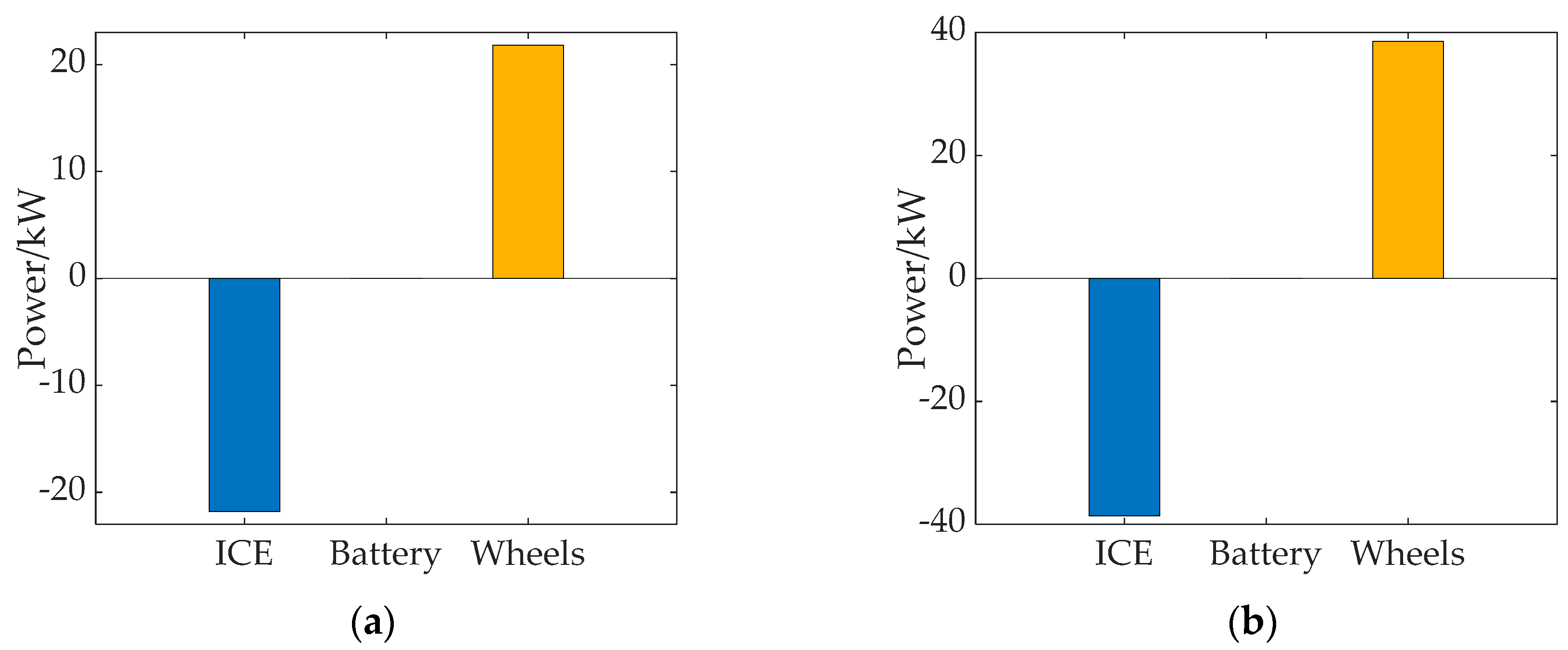
| Operation Modes | Rotating Speed of Inner Rotor ωo | Rotating Speed of Outer Rotor ωi | Current Frequency f |
|---|---|---|---|
| Pure electric mode | 0 r/min | 500 r/min | 108.3 Hz |
| Pure mechanical mode | 1200 r/min | 1015 r/min | 0 Hz (DC) |
| Hybrid mode | 1200 r/min | 2000 r/min | 213.3 Hz |
| Regenerative braking mode | 0 r/min | 1000 r/min | 216.6 Hz |
| Sources | Illustrative Waveforms | Fourier Series Coefficients |
|---|---|---|
| Inner PM (Region III) | 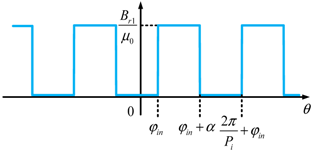 | |
| Outer PM (Only for DCP-MGM) (Region V) | 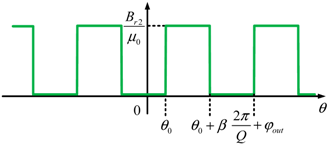 | |
| Stator windings (Region VIII) | 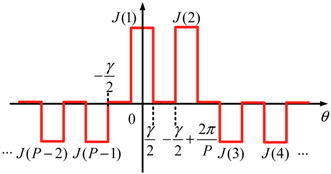 |
| Regions | Illustrative Waveforms | Coefficients |
|---|---|---|
| III | 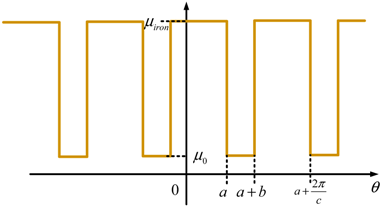 | a = φin, b = α, c = Pi |
| V | a = φin, b = β, c = Q | |
| VII | a = δ/2, b = 2π/Ps − δ, c = Ps | |
| VIII | a = γ/2, b = 2π/Ps − γ, c = Ps |
| Regions | SCP-MGM | DCP-MGM |
|---|---|---|
| III | 27.46 | 27.92 |
| V | 1309.15 | 1257.49 |
| VII | 888.05 | 838.35 |
| VIII | 1013.2 | 917.24 |
| Parameters | Symbols | Values | Units |
|---|---|---|---|
| Number of inner PM pole pairs | Pi | 11 | - |
| Number of modulator pieces | Q | 13 | - |
| Number of stator slots | P | 24 | - |
| Number of stator winding pole pairs | Ps | 2 | - |
| Axial length | L | 110 | mm |
| Outer radius of shaft | R1 | 25 | mm |
| Inner radius of inner PM | R2 | 55.5 | mm |
| Outer radius of inner rotor | R3 | 63.2 | mm |
| Inner radius of outer rotor | R4 | 63.8 | mm |
| Outer radius of outer rotor | R5 | 74.4 | mm |
| Inner radius of stator | R6 | 75 | mm |
| Radius of stator slot bottom | R7 | 78 | mm |
| Outer radius of stator slot | R8 | 109 | mm |
| Outer radius of stator | R9 | 120 | mm |
| Angle of inner PM arc | α | 0.286 | rad |
| Angle of Modulator piece | β | 0.242 | rad |
| Angle of slot opening | δ | 0.032 | rad |
| Angle of stator slot | γ | 0.168 | rad |
| Slot filling factor | Fa | 60% | - |
| Current density in stator windings | ID | 5 | A/mm2 |
| State | SCP-MGM | DCP-MGM | ||||||
|---|---|---|---|---|---|---|---|---|
| Inner Rotor | Outer Rotor | Inner Rotor | Outer Rotor | |||||
| ε1 | ε2 | ε1 | ε2 | ε1 | ε2 | ε1 | ε2 | |
| No-load | 9.3% | 0.55 T | 15.9% | 0.11 T | 11.4% | 1.06 T | 14.4% | 0.70 T |
| On-load | 14.2% | 1.62 T | 14.3% | 0.83 T | 20.8% | 3.11 T | 16.7% | 1.36 T |
| Mode | SCP-MGM | DCP-MGM | ||||||
|---|---|---|---|---|---|---|---|---|
| Inner Rotor | Outer Rotor | Inner Rotor | Outer Rotor | |||||
| ε1 | ε2 | ε1 | ε2 | ε1 | ε2 | ε1 | ε2 | |
| 1 | 3.59% | 12.1 Nm | 2.64% | 14.8 Nm | 3.55% | 22.5 Nm | 4.46% | 30.3 Nm |
| 2 | 3.00% | 7.85 Nm | 7.39% | 37.2 Nm | 2.57% | 14.9 Nm | 5.88% | 48.6 Nm |
| 3 | 2.75% | 8.9 Nm | 3.61% | 15.2 Nm | 2.27% | 15.3 Nm | 3.27% | 30.3 Nm |
| 4 | 5.73% | 18.1 Nm | 5.06% | 30.0 Nm | 3.50% | 28.4 Nm | 4.56% | 43.0 Nm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Liu, C.; Song, Z.; Yu, J. Analytical Modeling and Comparison of Two Consequent-Pole Magnetic-Geared Machines for Hybrid Electric Vehicles. Energies 2019, 12, 1888. https://doi.org/10.3390/en12101888
Zhao H, Liu C, Song Z, Yu J. Analytical Modeling and Comparison of Two Consequent-Pole Magnetic-Geared Machines for Hybrid Electric Vehicles. Energies. 2019; 12(10):1888. https://doi.org/10.3390/en12101888
Chicago/Turabian StyleZhao, Hang, Chunhua Liu, Zaixin Song, and Jincheng Yu. 2019. "Analytical Modeling and Comparison of Two Consequent-Pole Magnetic-Geared Machines for Hybrid Electric Vehicles" Energies 12, no. 10: 1888. https://doi.org/10.3390/en12101888
APA StyleZhao, H., Liu, C., Song, Z., & Yu, J. (2019). Analytical Modeling and Comparison of Two Consequent-Pole Magnetic-Geared Machines for Hybrid Electric Vehicles. Energies, 12(10), 1888. https://doi.org/10.3390/en12101888








