Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs
Abstract
1. Introduction
2. Materials and Methods
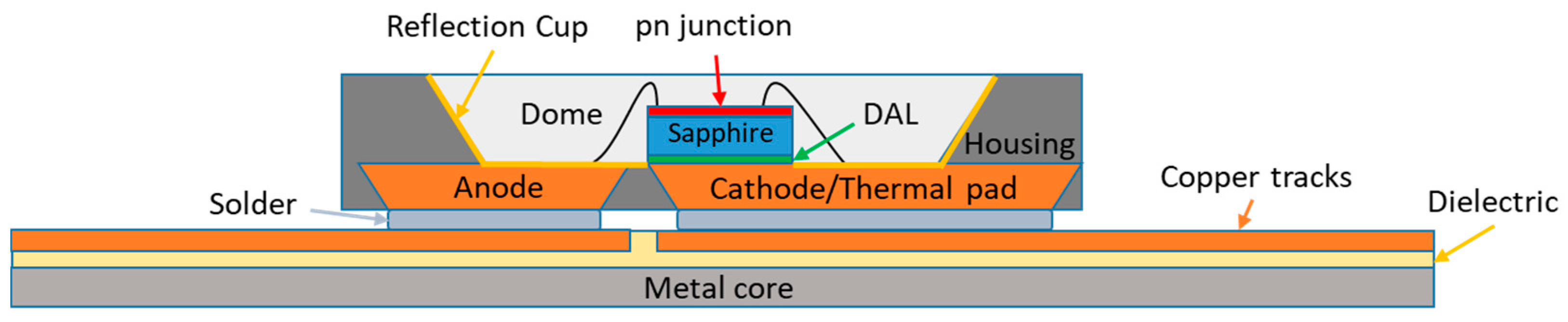
2.1. LEDs Architecture
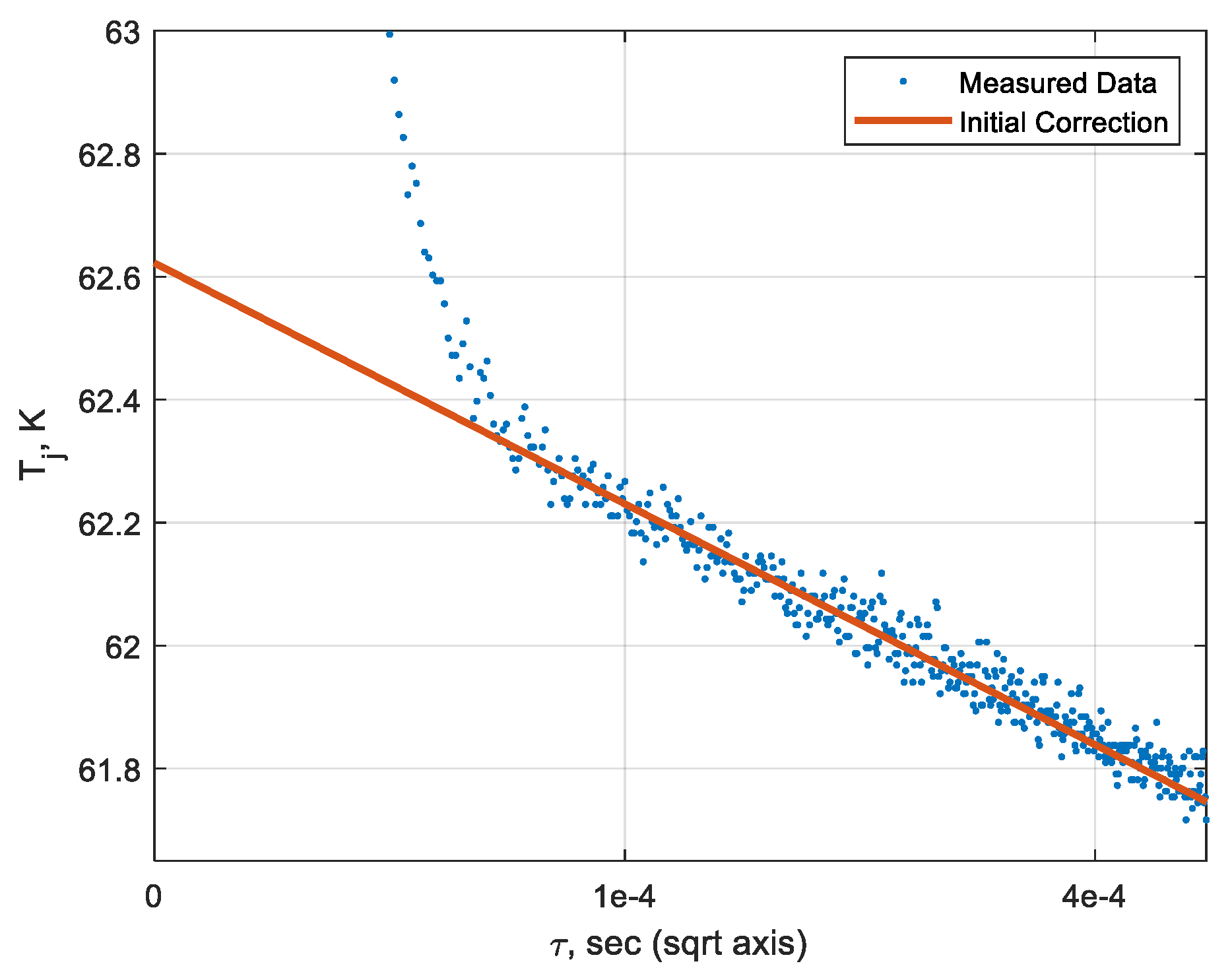
2.2. Thermal Transient Analysis
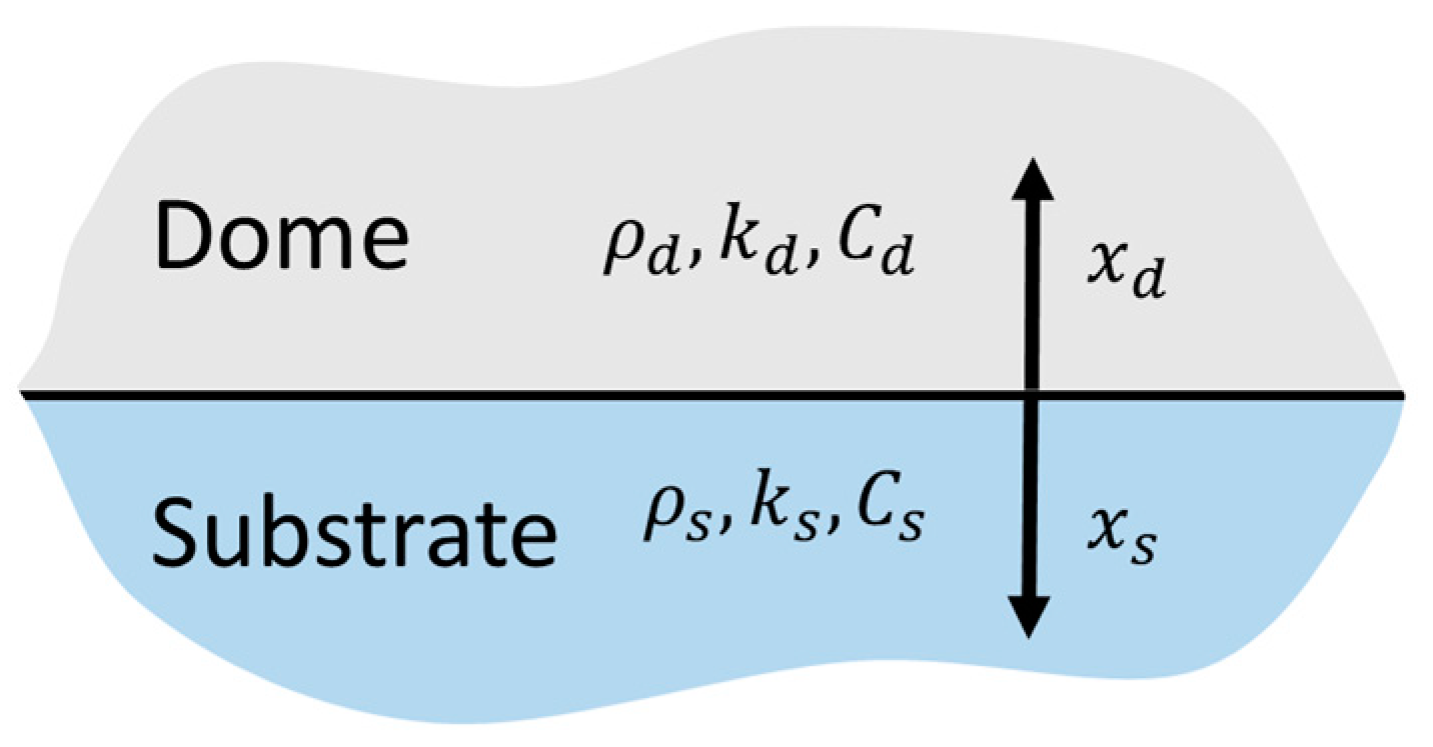
2.3. Thermal FEA Modeling
2.4. Experimental Setup and Physical Specimens
2.5. Multiple Heat Source Characterization
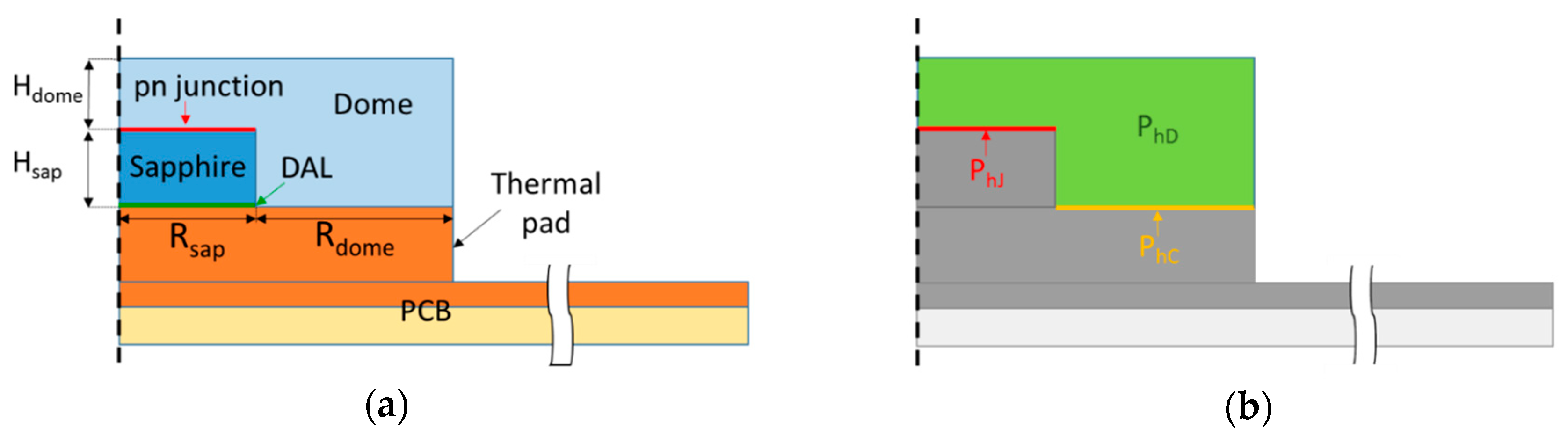
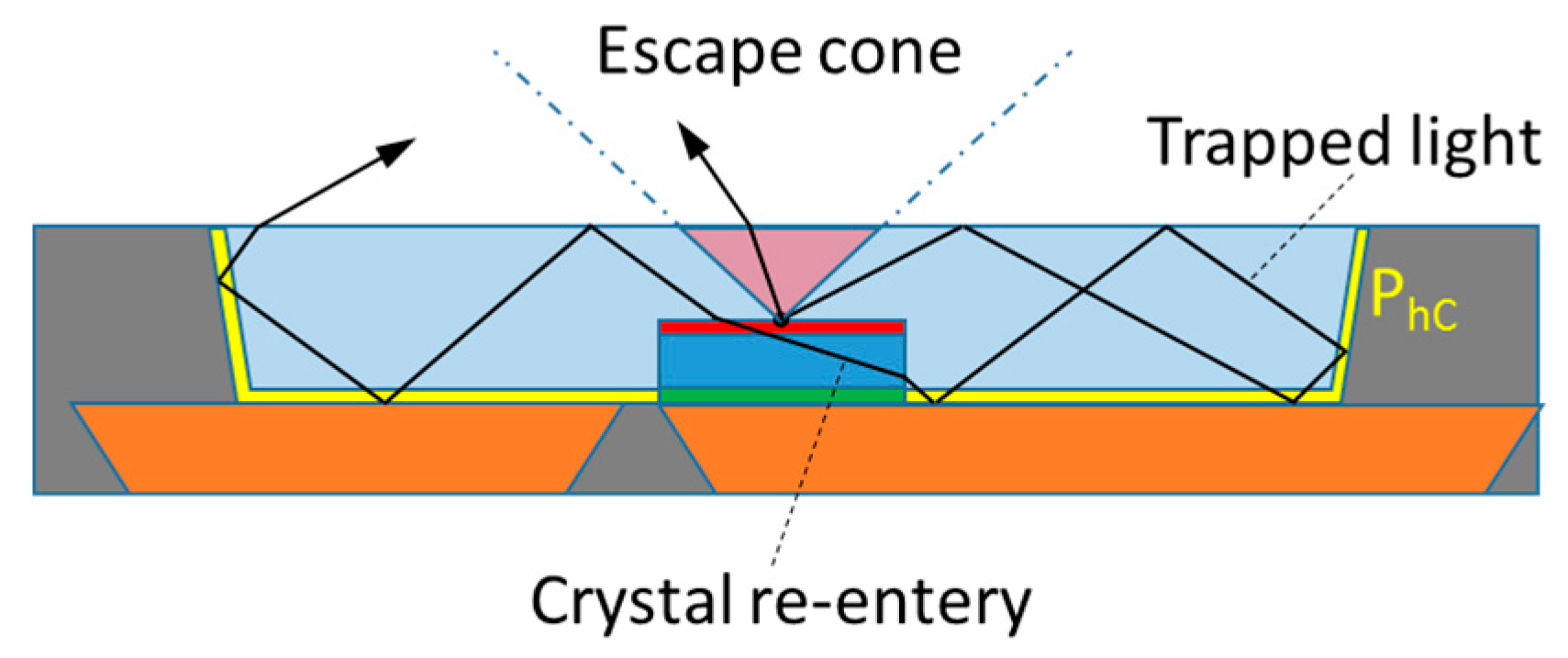
2.5.1. Secondary Heat Sources
2.5.2. Estimation of the Secondary Heat Sources
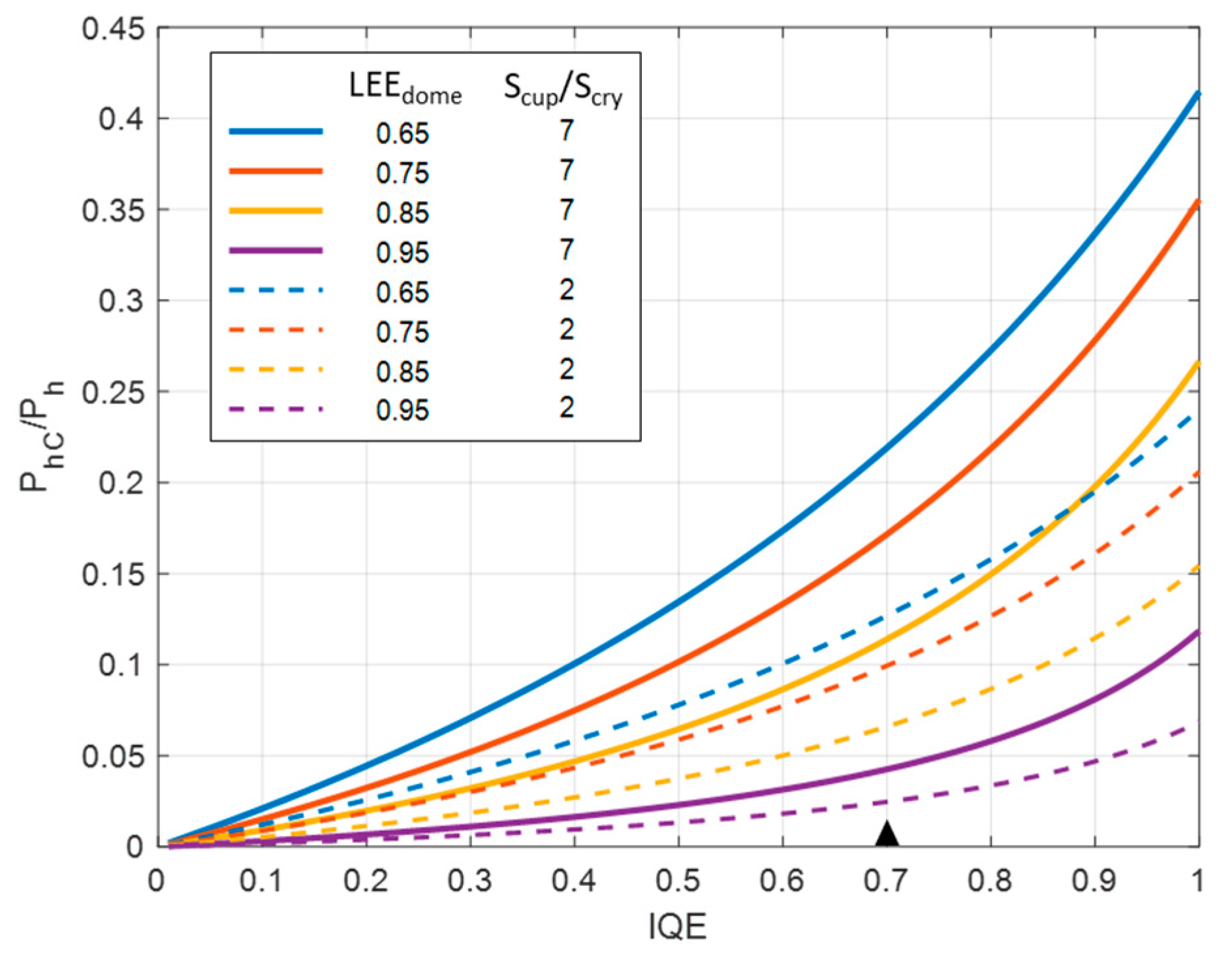
2.5.3. Applicability of the Approach for LEDs with Phosphor Light Conversion
3. Results
3.1. Numerical Simulations
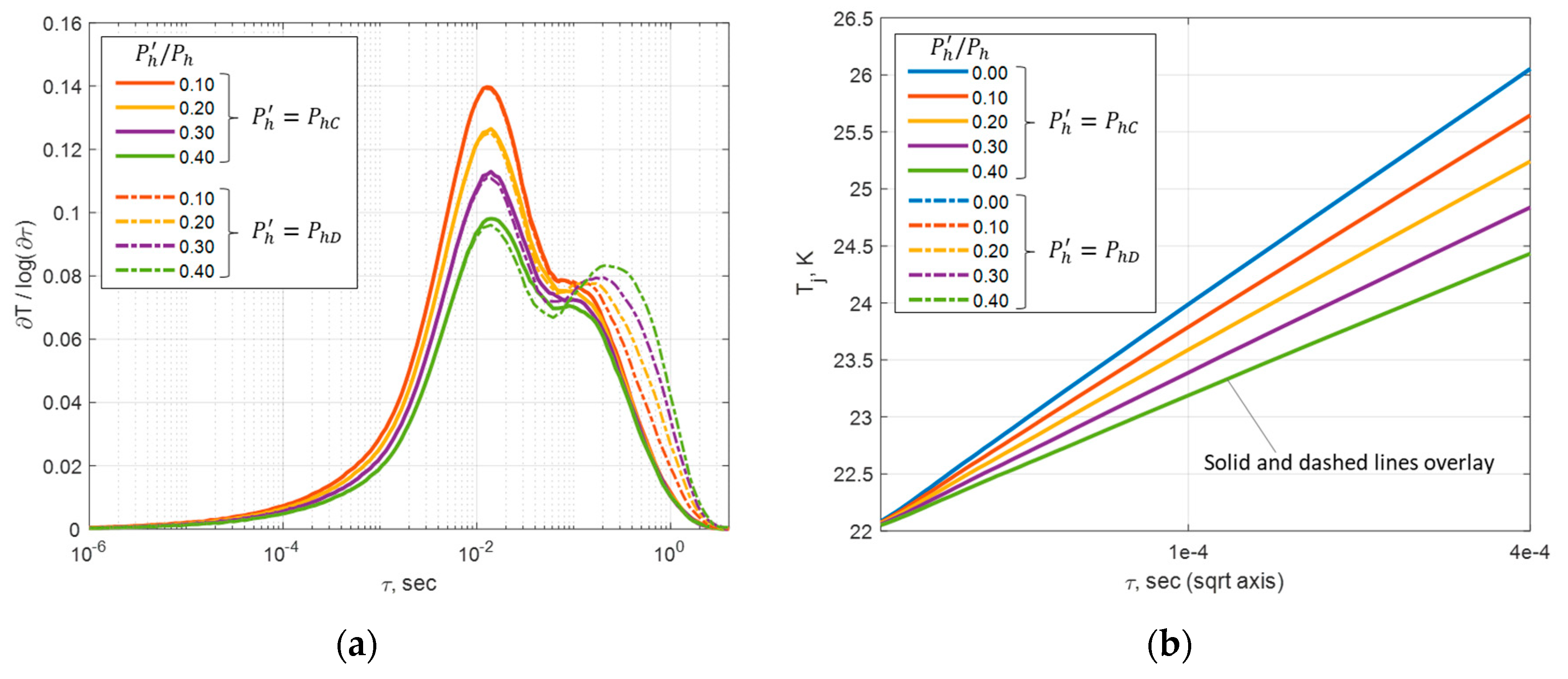
3.1.1. Secondary Heat Sources Impact on Junction Thermal Transient
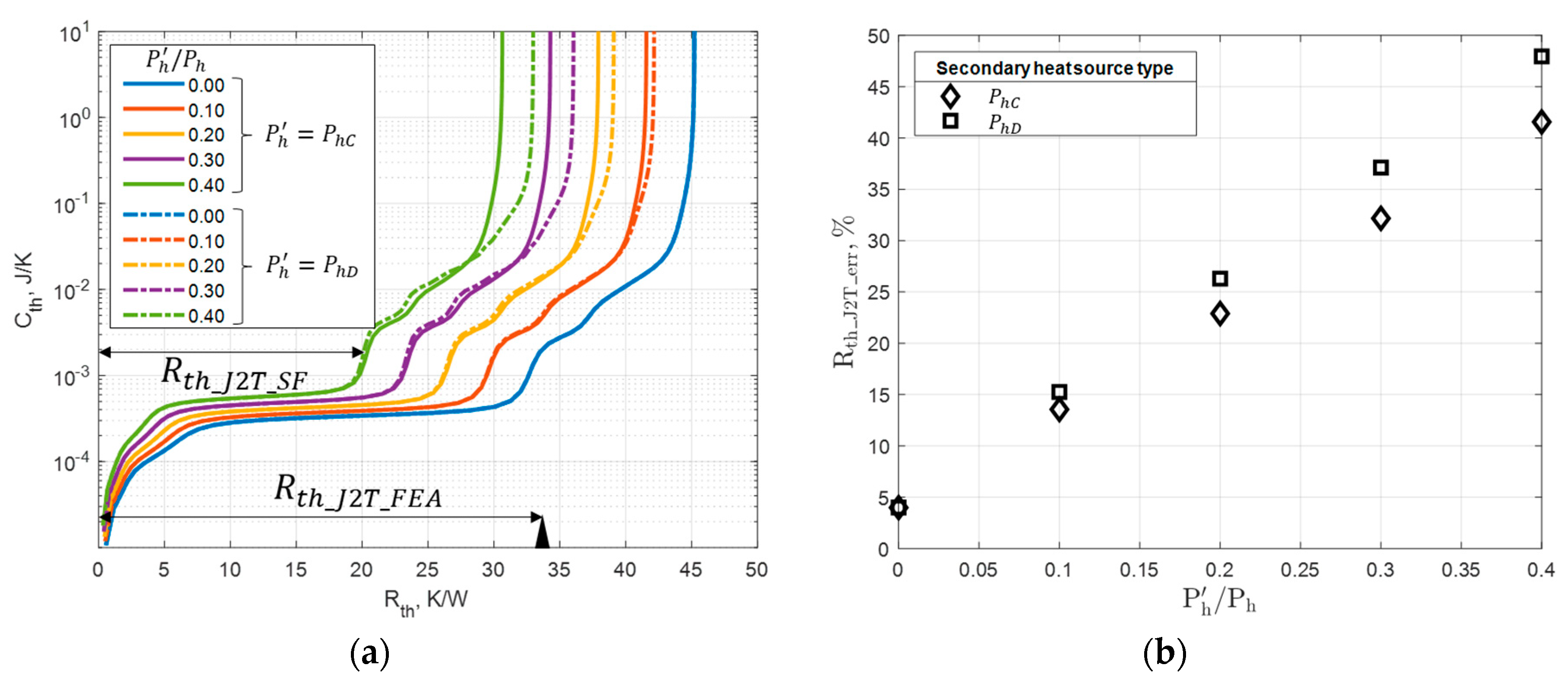
3.1.2. Secondary Heat Sources Estimation Verification
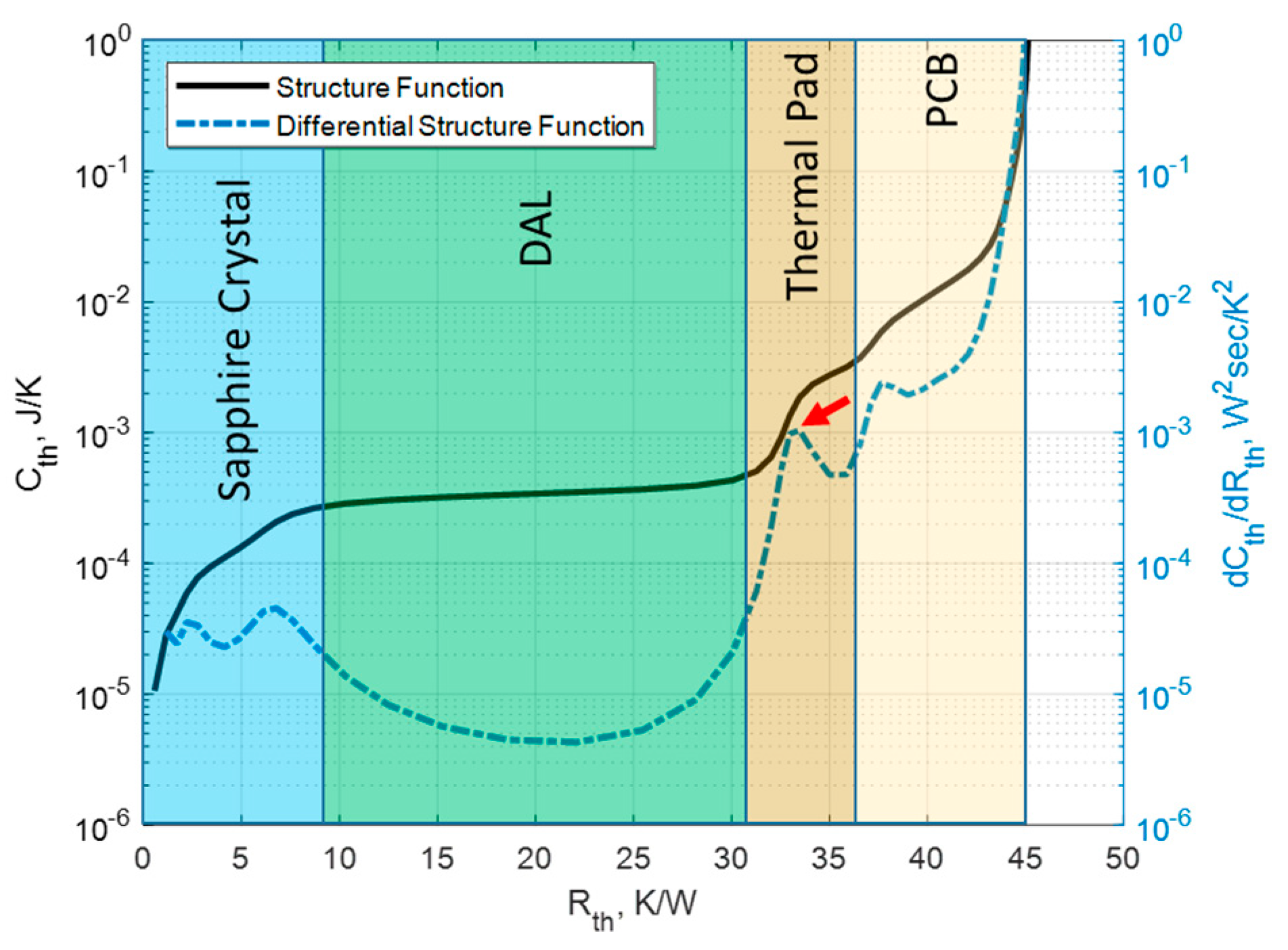
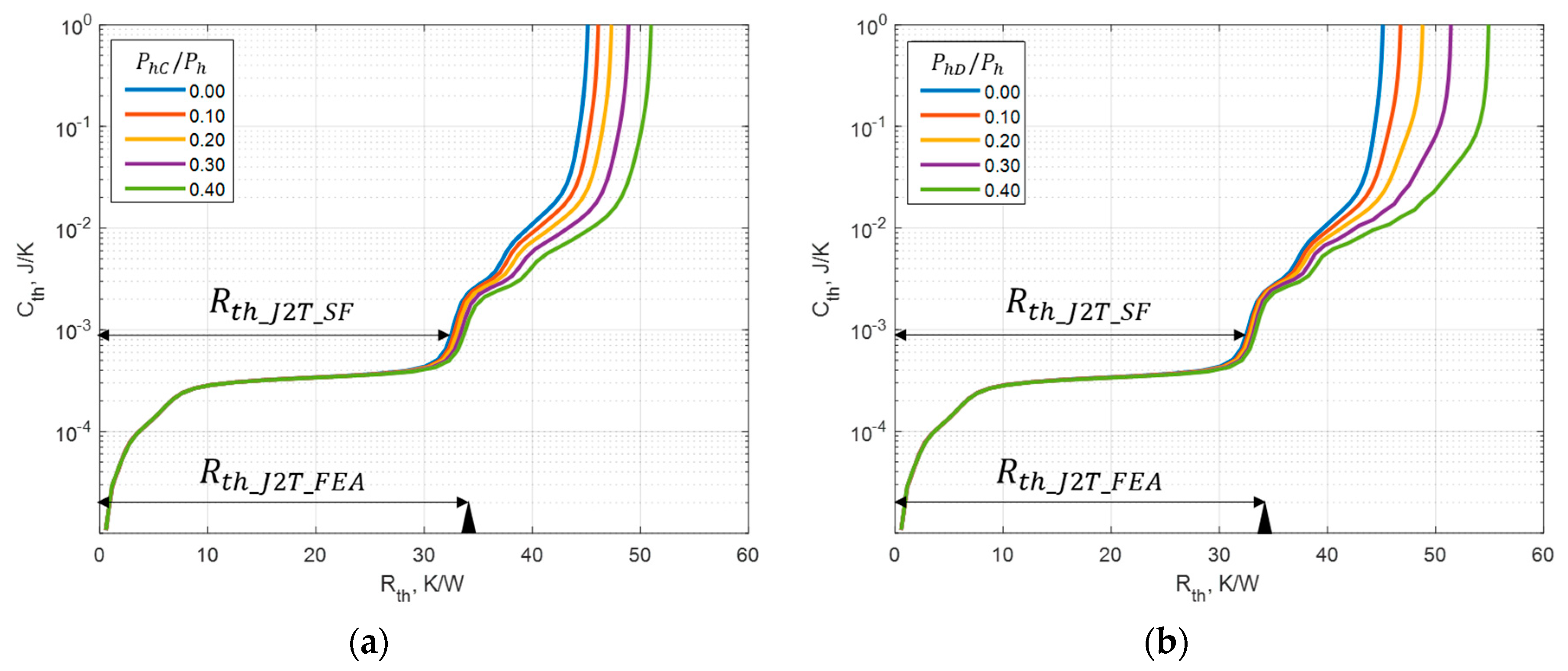
3.1.3. Secondary Heat Sources Impact on Structure Functions
3.1.4. Die and DAL Thermal Characterization
3.2. Experimental Verification
- The silicone dome enhances the light extraction from the chip into the encapsulant;
- The enhanced light extraction from the chip leads to a reduction of (Table 3); and
- The light is trapped in silicone dome due to TIR and is absorbed on the reflector surfaces, this effect increases .
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CTM | Compact thermal model |
| DAL | Die attach layer |
| DUT | Device Under Test |
| FEA | Finite Element Analysis |
| LED | Light-emitting diode |
| PCB | Printed circuit board |
| MCPCB | Metal core PCB |
| MP | Mid-power |
| SF | Structure function |
| TIR | Total internal reflection |
| External quantum efficiency | |
| Internal quantum efficiency | |
| Current | |
| Nondimensional parameter characterizing composite particles | |
| Phosphor particles volume fraction | |
| Crystal light re-absorption correction coefficient | |
| Electric power | |
| Radiant flux | |
| Total thermal power | |
| Combined secondary heat sources thermal power | |
| Thermal power dissipated in a pn junction | |
| Thermal power dissipated in a crystal during the trapped light re-entries | |
| Thermal power dissipated on the cup reflector surface | |
| Thermal power dissipated in the dome volume | |
| Thermal capacitance | |
| Thermal resistance | |
| Heat flow | |
| suffix made of two capital letters separated by “2”. The letters are can be “J”, “”, “”, and “”, denoting pn junction, and the LEDs’ dome, top of the thermal pad and case. The suffix denotes elements connecting two entities. The suffix can be followed by “FEA” which designates value derived directly from finite element analysis, “SF” which designates value derived from a structure function and “err” which designated the relative error of the value. | |
| pn junction area | |
| Reflector cup area | |
| Crystal chip area | |
| Average number of the photons bouncing off the cup walls | |
| Average number of crystal re-entries by photons | |
| Time | |
| Temperature | |
| Density | |
| Thermal conductivity | |
| Specific heat | |
| Spatial coordinate | |
| Heat flux | |
| Height | |
| Radius | |
| Volume | |
| suffix that can be “a”, “j”, “”, “”, “”, “”, and “” denoting ambient, pn junction, LEDs’ dome, pn junction substrate, silicone, phosphor, and sapphire materials, respectively | |
| Unilateral heat propagation initial transient constant | |
| Bilateral heat propagation initial transient constant | |
| Total light extraction efficiency | |
| Chip to dome light extraction efficiency | |
| Dome to ambient light extraction efficiency |
Appendix A
Appendix B
Appendix C
References
- Schilders, W.H.; Van der Vorst, H.A.; Rommes, J. (Eds.) Model Order Reduction: Theory, Research Aspects and Applications; Mathematics in Industry; Springer: Berlin/Heidelberg, Germany, 2008; Volume 13, ISBN 978-3-540-78840-9. [Google Scholar]
- Lasance, C.; Vinke, H.; Rosten, H.; Weiner, K.-L. A novel approach for the thermal characterization of electronic parts. In Proceedings of the 1995 IEEE/CPMT 11th Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), San Jose, CA, USA, 7–9 February 2011; Volume 36, pp. 1–9. [Google Scholar]
- Sabry, M. Compact thermal models for electronic systems. IEEE Trans. Components Packag. Technol. 2003, 26, 179–185. [Google Scholar] [CrossRef]
- Alexeev, A.; Bornoff, R.; Lungten, S.; Martin, G.; Onushkin, G.; Poppe, A.; Rencz, M.; Yu, J. Requirements specification for multi-domain LED compact model development in Delphi4LED. In Proceedings of the 2017 18th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Dresden, Germany, 3–5 April 2017; pp. 1–8. [Google Scholar]
- Bornoff, R.; Hildenbrand, V.; Lugten, S.; Martin, G.; Marty, C.; Poppe, A.; Rencz, M.; Schilders, W.H.A.; Yu, J. Delphi4LED—From measurements to standardized multi-domain compact models of LED: A new European R & D project for predictive and efficient multi-domain modeling and simulation of LEDs at all integration levels along the SSL supply chain. In Proceedings of the 2016 22nd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Budapest, Hungary, 21–23 September 2016; pp. 174–180. [Google Scholar]
- Lungten, S.; Bornoff, R.; Dyson, J.; Maubach, J.M.L.; Schilders, W.H.A.; Warner, M. Dynamic compact thermal model extraction for LED packages using model order reduction techniques. In Proceedings of the 2017 23rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Amsterdam, The Netherlands, 27–29 September 2017; pp. 1–6. [Google Scholar]
- Bornoff, R.; Farkas, G.; Gaal, L.; Rencz, M.; Poppe, A. LED 3D thermal model calibration against measurement. In Proceedings of the 2018 19th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Toulouse, France, 15–18 April 2018; pp. 1–7. [Google Scholar]
- Meyer, J.; Thomas, C.; Tappe, F.; Ogbazghi, T. In Depth Analyses of LEDs by a Combination of X-ray Computed Tomography (CT) and Light Microscopy (LM) Correlated with Scanning Electron Microscopy (SEM). J. Vis. Exp. 2016. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Lee, K.H. Evaluation of the internal quantum efficiency in light-emitting diodes. J. Korean Phys. Soc. 2015, 67, 658–662. [Google Scholar] [CrossRef]
- Ryu, H.Y.; Ryu, G.H.; Lee, S.H.; Kim, H.J. Evaluation of internal quantum efficiency in blue and green light-emitting diodes using rate equation model. In Proceedings of the 2013 Conference on Lasers and Electro-Optics Pacific Rim (CLEOPR), Kyoto, Japan, 30 June–4 July 2013; pp. 1–2. [Google Scholar]
- Lin, Y.; Tran, N.; Zhou, Y.; He, Y.; Shi, F. Materials Challenges and Solutions for the Packaging of High Power LEDs. In Proceedings of the 2006 International Microsystems, Package, Assembly Conference Taiwan, Taipei, Taiwan, 18–20 October 2006; pp. 1–4. [Google Scholar]
- Diodes, R.P.L.; Ma, Y.; Yu, X.; Xie, B.; Hu, R.; Luo, X. Analysis of Phosphor Heat Generation and Temperature Distribution in Analysis of Phosphor Heat Generation and Temperature Distribution in Remote- plate Phosphor-Converted Light-Emitting Diodes. In Proceedings of the Asian Conferenceon Thermal Sciences 2017, Jeju Island, Korea, 26–30 March 2017; pp. 1–6. [Google Scholar]
- Juntunen, E.; Tapaninen, O.; Sitomaniemi, A.; Heikkinen, V. Effect of Phosphor Encapsulant on the Thermal Resistance of a High-Power COB LED Module. IEEE Trans. Components Packag. Manuf. Technol. 2013, 3, 1148–1154. [Google Scholar] [CrossRef]
- Kim, J.K.; Luo, H.; Schubert, E.F.; Cho, J.; Sone, C.; Park, Y. Strongly Enhanced Phosphor Efficiency in GaInN White Light-Emitting Diodes Using Remote Phosphor Configuration and Diffuse Reflector Cup. Jpn. J. Appl. Phys. 2005, 44, L649–L651. [Google Scholar] [CrossRef]
- Alexeev, A.; Martin, G.; Hildenbrand, V.; Bosschaart, K.J. Influence of dome phosphor particle concentration on mid-power LED thermal resistance. In Proceedings of the 2016 32nd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 14–17 March 2016; pp. 33–43. [Google Scholar]
- Treurniet, T.; Lammens, V. Thermal management in color variable multi-chip led modules. In Proceedings of the Twenty-Second Annual IEEE Semiconductor Thermal Measurement And Management Symposium, Dallas, TX, USA, 14–16 March 2006; pp. 173–177. [Google Scholar]
- Poppe, A.; Zhang, Y.; Wilson, J.; Farkas, G.; Szabo, P.; Parry, J.; Rencz, M.; Szekely, V. Thermal Measurement and Modeling of Multi-Die Packages. IEEE Trans. Components Packag. Technol. 2009, 32, 484–492. [Google Scholar] [CrossRef]
- Mah, J.W.; Lee, B.K.; Devarajan, M. Thermal Impedance Measurement on Different Chip Arrangements for Various Multichip LEDs Application. IEEE Trans. Electron Devices 2015, 62, 2906–2912. [Google Scholar] [CrossRef]
- Qian, X.; Zou, J.; Shi, M.; Yang, B.; Li, Y.; Wang, Z.; Liu, Y.; Liu, Z.; Zheng, F. Development of optical-thermal coupled model for phosphor-converted LEDs. Front. Optoelectron. 2019. [Google Scholar] [CrossRef]
- Luo, X.; Hu, R. Calculation of the phosphor heat generation in phosphor-converted light-emitting diodes. Int. J. Heat Mass Transf. 2014, 75, 213–217. [Google Scholar] [CrossRef]
- Alexeev, A.; Cassarly, W.; Hildenbrand, V.D.; Tapaninen, O.; Sitomaniemi, A.; Wondergem, A. Simulating light conversion in mid-power LEDs. In Proceedings of the 2016 17th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Montpellier, France, 18–20 April 2016; pp. 1–7. [Google Scholar]
- Ma, Y.; Hu, R.; Yu, X.; Shu, W.; Luo, X. A modified bidirectional thermal resistance model for junction and phosphor temperature estimation in phosphor-converted light-emitting diodes. Int. J. Heat Mass Transf. 2017, 106, 1–6. [Google Scholar] [CrossRef]
- Lasance, C.J.M.S. Thermal Management for LED Applications; Lasance, C.J.M., Poppe, A., Eds.; Solid State Lighting Technology and Application Series; Springer: New York, NY, USA, 2014; Volume 2, ISBN 978-1-4614-5090-0. [Google Scholar]
- Profumo, F.; Tenconi, A.; Faceili, S.; Passerini, B. Implementation and validation of a new thermal model for analysis, design, and characterization of multichip power electronics devices. IEEE Trans. Ind. Appl. 1999, 35, 663–669. [Google Scholar] [CrossRef]
- Poppe, A.; Szalai, A. Practical aspects of implementation of a multi-domain LED model. In Proceedings of the 2014 Semiconductor Thermal Measurement and Management Symposium (SEMI-THERM), San Jose, CA, USA, 9–13 March 2014; pp. 153–158. [Google Scholar]
- Mitterhuber, L.; Defregger, S.; Magnien, J.; Rosc, J.; Hammer, R.; Goullon, L.; Hutter, M.; Schrank, F.; Hörth, S.; Kraker, E. Thermal transient measurement and modelling of a power cycled flip-chip LED module. Microelectron. Reliab. 2018, 81, 373–380. [Google Scholar] [CrossRef]
- Monavarian, M. Beyond Conventional c-Plane GaN-Based Light Emitting Diodes: A Systematic Exploration of LEDs on Semi-Polar Orientations. Ph.D. Disseration, Virginia Commonwealth University, Richmond, VA, USA, 2016. [Google Scholar]
- Van Bien, T.; Szekely, V. Fine structure of heat flow path in semiconductor devices: A measurement and identification method. Solid. State. Electron. 1988, 31, 1363–1368. [Google Scholar]
- Székely, V. A new evaluation method of thermal transient measurement results. Microelectron. J. 1997, 28, 277–292. [Google Scholar] [CrossRef]
- Rencz, M.; Szekely, V. Structure function evaluation of stacked dies. In Proceedings of the Twentieth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (IEEE Cat. No.04CH37545), San Jose, CA, USA, 11 March 2004; pp. 50–54. [Google Scholar]
- Poppe, A. Testing of Power LEDs: The Latest Thermal Testing Standards from JEDEC. Electron. Cool. Mag. 2013. Available online: https://www.electronics-cooling.com/2013/09/testing-of-power-leds-the-latest-thermal-testing-standards-from-jedec/ (accessed on 13 May 2019).
- JESD51-50—Overview of Methodologies for the Thermal Measurement of Single- and Multi-Chip, Single- and Multi-PN-Junction Light-Emitting Diodes (LEDs). Available online: https://www.jedec.org/system/files/docs/JESD51-50.pdf (accessed on 13 May 2019).
- JESD51-51—Implementation of the Electrical Test Method for the Measurement of Real Thermal Resistance and Impedance of Light-Emitting Diodes with Exposed Cooling. Available online: https://www.jedec.org/system/files/docs/JESD51-51.pdf (accessed on 13 May 2019).
- JESD51-52—Guidelines for Combining CIE 127-2007 Total Flux Measurements with Thermal Measurements of LEDs with Exposed Cooling Surface. Available online: https://www.jedec.org/system/files/docs/JESD51-52.pdf (accessed on 13 May 2019).
- JESD51-53—Terms, Definitions and Units Glossary for LED Thermal Testing. Available online: https://www.jedec.org/system/files/docs/JESD51-53.pdf (accessed on 13 May 2019).
- Rencz, M.R.; Székely, V. Measuring partial thermal resistances in a heat-flow path. IEEE Trans. Components Packag. Technol. 2002, 25, 547–553. [Google Scholar] [CrossRef]
- Rencz, M.; Szekely, V.; Morelli, A.; Villa, C. Determining partial thermal resistances with transient measurements, and using the method to detect die attach discontinuities. In Proceedings of the Eighteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 12–14 March 2002; pp. 15–20. [Google Scholar]
- He, P.; Zhang, J.; Zhang, J.; Yin, L. Effects of Die-Attach Quality on the Mechanical and Thermal Properties of High-Power Light-Emitting Diodes Packaging. Adv. Mater. Sci. Eng. 2017, 2017, 8658164. [Google Scholar] [CrossRef]
- Chen, C.J.; Chen, C.M.; Horng, R.H.; Wuu, D.S.; Hong, J.S. Thermal management and interfacial properties in high-power GaN-based light-emitting diodes employing diamond-added Sn-3 wt.%Ag-0.5 wt.%Cu solder as a die-attach material. J. Electron. Mater. 2010, 39, 2618–2626. [Google Scholar] [CrossRef]
- Bornoff, R.; Merelle, T.; Sari, J.; Di Bucchianico, A.; Farkas, G. Quantified Insights into LED Variability. In Proceedings of the 2018 24rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Stockholm, Sweden, 26–28 September 2018; pp. 1–6. [Google Scholar]
- Alexeev, A.; Martin, G.; Onushkin, G.; Linnartz, J.-P. Accurate Thermal Transient Measurements Interpretation of Monochromatic LEDs. In Proceedings of the Semi-Therm 35, San-Jose, CA, USA, 18–22 March 2019, unpublished. [Google Scholar]
- Tran, N.T.; Shi, F.G. LED package design for high optical efficiency and low viewing angle. In Proceedings of the 2007 International Microsystems, Packaging, Assembly and Circuits Technology, Taipei, Taiwan, 1–3 October 2007; pp. 10–13. [Google Scholar]
- Alexeev, A.; Martin, G.; Onushkin, G. Multiple heat path dynamic thermal compact modeling for silicone encapsulated LEDs. Microelectron. Reliab. 2018, 87, 89–96. [Google Scholar] [CrossRef]
- Arik, M.; Becker, C.A.; Weaver, S.E.; Petroski, J. Thermal management of LEDs: Package to system. In Proceedings of the Third International Conference on Solid State Lighting, Denver, CO, USA, 3–6 August 2004; pp. 64–76. [Google Scholar]
- Hantos, G.; Hegedus, J.; Poppe, A. Different questions of today’s LED thermal testing procedures. In Proceedings of the 2018 34th Thermal Measurement, Modeling & Management Symposium, San Jose, CA, USA, 19–23 March 2018; pp. 63–70. [Google Scholar]
- Hantos, G.; Hegedus, J. K-factor calibration issues of high power LEDs. In Proceedings of the 2017 23rd International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Amsterdam, The Netherlands, 27–29 Septermber 2017; pp. 1–6. [Google Scholar]
- Schubert, E.F. Light-Emitting Diodes; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780511790546. [Google Scholar]
- Zou, H.; Wang, J.; Feng, M.; Shieh, B.; Lee, S.W.R. A novel chip-on-board white light-emitting diode design for light extraction enhancement. In Proceedings of the 2016 13th China International Forum on Solid State Lighting (SSLChina), Beijing, China, 15–17 November 2016; Volume 2, pp. 24–27. [Google Scholar]
- Wu, D.; Wang, K.; Liu, S. Enhancement of light extraction efficiency of multi-chips light-emitting diode array packaging with various microstructure arrays. In Proceedings of the 2011 IEEE 61st Electronic Components and Technology Conference, Lake Buena Vista, FL, USA, 31 May–3 June 2011; pp. 242–245. [Google Scholar]
- Li, Z.T.; Wang, Q.H.; Tang, Y.; Li, C.; Ding, X.R.; He, Z.H. Light extraction improvement for LED COB devices by introducing a patterned leadframe substrate configuration. IEEE Trans. Electron Devices 2013, 60, 1397–1403. [Google Scholar] [CrossRef]
- Chen, T.; Hsu, T.-C.; Luo, C.; Hsu, M.; Lee, T. Improvement in light extraction efficiency of high brightness In GaN-Based Light Emitting Diodes. In Gallium Nitride Materials and Devices IV; SPIE - International Society For Optics and Photonics: San Jose, CA, USA, 2009; Volume 7216, pp. 72161T1–72161T10. [Google Scholar]
- Chung, S.-C.; Li, D.-R.; Lee, T.-X.; Yang, T.-H.; Ho, P.-C.; Sun, C.-C. Effect of chip spacing on light extraction for light-emitting diode array. Opt. Express 2015, 23, A640. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer, D.; Pape, H.; Kutscherauer, R.; Walder, M. How to evaluate transient dual interface measurements of the Rth-JC of power semiconductor packages. In Proceedings of the 2009 25th Annual IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 15–19 March 2009; pp. 172–179. [Google Scholar]
- Glavanovics, M.; Zitta, H. Thermal destruction testing: An indirect approach to a simple dynamic thermal model of smart power switches. In Proceedings of the 27th European Solid-State Circuits Conference, Villach, Austria, 18–20 September 2001; pp. 2–5. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Pietrak, K.; Winiewski, T.S. A review of models for effective thermal conductivity of composite materials. J. J. Power Technol. 2015, 95, 14–24. [Google Scholar]
- Hasselman, D.P.H.; Johnson, L.F. Effective Thermal Conductivity of Composites with Interfacial Thermal Barrier Resistance. J. Compos. Mater. 1987, 21, 508–515. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Every, A.G.; Tzou, Y.; Hasselman, D.P.H.; Raj, R. The effect of particle size on the thermal conductivity of ZnS/diamond composites. Acta Metall. Mater. 1992, 40, 123–129. [Google Scholar] [CrossRef]
- Zhang, Q.; Pi, Z.; Chen, M.; Luo, X.; Xu, L.; Liu, S. Effective thermal conductivity of silicone/phosphor composites. J. Compos. Mater. 2011, 45, 2465–2473. [Google Scholar] [CrossRef]
- Submitted, D.T. Thermal Properties of Yttrium Aluminum Garnett From Molecular Dynamics Simulations. In Proceedings of the ASME/JSME 2011 8th Thermal Engineering Joint Conference, Hawaii, HI, USA, 13–17 March 2011. [Google Scholar]
- Dal Lago, M.; Meneghini, M.; Trivellin, N.; Mura, G.; Vanzi, M.; Meneghesso, G.; Zanoni, E. Phosphors for LED-based light sources: Thermal properties and reliability issues. Microelectron. Reliab. 2012, 52, 2164–2167. [Google Scholar] [CrossRef]
- Fulmek, P.; Nicolics, J.; Nemitz, W.; Schweitzer, S.; Sommer, C.; Hartmann, P.; Schrank, F.; Wenzl, F.P. The impact of the thermal conductivities of the color conversion elements of phosphor converted LEDs under different current driving schemes. J. Lumin. 2016, 169, 559–568. [Google Scholar] [CrossRef]
- Chung, T.Y.; Chiou, S.C.; Chang, Y.Y.; Sun, C.C.; Yang, T.H.; Chen, S.Y. Study of Temperature Distribution Within pc-WLEDs Using the Remote-Dome Phosphor Package. IEEE Photonics J. 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Hu, R.; Luo, X. A model for calculating the bidirectional scattering properties of phosphor layer in white light-emitting diodes. J. Light. Technol. 2012, 30, 3376–3380. [Google Scholar] [CrossRef]
- Huang, M.; Yang, L. Heat generation by the phosphor layer of high-power white LED emitters. IEEE Photonics Technol. Lett. 2013, 25, 1317–1320. [Google Scholar] [CrossRef]
- Schweitzer, D.; Pape, H.; Chen, L.; Kutscherauer, R.; Walder, M. Transient dual interface measurement A new JEDEC standard for the measurement of the junction-to-case thermal resistance. In Proceedings of the 2011 27th Annual IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 20–24 March 2011; pp. 222–229. [Google Scholar]
- Chen, H.T.; Tan, S.C.; Hui, S.Y.R. Analysis and modeling of high-power phosphor-coated white light-emitting diodes with a large surface area. IEEE Trans. Power Electron. 2015, 30, 3334–3344. [Google Scholar] [CrossRef]
- Alexeev, A.; Martin, G.; Hildenbrand, V. Structure function analysis and thermal compact model development of a mid-power LED. In Proceedings of the 2017 33rd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 13–17 March 2017; pp. 283–289. [Google Scholar]
- Yan, B.; Tran, N.T.; You, J.P.; Shi, F.G. Can junction temperature alone characterize thermal performance of white LED emitters? IEEE Photonics Technol. Lett. 2011, 23, 555–557. [Google Scholar] [CrossRef]
- Kusama, H.; Sovers, O.J.; Yoshioka, T. Line shift method for phosphor temperature measurements. Jpn. J. Appl. Phys. 1976, 15, 2349–2358. [Google Scholar] [CrossRef]
- Khalid, A.H.; Kontis, K. Thermographic phosphors for high temperature measurements: Principles, current state of the art and recent applications. Sensors 2008, 8, 5673–5744. [Google Scholar] [CrossRef] [PubMed]
- Fuhrmann, N.; Baum, E.; Brübach, J.; Dreizler, A. High-speed phosphor thermometry. Rev. Sci. Instrum. 2011, 82. [Google Scholar] [CrossRef]
- Yang, T.H.; Huang, H.Y.; Sun, C.C.; Glorieux, B.; Lee, X.H.; Yu, Y.W.; Chung, T.Y. Noncontact and instant detection of phosphor temperature in phosphor-converted white LEDs. Sci. Rep. 2018, 8, 296. [Google Scholar] [CrossRef]
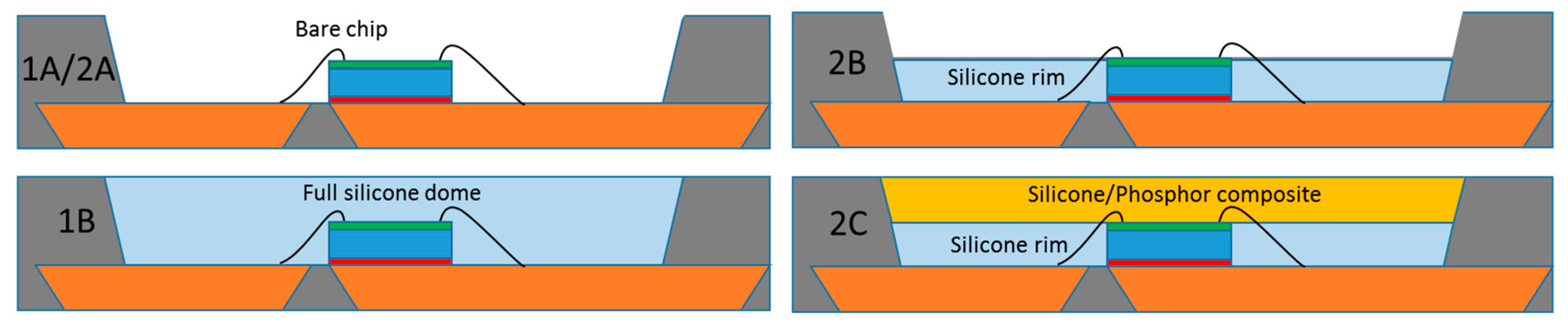
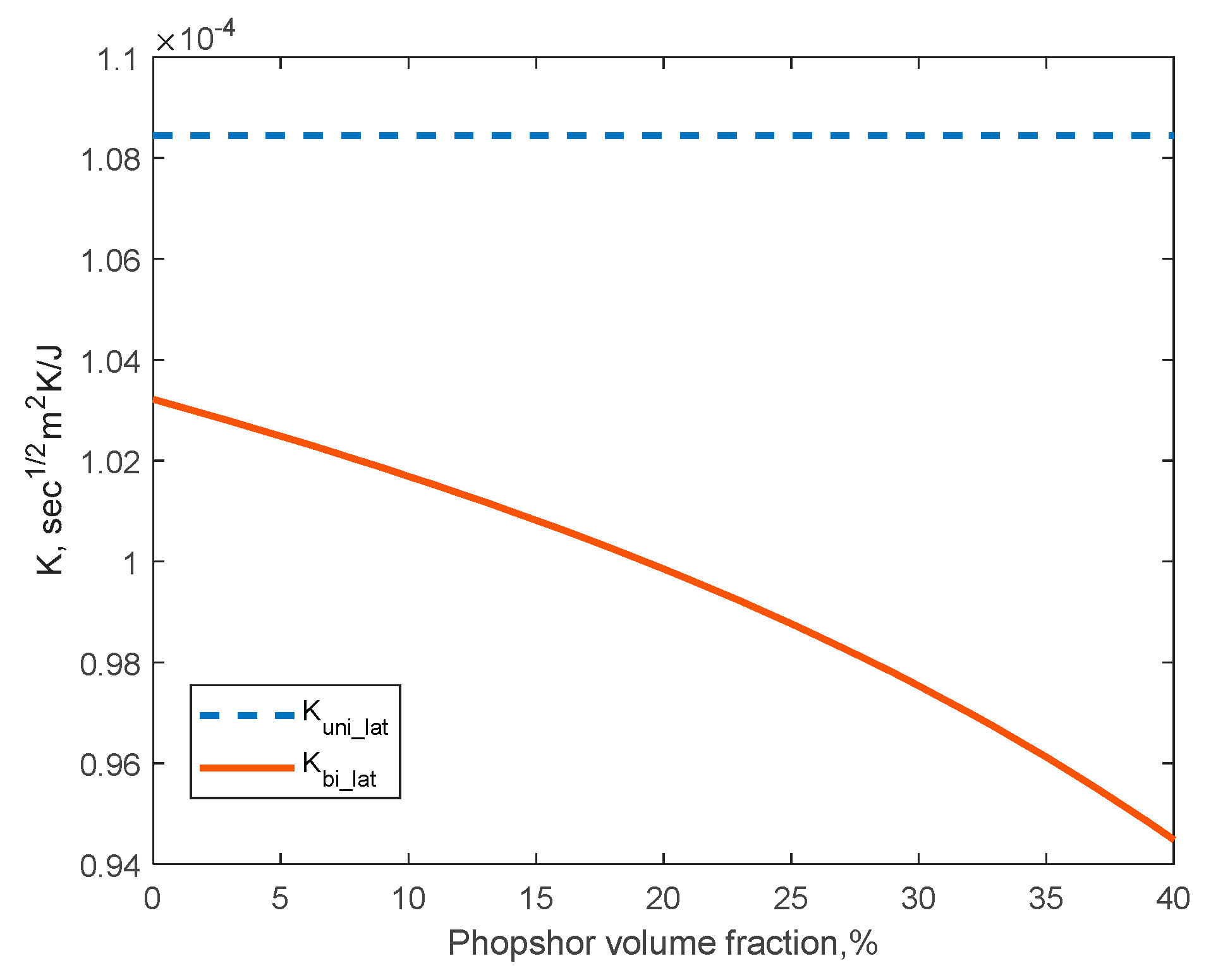
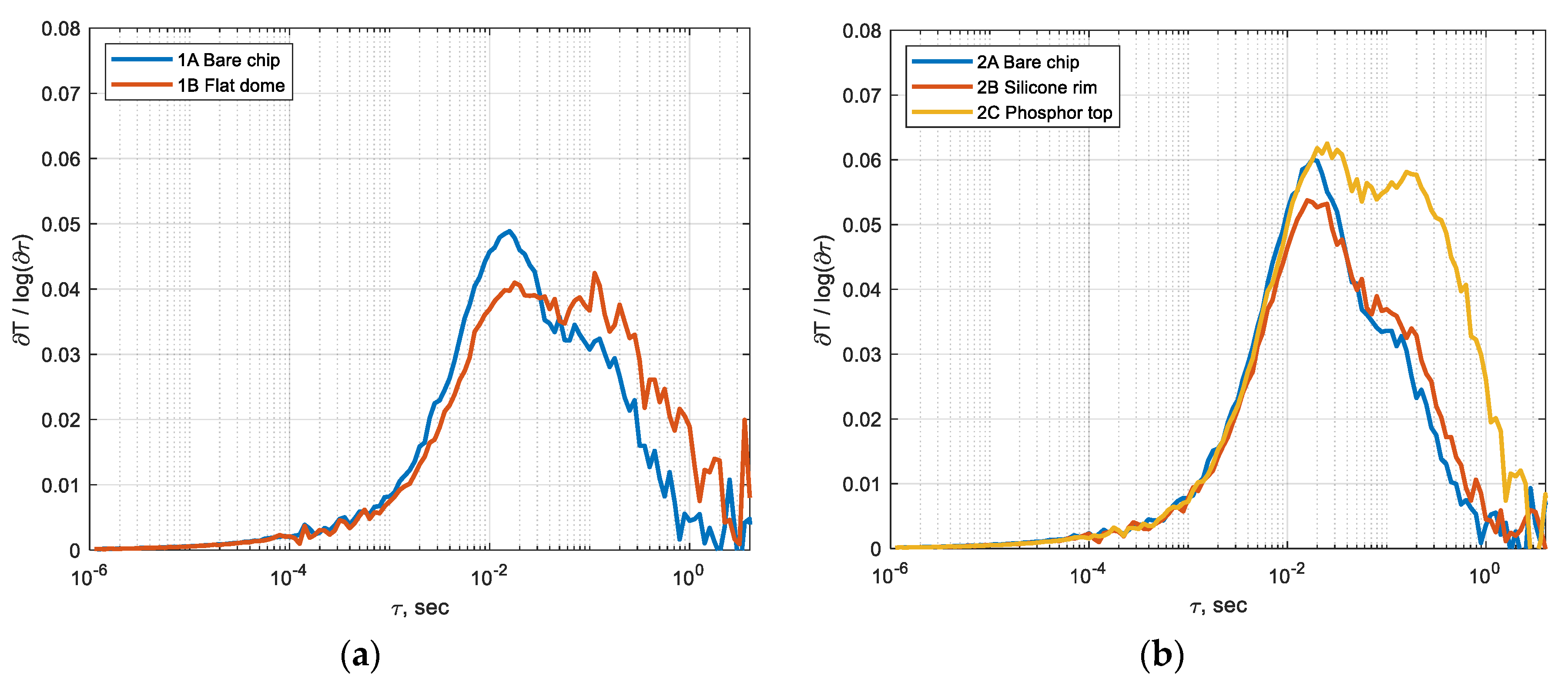
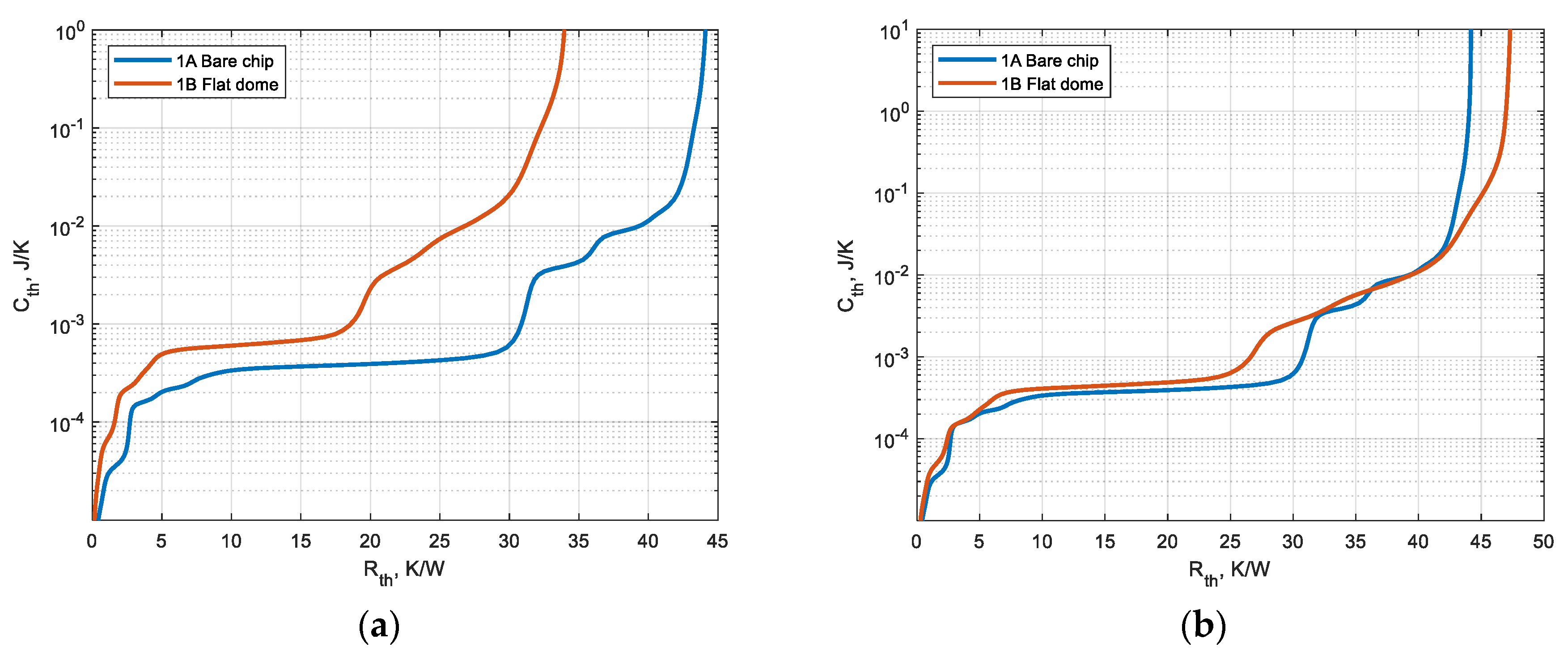
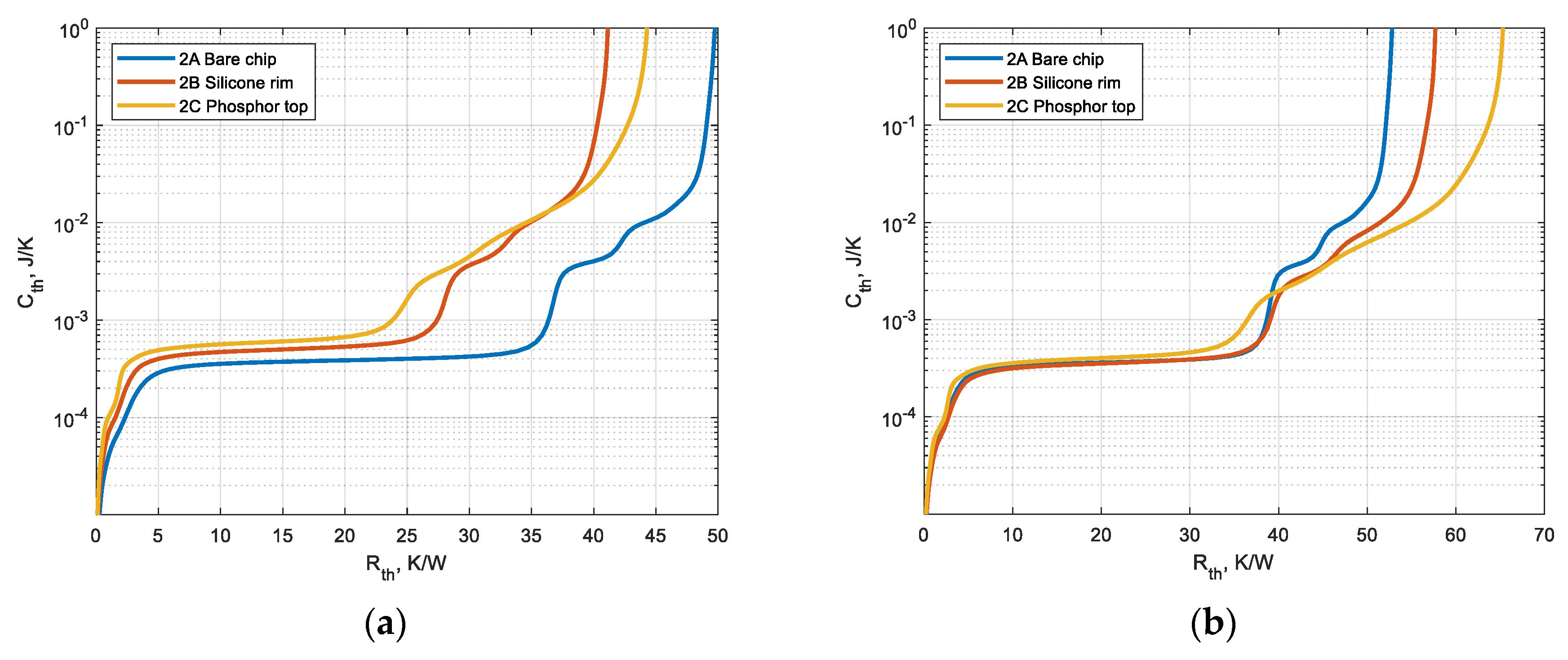
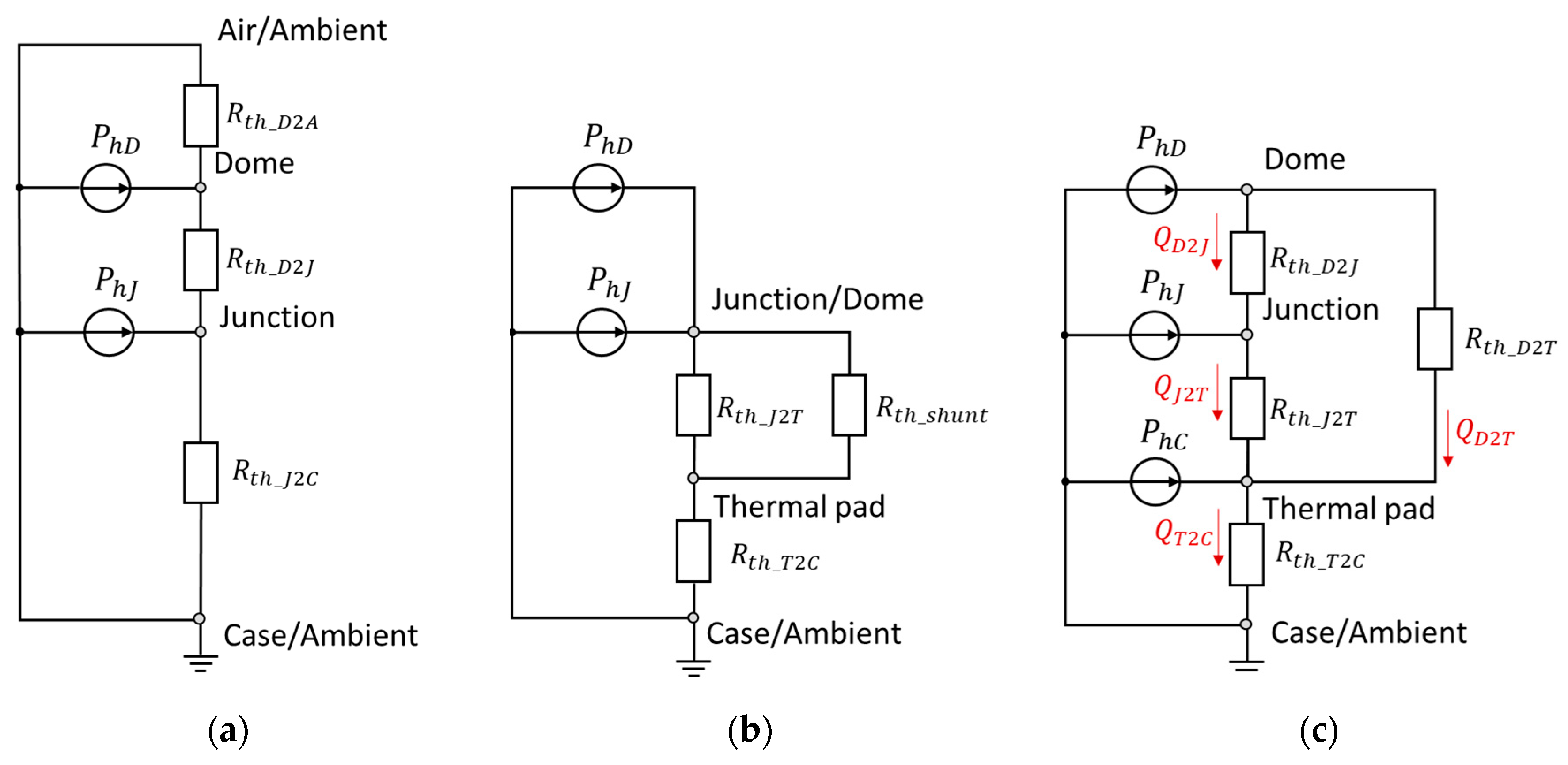
| Element | Material | Radius (mm) | Height (mm) | (g/mm3) | (J/gK) | (W/mK) |
|---|---|---|---|---|---|---|
| Crystal | Sapphire | 0.4 | 0.2 | 3.98 | 0.85 | 32 |
| DAL | - | 0.4 | 0.002 | - | - | 0.1 |
| Thermal pad | Copper | 1.2 | 0.25 | 8.93 | 0.39 | 380 |
| Dome | Silicone phosphor | 0.8 | 0.2 | 1.10* | 1.15* | 0.2* |
| MCPCB tracks | Copper | 10 | 0.07 | 8.93 | 0.39 | 380 |
| MCPCB dielectric | FR4 | 10 | 0.1 | 1.90 | 1.2 | 0.2 |
| Phosphor Volume Fraction | |||
|---|---|---|---|
| FEA Reference | Bilateral Estimation | Unilateral Estimation | |
| 0 | 4.1 | 4.1 | 4.3 |
| 0.4 | 3.7 | 3.7 | 4.3 |
| LED Sample | Dome Configuration | |||||
|---|---|---|---|---|---|---|
| 1A | Bare chip | 0.444 | 0.189 | 0.255 | 0.250 | 0.02 |
| 1B | Flat silicone | 0.445 | 0.122 | 0.323 | 0.229 | 0.29 |
| 2A | Bare chip | 0.441 | 0.199 | 0.242 | 0.221 | 0.09 |
| 2B | Rim dome | 0.442 | 0.159 | 0.283 | 0.203 | 0.28 |
| 2C | Phosphor top | 0.441 | 0.091 | 0.350 | 0.233 | 0.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexeev, A.; Onushkin, G.; Linnartz, J.-P.; Martin, G. Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs. Energies 2019, 12, 1860. https://doi.org/10.3390/en12101860
Alexeev A, Onushkin G, Linnartz J-P, Martin G. Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs. Energies. 2019; 12(10):1860. https://doi.org/10.3390/en12101860
Chicago/Turabian StyleAlexeev, Anton, Grigory Onushkin, Jean-Paul Linnartz, and Genevieve Martin. 2019. "Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs" Energies 12, no. 10: 1860. https://doi.org/10.3390/en12101860
APA StyleAlexeev, A., Onushkin, G., Linnartz, J.-P., & Martin, G. (2019). Multiple Heat Source Thermal Modeling and Transient Analysis of LEDs. Energies, 12(10), 1860. https://doi.org/10.3390/en12101860





