Abstract
In the smart grid, residential consumption scheduling in demand-side management (DSM) is one of the key technologies to facilitate utility companies and users in order to achieve systems optimality such as minimizing energy cost and demand peak. The success of DSM implementation depends on the level of user participation. While most of the prior works on DSM have reported good optimal results, they show a lack of focus towards user-centric issues such as user preferences, consumption deviation, and system fairness. Failure to account for such issues may lead to lower user participation in DSM programs. To address this problem, we propose user-centric consumption scheduling and fair billing mechanism for DSM program which consider economic as well as comfort aspects. First, a user’s discomfort cost is integrated into price incentives for determining consumption schedules. Second, consumption rescheduling mechanism is designed to allow users to change their preferences if necessary, and request new schedules. Finally, to improve the level of system fairness and avoid strategic players who try to manipulate the consumption profile for their benefit, a fair billing mechanism is proposed at the end of the scheduling period which takes into account both rescheduling users and user’s consumption deviation level. Simulation results show the effectiveness of the proposed method in terms of energy cost saving and improving fairness in the user’s billing.
1. Introduction
In the past decade, the world energy crisis has received greater attention as the concerns about climate change, greenhouse gas emissions, and increasing global electricity demand rise [1]. Electricity utility companies are forced to find newer and more efficient ways of electricity generation and delivery since the current electricity system design is out-of-date [2]. To solve the limitation of the traditional electricity grid, the concept of the smart grid had been proposed. The smart grid integrates information technology and automation control to meet the current and future demand requirements. The smart grid is an electricity network that is able to collect information at various stages, starting from the energy generation phase all the way to end-user power consumption, and take intelligent control decisions in order to keep a stable and efficient operation of the system [3]. One of the important applications in the smart grid that recently gained attention in both academia and industry is residential demand-side management (DSM) [4] The main concept of DSM is related to activities that reshape the user’s consumption profile to match the supply, reduce peak-to-average ratio (PAR), and minimize energy cost. Home energy management system (HEMS) solutions can be deployed to connect with the utility company through a smart meter for autonomously scheduling and managing the consumption using real-time price signal. From the perspective of the utility company, a shifting of load consumption can reduce peak demand and thus total energy cost in the grid. However, only considering user’s economic incentives may not be enough to motivate users to actively participate and contribute in the DSM program, leading to an unsuccessful DSM deployment [5]. According to the CHANGING BEHAVIOUR project [5], both theoretical and empirical works have shown insights regarding crucial conditions to make DSM programs more successful. Three disciplinary perspectives (economics, psychological, and sociological) have been identified and suggest various approaches for reducing energy demand. Therefore, it is important to design a DSM program that focuses on improving user participation and involvement. Such a DSM program should give users freedom of choice and ability to specify the level of participation in the community grid. Also, system fairness should be maintained among participants, especially in determining users’ electricity bills. A system without considering a proper billing fairness would result in a lack of user participation and may not be successful in achieving the program objectives.
1.1. Background Research and Limitations
Numerous works in the literature have proposed DSM algorithms to manage user flexibility [6,7,8,9,10,11,12,13,14,15,16,17]. In [6], automated demand response algorithms running at home is proposed to schedule home electric devices. Different demand response approaches including a flat price, a real-time price, or a maximum allowable power are presented. The results show that the algorithms are resilient to different approaches and can flat out the electricity usage, thus lower the total energy cost. In [7], the authors modeled household electricity consumers as a price-responsive user using stochastic finite impulse response models which account for uncertainties in their consumption pattern and responses to price variations. The optimal price signal is used to motivate change in consumption profiles, an approach which helped to smooth the consumption peak. In [8], various household appliance types are considered for consumption scheduling problem. They proposed the scheduling algorithm to maximize the total utility of appliances while satisfying a budget limit. The results show that different appliance types are effectively scheduled according to their constraints and user preferences. Agent-Based Control approach for DSM is proposed in [9] to manage smart home demand consumption on the large scale. The proposed scheduling mechanisms aim to reduce demand peak and carbon emission which the participants receive economic incentives. A game-theoretic framework-based consumption scheduling algorithm, a promising tool to manage the customer’s load profile and the interaction between utility companies and consumers, is proposed in [10]. The authors originally formulated the energy consumption scheduling for a residential community. A user has preferences regarding the use of flexible appliances and also tries to find an energy consumption schedule that minimizes his own electricity bills. The user’s energy cost is affected not only by his consumption but also by the total energy cost of the community.
Different viewpoints on system fairness also have been examined in the DSM consumption scheduling. In [11], a billing mechanism is proposed in which different electricity prices are applied to the users based on income and type. However, these assumptions are not considered practical in real-world scenarios. In [12], appliance operation delay is considered as a fairness index. A scheduling algorithm based on the water-filling method is proposed in order to assign schedules to the users with the same average delay. In [13], the authors attempt to improve energy cost allocation fairness by considering network congestion and load share ratio. The results show that their method is effective in allocating energy costs in proportion to benefit gained from participation. In [14], the Shapley value concept is used to fairly distribute revenue gained from DSM program among participants based on the level of user’s contribution to the overall cost. The authors proposed a reinforcement learning heuristic technique to estimate the amount of cost distribution. In [15,16], hourly billing mechanisms are proposed. Instead of calculating the bill based on daily consumption, the user’s bills are determined hourly. This improves the level of fairness in the user’s payment by determining users’ electricity bills in proportion to their consumption and flexibility. In [17], the authors consider a billing mechanism when users violate the optimal schedules. The proposed mechanism penalizes the users who increase their consumption from the optimal schedules but do not consider other possible variations.
However, there are several limitations which still need to be addressed. First, focusing on energy cost saving may not be a suitable approach for addressing the needs of the residential community sector. The residential users are more aware of their quality of life than in other sectors and thus, the aspect of welfare should be incorporated into the decision making when determining the consumption schedules. In addition, an ideal DSM program should give participating users the freedom to choose how much they want to contribute towards the community and receive incentives according to their action while maintaining the level of comfort they preferred. Moreover, one of the important aspects of fairness which is often overlooked is a consideration of users deviating from the optimal consumption schedules after their assignment. In the conventional approach, an identical price is applied to all users regardless of individual behavior or commitment to the assigned schedules. However, in the case when a user deviates from his schedule, the total community load profile changes. This change affects the electricity bills of other users in the community and thus may raise fairness concerns.
1.2. Addressing Limitations: Our Approach
In this paper, we address the limitations stated above by designing a user-centric consumption scheduling model with a fair billing mechanism for DSM program. First, we propose a user utility cost function that incorporates energy cost and discomfort measure into the consumption scheduling problem. The discomfort cost, which caused by shifting appliance consumption, will influence the scheduling decision based on the user’s preference. In addition, users can make a choice on how much they would contribute to the community while maintaining their preferred level of comfort. Second, a consumption rescheduling algorithm that copes with the users who change their appliance preference during the operation period is proposed based on our previous work in [18]. This algorithm provides the users with a chance to reevaluate their consumption promises. At the same time, the algorithm uses information regarding the energy consumption of other users in order to generate consumption schedules that still achieve reduced demand peaks and overall community energy cost. Finally, a fair billing mechanism is introduced and integrated into the DSM program. As an extension of our previous work in [19], we proposed rescheduling compensation bill and consumption deviation bill which accounts for rescheduling and consumption deviating users respectively. Any cost differences (i.e., differences between hourly scheduled and actual consumption) are distributed among the members of the community based on their individual actions and contributions. This billing mechanism maintains the level of fairness in determining users’ electricity bill as well as preventing strategic players from manipulating the consumption profile for their own benefit.
The main contributions of our work can be listed as follows:
- The proposed consumption scheduling model provides participating users with an intuitive way to specify the balance between their personal comfort and their level of participation in the energy saving efforts of the community. This allows users to maintain their preferred daily lifestyle while also receiving lower electricity bills due to reductions in the total community energy cost.
- The rescheduling algorithm provides an opportunity to reevaluate consumption schedules even in the case of last-minute preference changes, such that demand peaks and unnecessary energy costs are avoided.
- The billing mechanism improves fairness in DSM program. The impact from rescheduling users and consumption deviation are taken into account when distributing the total energy cost to all user based on their individual action.
The combination of increased freedom of choice for the user, reduced community costs through the rescheduling algorithm as well as improved fairness due to the proposed billing mechanism results in a user-centric DSM program design which will help increase the level of participation and lead to a successful implementation of the program.
1.3. Paper Organization
The rest of this paper is organized as follows. Section 2 presents an overview of the residential community model. In Section 3, the details and solution of scheduling optimization problems are discussed. User billing mechanisms are proposed in Section 4. Numerical simulation results and discussion are given in Section 5. The conclusion of the paper is drawn in Section 6.
2. Overview of Residential Community System Model
In this paper, a residential community that consists of a set of users associate with each house is considered. All users are sharing the same energy source from the utility grid. Each user is equipped with a HEMS for consumption scheduling. Moreover, it can change the schedules on behalf of appliances autonomously based on the time preference by users. The residential community is assumed to have a two-way communication network infrastructure that can provide communication among user’s HEMS and also connected to the utility company. The detailed of the system model is shown in Figure 1. The time during the operation period is represented by time slot h (e.g., hours in a day) such that . Without loss of generality and for simplicity purpose, we use h.
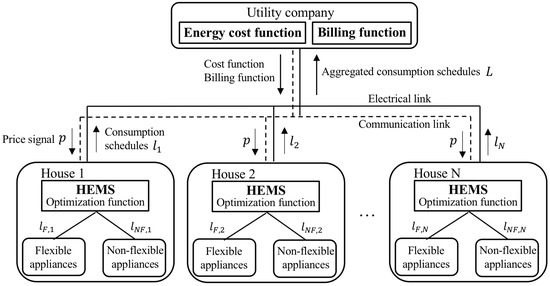
Figure 1.
Residential community model.
2.1. User Profile Model
Each user has various appliances which consume energy on a daily basis, classified into two types.
- Non-flexible: Appliances which their operation schedule cannot be shifted is called non-flexible appliances. Their consumption schedules must be kept as their original schedules. The examples of such appliances are a refrigerator, lighting, etc.
- Flexible: Appliances which can shift their operation time form their original schedules, respected to some constraints, are called flexible appliances such as washing machine, dishwasher, etc.
Let a set of non-flexible appliances of user n identified as and a set of flexible appliances is denoted as . To simplify the notation, we use to denote a flexible appliance of user n. For each hour h, the total consumption schedule contains sum of non-flexible and flexible appliance power levels, in which power levels by non-flexible appliance always kept as base power level, are expressed as follows:
Thus, total residential community consumption in hour h is the sum of consumption profile of all user that can be expressed as
For each flexible appliance , a daily energy requirement to fulfill its task is denoted as
Each flexible appliance is also restricted by maximum and minimum operating power limit in each time slot as
2.2. User Preference Model
User time preference for using each flexible appliance is modeled using parameters which specify a range of starting and ending hours that user n prefers the appliance to be operated as
where , are the mentioned hours of the day in the range of and . For example, the user may set 13:00 and 17:00 for a dishwasher to finish be for dinner time.
In addition, users also rank their flexible appliances with priority values . The appliance priority value indicates how important the appliance is and would affect how much the appliance operation can be shifted. The large value of means that the importance of an appliance is high and thus, causes high discomfort to the user when the appliance is shifted from the preferred time.
2.3. Energy Cost Model
An energy generation cost function, denoted as , is used to indicate the cost of required energy to serve all the residential user load during hour h. The widely accepted assumption is that marginal generation costs increase with load demand [10]. Thus, it is intuitive to assume properties of the cost function as follows:
Assumption 1.
The cost function is an increasing function with the total load. That is,
Assumption 2.
The cost function is strictly convex [20]. That is,
where , and .
An example of the cost function that satisfies the above assumptions is a smooth differentiable quadratic function, as also used in the thermal generation [21].
where , , and are coefficients of the cost function at each . Therefore, we adopt the same cost function in this paper. Please note that this cost function is general and can represent the actual energy cost or an artificial cost signal used by the utility company to impose a proper consumption scheduling. The electricity price, represented as an energy cost in terms of unit price per kWh, in each hour h can be calculated as
Electricity bill of user n in hour h can be calculated as
2.4. Discomfort Cost Function
An important factor of energy consumption scheduling in demand side is the user’s discomfort to shift flexible appliance load, as their value toward load shifting is different among users. For users, if they do not concern about the reduction of electricity bill, offered by the DSM incentive, the load profile of the flexible appliances will be within their time preference. Otherwise, their load profile will be scheduled in response to the price and will affect their comfort such that the appliances would be operated outside their specified time preferences. The discomfort caused by shifting appliance load outside its preferred time is measured by the time changes from its time preference and the corresponding power consumption. We propose the equivalent discomfort cost of user n and define as
where is the cost of discomfort in shifting the flexible appliances. The discomfort cost indicates that when the appliance is scheduled to operate in its time preference , the user n will be satisfied and his discomfort is zero. However, if the schedule lies outside the time preference range, the discomfort cost is increased proportional to the time and amount of consumption being scheduled, taking into account both before and after. Moreover, if the appliance operation time is shifted further away from the preferred time and/or the shifted consumption amount is higher, an increasing rate of discomfort is even higher as indicated by the squared term in Equation (14). For the choice of , as mentioned, the large value of means that the appliance is important to user n and the user is not willing to trade the discomfort caused by shifting the appliance with a lower electricity bill.
2.5. User’s Utility Cost Functions
The utility cost of user n is the integration of the electricity bill and the discomfort cost, which is defined as
where the utility cost consists of two terms: electricity bill and discomfort cost . The parameter is a user’s weight factor which uses for quantifying the user consideration between electricity bill and discomfort cost. A small means that user n concerns more about the electricity bill reduction than the discomfort caused by load shifting. The weight factor can also be interpreted as a community point of view of the users which they value between personal and community interest. For example, means that the user’s interest is toward the community benefit in reducing the energy cost and not concern about discomfort in shifting the appliances. On the other hand, indicates that the user only cares about personal interest and prefers the most comfort without considering the community overall energy cost. The value shows that the user balances the consideration between overall community energy cost and personal comfort. Thus, the proposed user’s utility cost function gives participating users a choice to contribute to the overall community objective, in which the degree of contribution can be different among users in the shared energy community environment.
3. Optimization Problem Formulation
In this section, we present the optimization problems and solutions for determining users’ consumption schedules. The detail of a day-ahead scheduling algorithm is presented which determine all user consumption schedules the night before. Then, a rescheduling algorithm is proposed to find consumption schedules when users have changed their original preferences during the operation period.
3.1. Day-Ahead Consumption Scheduling
An optimization problem for day-ahead consumption scheduling that minimizes user’s utility cost function, which consists of electricity bill and discomfort cost is formulated. The purpose of this model is to determine schedule of energy consumption for each user in the community in order to achieve optimal electricity bill savings and preserve the user’s comfort while reducing total energy generation cost of the whole community. Let us define user n’s energy consumption scheduling vector as
and denote
for a feasible strategy set of user . The optimization problem for user n is formulated as
where denotes the energy consumption scheduling vectors of all users other than user n. The constraints express that a fixed daily amount of energy is required for each flexible appliance of user n and appliance physical power limitation is bounded in each time slot h. In the user’s utility objective function , the electricity bill of user n depends not only to his own energy consumption but also energy consumption from all other users in the community . Thus, there is a dependency among users in the community which shared a common energy source.
To solve the optimization problem in Equation (19), a distributed iterative algorithm is used. The overall process is implemented in a closed-loop iterative fashion and summarized in Algorithm 1.
| Algorithm 1 Day-ahead consumption scheduling: executed by each user |
|
For each user , chooses any starting point in the feasible set for initial energy consumption vectors. Since no information about other user is available at the beginning of the process, the user also randomly initializes vector of all other users energy consumption vectors. The utility company can provide coordination of execution time for all user so that no user simultaneously solving the optimization problem at the same time. For simplicity, a round-robin scenario is used. Once, the user receives execution command allow for scheduling, the user’s HEMS locally solves the optimization problem in Equation (19). That is, each user tries to minimize its utility function assuming that energy consumption of all other users is fixed. Once the schedule solution has been found, the user compares the utility cost with the previous solution and updates if the new solution is better or otherwise keep the old solution. If the user updates new schedule, then he broadcasts the aggregated consumption vector to all other users in the community. In this way, a detail of each appliance consumption schedule is not revealed to other users and the privacy of the user is preserved. For other users, once received the consumption vector, they also update their community consumption knowledge for further scheduling. The algorithm terminates once no update is received or reached a maximum number of iteration threshold. Please note that the iterative algorithm is intended to schedule the energy consumption of a local community. To achieve nation-wide scaling, a divide-and-conquer approach can be used; it is possible to have clusters of communities running separate instances of the local energy consumption scheduling.
3.2. Energy Consumption Rescheduling
Most of the works in the literature assumed that every user would fully commit to the schedules, that is, during the operation period no user changes the time preference of flexible appliance and its operation will be fulfilled according to the assigned consumption level. However, in practical scenarios, some users may not be able to commit to the schedules determined in the previous day. Those users may want to change their preferences. To accommodate such last-minute changes, an algorithm that allows the users to reschedule their consumption is required. Based on these assumptions, we extend our previous work [18] regarding an energy consumption rescheduling algorithm so that it takes into account the user’s discomfort, using the discomfort cost function presented in Section 2.4.
Let us consider an event after the day-ahead consumption schedules are determined. From the mentioned assumptions, we assume that a user , where is a set of users who changed appliance time preference during the operation period and alter their schedules while the energy consumption schedules of all other users remain the same. During this period, at time , let us assume user m changes time preference of a flexible appliance , which not yet starts its operation, from to new time preference . The new user preference reflected in the HEMS. Then, the HEMS locally calculates new energy consumption schedule constrained by the new preference with scheduling period based on current energy consumption of the community as in the following optimization problem:
where a set of feasible energy consumption for the user is updated as
The updated energy consumption vector is then announced to the utility company and all other users. The rescheduling algorithm provides an opportunity for users to change their time preferences while also selecting the best possible schedule for the appliance corresponding to the new time preference. Please note that when a user reschedules other users electricity bills may be affected. However, the schedules of other users remain unaffected from this individual rescheduling event. The cost discrepancy will be addressed in the following section. The summary of the rescheduling algorithm is shown in Algorithm 2.
| Algorithm 2 Individual rescheduling for user m |
|
4. User Billing Mechanism
In this section, the details of the proposed fair billing mechanism are explained. As mentioned before, an optimal consumption schedule for each user is computed using Equation (19). Equations (11) and (13) are used to determine the user’s electricity bill which is proportional to the amount of energy consumed. However, this billing mechanism is fair for all users only when there is no consumption deviation. In practice, deviation is likely to occur, e.g., when users change their preferences and thus violate the schedules. This would have a negative fairness impact on the traditional billing. An alternative fair billing mechanism which takes a user’s action into consideration is required.
The proposed billing mechanism consists of two parts: rescheduling compensation and consumption deviation bills. In the first part, energy cost differences from rescheduling process are calculated. The rescheduling user will take responsibility for the corresponding change of electricity bill from all other users. In the second part, the actual consumption profile of each user is compared with the assigned schedule to calculate our defined penalty and reward metric. Then, in order to determine the user’s final electricity bill, the amount of penalty or reward is given to each user based on these metrics.
4.1. Rescheduling Compensation Bill
The rescheduling compensation bill is designed to compensate any cost that affect other users when rescheduling. That is, all other users bills should be kept the same as their day-ahead schedules while the rescheduling user takes responsible for any cost differences. Considering each rescheduling user , in each time slot , we denote total load before user m reschedule as and the corresponding energy cost as . The bill of user n before user m reschedule in time slot h is
Similarly, let us denote total load after user m reschedule as and the corresponding energy cost as . The bill of user n after user m rescheduled in time slot h is
The different in bill of user n before and after user m rescheduled at time slot h is calculated as
where for is 0. Bill compensation for user n in time slot h is calculated as
The bill compensation adjusts electricity cost for all users such that the rescheduling user m takes responsibility of the cost induced by his action. In Equation (25), the bill compensation of each user n is and for the rescheduling user m is the sum of bill differences from all other users. This bill compensation is calculated for all rescheduling user and will be added to the user’s final electricity bill.
4.2. Consumption Deviation Bill
After the bill compensation is determined, all user will be billed based on a billing mechanism extended from our work in [19] which takes into account any cost differences between actual and assigned consumption schedules. The proposed consumption deviation bill aims to fairly determine the user’s electricity bill based on the following fairness criteria:
- User’s electricity bills are determined proportional to their energy consumption.
- Users who consume energy according to their assigned day-ahead schedules will not pay more than the estimated electricity bills.
- In case when the users deviate their consumption from the assigned schedules, the cost differences are distributed to the users proportional to the amount of deviation.
Based on the fairness criteria, we defined penalty and reward metrics and assign to the users proportional to the amount of consumption they deviated from the assigned schedules. Let be the actual consumption and be the assigned consumption of user n for . Please note that the assigned schedule is including the schedule updated after user reschedules. The energy generation cost calculated from the assigned schedule is
Thus, the estimated electricity price becomes
Similarly, the actual energy generation cost calculated from the actual consumption is
and the actual electricity price is
Let us define a penalty metric and assign to user n based on the amount of consumption deviation relative to all other users in time slot h as
where . The penalty metric indicates how much the user n deviates consumption in time slot h from the assigned schedule compare to the total community consumption deviation. A large means that the user n relatively deviates more consumption in time slot h than other users. We also define a reward metric and assign to user n based on the amount of consumption committed relative to all other users in time slot h as
where is the maximum amount of consumption deviation in time slot h. The reward metric indicates how much the user n commits to the assigned consumption schedule compare to the total community schedule commitment. A large means that the user n relatively follows the assigned consumption in time slot h than other users. The energy cost different caused by consumption deviation of all users can be calculated as
Thus, the consumption deviation bill is calculated as follows
In Equation (34), the first term of the consumption deviation bill is a base energy bill, which users need to pay for their actual use of energy and being charged with the price . In the second term, there are two cases. The first case is when the energy cost of the actual consumption (deviated schedules) is higher than the energy cost of the assigned consumption . This extra cost is distributed to all users based on the amount of their deviated consumption, which is indicated by the penalty metric . This means that the higher consumption deviation the more penalty is given. The second case is when the actual energy cost is lower or equal to the energy cost of the assigned consumption . In this case, rewards are given to users based on their schedule commitments, which indicated by the reward metric . That is, the more user commits to the assigned schedules the more reward is given. Please note that the value of becomes negative in the second case, and thus lower the bill. Moreover, the deviating users are penalized for consumption deviation in both up and down direction to prevent strategic players who intentionally deviate from their schedules for economic benefits. An example of such strategy includes a user who constantly under-consume, a behavior that could otherwise be exploited to achieve cheaper electricity bills.
Finally, the final determination of user’s electricity bill for is calculated as the sum of and as
The summary of the proposed billing mechanism is shown in Algorithm 3. The utility company calculates electricity bill for each user at the end of the operation period and before starting of the next consumption scheduling. First, for each user , the bill compensation is initialized to zero. Then, the compensation bill is calculated according to Equation (26) for each rescheduling user . Once, the compensation bill is determined, the actual and assigned consumption level are compared in each time slot to calculate the penalty and reward metrics for each user. The consumption deviation bill is then calculated using Equations (33) and (34). Finally, the compensation bill is added to each user for the final electricity bill as in Equation (36).
| Algorithm 3 User Billing: calculate electricity bill for each user at the end of operation period |
|
Please note that we assume a budget-balanced billing system , i.e., the sum of the user’s bills equals the energy generation cost. It is possible for the utility to make a profit by multiplying the energy generation cost with some weight factor (e.g., ). Then, the difference between the total charges to the users and the total energy cost would indicate the profit of the utility. The proposed fair billing mechanism also retains this budget-balanced scheme; it only redistributes the generation cost more fairly based on the user’s actions and deviations. The users receive economic benefits from scheduling the consumption profiles more efficiently and by avoiding the use of energy during high demand periods.
5. Simulation Results
In this section, various simulation scenario and performance analysis of our proposed energy consumption scheduling algorithms and billing mechanisms are presented.
5.1. Simulation Setting
In the simulations that follow, the CREST demand model [22] was used as the residential user demand consumption. This model is a high-resolution (one-minute resolution) stochastic model of domestic electricity demand that incorporates appliance composition, human occupancy model and electrical parameters derived from time-use survey data. In the simulations, a population of 20 households on one ordinary weekend day in winter was considered. Please note that this number was chosen just for demonstration purposes. Simulating a larger number of users is possible. Appliance types and power rating parameters, the human occupancy and user demand were gathered by randomly sampling from the CREST model. Example of non-flexible appliances (i.e., critical appliances that their energy consumption cannot be shifted and must keep the power level as the original schedules) include refrigerator, television, personal computer, and lighting. Flexible appliances, including dishwasher, washing machine and electric shower, were modeled by Equations (5) and (6). The full list of 34 appliances used in the simulation can be found in Appendix A. The number of appliances each user own is determined by the result of sampling from a given probability distribution based on realistic statistics from a time-use survey. Please note that not all appliances in the list are occupied by every user. We assumed the daily energy requirement for each appliance corresponds to the data sampled. For appliance power constraints, we set and equal to the maximum observed value. The user time preference is randomly assigned for each flexible appliance considering the original schedule. The coefficients of energy generation cost function are set as , , and for and the cost function is given in Japanese Yen. We assumed all users equally value their flexible appliances needs and set the appliance priority value for all and balanced consideration between electricity bill and discomfort cost with the weight factor , unless otherwise stated. With consideration to electric vehicles, EV charging is possible and can be viewed as a consumption load. However, the use of EV as an energy source (i.e., a battery that can be scheduled for discharging) is not considered in this paper and is left as future work. The optimization in Equations (19) and (20) were solved using MATLAB optimization toolbox with a limiting number of 100 iterations, which in practice was sufficient for convergence.
5.2. Results of Consumption Scheduling Algorithm
First, the convergence of the proposed DSM consumption scheduling algorithm is investigated. Figure 2a,b show aggregated community and 20 individual users energy cost as the iteration number increases. The results show that the algorithm converges in less than 60 iterations in total, that is, each user approximately computes its consumption schedule for 3 times.
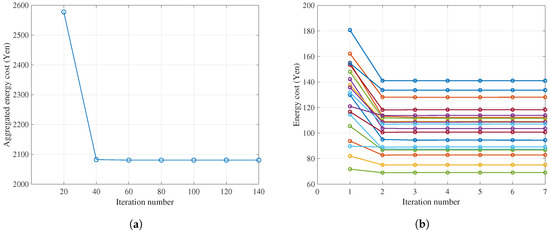
Figure 2.
The convergence of the proposed DSM consumption scheduling algorithm. (a) Aggregated energy cost of 20 users; (b) Individual energy cost of 20 users.
Figure 3 illustrates different aggregated consumption profiles without and with the proposed DSM consumption scheduling. We consider the base case of not using DSM consumption scheduling. In this case, the users use their appliances according to the original schedules without considering the energy price signal from the utility. Comparing this base case to a case that uses the proposed DSM consumption scheduling, the result shows that peak consumption was reduced by shifting consumption to the off-peak periods. The PAR value of 20 users has been reduced from 1.83 to 1.40 (−23.5%) by the proposed DSM consumption scheduling. The corresponding energy generation cost of the community also reduced from 4359.17 Yen to 4088.21 Yen (−6.22%). The reason for cost and PAR reduction is because the energy consumption of the users are scheduled more efficiently based on other users load information. Please note that the proposed scheduling mechanism also preserves the user’s preferred lifestyle by considering the discomfort caused by shifting appliance according to the user’s choice of preferences.

Figure 3.
Aggregated consumption profiles of 20 users.
The weight factor parameter is used to quantify the user’s point of view in the community toward energy cost saving and individual comfort. With a different value of , the result of the aggregated energy cost of the community is shown in Figure 4a under different appliance’s priority value of 1, 5, and 10. As the value of increases, the optimal energy cost increased in all cases. This is due to the fact that as the users concern more about their comfort, the system has less flexibility in shifting appliances in order to reduce the energy cost. Similarly, Figure 4b shows how the overall community PAR changes in response to different values of . The results show a similar trend as PAR increases when increases. In both results, the smaller value of causes the discomfort cost to be relatively low when compared to the electricity bill of users and thus, reducing energy cost and PAR more than the case of high values.
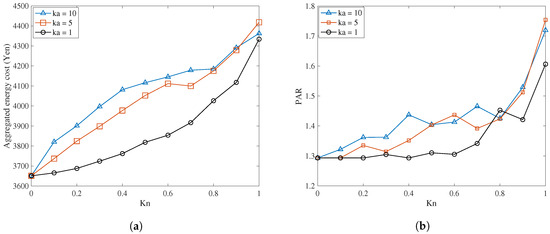
Figure 4.
Impact of for . (a) Aggregated energy cost of the community; (b) PAR of the community.
5.3. Results of Rescheduling Algorithm
In this section, the performance of rescheduling algorithm is demonstrated in 3 different scenarios. In the day-ahead schedules, the consumption profile is used as the optimal consumption schedules determined a day before. The deviated schedules referred to the case when users have changed their time preference of appliances. Without applying the rescheduling algorithm, users will change the operation time of the appliances and use them as early as possible according to their new preferences. For the schedule with rescheduling, the user requests for a new appliance schedule with the new preference considering other users consumption profiles. For the purpose of demonstration, we set 10 out of 20 users to randomly change a single flexible appliance’s time preference and request for rescheduling during 5:00 to 14:00. Figure 5 shows the corresponding aggregated consumption of the community in different scenarios. As we can see, when the user changes appliance operation time without considering other users load in the community, a high peak demand occurred and increased the total energy cost of the community. When rescheduling algorithm is applied, the resulting consumption profile is flattened with lower PAR, resulting in similar profile with the optimal day-ahead schedule. This is because of the rescheduling algorithm schedules devices in such a way as to reduce peak consumption.
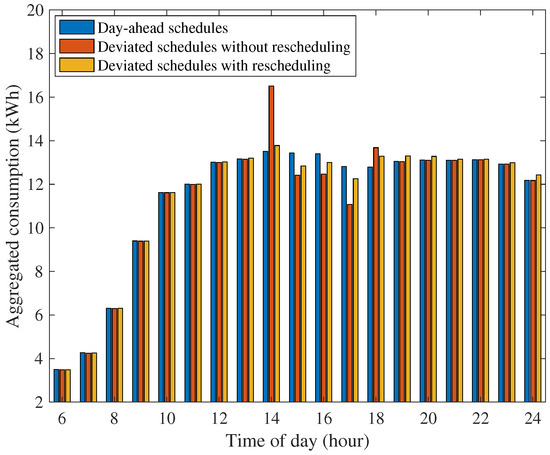
Figure 5.
Aggregated consumption profile of 20 users in the case of day-ahead schedules, deviated schedules without and with rescheduling.
We further show the impact of the proposed rescheduling algorithm by varying a different number of rescheduling users. The normalized aggregated energy cost is shown in Figure 6 for the case of with and without rescheduling algorithm as the number of rescheduling user increases. The result shows that when the number of rescheduling users increased, the greater cost reduction of the proposed rescheduling algorithm can be achieved when compared to the without-rescheduling scenario. This is because the rescheduling algorithm has even more chances to optimize various consumption loads, avoiding further consumption peaks. These results demonstrate the effectiveness of the proposed rescheduling algorithm when it comes to avoiding consumption peaks and thus flattening the total consumption profiles, resulting in lower total energy costs.
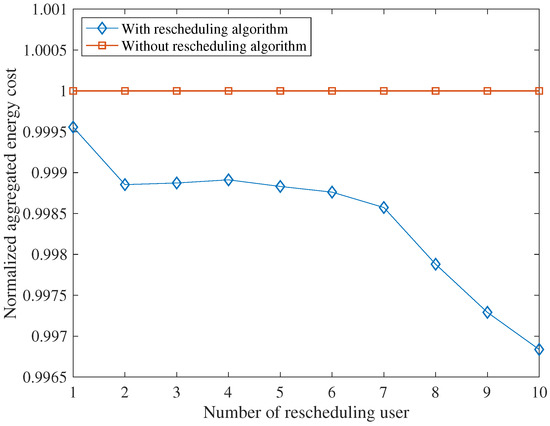
Figure 6.
Aggregated energy cost (normalized) per number of rescheduling users.
5.4. Results of Billing Mechanism
In this section, results of the proposed billing mechanism are investigated for the rescheduling and consumption deviation scenarios. The optimal day-ahead billing uses Equation (13) to calculate the user’s electricity bill. The rescheduling billing added bills compensation from Equation (26) to compensate the cost different caused by rescheduling users. Figure 7 shows the electricity bill of users for the optimal day-ahead and rescheduling billings with users 1–10 rescheduled their appliances. The results illustrate that the electricity bill of the rescheduling users are adjusted such that the electricity bill of non-rescheduling users (users 11–20) remain the same as their optimal day-ahead bills and those users who reschedule their appliance take responsibility for the bill discrepancies they caused. Thus, the proposed billing provides fairness to the non-rescheduling users.
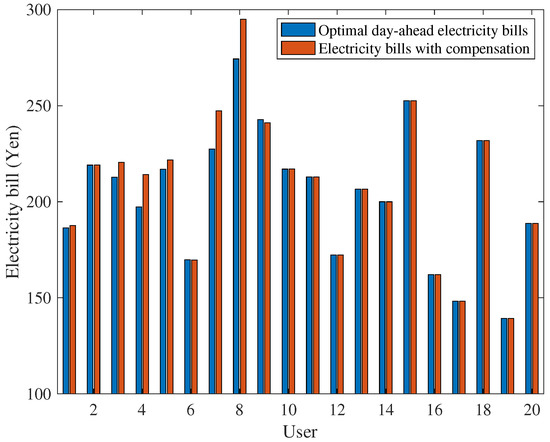
Figure 7.
User’s electricity bill before and after rescheduling.
As mentioned before, in a practical scenario we cannot assume that every user will follow the assigned schedules and consumption deviation is possible at any time after the schedules have been determined. Thus, in this scenario, energy costs are changed by changes in consumption, which in turn, affects all user’s electricity bills. To demonstrate the effect of deviated schedules, we set users 11–20 to deviate their consumption from the assigned schedules. The amount of deviation for each user is randomly selected from a uniform distribution in the range kWh in each time slot. Figure 8a shows the electricity bill of 20 users with consumption deviation using billing Equation (13). The results show that the electricity bill of non-deviating users (users 1–10) are increased from their predetermined electricity bills although they committed to the assigned schedules which considered unfair. This is because the actual consumption is different from the assigned schedules caused by users who deviate the consumption. In the same setting, Figure 8b shows the results of the proposed billing mechanism in Equation (36). The electricity bill of non-deviating users (users 1–10) are reduced as they received rewards for being committed to the assigned schedules while the bill of deviating users (users 11–20) are subjected to the penalty according to the amount of consumption deviation. That is, the proposed billing mechanism calculates users’ bills based on their consumption level compared to the assigned schedule in each time slot while the bills of non-deviating users are reduced from the given rewards. Electricity bills of deviating users are proportionally calculated based on the amount of deviation. Therefore, the proposed billing mechanism improves the fairness level in the billing process and prevents the strategic players from manipulating schedule for their economic benefits. This will motivate the users to participate in DSM program by maintaining fairness among users in the shared energy community.
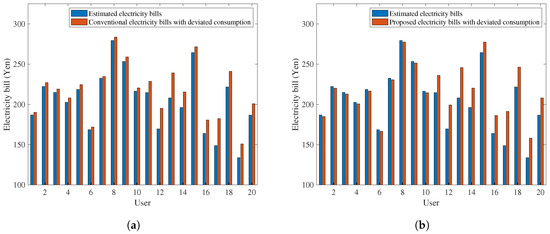
Figure 8.
User’s electricity bill with consumption deviation. (a) Conventional billing mechanism; (b) Proposed billing mechanism.
6. Conclusions
In this paper, we proposed user-centric consumption scheduling and fair billing mechanism for DSM program which consider economic incentives and user comfort. First, consumption scheduling is determined in a distributed iterative fashion in order to maximize individual user electricity bill savings while preserving the preferred level of discomfort caused by load shifting. Moreover, users also have a choice to determine the amount of contribution toward the community as a trade-off for their comfort. In addition, the rescheduling algorithm is proposed to cope with the users who have changed their preference and request new schedules whenever necessary. Finally, a fair billing mechanism is designed to improve the fairness level in determining final electricity bills of the users which considers both rescheduling users and the amount of consumption deviation from the assigned schedules.
The simulation results have shown the effectiveness of the proposed DSM mechanism, in the aspects of cost saving and PAR reduction in both day-ahead scheduling and rescheduling cases. The algorithm is shown to converge within a reasonable iteration count and able to achieve significant energy cost savings. The impact of different user’s weight factor and appliance priority values to the aggregated energy cost and PAR are analyzed. Finally, the results of the proposed billing mechanism shown an improvement in fairness level of the DSM program.
The integration of the proposed features result in a user-centric DSM program which is expected to attain higher levels of user participation and achieve a practical DSM deployment in the future smart grid. Future work could address the integration of distributed generation as well as further research on peer-to-peer energy sharing.
Author Contributions
Conceptualization, P.C., M.S., S.J., C.C., Y.L. and Y.T.; Methodology, P.C., M.S. and S.J.; Writing-Original Draft Preparation, P.C.; Writing-Review & Editing, M.S., S.J., C.C. and Y.L.; Supervision, C.C., Y.L. and Y.T.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The list of appliance is taken from CREST model specification sheet [22] as shown in Table A1. Please note thatthe classification of activities as shiftable or non-shiftable may be perceived as arbitrary. However, by applying different user preferences, an activity can be effectively reclassified as to fulfill the user’s needs.

Table A1.
List of appliances.
Table A1.
List of appliances.
| Non-Flexible Appliance | Flexible Appliance |
|---|---|
| Chest freezer | Iron |
| Fridge freezer | Vacuum |
| Refrigerator | Hob |
| Upright freezer | Oven |
| Answer machine | Microwave |
| Cassette/CD player | Kettle |
| Hi-Fi | Small cooking group |
| Clock | Dish washer |
| Cordless telephone | Tumble dryer |
| Fax | Washing machine |
| Personal computer | Washer dryer |
| Printer | Electric shower |
| TV 1 | |
| TV 2 | |
| TV 3 | |
| VCR/DVD | |
| TV receiver box | |
| Electric space heating | |
| Storage heaters | |
| Domestic Electric Storage Water Heater | |
| Electric instantaneous water heater | |
| Lighting |
References
- Nexans Home Page. Deploying a Smarter Grid through Cable Solutions and Services. Available online: https://www.nexans.co.uk/Corporate/2010/WHITE_PAPER_SMART_GRIDS_2010.pdf (accessed on 13 November 2018).
- Energypost Home Page. The Idea of Large Power Stations for Baseload Is Outdated. Available online: http://energypost.eu/interview-steve-holliday-ceo-national-grid-idea-large-power-stations-baseload-power-outdated/ (accessed on 5 November 2018).
- Paun, M.; Lorenz, G. Smart grids and networks of the future—Eurelectric views. In Proceedings of the CIRED 2009—20th International Conference and Exhibition on Electricity Distribution—Part 1, Prague, Czech Republic, 8–11 June 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Meyabadi, A.; Deihimi, M. A review of demand-side management: Reconsidering theoretical framework. Renew. Sustain. Energy Rev. 2017, 80, 367–379. [Google Scholar] [CrossRef]
- Breukers, S.; Heiskanen, E.; Brohmann, B.; Mourik, R.; Feenstra, C. Connecting research to practice to improve energy demand-side management (DSM). Energy 2011, 36, 2176–2185. [Google Scholar] [CrossRef]
- Li, Y.; Trayer, M. Automated residential demand response: Algorithmic implications of pricing models. In Proceedings of the 2012 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 13–16 January 2012; pp. 626–629. [Google Scholar] [CrossRef]
- Dorini, G.; Pinson, P.; Madsen, H. Chance-Constrained Optimization of Demand Response to Price Signals. IEEE Trans. Smart Grid 2013, 4, 2072–2080. [Google Scholar] [CrossRef]
- Roh, H.; Lee, J. Residential Demand Response Scheduling with Multiclass Appliances in the Smart Grid. IEEE Trans. Smart Grid 2016, 7, 94–104. [Google Scholar] [CrossRef]
- Ramchurn, S.D.; Vytelingum, P.; Rogers, A.; Jennings, N. Agent-based Control for Decentralised Demand Side Management in the Smart Grid. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems—Volume 1, AAMAS’11, Taipei, Taiwan, 2–6 May 2011; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2011; pp. 5–12. [Google Scholar]
- Mohsenian-Rad, A.H.; Wong, V.W.S.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous Demand-Side Management Based on Game-Theoretic Energy Consumption Scheduling for the Future Smart Grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Vuppala, S.K.; Padmanabh, K.; Bose, S.K.; Paul, S. Incorporating fairness within Demand response programs in smart grid. In Proceedings of the ISGT 2011, Anaheim, CA, USA, 17–19 January 2011; pp. 1–9. [Google Scholar] [CrossRef]
- Shinwari, M.; Youssef, A.; Hamouda, W. A Water-Filling Based Scheduling Algorithm for the Smart Grid. IEEE Trans. Smart Grid 2012, 3, 710–719. [Google Scholar] [CrossRef]
- Negash, A.I.; Haring, T.W.; Kirschen, D.S. Allocating the Cost of Demand Response Compensation in Wholesale Energy Markets. IEEE Trans. Power Syst. 2015, 30, 1528–1535. [Google Scholar] [CrossRef]
- O’Brien, G.; Gamal, A.E.; Rajagopal, R. Shapley Value Estimation for Compensation of Participants in Demand Response Programs. IEEE Trans. Smart Grid 2015, 6, 2837–2844. [Google Scholar] [CrossRef]
- Baharlouei, Z.; Narimani, H.; Mohsenian-Rad, H. Tackling co-existence and fairness challenges in autonomous Demand Side Management. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 3159–3164. [Google Scholar] [CrossRef]
- Baharlouei, Z.; Hashemi, M.; Narimani, H.; Mohsenian-Rad, H. Achieving Optimality and Fairness in Autonomous Demand Response: Benchmarks and Billing Mechanisms. IEEE Trans. Smart Grid 2013, 4, 968–975. [Google Scholar] [CrossRef]
- Assaf, T.; Osman, A.H.; Hassan, M. Fair Autonomous Energy Consumption Scheduling Based on Game-Theoretic Approach for the Future Smart Grid. In Proceedings of the 2016 UKSim-AMSS 18th International Conference on Computer Modelling and Simulation (UKSim), Cambridge, UK, 6–8 April 2016; pp. 235–239. [Google Scholar] [CrossRef]
- Charoen, P.; Javaid, S.; Lim, Y.; Tan, Y.; Charoenlarpnopparut, C. Adaptive Rescheduling of Energy Consumption Based on User Preferences for the Future Smart Grid. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 36–41. [Google Scholar] [CrossRef]
- Charoen, P.; Sioutis, M.; Javaid, S.; Lim, Y.; Tan, Y. Fair Billing Mechanism for Energy Consumption Scheduling with User Deviation in the Smart Grid. In Proceedings of the 2018 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–15 August 2018; pp. 84–88. [Google Scholar] [CrossRef]
- Lemaréchal, C.S.; Boyd, L. Vandenberghe, Convex Optimization, Cambridge University Press, 2004 hardback, ISBN 0 521 83378 7. Eur. J. Oper. Res. 2006, 170, 326–327. [Google Scholar] [CrossRef]
- Samadi, P.; Schober, R.; Wong, V.W.S. Optimal energy consumption scheduling using mechanism design for the future smart grid. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 369–374. [Google Scholar] [CrossRef]
- McKenna, E.; Thomson, M. High-resolution stochastic integrated thermal–electrical domestic demand model. Appl. Energy 2016, 165, 445–461. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).