Abstract
Increasing energy efficiency is commonly viewed as providing a key stimulus to economic growth, through investment in efficient technologies, reducing energy use and costs, enabling productivity gains, and generating jobs. However, this view is received wisdom, as empirical validation has remained elusive. A central problem is that current energy-economy models are not thermodynamically consistent, since they do not include the transformation of energy in physical terms from primary to end-use stages. In response, we develop the UK MAcroeconometric Resource COnsumption (MARCO-UK) model, the first econometric economy-wide model to explicitly include thermodynamic efficiency and end energy use (energy services). We find gains in thermodynamic efficiency are a key ‘engine of economic growth’, contributing 25% of the increases to gross domestic product (GDP) in the UK over the period of 1971–2013. This confirms an underrecognised role for energy in enabling economic growth. We attribute most of the thermodynamic efficiency gains to endogenised technical change. We also provide new insights into how the ‘efficiency-led growth engine’ mechanism works in the whole economy. Our results imply a slowdown in thermodynamic efficiency gains will constrain economic growth, whilst future energy-GDP decoupling will be harder to achieve than we suppose. This confirms the imperative for economic models to become thermodynamically consistent.
1. Introduction
The adoption of more efficient energy technologies and practices (usually described as ‘energy efficiency’) is a key pillar of global energy policies [1,2,3], with two common aims. First, it is widely considered as the most cost-effective intervention to achieve rapid reductions in energy demand and carbon dioxide emissions [3,4], which are required to limit global temperature rises [5]. However, due to an energy ‘rebound’ effect [6,7], its success in this role remains disputed [8,9]. Second, investment in efficient technologies is thought to stimulate economic growth [10] by enabling productivity gains and generating jobs [11,12]. Despite being theoretically preferable [13,14], current economy-wide models do not explicitly include thermodynamic (energy conversion) efficiency. Instead, they rely on broader proxies based on the anticipated effects of energy efficiency, such as price and technical progress effects [15,16,17], or intended energy reductions [18]. Therefore, the view of thermodynamic efficiency’s role as being a key ‘engine of economic growth’ is received wisdom, rather than empirically established fact.
In response, we develop the UK MAcroeconometric Resource COnsumption (MARCO-UK) model, which, to our knowledge, is the first energy-economy-wide model to include thermodynamic efficiency and energy services as explicit integral components. We also expand on existing macroeconometric models [19,20] by including the useful stage of energy consumption (as useful exergy), as shown in Figure 1. The inclusion of thermodynamic efficiency and useful exergy allows us to investigate their roles in economic growth. Useful exergy is the energy used at the last energy conversion stage before exchange for energy services, and so we adopt useful exergy as a proxy from this point for the more intuitive label of energy services. Following Ertesvag’s [21] distinction, we follow the ‘energy carriers for energy use’ thermoeconomics-based exergy analysis boundaries, first adopted at a national scale by Reistad [22], as opposed to the extended exergy analysis boundary of Wall [23] and Sciubba [24], where all energy and material exergy flows are considered through an economy.
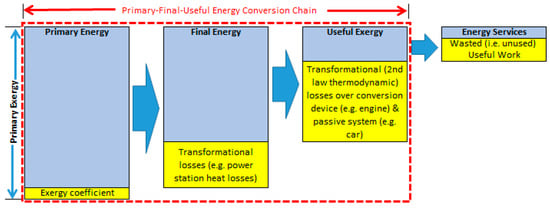
Figure 1.
Primary-to-final-to-useful energy conversion stages. Adapted from [30].
The final-to-useful stage is rarely studied at an economy-wide level [25,26,27] but, as Figure 1 illustrates, it is where most thermodynamic energy conversion losses occur. Referring to Figure 1, a key variable utilized in our analysis is thermodynamic efficiency for the key final-to-useful energy conversion stage, which we define in relation to the second law of thermodynamics following Carnahan et al. [28] and Patterson [13] as the ratio of useful energy (out) to useful energy (in) as (1):
Its inclusion within modelling frameworks could therefore be important for improving the evidence base for energy efficiency policy [29].
In this article, we use a counterfactual simulation approach to isolate and quantify the effect of thermodynamic efficiency gains on economic growth. Comparisons are made to other simulations, which isolate the effects of other variables, including labour, capital investment, and energy supply. We then explain the efficiency-led growth mechanism, before finally discussing the main implications for modelling and energy policy. Because the UK has exhibited similar economic growth and structural changes to other large industrialised economies [31,32], it is a good case study for illustrating the global reach and importance of the findings.
2. Materials and Methods
We utilise MARCO-UK in order to understand the role of thermodynamic efficiency in economic growth. MARCO-UK’s statistically robust construction is based on established econometric methods, and has involved significant empirical testing, validation, and peer-review. Four important characteristics of MARCO-UK form its architectural framing. First, the model contains post-Keynesian characteristics, where demand plays an essential role in the economy [33,34]. Second, the supply-side is represented via modified aggregate production functions involving capital, labour, and energy. Third, we include elements of ecological economics, specifically the assumption that energy plays a larger role in the economy than suggested by its cost-share [35,36]. Fourth, the ability to test elements of exergy economics, i.e., the influence on economic growth of useful exergy [37,38] and thermodynamic efficiency [39]. Moreover, econometric models have the distinct advantage of allowing ex-post and ex-ante simulations [40]. It also allows interrelationships of variables and coefficients to be estimated econometrically, rather than being specified a priori.
2.1. Model Construction
Figure 2 shows the simplified schematic of the relationships between the key energy and economic variables found at the core of MARCO-UK (see Supplementary Materials, for the complete set of variables and equations). Key energy variables include energy use (in GJ) at primary, final, and useful stages, and thermodynamic conversion efficiencies at primary-to-final and final-to-useful stages. Energy use at the primary and useful stage are aggregate totals. Figure 2 also shows MARCO-UK contains three energy ‘consuming’ sectors at the final energy stage: Households (C), Industry (IND), and Other (OTH) (e.g., agriculture, government, and services). These energy variables are fully integrated into MARCO-UK’s structure, as opposed to more conventional soft-linking of energy and economy modules [19,41].
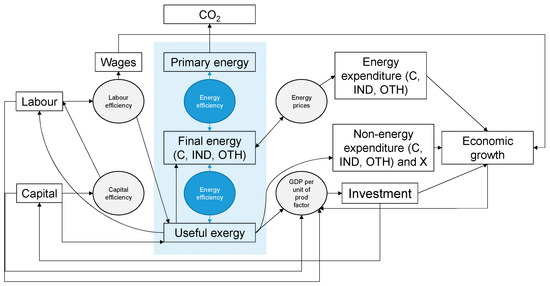
Figure 2.
Schematic MARCO-UK model structure.
MARCO-UK follows the tradition of post-Keynesian-based models. As such, it emphasises the role of aggregate demand as a key driver of economic growth, assuming that supply adjusts to meet demand. Moreover, the model’s structure is based on the system of national accounts. The model, in this sense, does not adhere to the principle of general equilibrium, as it is understood in supply-driven modelling frameworks (i.e., computable general equilibrium models). Rather, the relationship between aggregate demand and supply is given by national accounting definitions.
Total income must be equal to total expenditure in each time period. The level of aggregate demand (i.e., private and public expenditure), in turn, hinges on decisions to consume and invest. Households consume goods according to the income they receive, while government spending is assumed to be exogenous and not related to national income. Investment in capital stock is assumed to depend on the productivity of the factors of production (i.e., capital, labour and energy), while ‘crowding-out’ effects (i.e., limited availability of capital investment in some sectors due to the decision to invest in others) are endogenous. Investment in energy efficiency and other types of investment are not separated in the model. In fact, it is often difficult to separate these two categories of investment. For example, most new machines, houses, cars, and other goods are now more energy efficient than older ones, although they have not been considered as energy efficiency investments per se.
Drawing from the field of ecological economics, the model assumes that while energy and capital can be substitutable to a certain extent, they are mostly complementary inputs (e.g., additional energy is required to operate an extra machine). Investment in capital is also required to activate energy efficiency gains. Moreover, it is assumed that energy services have a closer link to economic growth, rather than primary and final energy. Demand for energy services drives the use of primary and final energy and, hence, stimulate capital investment and generate growth. In this respect, useful exergy is used in the model as a proxy for energy services. Moreover, demand for final energy is determined by energy prices, which are assumed to have been influenced during the modelling time period by the existing energy market structures in the UK (see additional assumptions in the Supplementary Materials).
2.2. MARCO-UK Equations
Like other macroeconometric models, MARCO-UK is essentially a system of equations. We outline how these are constructed, with examples of key variables from Figure 2. A full description of all 57 MARCO-UK equations is given in the Supplementary Materials.
MARCO-UK’s equations can be of two different types. The first type involves identities’, which represent definitional relationships between given variables and must hold true in all time periods. The main identities are based on definitions provided by the system of national accounts. For instance, (2) gives gross domestic product (GDP), defined from the expenditure side (Y) as the sum of private (C) and public (G) consumption, investment (I), and net exports (X−M). From the income side, (3) states that GDP (Y) is defined by total national income (i.e., compensation of employees (W), profits received by firms (YF), etc.) plus net taxes (YG). These two identities must hold for each time period. Most of the components of these GDP identities are themselves estimated individually as econometric equations:
The second type of equations are empirically-based, and contain parameters estimated econometrically. They are also known as ‘behavioural’ or ‘stochastic’ equations, but for simplicity, we use the term, ‘econometric equation’. Econometric equations exist for many of the model’s key variables, including capital, labour, prices, and energy consumption, etc. For example, labour (L) in (4) is a function of GDP (Y) and the other two factors of production: Capital services (K_SERV) and total useful exergy (UEX_TOT). Total useful exergy (UEX_TOT) in (5) is a function of its own level in time t−1, quality-adjusted labour (HL), gross capital stock (K_GRS), and GDP (Y). Last, the general level of prices in (6) is represented by the consumer price index (CPI), which is a function of the general price of energy (CPI_E), the price of imports (PM), wage productivity (W/Y), and the real exchange rate (E_INDEX_REAL):
We should also note that identities are commonly formed from econometrically estimated variables. One example, given in (7), is the endogenous energy variable of final-to-useful thermodynamic efficiency (EXEFF_FU), which is set as the ratio of consumed useful exergy (UEX_TOT) to final energy (FEN_T), which are themselves econometrically estimated variables. A second example is given in (8), where total final energy (FEN_T) is the sum of final energy used by households (FEN_C), industry (FEN_IND), and the remaining sectors (i.e., agriculture and services) (FEN_OTH):
The particular functional forms and choice of explanatory variables are empirically validated and tested using econometric techniques. The present version of the model contains 57 equations: 30 are identities and 27 are econometric (see Supplementary Materials).
2.3. Data and Estimation Process
The model is based on annual time series data for 75 variables covering the period of 1971–2013. Economic variables are expressed in constant (real) terms based on 2011 UK prices. Data was collected from internationally reputable data sources, including the UK Office for National Statistics, World Bank, Penn World Tables, and the United Nations (see Supplementary Materials).
The parameters contained in the econometric equations were estimated using Ordinary Least Squares (OLS) techniques, with variables expressed in logarithms, generally following the procedures suggested by Brillet [42]. Stationarity and cointegration tests were applied to determine the existence of common long-term equilibrium relationships between variables. When cointegrating relationships were identified, econometric equations were estimated using long-run and short-run specifications. The latter involve variables expressed in log differences, and include time lags and an error correction term. All the estimated variables were examined in terms of their goodness of fit (i.e., adjusted R2). Coefficients were checked for statistical significance, and their direction (signs) should not contradict theoretical expectations. Moreover, residuals were tested for normality, heteroscedasticity, and autocorrelation.
2.4. Basefit Model and Validation
Once all the econometric equations were estimated, they form a system of linear equations together with the identities. It is important to highlight that the model solution does not entail the optimisation of any particular variable. In other words, no optimal behaviour is implied. The system is dynamically solved for each time period using the established Gauss-Seidel iterative method [43]. This technique allows determination of the values of the endogenous variables, based on the known values of the exogenous variables (there are 17 exogenous variables, which can be consulted in the Supplementary Materials). The method also requires the actual values of the endogenous variables to be provided for the starting time periods (1971 to 1975 due to the use of time lags), and subsequently uses their estimated values to solve the system for the remaining time periods.
Dummy variables were included in order to capture break points in the variables’ trends. Dummies were applied once a structural break test had been applied, and were mostly used to account for the recessions in the mid 1970’s, early 1980’s, and the financial crisis of 2009. (Refer also to Supplementary Materials, section S4 for additional description of this process.) Once the model has been solved, the solution represents the basefit.
The model validation process involved several steps. First, the annual datasets for variables were sourced and validated. Second, using the annual datasets, the individual equations were assembled to form the basic model architecture, using mainly standard and post-Keynesian economic theory. Third, the basic model results and statistical test results were reviewed, with amendments made to correct any diagnostic errors. Fourth, the improved model was then peer reviewed, and several further refinements were made from the feedback received. A final stage then occurred to review the models results, and making required improvements to improve fitting to meet statistical tests. The end product was the basefit model, used for the counterfactual simulations.
2.5. Counterfactual (ex-post) Simulations
Counterfactual simulations are ideally suited to our guiding research question: What is the role of thermodynamic (energy) efficiency in economic growth? We ran ex-post simulations over the historical MARCO-UK time frame (1971–2013), enabling isolation of the effects on the whole economy caused by changes to any variable (e.g., thermodynamic efficiency). The ability to perform such isolation provides an advantage over other modelling approaches, such as Computable General Equilibrium (CGE) models [15,44]. For our study, we ran six simulations, where values of the following six variables were each successively held constant at 1971 levels during the entire time period (i.e., 1971–2013):
- Thermodynamic efficiency (final-to-useful energy conversion efficiency);
- Final energy use (total, i.e., sum of Households, Industry, and Other sectors);
- Useful exergy (total);
- Energy prices (paid by Households, Industry, and Other sectors);
- Investment in fixed capital (annual); and
- Labour (number of employed people).
3. Results: Thermodynamic Efficiency Gains Revealed as a Key ‘Engine of Economic Growth’
3.1. Simulation Results
The level of aggregate economic output in each of the simulations was compared to the basefit model solution in Figure 3, revealing the effect that changes in each variable exerted on economic growth. Though all simulations began at the same starting point (1971), they only became visible in 1976, once the highest lagged variable in all equations was cleared. The two largest historical influences on GDP are seen in Figure 3 as thermodynamic efficiency gains and capital investment. Constraining either variable to 1971 levels led to a counterfactual reduction in economic growth of 25% in 2013.
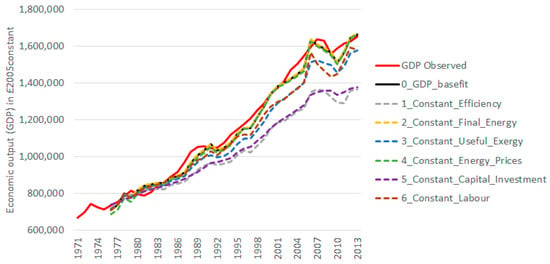
Figure 3.
Economic output GDP under counterfactual simulations.
More detail is given in Table 1, which shows the effects on economic growth of each simulation in different time periods. We followed the approach of Kander and Stern, both in terms of the format of Table 1, and their caveat (p.63) that “the contributions of each variable do not add up to the total growth rate” [45]. Therefore, Table 1 should be seen as providing a quantitative measure –for the variables tested in our counterfactual simulations– as to which have had the largest influences. In each time period, thermodynamic efficiency and capital investment consistently exert the most significant influence. The roles of the other variables in Table 1 were observed to be less strong.

Table 1.
Simulations—contributions to GDP growth rate.
3.2. The Strong Role(s) of Energy in Economic Growth
There are several important findings in relation to the role of energy in economic growth. First, as noted above, there was a significant role for thermodynamic efficiency gains in economic growth. This supports the earlier modelling work of Ayres and Warr in their Resource-EXergy Services (REXS) model [39], where they found thermodynamic efficiency gains had (and will have) a significant role in US economic growth.
Second, energy services (via our proxy of useful exergy) had a stronger effect on economic growth than final energy or energy prices, and was found to be the energy variable that affects economic growth the most in our model –when compared to the contribution from energy prices or energy supply (final energy). This supports the assertions of Ayres and others [38,46,47] in the field of exergy economics, who advocate that the useful stage of energy has a close link to economic growth. We found the relationship between energy supply (final energy) and economic growth to be weaker than Kander and Stern’s case study of Sweden [45]. This is because MARCO-UK includes final-to-useful thermodynamic efficiency as an additional energy variable, whose strong role in economic growth thereby reduces the influence of the final energy supply and potentially other explanatory variables, such as capital and labour.
Thirdly, we can split thermodynamic efficiency gains (and thus its contribution to economic growth) into two components: ‘Technical progress’ and ‘energy services demand’, as shown in Figure 4. In many economic models, there is often an unaccounted for portion of economic growth, which cannot be attributed to changes in factor inputs, such as labour, capital, and energy. This is commonly known as the Solow residual or ‘technical progress’ [48]. In our case, MARCO-UK endogenises technical progress, since our model attributes all economic growth to elements within the model. In Figure 4, the blue line shows the simulation where energy services demand is held constant. Thermodynamic efficiency rose significantly in this case (relative to the grey constant efficiency line), suggesting there is a ‘natural’ economy-wide thermodynamic efficiency gain that occurs year-to-year –in effect, this was ‘technical progress’ endogenised in our model. This confirms the crucial role that energy augmenting technical progress plays as a driver of economic growth, as previously suggested by others, including Berndt [49], and Turner and Hanley [50]. Separately, the black line shows thermodynamic efficiency in the basefit case. The increase to thermodynamic efficiency in this case (relative to the blue line), was therefore stimulated by the increased demand for energy services, and is part of the overall efficiency-led growth mechanism presented in the next section.
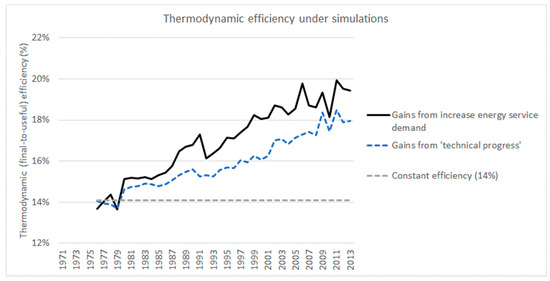
Figure 4.
Thermodynamic efficiency gains from technical progress and increased energy services.
3.3. The Divergent Influences of Capital and Labour
First, our results confirmed the strong role of capital in economic growth, but the traditional view of labour as a key input (alongside capital) was only partially supported from our model. Table 1 suggests a low overall contribution (less than 10%), but with stronger (1990–2000) and weaker (2000–2013) periods of influence. Second, our results showed that energy and capital behave as complements, and the energy-capital composite acts as a substitute for labour. This is most clearly seen in the Supplementary Materials, where Figure S3 shows how capital decreased when energy was constrained, whilst Figure S8 shows how energy-capital increased under a constrained labour supply. Third, Figure 5 shows the simulations’ effect on capital productivity (i.e., GDP per unit of capital stock) and labour productivity (GDP per person employed), which are important macroeconomic indicators [51,52]. UK capital productivity has been remarkably stable over time, at around 0.25 (measured in constant £2005 GBP). This stable range was maintained for all simulations –except for the outlier case where capital investment was constrained (economic growth slows, but capital stock peaks and then declines). Such stability reinforces our finding of the crucial role of capital investment. Conversely, labour productivity in the simulations showed significant variation around the basefit results. The weaker coupling between labour and GDP supports the earlier finding: Labour has a much lower effect (than capital) on economic growth. The strong role of energy displacing that of labour may be controversial in mainstream economic circles (given that only capital and labour exist as production factors), but support Hannon and Joyce [53], who found “the inclusion of energy in the … production function does not explain the contribution of technological process ... unless … one is able to make the seemingly unreasonable assumption that labor should not appear in the production function”.
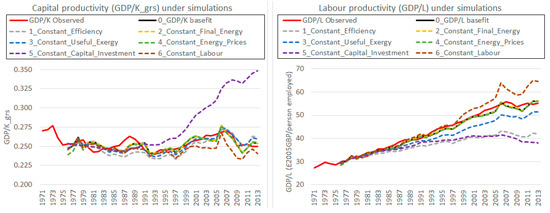
Figure 5.
Capital and labour productivity under simulations.
4. Discussion: The ‘Efficiency-led Growth Engine’ Mechanism
Having isolated and quantified the contribution of thermodynamic efficiency gains to economic growth, we now explain in more detail the ‘efficiency-led growth engine’ mechanism. In the mechanism, there are several feedback channels for efficiency gains leading to economic growth, as shown in Figure 6.
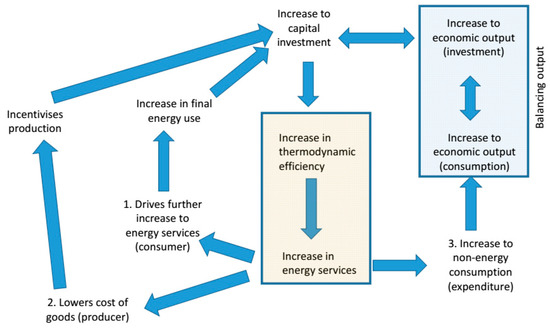
Figure 6.
The ‘efficiency-led growth engine’ mechanism.
To explain in more detail the growth mechanism in Figure 6, we start with capital investment, (e.g., through purchase of insulation or a more efficient domestic boiler), which causes an increase in thermodynamic efficiency from the final-to-useful stage. The effect is an increase in energy services (i.e., useful exergy) in the economic system. In other words, the same level of final energy supply delivers a greater flow of energy services. Apart from the initial capital investments, which generate economic growth, three other mechanisms are at play. First, there is a consumer-sided effect: The additional supply of energy services, at a lower final energy cost, drives an expansion in consumer demand for energy services. This effect is triggered in two stages. Initially, we see a redistribution of energy cost savings via an energy ‘rebound’ effect [54]. For example, increased use of higher efficiency lighting, or via demand for alternative energy services. The second stage is an increase in the consumption of additional energy services [55]. In total, the higher energy services demand is then satisfied, in turn, by increases to final energy use and capital investment, leading to higher economic output. The second mechanism occurs on the producer side, whereby the cost of production has been lowered, leading to productivity gains. This, in turn, stimulates increased production of goods through additional capital investment. The third mechanism involves the additional consumption of energy services, which requires and stimulates the additional demand for complementary non-energy goods. To balance output, Figure 6 shows this requires a further increase in economic output on the production side.
Our mechanisms of efficiency-stimulated economic growth expands the Salter-type economic growth cycle proposed by Ayres et al. [56], supported by empirical evidence. A key aspect of our modelling approach is that capital and energy are treated as complementary inputs: Final energy is needed to activate capital, and vice versa [57,58]. Therefore, higher levels of final energy supply leads to increased capital investment and subsequently higher economic growth.
5. Conclusions
5.1. The Underrecognised Role of Energy
Our study supports the view of Kummel and others [36,59] that energy has a much more significant role in economic growth than its 5–10% ‘cost-share’ in production costs would suggest. Such non-linearity demonstrates the importance of energy to the economy. Several key findings stand out. First is the quantified, significant role of thermodynamic efficiency gains and capital investment, which are revealed as key drivers of economic growth. Second, we identified that thermodynamic efficiency gains comprise two parts: A natural/technical (supply-side) gains (i.e., endogenised technical change), and a demand-side component, where increased demand for energy services accelerates thermodynamic efficiency gains. Third, demand for energy services had more influence on economic growth than either energy supply or energy prices, which supports those who suggest that the energy stage closest to energy services is most tightly linked to economic output [60]. Last, we set out the efficiency-led growth mechanism as represented in Figure 6.
5.2. Energy Efficiency as a Good Return on Investment
The investment in capital and energy efficiency gains can be seen as being essential to delivering economic growth, alongside other benefits, including wider access to energy services, job creation, and improving income per capita [12]. This crucial role of thermodynamic efficiency serves as key support for continued policy effort and investment in efficiency measures. Such investments (e.g., energy efficient machines, appliances, etc.) are also often associated with further productivity gains, like improvements in labour, material, and resource productivity, and economies of scale. However, by implication, economic growth could be hindered if future thermodynamic efficiency gains become harder to achieve, as previously suggested [39]. (Though, having said this, future efficiency policies can be targeted to increase energy services (useful exergy) whilst constraining final energy. An example could be a largescale domestic building retrofit programme).
Such thermodynamic constraint to an economy is a credible current scenario, as national-level thermodynamic efficiency gains have been slowing in developed countries, including the UK [61,62,63]. It may be, therefore, no coincidence that there also has been a slowdown in economic growth in OECD countries. In turn, this suggests a slowdown in thermodynamic efficiency gains may provide an alternative causation –often attributed to labour productivity [64]– for secular stagnation.
5.3. Developing Thermodynamically-Consistent Modelling
Capital, labour, and (final or primary) energy use are included in many energy-economy models as the three key inputs to ‘production’ [65,66]. However, thermodynamic efficiency and end energy use (energy services) are not, meaning such models are not thermodynamically consistent. Given our findings of the impacts of both efficiency gains and energy services on economic growth, this is a crucial omission. Developing thermodynamically-consistent economic models, which include thermodynamic efficiency and energy services, will enable a better understanding of the role of energy in the economy, and in turn provide better evidence for policy. It will also mean that the possible impacts of constraints to future thermodynamic (energy) efficiency gains on economic growth can be explored [39]. Such scenario modelling can help to quantify how slower/lower efficiency gains may constrain economic growth, and consider the best policy response, e.g., providing a firm, economic rationale for increased energy efficiency investment.
5.4. The Decoupling Challenge
The tight coupling between global energy use and GDP [67,68,69] can be explained because of –not in spite of– decades of global energy efficiency investment. Policy efforts to decouple energy from GDP are therefore more challenging than we may have supposed. However, the identification of the explicit role of thermodynamic efficiency in the economy serves as the first step to identify a way forward. Subsequent steps can utilise thermodynamically-consistent modelling to study the impacts of alternative policy measures on energy efficiency. One example is energy taxes [70], which can be adopted to reduce energy feedbacks/rebound. In MARCO-UK, this can be modelled via exogenous energy price increases. A second example is a faster transition to renewables to leave more unburnable fossil fuels [71,72]. In MARCO-UK, this can be modelled in a planned Version 2, which splits energy inputs between fossil fuels and renewables. A third example are sufficiency caps [73], which seek to place a limit on future energy use. In MARCO-UK, final energy can be exogenously constrained.
Finally, the UK has exhibited similar economic growth, and characteristics of structural change and thermodynamic efficiency gains to other large industrialised economies. Therefore, our findings have direct relevance to energy modelling and policy communities globally.
Supplementary Materials
The following are available online at http://www.mdpi.com/1996-1073/12/1/110/s1, Supplementary Materials: The UK MAcroeconometric Resource COnsumption Model (MARCO-UK).
Author Contributions
Conceptualization, J.B., M.S., P.G.T. and P.E.B.; methodology, M.S. and P.E.B.; software, M.S. and P.E.B.; validation, M.S., P.G.T. and P.E.B.; formal analysis, M.S. and P.E.B.; investigation, M.S. and P.E.B.; resources, J.B., data curation, M.S. and P.E.B.; writing—original draft preparation, M.S. and P.E.B.; writing—review and editing, J.B. and P.G.T.; visualization, M.S.; supervision, P.G.T.; project administration, J.B.; funding acquisition, J.B. and P.G.T.
Funding
This work was supported by the research programme of the UK Energy Research Centre, supported by the UK Research Councils under [EPSRC award EP/L024756/1] and the RCUK Energy Program’s funding for the Centre for Industrial Energy, Materials and Products [grant reference EP/N022645/1]. We also acknowledge the support for P.E.B. under EPSRC award EP/R024251/1, and for P.G.T. from the University of Leeds’ Low Carbon Energy Research Group and the Centre for Integrated Energy Research.
Acknowledgments
We would like to thank Cambridge Econometrics, Steve Keen, Tiago Domingos and Zia Wadud for their insightful comments on the MARCO-UK model during its construction as part of our peer review process. We also appreciate the comments and insights provided by the several anonymous reviewers who read this article and contributed to improve its quality.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- European Parliament. Directive 2012/27/EU of the European Parliament and of the Council of 25 October 2012 on energy efficiency. Off. J. Eur. Union Dir. 2012, 315, 1–56. [Google Scholar] [CrossRef]
- An-gang, H.U. The Five-Year Plan: A new tool for energy saving and emissions reduction in China. Adv. Clim. Change Res. 2017, 7, 222–228. [Google Scholar] [CrossRef]
- Geller, H.; Harrington, P.; Rosenfeld, A.H.; Tanishima, S.; Unander, F. Polices for increasing energy efficiency: Thirty years of experience in OECD countries. Energy Policy 2006, 34, 556–573. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Energy Efficiency—Market Report 2016. Available online: https://www.iea.org/eemr16/files/medium-term-energy-efficiency-2016_web.pdf (accessed on 26 December 2018).
- Meinshausen, M.; Meinshausen, N.; Hare, W.; Raper, S.C.B.; Frieler, K.; Knutti, R.; Frame, D.J.; Allen, M.R. Greenhouse-gas emission targets for limiting global warming to 2 °C. Nature 2009, 458, 1158–1162. [Google Scholar] [CrossRef] [PubMed]
- Herring, H. Does energy efficiency save energy? The debate and its consequences. Appl. Energy 1999, 63, 209–226. [Google Scholar] [CrossRef]
- Sorrell, S. Energy Substitution, Technical Change and Rebound Effects. Energies 2014, 7, 2850–2873. [Google Scholar] [CrossRef]
- Schipper, L.; Grubb, M. On the rebound? Feedback between energy intensities and energy uses in IEA countries. Energy Policy 2000, 28, 367–388. [Google Scholar] [CrossRef]
- Gillingham, K.; Kotchen, M.J.; Rapson, D.S.; Wagner, G. Energy policy: The rebound effect is overplayed. Nature 2013, 493, 475–476. [Google Scholar] [CrossRef]
- Ayres, R.U.; Warr, B. The Economic Growth Engine: How Energy and Work Drive Material Prosperity; Edward Elgar: Cheltenham, UK, 2010. [Google Scholar]
- McKinsey & Company. Energy Efficiency: A Compelling Global Resource. 2010, pp. 1–74. Available online: https://www.mckinsey.com/~/media/mckinsey/dotcom/client_service/Sustainability/PDFs/A_Compelling_Global_Resource.ashx (accessed on 26 December 2018).
- International Energy Agency (IEA). Capturing the Multiple Benefits of Energy Efficiency. Available online: https://www.iea.org/publications/freepublications/publication/captur_the_multiplbenef_ofenergyeficiency.pdf (accessed on 26 December 2018).
- Patterson, M.G. What is energy efficiency? Energy Policy 1996, 24, 377–390. [Google Scholar] [CrossRef]
- Madlener, R.; Alcott, B. Energy rebound and economic growth: A review of the main issues and research needs. Energy 2009, 34, 370–376. [Google Scholar] [CrossRef]
- Koesler, S.; Swales, K.; Turner, K. International spillover and rebound effects from increased energy efficiency in Germany. Energy Econ. 2016, 54, 444–452. [Google Scholar] [CrossRef]
- Bataille, C.; Melton, N. Energy efficiency and economic growth: A retrospective CGE analysis for Canada from 2002 to 2012. Energy Econ. 2017, 64, 118–130. [Google Scholar] [CrossRef]
- Kasahara, S.; Paltsev, S.; Reilly, J.; Jacoby, H.; Ellerman, A.D. Climate change taxes and energy efficiency in Japan. Environ. Resour. Econ. 2007, 37, 377–410. [Google Scholar] [CrossRef]
- Barker, T.; Dagoumas, A.; Rubin, J. The macroeconomic rebound effect and the world economy. Energy Effic. 2009, 2, 411–427. [Google Scholar] [CrossRef]
- E3ME Technical Manual; Version 6; Cambridge Econometrics: Cambridge, UK, 2014.
- Sijm, J.; Lehmann, P.; Chewpreecha, U.; Gawel, E.; Mercure, J.-F.; Pollitt, H.; Strunz, S. EU Climate and Energy Policy beyond 2020: Are Additional Targets and Instruments for Renewables Economically Reasonable? UFZ Discuss Pap No 3/2014. 2014, pp. 1–36. Available online: http://hdl.handle.net/10419/103564 (accessed on 26 December 2018).
- Ertesvåg, I.S. Society exergy analysis: A comparison of different societies. Energy 2001, 26, 253–270. [Google Scholar] [CrossRef]
- Reistad, G. Available Energy Conversion and Utilization in the United States. ASME Trans. Ser. J. Eng. Power 1975, 97, 429–434. [Google Scholar] [CrossRef]
- Wall, G. Exergy conversion in the Swedish society. Resour. Energy 1987, 9, 55–73. [Google Scholar] [CrossRef]
- Sciubba, E. Beyond thermoeconomics? The concept of Extended Exergy Accounting and its application to the analysis and design of thermal systems. Exergy Int. J. 2001, 1, 68–84. [Google Scholar] [CrossRef]
- Serrenho, A.C.; Sousa, T.; Warr, B.; Ayres, R.U.; Domingos, T. Decomposition of useful work intensity: The EU (European Union)-15 countries from 1960 to 2009. Energy 2014, 76, 704–715. [Google Scholar] [CrossRef]
- Ayres, R.U.; Ayres, L.W.; Warr, B. Exergy, power and work in the US economy, 1900–1998. Energy 2003, 28, 219–273. [Google Scholar] [CrossRef]
- Serrenho, A.C.; Warr, B.; Sousa, T.; Ayres, R.U. Structure and dynamics of useful work along the agriculture-industry-services transition: Portugal from 1856 to 2009. Struct. Change Econ. Dyn. 2016, 36, 1–21. [Google Scholar] [CrossRef]
- Technical Aspects of the More Efficient Utilization of Energy: Chapter 2—Second law efficiency: The Role of the Second Law of Thermodynamics in Assessing the Efficiency of Energy Use. Available online: https://aip.scitation.org/doi/pdf/10.1063/1.30306 (accessed on 26 December 2018).
- American Physical Society. Energy Future: Think Efficiency 2008. Available online: http://www.aps.org/energyefficiencyreport/index.cfm (accessed on 29 December 2018).
- Brockway, P.E.; Steinberger, J.K.; Barrett, J.R.; Foxon, T.J. Understanding China’s past and future energy demand: An exergy efficiency and decomposition analysis. Appl. Energy 2015, 155, 892–903. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Worldwide Trends in Energy Use and Efficiency: Key Insights from IEA Indicator Analysis 2008; IEA: Paris, France, 2008. [Google Scholar]
- Liddle, B. OECD energy intensity: Measures, trends, and convergence. Energy Effic. 2012, 5, 583–597. [Google Scholar] [CrossRef]
- Klein, L.R. Economic Fluctuations in the United States, 1921–1941, 1st ed.; John Wiley and Sons Ltd.: London, UK, 1950. [Google Scholar]
- Lavoie, M. Post-Keynesian Economics: New Foundations; Edward Elgar: Cheltenham, UK, 2014. [Google Scholar]
- King, C.W. Comparing World Economic and Net Energy Metrics, Part 3: Macroeconomic Historical and Future Perspectives. Energies 2015, 8, 12997–13020. [Google Scholar] [CrossRef]
- Kümmel, R. Why energy’s economic weight is much larger than its cost share. Environ. Innov. Soc. Transit. 2013, 9, 33–37. [Google Scholar] [CrossRef]
- Santos, J.; Domingos, T.; Sousa, T.; St. Aubyn, M. Useful Exergy Is Key in Obtaining Plausible Aggregate Production Functions and Recognizing the Role of Energy in Economic Growth: Portugal 1960–2009. Ecol. Econ. 2018, 148, 103–120. [Google Scholar] [CrossRef]
- Guevara, Z.; Sousa, T.; Domingos, T. Insights on Energy Transitions in Mexico from the Analysis of Useful Exergy 1971–2009. Energies 2016, 9, 488. [Google Scholar] [CrossRef]
- Warr, B.; Ayres, R. REXS: A forecasting model for assessing the impact of natural resource consumption and technological change on economic growth. Struct. Change Econ. Dyn. 2006, 17, 329–378. [Google Scholar] [CrossRef]
- Hall, L.M.H.; Buckley, A.R. A review of energy systems models in the UK: Prevalent usage and categorisation. Appl. Energy 2016, 169, 607–628. [Google Scholar] [CrossRef]
- Zha, D.; Zhou, D. The elasticity of substitution and the way of nesting CES production function with emphasis on energy input. Appl. Energy 2014, 130, 793–798. [Google Scholar] [CrossRef]
- Brillet, J.L. Structural Econometric Modelling: Methodology and Tools with Applications under EViews 2016. Available online: http://www.eviews.com/StructModel/structmodel.pdf (accessed on 26 December 2018).
- Varga, R.S. Basic Iterative Methods and Comparison Theorems. In Matrix Iterative Analysis; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 27, Available online: https://doi.org/10.1007/978-3-642-05156-2_3 (accessed on 26 December 2018).
- Allan, G.; Gilmartin, M.; Turner, K.; McGregor, P.; Swales, K. Review of Evidence for the Rebound Effect Technical Report 4: Computable General Equilibrium Modelling Studies. UKERC Work Pap UKERC/WP/TPA/2007/012. 2007. Available online: http://www.ukerc.ac.uk/publications/ukerc-review-of-evidence-for-the-rebound-effect-technical-report-4-computable-general-equilibrium-modelling-studies.html (accessed on 26 December 2018).
- Kander, A.; Stern, D.I. Economic growth and the transition from traditional to modern energy in Sweden. Energy Econ. 2014, 46, 56–65. [Google Scholar] [CrossRef]
- Ayres, R.U.; Warr, B. Accounting for growth: The role of physical work. Struct. Change Econ. Dyn. 2005, 16, 181–209. [Google Scholar] [CrossRef]
- Stresing, R.; Lindenberger, D.; Kümmel, R. Cointegration of output, capital, labor, and energy. Eur. Phys. J. B 2008, 66, 279–287. [Google Scholar] [CrossRef]
- Solow, R.M. Technical Change and the Aggregate Production Function. Rev. Econ. Stat. 1957, 39, 312–320. [Google Scholar] [CrossRef]
- Berndt, E.R. Energy use, technical progress and productivity growth: A survey of economic issues. J. Prod. Anal. 1990, 2, 67–83. [Google Scholar] [CrossRef]
- Turner, K.; Hanley, N. Energy efficiency, rebound effects and the environmental Kuznets Curve. Energy Econ. 2011, 33, 709–720. [Google Scholar] [CrossRef]
- Hulten, C.R.; Growth Accounting. Natl Bur Econ Res Work Pap 15341. Available online: www.nber.org/papers/w15341 (accessed on 26 December 2018).
- Schreyer, P. Capital Stocks, Capital Services and Multi-factor Productivity Measures. OECD Econ. Stud. 2004, 2003, 163–184. [Google Scholar] [CrossRef]
- Hannon, B.; Joyce, J. Energy and technical progress. Energy 1981, 6, 187–195. [Google Scholar] [CrossRef]
- Chitnis, M.; Sorrell, S.; Druckman, A.; Firth, S.K.; Jackson, T. Who rebounds most? Estimating direct and indirect rebound effects for different UK socioeconomic groups. Ecol. Econ. 2014, 106, 12–32. [Google Scholar] [CrossRef]
- Nel, W.P.; van Zyl, G. Defining limits: Energy constrained economic growth. Appl. Energy 2010, 87, 168–177. [Google Scholar] [CrossRef]
- Ayres, R.U.; Turton, H.; Casten, T. Energy efficiency, sustainability and economic growth. Energy 2007, 32, 634–648. [Google Scholar] [CrossRef]
- Berndt, E.R.; Wood, D.O. Technology, Prices and Derived Demand for Energy. Rev. Econ. Stud. Stat. 1975, 57, 259–268. [Google Scholar] [CrossRef]
- Stern, D.I. Elasticities of substitution and complementarity. J. Prod. Anal. 2011, 36, 79–89. [Google Scholar] [CrossRef]
- Ayres, R.U.; Voudouris, V. Introduction to: The enigma of economic growth: Beyond Solow-type macroeconomic perspectives. Energy Policy 2015, 86, 802–803. [Google Scholar] [CrossRef]
- Kümmel, R.; Ayres, R.U.; Lindenberger, D. Thermodynamic laws, economic methods and the productive power of energy. J. Non-Equilib. Thermodyn. 2010, 35, 145–179. [Google Scholar] [CrossRef]
- Warr, B.; Ayres, R.; Eisenmenger, N.; Krausmann, F.; Schandl, H. Energy use and economic development: A comparative analysis of useful work supply in Austria, Japan, the United Kingdom and the US during 100 years of economic growth. Ecol. Econ. 2010, 69, 1904–1917. [Google Scholar] [CrossRef]
- Voudouris, V.; Ayres, R.; Serrenho, A.C.; Kiose, D. The economic growth enigma revisited: The EU-15 since the 1970s. Energy Policy 2015, 86, 812–832. [Google Scholar] [CrossRef]
- Brockway, P.E.; Barrett, J.R.; Foxon, T.J.; Steinberger, J.K. Divergence of trends in US and UK aggregate exergy efficiencies 1960–2010. Environ. Sci. Technol. 2014, 48, 9874–9881. [Google Scholar] [CrossRef]
- O’Mahony, M.; Timmer, M.P. Output, input and productivity measures at the industry level: The EU KLEMS database. Econ. J. 2009, 119, 374–403. [Google Scholar] [CrossRef]
- van der Werf, E. Production functions for climate policy modeling: An empirical analysis. Energy Econ. 2008, 30, 2964–2979. [Google Scholar] [CrossRef]
- Mundaca, L.; Neij, L.; Worrell, E.; McNeil, M. Evaluating Energy Efficiency Policies with Energy-Economy Models. Annu. Rev. Environ. Resour. 2010, 35, 305–344. [Google Scholar] [CrossRef]
- Sharma, S.S. The relationship between energy and economic growth: Empirical evidence from 66 countries. Appl. Energy 2010, 87, 3565–3574. [Google Scholar] [CrossRef]
- Semieniuk, G. Fossil Energy in Economic Growth: A Study of the Energy Direction of Technical Change, 1950–2012. SPRU Work Pap Ser (SWPS), 2016-11. 2016, pp. 1–37. Available online: http://dx.doi.org/10.2139/ssrn.2795424 (accessed on 26 December 2018).
- Csereklyei, Z.; Stern, D.I. Global Energy Use: Decoupling or Convergence? Energy Econ. 2015, 51, 633–641. [Google Scholar] [CrossRef]
- Rosen, M.A. A Concise Review of Exergy-Based Economic Methods. In Proceedings of the 3rd IASME/WSEAS International Conference on Energy & Environment, Cambridge, UK, 23–25 February 2008; pp. 136–144. [Google Scholar]
- McGlade, C.; Ekins, P. The geographical distribution of fossil fuels unused when limiting global warming to 2’C. Nature 2015, 517, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Bumpus, A.; Comello, S. Emerging clean energy technology investment trends. Nat. Clim. Change 2017, 7, 382–385. [Google Scholar] [CrossRef]
- Alcott, B. Impact caps: Why population, affluence and technology strategies should be abandoned. J. Clean. Prod. 2010, 18, 552–560. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).