Correlations to Predict Elemental Compositions and Heating Value of Torrefied Biomass
Abstract
1. Introduction
2. Methodology
2.1. Biomass Samples
2.2. Data Analysis
2.3. Error Estimation
3. Results
3.1. Elemental Compositions
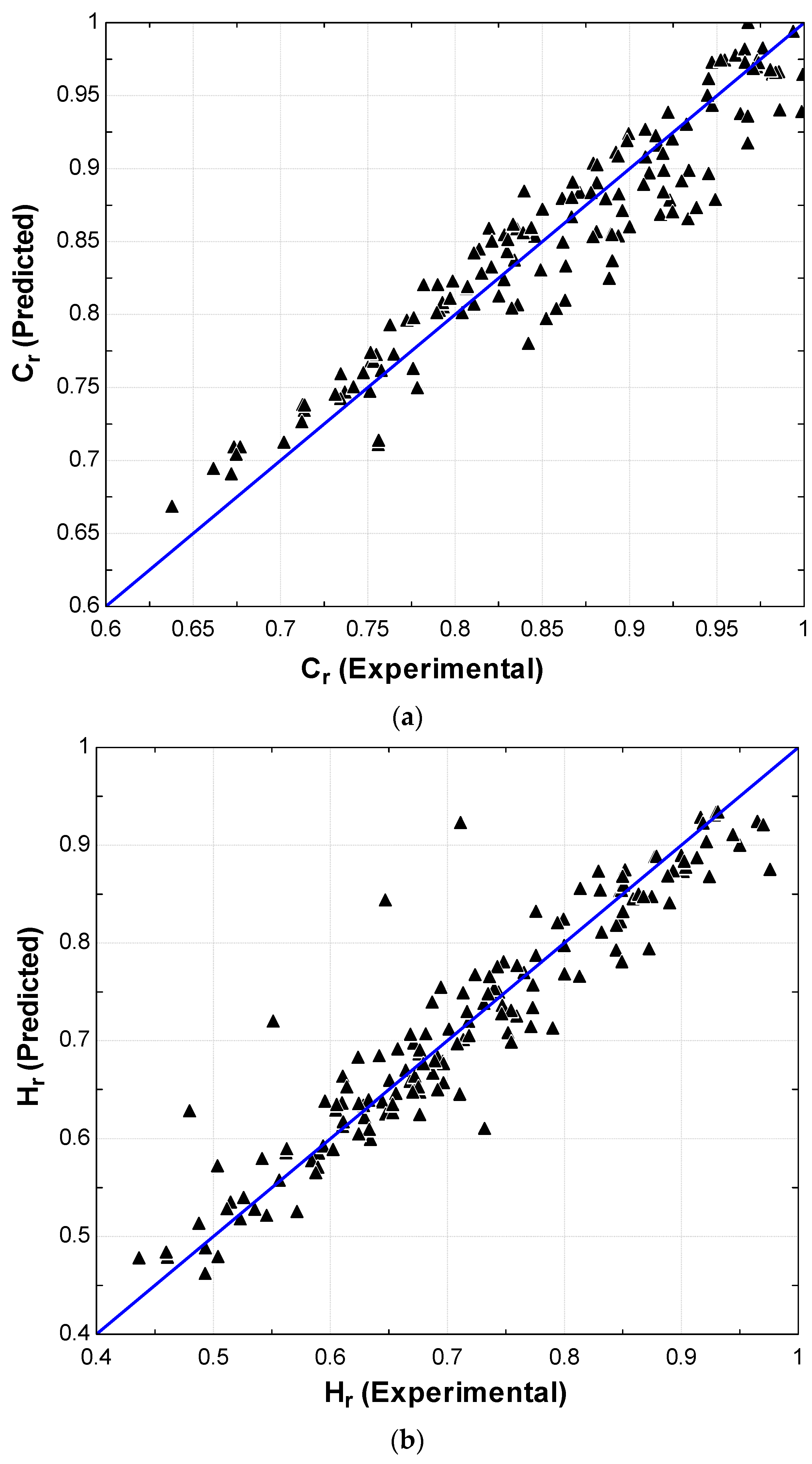
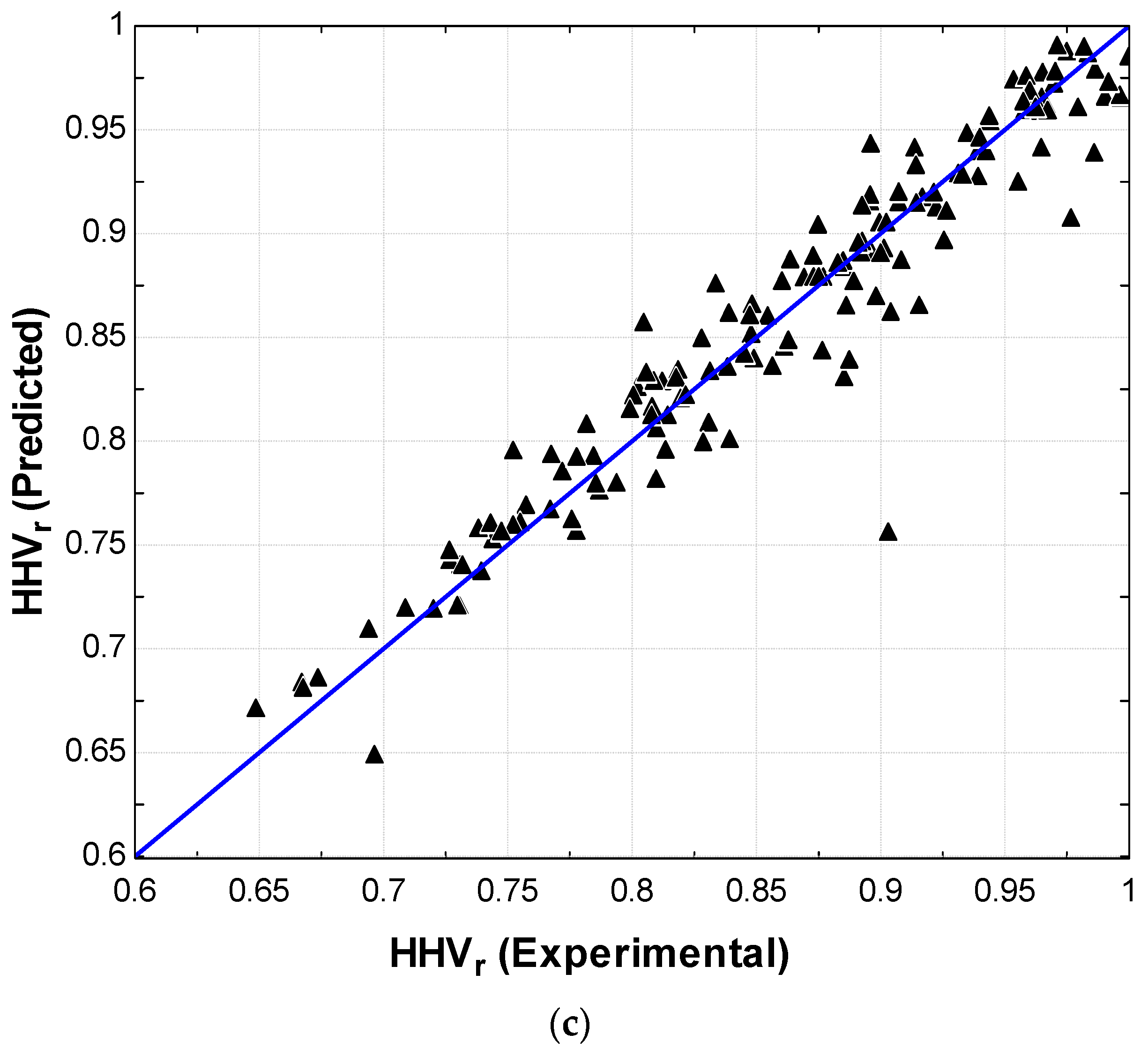
3.2. Modeling of C, H and HHV
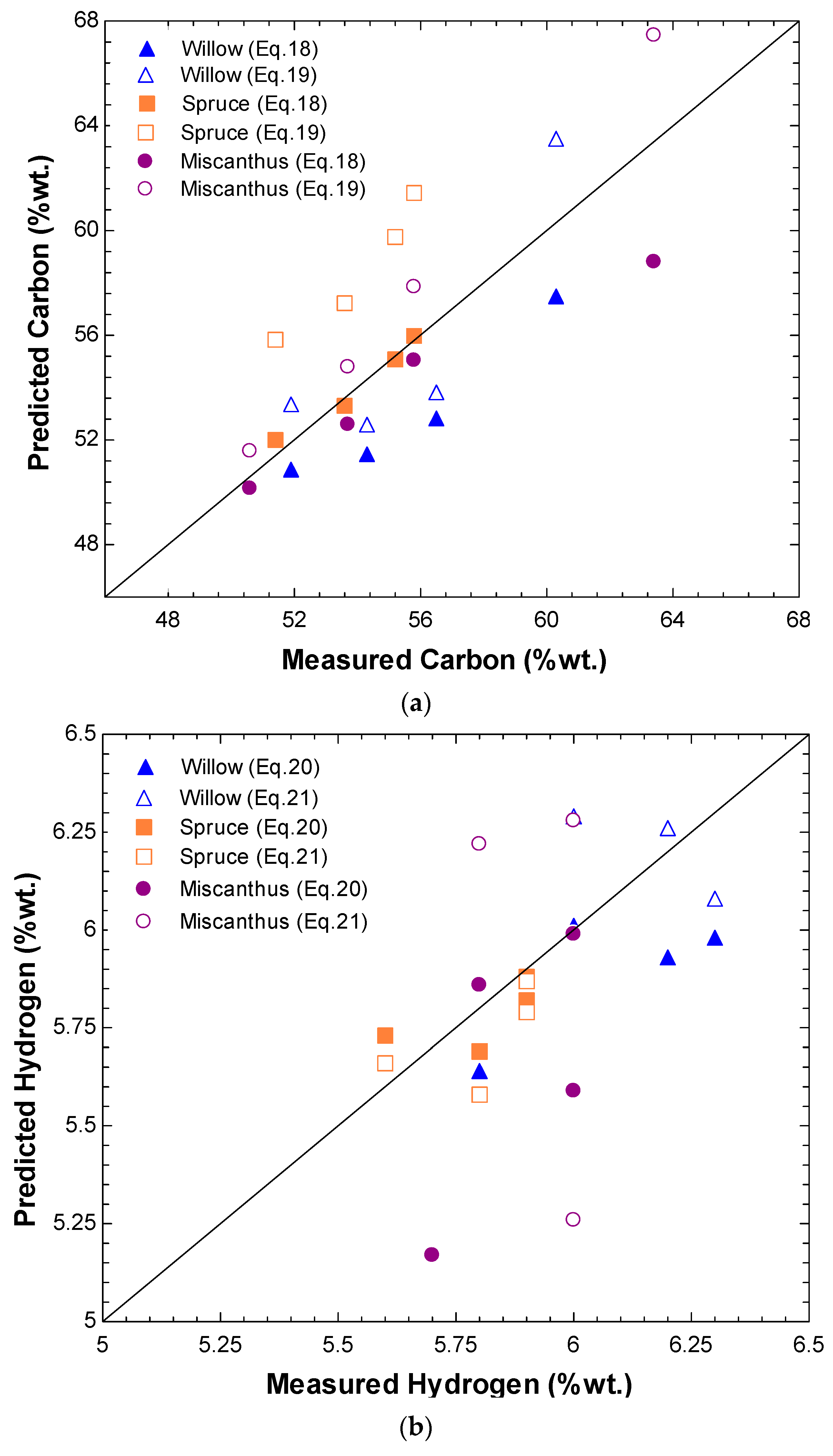
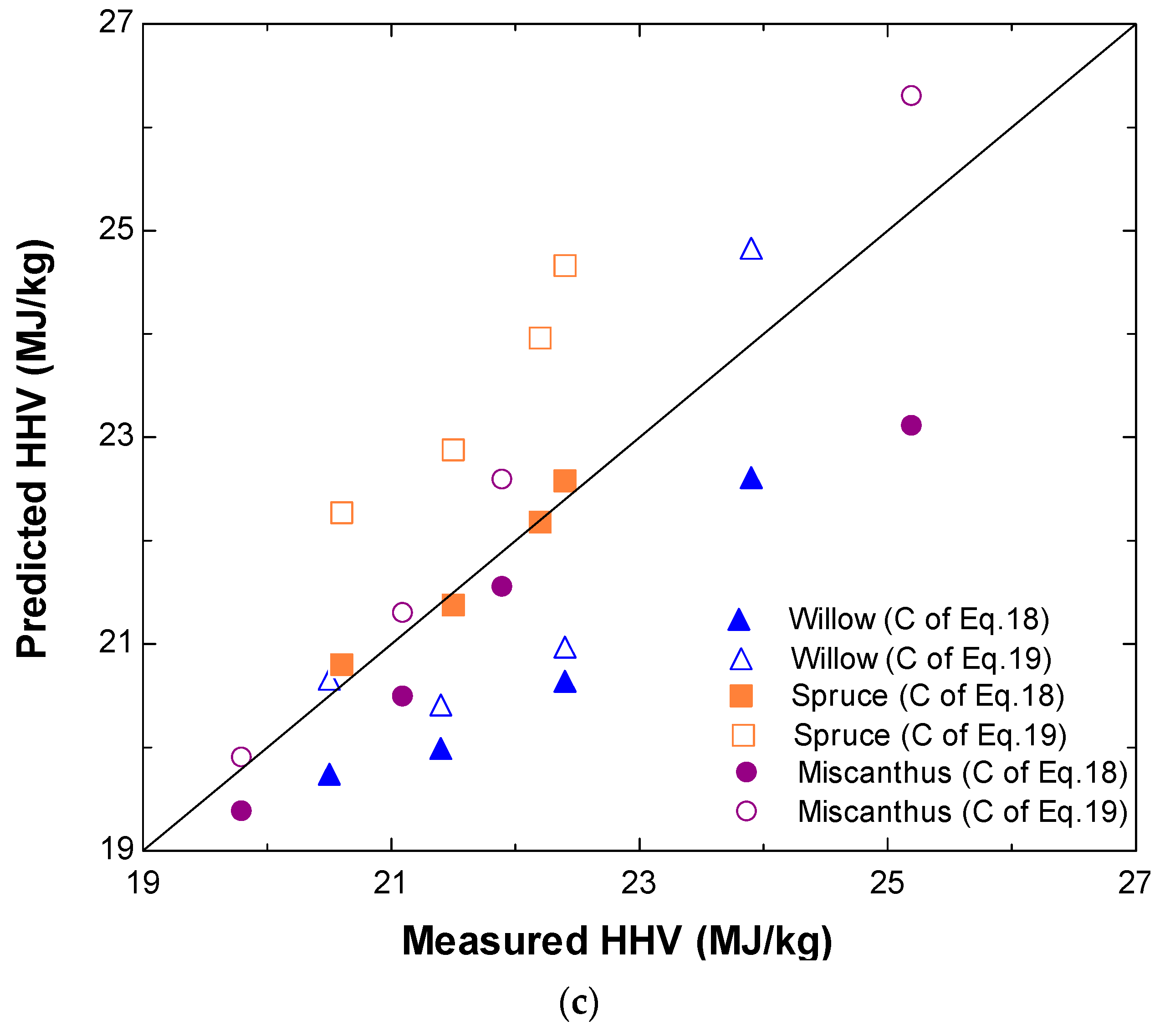
3.3. Comparison with the Existing Correlations in the Literature and Experimental Data
4. Conclusions
Nomenclature and Subscript
| C | Carbon content (%wt.) |
| O | Oxygen content (%wt.) |
| HHV | Higher heating value (MJ/kg) |
| VM | Volatile matter (%) |
| Solid mass yield (%) | |
| Predicted value | |
| Average value | |
| daf | Dry and ash free |
| RMSE | Root mean square error |
| H | Hydrogen content (%wt.) |
| N | Nitrogen content (%wt.) |
| FC | Fixed carbon (%) |
| ASH | Ash content (%) |
| n | Number of measurements |
| y | Measured value |
| N | Number of data |
| ABE | Average biased error (%) |
| o | Raw biomass |
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, W.; Peng, J.; Bi, X. A state-of-the-art review of biomass torrefation, densification and applications. Renew. Sustain. Energy Rev. 2015, 44, 847–866. [Google Scholar] [CrossRef]
- Mohr, S.H.; Wang, J.; Ellem, G.; Ward, J.; Giurco, D. Projection of world fossil fuels by country. Fuel 2015, 141, 120–135. [Google Scholar] [CrossRef]
- Shafiee, S.; Topal, E. When will fossil fuel reserves be diminished? Energy Policy 2009, 37, 181–189. [Google Scholar] [CrossRef]
- Madanayake, B.N.; Gan, S.; Eastwick, C.; Ng, H.K. Biomass as an energy source in coal co-firing and its feasibility enhancement via pre-treatment techniques. Fuel Process. Technol. 2017, 159, 287–305. [Google Scholar] [CrossRef]
- Herbert, G.M.J.; Krishnan, A.U. Quantifying environmental performance of biomass energy. Renew. Sustain. Energy Rev. 2016, 592, 92–308. [Google Scholar]
- Van der Stelt, M.J.C.; Gerhauser, H.; Kiel, J.H.A.; Ptasinski, K.J. Biomass upgrading by torrefaction for the production of biofuel: A Riview. Biomass Bioenergy 2011, 35, 3748–3762. [Google Scholar] [CrossRef]
- Haseli, Y. Process modeling of a biomass torrefaction plant. Energy Fuels 2018, 32, 5611–5622. [Google Scholar] [CrossRef]
- Repellin, V.; Govin, A.; Rolland, M.; Guyonnet, R. Energy requirement for fine grinding of torrefied wood. Biomass Bioenergy 2010, 34, 923–930. [Google Scholar] [CrossRef]
- Demirbas, A. Calculation of higher heating values of biomass fuel. Fuel 1997, 76, 431–434. [Google Scholar]
- Parikh, J.; Channiwala, S.A.; Ghosal, G.K. A correlation for calculating elemental composition from proximate analysis of biomass materials. Fuel 2007, 86, 1710–1719. [Google Scholar] [CrossRef]
- Shen, J.; Zhu, S.; Liu, X.; Zhang, H.; Tan, J. The prediction of elemental composition of biomass based on proximate analysis. Energy Convers. Manag. 2010, 51, 983–987. [Google Scholar] [CrossRef]
- Yin, C.Y. Prediction of higher heating values of biomass from proximate. Fuel 2011, 90, 1128–1132. [Google Scholar] [CrossRef]
- Friedl, A.; Padouvas, E.; Rotter, H.; Varmuza, K. Prediction of heating values of biomass fuel from elemental composition. Anal. Chim. Acta 2005, 544, 191–198. [Google Scholar] [CrossRef]
- Vargas-Morenoa, J.M.; Callejón-Ferrea, A.J.; Pérez-Alonsoa, J.; Velázquez-Martí, B. A review of the mathematical models for predicting the heating value of biomass materials. Renew. Sustain. Energy Rev. 2012, 16, 3065–3083. [Google Scholar] [CrossRef]
- Bridgeman, T.G.; Jones, J.M.; Shield, I.; Williams, P.T. Torrefaction of reed canary grass, wheat straw and willow to enhance solid fuel qualities and combustion properties. Fuel 2008, 87, 844–856. [Google Scholar] [CrossRef]
- Joshi, Y.; de Vries, H.; Woudstra, T.; de Jong, W. Torrefaction: Unit operation modelling and process simulation. Appl. Therm. Eng. 2015, 74, 83–88. [Google Scholar] [CrossRef]
- Nhucchen, D.R. Prediction of carbon, hydrogen, and oxygen compositions of raw and torrefied biomass using proximate analysis. Fuel 2016, 180, 348–356. [Google Scholar] [CrossRef]
- Nhuccen, D.R.; Afzal, M.T. HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses. Bioengineering 2017, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Soponpongpipat, N.; Sittikul, D.; Comsawang, P. Prediction model of higher heating value of torrefied biomass based on the kinetics of biomass decomposition. J. Energy Inst. 2015, 89, 425–435. [Google Scholar] [CrossRef]
- Sarvaramini, A.; Assima, G.P.; Larachi, F. Dry torrefaction of biomass-Torrefied products and torrefaction kinetics using the distributed activation energy model. Chem. Eng. J. 2013, 229, 498–507. [Google Scholar] [CrossRef]
- Bach, Q.V.; Tran, K.Q.; Skreiberg, O.; Trinh, T.T. Effects of wet torrefaction on pyrolysis of woody biomass fuels. Energy 2015, 88, 443–456. [Google Scholar] [CrossRef]
- Pach, M.; Zanzi, R.; Björnbom, E. Torrefied Biomass a Substitute for Wood and Charcoal. In Proceedings of the 6th Asia-Pacific International Symposium on Combustion and Energy Utilization, Kuala Lumpur, Malaysia, 20–22 May 2002. [Google Scholar]
- Tapasvi, D.; Khalil, R.; Tran, K.Q. Torrefaction of Norwegian Birch and Spruce: An Experimental Study Using Macro-TGA. Energy Fuels 2012, 26, 5232–5240. [Google Scholar] [CrossRef]
- Shoulaifar, T.K.; DeMartini, N. Ash-Forming Matter in Torrefied Birch Wood: Changes in Chemical Association. Energy Fuels 2013, 27, 5684–5690. [Google Scholar] [CrossRef]
- Arteaga-Pérez, L.E.; Segura, C. Torrefaction of Pinus radiata and Eucalyptus globulus: A combined experimental and modeling approach to process synthesis. Energy Sustain. Dev. 2015, 29, 13–23. [Google Scholar] [CrossRef]
- Phanphanich, M.; Mani, S. Impact of torrefaction on the grindability and fuel characteristics of forest biomass. Bioresour. Technol. 2011, 102, 1246–1253. [Google Scholar] [CrossRef] [PubMed]
- Li, M.F.; Chen, L.X. Evaluation of the structure and fuel properties of lignocelluloses through carbon dioxide torrefaction. Energy Convers. Manag. 2016, 119, 463–472. [Google Scholar] [CrossRef]
- Carmona, S.R.; Oerez, J.F. Effect of torrefaction temperature on properties of Patula pine. Maderas-Cienc. Tecnol. 2017, 19, 39–50. [Google Scholar]
- McNamee, P.; Adams, P.W.R.; McManus, M.C. An assessment of the torrefaction of North American pine and life cycle greenhouse gas emissions. Energy Convers. Manag. 2016, 113, 17–188. [Google Scholar] [CrossRef]
- Zheng, Y.; Tao, L.; Yang, X. Effect of the torrefaction Temperature on structural properties and pyrolysis behavior of biomass. BioResource 2017, 12, 3425–3447. [Google Scholar] [CrossRef]
- Grigiante, M.; Antolini, D. Mass yield as guide parameter of the torrefaction process. An experimental study of the solid fuel properties referred to two types of biomass. Fuel 2015, 153, 499–509. [Google Scholar] [CrossRef]
- Nanou, P.; Carbo, M.C.; Keil, J. Detailed mapping of the mass and energy balance of a continuous biomass torrefaction plant. Biomass Bioenergy 2016, 89, 67–77. [Google Scholar] [CrossRef]
- Larsson, S.H.; Rudolfsson, M. Effects of moisture content, torrefaction temperature, and die temperature in pilot scale pelletizing of torrefied Norway spruce. Appl. Energy 2013, 102, 827–832. [Google Scholar] [CrossRef]
- Ibrahim, R.H.H.; Dravell, L.I.; Jones, J.M.; Williams, A. Physicochemical characterisation of torrefied biomass. J. Anal. Appl. Pyrolysis 2013, 103, 21–30. [Google Scholar] [CrossRef]
- Chen, W.H.; Cheng, W.Y.; Lu, K.M.; Huang, Y.P. An evaluation on improvement of pulverized biomass property for solid fuel through torrefaction. Appl. Energy 2011, 88, 3636–3644. [Google Scholar] [CrossRef]
- Arias, B.; Pevida, C.; Fermoso, J.; Plaza, M.G.; Rubiera, F.; Pis, J.J. Influence of torrefaction on the griandability and reactivity of woody biomass. Fuel Process. Technol. 2008, 89, 169–175. [Google Scholar] [CrossRef]
- Na, B.; Ahn, B.J.; Lee, J.W. Changes in chemical and physical properties of yellow poplar (Liriodendron tulipifera) during torrefaction. Wood Sci. Technol. 2015, 49, 257–272. [Google Scholar] [CrossRef]
- Gucho, E.M.; Shahzad, K.; Bramer, E.A.; Brem, G. Experimental Study on Dry Torrefaction of Beech Wood and Miscanthus. Energies 2015, 8, 3903–3923. [Google Scholar] [CrossRef]
- Wannapeera, J.; Worasuwannarak, N. Examinations of chemical properties and pyrolysis behaviors oftorrefied woody biomass prepared at the same torrefactionmass yields. J. Anal. Appl. Pyrolysis 2015, 115, 279–287. [Google Scholar] [CrossRef]
- Huang, Y.F.; Sung, H.T.; Chiueh, P.T.; Lo, S.L. Microwave torrefaction of sewage sludge and leucaena. J. Taiwan Inst. Chem. Eng. 2017, 70, 236–243. [Google Scholar] [CrossRef]
- Wilk, M.; Magdziarz, A.; Kalemba, I. Characterisation of renewable fuels’ torrefaction process with different instrumental techniques. Energy 2015, 87, 259–269. [Google Scholar] [CrossRef]
- Yoo, H.S.; Choi, H.S. A study on torrefaction characteristics of waste sawdust in an auger type pyrolyzer. J. Mater. Cycles Waste Manag. 2016, 18, 460–468. [Google Scholar] [CrossRef]
- Mei, Y.; Liu, R.; Yang, Q.; Yang, H.; Shao, J.; Draper, C.; Zhang, S.; Chen, H. Torrefaction of cedarwood in a pilot scale rotary kiln and the influence of industrial flue gas. Bioresour. Technol. 2015, 177, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Barta-Rajnai, E.; Jakab, E.; Sebestyen, Z.; May, Z.; Barta, Z.; Wang, L.; Skreiberg, O.; Gronil, M.; Bozi, J.; Czegeny, Z. Comprehensive Compositional Study of Torrefied Wood and Herbaceous Materials by Chemical Analysis and Thermoanalytical Methods. Energy Fuels 2016, 30, 8019–8030. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; John Wiley & Sons, Incorporated: New York, NY, USA, 2012. [Google Scholar]
- Comrie, A.C. Comparing Neural Networks and Regression Models for Ozone Forecasting. J. Air Waste Manag. Assoc. 1997, 47, 653–663. [Google Scholar] [CrossRef]
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Am. Metrol. Soc. 1982, 63, 1309–1317. [Google Scholar] [CrossRef]
- Bridgeman, T.G.; Jones, J.M.; Williams, A.; Waldron, D.J. An investigation of the grindability of two torrefied energy crops. Fuel 2010, 89, 3911–3918. [Google Scholar] [CrossRef]
- Brostrom, M.; Nordin, A.; Pommer, L.; Branca, C.; Blasi, C.D. Influence of torrefaction on the devolatilization and oxidation kinetics of wood. J. Anal. Appl. Pyrolysis 2012, 96, 100–109. [Google Scholar] [CrossRef]
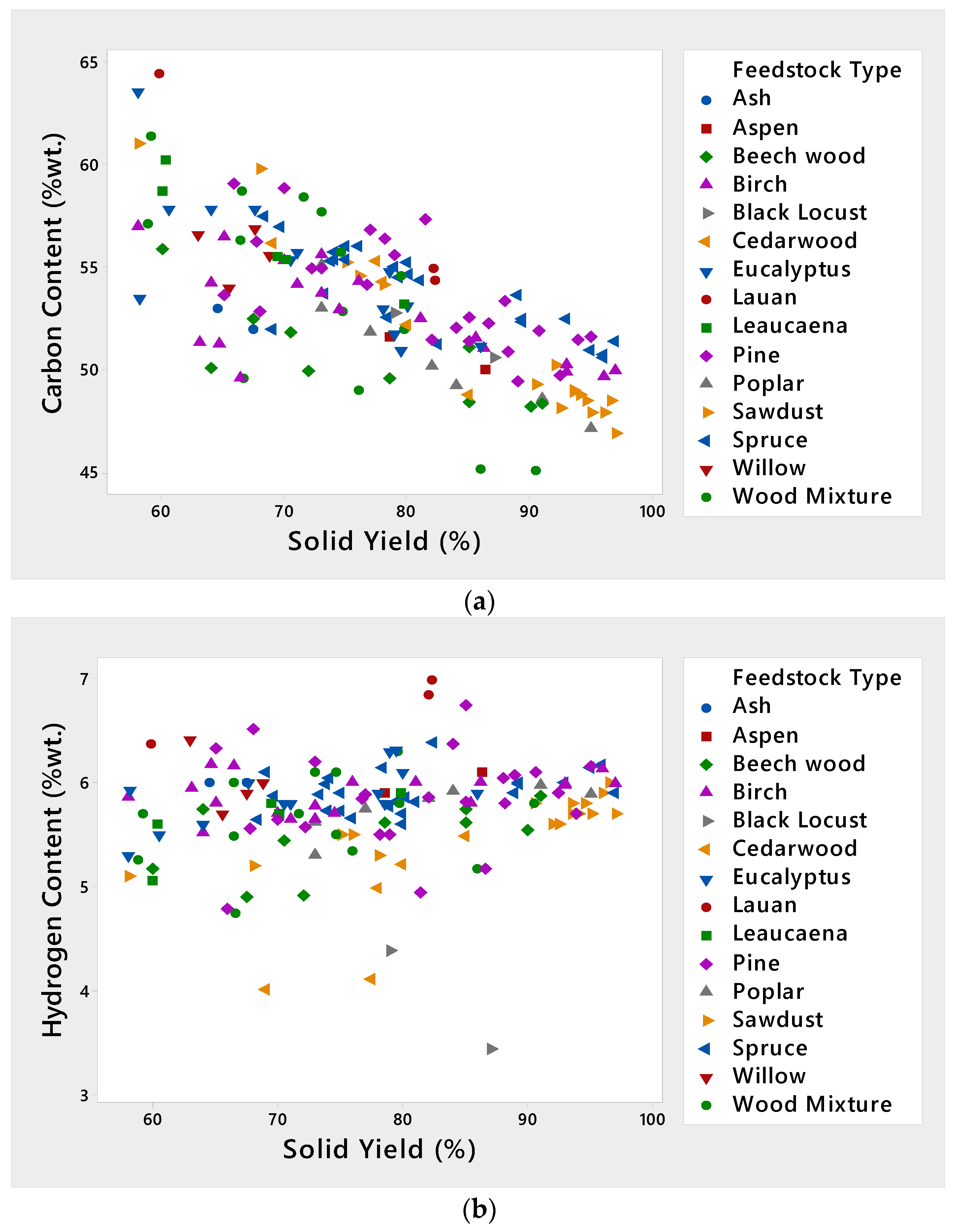
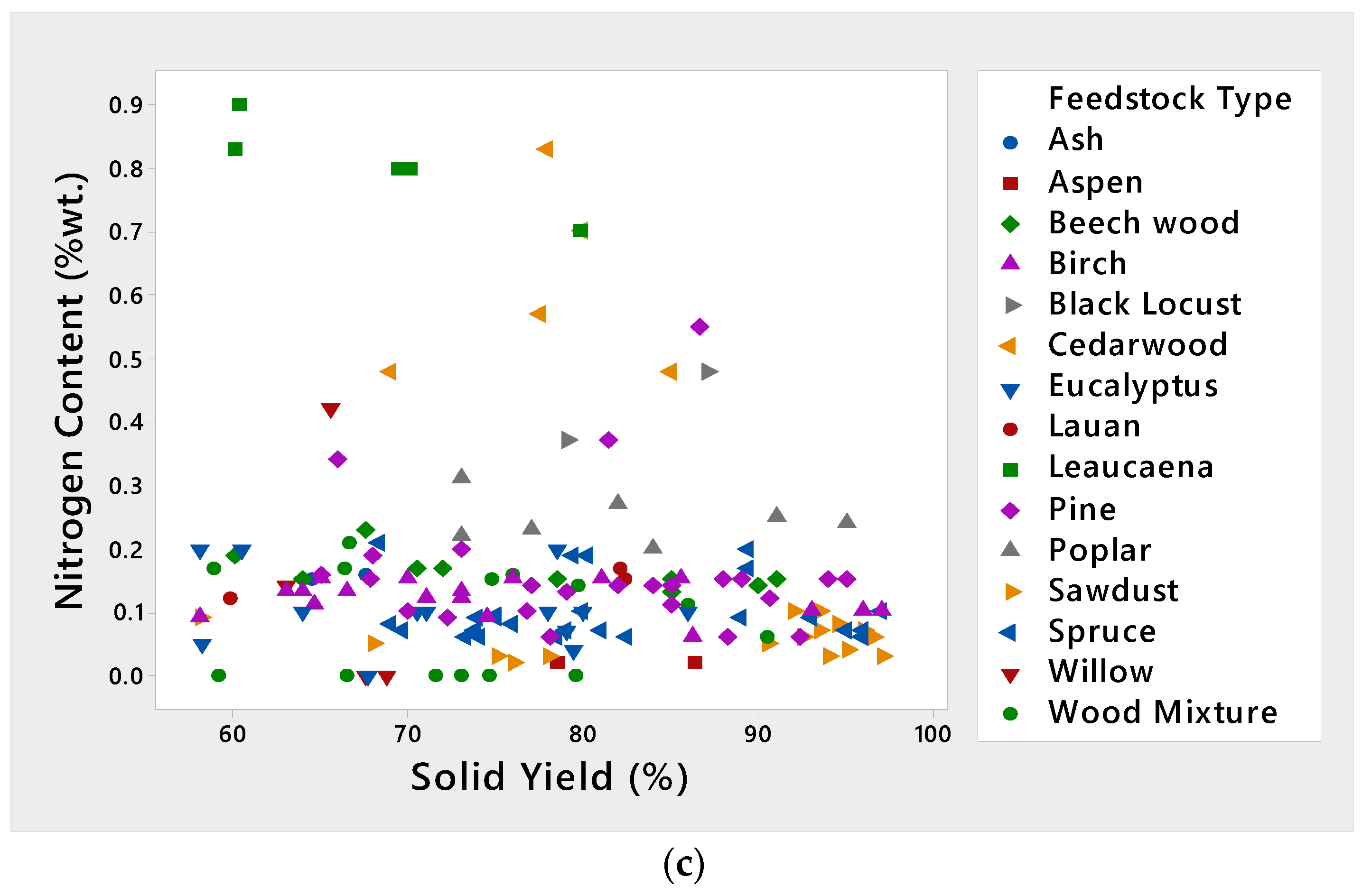
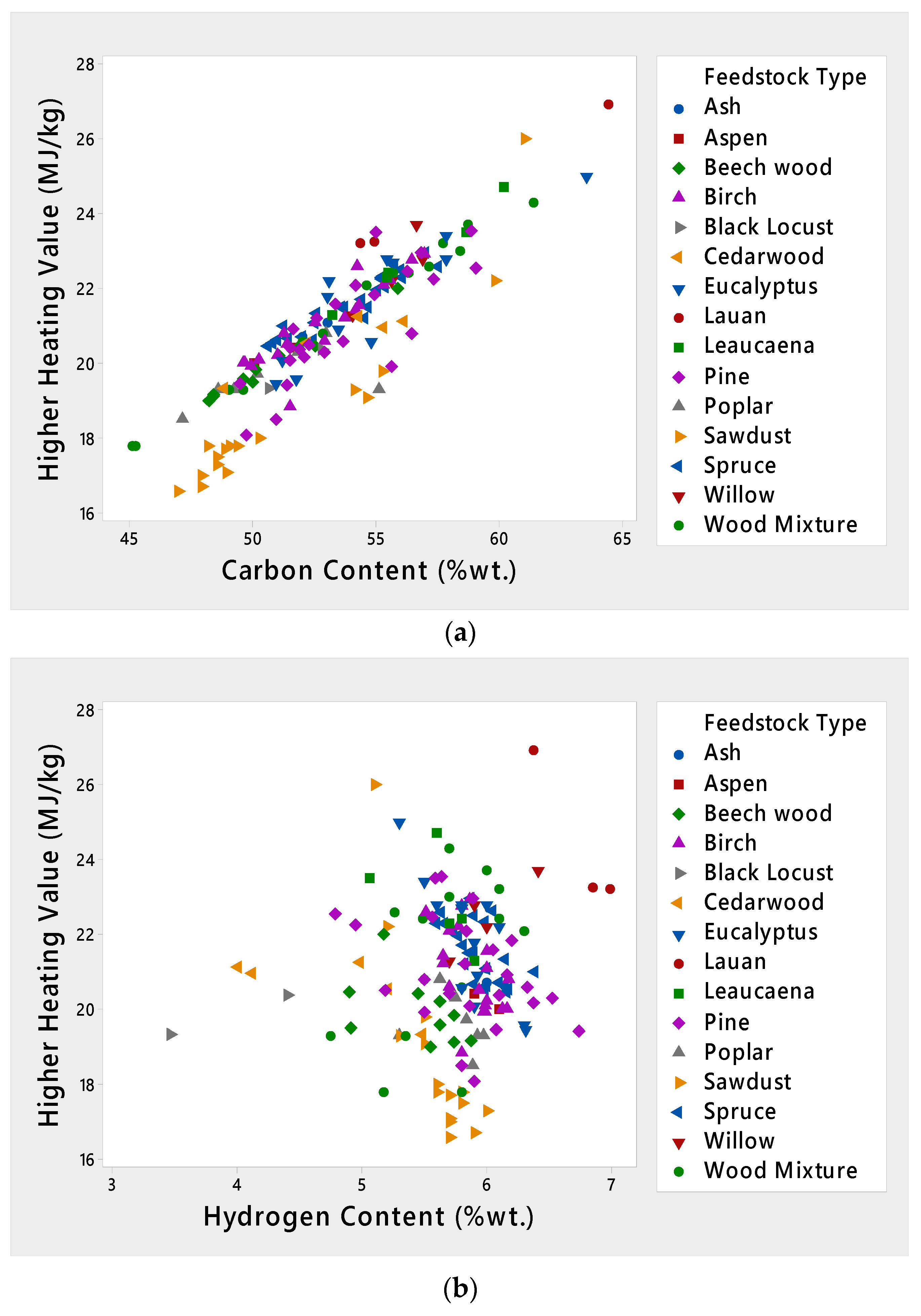
| Feedstock Type | Temperature (°C) | Residence Time (min) | References | ||
|---|---|---|---|---|---|
| Minimum | Maximum | Minimum | Maximum | ||
| Birch | 200 | 280 | 10 | 60 | [20,21,22,23,24] |
| Pine | 200 | 300 | 15 | 60 | [22,25,26,27,28,29,30] |
| Spruce | 200 | 300 | 5 | 60 | [21,23,31,32,33] |
| Willow | 230 | 300 | 30 | 60 | [32,34,35] |
| Eucalyptus | 240 | 290 | 15 | 60 | [25,34,36] |
| Poplar | 220 | 300 | 20 | 50 | [27,37] |
| Beech Wood | 240 | 300 | 15 | 60 | [38] |
| Leaucaena | 240 | 300 | 5 | 40 | [39,40] |
| Wood Mixture | 230 | 290 | 30 | 60 | [34,41] |
| Lauan | 220 | 250 | 30 | 60 | [35] |
| Sawdust | 220 | 300 | 10 | 60 | [42] |
| Cedarwood | 200 | 290 | 50 | 50 | [43] |
| Black Locust | 225 | 250 | 60 | 60 | [44] |
| Ash | 250 | 265 | 39 | 43 | [32] |
| Aspen | 240 | 280 | 15 | 60 | [20] |
| Wood | Parameter | n | Min | Max | Mean | Wood | Parameter | n | Min | Max | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Birch | (%) | 19 | 58.01 | 97 | 76.33 | Pine | (%) | 24 | 65 | 95 | 80.53 |
| C (% wt.) | 19 | 49.61 | 56.92 | 52.65 | C (% wt.) | 24 | 49.47 | 59.03 | 53.74 | ||
| N (% wt.) | 19 | 0.06 | 0.15 | 0.12 | N (% wt.) | 24 | 0.06 | 0.55 | 0.17 | ||
| H (% wt.) | 19 | 5.51 | 6.18 | 5.88 | H (% wt.) | 24 | 4.78 | 6.74 | 5.8 | ||
| HHV (MJ/kg) | 19 | 18.83 | 22.93 | 20.97 | HHV (MJ/kg) | 24 | 18.07 | 25.38 | 20.96 | ||
| Spruce | (%) | 26 | 68.40 | 97 | 81.3 | Eucalyptus | (%) | 13 | 58 | 86.0 | 71.64 |
| C (% wt.) | 26 | 50.6 | 57.49 | 53.89 | C (% wt.) | 13 | 50.92 | 63.5 | 55.37 | ||
| N (% wt.) | 26 | 0.06 | 0.21 | 0.1 | N (% wt.) | 13 | 0.00 | 0.2 | 0.1 | ||
| H (% wt.) | 26 | 5.60 | 6.39 | 5.9 | H (% wt.) | 13 | 5.3 | 6.31 | 5.85 | ||
| HHV (MJ/kg) | 26 | 20.46 | 22.97 | 21.6 | HHV (MJ/kg) | 13 | 19.45 | 25 | 21.9 | ||
| Willow | (%) | 4 | 63 | 68.76 | 66.09 | Poplar | (%) | 7 | 73 | 95.0 | 82.14 |
| C (% wt.) | 4 | 54.0 | 56.9 | 55.65 | C (% wt.) | 7 | 47.12 | 55.1 | 50.69 | ||
| N (% wt.) | 4 | 0.00 | 0.42 | 0.16 | N (% wt.) | 7 | 0.2 | 0.31 | 0.24 | ||
| H (% wt.) | 4 | 5.7 | 6.41 | 6.02 | H (% wt.) | 7 | 5.3 | 5.98 | 5.78 | ||
| HHV (MJ/kg) | 4 | 21.3 | 23.71 | 22.5 | HHV (MJ/kg) | 7 | 18.5 | 20.8 | 19.6 | ||
| Beech Wood | (%) | 10 | 60 | 91 | 76.35 | Leaucaena | (%) | 5 | 60.0 | 79.8 | 67.92 |
| C (% wt.) | 10 | 48.22 | 55.86 | 50.6 | C (% wt.) | 5 | 53.2 | 60.2 | 56.59 | ||
| N (% wt.) | 10 | 0.13 | 0.23 | 0.16 | N (% wt.) | 5 | 0.7 | 0.9 | 0.81 | ||
| H (% wt.) | 10 | 4.9 | 5.88 | 5.46 | H (% wt.) | 5 | 5.06 | 5.9 | 5.61 | ||
| HHV (MJ/kg) | 10 | 19.01 | 22.00 | 19.93 | HHV (MJ/kg) | 5 | 21.3 | 24.7 | 22.84 | ||
| Lauan | (%) | 3 | 59.8 | 82.3 | 74.73 | Sawdust | (%) | 16 | 58.0 | 97 | 86.85 |
| C (% wt.) | 3 | 54.33 | 64.4 | 57.88 | C (% wt.) | 16 | 46.9 | 61.0 | 51.16 | ||
| N (% wt.) | 3 | 0.12 | 0.17 | 0.15 | N (% wt.) | 16 | 0.02 | 0.1 | .06 | ||
| H (% wt.) | 3 | 6.37 | 6.99 | 6.73 | H (% wt.) | 16 | 5.1 | 6.0 | 5.61 | ||
| HHV (MJ/kg) | 3 | 23.2 | 26.92 | 24.45 | HHV (MJ/kg) | 16 | 16.6 | 26.0 | 18.61 | ||
| Wood Mixture | (%) | 14 | 58.8 | 90.5 | 73.07 | Cedar Wood | (%) | 5 | 69 | 85 | 77.9 |
| C (% wt.) | 14 | 45.1 | 61.4 | 53.82 | C (% wt.) | 5 | 48.82 | 56.13 | 53.34 | ||
| N (% wt.) | 14 | 0.0 | 0.21 | 0.83 | N (% wt.) | 5 | 0.48 | 0.83 | 0.61 | ||
| H (% wt.) | 14 | 4.75 | 6.3 | 5.64 | H (% wt.) | 5 | 4.01 | 5.49 | 4.76 | ||
| HHV (MJ/kg) | 14 | 17.8 | 24.3 | 21.34 | HHV (MJ/kg) | 5 | 19.35 | 21.25 | 20.62 | ||
| Black Locust | (%) | 2 | 79 | 87.0 | 83 | Ash & Aspen | (%) | 4 | 64.5 | 86.4 | 74.23 |
| C (% wt.) | 2 | 50.59 | 52.77 | 51.68 | C (% wt.) | 4 | 50.0 | 53.0 | 51.65 | ||
| N (% wt.) | 2 | 0.21 | 0.23 | 0.22 | N (% wt.) | 4 | 0.02 | 0.16 | 0.08 | ||
| H (% wt.) | 2 | 3.45 | 4.39 | 3.92 | H (% wt.) | 4 | 5.9 | 6.1 | 6.0 | ||
| HHV (MJ/kg) | 2 | 19.35 | 20.38 | 19.86 | HHV (MJ/kg) | 4 | 20.0 | 21.1 | 20.55 |
| Dependent Variable | Independent Variable(s) | RMSE | Bias | Eq. No. | |
|---|---|---|---|---|---|
| 0.037 | 81.52 | 13 | |||
| , C | 0.028 | 89.86 | 14 | ||
| 0.059 | 79.01 | 15 | |||
| , H | 0.043 | 88.45 | 16 | ||
| 0.023 | 92.80 | 17 |
| Eq. No | Eq. No | |||||
|---|---|---|---|---|---|---|
| 13 | 14 | |||||
| 0.2847 | −0.47289 | |||||
| 15 | 16 | |||||
| −0.1145 | −0.55735 | |||||
| 17 | ||||||
| 0.94497 |
| Correlation | Reference | ABE a (%) | RMSE |
|---|---|---|---|
| Current Study | −2.4 4.0 | 2.12 3.30 | |
| [10] | −12.1 | 7.39 | |
| [11] | −11.7 | 7.23 | |
| [17] | −6.1 | 3.86 | |
| Current Study | −2.4 −4.8 | 0.24 0.88 | |
| [10] | −1.8 | 0.26 | |
| [11] | −1.4 | 0.26 | |
| [17] | 11.9 | 0.82 | |
| Current Study | −3.1 b | 1.02 | |
| 2.93 c | 1.24 | ||
| [12] [12] | −8.7 | 2.32 | |
| −3.2 | 0.92 | ||
| [13] | 1.3 | 0.44 | |
| [18] [18] | −0.6 | 0.78 | |
| 2.2 | 0.55 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.; Haseli, Y.; Karadogan, E. Correlations to Predict Elemental Compositions and Heating Value of Torrefied Biomass. Energies 2018, 11, 2443. https://doi.org/10.3390/en11092443
Hasan M, Haseli Y, Karadogan E. Correlations to Predict Elemental Compositions and Heating Value of Torrefied Biomass. Energies. 2018; 11(9):2443. https://doi.org/10.3390/en11092443
Chicago/Turabian StyleHasan, Mahmudul, Yousef Haseli, and Ernur Karadogan. 2018. "Correlations to Predict Elemental Compositions and Heating Value of Torrefied Biomass" Energies 11, no. 9: 2443. https://doi.org/10.3390/en11092443
APA StyleHasan, M., Haseli, Y., & Karadogan, E. (2018). Correlations to Predict Elemental Compositions and Heating Value of Torrefied Biomass. Energies, 11(9), 2443. https://doi.org/10.3390/en11092443




