Heat Transfer Behaviors in Horizontal Wells Considering the Effects of Drill Pipe Rotation, and Hydraulic and Mechanical Frictions during Drilling Procedures
Abstract
:1. Introduction
2. Wellbore Geometry and Heat Transfer Mathematical Model
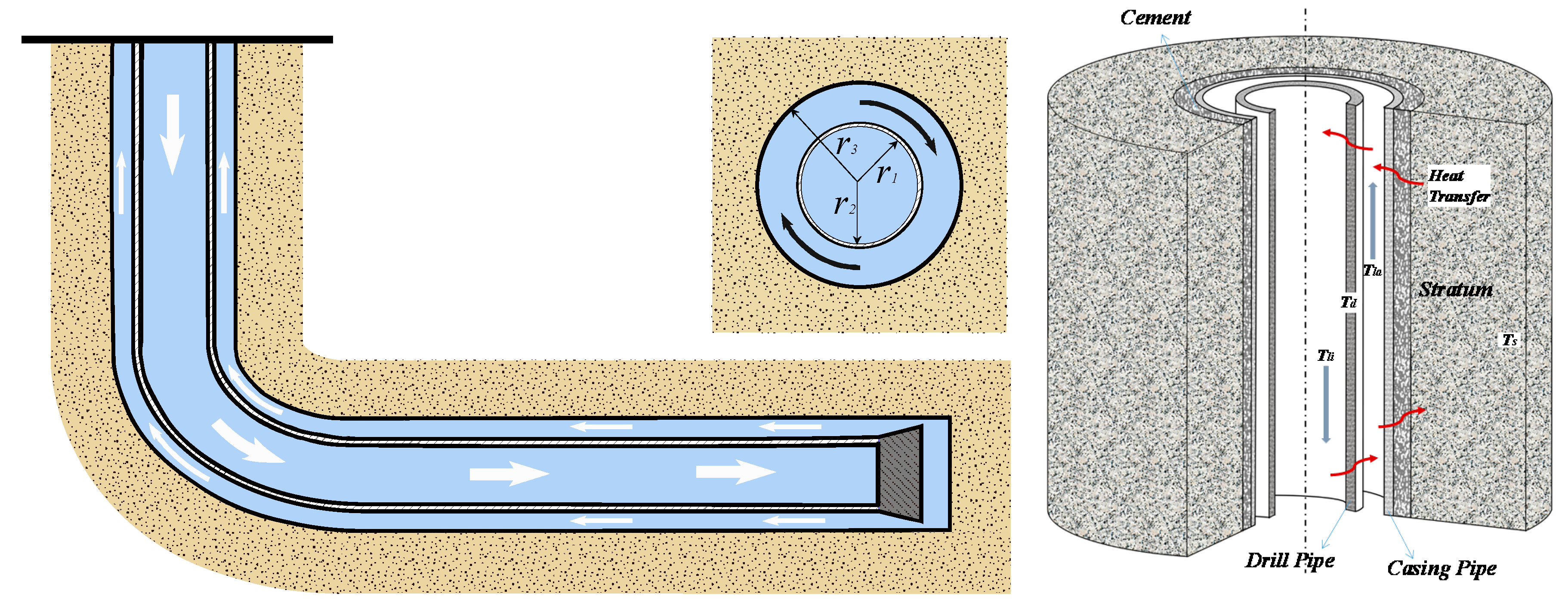
2.1. Description of Wellbore Geometry
- (1)
- For horizontal wells, the drill pipes in vertical segments were either concentric or eccentric at a constant eccentricity. Built-up segments were linearly and increasingly eccentric along the wellbore axis, with the eccentricity increasing from e = 0, at the kick-off point, to e = 1, at the heel of the horizontal segment; the mean eccentricity was e = 0.62. The horizontal segments were totally eccentric (e = 1).
- (2)
- No buckling segments existed along the entire well, and the shapes of drill pipes and annuli were regular.
- (3)
- The effect of casing pipes was not considered as its high heat conductivity. Moreover, the effects of heat radiation and conduction in the drilling fluid along the depth direction were neglected, merely considering the main forms of heat transfer conduction in solid parts and convection in fluid zones.
- (4)
- The initial geothermal temperature in the formation along the depth linearly increased. Based on the above assumptions, the heat transfer model was established according to the law of thermodynamic energy conservation. Accordingly, they were used to estimate the temperature variation during the drilling procedure.
2.2. Mathematical Model of Heat Transfer
2.2.1. Thermal Equilibrium Equations
2.2.2. Boundary and Initial Conditions
- (1)
- Boundary conditions:
- Inlet condition: ;
- Temperatures at the wellbore bottom: ;
- Coupled conditions at the wellbore wall: ;
- Far field boundary: ();
- (2)
- Initial conditions:
- Stratum retaining the original temperature: ;
- Drilling fluid in the drill pipe: ;
- Drilling fluid in the annulus: ;
2.3. Calculation of Heat Transfer Coefficients
2.3.1. Methods of Determining Heat Transfer Coefficients in Previous Studies
2.3.2. Heat Transfer Coefficients Involving Drill-Pipe Rotation
2.4. Calculation of Internal Heat Sources
2.4.1. Heat Sources Induced by Mechanical Friction
- (a)
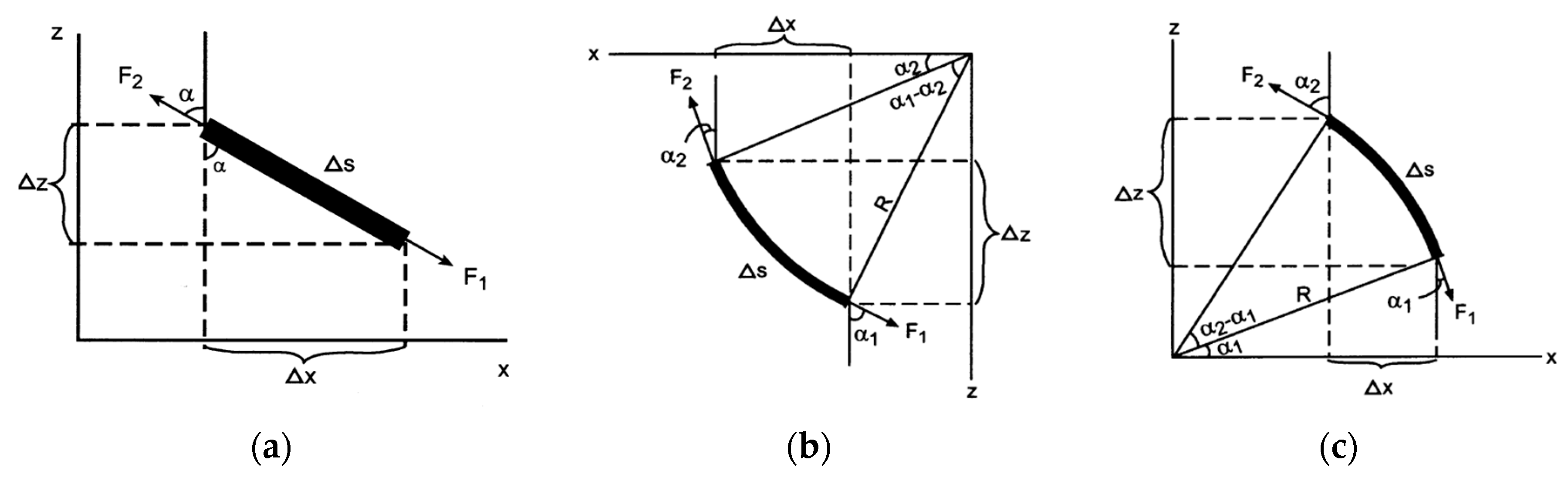
- Drop-off sectionWhen pulling up drill pipes, the force at the upper side of each section was:When lowering down the drill pipe, the force at the upper side was:The torque was given by:
- (b)
- Built-up sectionWhen pulling up drill pipes:When lowering down drill pipes:The torque was:
- (c)
- Straight inclined hole
2.4.2. Heat Sources of Circulating Pressure Losses in Dill Pipe, Annulus, and Drill Bit
- Drill String:
- Drill Bit:
- Annulus:
- ①
- Laminar regime:
- ②
- Turbulent regime:
3. Analysis of Wellbore Temperature Behavior during Deep Horizontal Well Drilling
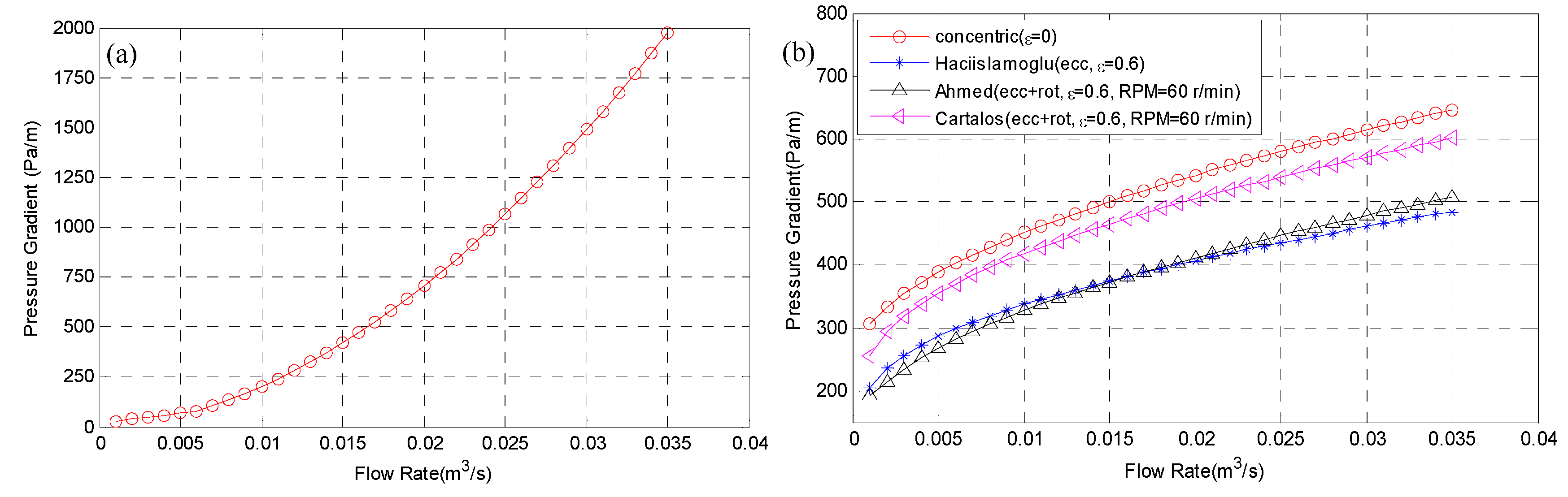
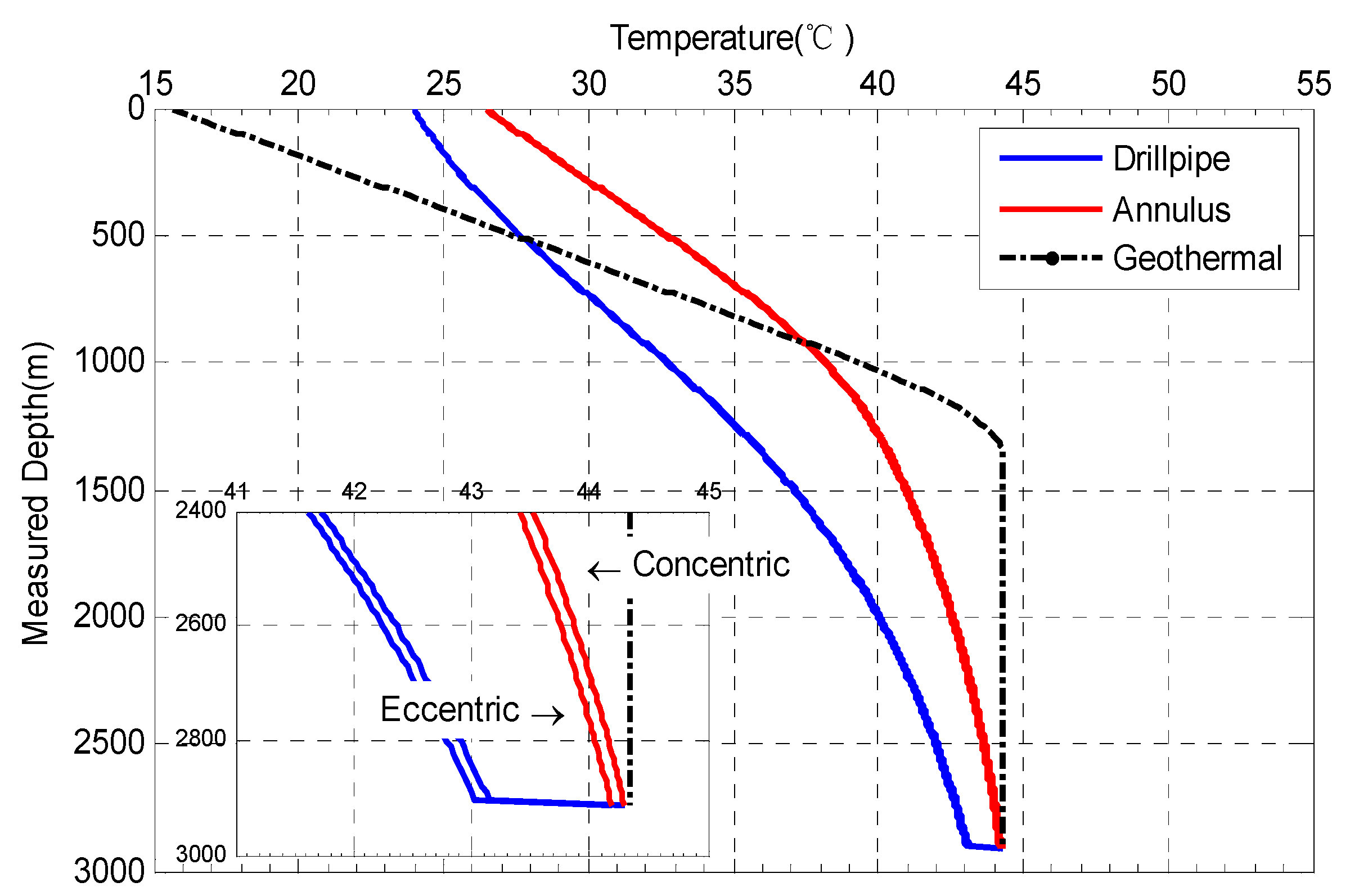
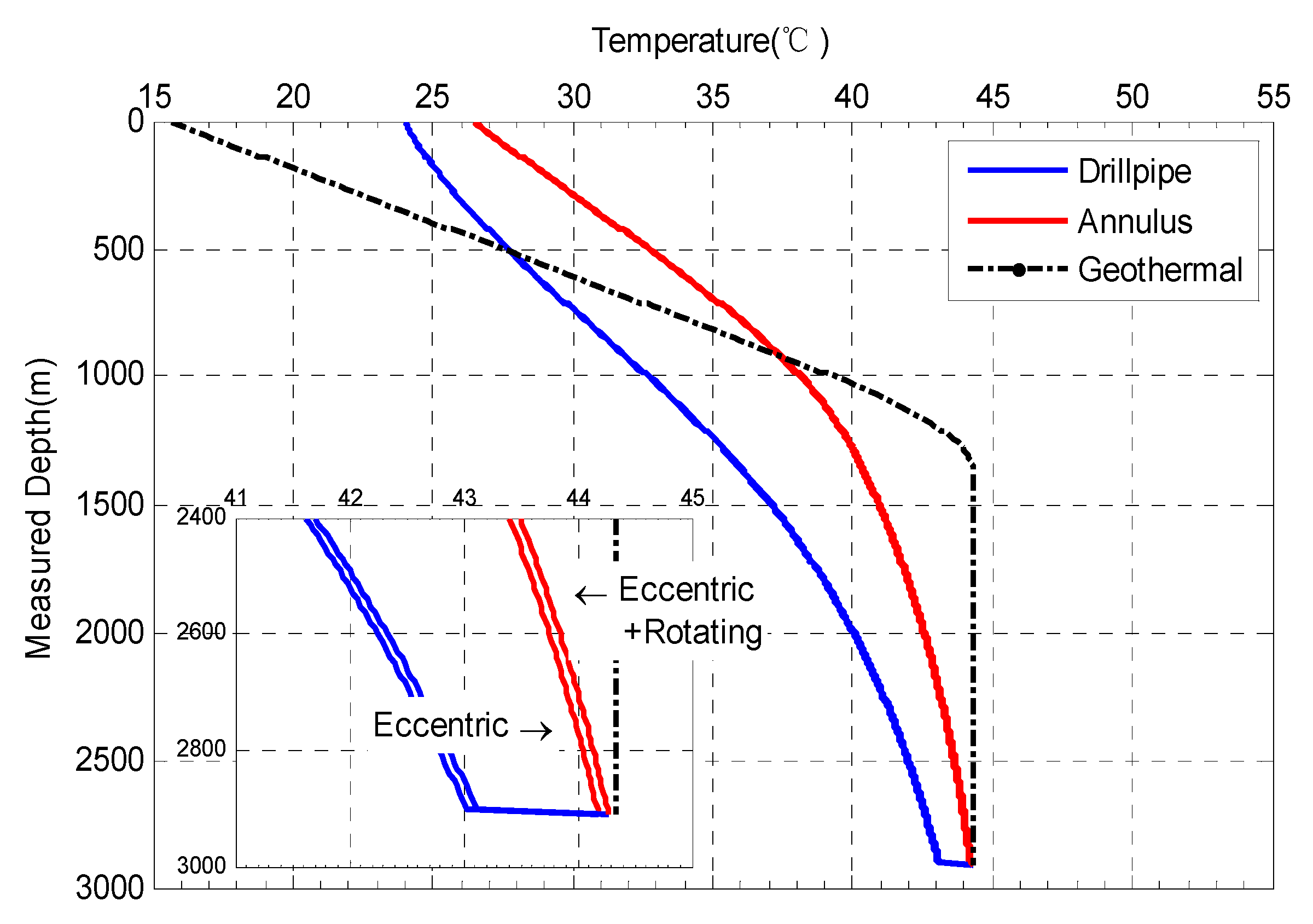
3.1. Influences of Circulating Pressure Drop under Various Rotation Rates and Eccentricities of Drill Pipes
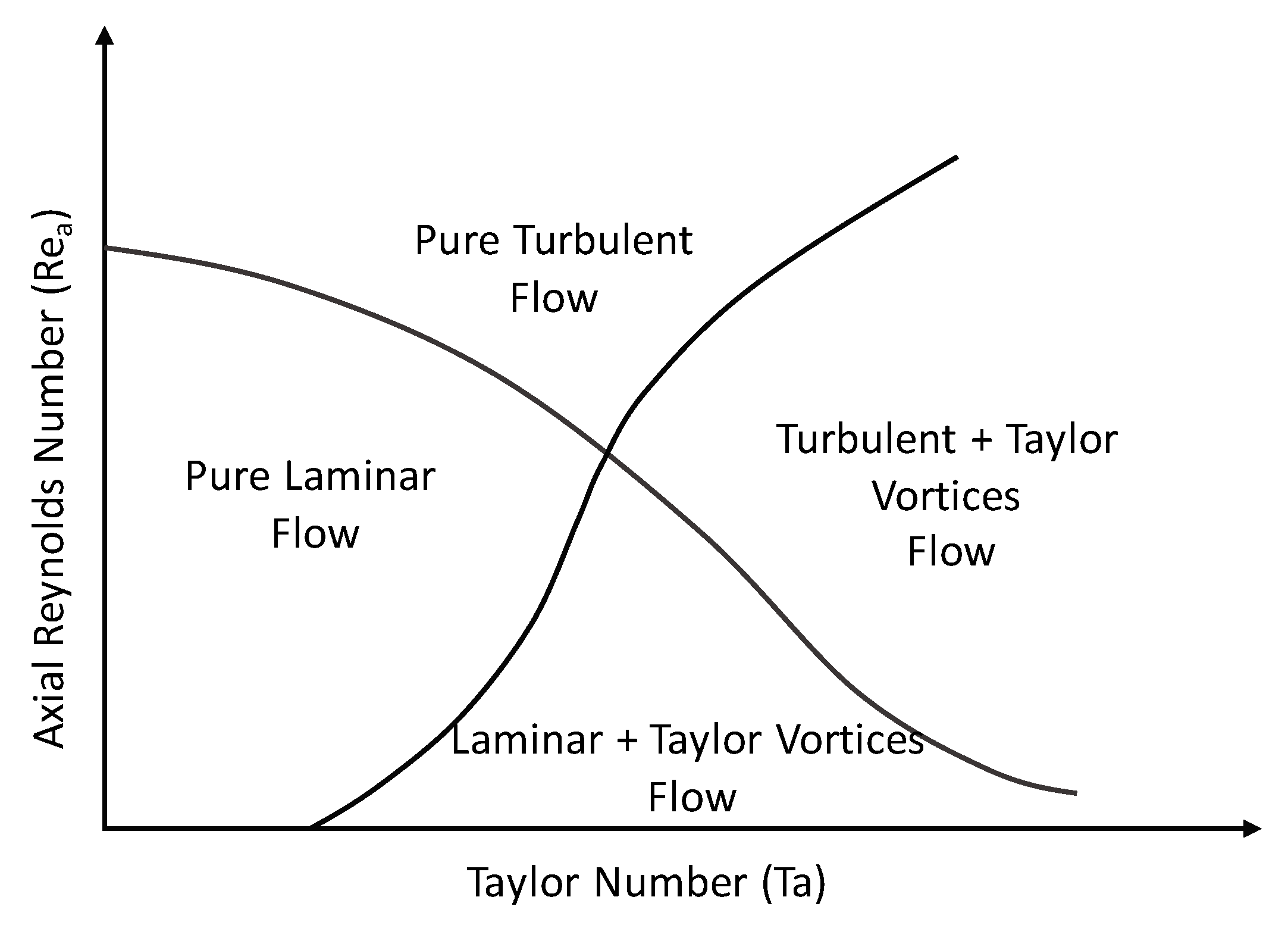
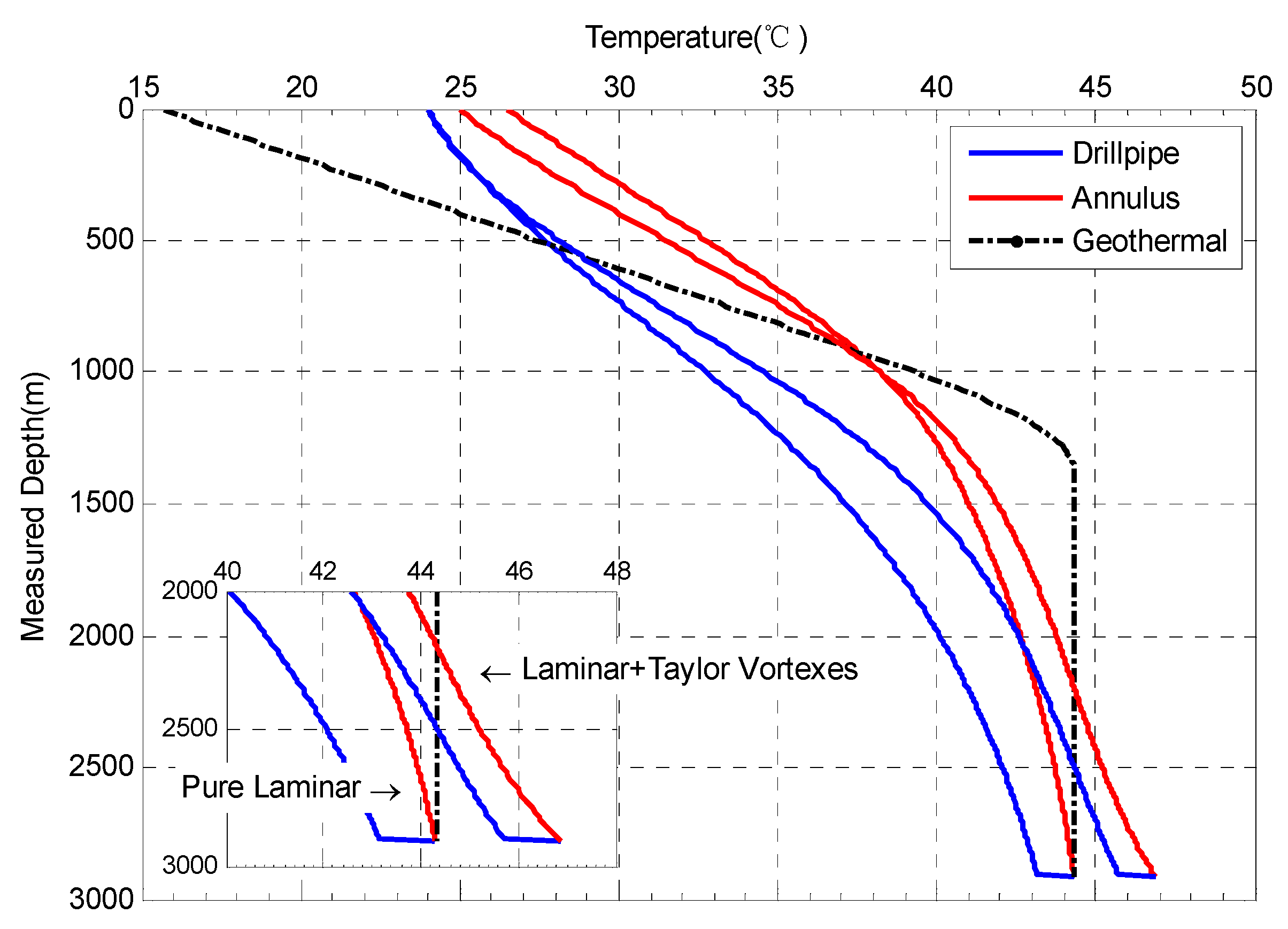
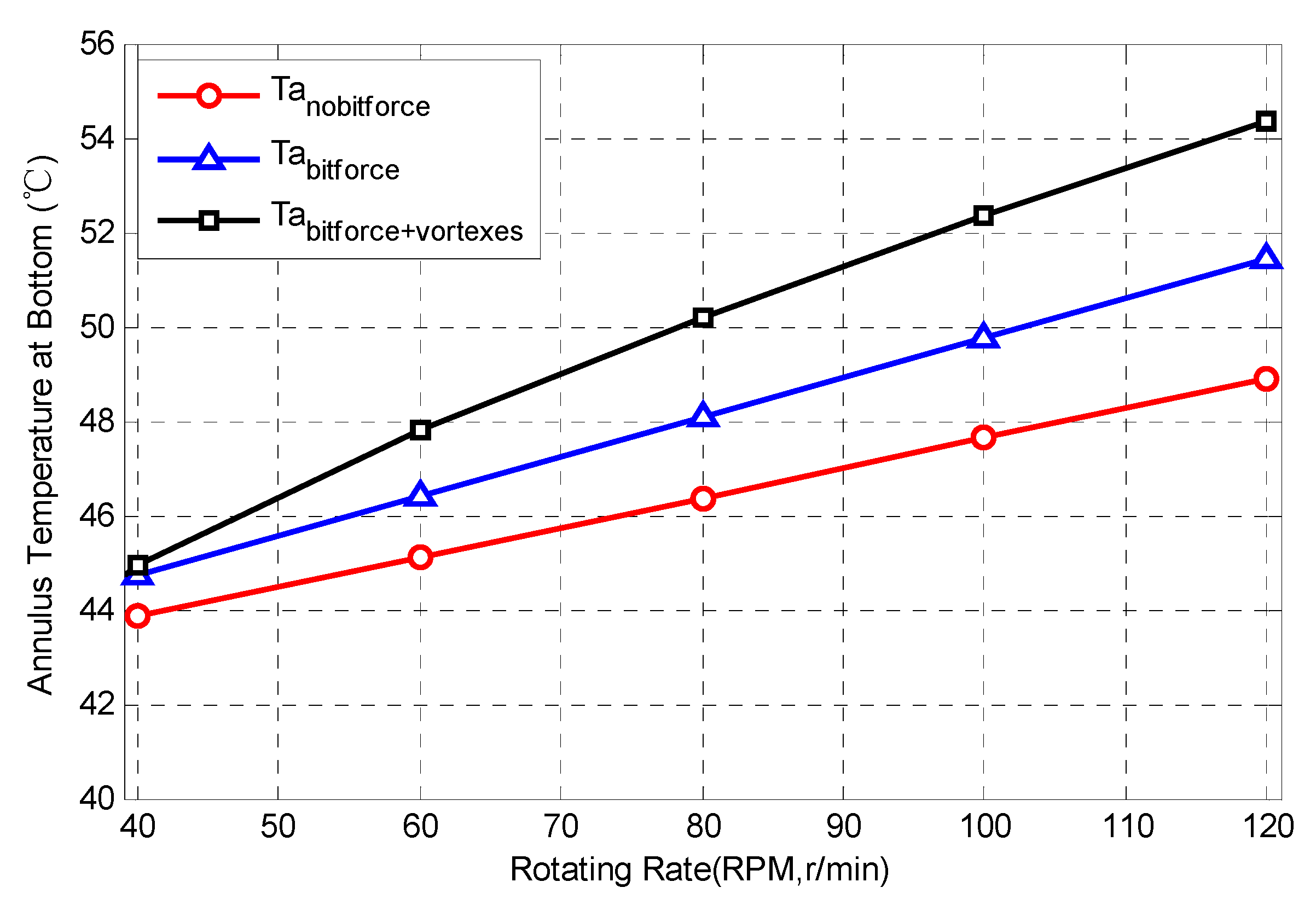
3.2. Influence of Nu with Taylor Vortex under Various Rotation Rates of Drill Pipe
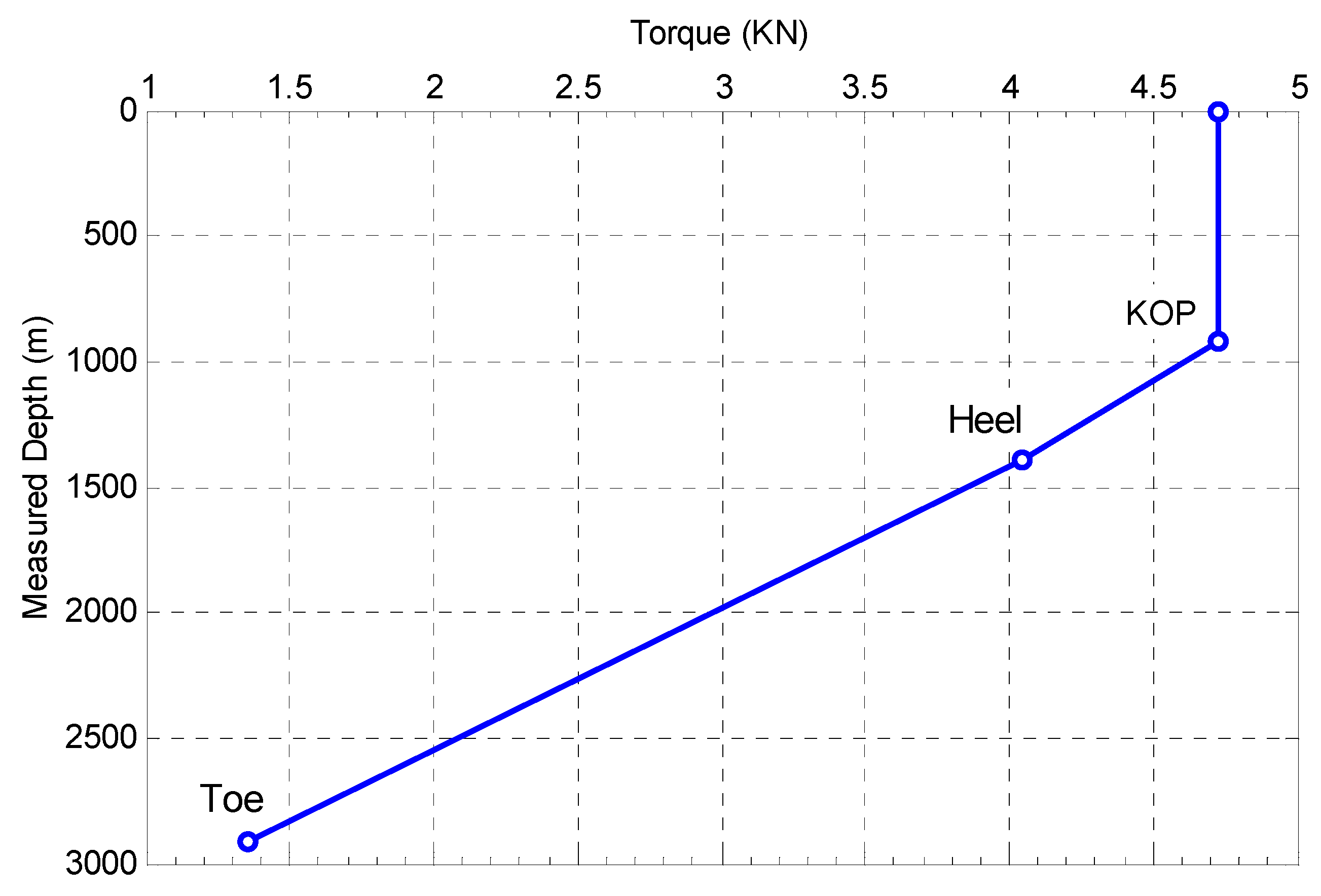
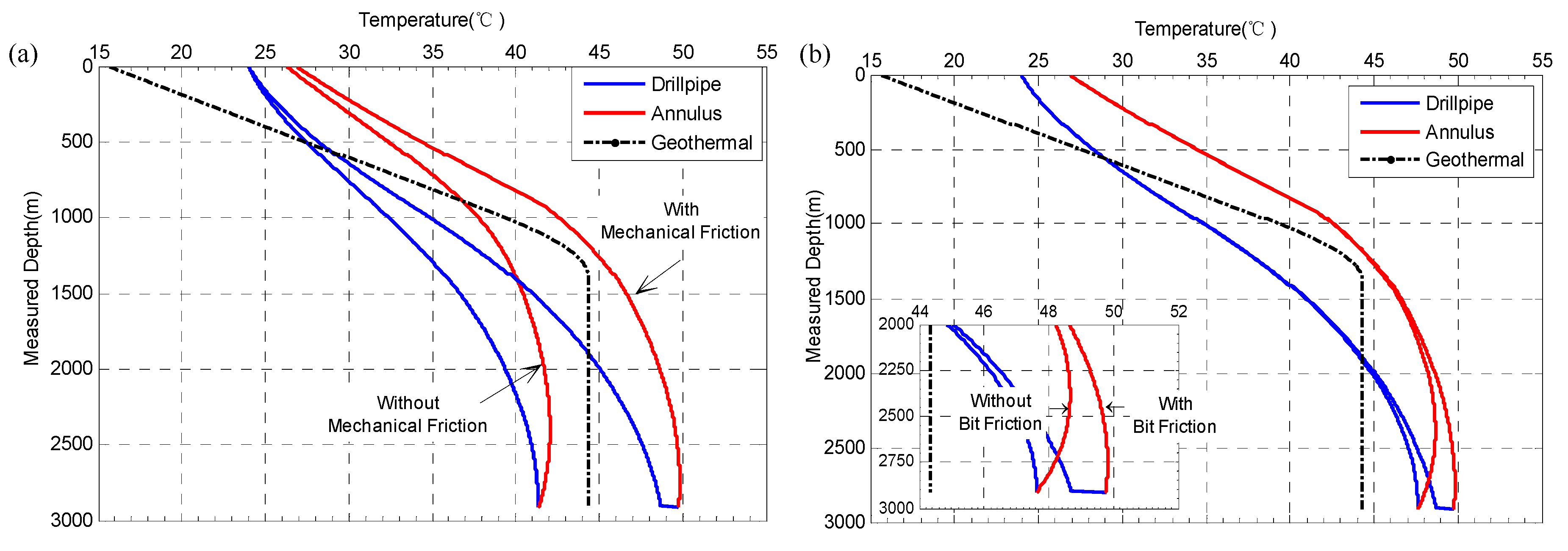
3.3. The Influence of Mechanical Friction under Various Rotation Rates of the Drill Pipe
4. Conclusions
- (1)
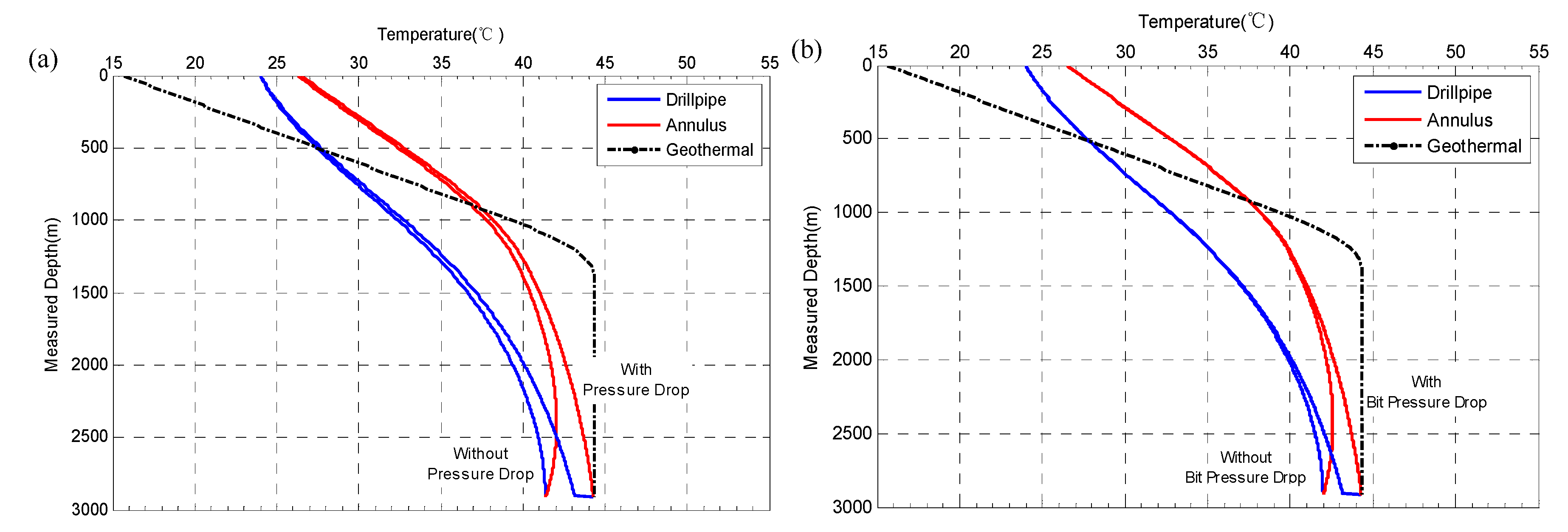
- The pressure drops in drill pipes and annuli during horizontal well drilling had negligible effects on temperature distributions. Consequently, it was more reasonable to take into consideration the pressure drop at the drill bit. When all pressure drops were considered, the temperature difference at the wellbore bottom was 3 °C. However, if the pressure drop at the drill bit was ignored but pressure drops in the drill pipe and annulus were considered, the difference is still 2 °C. But for the pressure drop influenced by drill pipe rotation and eccentricity, it only leads to 0.2 °C difference in bottom hole temperature, which can reasonably be neglected.
- (2)
- When the effect of drill pipe rotation on convection heat transfer in the annulus was considered, the occurrence of the Taylor vortex enhanced the heat transfer process. Compared to the heat transfer under the pure laminar regime, the temperature in the upper annulus was lower than that without the consideration of the effect of the drill pipe rotation, whereas the temperature in the lower annulus was greater.
- (3)
- The mechanical friction at the drill bit and drill pipes had a great influence on the wellbore temperature. This effect increased as the rotation rate increased. Hence, the effect of mechanical friction cannot be ignored. When RPM = 100 r/min, the annulus temperature difference at the wellbore bottom between the conditions where mechanical friction was considered and neglected reached up to 8 °C, which was a 19% increase.
- (4)
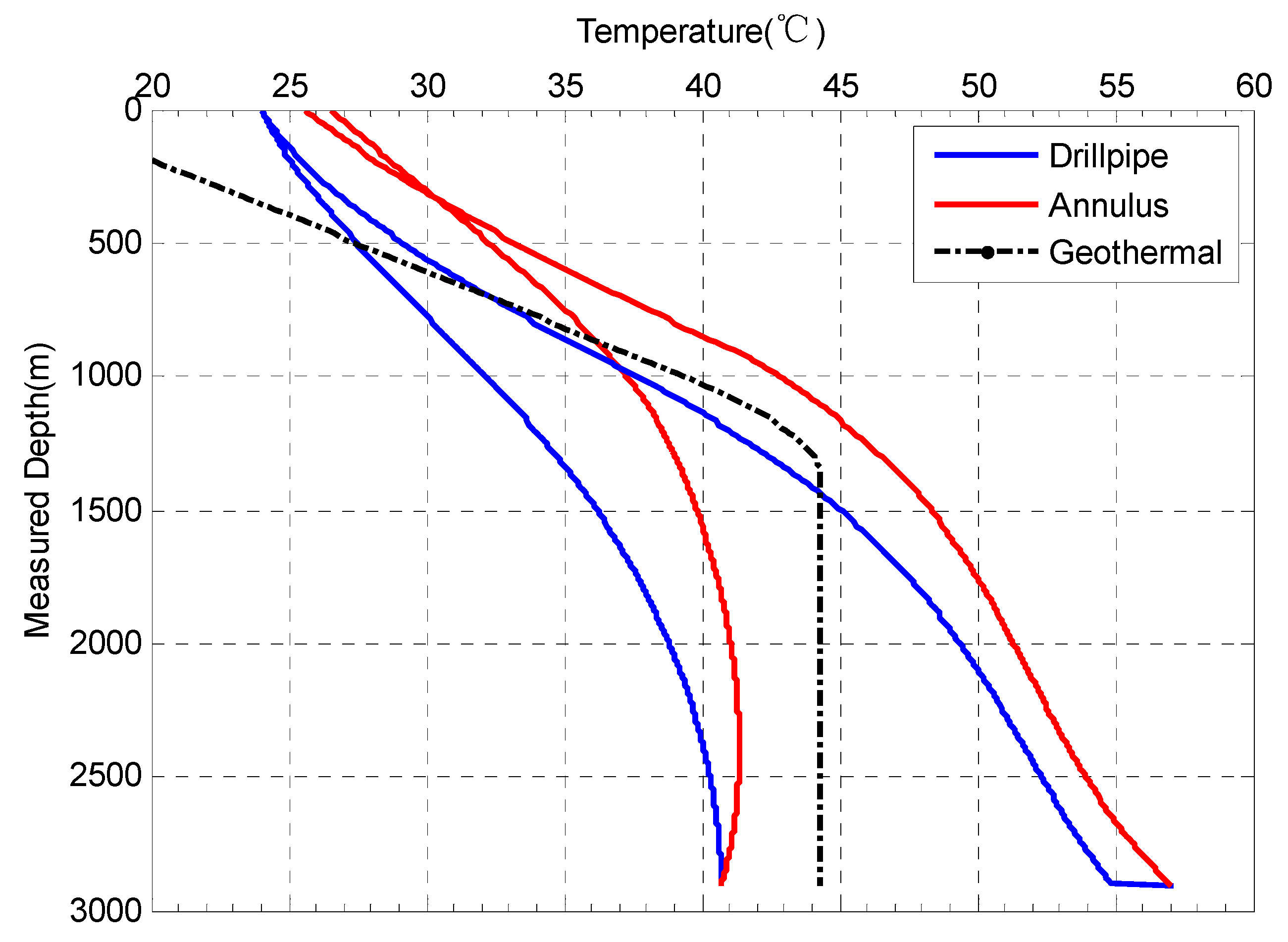
- The annulus temperature difference at the wellbore bottom between the conditions in which all effects, including drill pipe rotation, and hydraulic and mechanical frictions, were considered and neglected reached up to 16 °C, which was approximately a 38% increase. Moreover, it was possible for the temperature at the horizontal section to be greater than the original geothermal temperature when the abovementioned effects were taken into consideration.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| cd, cl, cr | heat capacity of drill pipe, mud and formation, J/(kg·°C); |
| Ddi, Ddo, Dw | inner and outer diameters of drillpipes, the wellbore diameter, respectively, m; |
| Dn1, Dn2, Dn3 | diameters of three nozzles at drill bit, mm; |
| DH | hydraulic diameter, m; |
| dP/dL | pressure drop gradient along drill pipe, Pa/m; |
| e | eccentricity of drill pipe, -; |
| F1, F2 | the force at the lower and upper end of a drillpipe segment, respectively, N; |
| Fbit | bit efficiency, -; |
| f | hydraulic friction factor, -; |
| fn | nozzle orifice coefficient, - |
| GT | geothermal gradient, °C/m; |
| H | a certain well depth, m; |
| Hheel | measured depth of the heel of horizontal section, m; |
| i | the number of radial grid layer, -; |
| j | the number of axial grid layer, -; |
| K | fluid consistency index, Pa·sn; |
| Nu | Nusselt number, dimensionless; |
| n | fluid flow behavior index, -; or the time step in the differential equations; |
| Pr | Prandtl number, dimensionless; |
| Qi, Qo | heat sources within the drill pipe and that within annulus, J; |
| q | circulating rate, m3/h; |
| R | reservoir radius, m; |
| Rb | radius of built-up section, m; |
| Recc | ratio of pressure drop along eccentric annulus to that along concentric annulus, -; |
| Rrot | ratio of pressure drop in annulus with a rotating drill pipe to that in annulus with a stationary drill pipe, -; |
| Re | Reynolds number, dimensionless; |
| Rea | axial Reynolds number, dimensionless; |
| Reeff | effective Reynolds number, dimensionless; |
| r1, r2, r3 | inner and outer radius of drillpipes, the wellbore radius, respectively, m; |
| T | torque along wellbore, kN·m; |
| Ta, Ta* | Taylor number, dimensionless; |
| Tbit | torque on bit, kN·m; |
| Tin, Ts | inlet and surface temperature, respectively, °C; |
| Tl, Td, Tla, Tr, Tb | temperature of mud in drill pipe, drill pipe, mud in annulus, formation and wellbore wall, respectively, °C; |
| t | circulating time, s; |
| w, wd | weight of drill pipe per meter in mud and air, respectively, kN/m; |
| z | the measured depth of well, m; |
| Greek Letters | |
| α1, α2 | inclination angle at the lower and upper end of a drill pipe segment, respectively, °; |
| αdi, αb | convective heat-transfer coefficient at the inner face of the drill pipe and the wellbore wall, respectively, W/(m2·°C); |
| β | buoyancy factor, -; |
| μ | mechanical friction factor (Equations (23)–(30)), -; or dynamic viscosity of mud (Equation (8); Equation (13)), Pa∙s; |
| ω | rotary speed per minute, r/min; |
| ρd, ρl, ρr | density of drill pipe, mud and formation rock, respectively, kg/m3; |
| δ | the annulus space gap, m; |
| Δs | length of a drill pipe segment, m; |
| λd, λl, λr | thermal conductivity of drill pipe, mud and formation, respectively, W/(m·K); |
| τy | fluid yield stress, Pa; |
| Abbreviations | |
| KOP | kick off point, m; |
| RPM, RPS | rotary speed per minute/second, r/min or r/s; |
| ROP | rate of penetration, m/h; |
| WOB | weight on bit, kN; |
| W, C, E, N, S | the name of grids, i.e., West(W), Center(C), East(E), North(N), South(S); |
Appendix A
Appendix A.1. Discretization of Heat Transfer Model

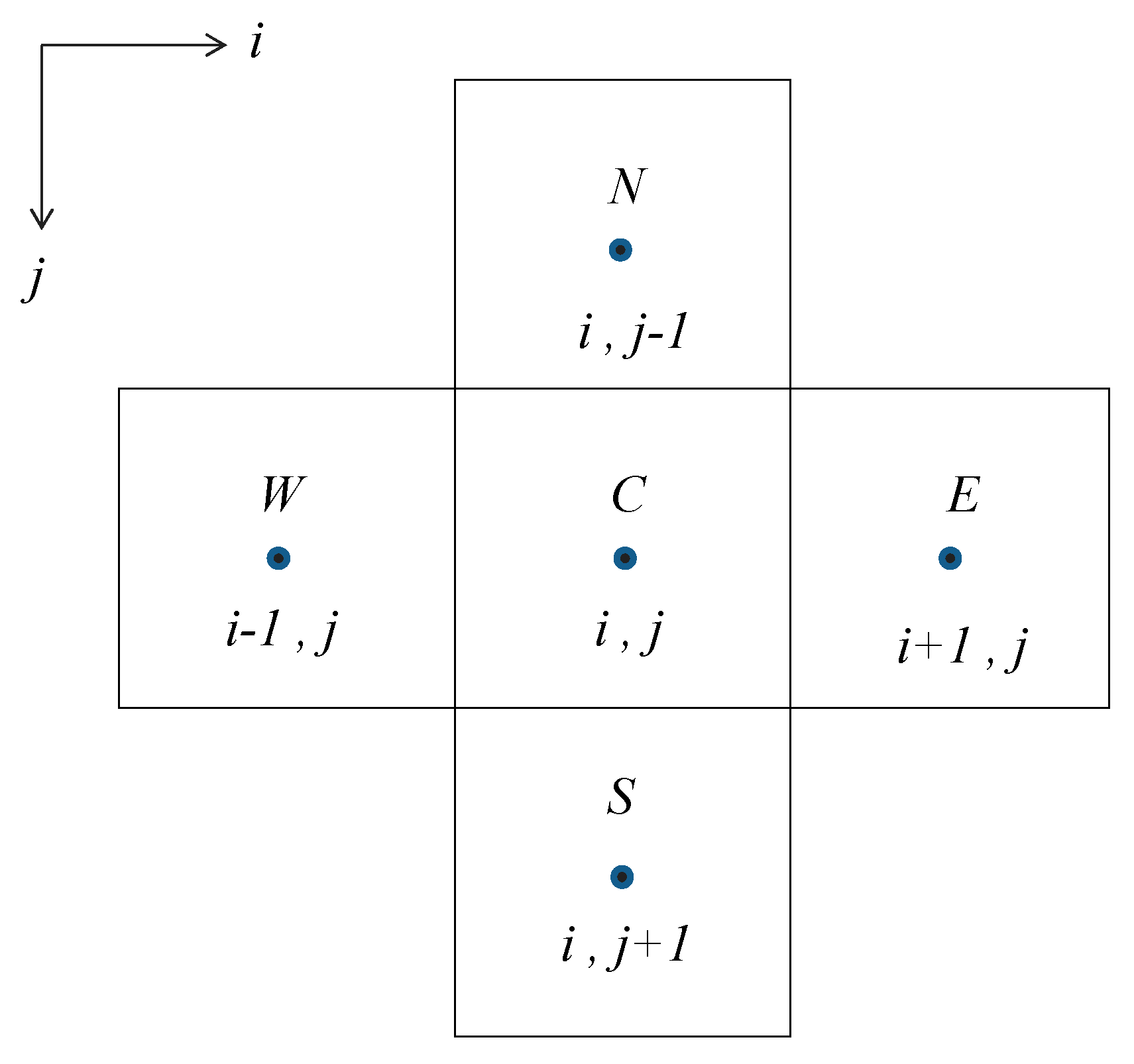
- (1)
- Drilling fluid in drill pipe
- (2)
- Drill pipe
- (3)
- Drilling fluid in annulus
- (4)
- Formation
- (5)
- Boundary and Initial conditions
- Inlet condition:
- Temperatures at wellbore bottom:
- Coupled condition at wellbore wall:
- Far field boundary:
- Stratum holds the original temperature:
- Drilling fluid in drill pipe:
- Drilling fluid in annulus:
Appendix A.2. Input Data and Calculation Procedure
| Parameters | Value | Unit | Parameters | Value | Unit |
|---|---|---|---|---|---|
| Circulating time, t | 21,600 | s | Rotary speed, RPM | 100 | r/min |
| Reservoir radius, R | 3 | m | Torque on bit, Tbit | 1.35 | kN·m |
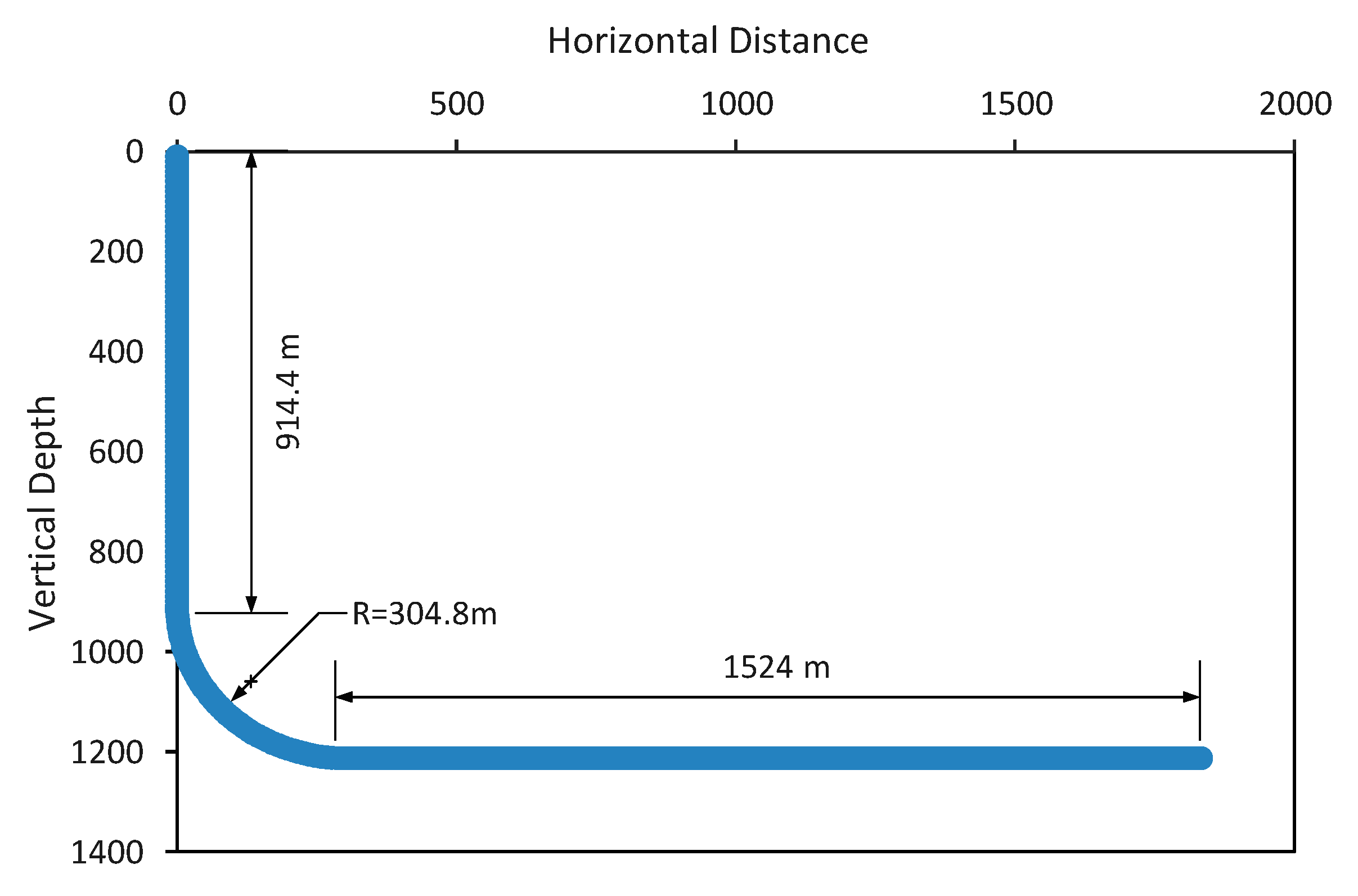
| Kick off point, KOP | 914.4 | m | Inlet temperature, Tin | 23.89 | °C |
| Heel of horizontal section, Hheel | 1393.18 | m | Surface temperature, Ts | 15.56 | °C |
| Radius of built-up section, Rb | 304.8 | m | Geothermal gradient, GT | 0.0238 | °C/m |
| Diameter of Nozzle #1, Dn1 | 18 | mm | Mud thermal conductivity, λl | 1.73 | W/(m·K) |
| Diameter of Nozzle #2, Dn2 | 18 | mm | Formation thermal conductivity, λr | 2.249 | W/(m·K) |
| Diameter of Nozzle #3, Dn3 | 16 | mm | Drill pipe thermal conductivity, λd | 34.6 | W/(m·K) |
| Fluid yield stress, τy | 5.75 | Pa | Mud heat capacity, cl | 1674.8 | J/(kg·°C) |
| Fluid consistency index, K | 0.3832 | Pa·sn | Formation heat capacity, cr | 837.4 | J/(kg·°C) |
| Fluid flow behavior index, n | 0.7 | - | Drill pipe heat capacity, cd | 460.57 | J/(kg·°C) |
| Circulating rate, q | 47.696 | m3/h | Mud density, ρl | 1198 | kg/m3 |
| Drill pipe inner diameter, Ddi | 0.101 | m | Drill pipe density, ρd | 8000 | kg/m3 |
| Drill pipe outer diameter, Ddo | 0.114 | m | Formation density, ρr | 2645 | kg/m3 |
| Wellbore diameter, Dw | 0.216 | m | Mechanical friction factor, μ | 0.2 | - |
| Weight of drill pipe per meter, wd | 0.186 | kN/m | Bit efficiency, Fbit | 0.8 | - |
| Rate of penetration, ROP | 14.4 | m/h | Nozzle orifice coefficient, fn | 0.95 | - |
| Weight on bit, WOB | 22.241 | kN |
References
- Edwardson, M.J.; Girner, H.M.; Parkison, H.R.; Williams, C.D.; Matthews, C.S. Calculation of Formation Temperature Disturbances Caused by Mud Circulation. J. Pet. Technol. 1962, 14, 416–426. [Google Scholar] [CrossRef]
- Ramey, H.J.J. Wellbore Heat Transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Holmes, C.S.; Swift, S.C. Calculation of Circulating Mud Temperatures. J. Pet. Technol. 1970, 22, 670–674. [Google Scholar] [CrossRef]
- Arnold, F.C. Temperature Variation in a Circulating Wellbore Fluid. J. Energy Resour. Technol. 1990, 112, 79–83. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Heat Transfer during Two-Phase Flow in Wellbores; Part I—Formation Temperature. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar] [CrossRef]
- Karstad, E.; Aadnoy, B.S. Analysis of Temperature Measurements during Drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–8 October 1997. [Google Scholar] [CrossRef]
- Kabir, C.S.; Hasan, A.R.; Kouba, G.E.; Ameen, M. Determining Circulating Fluid Temperature in Drilling, Workover, and Well Control Operations. SPE Drill. Complet. 1996, 11, 74–79. [Google Scholar] [CrossRef]
- Aniket, A.; Pratap Singh, A.; Samuel, R. Analytical Model to Predict the Effect of Pipe Friction on Downhole Temperatures for Extended Reach Drilling (ERD). In Proceedings of the IADC/SPE Drilling Conference and Exhibition, San Diego, CA, USA, 6–8 March 2012. [Google Scholar] [CrossRef]
- Kumar, A.; Samuel, R. Analytical Model to Estimate the Downhole Temperatures for Casing while Drilling Operations. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar] [CrossRef]
- Livescu, S.; Wang, X. Analytical Downhole Temperature Model for Coiled Tubing Operations. In Proceedings of the SPE/ICoTA Coiled Tubing and Well Intervention Conference and Exhibition, The Woodlands, TX, USA, 25–26 March 2014. [Google Scholar] [CrossRef]
- Raymond, L.R. Temperature Distribution in a Circulating Drilling Fluid. J. Pet. Technol. 1969. [Google Scholar] [CrossRef]
- Keller, H.H.; Couch, E.J.; Berry, P.M. Temperature Distribution in Circulating Mud Columns. Soc. Pet. Eng. J. 1973, 13, 23–30. [Google Scholar] [CrossRef]
- Marshall, D.W.; Bentsen, R.G. A Computer Model to Determine the Temperature Distributions in a Wellbore. J. Can. Pet. Technol. 1982. [Google Scholar] [CrossRef]
- Song, X.; Guan, Z. Coupled modeling circulating temperature and pressure of gas–liquid two phase flow in deep water wells. J. Pet. Sci. Eng. 2012, 92–93, 124–131. [Google Scholar] [CrossRef]
- Yang, M.; Yingfeng, M.; Gao, L.; Li, Y.; Chen, Y.; Zhao, X.; Li, H. Estimation of Wellbore and Formation Temperatures during the Drilling Process under Lost Circulation Conditions. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Gorman, J.M.; Abraham, J.P.; Sparrow, E.M. A novel, comprehensive numerical simulation for predicting temperatures within boreholes and the adjoining rock bed. Geothermics 2014, 50, 213–219. [Google Scholar] [CrossRef]
- Li, M.; Liu, G.; Li, J.; Zhang, T.; He, M. Thermal performance analysis of drilling horizontal wells in high temperature formations. Appl. Therm. Eng. 2015, 78, 217–227. [Google Scholar] [CrossRef]
- Bassam, A.; Santoyo, E.; Andaverde, J.; Hernández, J.A.; Espinoza-Ojeda, O.M. Estimation of static formation temperatures in geothermal wells by using an artificial neural network approach. Comput. Geosci. 2010, 36, 1191–1199. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, X.; Jeffrey, R.G. A model for downhole fluid and rock temperature prediction during circulation. Geothermics 2014, 50, 202–212. [Google Scholar] [CrossRef]
- Siu, A.; Li, Y.; Nghlem, L.; Redford, D. Numerical Modelling of a Thermal Horizontal Well. In Annual Technical Meeting; Petroleum Society of Canada: Calgary, AB, Canada, 1990. [Google Scholar]
- Yoshioka, K.; Zhu, D.; Hill, A.D.; Dawkrajai, P.; Lake, L.W. A Comprehensive Model of Temperature Behavior in a Horizontal Well. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar] [CrossRef]
- Yoshioka, K.; Zhu, D.; Hill, A.D.; Dawkrajai, P.; Lake, L.W. Prediction of Temperature Changes Caused by Water or Gas Entry into a Horizontal Well. SPE Prod. Oper. 2007, 22, 425–433. [Google Scholar] [CrossRef]
- Muradov, K.M.; Davies, D.R. Novel Analytical Methods of Temperature Interpretation in Horizontal Wells. Soc. Pet. Eng. 2011. [Google Scholar] [CrossRef]
- Trichel, D.K.; Fabian, J.A. Understanding and Managing Bottom Hole Circulating Temperature Behavior in Horizontal HT Wells—A Case Study Based on Haynesville Horizontal Wells. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Amsterdam, The Netherlands, 1–3 March 2011. [Google Scholar] [CrossRef]
- Nguyen, D.A.; Miska, S.Z.; Yu, M.; Saasen, A. Modeling Thermal Effects on Wellbore Stability. In Proceedings of the Trinidad and Tobago Energy Resources Conference, Port of Spain, Trinidad, 27–30 June 2010. [Google Scholar] [CrossRef]
- Santoyo-Gutierrez, E. Transient numerical simulation of heat transfer processes during drilling of geothermal wells. In Water Resources Research Group; University of Salford: Salford, UK, 1997. [Google Scholar]
- García, A.; Santoyo, E.; Espinosa, G.; Hernández, I.; Gutierrez, H. Estimation of Temperatures in Geothermal Wells during Circulation and Shut-in in the Presence of Lost Circulation. Transp. Porous Media 1998, 33, 103–127. [Google Scholar] [CrossRef]
- Bergman, T.L.; Incropera, F.P. Introduction to Heat Transfer; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Diersch, H.-J.G.; Bauer, D.; Heidemann, W.; Rühaak, W.; Schätzl, P. Finite element modeling of borehole heat exchanger systems: Part 1. Fundamentals. Comput. Geosci. 2011, 37, 1122–1135. [Google Scholar] [CrossRef]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Transient heat transfer in a coaxial borehole heat exchanger. Geothermics 2014, 51, 470–482. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Deng, J.; Meng, Y.; Li, G. Prediction of wellbore and formation temperatures during circulation and shut-in stages under kick conditions. Energy 2015, 91, 1018–1029. [Google Scholar] [CrossRef]
- Petersen, J.; Bjørkevoll, K.S.; Lekvam, K. Computing the Danger of Hydrate Formation Using a Modified Dynamic Kick Simulator. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 27 February–1 March 2001. [Google Scholar] [CrossRef]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiator of the tubular type. Int. Commun. Heat Mass Transf. 1930, 2, 3–22. [Google Scholar] [CrossRef]
- Sieder, E.N.; Tate, G.E. Heat Transfer and Pressure Drop of Liquids in Tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Petukhov, B.S. Heat Transfer and Friction in Turbulent Pipe Flow with Variable Physical Properties. Adv. Heat Transf. 1970, 6, 503–564. [Google Scholar] [CrossRef]
- Gnielinski, V. New Equations for Heat and Mass Transfer in Turbulent Pipe and Channel Flows. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Gnielinski, V. Heat Transfer Coefficients for Turbulent Flow in Concentric Annular Ducts. Heat Transf. Eng. 2009, 30, 431–436. [Google Scholar] [CrossRef]
- Gnielinski, V. On heat transfer in tubes. Int. J. Heat Mass Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- Tragesser, A.F.; Crawford, P.B.; Crawford, H.R. A Method for Calculating Circulating Temperatures. J. Pet. Technol. 1967, 19, 1507–1512. [Google Scholar] [CrossRef]
- Becker, K.M. An Experimental and Theoretical Study of Heat Transfer in an Annulus with an Inner Rotating Cylinder; Massachusetts Institute of Technology, Dept. of Mechanical Engineering: Massachusetts, MA, USA, 1957. [Google Scholar]
- Kaye, J. Modes of Adiabatic and Diabatic Fluid Flow in an Annulus with an Inner Rotating Cylinder. Trans. ASME 1958, 80, 753–765. [Google Scholar]
- Astill, K.N. Studies of the Developing Flow between Concentric Cylinders with the Inner Cylinder Rotating. J. Heat Transf. 1964, 86, 383–391. [Google Scholar] [CrossRef]
- Gazley, C., Jr. Heat-transfer characteristics of rotational and axial flow between concentric cylinders. Trans. ASME 1958, 80, 79–90. [Google Scholar]
- Li, G.; Yang, M.; Meng, Y.; Wen, Z.; Wang, Y.; Yuan, Z. Transient heat transfer models of wellbore and formation systems during the drilling process under well kick conditions in the bottom-hole. Appl. Therm. Eng. 2016, 93, 339–347. [Google Scholar] [CrossRef]
- Taylor, G.I. Stability of a Viscous Liquid Contained between Two Rotating Cylinders. Philos. Trans. R. Soc. Lond. 1923, 233, 289–343. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The stability of viscous flow between rotating cylinders in the presence of a magnetic field. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1953, 262, 293–309. [Google Scholar] [CrossRef]
- Goldstein, S. The stability of viscous fluid flow between rotating cylinders. Math. Proc. Camb. Philos. Soc. 1937, 33, 41–61. [Google Scholar] [CrossRef]
- Simmers, D.A.; Coney, J.E.R. A Reynolds analogy solution for the heat transfer characteristics of combined Taylor vortex and axial flows. Int. J. Heat Mass Transf. 1979, 22, 679–689. [Google Scholar] [CrossRef]
- Metzner, A.; Vaughn, R.; Houghton, G. Heat transfer to non-newtonian fluids. AIChE J. 1957, 3, 92–100. [Google Scholar] [CrossRef]
- Aoki, H.; Nohira, H.; Arai, H. Convective Heat Transfer in an Annulus with an Inner Rotating Cylinder. Bull. JSME 1967, 10, 523–532. [Google Scholar] [CrossRef]
- Cannon, J.N.; Kays, W.M. Heat Transfer to a Fluid Flowing Inside a Pipe Rotating About Its Longitudinal Axis. J. Heat Transf. 1969, 91, 135–139. [Google Scholar] [CrossRef]
- Warren, T.M. Factors Affecting Torque for a Roller Cone Bit. J. Pet. Technol. 1984, 36, 1500–1508. [Google Scholar] [CrossRef]
- Aadnøy, B.S.; Andersen, K. Design of oil wells using analytical friction models. J. Pet. Sci. Eng. 2001, 32, 53–71. [Google Scholar] [CrossRef]
- Aadnoy, B.S.; Fazaelizadeh, M.; Hareland, G. A 3D Analytical Model for Wellbore Friction. J. Can. Pet. Technol. 2010, 49, 25–36. [Google Scholar] [CrossRef]
- Kumar, A.; Samuel, R. Analytical Model to Predict the Effect of Pipe Friction on Downhole Fluid Temperatures. SPE Drill. Complet. 2013, 28, 270–277. [Google Scholar] [CrossRef]
- Craig, S. A multi-well review of coiled tubing force matching. In Proceedings of the SPE/ICoTA Coiled Tubing Conference and Exhibition, Houston, TX, USA, 8–9 April 2003. [Google Scholar] [CrossRef]
- Samuel, R. Friction factors: What are they for torque, drag, vibration, bottom hole assembly and transient surge/swab analyses? J. Pet. Sci. Eng. 2010, 73, 258–266. [Google Scholar] [CrossRef]
- Reed, T.D.; Pilehvari, A.A. A New Model for Laminar, Transitional, and Turbulent Flow of Drilling Muds. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, OK, USA, 21–23 March 1993. [Google Scholar] [CrossRef]
- Kelessidis, V.C.; Dalamarinis, P.; Maglione, R. Experimental study and predictions of pressure losses of fluids modeled as Herschel–Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows. J. Pet. Sci. Eng. 2011, 77, 305–312. [Google Scholar] [CrossRef]
- Cartalos, U.; Dupuis, D. An analysis accounting for the combined Effect of drillstring Rotation and eccentricity on Pressure Losses in Slimhole Drilling. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 22–25 February 1993. [Google Scholar] [CrossRef]
- Ooms, G.; Burgerscentrum, J.M.; Kampman-Reinhartz, B.E. Influence of Drillpipe Rotation and Eccentricity on Pressure Drop over Borehole during Drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar] [CrossRef]
- Ahmed, R.M.; Enfis, M.S.; El Kheir, H.M.; Laget, M.; Saasen, A. The Effect of Drillstring Rotation on Equivalent Circulation Density: Modeling and Analysis of Field Measurements. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 20–22 September 2010. [Google Scholar] [CrossRef]
- Anifowoshe, O.L.; Osisanya, S.O. The Effect of Equivalent Diameter Definitions on Frictional Pressure Loss Estimation in an Annulus with Pipe Rotation. In Proceedings of the SPE Deepwater Drilling and Completions Conference, Galveston, TX, USA, 20–21 June 2012. [Google Scholar] [CrossRef]
- Haciislamoglu, M.; Langlinais, J. Non-Newtonian Flow in Eccentric Annuli. J. Energy Resour. Technol. 1990, 112, 163–169. [Google Scholar] [CrossRef]
- Haciislamoglu, M. Practical Pressure Loss Predictions in Realistic Annular Geometries. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 25–28 September 1994. [Google Scholar] [CrossRef]
- Pilehvari, A.; Serth, R. Generalized Hydraulic Calculation Method for Axial Flow of Non-Newtonian Fluids in Eccentric Annuli. SPE Drill. Complet. 2009, 24, 553–563. [Google Scholar] [CrossRef]
- Nguyen, D.; Miska, S.; Mengjiao, Y.; Mitchell, R. Temperature profiles in directional and horizontal wells-the effect of drag forces. Wiertnictwo Nafta Gaz 2009, 26, 247–264. [Google Scholar]
- Wu, W.; Aubry, N.; Antaki, J.; McKoy, M.; Massoudi, M. Heat transfer in a drilling fluid with geothermal applications. Energies 2017, 10, 1349. [Google Scholar] [CrossRef]
- Miao, L.; Massoudi, M. Effects of shear dependent viscosity and variable thermal conductivity on the flow and heat transfer in a slurry. Energies 2015, 8, 11546–11574. [Google Scholar] [CrossRef]

| Fluid Type | Friction Factors | |
|---|---|---|
| Cases Hole | Open Hole | |
| Oil-based | 0.16–0.20 | 0.17–0.25 |
| Water-based | 0.25–0.35 | 0.25–0.40 |
| Brine | 0.30–0.4 | 0.3–0.4 |
| Polymer-based | 0.15–0.22 | 0.2–0.3 |
| Synthetic-based | 0.12–0.18 | 0.15–0.25 |
| Foam | 0.30–0.4 | 0.35–0.55 |
| Air | 0.35–0.55 | 0.40–0.60 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, X.; Zhou, J.; Guo, Y.; He, S.; Wang, L.; Chen, Y.; Tang, M.; Jian, R. Heat Transfer Behaviors in Horizontal Wells Considering the Effects of Drill Pipe Rotation, and Hydraulic and Mechanical Frictions during Drilling Procedures. Energies 2018, 11, 2414. https://doi.org/10.3390/en11092414
Chang X, Zhou J, Guo Y, He S, Wang L, Chen Y, Tang M, Jian R. Heat Transfer Behaviors in Horizontal Wells Considering the Effects of Drill Pipe Rotation, and Hydraulic and Mechanical Frictions during Drilling Procedures. Energies. 2018; 11(9):2414. https://doi.org/10.3390/en11092414
Chicago/Turabian StyleChang, Xin, Jun Zhou, Yintong Guo, Shiming He, Lei Wang, Yulin Chen, Ming Tang, and Rui Jian. 2018. "Heat Transfer Behaviors in Horizontal Wells Considering the Effects of Drill Pipe Rotation, and Hydraulic and Mechanical Frictions during Drilling Procedures" Energies 11, no. 9: 2414. https://doi.org/10.3390/en11092414
APA StyleChang, X., Zhou, J., Guo, Y., He, S., Wang, L., Chen, Y., Tang, M., & Jian, R. (2018). Heat Transfer Behaviors in Horizontal Wells Considering the Effects of Drill Pipe Rotation, and Hydraulic and Mechanical Frictions during Drilling Procedures. Energies, 11(9), 2414. https://doi.org/10.3390/en11092414






