Modelling, Parameter Identification, and Experimental Validation of a Lead Acid Battery Bank Using Evolutionary Algorithms
Abstract
1. Introduction
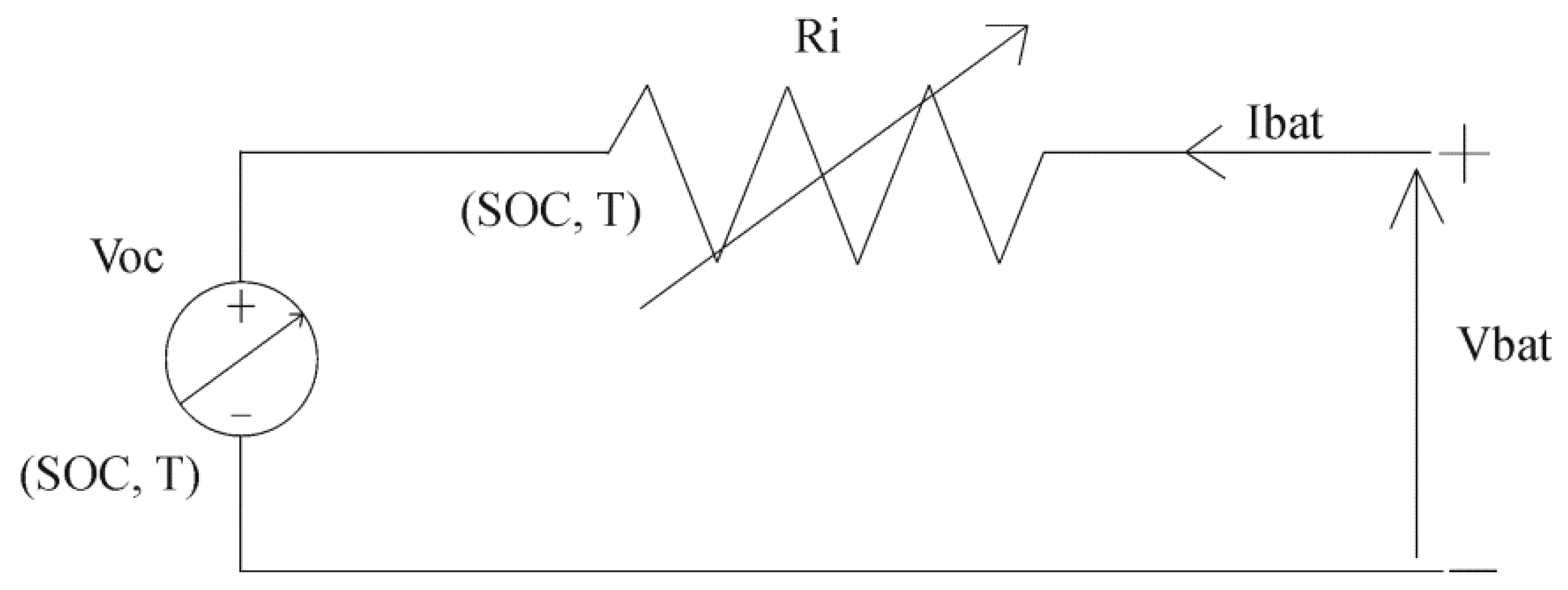
2. Battery Model Test
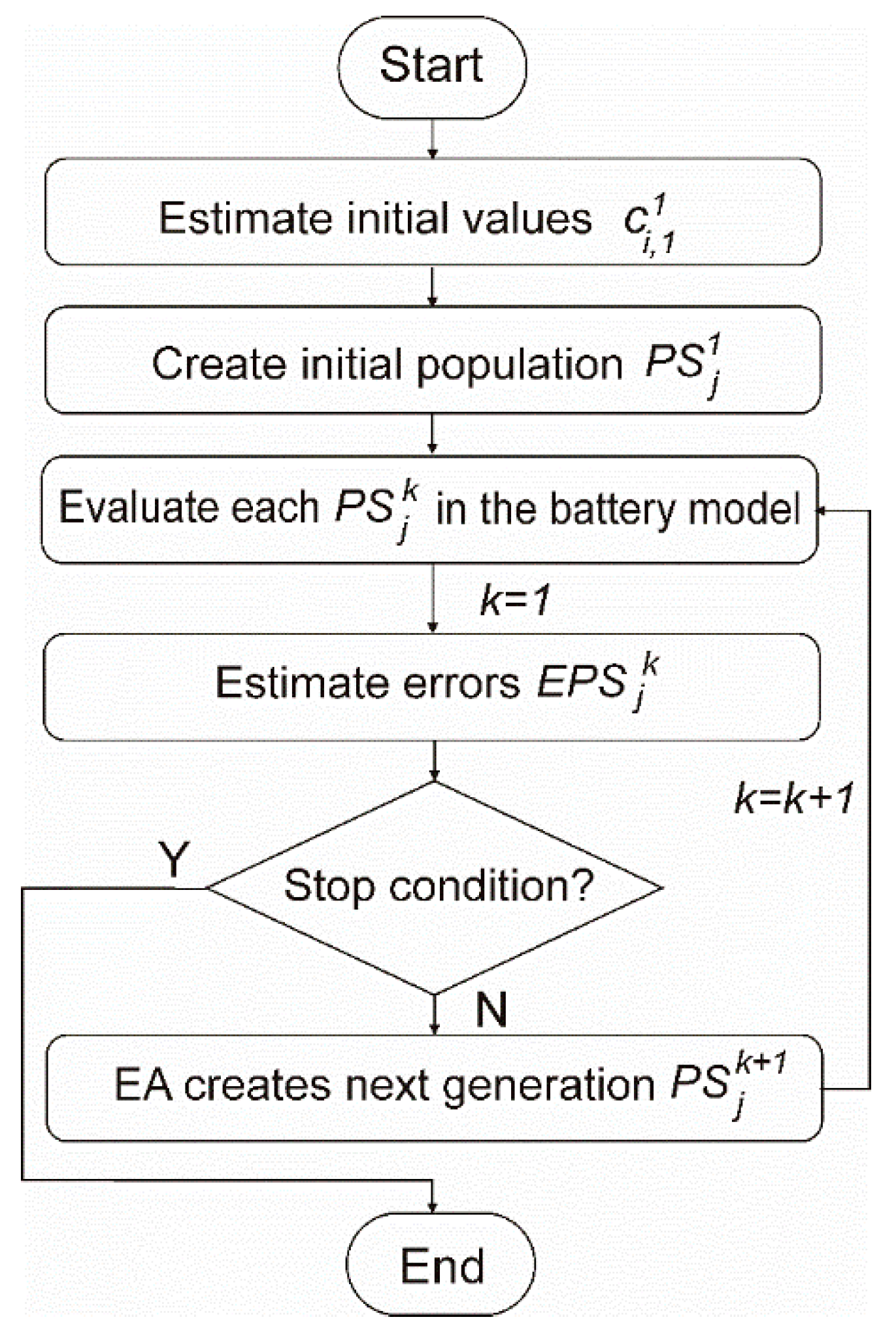
3. Parameter Identification
3.1. EAs’ Descriptions
3.2. New Proposal
3.3. Algorithms Configuration Criteria
4. Results and Discussion
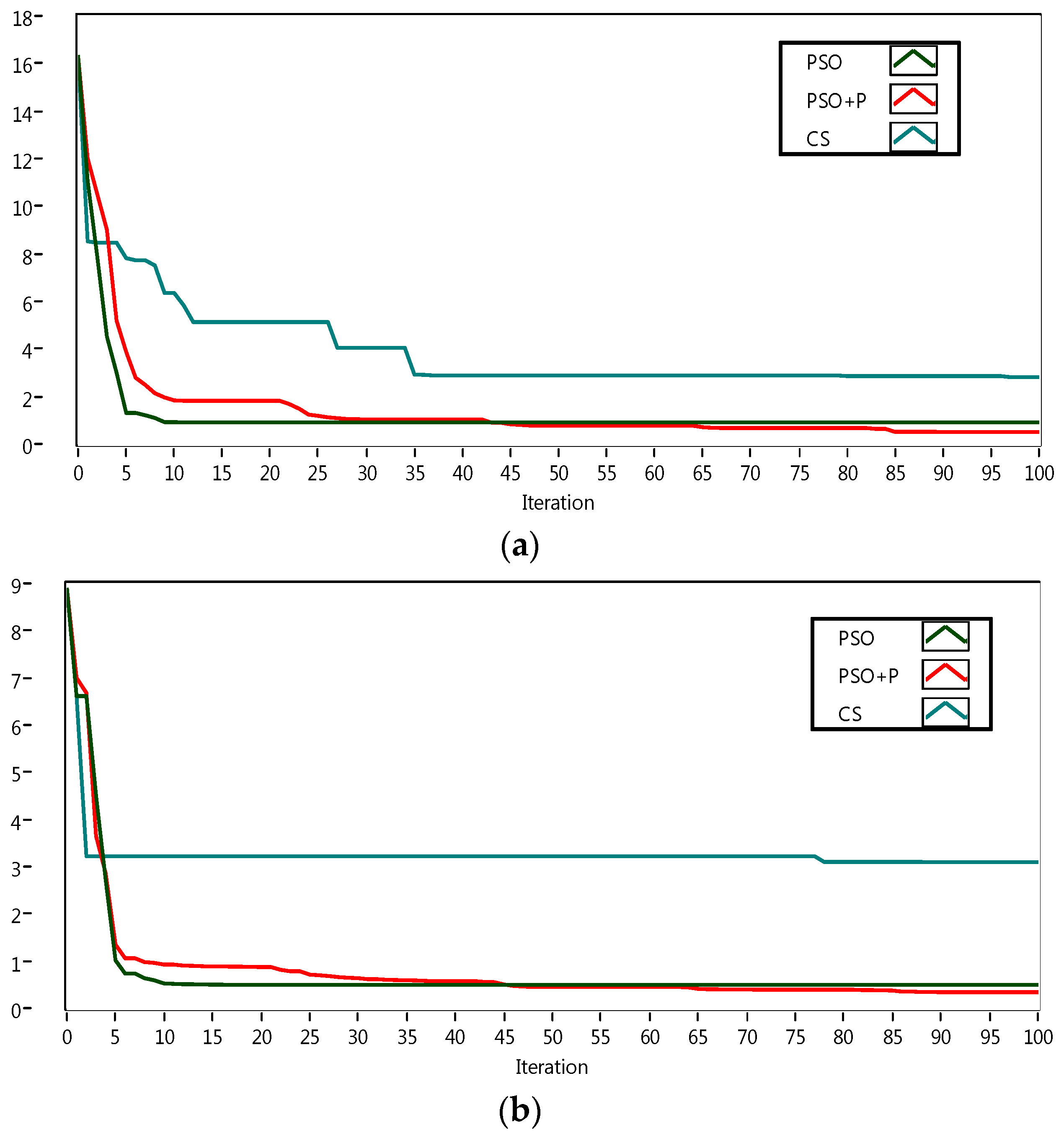
4.1. Optimization Results
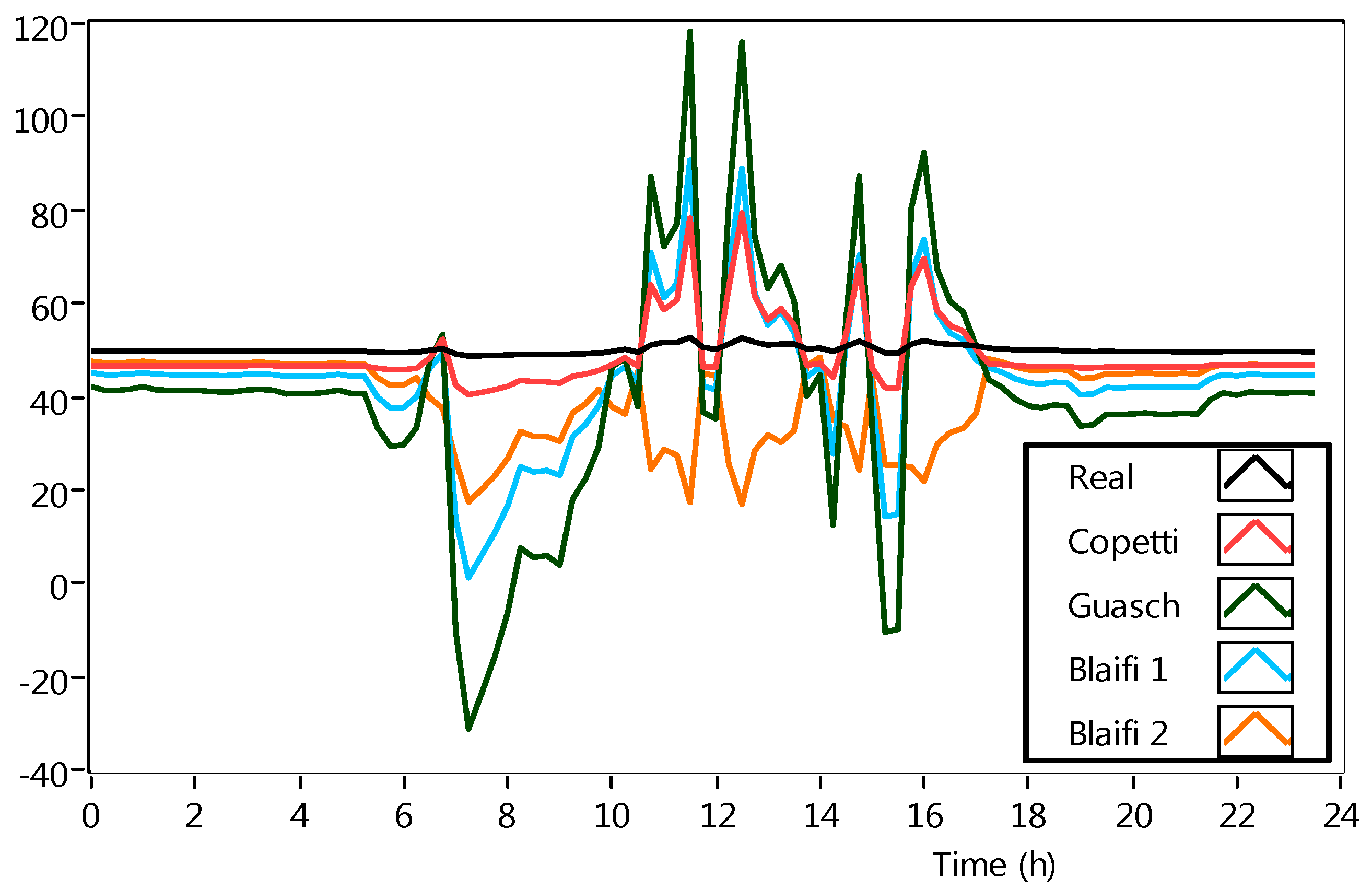
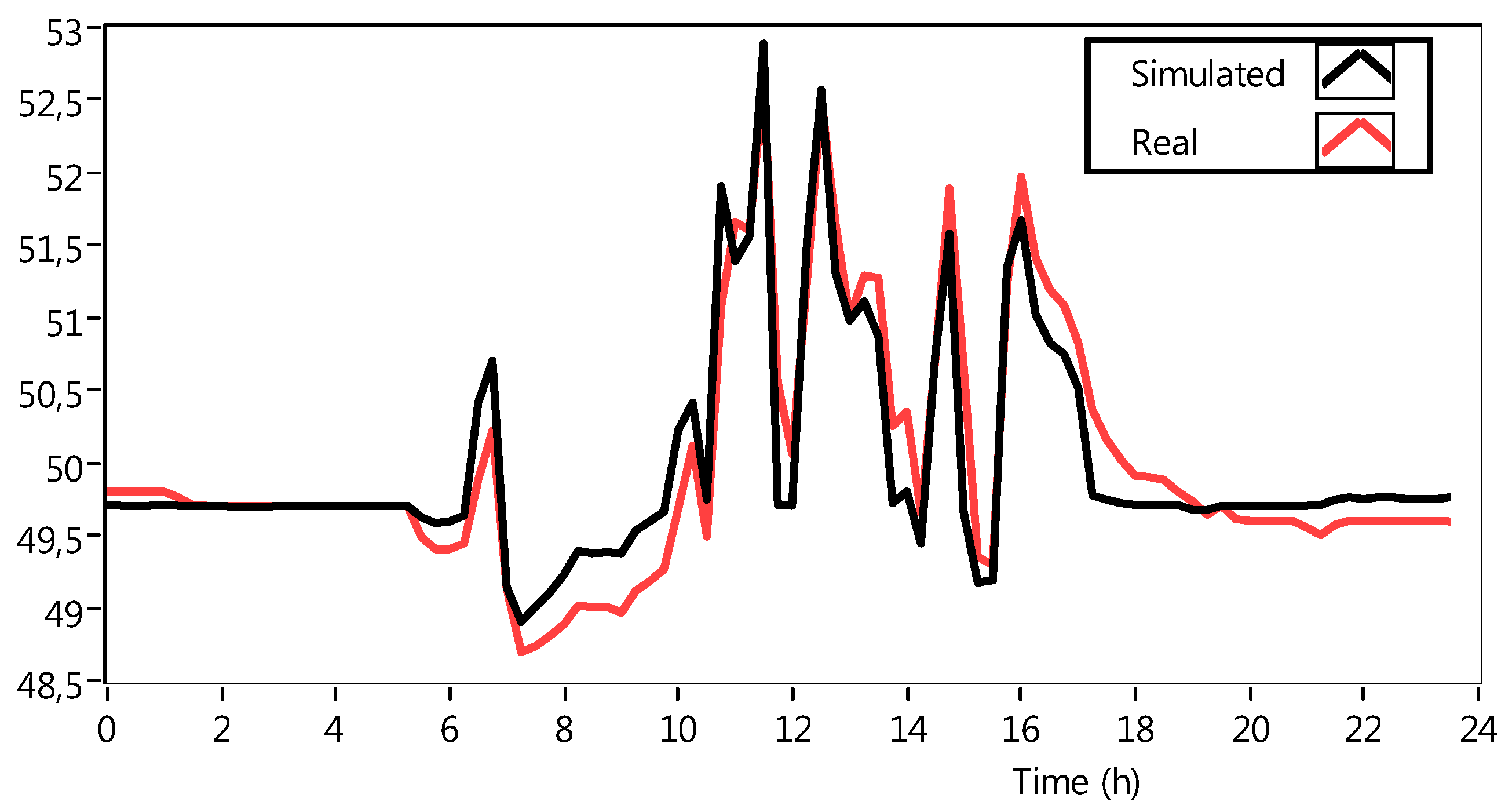
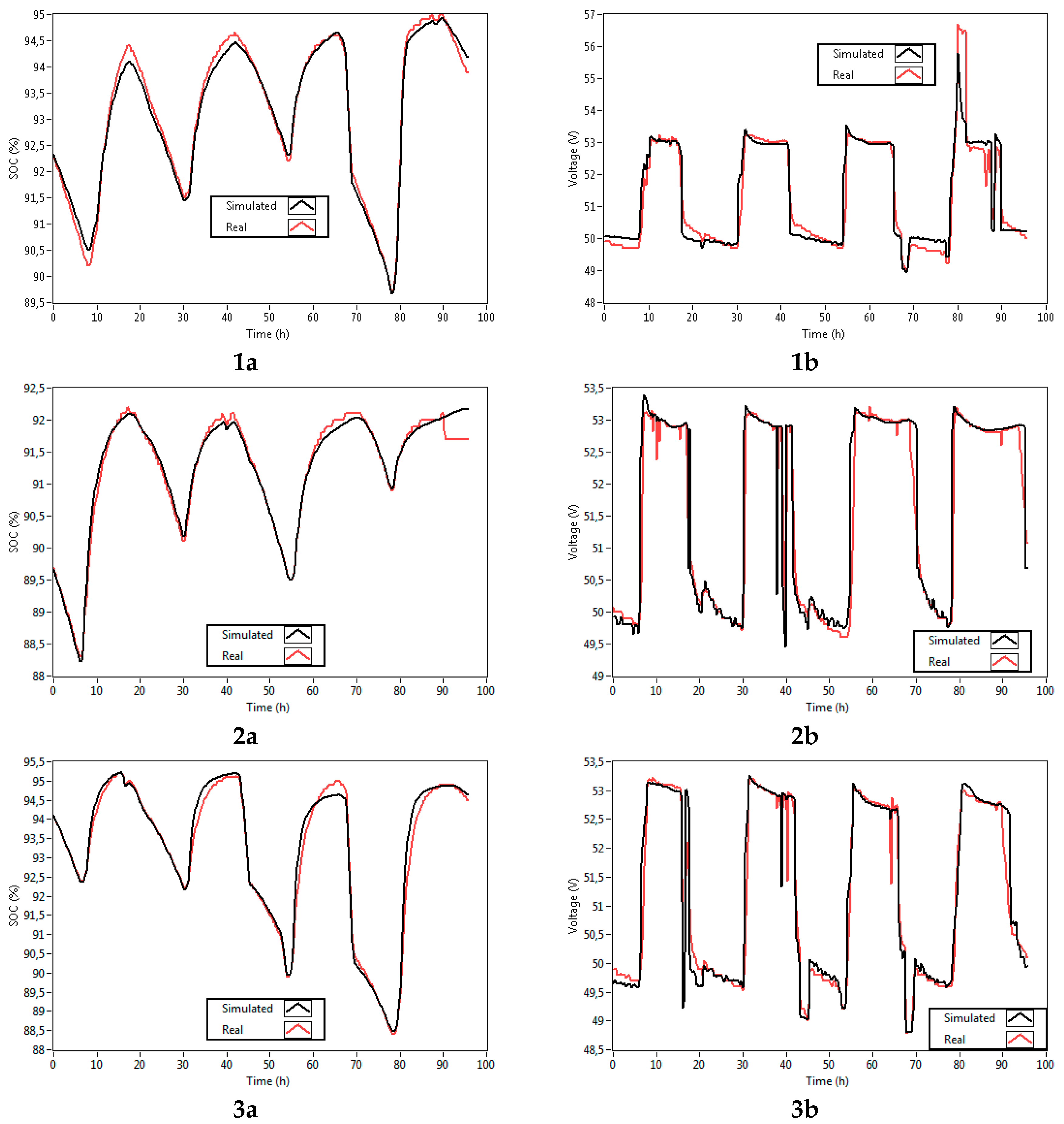
4.2. Model Performance and Validation
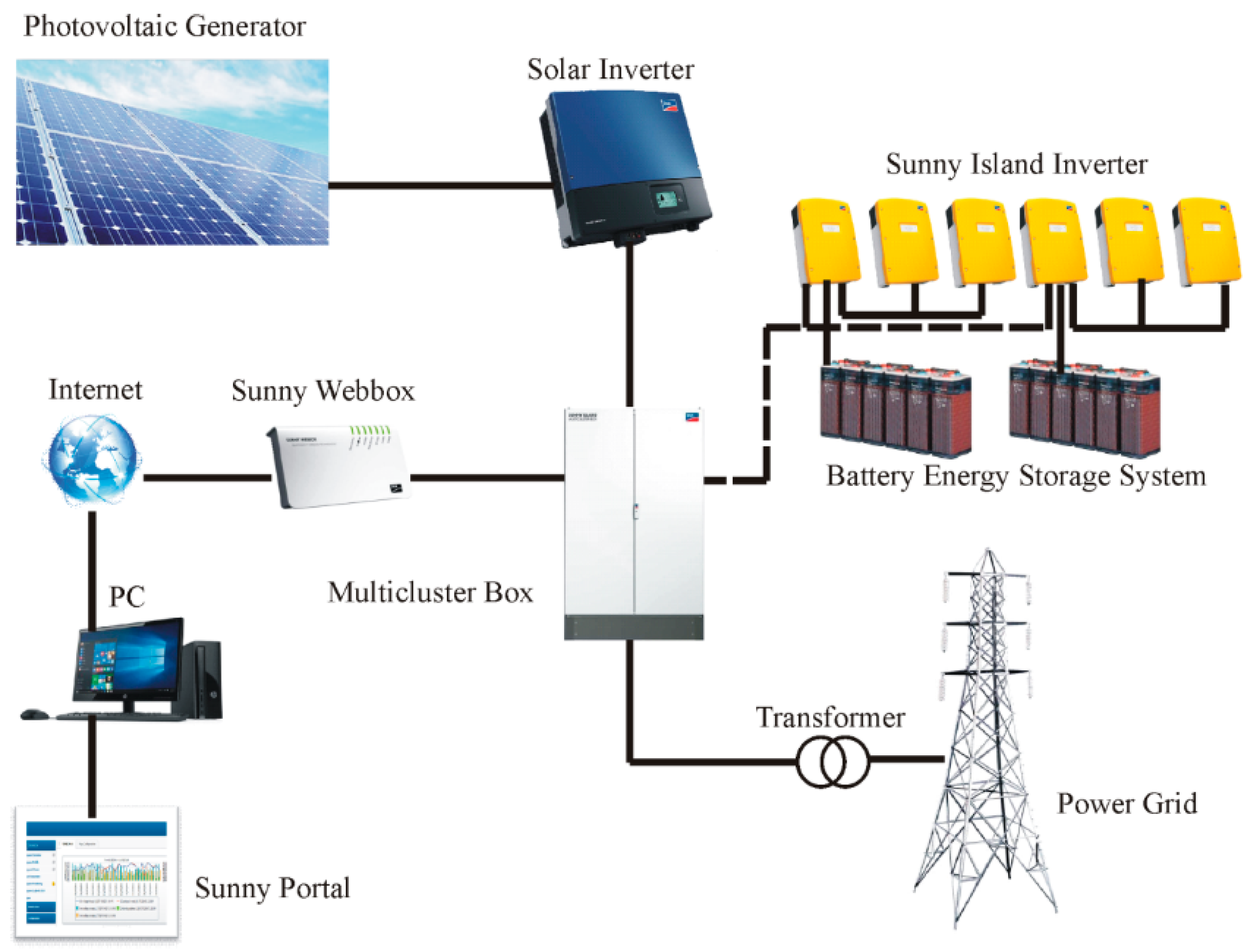
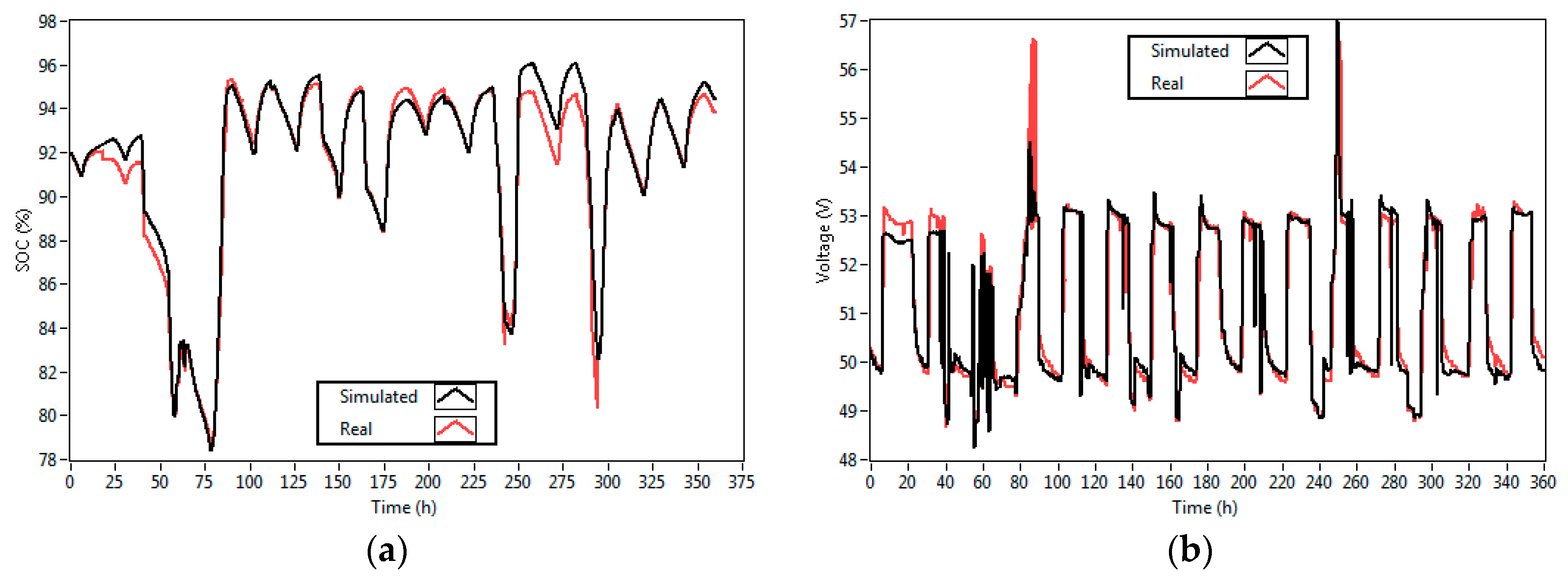
4.3. Experimental Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Banguero, E.; Correcher, A.; Pérez-Navarro, Á.; Morant, F.; Aristizabal, A. A Review on Battery Charging and Discharging Control Strategies: Application to Renewable Energy Systems. Energies 2018, 11, 1021. [Google Scholar] [CrossRef]
- Genc, R.; Alas, M.O.; Harputlu, E.; Repp, S.; Kremer, N.; Castellano, M.; Colak, S.G.; Ocakoglu, K.; Erdem, E. High-Capacitance Hybrid Supercapacitor Based on Multi-Colored Fluorescent Carbon-Dots. Sci. Rep. 2017, 7, 11222. [Google Scholar] [CrossRef] [PubMed]
- Repp, S.; Harputlu, E.; Gurgen, S.; Castellano, M.; Kremer, N.; Pompe, N.; Wörner, J.; Hoffmann, A.; Thomann, R.; Emen, F.M.; et al. Synergetic effects of Fe3+ doped spinel Li4Ti5O12 nanoparticles on reduced graphene oxide for high surface electrode hybrid supercapacitors. Nanoscale 2018, 10, 1877–1884. [Google Scholar] [CrossRef] [PubMed]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Evans, A.; Strezov, V.; Evans, T.J. Assessment of utility energy storage options for increased renewable energy penetration. Renew. Sustain. Energy Rev. 2012, 16, 4141–4147. [Google Scholar] [CrossRef]
- Ferreira, H.L.; Garde, R.; Fulli, G.; Kling, W.; Lopes, J.P. Characterisation of electrical energy storage technologies. Energy 2013, 53, 288–298. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Tyagi, V.V.; Rahim, N.A.; Panwar, N.L.; Mokhlis, H. Emergence of energy storage technologies as the solution for reliable operation of smart power systems: A review. Renew. Sustain. Energy Rev. 2013, 25, 135–165. [Google Scholar] [CrossRef]
- Kousksou, T.; Bruel, P.; Jamil, A.; el Rhafiki, T.; Zeraouli, Y. Energy storage: Applications and challenges. Sol. Energy Mater. Sol. Cells 2014, 120, 59–80. [Google Scholar] [CrossRef]
- Kaiser, R. Optimized battery-management system to improve storage lifetime in renewable energy systems. J. Power Sources 2007, 168, 58–65. [Google Scholar] [CrossRef]
- Sayigh, A. Renewable Energy in the Service of Mankind Vol I: Selected Topics from the World Renewable Energy Congress WREC 2014; Springer: New York, NY, USA, 2015. [Google Scholar]
- Armstrong, S.; Glavin, M.E.; Hurley, W.G. Comparison of battery charging algorithms for stand alone photovoltaic systems. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1469–1475. [Google Scholar]
- Yin, Y.; Luo, X.; Guo, S.; Zhou, Z.; Wang, J. A battery charging control strategy for renewable energy generation systems. In Proceedings of the World Congress on Engineering, London, UK, 2–4 July 2008; Volume 1, pp. 2–4. [Google Scholar]
- Saiju, R.; Heier, S. Performance analysis of lead acid battery model for hybrid power system. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–6. [Google Scholar]
- Tsang, K.M.; Chan, W.L.; Wong, Y.K.; Sun, L. Lithium-ion battery models for computer simulation. In Proceedings of the 2010 IEEE International Conference on Automation and Logistics (ICAL), Hong Kong/Macau, China, 16–20 August 2010; pp. 98–102. [Google Scholar]
- Nikdel, M. Various battery models for various simulation studies and applications. Renew. Sustain. Energy Rev. 2014, 32, 477–485. [Google Scholar]
- Zhu, W.H.; Zhu, Y.; Tatarchuk, B.J. A simplified equivalent circuit model for simulation of Pb-acid batteries at load for energy storage application. Energy Convers. Manag. 2011, 52, 2794–2799. [Google Scholar] [CrossRef]
- Fendri, D.; Chaabene, M. Dynamic model to follow the state of charge of a lead-acid battery connected to photovoltaic panel. Energy Convers. Manag. 2012, 64, 587–593. [Google Scholar] [CrossRef]
- Hittinger, E.; Wiley, T.; Kluza, J.; Whitacre, J. Evaluating the value of batteries in microgrid electricity systems using an improved Energy Systems Model. Energy Convers. Manag. 2015, 89, 458–472. [Google Scholar] [CrossRef]
- Ansari, A.B.; Esfahanian, V.; Torabi, F. Discharge, rest and charge simulation of lead-acid batteries using an efficient reduced order model based on proper orthogonal decomposition. Appl. Energy 2016, 173, 152–167. [Google Scholar] [CrossRef]
- Achaibou, N.; Haddadi, M.; Malek, A. Modeling of lead acid batteries in PV systems. Energy Procedia 2012, 18, 538–544. [Google Scholar] [CrossRef]
- Achaibou, N.; Haddadi, M.; Malek, A. Lead acid batteries simulation including experimental validation. J. Power Sources 2008, 185, 1484–1491. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, S.; Xiong, B.; Ji, D.; Tseng, K.J. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer. Appl. Energy 2016, 181, 332–341. [Google Scholar] [CrossRef]
- Devarakonda, L.; Hu, T. Algebraic method for parameter identification of circuit models for batteries under non-zero initial condition. J. Power Sources 2014, 268, 928–940. [Google Scholar] [CrossRef]
- Selmani, A.; Outanoute, M.; Lachhab, A.; Guerbaoui, M.; Bouchikhi, B. Performance Evaluation of Modelling and Simulation of Lead Acid Batteries for Photovoltaic Applications. Int. J. Power Electron. Drive Syst. 2016, 7, 472–480. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Ji, D.; Tseng, K.J. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model. Appl. Energy 2017, 204, 1264–1274. [Google Scholar] [CrossRef]
- Wei, Z.; Bhattarai, A.; Zou, C.; Meng, S.; Lim, T.M.; Skyllas-Kazacos, M. Real-time monitoring of capacity loss for vanadium redox flow battery. J. Power Sources 2018, 390, 261–269. [Google Scholar] [CrossRef]
- Thirugnanam, K.; Ezhil TP, E.R.J.; Singh, M.; Kumar, P. Mathematical modeling of Li-ion battery using genetic algorithm approach for V2G applications. IEEE Trans. Energy Convers. 2014, 29, 332–343. [Google Scholar]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online battery state of health estimation based on Genetic Algorithm for electric and hybrid vehicle applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Liu, W.; Liu, L.; Chung, I.-Y.; Cartes, D.A. Real-time particle swarm optimization based parameter identification applied to permanent magnet synchronous machine. Appl. Soft Comput. 2011, 11, 2556–2564. [Google Scholar] [CrossRef]
- Guo, L.; Meng, Z.; Sun, Y.; Wang, L. Parameter identification and sensitivity analysis of solar cell models with cat swarm optimization algorithm. Energy Convers. Manag. 2016, 108, 520–528. [Google Scholar] [CrossRef]
- Nyarko, E.K.; Scitovski, R. Solving the parameter identification problem of mathematical models using genetic algorithms. Appl. Math. Comput. 2004, 153, 651–658. [Google Scholar] [CrossRef]
- García-Triviño, P.; Gil-Mena, A.J.; Llorens-Iborra, F.; García-Vázquez, C.A.; Fernández-Ramírez, L.M.; Jurado, F. Power control based on particle swarm optimization of grid-connected inverter for hybrid renewable energy system. Energy Convers. Manag. 2015, 91, 83–92. [Google Scholar] [CrossRef]
- Al-Falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Rahman, M.A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Malik, A.; Zhang, Z.; Agarwal, R.K. Extraction of battery parameters using a multi-objective genetic algorithm with a non-linear circuit model. J. Power Sources 2014, 259, 76–86. [Google Scholar] [CrossRef]
- Brand, J.; Zhang, Z.; Agarwal, R.K. Extraction of battery parameters of the equivalent circuit model using a multi-objective genetic algorithm. J. Power Sources 2014, 247, 729–737. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L.; Hinds, G.; Lyu, C.; Zheng, J.; Li, J. Multi-objective optimization of lithium-ion battery model using genetic algorithm approach. J. Power Sources 2014, 270, 367–378. [Google Scholar] [CrossRef]
- Guasch, D.; Silvestre, S. Dynamic battery model for photovoltaic applications. Prog. Photovolt. Res. Appl. 2003, 11, 193–206. [Google Scholar] [CrossRef]
- Copetti, J.B.; Lorenzo, E.; Chenlo, F. A general battery model for PV system simulation. Prog. Photovolt. Res. Appl. 1993, 1, 283–292. [Google Scholar] [CrossRef]
- Blaifi, S.; Moulahoum, S.; Colak, I.; Merrouche, W. An enhanced dynamic model of battery using genetic algorithm suitable for photovoltaic applications. Appl. Energy 2016, 169, 888–898. [Google Scholar] [CrossRef]
- Blaifi, S.; Moulahoum, S.; Colak, I.; Merrouche, W. Monitoring and enhanced dynamic modeling of battery by genetic algorithm using LabVIEW applied in photovoltaic system. Electr. Eng. 2017, 100, 1021–1038. [Google Scholar] [CrossRef]
- Blaifi, S.; Moulahoum, S.; Kabache, N.; Colak, I. An improved dynamic battery model suitable for photovoltaic applications. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 694–698. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Berrazouane, S.; Mohammedi, K. Parameter optimization via cuckoo optimization algorithm of fuzzy controller for energy management of a hybrid power system. Energy Convers. Manag. 2014, 78, 652–660. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Fister, I., Jr.; Yang, X.-S.; Fister, I.; Brest, J.; Fister, D. A Brief Review of Nature-Inspired Algorithms for Optimization. arXiv 2013, arXiv:13074186. [Google Scholar]
- Aristizabal, A.; Banguero, E.; Murillo, W. A Verification Study for Grid-Connected 20 kW Solar PV System Operating in Chocó, Colombia. Energy Procedia 2017, 141, 96–101. [Google Scholar]
- Chan, H.L. A new battery model for use with battery energy storage systems and electric vehicles power systems. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000; Volume 1, pp. 470–475. [Google Scholar]
- Szumanowski, A.; Chang, Y. Battery management system based on battery nonlinear dynamics modeling. IEEE Trans. Veh. Technol. 2008, 57, 1425–1432. [Google Scholar] [CrossRef]
- Burgos, C.; Sáez, D.; Orchard, M.E.; Cárdenas, R. Fuzzy modelling for the state-of-charge estimation of lead-acid batteries. J. Power Sources 2015, 274, 355–366. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.; Wang, Y.; Liu, S.; Jia, J. Parameter Identification for PEM Fuel-Cell Mechanism Model Based on Effective Informed Adaptive Particle Swarm Optimization. IEEE Trans. Ind. Electron. 2011, 58, 2410–2419. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter identification for proton exchange membrane fuel cell model using particle swarm optimization. Int. J. Hydrog. Energy 2009, 34, 981–989. [Google Scholar] [CrossRef]
| Parameters | Guasch [39] | Copetti [40] | Blaifi [41,42] | Blaifi [43] |
|---|---|---|---|---|
| Vbodc (V) | 2.147 | 2.085 | 2.148 | 2.1612 |
| Kbodc (V) | 0.284 | 0.12 | 0.127 | 0.219 |
| P1dc (VAh) | 4.083 | 4 | 0.406 | 9.5044 |
| P2dc | −6.634 | 1.3 | 3.041 | 4.9361 |
| P3dc (Vh) | 0.27 | 0.27 | 1.218 | 0.9311 |
| P4dc | 1.5 | 1.5 | 0.7812 | 0.037 |
| P5dc (Vh) | 0.02 | 0.02 | 0.484 | 1.8837 |
| αrdc (°C−1) | 0.007 | 0.007 | 0.0197 | 0.0167 |
| Vboc (V) | 1.98 | 2 | 1.781 | 1.9016 |
| Kboc (V) | 0.149 | 0.16 | 0.5313 | 0.16 |
| P1c (VAh) | 5.923 | 6 | 7.234 | 6.0809 |
| P2c | 0.024 | 0.86 | 0.667 | 1.6701 |
| P3c (Vh) | 0.48 | 0.48 | 0.078 | 0.3375 |
| P4c | 1.2 | 1.2 | 0.492 | 0.9853 |
| P5c (Vh) | 0.036 | 0.036 | 0.7421 | 1.7838 |
| αrc (°C−1) | 0.025 | 0.025 | 0.43 | 0.01 |
| Criteria | PSO | PSO + P | CS |
|---|---|---|---|
| Population size | 1000 | 1000 | 1000 |
| Iterations | 100 | 100 | 100 |
| Weight initial (ω1) | 0.9 | 0.9 | - |
| Weight final (ω2) | 0.1 | 0.1 | - |
| c1 | 1 | 1 | - |
| c2 | 1 | 1 | - |
| vd | 5 | 5 | 5 |
| Iteration to perturb | - | 10 | - |
| Pa | - | - | 0.5 |
| α | - | - | 1 |
| λ | - | - | 2 |
| Criteria/Algorithm | PSO | PSO + P | Cuckoo | ||||
|---|---|---|---|---|---|---|---|
| d * | c * | d * | c * | d * | c * | ||
| Precision (error) | Value | 0.50 | 0.91 | 0.34 | 0.51 | 3.09 | 2.81 |
| Score | 1.48 | 1.78 | 1.00 | 1.00 | 9.23 | 5.53 | |
| Velocity (iteration) | Value | 17.00 | 11.00 | 91.00 | 90.00 | 89.00 | 97.00 |
| Score | 1.00 | 1.00 | 5.35 | 8.18 | 5.24 | 8.82 | |
| Computational cost (ms/iteration) | Value | 0.41 | 0.41 | 0.42 | 0.42 | 0.71 | 0.71 |
| Score | 1.00 | 1.00 | 1.03 | 1.03 | 1.72 | 1.72 | |
| Discharge | Charge | ||
|---|---|---|---|
| Vbodc (V) | 2.3003 | Vboc (V) | 2.2823 |
| Kbodc (V) | 0.1898 | Kboc (V) | 1.0227 |
| P1dc (VAh) | 20.4751 | P1c (VAh) | 2.4048 |
| P2dc | 0.9282 | P2c | 1.1928 |
| P3dc (Vh) | 0.1481 | P3c (Vh) | 0.0061 |
| P4dc | 2.3350 | P4c | 0.0285 |
| P5dc (Vh) | 0.0362 | P5c (Vh) | 0.0054 |
| αrdc (°C−1) | 0.0365 | αrc (°C−1) | 0.1008 |
| kIdc * | 2.2087 | kIc * | 0.3254 |
| kc_batdc * | 2.5517 | kc_batc * | 0.3603 |
| ksocdc * | 2.5509 | ksocc * | 16.7918 |
| kc120dc * | 0.0470 | kc120c * | 0.3097 |
| Signal | SOC | Voltage | ||||
|---|---|---|---|---|---|---|
| Month | (1) | (2) | (3) | (1) | (2) | (3) |
| Charge mode error (%) | 0.0606 | 0.0827 | 0.1787 | 0.2163 | 0.2504 | 0.2446 |
| Discharge mode error (%) | 0.1223 | 0.1335 | 0.1383 | 0.3824 | 0.3347 | 0.5242 |
| Mean (%) | 0.0956 | 0.1076 | 0.1602 | 0.3075 | 0.2904 | 0.3582 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ariza Chacón, H.E.; Banguero, E.; Correcher, A.; Pérez-Navarro, Á.; Morant, F. Modelling, Parameter Identification, and Experimental Validation of a Lead Acid Battery Bank Using Evolutionary Algorithms. Energies 2018, 11, 2361. https://doi.org/10.3390/en11092361
Ariza Chacón HE, Banguero E, Correcher A, Pérez-Navarro Á, Morant F. Modelling, Parameter Identification, and Experimental Validation of a Lead Acid Battery Bank Using Evolutionary Algorithms. Energies. 2018; 11(9):2361. https://doi.org/10.3390/en11092361
Chicago/Turabian StyleAriza Chacón, H. Eduardo, Edison Banguero, Antonio Correcher, Ángel Pérez-Navarro, and Francisco Morant. 2018. "Modelling, Parameter Identification, and Experimental Validation of a Lead Acid Battery Bank Using Evolutionary Algorithms" Energies 11, no. 9: 2361. https://doi.org/10.3390/en11092361
APA StyleAriza Chacón, H. E., Banguero, E., Correcher, A., Pérez-Navarro, Á., & Morant, F. (2018). Modelling, Parameter Identification, and Experimental Validation of a Lead Acid Battery Bank Using Evolutionary Algorithms. Energies, 11(9), 2361. https://doi.org/10.3390/en11092361





