Theoretical and Experimental Contributions on the Use of Smart Composite Materials in the Construction of Civil Buildings with Low Energy Consumption
Abstract
1. Introduction
- a small energy exchange with the exterior, ensured by thermal insulation;
- the use of renewable energy sources;
- reducing energy requirements by using phase change materials.
- -
- determination of new materials with phase change, that can be used in thermal insulation of buildings to increase the energy efficiency of them;
- -
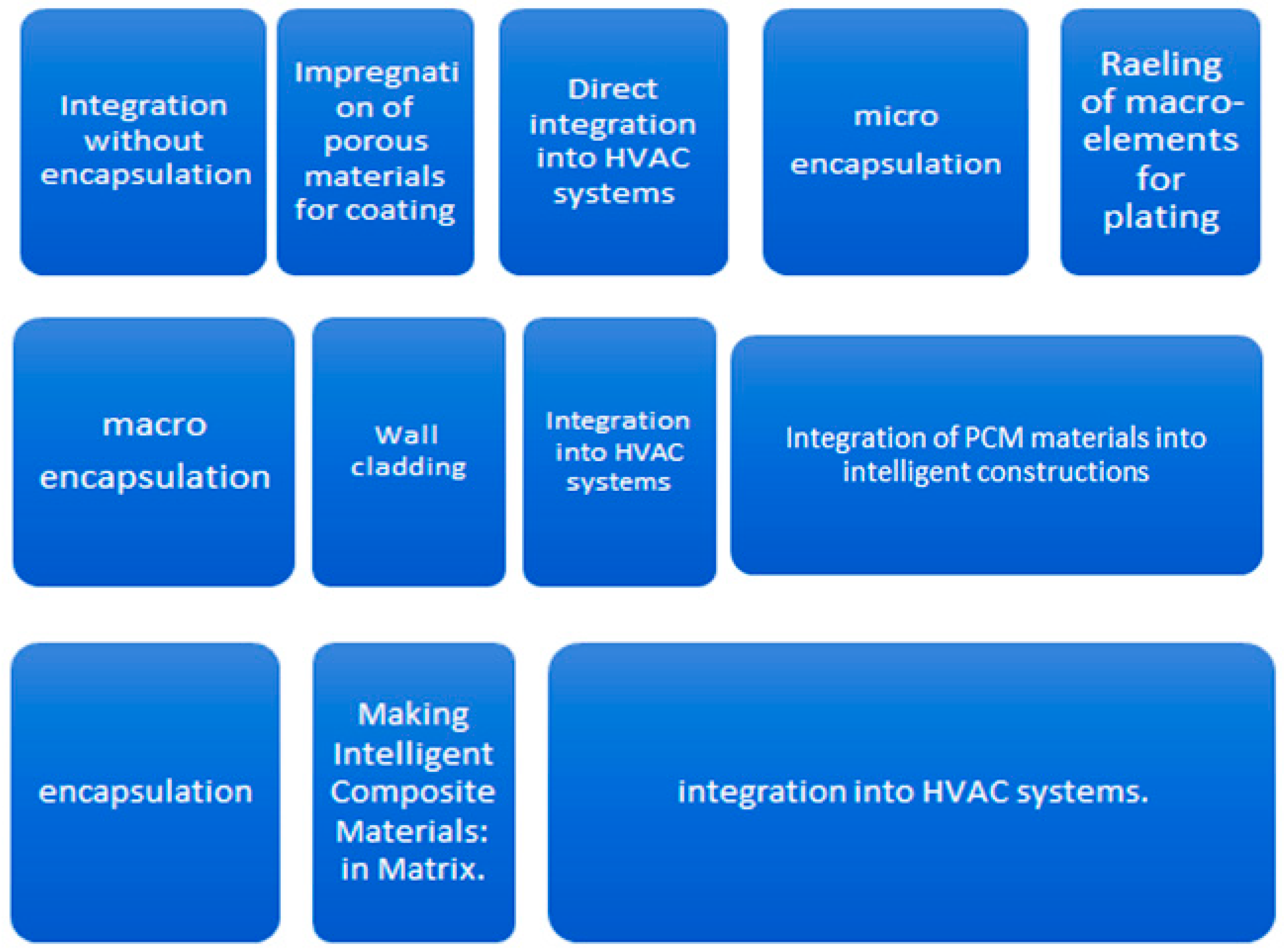
- identifying a technologies of integration of materials with phase change in order to achieve an intelligent composite material;
- -
- establishing the energy efficiency offered by intelligent composite material.
2. Materials and Methods
2.1. Experimental Realization of Intelligent Composite Material with Phase Change
2.2. The Theoretical Contributions on the Mathematical Model of Heat Transfer through the Proposed Composite Intelligent Composite Material to Be Achieved
3. Results and Discussion
3.1. Characterization of Thermal Behavior of Composite Material Made of Cement Matrix and PCM-RB01 Butyl Stearate Microcapsules
- -
- positioning of temperature sensors at the interface between the sample-cold plate and the sample-warm plate:
- -
- three thermistors in the center of resistance zone, the upper part;
- -
- three thermistors in the center of resistance zone, the lower part;
- -
- one thermistor in the protection slot area, the upper part;
- -
- one thermistor in the area of the protection slot, the lower part;
- -
- three thermistors in the resistance protection area, the upper part;
- -
- three thermistors in the resistance protection area, the lower part;
- -
- insertion of the assembly into the measuring enclosure (Figure 10);
- -
- connecting the cold plates to the water;
- -
- starting the power sources and connecting the hot plate to them;
- -
- adjusting the heating/heating current of the centerline resistance;
- -
- connecting to the PC the purchase plate and starting the data acquisition program;
- -
- setting the operating range of the vacuum pump and starting it in the “automatic” mode of the program interface;
- -
- initial temperature stabilization (2 ... 3 h);
- -
- adjusting the voltage/heating current of resistance protection area to obtain a maximum temperature difference of 0.4 °C between it and the central measuring zone;
- -
- secondary temperature stabilization (4 ... 6 h);
- -
- collecting data.
3.2. Characterization of Thermal Behavior of PCM-RB01 Microcapsules
4. Conclusions
- (1)
- Any building with a high thermal efficiency needs a wall with a high degree of thermal insulation that ensures minimal energy consumption. From this point of view, the storage of thermal energy in the wall is a key factor;
- (2)
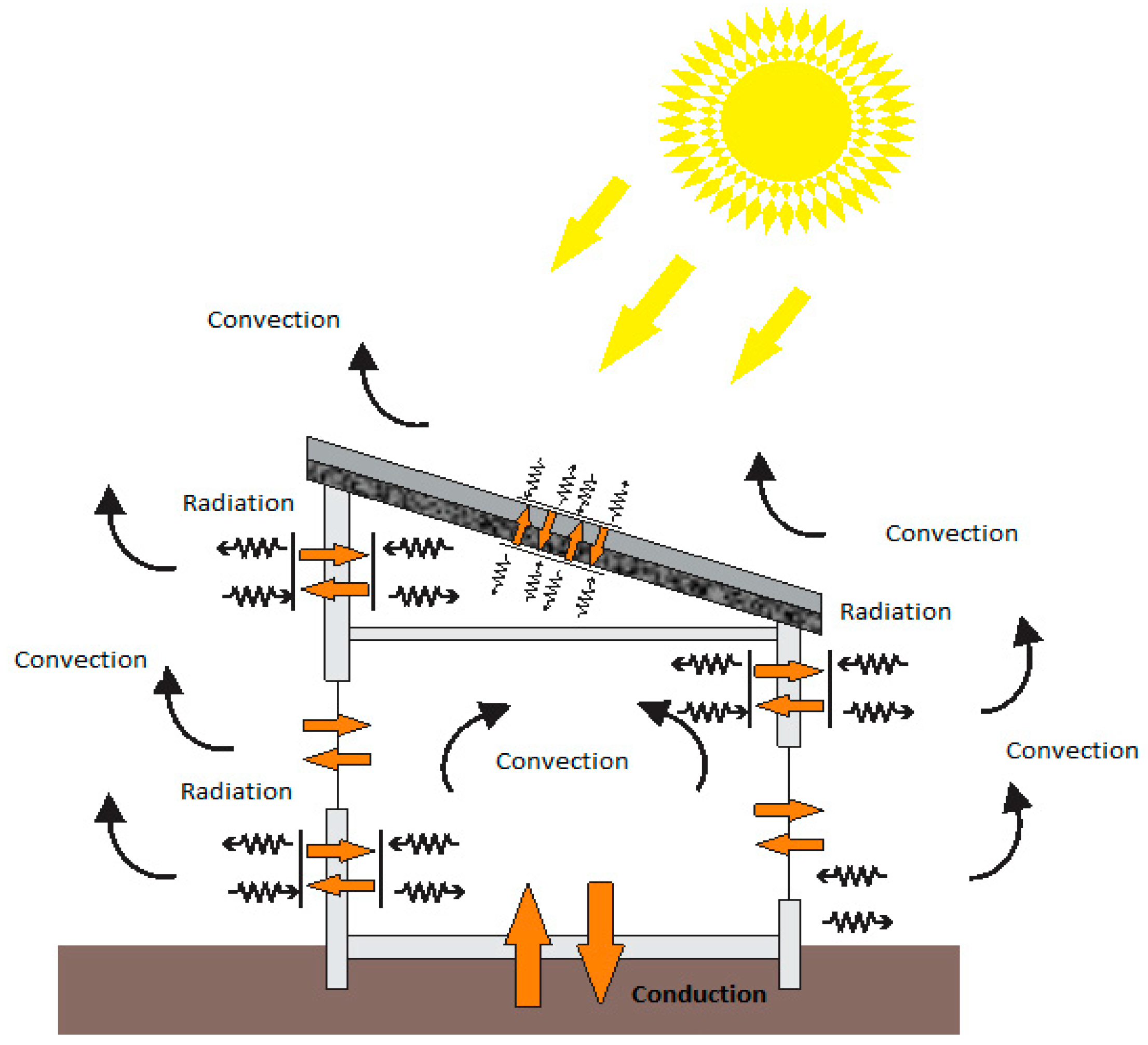
- Inside the building, the heat transfer process between walls and applicators is mainly achieved by free air convection upon contact with various surfaces and IR short wave radiation;
- (3)
- Use of PCMs ensures a reduction of thermal fluctuations on the inside by heat storage in the form of phase change;
- (4)
- The main factors in designing such systems are: the temperature limits between which the system must operate; the melting/solidification temperature of the PCM; latent heat of the PCM; degree of thermal loading; configuration of the PCM capsule bed;
- (5)
- Use of PCM micro-capsules can also be done by creating a “Solar Wall” where the incident solar radiation is absorbed by the PCM embedded in the wall, so the stored heat is used for heating and ventilating a house;
- (6)
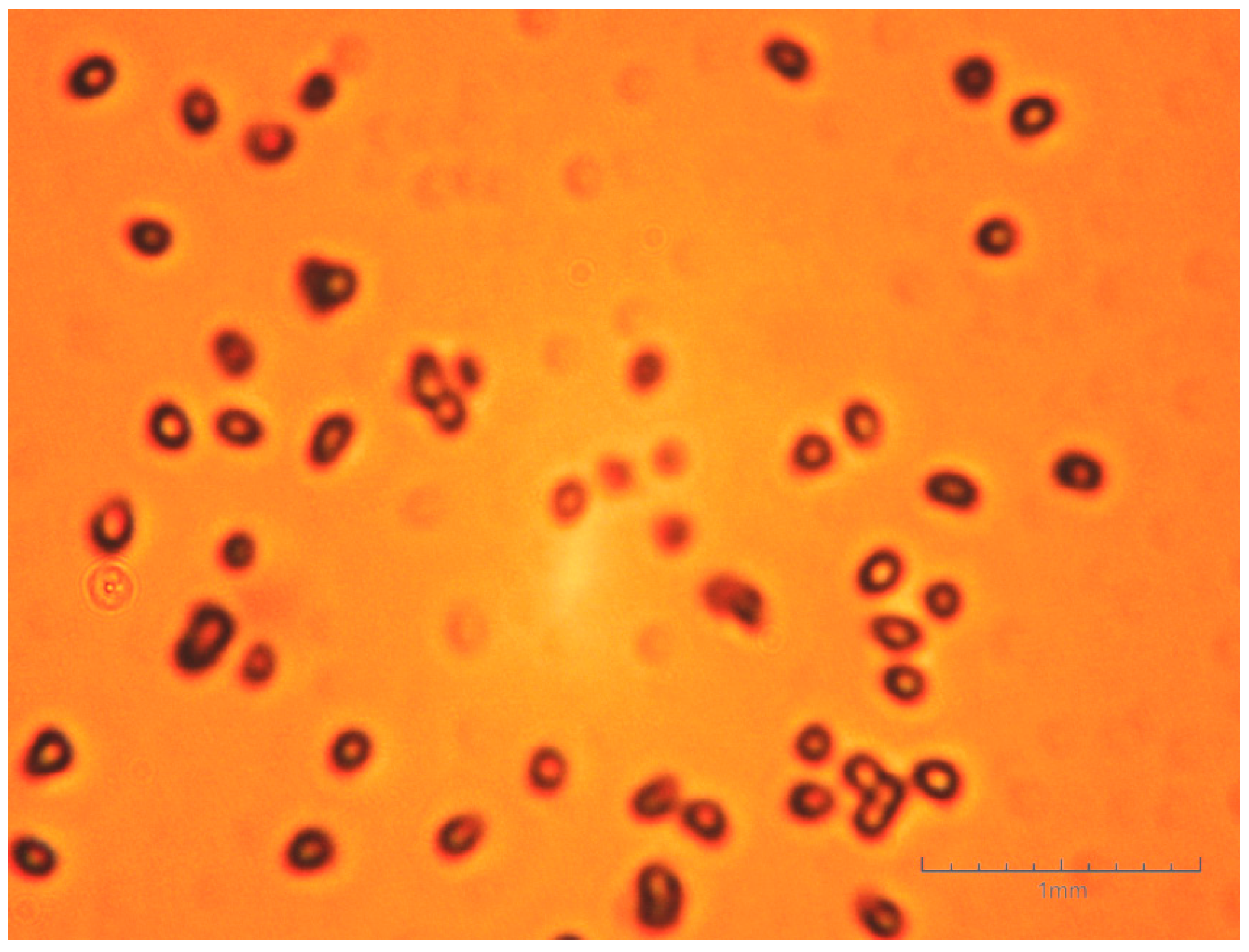
- The obtained butyl stearate microparticles are in the form of a white powder with a grain size of 0.5–3 mm and the constituent granules exhibit a high friability;
- (7)
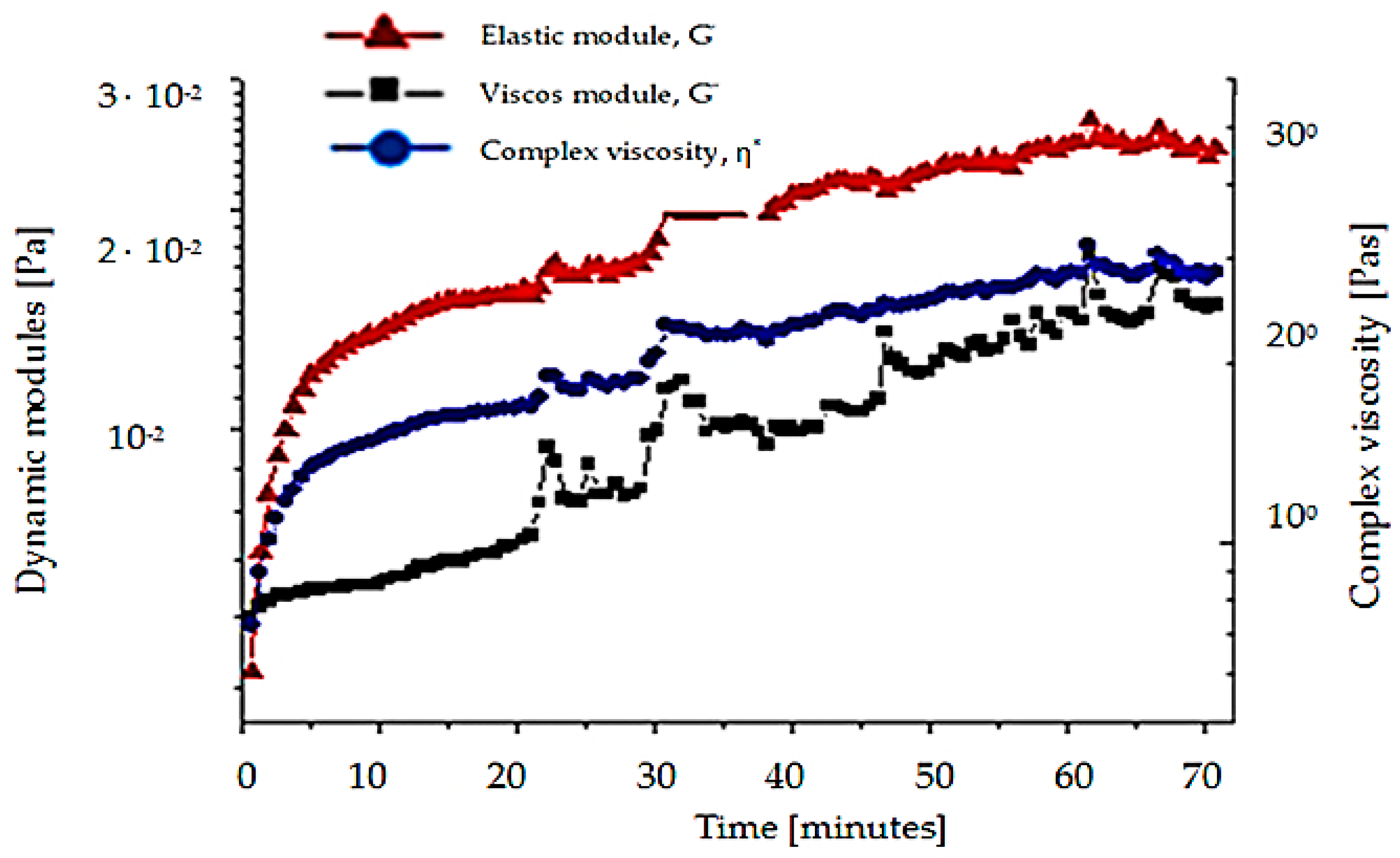
- Testing for butyl stearate has a complex viscosity 9 times greater than that of water; the viscous module being greater than the elastic modulus 10 times and all three sizes are approximately constant during the measurement;
- (8)
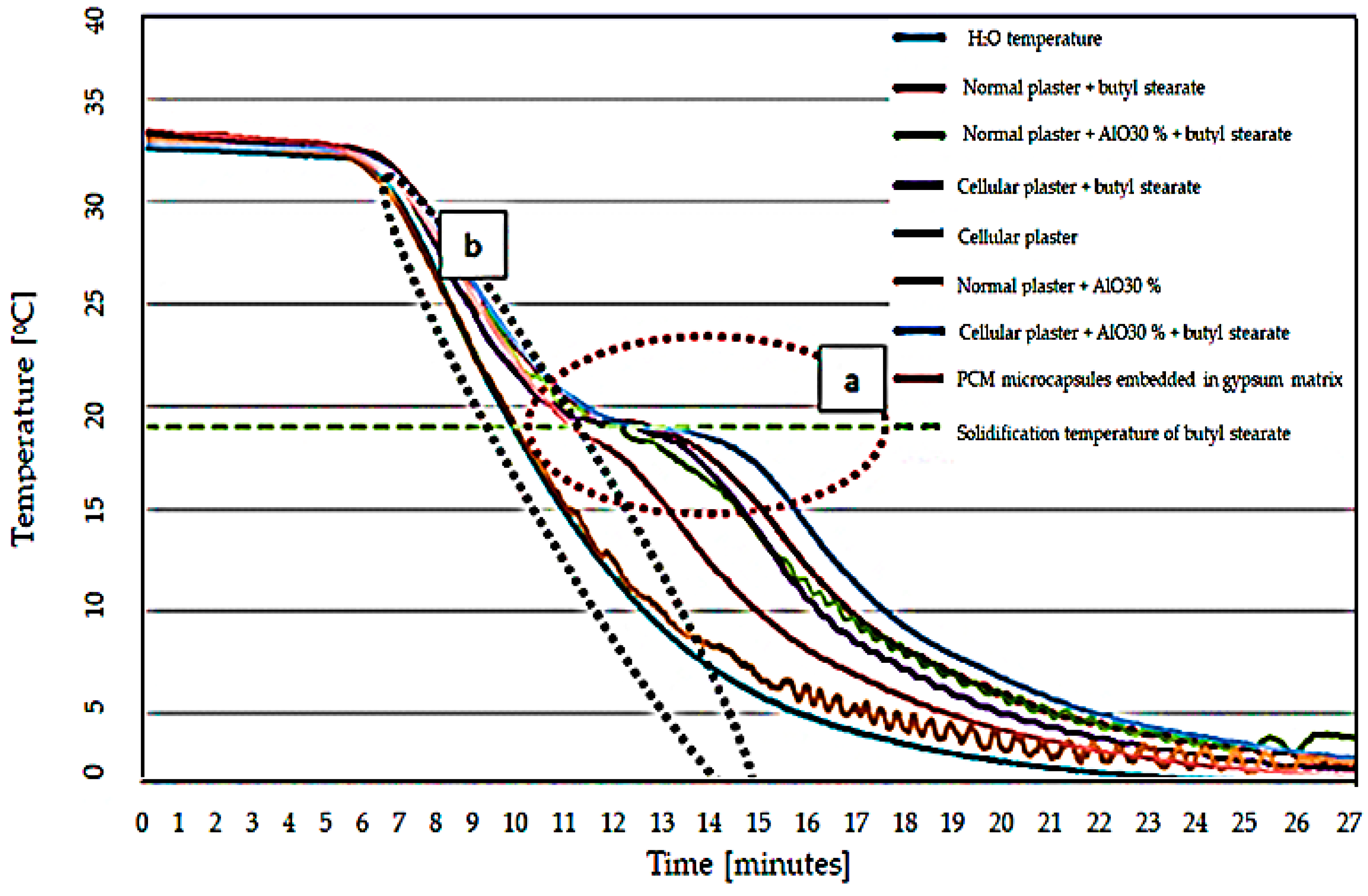
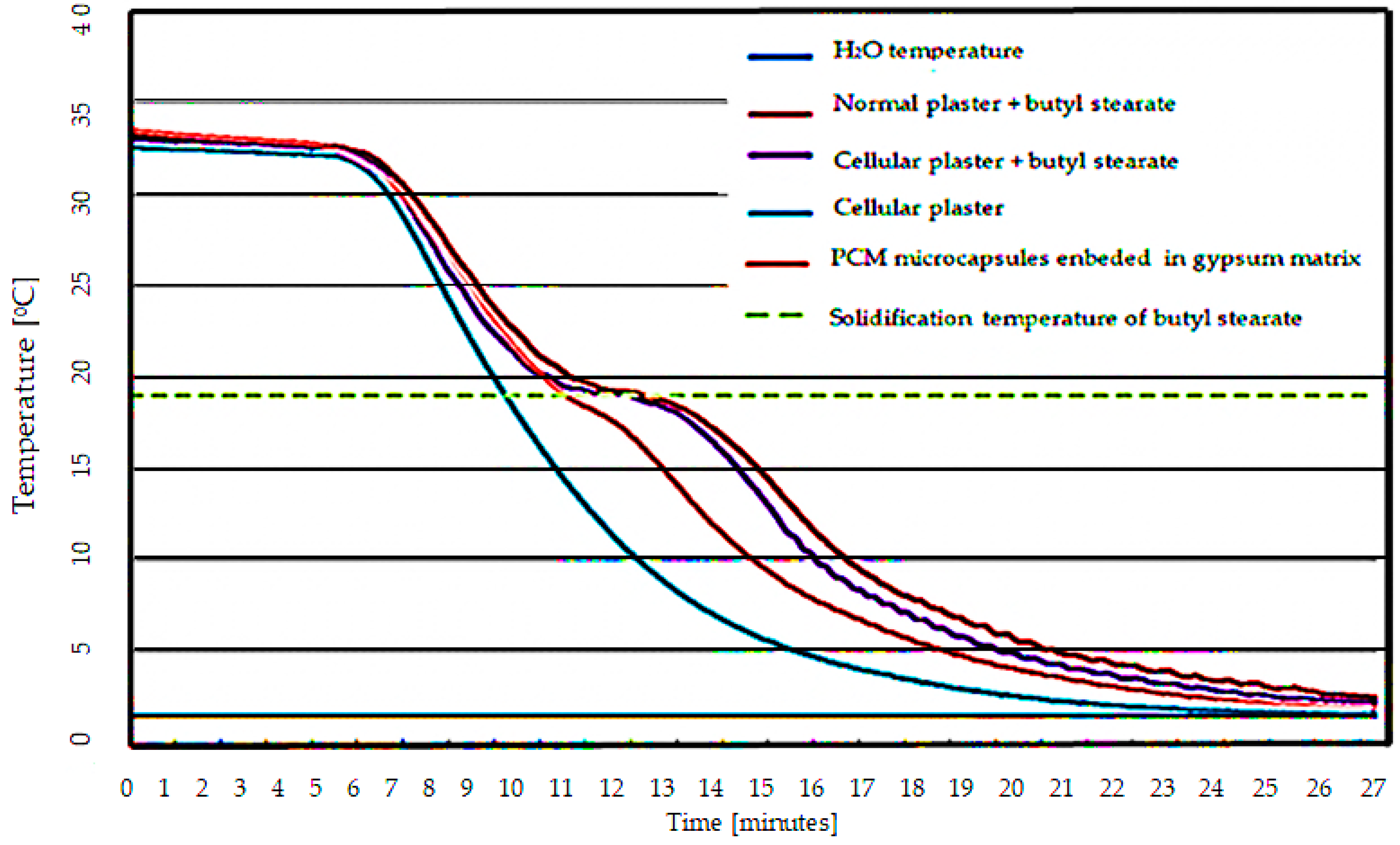
- Experimental results indicated a characteristic “S” type in the temperature variation plot for the butyl stearate-containing specimens, this form is explained through heat absorption at the phase change of the PCM material;
- (9)
- Although the thermal energy absorption capacity is lower for the developed material, it provides a net superior physical stability to the specimen compared to the classical types of integration;
- (10)
- Experimental research has shown that PCM developed material allows a maximum room temperature reduction of about 4 °C during the day and can reduce the night-time heating load;
- (11)
- Of the temperature variation graphs, a lesser thermal energy absorption capacity was observed for the PCM-RB01 containing sample compared to the vacuum-sucked butyl stearate specimen. This is explained by the lower packing factor (20.7% vs. 36%) for the PCM-RB01 microcapsule sample;
- (12)
- PCM material-free specimens did not exhibit a characteristic S-shape, the temperature of the specimen being characterized only by the sensible heat of the material;
- (13)
- The use of the PCM-RB01 material created in the thermal insulation of the buildings leads to a substantial reduction in energy consumption in both heating and cooling;
- (14)
- Despite the lower thermal energy absorption capacity, the developed PCM-RB01 material provides a superior physical stability to the specimen compared to the classical types of integration.
Author Contributions
Funding
Conflicts of Interest
References
- Kenisarin, M.; Mahkamov, K. Solar energy storage using phase change materials. Renew. Sustain. Energy Rev. 2007, 11, 1913–1965. [Google Scholar] [CrossRef]
- Ahmet, S.; Cemil, A.; Ali, K.; Orhan, U. Microencapsulated n-octacosane as a phase change material for thermal energy storage. Sol. Energy 2009, 83, 1757–1763. [Google Scholar]
- Bland, A.; Khzouz, M.; Statheros, T.; Gkanas, E.I. PCMs for Residential Building Applications: A Short Review Focused on Disadvantages and Proposals for Future Development. Buildings 2017, 7, 78. [Google Scholar] [CrossRef]
- Branko, Š. Smart Crack Control in Concrete through Use of Phase Change Materials (PCMs): A Review. Materials 2018, 11, 654. [Google Scholar]
- Alawadhi, E.M. Thermal analysis of building brick containing phase change material. Energy Build. 2008, 40, 351–357. [Google Scholar] [CrossRef]
- Chung, M.H.; Park, J.C. An Experimental Study on the Thermal Performance of Phase-Change Material and Wood-Plastic Composites for Building Roofs. Energies 2017, 10, 195. [Google Scholar] [CrossRef]
- Bendic, R.; Amza, G. Encapsulation of butyl stearate as a phase change material for thermal energy storage in intelligent building walls. In Proceedings of the 4th International Conference on Structural Analysis of Advanced Materials, ICSAAM, Sinaia, Romania, 7–11 September 2011. [Google Scholar]
- Schossig, P.; Henning, H.-M.; Gschwander, S.; Haussmann, T. Micro-encapsulated phase-change materials integrated into building materials. Sol. Energy Mater. Sol. Cells 2005, 89, 297–306. [Google Scholar] [CrossRef]
- Tyagi, V.V.; Buddhi, D. PCM thermal storage in buildings: A state of art. Renew. Sustain. Energy Rev. 2007, 11, 1146–1166. [Google Scholar] [CrossRef]
- Amza, G.; Milica, A.; Bendic, R. Contributions on the use of ultrasonic remaking process of printing plates. In Proceedings of the Annual Symposium of the Institute of Solid Mechanics SISOM 2010 and Session of the Commission of Acoustics, Bucharest, Romania, 27–28 May 2010. [Google Scholar]
- Zhang, Y.; Zhou, G.; Lin, K.; Zhang, Q.; Di, H. Application of latent thermal energy storage in buildings: State-of-the-art and outlook. Build. Environ. 2007, 42, 2197–2209. [Google Scholar] [CrossRef]
- Chen, F. Leakage Control and Characterization of Form Stable Phase Change Materials: Polymer (Matrix)/Polymer (PCM) Binary Blends and Natural Fiber/Polymer(Matrix)/Polymer (PCM) Ternary Composites; Washington State University: Pullman, WA, USA, 2013; Volume 131. [Google Scholar]
- Chen, F.; Wolcott, M.P. Miscibility studies of paraffin/polyethylene blends as form-stable phase change materials. Eur. Polym. J. 2014, 52, 44–52. [Google Scholar] [CrossRef]
- Khudhair, A.M.; Farid, M.M. A review on energy conservation in building applications with thermal storage by latent heat using phase change materials. Energy Convers. Manag. 2004, 45, 263–275. [Google Scholar] [CrossRef]
- Chen, F.; Wolcott, M.P. Polyethylene/paraffin binary composites for phase change material energy storage in building: A morphology, thermal properties, and paraffin leakage study. Sol. Energy Mater. Sol. Cells 2015, 137, 79–85. [Google Scholar] [CrossRef]
- Rufuss, D.D.W.; Suganthi, L.; Iniyan, S.; Davies, P.A. Effects of nanoparticle-enhanced phase change material (NPCM) on solar still productivity. J. Clean. Prod. 2018, 192, 9–29. [Google Scholar] [CrossRef]
- Beginn, U. Applicability of frozen gels from ultrahigh molecular weight polyethylene and paraffin waxes as shape persistent solid/liquid phase change materials. Macromol. Mater. Eng. 2003, 288, 245–251. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, C.Y.; Tian, Y. Review on thermal energy storage with phase change materials (PCMs) in building applications. Appl. Energy 2012, 92, 593–605. [Google Scholar] [CrossRef]
- Johan, H.; Chris, B.; Viktoria, M. Combining thermal energy storage with buildings—A review. Renew. Sustain. Energy Rev. 2015, 42, 1305–1325. [Google Scholar]
- Gracia, A.; Cabeza, L. Phase change materials and thermal energy storage for buildings. Energy Build. 2015, 103, 414–419. [Google Scholar] [CrossRef]
- Ye, R.; Fang, X.; Zhang, Z.; Gao, X. Preparation, Mechanical and Thermal Properties of Cement Board with Expanded Perlite Based Composite Phase Change Material for Improving Buildings Thermal Behavior. Materials 2015, 8, 7702–7713. [Google Scholar] [CrossRef] [PubMed]
- Konuklu, Y.; Ostry, M.; Paksoy, O.H.; Charvat, P. Review on using microencapsulated phase change materials (PCM) in building applications. Energy Build. 2015, 106, 134–155. [Google Scholar] [CrossRef]
- Vyas, G.S.; Jha, K.N. Benchmarking green building attributes to achieve cost effectiveness using a data envelopment analysis. Sustain. Cities Soc. 2017, 28, 127–134. [Google Scholar] [CrossRef]
- Rwei, S.P.; Tuan, H.N.; Chiang, W.Y.; Way, T.F. Synthesis and Characterization of pH and Thermo Dual-Responsive Hydrogels with a Semi-IPN Structure Based on N-Isopropylacrylamide and Itaconamic Acid. Materials 2018, 11, 696. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.R.; Roman, J.S. Smart Polymers and Their Applications; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kumar, A.; Srivastava, A.; Galaev, I.Y.; Mattiasson, B. Smart polymers: Physical forms and bioengineering applications. Prog. Polym. Sci. 2007, 32, 1203–1237. [Google Scholar] [CrossRef]
- Guillame-Gentil, O.; Semeno, O.; Roca, A.S.; Groth, T.; Zahn, R.; Voros, J.; Zenobi Wong, M. Engineering the extracellular environment: Strategies for building 2D and 3D cellular structures. Adv. Mater. 2010, 22, 5443–5462. [Google Scholar] [CrossRef] [PubMed]
- Alam, T.E. Experimental Investigation of Encapsulated Phase Change Materials for Thermal Energy Storage. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2015. [Google Scholar]
- Guarino, F.; Longo, S.; Ceilura, M.; Mistreta, M.; La Rocca, V. Phase Change Materials Applications to Optimize Cooling Performance of Buildings in the Mediterranean Area: A Parametric Analysis. Energy Procedia 2015, 78, 1708–1713. [Google Scholar] [CrossRef]
- Memon, S.A.; Liao, W.; Yang, S.; Cui, H.; Shah, S.F.A. Development of Composite PCMs by Incorporation of Paraffin into Various Building Materials. Materials 2015, 8, 499–518. [Google Scholar] [CrossRef] [PubMed]
- Farnam, Y.; Krafc, M.; Liston, L.; Washington, T.; Erk, K.; Tao, B.; Weiss, W.J. Evaluating the use of phase change materials in concrete pavement to melt ice and snow. J. Mater. Civ. Eng. 2015, 28, 04015161. [Google Scholar] [CrossRef]
- Yang, H.; Memon, S.A.; Bao, X.; Cui, H.; Li, D. Design and Preparation of Carbon Based Composite Phase Change Material for Energy Piles. Materials 2017, 10, 391. [Google Scholar] [CrossRef] [PubMed]
- Amza, G.; Bendic, R. Utilization of ultrasound emulsion in complex coacervation of polymeric microcapsules. In Proceedings of the Annual Symposium of the Institute of Solid Mechanics SISOM 2011 and Session of the Commission of Acoustics, Bucharest, Romania, 25–26 May 2011. [Google Scholar]
- Aguayo, M.; Das, S.; Castro, C.; Kabay, N.; Sant, G.; Neithalath, N. Porous inclusions as hosts for phase change materials in cementitious composites: Characterization, thermal performance, and analytical models. Constr. Build. Mater. 2017, 134, 574–584. [Google Scholar] [CrossRef]
- Norvell, C.; Sailor, D.J.; Dusicka, P. The effect of microencapsulated phase-change material on the compressive strength of structural concrete. J. Green Build. 2013, 8, 116–124. [Google Scholar] [CrossRef]








| The Phases of Micro-Encapsulation Process | Time | Components | Quantity |
|---|---|---|---|
| Emulsification I | 30 min | Water | 100 mL |
| Butyl stearate | 25 g | ||
| Pluronic PE6200 | 2 g | ||
| Emulsification II | 30 min | EM1 | - |
| PMMA | 25 g | ||
| alil-MMA | 2.5 g | ||
| Sol. FeSO4-7H2O | 1 mL | ||
| Ammonium persulphate | 0.25 g | ||
| Emulsification III | 1 h | EM2 | - |
| Na2S2O7 | 0.25 g | ||
| AZDN | 1 g | ||
| Precipitation | 6–8 h | - | - |
| Dry precipitation | 24–36 h | - | - |
| No. Sample | Sample | Method of Integrating PCM Material | Mass of Sample before Insertion of PCM Material [g] | Mass of Specimen after Insertion of PCM Material [g] | Packaging Report |
|---|---|---|---|---|---|
| 1 | Expanded plaster | n.a. | 68.2 | 68.2 | 0.0% |
| 2 | Expanded plaster + Butyl stearate | Soaking under vacuum | 67.8 | 90.7 | 33.8% |
| 3 | Expanded plaster + AlO 30% | n.a. | 73.2 | 73.2 | 0.0% |
| 4 | Expanded plaster+ AlO 30% + Butyl stearate | n.a. | 79.2 | 97.2 | 22.7% |
| 5 | Plaster + Butyl stearate | Soaking under vacuum | 70.8 | 96.3 | 36.0% |
| 6 | Plaster + AlO 30% + Butyl stearate | Soaking under vacuum | 73.6 | 97.6 | 32.6% |
| 7 | PMMA microcapsules embedded in plaster | Microcapsule blend before casting | 61.1 | 95.42 | 13.3% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bendic, V.; Dobrotă, D. Theoretical and Experimental Contributions on the Use of Smart Composite Materials in the Construction of Civil Buildings with Low Energy Consumption. Energies 2018, 11, 2310. https://doi.org/10.3390/en11092310
Bendic V, Dobrotă D. Theoretical and Experimental Contributions on the Use of Smart Composite Materials in the Construction of Civil Buildings with Low Energy Consumption. Energies. 2018; 11(9):2310. https://doi.org/10.3390/en11092310
Chicago/Turabian StyleBendic, Vasile, and Dan Dobrotă. 2018. "Theoretical and Experimental Contributions on the Use of Smart Composite Materials in the Construction of Civil Buildings with Low Energy Consumption" Energies 11, no. 9: 2310. https://doi.org/10.3390/en11092310
APA StyleBendic, V., & Dobrotă, D. (2018). Theoretical and Experimental Contributions on the Use of Smart Composite Materials in the Construction of Civil Buildings with Low Energy Consumption. Energies, 11(9), 2310. https://doi.org/10.3390/en11092310






