Numerical Modeling and Validation of a Novel 2D Compositional Flooding Simulator Using a Second-Order TVD Scheme
Abstract
1. Introduction
1.1. Previous Numerical Work
1.2. Aim of this Work
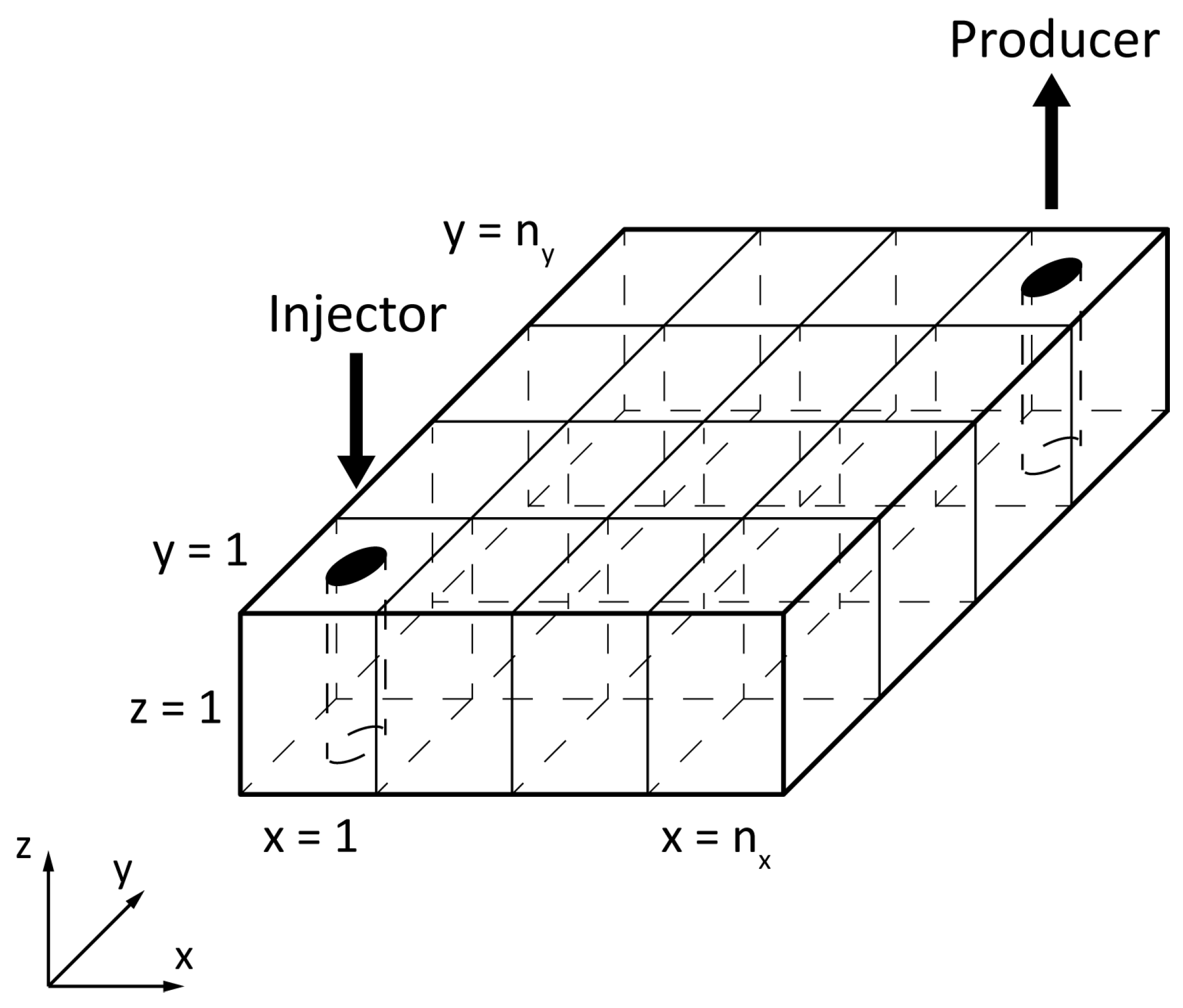
2. Physical Model
3. Mathematical Model
3.1. Flow Equations
3.2. Physical Properties
3.2.1. Residual Saturation
3.2.2. Relative Permeabilities
3.2.3. Capillary Pressure
3.3. Boundary Conditions
3.4. Discretization of the Partial Differential Equations
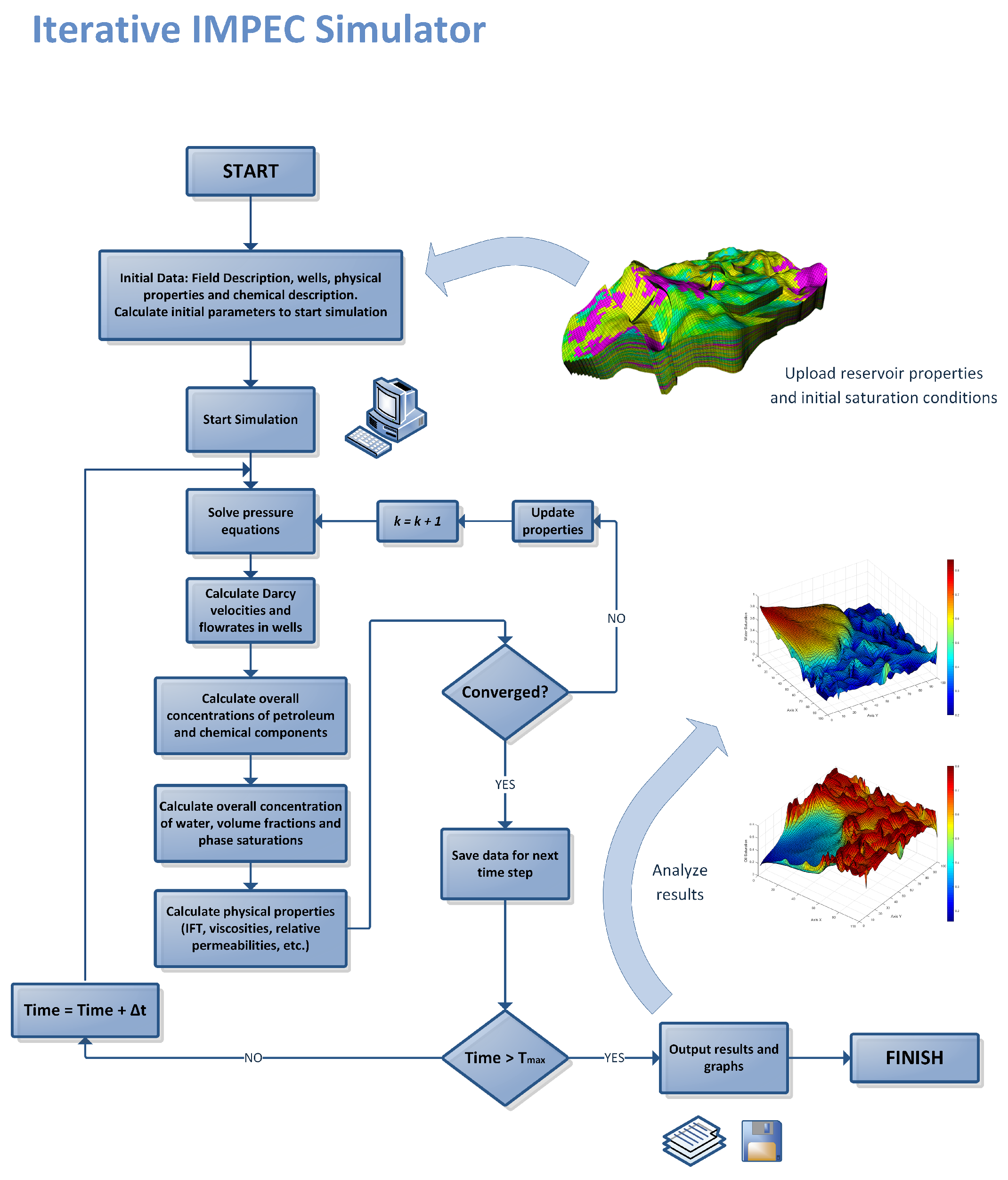
3.5. Solution Algorithm
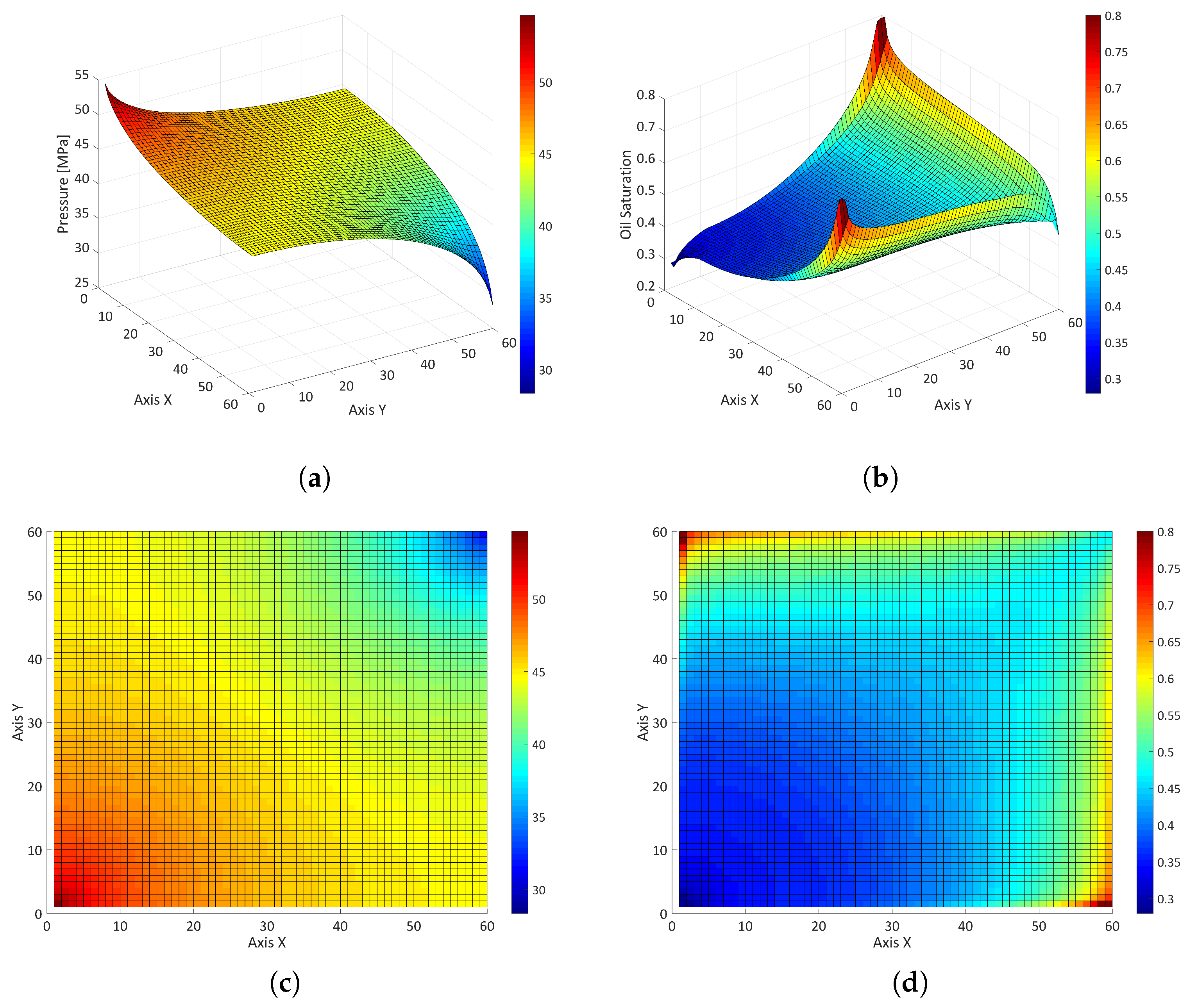
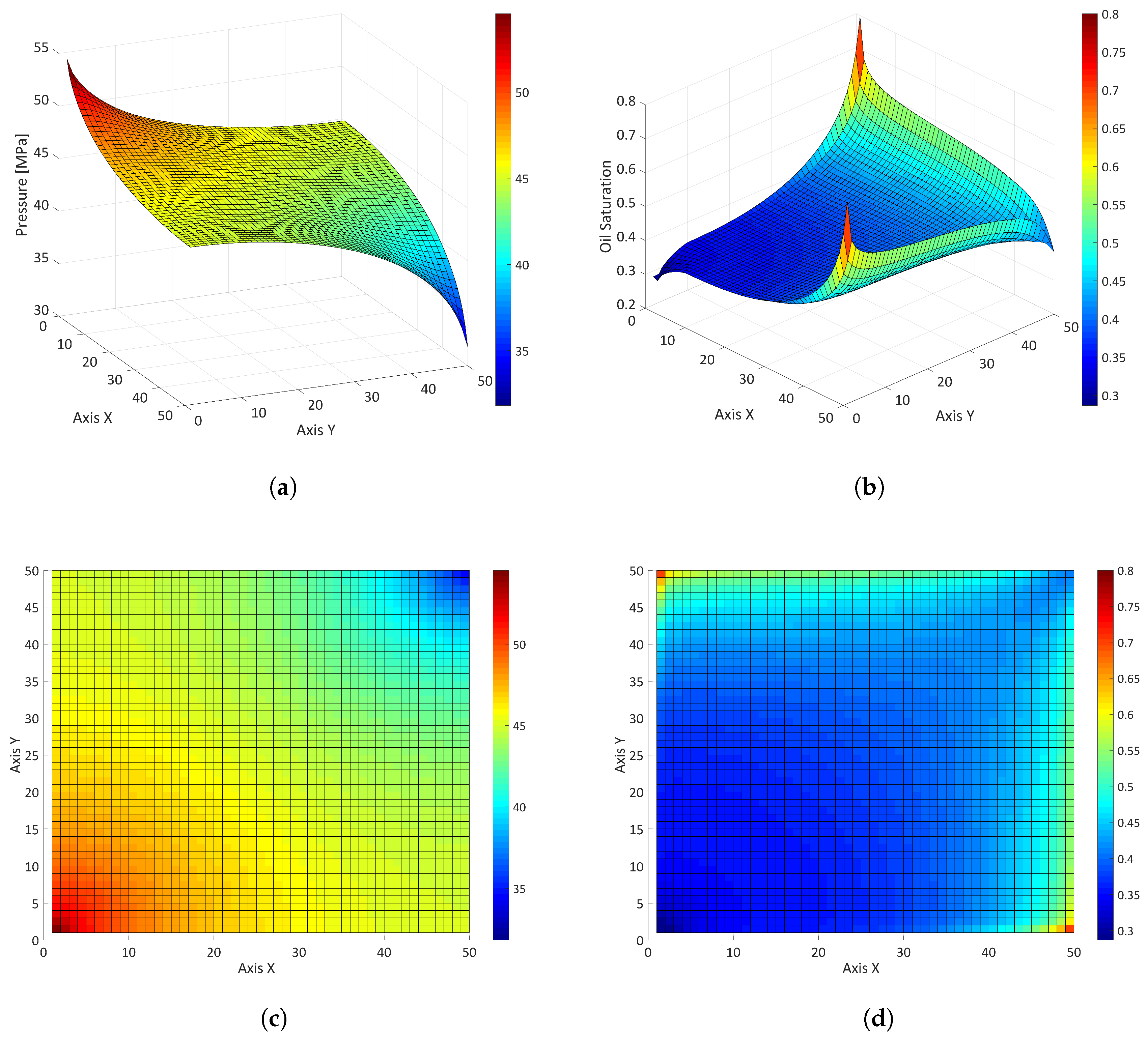
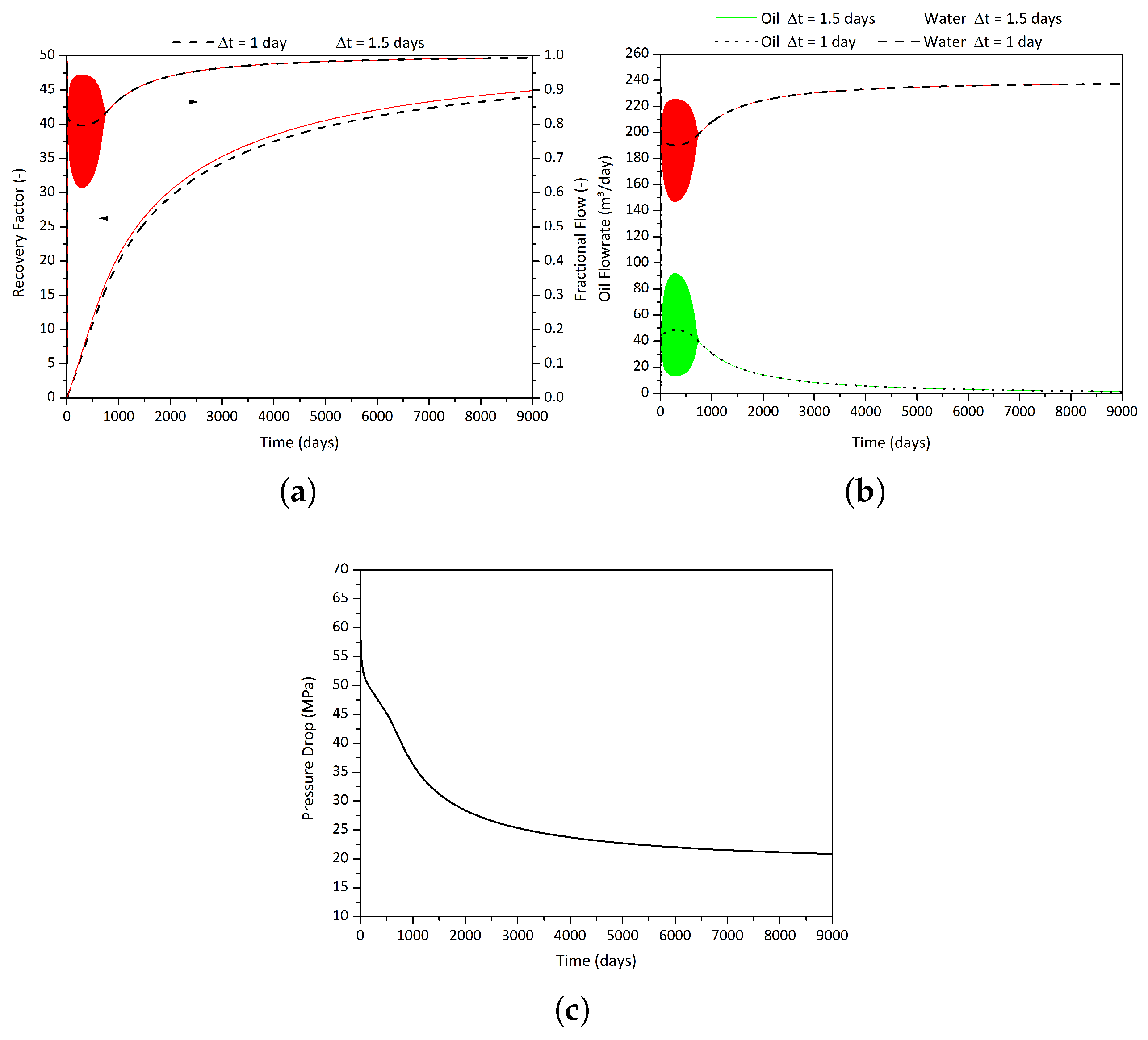
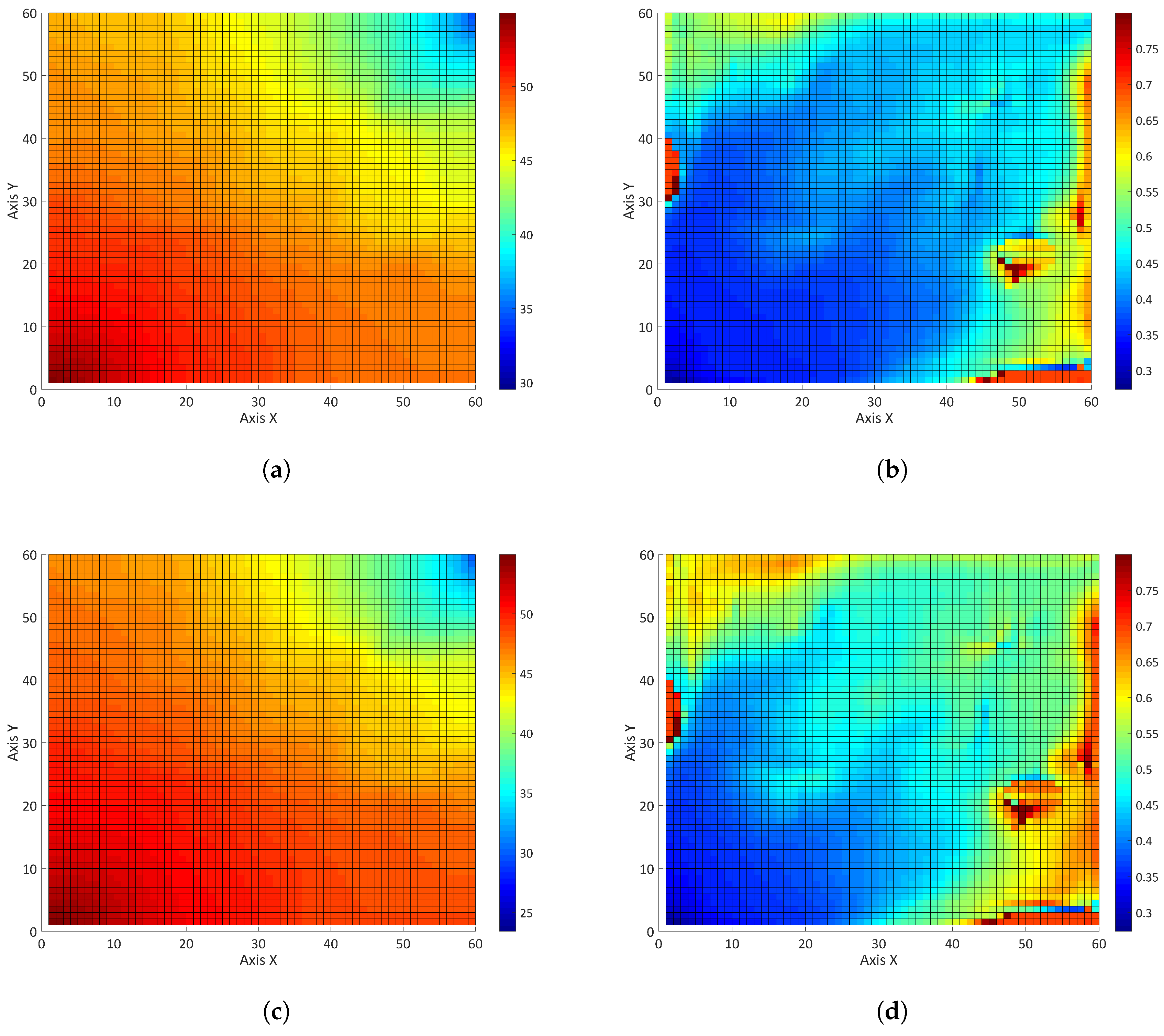
4. Results and Discussion
4.1. Data
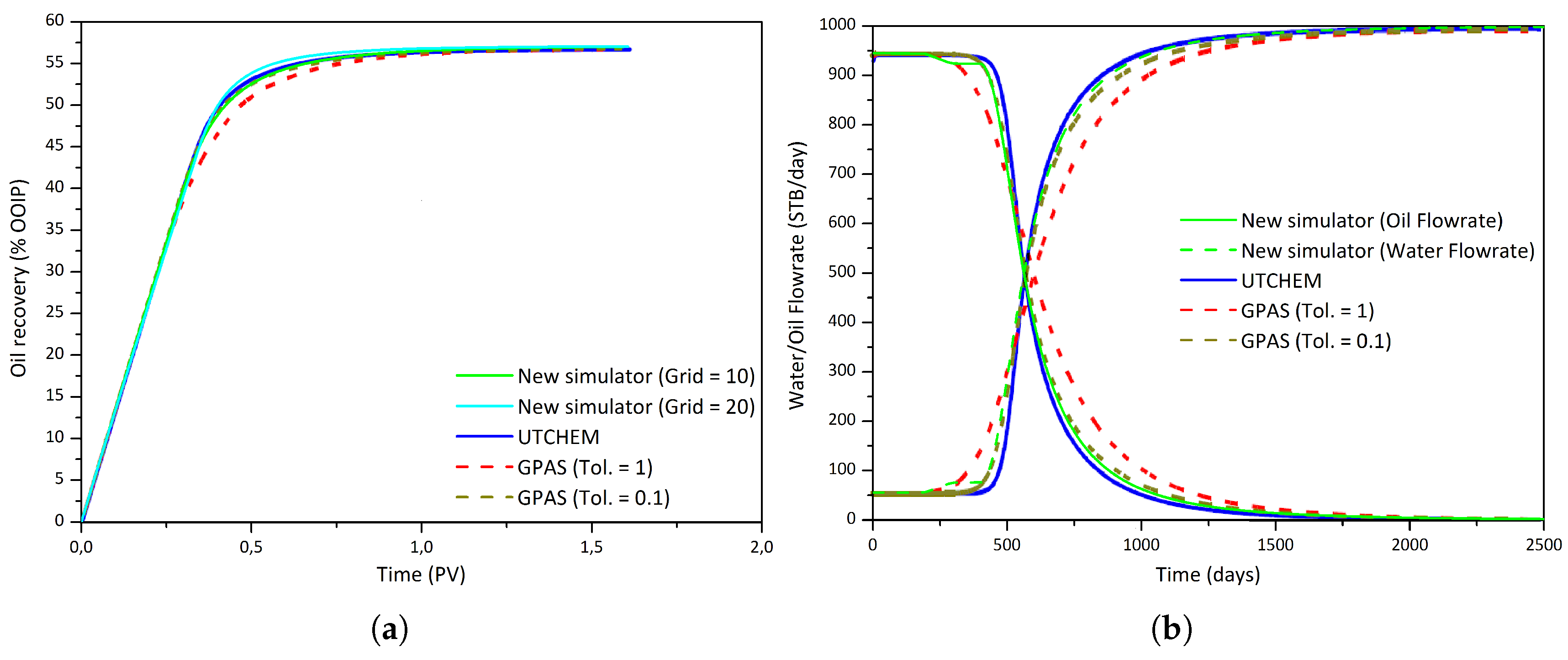
4.2. Validation of the Model
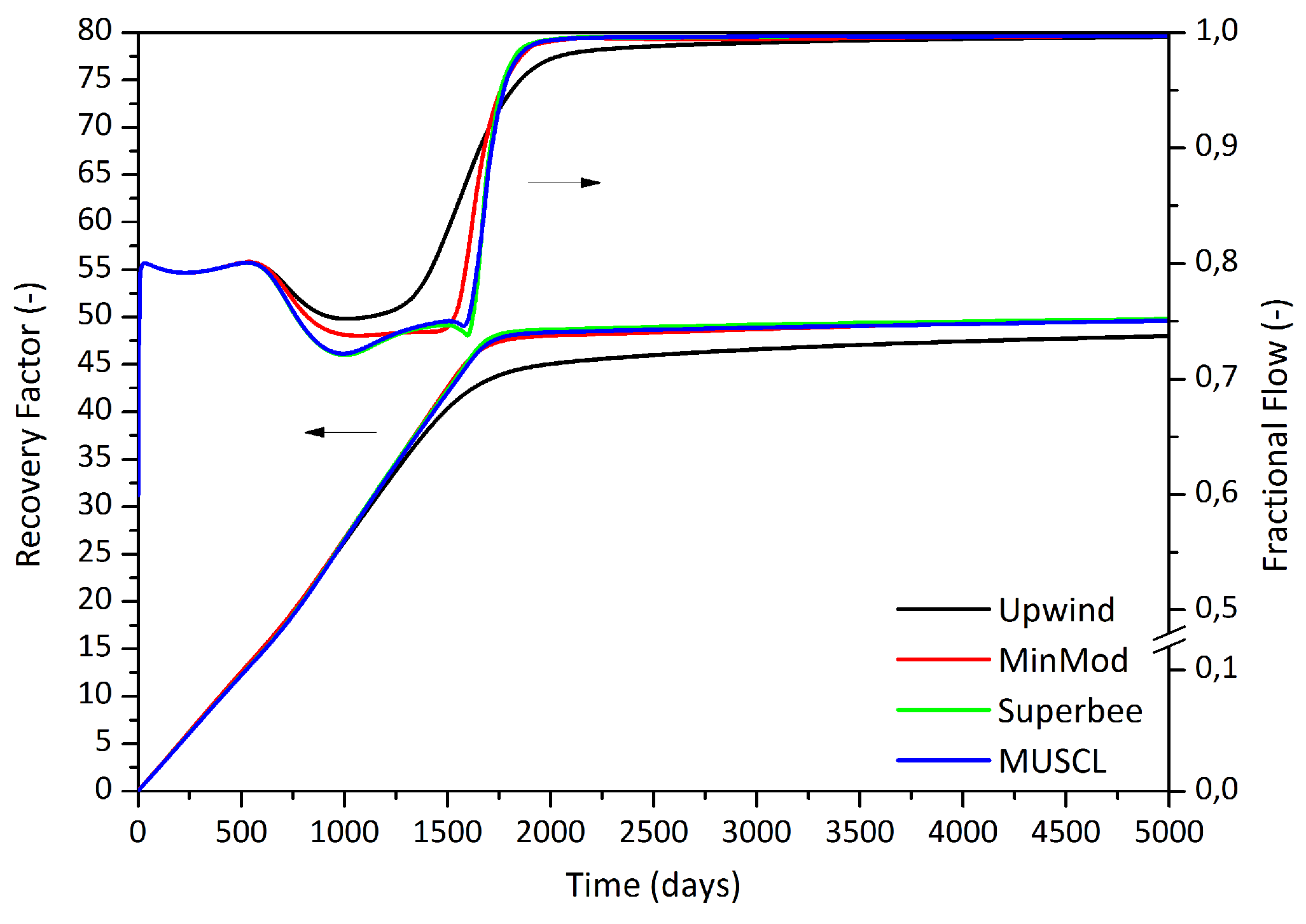
4.3. Waterflooding
4.3.1. Iterative Process
4.3.2. Non-Iterative Process
4.3.3. Random Permeability Field
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EOR | Enhanced Oil Recovery |
| TDS | Total Dissolved Solids |
| IAPV | Inaccessible Pore Volume |
| FENE | Finite non-Linear Elastic |
| UCM | Upper Convected Maxwell |
| TVD | Total Variation Diminishing |
| PDE | Partial Differential Equation |
| IFT | Interfacial Tension |
| REV | Representative Elementary Volume |
| IMPES | Implicit in Pressure, Explicit in Saturation |
| IMPEC | Implicit in Pressure, Explicit in Concentration |
| OOIP | Original Oil in Place |
| CFL | Courant-Friedrichs-Lewy |
Nomenclature
| Courant Number | Interfacial Tension [mN/m] | |||
| Dispersion Tensor | Reservoir Domain | |||
| Molecular Diffusion [m/s] | ||||
| Longitudinal Dispersion [m/s] | Superscripts | |||
| Transversal Dispersion [m/s] | a | Aqueous Phase | ||
| Flux Limiter Function | H | Water-Oil System (no Chemical) | ||
| Relative Permeability | j | Phase | ||
| p | Reservoir Pressure [Pa] | Iteration Number | ||
| Bottomhole Pressure [Pa] | Time-Step | |||
| r | Volumetric Concentration Gradient | o | Oleous Phase | |
| Well Radius [m] | r | Residual | ||
| S | Phase Saturation | |||
| s | Well Skin Factor | Subscripts | ||
| V | Volumetric Concentration | c | Chemical Component | |
| z | Overall Concentration | i | Component | |
| Injection | ||||
| Greek Letters | Spatial Grid Blocks | |||
| Domain Boundary | p | Petroleum Component | ||
| Kronecker Delta | t | Total | ||
| Phase Mobility [m/(Pa·s)] | w | Water Component | ||
| Absolute Viscosity [Pa·s] | ||||
Appendix A. Discretization of the PDE
References
- IEA. Resources to Reserves; Organisation for Economic Co-operation and Development: Paris, France, 2013; ISBN 978-9-26408-354-7. [Google Scholar] [CrossRef]
- Dake, L.P. Fundamentals of Reservoir Engineering; Elsevier: Amsterdam, The Netherlands, 1978; ISBN 0-444-41830-X. [Google Scholar]
- Lake, L.W. Enhanced Oil Recovery; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1989; ISBN 0-13-281601-6. [Google Scholar]
- Green, D.W.; Willhite, G.P. Enhanced Oil Recovery; Society of Petroleum Engineers: Richardson, TX, USA, 1989; ISBN 978-1-55563-077-5. [Google Scholar]
- Druetta, P.; Tesi, P.; Persis, C.D.; Picchioni, F. Methods in Oil Recovery Processes and Reservoir Simulation. Adv. Chem. Eng. Sci. 2016, 6, 39. [Google Scholar] [CrossRef]
- Donaldson, E.C.; Chilingarian, G.V.; Yen, T.F. Enhanced Oil Recovery, I: Fundamentals and Analyses; Elsevier Science: Amsterdam, The Netherlands, 1985; ISBN 978-0-08086-872-1. [Google Scholar]
- Baehr, A.; Corapcioglu, M. A Compositional Multiphase Model for Groundwater Contamination by Petroleum-Products. 1. Theoretical Considerations. Water Resour. Res. 1987, 23, 191–200. [Google Scholar] [CrossRef]
- Baehr, A.; Corapcioglu, M. A Compositional Multiphase Model for Groundwater Contamination by Petroleum-Products. 2. Numerical-Solution. Water Resour. Res. 1987, 23, 201–213. [Google Scholar] [CrossRef]
- Smaoui, H.; Zouhri, L.; Ouahsine, A. Flux-limiting techniques for simulation of pollutant transport in porous media: Application to groundwater management. Math. Comput. Model. 2008, 47, 47–59. [Google Scholar] [CrossRef]
- Wang, B.; Bauer, S. Pressure response of large-scale compressed air energy storage in porous formations. Energy Procedia 2017, 125, 588–595. [Google Scholar] [CrossRef]
- Peter, B.; Johannes, K.; Robert, S.; Mary, W. Simulation of Flow in Porous Media, Applications in Energy and Environment; De Gruyter: Berlin, Germany, 2013; ISBN 978-3-11-028224-5. [Google Scholar] [CrossRef]
- Ahusborde, E.; Ossmani, M.E. A sequential approach for numerical simulation of two-phase multicomponent flow with reactive transport in porous media, 2017. Math. Comput. Simul. 2017, 137, 71–89. [Google Scholar] [CrossRef]
- Sleep, B.E. A method of characteristics model for equation of state compositional simulation of organic compounds in groundwater. J. Contam. Hydrol. 1995, 17, 189–212. [Google Scholar] [CrossRef]
- Lake, L.; Pope, G.; Carey, G.; Sepehrnoori, K. Isothermal, Multiphase, Multicomponent Fluid-Flow in Permeable Media. 1. Description and Mathematical Formulation. In Situ 1984, 8, 1–40. [Google Scholar]
- Pope, G.A.; Carey, G.F.; Sepehrnoori, K. Isothermal, Multiphase, Multicomponent Fluid-Flow in Permeable Media. 2. Numerical Techniques and Solution. In Situ 1984, 8, 41–97. [Google Scholar]
- Helfferich, F. Theory of Multicomponent, Multiphase Displacement in Porous-Media. Soc. Pet. Eng. J. 1981, 21, 51–62. [Google Scholar] [CrossRef]
- Fleming, P.; Thomas, C.; Winter, W. Formulation of a General Multiphase, Multicomponent Chemical Flood Model. Soc. Pet. Eng. J. 1981, 21, 63–76. [Google Scholar] [CrossRef]
- Hirasaki, G.J. Application of the Theory of Multicomponent, Multiphase Displacement to 3-Component, 2-Phase Surfactant Flooding. Soc. Pet. Eng. J. 1981, 21, 191–204. [Google Scholar] [CrossRef]
- Li, Z.; Luo, H.; Bhardwaj, P.; Wang, B.; Delshad, M. Modeling dynamic fracture growth induced by non-Newtonian polymer injection. J. Pet. Sci. Eng. 2016, 147, 395–407. [Google Scholar] [CrossRef]
- Bao, K.; Lie, K.A.; Moyner, O.; Liu, M. Fully implicit simulation of polymer flooding with MRST. Computat. Geosci. 2017, 21, 1219–1244. [Google Scholar] [CrossRef]
- Krogstad, S.; Lie, K.A.; Nilsen, H.M.; Berg, C.F.; Kippe, V. Efficient flow diagnostics proxies for polymer flooding. Computat. Geosci. 2017, 21, 1203–1218. [Google Scholar] [CrossRef]
- Mykkeltvedt, T.S.; Raynaud, X.; Lie, K.A. Fully implicit higher-order schemes applied to polymer flooding. Computat. Geosci. 2017, 21, 1245–1266. [Google Scholar] [CrossRef]
- Delshad, M.; Pope, G.; Sepehrnoori, K. UTCHEM Version 9.0 Technical Documentation; Center for Petroleum and Geosystems Engineering, The University of Texas at Austin: Austin, TX, USA, 2000; Volume 78751. [Google Scholar]
- Bourgeat, A.; Granet, S.; Smai, F. Compositional two-phase flow in saturated–unsaturated porous media: benchmarks for phase appearance/disappearance. In Simulation of Flow in Porous Media Applications in Energy and Environment; Bastian, P., Kraus, J., Scheichl, R., Wheeler, M., Eds.; De Gruyter: Berlin, Germany, 2013; pp. 81–106. ISBN 978-3-11-028224-5. [Google Scholar]
- Braconnier, B.; Preux, C.; Flauraud, E.; Tran, Q.H.; Berthon, C. An analysis of physical models and numerical schemes for polymer flooding simulations. Computat. Geosci. 2017, 21, 1267–1279. [Google Scholar] [CrossRef]
- Cao, R.; Cheng, L.; Lian, P. Flow Behavior of Viscoelastic Polymer Solution in Porous Media. J. Dispers. Sci. Technol. 2015, 36, 41–50. [Google Scholar] [CrossRef]
- Dang, C.; Nghiem, L.; Nguyen, N.; Chen, Z.; Nguyen, Q. Evaluation of CO2 Low Salinity Water-Alternating-Gas for enhanced oil recovery. J. Nat. Gas Sci. Eng. 2016, 35, 237–258. [Google Scholar] [CrossRef]
- Ebaga-Ololo, J.; Chon, B.H. Prediction of Polymer Flooding Performance with an Artificial Neural Network: A Two-Polymer-Slug Case. Energies 2017, 10, 844. [Google Scholar] [CrossRef]
- Hilden, S.T.; Moyner, O.; Lie, K.A.; Bao, K. Multiscale Simulation of Polymer Flooding with Shear Effects. Transp. Porous Media 2016, 113, 111–135. [Google Scholar] [CrossRef]
- Janiga, D.; Czarnota, R.; Stopa, J.; Wojnarowski, P.; Kosowski, P. Performance of nature inspired optimization algorithms for polymer Enhanced Oil Recovery process. J. Pet. Sci. Eng. 2017, 154, 354–366. [Google Scholar] [CrossRef]
- Lotfollahi, M.; Farajzadeh, R.; Delshad, M.; Al-Abri, A.K.; Wassing, B.M.; Al-Mjeni, R.; Awan, K.; Bedrikovetsky, P. Mechanistic Simulation of Polymer Injectivity in Field Tests. SPE J. 2016, 21, 1178–1191. [Google Scholar] [CrossRef]
- Lotfollahi, M.; Koh, H.; Li, Z.; Delshad, M.; Pope, G.A. Mechanistic Simulation of Residual Oil Saturation in Viscoelastic Polymer Floods. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 21–23 March 2016. [Google Scholar] [CrossRef]
- Bidner, M.S.; Savioli, G.B. On the Numerical Modeling for Surfactant Flooding of Oil Reservoirs. Mecanica Comput. 2002, XXI, 566–585. [Google Scholar]
- Jonsson, K.; Jonsson, B. Fluid-Flow in Compressible Porous-Media. 1. Steady-State Conditions. AIChE J. 1992, 38, 1340–1348. [Google Scholar] [CrossRef]
- Jonsson, K.; Jonsson, B. Fluid-Flow in Compressible Porous-Media. 2. Dynamic Behavior. AIChE J. 1992, 38, 1349–1356. [Google Scholar] [CrossRef]
- Bidner, M.; Porcelli, P. Influence of phase behavior on chemical flood transport phenomena. Transp. Porous Media 1996, 24, 247–273. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids In Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972; ISBN 978-0-44400-114-6. [Google Scholar]
- Wang, J.; Liu, H.Q.; Xu, J. Mechanistic Simulation Studies on Viscous-Elastic Polymer Flooding in Petroleum Reservoirs. J. Dispers. Sci. Technol. 2013, 34, 417–426. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Macroscopic Modeling of Transport Phenomena in Porous-Media. 2. Applications to Mass, Momentum and Energy-Transport. Transp. Porous Media 1986, 1, 241–269. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; p. 523. ISBN 978-0-898716-06-1. [Google Scholar] [CrossRef]
- Camilleri, D.; Engelson, S.; Lake, L.W.; Lin, E.C.; Ohnos, T.; Pope, G.; Sepehrnoori, K. Description of an Improved Compositional Micellar/Polymer Simulator. SPE Reserv. Eng. 1987, 2, 427–432. [Google Scholar] [CrossRef]
- Camilleri, D.; Fil, A.; Pope, G.A.; Rouse, B.A.; Sepehrnoori, K. Comparison of an Improved Compositional Micellar/Polymer Simulator With Laboratory Corefloods. SPE Reserv. Eng. 1987, 2, 441–451. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of Well-Block Pressures in Numerical Reservoir Simulation (includes associated paper 6988). Soc. Pet. Eng. J. 1978, 18, 183–194. [Google Scholar] [CrossRef]
- Saad, N.; Pope, G.A.; Sepehrnoori, K. Application of higher-order methods in compositional simulation. SPE Reserv. Eng. (Soc. Pet. Eng.) 1990, 5, 623–630. [Google Scholar] [CrossRef]
- Kamalyar, K.; Kharrat, R.; Nikbakht, M. Numerical Aspects of the Convection-Dispersion Equation. Pet. Sci. Technol. 2014, 32, 1729–1762. [Google Scholar] [CrossRef]
- Liu, J.; Delshad, M.; Pope, G.A.; Sepehrnoori, K. Application of higher-order flux-limited methods in compositional simulation. Transp. Porous Media 1994, 16, 1–29. [Google Scholar] [CrossRef]
- Druetta, P.; Picchioni, F. Influence of the Polymer Properties and Numerical Schemes on Tertiary Oil Recovery Processes. 2018; submitted for publication. [Google Scholar]
- Druetta, P.; Yue, J.; Tesi, P.; Persis, C.D.; Picchioni, F. Numerical modeling of a compositional flow for chemical EOR and its stability analysis. Appl. Math. Model. 2017, 47, 141–159. [Google Scholar] [CrossRef]
- Najafabadi, N.F. Modeling chemical EOR Processes Using IMPEC and Fully IMPLICIT Reservoir Simulators. Ph.D. Thesis, The University of Texas at Austin, Austin, OH, USA, 2009. [Google Scholar]
- Kuzmin, D. A Guide to Numerical Methods for Transport Equations; University Erlangen-Nuremberg: Bavaria, Germany, 2010. [Google Scholar]
- Kuzmin, D.; Turek, S. High-resolution FEM-TVD schemes based on a fully multidimensional flux limiter. J. Computat. Phys. 2004, 198, 131–158. [Google Scholar] [CrossRef]
- Fazio, R.; Jannelli, A. Second order positive schemes by means of flux limiters for the advection equation. IAENG Int. J. Appl. Math. 2009, 39, 1–11. [Google Scholar]
- Lai, J.; Lin, G.; Guo, W. An upstream flux-splitting finite-volume scheme for 2D shallow water equations. Int. J. Numer. Methods Fluids 2005, 48, 1149–1174. [Google Scholar] [CrossRef]





| Flux Limiter | Function |
|---|---|
| Upwind | 0 |
| Superbee | |
| Minmod | |
| MUSCL |
| Reservoir Geometrical Dimensions | |||||
| Length (axis X) | 500 m | Length (axis Y) | 500 m | Layer thickness | 10 m |
| 25 elements | 25 elements | ||||
| Rock Formation Properties | |||||
| Porosity | 0.25 | 200 mD | 200 mD | ||
| Initial Conditions | |||||
| 0.70 | (EOR) | 0.35 | 0.15 | ||
| Reservoir Simulation Data | |||||
| Simulation time | 9000 days | Chem. injection time | - days | - | |
| Phases’ Properties | |||||
| 1 cP | 10 cP | Oil density | 850 kg/m | ||
| Water density | 1020 kg/m | IFT | 50 mN/m | ||
| Physical Data | |||||
| Number of wells | 2 | Radius | 0.25 m | Skin factor | 0 |
| Operation Conditions | |||||
| Flowrate (total) | 1500 STB/day | Bottomhole pressure | 55,160 kPa | ||
| Interfacial Tension | Capillary Pressure | Adsorption | |||||||||
| −1.7 | −0.02 | C | 0 | n | 1 | 0 | 0 | ||||
| Viscosity | Residual Saturation | Relative Permeabilities | |||||||||
| 0 | 0 | −0.25 | −0.50 | 1 | 0.2 | ||||||
| 1 | 1.57 | −0.70 | 1.5 | 1.5 | |||||||
| Number of Elements | Grid Size | Time Step | Relative Simulation Time | Cumulative Oil Production |
|---|---|---|---|---|
| - | m | days | - | |
| 25 | 20 | 0.5 | 3.91 | 97,652 |
| 25 | 20 | 1 | 1.33 | 97,605 |
| 25 | 20 | 2 | 1 | 97,316 |
| 25 | 20 | 4 | 3.57 | 92,143 |
| 50 | 10 | 0.5 | 9.46 | 97,662 |
| 60 | 8.333 | 0.5 | 37.42 | 97,531 |
| Grid Size | Time Step | Cumulative Oil Production | Cumulative Oil Production (Iterative) | Difference |
|---|---|---|---|---|
| - | days | % | ||
| 25 | 6 | 97,748 | 97,605 | 0.15 |
| 50 | 1.5 | 97,717 | 97,662 | 0.06 |
| 60 | 1 | 98,356 | 97,531 | 0.85 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Druetta, P.; Picchioni, F. Numerical Modeling and Validation of a Novel 2D Compositional Flooding Simulator Using a Second-Order TVD Scheme. Energies 2018, 11, 2280. https://doi.org/10.3390/en11092280
Druetta P, Picchioni F. Numerical Modeling and Validation of a Novel 2D Compositional Flooding Simulator Using a Second-Order TVD Scheme. Energies. 2018; 11(9):2280. https://doi.org/10.3390/en11092280
Chicago/Turabian StyleDruetta, Pablo, and Francesco Picchioni. 2018. "Numerical Modeling and Validation of a Novel 2D Compositional Flooding Simulator Using a Second-Order TVD Scheme" Energies 11, no. 9: 2280. https://doi.org/10.3390/en11092280
APA StyleDruetta, P., & Picchioni, F. (2018). Numerical Modeling and Validation of a Novel 2D Compositional Flooding Simulator Using a Second-Order TVD Scheme. Energies, 11(9), 2280. https://doi.org/10.3390/en11092280






