An Improved Multi-Timescale Coordinated Control Strategy for Stand-Alone Microgrid with Hybrid Energy Storage System
Abstract
:1. Introduction
- (1)
- HESS is not included as an element of coordinated control; thus, applicability is limited.
- (2)
- The SOC balance of HESS in daily dispatch period has not received enough attention.
- (3)
- The multi-timescale framework is relatively simple, with large gap between different timescales.
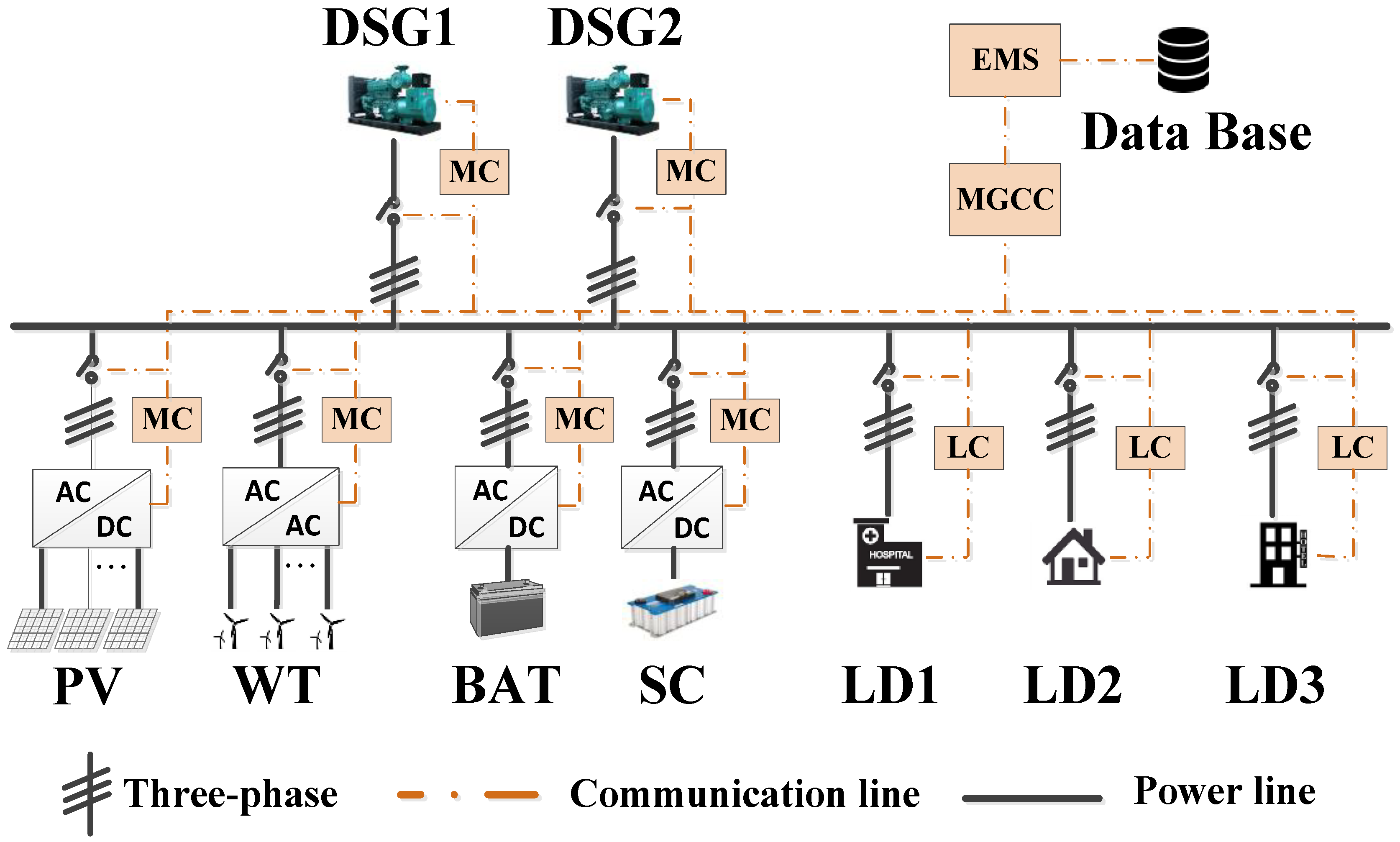
2. Typical Topology of Stand-Alone Microgrid with Hybrid Energy Storage System
- (1)
- The first layer is the optimal schedule layer and the corresponding control unit is EMS (energy management system). The DAO and IDR algorithm in EMS is used to realize coordinated control strategy of a large time scale and provide scheduling curve for MGCC (microgrid central controller).
- (2)
- The second layer is the MG control layer and the corresponding control unit is MGCC. The QRTC and RTCC in MGCC based on logical judgment is used to correct the deviation between the actual operating state and the ideal state of the MG and issue control commands to the device controller.
- (3)
- The third layer is the local control layer and the corresponding control unit is device controllers. Control commands from the MG real-time control layer are executed by DGs/load/HESS.
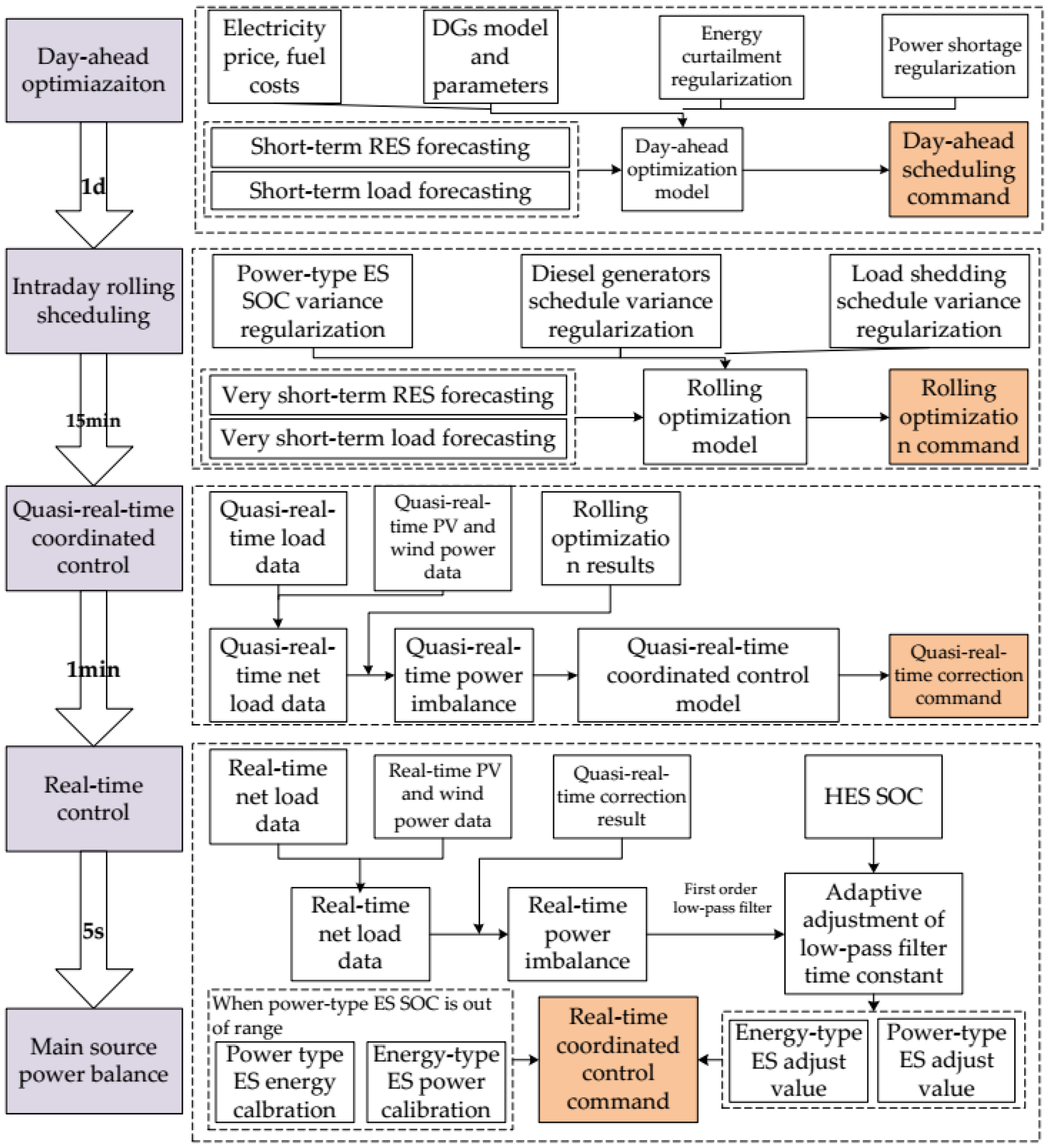
3. Multi-time Scale Coordinated Control
3.1. Multi-time Scale Coordinated Control Framework
- (1)
- Day-ahead optimization model: Based on the short-term load forecasting results, DGs’ hourly output scheduling curve (except PTESS) and load switching scheme are determined by DAO Day-ahead optimization model in the EMS. The execution cycle of this model is 1 day.
- (2)
- Intraday rolling model: Based on the ultra short-term power forecasting results, the DAO results are continuously corrected by the time-limited rolling optimization scheduling. The time scale of the rolling time window is 4h (same as the ultra short-term prediction). The model has an execution cycle of 15 min.
- (3)
- Quasi-real-time coordinated control model: The deviation between the constantly updated intraday rolling scheduling plan and the actual operating conditions of MG is calculated by the real-time collected data and will be corrected quickly. An integrated criterion is introduced to decide the adjustment priority of the distributed generations. The execution cycle of this model is 1 min.
- (4)
- Real-time coordinated control model: Under the condition of ensuring frequency and voltage stability, real-time control commands are determined to follow the command from quasi-real-time coordinated control as much as possible in second time scale and real-time smooth control strategy for HESS based on logic judgment is used to smooth unbalanced power of second time scale. The execution cycle of this model is 5 s.
3.2. Day-Ahead Optimization Model
3.2.1. Decision Variables
3.2.2. Objective Function and Constraints
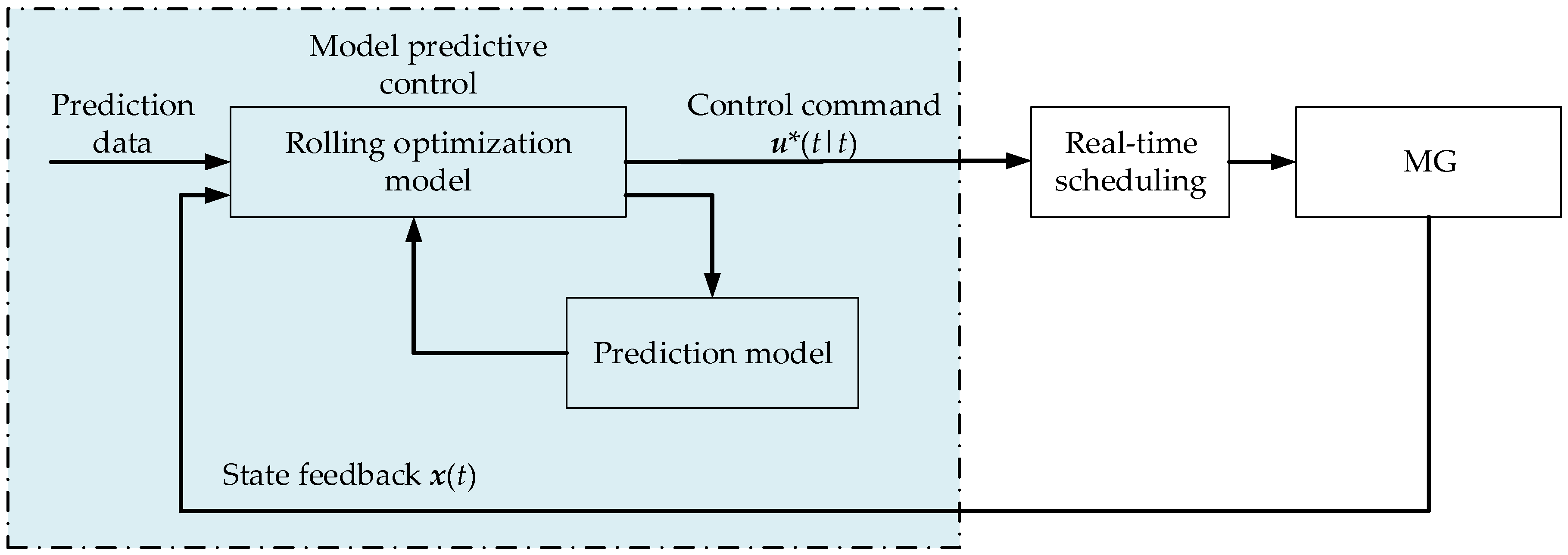
3.3. Intraday Rolling Optimization Based on Model Predictive Control
3.3.1. Model Predictive Control Framework
- (1)
- Prediction model: Based on the measured output data of generators and the predictive data of RES and load data in the next time period, this model is used to predict the future output of generators.
- (2)
- Rolling optimization: Repeated online optimization negates the influence caused by uncertain factors such as RE fluctuations.
- (3)
- Feedback control: The measured data feedback is used to correct the actual output state of the generators in the model and ensure that the next optimization calculation is based on the latest measured data.
3.3.2. Decision Variables
3.3.3. Objective Function and Constraints
3.4. Comprehensive Criteria Based Quasi-Real-Time Coordinated Control
- (1)
- When ①③⑤ are satisfied, increase the discharge power of ETESS with high priority. The increment is calculated by SOC error and rated capacity, as described by the following equation:where is the resting time until next rolling optimization.
- (2)
- When ①③⑥ are satisfied, increase the output of diesel generators with high priority. The increment takes rated power and spinning reserve margin into consideration, as described by the following equation:where is the command of rolling optimization for diesel generators and is the spinning reserve margin.
- (3)
- When ①④⑤ are satisfied, decrease the charge power of ETESS with high priority. is described by the following equation:
- (4)
- When ①④⑥ are satisfied, the strategy is the same as Equation (2).
- (5)
- When ②③⑤ are satisfied, decrease the output of diesel generators with high priority. The increment needs to take minimum load limitation into consideration, as described by the following equation:
- (6)
- When ②③⑥ are satisfied, decrease the discharge power of ETESS with high priority. is described by the following equation:
- (7)
- When ②④⑤ are satisfied, the strategy is the same as Equation (5).
- (8)
- When ②④⑥ are satisfied, increase the charge power of ETESS with high priority. is described by the following equation:
3.5. Real-Time Correction Control of Hybrid Energy Storage
4. Case Study
4.1. Basic Data
4.2. Analysis of Multi-Timescale Coordinated Control
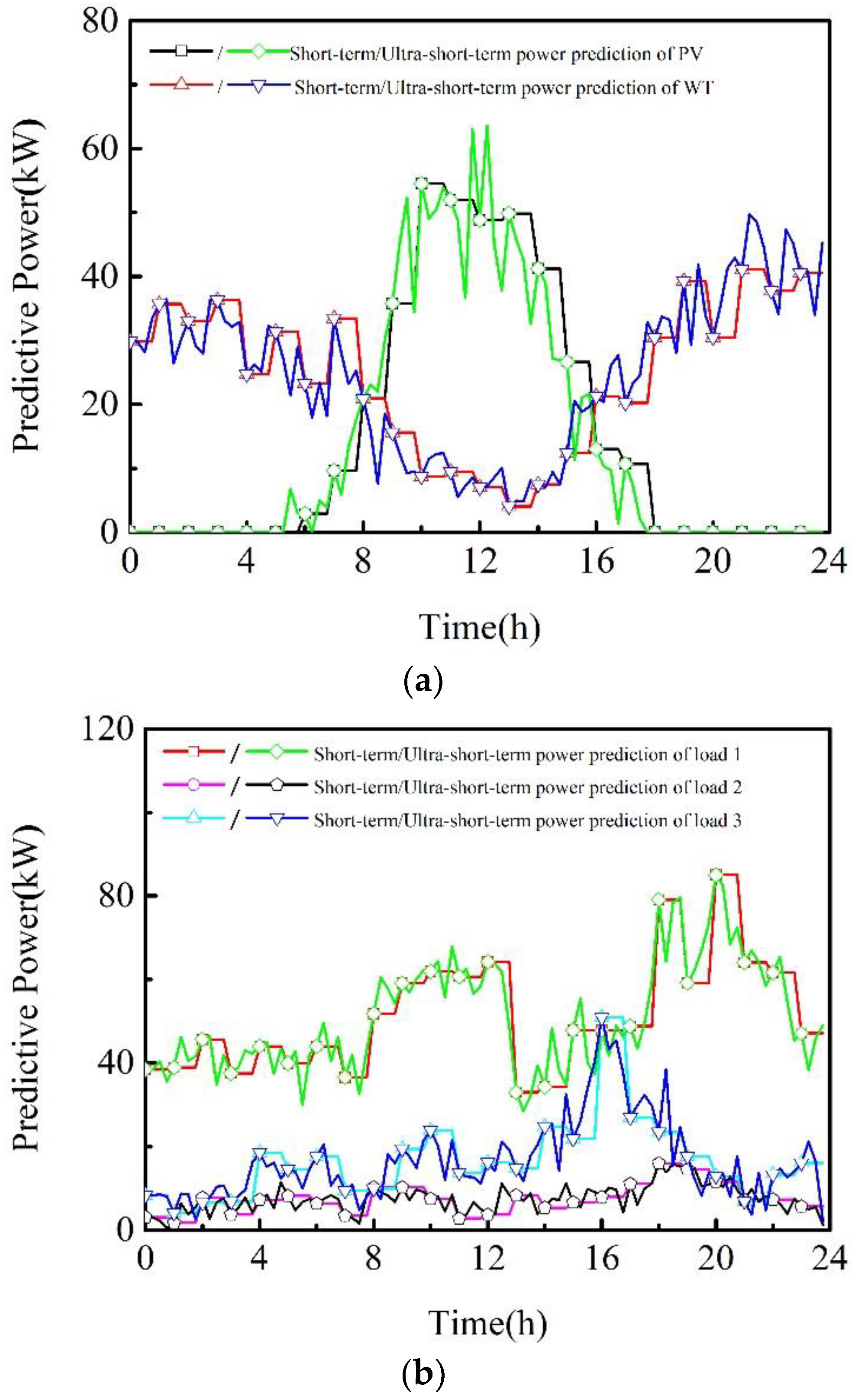
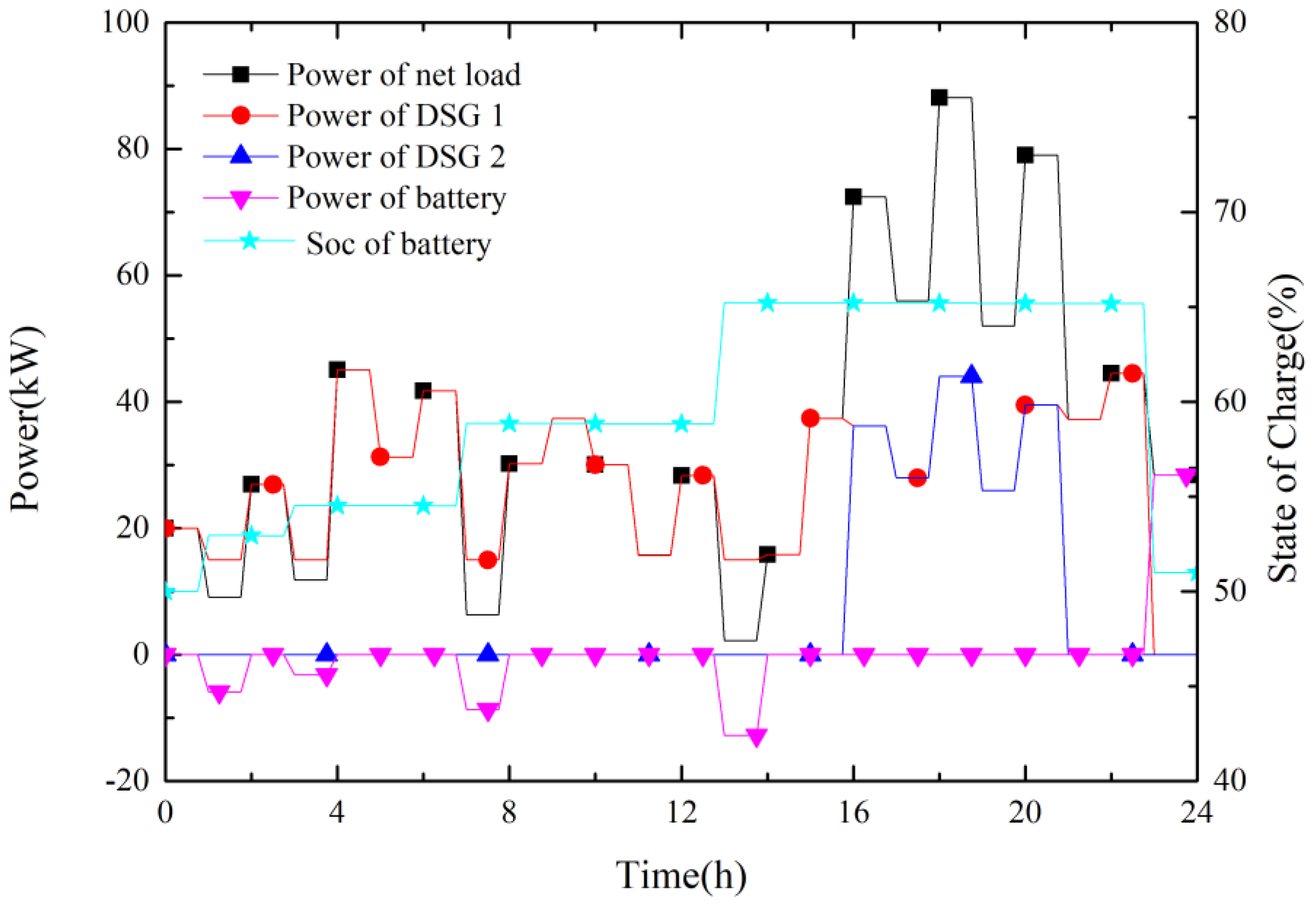
4.2.1. Analysis of Day-Ahead Optimization
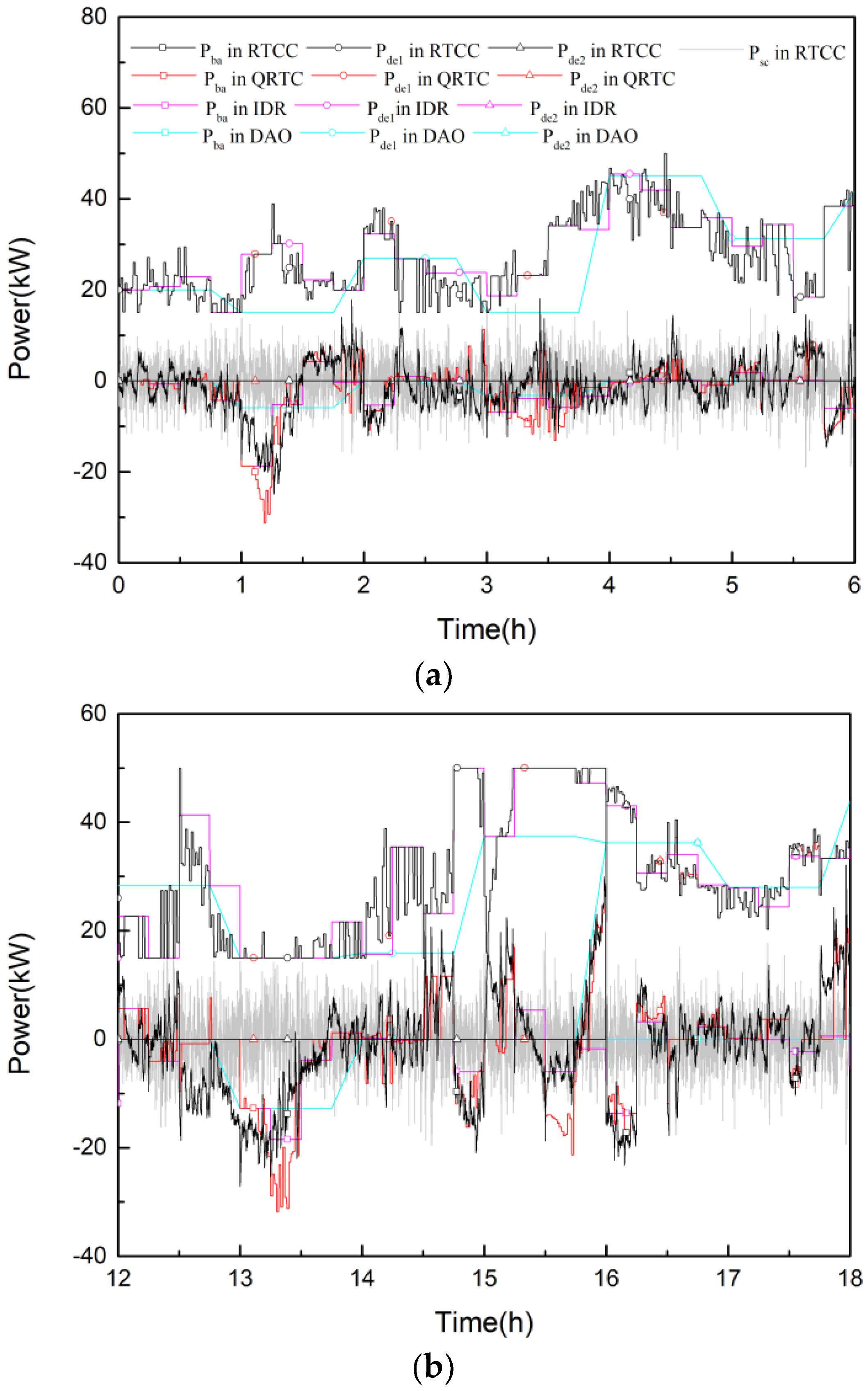
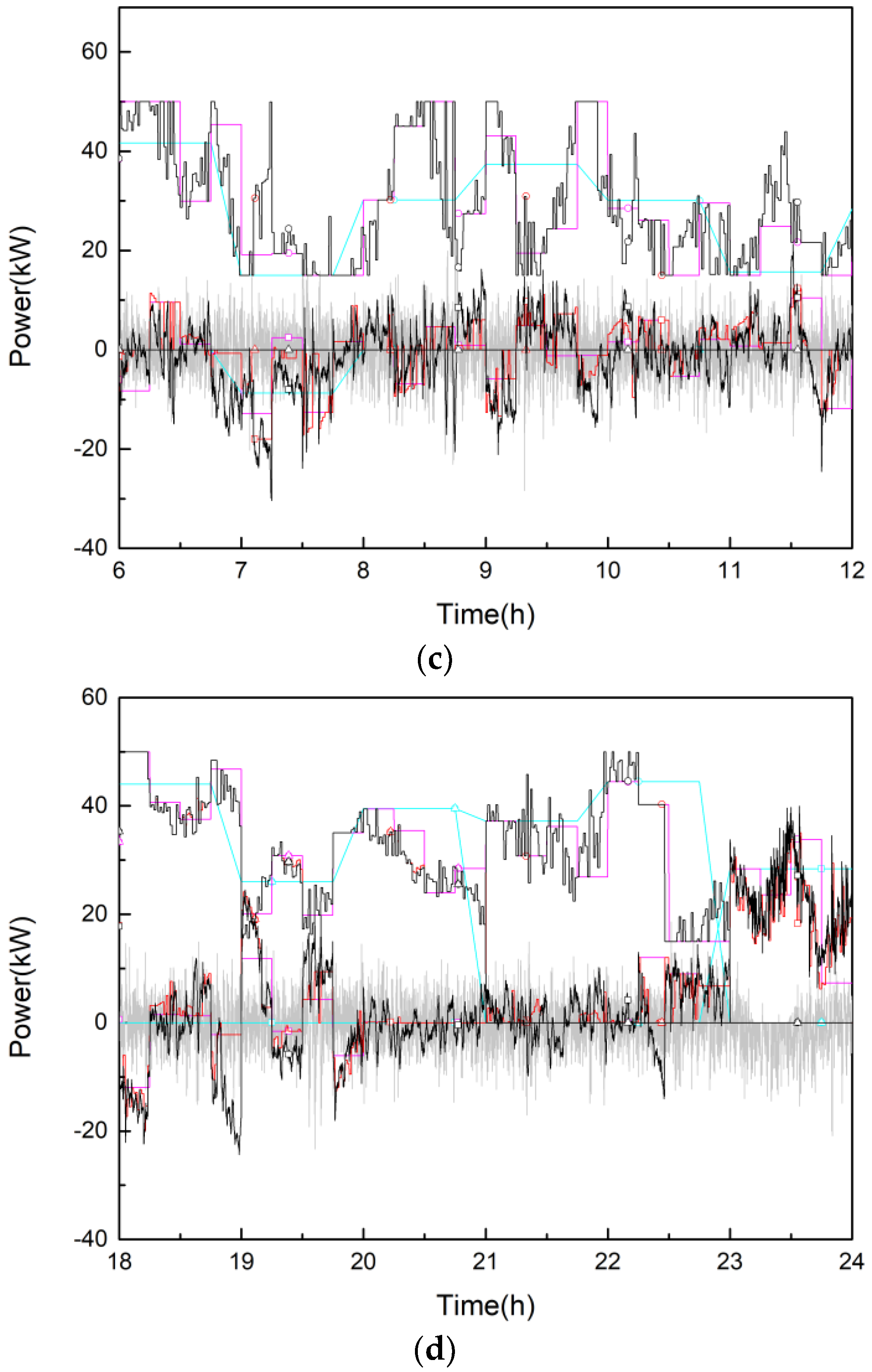
4.2.2. Analysis of Intraday, Quasi-Real-Time and Real-Time Coordinated Control
- (1)
- The essential of seconds-scale real-time coordinated control is to use HESS to compensate the power imbalance in the interval of quasi-real-time coordinated control, so the power curve of DSG in real-time coordinated control is basically overlapped with that in quasi-real-time coordinated control.
- (2)
- The power curve of DSG is more accurate in the shorter timescale. Compared to real-time power curve, the mean error of quasi-real-time curve is 0.19% while the mean error of intraday rolling curve is 11.73% and for day-ahead scheduling, 26.09%.
- (1)
- ETESS needs to compensate the low frequency unbalanced power in real-time timescale, so its real-time operating power curve is slightly different from the quasi-real-time curve.
- (2)
- Though intraday and day-ahead curves differ from the real-time curve greatly, they still reflect the overall change of the energy of ETESS.
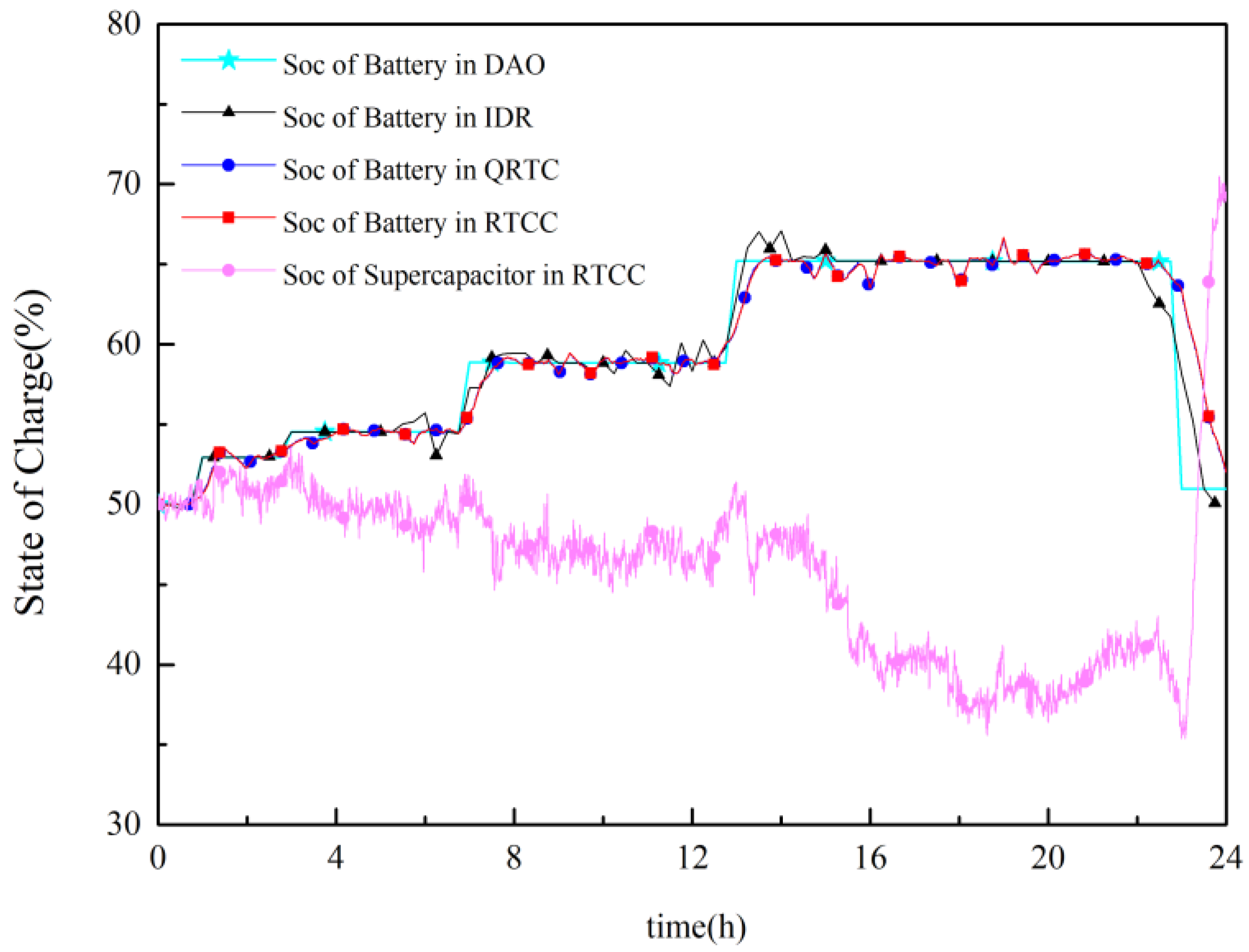
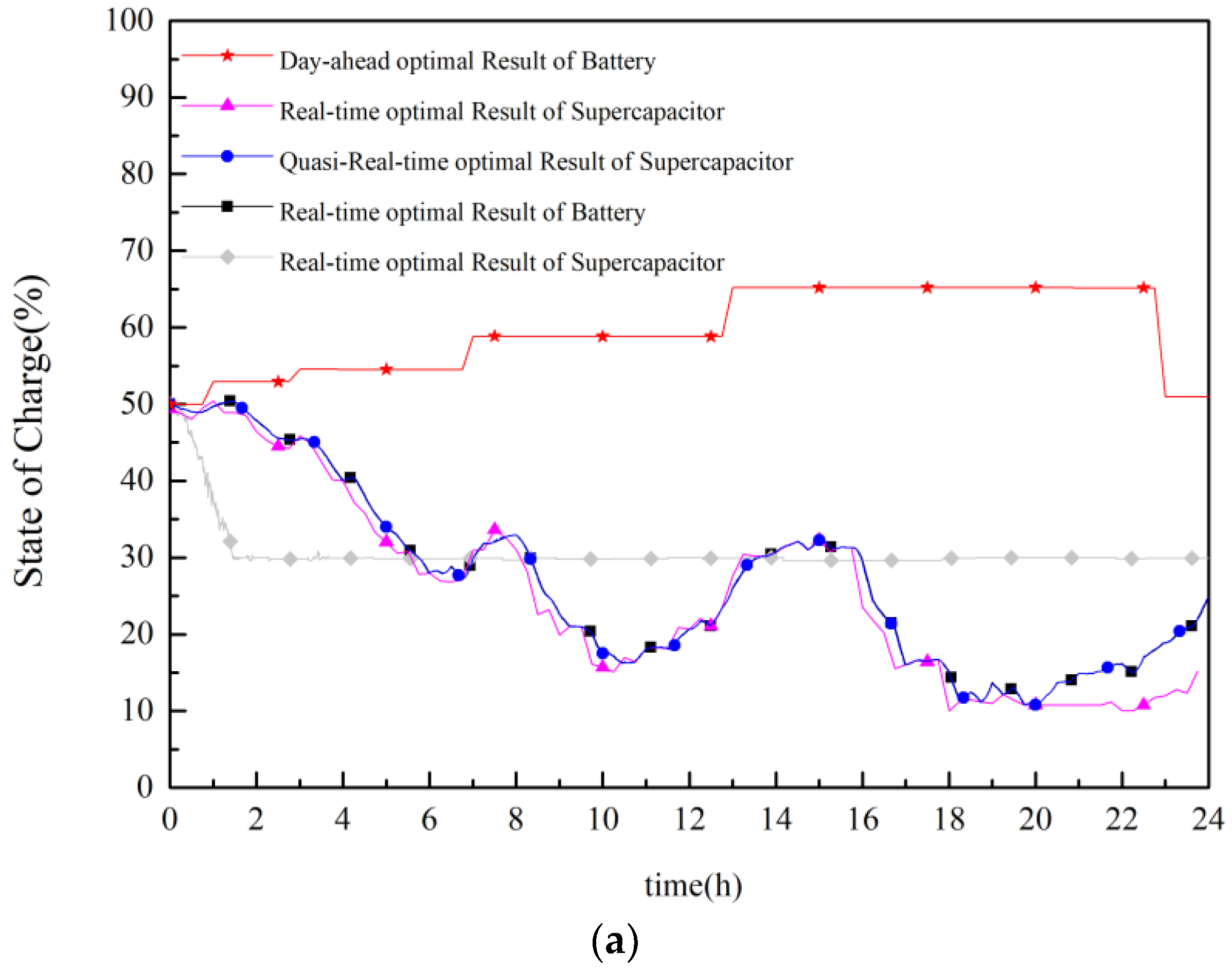
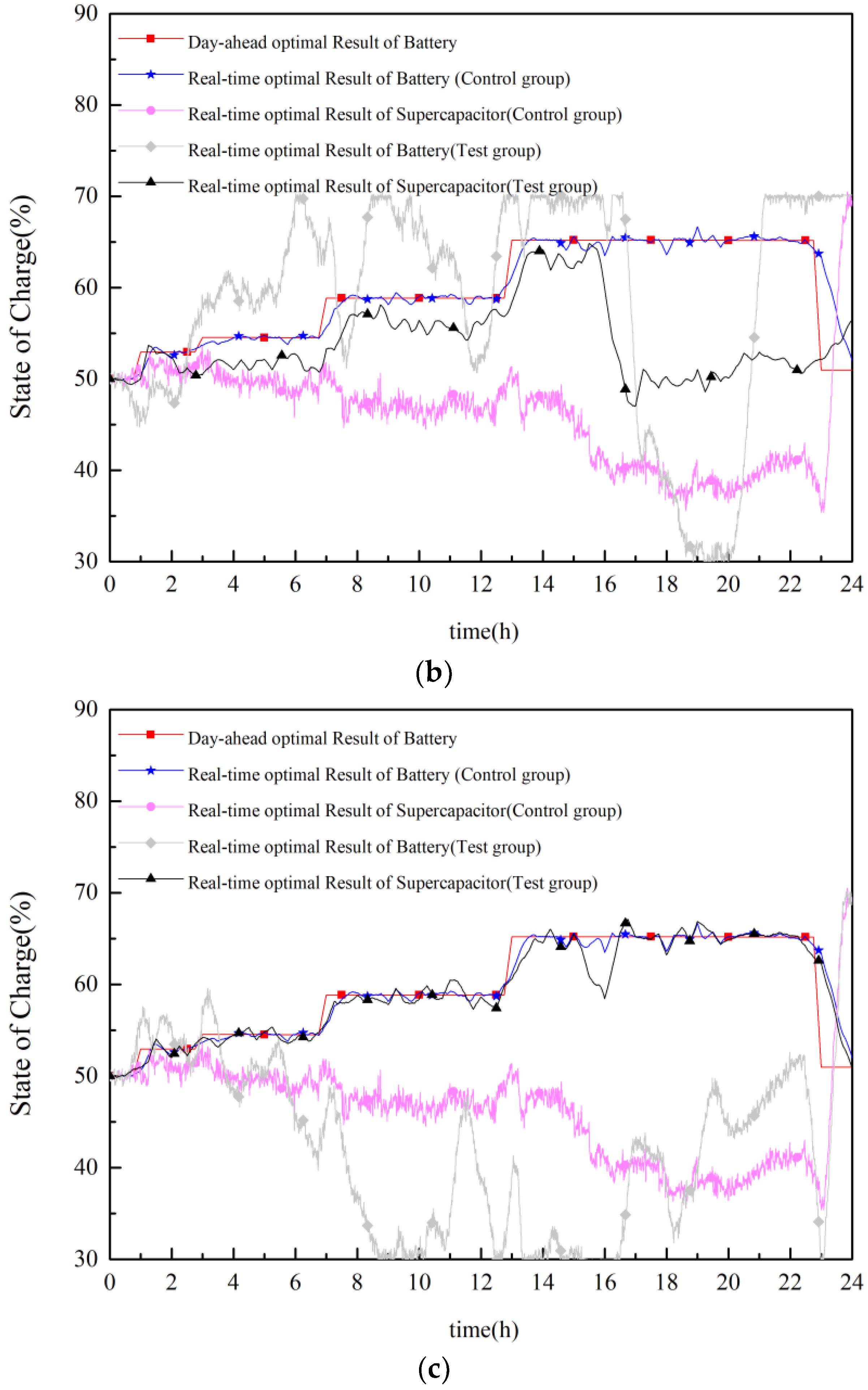
4.2.3. Analysis of Daily SOC Balance of ETESS
4.2.4. Analysis of the DSG Unit Commitment Correction Regularization
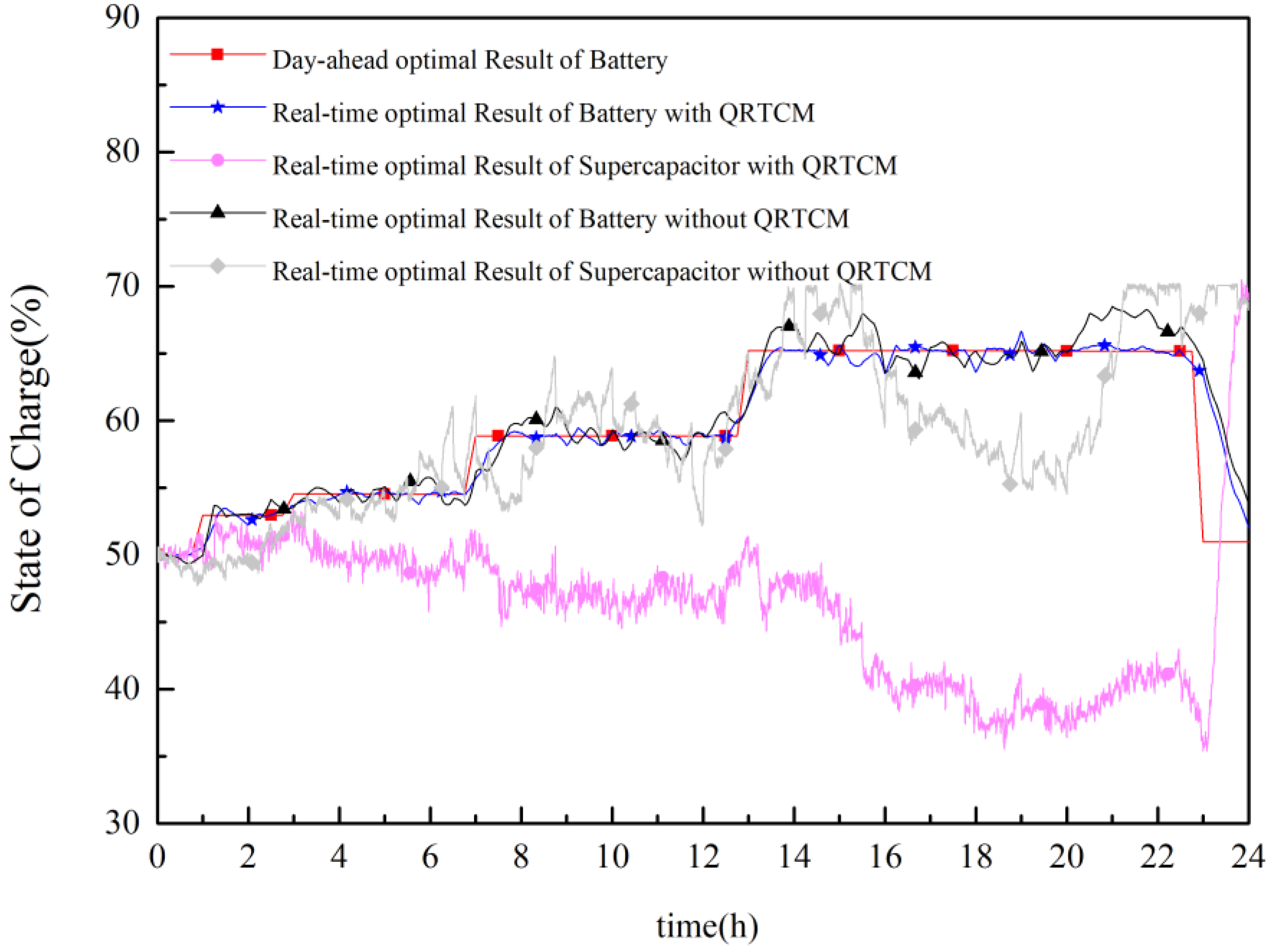
4.2.5. Analysis of the Necessity of Introducing Quasi-Real-Time Coordinated Control
5. Conclusions
- (1)
- Introduce power shortage regularization term in day-ahead optimization model can significantly improve the power supply reliability but at the cost of some economic profit.
- (2)
- Based on ultra-short-term forecasting, which has smaller prediction error, the intraday rolling optimization model can adjust the day-ahead schedule for DGs output power appropriately. When the day-ahead prediction error is large, DG unit commitment and load switching schedule will be correct to the robustness of the MG system.
- (3)
- To keep the ETESS SOC balance at the beginning and end of the day period, it is necessary to add ETESS SOC error regularization term in the intraday rolling optimization model. Besides, the comprehensive criterial proposed in quasi-real-time model can improve the ETESS’s ability to follow the day-ahead schedule and reducing the HESS operations risk at the same time.
- (1)
- To overcome the shortcomings of large error in day-ahead power prediction and increase the credibility of the optimization results, uncertainty optimization theory can be introduced, such as robust optimization, fuzzy programming and stochastic programming.
- (2)
- In large scale stand-alone MG system, it may contain multiple HESSs. How to manage the charge and discharge commands and the SOC of each HESS in quasi-real-time and real-time timescale, is a problem to be solved.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hartono, B.S.; Budiyanto; Setiabudy, R. Review of microgrid technology. In Proceedings of the 2013 International Conference on QiR, Yogyakarta, Indonesia, 25–28 June 2013. [Google Scholar]
- Lasseter, R.H.; Paigi, P. Microgrid: A conceptual solution. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004. [Google Scholar]
- He, M.; Giesselmann, M. Reliability-constrained self-organization and energy management towards a resilient microgrid cluster. In Proceedings of the 2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015. [Google Scholar]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Dougal, R.A.; Liu, S.; White, R.E. Power and life extension of battery-ultracapacitor hybrids. IEEE Trans. Compon. Packag. Technol. 2002, 25, 120–131. [Google Scholar] [CrossRef]
- Cagnano, A.; Bugliari, A.C.; De Tuglie, E. A cooperative control for the reserve management of isolated microgrids. Appl. Energy 2018, 218, 256–265. [Google Scholar] [CrossRef]
- Lasseter, R.H. Microgrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002. [Google Scholar]
- Liu, M.; Guo, L.; Wang, C.; Zhao, B.; Zhang, X.; Liu, Y. A coordinated operating control strategy for hybrid isolated microgrid including wind power, photovoltaic system, diesel generator and battery storage. Autom. Electr. Power Syst. 2012, 36, 19–24. [Google Scholar]
- Zhang, X.; Yeh, W.; Jiang, Y.; Huang, Y.; Xiao, Y.; Li, L. A case study of control and improved simplified swarm optimization for economic dispatch of a stand-alone modular microgrid. Energies 2018, 11, 793. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2016, 7, 1034–1043. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Huang, C.; Yue, D.; Deng, S.; Xie, J. Optimal scheduling of microgrid with multiple distributed resources using interval optimization. Energies 2017, 10, 339. [Google Scholar] [CrossRef]
- Dutta, S.; Sharma, R. Optimal storage sizing for integrating wind and load forecast uncertainties. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012. [Google Scholar]
- Fan, S.; Ai, Q.; Piao, L. Hierarchical energy management of microgrids including storage and demand response. Energies 2018, 11, 1111. [Google Scholar] [CrossRef]
- Guo, S.; Yuan, Y.; Zhang, X.; Bao, W.; Liu, C.; Cao, Y.; Wang, H. Energy Management Strategy of Isolated Microgrid Based on Multi-time Scale Coordinated Control. Trans. China Electrotech. Soc. 2014, 29, 122–129. [Google Scholar]
- Zhang, C.; Xu, Y.; Dong, Z.Y.; Ma, J. Robust operation of microgrids via two-stage coordinated energy storage and direct load control. IEEE Trans. Power Syst. 2017, 32, 2858–2868. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Mixed-integer-linear-programming-based energy management system for hybrid PV-wind-battery microgrids: Modeling, design and experimental verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef]
- Lee, W.-P.; Choi, J.-Y.; Won, D.-J. Coordination strategy for optimal scheduling of multiple microgrids based on hierarchical system. Energies 2017, 10, 1336. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A battery/ultracapacitor hybrid energy storage system for implementing the power management of virtual synchronous generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Nguyen-Hong, N.; Nguyen-Duc, H.; Nakanishi, Y. Optimal sizing of energy storage devices in isolated wind-diesel systems considering load growth uncertainty. IEEE Trans. Ind. Appl. 2018, 54, 1983–1991. [Google Scholar] [CrossRef]
- Momayyezan, M.; Abeywardana, D.B.W.; Hredzak, B.; Agelidis, V.G. Integrated reconfigurable configuration for battery/ultracapacitor hybrid energy storage systems. IEEE Trans. Energy Convers. 2016, 31, 1583–1590. [Google Scholar] [CrossRef]
- Ju, C.; Wang, P.; Goel, L.; Xu, Y. A two-layer energy management system for microgrids with hybrid energy storage considering degradation costs. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Xu, G.; Shang, C.; Fan, S.; Hu, X.; Cheng, H. A hierarchical energy scheduling framework of microgrids with hybrid energy storage systems. IEEE Access 2018, 6, 2472–2483. [Google Scholar] [CrossRef]
- Li, J.; Zheng, X.; Ai, X.; Wen, J.; Sun, S.; Li, G. Optimal design of capacity of distributed generation in island standalone microgrid. Trans. China Electrotech. Soc. 2016, 31, 176–184. [Google Scholar]
- Chen, J. Research on Optimal Sizing of Wind/Solar/Battery(/Diesel Generator) Microgrid. Ph.D. Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- Mohamed, E.A.A.E.; Yusuff, M.A.; Wahab, D.A. Application of rainflow cycle counting in the reliability prediction of automotive front corner module system. In Proceedings of the 2009 16th International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009. [Google Scholar]

| Quasi-Real-Time Power Imbalance | Power of ETESS in Rolling Optimization | Quasi-Real-Time SOC of ETESS |
|---|---|---|
| ① | ③ | ⑤ |
| ② | ④ | ⑥ |
| Serial Number of DSG | Rated Power (kW) | Startup Cost (CNY/Per Time) | Shutdown Cost (CNY/Per Time) | Coefficient of Operation Cost (CNY/kWh) | Fuel Cost (CNY/kWh) | Fuel Curve Slope (L/kWh) | Minimum Load Factor (%) |
|---|---|---|---|---|---|---|---|
| 1 | 50 | 2 | 2 | 0.0088 | 7 | 0. | 30 |
| 2 | 50 | 2 | 2 | 0.0088 | 7 | 0.3 | 30 |
| Type | Rated Power (kW) | Coefficient of Operation Cost (CNY/kWh) |
|---|---|---|
| Wind power | 50 | 0.0296 |
| PV power | 50 | 0.0096 |
| Type | Rated Power/Capacity (kW/kWh) | Initial Investment Cost (CNY/kWh) | Coefficient of Operation Cost (CNY/kWh) | Energy Per Unit Capacity (kWh) | Permitted SOC Range (%) | SOC Warning Range (%) | Initial SOC (%) |
|---|---|---|---|---|---|---|---|
| ETESS | 50/200 | 2 | 0.0088 | 250 | [10, 90] | [30, 70] | 50 |
| PTESS | 50/5 | 11.4 | 0 | ∞ | [10, 90] | [30, 70] | 50 |
| Energy Balance Error in a Cycle (%) | DSG Minimum Operation (Shutdown) Time (h) | Reserve Capacity (kW) | Regularization Parameter of RE Curtailment | Regularization Parameter of Power Shortage | Regularization Parameter of DSG Unit Commitment Correction | Regularization Parameter of SOC Error Correction |
|---|---|---|---|---|---|---|
| 10 | 2 | 10 | 5000 | 10000 | 10000 | 500 |
| Adjusting Coefficient for Time Constant of FOLPF | Reference Value for Time Constant of FOLPF |
|---|---|
| 15 | 30 |
| Day-Ahead Optimization Results | Without Regularization Terms | With Regularization Term |
|---|---|---|
| RE curtailment (%) | 0.00095619 | 0 |
| Power shortage (%) | 28.3567 | 0 |
| MG operation cost (CNY) | −1049.9027 | −645.8309 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yang, P.; Peng, J.; Huang, Y.; Chen, Y.; Zeng, Z. An Improved Multi-Timescale Coordinated Control Strategy for Stand-Alone Microgrid with Hybrid Energy Storage System. Energies 2018, 11, 2150. https://doi.org/10.3390/en11082150
Chen J, Yang P, Peng J, Huang Y, Chen Y, Zeng Z. An Improved Multi-Timescale Coordinated Control Strategy for Stand-Alone Microgrid with Hybrid Energy Storage System. Energies. 2018; 11(8):2150. https://doi.org/10.3390/en11082150
Chicago/Turabian StyleChen, Jingfeng, Ping Yang, Jiajun Peng, Yuqi Huang, Yaosheng Chen, and Zhiji Zeng. 2018. "An Improved Multi-Timescale Coordinated Control Strategy for Stand-Alone Microgrid with Hybrid Energy Storage System" Energies 11, no. 8: 2150. https://doi.org/10.3390/en11082150
APA StyleChen, J., Yang, P., Peng, J., Huang, Y., Chen, Y., & Zeng, Z. (2018). An Improved Multi-Timescale Coordinated Control Strategy for Stand-Alone Microgrid with Hybrid Energy Storage System. Energies, 11(8), 2150. https://doi.org/10.3390/en11082150




