Application of Markov Model to Estimate Individual Condition Parameters for Transformers

Abstract

This paper presents a study to estimate individual condition parameters of the transformer population based on Markov Model (MM). The condition parameters under study were hydrogen (H₂), methane (CH₄), acetylene (C₂H₂), ethylene (C₂H₄), ethane (C₂H₆), carbon monoxide (CO), carbon dioxide (CO₂), dielectric breakdown voltage, interfacial tension, colour, acidity, water content, and 2-furfuraldehyde (2-FAL). First, the individual condition parameter of the transformer population was ranked and sorted based on recommended limits as per IEEE Std. C57. 104-2008 and IEEE Std. C57.106-2015. Next, the mean for each of the condition parameters was computed and the transition probabilities for each condition parameters were obtained based on non-linear optimization technique. Next, the future states probability distribution was computed based on the MM prediction model. Chi-square test and percentage of absolute error analysis were carried out to find the goodness-of-fit between predicted and computed condition parameters. It is found that estimation for majority of the individual condition parameter of the transformer population can be carried out by MM. The Chi-square test reveals that apart from CH₄ and C₂H₄, the condition parameters are outside the rejection region that indicates agreement between predicted and computed values. It is also observed that the lowest and highest percentages of differences between predicted and computed values of all the condition parameters are 81.46% and 98.52%, respectively.

1. Introduction

Transformer is an integral component to ensure the reliability of power delivery in any utilities. Thus, monitoring its operational performance is very crucial to prevent failures. Although transformers are proven as reliable equipment in normal in-service operation, its failure could cause interruption in the power delivery that could result in direct or indirect repair costs to the utilities. Nowadays, asset owners have adopted a mechanism known as Condition-Based Monitoring (CBM) to monitor the operational parameter characteristics and it can provide a comprehensive diagnosis on transformers health to prevent the recurrence of failures. Condition parameter trends which point out the deterioration of transformers condition can be detected early via operational parameter monitoring, hence can be used for estimation of transformers condition [1,2,3].

Health Index (HI) is a common tool used for CBM purpose. It integrates all condition parameter data using a single quantitative index to represent transformer overall health status. This approach is useful to evaluate the long-term deterioration level based on the health condition that may not be viable to be identified by routine inspections and individual CBM techniques [4,5]. Besides, it also addresses the interaction between parameter characteristics and attributes of these techniques which is not considered in the conventional method. The drawback of this approach has positioned the asset owner in difficult situations to identify and point out the underlying root causes that lead to the deterioration of transformers health. Hence, modelling the deterioration of transformers using individual condition parameters could assist to provide a detail diagnosis on transformers population by looking at specific condition parameter deterioration curve rather than just providing the overall condition deterioration status.

There are many studies that have been carried out to analyse and provide comprehensive diagnostic interpretations for individual condition parameter data such as hydrogen (H₂), methane (CH₄), acetylene (C₂H₂), ethylene (C₂H₄), ethane (C₂H₆), carbon monoxide (CO), carbon dioxide (CO₂), dielectric breakdown voltage, interfacial tension, colour, acidity, water content and 2-furfuraldehyde. The studies are mainly centred on 3 common categories, namely deterministic, statistical and Artificial Intelligence (AI)-based models. Among the examples of deterministic models that have been used to interpret condition parameter data are Key Gas Method, Doernenburg Ratio Method, Rogers Ratio Method, IEC Ratio Method, IEC TC10 Database, IEC 60599, IEEE C57.104 and Duval Triangle Method [6,7]. Statistical-based models such as time series correlation technique [8] and rough set approach [9] are among the frequently used methods used to interpret the condition parameter data. Fuzzy set theory [10], Artificial Neural Network (ANN) [11], support vector machine [12], fuzzy-evidential reasoning [13], genetic algorithm [14,15], genetic programming [16,17] and particle swarm optimization [18,19] techniques are among the AI-based techniques that have been used to evaluate condition parameter data. Generally, these deterministic, statistical and AI techniques are used to evaluate the current condition of transformers.

Several studies have attempted to model the reliability of a transformer. It is often quite difficult to assess its reliability using conventional methods based on frequency of failures due to inadequate failures data record. Nevertheless, transformers have operational characteristics of which deterioration over the operating time can be correlated with its reliability. Thus, if the deterioration phenomenon of transformers is carefully monitored and adequately modelled, it is possible to assess its reliability. In addition, this approach allows the asset owner to estimate the remaining life, hence to derive a comprehensive maintenance strategy and plan for the maintenance expenditures [20]. Presently, there are only a few studies on modelling the future deterioration of transformers as most of the studies focus on modelling the reliability of power transformer based on failures data [21,22]. Markov chain is among the most well-known stochastic processes-based approach that are commonly implemented to model the deterioration process of facilities and equipment.

Markov process is used in non-time variant statistical deterioration prediction modelling. Markov chain is commonly used in civil engineering especially for structural deterioration assessment such as buildings [23], bridge [24], bridge element [25], pavement [26] and storm water pipe [27]. Markov chain also has been utilized to assess the oil degradation in oil-filled switchgear [28] and to determine spare requirement for power transformers [29,30].

In this study, MM based on individual condition parameter data is proposed to model the future deterioration of distribution transformer population. In total, 1322 oil samples from 373 distribution transformers of 33/11 kV voltage level and 30 MVA power rating are used for the case study. The age range for the transformer population is between 1 and 25 years. The first section of this study is on modelling of future condition of transformer population based on MM and individual condition parameter of transformers. The second section is on application of Markov chain model on the condition parameter data. The final section is on the analysis based on Chi-square test to find the goodness-of-fit between predicted and computed values for consistency to the hypothesized distribution and percentage of absolute error for results accuracy.

2. Modelling of Transformer Future Condition

MM was implemented to evaluate the future states of individual condition parameter data for the transformer population. The overall framework for modelling transformer future condition based on individual condition parameter can be seen in Figure 1. The individual condition parameter of the transformer population was ranked and sorted based on recommended limits as per IEEE Std. C57.104-2008 and IEEE Std. C57. 106-2015. Next, the average and transition probabilities for each of the condition parameters were computed based on a non-linear optimization technique. The final step was to determine the future condition states probability distribution based on the MM algorithm. Analysis was carried out based on Chi-square test and percentage of absolute error.

Figure 1. Framework for modelling the future condition parameters of the transformer population according to Markov Model (MM).

Future condition process of transformers was modelled based on discrete time stochastic processes approach for random variables known as MM which can be seen in Figure 2.

Figure 2. Five-states Markov process model for transformer future condition [24].

Future state was decided based on individual condition parameter data of employed CBM techniques, namely H₂, CH₄, C₂H₆, C₂H₄, C₂H₂, CO, CO₂, dielectric breakdown voltage, interfacial tension, colour, acidity, water content and 2-furfuraldehyde. The measured concentrations of these parameters were grouped into five discrete categories known as “very good”, “good”, “fair”, “poor” and “very poor” based on recommended limits by IEEE Std. C57. 104-2008 and IEEE Std. C57.106-2015 as tabulated in Table 1 and Table 2 [4,31,32]. State 1 and State 5 represent “very good” and “very poor” conditions respectively. However, the final states for dissolved gases and oil quality would only end up into “poor” state except for 2-FAL which could reach to “very poor” state.

Table 1. Recommended condition parameter data limit and condition for dissolved gases.

State	Condition	H2	CH4	C2H2	C2H4	C2H6	CO	CO2
		ppm	ppm	ppm	ppm	ppm	ppm	ppm
1	Very good	≤100	≤120	≤1	≤50	≤65	≤350	≤2500
2	Good	101−700	121−400	2−9	51−100	66−100	351−570	2501−4000
3	Fair	701−1800	401−1000	10−35	101−200	101−150	571−1400	4001−10,000
4	Poor	>1800	>1000	>35	>200	>150	>1400	>10,000

Table 2. Recommended condition parameter limit and condition for oil quality.

State	Condition	Dielectric Breakdown Voltage	Interfacial Tension	Colour	Acidity	Water Content	2-FAL
		kV	mN/m	g/cm3	mg KOH/g	ppm	ppb
1	Very good	≥45	≥25	≤1.5	≤0.05	≤30	0–100
2	Good	35−45	20−25	1.5−2.0	0.05−0.1	30−35	100−500
3	Fair	30−35	15−20	2.0−2.5	0.1−0.2	35−40	500−1000
4	Poor	≤30	≤15	≥2.5	≥0.2	≥40	1000−5000
5	Very poor	-	-	-	-	-	>5000

A typical MM for facilities deterioration based on [33] is shown in Equation (1). The transition probability matrix $T$ describes the probability of transitioning states within each time interval,

$$T=\left[\begin{array}{ccccc}{T}_{11}& T_{12}& T_{13}& T_{14}& T_{15}\\ 0& T_{22}& T_{23}& T_{24}& T_{25}\\ 0& 0& T_{33}& T_{34}& T_{35}\\ 0& 0& 0& T_{44}& T_{45}\\ 0& 0& 0& 0& T_{55}\end{array}\right]$$

(1)

where $T_{ij}$ is equal to the probability of a condition parameter to move from state $i$ to state $j$ in one year. Note that $T_{ij}=0$ for terms where $j$ is greater than $i.$ This imposes that the individual condition parameter cannot improve and transfer to its previous state. In total, 2 assumptions were considered in this study for simplification of the model. First, the future condition model only considered normal distribution and monotonic. Second, the summation of probabilities in each row of MM transition matrix was made equal to one. Only five $T_{ij}$ terms were needed to define MM transition matrix used in this study as shown in Equation (2).

$$T=\left[\begin{array}{ccccc}{T}_{11}& 1-T_{11}& 0& 0& 0\\ 0& T_{22}& 1-T_{22}& 0& 0\\ 0& 0& T_{33}& 1-T_{33}& 0\\ 0& 0& 0& T_{44}& 1-T_{44}\\ 0& 0& 0& 0& 1\end{array}\right]$$

(2)

The last term $T_{55}=1$, because the future condition was assumed to end up in the poorest condition. Since MM is memoryless and given an initial distribution, $q_0$, the distribution of the condition in year $n$ can be represented by Equation (3).

$$q_n=q_0{T}_n$$

(3)

Based on Equation (3), the initial condition state vector was assumed as an initial condition of a newly installed transformer where $q_0=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\end{array}\right]$. Finally, the condition state of the transformer population at $\mathrm{n}$ year can be obtained by multiplying the probability distribution for that year with transform matrix, $R^T$ as shown in Equation (4). The matrix was formed using the input from the upper limit value of each recommended limit for each parameter in each of the analyses.

$$D=q_n{R}^T$$

(4)

where $D$ is the condition value for each parameter and $R^T$ is the transform matrix.

Transition Probability Derivation

According to [34,35], there are two non-linear functions based on regression technique that can be used to compute the terms $T_{11}-T_{44}$ in the transition matrix. The first technique is minimization of summation of the squared difference between the relative frequency and discrete distribution and the second technique is minimization of the mean-square error for each row in the transition matrix. In this study, minimization of absolute difference between the predicted and computed average individual condition parameter data was employed as a nonlinear optimization technique as seen in Equation (5).

$$min\sum _{n=1}^{25}\left|C\left(n\right)-P\left(n,T\right)\right| subject to 0\le T\le 1$$

(5)

where $n$ is the number of years in each zone, $T$ is the transition probabilities ($T_{11,}{T}_{22,}{T}_{33,}{T}_{44,}$), $C\left(n\right)$ is the average of computed single-parameter data at year $n$, and $E\left(n, T\right)$ is the predicted values of conditions single-parameter data by Markov chain at year $n$. The transition matrix for each zone was then computed based on Equations (4) and (5).

3. Case Study

3.1. Application of Markov Chain Model to Transformer Condition Data

In total, 1322 oil samples from 373 distribution transformers with voltage and power ratings of 33 kV and 30 MVA were analysed. The range of age for the transformer population is between 1 to 25 years. In total, the oil samples were clustered into 5 zones of age as shown in Figure 3.

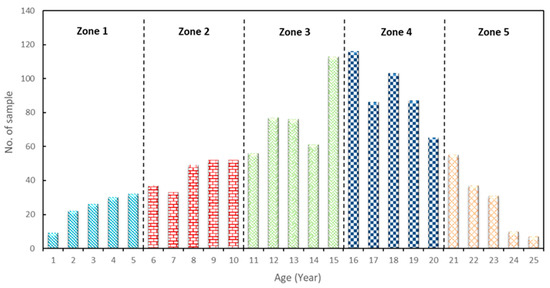
Figure 3. Distribution of oil samples used in case study.

Next, the average of each of the individual condition parameter data for age 1 to 25 were computed. Based on the computed values, the transition probabilities ($T_{11,}{T}_{22},T_{33},T_{44}$) were determined by minimization of the summation of the squared difference between the relative frequency in each year based on Equation (4). The example of the transition matrices obtained for hydrogen and 2-furfuraldehyde by each zone are tabulated in Table 3.

Table 3. Transition matrix for hydrogen and 2-furfuraldehyde according to zone.

Zone	Hydrogen, H2					2-Furfuraldehyde, 2-FAL
1	0.9766	0.0234	0	0	0	0.9900	0.0100	0	0	0
	0	0.8333	0.1667	0	0	0	0.9900	0.0100	0	0
	0	0	0.0100	0.9900	0	0	0	0.8136	0.1864	0.0000
	0	0	0	0.0100	0.9900	0	0	0	0.0252	0.9748
	0	0	0	0	1	0	0	0	0	1
2	0.9900	0.0100	0	0	0	0.9899	0.0101	0	0	0
	0	0.0100	0.9900	0	0	0	0.3947	0.6053	0	0
	0	0	0.0100	0.9900	0	0	0	0.9460	0.0594	0
	0	0	0	0.0100	0.9900	0	0	0	0.9360	0.0638
	0	0	0	0	1	0	0	0	0	1
3	0.9900	0.0100	0	0	0	0.6301	0.3699	0	0	0
	0	0.9900	0.0100	0	0	0	0.9899	0.0101	0	0
	0	0	0.0100	0.9900	0	0	0	0.9456	0.0544	0
	0	0	0	0.0100	0.9900	0	0	0	0.3139	0.6860
	0	0	0	0	1	0	0	0	0	1
4	0.9157	0.0013	0	0	0	0.0343	0.9657	0	0	0
	0	0.1164	0.8836	0	0	0	0.9899	0.0100	0	0
	0	0	0.0100	0.9900	0	0	0	0.6246	0.3754	0
	0	0	0	0.0100	0.9900	0	0	0	0.3377	0.6623
	0	0	0	0	1	0	0	0	0	1
5	0.9900	0.0100	0	0	0	0.0100	0.9900	0	0	0
	0	0.9900	0.0100	0	0	0	0.9664	0.0336	0	0
	0	0	0.0100	0.9900	0	0	0	0.2921	0.7079	0
	0	0	0	0.0100	0.9900	0	0	0	0.3099	0.6901
	0	0	0	0	1	0	0	0	0	1

Next, the future condition of the transformer for hydrogen and 2-furfuraldehyde were determined based on MM algorithm in Equation (3). The probability distribution for each year hydrogen and 2-furfuraldehyde can be seen in Equations (6) and (7), respectively.

$$\left[\begin{array}{c}{q}_1\\ q_2\\ q_3\\ q_4\\ q_5\end{array}\right]=\left[\begin{array}{ccc}{q}_0& \times & T_1\\ q_1& \times & T_2\\ q_2& \times & T_3\\ q_3& \times & T_4\\ q_4& \times & T_5\end{array}\right]=\left[\begin{array}{ccccc}0.9766& 0.0234& 0& 0& 0\\ 0.9538& 0.0423& 0.0039& 0& 0\\ 0.9315& 0.0576& 0.0071& 0& 0\\ 0.9097& 0.0698& 0.0097& 0.0071& 0\\ 0.8884& 0.0794& 0.0117& 0.0096& 0.0108\end{array}\right]$$

(6)

$$\left[\begin{array}{c}{q}_1\\ q_2\\ q_3\\ q_4\\ q_5\end{array}\right]=\left[\begin{array}{ccc}{q}_0& \times & T_1\\ q_1& \times & T_2\\ q_2& \times & T_3\\ q_3& \times & T_4\\ q_4& \times & T_5\end{array}\right]=\left[\begin{array}{ccccc}0.9900& 0.0100& 0& 0& 0\\ 0.9801& 0.0198& 0.0001& 0& 0\\ 0.9703& 0.0294& 0.0003& 0& 0\\ 0.9606& 0.0388& 0.0005& 0.0001& 0\\ 0.9510& 0.0480& 0.0008& 0.0001& 0.0001\end{array}\right]$$

(7)

Similar process was repeated to find the probability distribution for zone 2 to the last zone. The initial state, $q_0$ of the next zone was revised to the last distribution probability obtained in the previous zone. The corresponding matrices for initial state vectors used to obtain the probability distribution for hydrogen and 2-furfuraldehyde are shown in Equations (8) and (9), respectively.

$$\left[\begin{array}{c}\mathrm{Zone}1\\ \mathrm{Zone}2\\ \mathrm{Zone}3\\ \mathrm{Zone}4\\ \mathrm{Zone}5\end{array}\right]=\left[\begin{array}{ccccc}1.0000& 0& 0& 0& 0\\ 0.8884& 0.0794& 0.0117& 0.0096& 0.0108\\ 0.8449& 0.0086& 0.0087& 0.0088& 0.1290\\ 0.8035& 0.0488& 0.0004& 0.0003& 0.1470\\ 0.5172& 0.0008& 0.0008& 0.0010& 0.1983\end{array}\right]$$

(8)

$$\left[\begin{array}{c}\mathrm{Zone} 1\\ \mathrm{Zone} 2\\ \mathrm{Zone} 3\\ \mathrm{Zone} 4\\ \mathrm{Zone} 5\end{array}\right]=\left[\begin{array}{ccccc}1.0000& 0& 0& 0& 0\\ 0.9510& 0.0480& 0.0008& 0.0001& 0.0001\\ 0.9041& 0.0156& 0.0686& 0.0107& 0.0010\\ 0.0898& 0.8061& 0.0742& 0.0055& 0.0245\\ 0& 0.8529& 0.0279& 0.0191& 0.1001\end{array}\right]$$

(9)

The computed average for all condition parameters for zones 1 to 2 were used in the transition matrix for training and testing purposes, meanwhile the computed data for zones 3, 4 and 5 were used as validation to the predicted individual condition parameter data obtained from MM algorithm.

The comparison between predicted and computed individual condition parameter data throughout the sampling period are plotted in Figure 4, Figure 5 and Figure 6 respectively. The majority of the predicted H₂ are higher than computed H₂ as shown in Figure 4. The predicted and computed H₂ are in “good” condition until 8 years and 15 years, respectively. Both predicted and computed H₂ reinstate to “very good” condition until 25 years. The predicted CH₄ is higher than computed CH₄ during the first 9 years. After 9 years, the predicted CH₄ is close with computed CH₄. The predicted CH₄ is in “good” condition during the first 5 years. Between 5 and 9 years, it ends up in “fair” condition. After 9 years, it reinstates to “very good” condition. The computed CH₄ maintains in “very good” condition for 25 years. The predicted C₂H₂ is in-line with computed C₂H₂ during the first 12 years. After 13 years, the predicted C₂H₂ starts to fluctuate at values higher than computed C₂H₂. The predicted C₂H₂ is in “good” condition during the first 9 years. Between 10 and 23 years, the predicted C₂H₂ is “fair” condition. After 23 years, it reinstates to “good” condition. The computed C₂H₂ is in “very good” condition during the first 13 years. The computed C₂H₂ is in “good” condition between 14 and 24 years. After 24 years, it reinstates to “very good” condition. The trend for predicted C₂H₄ is similar to CH₄ where it is higher than computed C₂H₄ during the first 5 years and remains close to each other after 6 years. The predicted C₂H₄ is in “good” condition during the first 3 years. After 3 years, the predicted C₂H₄ ends up in “very good” condition. The computed C₂H₄ maintains in “very good” condition for 25 years. The predicted C₂H₆ shows an agreement with the computed C₂H₆ during the first 17 years. The predicted C₂H₆ deviates from computed C₂H₆ after 17 years. The predicted C₂H₆ is in “good” condition during the first 5 years. The predicted C₂H₆ enters “fair” condition between 6 and 13 years. After 13 years, it reinstates to “very good” condition. The computed C₂H₆ is in “good” condition during the first 4 years. Between 9 and 11 years, the computed C₂H₆ enters “fair” condition. After 11 years, it reinstates to “very good” condition. The predicted CO is higher than computed CO during the first 4 years. After 4 years, the majority of predicted CO shows reasonable agreements with computed CO. The predicted CO maintains in “good” condition for 25 years. The computed CO is in “very good” condition during the first 4 years. The computed CO is in “good” condition between 5 and 23 years. After 23 years, it ends up in “very good” condition. The predicted CO₂ is higher than computed CO₂ during the first 3 years. After 3 years, the majority of both predicted CO₂ shows reasonable agreements with computed CO₂. The predicted CO₂ is in “good” condition during the first 5 years. The predicted CO₂ is in “fair” condition between 6 and 23 years. After 23 years, the predicted CO₂ reinstates to “good” condition. The computed CO₂ is in “very good” condition during the first 3 years. The computed CO₂ is in “good” condition between 4 and 6 years. It enters “fair” condition between 7 and 23 years. After 23 years, the computed CO₂ reinstates to “good” condition.

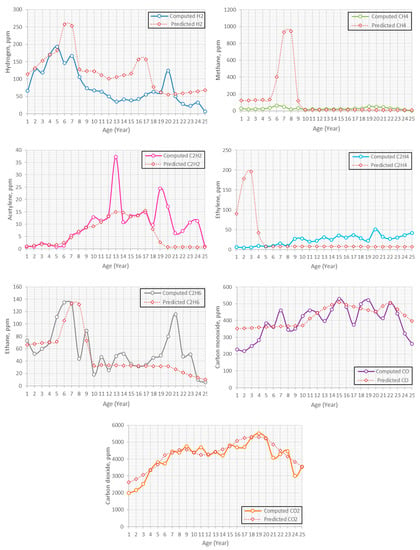
Figure 4. Comparison between computed and predicted hydrogen, methane, acetylene, ethylene, ethane, carbon monoxide and carbon dioxide.

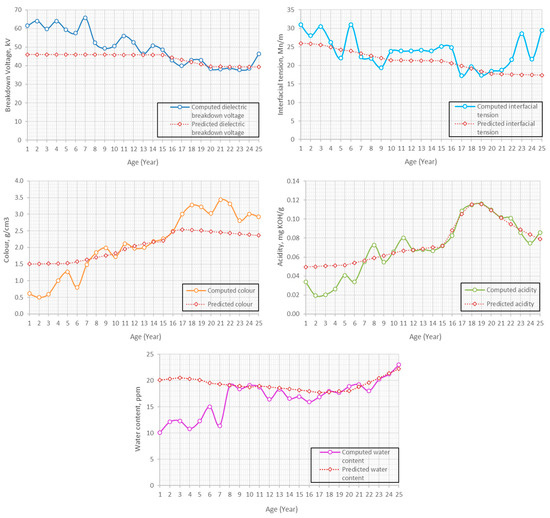
Figure 5. Comparison between computed and predicted dielectric breakdown voltage, interfacial tension, colour, acidity and water content.

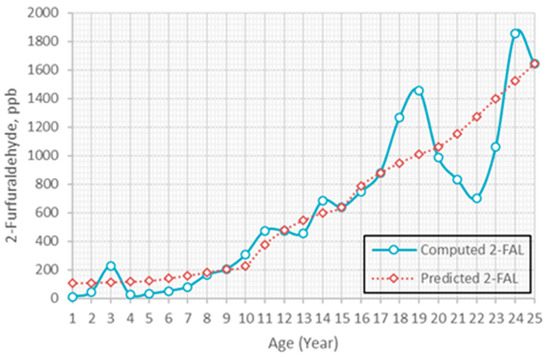
Figure 6. Comparison between computed and predicted 2-FAL.

The predicted dielectric breakdown voltage is lower than computed dielectric breakdown voltage during the first 12 years. After 12 years, the predicted dielectric breakdown voltage is close to the computed dielectric breakdown voltage. The predicted and computed dielectric breakdown voltages are in “very good” condition during the first 15 years. After 16 years, the predicted and computed dielectric breakdown voltages end up in “good” condition. The predicted interfacial tension shows an agreement with the computed interfacial tension during the first 21 years. The predicted interfacial tension deviates from computed interfacial tension starting from 22 years. The predicted interfacial tension is in “very good” condition in the first 3 years. It is in “good” condition between 3 and 16 years. The predicted interfacial tension ends up in “fair” condition after 16 years. The computed interfacial tension is in “very good” condition in the first 4 years. It is in “fair” condition between 5 and 16 years. After 16 years, the computed interfacial tension enters “fair” condition. The predicted colour is higher than computed colour during the first 7 years. The predicted colour is in-line with computed colour until 16 years and deviates after 16 years. The predicted colour is in “good” condition during the first 11 years. The predicted colour is in “fair” condition between 12 and 16 years. It enters “poor” condition between 17 and 19 years. After 19 years, the predicted colour reinstates to “fair” condition. The computed colour is in “very good” condition during the first 7 years. It is in “fair” condition between 8 and 13 years. The computed enters “fair” condition between 14 and 16 years. After 16 years, it ends up in “poor” condition. The predicted acidity is higher than computed acidity during the first 7 years. After 7 years, the predicted acidity is close with the computed acidity. The predicted and computed acidity are in “very good” condition during the first 7 years. Between 8 and 16 years, the predicted and computed acidity are in “good” condition. After 17 years, the predicted and computed acidity end up in “fair” condition. The trend for predicted water content is the same as acidity where it is higher than computed value during the first 7 years and remains close to each other after 8 years. The predicted and computed water content maintain in “very good” condition for 25 years.

The trend for predicted 2-FAL is higher than computed 2-FAL during the first 8 years and remains close to each other between 8 and 17 years. The predicted 2-FAL deviates from computed C2H6 starting from 18 years. The predicted 2-FAL is in “good” condition during the first 12 years. It is in “fair” condition between 13 and 18 years. After 18 years, it ends up in “poor” condition. The computed 2-FAL is in “very good” condition during the first 7 years. It is in “good” condition between 8 and 13 years. The computed 2-FAL enters “fair” condition between 14 and 22 years. After 22 years, it ends up in “poor” condition.

3.2. Chi-Square Test and Percentage of Absolute Error

The Chi-square test shown in Equation (10) was applied for individual condition parameters to find the goodness-of-fit between predicted and computed values for consistency to the hypothesized distribution.

$${\mathrm{X}}^2={\sum }_{n=1}^{25}\frac{{\left(P_n-C_n\right)}^2}{C_n}$$

(10)

where $n$ is the number of observations, $C_n$ is the computed value at $n$ year, $P_n$ is the predicted value at $t$ year and ${\mathrm{X}}^2$ is a Chi-square distribution coefficient with degree of freedom, $n-1$. In this study, the degree of freedom was considered as 0.05, therefore the area of rejection, $\mathsf{\alpha }$ fall after 13.85. The ${\mathrm{X}}^2$ results for H₂, CH₄, C₂H₂, C₂H₄, C₂H₆, CO, CO₂, dielectric breakdown voltage, interfacial tension, colour, acidity, water content, and 2-furfuraldehyde are tabulated in Table 4 and Table 5, respectively. The majority of the predicted values for H₂, C₂H₂, C₂H₆, CO and CO₂ fall close to the computed values as shown in Table 4. The ${\mathrm{X}}^2$ for CH₄ and C₂H₄ fall in the area of rejection due to mainly by higher discrepancies between the predicted and computed values in Zone 1 for both gases.

Table 4. Chi-square distribution coefficient for dissolved gases.

	H2	CH4	C2H2	C2H4	C2H6	CO	CO2
$X^2$	1.12	68.55	2.32	69.23	2.57	0.31	0.12

Table 5. Chi-square distribution coefficient for oil quality.

	Dielectric Breakdown Voltage	Interfacial Tension	Colour	Acidity	Water Content	2-FAL
$X^2$	0.76	0.71	2.78	0.71	1.03	0.59

The majority of predicted values for dielectric breakdown voltage, interfacial tension, colour, acidity, water content and 2-FAL are observed to fall close to the computed values which indicate consistency to the hypothesized distribution as shown in Table 5.

The average percentage error between the predicted and computed of individual condition parameter curves was carried out based on Equation (11).

$$Average percentage error (\%)=\frac{{\sum }_{n=1}^{25}\left(\frac{\left|Y_n-X_n\right|}{\left|Y_n\right|}\times 100\%\right)}{n}$$

(11)

where $Y_n$ is the computed individual condition parameter, $X_n$ is the predicted individual condition parameter, and $n$ is the age of the transformer. The computed average percentage error for individual condition parameter and accuracy levels are tabulated in Table 5 and Table 6, respectively. The highest average percentage error in zone 1–5 is C₂H₄ and the lowest is H₂ for a period of 25 years as shown in Table 6. Zooming into zone 3–5, the highest average percentage error is C₂H₂ and the lowest is CO₂. In term of accuracy level, CH₄ has the highest accuracy followed by H₂, CO, CO₂, C₂H₄, C₂H₆, C₂H₂. The distribution of absolute percentage errors for H₂, CH₄, C₂H₂, C₂H₄, C₂H₆, CO and CO₂ are shown in Figure 7.

Table 6. Average percentage error and accuracy level for dissolved gases.

	H2	CH4	C2H2	C2H4	C2H6	CO	CO2
Average percentage error for zone 1–5 (%)	2.68	11.90	12.09	17.65	13.67	3.95	2.83
Average percentage error zone 3–5 (%)	2.91	1.48	18.66	11.84	13.10	3.44	2.81
Accuracy level (%)	97.09	98.52	81.34	88.16	86.90	96.56	97.19

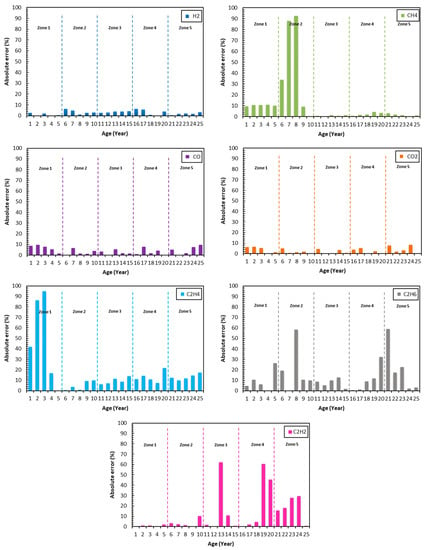
Figure 7. Percentage of absolute error between computed and predicted hydrogen, methane, acetylene, ethylene, ethane, carbon monoxide, carbon dioxide.

Colour has the highest average percentage error in zone 1–5 followed by dielectric breakdown voltage, interfacial tension, water content, acidity and 2-FAL for a period of 25 years as shown in Table 7. In zone 3–5, the highest and lowest average percentage errors are colour and acidity. Acidity has the highest accuracy while colour has the lowest accuracy. Figure 8 and Figure 9 show the distribution of absolute percentage errors for dielectric breakdown voltage, interfacial tension, colour, acidity, water content and 2-FAL.

Table 7. Average percentage error and accuracy level for oil quality.

	Dielectric Breakdown Voltage	Interfacial Tension	Colour	Acidity	Water Content	2-FAL
Average percentage error for zone 1–5 (%)	14.79	13.22	17.44	3.96	6.83	2.71
Average percentage error zone 3–5 (%)	6.62	14.51	16.24	1.66	2.12	3.58
Accuracy level (%)	93.38	84.49	83.76	98.34	97.88	96.42

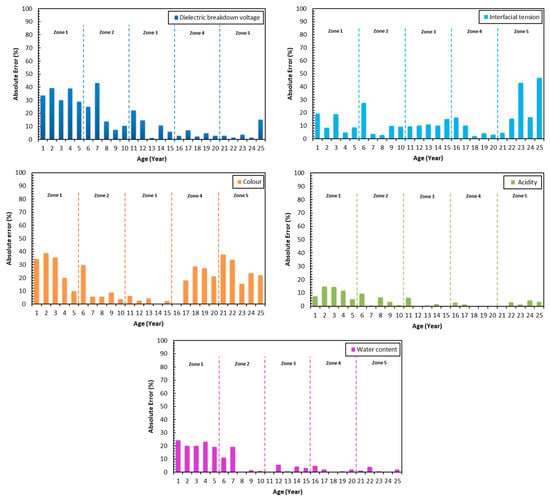
Figure 8. Percentage of absolute error between computed and predicted dielectric breakdown voltage, interfacial tension, colour, acidity and water content.

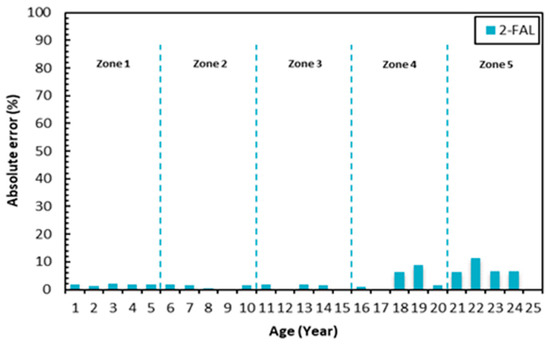
Figure 9. Percentage of absolute error between computed and predicted 2-furfuraldehyde.

4. Conclusions

It is found that MM can be used to represent approximate majority of the condition parameters. The prediction accuracy depends on the availability of the data at different zones. Overall, the trends of the predicted are close to computed condition parameters. Analysis based on Chi-squared test for goodness-of-fit reveals that the ${\mathrm{X}}^2$ values of majority condition parameters data fall outside the rejection area, $\mathsf{\alpha }=13.85$ for 0.05 degree of freedom. However, the ${\mathrm{X}}^2$ for CH₄ and C₂H₄ fall in the area of rejection which are 68.55 and 69.23, where it is mainly contributed by higher discrepancies between predicted and computed condition parameters in Zone 1. It is also observed that the lowest and highest accuracy levels for all the predicted values of all the condition parameters are 81.46% and 98.52%. Overall, MM can be implemented by utilities that utilize CBM data in their asset management approach for prediction of transformers future condition.