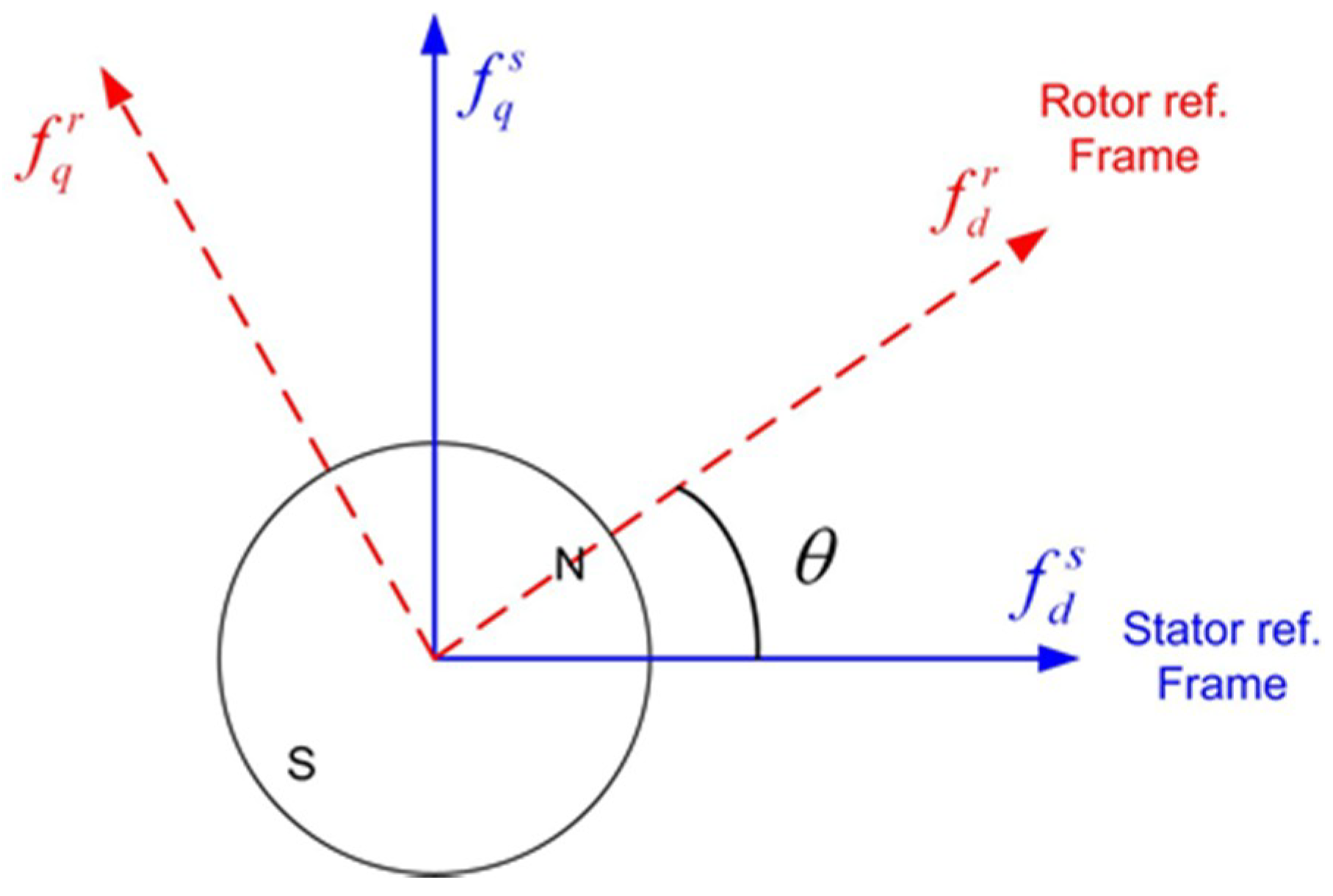
1. Introduction
Deadbeat direct torque and flux control (DB-DTFC) was developed by combining the features of deadbeat control and direct torque control (DTC) for induction motor drive systems [
1,
2]. DB-DTFC has been implemented for various types of electrical machine drives such as IPMSM (interior permanent magnet synchronous motor) drives [
3], wound field synchronous machine drives [
4], and synchronous reluctance machine drives [
5]. Recently, DB-DTFC has been applied for implementation of self-sensing control [
6,
7] and fault-tolerant control [
8]. In [
2,
3,
4,
5], it has been presented that DB-DTFC shows advantages over other motor control algorithms, for example, fast dynamic performance and less torque ripple. However, parameter sensitivity is one of the critical issues to be investigated because DB-DTFC algorithm is developed based on an inverse electrical machine model. The parameter sensitivity issue can be reduced by using online parameter identification methods but the methods are typically complicated to implement [
9,
10,
11]. In [
12,
13], robustness evaluation of DB-DTFC is presented with respect to parameter variations for induction machine (IM) drives and IPMSM drives, respectively. While the torque error, command tracking performance of DB-DTFC for IM, and IPMSM drives have been analyzed, the stability of DB-DTFC with respect to machine parameter variations has not been investigated. In [
14], disturbance to a system is estimated using a hybrid Kalman estimator and improvement of robustness is achieved. Not only robustness but also stable operation of motor drives is important, especially for transportation applications, for example, aircraft and electric vehicles.
Though DB-DTFC has shown higher dynamic performance and robustness from previous research, parameter sensitivity is still an important issue to investigate because DB-DTFC is an algorithm developed based on machine model and estimated parameters. In particular, the stability of DB-DTFC with respect to parameter variations should be investigated for practical applications and has not been investigated in other research. Therefore, investigating the stability of a DB-DTFC motor drive with respect to parameter variations is necessary. A few stability evaluation methods for motor drive systems have been presented. The Lyapunov stability theory is applied for stability evaluation of an induction machine drive in [
15,
16,
17]. Using the Lyapunov stability theory, it can be determined if a nonlinear system is (1) Lyapunov stable, (2) asymptotically stable, or (3) exponentially stable. However, the dynamic characteristics of the system are disregarded. In [
18], a load angle limiting method is applied to determine a stable region of motor drives. However, the load angle limiting method is torque limitation methods for stable operation of motor drives. A pole-zero migration method is used to investigate stability of motor drives in [
19,
20,
21]. From the pole-zero migration, not only system stability can be investigated but also system dynamic properties, such as frequency of oscillation and rate of decay. Also, the pole-zero migration can be clearly shown in the s-domain and z-domain for analog and digital systems, respectively. Since DB-DTFC is developed based on discrete time model of electrical motors, eigenvalue migration at z-domain is presented in this paper. The eigenvalue migration can be implemented in a linear system while CVC (current vector control) and DB-DTFC IPMSM drives are nonlinear systems. Therefore, deriving linear system models of both IPMSM drives is required. A small signal model or an operating point model is a modeling method used to approximate the dynamics of systems, including nonlinear components, with a linear equation. Using a small signal model of a nonlinear system, the dynamic response and characteristics of the system can be investigated when a small perturbation is applied. Therefore, small signal modeling has been applied for stability analysis of motor control systems and power converters [
22,
23,
24]. In this paper, small signal models of CVC and DB-DTFC IPMSM drives are derived for implementation of EV (eigenvalue) migration.
This paper begins with a brief introduction of a DB-DTFC algorithm and state observers for IPMSM drives. Using the DB-DTFC equation, an operating point model is derived. Then, the eigenvalue migration of DB-DTFC and CVC at z-domain is compared by applying the US06 supplemental federal test procedure (SFTP) driving cycle for practical verification in simulations and experiments.
3. Derivation of Operating Point Model of CVC and DB-DTFC IPMSM Drives
3.1. Operating Point Model of IPMSMs
It is known that a nonlinear system behaves similarly to its linearized approximation around an equilibrium point [
26]. Therefore, the nonlinear model can be linearized using an operating point model (small signal model). In addition, the stability of a system can be investigated using the operating point model. The operating point models of IPMSM drives can be described by the following equations from [
20]:
In Equations (10) to (14), Δ indicates the perturbation of each state,
p represents the derivatives of corresponding variables, and o denotes steady state values. The operating point model of IPMSM drives can be formed in a state-space representation. Based on the operating point models in continuous time, Equations (10) through (14), the operating point models in discrete time can be derived as in Equations (15) through (19).
The voltage and current operating point (small signal) model equations, Equations (15) and (16), can be formed in a matrix as in Equation (20):
where
The torque and stator flux linkage operating point (small signal) model equations, Equations (17) and (18), can be formed in a matrix as in Equation (21):
where
.
Then, the operating point model between torque and voltage can be written as in Equation (22):
where
.
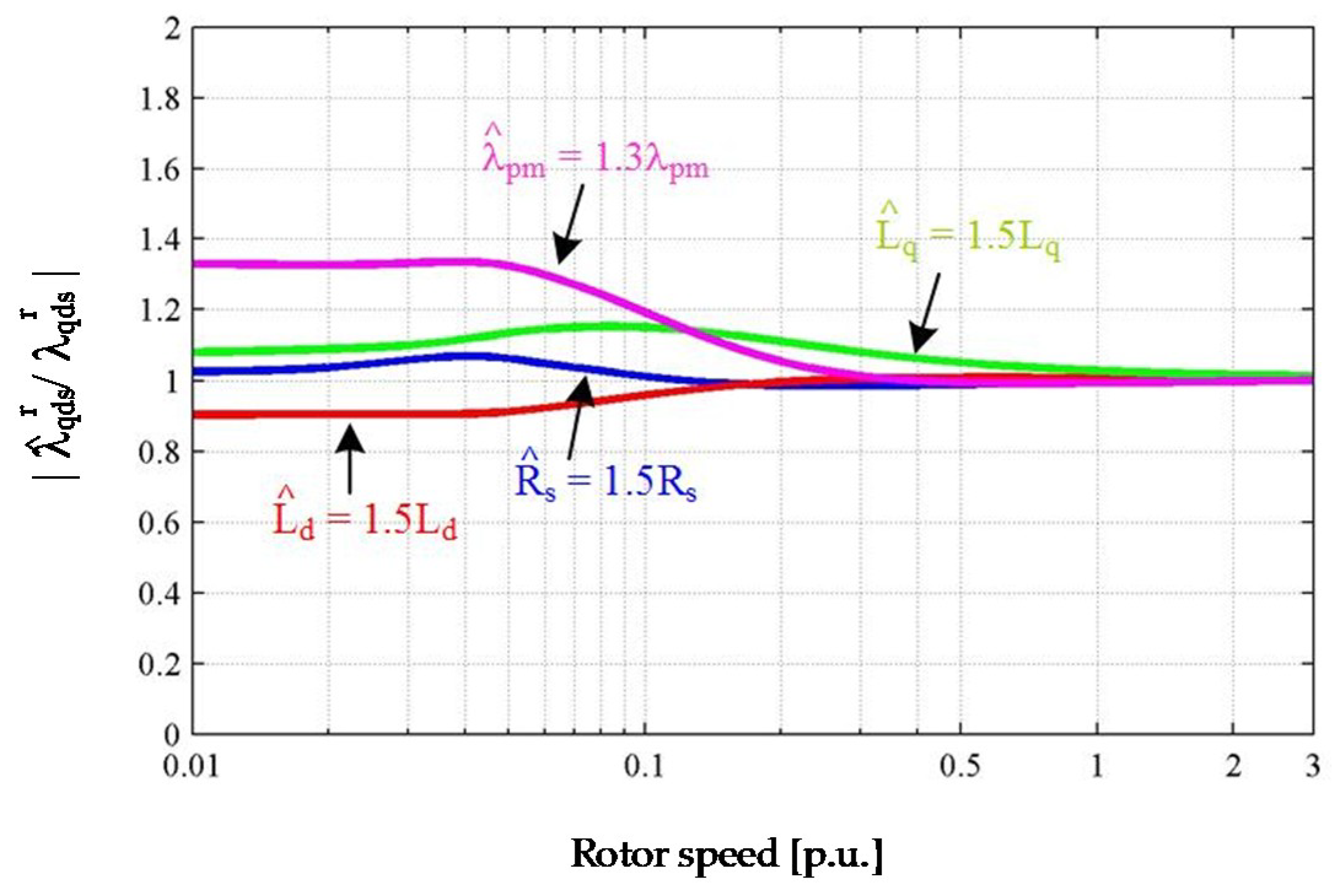
The operating point model, Equation (22), only covers a physical system, i.e., an IPMSM, and its dynamics. Therefore, a controller of an IPMSM is not included in Equation (22). It should be noted that the derived operating point model is sensitive to machine parameter variations such as q-axis inductance saturation with respect to stator current magnitude and permanent magnet flux linkage with respect to temperature. For more accurate modeling, either of the following can be applied as parameters in the operating point model: (1) Look-up table-based parameters varying as a function of operating conditions, or (2) calculated parameters by online estimation method. In this paper, constant parameters are used for analysis. In the following section, operating point models including DB-DTFC and CVC are derived.
3.2. Operating Point Model of DB-DTFC IPMSM Drives
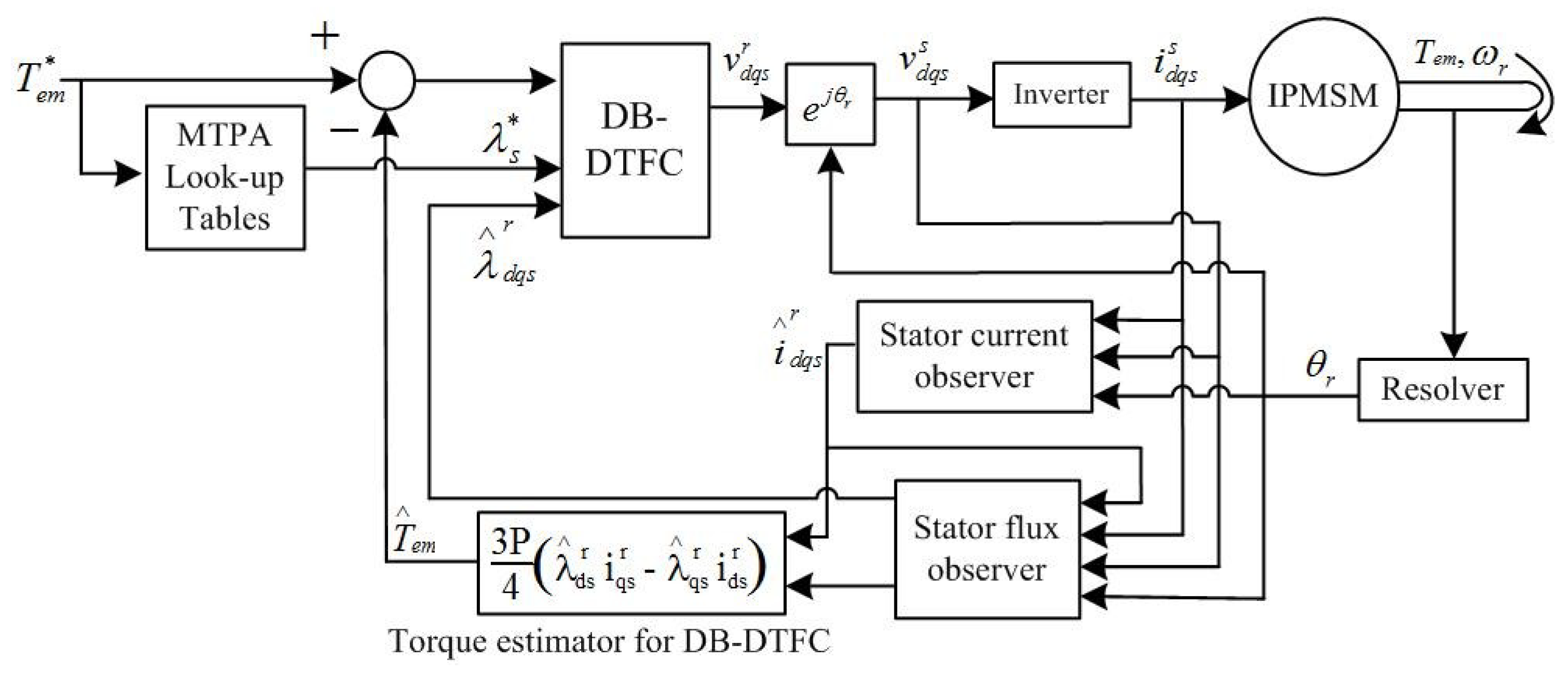
In
Figure 6, a block diagram of a DB-DTFC IPMSM drive is shown.
As shown in
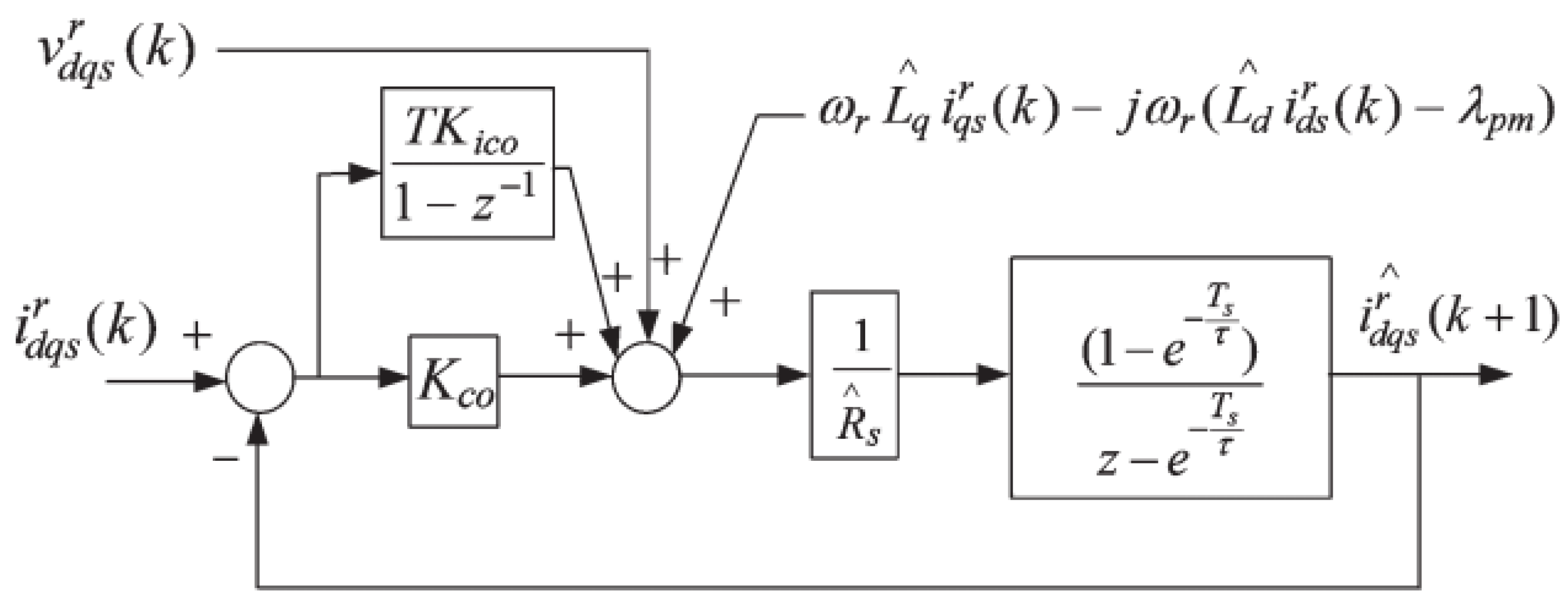
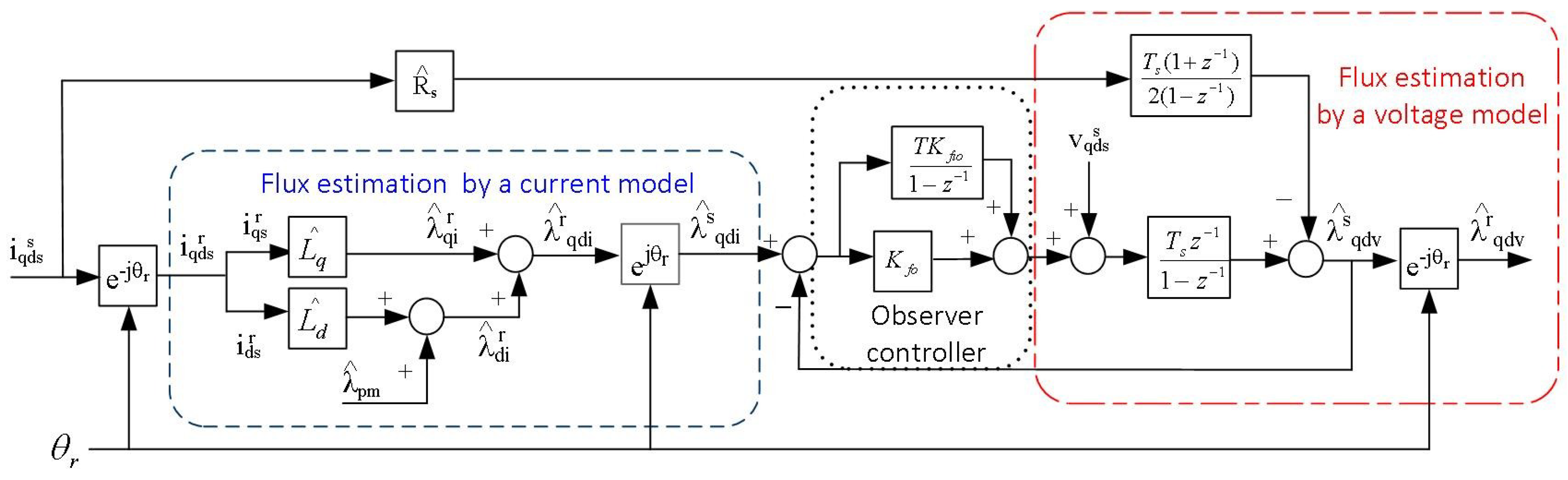
Figure 6, torque and stator flux linkage commands, estimated torque and estimated stator flux linkage are input signals of the DB-DTFC algorithm block. For efficient operation of a DB-DTFC IPMSM drive, pre-calculated copper loss minimizing stator flux linkage is selected from a maximum torque per ampere (MTPA) look-up table as stator flux linkage command. For estimation of torque and stator flux linkage, a stator current observer and a stator flux linkage observer are used in a DB-DTFC IPMSM drive. Block diagrams of observers can be found in
Figure 2 and
Figure 4.
In this section, an operating point model (or a small signal model) of a DB-DTFC IPMSM drive is derived. Since DB-DTFC is a model inverse solution, a closed-loop system including DB-DTFC can be written as in Equation (23):
A transfer function of a closed loop DB-DTFC system can be derived as in Equation (24) by expanding Equation (23):
If the estimated machine parameters match the actual machine parameters, that is,
A =
,
B =
,
C =
, and
D =
, the transfer function becomes deadbeat as in Equation (25):
If estimated parameters do not match the actual machine parameters, the characteristic equation, the denominator of the transfer function of the closed loop DB-DTFC system becomes Equation (26):
The roots of the characteristic equations are the eigenvalues (EVs) of the closed loop DB-DTFC system. The EV migration on a z-plane shows properties of IPMSM dynamics, such as stability, response time, and oscillation.
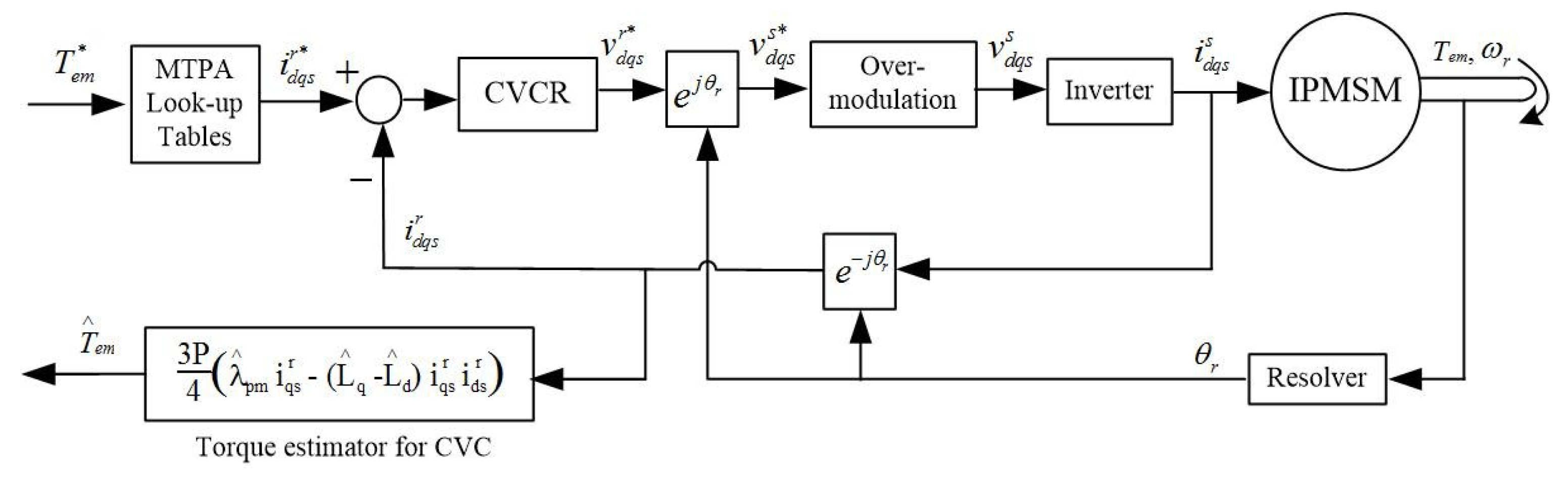
3.3. Operating Point Model of CVC IPMSM Drives
A block diagram of a current vector controlled (CVC) IPMSM drive is seen in
Figure 7.
For CVC, a closed loop system including PI controllers can be derived as in Equations (27) and (28):
The operating point model equations of the closed loop CVC system can be written as in Equations (29) and (30):
By substituting Equation (19) into Equations (29) and (30), Equations (29) and (30) become functions of
and
, as shown in Equations (31) and (32):
Equations (31) and (32) can be written in a matrix form as in Equation (33):
where
The operating point (small signal) models for the DB-DTFC and CVC IPMSM drives are derived in Equations (26) and (33), respectively. Using the operating point (small signal) models, the EV migration of each motor drive is analyzed in simulations and experiments.
4. Simulation Results
Since most driving cycles cover a wide operating space of a motor drive, a driving cycle is chosen as the load and command trajectories for a stability evaluation of DB-DTFC and CVC IPMSM drives. Among automotive driving cycles, the US06 SFTP automotive driving cycle is selected as a stability test trajectory in this paper because it contains high acceleration conditions, which are more suitable for dynamic operation testing of a motor drive. Torque command trajectory for US06 SFTP is developed by multiplying traction force and wheel radius of a test vehicle as in Equation (34), where
Ttr is the traction torque,
Ftr is the fraction force, and
Rwh is the wheel radius of a test vehicle:
Equation (35) is an equation to calculate traction force;
Km is the rotational inertia,
mv is the mass of a test vehicle in kg,
av is the acceleration of a test vehicle, and
Fdrag is the drag force. The drag force in Equation (35) can be calculated using Equation (36):
In Equation (36), Dair is air density and Cd is the aerodynamic parameter, which is typically 0.2~0.4. Af is the front area of a test vehicle and vx is the velocity of a test vehicle in meters per second. For more accurate torque trajectory development, additional forces such as rolling resistance force can be applied. Since the actual speed and torque trajectories of the US06 driving cycle cannot be applied directly, the trajectories are adjusted to fit to the rated capacity of the test IPMSM. Time range and scale are also changed so that the data size of the simulation results does not exceed the memory capacity of a computer.
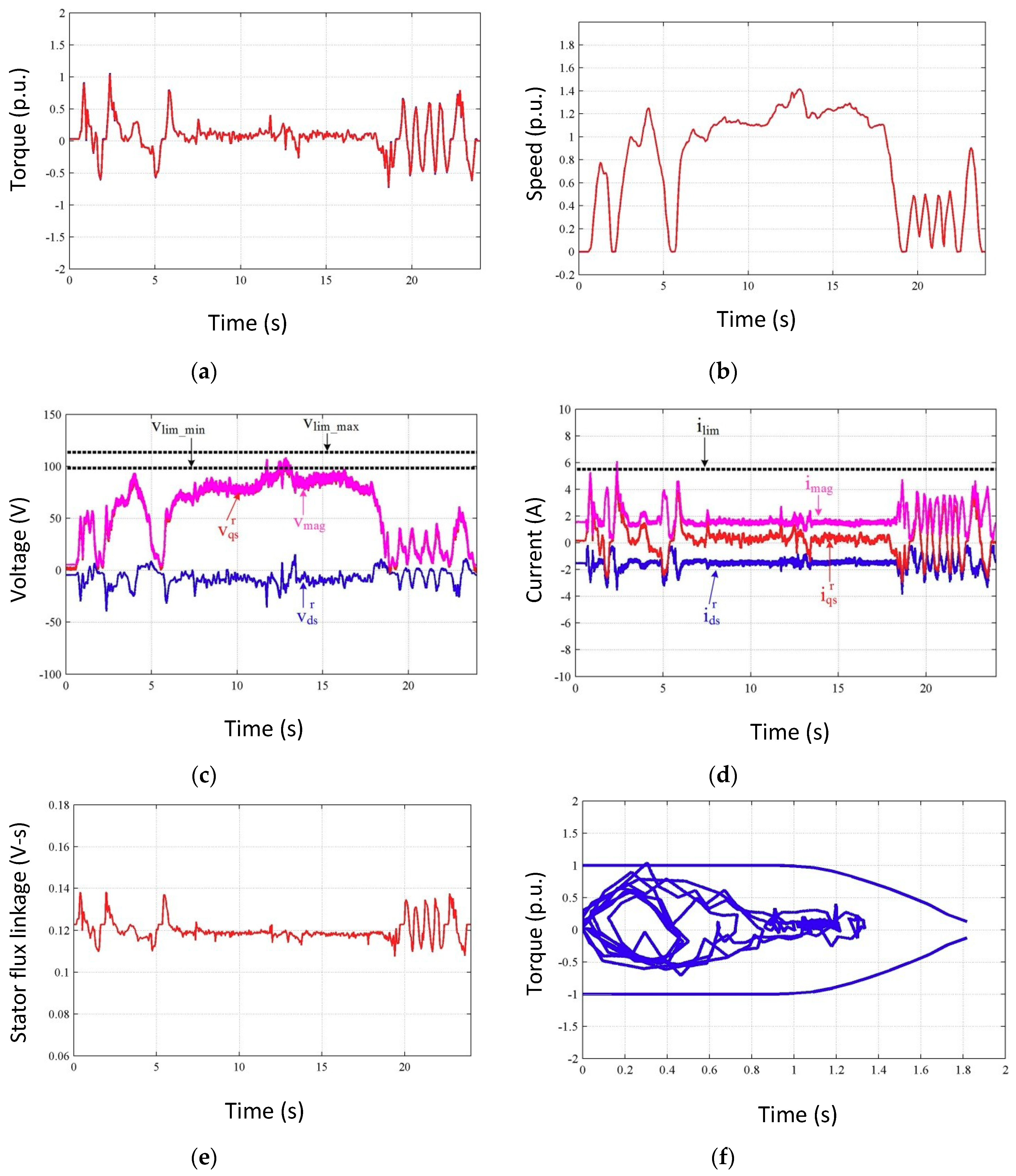
The simulation results for the US06 SFTP automotive driving cycle using DB-DTFC and CVC are shown in
Figure 8. Since simulation results using both control algorithms are the same, the results are overlaid. As shown in the simulation results, the operating speed range is increased over the rated speed (
Figure 8b), including flux weakening operation (
Figure 8e,f), and the torque trajectory of the driving cycle covers up to the rated torque of the test IPMSM (
Figure 8a). In addition to operation within a rated operating condition, operation at voltage and current limits (
Figure 8c,d) is also investigated when the test IPMSM is driven along the US06 automotive driving cycle. Since the MTPA look-up tables applied for DB-DTFC and CVC shown in
Figure 6 and
Figure 7 are developed using identical parameters and conditions, the d and q axis current vectors are the same for both control methods. For implementation of DB-DTFC, stator flux linkage and stator current observers are required. Therefore, the complexity and computational effort are higher than in CVC. From the simulation results in
Figure 8, the advantages of DB-DTFC over CVC are not directly shown. Though the US06 SFTP is one representative dynamic driving cycle, the corresponding speed and torque trajectories are relatively smooth to present the performance difference between the CVC and DB-DTFC algorithms. A comparison of the CVC and DB-DTFC algorithms based on the simulation results is given in
Table 1.
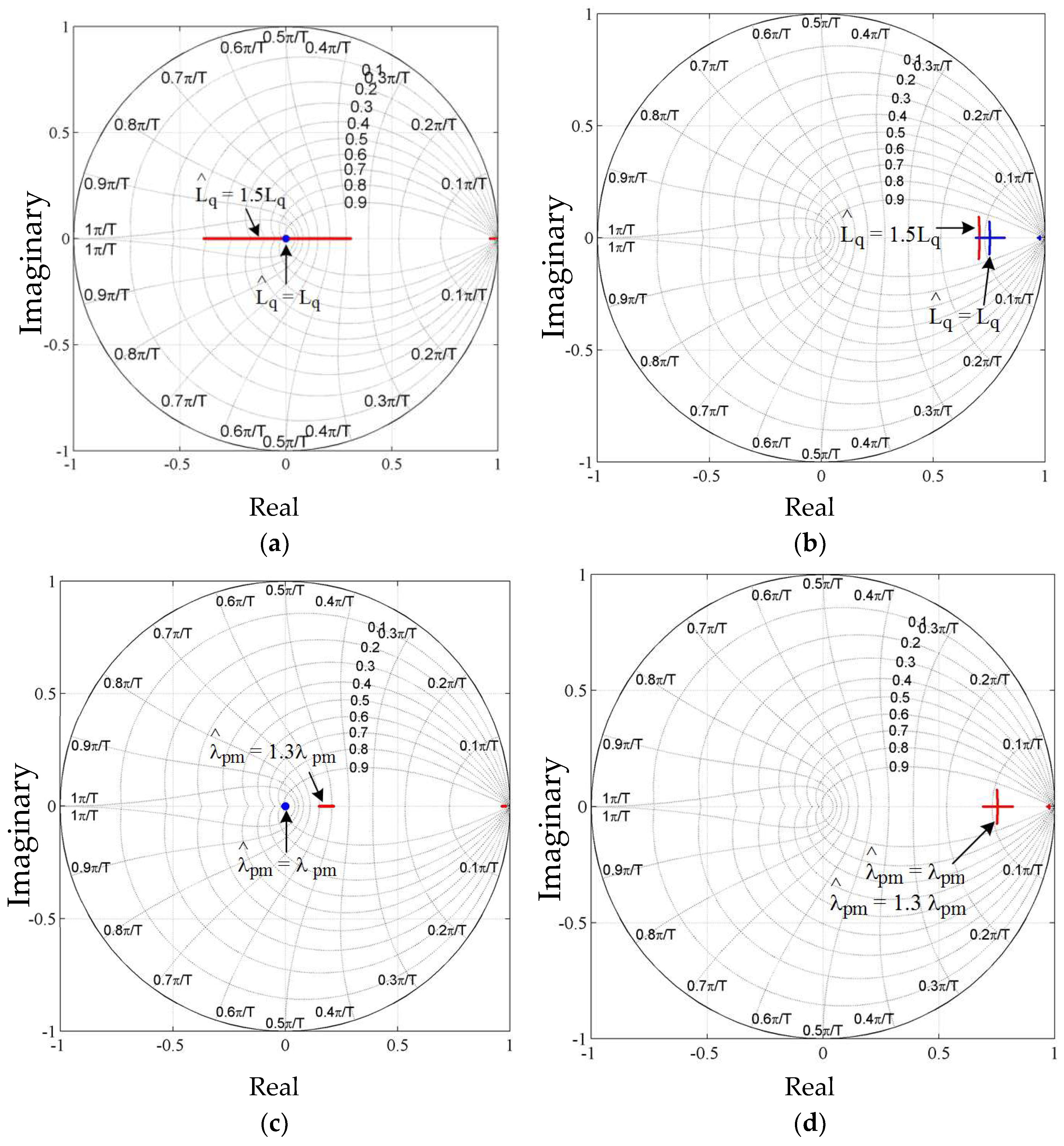
In addition to analyzing CVC and DB-DTFC using time domain simulation results, the EV migration of CVC and DB-DTFC is compared at different points. Utilizing data from the simulation results in
Figure 8 and the derived operating point (small signal) models of DB-DTFC and CVC IPMSM drives, the EV migration of each system can be investigated as shown in
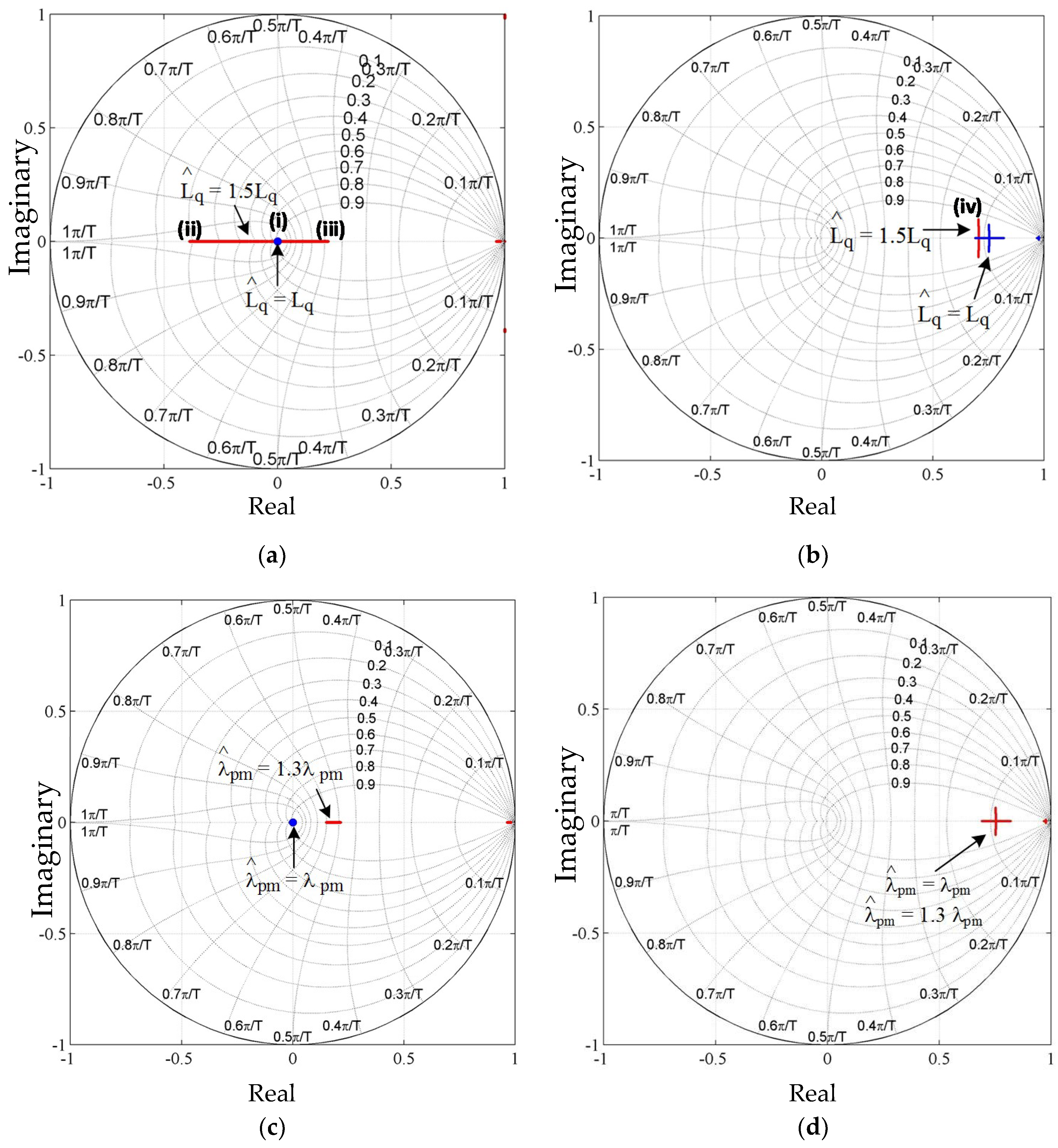
Figure 9. To investigate the EV migration characteristics of the CVC and DB-DTFC IPMSM drive systems with respect to machine parameter variations, q-axis inductance is detuned by 50% of its actual value intentionally, as shown in
Figure 9a,b, and permanent magnetic flux linkage is also detuned by 30% of its actual value, as shown in
Figure 9c,d. In the case of a DB-DTFC IPMSM drive, poles are always located at the center of a z-plane, as seen in
Figure 9a,c, if the estimated parameters used for the DB-DTFC algorithm exactly match the actual electrical machine parameters. This means that the deadbeat response is achieved along the torque and speed trajectories. If the parameters in the DB-DTFC and the machine parameters are different, the poles move away from a center of a z-plane, as seen in the red trajectories in
Figure 9a,c. As a pole moves away from the center of a z-plane, the dynamic response becomes slower, which means that deadbeat response is not achieved any more. Though deadbeat response is not achieved when machine parameters do not match, faster dynamic response can still be achieved using DB-DTFC than CVC. In the case of a CVC IPMSM drive, poles are located and move around near the bandwidth of the current vector controller, as shown in
Figure 9a,c. The location of poles is changed as shown in
Figure 9b when detuned q-axis inductance is used because inductance is used for calculation of controller gains of a current vector controller.
Since 50% higher q-axis inductance is used for controller gain calculation, the bandwidth of the controller becomes higher and a faster dynamic response is achieved than the desired dynamic response shown in
Figure 9b. Unlike q-axis inductance variation, a change in the permanent magnet flux linkage does not affect the dynamic characteristics, as shown in
Figure 9d, because permanent magnet flux linkage is not used for controller gain tuning. As seen in the simulation results in
Figure 9, eigenvalues are located within the unit circle in the z-plane for both the CVC and the DB-DTFC IPMSM drives. This means that the operation of both motor drive systems is stable along the US06 automotive driving cycle regardless of the machine parameter variations.
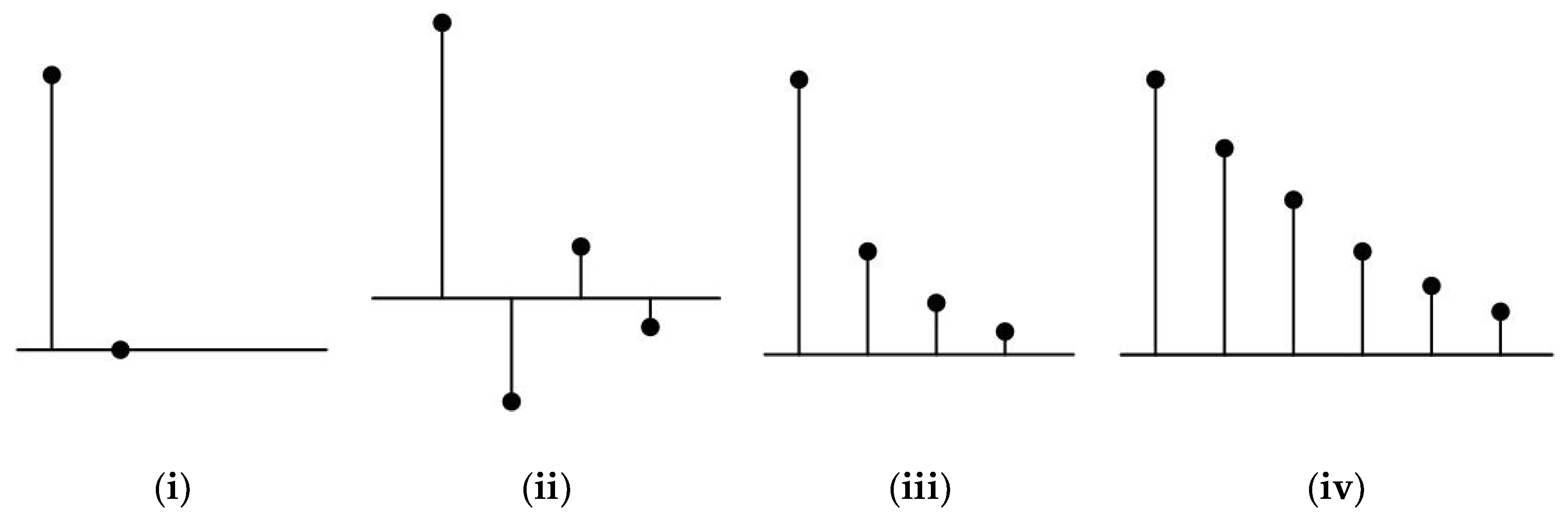
Figure 10 shows corresponding impulse responses with respect to EV locations of the DB-DTFC and CVC IPMSM drives specified in
Figure 9.
As shown in
Figure 10a, deadbeat response can be achieved when an accurately estimated parameter is used for the implementation of DB-DTFC. However, DB-DTFC sometimes results in forced oscillations, as seen in
Figure 10b, or a deadbeat response is not achieved, as seen in
Figure 10c, when an inaccurate machine parameter is used for the implementation of DB-DTFC. Though forced oscillation occurs, the oscillation does not continue for a long time. This means that the dynamic performance of DB-DTFC is still faster than that of CVC, regardless of the forced oscillation.
5. Experimental Results
Following simulation, the eigenvalue migration of DB-DTFC and CVC IPMSM drives is implemented and verified experimentally. The experimental test set-up is shown in
Figure 11 and the specifications of the test IPMSM are summarized in
Table 2.
In
Figure 11, the test IPMSM is controlled in a torque control mode and a load SPMSM is controlled in a speed control mode. Between the IPMSM and the SPMSM in
Figure 11, a torque detector (SS-505, Ono Sokki, Yokohama, Japan) is mounted and a shaft torque of the IPMSM is measured; the torque measurement is displayed through a torque meter. During the experiment, an AIX DSP control development system (XCS2000, Analog Devices, Norwood, MA, United States) is used for controlling and sensing signals. Control algorithms are developed using C++ language and downloaded to a DSP. The line current of a motor is measured by a hall-type LEM LA 55-P current sensor and 10 kHz of PWM sampling frequency is applied during experiment. For an inverter drive, a Semikron power converter (Semitop Stack, Semikron, Nuremberg, Germany) rated for 350 V
dc and 26 A is used.
Figure 12 shows the Semikron power converter used during the experiment.
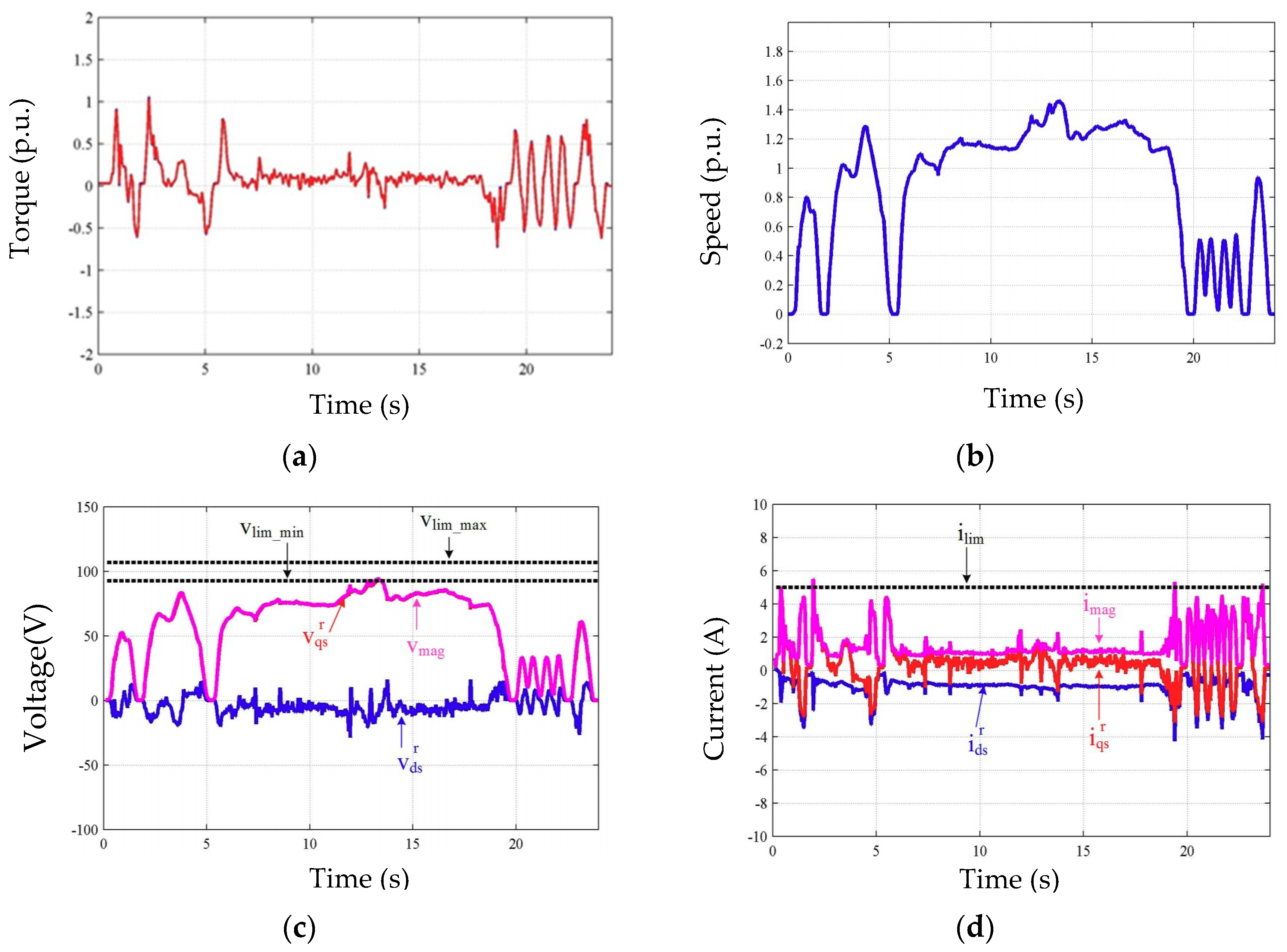
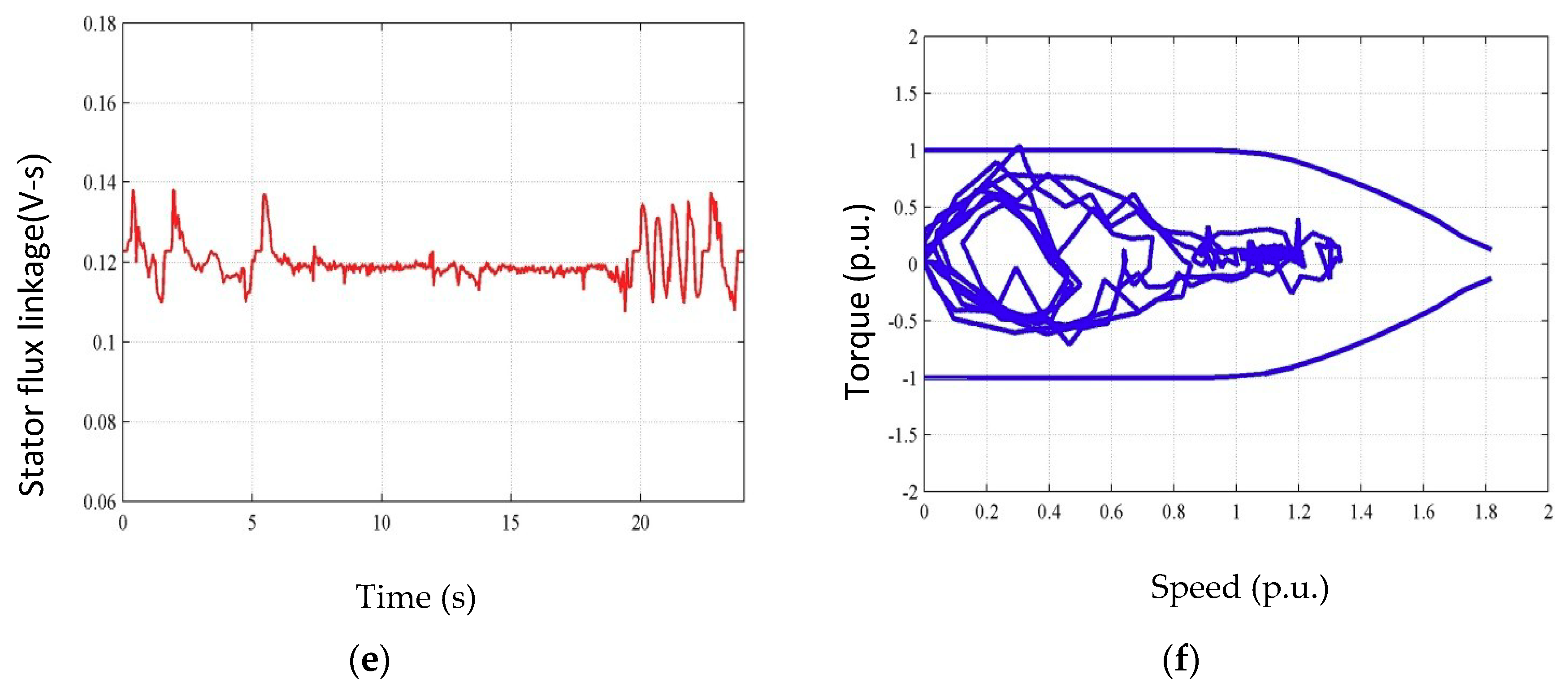
For stable operation of CVC and DB-DTFC motor drives, the US06 SFTP automotive driving cycle was applied. Rather than using actual torque and speed trajectories, the trajectories of the US06 driving cycle are scaled. During the experiment, a reduced DC link voltage is applied for safe operation of the test IPMSM drive, the load machine drive, and the torque sensor. The time range is also scaled down so that the saved data size does not exceed the memory capacity of a controller. The experimental results for the US06 SFTP automotive driving cycle using DB-DTFC are shown in
Figure 13.
The torque trajectory increases up to the rated torque of the test IPMSM and the speed trajectory is increased beyond the rated speed of the test IPMSM as shown in
Figure 13a,b,f. Also, the voltage and current limited operation can be observed in
Figure 13c,d when the test motor drive is operated along the US06 automotive driving cycle. In
Figure 13d, a rated current of the test IPMSM is marked as the current limit. A city driving cycle and a high driving cycle are combined in the US06 SFTP. Therefore, it is observed in
Figure 13f that the test IPMSM operates at both low speeds and high torque conditions and at high speeds and low torque operating conditions, which correspond to a city driving cycle and a highway driving cycle, respectively.
The operating point (small signal) models for the DB-DTFC and CVC IPMSM drives are derived in Equations (21) and (28), respectively. The EV migration of each motor drive is analyzed using the operating point (small signal) models derived for DB-DTFC and CVC IPMSM drives in Equations (21) and (28) and the experimental data shown in
Figure 14. For evaluation of the parameter sensitivity of eigenvalue migration for each control algorithm, the q-axis inductance is detuned by 50% of its actual value and the permanent magnetic flux linkage is detuned by 30% of its actual value. The EV migration results of DB-DTFC and CVC IPMSM drives are shown in
Figure 14.
Both the DB-DTFC and the CVC IPMSM drives are shown to be operating at a stable region when the torque and speed trajectories for the US06 automotive driving cycle are applied because the eigenvalues are located within the unit circle in the z-plain, as seen in
Figure 14. As seen in
Figure 14a,c, a deadbeat response can be achieved when the accurate estimated parameter is used. When the machine parameters, a permanent magnetic flux linkage and a q-axis inductance, are detuned, the DB-DTFC IPMSM drive still shows faster dynamic performance than the CVC IPMSM drive. However, a deadbeat response cannot be perfectly achieved, and a well-damped forced oscillation property is observed in the DB-DTFC IPMSM drive.