Abstract
A smart grid facilitates more effective energy management of an electrical grid system. Because both energy consumption and associated building operation costs are increasing rapidly around the world, the need for flexible and cost-effective management of the energy used by buildings in a smart grid environment is increasing. In this paper, we consider an energy management system for a smart energy building connected to an external grid (utility) as well as distributed energy resources including a renewable energy source, energy storage system, and vehicle-to-grid station. First, the energy management system is modeled using a Markov decision process that completely describes the state, action, transition probability, and rewards of the system. Subsequently, a reinforcement-learning-based energy management algorithm is proposed to reduce the operation energy costs of the target smart energy building under unknown future information. The results of numerical simulation based on the data measured in real environments show that the proposed energy management algorithm gradually reduces energy costs via learning processes compared to other random and non-learning-based algorithms.
1. Introduction
The term “smart grid” refers to a method of operating within the electrical grid system that is associated with smart energy meters, Energy Storage Systems (ESSs), Renewable Energy Sources (RESs), and communication networks among others [1]. In a smart grid environment, where energy supply and demand are rapidly increasing in modern times, one of the most important issues is developing an effective Energy Management System (EMS) to achieve various goals such as reducing energy consumption, balancing energy supply and demand, increasing the utilization of RES, and minimizing energy costs [2]. However, energy management in a smart grid is a very challenging task given the informational unknowns about factors that change over time, such as load requirements, energy prices, and amount of energy generation. For example, the amount of energy generated by RES such as a Photovoltaic (PV) system is strongly influenced by weather conditions that change over time. The variability of weather conditions makes the amount of energy generation hard to be predicted, consequently leading to the difficulty in the energy management.
In recent years, many research groups working on the smart grid have focused on improving EMS in various environments. Many studies, including [3,4], have focused on energy management for Thermostatically Controlled Loads (TCLs). These works have tried to derive the optimal control policy of TCLs in order to reduce the energy consumption of the smart grid or to meet the requirement of ancillary services while guaranteeing users’ comfort. The energy management of ESS in microgrid environments has been researched in literature. The term “microgrid”, which refers to a localized small electricity grid, can be occasionally disconnected from the traditional centralized grid and operate in an island-mode by leveraging backup energy resources such as ESS, fuel generators, and RES. These research efforts in [5,6,7,8] focused on decreasing dependency on the external grid or balancing between energy supply and demand by increasing ESS utilization in the microgrids. There has also been a considerable increase in the interest in energy management of Vehicle-to-Grid (V2G) systems [9,10,11,12]. By intelligent management of Electric Vehicles (EVs) charging and discharging scheduling, the profits of V2G station or the costs charged to EV users are optimized.
As reported by the U.S. Energy Information Administration in [13], buildings accounted for the consumption of more than 20% of the total energy delivered worldwide in 2016. This percentage is expected to increase by an average of 1.5% per year through 2040. To prepare for a significant amount of energy consumption in buildings, many research groups have actively worked to develop an EMS for smart energy buildings. The smart energy building represents an Information Technology (IT) centric building that automates its energy operation for achieving the optimal energy consumption. These smart energy buildings can be considered as a type of microgrid systems since they can operate in island-mode with the help of ESS, RES, or V2G systems. The literatures of [14,15,16,17,18,19,20,21] aimed at optimizing the energy consumptions or minimizing operation costs by flexibly and intelligently managing the various kinds of controllable energy sources and loads such as ESS, RES, and V2G system in the smart energy building.
In basic terms, the Reinforcement Learning (RL) is the problem in an area of machine learning concerned with how a learning agent learns what to do (action) in a given situation (state) by interacting with an environment to maximize or minimize numerical returns (rewards) [22]. Because the actions of the agent can affect all subsequent rewards, including the instant reward and its later actions, RL is a closed-loop system. As one of popular methods in RL, Q-learning is widely used for its model-free characteristic, which requires no prior knowledge regarding rewards or transition probabilities in the system, which makes it suitable for operating a system dealing with real-time data without future information or any prediction process. For this reason, many researchers focusing on EMS in the smart grid, especially for TCLs, ESS, and V2G systems in [3,4,6,11,12], have adopted Q-learning in their algorithms to control energy by using real-time information. However, the extant literature contains little evidence of the use of Q-learning for managing energy in smart energy buildings. Much of the research regarding smart energy buildings is on calculating energy schedules by using given or predicted day-ahead information rather than real-time information.
In this study, an EMS for a smart energy building is considered. This study is motivated by a Research and Development (R&D) project that aims at developing an EMS for a smart energy building in the campus of Gwangju Institute of Science and Technology (GIST) in Republic of Korea. The main objective of this project is to reduce the energy costs of a campus building by applying Artificial Intelligence (AI) techniques to the EMS. The smart energy building investigated in this paper is associated with a utility, a PV system, an ESS, and a V2G station, and it can exchange energy with those systems in real-time. The EMS is modeled using a Markov Decision Process (MDP) that completely describes the state space, action space, transition probability, and reward function. Furthermore, the system accounts for all unknowns associated with future information on the load demand of the building, amount of PV generation, load demand of V2G station, and energy prices of utility and V2G. To reduce the energy operation costs associated with this unknown information, a Q-learning-based energy management algorithm is proposed that improves the recommended actions for energy dispatch at every moment by learning through experience without any prior knowledge. Through numerical simulation results, we verify that the proposed Q-learning-based energy management algorithm gradually reduces the daily energy cost of smart energy building as its learning process progresses. The main contributions of this study can be summarized as follows:
- The energy management of a smart energy building is modeled using MDP to completely describe the state space, action space, transition probability, and reward function.
- We propose a Q-learning-based energy management algorithm that provides an optimal action of energy dispatch in the smart energy building. The proposed algorithm can minimize the total energy cost that takes into consideration the future cost by using only current system information, while most existing work for energy management of smart energy buildings focuses on the optimization based on 24 h ahead given or predicted future information.
- To reduce the convergence time of the Q-learning-based algorithm, we propose a simple Q-table initialization procedure, in which each value of Q-table is set to an instantaneous reward directly obtained by the reward function with an initial system condition.
- From the simulations using real-life data sets of building energy demand, PV generation, and vehicles parking records, it is verified that the proposed algorithm significantly reduces the energy cost of smart energy building under both Time-of-Use (ToU) and real-time energy pricing approaches, compared to a conventional optimization-based approach as well as the greedy and random approaches.
The remainder of this paper is organized as follows: an overview of related work is presented in Section 2. In Section 3, the overall system structure of the smart energy building considered in this paper is described, and the system model is formulated using an MDP. In Section 4, a Q-learning-based energy management algorithm is proposed for the smart energy building. Section 5 presents a performance evaluation, and Section 6 concludes this paper.
2. Related Work
In this section, we briefly summarize the related work on energy management in the smart grid environment into three categories: energy management in microgrid, energy management in V2G, and energy management in smart energy building.
2.1. Energy Management in Microgrid
As previously defined in Section 1, the microgrid represents a small electricity grid that is able to operate in island-mode without the help of the external grid by utilizing its own backup energy resources. Most research work in this category focuses on the optimal ESS control for reducing the dependency on the external grid or balancing the energy supply and demand. Ju et al. [5] have proposed a two-layer EMS for a microgrid, where ESS is integrated to maintain energy balancing and minimize the operation cost. The lower layer is formulated as a quadratic mixed-integer problem to minimize power fluctuations induced by demand forecast errors, and the upper layer is formulated as a nonlinear mixed-integer problem to obtain the power dispatch schedules that minimize the total operation cost. In [6], Kuznetsova et al. have suggested an two steps-ahead Q-learning-based ESS scheduling algorithm that determines whether to charge or discharge the ESS under the unknown information about future load demands and wind power generation. The simulation results of a case study have verified that the algorithm increases the utilization of the ESS and wind turbine while reducing grid dependency. In [7], an optimal ESS control strategy in a grid-connected microgrid has been proposed. Especially, to improve the accuracy of State of Charge (SoC) calculation, the authors have applied an extended ESS model, which utilizes 2D efficiency maps of power and SoC, to the optimization problem. The simulation results have verified that the proposed strategy with the extended ESS model guarantees the cost robustness regardless of demand forecast errors. Farzin et al. [8] have focused on managing ESS under two possible scenarios in a microgrid: normal operation mode and unscheduled islanding event. To deal with the trade-off between minimizing the operation cost in the normal mode and increasing the load curtailment in the islanding event, the authors have proposed a multi-objective optimization-based ESS scheduling framework that can simultaneously optimize the cost and curtailment in each corresponding scenario.
2.2. Energy Management in V2G
The research efforts in this category focus on the charging and discharging scheduling of EVs at V2G station for optimizing the benefits of the V2G station or reducing the costs charged to EV users. He et al. [9] have developed a scheduling algorithm for charging and discharging multiple EVs that aims to minimize the costs charged to EV users. To optimize scheduling, they have proposed global and local optimization problems expressed as convex optimization problems and verified that the local optimization problem is more appropriate for a practical environment with a large population and dynamic arrivals of EVs while providing performance close to that of the global optimization problem. Yet another optimal scheduling model for EV charging and discharging has been proposed in [10], where the authors have considered not only the costs charged to EV users but also user preferences and battery lifetime of EVs. However, this model is not operated with real-time information, meaning that scheduling is based on given day-ahead energy information rather than real-time information. EV charging and discharging scheduling algorithms using real-time information have been suggested in [11,12]. Given the unknown future energy price information, these algorithms determine the optimal scheduling at each moment by using the RL technique based only on the current information regarding energy prices to increase the daily profit for an EV user. However, these algorithms are limited in that they can be applied only to a single EV.
2.3. Energy Management in Smart Energy Building
The research efforts in this category generally focus on the energy consumption optimization or the operation cost minimization in smart energy buildings by managing various kinds of controllable energy sources and loads. In [14], Zhao et al. have described the framework and algorithmic aspects of a Cyber Enabled Building EMS, called CEBEMS. The objective of CEBEMS is to minimize the energy cost of a building while satisfying the occupants’ set lighting and cooling system points using decision-making control optimization. A case study involving a typical food service center as a test building has been executed to demonstrate the applicability of this framework to commercial buildings. Wang et al. [15] have proposed an intelligent multi-agent optimizer system to maximize occupant comfort and minimize building energy consumption. The multi-agent consists of a central coordinator-agent that coordinates the energy dispatch to local controller-agents and maximizes occupant comfort, and three local controller-agents that use multiple fuzzy logic controllers to satisfy different types of comfort demands. Within the range of set points for temperature, illumination level, and concentration given by the occupants in advance, this optimizer system derives the optimal points of the three elements to balance power consumption and comfort demands. In [16], Wang et al. also have applied the intelligent multi-agent optimizer system proposed in [15] to a V2G-integrated building to evaluate the impact of the aggregation of EVs on the building energy consumption as a Distributed Energy Resource (DER). The results of simulation, carried out using data of a 24 h period, have verified that a larger number of EVs are beneficial for satisfying the comfort demands of occupants while reducing energy consumption. Missaoui et al. in [17] have proposed an EMS for smart homes to obtain two solutions: comfort-preferred and cost-preferred. They have conducted a case study with given energy prices and verified that the EMS significantly reduces cost with both solutions. In [18], Basit et al. have proposed a home EMS aiming at optimizing the operation cost by scheduling household appliances without violating the required operation duration of non-schedulable devices. A day-ahead multi-objective optimization model for building energy management has been proposed in [19]. Based on the forecasted information on PV generation, load demand, and temperature, the synergetic dispatch of source-load-storage is scheduled to minimize the operation cost under ToU energy pricing while maintaining the users’ comfort. The EMSs operating in short-term to make real-time decisions have been considered in [20,21]. In [20], Yan et al. have focused on managing the EV charging station integrated with a commercial smart building. The chance-constrained optimization-based energy control algorithm that schedules power flows from and to the grid, EV charging and discharging, and ESS charging and discharging in real-time has been proposed to reduce the operational cost of the EV charging station. Piazza et al. [21] have proposed an EMS for smart energy buildings with a PV system and an ESS, where the system operates in two stages: planning stage that optimizes building energy cost by planning the grid-exchanged power profile and online replanning stage that aims at reducing building demand uncertainty.
Please note that our proposed Q-learning-based energy management algorithm falls into the third category. However, the proposed approach is distinct from existing work in that it determines real-time decisions of the optimal actions without any help of future information, while most existing work requires an additional prediction process or simply assume that a set of predicted data is available to solve optimization problems.
3. Energy Management System Model Using MDP
In this section, the overall system structure of a smart energy building is presented, and the system model is formulated using an MDP composed of a state space, action space, transition probabilities, and reward function.
3.1. Overall System Structure
The EMS of a smart energy building is considered with the aim of reducing building operation costs under unknown future information. Figure 1 describes the structure of the smart energy building considered in this paper. As shown, the smart energy building is connected to a utility and DERs including a PV system, ESS, and V2G station.
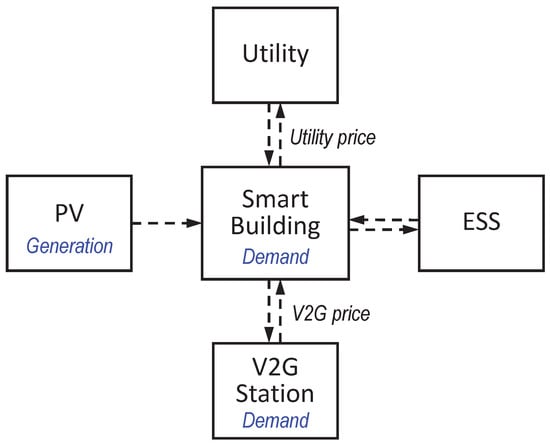
Figure 1.
Illustration of smart energy building associated with utility, PV, ESS, and V2G station.
The four components associated with the smart energy building are characterized as follows:
- “Utility” represents a company that supplies energy in real-time. It is assumed that the smart energy building is able to trade (buy and sell) energy with the utility company at any time at the prices determined by the utility company.
- “PV system” is a power supply system that converts sunlight into energy by means of photovoltaic panels. The energy generated by the PV system can be consumed to help meet the load demands of the smart energy building and V2G station.
- “V2G station” describes a system where EVs request charging (energy flow from the grid to EVs) or discharging (energy flow from EVs to the grid) services. It is assumed that the smart energy building trades energy based on the net demand of the V2G station, which can be either positive (if the number of EVs that require charging service is greater than the number of EVs that require discharging service) or negative (vice versa).
- “ESS” represents an energy storage system, capable of storing and releasing energy as needed in a flexible way. As a simple example, the smart energy building can utilize the ESS to decrease its operation cost by charging the ESS when energy prices are low and discharging the ESS when energy prices are high. We assume that the ESS considered in this paper consists of a combination of battery and super-capacitor. This hybrid ESS can take both the advantages of battery (high energy density and low cost per kWh) and super-capacitor (quick charging/discharging and extended lifetime) [23].
Let t denote the index of the present time step, and denote the length of each time step (min), during which all system variables are considered to be constant. The EMS operates in a discrete-time manner based on this time step, and the time step is repeated infinitely. In this study, we assume that there are five unknowns in future information as follows:
- “Building demand” represents the energy demand required by the smart energy building itself due to its internal energy consumption. The amount of energy demand of the building at each time step t is denoted by (kWh).
- “PV generation” represents the energy generated by the PV system, and is denoted by (kWh).
- “V2G demand” represents the energy demand of the V2G station, denoted by (kWh). Because the V2G station has bidirectional energy exchange capability with the building, there are two values of , a positive value when the V2G station draws energy from the building and a negative value when it supplies energy to the building.
- “Utility price” represents the prices for energy transaction between the building and the utility company, and is denoted by ($/kWh).
- “V2G price” represents the energy prices for energy transaction when EVs are charged or discharged at V2G station, and is denoted by ($/kWh).
The utility price is usually determined by the utility company in the form of a ToU pricing or a real-time pricing [24]. In the ToU pricing, the utility prices are just offered in a table with a few levels of prices according to time zone. In the real-time pricing, the prices are dynamically determined by wholesale energy market or energy supply and demand conditions. Likewise, V2G prices are available in several forms of pricing policy. The ToU pricing for V2G is generally determined by the utility company or V2G station itself in a way that the economic benefits are maximized. The real-time pricing policy for V2G is determined in accordance with the wholesale energy market or the real-time supply and demand condition by EVs charging and discharging [11]. Especially, there also exist some V2G pricing policies that provide discriminative incentives to EV users who permit the discharging in support of the grid operations [25]. Please note that no matter what policy the utility price and the V2G price follow, they are changing stochastically depending on the time of day, typically holding high values during the daytime and low values during the nighttime.
Future information on these five unknowns is not provided to the EMS at the present time step t, meaning that the information from time step is unknown, whereas past and current pieces of information are known to the system. The objective of the EMS is to gradually learn how to manage energy through experience gained over successive time steps under the unknowns of future information. In the following subsections, the state space, action space, transition probabilities, and reward function of the EMS are formulated using an MDP under this assumption of unknowns.
3.2. State Space
Let denote the SoC of the ESS at time step t, and represent the maximum capacity of the ESS. For safe use of the ESS, a guard ratio, denoted by , at both ends of the ESS capacity is considered as follows:
We define the net demand of the smart energy building at time step t, denoted by , as the sum of the energy demands from the building and the V2G station minus the energy generated by the PV system, as follows:
Because Building demand (), PV generation (), and V2G demand () are unknown variables, as mentioned in Section 3.1, the net demand of the smart energy building () is an unknown variable. Note it is assumed that there is no energy/exergy loss during the charging, discharging, and idling of the ESS.
The time step t basically reaches infinity over time. However, because time is repeated with a period of one day, the state of the time step is considered to be repeated with a period of one day as well. Therefore, the state of the time step, denoted by , can be defined as follows:
where h and m represent the number of hours per day (i.e., 24) and the number of minutes per hour (i.e., 60), respectively.
Taking all the above into consideration, the state of the EMS at time step t, denoted by , is defined as follows:
where is the state space of the EMS, and it is composed of five spaces: ESS SoC space , energy demand space , and time space . Thus, , where × represents Cartesian product. Please note that the values of utility price () and V2G price (), which are usually dependent on the state of the time step , are unknown, but they are not included in the state space. Instead, the stochastic price unknowns are included in the reward function to be used by the Q-learning.
3.3. Action Space
To satisfy in each time step t, the EMS of the smart energy building chooses one action from the action space , which is given by
where Buying represents the action of buying energy from the utility company to satisfy , Charging represents charging the ESS for later use, Discharging represents discharging the ESS to satisfy , and Selling denotes the action of selling energy to the utility company. Please note that Charging and Selling obviously include the actions of Buying and Discharging, respectively. For example, if the action Charging is selected, the EMS buys more energy than the amount required to satisfy the net demand, , and the remaining energy is used for charging into the ESS.
We define as the action taken at time step t, where denotes the possible action set in the action space under state . In each time step t, is constrained by ESS capacity, meaning that at time step t, only actions that satisfy the SoC condition of the ESS in the next time step , that is, , can be included in . Therefore, is determined as follows:
where denotes the energy unit for charging the ESS and selling to the utility company. Once the possible action set in each time step t is given by (6), the EMS selects one of the possible actions, , from according to a certain policy , which denotes the decision-making rule for action selection. More information about is covered in the next section.
Let denote the function of the amount of energy charged into the ESS with the taken action , represented by
where negative values represent energy discharge from the ESS.
Please note that the derived state and action spaces can be easily extended if the EMS includes other energy components in the smart energy building. For instance, if a Combined Heat and Power (CHP) system is deployed, the state space may include more parameters such as the amount of energy generation by CHP and the indoor temperature, and the action space includes the consuming energy from CHP to meet the demand and the selling energy from CHP to the utility.
3.4. Transition Probability
The transition probability of the EMS from state to state when action is taken can be represented as follows:
where and are given by
and
and is represented by the product of , , and as follows:
Because we assume that Building demand (), V2G demand (), and PV generation () are unknowns, the transition probability is not known to the system in time step t in advance. However, because the present study applies the RL technique, it is not necessary to know these transition probabilities. This is especially true for Q-learning, a model-free algorithm, in which the transition probabilities are learned implicitly through the experience gained over successive time steps.
3.5. Reward Function
Let denote the reward function that returns a cost value indicating how much money the smart energy building must pay for the energy used to operate the building. When action is taken at state , the reward function is defined by
where the negative value of implies that the smart energy building earns money, whereas the positive value is a cost that must be paid.
To account for the impact of the current action on future rewards, the total discounted reward at time step t under a given policy , denoted by , is defined as the sum of the instant reward at time step t and discounted rewards from the next time step, , as follows:
where denotes the discount factor that determines the importance of future rewards from the next time step, , to the infinity. For example, implies that the EMS will consider only the current reward, while implies that the system weighs both current reward and future long-term rewards equally. The objective of the EMS is to minimize the total discounted reward to reduce the operating cost of the smart energy building.
4. Energy Management Algorithm Using Q-Learning
In this section, we propose an RL-technique-based energy management algorithm that minimizes the total discounted reward defined by (13). Among the many types of algorithms included in the RL technique, the Q-learning algorithm was adopted owing to its model-free characteristic, in which transition probabilities can be learned implicitly through experience without any prior knowledge.
Let , denoting the action-value function that returns the expected total discounted reward when action is taken at state by following a given policy , be defined as follows:
The Q-learning algorithm tries to approximate the optimal action-value function , expressed as
by repeatedly updating the action-value function through experience of successive time steps.
To approximate the optimal action-value function , we must to estimate the values of for all state-action pairs. Let denote the greedy action minimizing the value of Q at state , that is,
and denote a positive small number between 0 and 1 (). To deal with the exploitation versus exploration tradeoff issue [26], we adopt a -greedy policy, where one of the actions from possible action set is selected randomly with a probability of for exploration, whereas for the majority of the time, the greedy action in is selected with a probability of for exploitation. As a result, the probability of selecting action at state under the policy , denoted by , is represented as follows:
Once the action is selected by following policy , the reward function is calculated using (12) and the state evolves to the next state, . Simultaneously, the action-value function is updated according to the following rule:
where is a learning rate that determines how much the newly obtained reward overrides the old value of . For instance, implies that the newly obtained information is ignored, whereas implies that the system considers only the latest information.
For the initialization problem, the typical Q-learning algorithm simply initializes the action-value function at time step 0, , with the value of 0 or ∞. However, convergence of the action-value function requires significant time because a large number of time steps is required to explore and update the values of for all state-action pairs at least once. To reduce the convergence time of the proposed algorithm, here we suggest that each value of is initialized to the total discounted reward with , which can be obtained easily as the instant reward at time step 0. That is, the values of for all state-action pairs can be explored preliminarily with instant rewards before the actual learning process begins. Through this simple additional initialization step, it is expected that the convergence time is significantly shortened.
Algorithm 1 shows the pseudocode of the main algorithm of the EMS using Q-learning. First, for all state-action pairs is initialized to the total discounted rewards with in line 1, and the learning parameters , , and are initialized in line 2. Lines 3–11 show the loop for each time step t. The possible action set satisfying the SoC condition of the ESS is determined in line 4, and the greedy action is obtained in line 5. In lines 6–7, one action () is selected from , which now includes the greedy action obtained in line 5, according to the probability of selecting an action under the policy , and the potential reward and the next state that will result from taking the selected action are observed. Based on this observation, is updated according to the update rule (18) in line 8; finally, in lines 9–10, the time step t and the state are transited to the next time step, , and the next state, , respectively.
| Algorithm 1 Energy management algorithm using Q-learning |
Figure 2 presents a simplified example of the Q-table updating procedure. The Q-table is given in the form of a matrix, with each row indicating the state and each column indicating the action. Suppose that the current state at time step t is . Then, Selling is supposed to be the greedy action because its Q-value, , is the minimum among all Q-values in the current state. According to the policy , the final action is selected from either Case I for exploitation or Case II for exploration. In Case I, the greedy action, Selling, is selected with a probability of . In Case II, an action is randomly chosen among all actions with a probability of regardless of Q-value. In both cases, the Q-value, , for the selected action is updated according to (18).
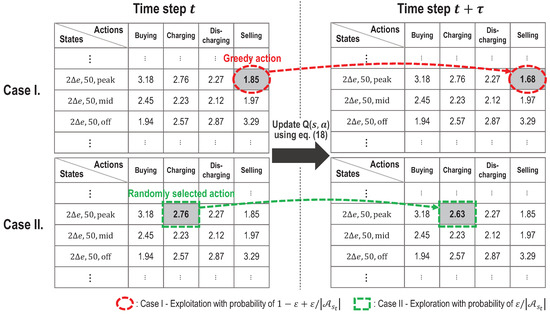
Figure 2.
Simplified example of Q-table updating.
5. Performance Evaluation
To evaluate the performance of the proposed energy management algorithm using Q-learning, we consider a smart energy building in a smart grid environment, which is associated with a utility and DERs, including PV system, ESS system, and V2G station, and perform numerical simulations based on the data measured in real environments. As a simulation framework, MATLAB 2017b is used.
5.1. Simulation Setting
In the simulations, the length of each time step was set to 5 min, and the ESS capacity was set to 500 kWh. The ESS guard ratio was set to , and the initial SoC of the ESS was set to be 250 kWh. Here, the final SoC of each day is constrained to be with a tolerance of %, i.e., [] kWh. The reason is that if the values of initial SoC vary every day, the initial condition of the learning process can differ from day to day. In this case, more explorations to learn the Q-values may be needed, resulting in longer convergence time. The energy unit for charging the ESS and selling to the utility company was set to kWh. We set the learning rate to . If is too large, the values of may oscillate significantly. On the other hand, if it is too small, it may cause long convergence time of the Q-learning algorithm. The -greedy parameter was set to , and the discount factor was set to , as many studies dealing with long-term future rewards in RL typically take with the values slightly less than 1 [4,12]. To examine the validity of these learning parameters setting, the performance of the proposed algorithm will be analyzed with respect to and through simulations in the next subsection (see Figures 10 and 11). The simulation input parameters are summarized in Table 1.

Table 1.
Simulation input parameters.
The building demand () and PV generation () follow the energy demand profile and PV generation profile, respectively, measured in a campus building in GIST during 100 weekdays (from 1 June 2016 to 18 October 2016) [27]. Examples of energy demand profile and PV generation profile for three days measured at intervals of 5 min are presented in Figure 3 and Figure 4. Likewise, Figure 5 shows an example of vehicle parking records for three days in the district office in Gwangju [28]. Based on these records, we simply modeled V2G demand (), in which the vehicles of commuters require charging and those of customers require discharging. Here, we assumed that every charger supports typical level 1 (dis)charging, where the (dis)charging rate is fixed to 7 kW/h ( kW per 5 min). For the utility price () and V2G price (), the ToU energy price tables given by Korea Electric Power Corporation in 2017 were used as follows:
where the peak-load periods are 10:00–12:00 and 13:00–17:00; mid-load periods are 09:00–10:00, 12:00–13:00, and 17:00–23:00; and off-peak-load period is 23:00–09:00 [29]. As we assumed that , , , , and are five unknown information in Section 3.1, the current values of them are measured at each time step t, but their future values are not available to the EMS.
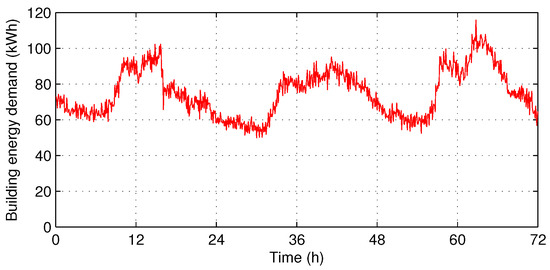
Figure 3.
Energy demand profile example for 3 days of campus building in GIST.
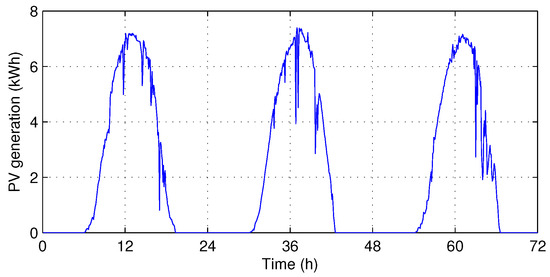
Figure 4.
PV generation profile example for 3 days of campus building in GIST.
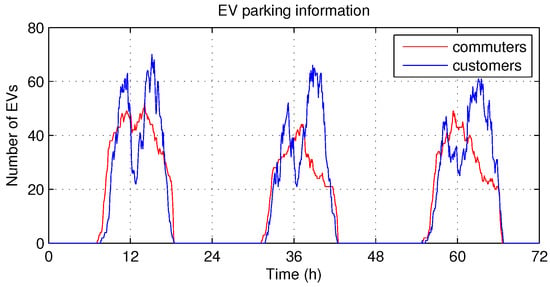
Figure 5.
Vehicle parking records of district office in Gwangju.
Please note that as an effort to reduce the number of state-action pairs in Q-table, we discretized each element in the state space as follows: into 20 levels, into 6 levels, and into 3 levels (peak-load, mid-load, and off-peak-load periods). This discretization of the state space is expected to be effective in shortening the convergence time of the proposed algorithm, cooperating with the Q-table initialization procedure proposed in Section 4.
5.2. Simulation Results
To verify the performance improvements achieved by applying the proposed algorithm, we compare the results obtained using the proposed algorithm to those obtained using three other algorithms, described as follows:
- Minimum instant reward—The system always chooses the action that gives the minimum instant reward in the present time step t, without considering future rewards. This algorithm is expected to provide similar results as the proposed algorithm with .
- Random action—The action is selected randomly from the possible action set , regardless of the value of .
- Previous action maintain—This algorithm tries to always maintain its previous action while keeping the SoC of the ESS () between ()% and ()% of the maximum capacity of the ESS (), regardless of any other information on the current state. Here, is set to 20 so that is kept between 30% and 70% of . For example, if the previous action is Buying or Charging with between 30% and 70%, the algorithm keeps selecting the Buying or Charging action until reaches 70%; then, it changes the action to Selling or Discharging.
- Hourly optimization in [21]—At the beginning of every hour, this algorithm schedules the energy dispatch by using the hourly forecasted profiles. We assume that the hourly profiles of building demand (Figure 3) and PV generation (Figure 4) are given an hour in advance with Normalized Root-Mean-Square Error (NRMSE) of % and %, respectively, as in [21].
The primary evaluation is devoted to investigating how the proposed energy management algorithm using Q-learning improves performance as the learning process progresses. As a metric of performance evaluation, daily cost is calculated as the sum of rewards over time steps. The simulation results of daily cost variation versus increasing number of days experienced are shown in Figure 6. The results show that the daily cost obtained using the proposed algorithm is close to that obtained using the previous action maintain algorithm on the 1st day, but it quickly converged (within about 3–5 days) to around $400, which is even lower than the hourly optimization algorithm, with the help of the simple additional initialization step suggested in Section 4. This is because the proposed algorithm selects better actions by using the learning process as it experiences more state-action pairs. It is worth noting that the daily cost obtained using the minimum instant reward algorithm is higher than that calculated using the random action algorithm because the minimum instant reward algorithm tends to always sell energy from the ESS, disregarding expected future rewards, only to minimize the instant reward value. From the overall results, it can be inferred that the higher the utilization of ESS capacity, the higher is the reduction in daily cost.
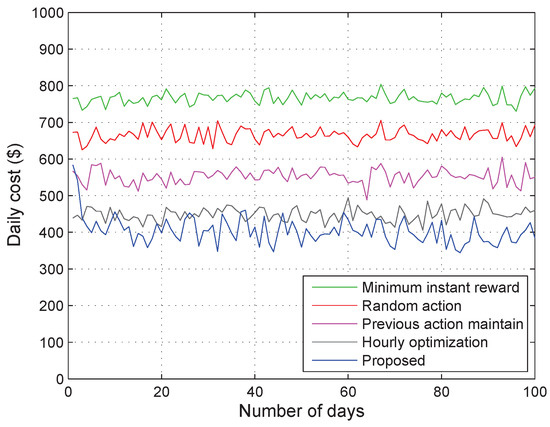
Figure 6.
Daily cost comparison with respect to time in days.
In Figure 7, we compare the amount of energy bought daily from the utility by four algorithms. At first glance, it may seem strange that the order of magnitude of the amount of energy bought daily from the utility is almost opposite to that of daily cost shown in Figure 6. However, this result is valid because the daily cost can be reduced through the process of buying (selling) more energy from (to) the utility when the utility price is low (high) by utilizing the ESS. Especially, the minimum instant reward algorithm buys the least amount of energy from the utility because it tends to always sell energy for minimizing the instant reward value, while the proposed algorithm intelligently buys and sells the largest amount of energy to reduce the daily cost.
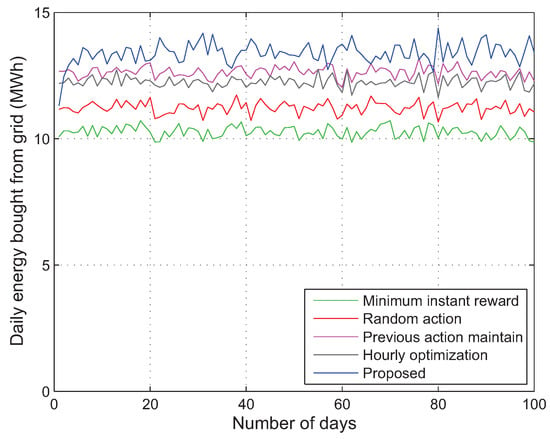
Figure 7.
Amount of energy bought daily from utility with respect to time in days.
To investigate the effect of ESS capacity on the average daily cost, we plotted the average daily cost for 100 days with varying ESS capacity, , between 0 and 1000 kWh in Figure 8. Here it is assumed that is set to the half of each . Overall, the proposed algorithm gives the lowest average daily cost, the same as in Figure 6. It can be seen that when is 0 kWh, all five algorithms provide the same, and highest, average daily costs because only the Buying action is possible for all five algorithms. However, as increases, the average daily costs determined using the random action, previous action maintain, hourly optimization, and proposed algorithms decrease until reaches 400 kWh because ESS capacity can be utilized to store and release energy by the Charging, Discharging, and Selling actions. For values larger than 400 kWh, the previous action maintain, hourly optimization, and proposed algorithms show slightly decreasing average daily costs with respect to increasing , whereas the random action algorithm is not affected by further changes in at all. This is because the three algorithms can utilize a larger amount of ESS capacity as the value of increases. However, increasing the ESS capacity generally requires a spike in purchasing and installation costs, with no remarkable performance improvements associated with increasing ESS capacity as shown in the Figure. Therefore, from the perspective of building operations, installing an ESS with a capacity between 400 and 600 kWh would be sufficient to ensure an average daily cost reduction.
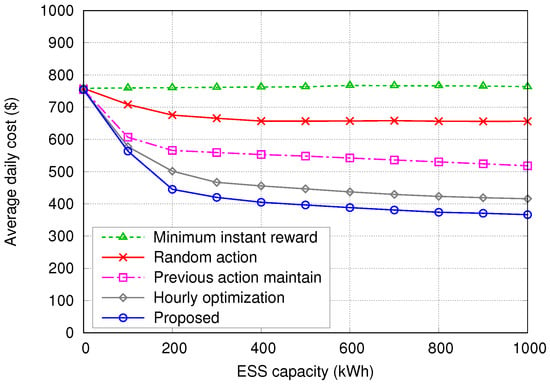
Figure 8.
Average daily cost with respect to ESS capacity.
To study the impact of the scale of the PV system, we scaled up and down the PV system by multiplying PV generation () with the scale factor , where . For example, means that the scale of the PV system is doubled, whereas means that the PV system is not associated with the smart energy building at all. Here, is set to 500 kWh. Figure 9 shows the simulation results of the average daily cost with respect to . Overall, the average daily costs decrease according to increasing . Especially, the proposed algorithm exhibits the lowest daily cost for any value of , and its rate of decrease becomes slightly larger compared to those of the other four algorithms as increases. This indicates that the proposed algorithm can reduce the daily cost by managing energy more intelligently with learning capability as the amount of energy generated by the PV system increases. Therefore, unless the installation cost of the PV system is taken into consideration, the larger the scale of the PV system, the more effective it would be for reducing the average daily cost of building operation.
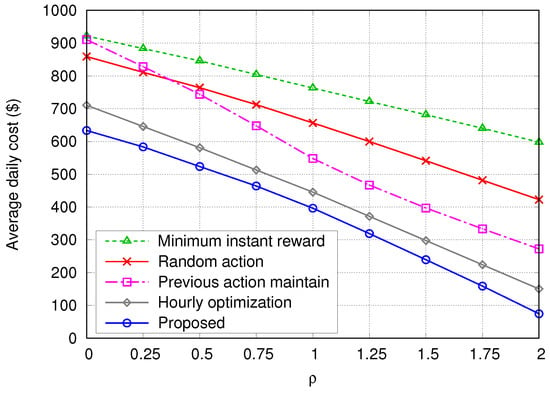
Figure 9.
Average daily cost with respect to scale factor of PV system.
In Figure 10 and Figure 11, we plotted the average daily cost variation of the proposed algorithm according to and , respectively, in order to examine the impact of these learning parameters on the performance. The costs of the four other algorithms are plotted for comparison. In Figure 10, the lowest average daily cost is achieved for , and when , almost the same cost as the random action algorithm is achieved because the action is always selected randomly. In Figure 11, the average daily cost gradually decreases as increases, and it becomes lower than the cost by the hourly optimization algorithm when . Also please note that when , the average daily cost of the proposed algorithm is the same as the minimum instant reward algorithm because the total discounted reward is composed of only the term of instant reward. These results imply that it was appropriate to set the learning parameters and to and , respectively.
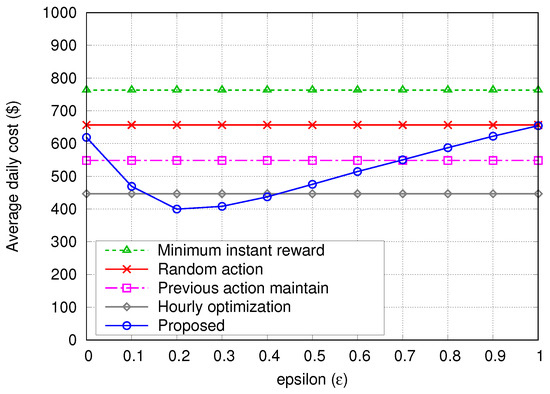
Figure 10.
Average daily cost variation with respect to -greedy parameter.
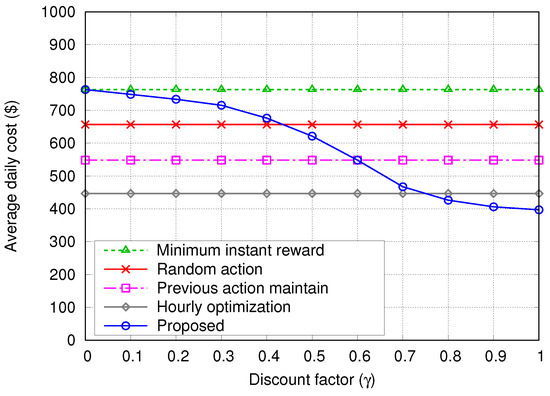
Figure 11.
Average daily cost variation with respect to discount factor .
Finally, we investigated the performance in a case of the real-time energy pricing. Figure 12 shows an example of the real-time hourly energy price profiles for the same three days of Figure 3, Figure 4 and Figure 5 in three U.S. states [30], and the average daily cost under the real-time pricing is presented in Figure 13. We simply assume that both and are the same as shown in Figure 12. Figure 13 shows that the proposed algorithm provides the lowest cost among the five algorithms for all the three real-time energy prices. Therefore, it can be concluded that the proposed algorithm is significantly effective for energy cost reduction regardless of the type of energy pricing policy.
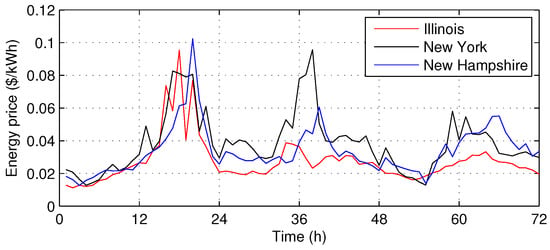
Figure 12.
Real-time hourly energy price example for 3 days in 3 U.S. states.
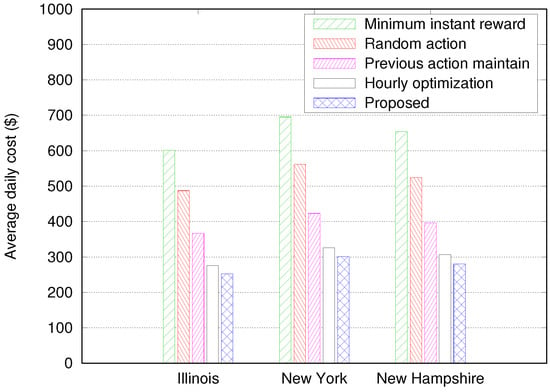
Figure 13.
Average daily cost with real-time energy prices.
6. Conclusions and Discussion
In this study, we proposed an RL based energy management algorithm for smart energy buildings in a smart grid environment. Smart energy buildings are capable of exchanging energy with an external grid and DERs such as a PV, an ESS, and a V2G station in real-time. We first developed the energy management system model by using a Markov decision process that completely describes the state space, action space, transition probability, and reward function. To reduce the energy costs of a building given unknown future information about the amount of building load demand, V2G station load demand, and energy generation by PV system, a Q-learning-based energy management algorithm that identifies better energy dispatch actions by learning through experience without prior knowledge was proposed. Through numerical simulations based on data measured in the real environments, we verified that the proposed algorithm significantly reduces energy costs compared to the random and other existing algorithms. We showed that the proposed algorithm successfully reduces energy costs under widely-used energy pricing policies of ToU and real-time. It is expected that the proposed learning-based energy management algorithm is applicable in various smart grid environments such as residential microgrids and smart energy factories under different energy pricing policies. As future work, we will extend the proposed algorithm so that it can work in more complicated cases with additional energy components such as CHP, TCLs, or wind turbines, and empirically validate the proposed algorithm in real smart buildings.
Author Contributions
S.K. designed the algorithm, performed the simulations, and prepared the manuscript as the first author. H.L. led the project and research and advised on the whole process of manuscript preparation. All authors discussed the simulation results and approved the publication.
Acknowledgments
This work was partially supported by GIST Research Institute (GRI) grant funded by the GIST in 2018, by the KETEP grant funded by MOTIE (No. 20171210200810), and by IITP grant funded by MSIT (No. 2014-0-00065, Resilient CPS Research), Republic of Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hashmi, M.; Hänninen, S.; Mäki, K. Survey of smart grid concepts, architectures, and technological demonstrations worldwide. In Proceedings of the IEEE PES Conference on Innovative Smart Grid Technologies (ISGT), Medellin, Colombia, 19–21 October 2011. [Google Scholar]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Kara, E.C.; Berges, M.; Krogh, B.; Kar, S. Using smart devices for system-level management and control in the smart grid: A reinforcement learning framework. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Tainan, Taiwan, 5–8 November 2012. [Google Scholar]
- Ruelens, F.; Claessens, B.J.; Vandael, S.; De Schutter, B.; Babuška, R.; Belmans, R. Residential demand response of thermostatically controlled loads using batch reinforcement learning. IEEE Trans. Smart Grid 2016, 8, 2149–2159. [Google Scholar] [CrossRef]
- Ju, C.; Wang, P.; Goel, L.; Xu, Y. A two-layer energy management system for microgrids with hybrid energy storage considering degradation costs. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Kuznetsova, E.; Li, Y.F.; Ruiz, C.; Zio, E.; Ault, G.; Bell, K. Reinforcement learning for microgrid energy management. Energy 2013, 59, 133–146. [Google Scholar] [CrossRef]
- Choi, J.; Shin, Y.; Choi, M.; Park, W.K.; Lee, I.W. Robust control of a microgrid energy storage system using various approaches. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A stochastic multi-objective framework for optimal scheduling of energy storage systems in microgrids. IEEE Trans. Smart Grid 2017, 8, 117–127. [Google Scholar] [CrossRef]
- He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Honarmand, M.; Zakariazadeh, A.; Jadid, S. Optimal scheduling of electric vehicles in an intelligent parking lot considering vehicle-to-grid concept and battery condition. Energy 2014, 65, 572–579. [Google Scholar] [CrossRef]
- Shi, W.; Wong, V.W. Real-time vehicle-to-grid control algorithm under price uncertainty. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011. [Google Scholar]
- Di Giorgio, A.; Liberati, F.; Pietrabissa, A. On-board stochastic control of electric vehicle recharging. In Proceedings of the IEEE Conference on Decision and Control (CDC), Florence, Italy, 10–13 December 2013. [Google Scholar]
- U.S. Energy Information Administration (EIA). International Energy Outlook 2016. Available online: https://www.eia.gov/outlooks/ieo/buildings.php (accessed on 3 March 2018).
- Zhao, P.; Suryanarayanan, S.; Simões, M.G. An energy management system for building structures using a multi-agent decision-making control methodology. IEEE Trans. Ind. Appl. 2013, 49, 322–330. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, R.; Wang, L. Multi-agent control system with intelligent optimization for smart and energy-efficient buildings. In Proceedings of the IEEE Conference on Industrial Electronics Society (IECON), Glendale, AZ, USA, 7–10 November 2010. [Google Scholar]
- Wang, Z.; Wang, L.; Dounis, A.I.; Yang, R. Integration of plug-in hybrid electric vehicles into energy and comfort management for smart building. Energy Build. 2012, 47, 260–266. [Google Scholar] [CrossRef]
- Missaoui, R.; Joumaa, H.; Ploix, S.; Bacha, S. Managing energy smart homes according to energy prices: Analysis of a building energy management system. Energy Build. 2014, 71, 155–167. [Google Scholar] [CrossRef]
- Basit, A.; Sidhu, G.A.S.; Mahmood, A.; Gao, F. Efficient and autonomous energy management techniques for the future smart homes. IEEE Trans. Smart Grid 2017, 8, 917–926. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, L.; Ren, H.; Liu, X.; Talari, S.; Shafie-khah, M.; Catalão, J.P. Multi-objective optimization model of source-load-storage synergetic dispatch for a building energy management system based on TOU price demand response. IEEE Trans. Ind. Appl. 2018, 54, 1017–1028. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized operational cost reduction for an EV charging station integrated with battery energy storage and PV generation. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Di Piazza, M.; La Tona, G.; Luna, M.; Di Piazza, A. A two-stage energy management system for smart buildings reducing the impact of demand uncertainty. Energy Build. 2017, 139, 1–9. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Manandhar, U.; Tummuru, N.R.; Kollimalla, S.K.; Ukil, A.; Beng, G.H.; Chaudhari, K. Validation of faster joint control strategy for battery-and supercapacitor-based energy storage system. IEEE Trans. Ind. Electron. 2018, 65, 3286–3295. [Google Scholar] [CrossRef]
- Burger, S.P.; Luke, M. Business models for distributed energy resources: A review and empirical analysis. Energy Policy 2017, 109, 230–248. [Google Scholar] [CrossRef]
- Mao, T.; Lau, W.H.; Shum, C.; Chung, H.S.H.; Tsang, K.F.; Tse, N.C.F. A regulation policy of EV discharging price for demand scheduling. IEEE Trans. Power Syst. 2018, 33, 1275–1288. [Google Scholar] [CrossRef]
- Kearns, M.; Singh, S. Near-optimal reinforcement learning in polynomial time. Mach. Learn. 2002, 49, 209–232. [Google Scholar] [CrossRef]
- Research Institute for Solar and Sustainable Energies (RISE). Available online: https://rise.gist.ac.kr/ (accessed on 15 February 2018).
- Gwangju Buk-Gu Office. Available online: http://eng.bukgu.gwangju.kr/index.jsp (accessed on 12 March 2018).
- Energy Price Table by Korea Electric Power Corporation (KEPCO). Available online: http://cyber.kepco.co.kr/ckepco/front/jsp/CY/E/E/CYEEHP00203.jsp (accessed on 17 March 2018).
- ISO New England. Available online: https://www.iso-ne.com/ (accessed on 28 March 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).