Energy Loss Allocation in Smart Distribution Systems with Electric Vehicle Integration
Abstract
:1. Introduction
- How much should an EV load pay for the incremental losses in the grid [3]?
- Should incremental losses produced by EVs connected to fast and slow charging stations be allocated in a proportional manner among all distribution loads [3]?
- Can a price signal for losses (sent in real-time via AMI and smart metering) force the EV loads to provide volt/var support in order to improve voltage profile and reduce system losses [4]?
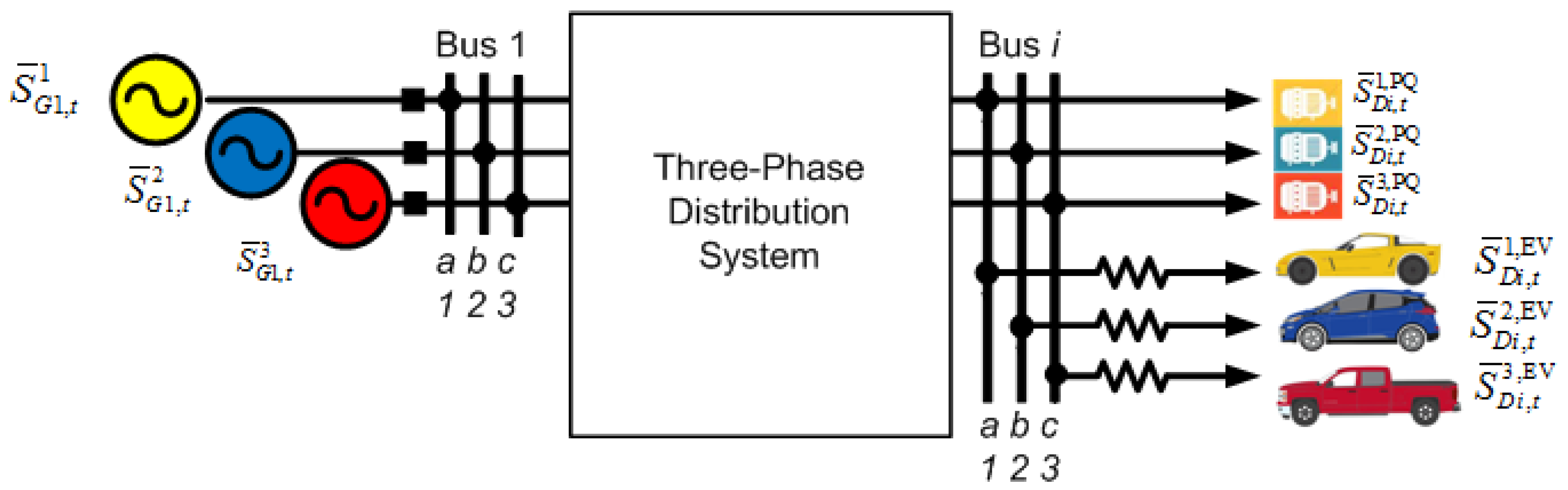
2. The Energy Loss Allocation Model
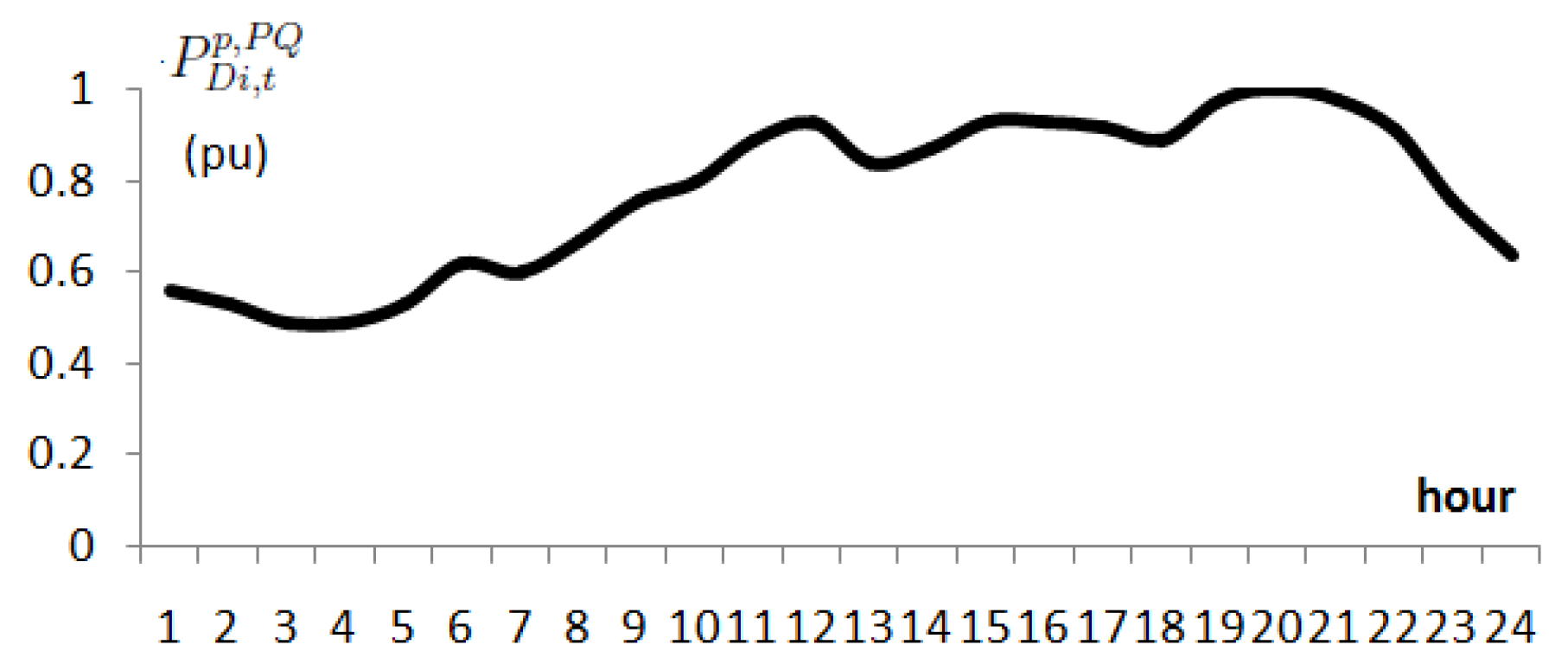
2.1. PQ and EV Load Modeling
2.2. Evaluation of Power Losses to Be Allocated among the Network Users
2.3. Energy Loss Allocation Procedures
- The proposed marginal allocation procedure per bus and per phase
- The standard pro rata or proportional allocation for comparison purposes [17]
2.3.1. Marginal Loss Allocation
2.3.2. Pro Rata or Proportional Allocation
3. Case Study
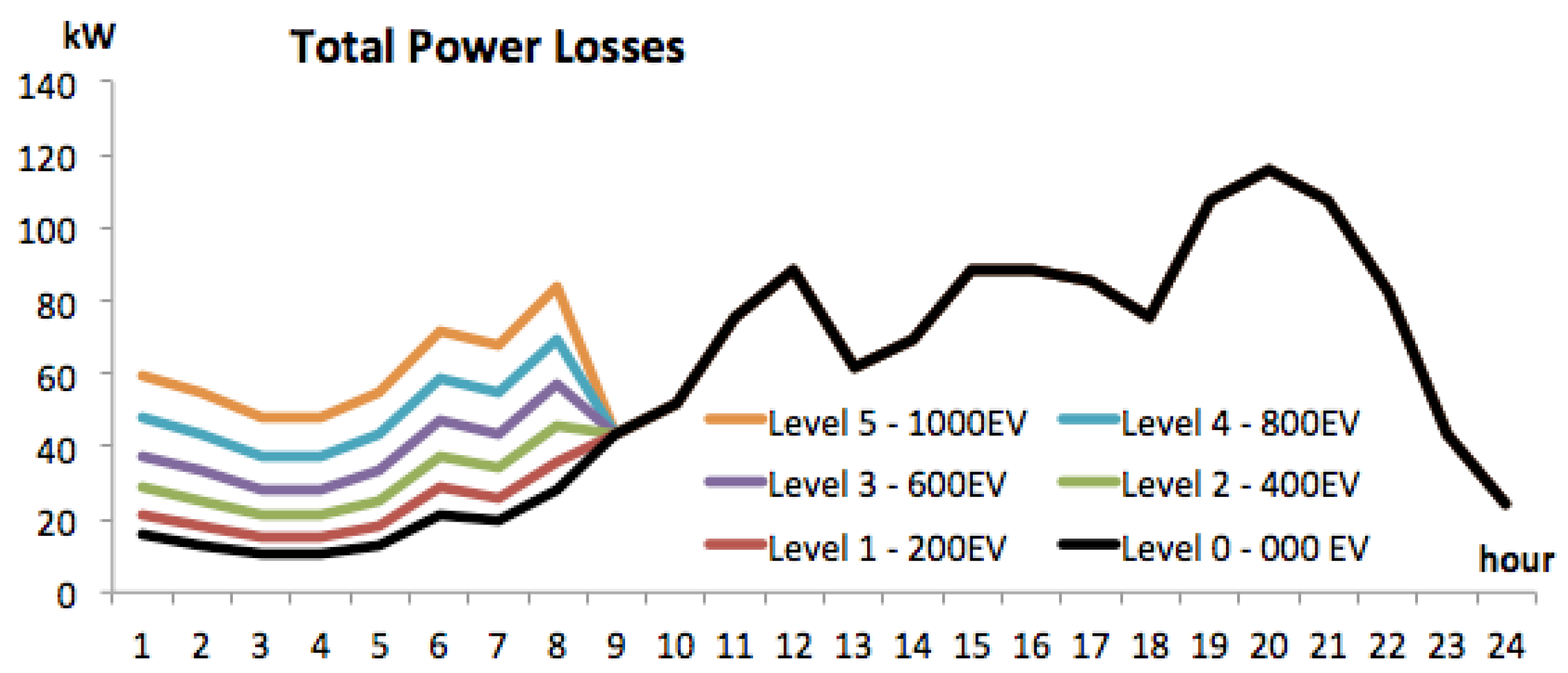
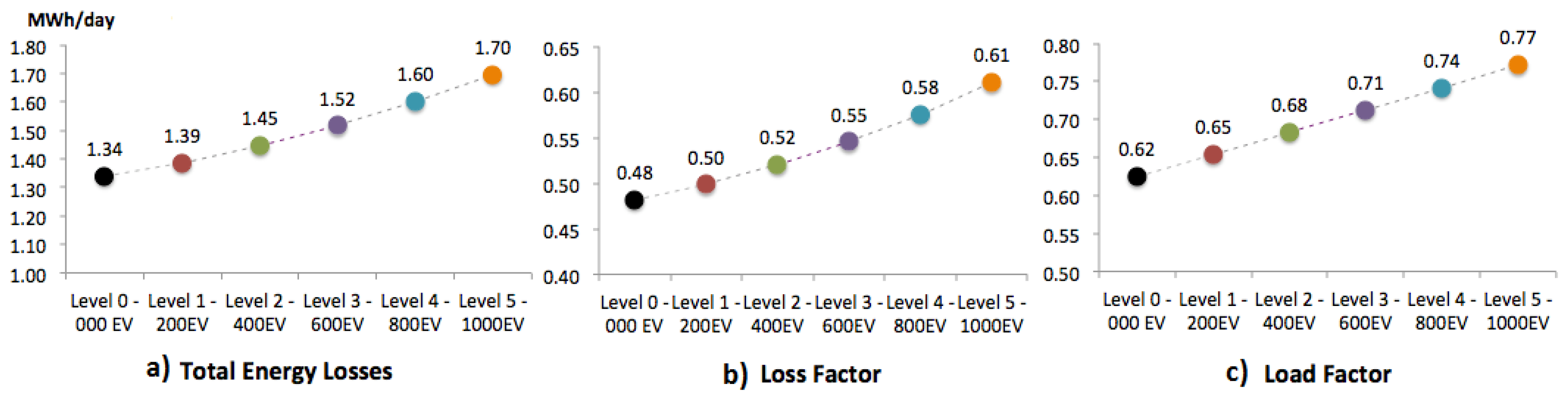
4. Results
- Slow charging at off-peak load conditions: 3.75 kW (16 A) 8 h.
- Fast charging at peak load conditions: 7.50 kW (32 A) 4 h.
4.1. Scenario 1: Slow Charging at Off-Peak Load Conditions
4.2. Scenario 2: Fast Charging at Peak Load Conditions
4.3. The Economical Effects in a Single EV Unit Under Off-Peak and Peak Load Conditions
4.4. The Impact of the EV Load Modeling on Loss Allocation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| ! Kersting NEV Test system |
| ! W. H. Kersting, A three-phase unbalanced line model with grounded |
| ! neutrals through a resistance, 2008 Ieee Power and Energy Society General |
| ! Meeting, Vols 1-11 (2008) 2651-2652 |
| ! 3 phase approach (kron’s reduction) with incremental load |
| clear |
| ! **** DEFINE SOURCE BUS |
| new circuit.KersNEV2nThreeP basekV = 12.47 phases = 3 !Define a 3-phase source |
| ~ mvasc3 = 2000000000 mvasc1 = 2100000000 |
| ! **** DEFINE DISTRIBUTION LINE |
| set earthmodel = carson |
| ! **** DEFINE WIRE DATA STRUCTURE |
| new wiredata.conductor Runits = mi Rac = 0.306 GMRunits = ft GMRac = 0.0244 Radunits = in Diam = 0.721 |
| new wiredata.neutral Runits = mi Rac = 0.592 GMRunits = ft GMRac = 0.00814 Radunits = in Diam = 0.563 |
| ! **** DEFINE LINE GEOMETRY; REDUCE OUT THE NEUTRAL WITH KRON |
| new linegeometry.4wire nconds = 4 nphases = 3 reduce = yes |
| ~ cond = 1 wire = conductor units = ft x = -4 h = 28 |
| ~ cond = 2 wire = conductor units = ft x = -1.5 h = 28 |
| ~ cond = 3 wire = conductor units = ft x = 3 h = 28 |
| ~ cond = 4 wire = neutral units = ft x = 0 h = 24 |
| ! **** 12.47 KV LINE! |
| new line.line1 geometry = 4wire length = 300 units = ft bus1 = sourcebus.1.2.3 bus2 = n1.1.2.3 |
| new line.line2 geometry = 4wire length = 300 units = ft bus1 = n1.1.2.3 bus2 = n2.1.2.3 |
| new line.line3 geometry = 4wire length = 300 units = ft bus1 = n2.1.2.3 bus2 = n3.1.2.3 |
| new line.line4 geometry = 4wire length = 300 units = ft bus1 = n3.1.2.3 bus2 = n4.1.2.3 |
| new line.line5 geometry = 4wire length = 300 units = ft bus1 = n4.1.2.3 bus2 = n5.1.2.3 |
| new line.line6 geometry = 4wire length = 300 units = ft bus1 = n5.1.2.3 bus2 = n6.1.2.3 |
| new line.line7 geometry = 4wire length = 300 units = ft bus1 = n6.1.2.3 bus2 = n7.1.2.3 |
| new line.line8 geometry = 4wire length = 300 units = ft bus1 = n7.1.2.3 bus2 = n8.1.2.3 |
| new line.line9 geometry = 4wire length = 300 units = ft bus1 = n8.1.2.3 bus2 = n9.1.2.3 |
| new line.line10 geometry = 4wire length = 300 units = ft bus1 = n9.1.2.3 bus2 = n10.1.2.3 |
| new line.line11 geometry = 4wire length = 300 units = ft bus1 = n10.1.2.3 bus2 = n11.1.2.3 |
| new line.line12 geometry = 4wire length = 300 units = ft bus1 = n11.1.2.3 bus2 = n12.1.2.3 |
| new line.line13 geometry = 4wire length = 300 units = ft bus1 = n12.1.2.3 bus2 = n13.1.2.3 |
| new line.line14 geometry = 4wire length = 300 units = ft bus1 = n13.1.2.3 bus2 = n14.1.2.3 |
| new line.line15 geometry = 4wire length = 300 units = ft bus1 = n14.1.2.3 bus2 = n15.1.2.3 |
| new line.line16 geometry = 4wire length = 300 units = ft bus1 = n15.1.2.3 bus2 = n16.1.2.3 |
| new line.line17 geometry = 4wire length = 300 units = ft bus1 = n16.1.2.3 bus2 = n17.1.2.3 |
| new line.line18 geometry = 4wire length = 300 units = ft bus1 = n17.1.2.3 bus2 = n18.1.2.3 |
| new line.line19 geometry = 4wire length = 300 units = ft bus1 = n18.1.2.3 bus2 = n19.1.2.3 |
| new line.line20 geometry = 4wire length = 300 units = ft bus1 = n19.1.2.3 bus2 = n20.1.2.3 |
| vsource.source.enabled = no |
| solve |
| Level 1 - 200EV | Level 2 - 400EV | Level 3 - 600EV | Level 4 - 800EV | Level 5 - 1000EV | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bus/Phase | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 1 |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 2 | 3 | 4 | 3 |
| 4 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 3 | 5 | 5 | 4 |
| 5 | 1 | 1 | 1 | 3 | 3 | 2 | 4 | 4 | 3 | 5 | 6 | 4 | 6 | 7 | 6 |
| 6 | 2 | 2 | 1 | 3 | 4 | 3 | 5 | 5 | 4 | 6 | 7 | 6 | 8 | 9 | 7 |
| 7 | 2 | 2 | 2 | 4 | 4 | 3 | 6 | 6 | 5 | 8 | 9 | 7 | 10 | 11 | 8 |
| 8 | 2 | 2 | 2 | 4 | 5 | 4 | 7 | 7 | 6 | 9 | 10 | 8 | 11 | 12 | 10 |
| 9 | 3 | 3 | 2 | 5 | 6 | 4 | 8 | 9 | 7 | 10 | 11 | 9 | 13 | 14 | 11 |
| 10 | 3 | 3 | 3 | 6 | 6 | 5 | 9 | 10 | 8 | 11 | 13 | 10 | 14 | 16 | 13 |
| 11 | 3 | 4 | 3 | 6 | 7 | 6 | 10 | 11 | 8 | 13 | 14 | 11 | 16 | 18 | 14 |
| 12 | 3 | 4 | 3 | 7 | 8 | 6 | 10 | 12 | 9 | 14 | 16 | 12 | 17 | 20 | 15 |
| 13 | 4 | 4 | 3 | 8 | 9 | 7 | 11 | 13 | 10 | 15 | 17 | 13 | 19 | 21 | 17 |
| 14 | 4 | 5 | 4 | 8 | 9 | 7 | 12 | 14 | 11 | 16 | 19 | 15 | 21 | 23 | 18 |
| 15 | 4 | 5 | 4 | 9 | 10 | 8 | 13 | 15 | 12 | 18 | 20 | 16 | 22 | 25 | 20 |
| 16 | 5 | 5 | 4 | 10 | 11 | 8 | 14 | 16 | 13 | 19 | 21 | 17 | 24 | 27 | 21 |
| 17 | 5 | 6 | 4 | 10 | 11 | 9 | 15 | 17 | 13 | 20 | 23 | 18 | 25 | 29 | 22 |
| 18 | 5 | 6 | 5 | 11 | 12 | 9 | 16 | 18 | 14 | 22 | 24 | 19 | 27 | 30 | 24 |
| 19 | 6 | 6 | 6 | 11 | 12 | 10 | 17 | 19 | 15 | 23 | 26 | 20 | 29 | 32 | 25 |
| 20 | 6 | 7 | 5 | 12 | 14 | 11 | 18 | 20 | 16 | 24 | 27 | 21 | 30 | 34 | 27 |
| 21 | 6 | 7 | 6 | 13 | 14 | 11 | 19 | 21 | 17 | 25 | 29 | 22 | 32 | 33 | 28 |
| SubTotal | 66 | 74 | 60 | 134 | 149 | 117 | 200 | 223 | 177 | 266 | 300 | 234 | 334 | 372 | 294 |
| Total | 200 | 400 | 600 | 800 | 1000 | ||||||||||
References
- Rotering, N.; Ilic, M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets. IEEE Trans. Power Syst. 2011, 26, 1021–1029. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of Electric Vehicle Charging Station Load on Distribution Network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Economic and technical management of an aggregation agent for electric vehicles: A literature survey. Int. Trans. Electr. Energy Syst. 2012, 22, 334–350. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Nair, N.C. Economic and pricing signals in electricity distribution systems: A bibliographic survey. In Proceedings of the IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–6. [Google Scholar]
- Pan, J.; Teklu, Y.; Rahman, S.; Jun, K. Review of usage-based transmission cost allocation methods under open access. IEEE Trans. Power Syst. 2000, 15, 1218–1224. [Google Scholar]
- Carpaneto, E.; Chicco, G.; Akilimali, J.S. Characterization of the loss allocation techniques for radial systems with distributed generation. Electr. Power Syst. Res. 2008, 78, 1396–1406. [Google Scholar] [CrossRef]
- Costa, P.M.; Matos, M.A. Loss allocation in distribution networks with embedded generation. IEEE Trans. Power Syst. 2004, 19, 384–389. [Google Scholar] [CrossRef]
- Bialek, J. Tracing the flow of electricity. IEE Proc. Gener. Transm. Distrib. 1996, 143, 313–320. [Google Scholar] [CrossRef]
- Galiana, F.D.; Conejo, A.J.; Kockar, I. Incremental transmission loss allocation under pool dispatch. IEEE Trans. Power Syst. 2002, 17, 26–33. [Google Scholar] [CrossRef]
- Weckx, S.; Driesen, J.; D’hulst, R. Optimal Real-Time Pricing for UnbalancedDistribution Grids with Network Constraints. In Proceedings of the IEEE Power and Energy SocietyGeneral Meeting (PESGM), Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Heydt, G.T.; Chowdhury, B.H.; Crow, M.L.; Haughton, D.; Kiefer, B.D.; Meng, F.J.; Sathyanarayana, B.R. Pricing and control in the next generation power distribution system. IEEE Trans. Smart Grid 2012, 3, 907–914. [Google Scholar] [CrossRef]
- De Oliveira-De Jesus, P.M.; Castronuovo, E.D.; De Leao, M.P. Reactive power response of wind generators under an incremental network-loss allocation approach. IEEE Trans. Energy Convers. 2008, 23, 612–621. [Google Scholar] [CrossRef]
- Kaur, M.; Ghosh, S. Effective Loss Minimization and Allocation of Unbalanced Distribution Network. Energies 2017, 10, 1931. [Google Scholar] [CrossRef]
- Hong, M. An approximate method for loss sensitivity calculation in unbalanced distribution systems. IEEE Trans. Power Syst. 2014, 29, 1435–1436. [Google Scholar] [CrossRef]
- Li, R.Y.; Wu, Q.W.; Oren, S.S. Distribution locational marginal pricing for optimal electric vehicle charging management. IEEE Trans. Power Syst. 2014, 29, 203–211. [Google Scholar] [CrossRef]
- Kongjeen, Y.; Bhumkittipich, K. Impact of Plug-in Electric Vehicles Integrated into Power Distribution System Based on Voltage-Dependent Power Flow Analysis. Energies 2018, 11, 1571. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Gorenstin, B.; Pereira, M.V. Some fundamental, technical concepts about cost based transmission pricing. IEEE Trans. Power Syst. 1996, 11, 1002–1008. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of load demand due to EV battery charging in distribution systems. IEEE Trans. Power Syst. 2011, 26, 802–810. [Google Scholar] [CrossRef]
- Hernandez, J.C.; Ruiz-Rodriguez, F.J.; Jurado, F. Modelling and assessment of the combined technical impact of electric vehicles and photovoltaic generation in radial distribution systems. Energy 2017, 141, 316–332. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Ozpineci, B.; Tolbert, L.M. EV/PHEV bidirectional charger assessment for V2G reactive power operation. IEEE Trans. Power Electr. 2011, 28, 5717–5727. [Google Scholar] [CrossRef]
- Dharmakeerthi, C.H.; Mithulananthan, N.; Saha, T.K. Impact of electric vehicle fast charging on power system voltage stability. Int. J. Electr. Power Energy Syst. 2014, 57, 241–249. [Google Scholar] [CrossRef]
- Wasley, R.G.; Shlash, M.A. Newton-Raphson algorithm for 3-phase load flow. Proc. Inst. Electr. Eng. 1974, 121, 630–638. [Google Scholar] [CrossRef]
- Arrillaga, J.A.; Arnold, J.P. Computer Analysis of Power Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990. [Google Scholar]
- De Oliveira-De Jesus, P.M.; Alvarez, M.A.; Yusta, J.M. Distribution power flow method based on a real quasi-symmetric matrix. Electric. Power Syst. Res. 2013, 95, 148–159. [Google Scholar] [CrossRef]
- Montenegro, D.; Hernandez, M.; Ramos, G.A. Real time OpenDSS framework for distribution systems simulation and analysis. In Proceedings of the 2012 Sixth IEEE/PES Transmission and Distribution: Latin America Conference and Exposition (T&D-LA), Montevideo, Uruguay, 3–5 September 2012. [Google Scholar]
- Mutale, J.; Strbac, G.; Curcic, S.; Jenkins, N. Allocation of losses in distribution systems with embedded generation. IEE Proc. Gener. Transm. Distrib. 2000, 147, 7–14. [Google Scholar] [CrossRef]
- Stoft, S. Power System Economics; IEEE Press & Wiley-Interscience: Hoboken, NJ, USA, 2002. [Google Scholar]
- Kersting, W.H. A three-phase unbalanced line model with grounded neutrals through a resistance. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-PESGM, Pittsburgh, PA, USA, 20–24 July 2008; pp. 12651–21652. [Google Scholar]
- Gonen, T. Electric Power Distribution Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Dugan, R.C.; McDermott, T.E. An open source platform for collaborating on smart grid research. In Proceedings of the IEEE Power Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–7. [Google Scholar]
- Mocci, S.; Natale, N.; Ruggeri, S.; Pilo, F. Multi-agent control system for increasing hosting capacity in active distribution networks with EV. In Proceedings of the IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 1409–1416. [Google Scholar]
- Kisacikoglu, M.C.; Erden, F.; Erdogan, N. Distributed control of PEV charging based on energy demand forecast. IEEE Trans. Ind. Inf. 2018, 14, 332–341. [Google Scholar] [CrossRef]
- Ruiz-Rodriguez, F.J.; Hernandez, J.C.; Jurado, F. Voltage behaviour in radial distribution systems under the uncertainties of photovoltaic systems and electric vehicle charging loads. Int. Trans. Electr. Energy Syst. 2018, 28, 2490. [Google Scholar] [CrossRef]
- Munkhammar, J.; Widen, J.; Ryden, J. On a probability distribution model combining household power consumption, electric vehicle home—Charging and photovoltaic power production. Appl. Energy 2015, 142, 135–143. [Google Scholar] [CrossRef]
- Ruiz-Rodriguez, F.J.; Hernandez, J.C.; Jurado, F. Probabilistic Load-Flow Analysis of Biomass-Fuelled Gas Engines with Electrical Vehicles in Distribution Systems. Energies 2017, 10, 1536. [Google Scholar] [CrossRef]
- ElNozahy, M.S.; Salama, M.M. A comprehensive study of the impacts of PHEVS on residential distribution networks. IEEE Trans. Sustain. Energy 2014, 5, 332–342. [Google Scholar] [CrossRef]
- Godina, R.; Paterakis, N.G.; Erdinc, O.; Rodrigues, E.M.G.; Catalão, J.P.S. Impact of EV charging-at-work on an industrial client distribution transformer in a Portuguese Island. In Proceedings of the 2015 Australasian Universities Power Engineering Conference (AUPEC), Wollongong, Australia, 27–30 September 2015; pp. 1–6. [Google Scholar]
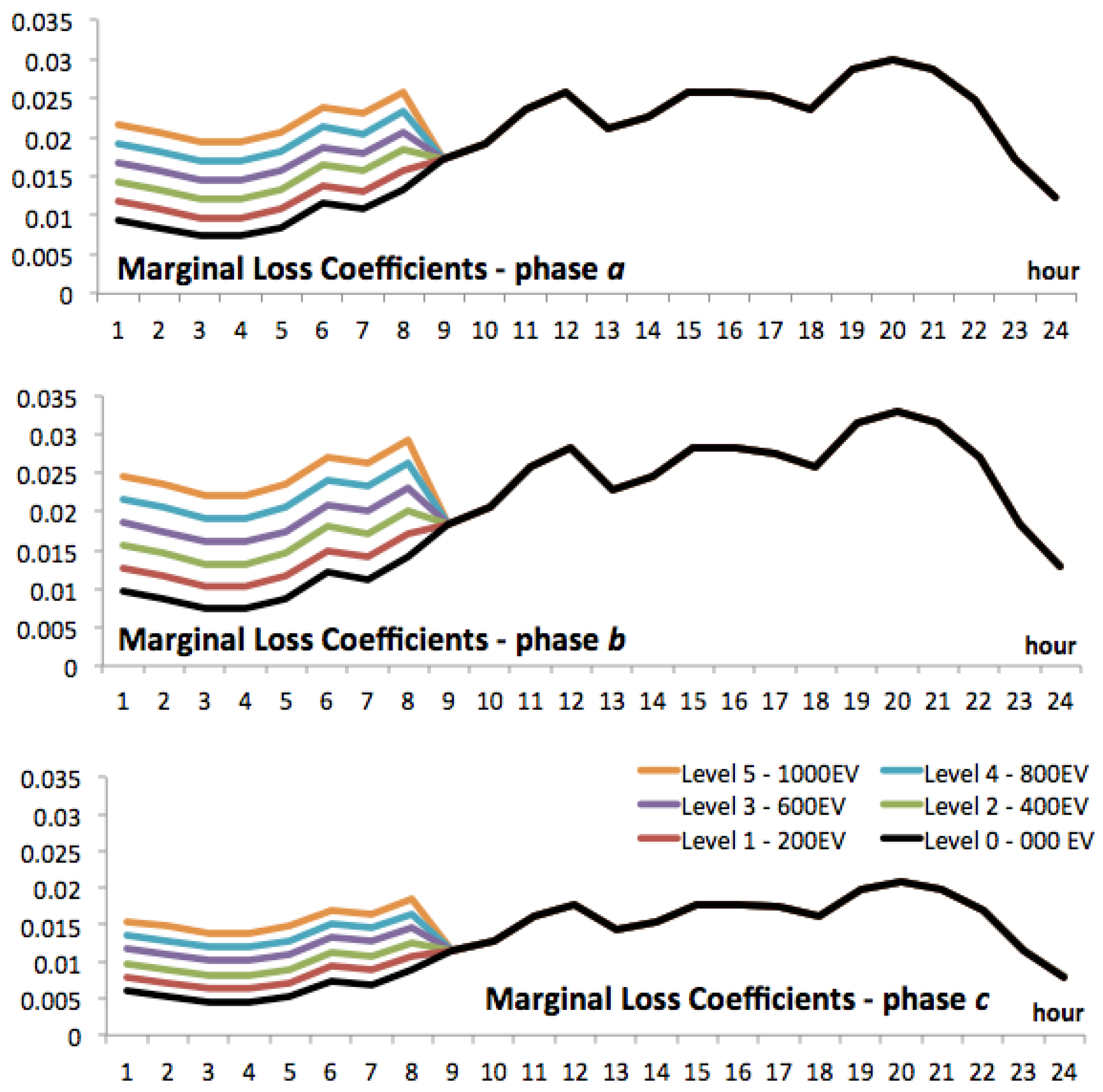
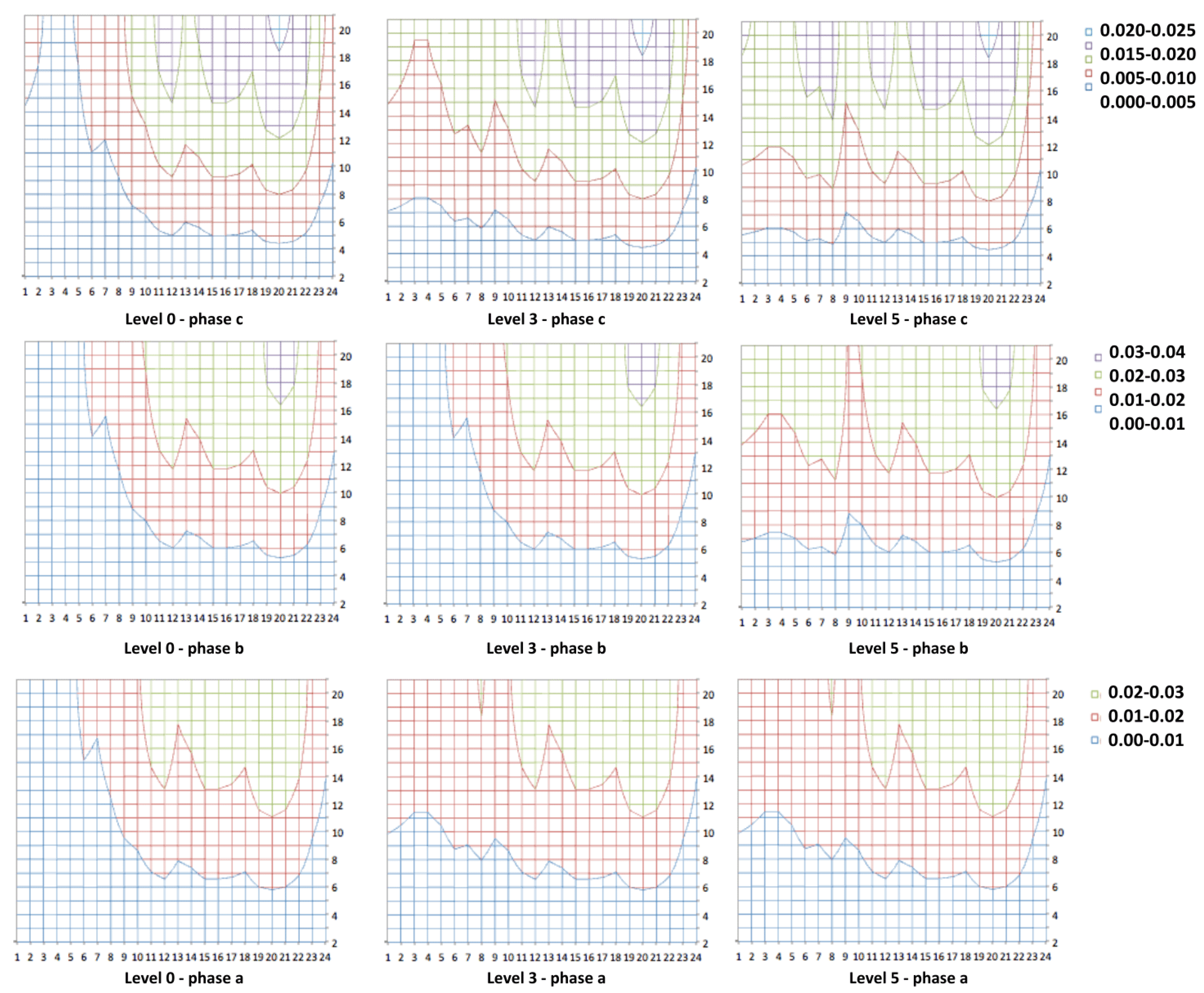
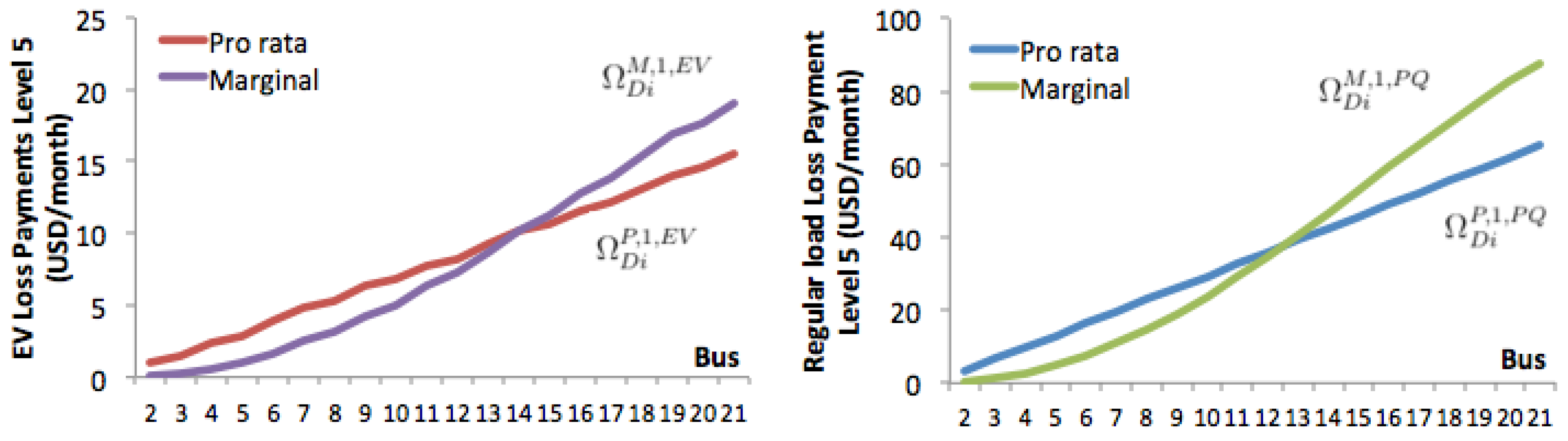
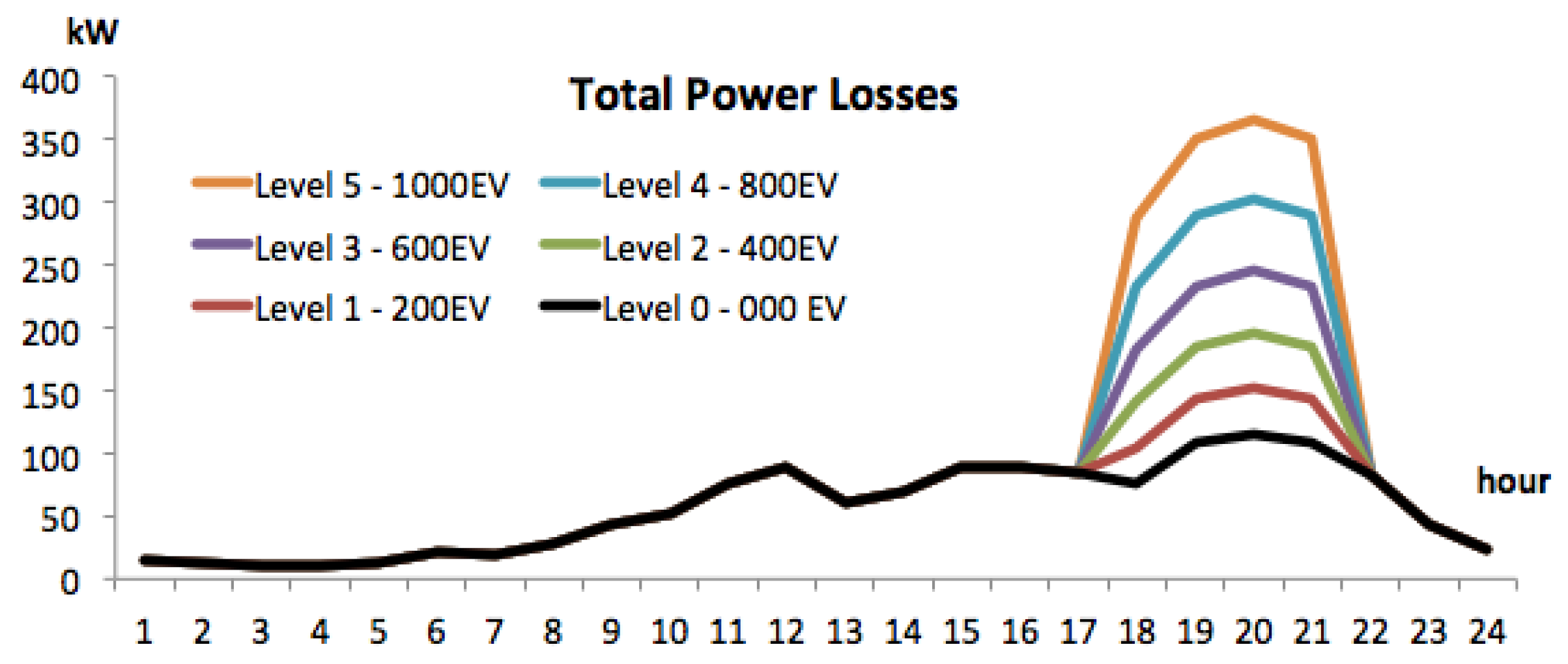
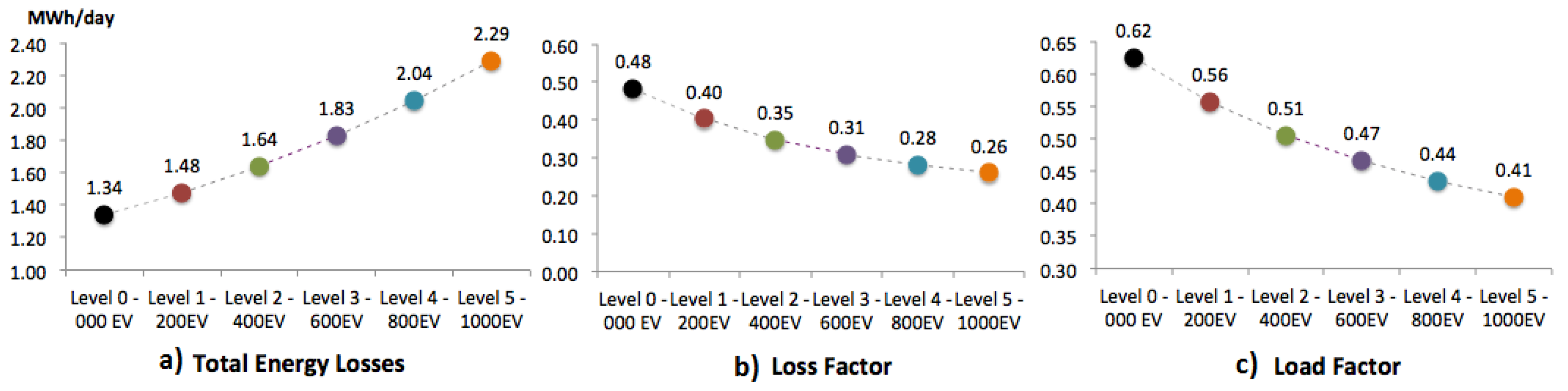
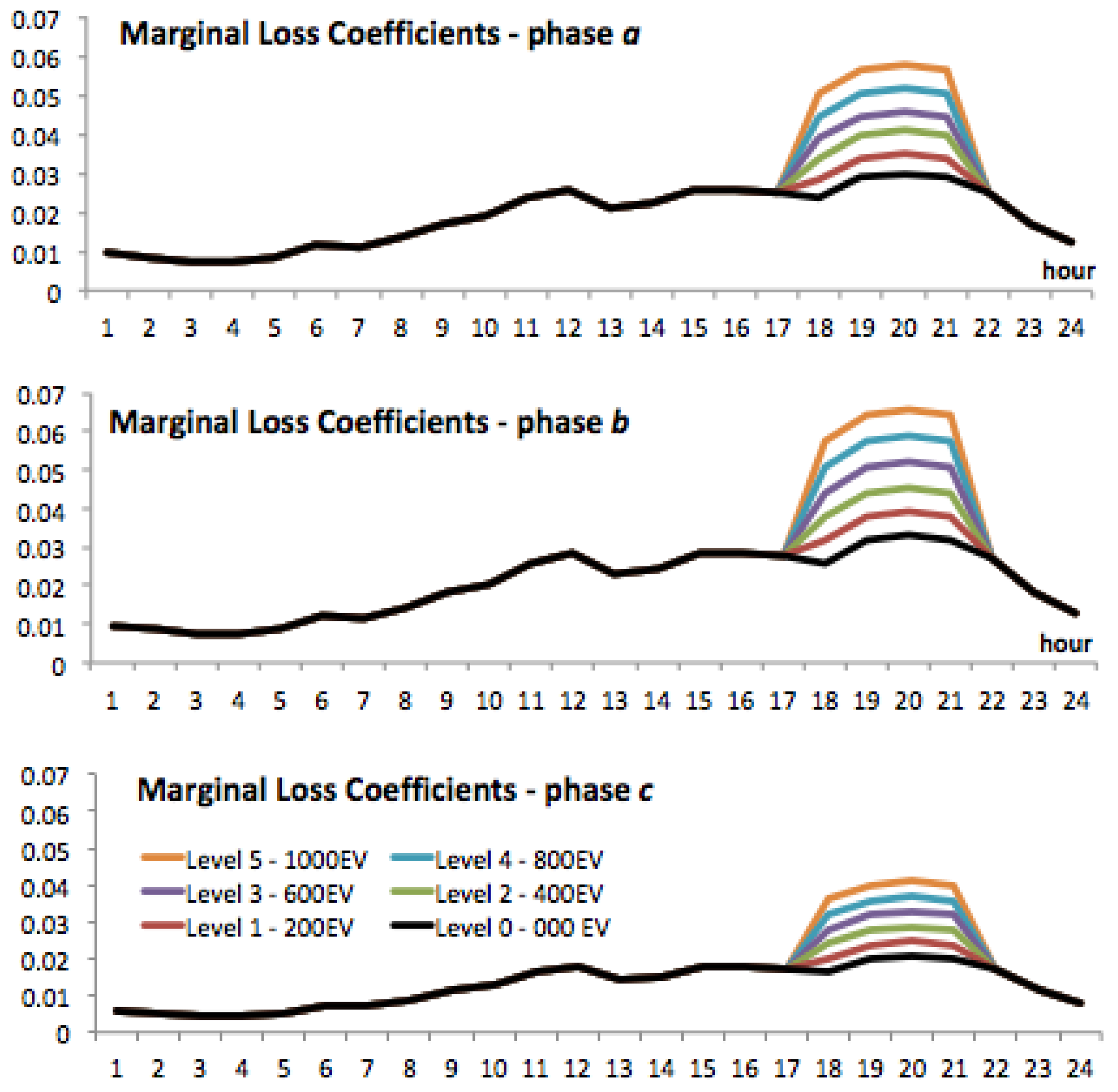

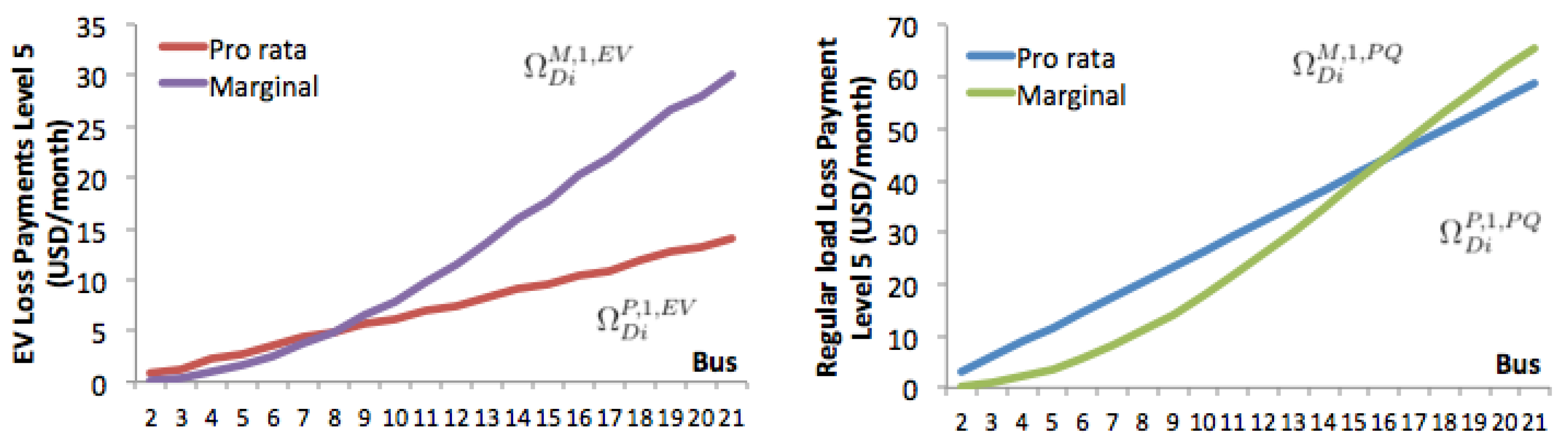
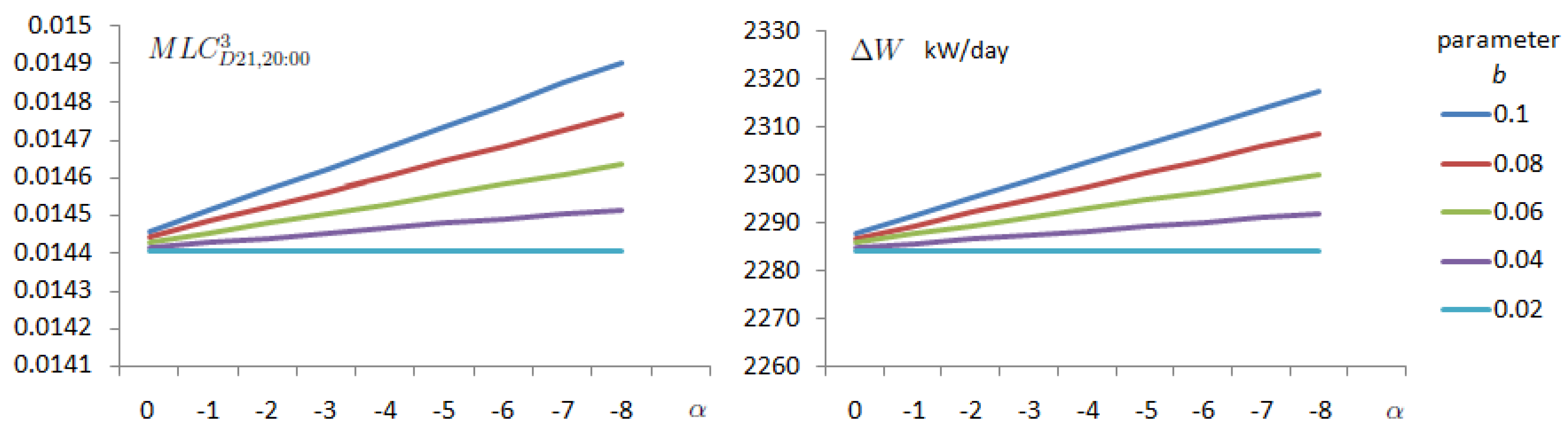
| Bus | Total | Phase 1 | Phase 2 | Phase 3 | ||||
|---|---|---|---|---|---|---|---|---|
| MW·h/day | kW | MW·h/day | kW | MW·h/day | kW | MWh/day | kW | |
| 2 | 0.6 | 0.04 | 0.2 | 0.01 | 0.2 | 0.02 | 0.2 | 0.01 |
| 3 | 1.2 | 0.08 | 0.4 | 0.03 | 0.5 | 0.03 | 0.4 | 0.02 |
| 4 | 1.8 | 0.12 | 0.6 | 0.04 | 0.7 | 0.05 | 0.5 | 0.04 |
| 5 | 2.4 | 0.16 | 0.8 | 0.05 | 0.9 | 0.06 | 0.7 | 0.05 |
| 6 | 3.0 | 0.20 | 1.0 | 0.07 | 1.1 | 0.08 | 0.9 | 0.06 |
| 7 | 3.7 | 0.24 | 1.2 | 0.08 | 1.4 | 0.09 | 1.1 | 0.07 |
| 8 | 4.3 | 0.28 | 1.4 | 0.09 | 1.6 | 0.11 | 1.2 | 0.08 |
| 9 | 4.9 | 0.32 | 1.6 | 0.11 | 1.8 | 0.12 | 1.4 | 0.10 |
| 10 | 5.5 | 0.37 | 1.8 | 0.12 | 2.1 | 0.14 | 1.6 | 0.11 |
| 11 | 6.1 | 0.41 | 2.0 | 0.14 | 2.3 | 0.15 | 1.8 | 0.12 |
| 12 | 6.7 | 0.45 | 2.2 | 0.15 | 2.5 | 0.17 | 2.0 | 0.13 |
| 13 | 7.3 | 0.49 | 2.4 | 0.16 | 2.7 | 0.18 | 2.1 | 0.14 |
| 14 | 7.9 | 0.53 | 2.6 | 0.18 | 3.0 | 0.20 | 2.3 | 0.15 |
| 15 | 8.5 | 0.57 | 2.8 | 0.19 | 3.2 | 0.21 | 2.5 | 0.17 |
| 16 | 9.1 | 0.61 | 3.0 | 0.20 | 3.4 | 0.23 | 2.7 | 0.18 |
| 17 | 9.7 | 0.65 | 3.2 | 0.22 | 3.6 | 0.24 | 2.9 | 0.19 |
| 18 | 10.3 | 0.69 | 3.4 | 0.23 | 3.9 | 0.26 | 3.0 | 0.20 |
| 19 | 11.0 | 0.73 | 3.6 | 0.24 | 4.1 | 0.27 | 3.2 | 0.21 |
| 20 | 11.6 | 0.77 | 3.8 | 0.26 | 4.3 | 0.29 | 3.4 | 0.23 |
| 21 | 12.2 | 0.81 | 4.0 | 0.27 | 4.6 | 0.30 | 3.6 | 0.24 |
| Total | 127.8 | 8.53 | 42.5 | 2.84 | 47.8 | 3.19 | 37.5 | 2.50 |
| Level | Base Load | EV Load | Total Load | Share |
|---|---|---|---|---|
| MW·h/day | % | |||
| Level 0—000EV | 127.8 | 0 | 127.8 | 0% |
| Level 1—200EV | 127.8 | 6 | 133.8 | 5% |
| Level 2—400EV | 127.8 | 12 | 139.8 | 10% |
| Level 3—600EV | 127.8 | 18 | 145.8 | 14% |
| Level 4—800EV | 127.8 | 24 | 151.8 | 19% |
| Level 5—1000EV | 127.8 | 30 | 157.8 | 25% |
| Level | Pro Rata | Marginal | Energy Losses | ||
|---|---|---|---|---|---|
| Level 0 | 1339.08, 100% | 0.00, 0% | 1339.08, 100% | 0.00 0,% | 1339.08 |
| Level 1 | 1324.41, 96% | 61.93, 4% | 1352.52, 98% | 33.82, 2% | 1386.34 |
| Level 2 | 1321.66, 91% | 124.55, 9% | 1363.84, 94% | 82.37, 6% | 1446.21 |
| Level 3 | 1329.09, 88% | 187.43, 12% | 1373.19, 91% | 143.32, 9% | 1516.51 |
| Level 4 | 1347.19, 84% | 253.33, 16% | 1381.59, 86% | 218.93, 14% | 1600.52 |
| Level 5 | 1372.92, 81% | 323.72, 19% | 1389.30, 82% | 307.33, 18% | 1696.64 |
| Level | Pro Rata | Marginal | Energy Losses | ||
|---|---|---|---|---|---|
| Level 0 | 1339.08, 100% | 0.00, 0% | 1339.08, 100% | 0.00, 0% | 1339.08 |
| Level 1 | 1410.22, 96% | 66.03, 4% | 1382.69, 94% | 93.57, 6% | 1476.26 |
| Level 2 | 1499.45, 91% | 141.52, 9% | 1426.40, 87% | 214.56, 13% | 1640.96 |
| Level 3 | 1601.37, 88% | 226.19, 12% | 1469.93, 80% | 357.63, 20% | 1827.56 |
| Level 4 | 1720.74, 84% | 324.16, 16% | 1516.01, 74% | 528.89, 26% | 2044.90 |
| Level 5 | 1851.48, 81% | 437.40, 19% | 1563.97, 68% | 724.91, 32% | 2288.88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Oliveira-De Jesus, P.M.; Rios, M.A.; Ramos, G.A. Energy Loss Allocation in Smart Distribution Systems with Electric Vehicle Integration. Energies 2018, 11, 1962. https://doi.org/10.3390/en11081962
De Oliveira-De Jesus PM, Rios MA, Ramos GA. Energy Loss Allocation in Smart Distribution Systems with Electric Vehicle Integration. Energies. 2018; 11(8):1962. https://doi.org/10.3390/en11081962
Chicago/Turabian StyleDe Oliveira-De Jesus, Paulo M., Mario A. Rios, and Gustavo A. Ramos. 2018. "Energy Loss Allocation in Smart Distribution Systems with Electric Vehicle Integration" Energies 11, no. 8: 1962. https://doi.org/10.3390/en11081962
APA StyleDe Oliveira-De Jesus, P. M., Rios, M. A., & Ramos, G. A. (2018). Energy Loss Allocation in Smart Distribution Systems with Electric Vehicle Integration. Energies, 11(8), 1962. https://doi.org/10.3390/en11081962







