Fluid Structure Interaction Modelling of Tidal Turbine Performance and Structural Loads in a Velocity Shear Environment
Abstract
1. Introduction
2. Modeling Approach
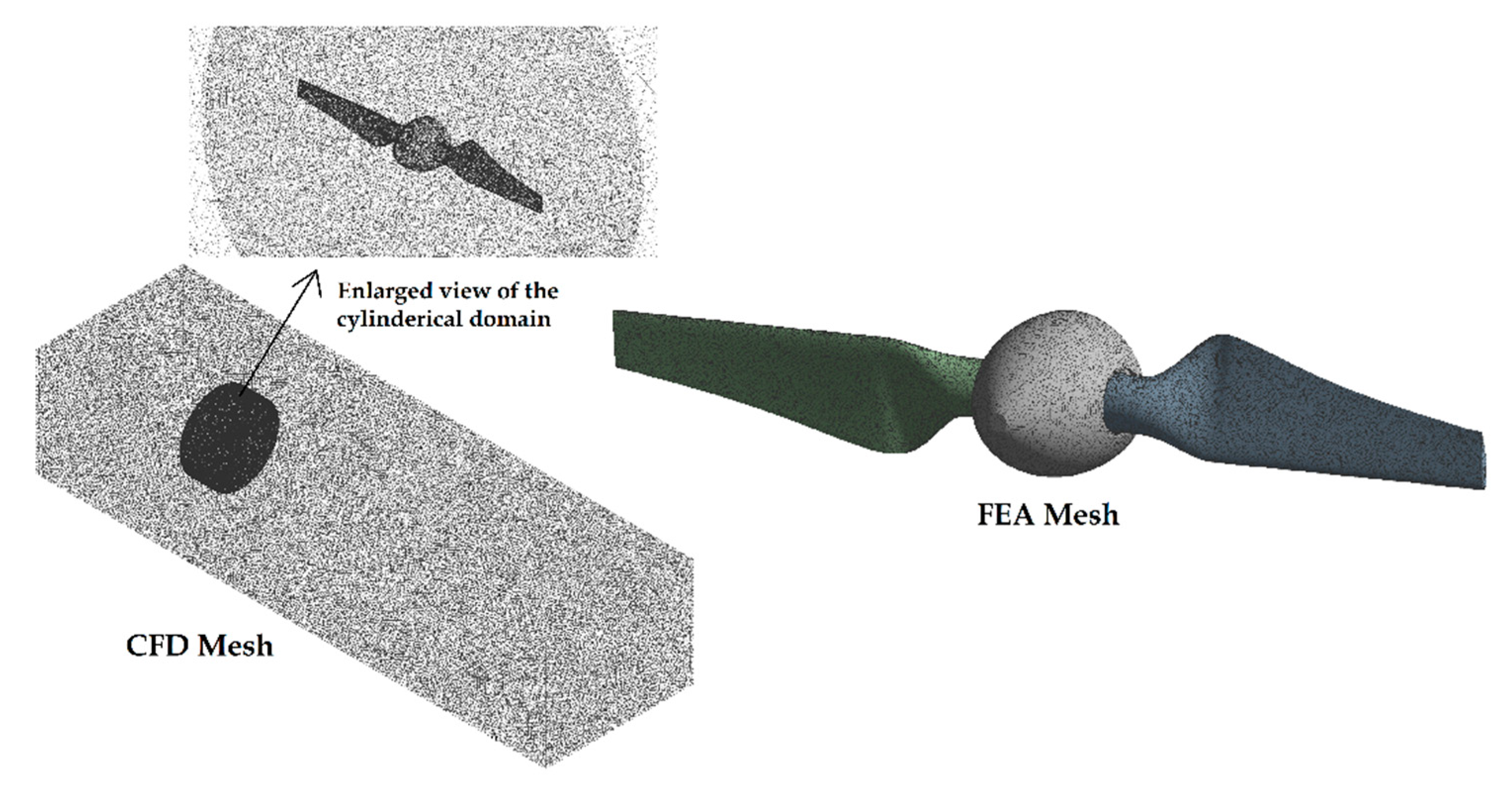
2.1. Transient CFD Model Setup
2.2. FEA Model Setup
2.3. System Coupling Setup
3. Results and Discussion
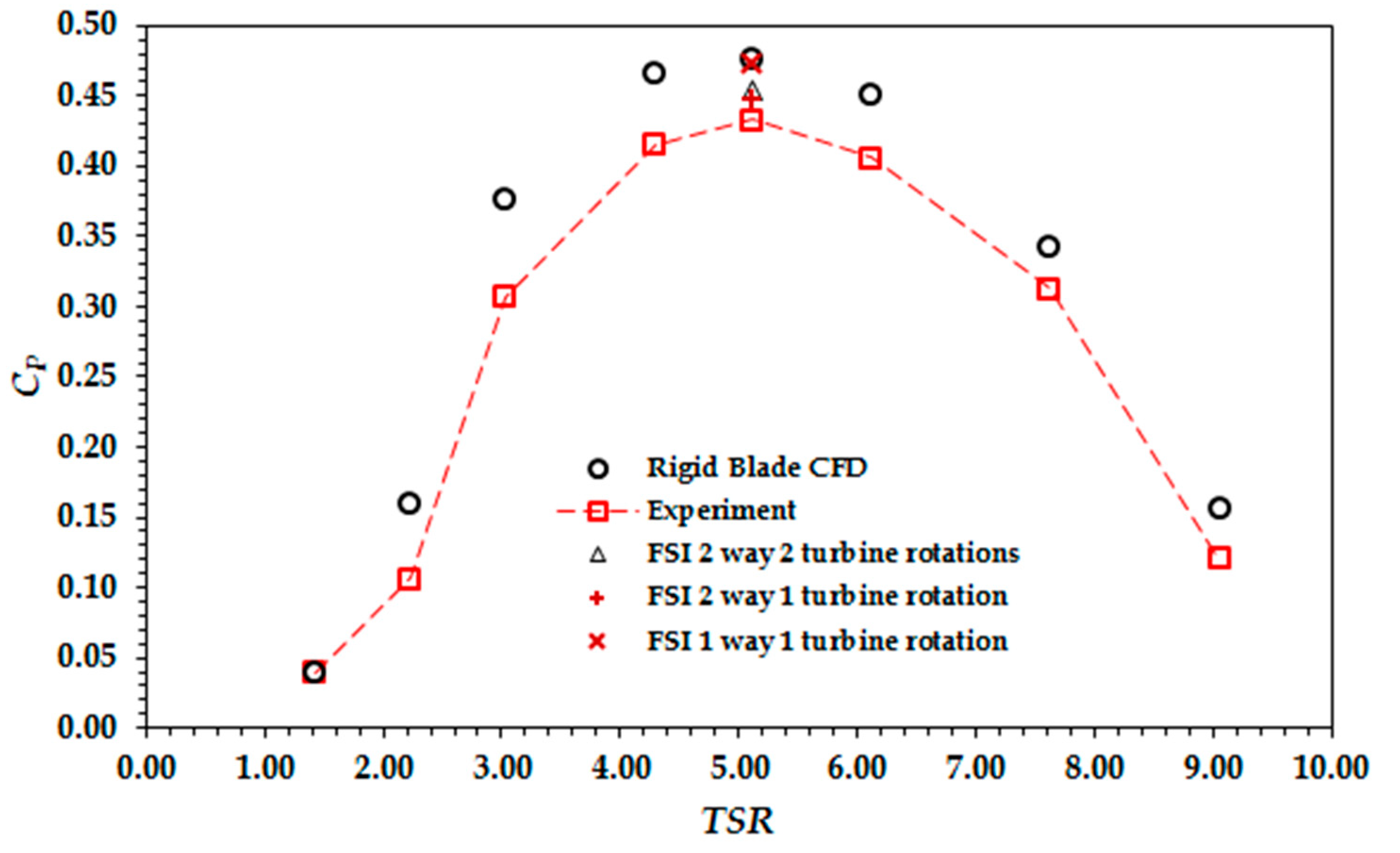
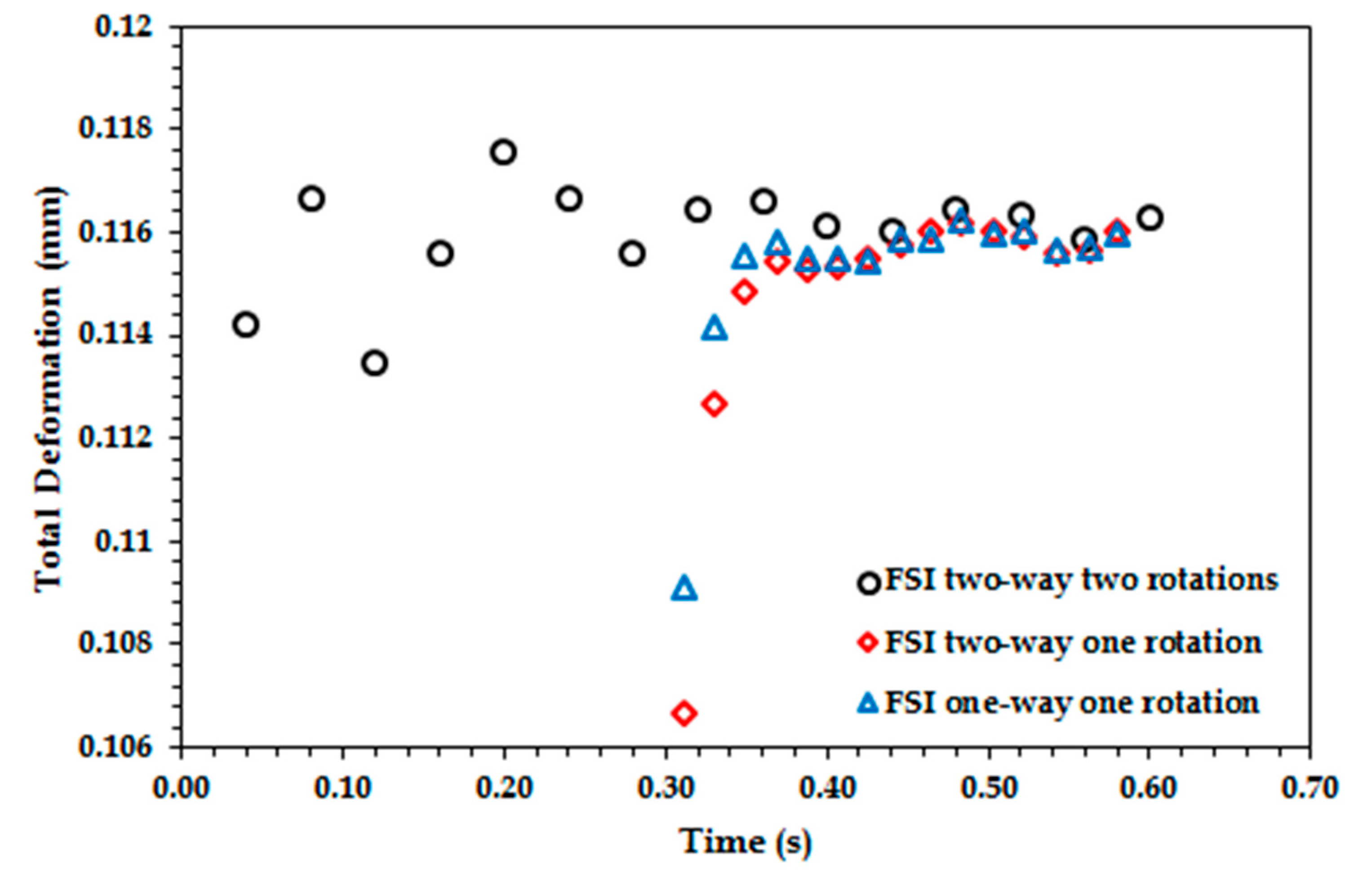
3.1. Development of the FSI Model
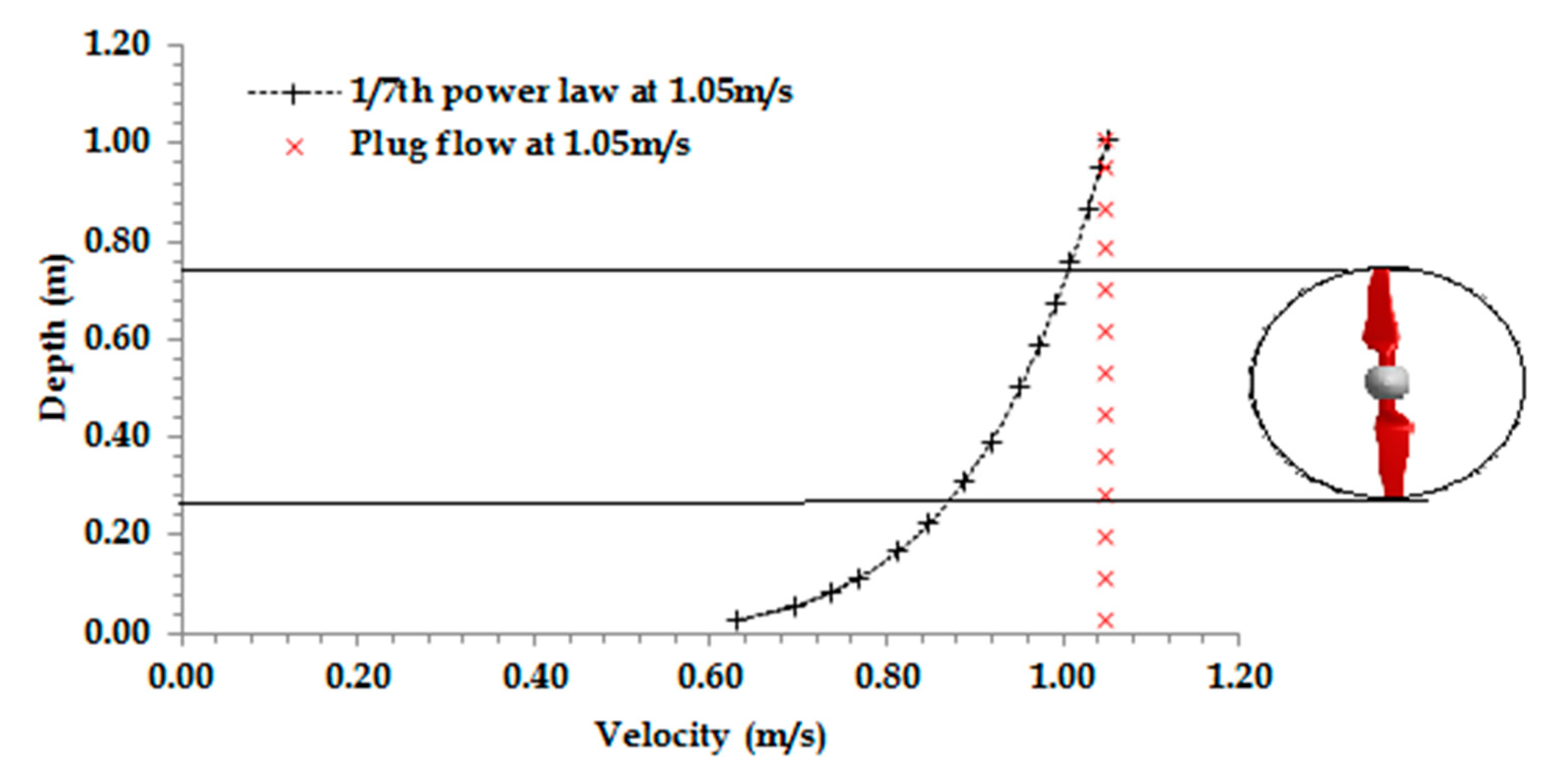
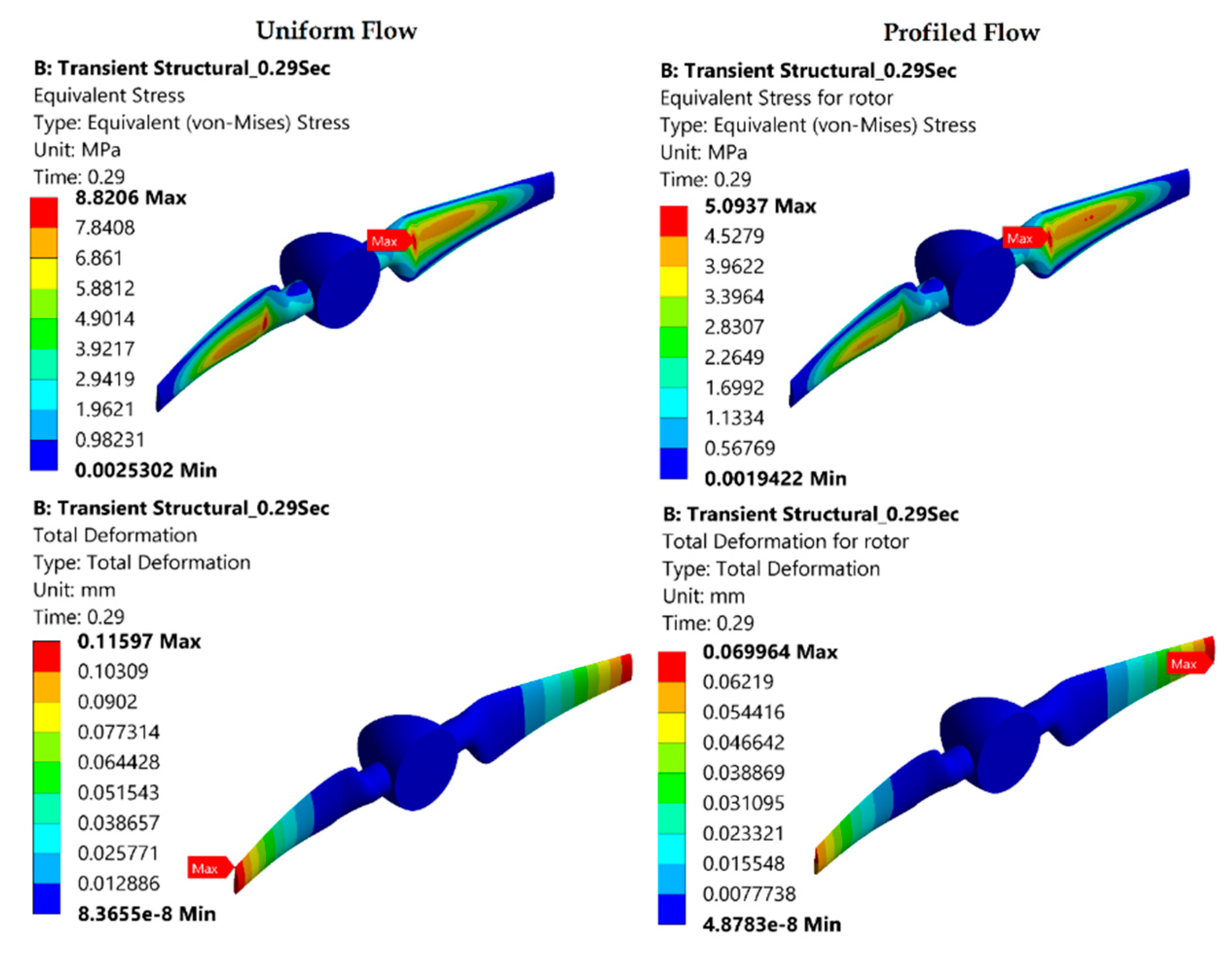
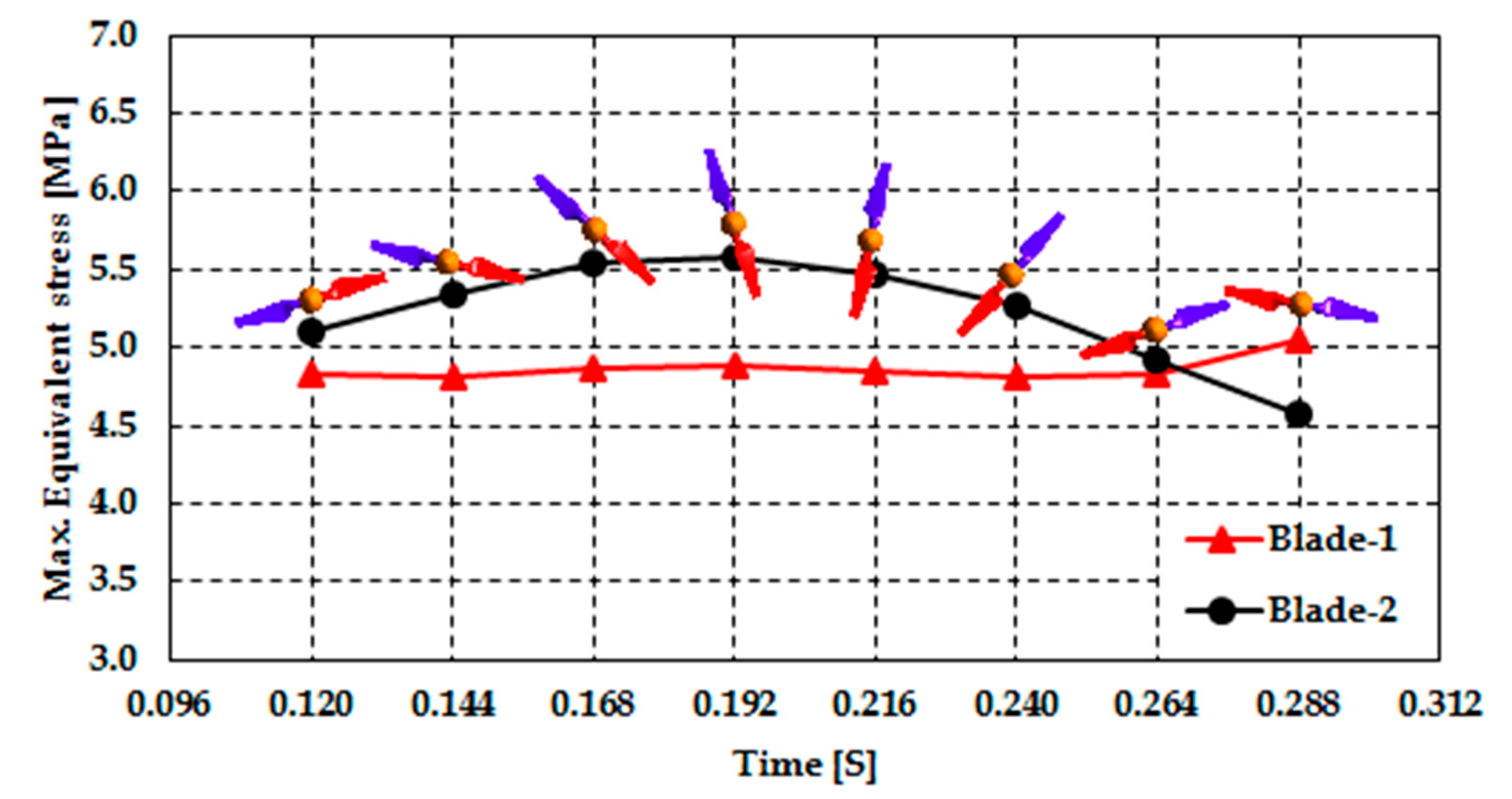
3.2. Effect of Velocity Profile on Performance and Structural Loads
4. Conclusions and Prospects
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Badshah, M.; Badshah, S.; Khalil, S.J. Hydrodynamic design of tidal current turbine and the effect of solidity on performance. J. Eng. Appl. Sci. 2017, 36, 45–54. [Google Scholar]
- Batten, W.; Bahaj, A.; Molland, A.; Chaplin, J. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
- Masters, I.; Chapman, J.; Willis, M.; Orme, J. A robust blade element momentum theory model for tidal stream turbines including tip and hub loss corrections. J. Mar. Eng. Technol. 2011, 10, 25–35. [Google Scholar]
- Mujahid, B.; VanZwieten, J.H.; Saeed, B.; Sakhi, J. A CFD study of blockage ratio and boundary proximity effects on the performance of a tidal turbine. IET Renew. Power Gen. under review.
- Nitin, K.; Arindam, B. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Tatum, S.; Allmark, M.; Frost, C.; O’Doherty, D.; Mason-Jones, A.; O’Doherty, T. CFD modelling of a tidal stream turbine subjected to profiled flow and surface gravity waves. Int. J. Mar. Energy 2016, 15, 156–174. [Google Scholar] [CrossRef]
- Tian, W.; VanZwieten, J.H.; Pyakurel, P.; Li, Y. Influences of yaw angle and turbulence intensity on the performance of a 20 kW in-stream hydrokinetic turbine. Energy 2016, 111, 104–116. [Google Scholar] [CrossRef]
- Liu, J.; Lin, H.; Purimitla, S.R.; ET, M.D. The effects of blade twist and nacelle shape on the performance of horizontal axis tidal current turbines. Appl. Ocean Res. 2017, 64, 58–69. [Google Scholar] [CrossRef]
- Nicholls-Lee, R.F. Adaptive Composite Blades for Horizontal Axis Tidal Turbines. Ph.D. Thesis, University of Southampton, Southampton, UK, 2011. [Google Scholar]
- Grogan, D.M.; Leen, S.B.; Kennedy, C.; Brádaigh, C.Ó. Design of composite tidal turbine blades. Renew. Energy 2013, 57, 151–162. [Google Scholar] [CrossRef]
- Zhou, F.; Mahfuz, H.; Alsenas, G.M.; Hanson, H.P. Static and fatigue analysis of composite turbine blades under random ocean current loading. Mar. Technol. Soc. J. 2013, 47, 59–69. [Google Scholar] [CrossRef]
- Turnock, S.; Wright, A. Directly coupled fluid structural model of a ship rudder behind a propeller. Mar. Struct. 2000, 13, 53–72. [Google Scholar] [CrossRef]
- Nicholls-Lee, R.F.; Turnock, S.R.; Boyd, S.W. Simulation Based Optimization of Marine Current Turbine Blades. In Proceedings of the 7th International Conference on Computer and IT Applications in the Maritime Industries (COMPIT’08), Liège, Belgium, 21–23 April 2008; pp. 314–328. [Google Scholar]
- Kim, B.; Bae, S.; Kim, W.; Lee, S.; Kim, M. A Study on the Design Assessment of 50 kW Ocean Current Turbine Using Fluid Structure Interaction Analysis. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Beijing, China, 19–23 August 2012; p. 042037. [Google Scholar]
- Jo, C.-H.; Kim, D.-Y.; Rho, Y.-H.; Lee, K.-H.; Johnstone, C. FSI analysis of deformation along offshore pile structure for tidal current power. Renew. Energy 2013, 54, 248–252. [Google Scholar] [CrossRef]
- Nicholls-Lee, R.; Turnock, S.; Boyd, S. Application of bend-twist coupled blades for horizontal axis tidal turbines. Renew. Energy 2013, 50, 541–550. [Google Scholar] [CrossRef]
- Tatum, S.; Frost, C.; Allmark, M.; O’Doherty, D.; Mason-Jones, A.; Prickett, P.; Grosvenor, R.; Byrne, C.; O’Doherty, T. Wave-current interaction effects on tidal stream turbine performance and loading characteristics. Int. J. Mar. Energy 2016, 14, 161–179. [Google Scholar] [CrossRef]
- Craig, H.; Vincent, S.N.; Budi, G.; Michele, G.; Fotis, S. U.S. Department of Energy Reference Model Program RM1: Experimental Results. Technical Report; 2014. Available online: https://www.osti.gov/biblio/1172793-department-energy-reference-model-program-rm1-experimental-results (accessed on 5 July 2018). [CrossRef]
- ANSYS Inc. ANSYS CFX-Solver Modelling Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2016; p. 170. [Google Scholar]
- Ageze, M.B.; Hu, Y.; Wu, H. Comparative Study on Uni-and Bi-Directional Fluid Structure Coupling of Wind Turbine Blades. Energies 2017, 10, 1499. [Google Scholar] [CrossRef]
- Morris, C.E.; O’Doherty, D.M.; O’Doherty, T.; Mason-Jones, A. Kinetic energy extraction of a tidal stream turbine and its sensitivity to structural stiffness attenuation. Renew. Energy 2016, 88, 30–39. [Google Scholar] [CrossRef]
- Morris, C. Influence of Solidity on the Performance, Swirl Characteristics, Wake Recovery and Blade Deflection of a Horizontal Axis Tidal Turbine. Ph.D. Thesis, Cardiff University, Wales, UK, 2014. [Google Scholar]
- Mason-Jones, A. Performance Assessment of a Horizontal Axis Tidal Turbine in a High Velocity Shear Environment. Ph.D. Thesis, Cardiff University, Wales, UK, 2009. [Google Scholar]



| S# | Simulation Name | Computational Time (h) | Thrust Force (N) |
|---|---|---|---|
| 1 | Two-way two turbine rotations | 283.3 | 99.29 |
| 2 | Two-way one turbine rotation | 105.6 | 98.66 |
| 3 | One-way one turbine rotation | 58.3 | 100.24 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badshah, M.; Badshah, S.; Kadir, K. Fluid Structure Interaction Modelling of Tidal Turbine Performance and Structural Loads in a Velocity Shear Environment. Energies 2018, 11, 1837. https://doi.org/10.3390/en11071837
Badshah M, Badshah S, Kadir K. Fluid Structure Interaction Modelling of Tidal Turbine Performance and Structural Loads in a Velocity Shear Environment. Energies. 2018; 11(7):1837. https://doi.org/10.3390/en11071837
Chicago/Turabian StyleBadshah, Mujahid, Saeed Badshah, and Kushsairy Kadir. 2018. "Fluid Structure Interaction Modelling of Tidal Turbine Performance and Structural Loads in a Velocity Shear Environment" Energies 11, no. 7: 1837. https://doi.org/10.3390/en11071837
APA StyleBadshah, M., Badshah, S., & Kadir, K. (2018). Fluid Structure Interaction Modelling of Tidal Turbine Performance and Structural Loads in a Velocity Shear Environment. Energies, 11(7), 1837. https://doi.org/10.3390/en11071837






